Assessment of PERSIANN Satellite Products over the Tulijá River Basin, Mexico
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Data
2.2.1. Rain Gauges
2.2.2. Rainfall Satellite-Based Products
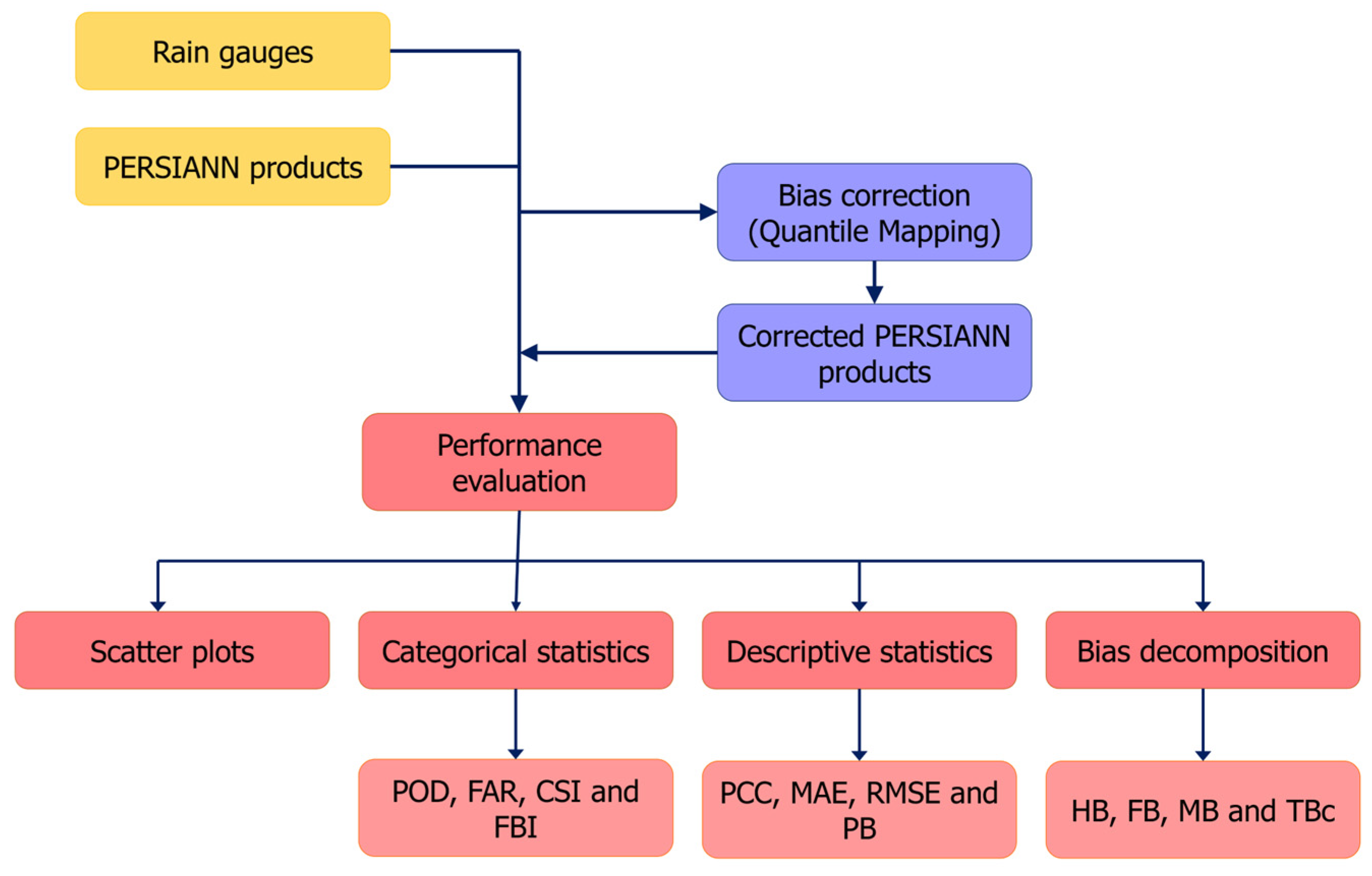
3. Methodology
3.1. Scatter Plots
3.2. Categorical Statistics
3.3. Descriptive Statistics
3.4. Bias Decomposition
3.5. Bias Correction: Quantile Mapping
4. Results
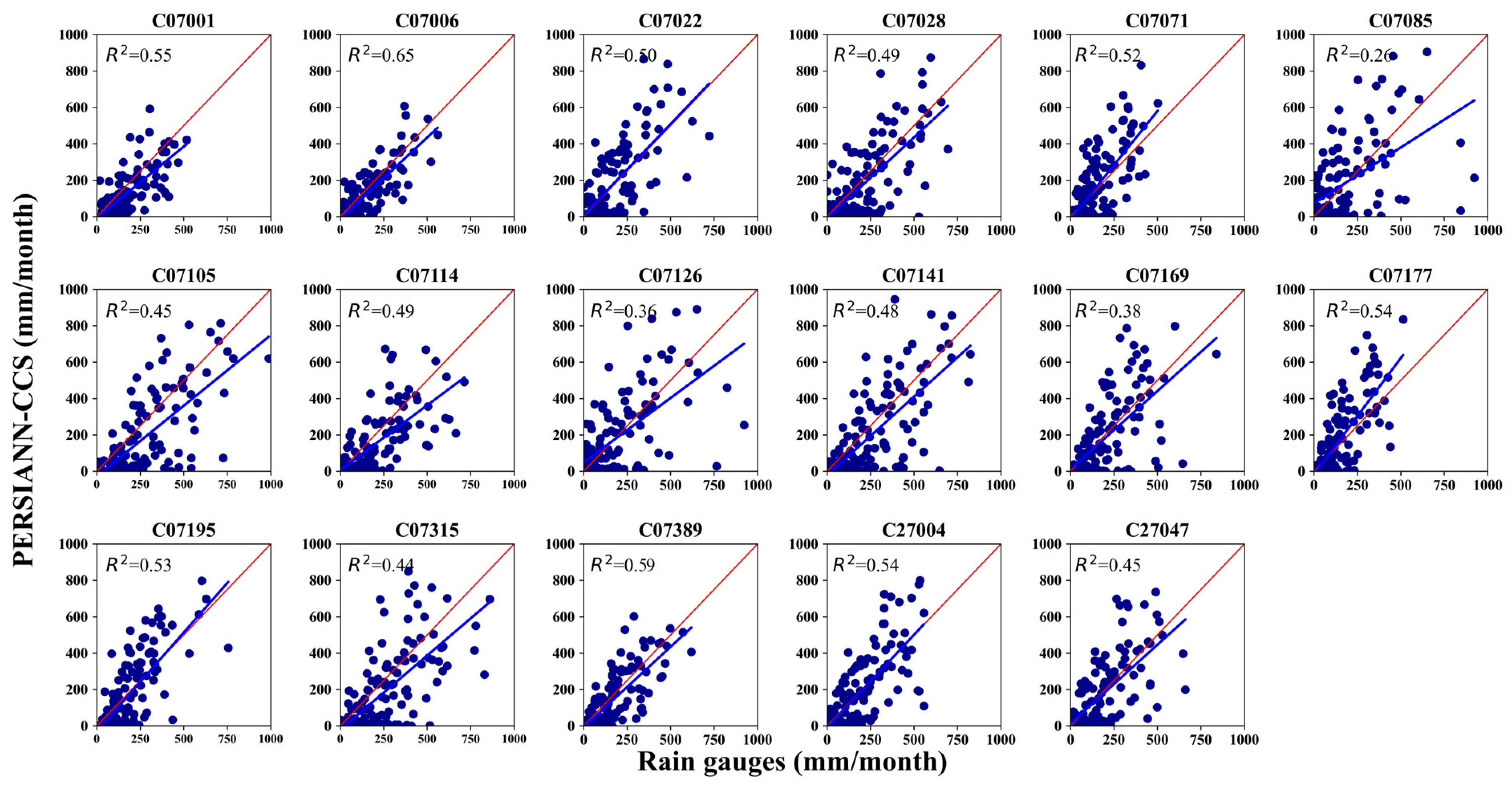
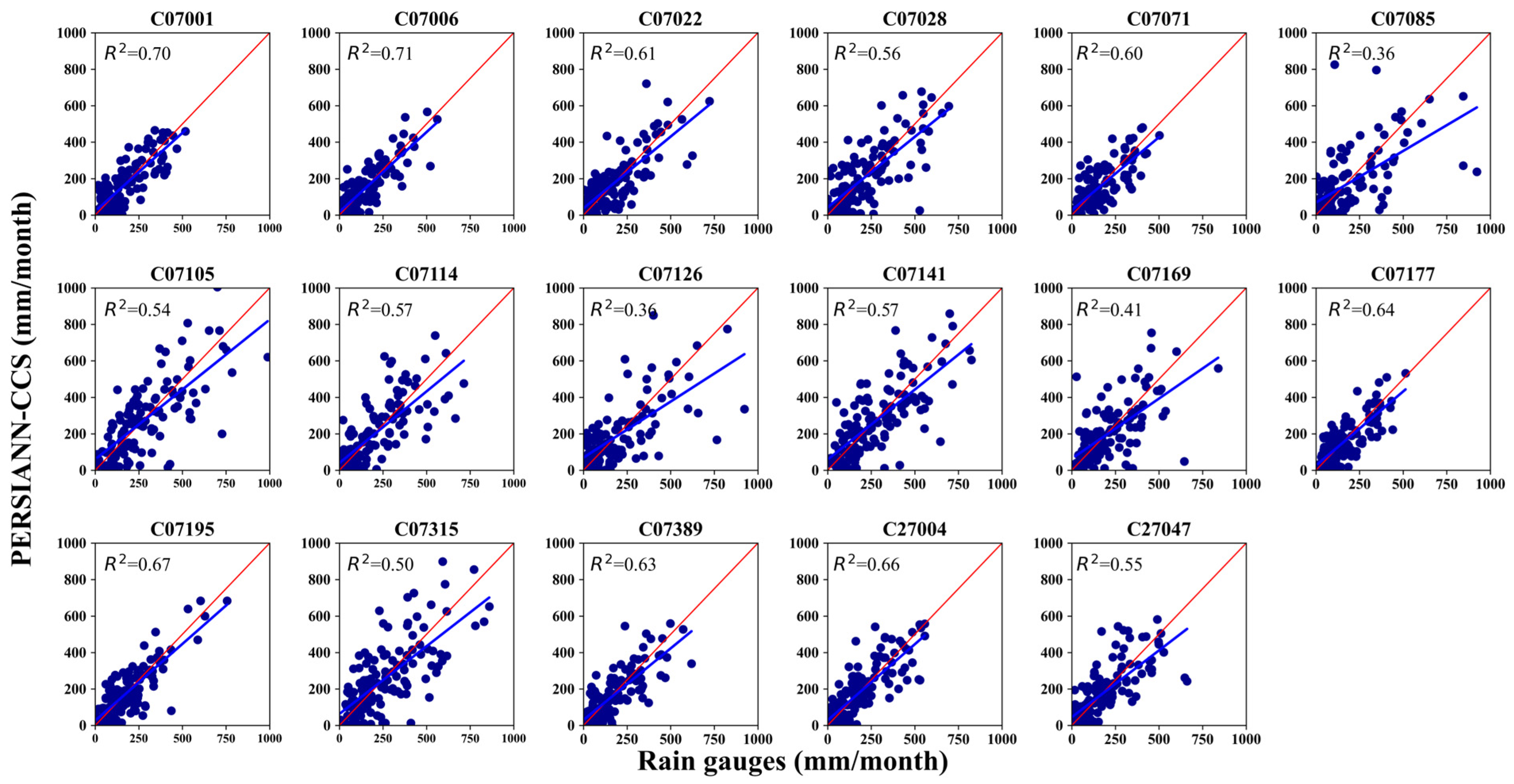
4.1. Graphic Comparison of Rain Gauges and SPPs (Scatter Plots)
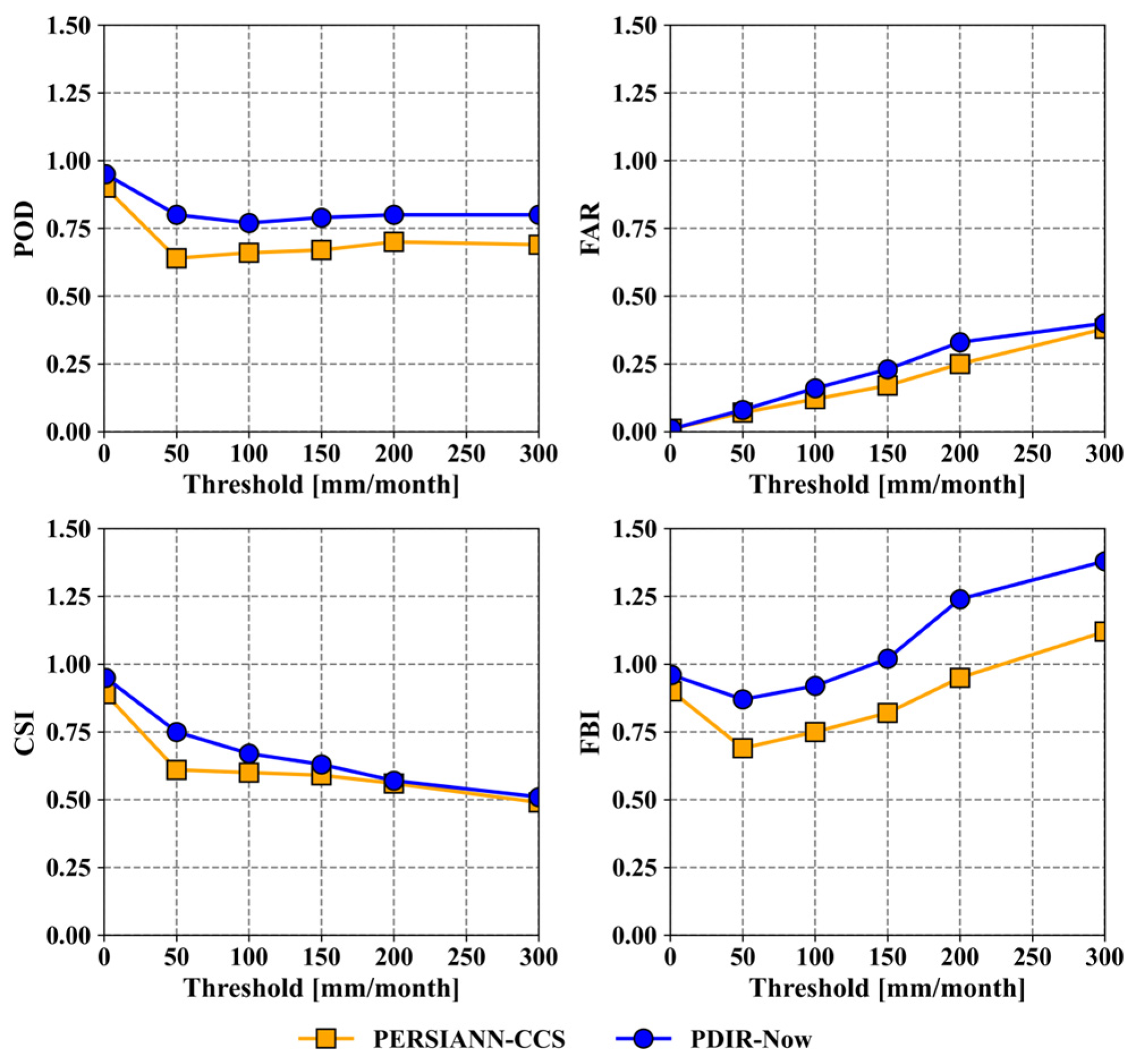
4.2. Performance of SPPs Based on Categorical Validation Statistics
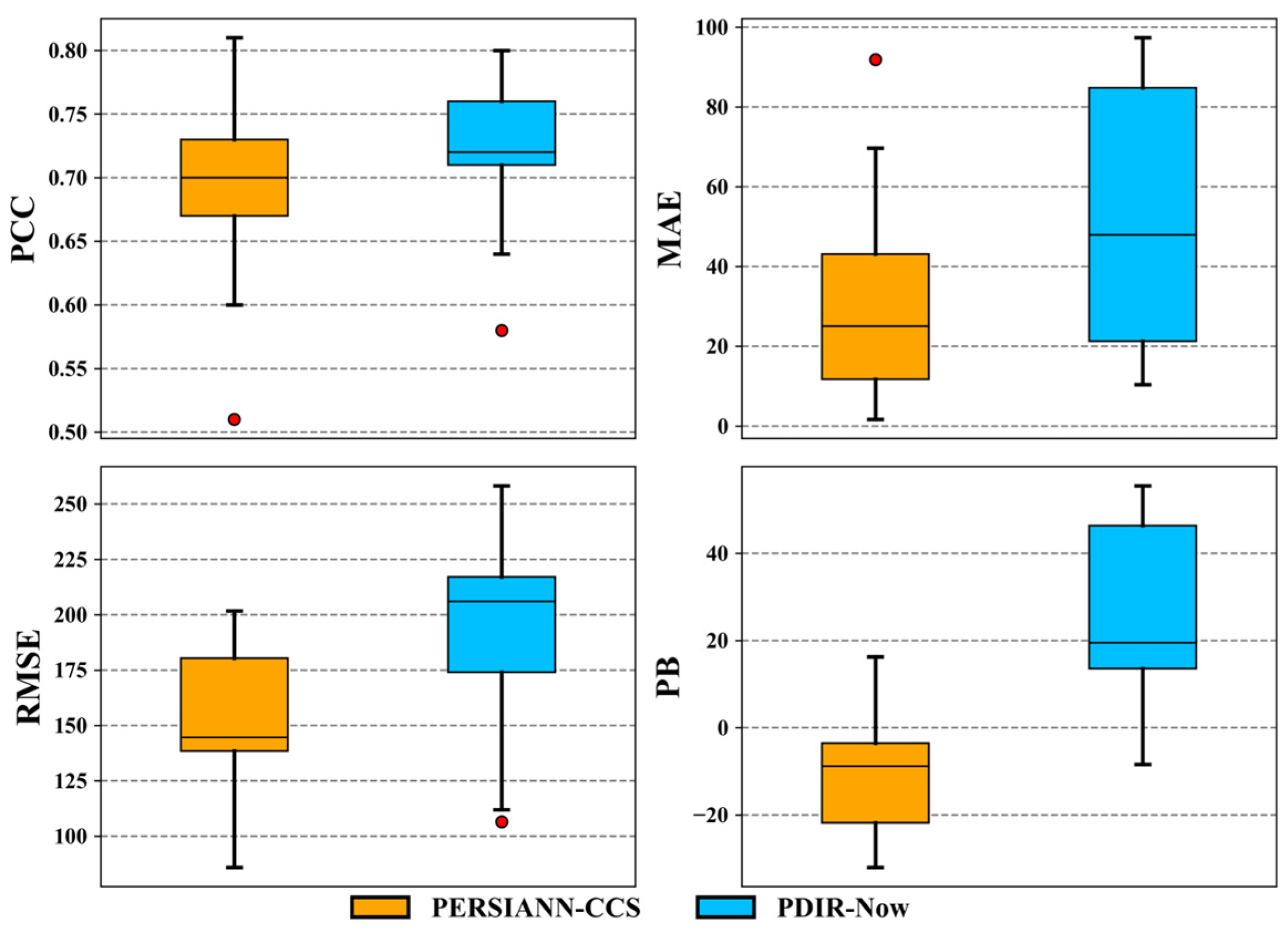
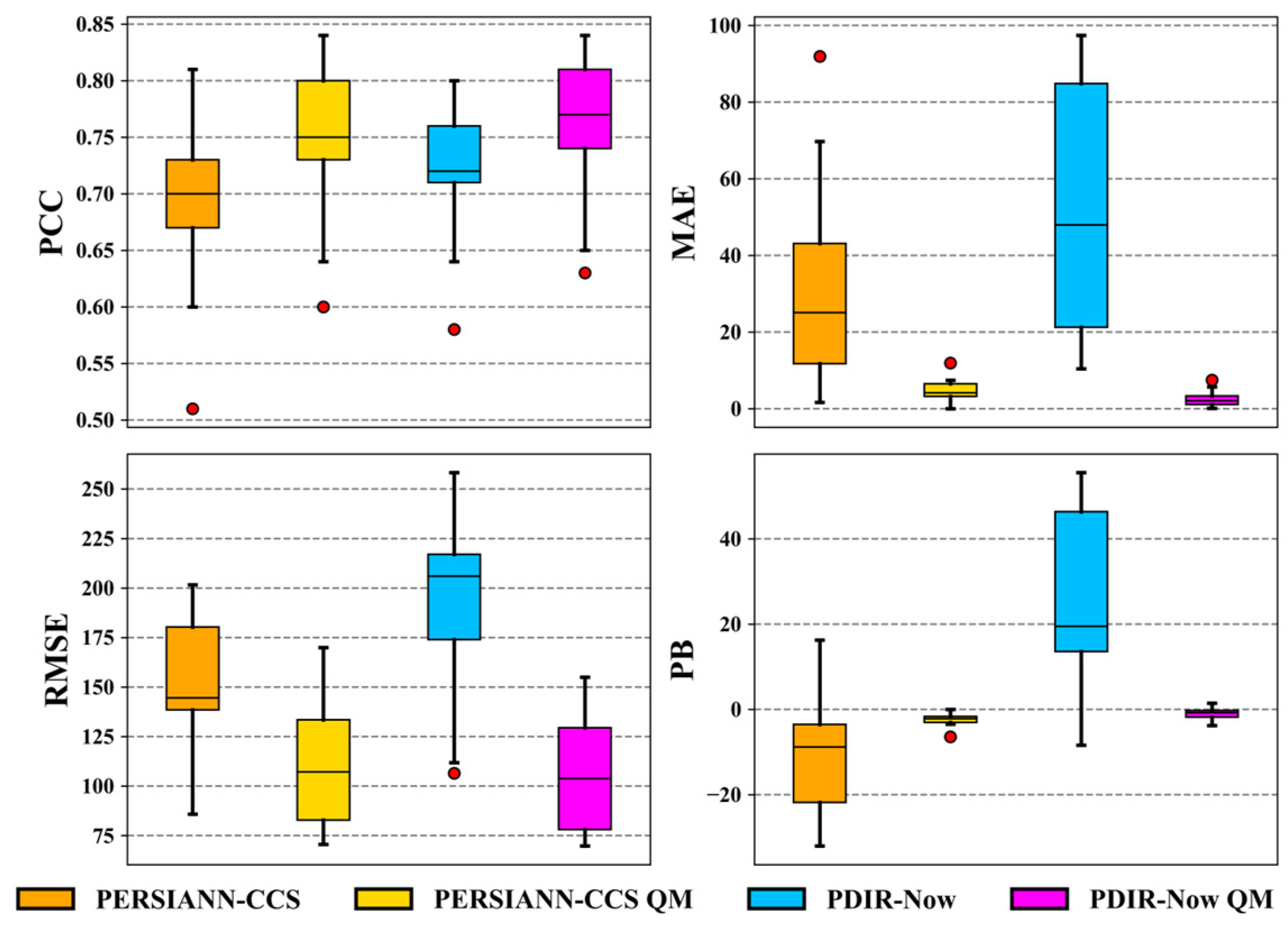
4.3. Performance of SPPs Based on Descriptive Validation Statistics
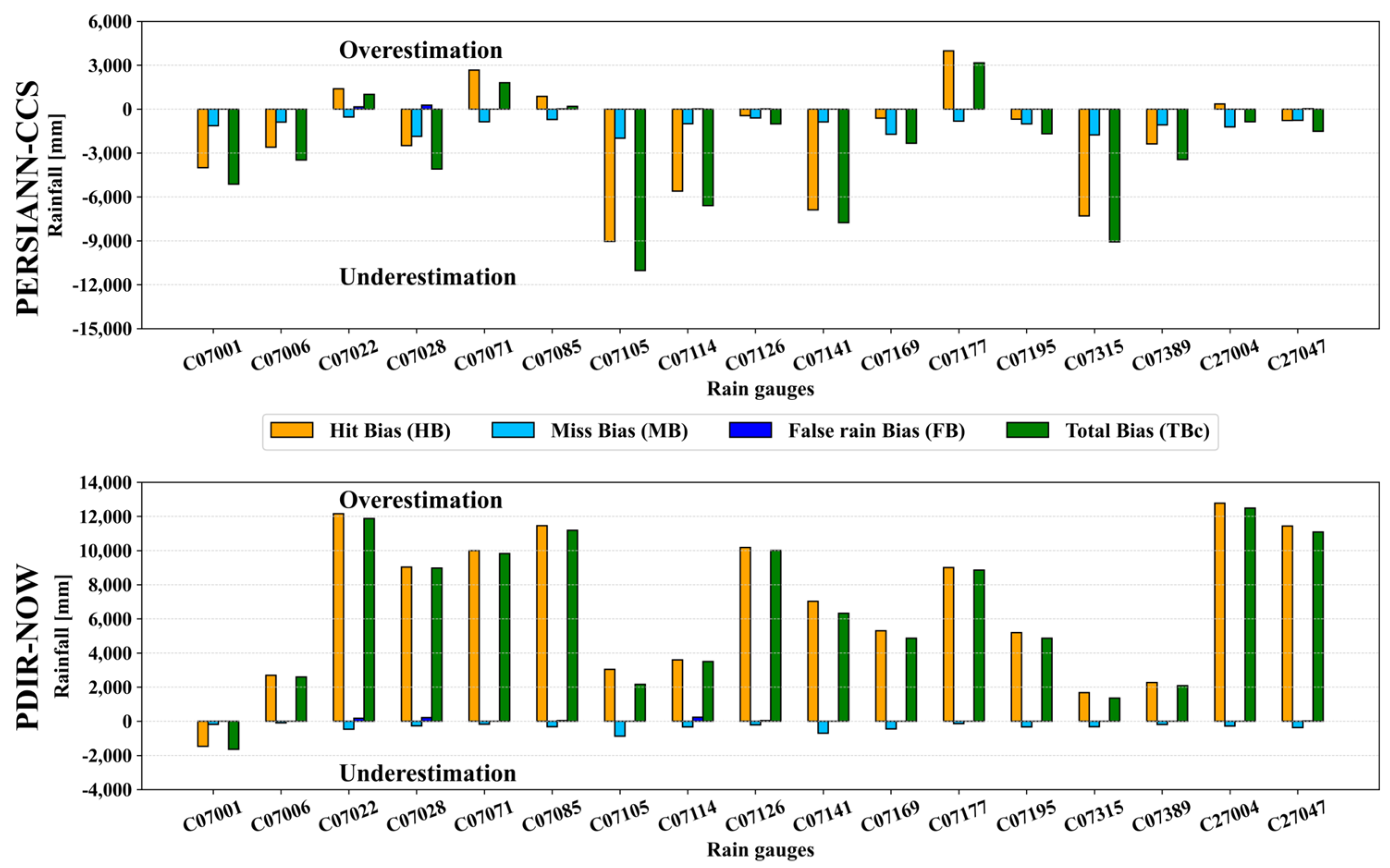
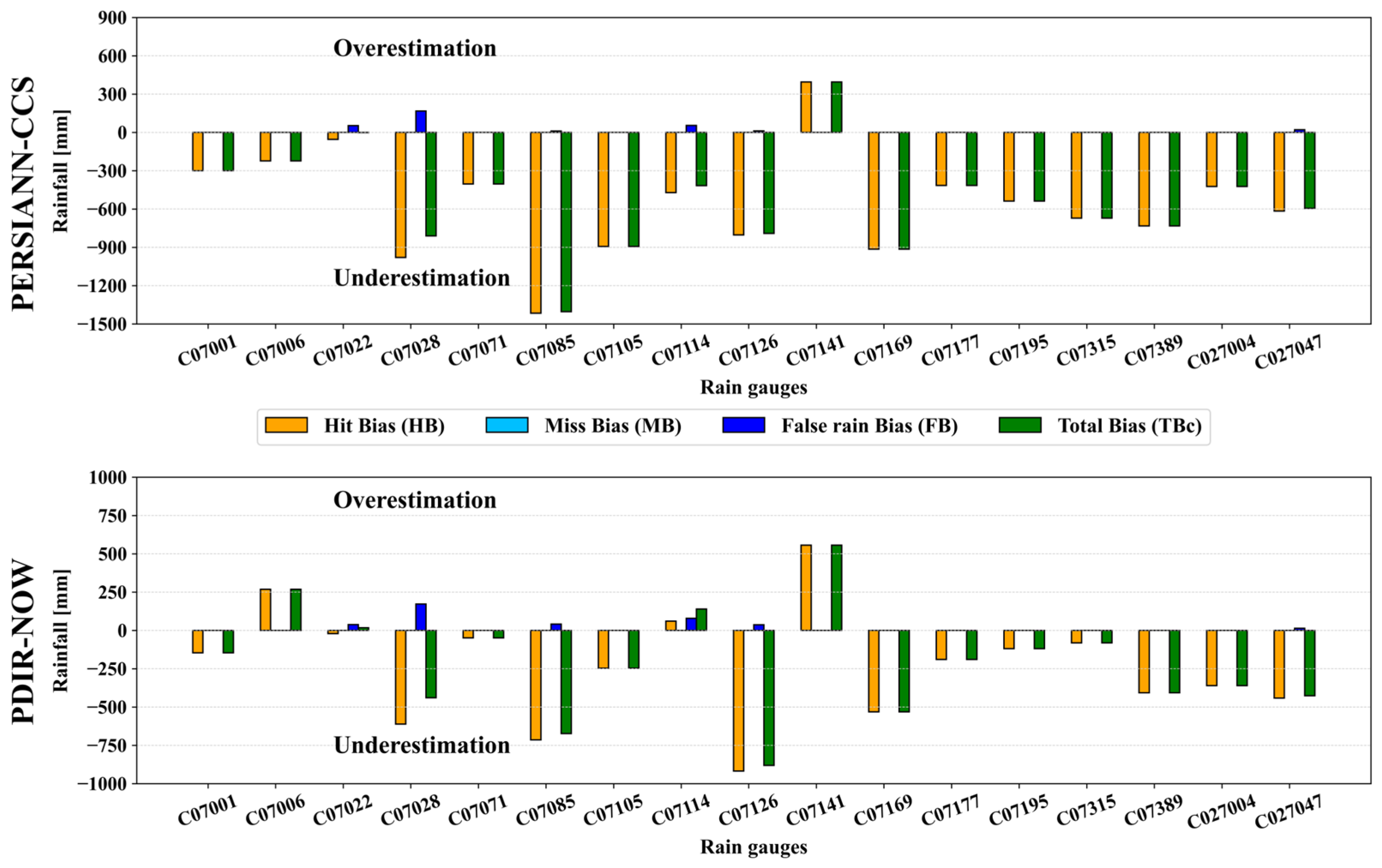
4.4. SPPs Bias Decomposition
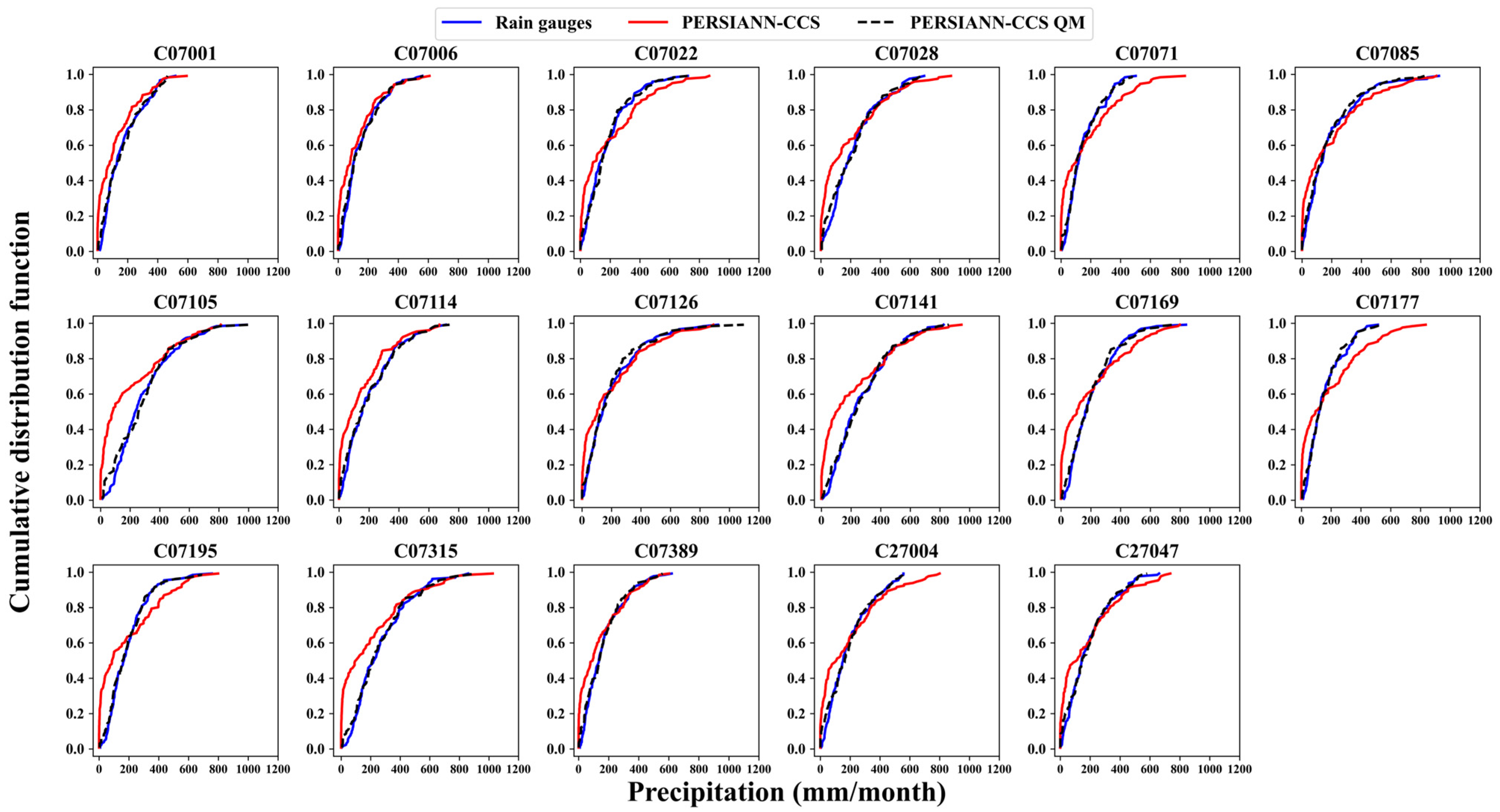
4.5. Bias Correction: Quantile Mapping
5. Discussion
6. Conclusions
- The SPPs show a good relationship with rain gauge records at the monthly level. Graphically, through scatter plots and with the help of a 1:1 line, the linear relationship between the data were evaluated, finding both overestimations and underestimations by the two SPPs, although PDIR-Now presents higher overestimation. Regarding the metrics of the categorical statistics (POD, FAR, CSI, and FBI), the performance of PDIR-Now is relatively better at all thresholds (intense or weak rains).
- The error of each SPP can be better understood by decomposing the total bias (difference in accumulated precipitation) of the SPPs and the rain gauges. It was indeed found that PDIR-Now tends to overestimate rainfall in large quantities. In contrast, PERSIANN-CCS underestimates it to a lesser extent. Therefore, it is demonstrated that both SPPs perform poorly in capturing the total volume of monthly rainfall over the TRB.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Budnik, S.V. Spatio-temporal change of atmospheric precipitation on territory of north-west of Ukraine. J. Atmos. Sci. Res. 2020, 2, 1–4. [Google Scholar] [CrossRef]
- Kidd, C.; Huffman, G. Global precipitation measurement. Meteorol. Appl. 2011, 18, 334–353. [Google Scholar] [CrossRef]
- Kim, K.B.; Bray, M.; Han, D. An improved bias correction scheme based on comparative precipitation characteristics. Hydrol. Process. 2015, 29, 2258–2266. [Google Scholar] [CrossRef]
- Overeem, A.; Leijnse, H.; van Leth, T.C.; Bogerd, L.; Priebe, J.; Tricarico, D.; Droste, A.; Uijlenhoet, R. Tropical rainfall monitoring with commercial microwave links in Sri Lanka. Environ. Res. Lett. 2021, 16, 074058. [Google Scholar] [CrossRef]
- Gilewski, P.; Nawalany, M. Inter-comparison of Rain-Gauge, Radar, and Satellite (IMERG GPM) precipitation estimates performance for rainfall-runoff modeling in a mountainous catchment in Poland. Water 2018, 10, 1665. [Google Scholar] [CrossRef]
- Jiang, S.; Ren, L.; Hong, Y.; Yong, B.; Yang, X.; Yuan, F.; Ma, M. Comprehensive evaluation of multi-satellite precipitation products with a dense rain gauge network and optimally merging their simulated hydrological flows using the Bayesian model averaging method. J. Hydrol. 2012, 452–453, 213–225. [Google Scholar] [CrossRef]
- Ashouri, H.; Hsu, K.L.; Sorooshian, S.; Braithwaite, D.K.; Knapp, K.R.; Cecil, L.D.; Nelson, B.R.; Prat, O.P. PERSIANN-CDR: Daily precipitation climate data record from multisatellite observations for hydrological and climate studies. Bull. Am. Meteorol. Soc. 2015, 96, 69–83. [Google Scholar] [CrossRef]
- Gavilán, V.; Lillo-Saavedra, M.; Holzapfel, E.; Rivera, D.; García-Pedrero, A. Seasonal crop water balance using harmonized Landsat-8 and Sentinel-2 time series data. Water 2019, 11, 2236. [Google Scholar] [CrossRef]
- Kulkarni, S.C.; Rege, P.P. Pixel level fusion techniques for SAR and optical images: A review. Inf. Fusion 2020, 59, 13–29. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Turk, F.J.; Petersen, W.; Hou, A.Y.; García-Ortega, E.; Machado, L.A.T.; Angelis, C.F.; Salio, P.; Kidd, C.; Huffman, G.J.; et al. Global precipitation measurement: Methods, datasets and applications. Atmos. Res. 2012, 104–105, 70–97. [Google Scholar] [CrossRef]
- Tapiador, F.J.; Kidd, C.; Hsu, K.L.; Marzano, F. Neural networks in satellite rainfall estimation. Meteorol. Appl. 2004, 11, 83–91. [Google Scholar] [CrossRef]
- Ceccato, P.; Dinku, T. Introduction to Remote Sensing for Monitoring Rainfall, Temperature, Vegetation and Water Bodies; IRI Technical Report 10-04; International Research Institute for Climate and Society: Palisades, NY, USA, 2010; p. 10. [Google Scholar] [CrossRef]
- Kidd, C.; Levizzani, V. Status of satellite precipitation retrievals. Hydrol. Earth Syst. Sci. 2011, 15, 1109–1116. [Google Scholar] [CrossRef]
- Sorooshian, S.; Gao, X.; Hsu, K.; Maddox, R.A.; Hong, Y.; Gupta, H.V.; Imam, B. Diurnal variability of tropical rainfall retrieved from combined GOES and TRMM satellite information. J. Clim. 2002, 15, 983–1001. [Google Scholar] [CrossRef]
- Herman, A.; Kumar, V.B.; Arkin, P.A.; Kousky, J.V. Objectively determined 10-day African rainfall estimates created for famine early warning systems. Int. J. Remote Sens. 1997, 18, 2147–2159. [Google Scholar] [CrossRef]
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Joyce, R.J.; Janowiak, J.E.; Arkin, P.A.; Xie, P. CMORPH: A method that produces global precipitation estimates from passive microwave and infrared data at high spatial and temporal resolution. J. Hydrometeorol. 2004, 5, 487–503. [Google Scholar] [CrossRef]
- Sorooshian, S.; Hsu, K.L.; Gao, X.; Gupta, H.V.; Imam, B.; Braithwaite, D. Evaluation of PERSIANN system satellite-based estimates of tropical rainfall. Bull. Am. Meteorol. Soc. 2000, 81, 2035–2046. [Google Scholar] [CrossRef]
- Beck, H.E.; Van Dijk, A.I.J.M.; Levizzani, V.; Schellekens, J.; Miralles, D.G.; Martens, B.; De Roo, A. MSWEP: 3-hourly 0.25° global gridded precipitation (1979-2015) by merging gauge, satellite, and reanalysis data. Hydrol. Earth Syst. Sci. 2017, 21, 589–615. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A Quasi-Global Precipitation Time Series for Drought Monitoring. US Geol. Surv. Data Ser. 2014, 832, 4. [Google Scholar] [CrossRef]
- Okamoto, K.; Ushio, T.; Iguchi, T.; Takahashi, N.; Iwanami, K. The Global Satellite Mapping of Precipitation (GSMaP) project. Int. Geosci. Remote Sens. Symp. (IGARSS) 2005, 5, 3414–3416. [Google Scholar] [CrossRef]
- Schneider, U.; Becker, A.; Finger, P.; Meyer-Christoffer, A.; Ziese, M.; Rudolf, B. GPCC’s new land surface precipitation climatology based on quality-controlled in situ data and its role in quantifying the global water cycle. Theor. Appl. Climatol. 2014, 115, 15–40. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Nelkin, E.J. The TRMM Multi-satellite Precipitation Analysis (TMPA). In Satellite Rainfall Applications for Surface Hydrology; Springer: Dordrecht, The Netherlands, 2010; pp. 3–22. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Kidd, C.; Nelkin, E.J.; Xie, P. NASA Global Precipitation Measurement (GPM) Integrated Multi-satellitE Retrievals for GPM (IMERG). Algorithm Theoretical Basis Document (ATBD) Version 4.5. 26 November 2015. Available online: https://pmm.nasa.gov/sites/default/files/document_files/IMERG_ATBD_V4.5.pdf (accessed on 5 February 2024).
- Rivera, J.A.; Marianetti, G.; Hinrichs, S. Validation of CHIRPS precipitation dataset along the Central Andes of Argentina. Atmos. Res. 2018, 213, 437–449. [Google Scholar] [CrossRef]
- Saeidizand, R.; Sabetghadam, S.; Tarnavsky, E.; Pierleoni, A. Evaluation of CHIRPS rainfall estimates over Iran. Q. J. R. Meteorol. Soc. 2018, 144, 282–291. [Google Scholar] [CrossRef]
- Erazo, B.; Bourrel, L.; Frappart, F.; Chimborazo, O.; Labat, D.; Dominguez-Granda, L.; Matamoros, D.; Mejia, R. Validation of satellite estimates (Tropical Rainfall Measuring Mission, TRMM) for rainfall variability over the Pacific slope and Coast of Ecuador. Water 2018, 10, 213. [Google Scholar] [CrossRef]
- Lekula, M.; Lubczynski, M.W.; Shemang, E.M.; Verhoef, W. Validation of satellite-based rainfall in Kalahari. Phys. Chem. Earth 2018, 105, 84–97. [Google Scholar] [CrossRef]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Katiraie-Boroujerdy, P.S.; Naeini, M.R.; Asanjan, A.A.; Chavoshian, A.; Hsu, K.L.; Sorooshian, S. Bias correction of satellite-based precipitation estimations using quantile mapping approach in different climate regions of Iran. Remote Sens. 2020, 12, 2102. [Google Scholar] [CrossRef]
- Shabalova, M.V.; van Deursen, W.P.A.; Buishand, T.A. Assessing future discharge of the river Rhine using regional climate model integrations and a hydrological model. Clim. Res. 2003, 23, 233–246. [Google Scholar] [CrossRef]
- Lenderink, G.; Buishand, A.; Van Deursen, W. Estimates of future discharges of the river Rhine using two scenario methodologies: Direct versus delta approach. Hydrol. Earth Syst. Sci. 2007, 11, 1145–1159. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias correction of regional climate model simulations for hydrological climate-change impact studies: Review and evaluation of different methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Themeßl, M.J.; Gobiet, A.; Heinrich, G. Empirical-statistical downscaling and error correction of regional climate models and its impact on the climate change signal. Clim. Chang. 2012, 112, 449–468. [Google Scholar] [CrossRef]
- Holthuijzen, M.; Beckage, B.; Clemins, P.J.; Higdon, D.; Winter, J.M. Robust bias-correction of precipitation extremes using a novel hybrid empirical quantile-mapping method: Advantages of a linear correction for extremes. Theor. Appl. Climatol. 2022, 149, 863–882. [Google Scholar] [CrossRef]
- Piani, C.; Weedon, G.P.; Best, M.; Gomes, S.M.; Viterbo, P.; Hagemann, S.; Haerter, J.O. Statistical bias correction of global simulated daily precipitation and temperature for the application of hydrological models. J. Hydrol. 2010, 395, 199–215. [Google Scholar] [CrossRef]
- Schmidli, J.; Frei, C.; Vidale, P.L. Downscaling from GCM precipitation: A benchmark for dynamical and statistical downscaling methods. Int. J. Climatol. 2006, 26, 679–689. [Google Scholar] [CrossRef]
- Gudmundsson, L.; Bremnes, J.B.; Haugen, J.E.; Engen-Skaugen, T. Technical Note: Downscaling RCM precipitation to the station scale using statistical transformations—A comparison of methods. Hydrol. Earth Syst. Sci. 2012, 16, 3383–3390. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Tsanis, I.K. Multisegment statistical bias correction of daily GCM precipitation output. J. Geophys. Res. Atmos. 2013, 118, 3150–3162. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Ayana, E.K.; Maathuis, B.H.P.; MacAlister, C.; Philpot, W.D.; Osorio Leyton, J.M.; Steenhuis, T.S. Performance of bias corrected MPEG rainfall estimate for rainfall-runoff simulation in the upper Blue Nile Basin, Ethiopia. J. Hydrol. 2018, 556, 1182–1191. [Google Scholar] [CrossRef]
- Bong, T.; Son, Y.H.; Yoo, S.H.; Hwang, S.W. Nonparametric quantile mapping using the response surface method—Bias correction of daily precipitation. J. Water Clim. Chang. 2018, 9, 525–539. [Google Scholar] [CrossRef]
- Devi, U.; Shekhar, M.S.; Singh, G.P.; Rao, N.N.; Bhatt, U.S. Methodological application of quantile mapping to generate precipitation data over Northwest Himalaya. Int. J. Climatol. 2019, 39, 3160–3170. [Google Scholar] [CrossRef]
- Heo, J.H.; Ahn, H.; Shin, J.Y.; Kjeldsen, T.R.; Jeong, C. Probability distributions for a quantile mapping technique for a bias correction of precipitation data: A case study to precipitation data under climate change. Water 2019, 11, 1475. [Google Scholar] [CrossRef]
- Serrat-Capdevila, A.; Merino, M.; Valdes, J.B.; Durcik, M. Evaluation of the performance of three satellite precipitation products over Africa. Remote Sens. 2016, 8, 836. [Google Scholar] [CrossRef]
- Shukla, A.K.; Ojha, C.S.P.; Singh, R.P.; Pal, L.; Fu, D. Evaluation of TRMM precipitation dataset over Himalayan Catchment: The upper Ganga Basin, India. Water 2019, 11, 613. [Google Scholar] [CrossRef]
- Ringard, J.; Seyler, F.; Linguet, L. A quantile mapping bias correction method based on hydroclimatic classification of the Guiana shield. Sensors 2017, 17, 1413. [Google Scholar] [CrossRef]
- Chow, V.; Maidment, D.; Mays, L. Hidrología Aplicada. Hidrologia Aplicada. 1994, p. 575. Available online: http://bases.bireme.br/cgi-bin/wxislind.exe/iah/online/?IsisScript=iah/iah.xis&src=google&base=REPIDISCA&lang=p&nextAction=lnk&exprSearch=158911&indexSearch=ID (accessed on 26 February 2024).
- Gallegos-Cedillo, J.; Arteaga-Ramírez, R.; Vázquez-Peña, M.A.; Juárez-Méndez, J.; Gallegos-Cedillo, J.; Arteaga-Ramírez, R.; Vázquez-Peña, M.A.; Juárez-Méndez, J. Estimation of missing daily precipitation and maximum and minimum temperature records in San Luis Potosí. Ing. Agrícola Biosist. 2016, 8, 3–16. [Google Scholar] [CrossRef]
- Toro Trujillo, A.M.; Arteaga Ramírez, R.; Alberto Vázquez Peña, M.; Alicia Ibáñez Castillo, L. Relleno de series diarias de precipitación, temperatura mínima, máxima de la región norte del Urabá Antioqueño. Rev. Mex. Cienc. Agrícolas 2015, 6, 577–588. [Google Scholar]
- Hong, Y.; Gochis, D.; Cheng, J.T.; Hsu, K.L.; Sorooshian, S. Evaluation of PERSIANN-CCS rainfall measurement using the NAME event rain gauge network. J. Hydrometeorol. 2007, 8, 469–482. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Gorooh, V.A.; Shearer, E.J.; Sadeghi, M.; Sorooshian, S.; Hsu, K.; Bolvin, D.; Ralph, M.F. Persiann dynamic infrared–rain rate (PDIR-now): A near-real-time, quasi-global satellite precipitation dataset. J. Hydrometeorol. 2020, 21, 2893–2906. [Google Scholar] [CrossRef]
- Sadeghi, M.; Nguyen, P.; Naeini, M.R.; Hsu, K.; Braithwaite, D.; Sorooshian, S. PERSIANN-CCS-CDR, a 3-hourly 0.04° global precipitation climate data record for heavy precipitation studies. Sci. Data 2021, 8, 157. [Google Scholar] [CrossRef]
- Li, J.; Yuan, D.; Liu, J.; Jiang, Y.; Chen, Y.; Hsu, K.L.; Sorooshian, S. Predicting floods in a large karst river basin by coupling PERSIANN-CCS QPEs with a physically based distributed hydrological model. Hydrol. Earth Syst. Sci. 2019, 23, 1505–1532. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical methods in the atmospheric sciences, second edition. In Meteorological Applications; Academic Press: London, UK, 2007; Volume 14. [Google Scholar]
- Gilbert, G.K. Finley’s Tornado Predictions. Am. Meteorol. J. 1884, 1, 166. [Google Scholar]
- Hossain, F.; Huffman, G.J. Investigating error metrics for satellite rainfall data at hydrologically relevant scales. J. Hydrometeorol. 2008, 9, 563–575. [Google Scholar] [CrossRef]
- Doswell, C.A.; Davies-Jones, R.; Keller, D.L. On Summary Measures of Skill in Rare Event Forecasting Based on Contingency Tables. Weather Forecast. 1990, 5, 576–585. [Google Scholar] [CrossRef]
- Logah, F.Y.; Adjei, K.A.; Obuobie, E.; Gyamfi, C.; Odai, S.N. Evaluation and Comparison of Satellite Rainfall Products in the Black Volta Basin. Environ. Process. 2021, 8, 119–137. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Habib, E.; Henschke, A.; Adler, R.F. Evaluation of TMPA satellite-based research and real-time rainfall estimates during six tropical-related heavy rainfall events over Louisiana, USA. Atmos. Res. 2009, 94, 373–388. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B.; Joyce, R.J.; Huffman, G.J.; Adler, R.F.; Hsu, K.L.; Turk, F.J.; Garcia, M.; Zeng, J. Component analysis of errors in Satellite-based precipitation estimates. J. Geophys. Res. Atmos. 2009, 114, D24101. [Google Scholar] [CrossRef]
- Xiao, S.; Zou, L.; Xia, J.; Yang, Z.; Yao, T. Bias correction framework for satellite precipitation products using a rain/no rain discriminative model. Sci. Total Environ. 2022, 818, 151679. [Google Scholar] [CrossRef]
- Adane, G.B.; Hirpa, B.A.; Lim, C.H.; Lee, W.K. Evaluation and comparison of satellite-derived estimates of rainfall in the diverse climate and terrain of central and northeastern ethiopia. Remote Sens. 2021, 13, 1275. [Google Scholar] [CrossRef]
- Belabid, N.; Zhao, F.; Brocca, L.; Huang, Y.; Tan, Y. Near-real-time flood forecasting based on satellite precipitation products. Remote Sens. 2019, 11, 252. [Google Scholar] [CrossRef]
- Cheng, S.; Wang, W.; Yu, Z. Evaluating the drought-monitoring utility of GPM and TRMM precipitation products over mainland china. Remote Sens. 2021, 13, 4153. [Google Scholar] [CrossRef]
- Chua, Z.W.; Kuleshov, Y.; Watkins, A.B.; Choy, S.; Sun, C. A Two-Step Approach to Blending GSMaP Satellite Rainfall Estimates with Gauge Observations over Australia. Remote Sens. 2022, 14, 1903. [Google Scholar] [CrossRef]
- Palharini, R.S.A.; Vila, D.A.; Rodrigues, D.T.; Quispe, D.P.; Palharini, R.C.; de Siqueira, R.A.; de Sousa Afonso, J.M. Assessment of the extreme precipitation by satellite estimates over South America. Remote Sens. 2020, 12, 2085. [Google Scholar] [CrossRef]
- Cánovas-García, F.; García-Galiano, S.; Alonso-Sarría, F. Assessment of satellite and radar quantitative precipitation estimates for real time monitoring of meteorological extremes over the southeast of the Iberian Peninsula. Remote Sens. 2018, 10, 1023. [Google Scholar] [CrossRef]
- Dehaghani, A.M.; Gohari, A.; Zareian, M.J.; Torabi Haghighi, A. A comprehensive evaluation of the satellite precipitation products across Iran. J. Hydrol. Reg. Stud. 2023, 46, 101360. [Google Scholar] [CrossRef]
- Nguyen, P.; Ombadi, M.; Sorooshian, S.; Hsu, K.; AghaKouchak, A.; Braithwaite, D.; Ashouri, H.; Rose Thorstensen, A. The PERSIANN family of global satellite precipitation data: A review and evaluation of products. Hydrol. Earth Syst. Sci. 2018, 22, 5801–5816. [Google Scholar] [CrossRef]
- Huang, W.R.; Liu, P.Y.; Hsu, J.; Li, X.; Deng, L. Assessment of near-real-time satellite precipitation products from gsmap in monitoring rainfall variations over Taiwan. Remote Sens. 2021, 13, 202. [Google Scholar] [CrossRef]
- Eini, M.R.; Rahmati, A.; Piniewski, M. Hydrological application and accuracy evaluation of PERSIANN satellite-based precipitation estimates over a humid continental climate catchment. J. Hydrol. Reg. Stud. 2022, 41, 101109. [Google Scholar] [CrossRef]
- Hsu, J.; Huang, W.R.; Liu, P.Y. Comprehensive Analysis of PERSIANN Products in Studying the Precipitation Variations over Luzon. Remote Sens. 2022, 14, 5900. [Google Scholar] [CrossRef]
- Gunathilake, M.B.; Senerath, T.; Rathnayake, U. Artificial neural network based PERSIANN data sets in evaluation of hydrologic utility of precipitation estimations in a tropical watershed of Sri Lanka. AIMS Geosci. 2021, 7, 478–489. [Google Scholar] [CrossRef]
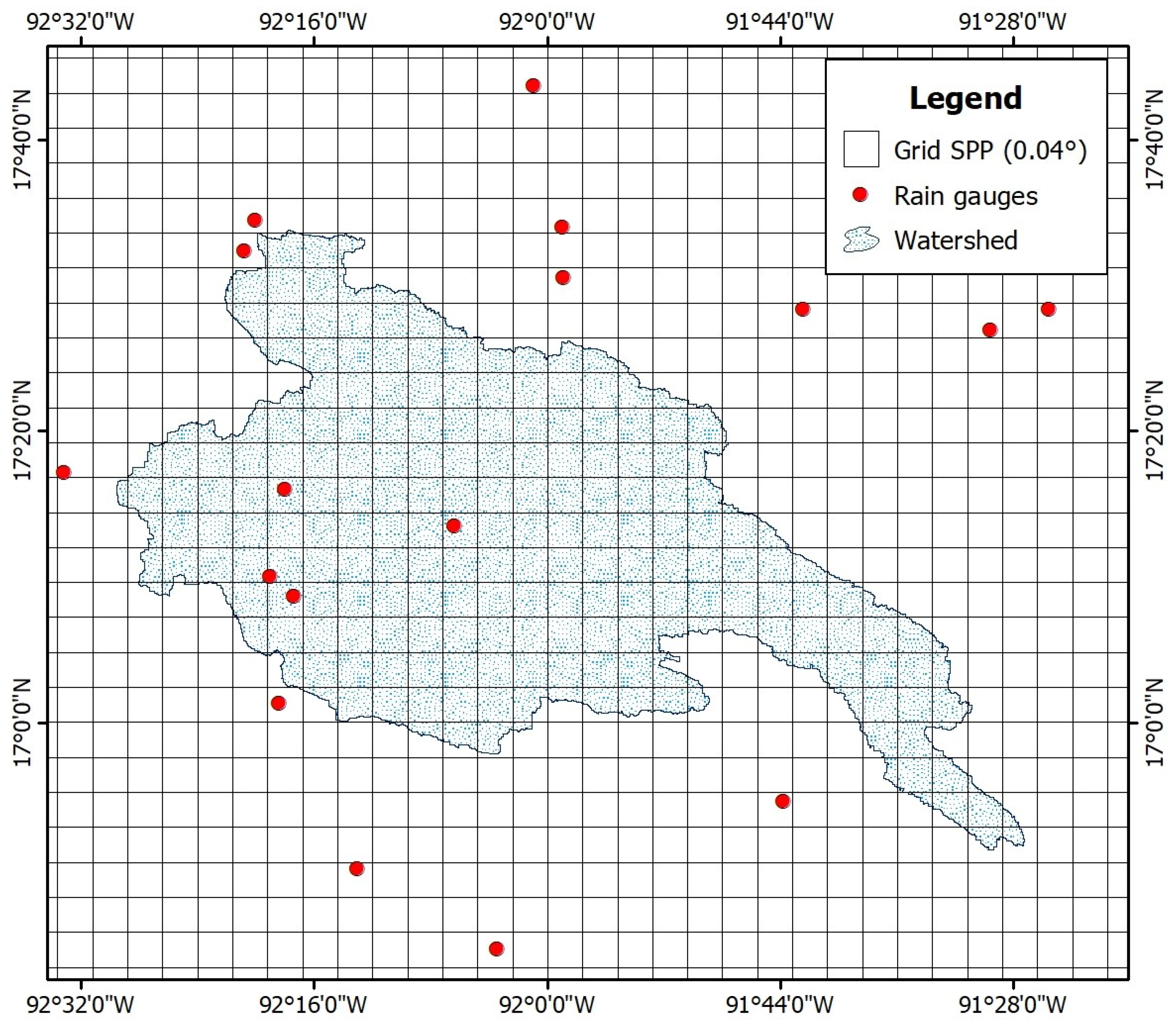




| Rain Gauge | Long (°W) | Lat (°N) | Elevation (m a.s.l) | Missing Data (%) | |
|---|---|---|---|---|---|
| ID Rg | Name | ||||
| C07001 | Abosolo Chiapas | −92.22 | 16.83 | 1280 | 8.51 |
| C07006 | Altamirano | −92.06 | 16.74 | 1240 | 7.71 |
| C07022 | Playas de Catazaja | −92.02 | 17.73 | 10 | 7.59 |
| C07028 | Chacamax | −91.71 | 17.47 | 60 | 6.30 |
| C07071 | Guaquitepec | −92.29 | 17.14 | 1160 | 0.02 |
| C07085 | Palenque | −91.98 | 17.51 | 60 | 10.30 |
| C07105 | Las nubes | −92.34 | 17.51 | 93 | 9.50 |
| C07114 | Yaquintela | −91.73 | 16.91 | 650 | 2.36 |
| C07126 | Palenque (DGE) | −91.98 | 17.57 | 60 | 11.12 |
| C07141 | Salto de agua (DGE) | −92.33 | 17.57 | 10 | 0.02 |
| C07169 | Tumbala | −92.30 | 17.27 | 1063 | 3.48 |
| C07177 | Yajalon | −92.32 | 17.17 | 660 | 4.83 |
| C07195 | Sabanilla | −92.55 | 17.29 | 300 | 2.74 |
| C07315 | Paso del cayuco | −92.11 | 17.23 | 291 | 1.52 |
| C07389 | Sitala | −92.31 | 17.02 | 1100 | 0.75 |
| C27004 | Boca del cerro | −91.49 | 17.45 | 14 | 0.00 |
| C27047 | Tenosique | −91.43 | 17.47 | 22 | 3.21 |
| Product | Abbreviation | Spatial Resolution | Temporal Resolution | Data Period | Reference |
|---|---|---|---|---|---|
| PERSIANN-Cloud Classification System | PERSIANN-CCS | 0.04° × 0.04° | Hourly, three-hourly, six-hourly, daily, monthly, yearly | January 2003–present | Hong et al. [51] |
| PERSIANN-Dynamic Infrared Rain Rate near-real-time | PDIR-Now | 0.04° × 0.04° | Hourly, three-hourly, six-hourly, daily, monthly, yearly | March 2000–present | Nguyen et al. [52] |
| Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks | PERSIANN | 0.25° × 0.25° | Hourly, three-hourly, six-hourly, daily, monthly, yearly | March 2000–present | Sorooshian et al. [18] |
| PERSIANN-Climate Data Record | PERSIANN-CDR | 0.25° × 0.25° | Daily, monthly, yearly | January 1983–present | Ashouri et al. [7] |
| PERSIANN-Cloud Classification System-Climate Data Record | PERSIANN-CCS-CDR | 0.04° × 0.04° | Three-hourly, six-hourly, daily, monthly, yearly | January 1983–present | Sadegui et al. [53] |
| Rain Gauge ≥ Threshold | Rain Gauge < Threshold | |
|---|---|---|
| Satellite ≥ Threshold | H | F |
| Satellite < Threshold | M | C |
| Statistic | Equation | Range | Best Value | |
|---|---|---|---|---|
| Categorical statistics | Probability of detection | 0 to 1 | 1 | |
| False alarm ratio | 0 to 1 | 0 | ||
| Critical success index | 0 to 1 | 1 | ||
| Frequency bias index | 0 to ∞ | 1 | ||
| Descriptive statistics | Pearson correlation coefficient | −1 to 1 | −1 or 1 | |
| Mean absolute error | 0 to ∞ | 0 | ||
| Root mean square error | 0 to ∞ | 0 | ||
| Percent bias | −∞ to ∞ | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ceferino-Hernández, L.; Magaña-Hernández, F.; Campos-Campos, E.; Morosanu, G.A.; Torres-Aguilar, C.E.; Mora-Ortiz, R.S.; Díaz, S.A. Assessment of PERSIANN Satellite Products over the Tulijá River Basin, Mexico. Remote Sens. 2024, 16, 2596. https://doi.org/10.3390/rs16142596
Ceferino-Hernández L, Magaña-Hernández F, Campos-Campos E, Morosanu GA, Torres-Aguilar CE, Mora-Ortiz RS, Díaz SA. Assessment of PERSIANN Satellite Products over the Tulijá River Basin, Mexico. Remote Sensing. 2024; 16(14):2596. https://doi.org/10.3390/rs16142596
Chicago/Turabian StyleCeferino-Hernández, Lorenza, Francisco Magaña-Hernández, Enrique Campos-Campos, Gabriela Adina Morosanu, Carlos E. Torres-Aguilar, René Sebastián Mora-Ortiz, and Sergio A. Díaz. 2024. "Assessment of PERSIANN Satellite Products over the Tulijá River Basin, Mexico" Remote Sensing 16, no. 14: 2596. https://doi.org/10.3390/rs16142596
APA StyleCeferino-Hernández, L., Magaña-Hernández, F., Campos-Campos, E., Morosanu, G. A., Torres-Aguilar, C. E., Mora-Ortiz, R. S., & Díaz, S. A. (2024). Assessment of PERSIANN Satellite Products over the Tulijá River Basin, Mexico. Remote Sensing, 16(14), 2596. https://doi.org/10.3390/rs16142596







