Development of an Adaptive Fuzzy Integral-Derivative Line-of-Sight Method for Bathymetric LiDAR Onboard Unmanned Surface Vessel

Abstract

Previous control methods developed by our research team cannot satisfy the high accuracy requirements of unmanned surface vessel (USV) path-tracking during bathymetric mapping because of the excessive overshoot and slow convergence speed. For this reason, this study developed an adaptive fuzzy integral-derivative line-of-sight (AFIDLOS) method for USV path-tracking control. Integral and derivative terms were added to counteract the effect of the sideslip angle with which the USV could be quickly guided to converge to the planned path for bathymetric mapping. To obtain high accuracy of the look-ahead distance, a fuzzy control method was proposed. The proposed method was verified using simulations and outdoor experiments. The results demonstrate that the AFIDLOS method can reduce the overshoot by 79.85%, shorten the settling time by 55.32% in simulation experiments, reduce the average cross-track error by 10.91% and can ensure a 30% overlap of neighboring strips of bathymetric LiDAR outdoor mapping when compared with the traditional guidance law.

1. Introduction

Unmanned surface vessels (USVs) have a multitude of applications in bathymetric mapping [1,2,3]. A bathymetric light detection and ranging (LiDAR) named “GQ-Cormorant 19”, developed by our research team, has been assembled on an unmanned surface vessel (USV), named “GQ-S20”, for near-shore three-dimensional (3D) bathymetric mapping [4,5,6]. Its basic working principle for bathymetric map is as follows: The LiDAR system emits a green laser ray to shoot the water surface. Part of the laser ray returns from water surface and part of it continues until it shoots the water bottom. The LiDAR receiving optical system receives the echoes from the water surface and the water bottom. The time difference of the laser ray’s round trip between water surface and water bottom is calculated. The three-dimensional coordinates of the laser footprints at water bottom can be calculated using the time difference of the laser ray trip and POS (position and orientation system) data [7,8,9]. Since one strip of LiDAR system usually cannot cover a large water field, multiple strips with a certain percentage of overlap (usually greater than 30%) are used to collect the bathymetric data covering a large field. Moreover, since the accuracy of the LiDAR points located in the margin of the strips is low, these points are usually tailored out. To ensure more than 30% overlap of the neighboring cross-strips and satisfy the accuracy requirements of bathymetric mapping of the point cloud data, a path-tracking functionality (system) must be developed for autonomous USV operation under different water environments such as lakes, reservoirs, and seas [10,11,12,13,14]. The path-tracking functionality (system) using the line-of-sight (LOS) guidance law for USV path-tracking developed earlier by our research team has exposed several shortcomings, such as excessive overshoot and slow convergence speed, which result in errors in 3D point cloud coordinates along the planned trajectory and insufficient overlap of successive cross-strips. Therefore, this study proposed an adaptive fuzzy integral-derivative line-of-sight (AFIDLOS) method.

Over the past few decades, significant efforts have been made to develop guidance laws [15]. These methods are mostly based on the LOS guidance law, which has been demonstrated by Abdurahman et al. [16], Fossen et al. [17], Fu and Wang [18], Huang et al. [19], Kelasidi et al. [20], Villa et al. [21], Liu et al. [22], Qu et al. [23], Shao et al. [24], Wang et al. [25], and Zhang et al. [26]. Early efforts can be classified into two main categories.

• LOS guidance law based on parameter optimization: Healey and Lienard [27] first combined LOS guidance law with sliding mode control for path-tracking control of USV. However, the values of look-ahead distance and acceptance radius in the traditional LOS guidance law are generally fixed. The fixed values of the parameters prevent the USV from adaptively adjusting according to the distance from the desired path, resulting in a reduction of the path-tracking accuracy. Therefore, Lekkas and Fossen [28] proposed a time-varying look-ahead distance LOS guidance law that establishes a relationship between the look-ahead distance and cross-track error. Therefore, the look-ahead distance can be adaptively adjusted according to the magnitude of the cross-track error, which improves the accuracy and speed of path-tracking. Liu et al. [29] proposed an LOS guidance law with a variable acceptance radius, where the acceptance radius could be adaptively adjusted according to the angle between the desired routes, thus enabling the USV to reduce the amount of overshoot and improve the path-tracking accuracy when turning. Although both improved guidance laws provide certain improvement in path-tracking performance, they lack a method for valuing the parameters in time-varying equations, and the performance of the functions may not be the best. Thus, Mu et al. [30] proposed an adaptive time-varying look-ahead distance LOS (ALOS) guidance law based on a fuzzy control optimization algorithm wherein the convergence rate in the time-varying look-ahead distance equation was calculated by the fuzzy controller through the change rate of the cross-track error. This guidance law was combined with a proportional-integral-derivative (PID) algorithm to form a path-tracking method, and practical experiments were conducted. However, experimental results show that this method produces a large overshoot when the USV turns. The PID algorithm is susceptible to environmental influences in practical applications, which can reduce the path-tracking accuracy.
• LOS guidance law based on sideslip angle prediction: During path-tracking, the USV can generate a sideslip angle under the influence of wind and waves, which can cause the USV to deviate from the planned path. Therefore, there is a demand to develop an LOS guidance law that can predict the sideslip angle. Borhaug et al. [31] proposed the ILOS guidance law by adding an integral term to the traditional LOS guidance law. This guidance law counteracts the effects arising from the sideslip angle by means of an integral term, and finally proves the stability of global asymptotic path-tracking. Zheng et al. [32] proposed an error-constrained line-of-sight (ECLOS) guidance law with a nonlinear perturbation observer to estimate external disturbances and demonstrated the reliability of the proposed method through simulation experiments. Wan et al. [33] proposed a time-varying look-ahead distance LOS guidance law related to the USV speed and cross-track error and designed a reduced-dimensional state observer to estimate the time-varying sideslip angle online to improve the path-tracking accuracy. Li et al. [34] proposed an extended state observer (ESO)-based ILOS guidance law that simultaneously predicts the heading angle and estimates the flow velocity. Yu et al. [35] proposed a finite-time predictor-based LOS guidance law (FPLOS) that could obtain the sideslip angle using an error predictor in finite time. Although the addition of observers and predictors can predict the sideslip angle more accurately, it also increases the complexity of the control system and requires more computational resources. The method is currently in the simulation stage and cannot be used for practical experiments. Liu et al. [36] proposed an adaptive line-of-sight (ALOS) algorithm to obtain the desired heading angle and a more accurate model predictive control (MPC) method to predict the sideslip angle. However, as discussed in this study, the use of an MPC method in practical experiments requires the controller to be computationally powerful and necessitates the use of more powerful CPUs, which is not conducive to a small USV or the processing of microcontrollers.

As discussed above, the existing guidance laws are based on parameter optimization and prediction of the sideslip angle. They exposed the same faults as our previous version of the USV path-tracking system, such as excessive overshoot and slow convergence speed, which resulted in unaffordable errors in seashore bathymetric mapping. Therefore, an AFIDLOS method is proposed in this study. The proposed AFIDLOS method innovatively adds integral and derivative terms to the traditional LOS guidance law for predicting and counteracting the effects of sideslip angle. To obtain a high accuracy of look-ahead distance, the fuzzy control is used to adaptively adjust the convergence rate in the proposed AFIDLOS method, which is implemented on the microcontroller. Compared with the existing methods, the proposed AFIDLOS method optimizes the parameters and greatly reduces the computational complexity of the controller. This paper is organized as follows: The background of this research was introduced in Section 1. The principle of the proposed AFIDLOS method for USV path-tracking control is presented in Section 2. Validation through simulations and outdoor experiments is designed and conducted in Section 3. Finally, the conclusions are presented in Section 4.

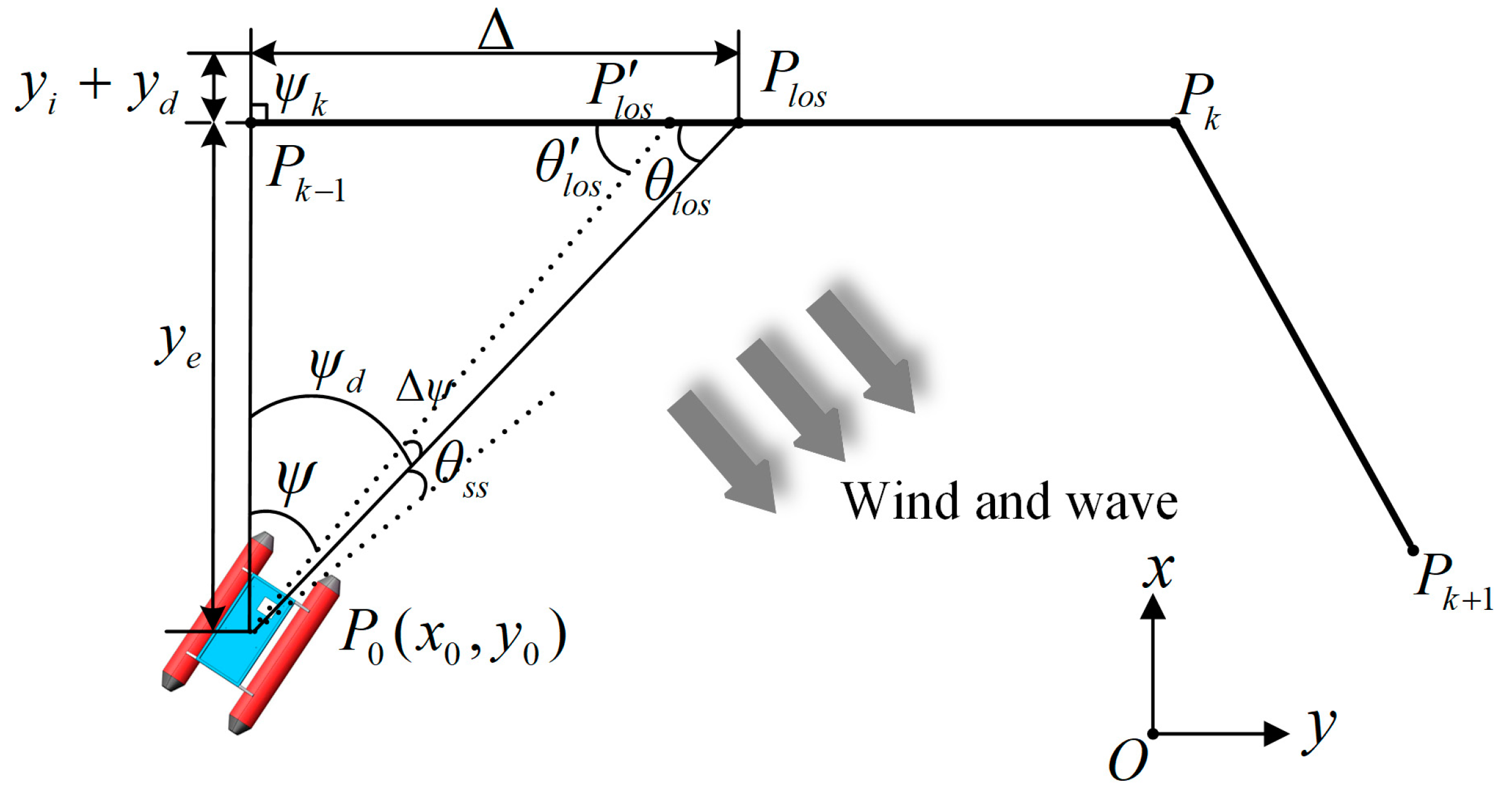
2. Development of AFIDLOS Method

2.1. Architecture of the Path-Tracking System

The architecture of the AFIDLOS method developed in this study for the USV path-tracking control system is depicted in Figure 1, which comprises the integral-derivative line-of-sight (IDLOS) method, fuzzy controller, and look-ahead distance computation. The IDLOS method is used to calculate the cross-track error $y_e$ and the change rate of the cross-track error ${\dot{y}}_e$ based on the coordinates, $X$ and $Y$, which are obtained from the GPS module. Based on the values of $y_e$ and ${\dot{y}}_e$, the fuzzy controller is used to calculate the convergence rate $\gamma$ and output it to the look-ahead distance calculator. Using $y_e$ and $\gamma$, the look-ahead distance computation is used to calculate the look-ahead distance $\Delta$. The IDLOS method is used to update the value of $\Delta$, estimate the sideslip angle, correct for the LOS angle, and then output the desired heading angle ${\psi }_d$. The control model of linear quadratic regulator (LQR) is used to control the difference of the heading angle $\Delta \psi$ and output control command $\Delta n$ based on $\Delta \psi$. The USV moves in terms of $\Delta n$, while sending coordinates, $X$ and $Y$, back to the AFIDLOS system for the next cycle.

2.2. Development of AFIDLOS Method

It is assumed that the USV is located at point $P_0$ with coordinates $\left(x_0,y_0\right)$ with respect to the local coordinate system, $O-x,y$, and the actual heading angle is $\psi$ (Figure 2). The USV is planned to move forward along the paths $P_{k-1}{P}_k$ and $P_k{P}_{k+1}$, which are designed with the desired heading angle ${\psi }_d$ in the direction of $P_0{P}_{los}$. However, the USV indeed derived from the planned path with a sideslip angle ${\theta }_{ss}$, owing to the distribution of factors such as sea wind, water flow direction, and sea waves.

Therefore, the basic concept of the IDLOS method proposed in this study involves minimizing the influence of the sideslip angle ${\theta }_{ss}$ and correcting the LOS angle ${\theta }_{los}$ to ${\theta }_{los}^{\prime }$ by adding the integral and derivative terms $y_i$ and $y_d$, respectively, that is,

$${\theta }_{los}^{\prime }=\arctan \left({\displaystyle \frac{y_e+y_i+y_d}{\Delta }}\right)$$

(1)

where ${\psi }_k$ represents the angle between the north and path $P_{k-1}{P}_k$; $y_e$ represents the cross-track error, which is defined as the vertical distance between the position of the USV and planned path; and $\Delta$ represents the look-ahead distance, which is defined as the distance between the vertical point and point $P_{los}$.

The integral term and derivative terms $y_i$, and $y_d$, respectively, are expressed as

$$y_i=k_i{\displaystyle {\int }_{t_1}^{t_2}{y}_{e}dt}$$

(2)

$$y_d=k_d{\dot{y}}_e$$

(3)

where $k_d$ is the constant derivative coefficient; $t_1$ and $t_2$ are the integral times; and $k_i$ is the adaptive factor calculated as

$$k_i=1-e^{-\lambda \left|y_e\right|}$$

(4)

where $\lambda$ is the dynamically adjustable parameter.

Observing Equation (1) and Figure 2, the added integral and derivative terms ($y_i+y_d$) change the LOS angle of the USV from ${\theta }_{los}$ to the corrected angle ${\theta }_{los}^{\prime }$; thus, the USV will probably track along the direction $P_0{P}_{los}^{\prime }$ to counteract the effect generated by the sideslip angle ${\theta }_{ss}$.

The traditional fixed value of look-ahead distance in Equation (1) affects the LOS angle, which in turn affects the path-tracking accuracy [30]. To solve the problem, an adaptive LOS method is developed using a time-vary equation

$$\Delta =\left({\Delta }_{\max }-{\Delta }_{\min }\right)e^{-\gamma \left|y_e\right|}+{\Delta }_{\min }$$

(5)

where ${\Delta }_{\max }$ and ${\Delta }_{\min }$ are the maximum and minimum look-ahead distances, respectively, which are usually two to four times the length of the USV [28], and $\gamma$ is the convergence rate.

A fixed value of the convergence rate in Equation (5) does not satisfy the requirement of the USV to reduce the cross-track error quickly or smoothly if the USV is in a position farther or closer to the planned path [28]. Thus, the AFIDLOS method was proposed to implement the adaptivity of the convergence rate, which is designed using the following steps:

First, if the value of the cross-track error exceeded 1.5 times the width of the USV, it was considered to be too far from the planned path; therefore, the domain of the cross-track error $y_e$ was set within $[-120\mathrm{cm},120\mathrm{cm}]$. Because the velocity of a USV is usually approximately 0.6 m/s while collecting 3D bathymetric point cloud data, the domain of the change rate of the cross-track error ${\dot{y}}_e$ was set as $[-60\mathrm{cm}/\mathrm{s},60\mathrm{cm}/\mathrm{s}]$. To represent the exact value of the domain by a fuzzy value, seven fuzzy subsets of $y_e$ and ${\dot{y}}_e$ were defined as follows:

$$\left[\begin{array}{ccccccc}NB& NM& NS& O& PS& PM& PB\end{array}\right]$$

(6)

where $NB$, $NM$ and $NS$ represent negative big, medium and small fuzzy values, respectively; $O$ represents zero; $PS$, $PM$ and $PB$ represent positive small, medium and big fuzzy values, respectively. The magnitude of each subsets represents the degree of magnitude of the value of $y_e$ and ${\dot{y}}_e$.

If the USV travels along the planned path, then the look-ahead distance in Equation (5) should take the maximum value ${\Delta }_{\max }$, that is, the convergence rate should be zero. If the USV is away from the planned path, then the look-ahead distance in Equation (5) should take the value closest to ${\Delta }_{\min }$, that is, the convergence rate should be one. Based on the above assumptions, the domain of the output $\gamma$ should be within $[0,1]$. Therefore, the five fuzzy subsets of $\gamma$ are defined as follows:

$$\left[\begin{array}{ccccc}VS& S& M& B& VB\end{array}\right]$$

(7)

where $VS$, $S$ and $M$ represent very small, small and medium fuzzy values, respectively; and $B$ and $VB$ represent big and very big fuzzy values, respectively. The magnitude of each subset represents the degree of magnitude of the value of $\gamma$.

Second, to achieve fuzzification of the domains, it is necessary to determine the degree of membership of the domains in Equations (6) and (7). Thus, we divided the range of values of $y_e$, ${\dot{y}}_e$ and $\gamma$ into $[-120\mathrm{cm},120\mathrm{cm}]$, $[-60\mathrm{cm}/\mathrm{s},60\mathrm{cm}/\mathrm{s}]$ and $[0,1]$, and used the triangular membership function as a membership function of the fuzzy subset for the degree of membership of the values of $y_e$, ${\dot{y}}_e$ and $\gamma$. The results are shown in Figure 3.

In Figure 3, each of the values in the domain can be represented by the degree of membership function of the fuzzy subset, which implements the process of fuzzification of the domains into fuzzy subsets. For example, if the value of $y_e$ is zero, the degree of membership is zero in all fuzzy subsets, except for the fuzzy subset $O$, where the degree of membership is one. This is because the value of zero is the closest approximation of the fuzzy subset $O$, and it is not within the range of the values of the other fuzzy subsets.

With the above steps, the next step is fuzzy reasoning for the fuzzy subsets. The basic idea is that if the path of the USV is far from the planned path, the cross-track error is probably large, and the convergence rate should be increased; whereas, if the path of the USV is close to the planned path, the cross-track error is probably small, and the convergence rate should be decreased. Based on this idea, an array of fuzzy control rules was designed, as presented in

Table 1. Array of fuzzy control rules.

$\mathit{\gamma }$		${\mathit{y}}_{\mathit{e}}$
		NB	NM	NS	O	PS	PM	PB
${\dot{y}}_e$	NB	VB	B	B	M	B	VB	VB
	NM	VB	B	B	M	M	B	VB
	NS	B	M	S	VS	S	M	B
	O	M	M	S	VS	S	M	M
	PS	B	M	S	VS	S	M	B
	PM	VB	B	M	S	M	B	VB
	PB	VB	VB	B	M	B	VB	VB

.

Analyzing Table 1, if the values of $y_e$ and ${\dot{y}}_e$ are large (PB), the USV must be adjusted to the planned path quickly; thus, $\gamma$ obtains the maximum value (VB). If the values of $y_e$ and ${\dot{y}}_e$ are very small (O), the USV must converge to the planned path smoothly; thus, the $\gamma$ obtains the minimum value (VS). The above analysis shows that the value the fuzzy subset of the $\gamma$ takes is determined by the fuzzy subset of $y_e$ and ${\dot{y}}_e$, indicating the fuzzy relationship among the three.

To defuzzy the fuzzy relationships between $y_e$, ${\dot{y}}_e$, and $\gamma$ in Table 1, it is necessary to convert the fuzzy relationships into exact numerical relationships between the domains. To this end, this paper uses the centroid method as the defuzzification method, which is based on selecting the center of gravity of the area enclosed by the fuzzy membership function and the horizontal coordinates as the exact value of the output [30]. With the Fuzzy toolbox of MATLAB R2021b software, the fuzzy input–output 3D surface with convergence rate can be obtained and is shown in Figure 4.

As shown in Figure 4, the fuzzy subsets of the cross-track error, change rate of the cross-track error, and convergence rate were divided into $[-120\mathrm{cm},120\mathrm{cm}]$, $[-60\mathrm{cm}/\mathrm{s},60\mathrm{cm}/\mathrm{s}]$, and $[0,1]$. The value of the convergence rate is shown in Figure 4, according to the value of the cross-track error and the change rate of the cross-track error; thus, the USV can obtain a more reasonable value of the look-ahead distance during the path-tracking process.

Finally, combining Equations (1) and (5), the AFIDLOS method is established using

$${\psi }_d={\psi }_k-\arctan \left({\displaystyle \frac{y_e+(1-e^{-\lambda \left|y_e\right|}){\displaystyle {\int }_{t_1}^{t_2}{y}_{e}dt}+k_d{\dot{y}}_e}{\left({\Delta }_{\max }-{\Delta }_{\min }\right)e^{-\gamma \left|y_e\right|}+{\Delta }_{\min }}}\right)$$

(8)

where the symbols are the same as above.

As compared with the traditional LOS guidance law, Equation (8), which is called “AFIDLOS”, adds an integral term, a derivative term and adaptive adjustment of the look-ahead distance.

2.3. Control Model of LQR

After the AFIDLOS method was developed, the next step was to develop a control model for the USV operation. From Figure 1, it can be understood that the input to the control model of the LQR was indeed the error of the heading angle $\Delta \psi$, which can be expressed as [37]

$$\Delta \psi ={\psi }_d-\psi$$

(9)

Derivation of Equation (9), we have

$$\Delta \dot{\psi }=-r$$

(10)

where $r$ is the angular velocity of the USV, whose derivation can be obtained from [38]

$$\dot{r}=-{\displaystyle \frac{d_{33}}{m_{33}}}r+{\displaystyle \frac{1}{m_{33}}}{\tau }_r$$

(11)

where $m_{33}$ is the mass coefficient, $d_{33}$ is the damping coefficient, and ${\tau }_r$ represents the rotational moment of the USV, which can be expressed as

$${\tau }_r={\displaystyle \frac{1}{2}}\left(F_l-F_r\right)d$$

(12)

where $F_l$ and $F_r$ represent the left and right thrusters of the USV, respectively, and $d$ represents the distance between the left and right thrusters.

Because the thrust of the USV thruster cannot be measured directly, it is controlled by varying the time of the high-level pulse width modulation (PWM) signal output from the STM32 chip. Therefore, it is necessary to establish a relationship between the control command and thrust of USV thrusters. Thus, it is assumed that the control command is proportional to the thrust by

$$\{\begin{array}{c}{F}_l=k\left(n_0+\Delta n\right)\\ F_r=k\left(n_0-\Delta n\right)\end{array}$$

(13)

where $k$ denotes the proportionality coefficient; $n_0$ is the initial control command; and $\Delta n$ is the variable control command.

By substituting Equation (13) into Equation (12), we obtain

$${\tau }_r=kd\Delta n$$

(14)

By substituting Equation (14) into Equation (11), the resulting equation for the control model of the USV is expressed as

$$\{\begin{array}{l}\dot{r}=-{\displaystyle \frac{d_{33}}{m_{33}}}r+{\displaystyle \frac{kd}{m_{33}}}\Delta n\\ \Delta \dot{\psi }=-r\end{array}$$

(15)

We rewrite Equation (15) in a state–space form

$$\left[\begin{array}{c}\dot{r}\\ \Delta \dot{\psi }\end{array}\right]=\left[\begin{array}{cc}-{\displaystyle \frac{d_{33}}{m_{33}}}& 0\\ -1& 0\end{array}\right]\left[\begin{array}{c}r\\ \Delta \psi \end{array}\right]+\left[\begin{array}{c}{\displaystyle \frac{kd}{m_{33}}}\\ 0\end{array}\right]\Delta n$$

(16)

where $x={\left[\begin{array}{cc}r& \Delta \psi \end{array}\right]}^T$ is the state matrix. Simplifying Equation (16) yields

$$\dot{x}=Ax+B\Delta n$$

(17)

where $\Delta n$ can be expressed by

$$\Delta n=-Kx$$

(18)

where $K={\left[\begin{array}{cc}{K}_1& K_2\end{array}\right]}^T$ is the state feedback matrix. To achieve optimal control, $K$ is calculated as follows [39]

$$K=R^{-1}{B}^{T}P$$

(19)

where $P$ is a positive semi-definite symmetric matrix, that satisfies the following Riccati equation [40]:

$$PA+A^{T}P+Q-PB{R}^{-1}{B}^{T}P=0$$

(20)

where $Q$ is a positive semidefinite matrix and $R$ is a positive definite symmetric array. The values of the $Q$ and $R$ are generally chosen by experience [41].

After solving for $P$ through Equation (20), the value of $K$ can also be given through Equation (19). Substituting the value of $K$ into Equation (18) yields the final expression of the control command by

$$\Delta n=-K_{1}r-K_2\Delta \psi$$

(21)

Using Equations (16) and (21), the control command can be obtained by determining the values of $K_1$ and $K_2$. The control model of the USV and the control law of the LQR for the control command were established, which provided the model and theoretical support for the experiments conducted below.

3. Experiments and Discussion

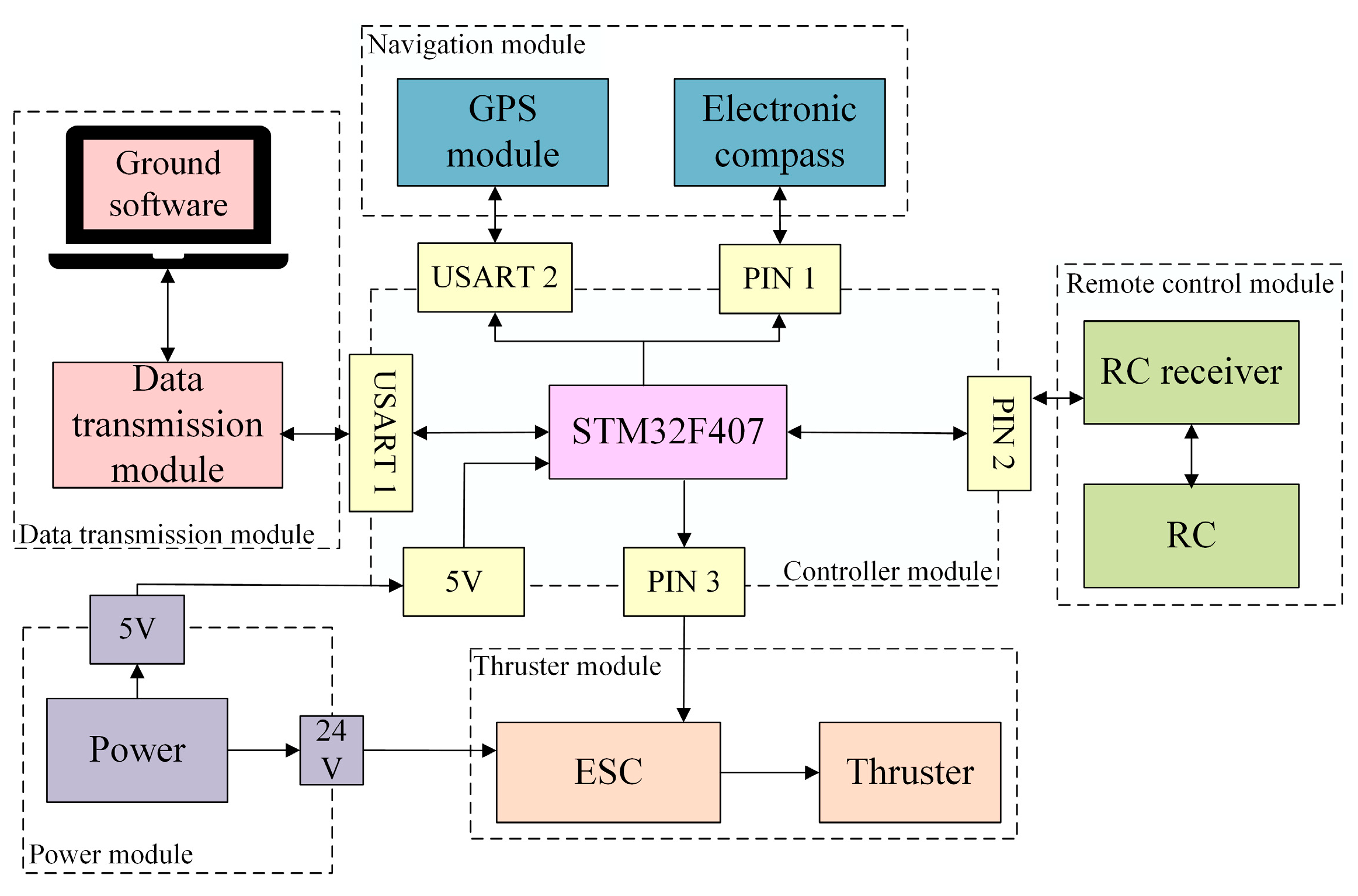
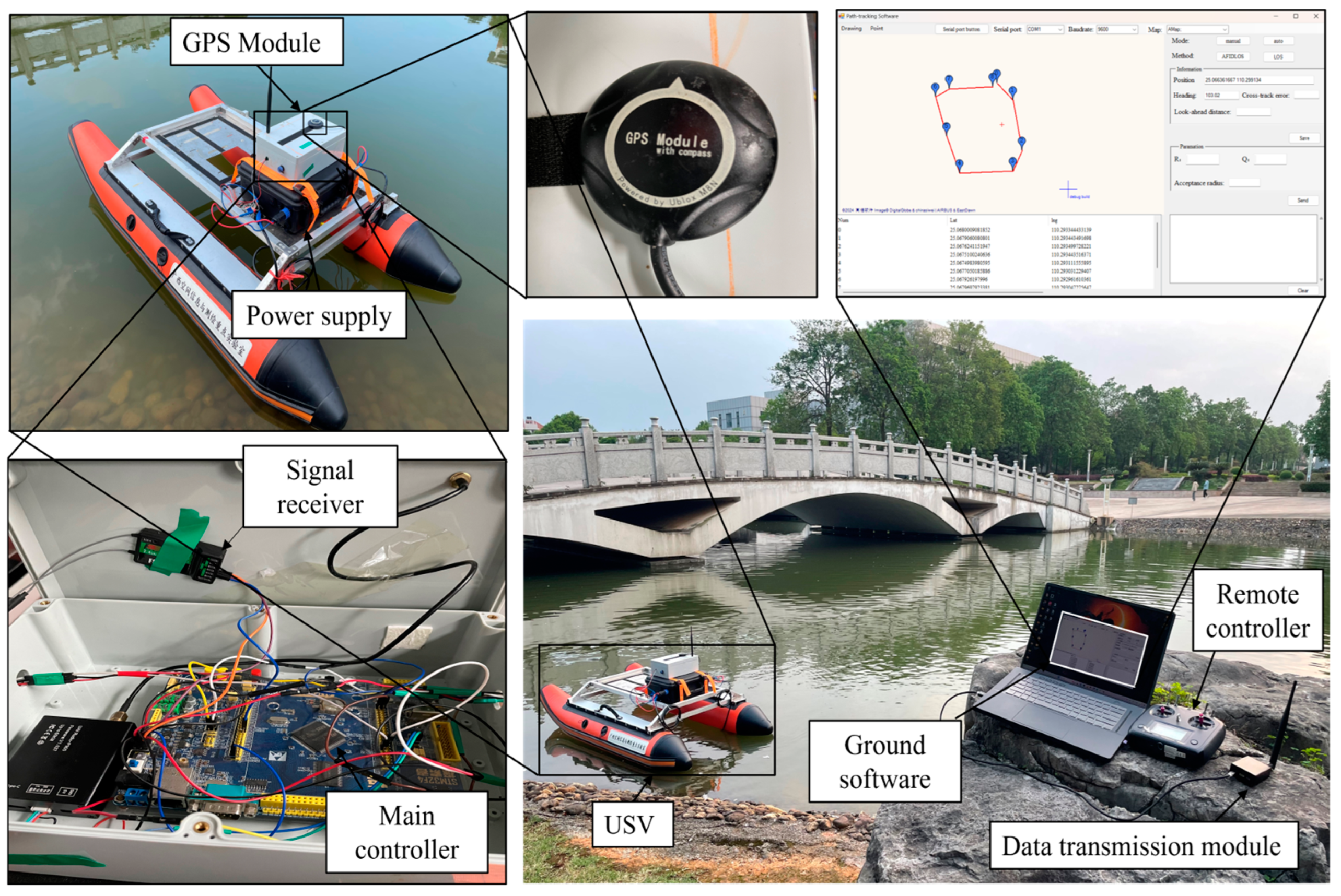
3.1. Implementation Using STM32 Microcontroller

The hardware framework for the proposed AFIDLOS method is shown in Figure 5, and mainly consists of the controller module (STM32 (ST Company, Geneva, Italy)), navigation module, thruster module, data transmission module, electronic speed controller (ESC), power module, remote control (RC) module and computer (equipped with ground software).

This paper uses the NEO-M8N GPS module (U-Blox Company, Thalwil, Switzerland), whose positioning accuracy is 2.5 m; the P900 data transmission module (Microhard Company, Calgary, Canada), which has a maximum transmission range of 60 km; and the T80-80 thruster (Cehai Technology Company, Shenzhen, China), which has a rating power of 520 W and can provide a maximum thrust of 80 N. The Fly Monster-120 ESC module (Flycolor Company, Shenzhen, China) is used to control the speed of the thruster. It can withstand a maximum current of 90 A and can meet the control requirements of the thruster. The FS-i6S RC (Flysky Company, Shenzhen, China), which uses 2.4 G wireless frequency with eight channels and has a maximum control distance of 1.5 km is used. Considering the control requirements of each peripheral device mentioned above and the high integration of the USV, the STM32 microcontroller (ST Company, Geneva, Italy) is used, whose internal clock is up to 168 MHz. It has six universal synchronous/asynchronous receiver transmitters (USARTs), 144 pins and 10 general-purpose timers, which can meet the design requirements of the USV path-tracking system (see Figure 6).

The proposed AFIDLOS method is implemented in STM32 through software programming as shown in Figure 7, which mainly consists of the navigation function, path function, calculation function, adaptive fuzzy (AF) LOS function, IDLOS function, LQR function and PWM function. The task of each function is programmed as follows.

• Navigation function: when USART2 is interrupted, the latitude, longitude and heading angle are extracted from the navigation module and output.
• Path function: based on the paths (input from data transmission module) and USV’s position data (latitude, longitude and heading angle input from navigation module), the planned path $P_{k-1}{P}_k$ is output (when the USV enters the “circle of acceptance”, the planned path is switched).
• Calculation function: the cross-track error $y_e$ and the change rate of the cross-track error ${\dot{y}}_e$ is calculated based on the USV position and the planned path.
• AFLOS function: based on $y_e$ and ${\dot{y}}_e$, the look-ahead distance $\Delta$ is obtained by adaptive fuzzy LOS method (see Equation (5) and Figure 4).
• IDLOS function: based on $\Delta$, the desired heading angle ${\psi }_d$ is obtained by the IDLOS method (see Equation (8)). Subtracting the current heading angle $\psi$ from ${\psi }_d$, the error of the heading angle $\Delta \psi$ is output (see Equation (9)).
• LQR function: based on $\Delta \psi$, the variable control command $\Delta n$ is obtained and output (see Equations (10) and (21)).
• PWM function: based on $\Delta n$ and initial control command $n_0$ (see Equation (13)), the pulse width modulation (PWM) waves with pulse width of $n_0+\Delta n$ and $n_0+\Delta n$ are output to the thruster module.

3.2. Calculation of Initial Values for the Control Model of USV

Before conducting the experimental verification of the proposed method, the initial values of Equation (16) must first be determined. If the USV carries dual thrusters with thrust $F$, range of $\left[-80N,80N\right]$, and control command $n$, range of $\left[-500,500\right]$, we can obtain the proportionality between the two using Equation (13) as $F=0.16N$ and $k=0.16$. The mass coefficient can be calculated as follows [42]

$$m_{33}\approx {\displaystyle \frac{m\left(L^2+W^2\right)+\frac{1}{2}\left(0.1m{d}^2+\rho \pi {D_P}^2{L}^3\right)}{12}}$$

(22)

where $m$ represents the weight of the USV, and has a value of 30 kg; $L$ is the length of the USV, and has a value of 1.7 m; $W$ is the width of the USV, and has a value of 0.82 m; $\rho$ is the density of water; $d$ has a value of 0.7 m; and $D_P$ is the depth of draft, and has a value of 0.15 m.

By substituting these parameters into Equation (22) we obtain $m_{33}=23.44$. In addition, to obtain the damping coefficient $d_{33}$, a USV rotation experiment was conducted, which mainly involved uniform circular motion of the USV. If the USV is allowed to perform uniform circular motion, the angular acceleration $\dot{r}$ is taken as zero. Thereby, Equation (16) can be rewritten as

$$r={\displaystyle \frac{0.112}{d_{33}}}\Delta n$$

(23)

To establish the relationship between the variable control command $\Delta n$ and angular velocity $r$, the angular velocity under different variable control commands was tested in the rotation experiment, and the data are listed in

Table 2. Data of the USV’s rotation experiment.

Parameters	Values
$\Delta n$	50	100	150	200	250	300	350	400	450
$r$	9.10	15.14	23.19	29.30	35.40	43.95	48.83	53.57	57.56
$\Delta n$	−50	−100	−150	−200	−250	−300	−350	−400	−450
$r$	−10.31	−16.10	−25.20	−30.52	−37.23	−44.56	−50.05	−54.80	−58.80

.

As shown in Table 2, the larger the variable control command, the larger the angular velocity of the USV. By linear fitting of all the data in Table 2, we can obtain the proportionality between the two as

$$r=0.157\Delta n$$

(24)

Substituting Equation (24) into Equation (23) yields $d_{33}=0.71$.

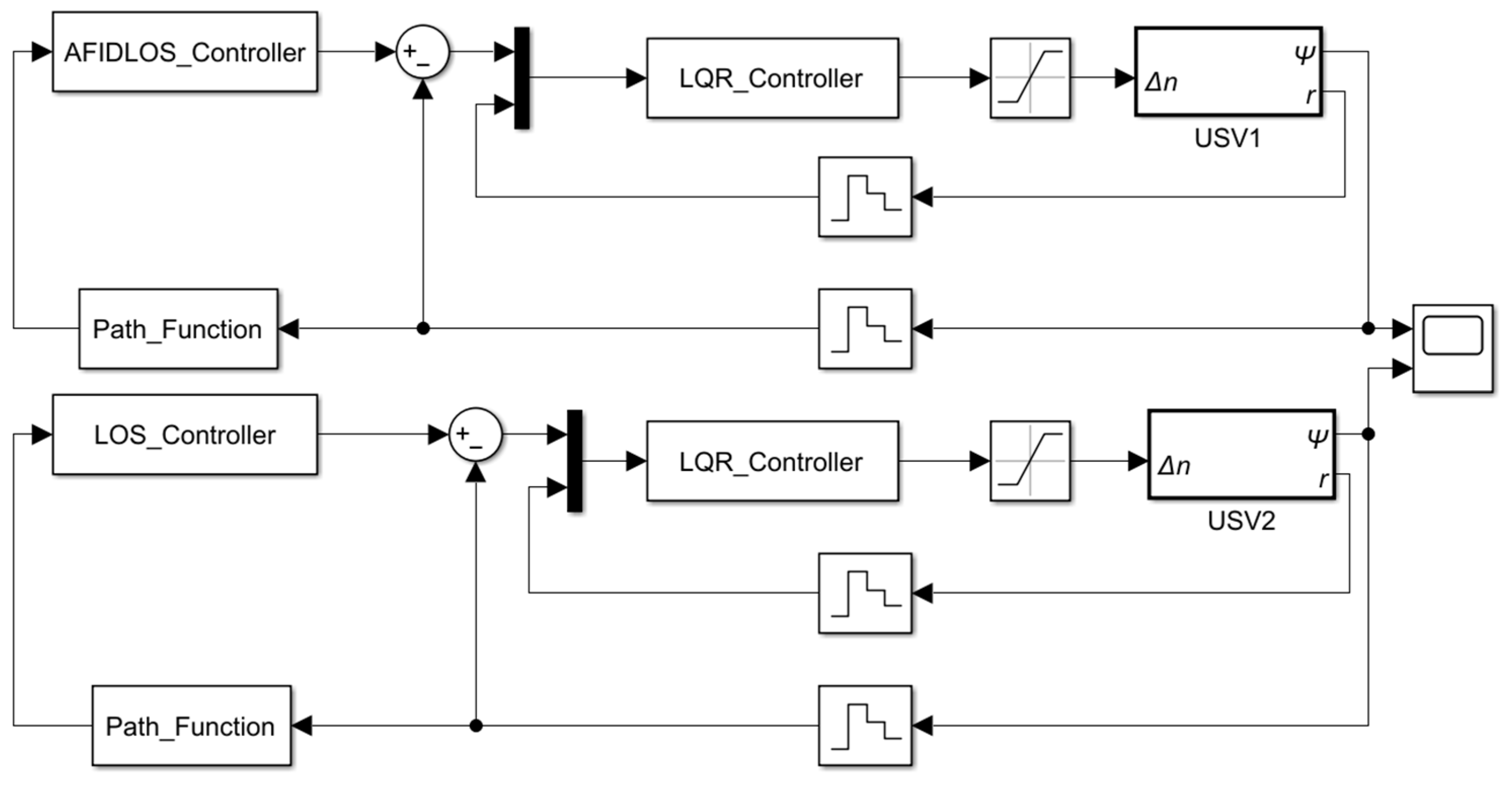
3.3. Verifications through Simulation Experiments

The proposed AFIDLOS method was verified via a simulation experiment. An “M-shape” path was planned with five points, noted A, B, C, D and E, whose coordinates were $\mathrm{A}\left(6,5\right),\mathrm{B}(26,20),\mathrm{C}(6,35),\mathrm{D}(26,50)$ and $\mathrm{E}(6,65)$ (Figure 8). The initial position of the USV was located at $\mathrm{S}(5,5)$, and the first planned waypoint was located at point $\mathrm{A}(6.5)$. The control parameters of the proposed AFIDLOS system were obtained as per the following steps:

• Setting the initial acceptance radius as 0.5 m;
• Substituting $Q=diag\left[\begin{array}{cc}1& 100\end{array}\right],R=0.01$ into Equations (19) and (20) to calculate $K=\left[\begin{array}{cc}76.64& -31.63\end{array}\right]$;
• Setting the constant derivative coefficient $k_d$ as 3.8.

Using the parameters calculated above and LQR control model in Equation (16) into the simulation model (Figure 9), the heading control performance of the AFIDLOS method and LOS guidance law can be observed using the oscilloscope in the simulation model (Figure 10). A comparison of the simulation data for the AFIDLOS method and LOS guidance law at the four turning points is presented in

Table 3. Comparison of the simulation data for AFIDLOS method and LOS guidance law.

Point	Guidance Law	Overshoot	Improvement Rate of Overshoot	Settling Time	Improvement Rate of Settling Time
A	AFIDLOS	3.90%	89.7%	4.84 s	55.19%
	LOS	37.80%		10.80 s
B	AFIDLOS	7.90%	68.90%	5.50 s	54.17%
	LOS	25.40%		12.00 s
C	AFIDLOS	2.70%	89.58%	5.80 s	59.30%
	LOS	25.90%		14.25 s
D	AFIDLOS	7.40%	71.21%	5.30 s	56.20%
	LOS	25.70%		12.10 s
Averages			79.85%		55.32%

.

As shown in Figure 10 and Table 3, the AFIDLOS method can reduce the amount of overshoot by 79.85% and shorten the settling time by 55.32% compared with the LOS guidance law for the entire simulation path. The USV has a higher improvement rate of overshoot when tracking turning points A and C and a lower improvement rate of overshoot at turning points B and D, indicating that the AFIDLOS method has a smaller overshoot and faster convergence speed when tracking smaller heading angles.

3.4. Verifications through Outdoor Experiments

Outdoor experiments were conducted to verify the reliability of the proposed AFIDLOS method for real scenarios. The initial parameters of the USV were set with the radius of the acceptance circle three times the width, i.e., 2.4 m, and the initial control command of the thruster $n_0=100$.

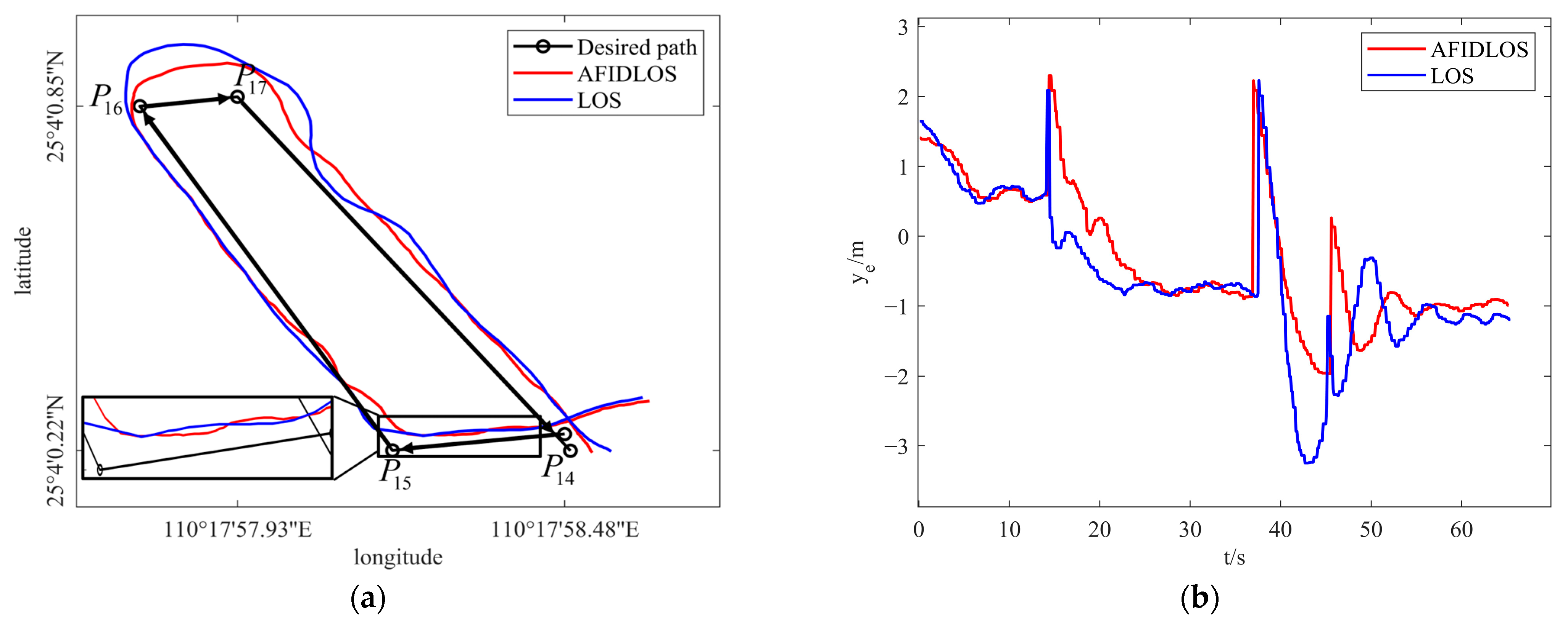
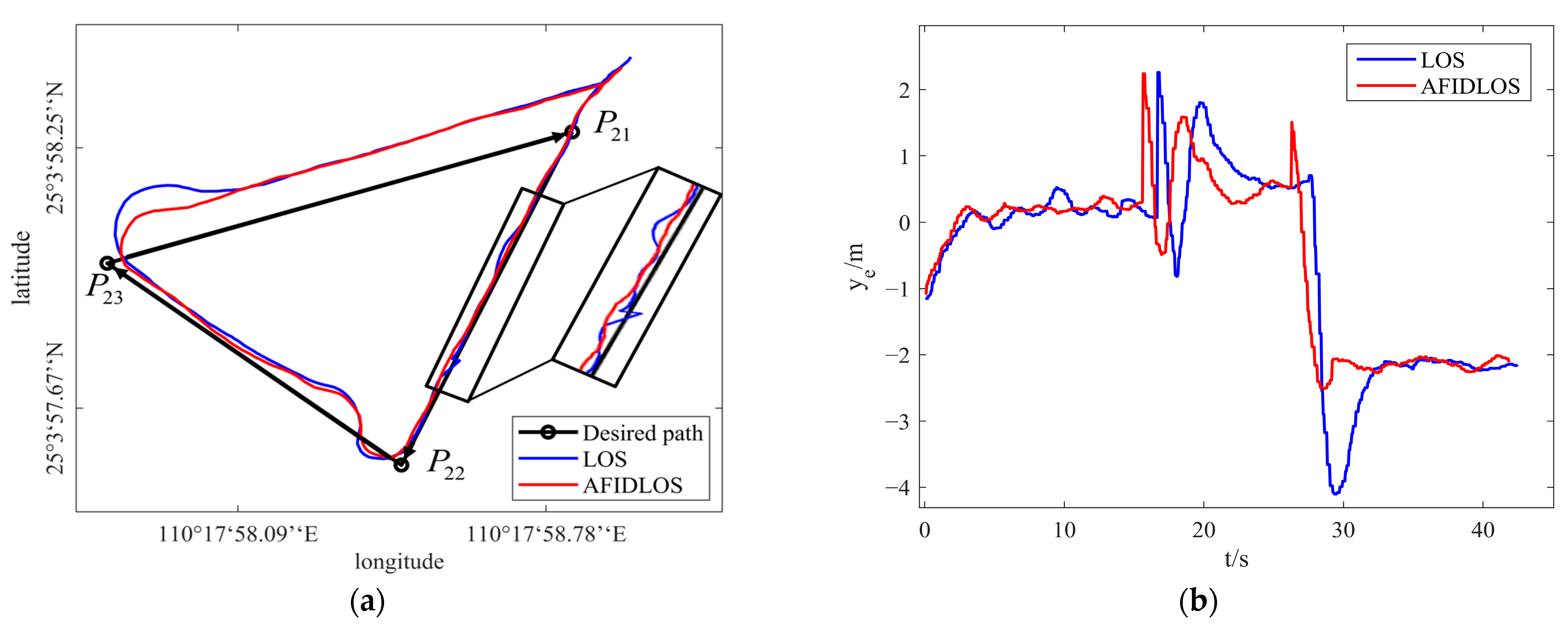
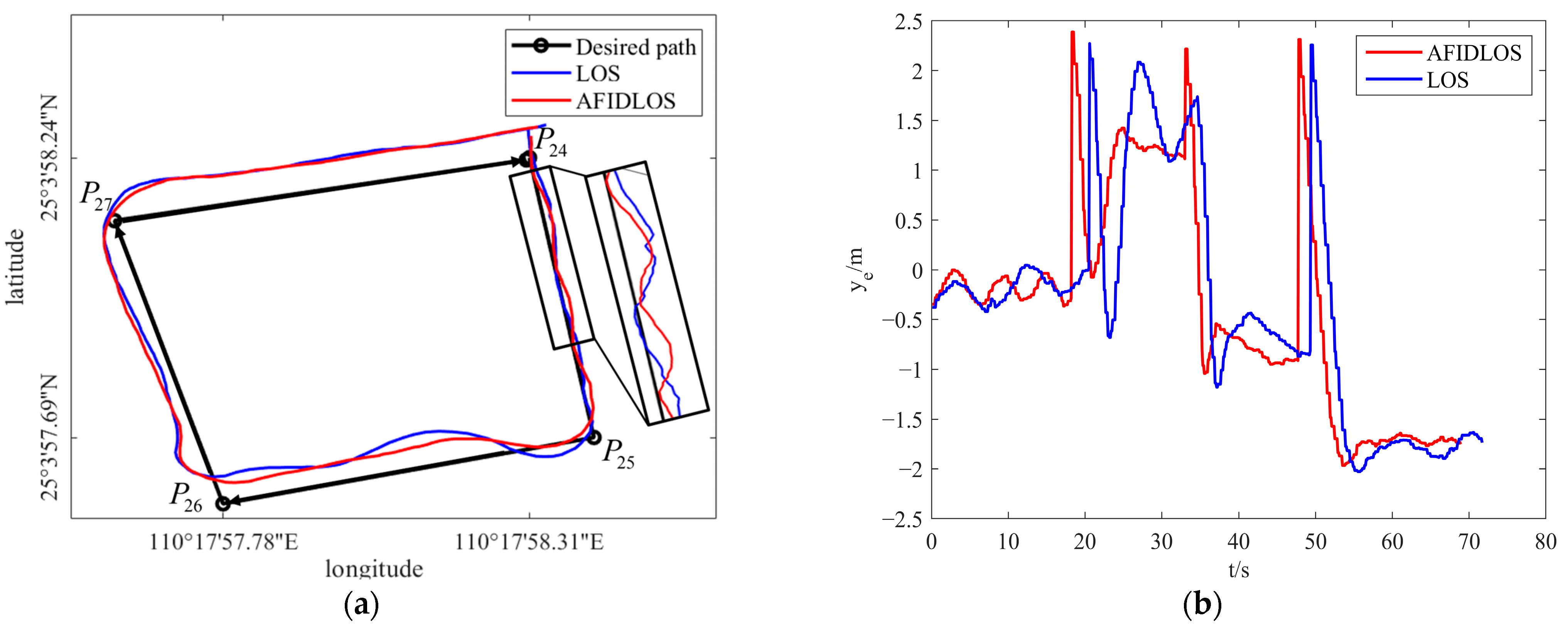
3.4.1. Verification in Artificial Lake

The experiment was conducted in a small artificial lake approximately 150 m long and 30 m wide (Figure 11). The experimental device was set up using a main controller (STM32F407 (ST Company, Geneva, Italy)), data transmission module, power supply, GPS module and other equipment installed on the hull of the USV. A computer equipped with software was used on the ground side. The ground software sends control commands to the USV through the data transmission module and monitors the status of the USV movement in real time, while the remote control is mainly responsible for the USV movement. To reduce the computational effort required by the USV’s main controller (STM32), the convergence rate during path-tracking was calculated using the ground software and sent to the USV.

The experiment was conducted as follows:

• Equip the modules of the USV, turn on the power switch of USV, and move USV to the starting point by remote control.
• Open software and connect the serial port to communicate with and receive data from the USV.
• Switch the control algorithm to LOS guidance law through the software and send the waypoints to the controller of the USV.
• Trace the triangular and quadrilateral paths separately, and save the data sent during the tracing process of the USV.
• Switch the control algorithm to AFIDLOS method through the software, and remotely control the USV to the starting point.
• Repeat Step 4.
• End the experiment. The results for trajectory comparison analysis are depicted in Figure 12 and

  Table 4. Data comparison of triangle path in an artificial lake.

  Path	Guidance Law	Average Cross-Track Error (Absolute Value)	Improvement Rate of Cross-Track Error
  $P_{11}{P}_{12}$	LOS	0.76 m	22.37%
  	AFIDLOS	0.59 m
  $P_{12}{P}_{13}$	LOS	0.71 m	9.86%
  	AFIDLOS	0.64 m
  $P_{13}{P}_{11}$	LOS	1.36 m	5.88%
  	AFIDLOS	1.28 m

  .

From Figure 12 and Table 4, the AFIDLOS method can reduce the cross-track errors by 22.37%, 9.86% and 5.88%, respectively, compared with the LOS guidance law. This is because the AFIDLOS method can adjust the look-ahead distance according to the cross-track error, which makes the cross-track error in a straight path $P_{11}{P}_{12}$ smaller than that in the LOS guidance law, resulting in a higher improvement rate. When tracking the path $P_{13}{P}_{14}$, the LOS guidance law has a large cross-track error of up to 2.50 m, whereas the AFIDLOS method has a maximum cross-track error of only 2.15 m and a smaller amount of overshoot during path-tracking. However, both produce similar average cross-track errors after convergence to the planned path, resulting in a lower improvement rate. These results demonstrate that the AFIDLOS method has a faster convergence speed and smaller overshoot.

Figure 13 shows the experimental results for the quadrilateral path in an artificial lake, and a comparison analysis is presented in

Table 5. Data comparison of quadrilateral path in an artificial lake.

Path	Guidance Law	Average Cross-Track Error (Absolute Value)	Improvement Rate of Cross-Track Error
$P_{14}{P}_{15}$	LOS	0.83 m	1.20%
	AFIDLOS	0.82 m
$P_{15}{P}_{16}$	LOS	0.68 m	4.41%
	AFIDLOS	0.71 m
$P_{16}{P}_{17}$	LOS	2.08 m	36.54%
	AFIDLOS	1.32 m
$P_{17}{P}_{14}$	LOS	1.21 m	15.70%
	AFIDLOS	1.02 m

.

From Figure 13 and Table 5, the AFIDLOS method can reduce the cross-track errors by 1.20%, 4.41%, 36.54%, and 15.70%, respectively, compared with the LOS guidance law. This is because when the USV tracks a straight path $P_{14}{P}_{15}$, its path distance is shorter. Thus, the path-tracking performance is similar for both guidance laws, resulting in a lower improvement rate. When the USV tracks the path $P_{16}{P}_{17}$, the LOS guidance law has a large cross-track error, which is up to 3.3 m, while AFIDLOS method has a maximum cross-track error of only 1.9 m and a smaller amount of overshoot during path-tracking, resulting in a higher improvement rate. These results demonstrate that the AFIDLOS method can converge faster to the planned path than the traditional guidance law because a smaller amount of overshoot during path-tracking implies a faster convergence speed.

3.4.2. Verification in a Natural Lake

A second experiment to verify the AFIDLOS method was conducted in the campus’s natural lake (Figure 14).

With similar operations conducted for the experiments, Figure 15 shows the experimental results for the triangular path in the natural lake, and the corresponding comparison analysis is presented in

Table 6. Data comparison of triangle path in natural lake.

Path	Guidance Law	Average Cross-Track Error (Absolute Value)	Improvement Rate of Cross-Track Error
$P_{21}{P}_{22}$	LOS	0.24 m	4.17%
	AFIDLOS	0.23 m
$P_{22}{P}_{23}$	LOS	0.84 m	10.71%
	AFIDLOS	0.75 m
$P_{23}{P}_{21}$	LOS	2.34 m	12.82%
	AFIDLOS	2.04 m

.

From Figure 15 and Table 6, the AFIDLOS method can reduce the cross-track errors by 4.17%, 15.48%, and 12.82%, respectively, compared with the LOS guidance law. This is because the tracking performance of the AFIDLOS method is more stable than that of the LOS guidance law when the USV tracks a straight path $P_{21}{P}_{22}$. However, both guidance laws produce similar cross-track errors, resulting in a lower improvement rate. When the USV tracks the path $P_{23}{P}_{21}$, the LOS guidance law has a large cross-track error, which is up to 4.1 m, while the AFIDLOS method has a maximum cross-track error of only 2.5 m and a smaller amount of overshoot during path-tracking, resulting in a higher improvement rate. These results demonstrate that the AFIDLOS method can converge faster to the planned path than the traditional guidance law because a smaller amount of overshoot during path-tracking implies a faster convergence speed.

Figure 16 shows the experimental results for the quadrilateral path of the natural lake, and the corresponding comparison analysis is presented in

Table 7. Data comparison of quadrilateral path in a natural lake.

Path	Guidance Law	Average Cross-Track Error (Absolute Value)	Reduction of Cross-Track Error
$P_{24}{P}_{25}$	LOS	0.18 m	5.56%
	AFIDLOS	0.17 m
$P_{25}{P}_{26}$	LOS	1.30 m	17.69%
	AFIDLOS	1.07 m
$P_{26}{P}_{27}$	LOS	0.82 m	3.66%
	AFIDLOS	0.85 m
$P_{27}{P}_{24}$	LOS	1.65 m	3.64%
	AFIDLOS	1.59 m

.

From Figure 16 and Table 7, the AFIDLOS method can reduce the cross-track errors by 5.56%, 17.69%, 3.66% and 3.64% compared with the LOS guidance law. This is because when the USV tracks the path $P_{25}{P}_{26}$, the LOS guidance law has a large cross-track error, which is up to 2.1 m, while the AFIDLOS method has a maximum cross-track error of only 1.3 m and a smaller amount of overshoot during path-tracking, resulting in a higher improvement rate. The tracking performance of the AFIDLOS method is more stable than that of the LOS guidance law when the USV tracks a straight path $P_{26}{P}_{27}$. However, both guidance laws produce similar cross-track errors, resulting in a lower improvement rate. These results demonstrate that the AFIDLOS method can converge faster to the planned path than the traditional guidance law because a smaller amount of overshoot during path-tracking implies a faster convergence speed.

3.4.3. Verification in the Beibu Gulf

To further verify the applicability of the AFIDLOS method proposed in this study, an experiment was conducted in the Beibu Gulf in Beihai City, Guangxi Province. To satisfy the requirements of the research team, a bathymetric LiDAR, POS system, controller, and other equipment were installed on the hull of the USV, as shown in Figure 17.

Figure 18 shows the experimental results for the quadrilateral path in the Beibu Gulf. The experimental data are listed in

Table 8. Data comparison of quadrilateral path in the Beibu Gulf.

Path	Guidance Law	Average Cross-Track Error (Absolute Value)	Reduction of Cross-Track Error
$P_{31}{P}_{32}$	LOS	1.02 m	16.67%
	AFIDLOS	0.85 m
$P_{32}{P}_{33}$	LOS	0.60 m	1.67%
	AFIDLOS	0.59 m
$P_{33}{P}_{34}$	LOS	0.57 m	3.51%
	AFIDLOS	0.55 m
$P_{34}{P}_{31}$	LOS	1.07 m	19.63%
	AFIDLOS	0.86 m

.

From Figure 18 and Table 8, the AFIDLOS method can reduce the cross-track errors by 16.67%, 1.67%, 3.51% and 19.63% compared with the LOS guidance law. This is because when the USV tracks a straight path $P_{32}{P}_{33}$, there are small oscillations in both guidance laws; however, the AFIDLOS method produces a slightly smaller cross-track error than the LOS guidance law, resulting in a lower improvement rate. When the USV tracks the path $P_{34}{P}_{31}$, the LOS guidance law has a large cross-track error, which is up to 3.6 m, while the AFIDLOS method has a maximum cross-track error of only 1.4 m and a smaller amount of overshoot during path-tracking, resulting in a higher improvement rate. These results demonstrate that the AFIDLOS method can converge faster to the planned path than the traditional guidance law because a smaller amount of overshoot during path-tracking implies a faster convergence speed.

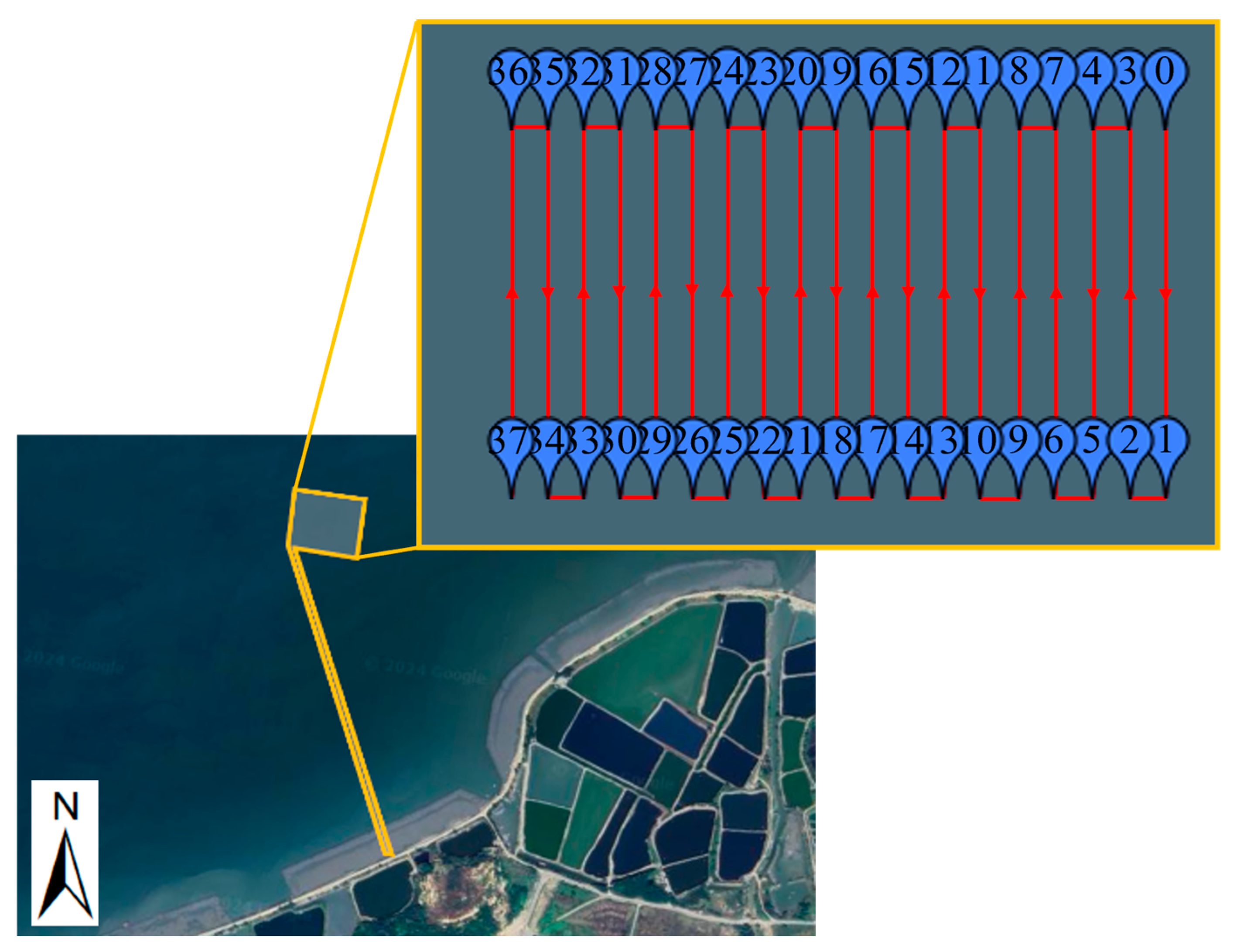
3.4.4. Verification through Multi-Strip Tracking in the Pinqing Lake

To ensure more than 30% overlap of the neighboring cross-strips and satisfy the accuracy requirements of bathymetric mapping of the point cloud data, this experiment was conducted using a USV named “GQ-S20” in the Pinqing Lake located in Shanwei City, Guangdong Province. The climate parameters collected on the day of the experiment were as follows: sunny, temperature of 21–30 °C, the wind direction was southeast, and the wind speed was 1.6 m/s–3.3 m/s. The experimental process is outlined as follows:

• All equipment, such as the GQ-Cormorant 19, POS, antenna, data transmission module and power supply, were loaded on the GQ-S20, and the initial values of GQ-Cormorant 19 were set.
• The AFIDLOS method was applied to the control system, where the path was planned using the ground software and sent to the control system.
• The USV was programmed to follow a planned path, as shown in Figure 19, which was a scanning strip with multiple round trips to both sides of the lake.
• Echo data were obtained by scanning the water through the GQ-Cormorant 19 and were stored in the control system for processing.
• The collected echo data were analyzed to generate the experimental results, as shown in Figure 20.

Based on the experimental results above, the following conclusions can be drawn. First, as observed in Figure 20a, the USV followed the planned paths correctly, and the echo signals were captured correctly by GQ-Cormorant 19, with a 30% overlap of neighboring cross-strips on both the water surface and the bottom. The point cloud data were separated and processed to observe their distribution on the water surface and bottom (Figure 20b,c), from which water depth information could be obtained. These results show that the proposed AFIDLOS method can satisfy the accuracy requirements of bathymetric mapping of point cloud data.

3.5. Discussion

All the experimental results obtained above are presented in

Table 9. Data comparison of all the experimental results.

Experimental Location	Average Improvement Rate of Cross-Track Error
Artificial lake	13.71%
Natural lake	10.37%
Beibu Gulf	8.32%

. From Table 9, the improvement rates of the cross-track error from the proposed AFIDLOS method in an artificial lake, a natural lake, and the Beibu Gulf reached 13.71%, 10.37% and 8.32%, respectively, when compared with the traditional LOS guidance law. The difference in results between the artificial lake and the Beibu Gulf is probably caused by the fact that the surface of the artificial lake is relatively calm without external influence, whereas Beibu Gulf suffered from a few external influences such as sea wind and waves, resulting in a relatively low improvement rate. In addition, all the experimental results again demonstrate that the AFIDLOS method has a higher path-tracking accuracy in all waters than the LOS guidance law has. The advantages of the AFIDLOS method are as follows:

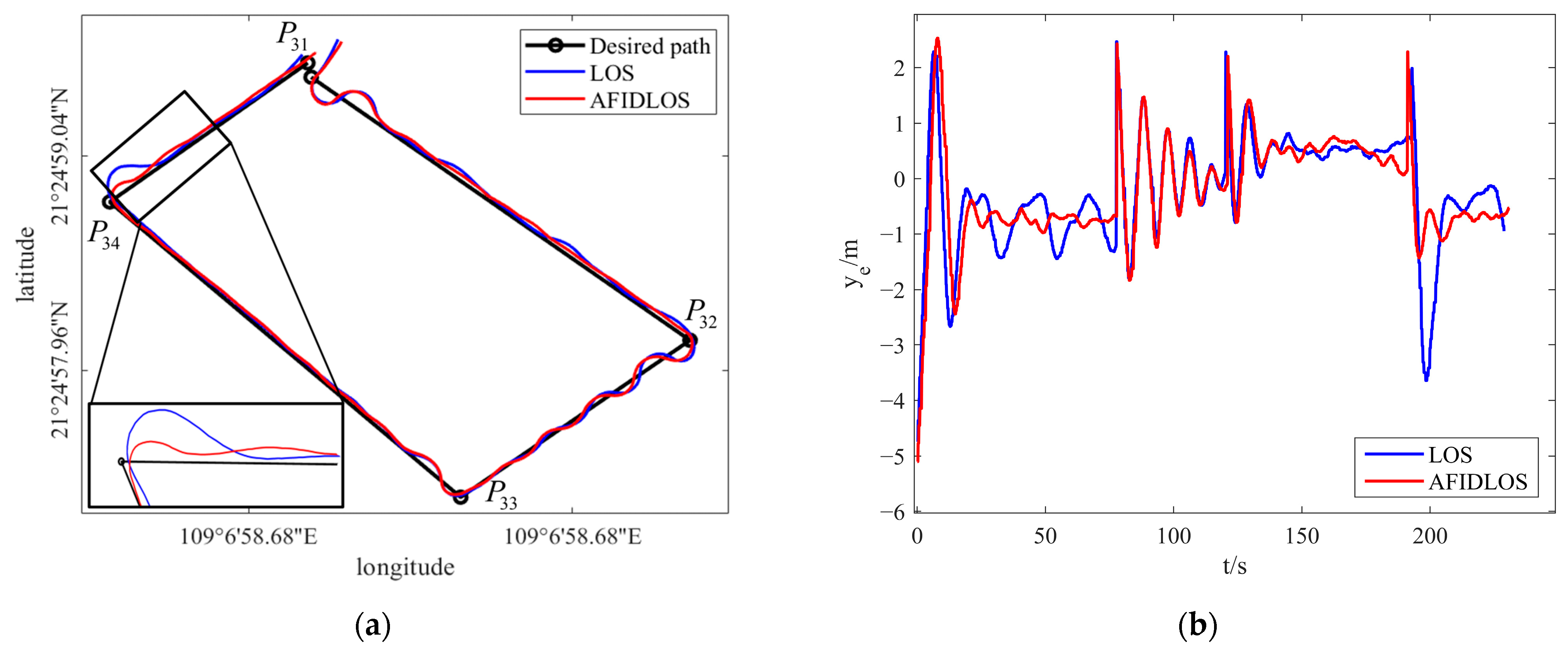
• Compared to the LOS guidance law, the proposed AFIDLOS method adds integral and derivative terms to Equation (1). If the cross-track error becomes larger, the integral term is enhanced to predict the sideslip angle ${\theta }_{los}$ and compensate for the LOS angle ${\theta }_{los}$; the derivative term is used to eliminate the overshoot and oscillation, so that the USV converges to the planned path faster. If the cross-track error decreases, the effect of the integral and derivative terms will be weakened, such that the USV converges smoothly to the planned path.
• Compared to the LOS guidance law, the proposed AFIDLOS method can obtain the optimal look-ahead distance value using fuzzy control. The optimal value of the convergence rate $\gamma$, was adjusted in real time using the value and change rate of the cross-track error in Equation (5) to render the value of the look-ahead distance more reasonable.
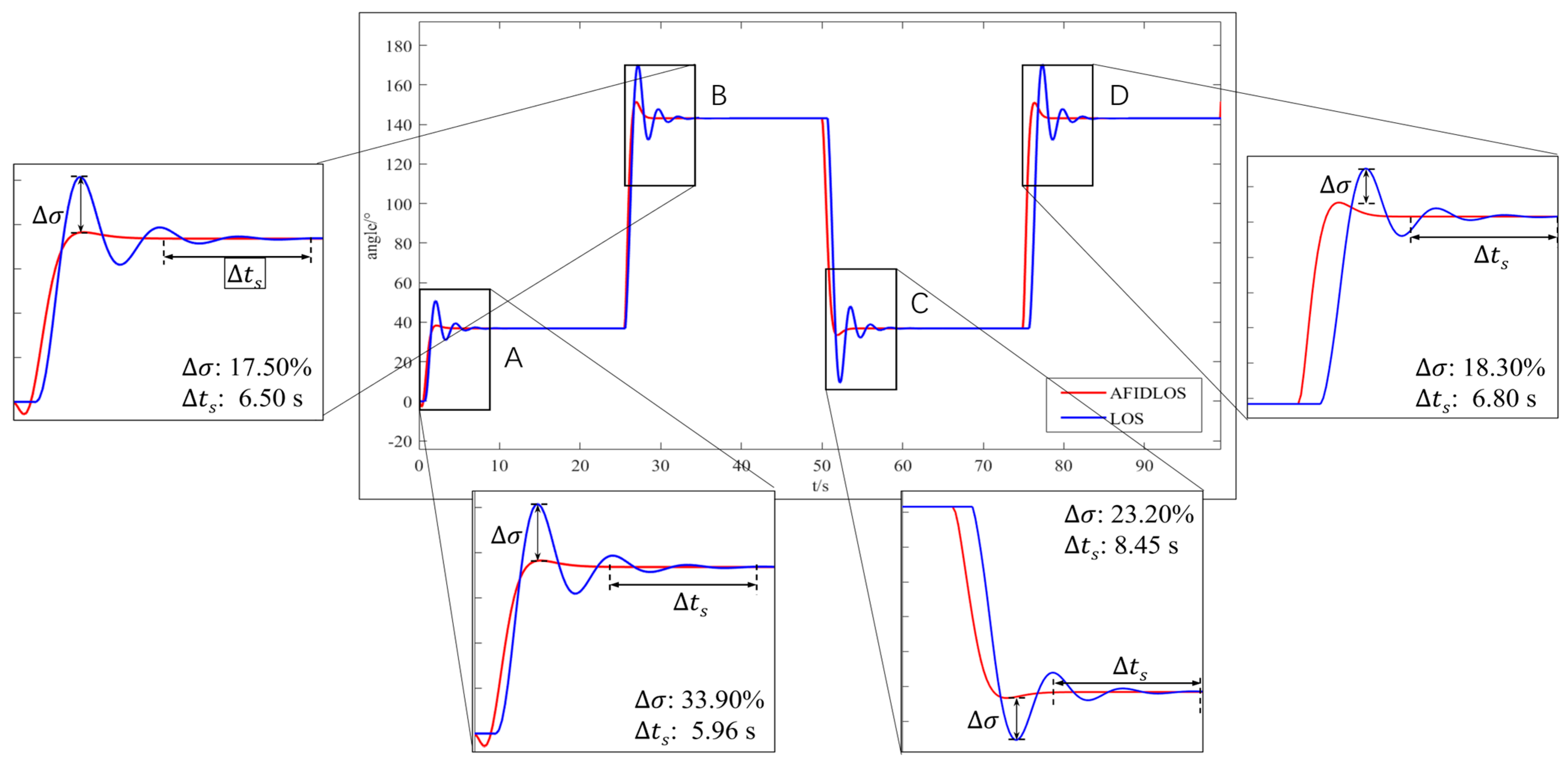
• Compared to the LOS guidance law, the AFIDLOS method exhibited better path-tracking performance with a smaller overshoot and faster convergence speed during USV path-tracking.

4. Conclusions

This study established an AFIDLOS method for the path-tracking of a USV carried with bathymetric LiDAR developed by our research team. The developed AFIDLOS method was implemented based on an STM32 chip and verified through heading control in simulations and real path-tracking outdoor experiments. Based on the experimental results, the following conclusions were drawn.

• The developed AFIDLOS method reduced the amount of overshoot by 79.85% and shortened the settling time by 55.32%, when compared with the traditional LOS guidance law in the simulation experiments.
• The developed AFIDLOS method reduced the average cross-track error by 10.91% compared with the traditional LOS guidance law in outdoor experiments.
• In Pinqing Lake, the path-tracking accuracy of the USV embedded with the bathymetric LiDAR satisfied the requirement of 3D bathymetry.

The above results demonstrate that the proposed AFIDLOS method is able to overcome the problems of large overshoot and slow convergence speed, which have been encountered with the traditional LOS guidance law when applied in the bathymetric LIDAR onboard a USV. The proposed AFIDLOS method especially ensures 30% overlap of the neighboring strips, which satisfies the accuracy requirement for bathymetric mapping.

The shortcomings of the USV model established in this study include the presence of linearization processes, which may prevent the controller from achieving the desired effect. In future research, the interference of external environmental factors will be considered to achieve more accurate modeling, and the control method will be optimized to improve the stability of the system.