BPG-Based Lossy Compression of Three-Channel Remote Sensing Images with Visual Quality Control
Abstract
:1. Introduction
- -
- The metric must rank highly for characterizing image visual quality, demonstrating a strong correlation with mean opinion scores across databases containing various types of distortions resulting from lossy compression.
- -
- -
- Understanding its fundamental properties is essential, including the distortion invisibility threshold [38].
- -
- The metric should be computationally efficient, allowing fast and straightforward calculations [28].
2. Advantages and Properties of the Considered Coder and Metric
3. Two-Step Procedure for BPG-Based Compression with Providing a Desired HaarPSI
4. Discussion and Practical Aspects
4.1. Verification Results
4.2. Classification Aspects
4.3. Other Practical Aspects
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mielke, C.; Boshce, N.K.; Rogass, C.; Segl, K.; Gauert, C.; Kaufmann, H. Potential Applications of the Sentinel-2 Multispectral Sensor and the ENMAP hyperspectral Sensor in Mineral Exploration. EARSeL eProc. 2014, 13, 93–102. [Google Scholar] [CrossRef]
- Kussul, N.; Lavreniuk, M.; Kolotii, A.; Skakun, S.; Rakoid, O.; Shumilo, L. A workflow for Sustainable Development Goals indicators assessment based on high-resolution satellite data. Int. J. Digit. Earth 2020, 13, 309–321. [Google Scholar] [CrossRef]
- Khorram, S.; van der Wiele, C.F.; Koch, F.H.; Nelson, S.A.C.; Potts, M.D. Future Trends in Remote Sensing. In Principles of Applied Remote Sensing; Springer International Publishing: Cham, Switzerland, 2016; pp. 277–285. ISBN 978-3-319-22559-3. [Google Scholar]
- Pillai, D.K. New Computational Models for Image Remote Sensing and Big Data. In Big Data Analytics for Satellite Image Processing and Remote Sensing; IGI Global: Hershey, PA, USA, 2018; pp. 1–21. [Google Scholar] [CrossRef]
- Blanes, I.; Magli, E.; Serra-Sagrista, J. A Tutorial on Image Compression for Optical Space Imaging Systems. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–26. [Google Scholar] [CrossRef]
- Radosavljevic, M.; Brkljač, B.; Lugonja, P.; Crnojevic, V.; Trpovski, Ž.; Xiong, Z.; Vukobratović, D. Lossy Compression of Multispectral Satellite Images with Application to Crop Thematic Mapping: A HEVC Comparative Study. Remote Sens. 2020, 12, 1590. [Google Scholar] [CrossRef]
- Bausys, R.; Kazakeviciute-Januskeviciene, G. Qualitative Rating of Lossy Compression for Aerial Imagery by Neutrosophic WASPAS Method. Symmetry 2021, 13, 273. [Google Scholar] [CrossRef]
- Santos, L.; Lopez, S.; Cali, G.M.; Lopez, J.F.; Sarmiento, R. Performance Evaluation of the H.264/AVC Video Coding Standard for Lossy Hyperspectral Image Compression. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 451–461. [Google Scholar] [CrossRef]
- Christophe, E. Hyperspectral Data Compression Tradeoff. In Optical Remote Sensing; Prasad, S., Bruce, L.M., Chanussot, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 9–29. ISBN 978-3-642-14211-6. [Google Scholar]
- Vasilyeva, I.; Li, F.; Abramov, S.K.; Lukin, V.V.; Vozel, B.; Chehdi, K. Lossy Compression of Three-Channel Remote Sensing Images with Controllable Quality. In Image and Signal Processing for Remote Sensing XXVII; Bruzzone, L., Bovolo, F., Benediktsson, J.A., Eds.; SPIE: Bellingham, WA, USA, 2021; p. 26. [Google Scholar] [CrossRef]
- Ye, N.; Perez-Ortiz, M.; Mantiuk, R.K. Visibility Metric for Visually Lossless Image Compression. In Proceedings of the 2019 Picture Coding Symposium (PCS), Ningbo, China, 12–15 November 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Bondžulić, B.; Pavlović, B.; Stojanović, N.; Petrović, V.; Bujaković, D. A Simple and Reliable Approach to Providing a Visually Lossless Image Compression. Vis. Comput. 2024, 40, 3747–3763. [Google Scholar] [CrossRef]
- Ponomarenko, N.N.; Lukin, V.V.; Kozhemiakin, R.A.; Egiazarian, K.O.; Chobanu, M.K. Lossy and Visually Lossless Compression of Single-Look SAR Images. Telecommun. Radio Eng. 2013, 72, 711–729. [Google Scholar] [CrossRef]
- Ozah, N.; Kolokolova, A. Compression Improves Image Classification Accuracy. In Advances in Artificial Intelligence; Meurs, M.-J., Rudzicz, F., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2019; Volume 11489, pp. 525–530. ISBN 978-3-030-18304-2. [Google Scholar]
- Chen, Z.; Hu, Y.; Zhang, Y. Effects of Compression on Remote Sensing Image Classification Based on Fractal Analysis. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4577–4590. [Google Scholar] [CrossRef]
- Sneyers, J. Contemplating Codec Comparisons. Available online: https://cloudinary.com/blog/contemplating-codec-comparisons (accessed on 10 May 2024).
- Cheng, Z.; Sun, H.; Takeuchi, M.; Katto, J. Performance Comparison of Convolutional AutoEncoders, Generative Adversarial Networks and Super-Resolution for Image Compression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Salt Lake City, UT, USA, 18–23 June 2018. [Google Scholar]
- Abramova, V.; Lukin, V.; Abramov, S.; Abramov, K.; Bataeva, E. Analysis of Statistical and Spatial Spectral Characteristics of Distortions in Lossy Image Compression. In Proceedings of the 2022 IEEE 2nd Ukrainian Microwave Week (UkrMW), Kharkiv, Ukraine, 14–18 November 2022; pp. 644–649. [Google Scholar] [CrossRef]
- Wallace, G. The JPEG Still Picture Compression Standard. Commun. ACM 1991, 34, 30–44. [Google Scholar] [CrossRef]
- Chen, Y.; Mukherjee, D.; Han, J.; Grange, A.; Xu, Y.; Parker, S.; Chen, C.; Su, H.; Joshi, U.; Chiang, C.-H.; et al. An Overview of Coding Tools in AV1: The First Video Codec from the Alliance for Open Media. SIP 2020, 9, e6. [Google Scholar] [CrossRef]
- Taubman, D.S.; Marcellin, M.W. JPEG2000: Image Compression Fundamentals, Standards, and Practice; Springer: Boston, MA, USA, 2002; ISBN 978-1-4613-5245-7. [Google Scholar]
- Zemliachenko, A.; Kozhemiakin, R.; Uss, M.; Abramov, S.; Ponomarenko, N.; Lukin, V.; Vozel, B.; Chehdi, K. Lossy compression of hyperspectral images based on noise parameters estimation and variance stabilizing transform. J. Appl. Remote Sens. 2014, 8, 083571. [Google Scholar] [CrossRef]
- Bellard, F. BPG Image Format. Available online: https://bellard.org/bpg/ (accessed on 10 May 2024).
- Yee, D.; Soltaninejad, S.; Hazarika, D.; Mbuyi, G.; Barnwal, R.; Basu, A. Medical Image Compression Based on Region of Interest Using Better Portable Graphics (BPG). In Proceedings of the 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Banff, AB, Canada, 5–8 October 2017; pp. 216–221. [Google Scholar]
- Du, Q.; Fowler, J.E. Hyperspectral image compression using JPEG2000 and principal component analysis. IEEE Geosci. Remote Sens. Lett. 2007, 4, 201–205. [Google Scholar] [CrossRef]
- Zemliachenko, A.; Lukin, V.; Ponomarenko, N.; Egiazarian, K.; Astola, J. Still Image/Video Frame Lossy Compression Providing a Desired Visual Quality. Multidimens. Syst. Signal Process. 2016, 27, 697–718. [Google Scholar] [CrossRef]
- Kovalenko, B.; Lukin, V. Analysis of color image compression by BPG coder. In Proceedings of the 2022 IEEE 3rd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 3–7 October 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Li, F.; Lukin, V.; Ieremeiev, O.; Okarma, K. Quality Control for the BPG Lossy Compression of Three-Channel Remote Sensing Images. Remote Sens. 2022, 14, 1824. [Google Scholar] [CrossRef]
- Li, F.; Abramov, S.; Dohtiev, I.; Lukin, V. Advantages and drawbacks of two-step approach to providing desired parameters in lossy image compression. Adv. Inf. Syst. 2024, 8, 57–63. [Google Scholar] [CrossRef]
- Yang, K.; Jiang, H. Optimized-SSIM Based Quantization in Optical Remote Sensing Image Compression. In Proceedings of the 2011 Sixth International Conference on Image and Graphics, Hefei, China, 12–15 August 2011; IEEE: New York, NY, USA, 2011; pp. 117–122. [Google Scholar]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A Feature Similarity Index for Image Quality Assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Ieremeiev, O.; Lukin, V.; Okarma, K.; Egiazarian, K. Full-Reference Quality Metric Based on Neural Network to Assess the Visual Quality of Remote Sensing Images. Remote Sens. 2020, 12, 2349. [Google Scholar] [CrossRef]
- Lukin, V.; Abramov, S.; Krivenko, S.; Kurekin, A.; Pogrebnyak, O. Analysis of Classification Accuracy for Pre-Filtered Multichannel Remote Sensing Data. Expert Syst. Appl. 2013, 40, 6400–6411. [Google Scholar] [CrossRef]
- Marsetic, A.; Kokalj, Z.; Ostir, K. The Effect of Lossy Image Compression on Object Based Image Classification—WorldView-2 Case Study. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 38, 187–192. [Google Scholar] [CrossRef]
- Gandor, T.; Nalepa, J. First Gradually, Then Suddenly: Understanding the Impact of Image Compression on Object Detection Using Deep Learning. Sensors 2022, 22, 1104. [Google Scholar] [CrossRef] [PubMed]
- Lukin, V.; Bataeva, E.; Abramov, S. Saliency Map in Image Visual Quality Assessment and Processing. Radioelectron. Comput. Syst. 2023, 1, 112–121. [Google Scholar] [CrossRef]
- Nafchi, H.Z.; Shahkolaei, A.; Hedjam, R.; Cheriet, M. Mean Deviation Similarity Index: Efficient and Reliable Full-Reference Image Quality Evaluator. IEEE Access 2016, 4, 5579–5590. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Lukin, V.; Astola, J.; Egiazarian, K. Analysis of HVS-metrics’ properties using color image database TID2013. In Advanced Concepts for Intelligent Vision Systems; Battiato, S., Blanc-Talon, J., Gallo, G., Philips, W., Popescu, D., Scheunders, P., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2015; Volume 9386, pp. 613–624. ISBN 978-3-319-25902-4. [Google Scholar]
- Reisenhofer, R.; Bosse, S.; Kutyniok, G.; Wiegand, T. A Haar Wavelet-Based Perceptual Similarity Index for Image Quality Assessment. Signal Process. Image Commun. 2018, 61, 33–43. [Google Scholar] [CrossRef]
- Kryvenko, L.; Krylova, O.; Lukin, V.; Kryvenko, S. Intelligent Visually Lossless Compression of Dental Images. Adv. Opt. Technol. 2024, 13, 1306142. [Google Scholar] [CrossRef]
- Lukin, V.; Li, F. Providing a Desired Compression Ratio for Better Portable Graphics Encoder of Color Images. In Advances and Challenges in Science and Technology Vol. 1; Jakóbczak, D.J., Ed.; B P International (a Part of Sciencedomain International): Hongkong, China, 2023; pp. 98–111. ISBN 978-81-19-49190-2. [Google Scholar]
- Kovalenko, B.; Lukin, V.; Kryvenko, S.; Naumenko, V.; Vozel, B. Prediction of Parameters in Optimal Operation Point for BPG-Based Lossy Compression of Noisy Images. Ukr. J. Remote Sens. 2022, 9, 4–12. [Google Scholar] [CrossRef]
- Ieremeiev, O.; Lukin, V.; Okarma, K.; Egiazarian, K.; Vozel, B. On Properties of Visual Quality Metrics in Remote Sensing Applications. Electron. Imaging 2022, 34, 354-1–354-6. [Google Scholar] [CrossRef]
- Ponomarenko, N.; Silvestri, F.; Egiazarian, K.; Carli, M.; Astola, J.; Lukin, V. On Between-Coefficient Contrast Masking of DCT Basis Functions. In Proceedings of the Third International Workshop on Video Processing and Quality Metrics for Consumer Electronics, Scottsdale, AZ, USA, 25–26 January 2007; pp. 1–4. [Google Scholar]
- Cameron, C.A.; Windmeijer, F.A.G. An R-Squared Measure of Goodness of Fit for Some Common Nonlinear Regression Models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Tong, X.-Y.; Lu, Q.; Xia, G.-S.; Zhang, L. Large-Scale Land Cover Classification in Gaofen-2 Satellite Imagery. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 3599–3602. [Google Scholar]
- Li, F.; Lukin, V.; Okarma, K.; Fu, Y. Providing a Desired Quality of BPG Compressed Images for FSIM Metric. In Proceedings of the 2021 IEEE 3rd International Conference on Advanced Trends in Information Theory (ATIT), Kyiv, Ukraine, 15–17 December 2021; pp. 10–14. [Google Scholar]
- Kovalenko, B.; Lukin, V. Usage of different Chroma Subsampling Modes in Image Compression by BPG Coder. Ukr. J. Remote Sens. 2022, 9, 11–16. [Google Scholar] [CrossRef]
- Proskura, G.; Vasilyeva, I.; Fangfang, L.; Lukin, V. Classification of Compressed Multichannel Images and Its Improvement. In Proceedings of the 2020 30th International Conference Radioelektronika (RADIOELEKTRONIKA), Bratislava, Slovakia, 15–16 April 2020; pp. 1–6. [Google Scholar]
- Yang, Q. Research on SVM Remote Sensing Image Classification Based on Parallelization. J. Phys. Conf. Ser. 2021, 1852, 032009. [Google Scholar] [CrossRef]
- Lukin, V.; Li, F.; Zhu, J.; Kryvenko, S. Peculiarities of SVM-based classification of BPG compressed three-channel images. In Proceedings of the 8th International Symposium of Space Optical Instrument and Application (ISSOIA), Beijing, China, 15–17 November 2023. in print. [Google Scholar]
- Chandler, D.M. Most Apparent Distortion: Full-Reference Image Quality Assessment and the Role of Strategy. J. Electron. Imaging 2010, 19, 011006. [Google Scholar] [CrossRef]
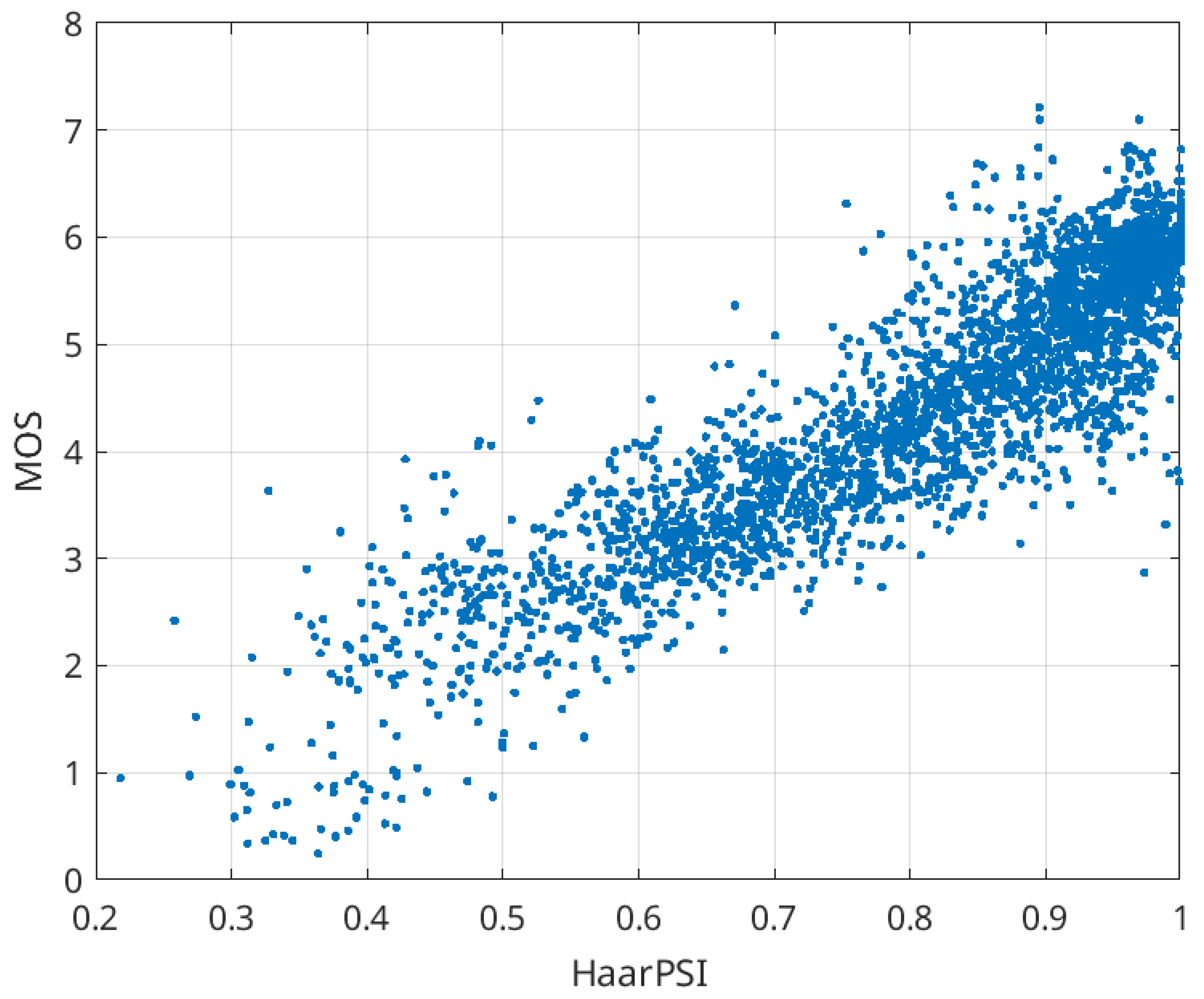
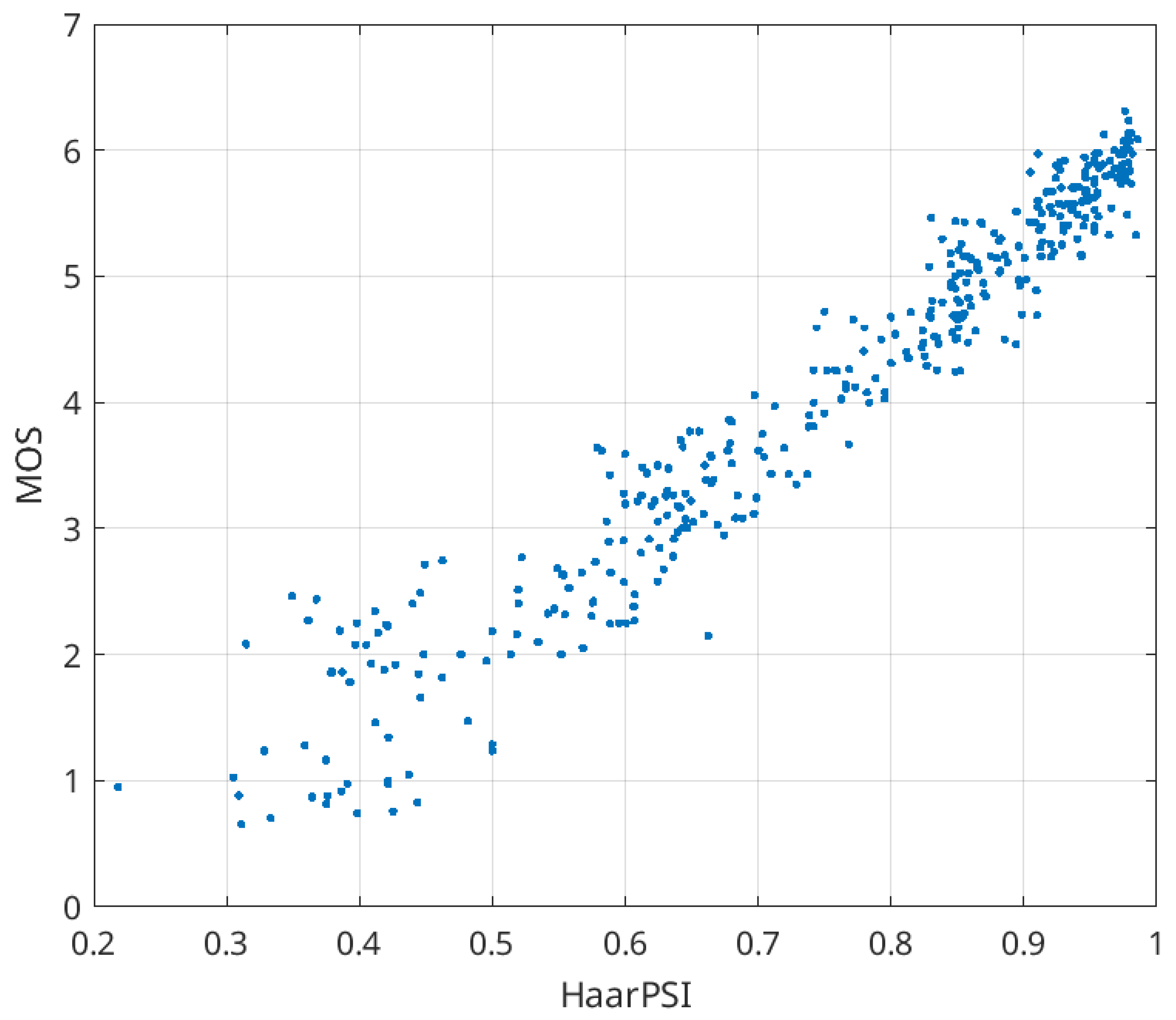


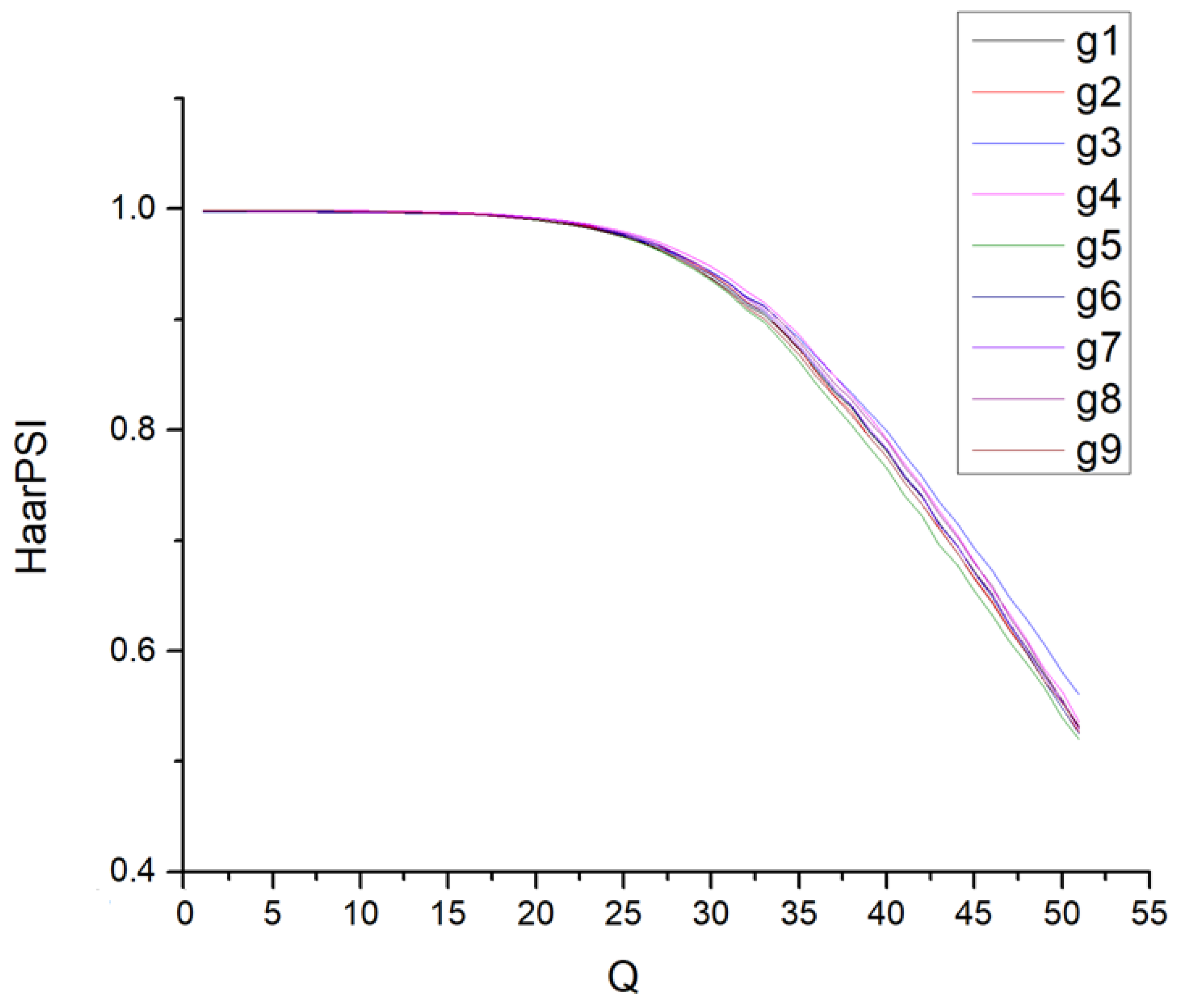

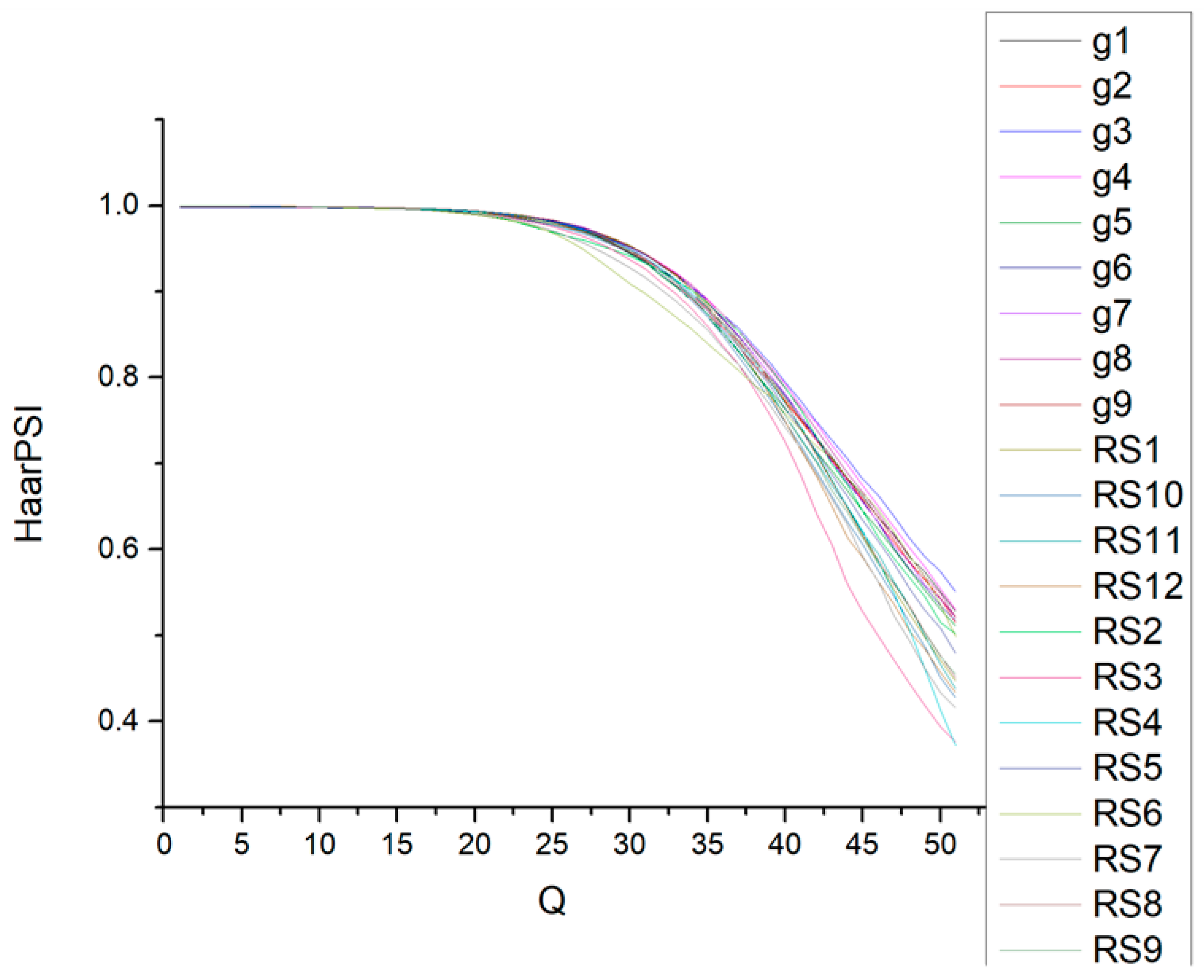
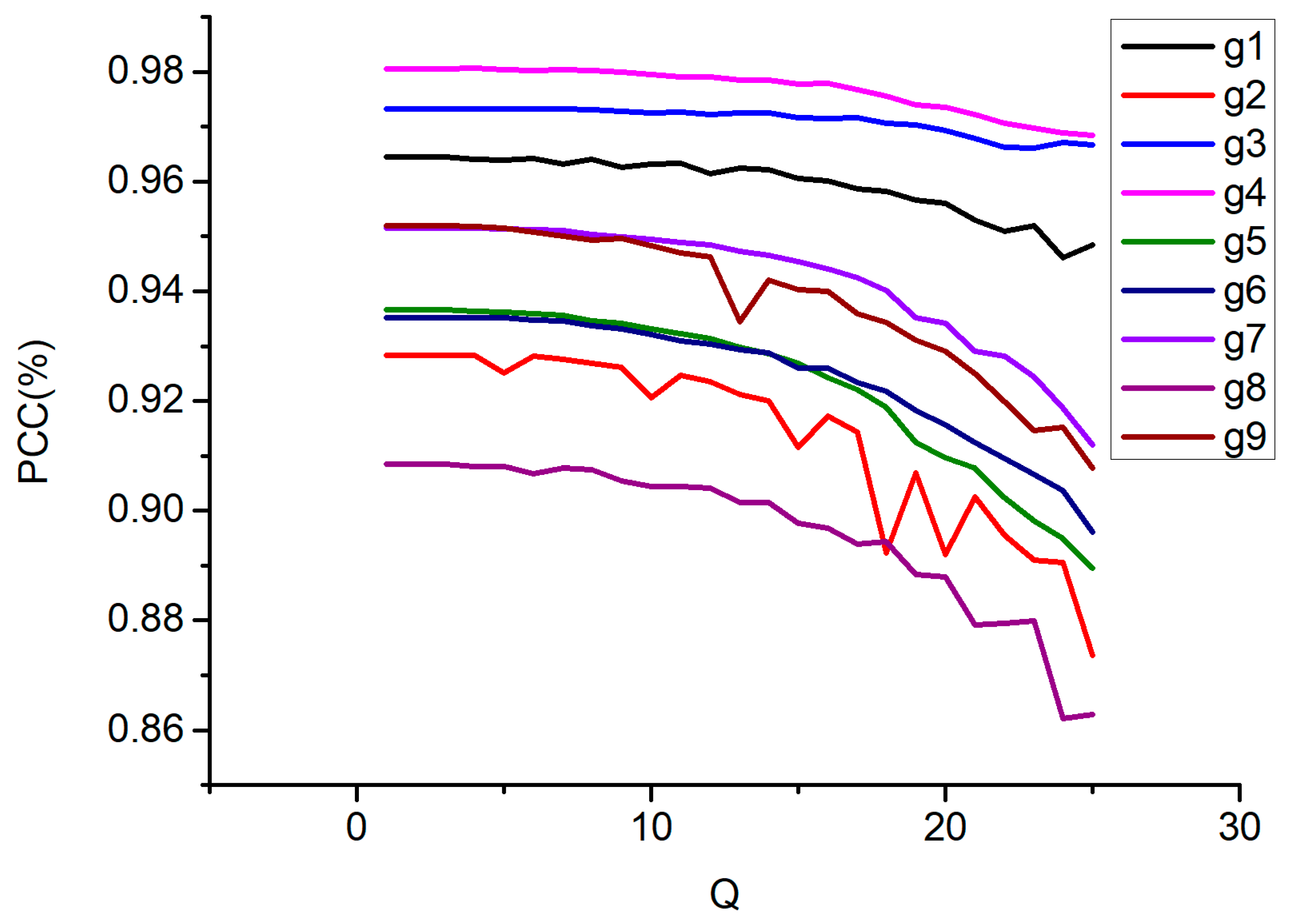
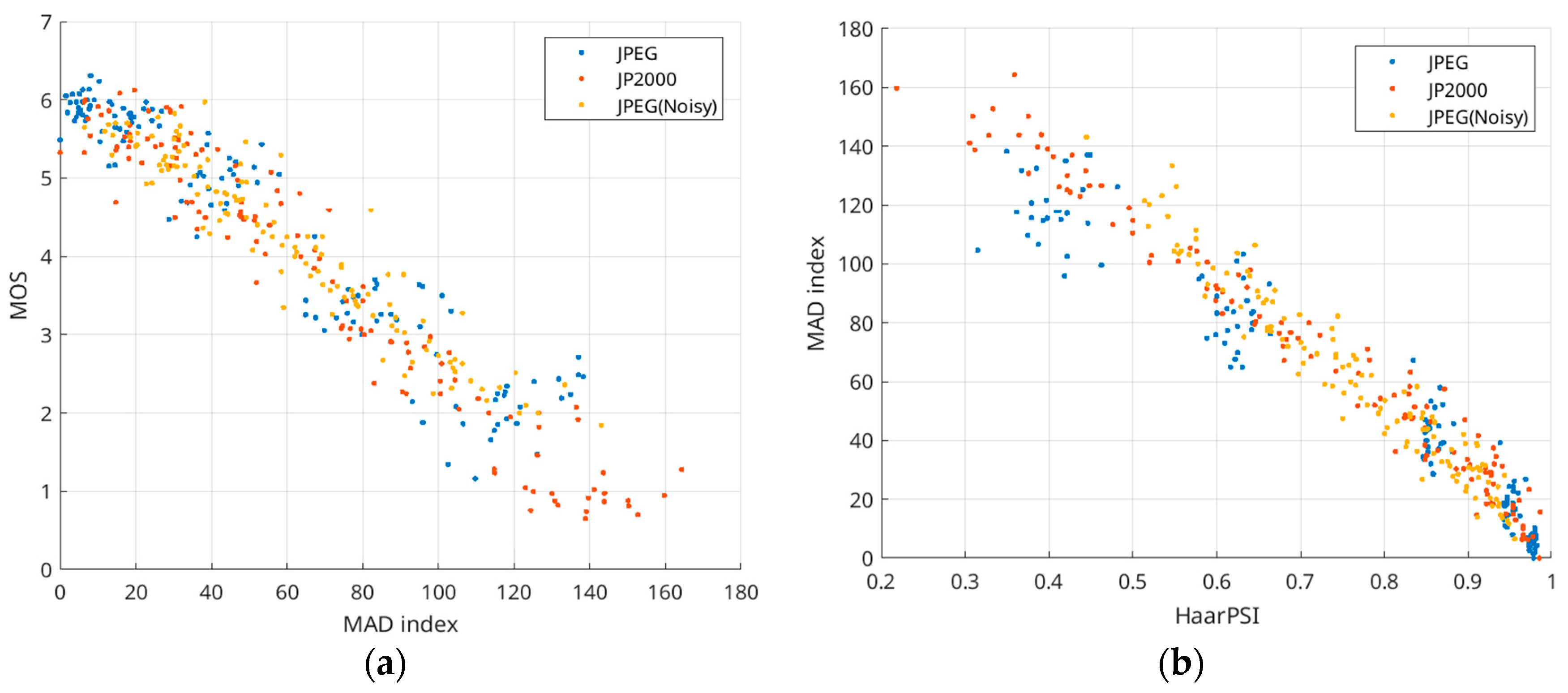
| Q | Average HaarPSI for the Mode 4:4:4 | Average HaarPSI for the Mode 4:2:2 | Average HaarPSI for the Mode 4:2:0 |
|---|---|---|---|
| 1 | 0.999618 | 0.99911 | 0.998718 |
| 2 | 0.999618 | 0.99911 | 0.998718 |
| 3 | 0.999618 | 0.99911 | 0.998718 |
| 4 | 0.999609 | 0.999099 | 0.998706 |
| 5 | 0.999597 | 0.999081 | 0.998687 |
| 6 | 0.999573 | 0.999053 | 0.998652 |
| 7 | 0.999525 | 0.998997 | 0.998587 |
| 8 | 0.999386 | 0.998841 | 0.998405 |
| 9 | 0.999212 | 0.998651 | 0.998175 |
| 10 | 0.99905 | 0.998469 | 0.997949 |
| 11 | 0.998846 | 0.998246 | 0.997681 |
| 12 | 0.998656 | 0.99803 | 0.997413 |
| 13 | 0.99842 | 0.997761 | 0.997095 |
| 14 | 0.998148 | 0.997445 | 0.996713 |
| 15 | 0.997816 | 0.99707 | 0.996244 |
| 16 | 0.997396 | 0.996576 | 0.99565 |
| 17 | 0.996793 | 0.995888 | 0.994828 |
| 18 | 0.996079 | 0.995068 | 0.993831 |
| 19 | 0.995085 | 0.993884 | 0.992431 |
| 20 | 0.993873 | 0.992518 | 0.990842 |
| 21 | 0.992499 | 0.990953 | 0.989041 |
| 22 | 0.990633 | 0.988835 | 0.986647 |
| 23 | 0.988258 | 0.98623 | 0.983686 |
| 24 | 0.985515 | 0.983136 | 0.980176 |
| 25 | 0.981961 | 0.979277 | 0.975889 |
| 26 | 0.977818 | 0.97456 | 0.970683 |
| 27 | 0.972998 | 0.969344 | 0.96491 |
| 28 | 0.966793 | 0.962459 | 0.957538 |
| 29 | 0.959384 | 0.954422 | 0.948902 |
| 30 | 0.951481 | 0.945826 | 0.939824 |
| 31 | 0.941972 | 0.935509 | 0.92883 |
| 32 | 0.930264 | 0.923002 | 0.91611 |
| 33 | 0.917892 | 0.909805 | 0.905264 |
| 34 | 0.903469 | 0.89488 | 0.88984 |
| 35 | 0.886685 | 0.877215 | 0.872335 |
| 36 | 0.867929 | 0.857726 | 0.852999 |
| 37 | 0.847834 | 0.837524 | 0.832716 |
| 38 | 0.826108 | 0.815065 | 0.813886 |
| 39 | 0.803486 | 0.792301 | 0.790896 |
| 40 | 0.778753 | 0.76762 | 0.768925 |
| 41 | 0.751935 | 0.740915 | 0.742817 |
| 42 | 0.725523 | 0.714471 | 0.718263 |
| 43 | 0.69802 | 0.68781 | 0.691514 |
| 44 | 0.669779 | 0.659982 | 0.66634 |
| 45 | 0.642877 | 0.633854 | 0.640157 |
| 46 | 0.615658 | 0.607032 | 0.614656 |
| 47 | 0.587955 | 0.580515 | 0.587563 |
| 48 | 0.560788 | 0.552955 | 0.560967 |
| 49 | 0.534194 | 0.527514 | 0.534221 |
| 50 | 0.507082 | 0.50065 | 0.506903 |
| 51 | 0.4825 | 0.476095 | 0.482055 |
| HaarPSIdes | Q1 | Mean1 | Mean2 | Var1 | Var2 | Values of Q2 |
|---|---|---|---|---|---|---|
| 0.98 | 26 | 0.9817 | 0.9801 | 0.000003 | 0.0000007 | 26, 27 |
| 0.90 | 36 | 0.8814 | 0.9008 | 0.00010 | 0.00003 | 34, 35, 36 |
| 0.80 | 41 | 0.7761 | 0.7980 | 0.00016 | 0.00006 | 39, 40, 41 |
| HaarPSIdes | Q1 | Mean1 | Mean2 | Var1 | Var2 | Values of Q2 |
|---|---|---|---|---|---|---|
| 0.98 | 25 | 0.9853 | 0.9817 | 0.0000019 | 0.000003 | 26 |
| 0.90 | 34 | 0.9143 | 0.9043 | 0.000068 | 0.000008 | 34, 35 |
| 0.80 | 39 | 0.8231 | 0.8055 | 0.00015 | 0.00003 | 39, 40, 41 |
| HaarPSIdes | Q1 | Mean1 | Mean2 | Var1 | Var2 | Limits of Q2 |
|---|---|---|---|---|---|---|
| 0.98 | 26 | 0.9717 | 0.9791 | 0.0000040 | 0.0000013 | 24, 25 |
| 0.90 | 35 | 0.8751 | 0.8992 | 0.00005 | 0.00002 | 33, 34 |
| 0.80 | 39 | 0.8006 | 0.7988 | 0.00010 | 0.00002 | 39, 40 |
| HaarPSIdes | Q1 | Mean1 | Mean2 | Var1 | Var2 | Values of Q2 |
|---|---|---|---|---|---|---|
| 0.98 | 25 | 0.9799 | 0.9796 | 0.000010 | 0.000002 | 24, 25, 26, 27 |
| 0.90 | 34 | 0.8888 | 0.8972 | 0.00024 | 0.00009 | 32, 33, 34, 35 |
| 0.80 | 39 | 0.7828 | 0.7967 | 0.00046 | 0.00014 | 37, 38, 39, 40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Ieremeiev, O.; Lukin, V.; Egiazarian, K. BPG-Based Lossy Compression of Three-Channel Remote Sensing Images with Visual Quality Control. Remote Sens. 2024, 16, 2740. https://doi.org/10.3390/rs16152740
Li F, Ieremeiev O, Lukin V, Egiazarian K. BPG-Based Lossy Compression of Three-Channel Remote Sensing Images with Visual Quality Control. Remote Sensing. 2024; 16(15):2740. https://doi.org/10.3390/rs16152740
Chicago/Turabian StyleLi, Fangfang, Oleg Ieremeiev, Vladimir Lukin, and Karen Egiazarian. 2024. "BPG-Based Lossy Compression of Three-Channel Remote Sensing Images with Visual Quality Control" Remote Sensing 16, no. 15: 2740. https://doi.org/10.3390/rs16152740
APA StyleLi, F., Ieremeiev, O., Lukin, V., & Egiazarian, K. (2024). BPG-Based Lossy Compression of Three-Channel Remote Sensing Images with Visual Quality Control. Remote Sensing, 16(15), 2740. https://doi.org/10.3390/rs16152740






.png)


