Improving the Gross Primary Productivity Estimation by Simulating the Maximum Carboxylation Rate of Maize Using Leaf Age
Abstract
:1. Introduction
2. Data Availability
2.1. Eddy Covariance Data
2.2. Remote Sensing Data
3. Method
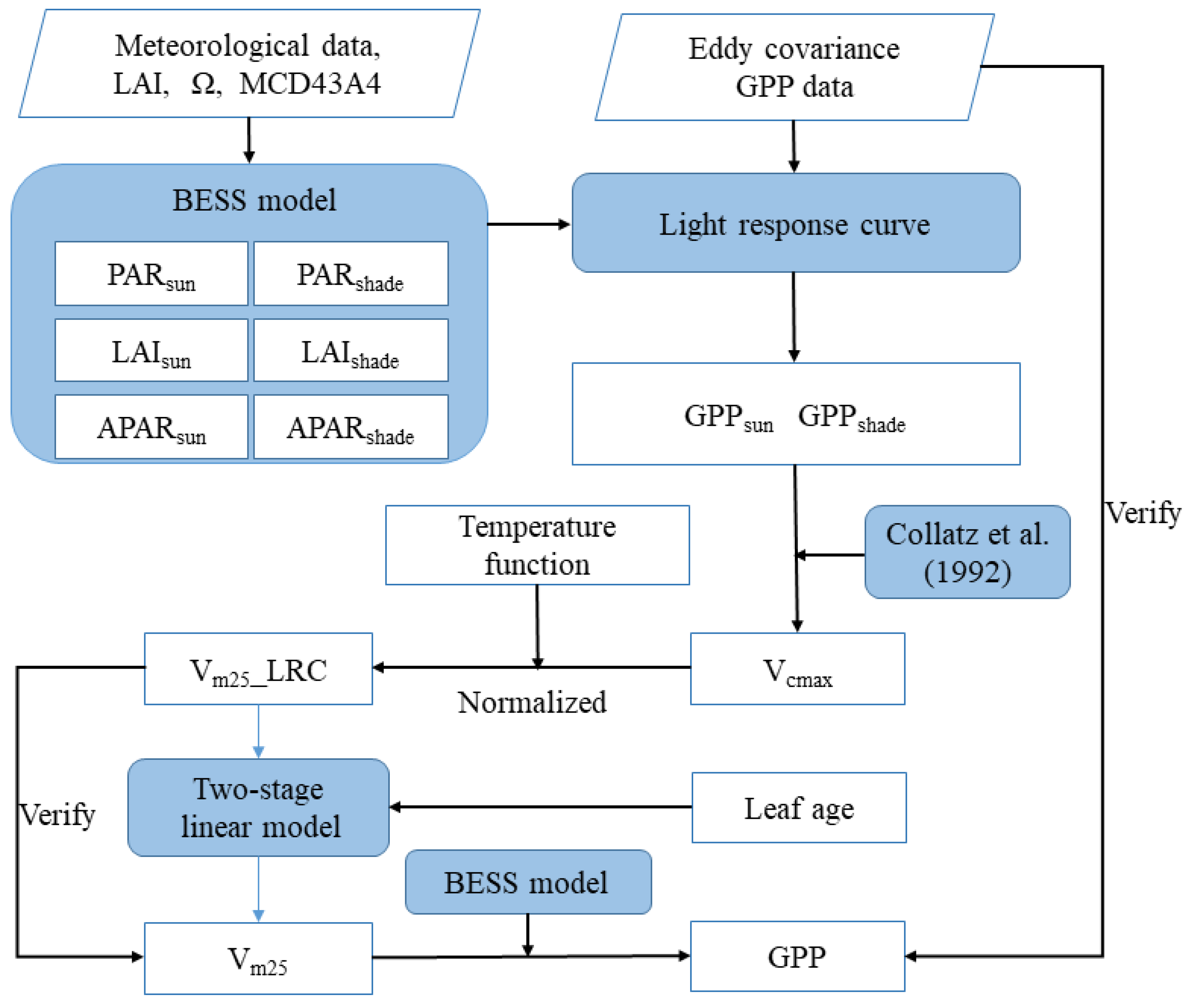
3.1. Inversely Solving Vm25 by Coupling the BESS and LRC
3.1.1. The Separation of Sunlit and Shaded GPP by BESS
3.1.2. Photosynthesis Rates of Sunlit and Shaded Leaves Estimated by LRC
3.1.3. The Inversion of Vcmax from Sunlit GPP
3.1.4. Normalizing Vcmax to 25 °C
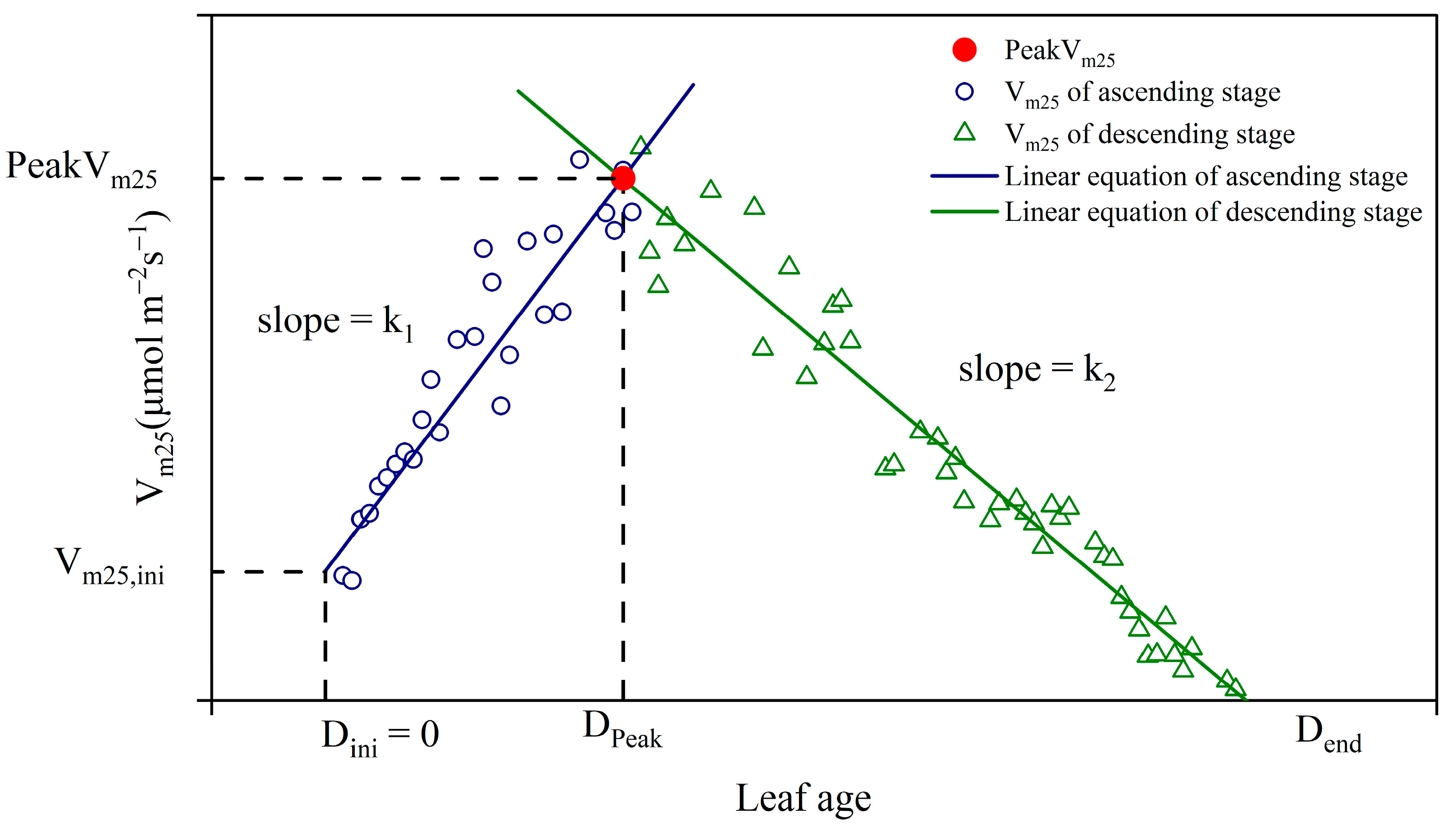
3.2. Two-Stage Linear Model
3.3. Model Validation
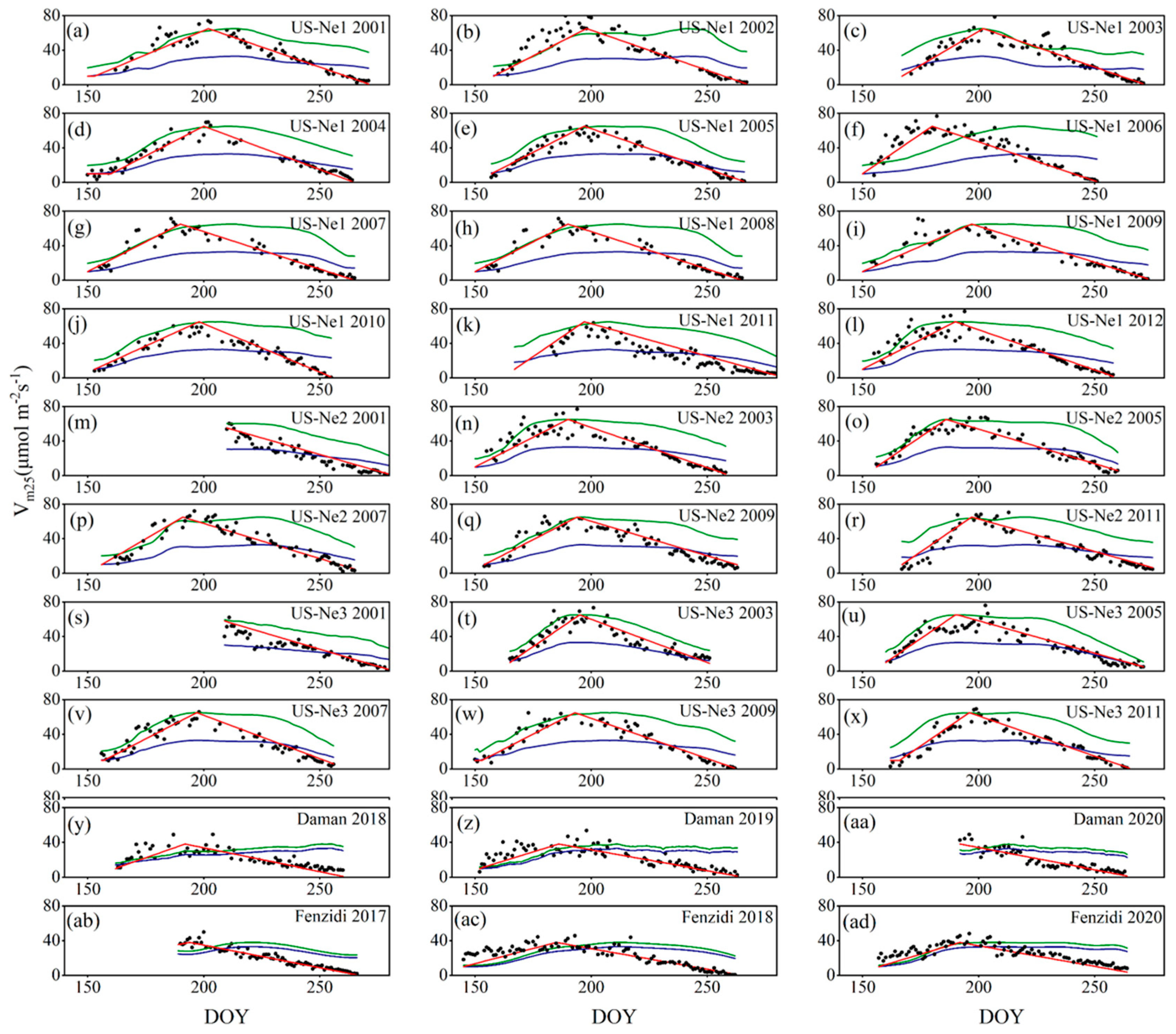
3.3.1. Calibration and Validation of Vm25
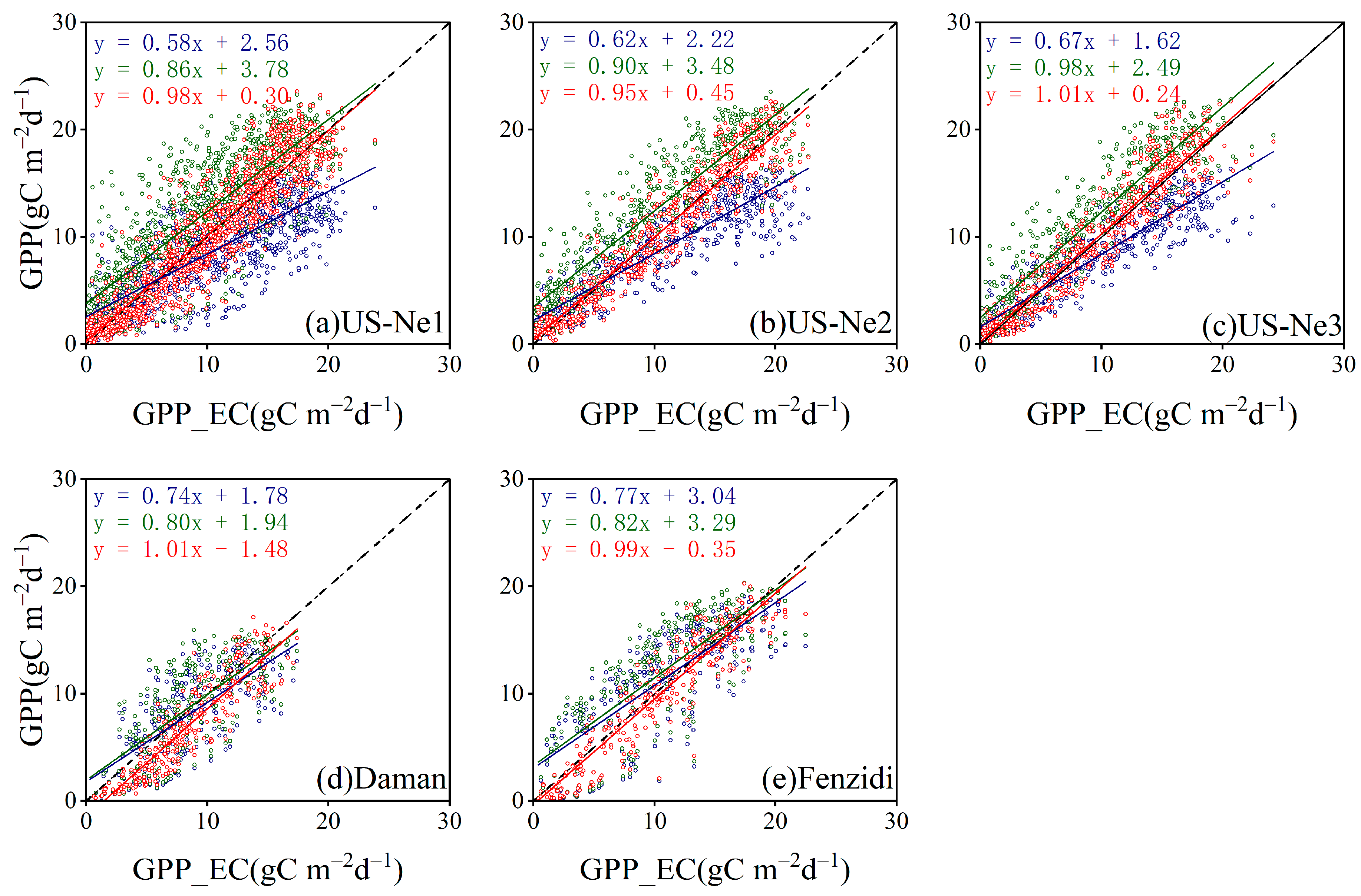
3.3.2. Comparison with the Vm25 Obtained by BESS
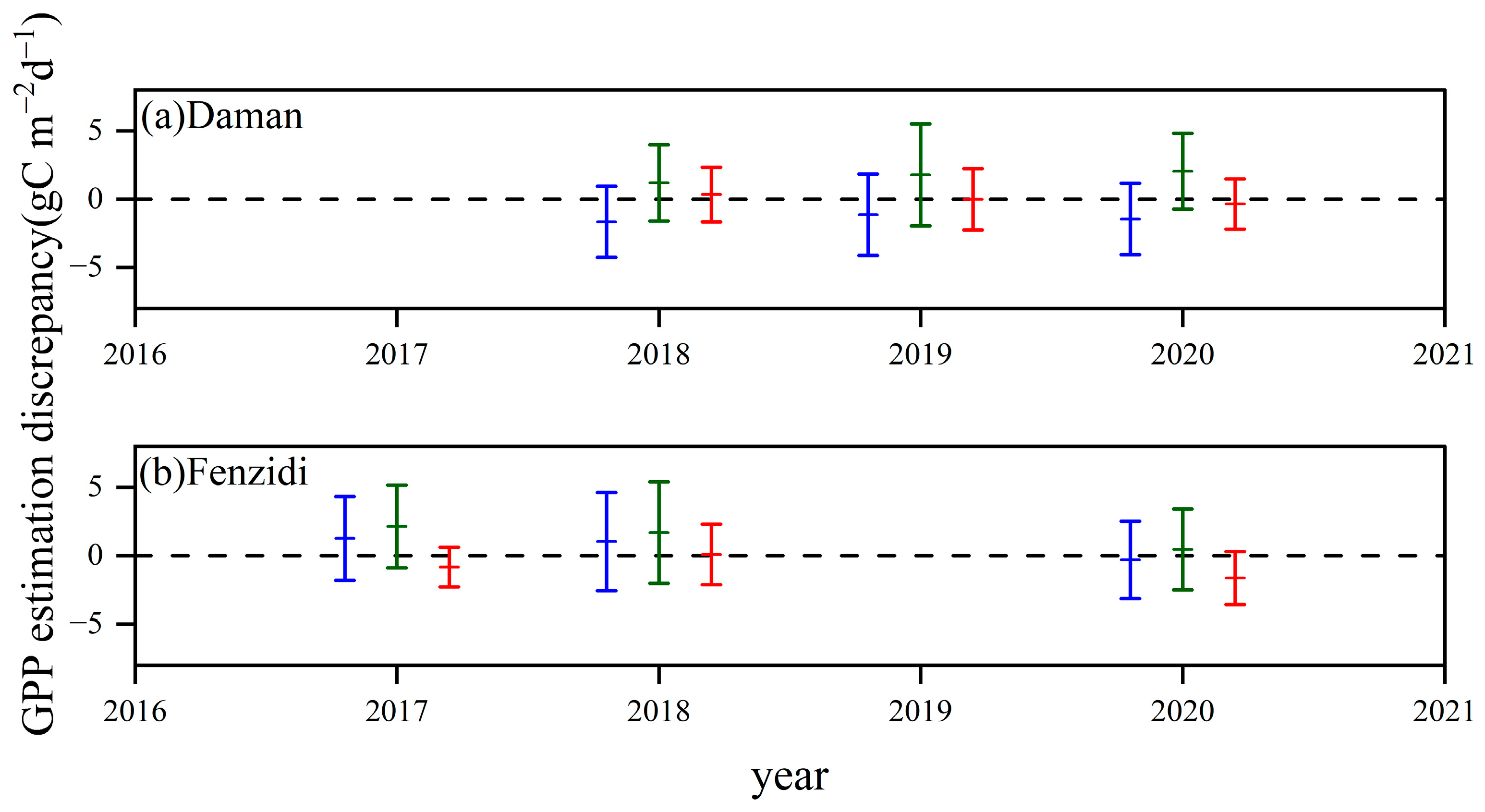
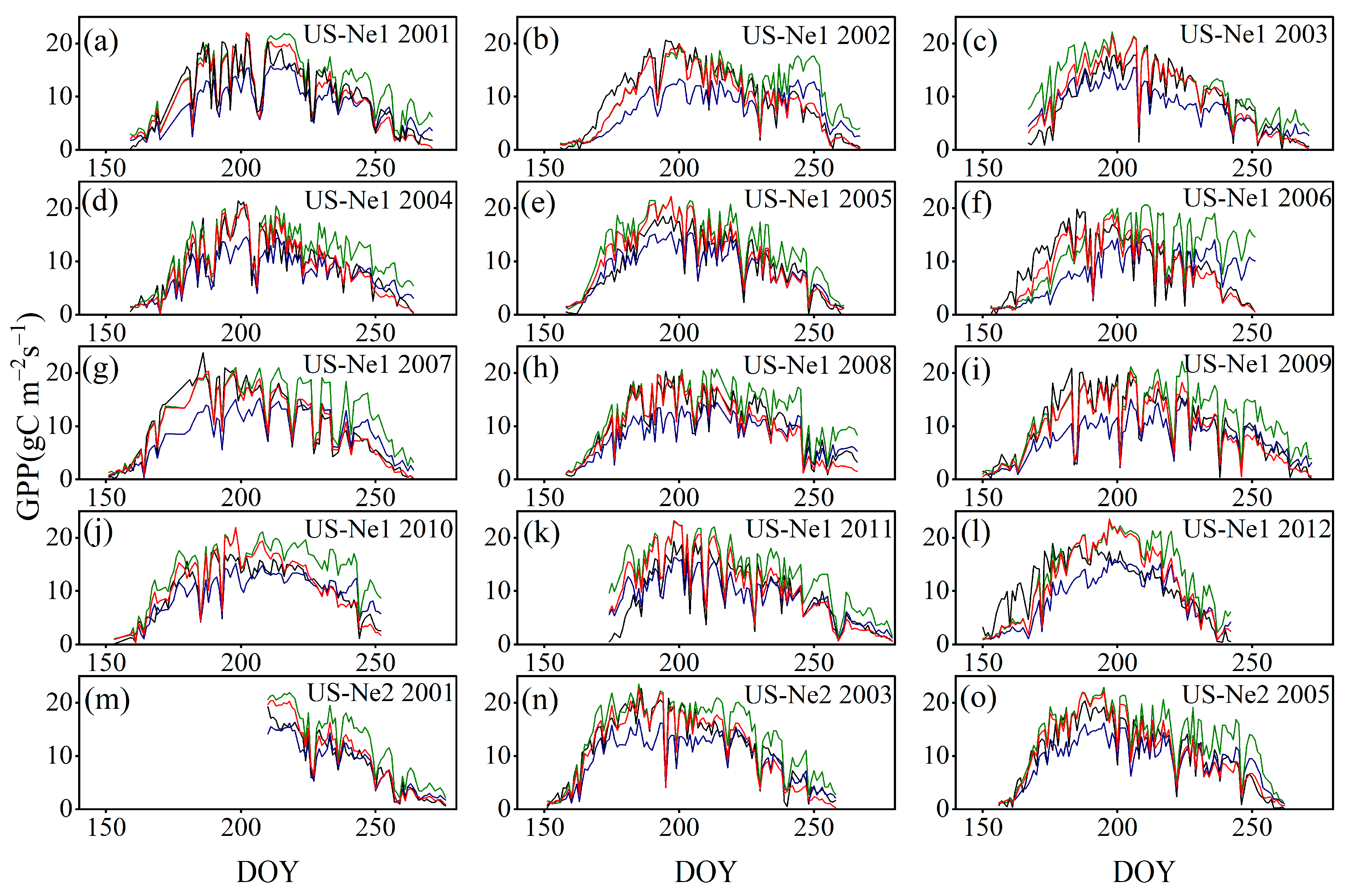
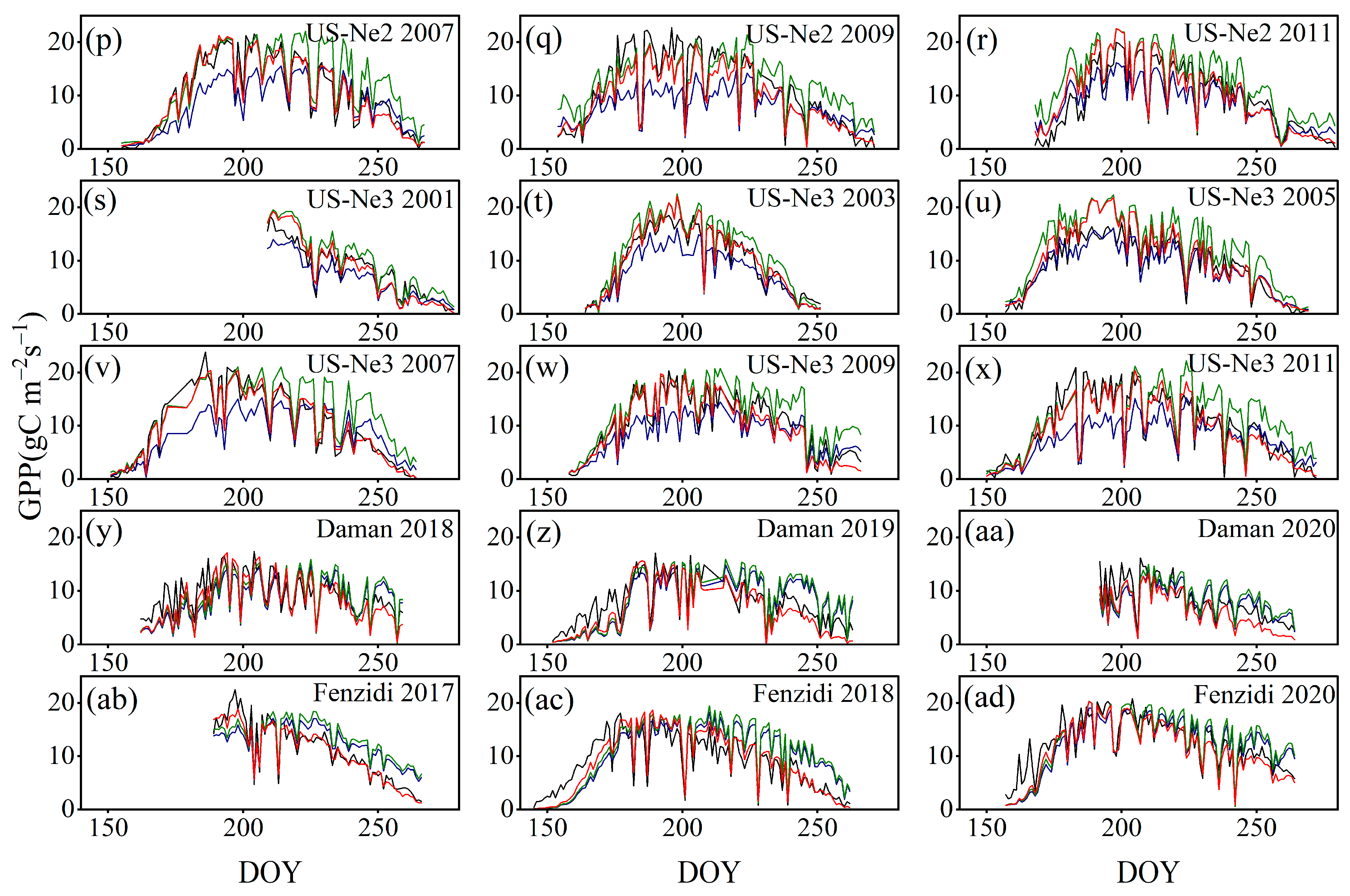
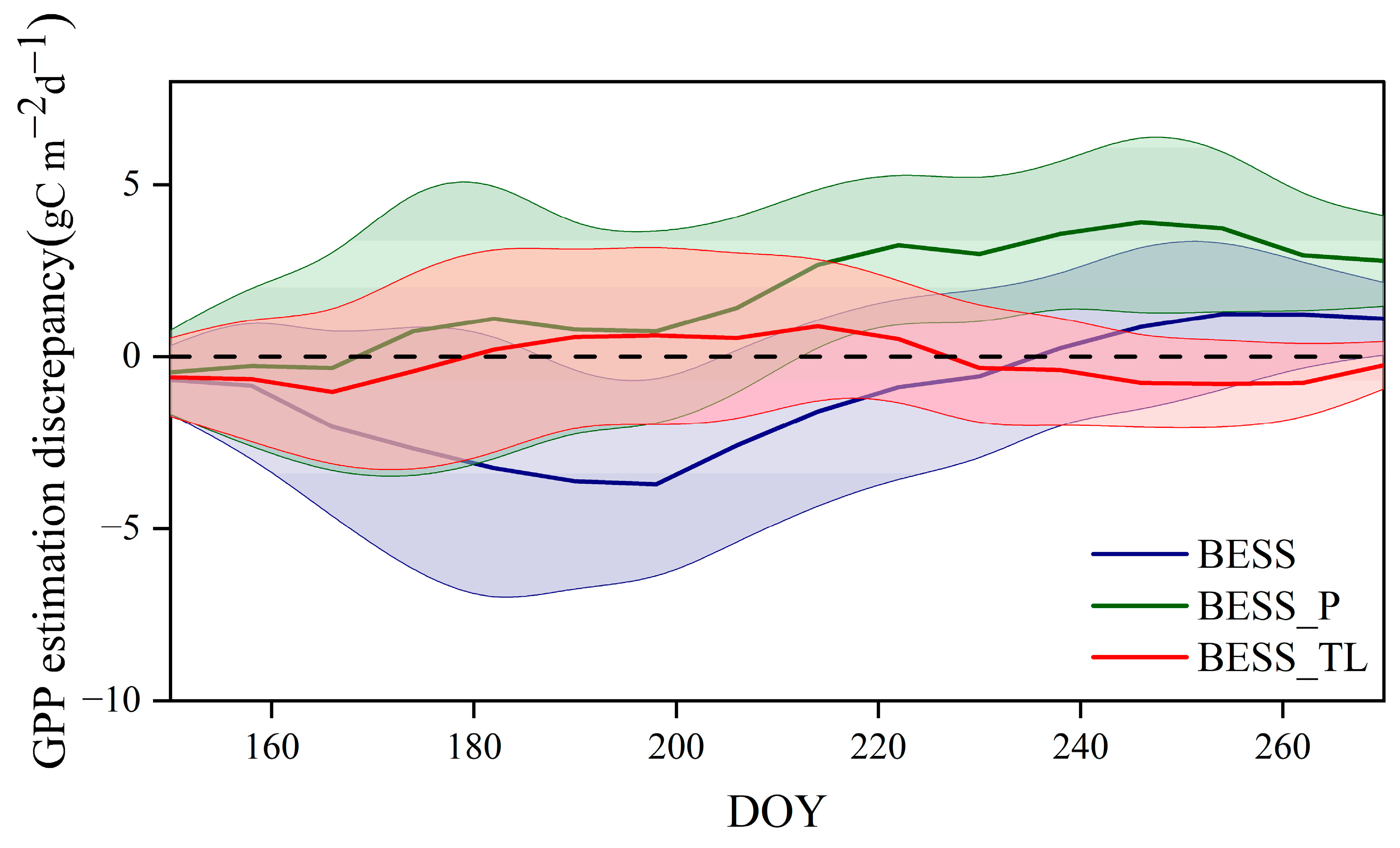
3.3.3. Comparison with the GPP Obtained by BESS
4. Results
4.1. Calibration and Validation of Vm25
4.2. Comparison with the Vm25 Obtained by BESS
4.3. Comparison with the GPP Obtained by BESS
5. Discussion
5.1. Foundation of Vm25 Estimation
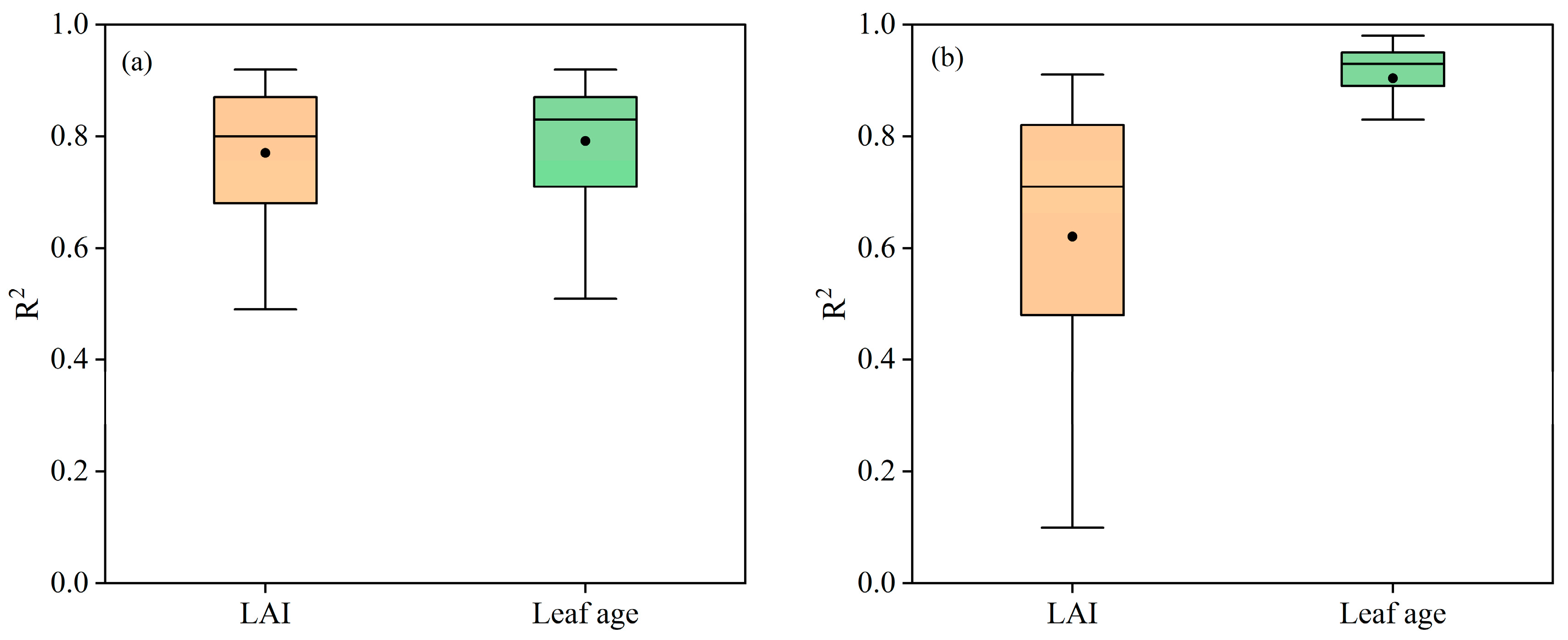
5.2. The Advantages of Leaf Age as a Vm25 Predictor
5.3. Readily Available Leaf Age
5.4. Model Limitations
6. Conclusions
- (1)
- Vm25 inversion: Considering the special photosynthetic process of C4 plants, we replaced the BEPS model with the BESS model coupled with the LRC to invert Vm25 at five maize sites. This method allowed us to obtain continuous Vm25 values throughout the growth period, enabling a detailed study of Vm25 variation trends.
- (2)
- Two-Stage Linear Model Development: We developed a new Two-stage linear model to determine the dynamics changes in maize Vm25. This method divides Vm25 into two stages during the growth process and uses leaf age as the key variable in the simulation, effectively capturing the seasonal variation characteristics of Vm25. Additionally, compared to using a fixed value, this method allows for the calibration of the PeakVm25 value, thereby enhancing model accuracy.
- (3)
- Model Performance and Comparison: The Two-stage linear method more accurately simulated the variation trend of Vm25 compared to the Vm25 of the original BESS model. Furthermore, implementing this method significantly improved the simulation results of GPP. BESS_TL outperforms the other two methods in this study, showing higher R2 and lower RMSE at each site. The GPP simulated by BESS_TL at both interannual and seasonal levels deviated less from the EC GPP. Overall, the developed Vm25 estimation method enhances the accuracy of farmland GPP simulation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
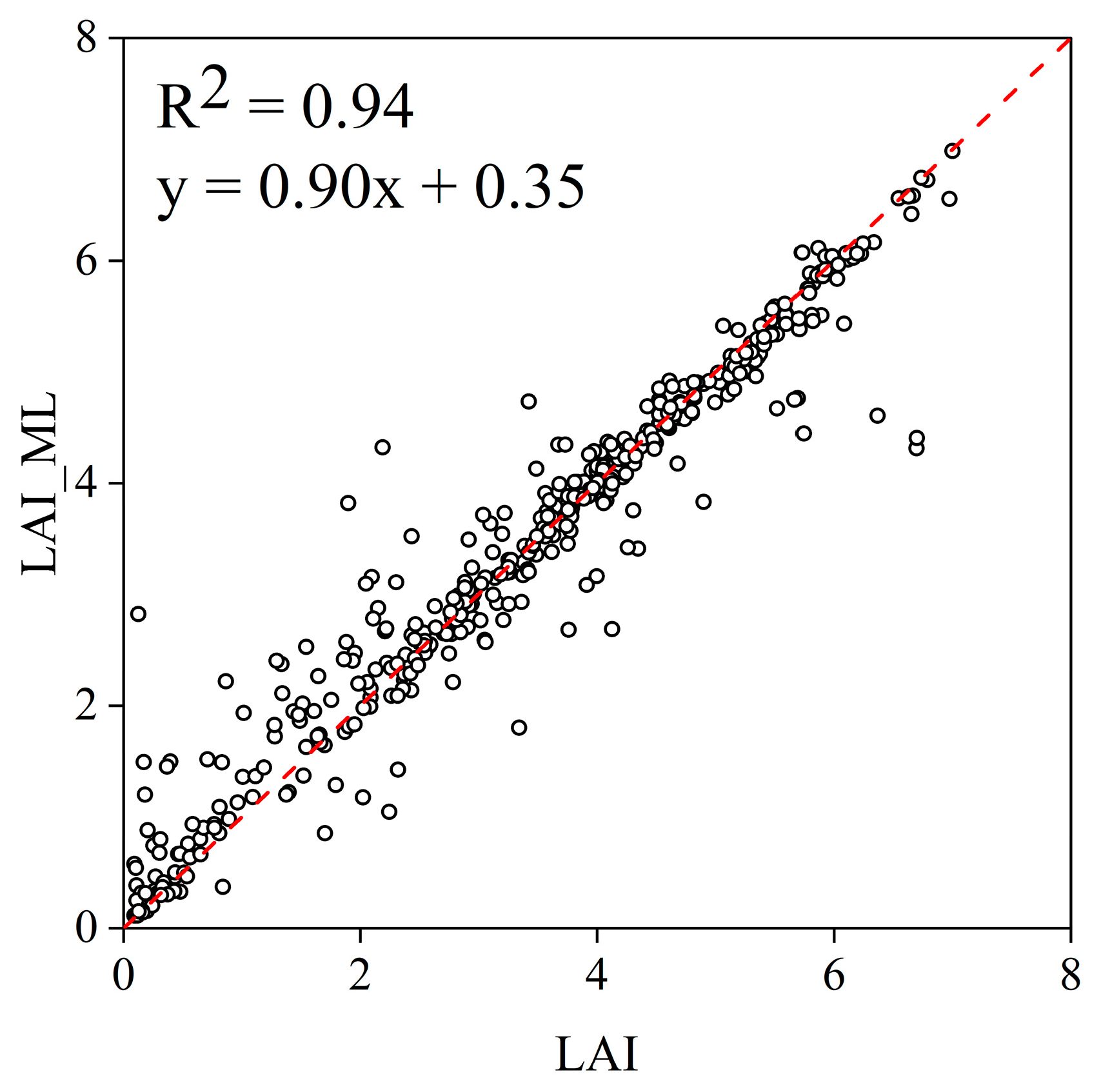
Appendix A. Result of Machine Learning Simulation of LAI
Appendix B. Two-Leaf Canopy Radiative Transfer Model in BESS
References
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rodenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial gross carbon dioxide uptake: Global distribution and covariation with climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Li, X.L.; Liang, S.L.; Yu, G.R.; Yuan, W.P.; Cheng, X.; Xia, J.Z.; Zhao, T.B.; Feng, J.M.; Ma, Z.G.; Ma, M.G.; et al. Estimation of gross primary production over the terrestrial ecosystems in China. Ecol. Model. 2013, 261, 80–92. [Google Scholar] [CrossRef]
- Yuan, W.P.; Liu, S.G.; Yu, G.R.; Bonnefond, J.M.; Chen, J.Q.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar] [CrossRef]
- Smith, N.G.; Keenan, T.F.; Colin Prentice, I.; Wang, H.; Wright, I.J.; Niinemets, Ü.; Crous, K.Y.; Domingues, T.F.; Guerrieri, R.; Ishida, F.Y.; et al. Global photosynthetic capacity is optimized to the environment. Ecol. Lett. 2019, 22, 506–517. [Google Scholar] [CrossRef] [PubMed]
- Zhu, X.J.; Yu, G.R.; Wang, Q.F.; Gao, Y.N.; He, H.L.; Zheng, H.; Chen, Z.; Shi, P.L.; Zhao, L.; Li, Y.N.; et al. Approaches of climate factors affecting the spatial variation of annual gross primary productivity among terrestrial ecosystems in China. Ecol. Indic. 2016, 62, 174–181. [Google Scholar] [CrossRef]
- Miner, G.L.; Bauerle, W.L. Seasonal responses of photosynthetic parameters in maize and sunflower and their relationship with leaf functional traits. Plant Cell Environ. 2019, 42, 1561–1574. [Google Scholar] [CrossRef]
- Rogers, A.; Medlyn, B.E.; Dukes, J.S.; Bonan, G.; von Caemmerer, S.; Dietze, M.C.; Kattge, J.; Leakey, A.D.; Mercado, L.M.; Niinemets, U.; et al. A roadmap for improving the representation of photosynthesis in Earth system models. New Phytol. 2017, 213, 22–42. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.Q.; Li, Y.; Ju, W.M.; Chen, B.; Chen, J.H.; Croft, H.; Mickler, R.A.; Yang, F.T. Estimation of Leaf Photosynthetic Capacity From Leaf Chlorophyll Content and Leaf Age in a Subtropical Evergreen Coniferous Plantation. J. Geophys. Res. Biogeosci. 2020, 125, e2019JG005020. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Kong, D.D.; Gan, R.; Chiew, F.H.S.; McVicar, T.R.; Zhang, Q.; Yang, Y.T. Coupled estimation of 500 m and 8-day resolution global evapotranspiration and gross primary production in 2002-2017. Remote Sens. Environ. 2019, 222, 165–182. [Google Scholar] [CrossRef]
- Liu, J.; Chen, J.M.; Cihlar, J. Mapping evapotranspiration based on remote sensing: An application to Canada’s landmass. Water Resources Res. 2003, 39, 1189. [Google Scholar] [CrossRef]
- Farquhar, G.D.; Caemmerer, S.V.; Berry, J.A. A biochemical model of photosynthetic assimilation in leaves of C3 species. Planta 1980, 149, 67–90. [Google Scholar] [CrossRef]
- Collatz, G.J.; Ribas-Carbo, M.; Berry, J.A. Coupled Photosynthesis-Stomatal Conductance Model for Leaves of C4 Plants. Aust. J. Plant Physiol. 1992, 19, 519–538. [Google Scholar] [CrossRef]
- Lebauer, D.S.; Wang, D.; Richter, K.T.; Davidson, C.C.; Dietze, M.C. Facilitating feedbacks between field measurements and ecosystem models. Ecol. Monogr. 2013, 83, 133–154. [Google Scholar] [CrossRef]
- Bonan, G.B.; Lawrence, P.J.; Oleson, K.W.; Levis, S.; Jung, M.; Reichstein, M.; Lawrence, D.M.; Swenson, S.C. Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from FLUXNET data. J. Geophys. Res. Biogeosci. 2011, 116, G02014. [Google Scholar] [CrossRef]
- Medvigy, D.; Jeong, S.J.; Clark, K.L.; Skowronski, N.S.; Schafer, K.V.R. Effects of seasonal variation of photosynthetic capacity on the carbon fluxes of a temperate deciduous forest. J. Geophys. Res. Biogeosci. 2013, 118, 1703–1714. [Google Scholar] [CrossRef]
- Grassi, G.; Vicinelli, E.; Ponti, F.; Cantoni, L.; Magnani, F. Seasonal and interannual variability of photosynthetic capacity in relation to leaf nitrogen in a deciduous forest plantation in northern Italy. Tree Physiol. 2005, 25, 349–360. [Google Scholar] [CrossRef] [PubMed]
- Yuan, D.K.; Zhang, S.; Li, H.J.; Zhang, J.H.; Yang, S.S.; Bai, Y. Improving the Gross Primary Productivity Estimate by Simulating the Maximum Carboxylation Rate of the Crop Using Machine Learning Algorithms. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4413115. [Google Scholar] [CrossRef]
- Qian, X.J.; Liu, L.Y.; Chen, X.D.; Zarco-Tejada, P. Assessment of Satellite Chlorophyll-Based Leaf Maximum Carboxylation Rate (Vcmax) Using Flux Observations at Crop and Grass Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5352–5360. [Google Scholar] [CrossRef]
- Houborg, R.; Cescatti, A.; Migliavacca, M.; Kustas, W.P. Satellite retrievals of leaf chlorophyll and photosynthetic capacity for improved modeling of GPP. Agric. For. Meteorol. 2013, 177, 10–23. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; van der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Kohler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Glob. Chang. Biol. 2014, 20, 3727–3742. [Google Scholar] [CrossRef]
- Chen, J.M.; Mo, G.; Pisek, J.; Liu, J.; Deng, F.; Ishizawa, M.; Chan, D. Effects of foliage clumping on the estimation of global terrestrial gross primary productivity. Glob. Biogeochem. Cycles 2012, 26, GB1019. [Google Scholar] [CrossRef]
- Gan, R.; Zhang, Y.Q.; Shi, H.; Yang, Y.T.; Eamus, D.; Cheng, L.; Chiew, F.H.S.; Yu, Q. Use of satellite leaf area index estimating evapotranspiration and gross assimilation for Australian ecosystems. Ecohydrology 2018, 11, e1974. [Google Scholar] [CrossRef]
- Dillen, S.Y.; Op de Beeck, M.; Hufkens, K.; Buonanduci, M.; Phillips, N.G. Seasonal patterns of foliar reflectance in relation to photosynthetic capacity and color index in two co-occurring tree species, Quercus rubra and Betula papyrifera. Agric. For. Meteorol. 2012, 160, 60–68. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Chang. Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef] [PubMed]
- Jiang, C.; Ryu, Y.; Wang, H.; Keenan, T.F. An optimality-based model explains seasonal variation in C3 plant photosynthetic capacity. Glob. Chang. Biol. 2020, 26, 6493–6510. [Google Scholar] [CrossRef] [PubMed]
- Bloomfield, K.J.; Prentice, I.C.; Cernusak, L.A.; Eamus, D.; Medlyn, B.E.; Rumman, R.; Wright, I.J.; Boer, M.M.; Cale, P.; Cleverly, J.; et al. The validity of optimal leaf traits modelled on environmental conditions. New Phytol. 2019, 221, 1409–1423. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Atkin, O.K.; Keenan, T.F.; Smith, N.G.; Wright, I.J.; Bloomfield, K.J.; Kattge, J.; Reich, P.B.; Prentice, I.C. Acclimation of leaf respiration consistent with optimal photosynthetic capacity. Glob. Chang. Biol. 2020, 26, 2573–2583. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wang, P.Y.; Wang, S.Q.; Ju, W.M.; Liu, Z.H.; Zhang, Y.H. Simulating canopy carbonyl sulfide uptake of two forest stands through an improved ecosystem model and parameter optimization using an ensemble Kalman filter. Ecol. Model. 2023, 475, 110212. [Google Scholar] [CrossRef]
- Mo, X.G.; Chen, J.M.; Ju, W.M.; Black, T.A. Optimization of ecosystem model parameters through assimilating eddy covariance flux data with an ensemble Kalman filter. Ecol. Model. 2008, 217, 157–173. [Google Scholar] [CrossRef]
- Xu, T.R.; Chen, F.; He, X.L.; Barlage, M.; Zhang, Z.; Liu, S.M.; He, X.P. Improve the Performance of the Noah-MP-Crop Model by Jointly Assimilating Soil Moisture and Vegetation Phenology Data. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002394. [Google Scholar] [CrossRef]
- Zheng, T.; Chen, J.; He, L.M.; Arain, M.A.; Thomas, S.C.; Murphy, J.G.; Geddes, J.A.; Black, T.A. Inverting the maximum carboxylation rate (V-cmax) from the sunlit leaf photosynthesis rate derived from measured light response curves at tower flux sites. Agric. For. Meteorol. 2017, 236, 48–66. [Google Scholar] [CrossRef]
- Xie, X.Y.; Li, A.N.; Jin, H.A.; Yin, G.F.; Nan, X. Derivation of temporally continuous leaf maximum carboxylation rate (V-cmax) from the sunlit leaf gross photosynthesis productivity through combining BEPS model with light response curve at tower flux sites. Agric. For. Meteorol. 2018, 259, 82–94. [Google Scholar] [CrossRef]
- Wang, X.P.; Chen, J.M.; Ju, W.M.; Zhang, Y.G. Seasonal Variations in Leaf Maximum Photosynthetic Capacity and Its Dependence on Climate Factors Across Global FLUXNET Sites. J. Geophys. Res. Biogeosci. 2022, 127, e2021JG006709. [Google Scholar] [CrossRef]
- Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Penuelas, J.; Valentini, R. Relationships between Ndvi, Canopy Structure, and Photosynthesis in 3 Californian Vegetation Types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef]
- Alton, P.B. Retrieval of seasonal Rubisco-limited photosynthetic capacity at global FLUXNET sites from hyperspectral satellite remote sensing: Impact on carbon modelling. Agric. For. Meteorol. 2017, 232, 74–88. [Google Scholar] [CrossRef]
- Ryu, Y.; Berry, J.A.; Baldocchi, D.D. What is global photosynthesis? History, uncertainties and opportunities. Remote Sens. Environ. 2019, 223, 95–114. [Google Scholar] [CrossRef]
- Jin, J.; Pratama, B.A.; Wang, Q. Tracing Leaf Photosynthetic Parameters Using Hyperspectral Indices in an Alpine Deciduous Forest. Remote Sens. 2020, 12, 1124. [Google Scholar] [CrossRef]
- Serbin, S.P.; Singh, A.; Desai, A.R.; Dubois, S.G.; Jablonsld, A.D.; Kingdon, C.C.; Kruger, E.L.; Townsend, P.A. Remotely estimating photosynthetic capacity, and its response to temperature, in vegetation canopies using imaging spectroscopy. Remote Sens. Environ. 2015, 167, 78–87. [Google Scholar] [CrossRef]
- Kattge, J.; Knorr, W.; Raddatz, T.; Wirth, C. Quantifying photosynthetic capacity and its relationship to leaf nitrogen content for global-scale terrestrial biosphere models. Glob. Chang. Biol. 2009, 15, 976–991. [Google Scholar] [CrossRef]
- Archontoulis, S.V.; Yin, X.; Vos, J.; Danalatos, N.G.; Struik, P.C. Leaf photosynthesis and respiration of three bioenergy crops in relation to temperature and leaf nitrogen: How conserved are biochemical model parameters among crop species? J. Exp. Bot. 2012, 63, 895–911. [Google Scholar] [CrossRef]
- Yamori, W.; Nagai, T.; Makino, A. The rate-limiting step for CO2 assimilation at different temperatures is influenced by the leaf nitrogen content in several C3 crop species. Plant Cell Environ. 2011, 34, 764–777. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.G.; Guanter, L.; Joiner, J.; Song, L.; Guan, K.Y. Spatially-explicit monitoring of crop photosynthetic capacity through the use of space-based chlorophyll fluorescence data. Remote Sens. Environ. 2018, 210, 362–374. [Google Scholar] [CrossRef]
- Luo, X.; Croft, H.; Chen, J.M.; He, L.; Keenan, T.F. Improved estimates of global terrestrial photosynthesis using information on leaf chlorophyll content. Glob. Chang. Biol. 2019, 25, 2499–2514. [Google Scholar] [CrossRef] [PubMed]
- Houborg, R.; McCabe, M.F.; Cescatti, A.; Gitelson, A.A. Leaf chlorophyll constraint on model simulated gross primary productivity in agricultural systems. Int. J. Appl. Earth Obs. Geoinf. 2015, 43, 160–176. [Google Scholar] [CrossRef]
- Qian, X.; Liu, L.; Croft, H.; Chen, J. Relationship Between Leaf Maximum Carboxylation Rate and Chlorophyll Content Preserved Across 13 Species. J. Geophys. Res. Biogeosci. 2021, 126, e2020JG006076. [Google Scholar] [CrossRef]
- Qian, B.X.; Ye, H.C.; Huang, W.J.; Xie, Q.Y.; Pan, Y.H.; Xing, N.C.; Ren, Y.; Guo, A.T.; Jiao, Q.J.; Lan, Y.B. A sentinel-2-based triangular vegetation index for chlorophyll content estimation. Agric. For. Meteorol. 2022, 322, 109000. [Google Scholar] [CrossRef]
- Genty, B.; Briantais, J.M.; Baker, N.R. The Relationship between the Quantum Yield of Photosynthetic Electron-Transport and Quenching of Chlorophyll Fluorescence. Biochim. Et Biophys. Acta (BBA)-Gen. Subj. 1989, 990, 87–92. [Google Scholar] [CrossRef]
- Yang, X.; Tang, J.W.; Mustard, J.F.; Lee, J.E.; Rossini, M.; Joiner, J.; Munger, J.W.; Kornfeld, A.; Richardson, A.D. Solar-induced chlorophyll fluorescence that correlates with canopy photosynthesis on diurnal and seasonal scales in a temperate deciduous forest. Geophys. Res. Lett. 2015, 42, 2977–2987. [Google Scholar] [CrossRef]
- He, L.; Chen, J.M.; Liu, J.; Zheng, T.; Wang, R.; Joiner, J.; Chou, S.; Chen, B.; Liu, Y.; Liu, R.; et al. Diverse photosynthetic capacity of global ecosystems mapped by satellite chlorophyll fluorescence measurements. Remote Sens. Environ. 2019, 232, 111344. [Google Scholar] [CrossRef]
- Camino, C.; Gonzalez-Dugo, V.; Hernandez, P.; Zarco-Tejada, P.J. Radiative transfer Vcmax estimation from hyperspectral imagery and SIF retrievals to assess photosynthetic performance in rainfed and irrigated plant phenotyping trials. Remote Sens. Environ. 2019, 231, 111186. [Google Scholar] [CrossRef]
- Chen, R.A.; Liu, L.Y.; Liu, X.J. Leaf chlorophyll contents dominates the seasonal dynamics of SIF/GPP ratio: Evidence from continuous measurements in a maize field. Agric. For. Meteorol. 2022, 323, 109070. [Google Scholar] [CrossRef]
- Jin, P.B.; Wang, Q.; Iio, A.; Tenhunen, J. Retrieval of seasonal variation in photosynthetic capacity from multi-source vegetation indices. Ecol. Inform. 2012, 7, 7–18. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Ju, W.M.; Sun, X.M.; Hu, Z.M.; Han, S.J.; Black, T.A.; Jassal, R.S.; Wu, X.C. Close relationship between spectral vegetation indices and V-cmax in deciduous and mixed forests. Tellus B Chem. Phys. Meteorol. 2014, 66, 23279. [Google Scholar] [CrossRef]
- Muraoka, H.; Noda, H.M.; Nagai, S.; Motohka, T.; Saitoh, T.M.; Nasahara, K.N.; Saigusa, N. Spectral vegetation indices as the indicator of canopy photosynthetic productivity in a deciduous broadleaf forest. J. Plant Ecol. 2013, 6, 393–407. [Google Scholar] [CrossRef]
- Wang, R.; Chen, J.M.; Luo, X.Z.; Black, A.; Arain, A. Seasonality of leaf area index and photosynthetic capacity for better estimation of carbon and water fluxes in evergreen conifer forests. Agric. For. Meteorol. 2019, 279, 107708. [Google Scholar] [CrossRef]
- Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; van Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; van Gorsel, E.; Knohl, A.; Law, B.E.; et al. Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales. Glob. Biogeochem. Cycles 2011, 25, GB4017. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhu, Z.; Zeng, H.; Myneni, R.B.; Zhang, Y.; Penuelas, J.; Piao, S. Seasonal peak photosynthesis is hindered by late canopy development in northern ecosystems. Nat. Plants 2022, 8, 1484–1492. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.; Xu, M.; Pan, H.; Yu, X. Leaf-age effects on temperature responses of photosynthesis and respiration of an alpine oak, Quercus aquifolioides, in southwestern China. Tree Physiol. 2015, 35, 1236–1248. [Google Scholar] [CrossRef] [PubMed]
- Locke, A.M.; Ort, D.R. Leaf hydraulic conductance declines in coordination with photosynthesis, transpiration and leaf water status as soybean leaves age regardless of soil moisture. J. Exp. Bot. 2014, 65, 6617–6627. [Google Scholar] [CrossRef]
- Reich, P.B.; Walters, M.B.; Ellsworth, D.S. Leaf Age and Season Influence the Relationships between Leaf Nitrogen, Leaf Mass Per Area and Photosynthesis in Maple and Oak Trees. Plant Cell Environ. 1991, 14, 251–259. [Google Scholar] [CrossRef]
- Richardson, A.D.; Anderson, R.S.; Arain, M.A.; Barr, A.G.; Bohrer, G.; Chen, G.S.; Chen, J.M.; Ciais, P.; Davis, K.J.; Desai, A.R.; et al. Terrestrial biosphere models need better representation of vegetation phenology: Results from the North American Carbon Program Site Synthesis. Glob. Chang. Biol. 2012, 18, 566–584. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Suyker, A.; Xiao, X.M. Modeling gross primary production of maize and soybean croplands using light quality, temperature, water stress, and phenology. Agric. For. Meteorol. 2015, 213, 160–172. [Google Scholar] [CrossRef]
- Wu, Q.L.; Song, C.H.; Song, J.L.; Wang, J.D.; Chen, S.Y.; Yang, L.; Xiang, W.H.; Zhao, Z.H.; Jiang, J. Effects of leaf age and canopy structure on gross ecosystem production in a subtropical evergreen Chinese fir forest. Agric. For. Meteorol. 2021, 310, 108618. [Google Scholar] [CrossRef]
- Meijide, A.; Roll, A.; Fan, Y.C.; Herbst, M.; Niu, F.R.; Tiedemann, F.; June, T.; Rauf, A.; Holoscher, D.; Knohl, A. Controls of water and energy fluxes in oil palm plantations: Environmental variables and oil palm age. Agric. For. Meteorol. 2017, 239, 71–85. [Google Scholar] [CrossRef]
- Li, S.; Fleisher, D.H.; Wang, Z.; Barnaby, J.; Timlin, D.; Reddy, V.R. Application of a coupled model of photosynthesis, stomatal conductance and transpiration for rice leaves and canopy. Comput. Electron. Agric. 2021, 182, 106047. [Google Scholar] [CrossRef]
- Wu, J.; Albert, L.P.; Lopes, A.P.; Restrepo-Coupe, N.; Hayek, M.; Wiedemann, K.T.; Guan, K.; Stark, S.C.; Christoffersen, B.; Prohaska, N.; et al. Leaf development and demography explain photosynthetic seasonality in Amazon evergreen forests. Science 2016, 351, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Kositsup, B.; Kasemsap, P.; Thanisawanyangkura, S.; Chairungsee, N.; Satakhun, D.; Teerawatanasuk, K.; Ameglio, T.; Thaler, P. Effect of leaf age and position on light-saturated CO2 assimilation rate, photosynthetic capacity, and stomatal conductance in rubber trees. Photosynthetica 2010, 48, 67–78. [Google Scholar] [CrossRef]
- Lu, X.H.; Ju, W.M.; Li, J.; Croft, H.; Chen, J.M.; Luo, Y.Q.; Yu, H.; Hu, H.J. Maximum Carboxylation Rate Estimation With Chlorophyll Content as a Proxy of Rubisco Content. J. Geophys. Res. Biogeosci. 2020, 125, e2020JG005748. [Google Scholar] [CrossRef]
- Pastorello, G.; Trotta, C.; Canfora, E.; Chu, H.S.; Christianson, D.; Cheah, Y.W.; Poindexter, C.; Chen, J.Q.; Elbashandy, A.; Humphrey, M.; et al. The FLUXNET2015 dataset and the ONEFlux processing pipeline for eddy covariance data. Sci. Data 2020, 7, 225. [Google Scholar] [CrossRef]
- Liu, S.M.; Xu, Z.W.; Wang, W.Z.; Jia, Z.Z.; Zhu, M.J.; Bai, J.; Wang, J.M. A comparison of eddy-covariance and large aperture scintillometer measurements with respect to the energy balance closure problem. Hydrol. Earth Syst. Sci. 2011, 15, 1291–1306. [Google Scholar] [CrossRef]
- Liu, S.M.; Li, X.; Xu, Z.W.; Che, T.; Xiao, Q.; Ma, M.G.; Liu, Q.H.; Jin, R.; Guo, J.W.; Wang, L.X.; et al. The Heihe Integrated Observatory Network: A Basin-Scale Land Surface Processes Observatory in China. Vadose Zone J. 2018, 17, 180072. [Google Scholar] [CrossRef]
- Suyker, A.E.; Verma, S.B. Gross primary production and ecosystem respiration of irrigated and rainfed maize-soybean cropping systems over 8 years. Agric. For. Meteorol. 2012, 165, 12–24. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.H.; Zhang, S.; Yao, F.M.; Magliulo, V. A remote sensing-based two-leaf canopy conductance model: Global optimization and applications in modeling gross primary productivity and evapotranspiration of crops. Remote Sens. Environ. 2018, 215, 411–437. [Google Scholar] [CrossRef]
- Chen, J.M.; Menges, C.H.; Leblanc, S.G. Global mapping of foliage clumping index using multi-angular satellite data. Remote Sens. Environ. 2005, 97, 447–457. [Google Scholar] [CrossRef]
- Chen, J.M.; Black, T.A. Foliage area and architecture of plant canopies from sunfleck size distributions. Agric. For. Meteorol. 1992, 60, 249–266. [Google Scholar] [CrossRef]
- He, L.M.; Chen, J.M.; Pisek, J.; Schaaf, C.; Strahler, A.H.; IEEE. Global clumping index map derived from modis BRDF products. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 24–29 July 2011; pp. 1255–1258. [Google Scholar] [CrossRef]
- He, L.M.; Chen, J.M.; Pisek, J.; Schaaf, C.B.; Strahler, A.H. Global clumping index map derived from the MODIS BRDF product. Remote Sens. Environ. 2012, 119, 118–130. [Google Scholar] [CrossRef]
- Lasslop, G.; Reichstein, M.; Papale, D.; Richardson, A.D.; Arneth, A.; Barr, A.; Stoy, P.; Wohlfahrt, G. Separation of net ecosystem exchange into assimilation and respiration using a light response curve approach: Critical issues and global evaluation. Glob. Chang. Biol. 2010, 16, 187–208. [Google Scholar] [CrossRef]
- Chen, J.M.; Liu, J.; Cihlar, J.; Goulden, M.L. Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications. Ecol. Model. 1999, 124, 99–119. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and drainage paper No. 56. Rome Food Agric. Organ. United Nations 1998, 56, e156. [Google Scholar]
- De Kauwe, M.G.; Lin, Y.S.; Wright, I.J.; Medlyn, B.E.; Crous, K.Y.; Ellsworth, D.S.; Maire, V.; Prentice, I.C.; Atkin, O.K.; Rogers, A.; et al. A test of the ‘one-point method’ for estimating maximum carboxylation capacity from field-measured, light-saturated photosynthesis. New Phytol. 2016, 210, 1130–1144. [Google Scholar] [CrossRef]
- Jiang, C.; Ryu, Y. Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS). Remote Sens. Environ. 2016, 186, 528–547. [Google Scholar] [CrossRef]
- Houborg, R.; Anderson, M.C.; Norman, J.M.; Wilson, T.; Meyers, T. Intercomparison of a ‘bottom-up’ and ‘top-down’ modeling paradigm for estimating carbon and energy fluxes over a variety of vegetative regimes across the U.S. Agric. For. Meteorol. 2009, 149, 1875–1895. [Google Scholar] [CrossRef]
- Bauerle, W.L.; Oren, R.; Way, D.A.; Qian, S.S.; Stoy, P.C.; Thornton, P.E.; Bowden, J.D.; Hoffman, F.M.; Reynolds, R.F. Photoperiodic regulation of the seasonal pattern of photosynthetic capacity and the implications for carbon cycling. Proc. Natl. Acad. Sci. USA 2012, 109, 8612–8617. [Google Scholar] [CrossRef] [PubMed]
- Stinziano, J.R.; Huner, N.P.; Way, D.A. Warming delays autumn declines in photosynthetic capacity in a boreal conifer, Norway spruce (Picea abies). Tree Physiol. 2015, 35, 1303–1313. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Shi, L.S.; Zha, Y.Y.; Liu, S.B.; Nie, C.W.; Xu, H.G.; Yang, H.Y.; Shao, M.C.; Yu, X.; Cheng, M.H.; et al. Estimating leaf age of maize seedlings using UAV-based RGB and multispectral images. Comput. Electron. Agric. 2023, 215, 108349. [Google Scholar] [CrossRef]
- Adams, M.L.; Norvell, W.A.; Peverly, J.H.; Philpot, W.D. Fluorescence and reflectance characteristics of manganese deficient soybean leaves: Effects of leaf age and choice of leaflet. Plant Soil 1993, 155–156, 235–238. [Google Scholar] [CrossRef]
- De Pury, D.G.G.; Farquhar, G.D. Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models. Plant Cell Environ. 1997, 20, 537–557. [Google Scholar] [CrossRef]


| Site | Latitude | Longitude | Crop Type | Year | LAI |
|---|---|---|---|---|---|
| US-Ne1 | 41.165°N | 96.477°W | Maize | 2001–2012 | — |
| US-Ne2 | 41.165°N | 96.470°W | Maize–Soybean | 2001–2012 | Literature * |
| US-Ne3 | 41.180°N | 96.440°W | Maize–Soybean | 2001–2012 | Literature * |
| Daman | 38.853°N | 100.376°E | Maize | 2018, 2019, 2021 | measured |
| Fenzidi | 41.153°N | 107.653°E | Maize | 2017, 2018, 2020 | measured |
| Site | BESS | BESS_P | BESS_TL | |||
|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| US-Ne1 | 18.93 | 0.23 | 25.07 | 0.23 | 7.54 | 0.85 |
| US-Ne2 | 16.58 | 0.52 | 22.67 | 0.52 | 6.82 | 0.88 |
| US-Ne3 | 14.70 | 0.67 | 19.46 | 0.67 | 6.82 | 0.87 |
| Daman | 14.55 | 0.02 | 16.99 | 0.02 | 6.44 | 0.71 |
| Fenzidi | 13.25 | 0.01 | 15.30 | 0.01 | 5.40 | 0.82 |
| Site | BESS | BESS_P | BESS_TL | |||
|---|---|---|---|---|---|---|
| RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| US-Ne1 | 3.69 | 0.66 | 4.07 | 0.70 | 2.29 | 0.86 |
| US-Ne2 | 3.48 | 0.80 | 3.53 | 0.83 | 2.03 | 0.90 |
| US-Ne3 | 2.99 | 0.83 | 3.32 | 0.85 | 2.04 | 0.89 |
| Daman | 2.96 | 0.53 | 3.02 | 0.53 | 2.32 | 0.82 |
| Fenzidi | 3.35 | 0.63 | 3.64 | 0.63 | 2.06 | 0.87 |
| Site | BESS | BESS_P | BESS_TL | |||
|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | |
| US-Ne1 | −1.56 | 3.35 | 2.39 | 3.30 | 0.12 | 2.29 |
| US-Ne2 | −1.69 | 3.03 | 2.40 | 2.59 | −0.02 | 2.03 |
| US-Ne3 | −1.56 | 2.56 | 2.31 | 3.32 | 0.29 | 2.02 |
| Daman | −0.43 | 2.92 | 0.22 | 3.01 | −1.42 | 1.82 |
| Fenzidi | −0.06 | 3.29 | −0.13 | 3.49 | 0.05 | 2.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wang, S.; Wang, W.; Rong, Y.; Zhang, C.; Wang, C.; Huo, Z. Improving the Gross Primary Productivity Estimation by Simulating the Maximum Carboxylation Rate of Maize Using Leaf Age. Remote Sens. 2024, 16, 2747. https://doi.org/10.3390/rs16152747
Zhang X, Wang S, Wang W, Rong Y, Zhang C, Wang C, Huo Z. Improving the Gross Primary Productivity Estimation by Simulating the Maximum Carboxylation Rate of Maize Using Leaf Age. Remote Sensing. 2024; 16(15):2747. https://doi.org/10.3390/rs16152747
Chicago/Turabian StyleZhang, Xin, Shuai Wang, Weishu Wang, Yao Rong, Chenglong Zhang, Chaozi Wang, and Zailin Huo. 2024. "Improving the Gross Primary Productivity Estimation by Simulating the Maximum Carboxylation Rate of Maize Using Leaf Age" Remote Sensing 16, no. 15: 2747. https://doi.org/10.3390/rs16152747
APA StyleZhang, X., Wang, S., Wang, W., Rong, Y., Zhang, C., Wang, C., & Huo, Z. (2024). Improving the Gross Primary Productivity Estimation by Simulating the Maximum Carboxylation Rate of Maize Using Leaf Age. Remote Sensing, 16(15), 2747. https://doi.org/10.3390/rs16152747










