System Design of Ocean Temperature Measurement System Using Brillouin Lidar Based on Dual Iodine Cells
Abstract
1. Introduction
2. Principle
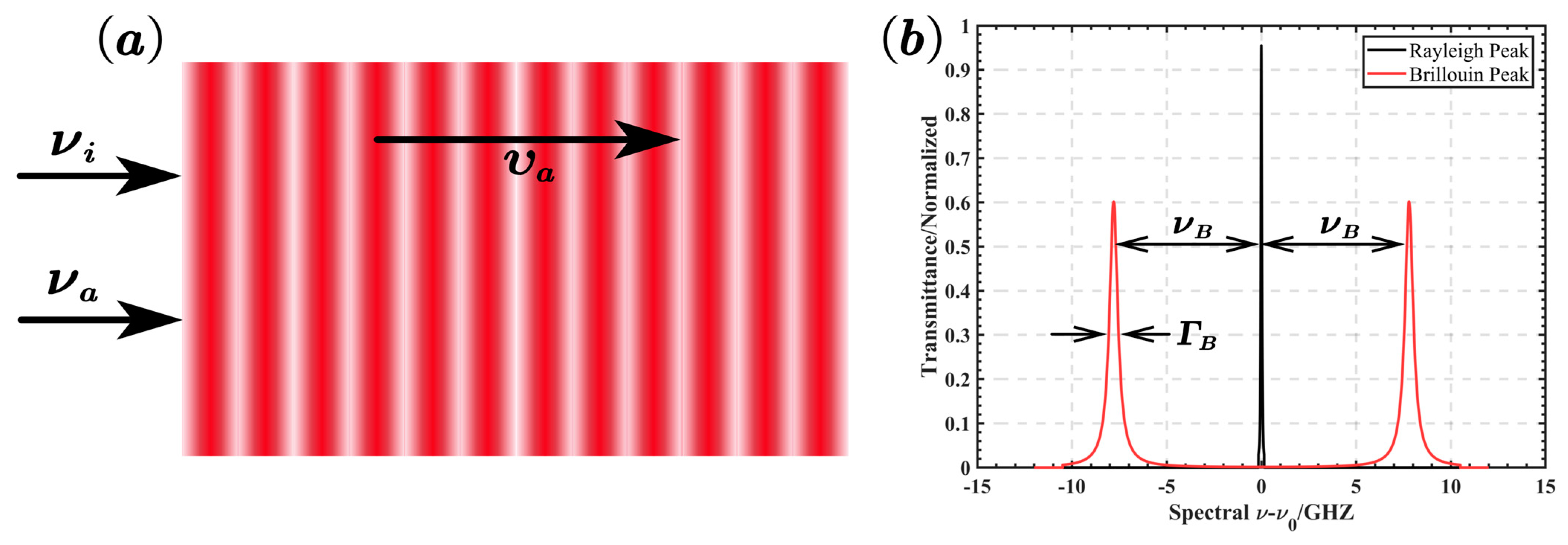
2.1. Brillouin Scattering Detection Based on Iodine Cells
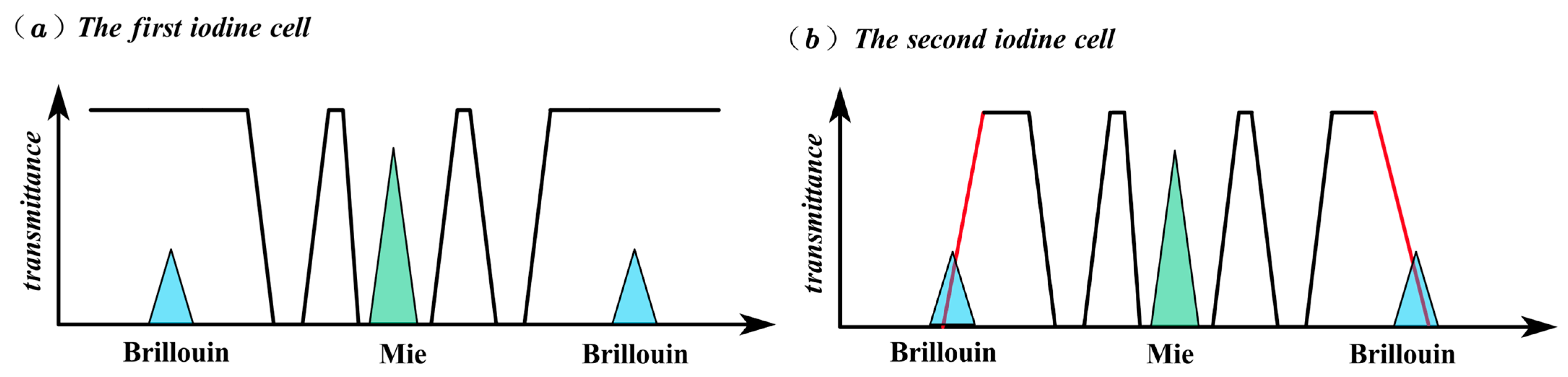
2.2. Dual Iodine Cells for Temperature Measurement
- Separate the elastic scattering and Brillouin scattering. The elastic scattering should be absorbed sufficiently completely, while the Brillouin scattering signals pass with high transmittance and are preserved as much as possible.
- The absorption rate of the elastic scattering should remain relatively stable when the laser frequency has a certain jitter.
- According to the principle of edge detection, the Brillouin signal should lie at the steep edge of the iodine cell absorption curve.
- It should meet several requirements regarding the relationship between the output signal intensity and temperature. First, the monotonicity should be uniform. Second, the slope should be as steep as possible. Third, it should remain relatively stable when the laser frequency has a certain jitter. Fourth, its value, influenced by the ratio of the Mie scattering intensity and Brillouin scattering intensity, should be kept as small as possible.
2.3. Laser Center Frequency
3. System Design
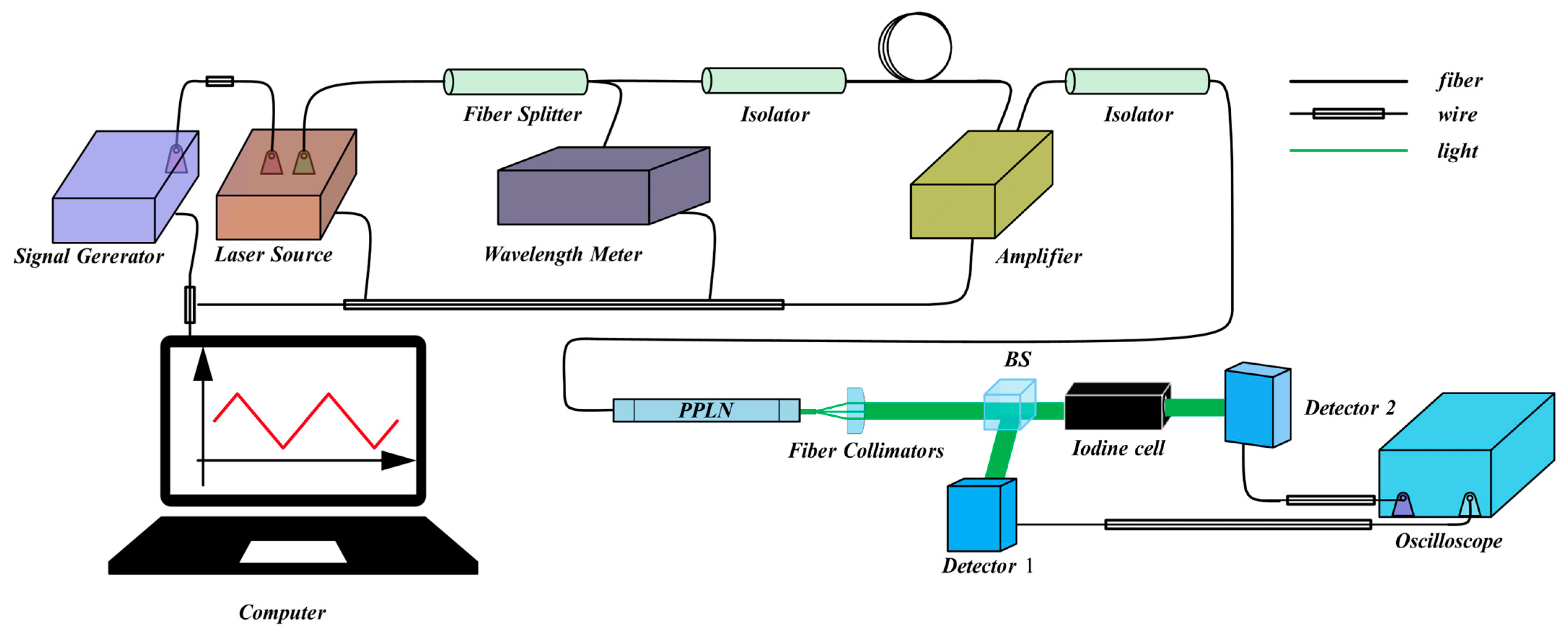
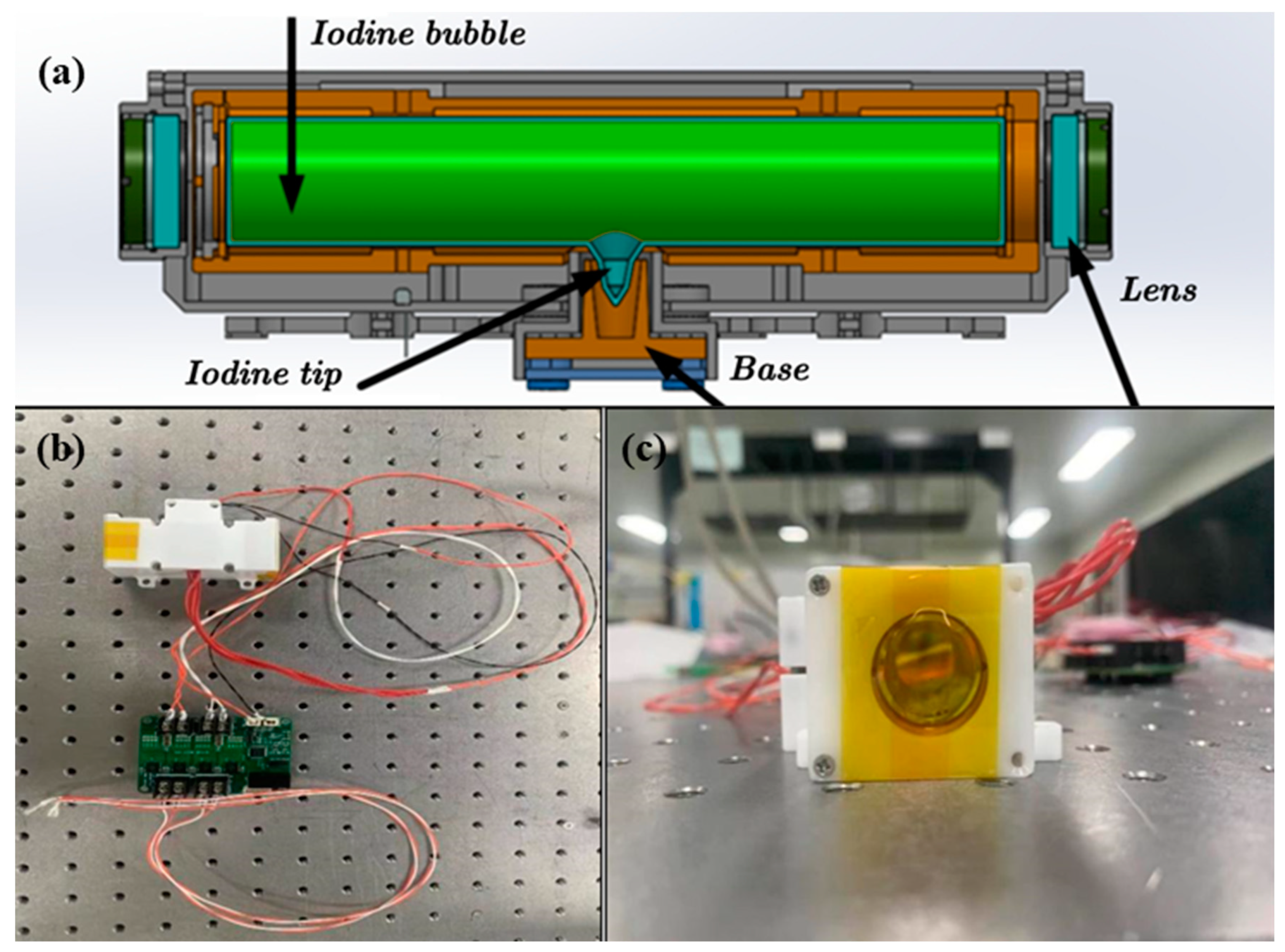
3.1. Real Iodine Cell Absorption Spectrum Testing Device
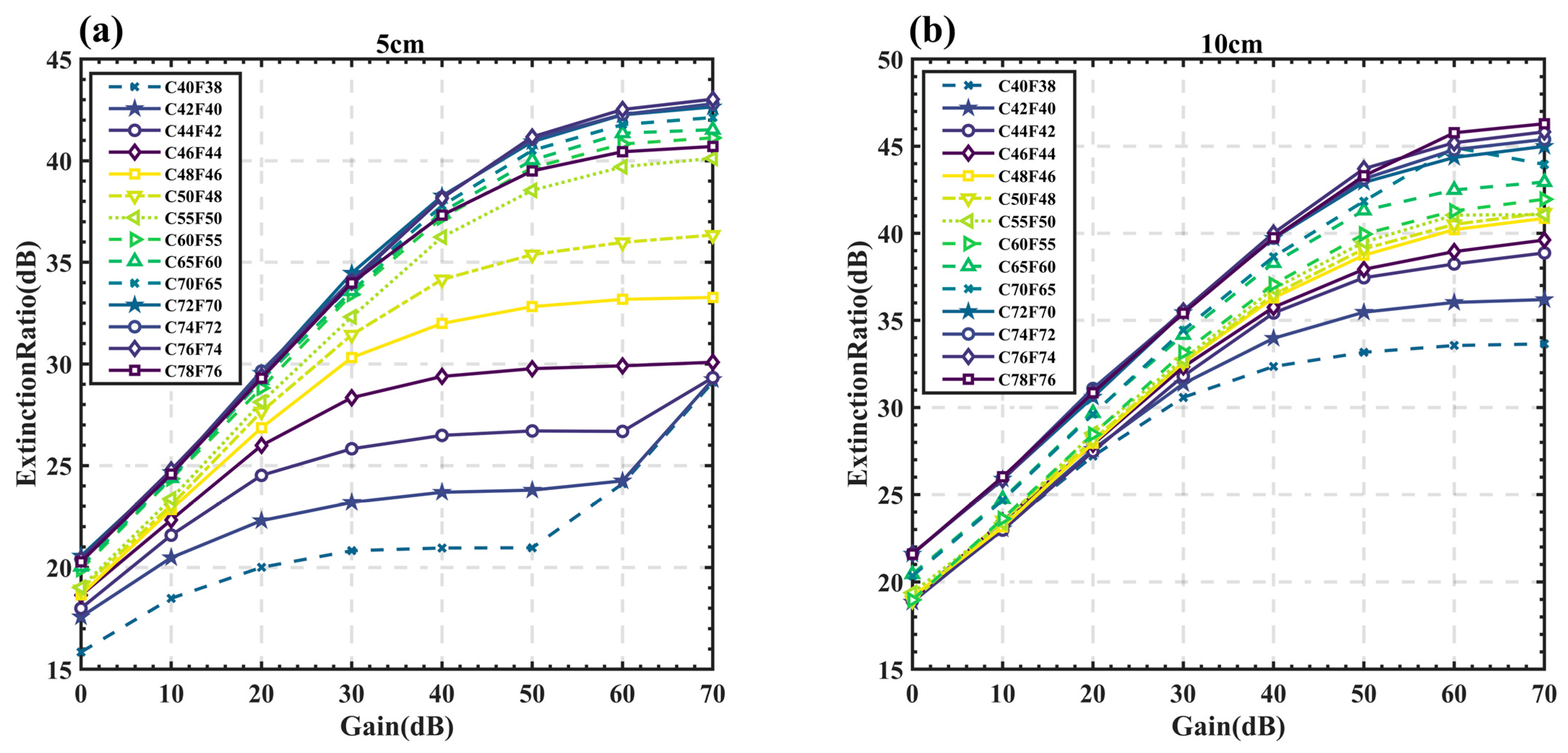
3.2. Extinction Ratio Test
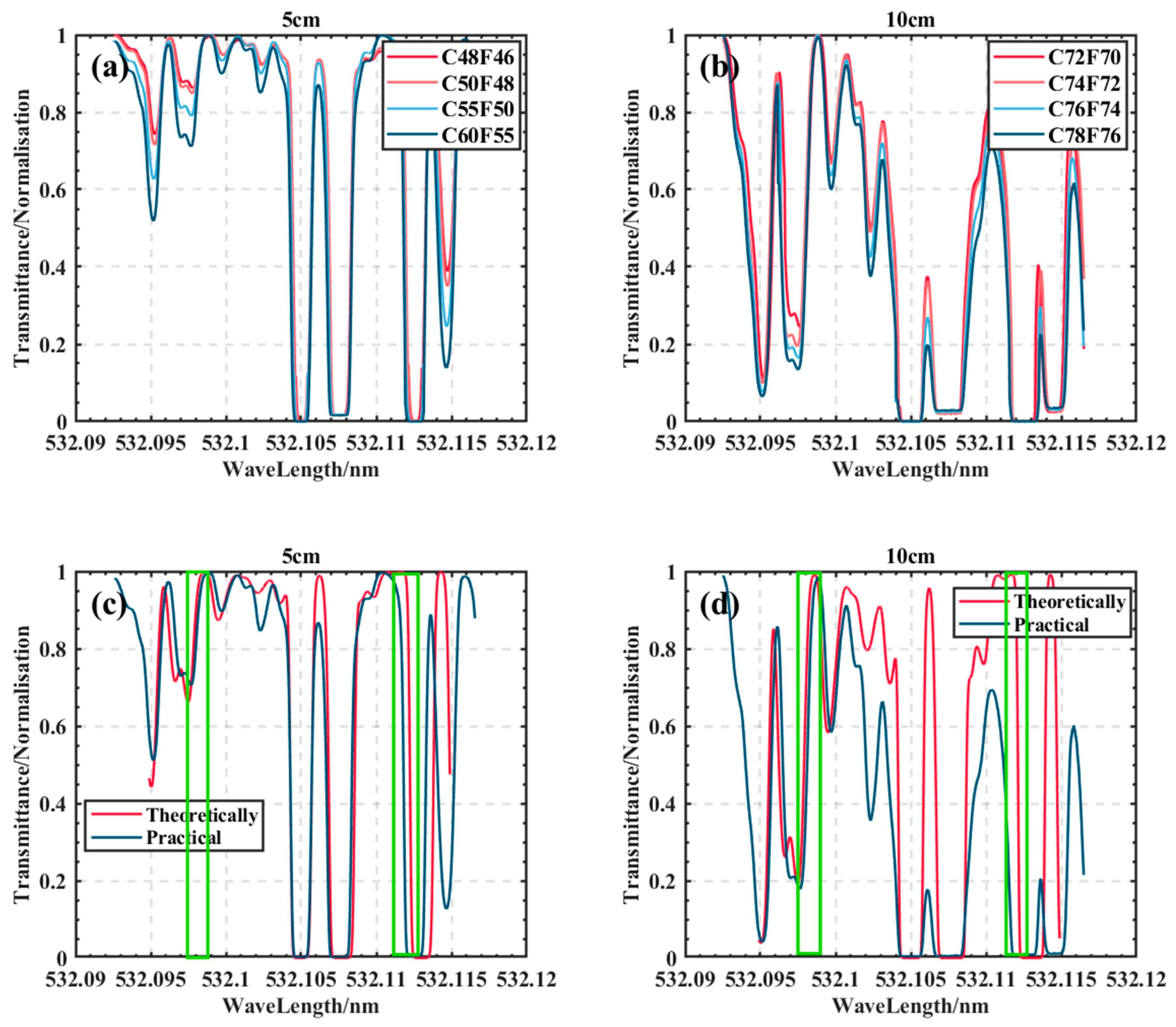
3.3. Iodine Absorption Spectra Test
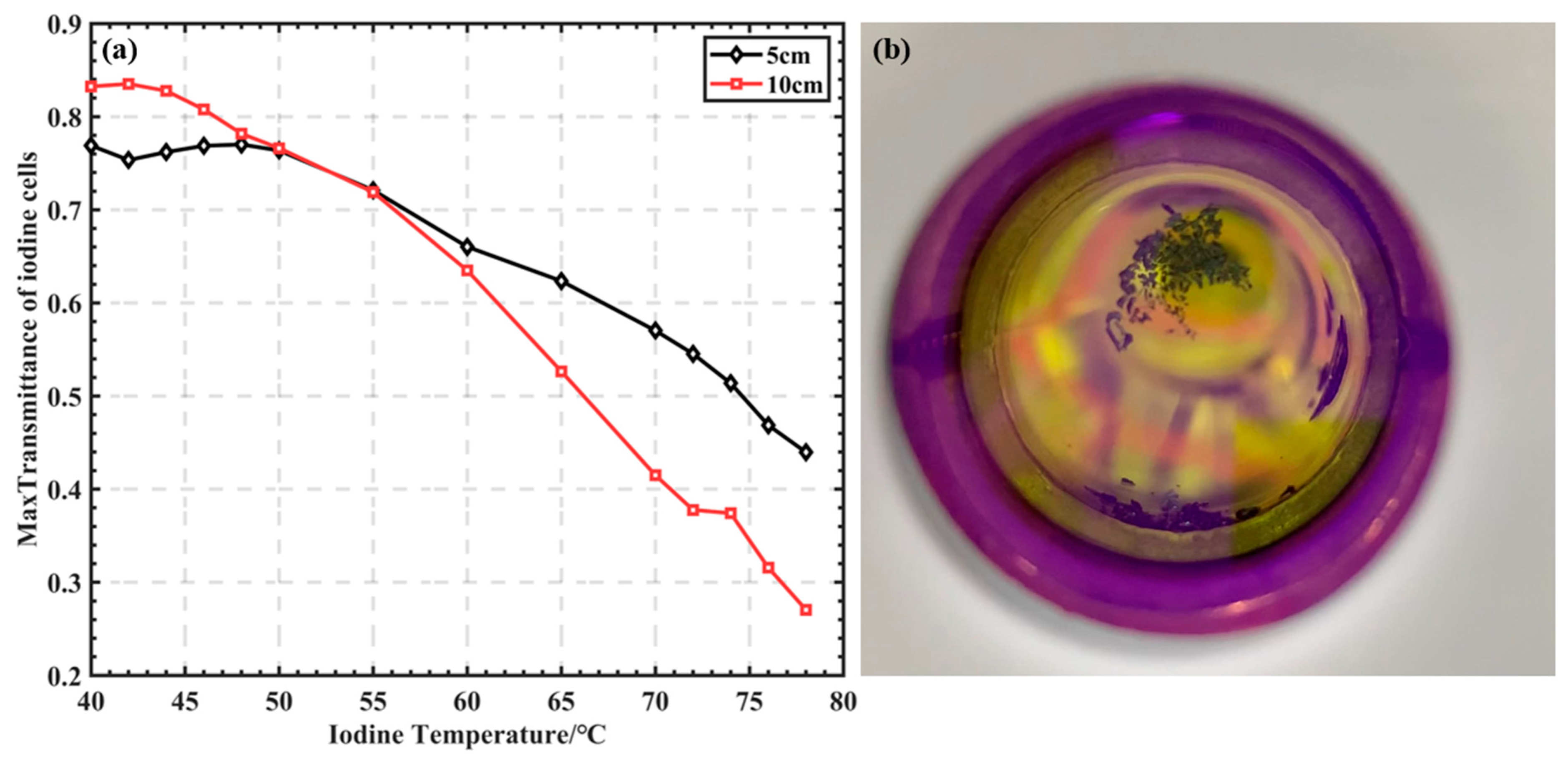
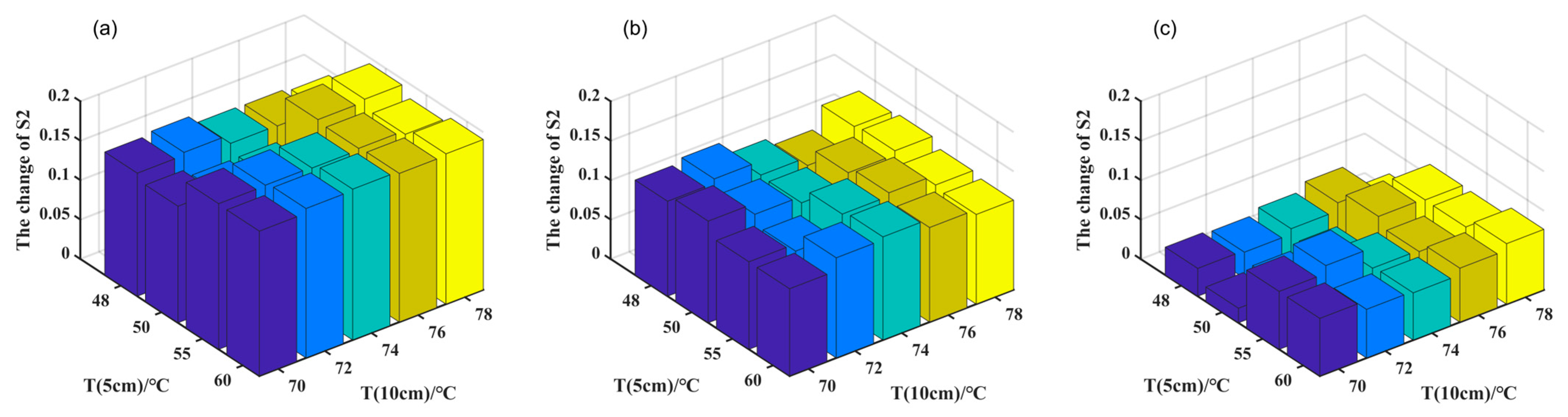
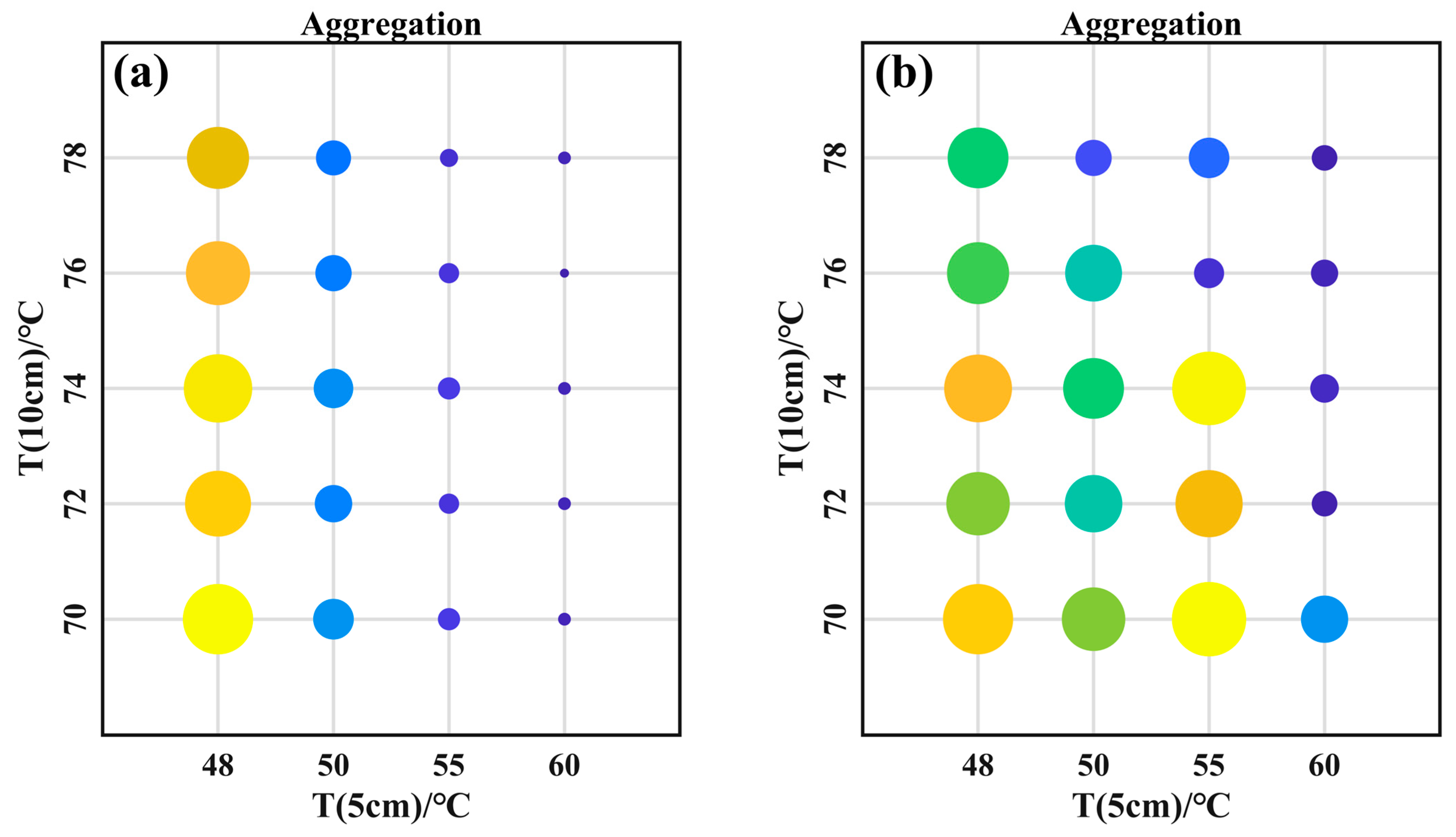
3.4. Iodine Cell Temperature Set Analysis
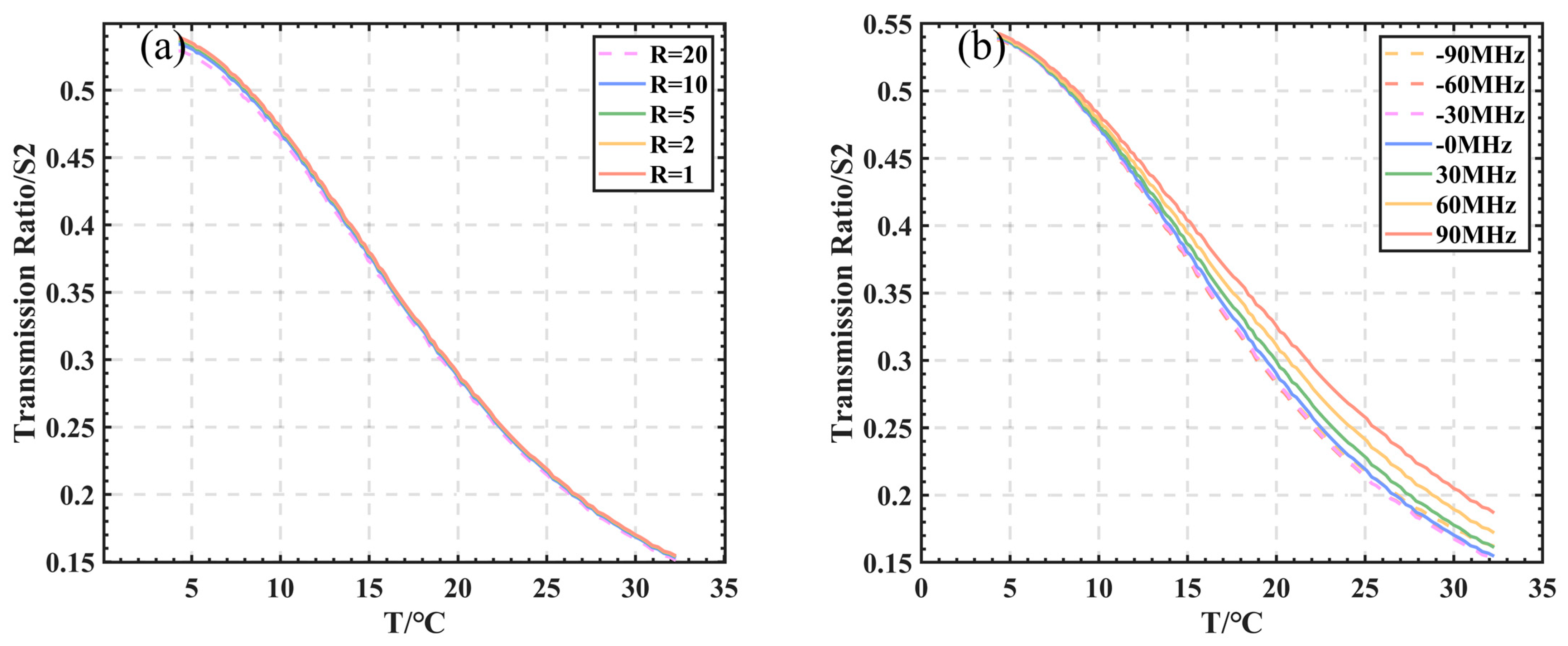
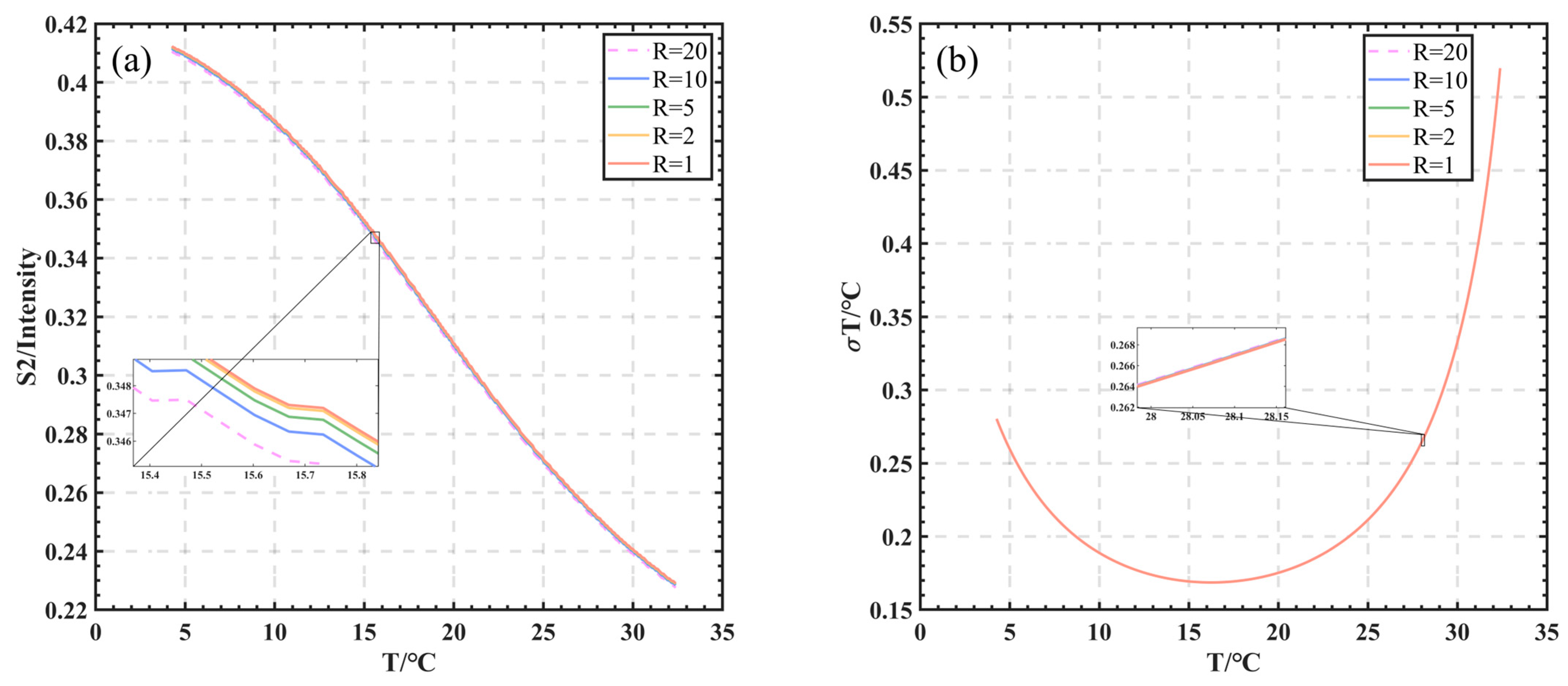
3.5. Temperature Measurement Accuracy Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brierley, A.S.; Kingsford, M.J. Impacts of Climate Change on Marine Organisms and Ecosystems. Curr. Biol. 2009, 19, R602–R614. [Google Scholar] [CrossRef] [PubMed]
- Harley, C.D.G.; Hughes, A.R.; Hultgren, K.M.; Miner, B.G.; Sorte, C.J.B.; Thornber, C.S.; Rodriguez, L.F.; Tomanek, L.; Williams, S.L. The impacts of climate change in coastal marine systems. Ecol. Lett. 2006, 9, 228–241. [Google Scholar] [CrossRef] [PubMed]
- Hiscock, K.; Southward, A.; Tittley, I.; Hawkins, S. Effects of changing temperature on benthic marine life in Britain and Ireland. Aquat. Conserv.-Mar. Freshw. Ecosyst. 2004, 14, 333–362. [Google Scholar] [CrossRef]
- Ingleby, B.; Huddleston, M. Quality control of ocean temperature and salinity profiles—Historical and real-time data. J. Mar. Syst. 2007, 65, 158–175. [Google Scholar] [CrossRef]
- Cullum, J.; Stevens, D.P.; Joshi, M.M. Importance of ocean salinity for climate and habitability. Proc. Natl. Acad. Sci. USA 2016, 113, 4278–4283. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wang, Y.J.; Song, S.; Li, F. Overview of Fibre Optic Sensing Technology in the Field of Physical Ocean Observation. Front. Phys. 2021, 9, 745487. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Chen, P.; Liang, K. Remote Sensing of Seawater Temperature and Salinity Profiles by the Brillouin Lidar Based on a Fizeau Interferometer and Multichannel Photomultiplier Tube. Sensors 2023, 23, 446. [Google Scholar] [CrossRef] [PubMed]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Conroy, J.L.; Domingues, C.M.; Fasullo, J.T.; Gilson, J.; et al. A review of global ocean temperature observations: Implications for ocean heat content estimates and climate change. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O.; Bulgin, C.E.; Block, T.; Corlett, G.K.; Fiedler, E.; Good, S.A.; Mittaz, J.; Rayner, N.A.; Berry, D.; et al. Satellite-based time-series of sea-surface temperature since 1981 for climate applications. Sci. Data 2019, 6, 223. [Google Scholar] [CrossRef]
- Amani, M.; Mohseni, F.; Layegh, N.F.; Nazari, M.E.; Fatolazadeh, F.; Salehi, A.; Ahmadi, S.A.; Ebrahimy, H.; Ghorbanian, A.; Jin, S.; et al. Remote Sensing Systems for Ocean: A Review (Part 2: Active Systems). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 1421–1453. [Google Scholar] [CrossRef]
- Amani, M.; Ghorbanian, A.; Asgarimehr, M.; Yekkehkhany, B.; Moghimi, A.; Jin, S.; Naboureh, A.; Mohseni, F.; Mahdavi, S.; Layegh, N.F. Remote Sensing Systems for Ocean: A Review (Part 1: Passive Systems). IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 210–234. [Google Scholar] [CrossRef]
- Moisan, J.R.; Rousseaux, C.S.; Stysley, P.R.; Clarke, G.B.; Poulios, D.P. Ocean Temperature Profiling Lidar: Analysis of Technology and Potential for Rapid Ocean Observations. Remote Sens. 2024, 16, 1236. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, J.; Zheng, Y.; Xu, Y.; Xu, J.; Jiao, J.; Su, Y.; Lu, H.-F.; Liang, K. Brillouin scattering spectrum for liquid detection and applications in oceanography. Opto-Electron. Adv. 2023, 6, 220016. [Google Scholar] [CrossRef]
- Schorstein, K.; Popescu, A.; Göbel, M.; Walther, T. Remote Water Temperature Measurements Based on Brillouin Scattering with a Frequency Doubled Pulsed Yb:doped Fiber Amplifier. Sensors 2008, 8, 5820–5831. [Google Scholar] [CrossRef] [PubMed]
- Liang, K.; Ma, Y.; Yu, Y.; Huang, J.; Li, H. Research on simultaneous measurement of ocean temperature and salinity using Brillouin shift and linewidth. Opt. Eng. 2012, 51, 066002. [Google Scholar] [CrossRef]
- Rudolf, A.; Walther, T. Laboratory demonstration of a Brillouin lidar to remotely measure temperature profiles of the ocean. Opt. Eng. 2014, 53, 051407. [Google Scholar] [CrossRef]
- Emery, Y.; Fry, E.S. Laboratory development of a LIDAR for measurement of sound velocity in the ocean using Brillouin scattering. In Proceedings of the Conference on Ocean Optics XIII, Halifax, NS, Canada, 22–25 October 1996; pp. 210–215. [Google Scholar]
- Xu, J.F.; Ren, X.B.; Gong, W.P.; Dai, R.; Liu, D.H. Measurement of the bulk viscosity of liquid by Brillouin scattering. Appl. Opt. 2003, 42, 6704–6709. [Google Scholar] [CrossRef] [PubMed]
- Shi, J.; Ouyang, M.; Gong, W.; Li, S.; Liu, D. A Brillouin lidar system using F-P etalon and ICCD for remote sensing of the ocean. Appl. Phys. B-Lasers Opt. 2008, 90, 569–571. [Google Scholar] [CrossRef]
- Liu, Z.; Sun, J.; Zhang, X.; Zeng, Z.; Xu, Y.; Luo, N.; He, X.; Shi, J. High-Accuracy Spectral Measurement of Stimulated-Brillouin-Scattering Lidar Based on Hessian Matrix and Steger Algorithm. Remote Sens. 2023, 15, 1511. [Google Scholar] [CrossRef]
- Dai, R.; Gong, W.; Xu, J.; Ren, X.; Liu, D. The edge technique as used in Brillouin lidar for remote sensing of the ocean. Appl. Phys. B-Lasers Opt. 2004, 79, 245–248. [Google Scholar] [CrossRef]
- Edward; Fry, S.; Emery, Y.; Quan, X.; Katz, J.W. Accuracy limitations on Brillouin lidar measurements of temperature and sound speed in the ocean. Appl. Opt. 1997, 36, 6887–6894. [Google Scholar] [CrossRef]
- Fry, E.S.; Katz, J.; Liu, D.H.; Walther, T. Temperature dependence of the Brillouin linewidth in water. J. Mod. Opt. 2002, 49, 411–418. [Google Scholar] [CrossRef]
- Gong, W.; Shi, J.; Li, G.; Liu, D.; Katz, J.W.; Fry, E.S. Calibration of edge technique considering variation of Brillouin line width at different temperatures of water. Appl. Phys. B-Lasers Opt. 2006, 83, 319–322. [Google Scholar] [CrossRef]
- Liang, K.; Zhang, R.; Sun, Q.; Xu, Y.; Wu, H.; Zhang, P.; Zhou, B. Brillouin shift and linewidth measurement based on double-edge detection technology in seawater. Appl. Phys. B 2020, 126, 160. [Google Scholar] [CrossRef]
- Smith, J.A.; Hostetler, C. Brillouin Asymmetric Spatial Heterodyne Oceanographic Lidar Receiver for Profiling Temperature, Salinity, and Sound Velocity; NASA: Hampton, VA, USA, 2024.
- Gelbwachs, J.A. Atomic Resonance Filters. IEEE J. Quantum Electron. 1988, 24, 1266–1277. [Google Scholar] [CrossRef]
- Miles, R.; Lempert, W.; Forkey, J. Instantaneous velocity fields and background suppression by filtered Rayleigh scattering. In Proceedings of the 29th Aerospace Sciences Meeting (AIAA), Reno, NV, USA, 7–10 January 1991. [Google Scholar]
- Forkey, J.N.; Lempert, W.R.; Miles, R.B. Corrected and calibrated I2 absorption model at frequency-doubled Nd:YAG laser wavelengths. Appl. Opt. 1997, 36, 6729–6738. [Google Scholar] [CrossRef]
- Boguszko, M.; Elliott, G.S. Property measurement utilizing atomic/molecular filter-based diagnostics. Prog. Aerosp. Sci. 2005, 41, 93–142. [Google Scholar] [CrossRef]





| m1 = 120.2 | m2 = −43.253 | m3 = 21.215 | m4 = 3.4079 | m5 = −60.661 |
| m6 = 13.645 | m7 = −0.0053 | m8 = 3.6607 | m9 = 6.1565 | m10 = −1.579 |
| Number | Temperature/K | Pressure/Torr | Length/CM |
|---|---|---|---|
| Low-temperature iodine cell | 353 | 1 | 10 |
| High-temperature iodine cell | 353 | 15 | 10 |
| Temperature/°C | Gain/dB | |
|---|---|---|
| Iodine cell of 5 cm | ≥48 | ≥30 |
| Iodine cell of 10 cm | ≥40 | ≥30 |
| Temperature Range/°C | 5 cm Iodine Cell Temperature/°C | 10 cm Iodine Cell Temperature/°C |
|---|---|---|
| 5~32 | 60 | 78 |
| 5~15 | 50 | 78 |
| 15~32 | 60 | 78 |
| Temperature Range/°C | 5 cm Temperature/°C | 10 cm Temperature/°C | Wavelength/nm |
|---|---|---|---|
| 5~32 | 50/60 | 78 | 532.10518/532.10495 |
| 5~15 | 50 | 78 | 532.10495 |
| 15~32 | 60 | 78 | 532.10518 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, F.; Chen, W.; Liang, L.; Fang, C.; He, Y. System Design of Ocean Temperature Measurement System Using Brillouin Lidar Based on Dual Iodine Cells. Remote Sens. 2024, 16, 2748. https://doi.org/10.3390/rs16152748
Yang F, Chen W, Liang L, Fang C, He Y. System Design of Ocean Temperature Measurement System Using Brillouin Lidar Based on Dual Iodine Cells. Remote Sensing. 2024; 16(15):2748. https://doi.org/10.3390/rs16152748
Chicago/Turabian StyleYang, Fu, Wenhao Chen, Luqiang Liang, Chunqi Fang, and Yan He. 2024. "System Design of Ocean Temperature Measurement System Using Brillouin Lidar Based on Dual Iodine Cells" Remote Sensing 16, no. 15: 2748. https://doi.org/10.3390/rs16152748
APA StyleYang, F., Chen, W., Liang, L., Fang, C., & He, Y. (2024). System Design of Ocean Temperature Measurement System Using Brillouin Lidar Based on Dual Iodine Cells. Remote Sensing, 16(15), 2748. https://doi.org/10.3390/rs16152748






