Super-Resolution Learning Strategy Based on Expert Knowledge Supervision
Abstract
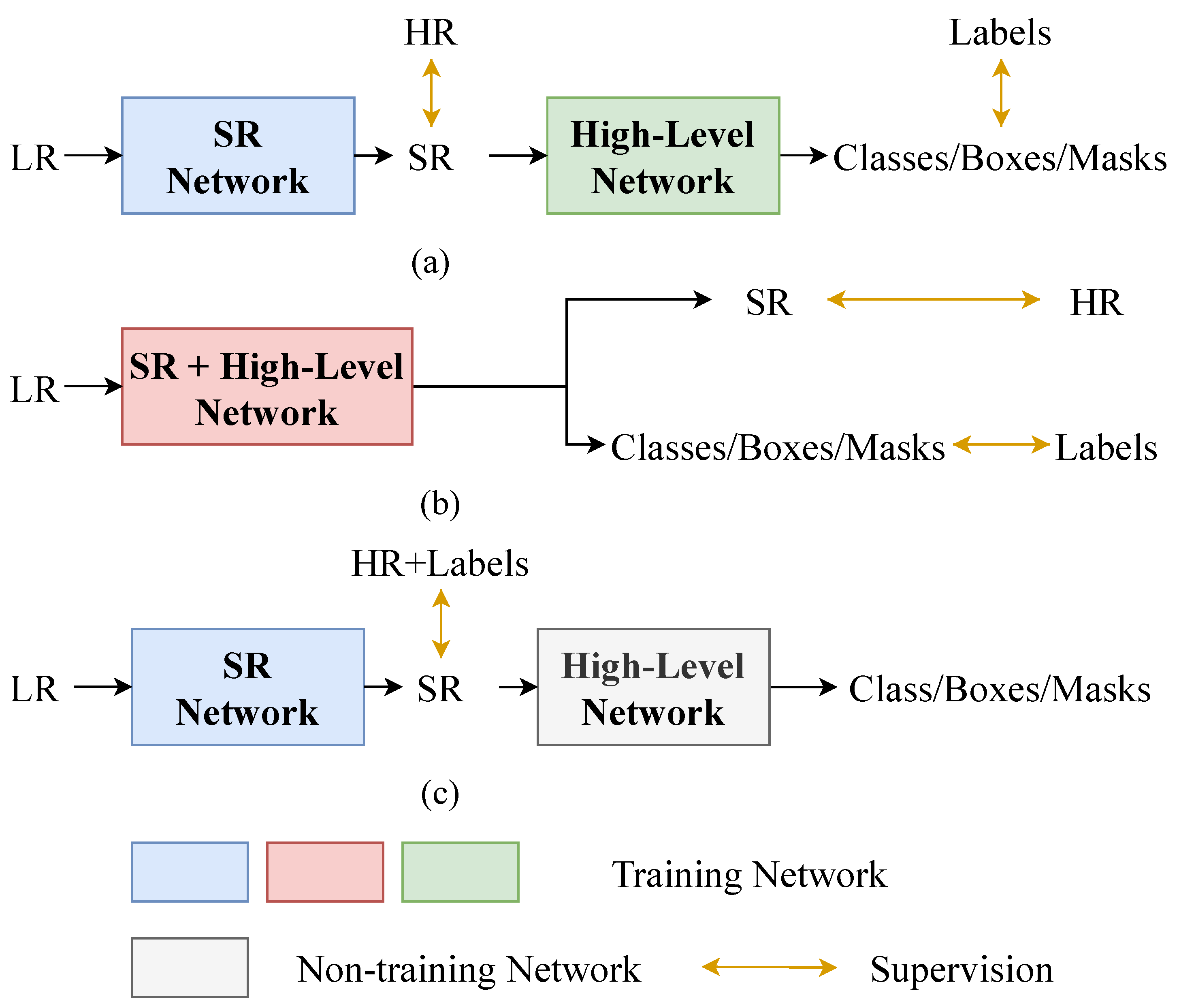
1. Introduction
- An Expert Knowledge Guided SR Framework: EKS-SR innovatively incorporates expert annotations for high-level tasks to supervise the SR network, achieving significant improvements in fine-grained tasks with coarse-grained annotations.
- Multi Constraint Approach to Focus on Object Reconstruction: Unlike existing learning strategies that overlook the challenge of object area recovery, EKS-SR leverages prior information from three perspectives: regional constraints, feature constraints, and attribution constraints, to guide the SR model in achieving more accurate reconstructions of multi-scale objects in RS, especially for small objects.
- Enhancing Practicality Under Limited Annotations without Increasing Inference-time: Even the expert annotations are limited, EKS-SR can improve practical task performance without increasing the model parameters and inference time, which provides a new solution for resource-limited RS devices.
- Plug-in and Play: The design of EKS-SR does not rely on specific SR models and high-level task models, which can be applied to any model and have strong scalability. The strong scalability ensures that as new models and tasks emerge, EKS-SR can continue to be relevant and beneficial, offering ongoing improvements in performance and utility.
2. Related Works
2.1. Single Image Super Resolution
2.2. Image Super-Resolution with High-Level Tasks
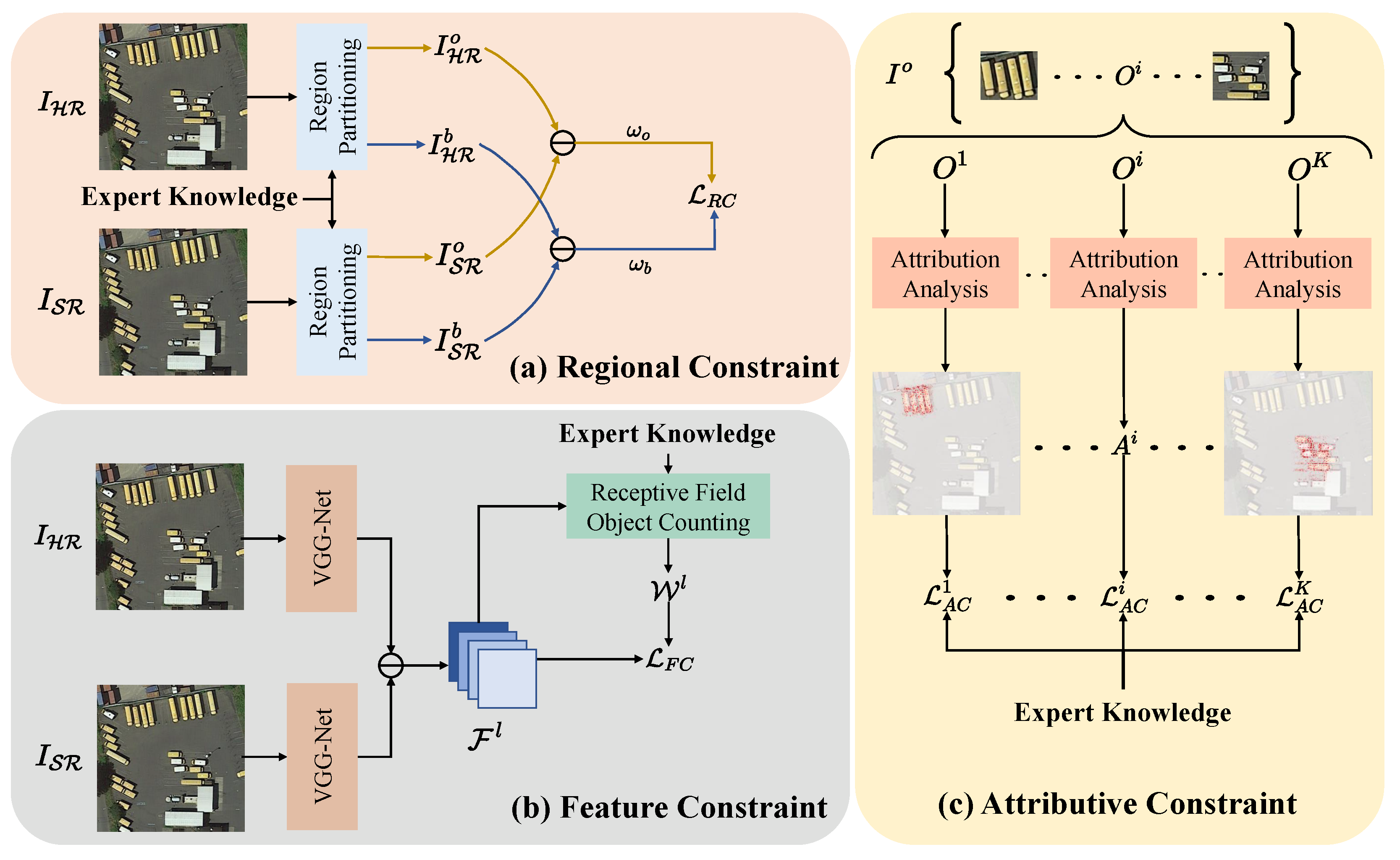
3. Method
3.1. Regional Constraint
3.2. Feature Constraint
3.3. Attributive Constraint
- Sensitivity: For any input image I and baseline image , when any part of the image changes and causes a change in the model’s prediction result, the AM should also be able to express this change.
- Implementation Invariance: For two networks, even though their implementation methods are different, if their outputs are equal for all inputs, then the AM obtained by performing attribution analysis on these two networks should be the same.
3.4. Proposed Learning Strategy
| Algorithm 1 EKS-SR Learning Strategy |
Input: A dataset of image pairs with expert knowledge , Initial model parameters , Number of iterations , Start iterations of attribute constraint begins , Attributive constraint frequency f. |
Output: Trained model parameters |
|
4. Experiments
4.1. Datasets and Evaluation Metrics
4.1.1. Datasets Description
- (1)
- iSAID: The iSAID dataset consists of 2806 images with different sizes and 655,451 annotated instances. Due to the large size of the original images in the iSAID dataset, we have divided them into image patches for training and testing. We have created the SR dataset using bicubic and Gaussian blur to get the LR image with sizes. The original training set is used as the training set for the SR task. Additionally, the validation set of iSAID is used as the test set for the SR task. The training set contains a total of 27,286 images and the test set contains a total of 9446 images.
- (2)
- COWC: The COWC is a large dataset of annotated cars from overhead, which consists of images from Selwyn in New Zealand, Potsdam and Vaihingen in Germany, Columbus and Utah in the United States, and Toronto in Canada. We crop the image to and randomly select 80% images in Potsdam for training, 10% images in Potsdam for validating, and others for testing. The LR images of the COWC dataset have a size of and , corresponding to and upscale factor SR tasks, respectively.
4.1.2. Evaluation Metrics for SR
- (1)
- PSNR: PSNR is the most widely used objective quality assessment metric in SR tasks. Given HR image and LR image , PSNR is defined aswhere represents the maximum pixel value (255 for 8-bit images) and represents the mean squared error (MSE) between and , which can be calculated aswhere m and n represent the height and width of the SR image . A larger PSNR value indicates greater similarity between the two images.
- (2)
- SSIM: SSIM is an index that quantifies the structural similarity between two images. Unlike PSNR, SSIM is designed to mimic the human visual system’s perception of structural similarity. SSIM quantifies the image’s attributes of brightness, contrast, and structure, using the mean to estimate brightness, variance to estimate contrast, and covariance to estimate structural similarity. SSIM is defined aswhere and denote the mean values of and , respectively. and denote the variance of and , respectively. denotes the covariance of and . and are two constants used to maintain the stability of the denominator. The SSIM value ranges from 0 to 1, with a higher value indicating greater similarity between the two images.
- (3)
- LPIPS: To better simulate human visual perception, Zhang et al. [60] proposed LPIPS, which measures the difference between two images in the feature domain by a pre-trained VGG [51] feature extract network . Compared to PSNR and SSIM, LPIPS evaluates the similarity between two images in a way that is more consistent with human visual habits. LPIPS is defined aswhere and represents the l-th layer of and its weights. and is the height and width of the SR image . A smaller LPIPS value indicates greater similarity between the two images.
4.1.3. Evaluation Metrics for Object Detection and Instance Segmentation
4.2. Implementation Details
4.3. Results Achieved Using the Learning Strategy EKS-SR on Different SR Models
4.3.1. Quantitative Results on COWC
4.3.2. Quantitative Results on iSAID
4.3.3. Qualitative Comparison
4.4. Performance under Different Upscale Factors
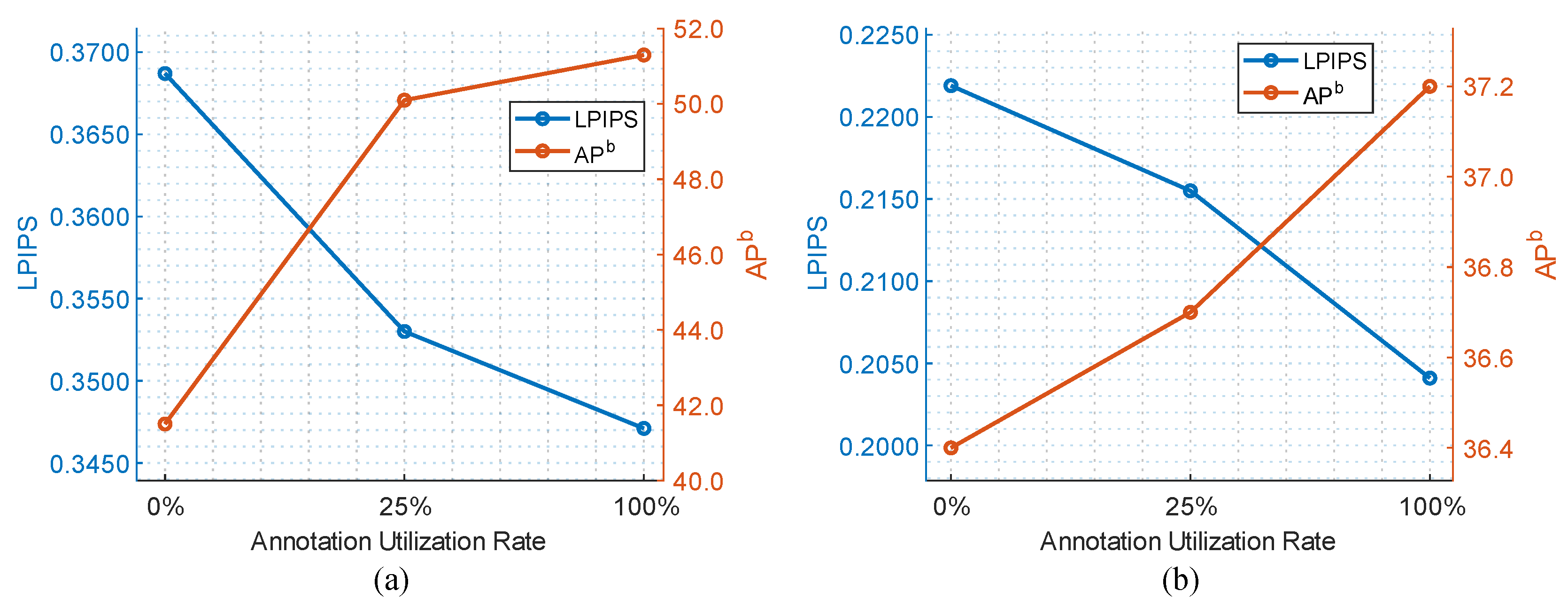
4.5. Performance under Limited Annotation
4.6. Ablation Studies
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SR | Super Resolution |
| DL | Deep Learning |
| RS | Remote Sensing |
| SISR | Single Image Super-Resolution |
| PSNR | Peak Signal-to-Noise Ratio |
| PSNR-SR | Peak Signal-to-Noise Ratio-Oriented Super Resolution |
| GAN | Generative Adversarial Network |
| GAN-SR | Generative Adversarial Network-Based Super Resolution |
| EKS-SR | Super-Resolution Learning Strategy Based on Expert Knowledge Supervision |
| LR | Low Resolution |
| HR | High Resolution |
| AM | Attribution Map |
| IG | Integrated Gradients |
| LAM | Local Attribution Map |
| SRGAN | Super-Resolution Generative Adversarial Network |
| SwinIR | Image restoration using Swin Transformer |
| iSAID | Instance Segmentation in Aerial Images Datase |
| COWC | Cars Overhead With Context |
| Faster R-CNN | Faster region-based Convolutional Neural Network |
| Mask R-CNN | Mask region-based Convolutional Neural Network |
| SSIM | Structural Similarity Index |
| LPIPS | Learned Perceptual Image Patch Similarity |
| MSE | Mean Squared Error |
| AP | Average Precision |
| IoU | Intersections over Union |
| GPU | Graphics processing unit |
References
- Shafique, A.; Cao, G.; Khan, Z.; Asad, M.; Aslam, M. Deep learning-based change detection in remote sensing images: A review. Remote Sens. 2022, 14, 871. [Google Scholar] [CrossRef]
- Wang, G.; Li, B.; Zhang, T.; Zhang, S. A network combining a transformer and a convolutional neural network for remote sensing image change detection. Remote Sens. 2022, 14, 2228. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Song, S.; Li, F.; Huang, G. Deep Siamese networks based change detection with remote sensing images. Remote Sens. 2021, 13, 3394. [Google Scholar] [CrossRef]
- He, L.; Zhang, W.; Shi, J.; Li, F. Cross-domain association mining based generative adversarial network for pansharpening. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7770–7783. [Google Scholar] [CrossRef]
- Tang, D.; Cao, X.; Hou, X.; Jiang, Z.; Meng, D. Crs-diff: Controllable generative remote sensing foundation model. arXiv 2024, arXiv:2403.11614. [Google Scholar]
- Rui, X.; Cao, X.; Pang, L.; Zhu, Z.; Yue, Z.; Meng, D. Unsupervised hyperspectral pansharpening via low-rank diffusion model. Inf. Fusion 2024, 107, 102325. [Google Scholar] [CrossRef]
- He, L.; Ren, Z.; Zhang, W.; Li, F.; Mei, S. Unsupervised Pansharpening Based on Double-Cycle Consistency. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5613015. [Google Scholar] [CrossRef]
- Cheng, G.; Yuan, X.; Yao, X.; Yan, K.; Zeng, Q.; Xie, X.; Han, J. Towards large-scale small object detection: Survey and benchmarks. IEEE Trans. Pattern Anal. Mach. Intell. 2023, 45, 13467–13488. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, F.; An, Y.; Zhang, X.; Sun, H. Towards Robust LiDAR-Camera Fusion in BEV Space via Mutual Deformable Attention and Temporal Aggregation. IEEE Trans. Circuits Syst. Video Technol. 2024, 34, 5753–5764. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, G.; Yang, L.; Li, Z.; Gao, M.; Yu, C.; Gong, E.; Long, H.; Hu, H. Dynamic monitoring of environmental quality in the Loess Plateau from 2000 to 2020 using the Google Earth Engine Platform and the Remote Sensing Ecological index. Remote Sens. 2022, 14, 5094. [Google Scholar] [CrossRef]
- Xu, D.; Cheng, J.; Xu, S.; Geng, J.; Yang, F.; Fang, H.; Xu, J.; Wang, S.; Wang, Y.; Huang, J.; et al. Understanding the relationship between China’s eco-environmental quality and urbanization using multisource remote sensing data. Remote Sens. 2022, 14, 198. [Google Scholar] [CrossRef]
- Ma, Y.; Chen, S.; Ermon, S.; Lobell, D.B. Transfer learning in environmental remote sensing. Remote Sens. Environ. 2024, 301, 113924. [Google Scholar] [CrossRef]
- Dong, C.; Loy, C.C.; He, K.; Tang, X. Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 38, 295–307. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, K.; Li, K.; Wang, L.; Zhong, B.; Fu, Y. Image Super-Resolution Using Very Deep Residual Channel Attention Networks. In Proceedings of the European Conference on Computer Vision Workshops, Munich, Germany, 8–14 September 2018; pp. 294–310. [Google Scholar]
- Dai, T.; Cai, J.; Zhang, Y.; Xia, S.T.; Zhang, L. Second-order Attention Network for Single Image Super-Resolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 11065–11074. [Google Scholar]
- Liang, J.; Cao, J.; Sun, G.; Zhang, K.; Van Gool, L.; Timofte, R. SwinIR: Image Restoration Using Swin Transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision Workshops, Montreal, BC, Canada, 11–17 October 2021; pp. 1833–1844. [Google Scholar]
- Huan, H.; Li, P.; Zou, N.; Wang, C.; Xie, Y.; Xie, Y.; Xu, D. End-to-end super-resolution for remote-sensing images using an improved multi-scale residual network. Remote Sens. 2021, 13, 666. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, L.; Liu, L.; Hu, H.; Tao, W. URNet: A U-shaped residual network for lightweight image super-resolution. Remote Sens. 2021, 13, 3848. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Zhou, J.; Qiao, Y.; Dong, C. Activating more pixels in image super-resolution transformer. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 22367–22377. [Google Scholar]
- Ledig, C.; Theis, L.; Huszar, F.; Caballero, J.; Cunningham, A.; Acosta, A.; Aitken, A.; Tejani, A.; Totz, J.; Wang, Z.; et al. Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4681–4690. [Google Scholar]
- Zhang, W.; Liu, Y.; Dong, C.; Qiao, Y. Ranksrgan: Generative adversarial networks with ranker for image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3096–3105. [Google Scholar]
- Ren, Z.; He, L.; Lu, J. Context aware Edge-Enhanced GAN for Remote Sensing Image Super-Resolution. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 1363–1376. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, S.; Feng, Y.; Mei, S.; Jia, S.; Du, Q. Hyperspectral imagery spatial super-resolution using generative adversarial network. IEEE Trans. Comput. Imaging 2021, 7, 948–960. [Google Scholar] [CrossRef]
- Rabbi, J.; Ray, N.; Schubert, M.; Chowdhury, S.; Chao, D. Small-object detection in remote sensing images with end-to-end edge-enhanced GAN and object detector network. Remote Sens. 2020, 12, 1432. [Google Scholar] [CrossRef]
- Feng, X.; Zhang, W.; Su, X.; Xu, Z. Optical remote sensing image denoising and super-resolution reconstructing using optimized generative network in wavelet transform domain. Remote Sens. 2021, 13, 1858. [Google Scholar] [CrossRef]
- Xu, Y.; Luo, W.; Hu, A.; Xie, Z.; Xie, X.; Tao, L. TE-SAGAN: An improved generative adversarial network for remote sensing super-resolution images. Remote Sens. 2022, 14, 2425. [Google Scholar] [CrossRef]
- Wang, X.; Yu, K.; Wu, S.; Gu, J.; Liu, Y.; Dong, C.; Qiao, Y.; Change Loy, C. Esrgan: Enhanced super-resolution generative adversarial networks. In Proceedings of the European Conference on Computer Vision Workshops, Munich, Germany, 8–14 September 2018; pp. 1–16. [Google Scholar]
- Guo, M.; Zhang, Z.; Liu, H.; Huang, Y. NDSRGAN: A novel dense generative adversarial network for real aerial imagery super-resolution reconstruction. Remote Sens. 2022, 14, 1574. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Zhang, L.; Dong, R.; Yuan, S.; Li, W.; Zheng, J.; Fu, H. Making low-resolution satellite images reborn: A deep learning approach for super-resolution building extraction. Remote Sens. 2021, 13, 2872. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, Y.; Ding, M.; Ghanem, B. Sod-mtgan: Small object detection via multi-task generative adversarial network. In Proceedings of the European Conference on Computer Vision, Munich, Germany, 8–14 September 2018; pp. 206–221. [Google Scholar]
- Wang, L.; Li, D.; Zhu, Y.; Tian, L.; Shan, Y. Dual super-resolution learning for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 3774–3783. [Google Scholar]
- Pereira, M.B.; Santos, J.A.d. An end-to-end framework for low-resolution remote sensing semantic segmentation. In Proceedings of the 2020 IEEE Latin American GRSS & ISPRS Remote Sensing Conference, Santiago, Chile, 22–26 March 2020; pp. 6–11. [Google Scholar]
- Abadal, S.; Salgueiro, L.; Marcello, J.; Vilaplana, V. A dual network for super-resolution and semantic segmentation of sentinel-2 imagery. Remote Sens. 2021, 13, 4547. [Google Scholar] [CrossRef]
- Zhang, J.; Lei, J.; Xie, W.; Fang, Z.; Li, Y.; Du, Q. SuperYOLO: Super resolution assisted object detection in multimodal remote sensing imagery. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5605415. [Google Scholar] [CrossRef]
- Xie, J.; Fang, L.; Zhang, B.; Chanussot, J.; Li, S. Super resolution guided deep network for land cover classification from remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5611812. [Google Scholar] [CrossRef]
- Salgueiro, L.; Marcello, J.; Vilaplana, V. SEG-ESRGAN: A multi-task network for super-resolution and semantic segmentation of remote sensing images. Remote Sens. 2022, 14, 5862. [Google Scholar] [CrossRef]
- Yang, L.; Han, Y.; Chen, X.; Song, S.; Dai, J.; Huang, G. Resolution adaptive networks for efficient inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2369–2378. [Google Scholar]
- Yang, L.; Zheng, Z.; Wang, J.; Song, S.; Huang, G.; Li, F. Adadet: An adaptive object detection system based on early-exit neural networks. IEEE Trans. Cogn. Dev. Syst. 2023, 16, 332–345. [Google Scholar] [CrossRef]
- Lu, T.; Wang, J.; Zhang, Y.; Wang, Z.; Jiang, J. Satellite image super-resolution via multi-scale residual deep neural network. Remote Sens. 2019, 11, 1588. [Google Scholar] [CrossRef]
- Xiao, Y.; Su, X.; Yuan, Q.; Liu, D.; Shen, H.; Zhang, L. Satellite video super-resolution via multiscale deformable convolution alignment and temporal grouping projection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5610819. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16 × 16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 10012–10022. [Google Scholar]
- Zhou, Y.; Li, Z.; Guo, C.L.; Bai, S.; Cheng, M.M.; Hou, Q. Srformer: Permuted self-attention for single image super-resolution. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 12780–12791. [Google Scholar]
- Jolicoeur-Martineau, A. The relativistic discriminator: A key element missing from standard GAN. arXiv 2018, arXiv:1807.00734. [Google Scholar]
- Bashir, S.M.A.; Wang, Y. Small object detection in remote sensing images with residual feature aggregation-based super-resolution and object detector network. Remote Sens. 2021, 13, 1854. [Google Scholar] [CrossRef]
- Yang, J.; Fu, K.; Wu, Y.; Diao, W.; Dai, W.; Sun, X. Mutual-feed learning for super-resolution and object detection in degraded aerial imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5628016. [Google Scholar] [CrossRef]
- Tang, Z.; Pan, B.; Liu, E.; Xu, X.; Shi, T.; Shi, Z. Srda-net: Super-resolution domain adaptation networks for semantic segmentation. arXiv 2020, arXiv:2005.06382. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Rao, S.; Böhle, M.; Parchami-Araghi, A.; Schiele, B. Studying How to Efficiently and Effectively Guide Models with Explanations. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 2–6 October 2023; pp. 1922–1933. [Google Scholar]
- Baehrens, D.; Schroeter, T.; Harmeling, S.; Kawanabe, M.; Hansen, K.; Müller, K.R. How to explain individual classification decisions. J. Mach. Learn. Res. 2010, 11, 1803–1831. [Google Scholar]
- Simonyan, K.; Vedaldi, A.; Zisserman, A. Deep inside convolutional networks: Visualising image classification models and saliency maps. arXiv 2013, arXiv:1312.6034. [Google Scholar]
- Sundararajan, M.; Taly, A.; Yan, Q. Axiomatic attribution for deep networks. In Proceedings of the International Conference on Machine Learning, Sydney, Australia, 6–11 August 2017; pp. 3319–3328. [Google Scholar]
- Springenberg, J.; Dosovitskiy, A.; Brox, T.; Riedmiller, M. Striving for Simplicity: The All Convolutional Net. In Proceedings of the International Conference on Learning Representations Workshop, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Gu, J.; Dong, C. Interpreting super-resolution networks with local attribution maps. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 9199–9208. [Google Scholar]
- Waqas Zamir, S.; Arora, A.; Gupta, A.; Khan, S.; Sun, G.; Shahbaz Khan, F.; Zhu, F.; Shao, L.; Xia, G.S.; Bai, X. isaid: A large-scale dataset for instance segmentation in aerial images. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Long Beach, CA, USA, 16–17 June 2019; pp. 28–37. [Google Scholar]
- Mundhenk, T.N.; Konjevod, G.; Sakla, W.A.; Boakye, K. A large contextual dataset for classification, detection and counting of cars with deep learning. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 785–800. [Google Scholar]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The unreasonable effectiveness of deep features as a perceptual metric. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster R-CNN: Towards real-time object detection with region proposal networks. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 39, 1137–1149. [Google Scholar] [CrossRef]
- Liang, J.; Zeng, H.; Zhang, L. Details or artifacts: A locally discriminative learning approach to realistic image super-resolution. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 5657–5666. [Google Scholar]
- Timofte, R.; Agustsson, E.; Van Gool, L.; Yang, M.H.; Zhang, L. Ntire 2017 challenge on single image super-resolution: Methods and results. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 114–125. [Google Scholar]
- Agustsson, E.; Timofte, R. Ntire 2017 challenge on single image super-resolution: Dataset and study. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, 21–26 July 2017; pp. 126–135. [Google Scholar]




| Model | Learning Strategy | PSNR ↑ | SSIM ↑ | LPIPS ↓ | ↑ | ↑ | ↑ |
|---|---|---|---|---|---|---|---|
| HR | - | - | - | - | 93.7 | 97.7 | 97.6 |
| SRGAN | Original | 26.526 | 0.6283 | 0.3687 | 41.5 | 62.3 | 47.8 |
| LDL | 27.432 | 0.6518 | 0.3488 | 48.1 | 68.6 | 57.3 | |
| EKS-SR | 27.083 | 0.6359 | 0.3471 | 51.3 | 73.0 | 61.7 | |
| SRFormer | Original | 31.580 | 0.8033 | 0.3488 | 70.5 | 84.7 | 82.1 |
| LDL | 27.689 | 0.6697 | 0.3412 | 48.8 | 71.4 | 58.3 | |
| EKS-SR | 32.348 | 0.8263 | 0.3233 | 77.5 | 88.7 | 87.7 | |
| SwinIR | Original | 33.205 | 0.8500 | 0.2922 | 80.5 | 90.8 | 89.7 |
| LDL 1 | 28.704 | 0.6847 | 0.4035 | 37.0 | 50.8 | 44.4 | |
| LDL 2 | 27.313 | 0.6219 | 0.2583 | 57.4 | 79.4 | 70.0 | |
| EKS-SR | 33.220 | 0.8505 | 0.2912 | 80.8 | 90.9 | 89.8 |
| Model | Learning Strategy | PSNR ↑ | SSIM ↑ | LPIPS ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ |
|---|---|---|---|---|---|---|---|---|---|---|
| HR | - | - | - | - | 44.2 | 63.1 | 46.7 | 36.5 | 59.3 | 39.4 |
| SRGAN | Original | 35.299 | 0.8516 | 0.2219 | 36.4 | 55.9 | 39.8 | 29.2 | 49.2 | 30.6 |
| EKS-SR | 36.352 | 0.8680 | 0.2041 | 37.2 | 56.7 | 41.0 | 29.8 | 50.4 | 31.3 | |
| Improvement | 1.053 | 0.0164 | 0.0178 | 0.8 | 0.8 | 1.2 | 0.6 | 1.2 | 0.7 | |
| SwinIR | Original | 38.533 | 0.9011 | 0.2182 | 37.8 | 57.0 | 41.7 | 30.7 | 50.9 | 32.9 |
| EKS-SR | 38.550 | 0.9015 | 0.2170 | 37.9 | 57.2 | 41.8 | 30.8 | 51.0 | 32.9 | |
| Improvement | 0.017 | 0.0004 | 0.0012 | 0.1 | 0.2 | 0.1 | 0.1 | 0.1 | 0.0 |
| Upscale | Learning Strategy | PSNR ↑ | SSIM ↑ | LPIPS ↓ | ↑ | ↑ | ↑ |
|---|---|---|---|---|---|---|---|
| HR | - | - | - | - | 93.7 | 97.7 | 97.6 |
| Original | 33.205 | 0.8500 | 0.2922 | 80.5 | 90.8 | 89.7 | |
| EKS-SR | 33.220 | 0.8505 | 0.2912 | 80.8 | 90.9 | 89.8 | |
| Improvement | 0.015 | 0.0005 | 0.0010 | 0.3 | 0.1 | 0.1 | |
| Original | 29.469 | 0.7655 | 0.3987 | 50.6 | 63.8 | 60.3 | |
| EKS-SR | 29.567 | 0.7690 | 0.3953 | 52.9 | 66.5 | 62.5 | |
| Improvement | 0.098 | 0.0035 | 0.0034 | 2.3 | 2.7 | 2.2 |
| Label Utilization Rate | PSNR ↑ | SSIM ↑ | LPIPS ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ |
|---|---|---|---|---|---|---|---|---|---|
| 100% | 36.352 | 0.8680 | 0.2041 | 37.2 | 56.7 | 41.0 | 29.8 | 50.4 | 31.3 |
| 25% | 35.960 | 0.8520 | 0.2155 | 36.7 | 56.3 | 40.4 | 29.4 | 49.9 | 30.6 |
| 0% | 35.299 | 0.8516 | 0.2219 | 36.4 | 55.9 | 39.8 | 29.2 | 49.2 | 30.6 |
| Label Utilization Rate | PSNR ↑ | SSIM ↑ | LPIPS ↓ | ↑ | ↑ | ↑ |
|---|---|---|---|---|---|---|
| 100% | 27.083 | 0.6359 | 0.3471 | 51.3 | 73.0 | 61.7 |
| 25% | 26.819 | 0.6261 | 0.3530 | 50.1 | 70.7 | 60.7 |
| 0% | 26.526 | 0.6283 | 0.3687 | 41.5 | 62.3 | 47.8 |
| Model | Learning Strategy | PSNR ↑ | SSIM ↑ | LPIPS ↓ | ↑ | ↑ | ↑ | ↑ | ↑ | ↑ |
|---|---|---|---|---|---|---|---|---|---|---|
| HR | - | - | - | - | 44.2 | 63.1 | 46.7 | 36.5 | 59.3 | 39.4 |
| SRGAN | + + | 35.299 | 0.8516 | 0.2219 | 36.4 | 55.9 | 39.8 | 29.2 | 49.2 | 30.6 |
| + + | 35.822 | 0.8516 | 0.2213 | 36.4 | 55.8 | 39.9 | 29.2 | 49.1 | 30.4 | |
| + + | 36.001 | 0.8511 | 0.2094 | 36.9 | 56.5 | 40.5 | 29.6 | 50.2 | 30.8 | |
| + + + | 36.352 | 0.8680 | 0.2041 | 37.2 | 56.7 | 41.0 | 29.8 | 50.4 | 31.3 | |
| SwinIR | 38.533 | 0.9011 | 0.2182 | 37.8 | 57.0 | 41.7 | 30.7 | 50.9 | 32.9 | |
| 38.541 | 0.9012 | 0.2178 | 37.9 | 57.1 | 41.9 | 30.7 | 51.0 | 32.7 | ||
| + | 38.550 | 0.9015 | 0.2170 | 37.9 | 57.2 | 41.8 | 30.8 | 51.0 | 32.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Z.; He, L.; Zhu, P. Super-Resolution Learning Strategy Based on Expert Knowledge Supervision. Remote Sens. 2024, 16, 2888. https://doi.org/10.3390/rs16162888
Ren Z, He L, Zhu P. Super-Resolution Learning Strategy Based on Expert Knowledge Supervision. Remote Sensing. 2024; 16(16):2888. https://doi.org/10.3390/rs16162888
Chicago/Turabian StyleRen, Zhihan, Lijun He, and Peipei Zhu. 2024. "Super-Resolution Learning Strategy Based on Expert Knowledge Supervision" Remote Sensing 16, no. 16: 2888. https://doi.org/10.3390/rs16162888
APA StyleRen, Z., He, L., & Zhu, P. (2024). Super-Resolution Learning Strategy Based on Expert Knowledge Supervision. Remote Sensing, 16(16), 2888. https://doi.org/10.3390/rs16162888






