Climatology of Polar Stratospheric Clouds Derived from CALIPSO and SLIMCAT
Abstract
1. Introduction
2. Materials and Methods
2.1. CALIPSO PSC Observations
2.2. TOMCAT/SLIMCAT 3D CTM
2.3. PSC Area Calculation
2.4. Relative Standard Deviation
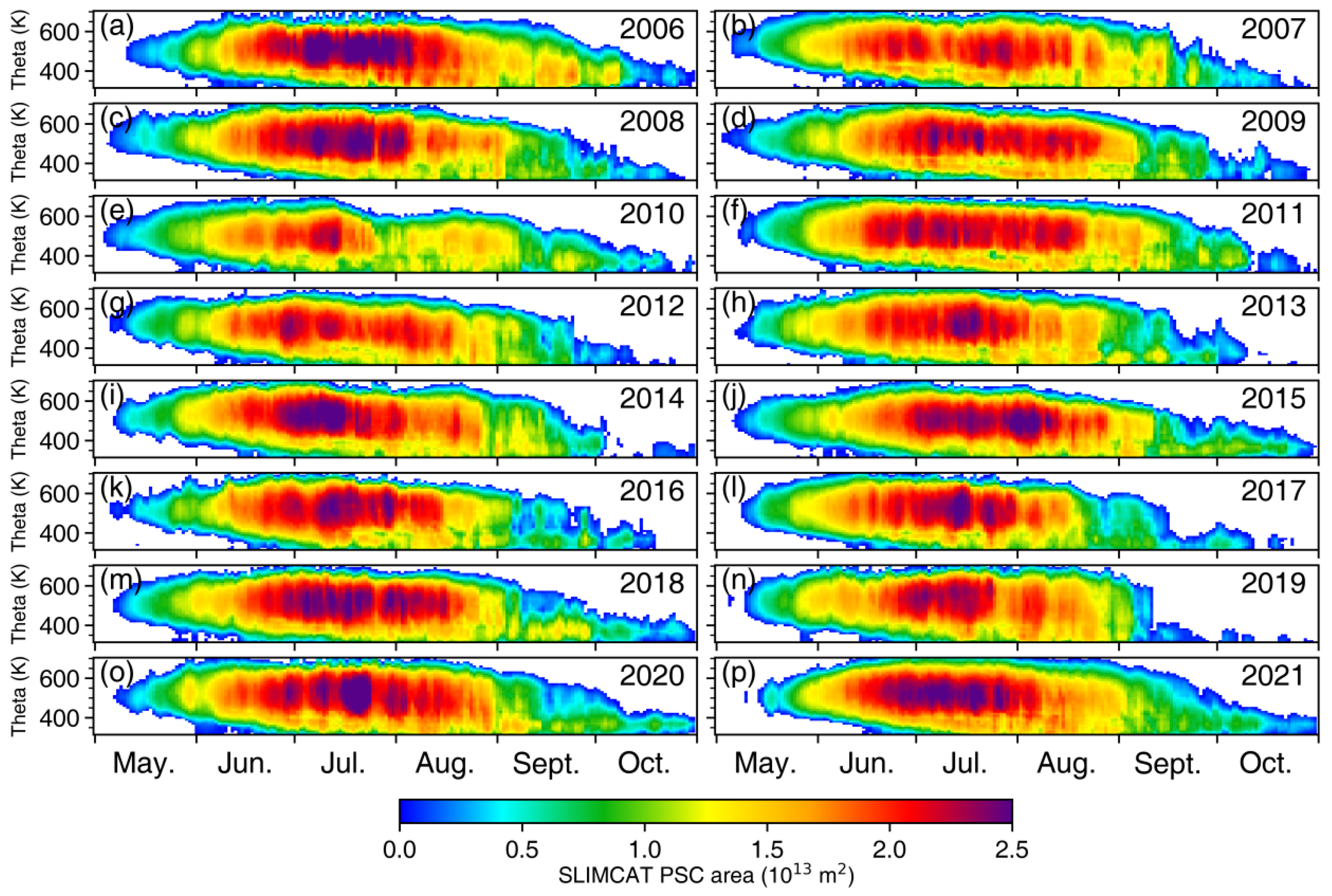
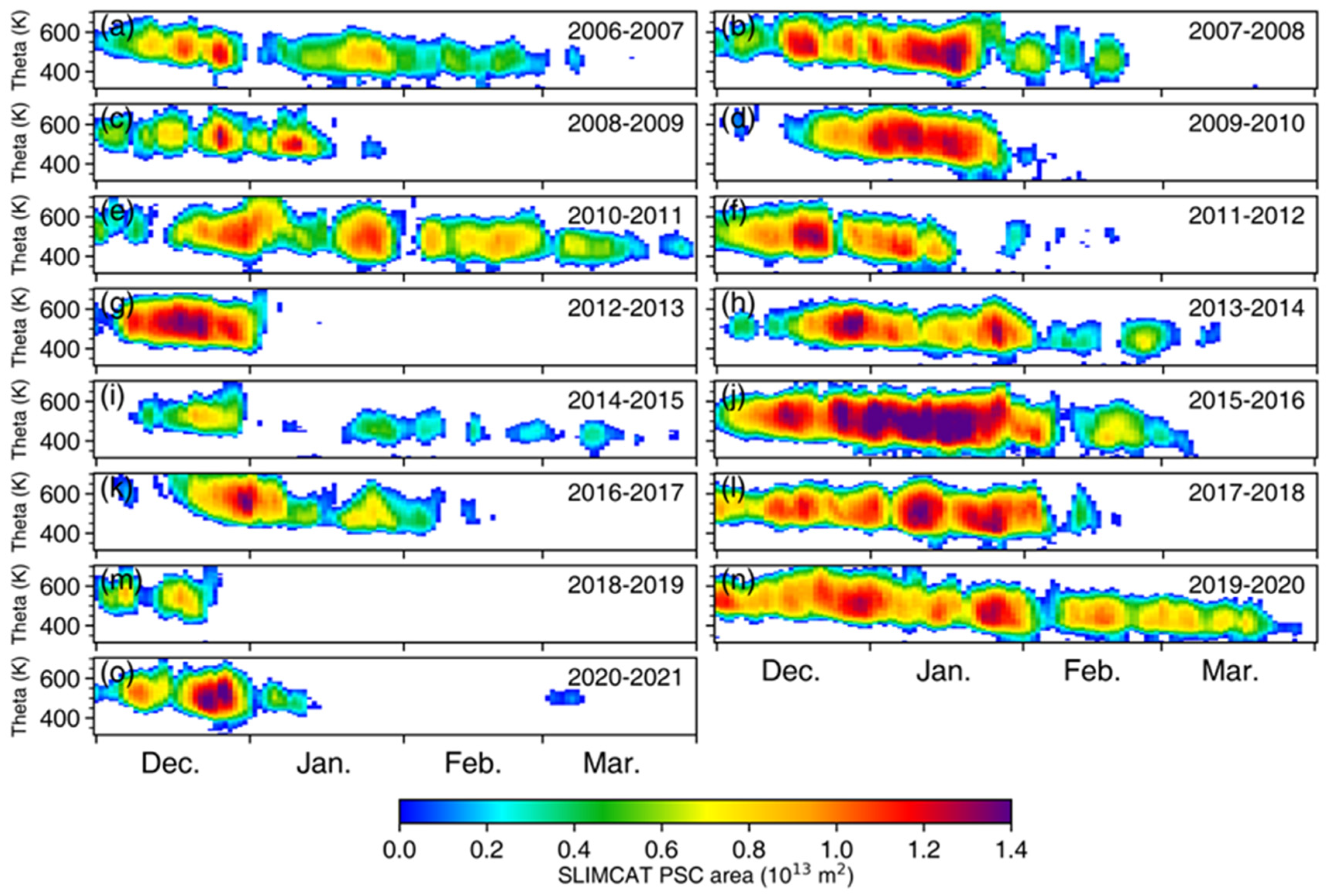
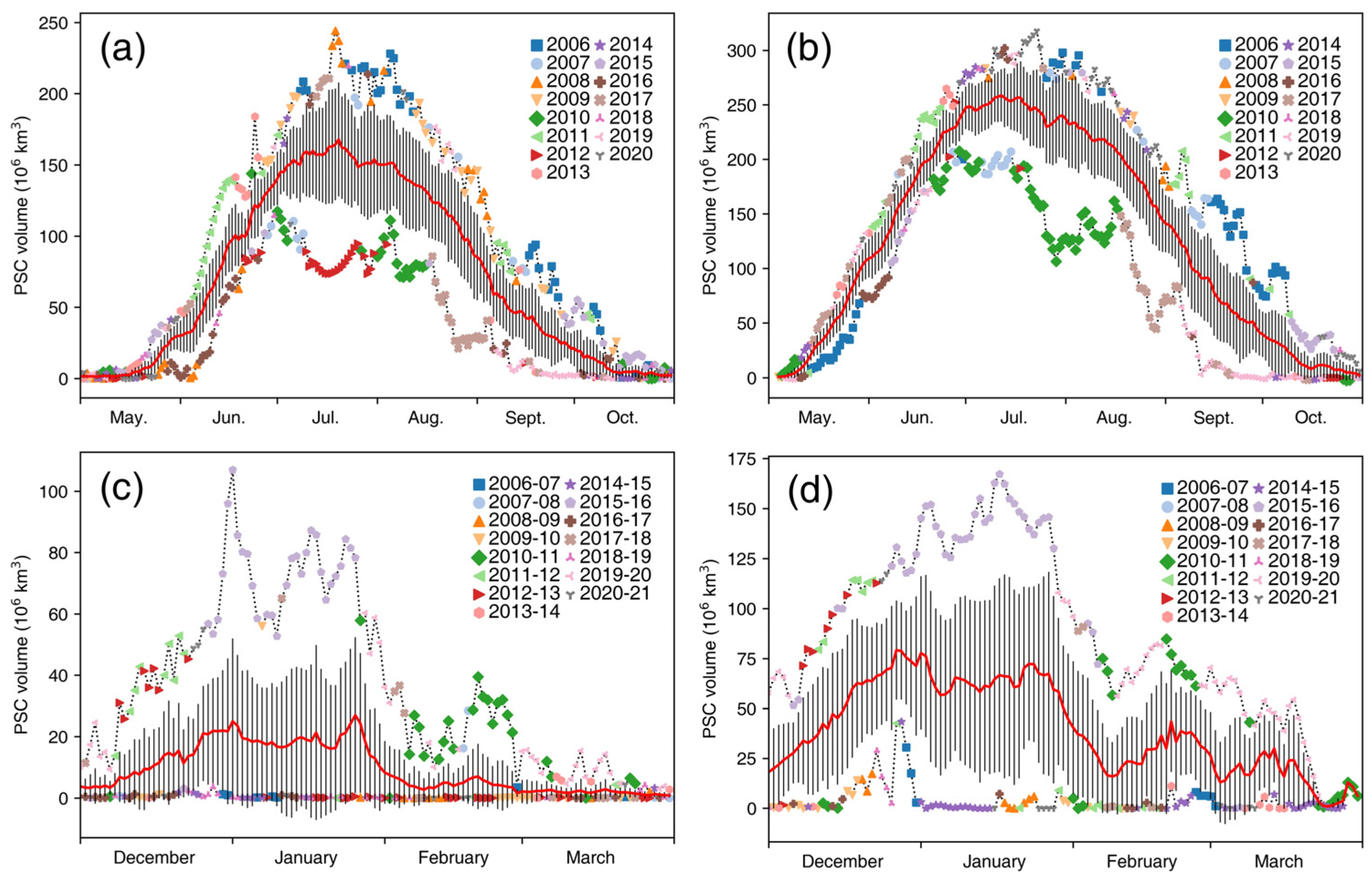
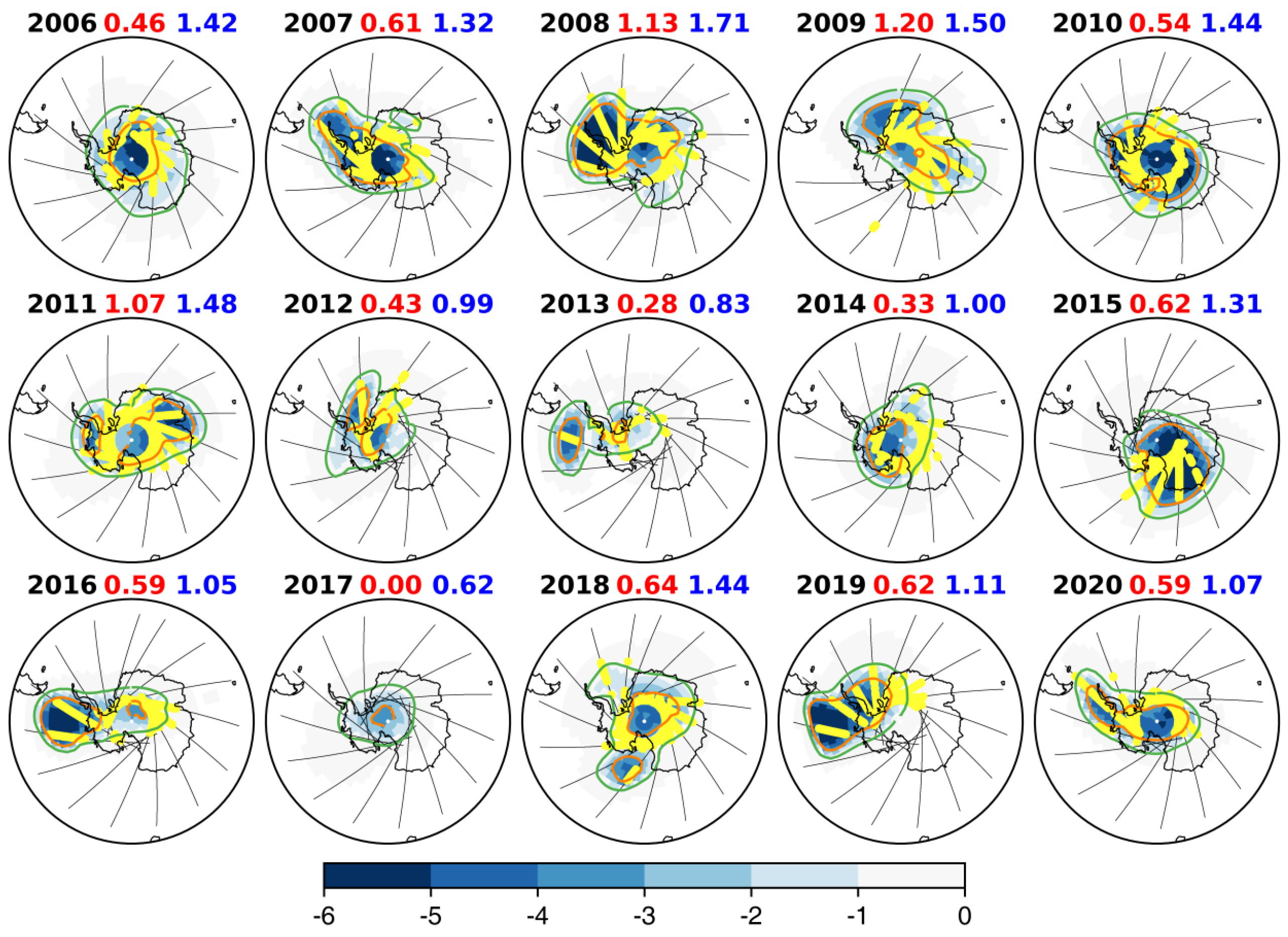
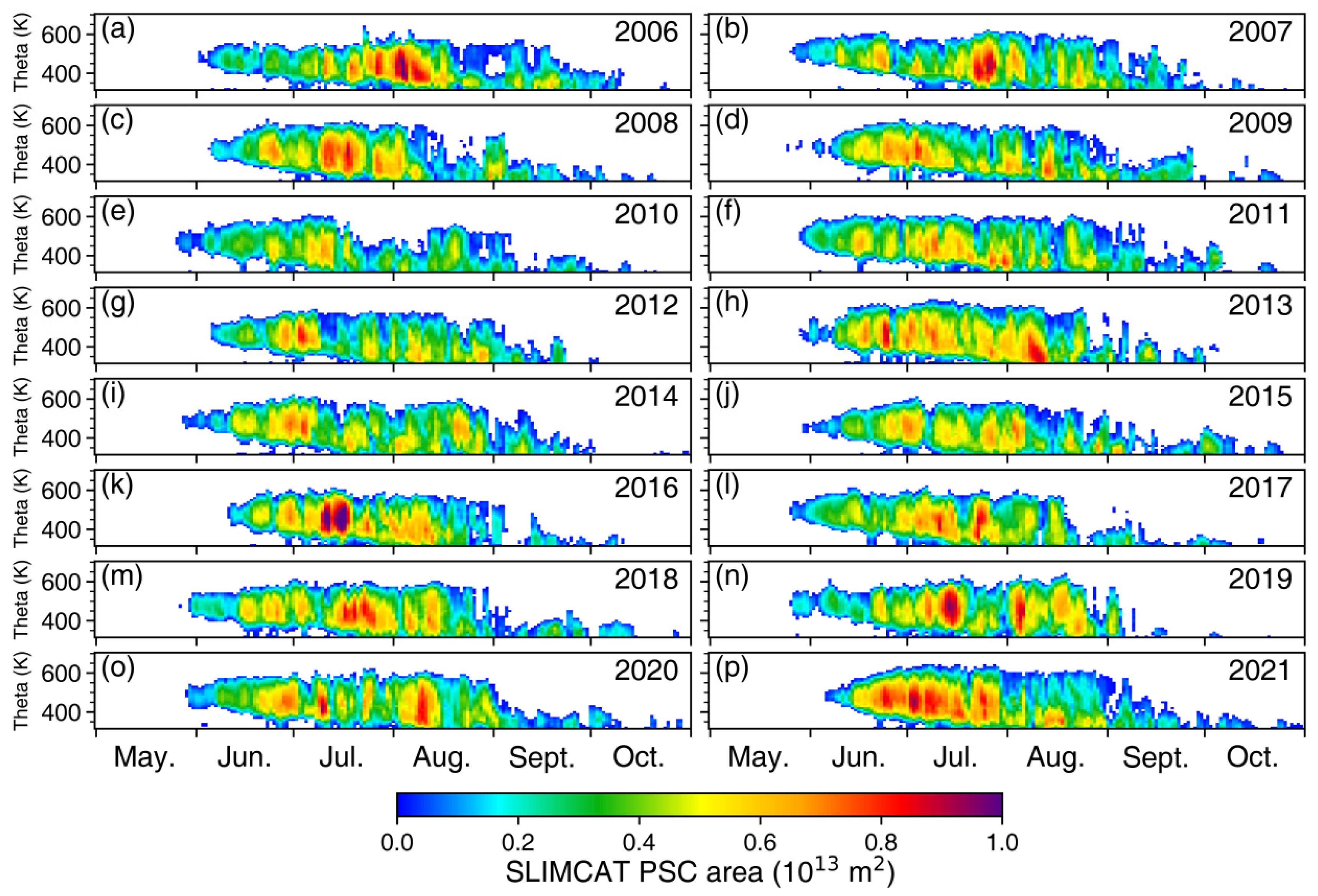
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Solomon, S.; Garcia, R.R.; Rowland, F.S.; Wuebbles, D.J. On the Depletion of Antarctic Ozone. Nature 1986, 321, 755–758. [Google Scholar] [CrossRef]
- Hanson, D.; Mauersberger, K. Laboratory Studies of the Nitric Acid Trihydrate: Implications for the South Polar Stratosphere. Geophys. Res. Lett. 1988, 15, 855–858. [Google Scholar] [CrossRef]
- Browell, E.V.; Butler, C.F.; Ismail, S.; Robinette, P.A.; Carter, A.F.; Higdon, N.S.; Toon, O.B.; Schoeberl, M.R.; Tuck, A.F. Airborne Lidar Observations in the Wintertime Arctic Stratosphere: Polar Stratospheric Clouds. Geophys. Res. Lett. 1990, 17, 385–388. [Google Scholar] [CrossRef]
- Toon, O.B.; Browell, E.V.; Kinne, S.; Jordan, J. An Analysis of Lidar Observations of Polar Stratospheric Clouds. Geophys. Res. Lett. 1990, 17, 393–396. [Google Scholar] [CrossRef]
- Carslaw, K.S.; Luo, B.P.; Clegg, S.L.; Peter, T.; Brimblecombe, P.; Crutzen, P.J. Stratospheric Aerosol Growth and HNO3 Gas Phase Depletion from Coupled HNO3 and Water Uptake by Liquid Particles. Geophys. Res. Lett. 1994, 21, 2479–2482. [Google Scholar] [CrossRef]
- Tabazadeh, A.; Turco, R.P.; Drdla, K.; Jacobson, M.Z.; Toon, O.B. A Study of Type I Polar Stratospheric Cloud Formation. Geophys. Res. Lett. 1994, 21, 1619–1622. [Google Scholar] [CrossRef]
- Tritscher, I.; Pitts, M.C.; Poole, L.R.; Alexander, S.P.; Cairo, F.; Chipperfield, M.P.; Grooß, J.-U.; Höpfner, M.; Lambert, A.; Luo, B.; et al. Polar Stratospheric Clouds: Satellite Observations, Processes, and Role in Ozone Depletion. Rev. Geophys. 2021, 59, e2020RG000702. [Google Scholar] [CrossRef]
- Carslaw, K.S.; Wirth, M.; Tsias, A.; Luo, B.P.; Dörnbrack, A.; Leutbecher, M.; Volkert, H.; Renger, W.; Bacmeister, J.T.; Peter, T. Particle Microphysics and Chemistry in Remotely Observed Mountain Polar Stratospheric Clouds. J. Geophys. Res. Atmos. 1998, 103, 5785–5796. [Google Scholar] [CrossRef]
- Wirth, M.; Tsias, A.; Dörnbrack, A.; Weiß, V.; Carslaw, K.S.; Leutbecher, M.; Renger, W.; Volkert, H.; Peter, T. Model-Guided Lagrangian Observation and Simulation of Mountain Polar Stratospheric Clouds. J. Geophys. Res. Atmos. 1999, 104, 23971–23981. [Google Scholar] [CrossRef]
- Lambert, A.; Santee, M.L.; Livesey, N.J. Interannual Variations of Early Winter Antarctic Polar Stratospheric Cloud Formation and Nitric Acid Observed by CALIOP and MLS. Atmos. Chem. Phys. 2016, 16, 15219–15246. [Google Scholar] [CrossRef]
- Ansmann, A.; Ohneiser, K.; Chudnovsky, A.; Knopf, D.A.; Eloranta, E.W.; Villanueva, D.; Seifert, P.; Radenz, M.; Barja, B.; Zamorano, F.; et al. Ozone Depletion in the Arctic and Antarctic Stratosphere Induced by Wildfire Smoke. Atmos. Chem. Phys. 2022, 22, 11701–11726. [Google Scholar] [CrossRef]
- Koop, T.; Ng, H.P.; Molina, L.T.; Molina, M.J. A New Optical Technique to Study Aerosol Phase Transitions: The Nucleation of Ice from H2SO4 Aerosols. J. Phys. Chem. A 1998, 102, 8924–8931. [Google Scholar] [CrossRef]
- Engel, I.; Luo, B.P.; Pitts, M.C.; Poole, L.R.; Hoyle, C.R.; Grooß, J.-U.; Dörnbrack, A.; Peter, T. Heterogeneous Formation of Polar Stratospheric Clouds—Part 2: Nucleation of Ice on Synoptic Scales. Atmos. Chem. Phys. 2013, 13, 10769–10785. [Google Scholar] [CrossRef]
- Voigt, C.; Dörnbrack, A.; Wirth, M.; Groß, S.M.; Pitts, M.C.; Poole, L.R.; Baumann, R.; Ehard, B.; Sinnhuber, B.-M.; Woiwode, W.; et al. Widespread Polar Stratospheric Ice Clouds in the 2015–2016 Arctic Winter—Implications for Ice Nucleation. Atmos. Chem. Phys. 2018, 18, 15623–15641. [Google Scholar] [CrossRef]
- Salawitch, R.J.; Wofsy, S.C.; Gottlieb, E.W.; Lait, L.R.; Newman, P.A.; Schoeberl, M.R.; Loewenstein, M.; Podolske, J.R.; Strahan, S.E.; Proffitt, M.H.; et al. Chemical Loss of Ozone in the Arctic Polar Vortex in the Winter of 1991–1992. Science 1993, 261, 1146–1149. [Google Scholar] [CrossRef] [PubMed]
- Hunt, B.G. Photochemistry of Ozone in a Moist Atmosphere. J. Geophys. Res. 1966, 71, 1385–1398. [Google Scholar] [CrossRef]
- Nicolet, M. The Origin of Nitric Oxide in the Terrestrial Atmosphere. Planet. Space Sci. 1970, 18, 1111–1118. [Google Scholar] [CrossRef]
- Spang, R.; Arndt, K.; Dudhia, A.; Höpfner, M.; Hoffmann, L.; Hurley, J.; Grainger, R.G.; Griessbach, S.; Poulsen, C.; Remedios, J.J.; et al. Fast Cloud Parameter Retrievals of MIPAS/Envisat. Atmos. Chem. Phys. 2012, 12, 7135–7164. [Google Scholar] [CrossRef]
- Spang, R.; Hoffmann, L.; Müller, R.; Grooß, J.-U.; Tritscher, I.; Höpfner, M.; Pitts, M.; Orr, A.; Riese, M. A Climatology of Polar Stratospheric Cloud Composition between 2002 and 2012 Based on MIPAS/Envisat Observations. Atmos. Chem. Phys. 2018, 18, 5089–5113. [Google Scholar] [CrossRef]
- Lecours, M.; Bernath, P.; Boone, C.; Crouse, J. Infrared Transmittance Spectra of Polar Stratospheric Clouds. J. Quant. Spectrosc. Radiat. Transf. 2023, 294, 108406. [Google Scholar] [CrossRef]
- Lavy, L.; Bernath, P.; Lecours, M.; English, D.; Fromm, M. Comparison between ACE and CALIPSO Observations of Antarctic Polar Stratospheric Clouds. J. Quant. Spectrosc. Radiat. Transf. 2024, 313, 108827. [Google Scholar] [CrossRef]
- Achtert, P.; Tesche, M. Assessing Lidar-based Classification Schemes for Polar Stratospheric Clouds Based on 16 Years of Measurements at Esrange, Sweden. J. Geophys. Res. Atmos. 2014, 119, 1386–1405. [Google Scholar] [CrossRef]
- Pitts, M.C.; Poole, L.R.; Gonzalez, R. Polar Stratospheric Cloud Climatology Based on CALIPSO Spaceborne Lidar Measurements from 2006 to 2017. Atmos. Chem. Phys. 2018, 18, 10881–10913. [Google Scholar] [CrossRef]
- Achtert, P.; Khosrawi, F.; Blum, U.; Fricke, K.H. Investigation of Polar Stratospheric Clouds in January 2008 by Means of Ground-Based and Spaceborne Lidar Measurements and Microphysical Box Model Simulations. J. Geophys. Res. Atmos. 2011, 116, D07201. [Google Scholar] [CrossRef]
- Achtert, P.; Karlsson Andersson, M.; Khosrawi, F.; Gumbel, J. On the Linkage between Tropospheric and Polar Stratospheric Clouds in the Arctic as Observed by Space–Borne Lidar. Atmos. Chem. Phys. 2012, 12, 3791–3798. [Google Scholar] [CrossRef]
- Zhu, Y.; Toon, O.B.; Pitts, M.C.; Lambert, A.; Bardeen, C.; Kinnison, D.E. Comparing Simulated PSC Optical Properties with CALIPSO Observations during the 2010 Antarctic Winter: Comparing Simulated PSC With CALIPSO. J. Geophys. Res. Atmos. 2017, 122, 1175–1202. [Google Scholar] [CrossRef]
- Zhu, Y.; Toon, O.B.; Lambert, A.; Kinnison, D.E.; Bardeen, C.; Pitts, M.C. Development of a Polar Stratospheric Cloud Model Within the Community Earth System Model: Assessment of 2010 Antarctic Winter. J. Geophys. Res. Atmos. 2017, 122, 10418–10438. [Google Scholar] [CrossRef]
- Tritscher, I.; Grooß, J.-U.; Spang, R.; Pitts, M.C.; Poole, L.R.; Müller, R.; Riese, M. Lagrangian Simulation of Ice Particles and Resulting Dehydration in the Polar Winter Stratosphere. Atmos. Chem. Phys. 2019, 19, 543–563. [Google Scholar] [CrossRef]
- Steiner, M.; Luo, B.; Peter, T.; Pitts, M.C.; Stenke, A. Evaluation of Polar Stratospheric Clouds in the Global Chemistry–Climate Model SOCOLv3.1 by Comparison with CALIPSO Spaceborne Lidar Measurements. Geosci. Model Dev. 2021, 14, 935–959. [Google Scholar] [CrossRef]
- Zhu, Y.; Toon, O.B.; Lambert, A.; Kinnison, D.E.; Brakebusch, M.; Bardeen, C.G.; Mills, M.J.; English, J.M. Development of a Polar Stratospheric Cloud Model within the Community Earth System Model Using Constraints on Type I PSCs from the 2010–2011 Arctic Winter. J. Adv. Model. Earth Syst. 2015, 7, 551–585. [Google Scholar] [CrossRef]
- Hanson, D.R.; Ravishankara, A.R. Reactive Uptake of ClONO2 onto Sulfuric Acid Due to Reaction with HCl and H2O. J. Phys. Chem. 1994, 98, 5728–5735. [Google Scholar] [CrossRef]
- Wegner, T.; Kinnison, D.E.; Garcia, R.R.; Solomon, S. Simulation of Polar Stratospheric Clouds in the Specified Dynamics Version of the Whole Atmosphere Community Climate Model: POLAR STRATOSPHERIC CLOUDS IN SD-WACCM 4. J. Geophys. Res. Atmos. 2013, 118, 4991–5002. [Google Scholar] [CrossRef]
- Dhomse, S.; Chipperfield, M.P.; Feng, W.; Haigh, J.D. Solar Response in Tropical Stratospheric Ozone: A 3-D Chemical Transport Model Study Using ERA Reanalyses. Atmos. Chem. Phys. 2011, 11, 12773–12786. [Google Scholar] [CrossRef]
- Chipperfield, M.P.; Bekki, S.; Dhomse, S.; Harris, N.R.P.; Hassler, B.; Hossaini, R.; Steinbrecht, W.; Thiéblemont, R.; Weber, M. Detecting Recovery of the Stratospheric Ozone Layer. Nature 2017, 549, 211–218. [Google Scholar] [CrossRef]
- Weber, M.; Arosio, C.; Feng, W.; Dhomse, S.S.; Chipperfield, M.P.; Meier, A.; Burrows, J.P.; Eichmann, K.; Richter, A.; Rozanov, A. The Unusual Stratospheric Arctic Winter 2019/20: Chemical Ozone Loss from Satellite Observations and TOMCAT Chemical Transport Model. J. Geophys. Res. Atmos. 2021, 126, e2020JD034386. [Google Scholar] [CrossRef]
- Chipperfield, M.P.; Dhomse, S.S.; Feng, W.; McKenzie, R.L.; Velders, G.J.M.; Pyle, J.A. Quantifying the Ozone and Ultraviolet Benefits Already Achieved by the Montreal Protocol. Nat. Commun. 2015, 6, 7233. [Google Scholar] [CrossRef]
- Dhomse, S.S.; Feng, W.; Montzka, S.A.; Hossaini, R.; Keeble, J.; Pyle, J.A.; Daniel, J.S.; Chipperfield, M.P. Delay in Recovery of the Antarctic Ozone Hole from Unexpected CFC-11 Emissions. Nat. Commun. 2019, 10, 5781. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Chipperfield, M.P.; Davies, S.; von der Gathen, P.; Kyrö, E.; Volk, C.M.; Ulanovsky, A.; Belyaev, G. Large Chemical Ozone Loss in 2004/2005 Arctic Winter/Spring. Geophys. Res. Lett. 2007, 34, L09803. [Google Scholar] [CrossRef]
- Wohltmann, I.; Wegner, T.; Müller, R.; Lehmann, R.; Rex, M.; Manney, G.L.; Santee, M.L.; Bernath, P.; Sumińska-Ebersoldt, O.; Stroh, F.; et al. Uncertainties in Modelling Heterogeneous Chemistry and Arctic Ozone Depletion in the Winter 2009/2010. Atmos. Chem. Phys. 2013, 13, 3909–3929. [Google Scholar] [CrossRef]
- Nakajima, H.; Wohltmann, I.; Wegner, T.; Takeda, M.; Pitts, M.C.; Poole, L.R.; Lehmann, R.; Santee, M.L.; Rex, M. Polar Stratospheric Cloud Evolution and Chlorine Activation Measured by CALIPSO and MLS, and Modeled by ATLAS. Atmos. Chem. Phys. 2016, 16, 3311–3325. [Google Scholar] [CrossRef]
- Feng, W.; Dhomse, S.S.; Arosio, C.; Weber, M.; Burrows, J.P.; Santee, M.L.; Chipperfield, M.P. Arctic Ozone Depletion in 2019/20: Roles of Chemistry, Dynamics and the Montreal Protocol. Geophys. Res. Lett. 2021, 48, e2020GL091911. [Google Scholar] [CrossRef]
- Kuttippurath, J.; Feng, W.; Müller, R.; Kumar, P.; Raj, S.; Gopikrishnan, G.P.; Roy, R. Exceptional Loss in Ozone in the Arctic Winter/Spring of 2019/2020. Atmos. Chem. Phys. 2021, 21, 14019–14037. [Google Scholar] [CrossRef]
- Ardra, D.; Kuttippurath, J.; Roy, R.; Kumar, P.; Raj, S.; Müller, R.; Feng, W. The Unprecedented Ozone Loss in the Arctic Winter and Spring of 2010/2011 and 2019/2020. ACS Earth Space Chem. 2022, 6, 683–693. [Google Scholar] [CrossRef]
- Winker, D.M.; Hunt, W.H.; McGill, M.J. Initial Performance Assessment of CALIOP. Geophys. Res. Lett. 2007, 34, L19803. [Google Scholar] [CrossRef]
- Pitts, M.C.; Thomason, L.W.; Poole, L.R.; Winker, D.M. Characterization of Polar Stratospheric Clouds with Spaceborne Lidar: CALIPSO and the 2006 Antarctic Season. Atmos. Chem. Phys. 2007, 7, 5207–5228. [Google Scholar] [CrossRef]
- Pitts, M.C.; Poole, L.R.; Lambert, A.; Thomason, L.W. An Assessment of CALIOP Polar Stratospheric Cloud Composition Classification. Atmos. Chem. Phys. 2013, 13, 2975–2988. [Google Scholar] [CrossRef]
- Pitts, M.C.; Poole, L.R.; Thomason, L.W. CALIPSO Polar Stratospheric Cloud Observations: Second-Generation Detection Algorithm and Composition Discrimination. Atmos. Chem. Phys. 2009, 9, 7577–7589. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Chipperfield, M.P. New Version of the TOMCAT/SLIMCAT off-Line Chemical Transport Model: Intercomparison of Stratospheric Tracer Experiments. Q. J. R. Meteor. Soc. 2006, 132, 1179–1203. [Google Scholar] [CrossRef]
- Feng, W.; Chipperfield, M.P.; Roscoe, H.K.; Remedios, J.J.; Waterfall, A.M.; Stiller, G.P.; Glatthor, N.; Höpfner, M.; Wang, D.-Y. Three-Dimensional Model Study of the Antarctic Ozone Hole in 2002 and Comparison with 2000. J. Atmos. Sci. 2005, 62, 822–837. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Xie, F.; Chipperfield, M.P.; Feng, W.; Son, S.-W.; Abraham, N.L.; Archibald, A.T.; Bekki, S.; Butchart, N.; et al. Stratospheric Ozone Loss over the Eurasian Continent Induced by the Polar Vortex Shift. Nat. Commun. 2018, 9, 206. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, C.; Zhang, K.; Xu, M.; Duan, J.; Chipperfield, M.P.; Feng, W.; Zhao, S.; Xie, F. The Role of Chemical Processes in the Quasi-Biennial Oscillation (QBO) Signal in Stratospheric Ozone. Atmos. Environ. 2021, 244, 117906. [Google Scholar] [CrossRef]
- Snels, M.; Scoccione, A.; Di Liberto, L.; Colao, F.; Pitts, M.; Poole, L.; Deshler, T.; Cairo, F.; Cagnazzo, C.; Fierli, F. Comparison of Antarctic Polar Stratospheric Cloud Observations by Ground-Based and Space-Borne Lidar and Relevance for Chemistry–Climate Models. Atmos. Chem. Phys. 2019, 19, 955–972. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteor. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Feng, W.; Chipperfield, M.P.; Dorf, M.; Pfeilsticker, K.; Ricaud, P. Mid-Latitude Ozone Changes: Studies with a 3-D CTM Forced by ERA-40 Analyses. Atmos. Chem. Phys. 2007, 7, 2357–2369. [Google Scholar] [CrossRef]
- Li, Y.; Dhomse, S.S.; Chipperfield, M.P.; Feng, W.; Chrysanthou, A.; Xia, Y.; Guo, D. Effects of Reanalysis Forcing Fields on Ozone Trends and Age of Air from a Chemical Transport Model. Atmos. Chem. Phys. 2022, 22, 10635–10656. [Google Scholar] [CrossRef]
- Coy, L.; Nash, E.R.; Newman, P.A. Meteorology of the Polar Vortex: Spring 1997. Geophys. Res. Lett. 1997, 24, 2693–2696. [Google Scholar] [CrossRef]
- Lawrence, Z.D.; Manney, G.L.; Wargan, K. Reanalysis Intercomparisons of Stratospheric Polar Processing Diagnostics. Atmos. Chem. Phys. 2018, 18, 13547–13579. [Google Scholar] [CrossRef] [PubMed]
- Ivy, D.J.; Solomon, S.; Kinnison, D.; Mills, M.J.; Schmidt, A.; Neely III, R.R. The Influence of the Calbuco Eruption on the 2015 Antarctic Ozone Hole in a Fully Coupled Chemistry-Climate Model. Geophys. Res. Lett. 2017, 44, 2556–2561. [Google Scholar] [CrossRef]
- Shen, X.; Wang, L.; Osprey, S. The Southern Hemisphere Sudden Stratospheric Warming of September 2019. Sci. Bull. 2020, 65, 1800–1802. [Google Scholar] [CrossRef]
- Manney, G.L.; Lawrence, Z.D. The Major Stratospheric Final Warming in 2016: Dispersal of Vortex Air and Termination of Arctic Chemical Ozone Loss. Atmos. Chem. Phys. 2016, 16, 15371–15396. [Google Scholar] [CrossRef]
- Khosrawi, F.; Kirner, O.; Sinnhuber, B.-M.; Johansson, S.; Höpfner, M.; Santee, M.L.; Froidevaux, L.; Ungermann, J.; Ruhnke, R.; Woiwode, W.; et al. Denitrification, Dehydration and Ozone Loss during the 2015/2016 Arctic Winter. Atmos. Chem. Phys. 2017, 17, 12893–12910. [Google Scholar] [CrossRef]
- Hu, J.; Li, T.; Xu, H. Relationship between the North Pacific Gyre Oscillation and the Onset of Stratospheric Final Warming in the Northern Hemisphere. Clim. Dyn. 2018, 51, 3061–3075. [Google Scholar] [CrossRef]
- Qin, Y.; Gu, S.; Dou, X.; Teng, C.; Li, H. On the Westward Quasi-8-Day Planetary Waves in the Middle Atmosphere During Arctic Sudden Stratospheric Warmings. J. Geophys. Res. Atmos. 2021, 126, e2021JD035071. [Google Scholar] [CrossRef]
- Manney, G.L.; Santee, M.L.; Rex, M.; Livesey, N.J.; Pitts, M.C.; Veefkind, P.; Nash, E.R.; Wohltmann, I.; Lehmann, R.; Froidevaux, L.; et al. Unprecedented Arctic Ozone Loss in 2011. Nature 2011, 478, 469–475. [Google Scholar] [CrossRef]
- Feng, W.; Chipperfield, M.P.; Davies, S.; Mann, G.W.; Carslaw, K.S.; Dhomse, S.; Harvey, L.; Randall, C.; Santee, M.L. Modelling the Effect of Denitrification on Polar Ozone Depletion for Arctic Winter 2004/2005. Atmos. Chem. Phys. 2011, 11, 6559–6573. [Google Scholar] [CrossRef]
- Hoffmann, L.; Spang, R.; Orr, A.; Alexander, M.J.; Holt, L.A.; Stein, O. A Decadal Satellite Record of Gravity Wave Activity in the Lower Stratosphere to Study Polar Stratospheric Cloud Formation. Atmos. Chem. Phys. 2017, 17, 2901–2920. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, W.; Chipperfield, M.P.; Xie, F.; Huang, J. Persistent Shift of the Arctic Polar Vortex towards the Eurasian Continent in Recent Decades. Nat. Clim. Change 2016, 6, 1094–1099. [Google Scholar] [CrossRef]
- Lambert, A.; Santee, M.L.; Wu, D.L.; Chae, J.H. A-Train CALIOP and MLS Observations of Early Winter Antarctic Polar Stratospheric Clouds and Nitric Acid in 2008. Atmos. Chem. Phys. 2012, 12, 2899–2931. [Google Scholar] [CrossRef]



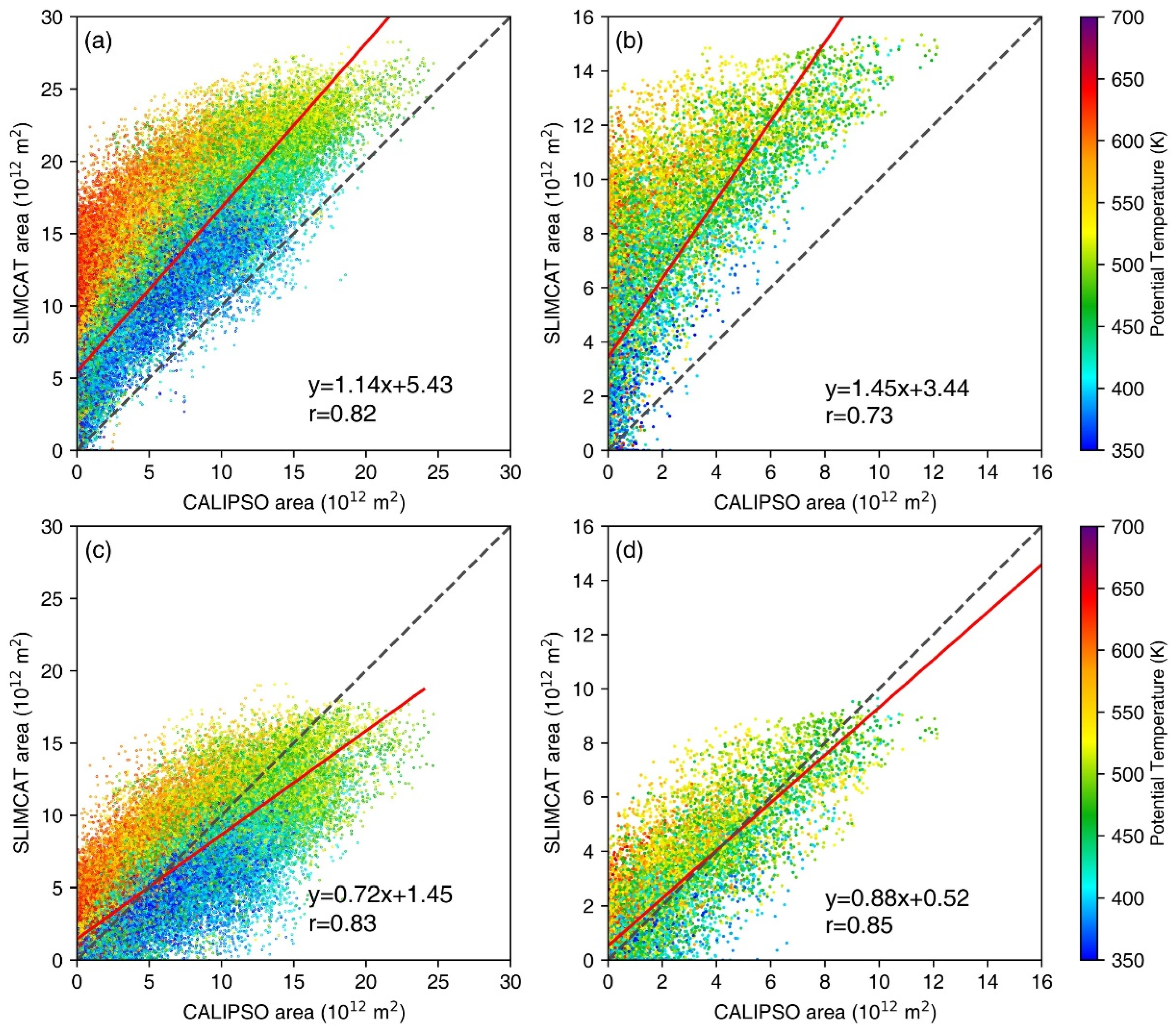
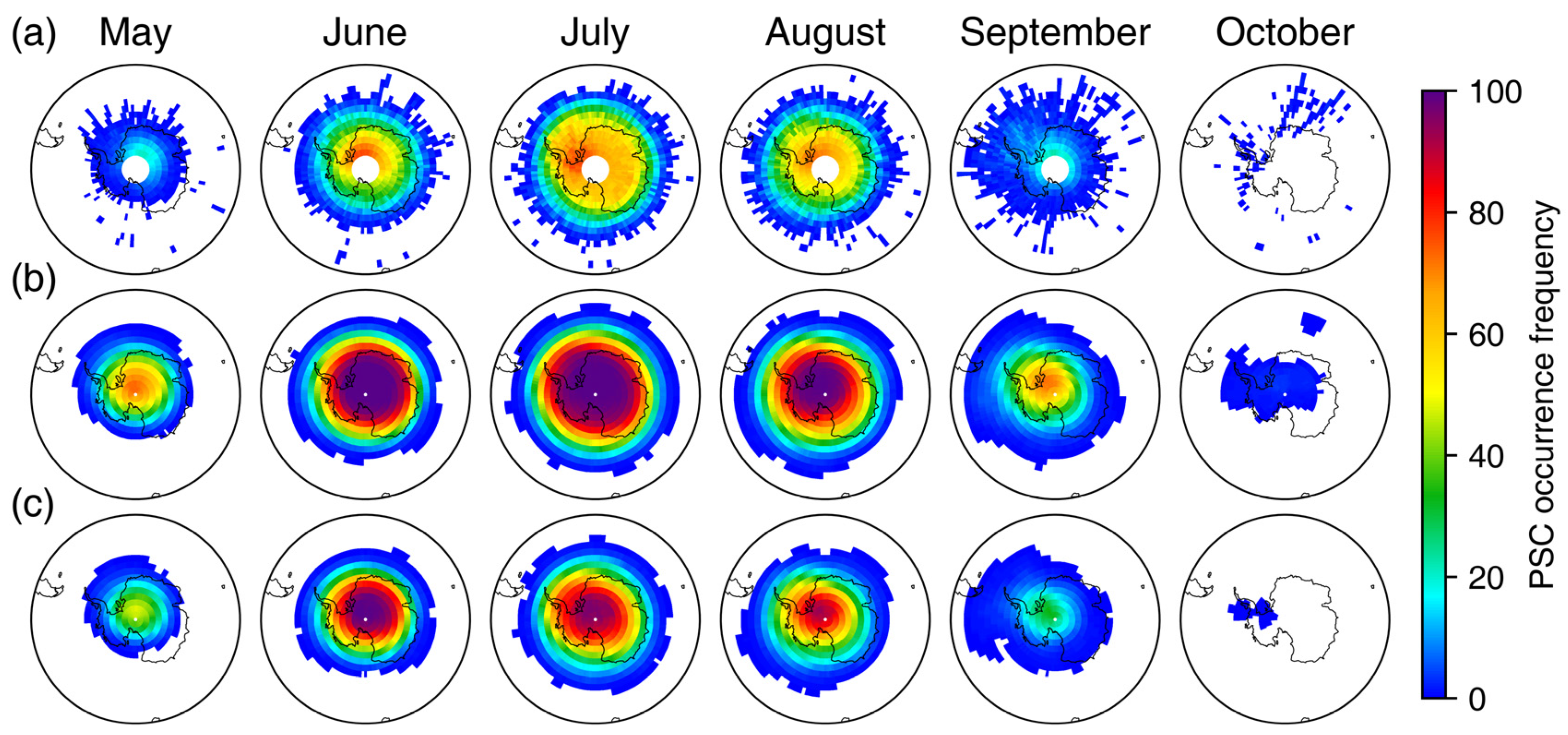
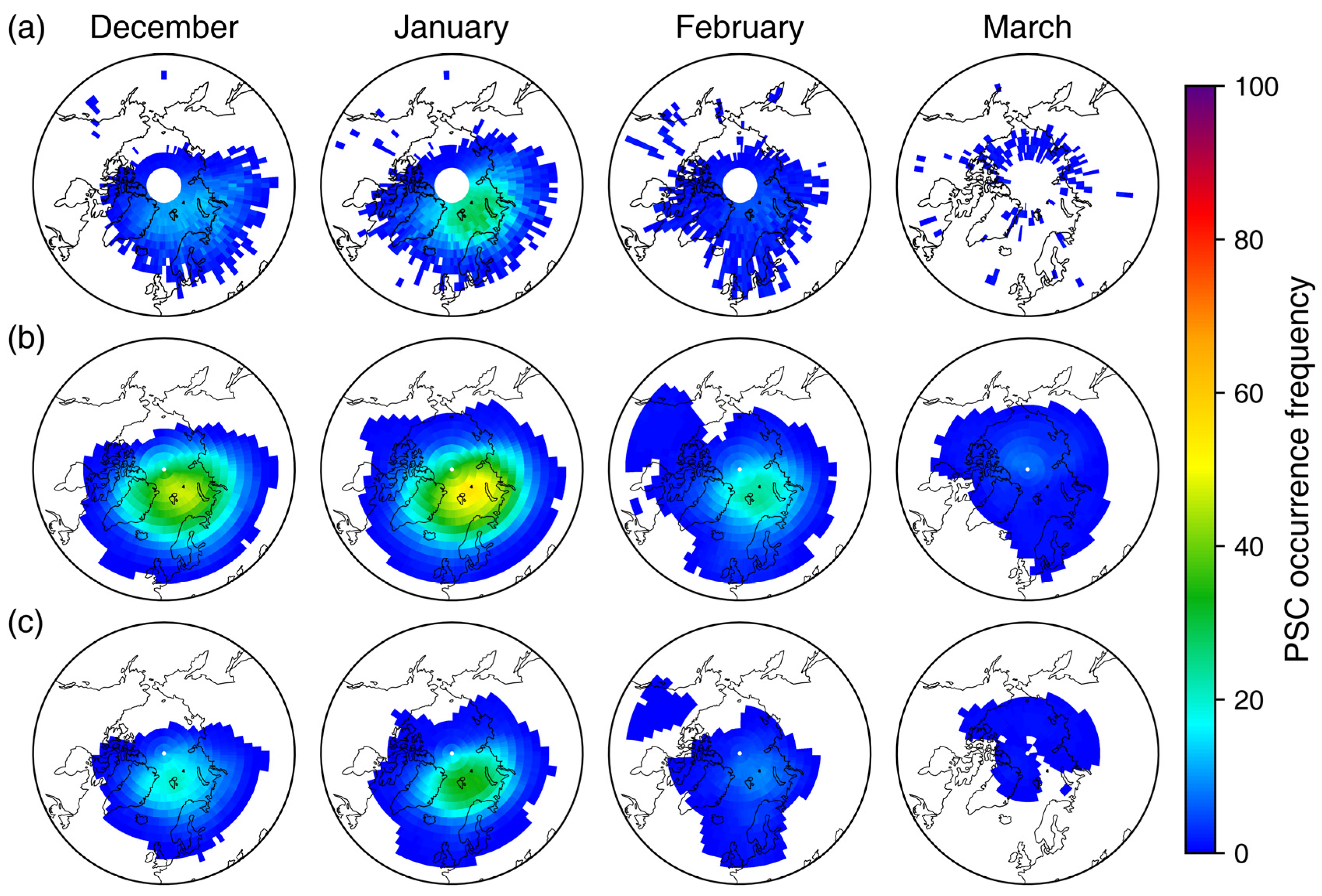
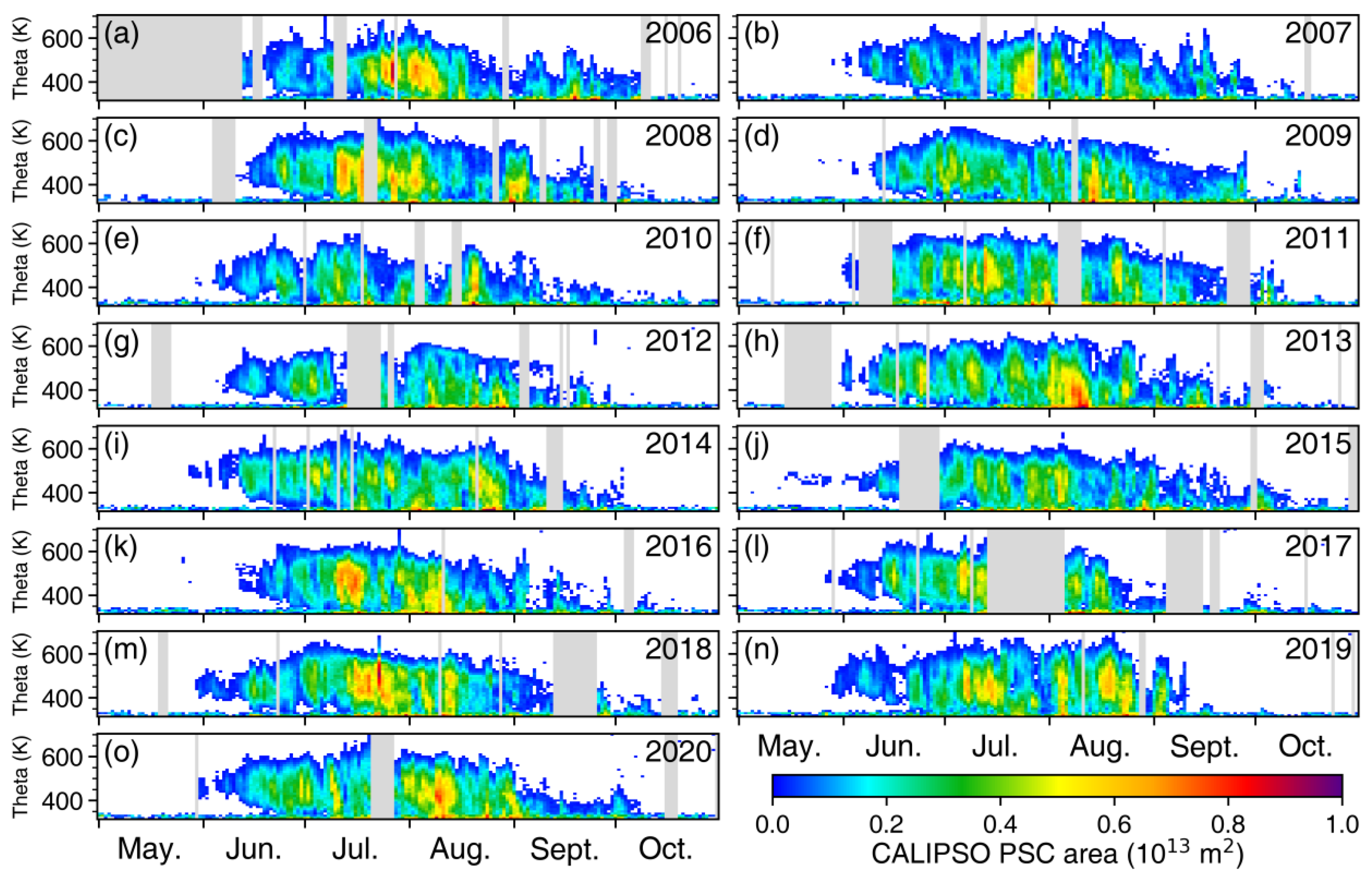

| Items | Antarctic | Arctic | ||
|---|---|---|---|---|
| CALIPSO | SLIMCAT | CALIPSO | SLIMCAT | |
| Mean value (106 km3) | 71.72 | 135.49 | 9.82 | 46.84 |
| Seasonal variation (%) | 86.39 | 67.49 | 148.23 | 75.08 |
| Interannual variation (%) | 41.12 | 36.02 | 128.92 | 74.95 |
| Linear trend (106 km3/year) | −1.21 ± 1.40 | 0.07 ± 0.89 | 0.05 ± 0.58 | 0.39 ± 1.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Wang, Z.; Li, S.; Zhang, J.; Feng, W. Climatology of Polar Stratospheric Clouds Derived from CALIPSO and SLIMCAT. Remote Sens. 2024, 16, 3285. https://doi.org/10.3390/rs16173285
Li D, Wang Z, Li S, Zhang J, Feng W. Climatology of Polar Stratospheric Clouds Derived from CALIPSO and SLIMCAT. Remote Sensing. 2024; 16(17):3285. https://doi.org/10.3390/rs16173285
Chicago/Turabian StyleLi, Douwang, Zhe Wang, Shun Li, Jiankai Zhang, and Wuhu Feng. 2024. "Climatology of Polar Stratospheric Clouds Derived from CALIPSO and SLIMCAT" Remote Sensing 16, no. 17: 3285. https://doi.org/10.3390/rs16173285
APA StyleLi, D., Wang, Z., Li, S., Zhang, J., & Feng, W. (2024). Climatology of Polar Stratospheric Clouds Derived from CALIPSO and SLIMCAT. Remote Sensing, 16(17), 3285. https://doi.org/10.3390/rs16173285









