Impact of a New Wave Mixing Scheme on Ocean Dynamics in Typhoon Conditions: A Case Study of Typhoon In-Fa (2021)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Programs
2.2. Introduction and Setup of the Coupling Model
2.3. Study Area and Datasets
3. Results
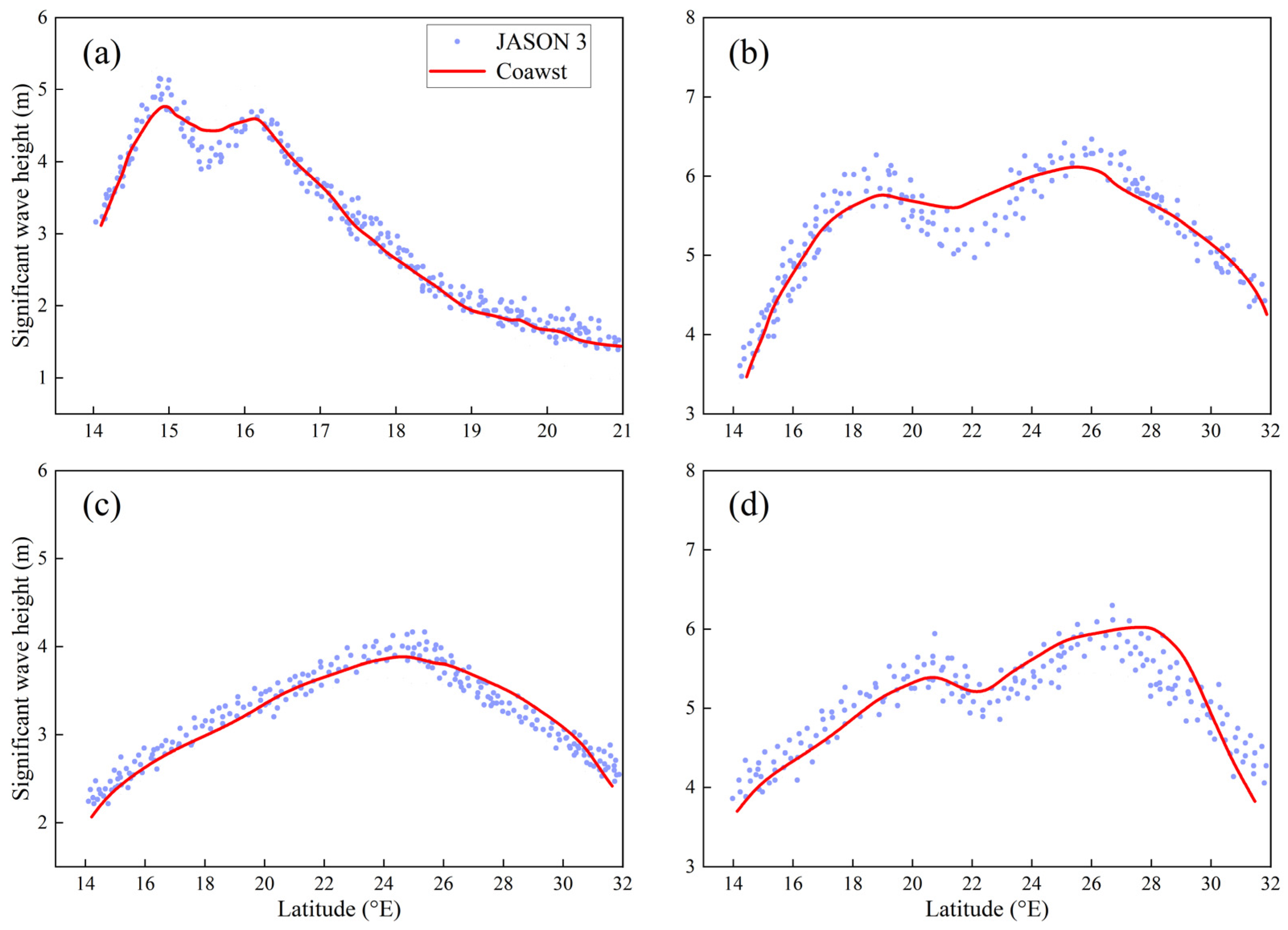
3.1. Wave-Simulation Results
3.2. Simulated Currents
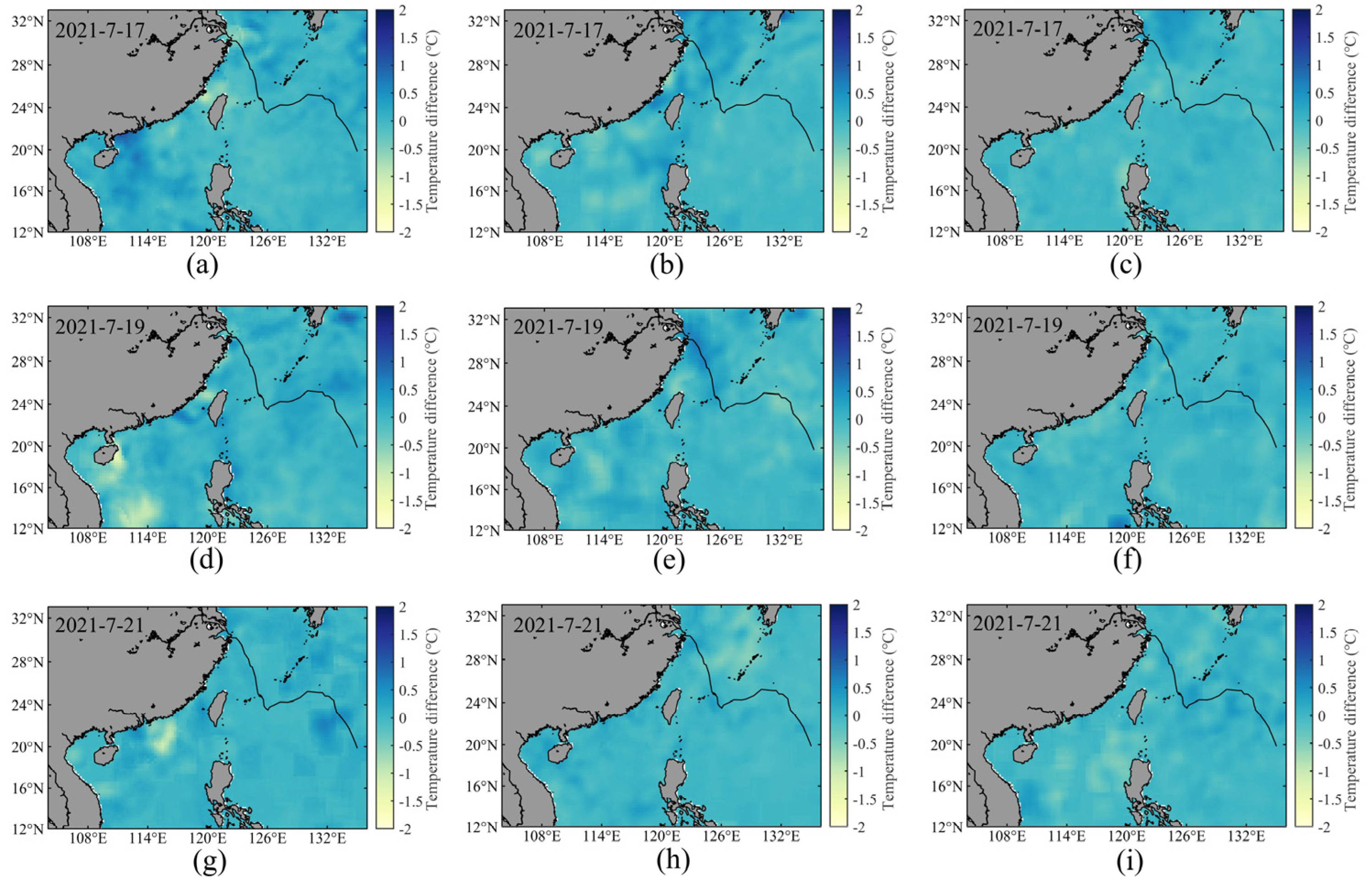
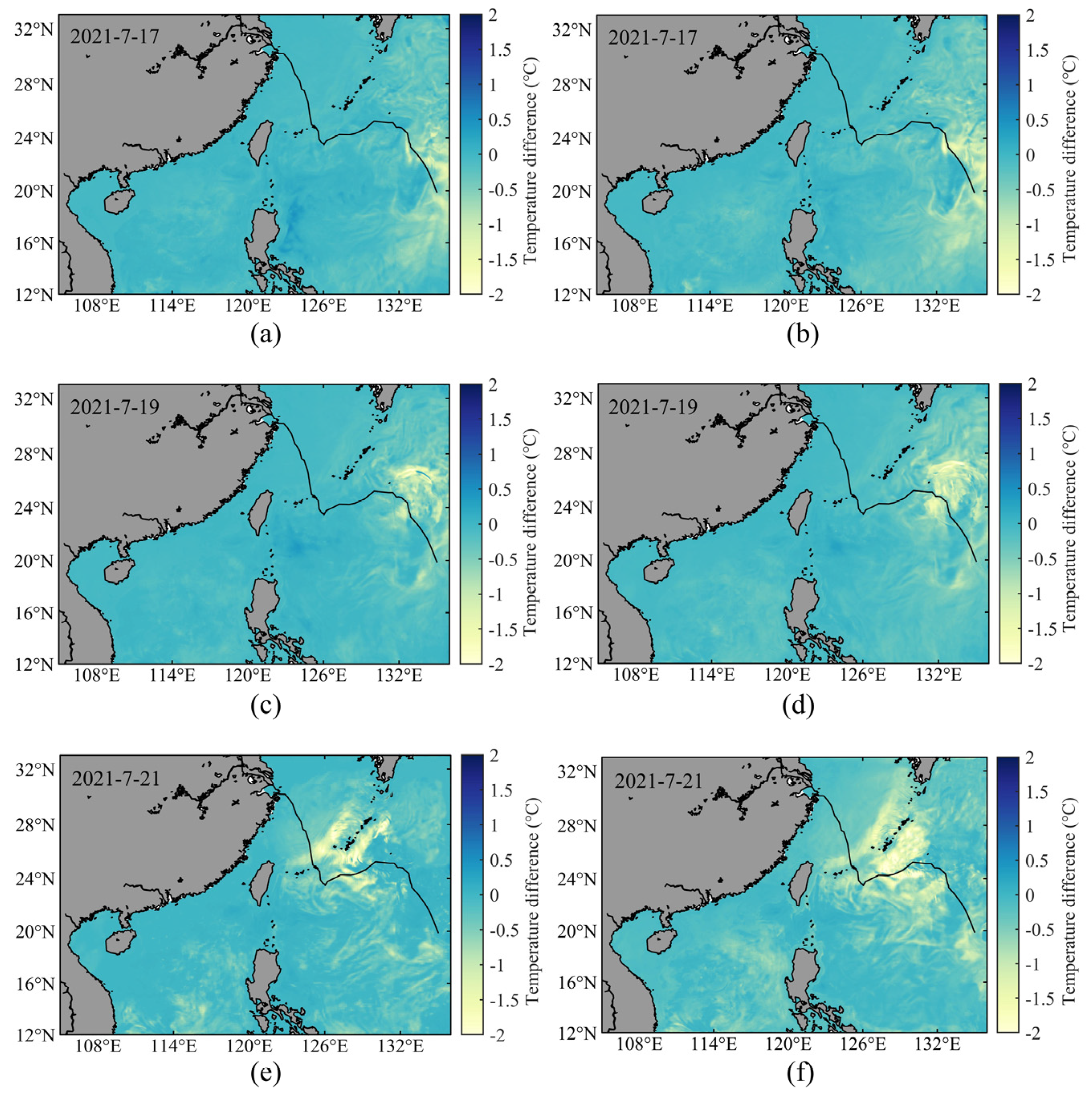
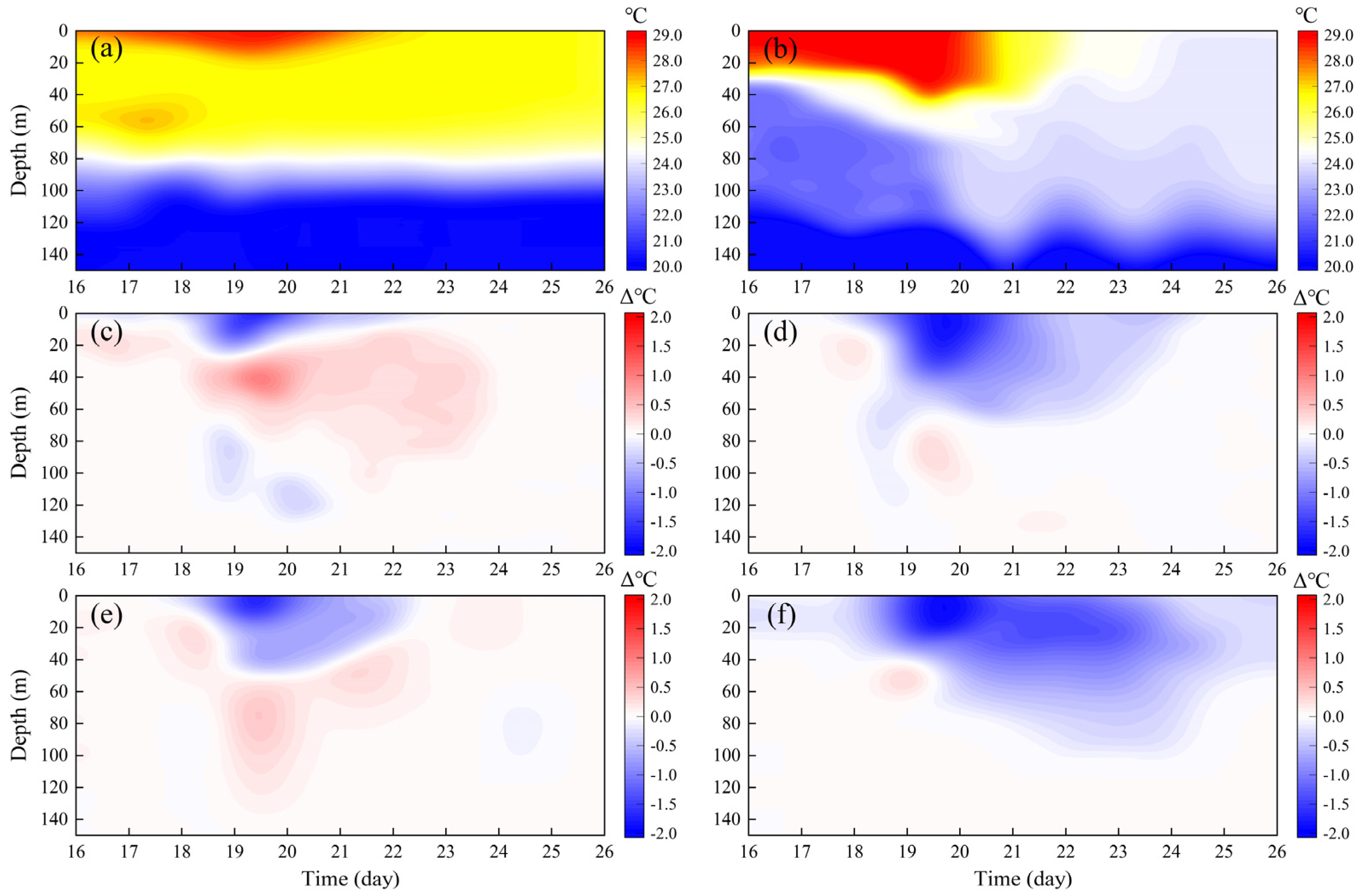
3.3. Simulated SST
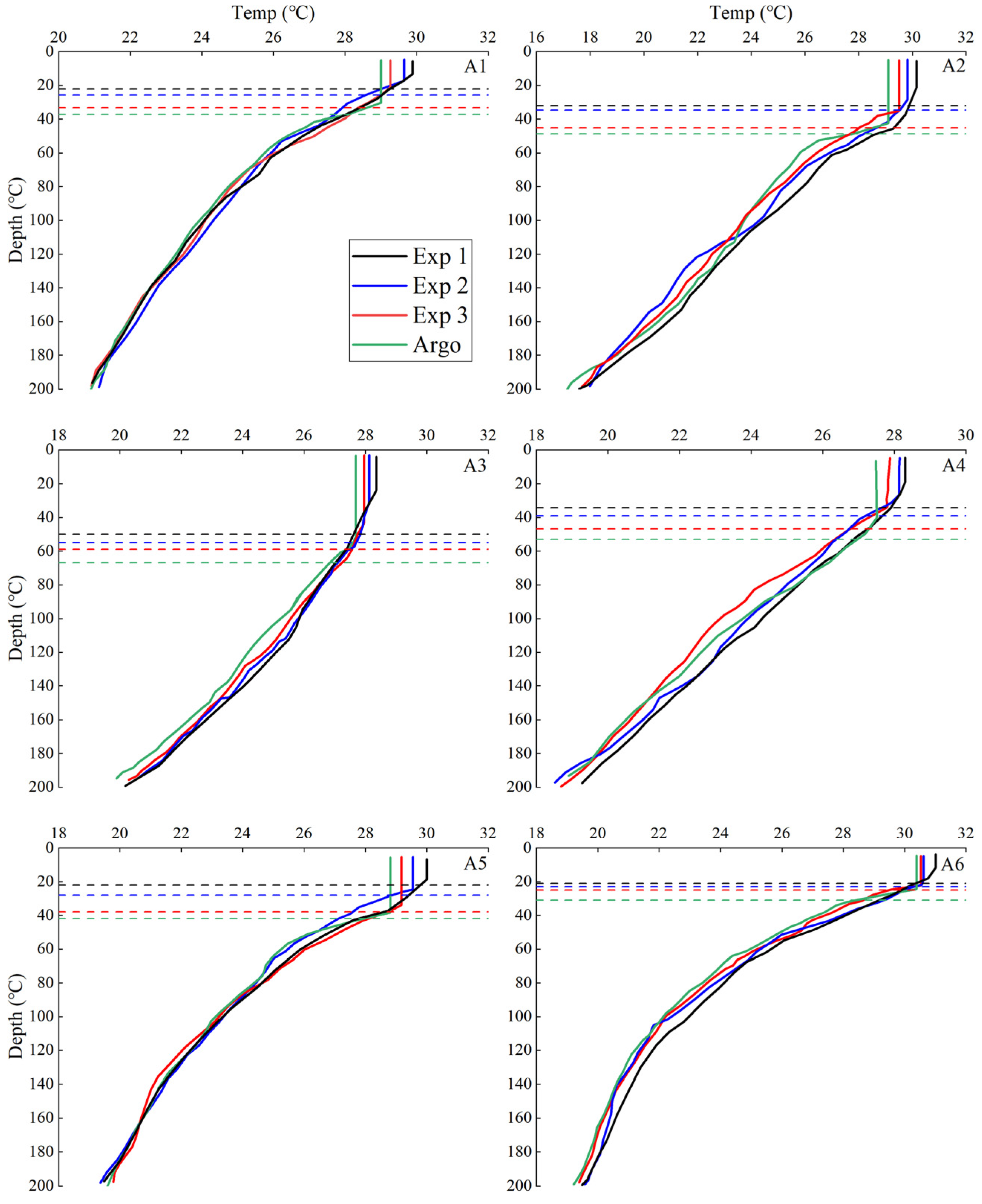
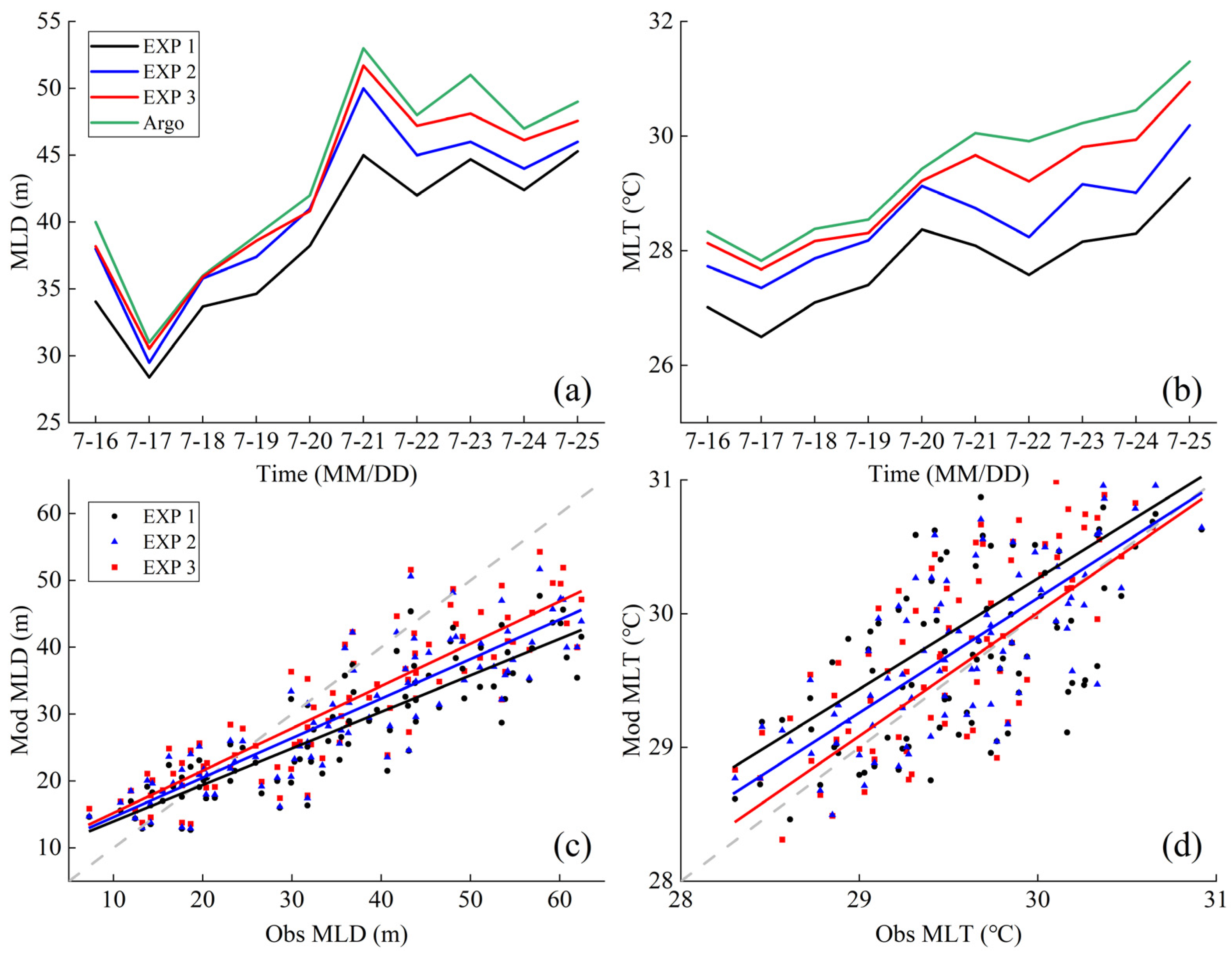
3.4. The Simulated Results of Mixed-Layer Temperature
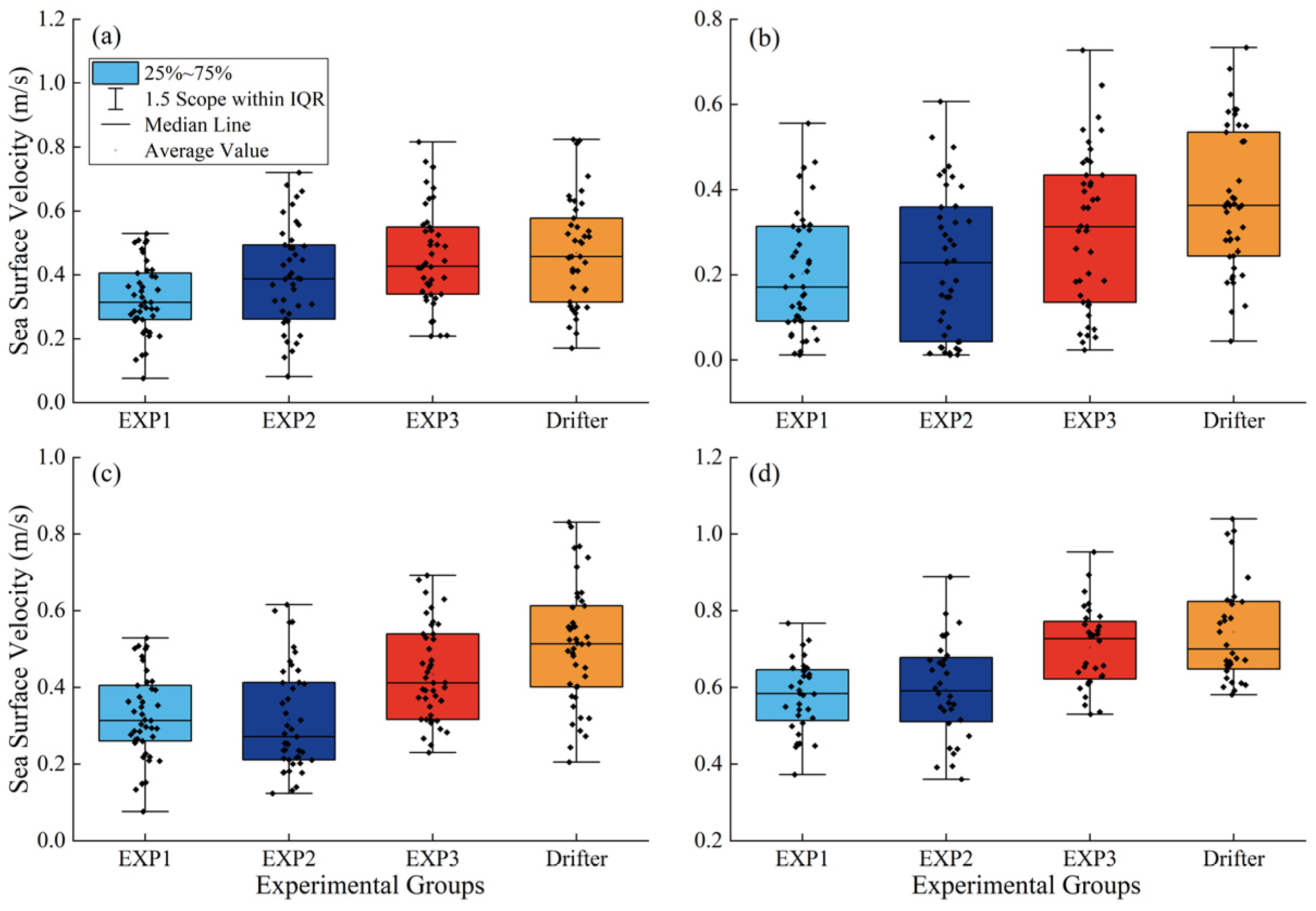
3.5. Effect on Surface Current Field
4. Conclusions
- (1)
- Using HYCOM data as the background field, GFS reanalysis wind fields and ERA5 reanalysis heat flux data as driving fields, the simulated significant wave heights, SST and other variables from the COAWST sea–wave–air coupled model closely match actual measurements. This accuracy suggests that the selection of background fields, initial conditions and physical parameters is appropriate, indicating that the model performs well in simulating sea–wave–air interactions and can serve as a reference for future simulations.
- (2)
- The inclusion of wave-induced mixing effects in the COAWST model reduces SST biases, particularly in areas affected by the typhoon. The spatial distribution of SST differences aligns with the distribution of significant wave heights, showing larger differences near the typhoon and smaller differences in calmer waters. Analysis reveals that wave-induced vertical mixing enhances current velocities during the typhoon, with a more pronounced effect on the right side of the typhoon path. This enhancement increases upper-layer water dispersion and upwelling, resulting in reduced SST. Furthermore, the MLD metrics in EXP3 demonstrate significant improvements, with the percentage error (PE) decreasing from 26.54 in EXP1 to 18.54, the mean absolute error (MAE) from 8.85 to 5.25 and the root mean square error (RMSE) from 11.05 to 6.13, while the correlation coefficient (COR) increased from 0.84 to 0.92, indicating a notable reduction in errors and enhanced predictive accuracy. For MLT, EXP3 achieves a PE reduction to 1.02, with MAE and RMSE values dropping to 0.41 and 0.46, respectively. Incorporating wave-induced mixing effects thus significantly improves the accuracy of upper-layer SST simulations.
- (3)
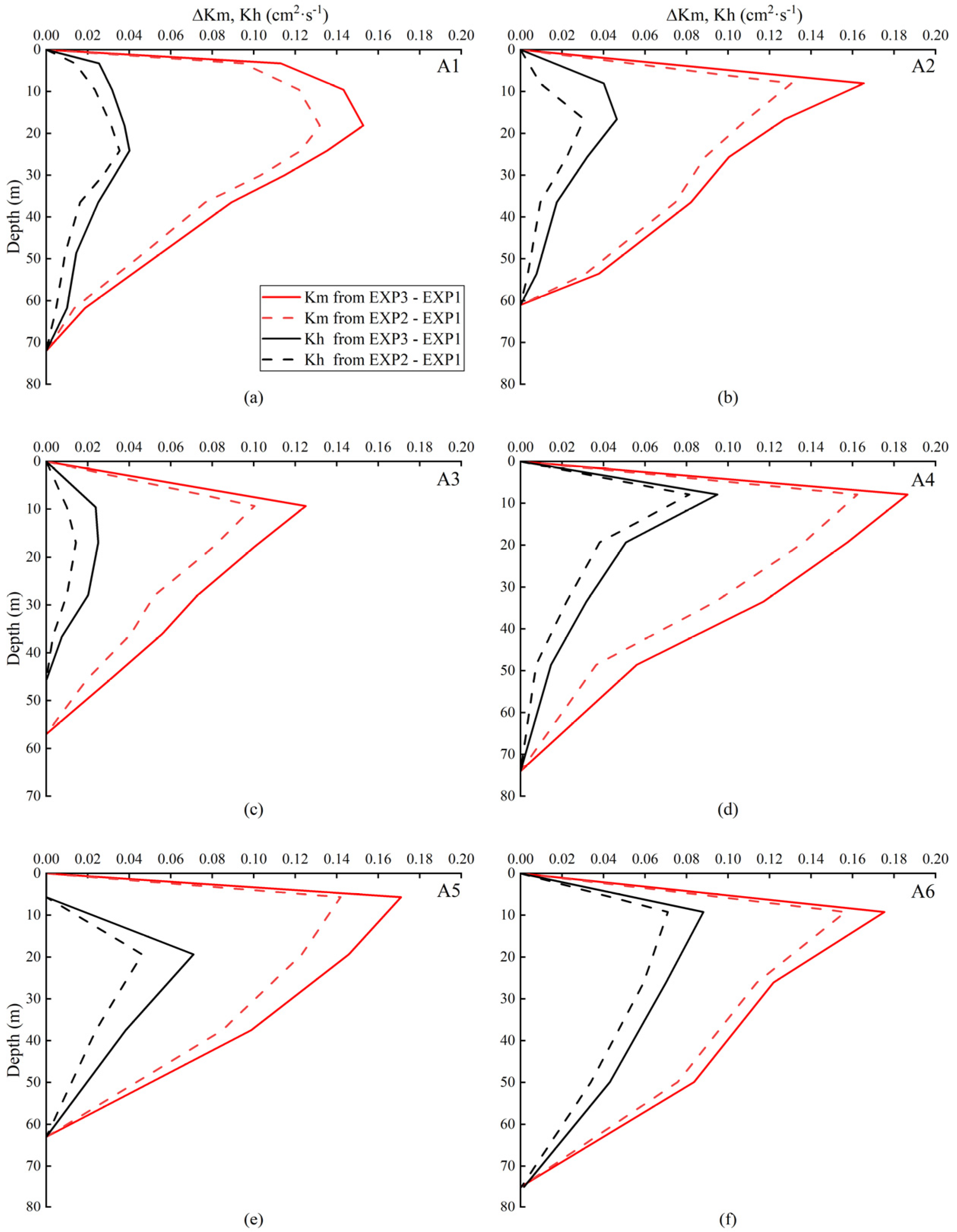
- The original COAWST model’s MY2.5 scheme (EXP1) tends to overestimate upper-ocean temperatures, while the previously proposed parameterization scheme (EXP2) underestimates turbulent mixing during typhoons. This paper proposes a new parameterization scheme (EXP3) that accounts for turbulence enhancement during typhoons. Compared to EXP1 and EXP2, EXP3 significantly improves simulations of temperature changes in both the sea surface layer and deep sea column, demonstrating more efficient vertical momentum and heat transfer. Due to strong wind stress and wave breaking caused by intense winds, the upper ocean experiences rapid mixing, leading to a sharp increase in turbulent kinetic energy (TKE), which peaks near the typhoon’s eye. Simulation results indicate that wave-induced mixing significantly enhances the generation and vertical transport of TKE. Specifically, the EXP3 scheme shows that with the inclusion of wave-induced mixing effects, TKE distribution becomes more widespread and intense, leading to an increase in mixed layer depth. This underscores the critical role of wave-induced mixing in enhancing vertical mixing and energy transfer, particularly near the typhoon path. Comparisons of the simulation results from EXP1, EXP2 and EXP3 reveal that the increase in TKE contributes to a more uniform energy distribution within the mixed layer, facilitating vertical heat and momentum exchange. As a result, sea surface temperatures decrease, and the temperature within the mixed layer becomes more uniform. Comparisons with Argo and Drifter buoy data show that EXP3 results are closer to observed measurements, highlighting the importance of incorporating wave-induced mixing and turbulence enhancement. The enhanced model offers better simulations of ocean temperature and current velocity changes during typhoons, improving forecasting accuracy and reliability. This method of improving wave–current interaction modeling is effective and recommended for forecasting sea states in the East China Sea and South China Sea, especially under typhoon conditions. In future research, we will explore the impact of multiple wave effects on the ocean during typhoons using the COAWST model, while also considering the extension of the new wave-induced mixing scheme to global climate models. This extension aims to verify its applicability across different ocean areas and assess its potential impact on the global climate system.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, X.; Gao, S.; Ji, X.; Zhu, X.; Zheng, J.; Guo, S. Impact of Typhoons on the Ecological Environment of the Pearl River Estuary in the Summer of 2021—A Study of an Algal Bloom Event. Front. Mar. Sci. 2024, 11, 1395804. [Google Scholar] [CrossRef]
- Woo, H.J.; Park, K.A. Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016). Remote Sens. 2021, 13, 1063. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, X.; Kou, Y.; Wu, F.; Zhao, D.; Yu, Z. Analysis of Extreme Sea States under the Impact of Typhoon in Different Periods: A Nested Stochastic Compound Distribution Applied in the South China Sea. Appl. Ocean Res. 2022, 127, 103298. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Du, X.; Liu, Q.; Liu, X. Temporal-Spatial Characteristics of Storm Surges and Rough Seas in Coastal Areas of Mainland China from 2000 to 2019. Nat. Hazards 2021, 107, 1273–1285. [Google Scholar] [CrossRef]
- Shi, X.; Han, Z.; Fang, J.; Tan, J.; Guo, Z.; Sun, Z. Assessment and Zonation of Storm Surge Hazards in the Coastal Areas of China. Nat. Hazards 2020, 100, 39–48. [Google Scholar]
- Huang, S.; Du, Y.; Yi, J.; Liang, F.; Qian, J.; Wang, N.; Tu, W. Understanding Human Activities in Response to Typhoon Hato from Multi-Source Geospatial Big Data: A Case Study in Guangdong, China. Remote Sens. 2022, 14, 1269. [Google Scholar] [CrossRef]
- Wang, T.; Yin, K.; Li, Y.; Chen, L.; Xiao, C.; Zhu, H.; van Westen, C. Physical Vulnerability Curve Construction and Quantitative Risk Assessment of a Typhoon-Triggered Debris Flow via Numerical Simulation: A Case Study of Zhejiang Province, SE China. Landslides 2024, 21, 1333–1352. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, S.; Wang, G. Spatiotemporal Variations in Meteorological Disasters and Vulnerability in China During 2001–2020. Front. Earth Sci. 2021, 9, 789523. [Google Scholar] [CrossRef]
- Song, G.; Zhao, L.; Chai, F.; Liu, F.; Li, M.; Xie, H. Summertime Oxygen Depletion and Acidification in Bohai Sea, China. Front. Mar. Sci. 2020, 7, 252. [Google Scholar] [CrossRef]
- He, T.; Li, J.; Xie, L.; Zheng, Q. Response of Chlorophyll-a to Rainfall Event in the Basin of the South China Sea: Statistical Analysis. Mar. Environ. Res. 2024, 199, 106576. [Google Scholar] [CrossRef]
- Wang, Y.; Qiao, F.; Fang, G.; Wei, Z. Application of Wave-Induced Vertical Mixing to the K Profile Parameterization Scheme. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. Development of a Turbulence Closure Model for Geophysical Fluid Problems. Rev. Geophys. 1982, 20, 851–875. [Google Scholar] [CrossRef]
- Price, J.F.; Weller, R.A.; Pinkel, R. Diurnal Cycling: Observations and Models of the Upper Ocean Response to Diurnal Heating, Cooling, and Wind Mixing. J. Geophys. Res. 1986, 91, 8411–8427. [Google Scholar] [CrossRef]
- Large, W.G.; McWilliams, J.C.; Doney, S.C. Oceanic Vertical Mixing: A Review and a Model with a Nonlocal Boundary Layer Parameterization. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef]
- Kraus, E.B.; Turner, J.S. A One-Dimensional Model of the Seasonal Thermocline II. Gen. Theory Its Conseq. Tellus 1967, 19, 98–106. [Google Scholar] [CrossRef]
- Mellor, G.L.; Yamada, T. A Hierarchy of Turbulence Closure Models for Planetary Boundary Layers. J. Atmos. Sci. 1974, 31, 1791–1806. Available online: https://journals.ametsoc.org/view/journals/atsc/31/7/1520-0469_1974_031_1791_ahotcm_2_0_co_2.xml (accessed on 8 July 2024). [CrossRef]
- Gaspar, P.; Grégoris, Y.; Lefevre, J. A Simple Eddy Kinetic Energy Model for Simulations of the Oceanic Vertical Mixing: Tests at Station Papa and Long-term Upper Ocean Study Site. J. Geophys. Res. 1990, 95, 16179–16193. [Google Scholar] [CrossRef]
- Craig, P.D.; Banner, M.L. Modeling Wave-Enhanced Turbulence in the Ocean Surface Layer. J. Phys. Oceanogr. 1994, 24, 2546–2559. Available online: https://journals.ametsoc.org/view/journals/phoc/24/12/1520-0485_1994_024_2546_mwetit_2_0_co_2.xml (accessed on 8 July 2024). [CrossRef]
- The Development of a Coastal Circulation Numerical Model: 1. Wave-Induced Mixing and Wave-Current Interaction. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=edacbbfeb14000b0eee6664d208ee0c5 (accessed on 25 July 2024).
- Uchiyama, Y.; McWilliams, J.C.; Shchepetkin, A.F. Wave–Current Interaction in an Oceanic Circulation Model with a Vortex-Force Formalism: Application to the Surf Zone. Ocean Model. 2010, 34, 16–35. [Google Scholar] [CrossRef]
- Qiao, F.; Yuan, Y.; Yang, Y.; Zheng, Q.; Xia, C.; Ma, J. Wave-induced Mixing in the Upper Ocean: Distribution and Application to a Global Ocean Circulation Model. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, Y.; Yu, C.; Teng, Y.; Sun, M. Study on Surface Wave-Induced Mixing of Transport Flux Residue under Typhoon Conditions. J. Ocean. Limnol. 2019, 37, 1837–1845. [Google Scholar] [CrossRef]
- Yuan, Y.; Qiao, F.; Yin, X.; Han, L. Analytical Estimation of Mixing Coefficient Induced by Surface Wave-Generated Turbulence Based on the Equilibrium Solution of the Second-Order Turbulence Closure Model. Sci. China Earth Sci. 2013, 56, 71–80. [Google Scholar] [CrossRef]
- McWilliams, J.C.; Sullivan, P.P. Vertical Mixing by Langmuir Circulations. Spill Sci. Technol. Bull. 2000, 6, 225–237. [Google Scholar] [CrossRef]
- Smyth, W.D.; Skyllingstad, E.D.; Crawford, G.B.; Wijesekera, H. Nonlocal Fluxes and Stokes Drift Effects in the K-Profile Parameterization. Ocean Dyn. 2002, 52, 104–115. [Google Scholar] [CrossRef]
- Roekel, L.P.V.; Fox-Kemper, B.; Sullivan, P.P.; Hamlington, P.E.; Haney, S.R. The Form and Orientation of Langmuir Cells for Misaligned Winds and Waves. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Noh, Y.; Ok, H.; Lee, E.; Toyoda, T.; Hirose, N. Parameterization of Langmuir Circulation in the Ocean Mixed Layer Model Using LES and Its Application to the OGCM. J. Phys. Oceanogr. 2016, 46, 57–78. [Google Scholar] [CrossRef]
- Qing, L.; Baylor, F.K. Assessing the Effects of Langmuir Turbulence on the Entrainment Buoyancy Flux in the Ocean Surface Boundary Layer. J. Phys. Oceanogr. 2017, 47, 2863–2886. [Google Scholar]
- Ali, A.; Christensen, K.H.; Breivik, Ø.; Malila, M.; Raj, R.P.; Bertino, L.; Chassignet, E.P.; Bakhoday-Paskyabi, M. A Comparison of Langmuir Turbulence Parameterizations and Key Wave Effects in a Numerical Model of the North Atlantic and Arctic Oceans. Ocean Model. 2019, 137, 76–97. [Google Scholar] [CrossRef]
- Wang, H.; Dong, C.; Yang, Y.; Gao, X. Parameterization of Wave-Induced Mixing Using the Large Eddy Simulation (LES) (I). Atmosphere 2020, 11, 207. [Google Scholar] [CrossRef]
- Han, S.; Wang, M.; Peng, B. Response of Temperature to Successive Typhoons in the South China Sea. J. Mar. Sci. Eng. 2022, 10, 1157. [Google Scholar] [CrossRef]
- Jacob, S.D.; Shay, L.K.; Mariano, A.J.; Black, P.G. The 3D Oceanic Mixed Layer Response to Hurricane Gilbert. J. Phys. Oceanogr. 2000, 30, 1407–1429. [Google Scholar] [CrossRef]
- Huang, P.; Sanford, T.B.; Imberger, J. Heat and Turbulent Kinetic Energy Budgets for Surface Layer Cooling Induced by the Passage of Hurricane Frances (2004). J. Geophys. Res. Oceans 2009, 114. [Google Scholar] [CrossRef]
- Kantha, L.H.; Clayson, C.A. An Improved Mixed Layer Model for Geophysical Applications. J. Geophys. Res. 1994, 99, 25235–25266. [Google Scholar] [CrossRef]
- Martin, P.J. Simulation of the Mixed Layer at OWS November and Papa with Several Models. J. Geophys. Res. 1985, 90, 903–916. [Google Scholar] [CrossRef]
- Wang, J.; Kuang, C.; Chen, K.; Fan, D.; Qin, R.; Han, X. Wave–Current Interaction by Typhoon Fongwong on Saline Water Intrusion and Vertical Stratification in the Yangtze River Estuary. Estuar. Coast. Shelf Sci. 2022, 279, 108138. [Google Scholar] [CrossRef]
- Zhang, W.; Li, R.; Zhu, D.; Zhao, D.; Guan, C. An Investigation of Impacts of Surface Waves-Induced Mixing on the Upper Ocean under Typhoon Megi (2010). Remote Sens. 2023, 15, 1862. [Google Scholar] [CrossRef]
- Qiao, F.; Yuan, Y.; Ezer, T.; Xia, C.; Yang, Y.; Lü, X.; Song, Z. A Three-Dimensional Surface Wave–Ocean Circulation Coupled Model and Its Initial Testing. Ocean Dyn. 2010, 60, 1339–1355. [Google Scholar] [CrossRef]
- Sun, Z.; Shao, W.; Yu, W.; Li, J. A Study of Wave-Induced Effects on Sea Surface Temperature Simulations during Typhoon Events. J. Mar. Sci. Eng. 2021, 9, 622. [Google Scholar] [CrossRef]
- Yao, R.; Shao, W.; Hao, M.; Zuo, J.; Hu, S. The Respondence of Wave on Sea Surface Temperature in the Context of Global Change. Remote Sens. 2023, 15, 1948. [Google Scholar] [CrossRef]
- Huang, C.J.; Qiao, F. Wave-Turbulence Interaction and Its Induced Mixing in the Upper Ocean. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
- Ma, H.; Dai, D.; Guo, J.; Qiao, F. Observational Evidence of Surface Wave-Generated Strong Ocean Turbulence. J. Geophys. Res. Oceans 2020, 12, e2019JC015657. [Google Scholar] [CrossRef]
- Study on Hydrodynamic Environment of the Bohai Sea, the Huanghai Sea and the East China Sea with Wave-Current Coupled Numerical Model. Available online: http://www.hyxbocean.cn/en/article/id/20040403 (accessed on 25 July 2024).
- Pleskachevsky, A.; Dobrynin, M.; Babanin, A.V.; Günther, H.; Stanev, E. Turbulent Mixing Due to Surface Waves Indicated by Remote Sensing of Suspended Particulate Matter and Its Implementation into Coupled Modeling of Waves, Turbulence, and Circulation. J. Phys. Oceanogr. 2011, 41, 708–724. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3; National Center for Atmospheric Research: Boulder, CO, USA, 2008; Volume 1, pp. 1–5. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A Third-generation Wave Model for Coastal Regions: 1. Model Description and Validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Shchepetkin, A.F.; McWilliams, J.C. The Regional Oceanic Modeling System (ROMS): A Split-Explicit, Free-Surface, Topography-Following-Coordinate Oceanic Model. Ocean Model. 2004, 9, 347–404. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) Modeling System. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, W.Z.; Wang, Y.; Chai, F. Mechanism of Oceanic Eddies in Modulating the Sea Surface Temperature Response to a Strong Typhoon in the Western North Pacific. Front. Mar. Sci. 2023, 10, 1117301. [Google Scholar] [CrossRef]
- Yang, B.; Hou, Y.; Hu, P.; Liu, Z.; Liu, Y. Shallow Ocean Response to Tropical Cyclones Observed on the Continental Shelf of the Northwestern S Outh C Hina S Ea. J. Geophys. Res. Oceans 2015, 120, 3817–3836. [Google Scholar] [CrossRef]
- Chen, H.; Li, S.; He, H.; Song, J.; Ling, Z.; Cao, A.; Zou, Z.; Qiao, W. Observational Study of Super Typhoon Meranti (2016) Using Satellite, Surface Drifter, Argo Float and Reanalysis Data. Acta Oceanol. Sin. 2021, 40, 70–84. [Google Scholar] [CrossRef]
- Song, Z.; Qiao, F.; Song, Y. Response of the Equatorial Basin-Wide SST to Non-Breaking Surface Wave-Induced Mixing in a Climate Model: An Amendment to Tropical Bias. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Sun, J.; Oey, L.-Y.; Chang, R.; Xu, F.; Huang, S.-M. Ocean Response to Typhoon Nuri (2008) in Western Pacific and South China Sea. Ocean Dyn. 2015, 65, 735–749. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Wu, R.; Chen, D.; Zhang, D.; Shang, X.; Wang, Y.; Song, X.; Jin, W.; Yu, L.; et al. Sea Surface Current Response Patterns to Tropical Cyclones. J. Mar. Syst. 2020, 208, 103345. [Google Scholar] [CrossRef]
- Hazelworth, J.B. Water Temperature Variations Resulting from Hurricanes. J. Geophys. Res. 1968, 73, 5105–5123. [Google Scholar] [CrossRef]
- Li, M.; Garrett, C.; Skyllingstad, E. A Regime Diagram for Classifying Turbulent Large Eddies in the Upper Ocean. Deep-Sea Res. Part I 2004, 52, 259–278. [Google Scholar] [CrossRef]
- Wadler, J.B.; Cione, J.J.; Michlowitz, S.; de la Cruz, B.J.; Shay, L.K. Improving the Statistical Representation of Tropical Cyclone In-Storm Sea Surface Temperature Cooling. Weather Forecast. 2024, 39, 847–866. [Google Scholar] [CrossRef]
- Roemmich, D.; Owens, W. The Argo Project: Global Ocean Observations for Understanding and Prediction of Climate Variability. Oceanography 2000, 13, 45–50. [Google Scholar] [CrossRef]
- Hasselmann, K. Wave-Driven Inertial Oscillations. Geophys. Fluid Dyn. 1970, 1, 463–502. [Google Scholar] [CrossRef]
- Clement, U.; Gérald, D.; Lucile, G.; Aurélien, P.; Fabrice, A.; Maxime, B.; Yannice, F. Reconstructing Ocean Surface Current Combining Altimetry and Future Spaceborne Doppler Data. J. Geophys. Res. Oceans 2021, 126. [Google Scholar] [CrossRef]
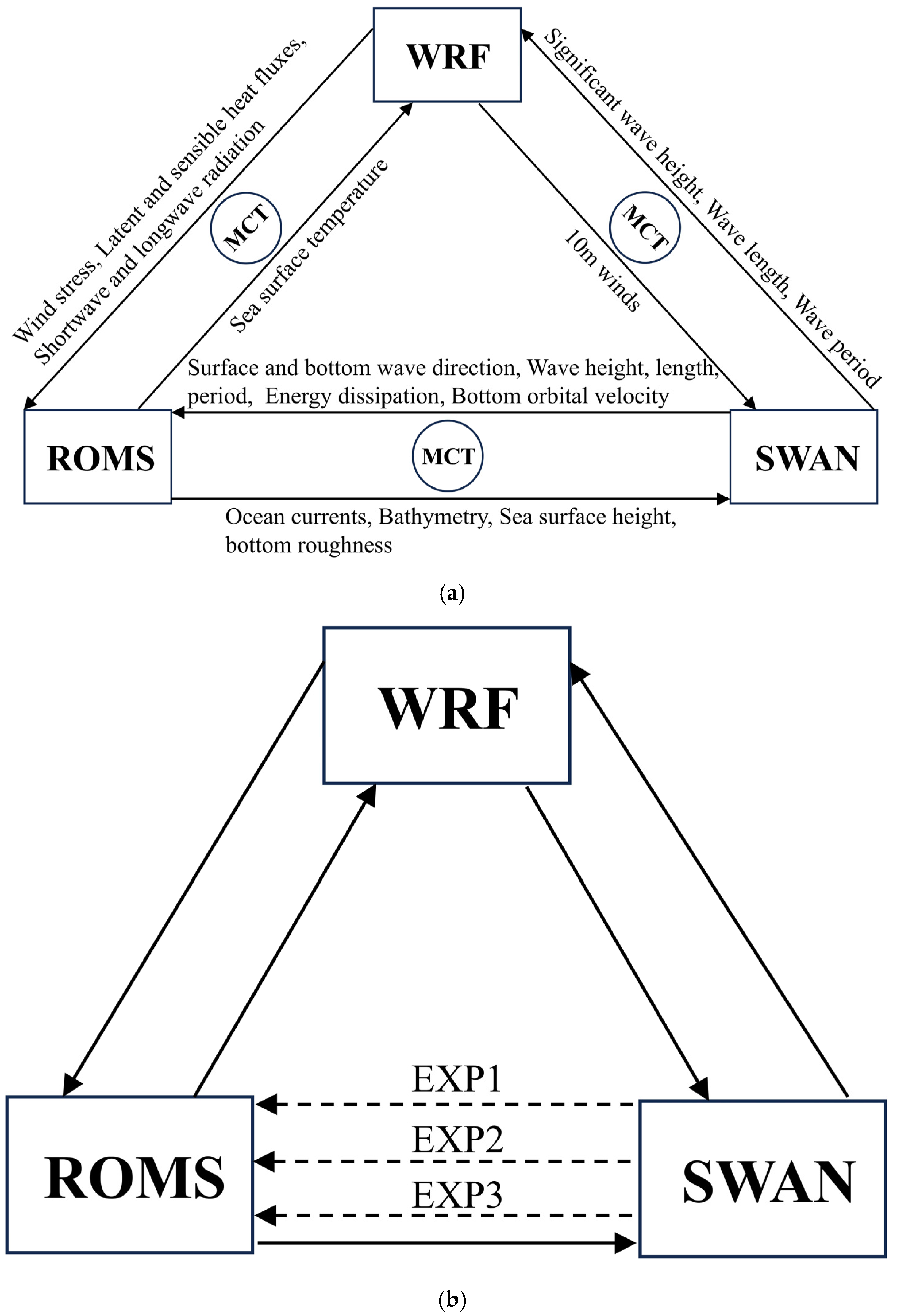


| WRF | SWAN | ROMS | |
|---|---|---|---|
| Domain | DO1: 140 × 116 (30 km) | DO1: 591 × 438 (10 km) | DO1: 590 × 437 (10 km) |
| DO2: 591 × 438 (10 km) | |||
| 50 eta levels | 40 sigma levels | ||
| Dynamics | DO1: dt = 48 s, DO2: dt = 16 s | dt = 60 s | dt = 60 s |
| Physics | Mp_physcis: WSM 6-class graupel | Whitecapping physics: KOMEN | Momentum equation physics: TS_U3HADVECTION |
| Ra_lw_physics: RRTMG | Whitecap crushed Physics: Hasselman | Vertical mixing physics: MY2.5 mixing | |
| Ra_sw_physics: RRTMG | Bottom Friction Physics: Collins | Tidal physics: UV_TIDES | |
| Sf_sfclay_physics: Monin-Obukhov | |||
| Sf_surface_physics: Noah | |||
| Bl_pbl_physics: TS_U | |||
| Cu_physics:Kain-Fritsch |
| Data | Data Sources |
|---|---|
| Topographic data | ETOPO1 (http://www.ngdc.noaa.gov/mgg/global/, accessed on 3 March 2024) |
| Wind data | GFS (https:/nomads.ncep.noaa.gov/, accessed on 3 March 2024) |
| Heat flux data | ERA5 (https://www.ecmwf.int/, accessed on 3 March 2024) |
| Initial field data | HYCOM (https://www.hycom.org/, accessed on 3 March 2024) |
| Validation data | JASON-3 (https://www.aviso.altimetry.fr/en/home.html, accessed on 3 March 2024) |
| OISST (https://www.hycom.org/, accessed on 3 March 2024) | |
| Argo (http://www.argo.org.cn/, accessed on 3 March 2024) Drifter (https://www.aoml.noaa.gov/global-drifter-program/, accessed on 3 March 2024) |
| Track | Satellite Peak (m) | Simulated Peak (m) | PE (m) | MAE (m) | RMSE (m) | COR |
|---|---|---|---|---|---|---|
| C1 | 5.152 | 4.767 | 0.385 | 0.342 | 0.366 | 0.871 |
| C2 | 6.463 | 6.146 | 0.317 | 0.392 | 0.389 | 0.836 |
| C3 | 4.177 | 3.918 | 0.259 | 0.296 | 0.314 | 0.943 |
| C4 | 6.291 | 6.025 | 0.266 | 0.287 | 0.294 | 0.951 |
| EXP1 | EXP2 | EXP3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PE (m) | MAE (m) | RMSE (m) | COR | PE (m) | MAE (m) | RMSE (m) | COR | PE (m) | MAE (m) | RMSE (m) | COR | |
| MLD (m) | 26.54 | 8.85 | 11.05 | 0.84 | 21.94 | 6.58 | 8.55 | 0.88 | 18.54 | 5.25 | 6.13 | 0.92 |
| MLT (°C) | 1.55 | 0.55 | 0.65 | 0.52 | 1.14 | 0.46 | 0.53 | 0.74 | 1.02 | 0.41 | 0.46 | 0.64 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, W.; Chen, J.; Shi, J.; Zhang, S.; Zhang, W.; Xia, J.; Wang, H.; Yi, Z.; Wu, Z.; Zhang, Z. Impact of a New Wave Mixing Scheme on Ocean Dynamics in Typhoon Conditions: A Case Study of Typhoon In-Fa (2021). Remote Sens. 2024, 16, 3298. https://doi.org/10.3390/rs16173298
Chen W, Chen J, Shi J, Zhang S, Zhang W, Xia J, Wang H, Yi Z, Wu Z, Zhang Z. Impact of a New Wave Mixing Scheme on Ocean Dynamics in Typhoon Conditions: A Case Study of Typhoon In-Fa (2021). Remote Sensing. 2024; 16(17):3298. https://doi.org/10.3390/rs16173298
Chicago/Turabian StyleChen, Wei, Jie Chen, Jian Shi, Suyun Zhang, Wenjing Zhang, Jingmin Xia, Hanshi Wang, Zhenhui Yi, Zhiyuan Wu, and Zhicheng Zhang. 2024. "Impact of a New Wave Mixing Scheme on Ocean Dynamics in Typhoon Conditions: A Case Study of Typhoon In-Fa (2021)" Remote Sensing 16, no. 17: 3298. https://doi.org/10.3390/rs16173298
APA StyleChen, W., Chen, J., Shi, J., Zhang, S., Zhang, W., Xia, J., Wang, H., Yi, Z., Wu, Z., & Zhang, Z. (2024). Impact of a New Wave Mixing Scheme on Ocean Dynamics in Typhoon Conditions: A Case Study of Typhoon In-Fa (2021). Remote Sensing, 16(17), 3298. https://doi.org/10.3390/rs16173298





