Resource Allocation of Netted Opportunistic Array Radar for Maneuvering Target Tracking under Uncertain Conditions
Abstract
:1. Introduction
- (1)
- The PC-CRLB of radar resource allocation for MTT is derived. We adopt the modified current statistical (MCS) model to characterize the motion state of maneuvering targets. The original state transition matrix and the input-acceleration matrix are combined to form the augmented state transition matrix in this model. And the process noise is periodically updated by the estimated error covariance to realize the self-adaption [32,33]. Considering the high maneuverability, the PC-CRLB instead of the PCRLB is utilized as the performance metric in resource allocation. The PC-CRLB provides a tighter lower bound since it is dependent on the actual measurement realizations. The mathematical expression of PC-CRLB for the centralized system is derived with the optimal fusion.
- (2)
- A closed-loop resource allocation strategy for the netted OAR system is formulated. The MCS-based strong tracking square-root cubature Kalman filter (ST-SCKF) is employed to obtain the global posterior distribution of the target conditioned on the CNA [32,33]. Based on the updated target state and the radar coordinates, the resource allocation strategy is performed with the objective of minimizing the total power consumption. In this strategy, the fuzzy logic inference system (FLIS) is used to select the most efficient radar group in line with the properties of targets relative to different radars [34,35]. The optimal power allocation for the next round can be implemented through the CCP model, subject to the uncertain constraints arising from the unknown RCS. The closed-loop signal processing framework is illustrated in Figure 1.
- (3)
- A hybrid intelligent optimization algorithm (HIOA) consisting of a stochastic simulation and a genetic algorithm (GA) is developed to solve the non-convex power optimization problem. Considering the uncertainty of the RCS, the resource allocation is modeled as the non-convex CCP. The stochastic simulation samples the random variables according to the probability distribution. The GA calculates the optimal solution of resource allocation based on all the sampling values meeting the constraint conditions. Superior to other solution methods, the HIOA could solve all the stochastic CCP.
2. System Model
2.1. Signal Model
2.2. Motion Model
2.3. Measurement Model
3. Centralized PC-CRLB
4. Resource Allocation Strategy for MTT
4.1. Tracking Performance Metric
4.2. Radar Node Selection
4.3. Optimization Modeling
4.4. Solution Strategy
4.4.1. Stochastic Simulation
4.4.2. Hybrid Intelligent Optimization Algorithm
4.4.3. Closed-Loop Signal Processing Framework
4.5. Further Statement
5. Simulations and Analysis
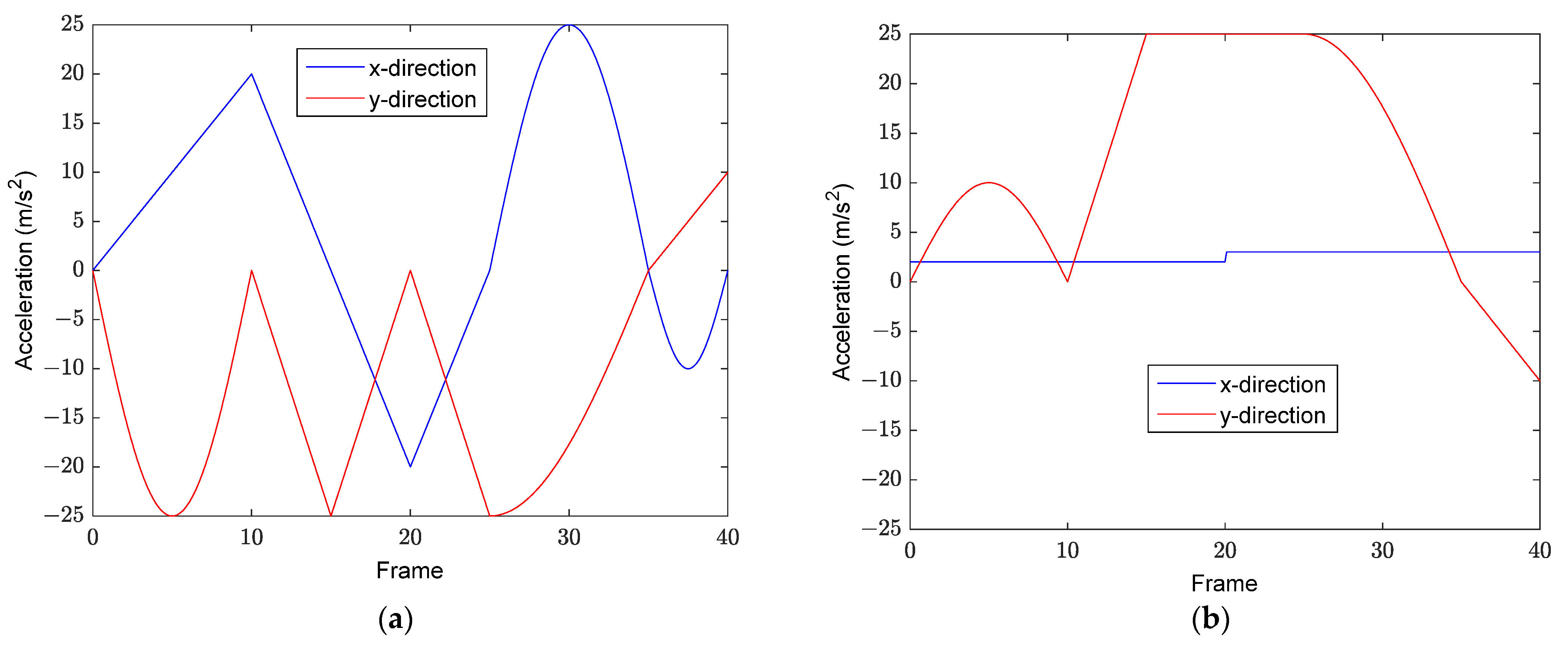
5.1. Case 1: 3 Radars and Acceleration Model 1
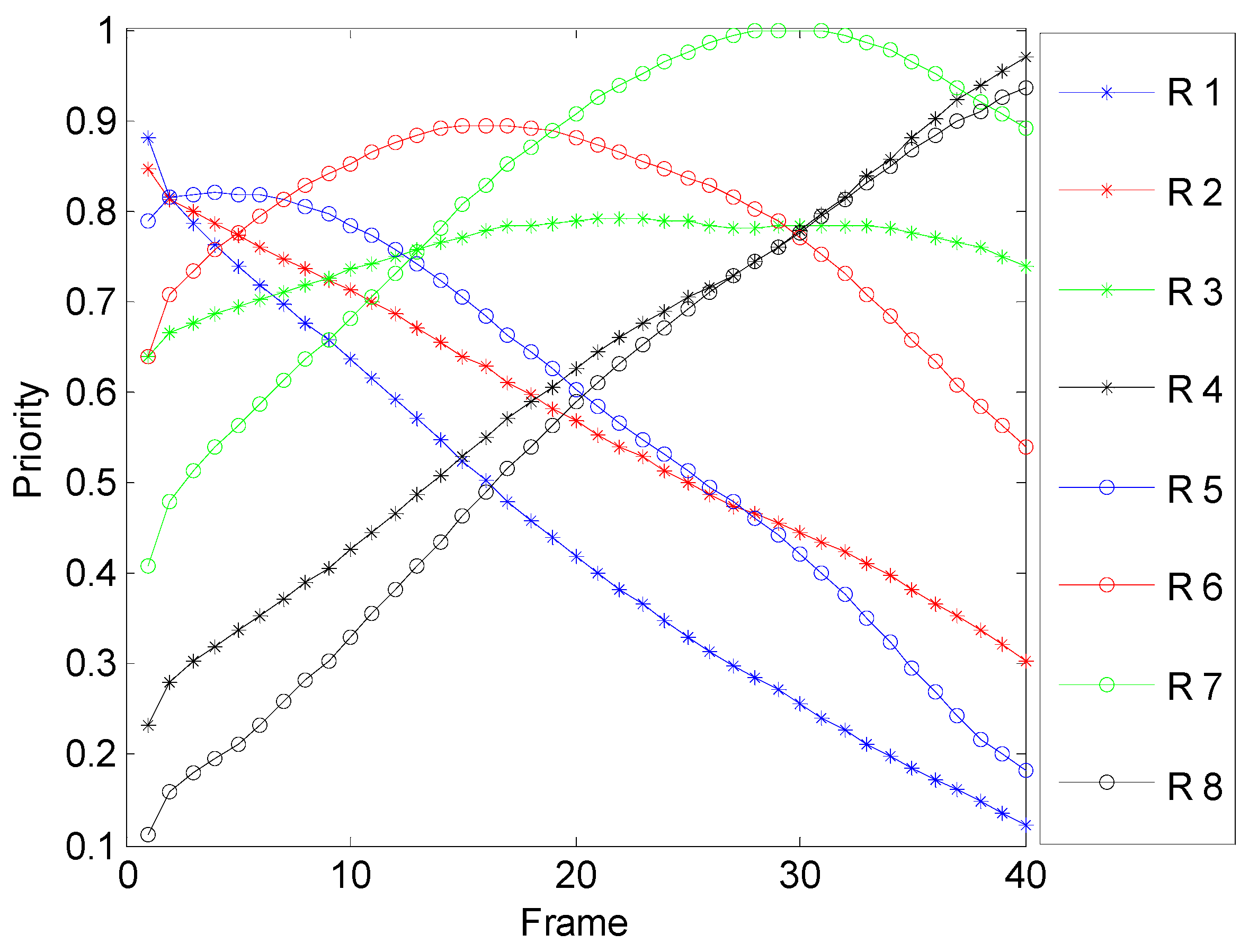
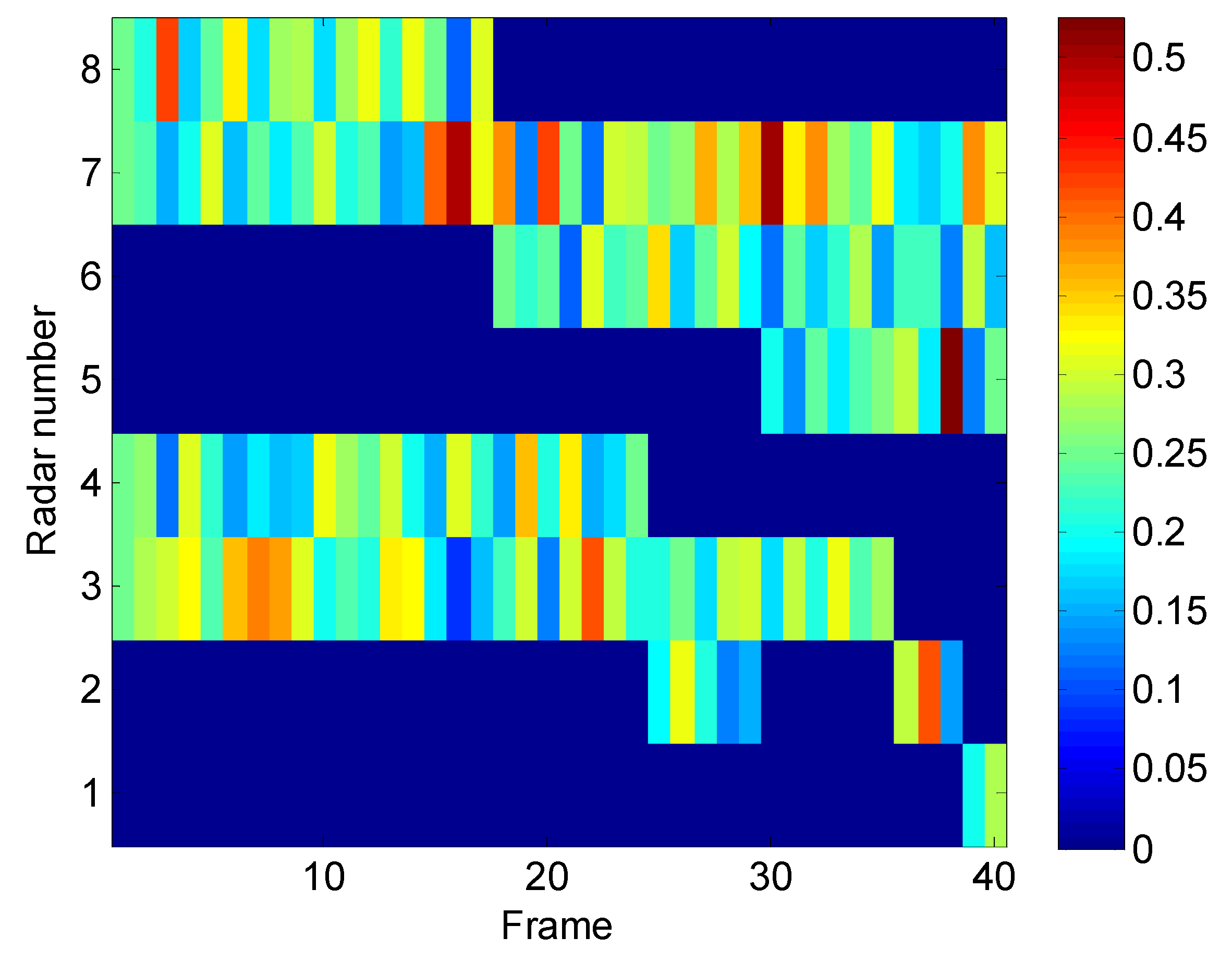
5.1.1. Adaptive Priority
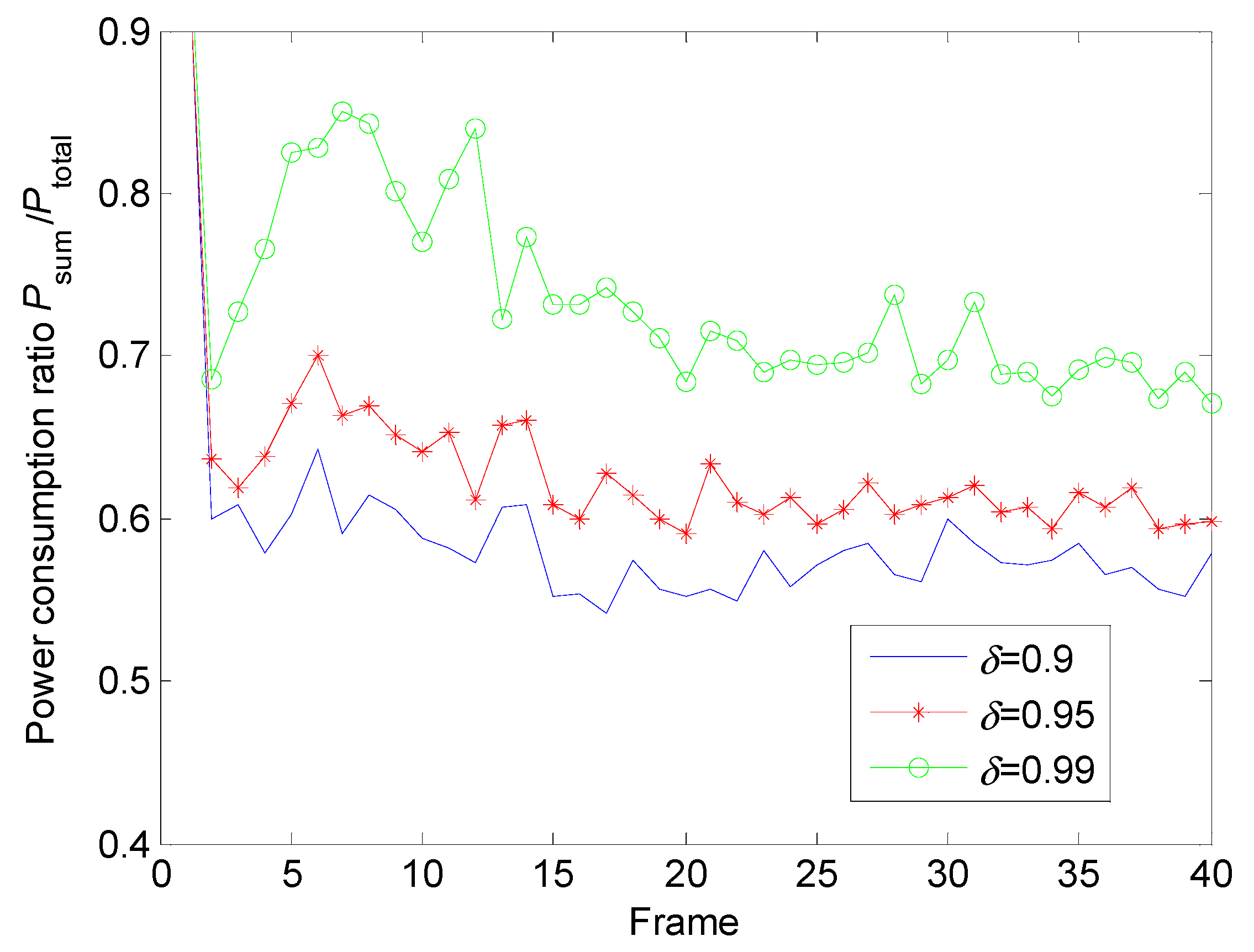
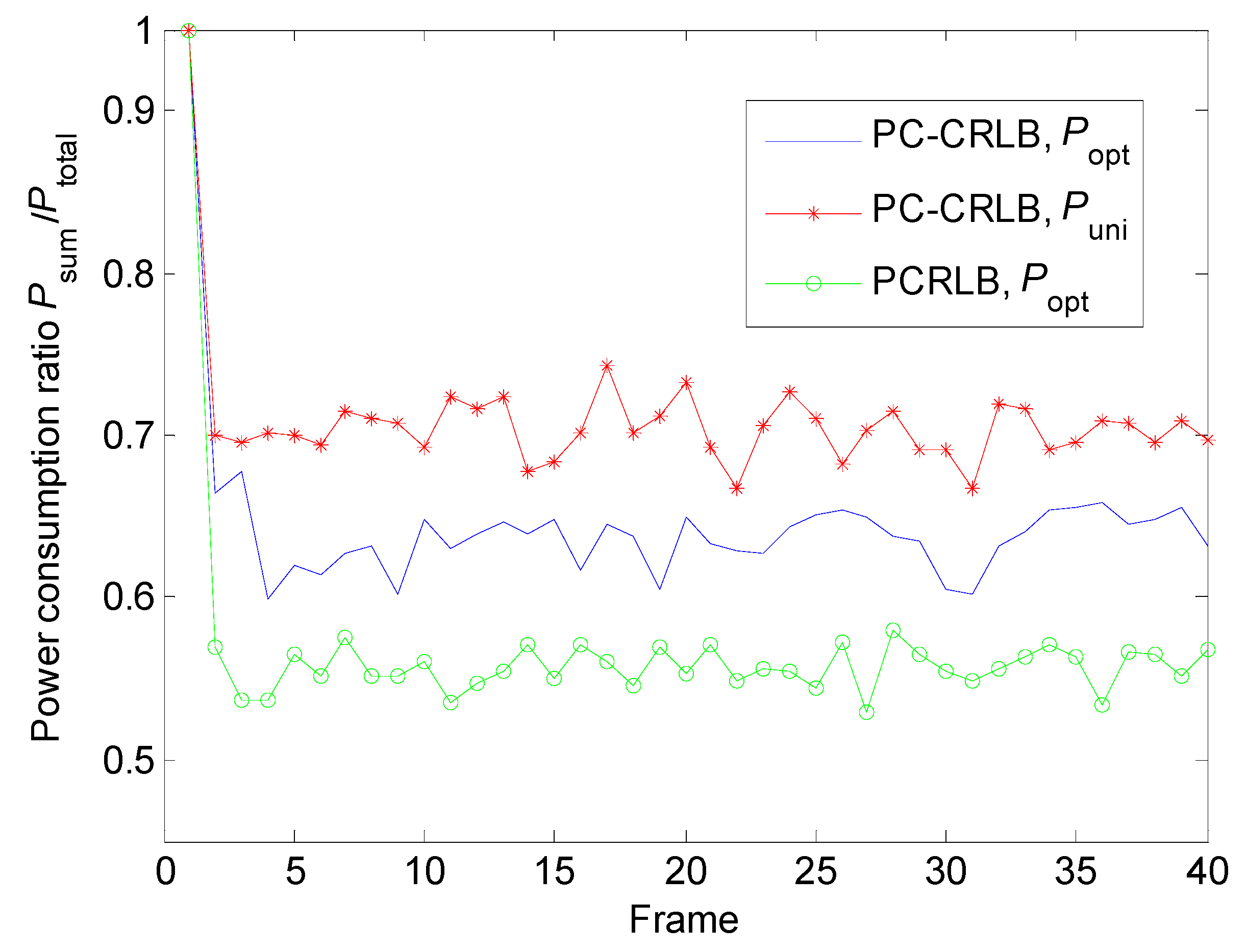
5.1.2. Power Allocation with Different Conditions
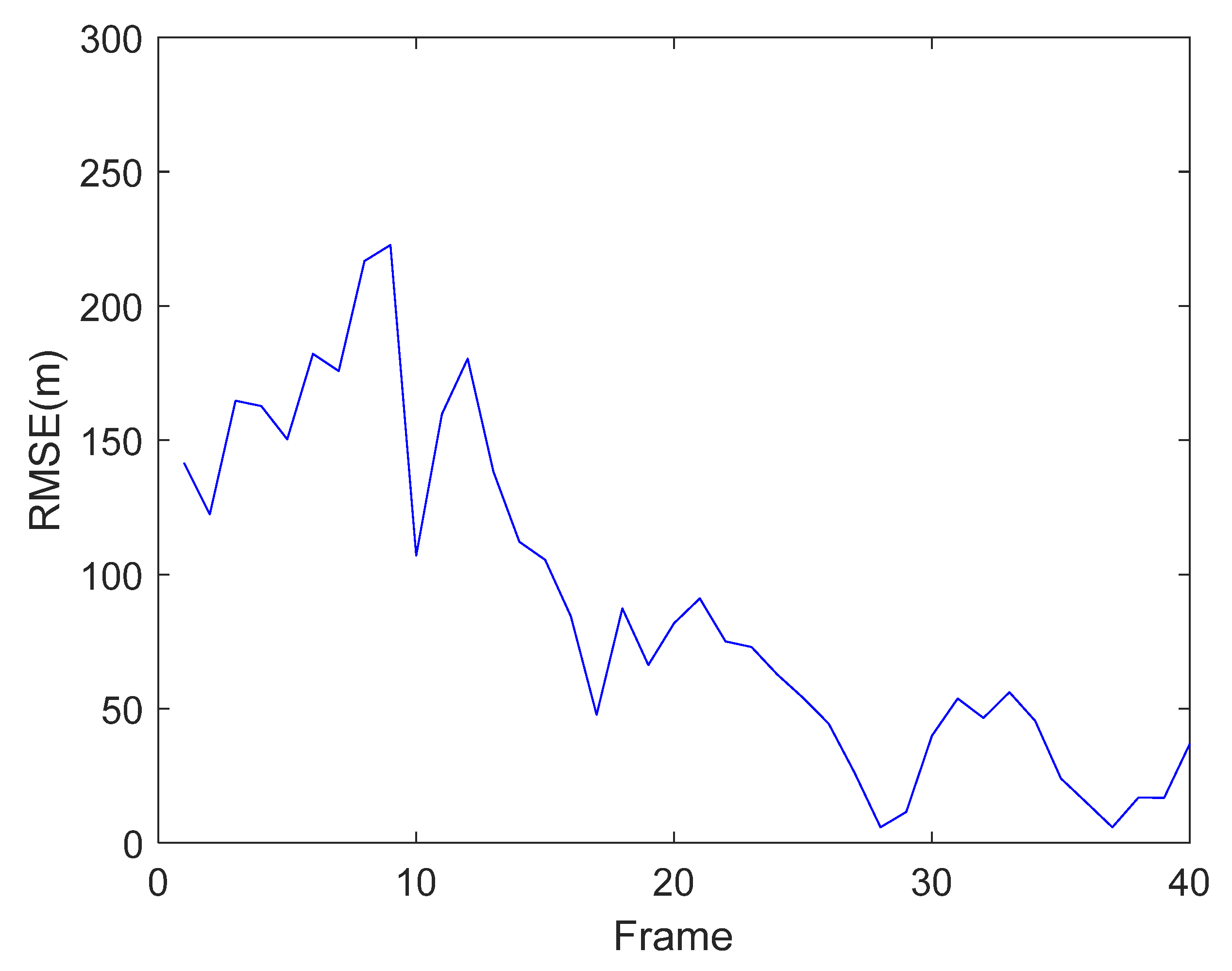
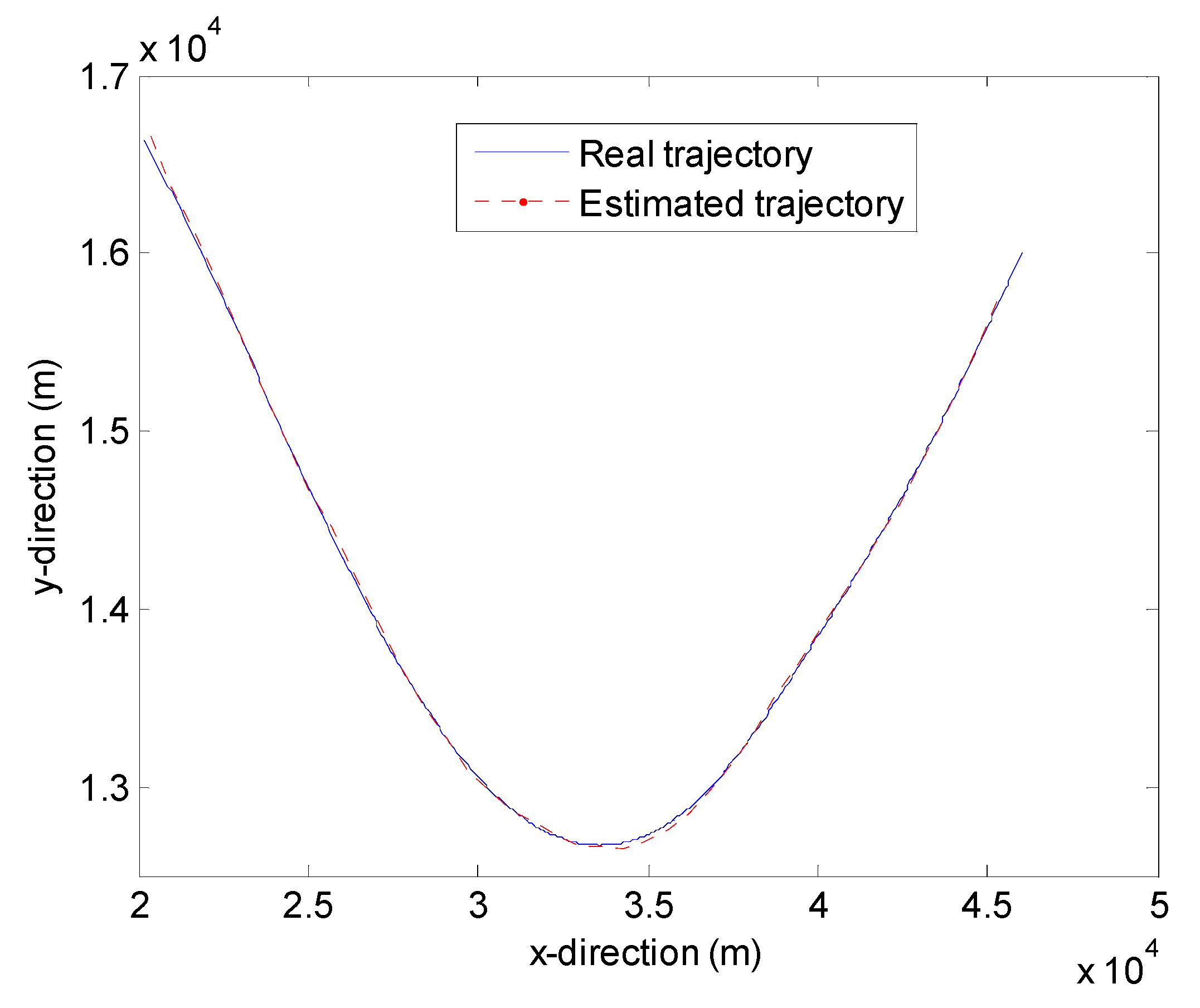
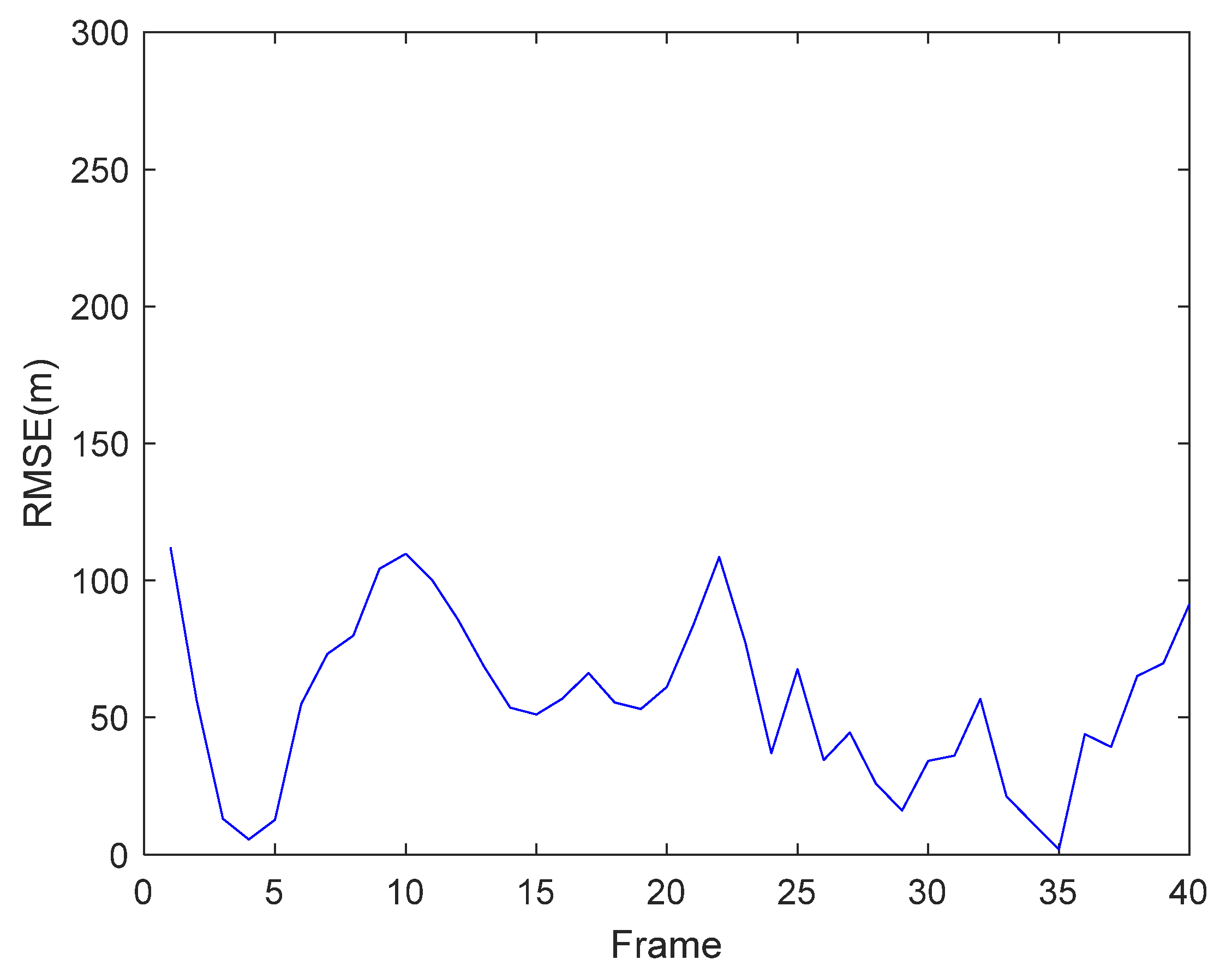
5.1.3. Target Tracking
5.2. Case 2: Four Radars and Acceleration Model 2
5.2.1. Adaptive Priority
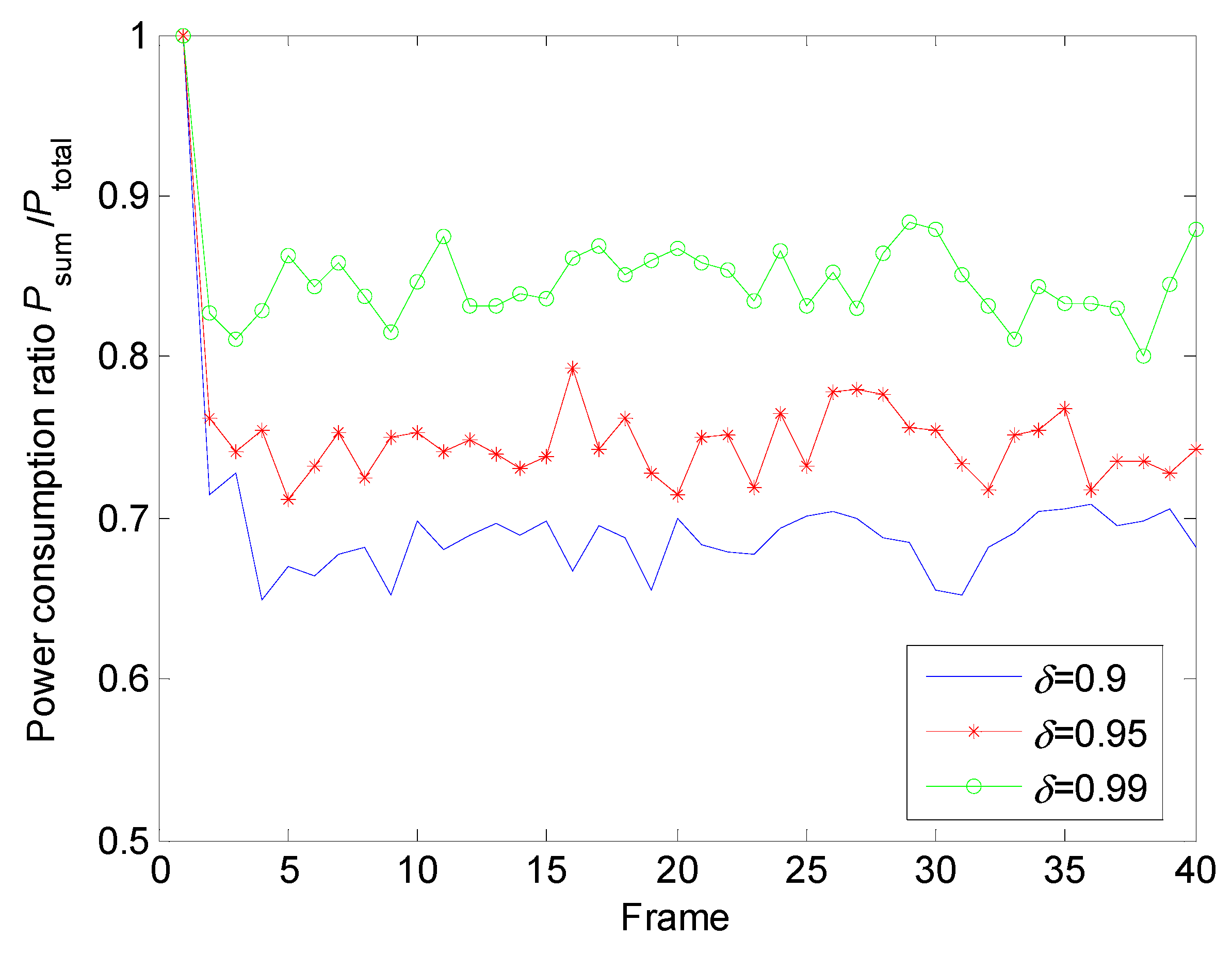
5.2.2. Power Allocation with Different Conditions
5.2.3. Target Track
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kocaman, İ. Distributed Beamforming in a Swarm UAV Network. Master’s Thesis, Naval Postgraduate School, Monterey, CA, USA, 2008. [Google Scholar]
- Long, W.J.; Ben, D.; Pan, M.H.; Shu, X.R.; Han, Y.M.; Pan, J.B. Opportunistic digital array radar and its technical characteristic analysis. In Proceedings of the IET International Radar Conference, Guilin, China, 20–22 April 2009. [Google Scholar]
- Han, Q.H.; Pan, M.H.; Liang, Z.L. Joint power and beam allocation of opportunistic array radar for multiple target tracking in clutter. Digit. Signal Process. 2018, 78, 136–151. [Google Scholar] [CrossRef]
- Han, Q.H.; Pan, M.H.; Long, W.J.; Liang, Z.L.; Shan, C.G. Joint adaptive sampling interval and power allocation for maneuvering target tracking in a multiple opportunistic array radar system. Sensors 2020, 20, 981. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J. Evolution of netted radar systems. IEEE Access 2020, 8, 124961–124977. [Google Scholar]
- Yan, J.K.; Liu, H.W.; Jiu, B.; Chen, B.; Liu, Z.; Bao, Z. Simultaneous multibeam resource allocation scheme for multiple target tracking. IEEE Trans. Signal Process. 2015, 63, 3110–3122. [Google Scholar] [CrossRef]
- Yuan, Y.; Yi, W.; Hoseinnezhad, R.; Varshney, P.K. Robust power allocation for resource-aware multi-target tracking with colocated MIMO radars. IEEE Trans. Signal Process. 2021, 9, 443–458. [Google Scholar] [CrossRef]
- Lu, X.J.; Yi, W.; Kong, L.J. Joint online route planning and resource optimization for multitarget tracking in airborne radar systems. IEEE Syst. J. 2022, 16, 4198–4209. [Google Scholar] [CrossRef]
- Yang, Y.Q.; Xia, Z.H.; Zhao, Z.L.; Zhang, T.; Li, K.; Yin, X.; Shi, H.F.; Peng, T. Intelligent resource management and optimization of clustered UAV airborne SAR system. In Proceedings of the 2021 IEEE 4th International Conference on Electronics Technology (ICET), Chengdu, China, 7–10 May 2021. [Google Scholar]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Power allocation strategies for target localization in distributed multiple-radar architectures. IEEE Trans. Signal Process. 2011, 59, 3226–3240. [Google Scholar] [CrossRef]
- Godrich, H.; Petropulu, A.P.; Poor, H.V. Sensor selection in distributed multiple-radar architectures for localization: A knapsack problem formulation. IEEE Trans. Signal Process. 2012, 60, 247–260. [Google Scholar] [CrossRef]
- Yan, J.K.; Pu, W.Q.; Liu, H.W.; Jiu, B.; Bao, Z. Robust chance constrained power allocation scheme for multiple target localization in colocated MIMO radar system. IEEE Trans. Signal Process. 2018, 66, 3946–3957. [Google Scholar] [CrossRef]
- Xie, M.C.; Yi, W.; Kirubarajan, T.; Kong, L.J. Joint node selection and power allocation strategy for multitarget tracking in decentralized radar networks. IEEE Trans. Signal Process. 2018, 66, 729–743. [Google Scholar] [CrossRef]
- Yan, J.K.; Pu, W.Q.; Zhou, S.H.; Liu, H.W.; Greco, M.S. Optimal resource allocation for asynchronous multiple targets tracking in heterogeneous radar networks. IEEE Trans. Signal Process. 2020, 68, 4055–4068. [Google Scholar] [CrossRef]
- Sun, H.; Li, M.; Zuo, L.; Cao, R.Q. Joint threshold optimization and power allocation of cognitive radar network for target tracking in clutter. Signal Process. 2020, 172, 107566. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Z.J.; Lu, W.L.; Xie, J.W. Joint target assignment and power allocation in multiple distributed MIMO radar networks. IEEE Syst. J. 2021, 15, 694–704. [Google Scholar] [CrossRef]
- Zhang, R.S.; Zhang, J.Y.; Yu, H.C. Review of modeling and control in UAV autonomous maneuvering flight. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation (ICMA), Changchun, China, 5–8 August 2018. [Google Scholar]
- Dong, F.; You, K.Y.; Zhang, J.Q. Flight control for UAV loitering over a ground target with unknown maneuver. IEEE Trans. Control Syst. Tech. 2020, 28, 2461–2473. [Google Scholar] [CrossRef]
- Guo, L.; Li, X.R.; Huang, H.; Jing, S.; He, Y.C.; Wang, C.Z. Intelligent penetration of UAV based on moth suppression algorithm. In Proceedings of the 2018 Chinese Automation Congress (CAC), Xi’an, China, 30 November–2 December 2018. [Google Scholar]
- Liang, L.; Deng, F.; Wang, J.N.; Lu, M.B.; Chen, J. A reconnaissance penetration game with territorial-constrained defender. IEEE Trans. Autom. Control 2022, 67, 6295–6302. [Google Scholar] [CrossRef]
- Nadarajah, N.; Tharmarasa, R.; McDonald, M.; Kirubarajan, T. IMM forward filtering and backward smoothing for maneuvering target tracking. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2673–2678. [Google Scholar] [CrossRef]
- Ma, J.; Guo, X.T. Combination of IMM algorithm and ASTRWCKF for maneuvering target tracking. IEEE Access 2020, 8, 143095–143103. [Google Scholar] [CrossRef]
- Zhang, Z.H.; Zhou, G.J. Maneuvering target state estimation based on separate modeling with high-order polynomials. Digit. Signal Process. 2022, 123, 103401. [Google Scholar] [CrossRef]
- Savage, C.O.; La Scala, B.F. Sensor management for tracking smart targets. Digit. Signal Process. 2009, 19, 968–977. [Google Scholar] [CrossRef]
- Zuo, L.R.; Niu, X.; Varshney, P.K. Conditional Posterior Cramér-Rao Lower Bounds for Nonlinear Sequential Bayesian Estimation. IEEE Trans. Signal Process. 2011, 59, 1–14. [Google Scholar] [CrossRef]
- Bell, K.L.; Baker, C.J.; Smith, G.E.; Johnson, J.T.; Rangaswamy, M. Cognitive radar framework for target detection and tracking. IEEE J. Sel. Topics Signal Process. 2015, 9, 1427–1439. [Google Scholar] [CrossRef]
- Chen, X.; Tharmarasa, R.; Kirubarajan, T. Multitarget multisensor tracking. In Academic Press Library in Signal Processing; Sidiropoulos, N.D., Gini, F., Chellappa, R., Theodoridis, S., Eds.; Academic Press: Cambridge, MA, USA, 2014; Volume 2, pp. 786–787. [Google Scholar]
- Li, X.T.; Zhang, T.X.; Yi, W.; Kong, L.J.; Yang, X.B. Radar selection based on the measurement information and the measurement compensation for target tracking in radar network. IEEE Sens. J. 2019, 19, 7923–7935. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.J.; Zhang, Q.; Fei, T.Y. A robust joint frequency spectrum and power allocation strategy in a coexisting radar and communication system. Chin. J. Aeronaut. 2024. [Google Scholar] [CrossRef]
- Skolnik, M.I. Introduction to Radar System, 3rd ed.; Tata McGraw-Hill Publishing Company Limited: New Delhi, India, 2001; pp. 49–73. [Google Scholar]
- Liu, B.D. Theory and Practice of Uncertain Programming, 2nd ed.; Springer: Berlin, Germany, 2009. [Google Scholar]
- Zhang, H.W.; Liu, W.J.; Zong, B.F.; Shi, J.P.; Xie, J.W. An efficient power allocation strategy for maneuvering target tracking in cognitive MIMO radar. IEEE Trans. Signal Process. 2021, 69, 1591–1602. [Google Scholar] [CrossRef]
- Zhang, H.W.; Xie, J.W.; Ge, J.A.; Lu, W.L.; Liu, B.Z. Strong tracking SCKF based on adaptive CS model for manoeuvring aircraft tracking. IET Radar Sonar Navig. 2018, 12, 742–749. [Google Scholar] [CrossRef]
- Miranda, S.L.C.; Baker, C.J.; Woodbridge, K.; Griffiths, H.D. Knowledge-based resource management for multifunction radar. IEEE Signal Process. Mag. 2006, 23, 66–76. [Google Scholar] [CrossRef]
- Miranda, S.L.C.; Baker, C.J.; Woodbridge, K.; Griffiths, H.D. Fuzzy logic approach for prioritisation of radar tasks and sectors of surveillance in multifunction radar. IET Radar Sonar Nav. 2007, 1, 131–141. [Google Scholar] [CrossRef]
- Van Trees, H.L. Detection, Estimation, Modulation Theory Part III; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Singer, R.A. Estimating optimal tracking filter performance for manned maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1970, AES-6, 473–483. [Google Scholar] [CrossRef]
- Zhou, H.; Kumar, K.S.P. A ‘current’ statistical model and adaptive algorithm for estimating maneuvering targets. AIAA J. Guid. 1984, 7, 596–602. [Google Scholar] [CrossRef]
- Mehrotra, K.; Mahapatra, P.R. A Jerk model for tracking highly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1997, 3, 1094–1105. [Google Scholar] [CrossRef]
- Zhang, H.W.; Liu, W.; Shi, J.P.; Fei, T.; Zong, B. Joint detection threshold optimization and illumination time allocation strategy for cognitive tracking in a networked radar system. IEEE Trans. Signal Process. 2022, 70, 5833–5847. [Google Scholar] [CrossRef]
- Van Trees, H.L. Optimum Array Processing: Detection, Estimation, Modulation Theory IV; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Van Trees, H.L.; Bell, K.L. Bayesian Bounds for Parameter Estimation and Nonlinear Filtering/Tracking; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Glass, J.D.; Smith, L.D. MIMO radar resource allocation using posterior Cramér-Rao lower bounds. In Proceedings of the 2011 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2011; pp. 1–9. [Google Scholar]
- Han, Q.H.; Pan, M.H.; Zhang, W.C.; Liang, Z.H. Time resource management of OAR based on fuzzy logic priority for multiple target tracking. J. Syst. Eng. Electron. 2018, 29, 742–755. [Google Scholar]
- Lee, C.C. Fuzzy logic in control systems: Fuzzy logic controller, parts I and II. IEEE Trans. Syst. Man Cybern. 1990, 20, 404–435. [Google Scholar] [CrossRef]
- Wang, L.X. A Course in Fuzzy Systems and Control (International Edition); Prentice-Hall: Upper Saddle River, NJ, USA, 1997. [Google Scholar]


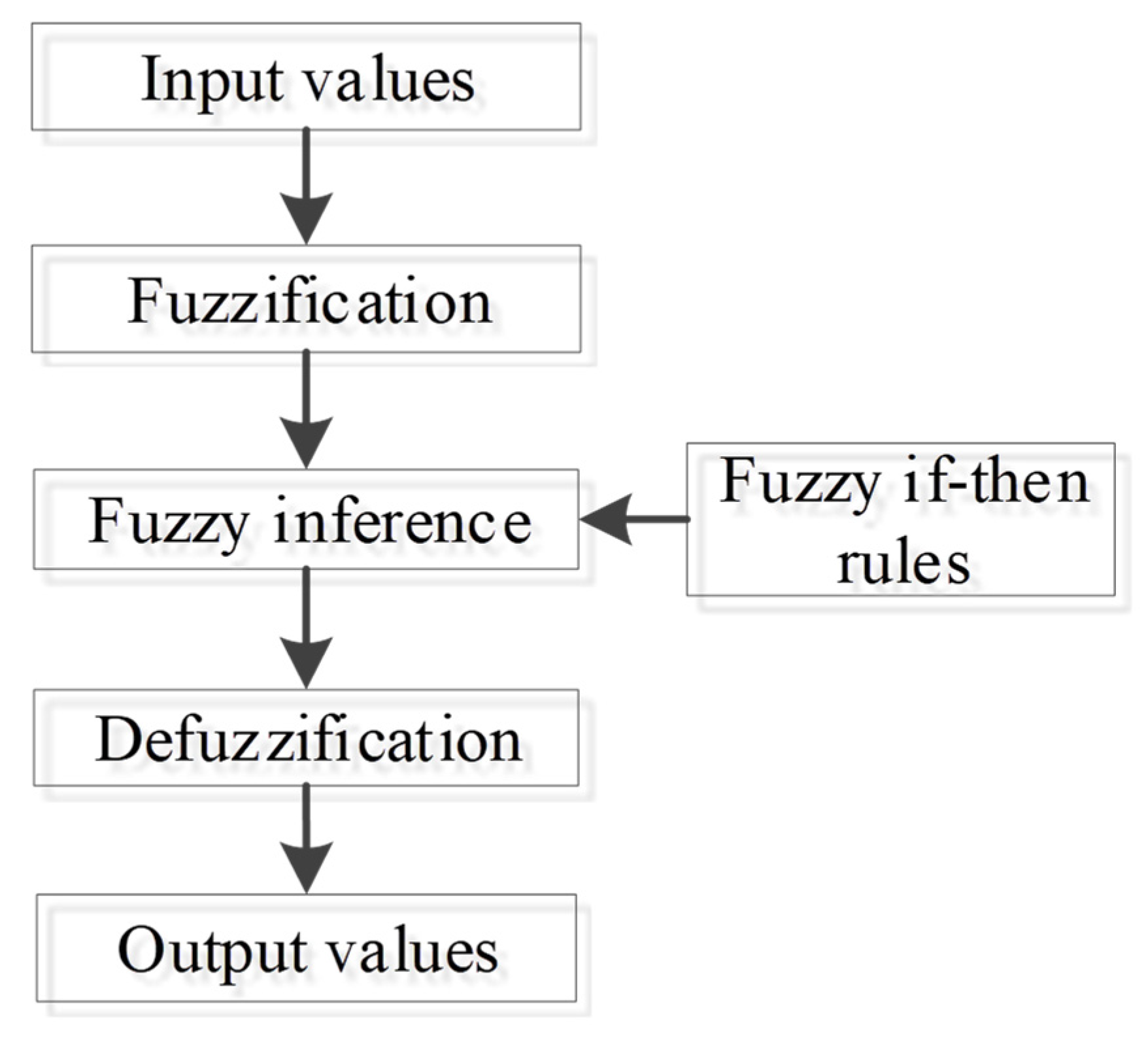







| Fuzzy Variable | Fuzzy Value |
|---|---|
| Range | very close, close, medium-close, medium, medium-far, far, very far |
| Radial velocity | very slow, slow, medium-slow, medium, medium-fast, fast, very fast |
| Priority | very low, low, medium-low, medium, medium-high, high, very high |
| Step 1 Let N′ = 0; |
| Step 2 Select (i = 1, 2, …, Nk) from the set and produce ; |
| Step 3 If ≤ ηk, N′ = N′ + 1; |
| Step 4 Repeat the second and third steps Nk times; |
| Step 5 = N′/Nk. If N′/Nk ≥ δ, the and meet the constraints, otherwise not. |
| (1) Initialize the population, and check the feasibility of the generated chromosomes by the stochastic simulation in Table 2. |
| (2) Update the chromosomes by crossover and mutation in which the feasibility of offspring can be checked by the stochastic simulation in Table 2. |
| (3) Calculate the objective function values of all the chromosomes. |
| (4) Compute the fitness of each chromosome according to the objective function values. |
| (5) Select the chromosomes by spinning the roulette wheel. |
| (6) Repeat the second to fifth steps for a given number of cycles. |
| (7) Report the best chromosome as the optimal solution . |
| (1) Let k = 1, initialize the (, ). |
| (2) The MCS-based ST-SCKF with the sequential updating technique is used to obtain the global state estimate. |
| (3) Based on the updated target state, obtain the optimal radar nodes according to the priority. |
| (4) Compute the centralized PC-CRLB conditioned on a particle filter, and adopt the HIOA to solve the CCP-based resource allocation for the optimal solution. |
| (5) Send the optimal allocation (, ) back to guide probing in next sampling instant. |
| (6) Let k = k + 1, and go to (2). |
| Index | Initial Position (km) | Velocity (m/s) |
|---|---|---|
| Radar 1 | (18, 0) | (-, -) |
| Radar 2 | (25, 0) | (-, -) |
| Radar 3 | (35, 5) | (-, -) |
| Radar 4 | (45, 10) | (-, -) |
| Radar 5 | (15, 20) | (-, -) |
| Radar 6 | (25, 24) | (-, -) |
| Radar 7 | (35, 24) | (-, -) |
| Radar 8 | (45, 24) | (-, -) |
| Case 1: Target | (20, 9) | (380, 440) |
| Case 2: Target | (46, 16) | (−600, −250) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Q.; Long, W.; Yang, Z.; Dong, X.; Chen, J.; Wang, F.; Liang, Z. Resource Allocation of Netted Opportunistic Array Radar for Maneuvering Target Tracking under Uncertain Conditions. Remote Sens. 2024, 16, 3499. https://doi.org/10.3390/rs16183499
Han Q, Long W, Yang Z, Dong X, Chen J, Wang F, Liang Z. Resource Allocation of Netted Opportunistic Array Radar for Maneuvering Target Tracking under Uncertain Conditions. Remote Sensing. 2024; 16(18):3499. https://doi.org/10.3390/rs16183499
Chicago/Turabian StyleHan, Qinghua, Weijun Long, Zhen Yang, Xishang Dong, Jun Chen, Fei Wang, and Zhiheng Liang. 2024. "Resource Allocation of Netted Opportunistic Array Radar for Maneuvering Target Tracking under Uncertain Conditions" Remote Sensing 16, no. 18: 3499. https://doi.org/10.3390/rs16183499
APA StyleHan, Q., Long, W., Yang, Z., Dong, X., Chen, J., Wang, F., & Liang, Z. (2024). Resource Allocation of Netted Opportunistic Array Radar for Maneuvering Target Tracking under Uncertain Conditions. Remote Sensing, 16(18), 3499. https://doi.org/10.3390/rs16183499







