Impact Analysis of Satellite Geometry Variation on ARAIM Integrity Risk over Exposure Interval
Abstract
:1. Introduction
2. Problem Definition
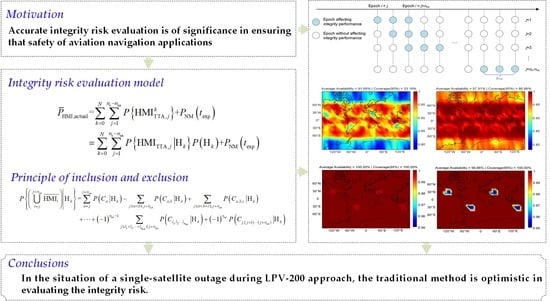
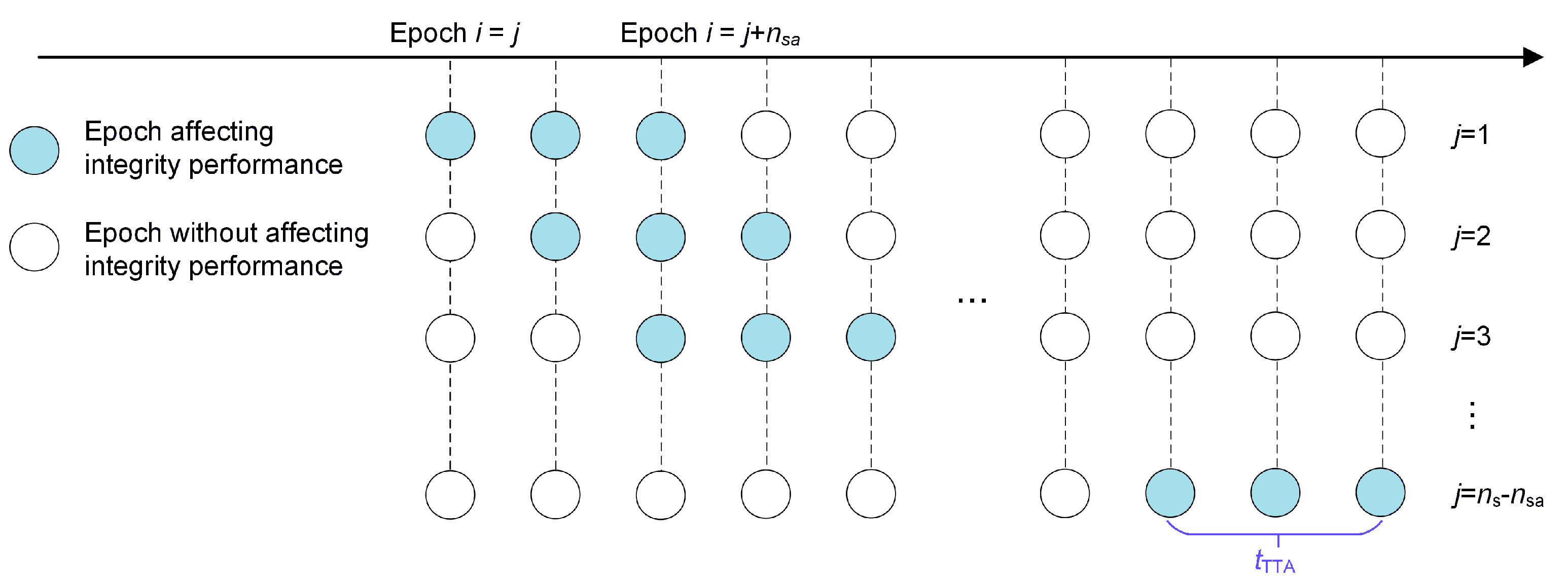
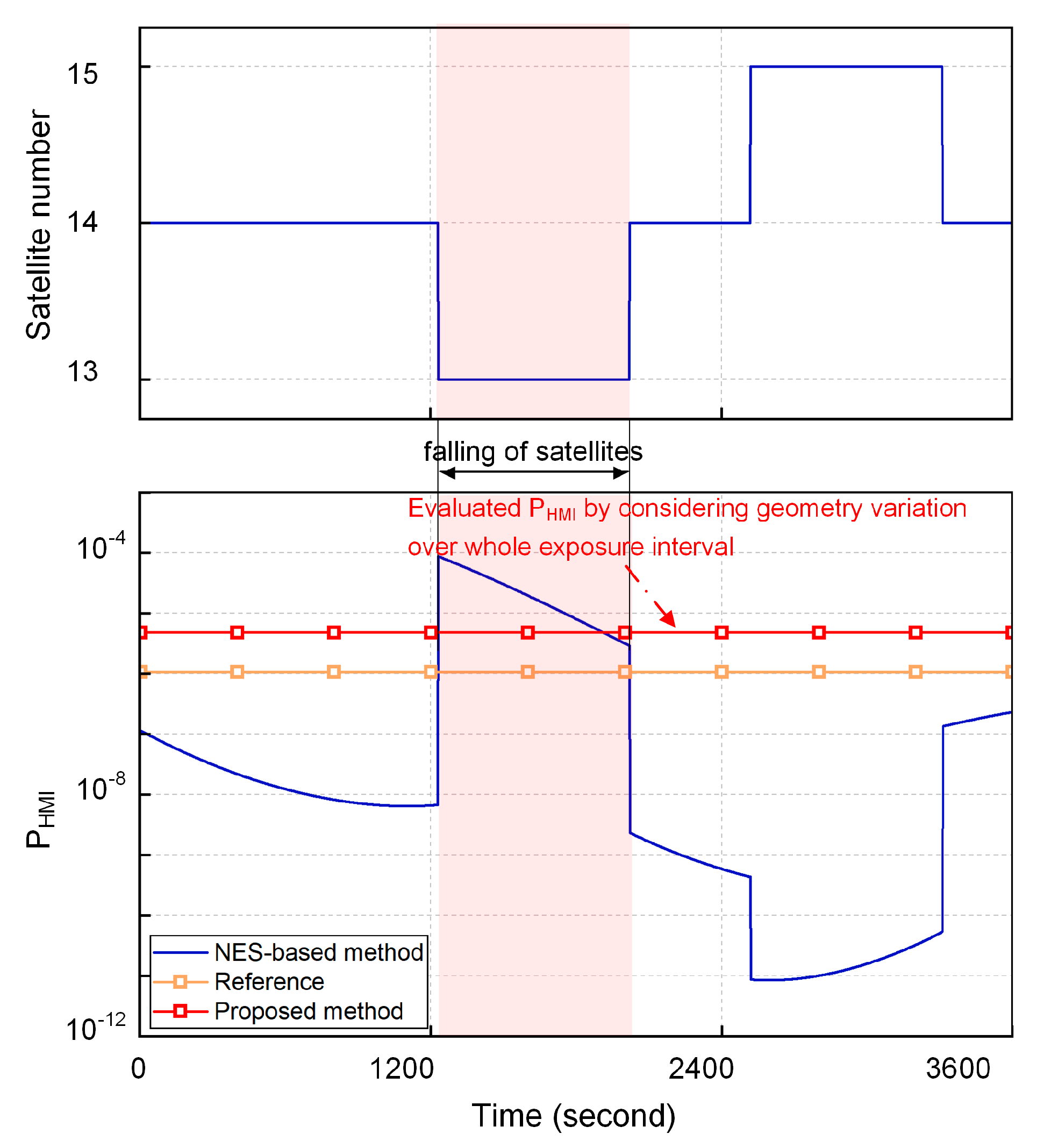
3. Integrity Risk Evaluation over the Exposure Interval
3.1. Hazardous Misleading Information
3.2. Evaluation of PHMI
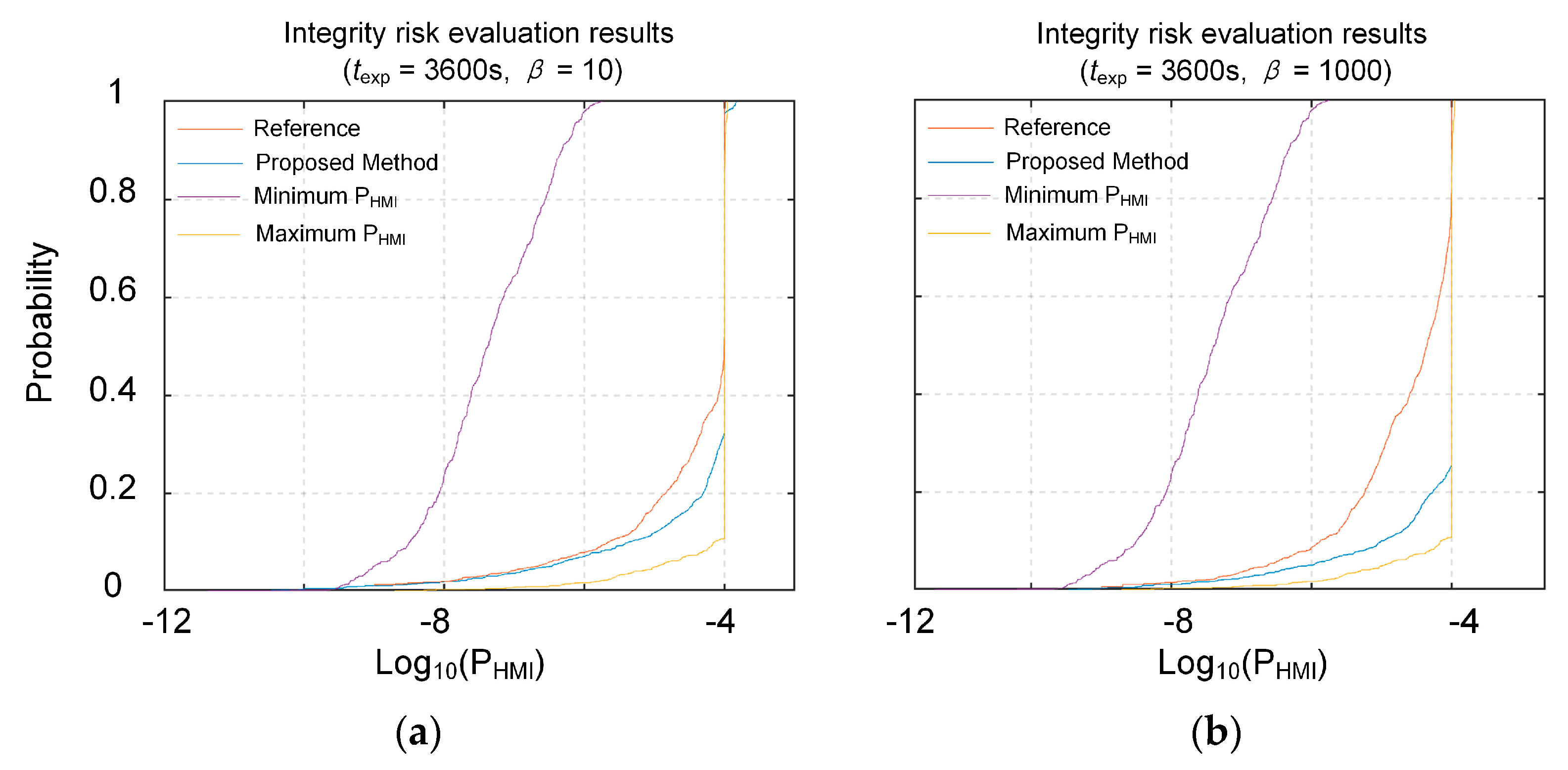
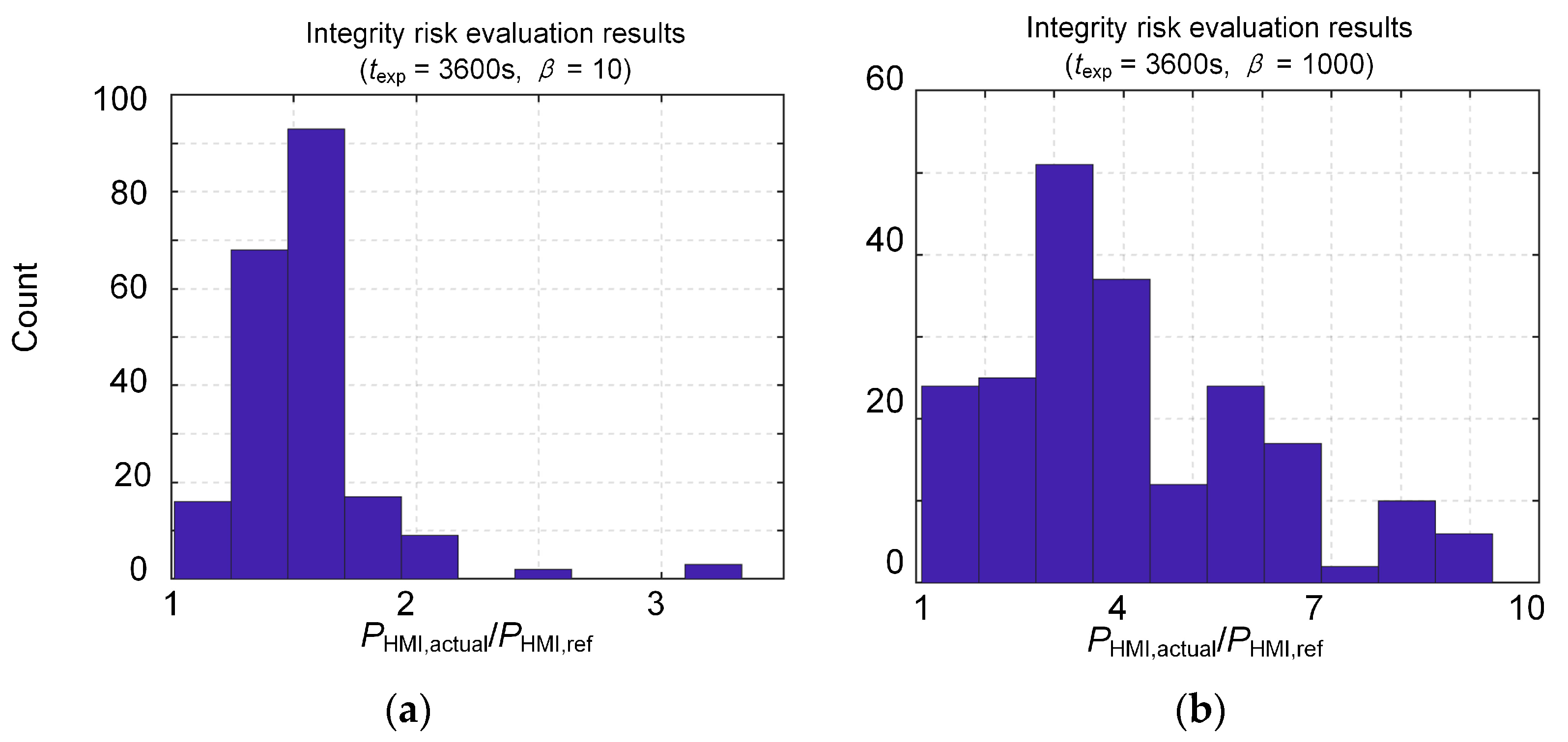
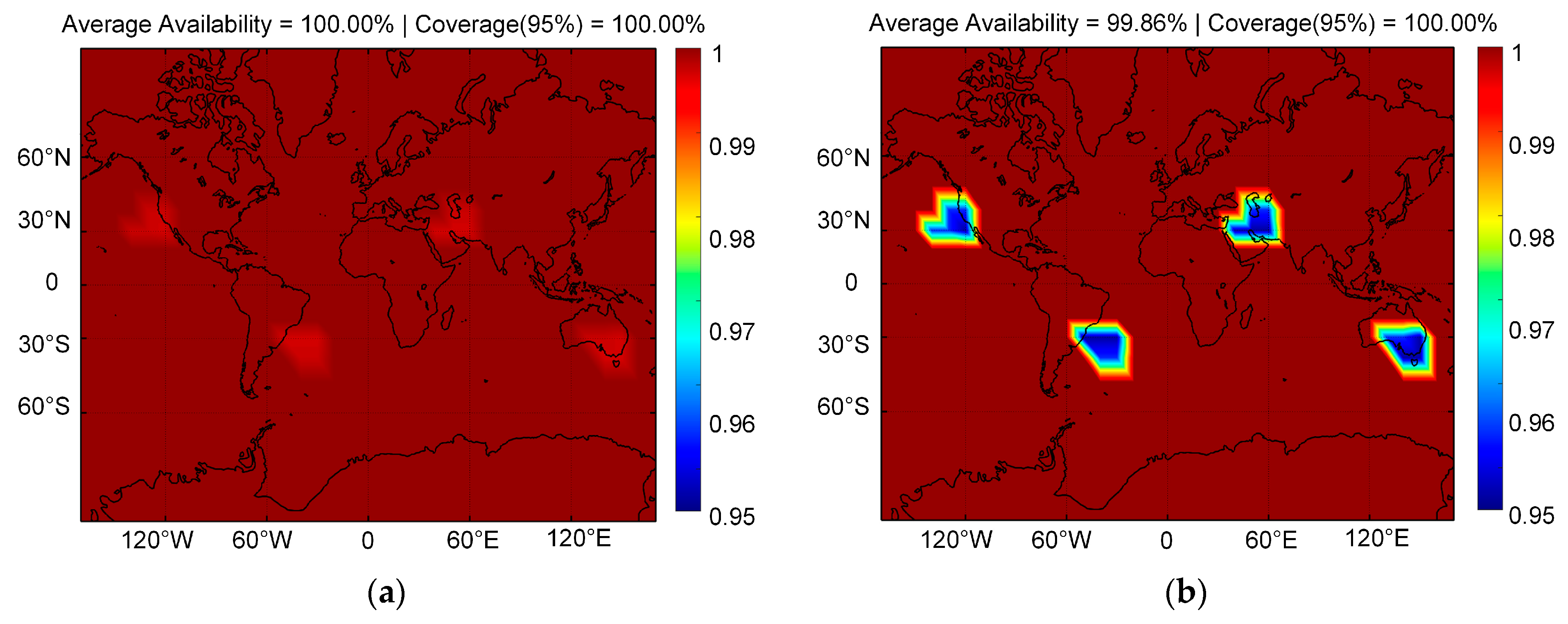
4. Experiment and Analysis
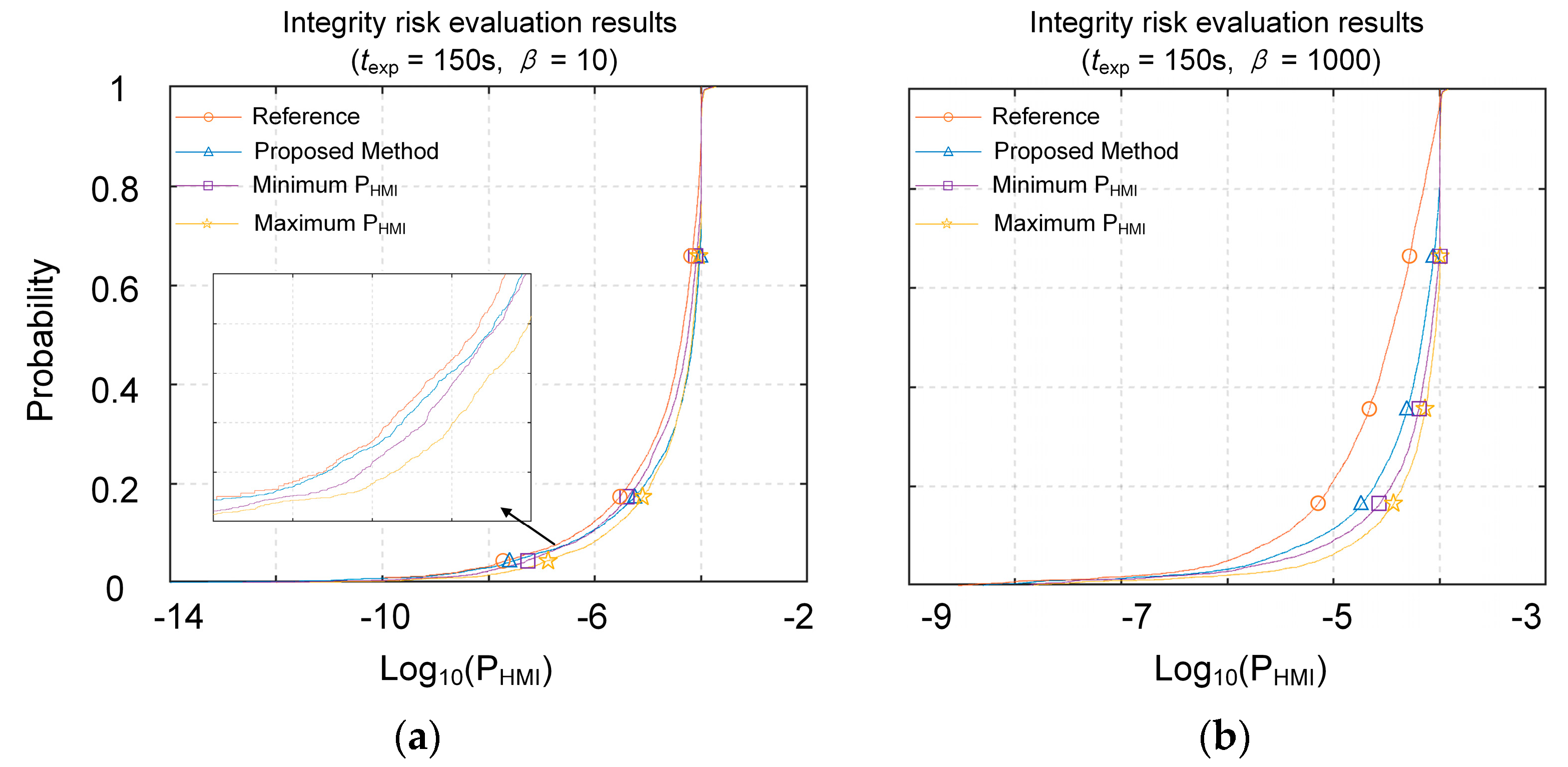
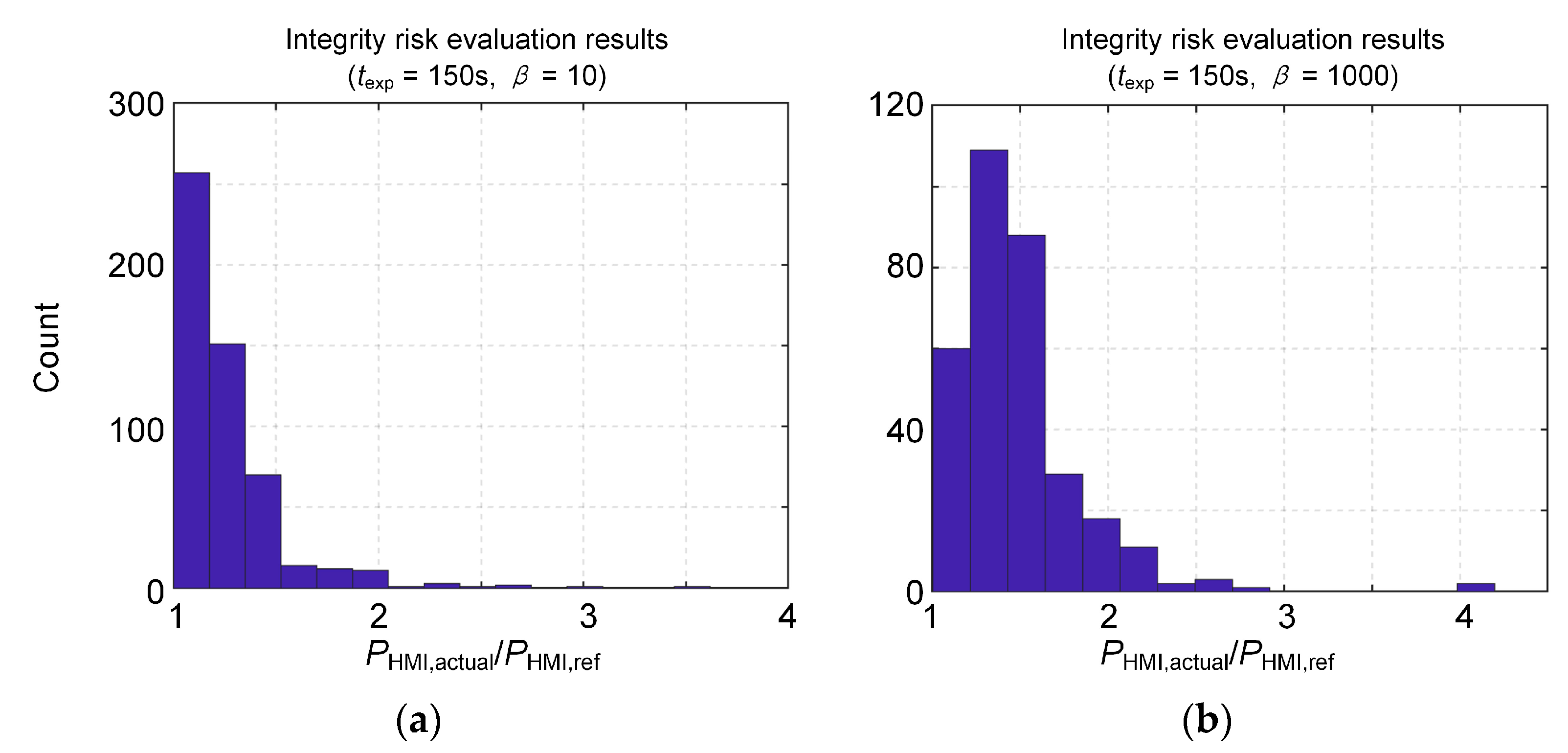
4.1. Tightness Analysis of Integrity Risk Evaluate Results
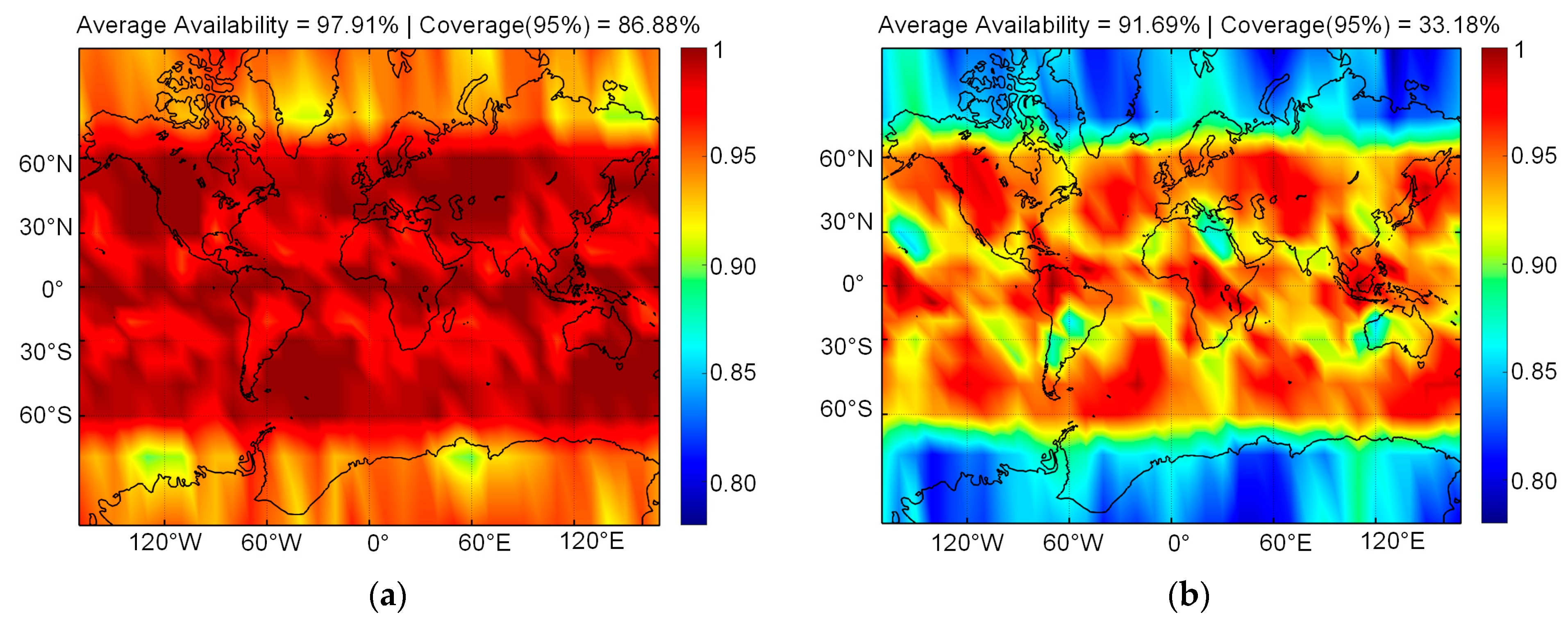
4.2. Evaluation of PHMI for Solution Separation ARAIM
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- WG-C Advanced RAIM Technical Subgroup (TSG). Advanced RAIM Technical Subgroup Reference Airborne Algorithm Description Document v4.1. 2022. Available online: https://www.ion.org/publications/abstract.cfm?articleID=18254 (accessed on 4 June 2023).
- Lee, Y.; Bian, B.; Odeh, A.; She, J. Sensitivity of advanced RAIM performance to mischaracterizations in integrity support message values. J. Navig. 2021, 68, 541–558. [Google Scholar] [CrossRef]
- Li, L.; Li, Z.; Yuan, H.; Wang, L.; Hou, Y. Integrity monitoring-based ratio test for GNSS integer ambiguity validation. GPS Solut. 2016, 20, 573–585. [Google Scholar] [CrossRef]
- Zhao, Y.; Cheng, C.; Li, L.; Wang, R.; Liu, Y.; Li, Z.; Zhao, L. BDS signal-in-space anomaly probability analysis over the last 6 years. GPS Solut. 2021, 25, 49. [Google Scholar] [CrossRef]
- Ma, X.; He, X.; Yu, K.; Montillet, J.P.; Lu, T.; Yan, L.; Zhao, L. Progress of global ARAIM availability of BDS-2/BDS-3 with TGD and ISB. Adv. Space Res. 2022, 70, 935–946. [Google Scholar] [CrossRef]
- Li, L.; Zhao, L.; Yang, F.; Li, N. A novel ARAIM approach in probability domain for combined GPS and Galileo. In Proceedings of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, 14–18 September 2015. [Google Scholar]
- Blanch, J.; Walter, T.; Enge, P. RAIM with optimal integrity and continuity allocations under multiple failures. IEEE Trans. Aerosp. Electron. Syst. 2010, 46, 1235–1247. [Google Scholar] [CrossRef]
- Bang, E.; Milner, C.; Macabiau, C. Cross-correlation effect of ARAIM test statistic on false alarm risk. GPS Solut. 2020, 24, 1–14. [Google Scholar] [CrossRef]
- Li, L.; Wang, H.; Jia, C.; Zhao, L.; Zhao, Y. Integrity and continuity allocation for the RAIM with multiple constellations. GPS Solut. 2017, 21, 1503–1513. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, W.; Guo, S.; Mao, Y.; Yang, Y. Introduction to BeiDou-3 navigation satellite system. Navigation 2019, 66, 7–18. [Google Scholar] [CrossRef]
- Joerger, M.; Chan, F.; Pervan, B. Solution separation versus residual-based RAIM. J. Navig. 2014, 61, 273–291. [Google Scholar] [CrossRef]
- Milner, C.; Ochieng, W.Y. Weighted RAIM for APV: The ideal protection level. J. Navig. 2011, 64, 61–73. [Google Scholar] [CrossRef]
- Blanch, J.; Walter, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline advanced RAIM user alogothrim and possible improvements. IEEE Trans. Aerosp Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Zhai, Y.; Zhan, X.; Pervan, B. Bounding Integrity Risk and False Alert Probability Over Exposure Time Intervals. IEEE Trans. Aerosp Electron. Syst. 2019, 56, 1873–1885. [Google Scholar] [CrossRef]
- Milner, C.; Pervan, B.; Blanch, J.; Joerger, M. Evaluating integrity and continuity over time in advanced RAIM. 2020. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium (PLANS), Portland, OR, USA, 20–23 April 2020. [Google Scholar]
- Blanch, J.; Walter, T.; Milner, C.; Joerger, M.; Pervan, B.; Bouvet, D. Baseline advanced RAIM user algorithm: Proposed updates. In Proceedings of the 2022 International Technical Meeting of The Institute of Navigation (ION ITM 2022), Long Beach, CA, USA, 25–27 January 2022. [Google Scholar]
- Du, J.; Wang, Z.; Fang, K.; Zhu, Y.; Dan, Z.; Wang, H.; Li, X. ARAIM integrity risk allocation over time. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022. [Google Scholar]
- Blanch, J.; Chen, Y.; Phelts, R.; Walter, T.; Enge, P. Mitigation of short duration satellite outages for Advanced RAIM and other integrity systems based on GNSS. In Proceedings of the 29th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2016), Portland, OR, USA, 12–16 September 2016. [Google Scholar]
- Nikiforov, I. From pseudorange overbounding to integrity risk overbounding. Navigation 2019, 66, 417–439. [Google Scholar] [CrossRef]
- Lee, Y.; She, J.; Odeh, A.; Bian, B. Horizontal advanced RAIM performance sensitivity to mischaracterizations in integrity support message values. In Proceedings of the 32nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2019), Miami, FL, USA, 16–20 September 2019. [Google Scholar]
- Bang, E.; and Milner, C. Integrity risk under temporal correlation for horizontal ARAIM. IEEE Trans. Aerosp Electron. Syst. 2021, 57, 3974–3987. [Google Scholar] [CrossRef]
- Joerger, M.; Pervan, B. Multi-constellation ARAIM exploiting satellite motion. Navigation 2020, 67, 235–253. [Google Scholar] [CrossRef]
- Zhai, Y. Ensuring Navigation Integrity and Continuity Using Multi-Constellation GNSS. Ph.D. Thesis, Department of Mechanical, Materials and Aerospace Engineering, Illinois Institute of Technology, Chicago, IL, USA, 2018. [Google Scholar]
- Joerger, M.; Stevanovic, S.; Langel, S.; Pervan, B. Integrity risk minimisation in RAIM part 1: Optimal detector design. J. Navig. 2016, 69, 449–467. [Google Scholar] [CrossRef]
- Chan, F.; Joerger, M.; Khanafseh, S.; Pervan, B. Bayesian fault-tolerant position estimator and integrity risk bound for GNSS navigation. J. Navig. 2014, 67, 753–775. [Google Scholar] [CrossRef]
- Cassel, R. Real-Time ARAIM Using GPS, GLONASS, and GALILEO. Master’s Thesis, Department of Mechanical, Materials and Aerospace Engineering, Illinois Institute of Technology, Chicago, IL, USA, 2017. [Google Scholar]
- Wang, L.; Luo, S.; Tu, R.; Fan, L.; Zhang, Y. ARAIM with BDS in the Asia-Pacific region. Adv. Space Res. 2018, 62, 707–720. [Google Scholar] [CrossRef]
- El-Mowafy, A.; Yang, C. Limited sensitivity analysis of ARAIM availability for LPV-200 over Australia using real data. Adv. Space Res. 2016, 57, 659–670. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Satellite clock and orbits correction error σURA (integrity) | V-ARAIM: 1.5 [m] H-ARAIM: 2.4 [m] |
| Satellite clock and orbits correction error σURE (accuracy and continuity) | (2/3) σURA [m] |
| PHMI,REQ | V-ARAIM: 9.8 × 10−8/150 s H-ARAIM: 1.0 × 10−7/h |
| PFA,REQ | V-ARAIM: 3.9 × 10−6/150 sH-ARAIM: 5.0 × 10−7/h |
| Rsat | 10−5/h for both GPS and Galileo |
| Rconst | 10−8/h (GPS); 1 × 10−4/h (Galileo) |
| MFD (mean fault duration) | 1 h for both GPS and Galileo |
| NES | texp/ts for both integrity and continuity |
| texp | 150 [s] (LPV-200); 3600 [s] (RNP 0.1) |
| ta | 6 [s] (LPV-200); 10 [s] (RNP 0.1) |
| ts | 2 [s] |
| PNM | 6 × 10−8 |
| Alarm limit | VAL: 35 [m]; HAL: 185 [m] |
| Method | β = 10 | β = 100 | β = 1000 | ||||
|---|---|---|---|---|---|---|---|
| Average | Coverage | Average | Coverage | Average | Coverage | ||
| LPV-200 nominal | Traditional | 98.41% | 93.67% | 98.41% | 93.67% | 98.41% | 93.67% |
| Actual | 98.17% | 92.44% | 97.59% | 91.05% | 97.71% | 90.74% | |
| Loss | 0.24% | 1.23% | 0.82% | 2.62% | 0.70% | 2.93% | |
| LPV-200 one-satellite outage | Traditional | 97.91% | 86.88% | 97.91% | 86.88% | 97.91% | 86.88% |
| Actual | 94.51% | 58.02% | 91.69% | 33.18% | 90.97% | 26.39% | |
| Loss | 3.40% | 28.86% | 6.22% | 53.70% | 6.94% | 60.49% | |
| RNP 0.1 | Traditional | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% | 100.00% |
| Actual | 99.86% | 100.00% | 99.86% | 100.00% | 99.83% | 100.00% | |
| Loss | 0.14% | 0.00% | 0.14% | 0.00% | 0.17% | 0.00% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Li, L.; Na, Z.; Duan, Y.; Xu, X.; Liu, Z. Impact Analysis of Satellite Geometry Variation on ARAIM Integrity Risk over Exposure Interval. Remote Sens. 2024, 16, 286. https://doi.org/10.3390/rs16020286
Li R, Li L, Na Z, Duan Y, Xu X, Liu Z. Impact Analysis of Satellite Geometry Variation on ARAIM Integrity Risk over Exposure Interval. Remote Sensing. 2024; 16(2):286. https://doi.org/10.3390/rs16020286
Chicago/Turabian StyleLi, Ruijie, Liang Li, Zhibo Na, Yangwang Duan, Xin Xu, and Zelin Liu. 2024. "Impact Analysis of Satellite Geometry Variation on ARAIM Integrity Risk over Exposure Interval" Remote Sensing 16, no. 2: 286. https://doi.org/10.3390/rs16020286
APA StyleLi, R., Li, L., Na, Z., Duan, Y., Xu, X., & Liu, Z. (2024). Impact Analysis of Satellite Geometry Variation on ARAIM Integrity Risk over Exposure Interval. Remote Sensing, 16(2), 286. https://doi.org/10.3390/rs16020286