Assessment of Radio Frequency Compatibility for New Radio Navigation Satellite Service Signal Design in the L6-Band
Abstract
:1. Introduction
2. Methodology
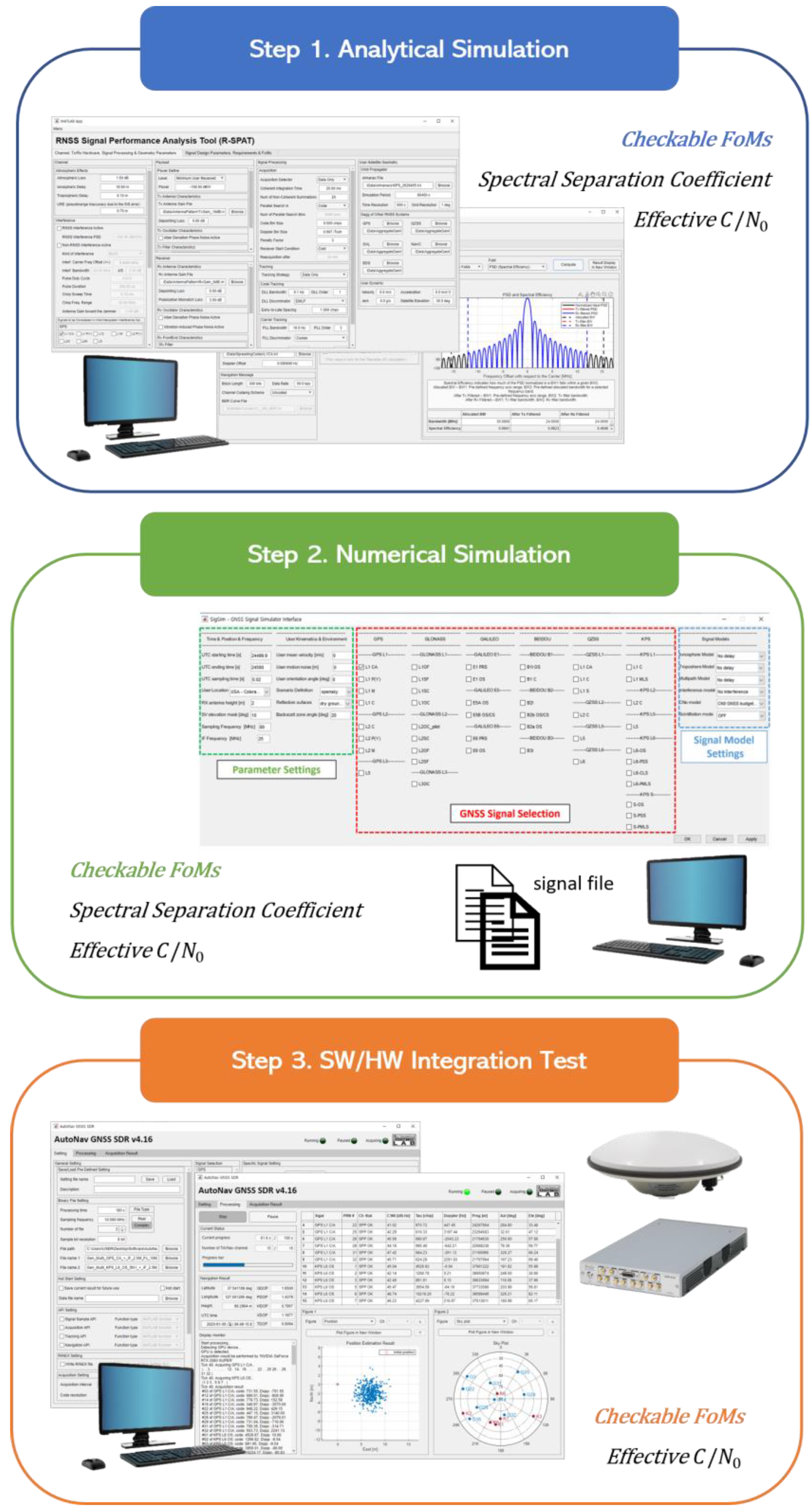
2.1. Analytical Simulation
2.2. Numerical Simulation
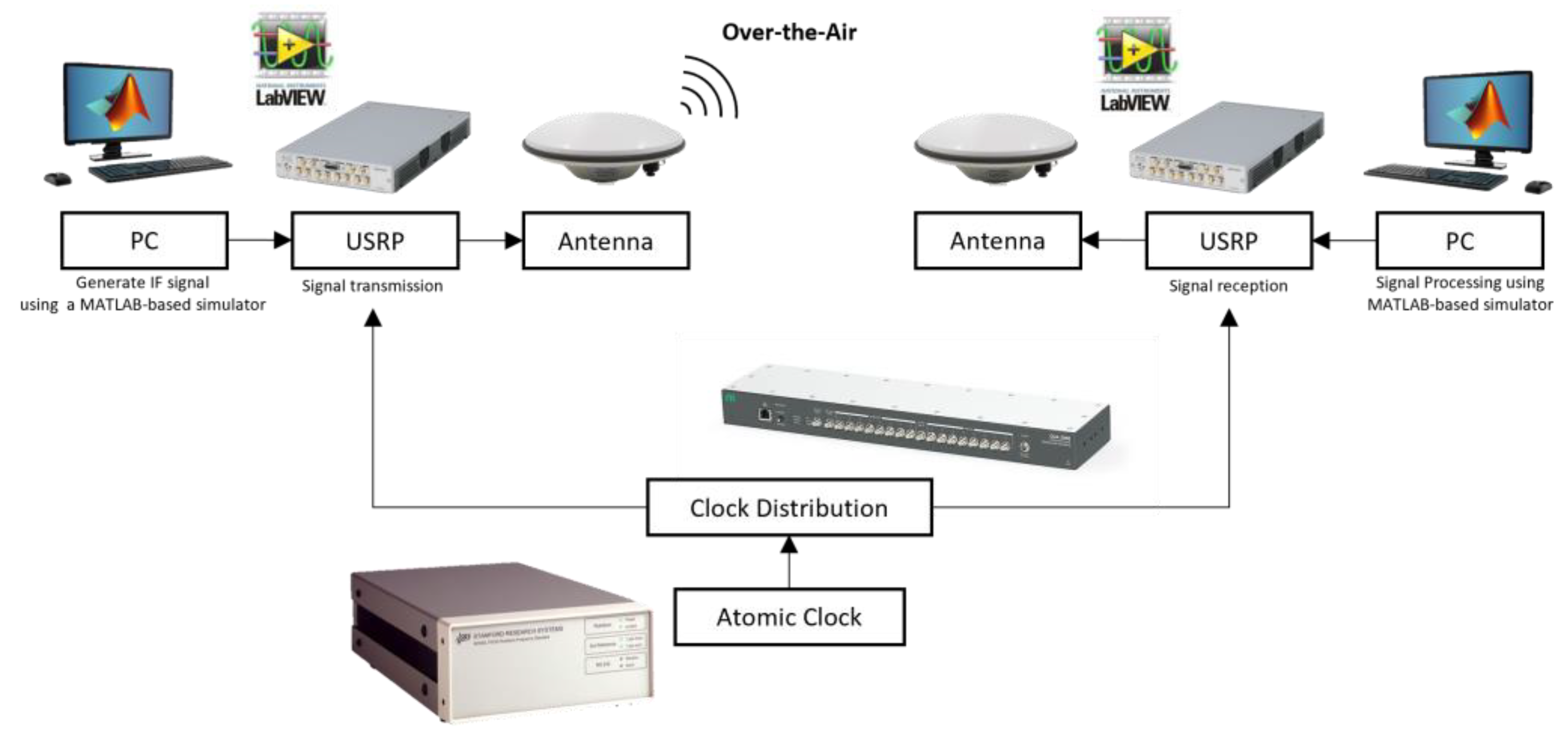
2.3. Software/Hardware Integration Test
3. Simulation Parameters
3.1. L6-Band Signals
3.2. Space Constellation
4. Results
4.1. Analytical Simulations
4.2. Numerical Simulations
4.3. Software/Hardware Integration Test
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kim, T. Korean Positioning System (KPS) and Korean Augmentation Satellite System (KASS) Update. In Proceedings of the Fifteenth Meeting of the International Committee on Global Navigation Satellite Systems (ICG-15), Vienna, Austria, 27 September–1 October 2021. [Google Scholar]
- Satellite Navigation System More Accurately. Available online: https://www.kari.re.kr/eng/sub03_08_01.do (accessed on 2 January 2023).
- ITU. Radio Regulations, 2020 ed; ITU: Geneva, Switzerland, 2020; Volume 1, pp. 96–126. ISBN 978-92-61-30301-3. [Google Scholar]
- ITU. Description of Systems and Networks in the Radionavigation-Satellite Service (Space-to-Earth and Space-to-Space) and Technical Characteristics of Transmitting Space Stations Operating in the Bands 1 164-1 215 MHz, 1 215-1 300 MHz and 1 559-1 610 MHz (Recommendation ITU-R M.1787-4); ITU: Geneva, Switzerland, 2022. [Google Scholar]
- Indian Space Research Organization. IRNSS Signal-in-Space Interface Control Document (ISRO-IRNSS-ICD-SPS-1.1); Indian Space Research Organization: Bengaluru, India, 2017. [Google Scholar]
- ITU. A Coordination Methodology for Radionavigation-Satellite Service Inter-System Interference Estimation (Recommendation ITU-R M.1831-1); ITU: Geneva, Switzerland, 2015. [Google Scholar]
- Betz, J.W. Effect of Partial-Band Interference on Receiver Estimation of C/N0: Theory. In Proceedings of the 2001 National Technical Meeting of the Institute of Navigation (ION NTM 2001), Long Beach, CA, USA, 22–24 January 2001. [Google Scholar]
- Betz, J.W.; Goldstein, D.B. Candidate Designs for an Additional Civil Signal in GPS Spectral Bands. In Proceedings of the 2002 National Technical Meeting of the Institute of Navigation (ION NTM 2002), San Diego, CA, USA, 28–30 January 2002. [Google Scholar]
- Liu, W.; Zhai, C.R.; Zhan, X.Q.; Zhang, Y.H. Assessment and analysis of radio frequency compatibility among several global navigation satellite systems. IET Radar Sonar Navig. 2011, 5, 128–136. Available online: https://digital-library.theiet.org/content/journals/10.1049/iet-rsn.2009.0241 (accessed on 20 October 2023). [CrossRef]
- Sun, Y.; Xue, R.; Zhao, D.; Wang, D. Radio Frequency Compatibility Evaluation of S Band Navigation Signals for Future BeiDou. Sensors 2017, 17, 1039. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Zhai, C.; Zhang, Y.; Zhan, X. Simulation Analysis of GPS/Galileo/Compass Radio Frequency Compatibility. In Proceedings of the 22nd International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2009), Savannah, GA, USA, 22–25 September 2009. [Google Scholar]
- Wallner, S.; Hein, G.W.; Pany, T.; Avila-Rodriguez, J.A.; Posfay, A. Interference computations between GPS and Galileo. In Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, 13–16 September 2005. [Google Scholar]
- Wallner, S.; Hein, G.W.; Avila-Rodriguez, J.A. Interference computations between several GNSS systems. ESA Navitec 2006, 11–13. Available online: https://www.researchgate.net/profile/Stefan-Wallner-7/publication/229047833_Interference_computations_between_several_GNSS_systems/links/54b38b970cf220c63cd284a3/Interference-computations-between-several-GNSS-systems.pdf (accessed on 20 October 2023).
- Han, K.; Shin, H.; Won, J.H. A Method of GNSS RF Compatibility Assessment for KPS Signal Design. In Proceedings of the ISGNSS 2019 in Conjunction with IPNT Conference, Jeju, Republic of Korea, 29 October–1 November 2019; Available online: http://ipnt.or.kr/2019proc/22 (accessed on 20 October 2023).
- Lee, S.; Han, K.; Won, J.H. A High-Level RF Compatibility Analysis for RNSS Signal Design. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MI, USA, 20–24 September 2021. [Google Scholar] [CrossRef]
- Lee, S.; Han, K.; Won, J.H. RF Compatibility Analysis of GNSS and KPS Signals at L6/S-band. J. Position. Navig. Timing 2021, 10, 21–28. [Google Scholar] [CrossRef]
- Akos, D.; Arribas, J.; Bhuiyan, M.Z.H.; Closas, P.; Dovis, F.; Fernandez-Hernandez, I.; Fernández–Prades, C.; Gunawardena, S.; Humphreys, T.; Kassas, Z.M.; et al. GNSS Software Defined Radio: History, Current Developments, and Standardization Efforts. In Proceedings of the 35th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2022), Denver, CO, USA, 19–23 September 2022. [Google Scholar] [CrossRef]
- Choi, B.H.; Song, Y.J.; Lee, S.; Won, J.H. Design of a Fully Reconfigurable Multi-Constellation and Multi-Frequency GNSS Signal Generator. J. Position. Navig. Timing 2023, 12, 295–306. [Google Scholar] [CrossRef]
- European Union. Galileo—Open Service—Signal in Space Interface Control Document (OS SIS ICD v2.0). January 2021. Available online: https://www.gsc-europa.eu/sites/default/files/sites/all/files/Galileo_OS_SIS_ICD_v2.0.pdf (accessed on 2 January 2023).
- China Satellite Navigation Office. BeiDou Navigation Satellite System Signal in Space Interface Control Document Open Service Signal B3I (Version 1.0). February 2018. Available online: http://en.beidou.gov.cn/SYSTEMS/ICD/201806/P020180608516798097666.pdf (accessed on 2 January 2023).
- Cabinet Office. Quasi-Zenith Satellite System Interface Specification Centimeter Level Augmentation Service (IS-QZSS-L6-005). September 2022. Available online: https://qzss.go.jp/en/technical/download/pdf/ps-is-qzss/is-qzss-l6-005.pdf?t=1682599378664 (accessed on 2 January 2023).
- Orbital and Technical Parameters. Available online: https://www.gsc-europa.eu/system-service-status/orbital-and-technical-parameters (accessed on 2 January 2023).
- Constellation Status. Available online: http://www.csno-tarc.cn/en/system/constellation (accessed on 2 January 2023).
- United Nations. The Interoperable Global Navigation Satellite Systems Space Service Volume, 2nd ed.; United Nations Office for Outer Space Affairs: Vienna, Austria, 2018; pp. 109–114. ISBN 9789211304367. [Google Scholar]
- Kogure, S. Update of QZSS. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MI, USA, 20–24 September 2021. [Google Scholar] [CrossRef]
- Choi, B.K.; Roh, K.M.; Ge, H.; Ge, M.; Joo, J.; Heo, M.B. Performance Analysis of the Korean Positioning System Using Observation Simulation. Remote Sens. 2020, 12, 3365. [Google Scholar] [CrossRef]
- Shin, M.; Lim, D.W.; Chun, S.; Heo, M.B. A Study on the Satellite Orbit Design for KPS Requirements. J. Position. Navig. Timing 2019, 8, 215–223. [Google Scholar] [CrossRef]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance, 2nd ed.; Ganga-Jamuna Press: Lincoln, MA, USA, 2006; pp. 393–427. ISBN 13:978-0970954411. [Google Scholar]
- Betz, J.W.; Titus, B.M. Intersystem and intrasystem interference with signal imperfections. In Proceedings of the PLANS 2004. Position Location and Navigation Symposium (IEEE Cat. No.04CH37556), Monterey, CA, USA, 26–29 April 2004. [Google Scholar] [CrossRef]
- Titus, B.M.; Betz, J.; Hegarty, C.; Owen, R. Intersystem and Intrasystem Interference Analysis Methodology. In Proceedings of the 16th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS/GNSS 2003), Portland, OR, USA, 9–12 September 2003. [Google Scholar]
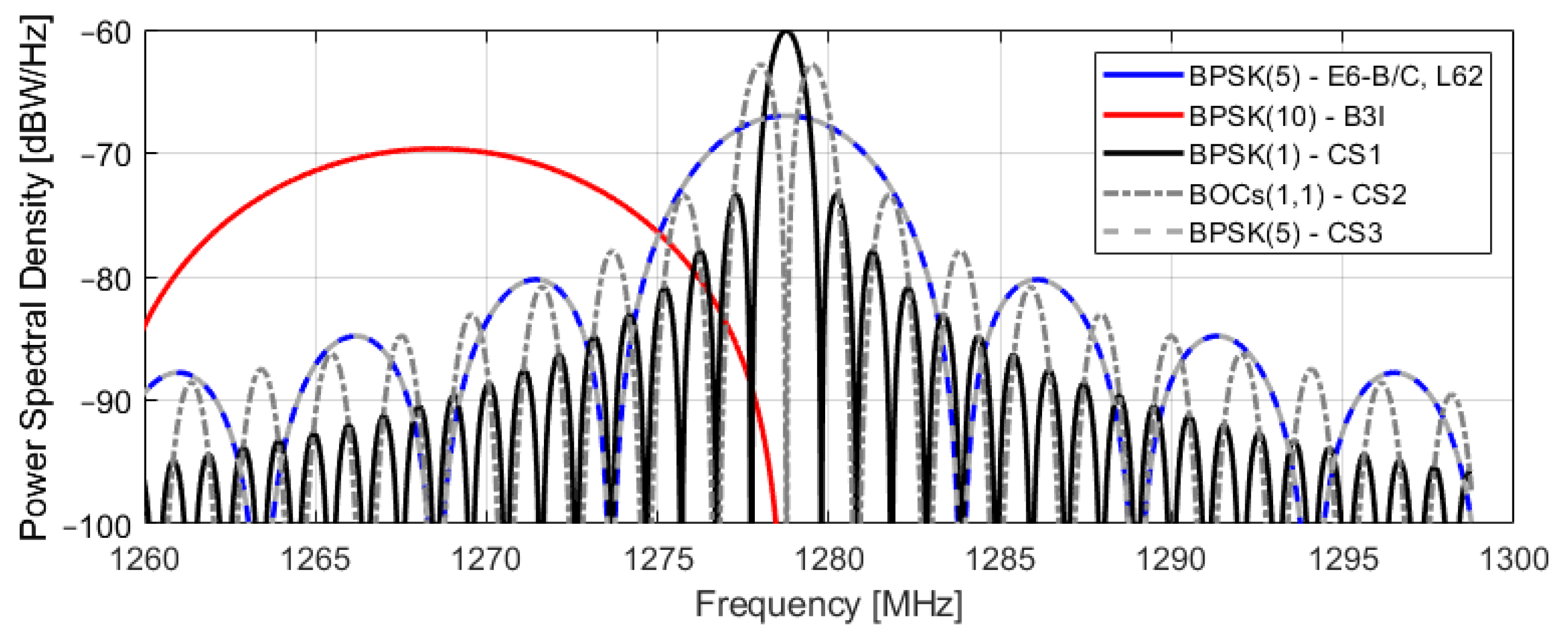

| System | Center Frequency [MHz] | Signal Name | Modulation | Primary Code Family (Length) | Secondary Code Family (Length) | Data Rate [bps] | |
|---|---|---|---|---|---|---|---|
| Galileo | 1278.75 | E6-B/C | E6-B | BPSK (5) | Memory(5115) | - | 500 |
| E6-C | BPSK (5) | Memory(5115) | CS 100(100) | - | |||
| BDS | 1268.52 | B3I | BPSK (10) | Gold(10230) | - | 50 * 500 ** | |
| QZSS | 1278.75 | L62 | code1 | BPSK (2.5) | Kasami(10320) | - | 2000 |
| code2 | BPSK (2.5) | Kasami(10320) | - | 2000 | |||
| New RNSS | 1278.75 | CS1 | BPSK (1) | Random(10320) | - | 50 | |
| CS2 | BOCs (1,1) | Random(10320) | - | 50 | |||
| CS3 | BPSK (5) | Random(10320) | - | 50 | |||
| Parameter | Galileo | BDS | QZSS | New RNSS |
|---|---|---|---|---|
| Constellation | 22 MEO | 7GEO + 10IGSO + 27MEO | 2GEO + 1QGEO + 4QZO | 3GEO + 5IGSO |
| Inclination | 56° | GEO: 0° IGSO/MEO: 55° | GEO: 0° QGEO: 3° QZO: 41° | GEO: 0° IGSO: 43° |
| Eccentricity | 0 | 0.003 | GEO: 0 QGEO: 0.008 QZO: 0.075 | GEO: 0 IGSO: 0.075 |
| Signal | Scenario | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | |
| E6-B/C | ○ | ● | ○ | ● | ○ | ● | ||||||
| B3I | ○ | ● | ○ | ● | ○ | ● | ||||||
| L62 | ○ | ● | ○ | ● | ○ | ● | ||||||
| CS1 | ● | ● | ● | ○ | ||||||||
| CS2 | ● | ● | ● | ○ | ||||||||
| CS3 | ● | ● | ● | ○ | ||||||||
| Interference Signal | SSC (dB/Hz) | |||||
|---|---|---|---|---|---|---|
| E6-B/C (BPSK (5)) | B3I (BPSK (10)) | L62 (BPSK (5)) | CS1 (BPSK (1)) | CS2 (BOCs (1,1)) | CS3 (BPSK (5)) | |
| E6-B/C | −68.63 | −83.19 | −68.63 | −67.25 | −67.88 | −68.63 |
| B3I | −83.97 | −70.98 | −83.97 | −91.13 | −86.30 | −83.97 |
| L62 | −68.63 | −83.19 | −68.63 | −67.25 | −67.88 | −68.63 |
| CS1 | −67.25 | −90.30 | −67.25 | −61.81 | −67.79 | −67.25 |
| CS2 | −67.88 | −85.48 | −67.88 | −67.79 | −64.74 | −67.88 |
| CS3 | −68.63 | −83.19 | −68.63 | −67.25 | −67.88 | −68.63 |
| Classification | Parameter | Value | Unit |
|---|---|---|---|
| Simulation | Time | 1 | day |
| Time resolution | 10 | min | |
| Grid resolution | 1 × 1 | deg | |
| Elevation mask | 5 | deg | |
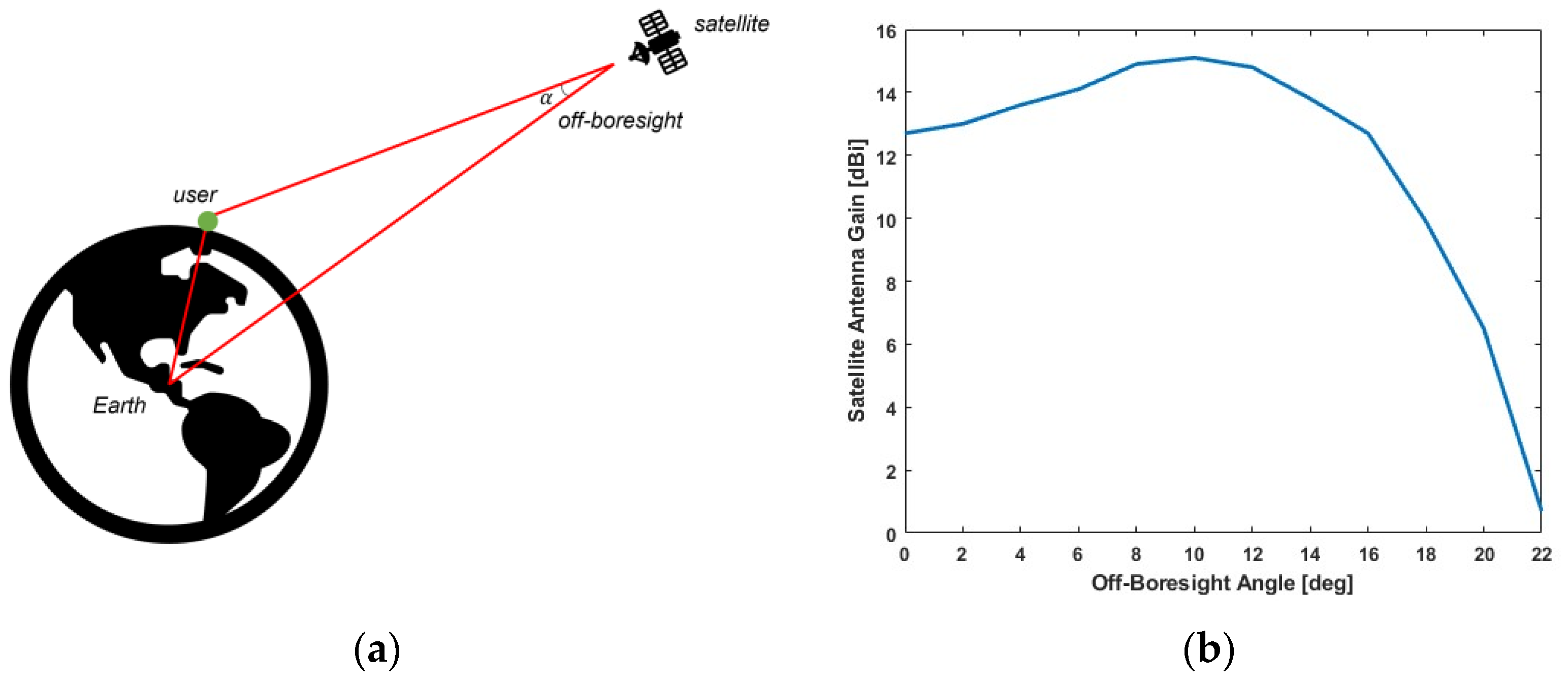
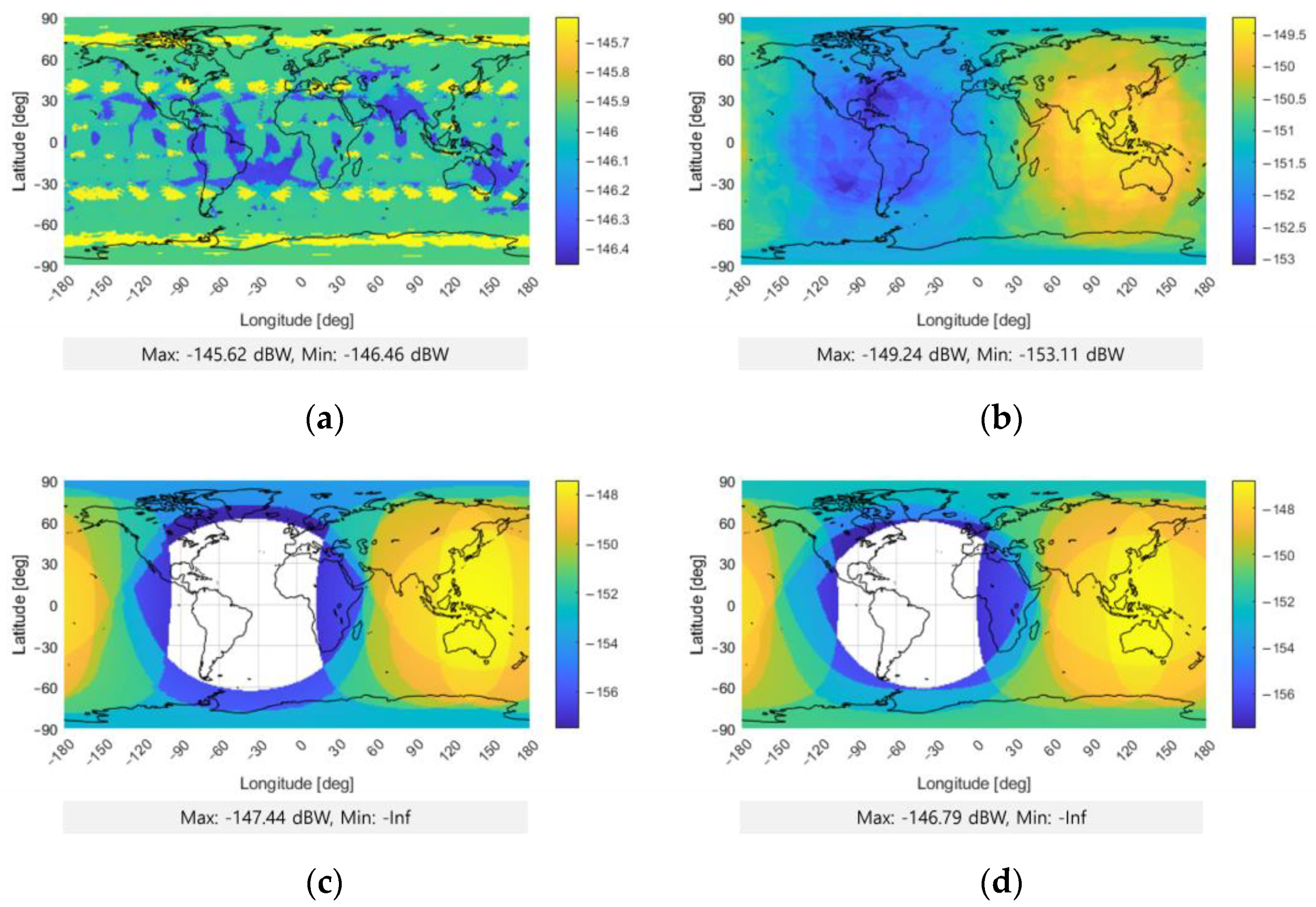
| Antenna gain | Satellite | Global: Figure 4b Regional: 16 | dBi |
| Receiver | 3 | dBi | |
| Loss | Distance | Equation (9) | dB |
| Polarization | 3 | dB | |
| Atmosphere | 1.5 | dB | |
| Processing | 1 | dB | |
| Received signal power | Minimum received power | Galileo: −155.25 BDS: −163 QZSS: −156.82 New RNSS: −157 | dBW |
| Interference Signal | SSC [dB/Hz] (βdiff) | |||||
|---|---|---|---|---|---|---|
| E6-B/C | B3I | L62 | CS1 | CS2 | CS3 | |
| (BPSK (5)) | (BPSK (10)) | (BPSK (5)) | (BPSK (1)) | (BOCs (1,1)) | (BPSK (5)) | |
| E6-B/C | −63.58 | −82.92 | −70.02 | −67.27 | −67.92 | −69.68 |
| (5.05) | (0.27) | (1.39) | (0.02) | (0.04) | (1.05) | |
| B3I | −83.87 | −60.09 | −90.04 | −91.83 | −86.80 | −89.07 |
| (0.10) | (10.89) | (6.07) | (0.70) | (0.50) | (5.10) | |
| L62 | −70.02 | −89.12 | −60.36 | −67.13 | −67.80 | −63.69 |
| (1.39) | (5.93) | (8.27) | (0.12) | (0.08) | (4.94) | |
| CS1 | −67.27 | −90.86 | −67.13 | −59.12 | −65.21 | −67.04 |
| (0.02) | (0.56) | (0.12) | (2.69) | (2.58) | (0.21) | |
| CS2 | −67.92 | −85.82 | −67.80 | −65.21 | −61.87 | −67.77 |
| (0.04) | (0.34) | (0.08) | (2.58) | (2.87) | (0.11) | |
| CS3 | −69.68 | −88.13 | −63.69 | −67.04 | −67.77 | −61.16 |
| (1.05). | (4.94) | (4.94) | (0.21) | (0.11) | (7.47) | |
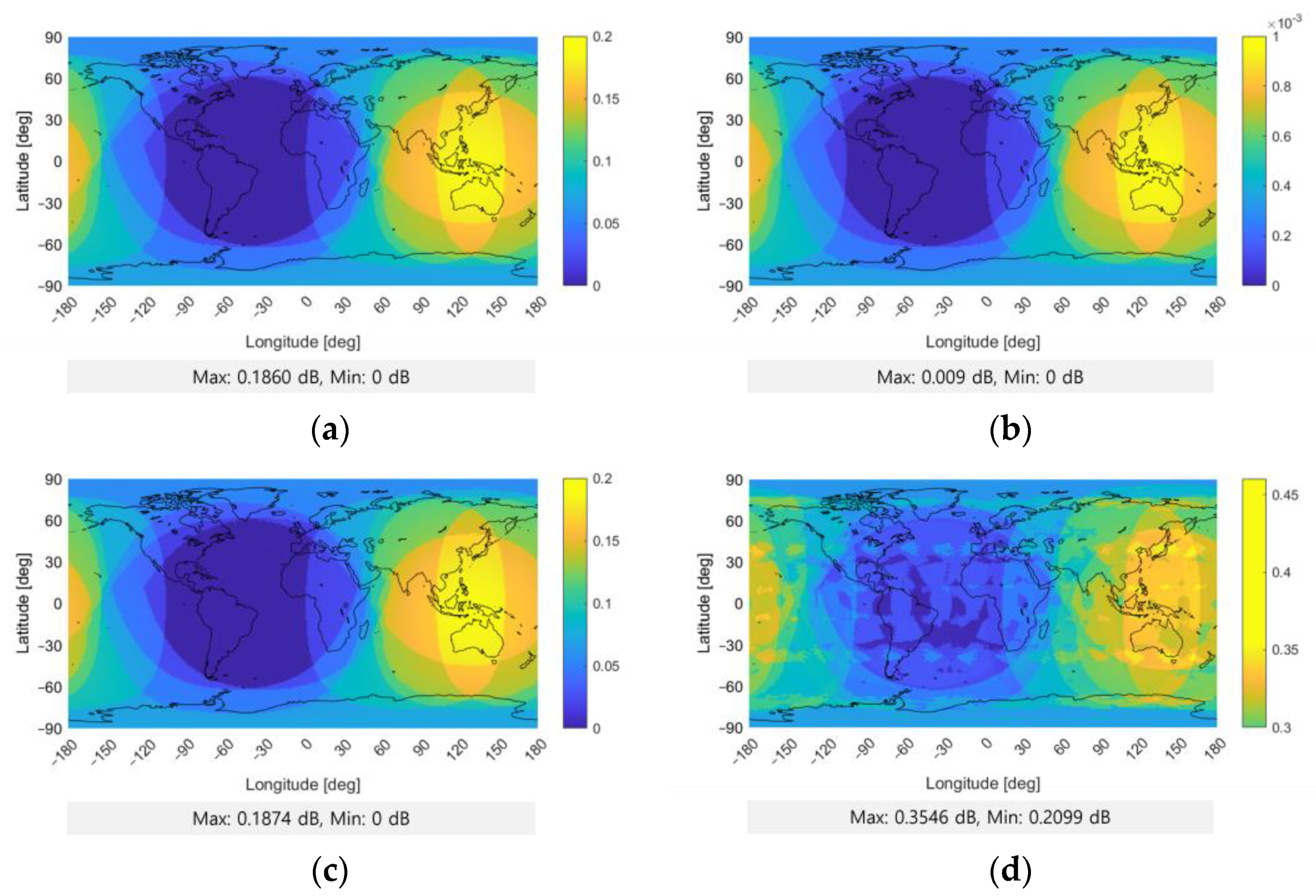
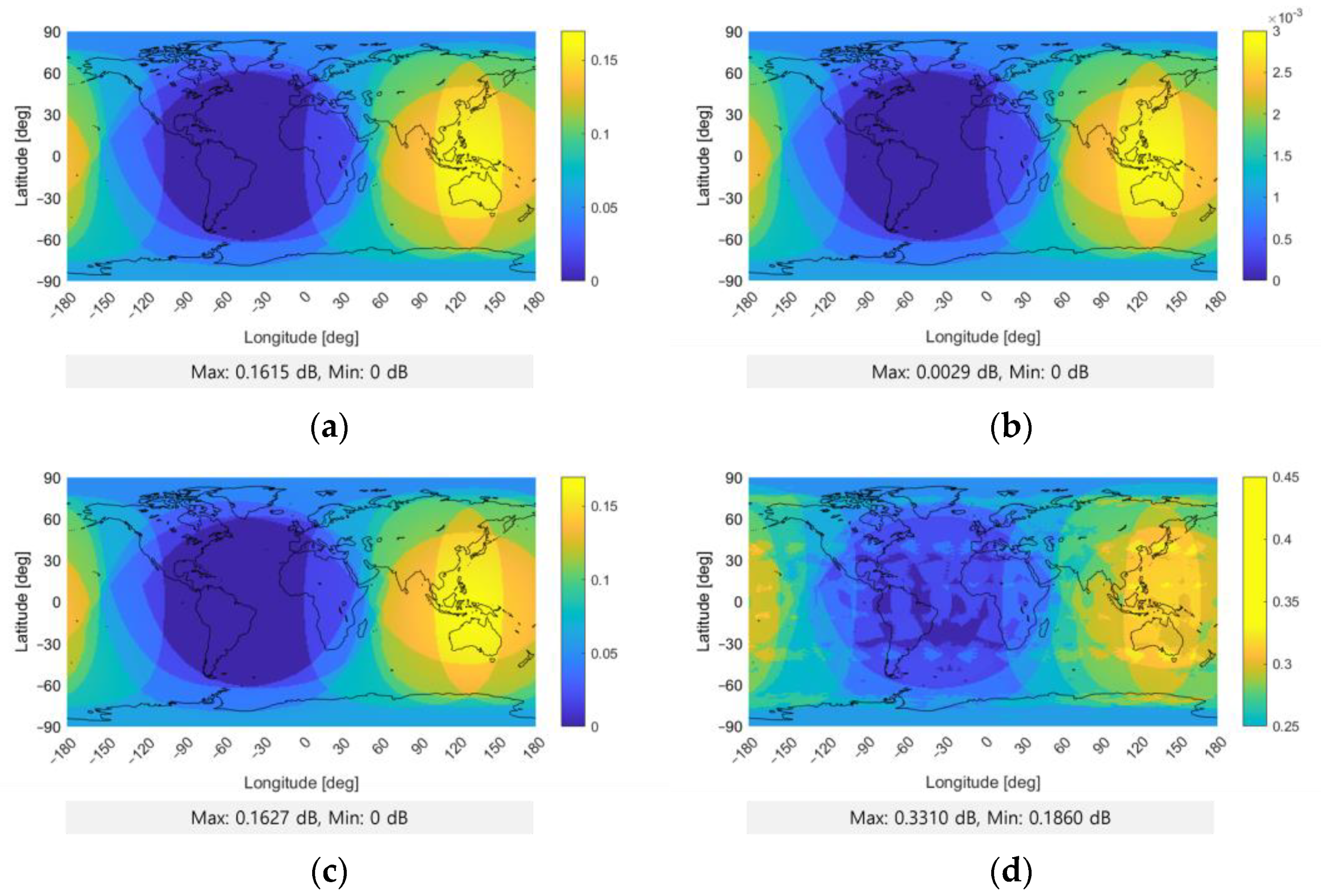
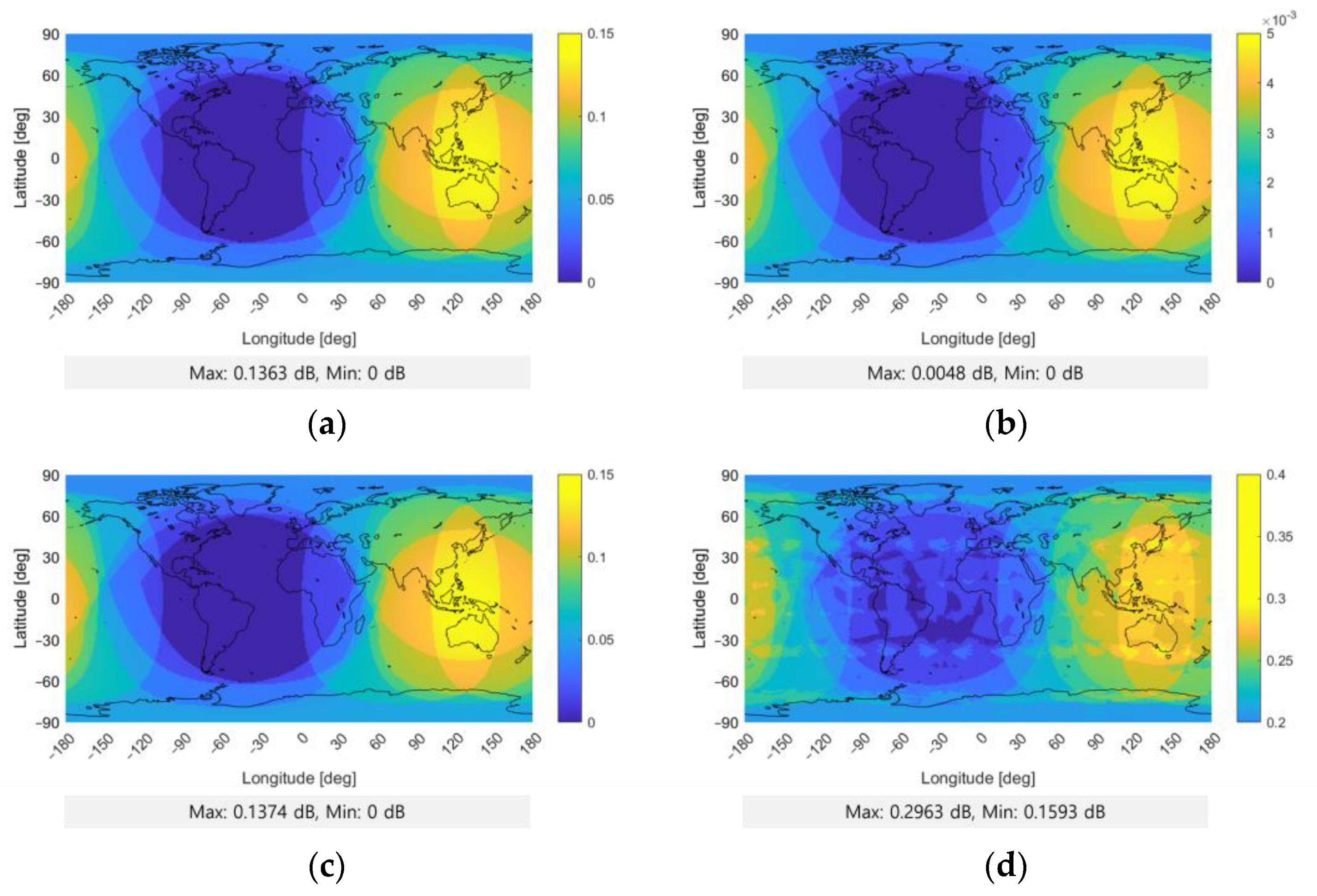
| Scenario | [dB] | | | |
|---|---|---|---|
| Analytical ) | Numerical ) | ||
| 1 | 0.19 | 0.17 | 0.02 |
| 2 | <0.01 | <0.01 | 0.00 |
| 3 | 0.19 | 0.17 | 0.02 |
| 4 | 0.35 | 0.33 | 0.02 |
| 5 | 0.16 | 0.15 | 0.01 |
| 6 | <0.01 | <0.01 | 0.00 |
| 7 | 0.16 | 0.14 | 0.02 |
| 8 | 0.33 | 0.31 | 0.02 |
| 9 | 0.14 | 0.10 | 0.04 |
| 10 | <0.01 | <0.01 | 0.00 |
| 11 | 0.14 | 0.36 | 0.22 |
| 12 | 0.30 | 0.43 | 0.13 |
| Classification | Parameter | Value | Unit |
|---|---|---|---|
| Simulation | Time | 60 | s |
| Start time of week | 24,492 | s | |
| User latitude | 37.4505 | deg | |
| User longitude | 126.6575 | deg | |
| User height | 113.2995 | m | |
| Tx | USRP model | NI-2944R | - |
| Analog gain | 30 | dB | |
| Digital gain | 50 | dB | |
| Sapling rate | 40 | MHz | |
| IF | 10 | MHz | |
| Rx | USRP model | NI-2950R | - |
| Analog gain | 0 | dB | |
| Digital gain | 0 | dB | |
| Sampling rate | 40 | MHz | |
| IF | 10 | MHz |
| Case | [dB] | Blue–Orange | |
|---|---|---|---|
| No Interference Signal (Blue) | With Interference Signal (Orange) | ||
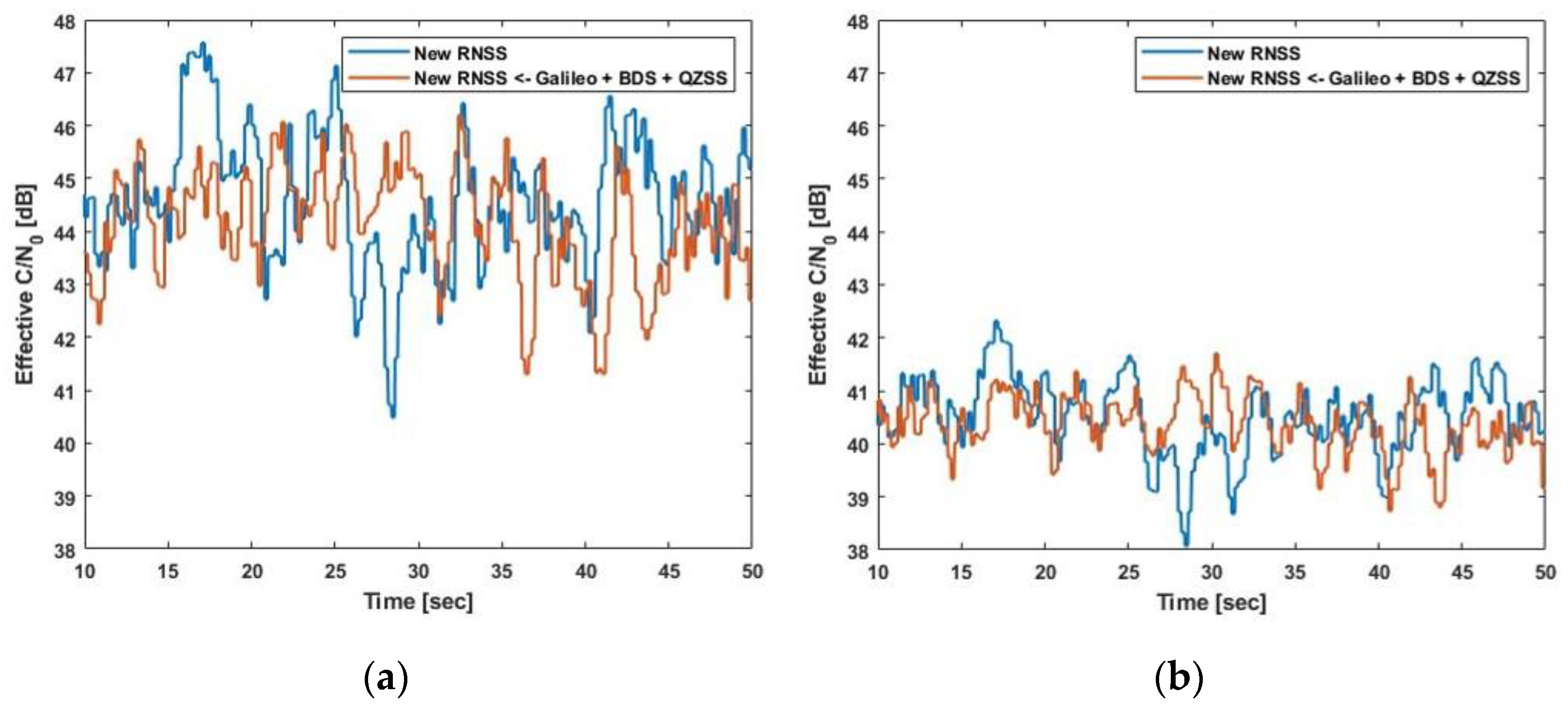
| PRN 4 | 44.5990 | 44.1386 | 0.4604 |
| PRN 6 | 40.5098 | 40.3733 | 0.1365 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.; Han, K.; Won, J.-H. Assessment of Radio Frequency Compatibility for New Radio Navigation Satellite Service Signal Design in the L6-Band. Remote Sens. 2024, 16, 319. https://doi.org/10.3390/rs16020319
Lee S, Han K, Won J-H. Assessment of Radio Frequency Compatibility for New Radio Navigation Satellite Service Signal Design in the L6-Band. Remote Sensing. 2024; 16(2):319. https://doi.org/10.3390/rs16020319
Chicago/Turabian StyleLee, Subin, Kahee Han, and Jong-Hoon Won. 2024. "Assessment of Radio Frequency Compatibility for New Radio Navigation Satellite Service Signal Design in the L6-Band" Remote Sensing 16, no. 2: 319. https://doi.org/10.3390/rs16020319
APA StyleLee, S., Han, K., & Won, J. -H. (2024). Assessment of Radio Frequency Compatibility for New Radio Navigation Satellite Service Signal Design in the L6-Band. Remote Sensing, 16(2), 319. https://doi.org/10.3390/rs16020319





