Tracking-by-Detection Algorithm for Underwater Target Based on Improved Multi-Kernel Correlation Filter

Abstract

Joint detection and tracking of weak underwater targets are challenging problems whose complexity is intensified when the target is disturbed by reverberation. In the low signal-to-reverberation ratio (SRR) environment, the traditional detection and tracking methods perform poorly in tracking robustness because they only consider the target motion characteristics. Recently, the kernel correlation filter (KCF) based on target features has received lots of attention and gained great success in visual tracking. We propose an improved multi-kernel correlation filter (IMKCF) tracking-by-detection algorithm by introducing the KCF into the field of underwater weak target detection and tracking. It is composed of the tracking-by-detection, the adaptive reliability check, and the re-detection modules. Specifically, the tracking-by-detection part is built on the multi-kernel correlation filter (MKCF), and it uses multi-frame data weighted averaging to update. The reliability check helps keep the tracker from corruption. The re-detection module, integrated with a Kalman filter, identifies target positions when the tracking is unreliable. Finally, the experimental data processing and analysis show that the proposed method outperforms the single-kernel methods and some traditional tracking methods.

1. Introduction

Underwater target detection and tracking in active sonar systems has always been a hot topic in underwater applications. The conventional approach to detect and track underwater targets involves threshold detection, followed by data association and filtering tracking [1,2,3,4]. However, practical sonar systems often encounter strong reverberation interference. In this low signal-to-reverberation ratio (SRR) environment, only setting a lower threshold can ensure that the target is not missed, but it also causes a lot of false alarms [5,6]. The higher false alarm rate adversely affects target associations, thereby increasing the risk of tracker drift during the tracking process.

In order to solve the problem of weak target detection and tracking in low SRR, the methods commonly used at present can be categorized into three groups. The first group involves traditional data association methods, such as joint probabilistic data association (JPDA) [7,8] and multiple hypothesis tracking (MHT) [9,10]. However, these approaches suffer from high computational costs when confronted with a high false alarm rate. The second group focuses on methods based on random finite set (RFS) [11,12], which eliminate the need for data association. These methods employ filtering techniques based on the motion characteristics of the target. A crucial aspect of accurate tracking filtering is establishing an appropriate motion model that aligns with the target’s motion type. The filtering algorithms with multiple models (MMs) and the jump Markov system (JMS) have been shown to be effective approaches for maneuvering target tracking [13,14,15]. In addition, Yue et al. established a multi-directional motion model set according to the motion characteristics of the diver target [16]. However, due to the diverse underwater target motion types, it is challenging to apply a single modeling method to all underwater targets of interest. Furthermore, in environments with reverberation interference, the aforementioned tracking methods face difficulties in accurately determining the target’s position solely based on trajectory information. The third group involves deep learning methods, such as Convolutional Neural Network (CNN) [17], Recurrent Neural Network (RNN) [18], and Siamese Network [19]. These approaches typically require a substantial number of samples for model training. However, in practical applications, it may not be feasible to collect a sufficient amount of sample data.

Nevertheless, the kernel correlation filter (KCF) algorithm, proposed by Joao F. Henriques et al., presents a promising solution for tracking multiple target types without the need for predefined target motion models [20,21]. Presently, the KCF algorithm is primarily used in the visual tracking field [22], and there has been no prior instance of its application in underwater target tracking domestically or internationally. Hence, the primary contribution of this study lies in the application of the KCF algorithm to resolve the detection and tracking challenges associated with underwater weak targets.

The effectiveness of single-feature-based tracking is limited due to the absence of prior knowledge about the target in the model-free kernelized correlation filter (KCF) algorithm [23,24,25,26]. To enhance robustness in tracking, researchers have explored multi-feature fusion tracking methods [27,28,29,30], which leverage a shared kernel function with multiple complementary features. However, these methods face challenges in achieving the optimal solution because different features may require distinct kernel functions. To adaptively use multiple complementary features, Tang et al. introduced multi-kernel learning (MKL) into the correlation filtering algorithm to dynamically update multiple nonlinear kernels, namely the multi-kernel correlation filter (MKCF) [31]. However, the MKCF algorithm only utilizes adjacent frame information for filter updates, which could lead to model update errors in the presence of reverberation occlusion. The second contribution of this paper is to utilize weighted information from historical samples to adaptively solve the parameters of multiple nonlinear kernels and make full use of multiple complementary features to enhance the robustness and tracking accuracy of the long-term tracking process.

In scenarios with low SRR, the involvement of non-target information in training frames may result in error propagation during the model update phase, increasing the risk of drift. Thus, it becomes crucial to assess the reliability of tracking results and identify a more dependable result when the tracking outcome is unreliable.

In terms of assessing the reliability of tracking results, Bolme [32] computed the peak-to-sidelobe ratio (PSR) score of the relevant response, comparing it with a fixed threshold to determine reliability. However, this method exhibited limited effectiveness in complex environments. Wang et al. (their tracker is abbreviated as RRLT) [33] proposed a more effective reliability criterion for evaluating the confidence of the current tracking result. This criterion adaptively updates the mean value of multi-frame PSR scores as a threshold, thereby improving the accuracy of evaluation results in complex environments. Regarding tracking methods, the long-term correlation tracker (LCT) employs an online random fern classifier to generate potential target locations [34], while Wang [33] utilizes a particle filter to generate numerous candidate target positions around the previous frame’s target position. Nonetheless, neither LCT nor the random RRLT tracker can successfully re-detect a target that has been obscured for an extended period [35]. The third contribution of this paper entails a real-time assessment of target tracking result reliability and proposes an effective re-detection module. The reliability check module adopts the approach outlined by Wang et al. [33] to evaluate the reliability of both detection and tracking results obtained using the MKCF. When the tracking result is deemed unreliable, the re-detection module utilizes the historical reliability tracking result to drive the Kalman filter, predicting the target candidate position. Subsequently, several candidate positions are generated around this predicted position, following a Gaussian distribution. Finally, a stringent replacement criterion is applied to determine the final tracking result.

In summary, this paper presents an improved multi-kernel correlation filter (IMKCF) algorithm for robust detection and tracking of weak underwater targets. A novel adaptation of the KCF algorithm from visual tracking to the domain of underwater multi-motion weak target detection and tracking is proposed. To address the issue of limited robustness in single-feature tracking, the weighted information from historical samples is utilized to adaptively resolve the coefficients of multiple nonlinear kernels. The MKCF algorithm is analyzed from a maximum likelihood perspective to determine the target position based on the maximum likelihood criterion. Real-time estimation of the target tracking result reliability is performed, and an effective re-detection module is introduced. The efficacy of the algorithm is validated through the analysis of sea trial data.

The rest of this article is organized as follows: Section 2 introduces the target model and sonar measurement model. Section 3 reviews the KCF algorithm. Section 4 introduces the framework of the IMKCF tracking-by-detection algorithm and introduces the components of each module in detail. Section 5 analyzes the performance of the algorithm by processing experimental data. Section 6 summarizes the work of this paper.

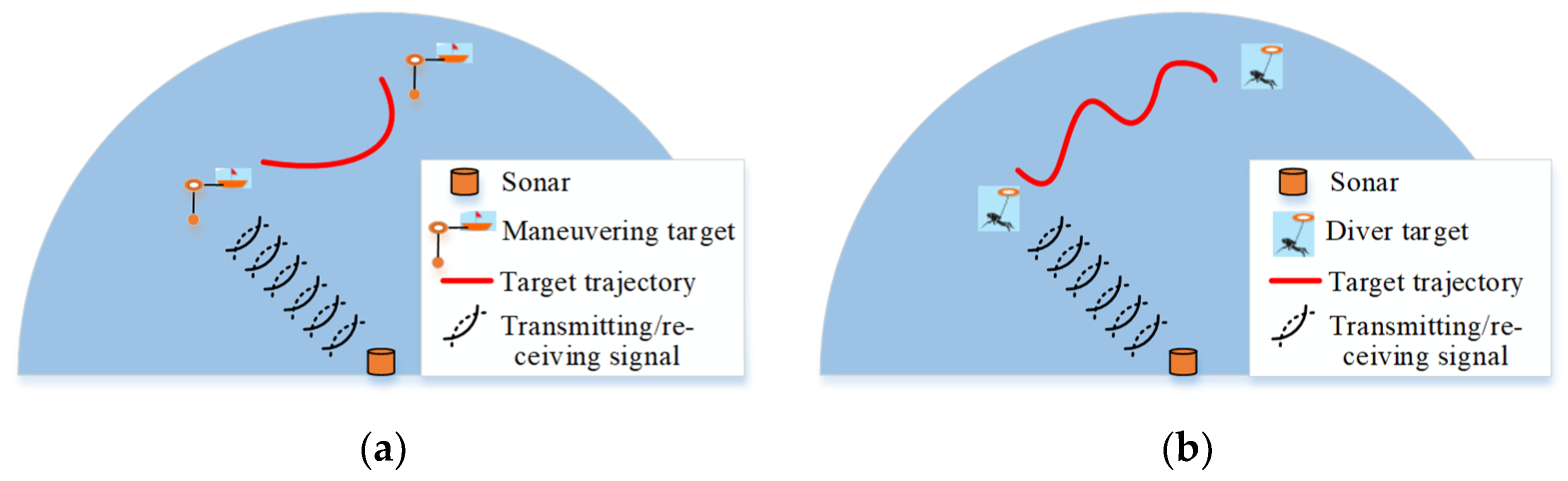
2. Model Establishment

2.1. Target Model

Given the position of the target $x^k$ at time $k$ denoted by $x_{p_k}$ and $y_{p_k}$, and the corresponding velocities $v_{x_k}$ and $v_{y_k}$, the state of the target can be represented by $x^k=\left[x_{p_k},y_{p_k},v_{x_k},v_{y_k}\right]$. The evolution of $x^k$ is formulated as a first-order Markov process,

$$x^{k\left|k-1\right.}=p\left(x^k\left|x^{k-1}\right.\right)$$

(1)

where the $p$ is the a priori probability density function. The specific form of $p$ is determined by the target model.

2.2. Measurement Model

The algorithm employs raw sonar data measurements in range-azimuth format. When the influence of noise is disregarded, the correlation between the range, angle of the sonar, and position of the target is established.

$$\left\{\begin{array}{l}{r}_k=\sqrt{x_{p_k}^2+y_{p_k}^2}\\ {\theta }_k=\arctan \left(\frac{x_{p_k}}{y_{p_k}}\right).\end{array}\right.$$

(2)

At time $k$, the resolution of the measurement area is $N_r\times N_b$. With the sonar position serving as the reference point or origin, the measurement area is characterized by a distance range $\left[R_{min},R_{max}\right]$, which is discretized into $N_r$ distance units, and an azimuth range $\left[{\theta }_{min},{\theta }_{max}\right]$, which is discretized into $N_b$ azimuth units.

$$N_r=\frac{2\left(R_{max}-R_{min}\right)}{c}\times F_s,$$

(3)

where $F_s$ is the sampling frequency, and $N_b$ can be determined by the azimuth resolution unit $∆\theta$. The element $z_k\left(x,y\right)$ of the $x\mathrm{t}\mathrm{h}$ azimuth and $y\mathrm{t}\mathrm{h}$ distance cell in the measurement $z_k$ is the signal echo intensity. $z_k\left(x,y\right)$ can be modeled as

$$z_k\left(x,y\right)=\left\{\begin{array}{l}{a}_{k}h\left(x,y;{\mathit{x}}_k\right)+{\mathit{w}}_k\mathrm{if}\mathrm{target}\mathrm{is}\mathrm{in}\left(x,y\right)\\ {\mathit{w}}_k\mathrm{otherwise}\hfill \end{array}\right.,$$

(4)

where $a_k$ is the peak amplitude of the target, $h$ is the point spread function, and ${\mathit{w}}_k$ is the measured noise and reverberation of the sonar system at moment $k$.

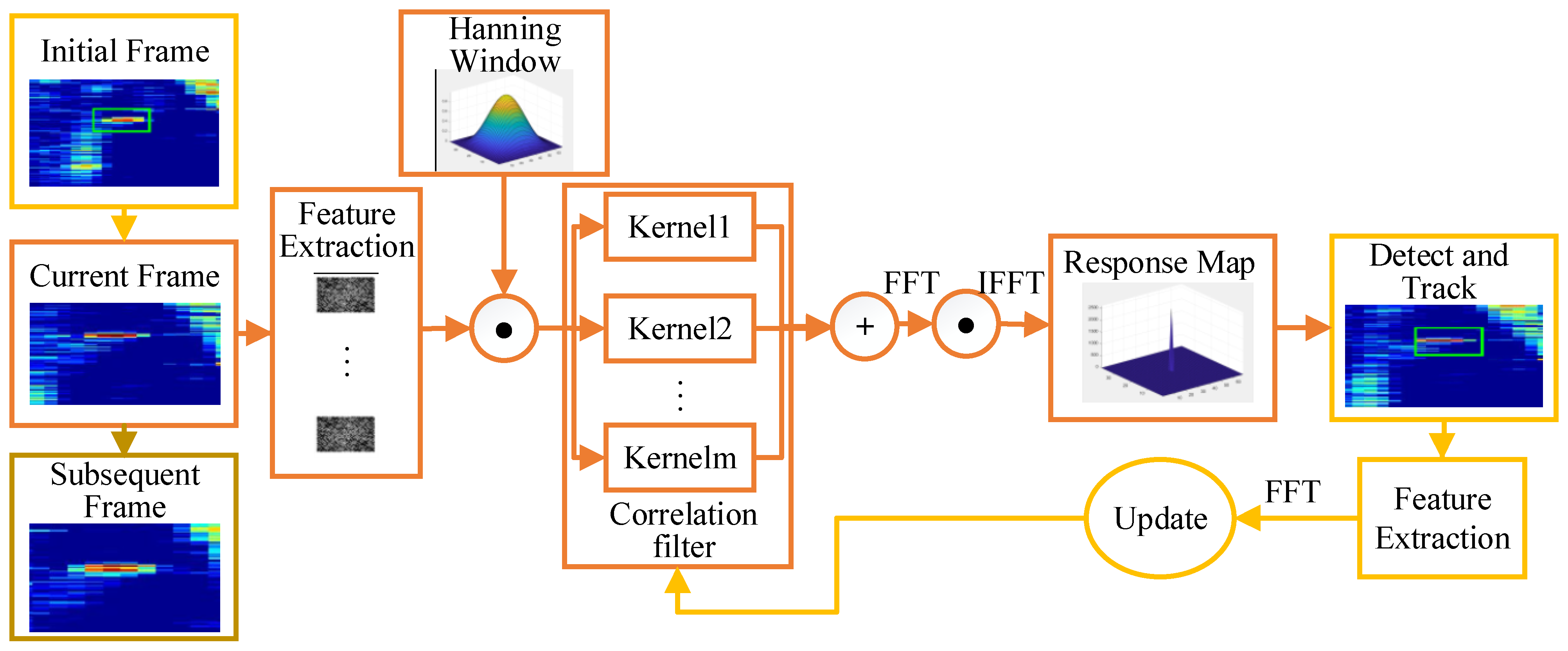
3. Preliminaries of the KCF Algorithm

The KCF algorithm involves three steps: training, detection, and updating. In the training step, it aims to optimize the correlation filter parameter using the training feature–label pairs ${{\{\mathit{x}}_i,y_i\}}_{i=1}^m$. It maps the input $\mathit{x}$ to a new space $\phi \left(\mathit{x}\right)$ with higher dimensions and puts the $\phi \left(\mathit{x}\right)$ into the optimization process. The kernel function $\kappa$ and the objective of optimization are as follows.

$$\kappa \left({\mathit{x}}_i,{\mathit{x}}_j\right)=〈\phi \left({\mathit{x}}_i\right),\phi \left({\mathit{x}}_j\right)〉.$$

(5)

$$\underset{w}{\min }{\displaystyle \sum _{i=1}^m{\left(y_i-{\displaystyle \sum _{j=1}^m{a}_j\kappa \left({\mathit{x}}_i,{\mathit{x}}_j\right)}\right)}^2+\lambda {‖\mathit{w}‖}^2},$$

(6)

where $\mathit{w}$ is defined as

$$\mathit{w}={\displaystyle \sum _{i=1}^m{a}_i\phi \left({\mathit{x}}_i\right)}.$$

(7)

The solution of (6) is given by employing the circulant structure for fast training and testing,

$$\mathit{\alpha }=F^{-1}\left(\frac{F\left(\mathbf{Y}\right)}{F^{*}\left({\mathbf{K}}_{xx}\right)+\lambda }\right),$$

(8)

where the * indicates the complex conjugate, and $F$ and $F^{-1}$ denote the Fourier transform and the inverse, respectively. ${\mathbf{K}}_{\mathit{x}\mathit{x}}$ denotes kernel matrix.

In the detection step, we can compute the probability of a new input $\mathit{z}$ being from the target feature.

$${\mathbf{Y}}^{\prime }=F^{-1}\left(F*\left({\mathbf{K}}_{xz}\right)F\left(\mathit{\alpha }\right)\right).$$

(9)

In the updating step, the reference feature $\mathit{x}$ and the correlation filter parameters are calculated as follows

$${\mathit{x}}_t={\mathit{z}}_t\times \eta +\left(1-\eta \right)\times {\mathit{x}}_{t-1},$$

(10)

$${\mathit{\alpha }}_t={\mathit{\alpha }}_{z_t}\times \eta +\left(1-\eta \right)\times {\mathit{\alpha }}_{t-1},$$

(11)

where $\eta$ is the learning rate.

As above, the KCF can be performed on general machines due to its high computational efficiency. However, the performance of KCF is related to the features extracted. Making full use of multiple complementary features can improve tracking accuracy and robustness. Therefore, in our proposed algorithm, to avoid the interference of different features in the single kernel, we use MKCF to assign a kernel for each feature.

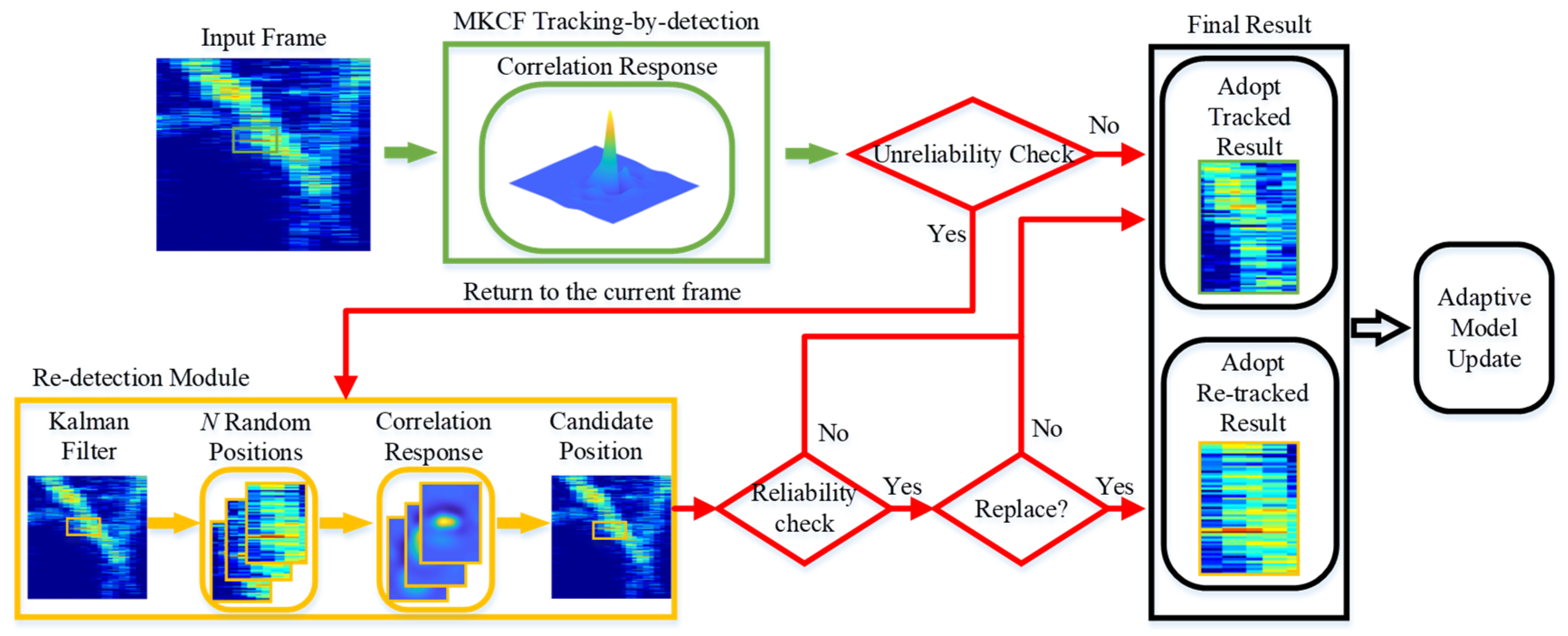
4. Improved MKCF Tracking-by-Detection

This study aims to tackle the challenge of detecting and tracking weak targets with various motion types in shallow sea environments. We propose an IMKCF tracking-by-detection algorithm, which consists of three components: the MKCF tracking-by-detection, the adaptive reliability check, and the re-detection modules. The overall framework of the proposed approach is depicted in Figure 1.

4.1. The MKCF Tracking-by-Detection

Studies have shown that the incorporation of multiple kernels can improve the discriminatory ability of classifiers in comparison to a single-kernel approach [36]. A prevalent approach is to employ a basis kernel, $k_m\left(m=1,\cdots ,M\right)$, and then view $k\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\mathbf{b}}^{\mathrm{T}}\mathbf{k}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$ as a composition of the basis kernels, where $\mathbf{k}\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)={\left(k_1({\mathbf{x}}_i,{\mathbf{x}}_j),\cdots ,k_M({\mathbf{x}}_i,{\mathbf{x}}_j)\right)}^{\mathrm{T}}$, $\mathbf{b}={\left(b_1,\cdots ,b_m\right)}^{\mathrm{T}}$, $\sum _{m=1}^M{b}_m=1$, and $b_m\ge 0$. Therefore $\mathbf{K}=\sum _{m=1}^M{b}_m{\mathbf{K}}_m$, ${\mathbf{K}}_m$ is the base core of group $m$, whose elements are $k_{ij}^m=k_m\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$. The optimization problem is used to minimize the loss,

$$\begin{array}{l}\underset{\mathit{\alpha },b}{\min }\frac{1}{2}{‖y-{\displaystyle \sum _{m=1}^M{b}_m{{\rm K}}_m\mathit{\alpha }}‖}_2^2+\frac{\mathit{\lambda }}{2}{\mathit{\alpha }}^{\mathrm{T}}{\displaystyle \sum _{m=1}^M{b}_m{{\rm K}}_m\mathit{\alpha }}=\underset{\mathit{\alpha },b}{\min }F\left(\mathit{\alpha },b\right)\\ \mathrm{s}.\mathrm{t}.{\displaystyle \sum _{m=1}^M{b}_m}=1,b_m\ge 0,m=1,\cdots ,M\end{array}.$$

(12)

The optimal solution can be expressed as Equation (13), and the * indicates the optimal.

$$f^{*}\left(x\right)={\displaystyle \sum _{i=0}^{l-1}{\alpha }_i{b}^{\mathrm{T}}k\left(x_i,x\right)}.$$

(13)

The diagram of the MKCF tracking-by-detection algorithm is presented in Figure 2.

In order to achieve localization robustness, the MKCF tracking-by-detection algorithm uses the weighted average of historical samples to update the training coefficients $\mathit{\alpha }$ and $\mathit{b}$. The optimization function is represented by

$$F_p\left({\mathit{\alpha }}_p,b_p\right)\equiv \frac{1}{2}{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{m=1}^M{\beta }_m^j{u}_{F\left(\mathit{\alpha },b\right)}^{j,m}}},$$

(14)

where ${\beta }^j$ is the weight of the sample optimization function of the $j\mathrm{t}\mathrm{h}$ frame, $u_{F\left(\mathit{\alpha },\mathbf{b}\right)}^{j,m}={‖{\mathbf{y}}_c-b_{m,p}{\mathbf{K}}_m^j{\mathit{\alpha }}_p‖}_2^2+\lambda b_{m,p}{\mathit{\alpha }}_p^{\mathrm{T}}{\mathbf{K}}_m^j{\mathit{\alpha }}_p$,$j=2,\cdots ,p$,${\beta }_m^1={\left(1-{\gamma }_m\right)}^{p-1}$,${\beta }_m^j={\gamma }_m{\left(1-{\gamma }_m\right)}^{p-j}$,${\mathit{\alpha }}_p={\left({\alpha }_{0,p},\cdots {,\alpha }_{l-1,p}\right)}^T$, ${\mathbf{b}}_p={\left(b_{1,p},\cdots {,b}_{M,p}\right)}^T$, $\sum _{m=1}^M{b}_{m,p}=1$, $p$ is the number of historical frames, ${\gamma }_m\in \left(\mathrm{0,1}\right)$ is the learning rate, and ${\mathbf{K}}_m^j$ is the Gram matrix of kernel $m$. The new optimization problem is

$$\begin{array}{l}\underset{{\mathit{\alpha }}_p,b_p}{\min }{F}_p\left({\alpha }_p,b_p\right)\\ \mathrm{s}.\mathrm{t}.{\displaystyle \sum _{m=1}^M{d}_{m,p}}=1\\ d_{m,p}\ge 0,m=1,\cdots ,M.\end{array}$$

(15)

First, given ${\mathbf{b}}_p$ to solve ${\mathit{\alpha }}_p$, the above optimization problem becomes an unconstrained optimization problem. Let ${\nabla }_{{\mathit{\alpha }}_p}{F}_p\left({\mathit{\alpha }}_p,{\mathbf{b}}_p\right)$, then,

$${\mathit{\alpha }}_p={\left({\displaystyle \sum _{j=1}^p{\displaystyle \sum _{m=1}^M{\beta }_m^j\left({\left(b_{m,p}{K}_m^j\right)}^2+\lambda b_{m,p}{K}_m^j\right)}}\right)}^{-1}\cdot {\displaystyle \sum _{j=1}^p{\displaystyle \sum _{m=1}^M{\beta }_m^j{b}_{m,p}{K}_m^j{y}_c}}.$$

(16)

The efficient evaluation can be achieved through the utilization of FFT.

$$A_p\equiv F\left({\mathit{\alpha }}_p\right)=\frac{{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{m=1}^M{\beta }_m^{j}F\left(b_{m,p}{k}_m^j\right)\odot F\left(y_c\right)}}}{{\displaystyle \sum _{j=1}^p{\displaystyle \sum _{m=1}^M{\beta }_m^{j}F\left(b_{m,p}{k}_m^j\right)\odot \left(F\left(b_{m,p}{k}_m^j\right)+\lambda \right)}}}.$$

(17)

Set

$$A_p=\frac{A_p^N}{A_p^D}=\frac{{\displaystyle \sum _{m=1}^M{A}_{m,p}^N}}{{\displaystyle \sum _{m=1}^M{A}_{m,p}^D}}.$$

(18)

when $p=1$,

$$\begin{array}{l}{A}_{m,1}^N=F\left(b_{m,1}{k}_m^1\right)\odot F\left(y_c\right)\\ A_{m,1}^D=F\left(b_{m,1}{k}_m^1\right)\odot \left(F\left(b_{m,1}{k}_m^1\right)+\lambda \right).\end{array}$$

(19)

when $p>1$,

$$\begin{array}{l}{A}_{m,p}^N=\left(1-{\gamma }_m\right)A_{m,p-1}^N+{\gamma }_{m}F\left(b_{m,p}{k}_m^p\right)\odot F\left(y_c\right)\\ A_{m,p}^D=\left(1-{\gamma }_m\right)A_{m,p-1}^D+{\gamma }_{m}F\left(b_{m,p}{k}_m^p\right)\odot \left(F\left(b_{m,p}{k}_m^p\right)+\lambda \right).\end{array}$$

(20)

The optimal solution ${\alpha }_p^{*}$ can be attained by means of the aforementioned iteration. Subsequently, when presented with the task of solving ${\mathbf{b}}_p$ given ${\mathit{\alpha }}_p$, the optimization problem outlined earlier transforms into a constrained optimization problem. To address this issue, we initially posit it as an unconstrained optimization problem and subsequently demonstrate that the resulting solution ${\mathbf{b}}_p$ conforms to the prescribed constraint conditions. Let ${\nabla }_{{\mathbf{b}}_p}{F}_p\left({\mathit{\alpha }}_p,{\mathbf{b}}_p\right)$, then,

$$b_{m,p}=\frac{{\displaystyle \sum _{j=1}^p{\beta }_m^j{\left(K_m^j{\mathit{\alpha }}_p\right)}^{\mathrm{T}}\left(2y_c-\lambda {\mathit{\alpha }}_p\right)}}{2{\displaystyle \sum _{j=1}^p{\beta }_m^j{\left(K_m^j{\mathit{\alpha }}_p\right)}^{\mathrm{T}}\left(K_m^j{\mathit{\alpha }}_p\right)}},$$

(21)

where $m=1,\cdots ,M$, let

$$b_{m,p}=\frac{b_{m,p}^N}{b_{m,p}^D}.$$

(22)

when $p=1$,

$$\begin{array}{l}{b}_{m,p}^N=\left(1-{\gamma }_m\right)b_{m,p-1}^N+{\gamma }_m{\left(K_m^p{\mathit{\alpha }}_p\right)}^{\mathrm{T}}\left(2y_c-\lambda {\mathit{\alpha }}_p\right)\\ b_{m,p}^D=\left(1-{\gamma }_m\right)b_{m,p-1}^D+2{\gamma }_m{\left(K_m^p{\mathit{\alpha }}_p\right)}^{\mathrm{T}}\left(K_m^p{\mathit{\alpha }}_p\right)\end{array}.$$

(23)

when $p>1$,

$$\begin{array}{l}{b}_{m,1}^N={\left(K_m^1{\mathit{\alpha }}_1\right)}^{\mathrm{T}}\left(2y_c-\lambda {\mathit{\alpha }}_1\right)\\ b_{m,1}^D=2{\left(K_m^1{\mathit{\alpha }}_1\right)}^{\mathrm{T}}\left(K_m^1{\mathit{\alpha }}_1\right)\end{array}.$$

(24)

The FFT method enables the rapid calculation of ${\mathbf{K}}_m^p{\mathit{\alpha }}_p$ as $F^{-1}\left(F^{\mathrm{*}}\left({\mathbf{k}}_m^p\right)⨀F\left({\alpha }_p\right)\right)=F^{-1}\left(F^{\mathrm{*}}\left({\mathbf{k}}_m^p\right)⨀A_p\right)$. Subsequently, the optimal solution can be attained through the aforementioned iteration. Finally, the solution is verified to conform to the prescribed constraint conditions.

The kernel function employed in this algorithm utilizes a Gaussian kernel, and the elements within the kernel matrix can be computed using the following formula,

$$k_m\left(x_i,x_j\right)=\exp \left(-\frac{1}{{\sigma }_k^2}\left({‖x_i-x_j‖}^2\right)\right).$$

(25)

The exponent within the exponential function $\mathrm{e}\mathrm{x}\mathrm{p}\left(·\right)$ used in this study is determined by the negative normalized Euclidean distance between ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$. The higher the similarity between ${\mathbf{x}}_i$ and ${\mathbf{x}}_j$ in Euclidean space, the greater the value of $k_m\left({\mathbf{x}}_i,{\mathbf{x}}_j\right)$. This function is commonly known as the likelihood function in filter-based tracking [37]. It enables the calculation of a value that represents the likelihood of the measured real target given any measurement. Based on the maximum likelihood estimation criterion, the target position is estimated by determining the peak position $y_p$ of the correlation response $\mathbf{y}$.

4.2. The Adaptive Reliability Check

In the correlation filter response map, a single peak is observed, and the sharpness of the peak corresponds to the reliability of the tracking result. The work conducted by Bolme [34] has proposed the idea that the peak-to-sidelobe ratio (PSR) possesses the potential to serve as an indicator of the sharpness of the response peak. The PSR is defined as

$$S_p=\frac{\max \left(R_p\right)-{\mu }_p}{{\sigma }_p},$$

(26)

where $R_p$ represents the response map calculated by the correlation filter at frame $p$, and ${\mu }_p$ and ${\sigma }_p$ are the mean and standard deviation of $R_p$, respectively. In cases where the tracking result is unreliable, as exemplified in Figure 3, the response map may exhibit multiple peaks with low values, resulting in a significant decrease in the PSR. Therefore, the PSR can serve as an indicator of tracking result quality to a certain degree.

It is not suitable to pre-define a constant threshold to judge the reliability of the current tracking because the PSR fluctuates between different values due to the uncertainty factor in different scenarios. In order to mitigate the impact of fluctuations in the PSR, we utilize the historical frames to compute the average score to determine the reliability of the tracking results. We combine the PSR values of the historical frames to $C=\left\{S_2,\cdots ,S_{p-1}\right\}$ with the mean of $M$. Furthermore, we introduce a small coefficient ${\tau }_1$, whereby the PSR $S_i$ of the $i\mathrm{t}\mathrm{h}$ frame is stored in $C$ if $S_i<{\tau }_1\cdot M$ and discarded otherwise. Finally, the evaluation criteria of the MKCF algorithm adaptively changes from frame to frame as the average of the multi-frame PSR is computed.

We check the reliability of the tracking result in each frame. The tracking result is deemed unreliable if $S_i<{\tau }_1\cdot M$ (“Unreliability Check” in Figure 1). On the other hand, the tracking result is likely to be reliable if it satisfies $S_i>{\tau }_2\cdot M$ (“Reliability Check” in Figure 1) and the coefficient ${\tau }_2$ is higher than ${\tau }_1$. Once the initial tracking result is determined to be unreliable, the re-detection module is initiated.

4.3. The Re-Detection Module

This section provides an introduction to the re-detection module, which plays a crucial role in generating candidate target locations and determining whether to substitute the initial tracking result with the optimal candidate target location. A key component of this module is the implementation of the Kalman filter, which utilizes reliable tracking results from the current frame for filter updates. Assuming that the motion between adjacent frames adheres to a linear Gaussian distribution as prior knowledge, the motion model in the Kalman filter can be established as a uniform linear motion model.

In cases where the track result is deemed unreliable, the target positions from the last reliable tracking results are saved and used to drive a Kalman filter, providing an estimated position ${position}_p$ for the current target position with the variance in $\psi \left({position}_p\right)$. Subsequently, $N$ random locations $g_j\left(j=1,\cdots ,N\right)$ are generated around the location ${position}_p$, following a Gaussian distribution with the mean ${position}_p$ and the variance $\psi \left({position}_p\right)$. With $g_j$ as the center, $N$ target candidate bounding boxes $B_j$ are generated. For the obtained $B_j$, their response maps $R_p^j$ are generated by Equation (6) and the maximum values of these maps, $q_j={\max }_u{R}_p^j\left(u\right)$, are also computed. Suppose $q_j^{*}$ is the maximum among $\left\{q_1,\dots ,q_N\right\}$. The best candidate bounding box of the target $B_j^{*}$ and the best candidate location of the target $g_j^{*}$ are determined accordingly. Finally, the decision of whether the best candidate location $g_j^{*}$ replaces the initial tracking result is determined through the following two steps.

(1) If it does not meet the reliability check $S_i>{\tau }_2\cdot M$, the initial tracking result is used;

(2) If it meets the reliability check $S_i>{\tau }_2\cdot M$, we compute the correlation response at the initial tracking location, and the highest response value is recorded as $k_p$. If (27) is met, the initial tracking result is replaced with $g_j^{*}$.

$$q_j^{*}\ge \gamma \times k_p,$$

(27)

where $\gamma$ is the penalty parameter, and the * indicates the optimal. If the above equation is not satisfied, the initial tracking result is not replaced.

5. Experimental Results

In this section, we apply the proposed method on two test scenarios and compare it with the traditional tracking methods and the original KCF algorithms. All the algorithms are implemented in MATLAB 2018b, utilizing an Intel i5-6200U CPU with a main frequency of 2.3 GHz and 8 GB of memory. We make a

Table 1. The abbreviations of various algorithms.

Algorithm	Abbreviation
Multiple Hypothesis Tracking	MHT
Joint Probabilistic Data Association	JPDA
Probability Hypothesis Density	PHD
Multi-Feature Kernel Correlation Filter	MF-KCF
Multi-Kernel Correlation Filter	MKCF
Improved Multi-Feature Kernel Correlation Filter	IMF-KCF
Improved Multi-Kernel Correlation Filter	IMKCF

to summarize the abbreviations of various algorithms.

5.1. Evaluation Metrics

Evaluation metrics of performance are discussed below.

(1) Root-mean-square error (RMSE) and precision: the average distance error between the estimated position and the actual position, defined as (28). Given a threshold $M$, the centroid position is properly estimated if its RMSE is less than $M$. The RMSE accuracy is defined as the percentage of the total number of frames for which the location is correctly estimated.

$$\mathrm{RMSE}=\sqrt{{\displaystyle \sum _{i=1}^m\left[{\left({\widehat{x}}_k^i-x_k\right)}^2+{\left({\widehat{y}}_k^i-y_k\right)}^2\right]}/m},$$

(28)

where m is the number of Monte Carlo experiments.

(2) Intersection over union (IOU) and precision: IOU is defined as (29). A larger IOU value indicates a more accurate estimation of the target. Given a threshold $N$, the target box is considered correctly estimated if its IOU is greater than $N$. The IOU accuracy is defined as the percentage of the total number of frames for which the target box is correctly estimated.

$$\mathrm{IOU}=\frac{E\cap G}{E\cup G},$$

(29)

where $E$ denotes the area of the estimated target and $G$ denotes the area of the real target. Operator $\cap$ represents intersection and $\cup$ means the union.

(3) Frames Per Second (FPS): The number of frames processed per second, the greater the FPS; the higher the efficiency of the algorithm.

5.2. Test Scenarios and Parameter Settings

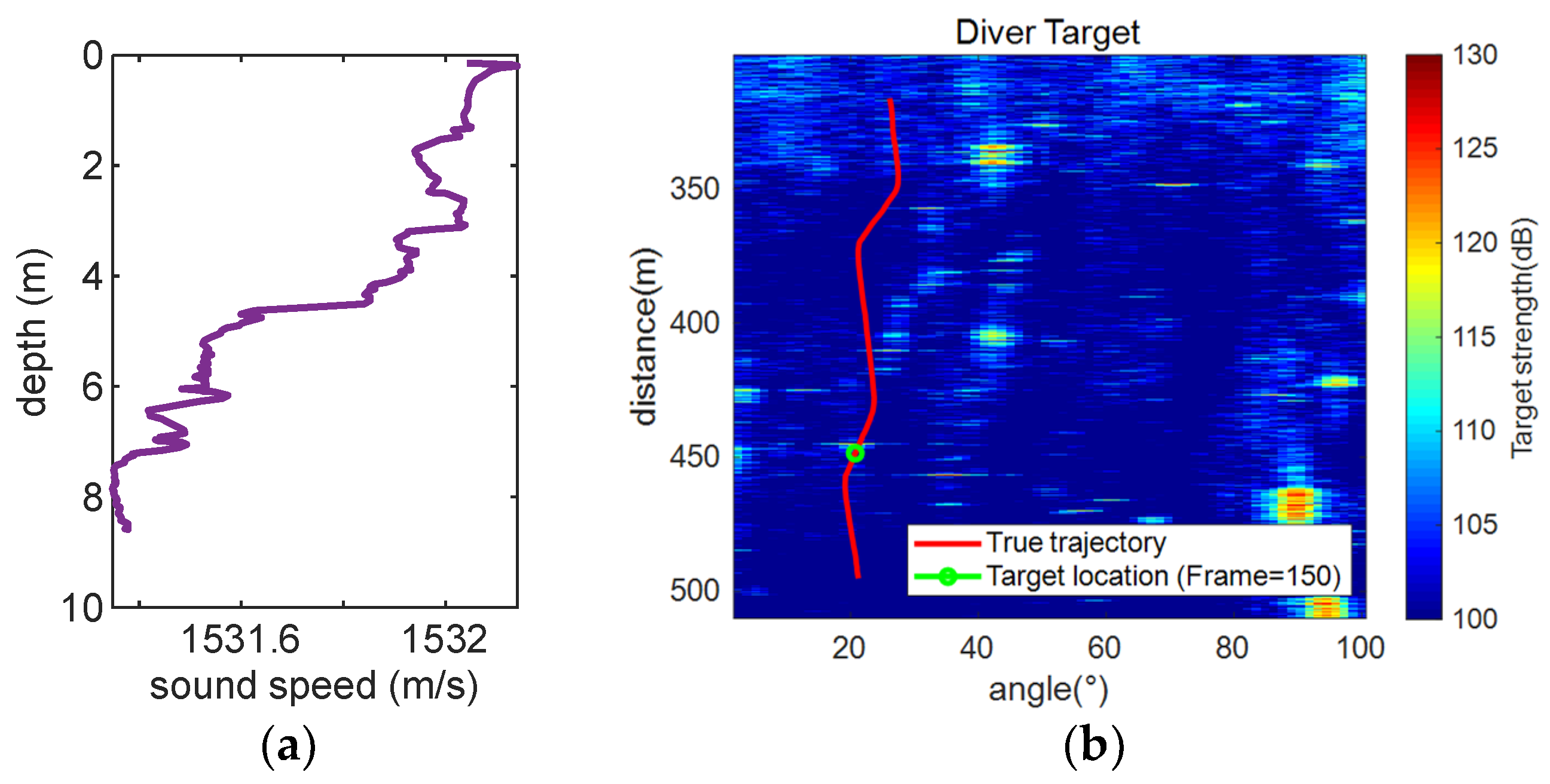
5.2.1. Test Scenarios

In order to verify the effect of the proposed algorithm on tracking targets exhibiting different types of motion, we have designed two scenarios. Notably, both the ball and the diver have equivalent target strength, with the difference lying in their respective motion types. The experiment used a GPS device to record the actual motion trajectory of the target. The GPS device is soft-connected to the target and floats on the ocean directly above the target.

(a) Maneuvering target: As shown in Figure 4a, the small boat drags the ball to perform a turning motion. Figure 5a is the sound speed profile of the experiment. The actual trajectory of the target is plotted in Figure 5b, represented by the red line. Subsequent to the 70th frame, the SRR is lower than 0 dB for the majority of frames within this specific scene.

(b) Diver target: As represented in Figure 4b, the closed diver moves in a Z-shaped manner. The sound speed profile is shown in Figure 6a. The actual trajectory of the target is plotted in Figure 6b, represented by the red line. In this scene, the SRR surpasses 0 dB for the majority of frames, indicating a higher quality data set.

5.2.2. Parameter Settings

In this paper, we use the histogram of oriented gradient (HOG) and invariant moment features. The HOG feature has nine gradient orientations, and the cell size is $4\times 4$. In the KCF, it uses a single Gaussian kernel with parameter $\sigma =0.5$ and the learning factor $\eta =0.01$. It is worth noting that the multi-feature KCF (MF-KCF) trains the tracker based on the above features’ fusion. The MKCF uses two Gaussian kernels with parameters ${\sigma }_1=0.3$ and ${\sigma }_2=0.3$ and learning factors $\eta =0.0175$ and $\eta =0.018$, respectively. Both methods employ a regularization parameter of $\lambda ={10}^{-4}$ [38]. In the adaptive reliability check module, the coefficients ${\tau }_1$ and ${\tau }_2$ are 0.75 and 0.9, respectively.

To address the issue of high-frequency noise caused by abrupt edges in samples after the cyclic shift, this study uses the Hanning window when processing sample features. The application of the Hanning window aids in smoothing boundaries and minimizing interference from background information, consequently enhancing overall tracking accuracy. Furthermore, due to the potential decline in detection and tracking performance associated with an excessive search area in the KCF, it becomes necessary to restrict the size of the search area. Hence, the search area is limited to 2.5 times the size of the target box [39].

5.3. Data Processing and Analysis

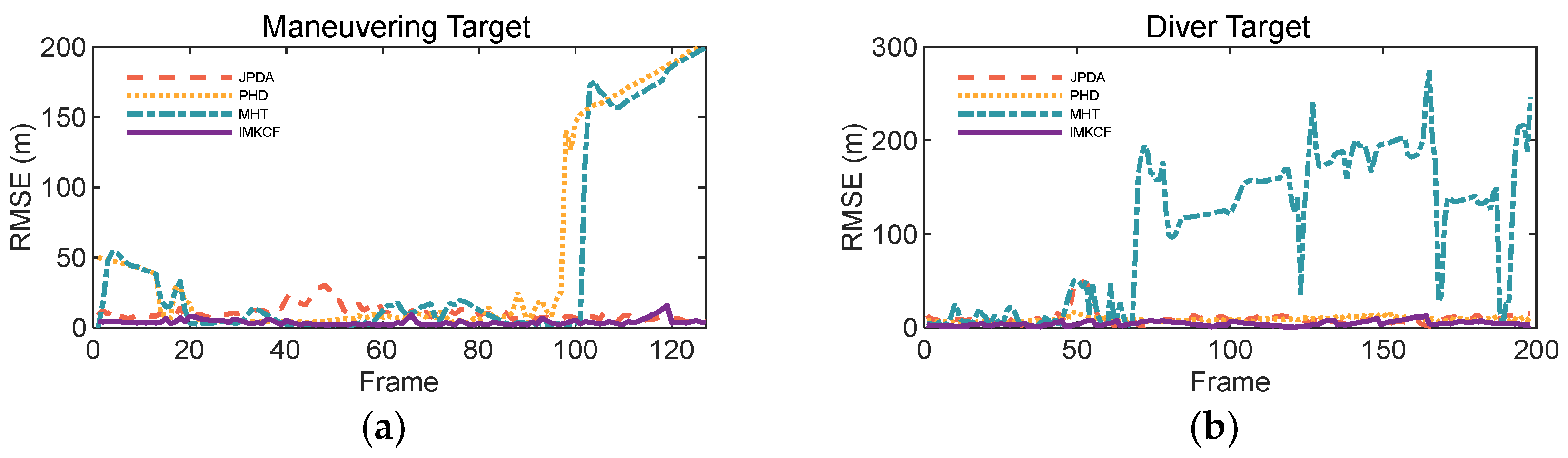
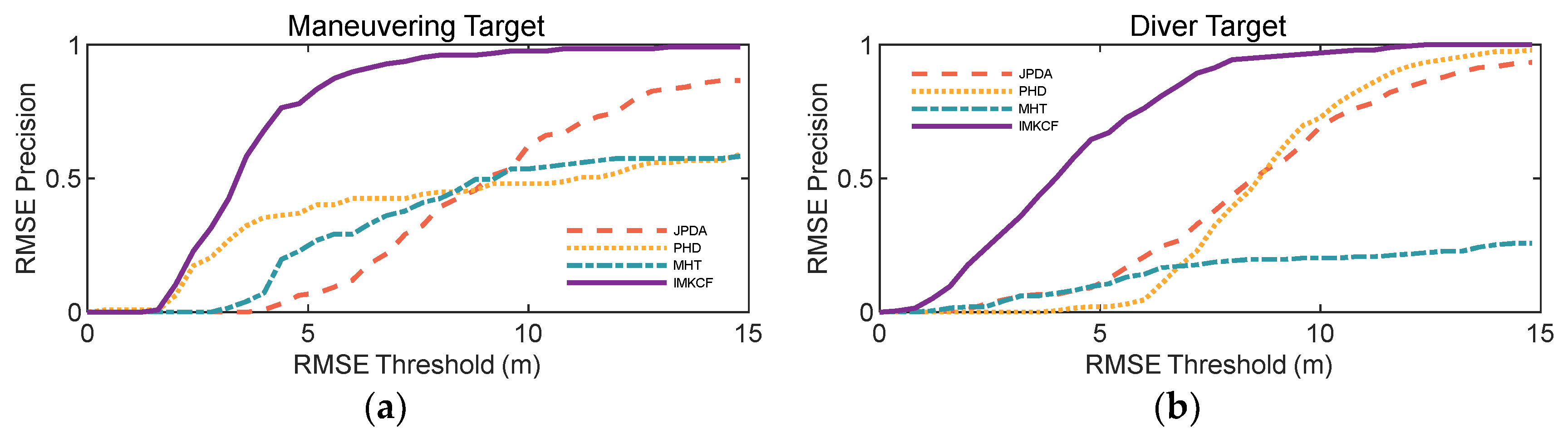
5.3.1. Comparison with Traditional Tracking Algorithms

In this section, a comparison is made between the proposed algorithm and three commonly used algorithms in underwater target detection and tracking: MHT, JPDA, and PHD. To minimize target loss during thresholding, a relatively low threshold is adopted in the data preprocessing stage. It should be noted that this approach can lead to an increased probability of false alarms, resulting in an increased number of false targets, thereby adding difficulties of data association and computational costs.

The outcomes of data processing for maneuvering and diver targets are depicted in Figure 7 and Figure 8. Analysis of these figures reveals that the proposed IMKCF algorithm consistently maintains a relatively low RMSE across the majority of frames in both maneuvering and diver target tracking processes, when compared to the other three algorithms. This superior performance can mainly be attributed to two factors. Firstly, our response map, which is based on target features, effectively identifies target areas. Secondly, the re-detection module with a Kalman filter estimates a reliable target location when the tracking result is deemed unreliable.

As shown in Figure 7, in the tracking of maneuvering targets, the three traditional tracking algorithms perform poorly, particularly the PHD and MHT algorithms. Both exhibit significant tracking drift at approximately 100 frames. The JPDA and PHD algorithms demonstrate satisfactory performance in tracking the diver target, while the MHT algorithm experiences tracking drift at about 70 frames. The JPDA algorithm excels in cluttered environments as it does not require prior information about the target and clutter, allowing for successful target tracking. Nevertheless, because this study focuses on a single-target tracking scenario, the JPDA algorithm performs relatively well. In contrast, the MHT algorithm necessitates prior information about the target and clutter, and the computational complexity increases exponentially with the clutter density. To enhance computational efficiency, we set a smaller value for N-scan pruning, but this compromises the tracking performance of the algorithm. The PHD algorithm, which is based on RFS theory, avoids the intricate correlation process associated with traditional methods and exhibits high computational efficiency. In the data processing of the two scenarios, we assume a uniform linear motion model for both the MHT and PHD algorithms. However, this motion constraint is not robust in low SRR environments, leading to the failure of the PHD algorithm in tracking maneuvering targets. Our proposed method surpasses these algorithms by utilizing multiple features and incorporating reliability estimation to identify a reliable re-detected target for self-correction.

Figure 8a,b display the percentage of frames within a given RMSE threshold for the error between the estimated position and the true position of the maneuvering target and the diver target, respectively. Analysis of these figures demonstrates that the IMKCF algorithm outperforms the other three tested algorithms in terms of RMSE precision. Specifically, when the RMSE threshold is set at 5, the IMKCF algorithm achieves an accuracy rate close to 80%, while the other algorithms only have approximately 50% accuracy when the RMSE threshold is 10.

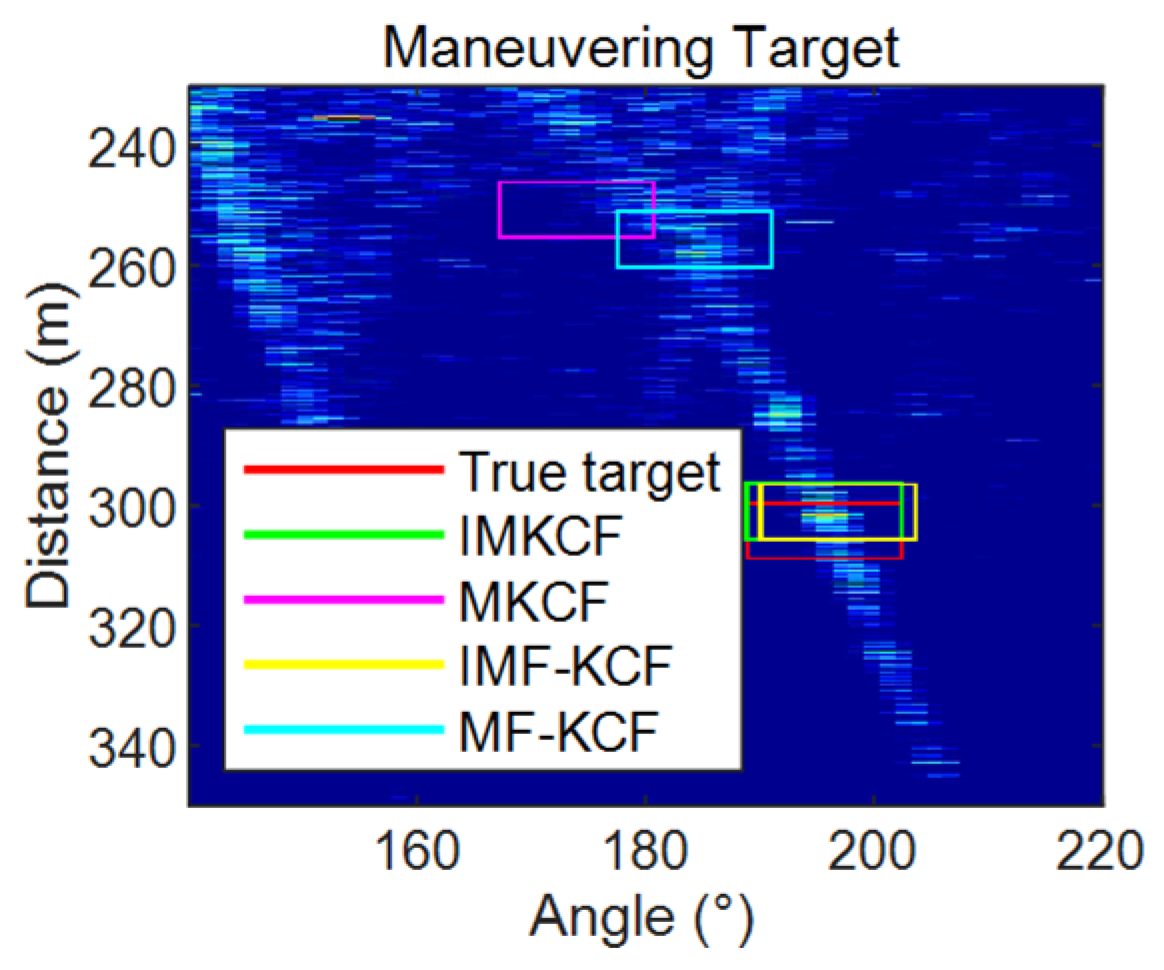
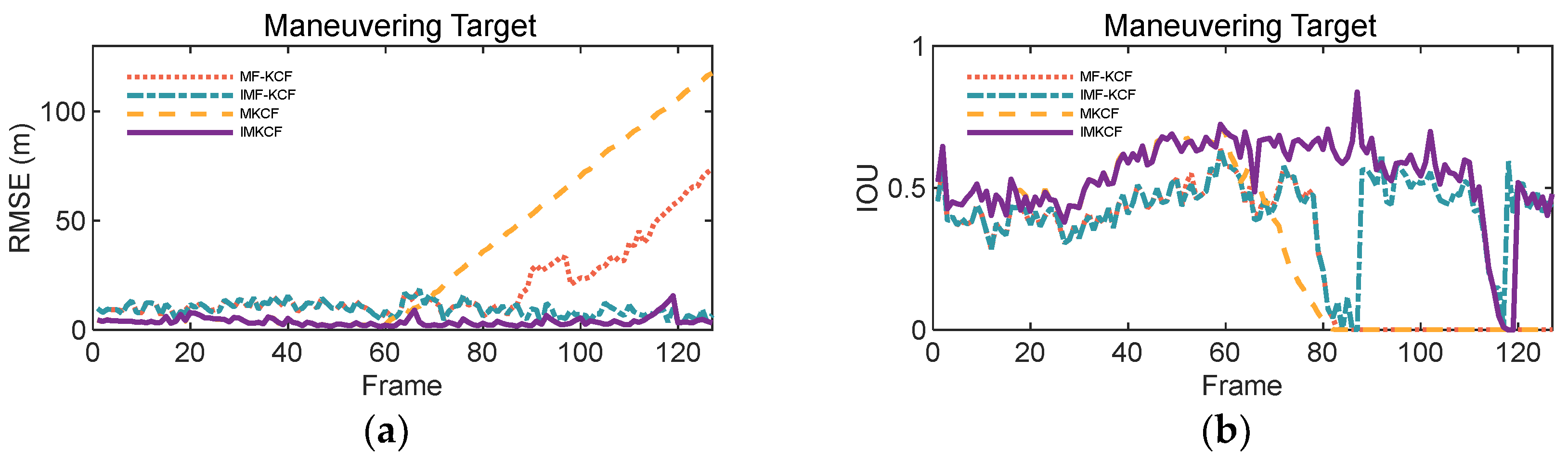
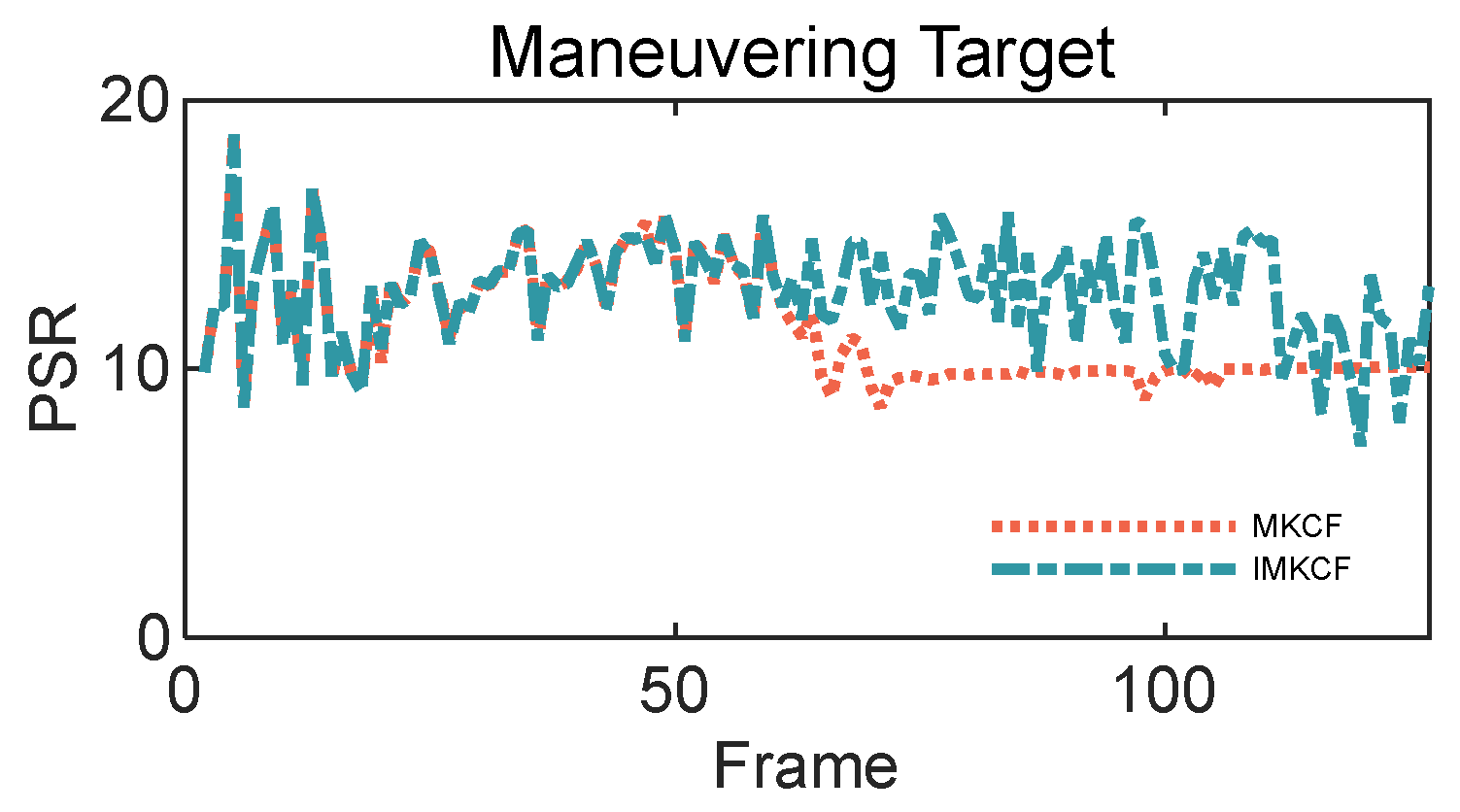
5.3.2. Comparison with Original KCF Algorithms

In this section, a comparative analysis is conducted between the proposed algorithm and three original KCF algorithms, namely, MF-KCF, improved MF-KCF (IMF-KCF), and MKCF. Figure 9 illustrates the target position in the final frame and tracking outcomes for all four algorithms. It can be observed from the figure that both the MF-KCF and MKCF algorithms fail to track the maneuvering target. Conversely, the IMF-KCF and IMKCF algorithms, incorporating adaptive reliability checks and a re-detection module, successfully track the target. At approximately the 70th frame, target tracking is interfered with by reverberation, and the training samples are contaminated, resulting in error propagation during model training and subsequent tracker drift. The IMKCF algorithm checks real-time reliability on target tracking results and re-detects the target position when deemed unreliable, preventing frame drift. The versatility of the re-detection module is demonstrated by its successful implementation in both algorithms.

To further elucidate tracking performance under low-SRR scenarios, Figure 10 presents the frame-by-frame RMSE and IOU of maneuvering target tracking. Higher IOU values and lower RMSE values signify more accurate tracking outcomes. As shown in Figure 10, both the MF-KCF and MKCF algorithms lose track of the targets around the 70th frame. The IMKCF algorithm outperforms the IMF-KCF algorithm, exhibiting relatively low RMSE and high IOU values across most frames, indicating superior accuracy. This improvement can be attributed to the MKCF tracking-by-detection module, which enables the algorithm to make full use of the complementary features and improve tracking accuracy.

Figure 11a depicts the RMSE precision. The figure reveals that when the RMSE threshold is set at 10, the IMKCF algorithm achieves nearly 100% precision, while the other three algorithms fall below 60%. Additionally, Figure 11b demonstrates the IOU precision. Notably, when the IOU threshold is set at 0.5, the IMKCF algorithm attains nearly 100% precision, whereas the other three algorithms exhibit less than 60%. The results show that, compared with the single-kernel correlation filter, the correlation filter based on multiple kernels has greater advantages in tracking accuracy.

Figure 12 illustrates the PSR curve during the tracking process of the MKCF and IMKCF algorithms. It can be observed that the PSR of the MKCF algorithm experiences a significant decline around the 70th frame, whereas the PSR of the IMKCF algorithm fluctuates steadily throughout the tracking process. These findings indicate that the PSR score serves as an indicator of tracking result reliability, and the adaptive reliability check and re-detection modules within the IMKCF algorithm play a vital role in enhancing tracking robustness.

5.3.3. Algorithm Efficiency

Table 2. FPS and the average of RMSE.

	MHT	JPDA	PHD	MF-KCF	MKCF	IMF-KCF	IMKCF
FPS	7.2	107.1	122.3	22.3	27.2	11.3	14.2
RMSEaver	44.82	10.26	50.83	19.94	33.52	9.6	3.86

displays the PFS and average RMSE of the above algorithms. The results indicate that the PHD algorithm has the highest FPS and computational efficiency but exhibits the poorest tracking accuracy. In contrast, the KCF algorithms exhibit relatively lower computational efficiency but has higher tracking accuracy compared to the classical filtering algorithm. The analysis suggests that MKCF exhibits a slight improvement in computational efficiency when compared MF-KCF. This implies that the incorporation of an additional kernel in kernel correlation filtering does not result in a significant increment in computational cost. Moreover, the results demonstrate that IMKCF achieves superior tracking accuracy in comparison to both IMF-KCF and MF-KCF. Notably, Table 2 reveals that the inclusion of a re-detection module can lead to an increase in computational cost, as it carries out target re-detection when the tracking results are deemed unreliable.

6. Conclusions

In this paper, we propose an IMKCF algorithm to solve the challenging problem of detecting and tracking weak targets with varying movements in a complex marine environment. The IMKCF algorithm consists of three modules: the MKCF tracking-by-detection, the adaptive reliability check, and the re-detection modules. The MKCF tracking-by-detection module employs a multi-frame data weighted average technique to adaptively update the coefficients of multiple kernels, thereby enhancing tracking accuracy. We conduct a comprehensive analysis of the MKCF algorithm using a maximum likelihood perspective and prove that the target location can be precisely determined based on the location of the maximum value of the correlation response. The remaining two modules work collaboratively to improve the robustness of target tracking. In particular, the previous reliable tracking results are utilized to drive a Kalman filter, generating a position estimate when the tracking result is considered unreliable. A decision is then made about whether to replace the original target position with the estimated one.

In data processing, we extracted HOG features and invariant moment features to train the proposed IMKCF algorithm, which has been compared with traditional tracking algorithms and original KCF algorithms. The experimental results demonstrate that our proposed algorithm not only exhibits the capability of effectively tracking underwater targets with diverse motion types but also achieves long-term robust tracking in low-SRR environments. Moreover, the tracking accuracy of our algorithm surpasses that of the single-core correlation filter. Currently, the method proposed in this paper is only suitable for single-target tracking. In future research, we plan to delve deeper into the challenges of multiple weak underwater target tracking. Additionally, we aim to mine more target feature information to enhance the algorithm’s robustness.