Multiscale Spatiotemporal Variations of GNSS-Derived Precipitable Water Vapor over Yunnan
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Description
2.2. Retrieval of PWV
3. Results
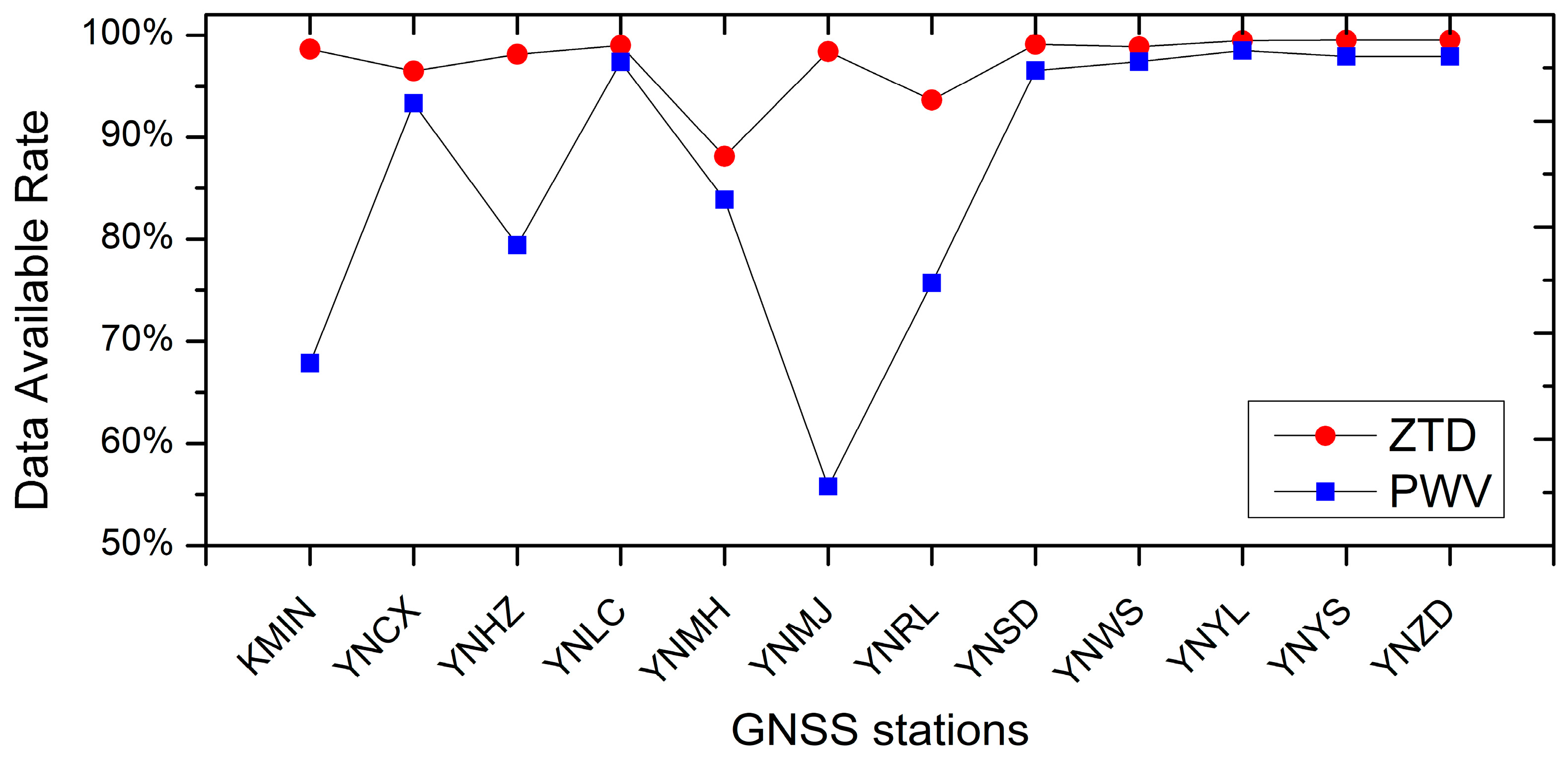
3.1. Continuity of GNSS ZTD and PWV Time Series
3.2. Evaluation of the GNSS PWV with Radiosonde Data
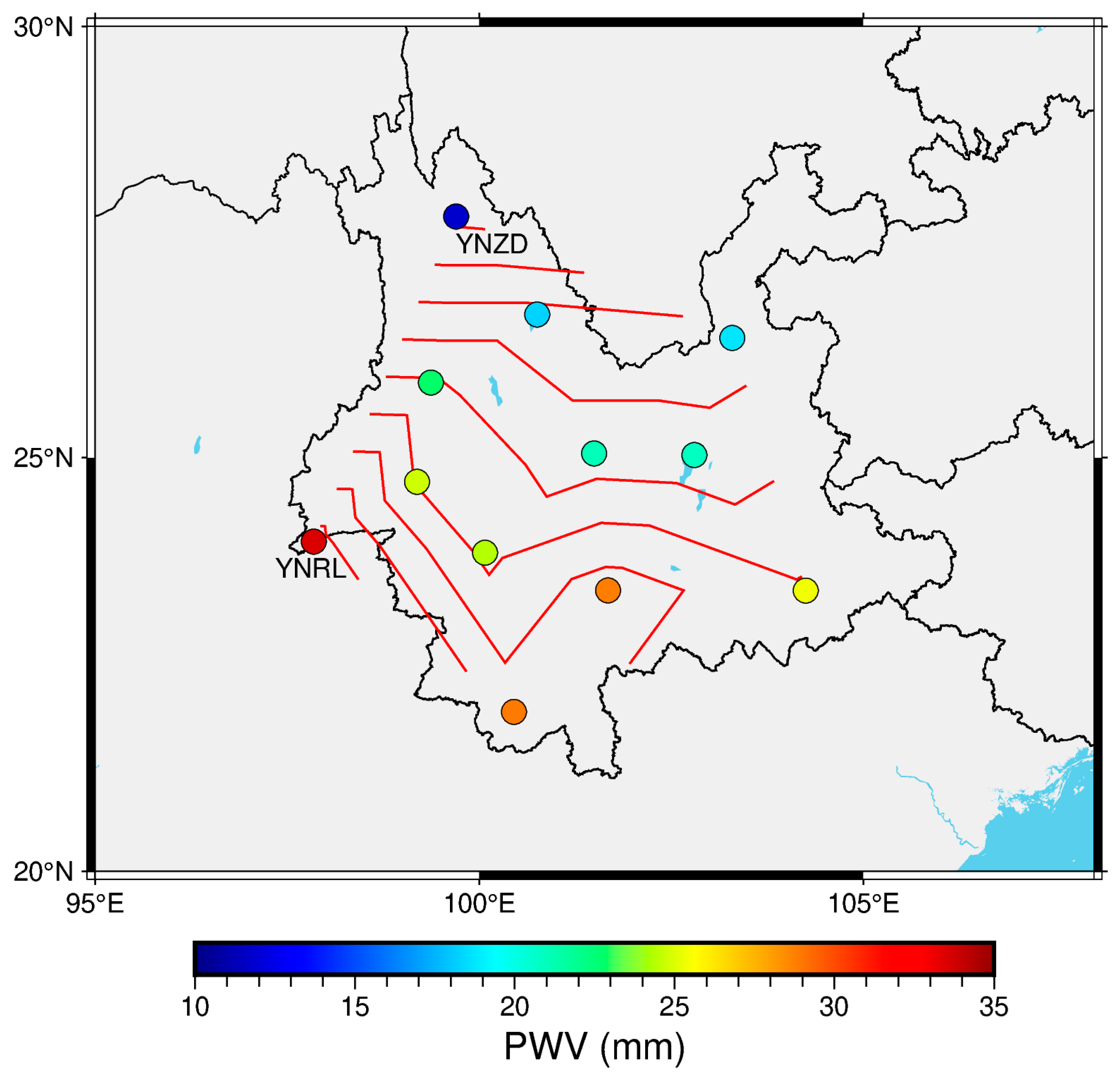
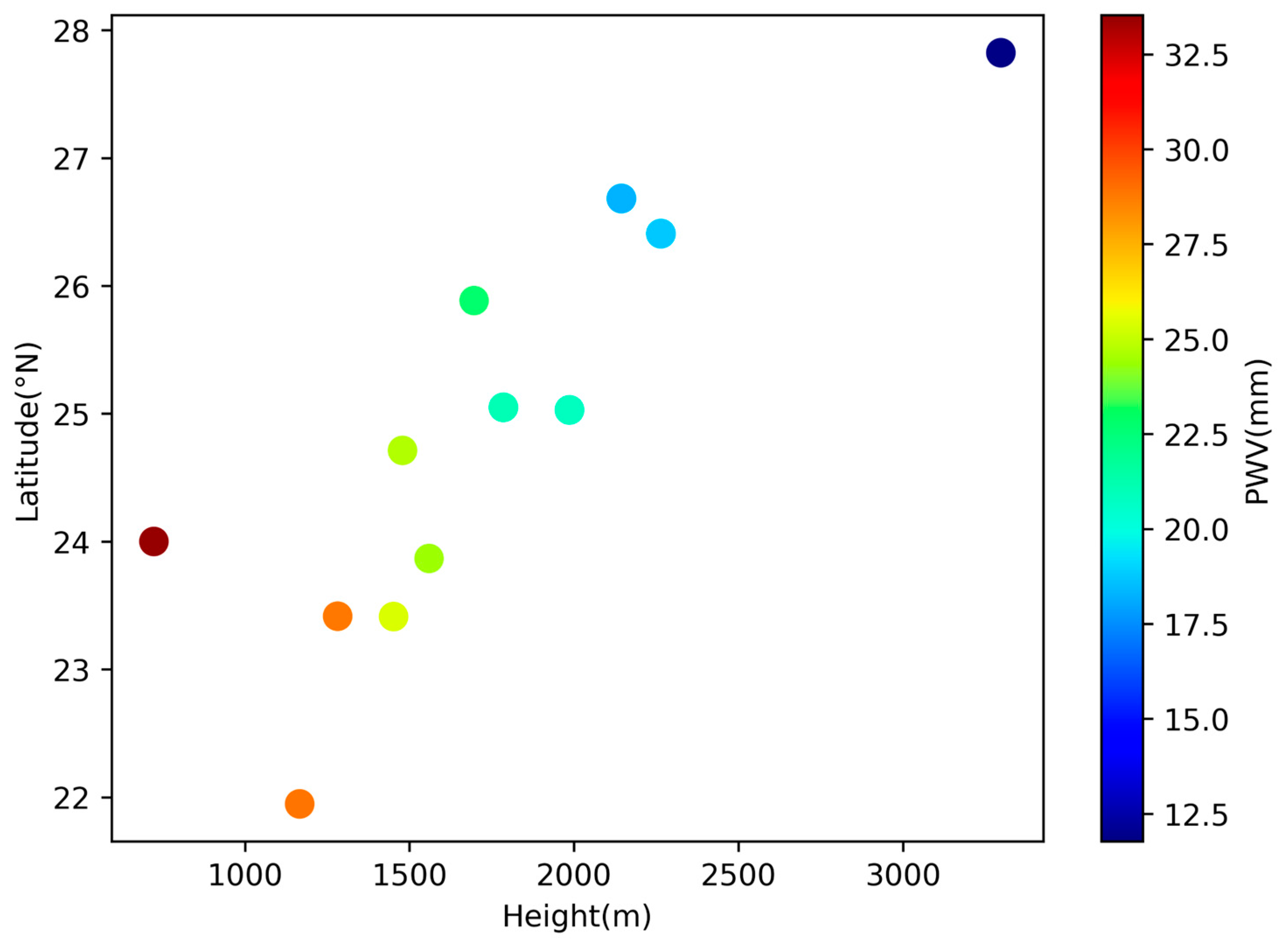
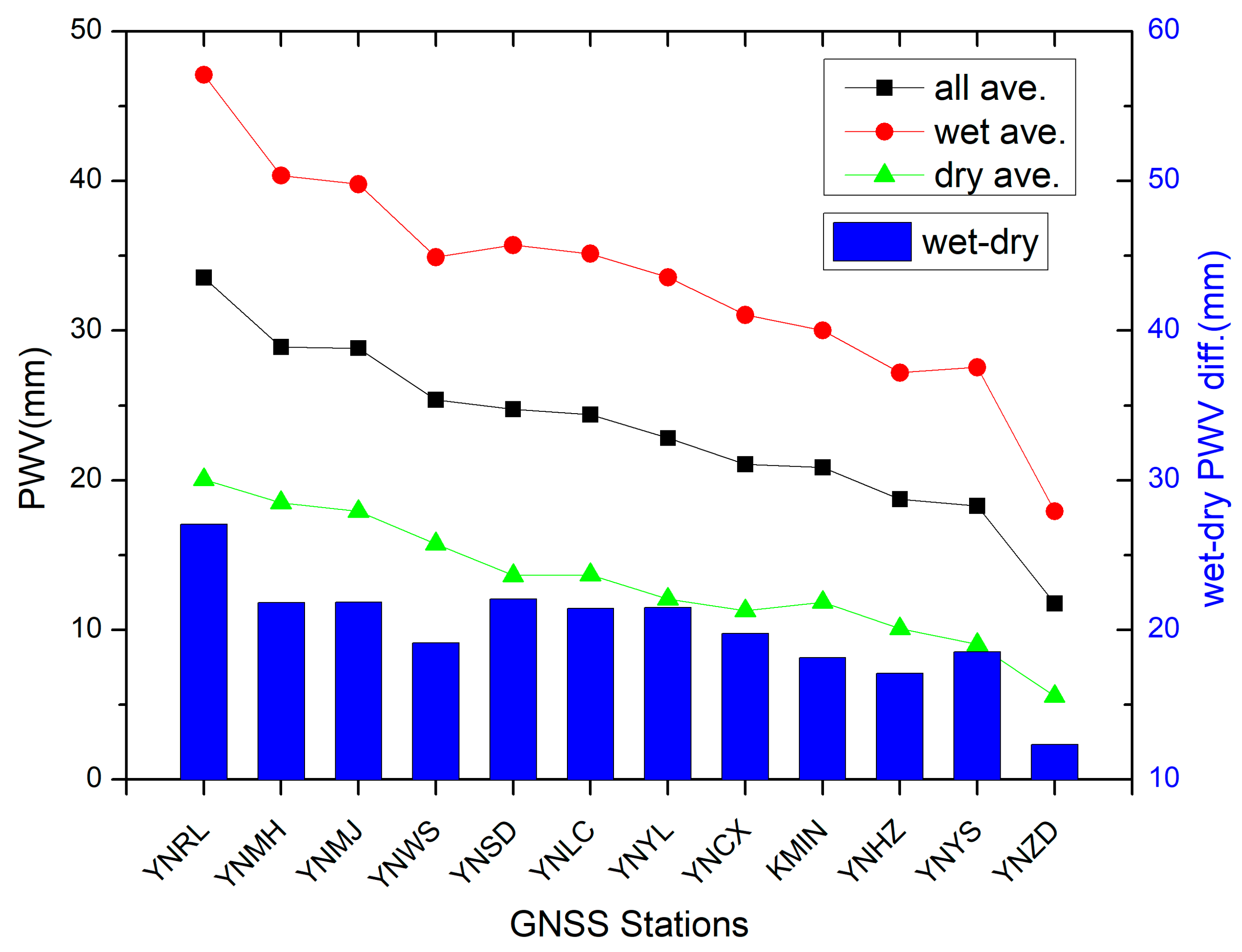
3.3. Average PWV and Spatial Distribution
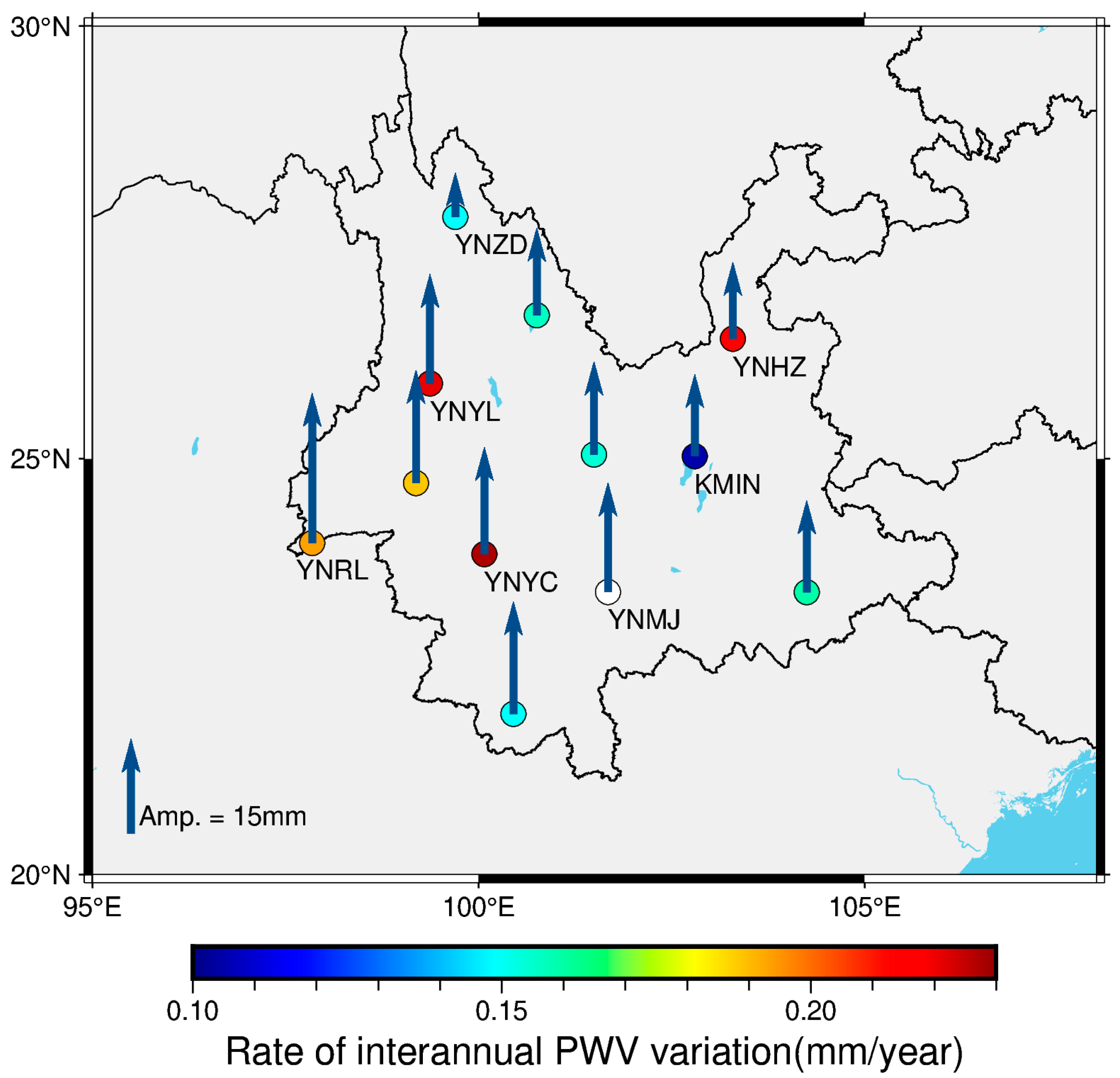
3.4. Secular, Annual and Semiannual Variations of PWV
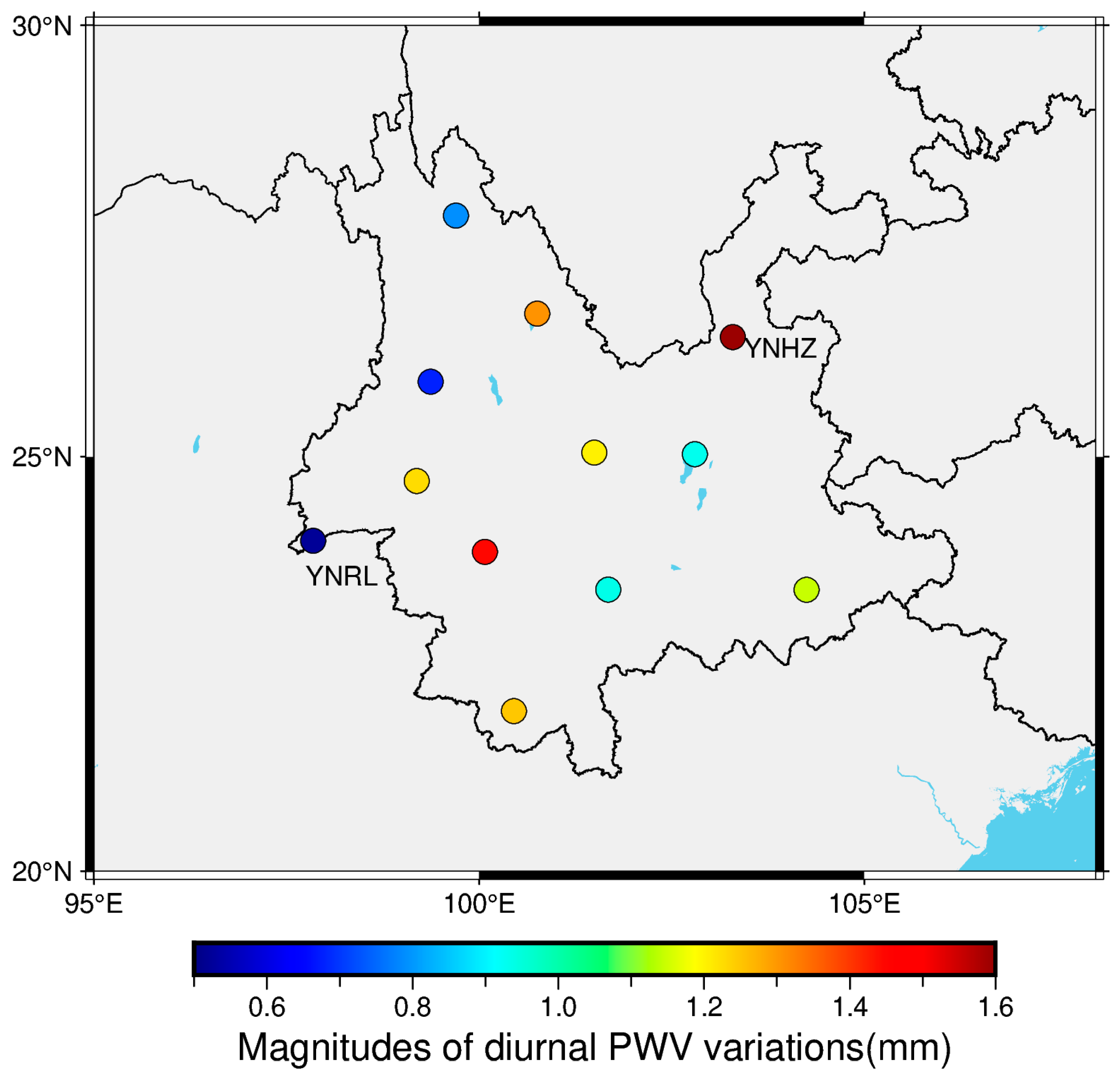
3.5. Monthly and Diurnal Variations of PWV
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Anand, K.; Inamdar, V.; Ramanathan, N.; Loeb, G. Satellite observations of the water vapor greenhouse effect and column longwave cooling rates: Relative roles of the continuum and vibration-rotation to pure rotation bands. J. Geophys. Res.-Atmos. 2004, 109, 1–9. [Google Scholar]
- Easterbrook, D. Greenhouse gases. In Evidence-Based Climate Science: Data Opposing CO2 Emissions as the Primary Source of Global Warming, 2nd ed.; Easterbrook, D., Ed.; Elsevier: Oxford, UK, 2016; pp. 163–173. [Google Scholar]
- Mills, E. Weather Studies: Introduction to Atmospheric Science, 6th ed.; American Meteorological Society: Boston, MA, USA, 2015. [Google Scholar]
- Salby, M. Fundamentals of Atmospheric Physics; Academic Press: San Diego, CA, USA, 1996; pp. 25–29. [Google Scholar]
- Wang, J.; Zhang, L.; Dai, A.; Immler, F.; Sommer, M.; Vomel, H. Radiation dry bias correction of Vaisala RS92 humidity data and its impacts on historical radiosonde data. J. Atmos. Ocean. Technol. 2013, 30, 197–214. [Google Scholar] [CrossRef]
- Rocken, C.; Ware, R.; Van Hove, T.; Solheim, F.; Alber, C.; Johnson, J.; Bevis, M.; Businger, S. Sensing atmospheric water vapor with the Global Positioning System. Geophy. Res. Lett. 1993, 20, 2631–2634. [Google Scholar] [CrossRef]
- Rocken, C.; Hove, T.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Chiswell, S.; Businger, S. GPS/STORM—GPS sensing of atmospheric water vapor for meteorology. J. Atmos. Ocean Tech. 1995, 12, 468–478. [Google Scholar] [CrossRef]
- Wang, M. The Assessment and Meteorological Applications of High Spatiotemporal Resolution GPS ZTD/PW Derived by Precise Point Positioning. Ph.D. Thesis, Tong University, Shanghai, China, 2019. [Google Scholar]
- Bevis, M.; Businger, S.; Herring, T.; Rocken, C.; Anthes, R.; Ware, R. GPS meteorology: Remote sensing of atmospheric water vapor using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Askne, J.; Nordius, H. Estimation of tropospheric delay for microwaves from surface weather data. Radio Sci. 1987, 22, 379–386. [Google Scholar] [CrossRef]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Rochen, C.; Solheim, F.; Van Hove, T.; Ware, R.; et al. GPS meteorology: Direct estimation of the absolute value of precipitable water. J. Appl. Meteorol. 1996, 35, 830–838. [Google Scholar] [CrossRef]
- Fang, P.; Bevis, M.; Bock, Y.; Gutman, S.; Wolfe, D. GPS meteorology: Reducing systematic errors in geodetic estimates for zenith delay. Geophys. Res. Lett. 1998, 25, 3583–3586. [Google Scholar] [CrossRef]
- Cao, Y.; Fang, Z.; Xia, Q. Relationship between GPS precipitable water vapor and precipitation. J. Appl. Meteorol. Sci. 2005, 16, 54–59. [Google Scholar]
- Van Baelen, J.; Reverdy, M.; Tridon, F.; Labbouz, L.; Dick, G.; Bender, M.; Hagen, M. On the relationship between water vapour field evolution and the life cycle of precipitation systems. Q. J. R. Meteorol. Soc. 2011, 137, 204–223. [Google Scholar] [CrossRef]
- Huang, L.; Mo, Z.; Xie, S.; Liu, L.; Chen, J.; Kang, C.; Wang, S. Spatiotemporal characteristics of GNSS-derived precipitable water vapor during heavy rainfall events in Guilin, China. Satell. Navig. 2021, 2, 13. [Google Scholar] [CrossRef]
- Brenot, H.; Neméghaire, J.; Delobbe, L.; Clerbaux, N.; De Meutter, P.; Deckmyn, A.; Deckmyn, A.; Deleloo, A.; Frappez, L.; Roozendael, M. Preliminary signs of the initiation of deep convection by GNSS. Atmos. Chem. Phys. 2013, 13, 5425–5449. [Google Scholar] [CrossRef]
- Adams, D.; Barbosa, H.; Gaitán De Los Ríos, K. A spatiotemporal water vapor-deep convection correlation metric derived from the Amazon dense GNSS meteorological network. Mon. Weather Rev. 2017, 145, 279–288. [Google Scholar] [CrossRef]
- Shi, C.; Zhou, L.; Fan, L.; Zhang, W.; Cao, Y.; Wang, C.; Xiao, F.; Lv, G.; Liang, H. Analysis of ‘21·7’ extreme rainstorm process in Henan Province using BeiDou/GNSS observation. Chin. J. Geophys.-CH 2022, 65, 186–196. [Google Scholar]
- Vedel, H.; Huang, X. Impact of ground based GPS data on numerical weather prediction. J. Meteorol. Soc. JPN 2004, 82, 459–472. [Google Scholar] [CrossRef]
- Bennitt, G.; Jupp, A. Operational assimilation of GPS zenith total delay observations into the Met Office numerical weather prediction models. Mon. Weather Rev. 2012, 140, 2706–2719. [Google Scholar] [CrossRef]
- Means, J. GPS precipitable water as a diagnostic of the north American monsoon in California and Nevada. J. Clim. 2013, 26, 1432–1444. [Google Scholar] [CrossRef]
- Moore, A.; Small, I.; Gutman, S.; Bock, Y.; Dumas, J.; Fang, P.; Haase, J.; Jackson, M.; Laber, J. National weather service forecasters use GPS precipitable water vapor for enhanced situational awareness during the Southern California Summer Monsoon. Bull. Am. Meteorol. Soc. 2015, 96, 1867–1877. [Google Scholar] [CrossRef]
- Wang, M.; Wang, J.; Bock, Y.; Liang, H.; Dong, D.; Fang, P. Dynamic mapping of the movement of landfalling atmospheric rivers over southern California with GPS data. Geophys. Res. Lett. 2019, 46, 3551–3559. [Google Scholar] [CrossRef]
- Zhao, Q.; Ma, X.; Yao, W.; Liu, Y.; Yao, Y. A drought monitoring method based on precipitable water vapor and precipitation. J. Clim. 2020, 33, 10727–10741. [Google Scholar] [CrossRef]
- Jin, S.; Li, Z.; Cho, J. Integrated water vapor field and multiscale variations over China from GPS measurements. J. Appl. Meteorol. Clim. 2008, 47, 3008–3015. [Google Scholar] [CrossRef]
- Jin, S.; Luo, O. Variability and climatology of PWV from global 13-year GPS observations. IEEE Trans. Geosci. Remote 2009, 47, 1918–1924. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L. Climate applications of a global 2-hourly atmospheric precipitable water dataset derived from IGS tropospheric products. J. Geod. 2009, 83, 209–217. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, W.; Cao, Y.; Lou, Y.; Liang, H.; Fan, L.; Satirapod, C.; Trakolkul, C. Atmospheric water vapor climatological characteristics over Indo-China region based on BeiDou/GNSS and relationships with precipitation. Acta Geod. Cartogr. Sin. 2020, 49, 1112–1119. [Google Scholar]
- Wu, M.; Jin, S.; Li, Z.; Cao, Y.; Ping, F.; Tang, X. High-precision GNSS PWV and its variation characteristics in China based on individual station meteorological data. Remote Sens. 2021, 13, 1296. [Google Scholar] [CrossRef]
- Fu, R.; Duan, X.; Liu, J.; Sun, J.; Wang, M.; Chen, X.; Liu, Y. Characteristics of ground-based GPS-retrieved PWV in Yunnan. Meteorol. Sci. Technol. 2010, 38, 456–462. [Google Scholar]
- Hai, Y.; Sun, J.; Chen, X. The analysis of GPS-retrieved PWV characteristic in Yunnan from 2007–2010. Yunnan Geogr. Environ. Res. 2011, 23, 78–84. [Google Scholar]
- Shen, Y.; Duan, W. Characteristics of temporal and spatial distribution of water vapor resource in Yunnan area. Environ. Sci. Surv. 2016, 35, 36–41. [Google Scholar]
- Li, Y.; Xu, A.; Dong, B. Variation characteristics of precipitable water volume observed by GPS in Dali. J. Meteorol. Res. Appl. 2020, 41, 32–37. [Google Scholar]
- Hu, H.; Cao, Y.; Shi, C.; Lei, Y.; Wen, H.; Liang, H.; Tu, M.; Wan, X.; Wang, H.; Liang, J.; et al. Analysis of the precipitable water vapor observation in Yunnan–Guizhou Plateau during the convective weather system in summer. Atmosphere 2021, 12, 1085. [Google Scholar] [CrossRef]
- Wang, M.; Cao, Y.; Liang, H.; Tu, M.; Liu, Z. On the accuracy of regional weighted mean temperature linear models over China. J. Nanjing Univ. Inf. Sci. Technol. (Nat. Sci. Ed.) 2021, 13, 161–169. [Google Scholar]
- Wang, M.; Chen, J.; Han, J.; Zhang, Y.; Fan, M.; Yu, M.; Sun, C.; Xie, T. Region-specific and weather-dependent characteristics of the relation between GNSS weighted mean temperature and surface temperature over China. Remote Sens. 2023, 15, 1538. [Google Scholar] [CrossRef]
- Niell, A. Preliminary evaluation of atmospheric mapping functions based on numerical weather models. Phys. Chem. Earth 2001, 26, 475–480. [Google Scholar] [CrossRef]
- Böhm, J.; Schuh, H. Vienna mapping functions in VLBI analyses. Geophy. Res. Lett. 2004, 31, L01603. [Google Scholar] [CrossRef]
- Neill, A. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Böhm, J.; Niell, A.; Tregoning, P.; Schuh, H. Global mapping function (GMF): A new empirical mapping function based on data from numerical weather model data. Geophys. Res. Lett. 2006, 33, L07304. [Google Scholar] [CrossRef]
- Davis, J.; Elgered, G.; Niell, A.; Kuehn, C. Ground based measurement of gradients in the “wet” radio refractivity of air. Radio Sci. 1993, 28, 1003–1018. [Google Scholar] [CrossRef]
- Saastamoinen, J. Atmospheric correction for troposphere and stratosphere in radio ranging of satellites. In The Use of Artificial Satellites for Geodesy; Henriksen, S., Mancini, A., Chovitz, B., Eds.; William Byrd Press: Richmond, VA, USA, 1972; Volume 15, pp. 247–252. [Google Scholar]
- Bevis, M.; Businger, S.; Chiswell, S.; Herring, T.; Anthes, R.; Rocken, C.; Ware, R. GPS meteorology: Mapping zenith wet delays onto precipitable water. J. Appl. Meteorol. 1994, 33, 379–386. [Google Scholar] [CrossRef]
- Davis, J.; Herring, T.; Shapiro, I.; Rogers, A.; Elgered, G. Geodesy by radio interferometry: Effects of atmospheric modeling errors on estimates of baseline length. Radio Sci. 1985, 20, 1593–1607. [Google Scholar] [CrossRef]
- Dach, R.; Lutz, S.; Walser, P.; Fridez, P. Bernese GNSS Software Version 5.2; User Manual; Astronomical Institute, University of Bern, Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar] [CrossRef]
- Chen, G.; Herring, T. Effects of atmospheric azimuthal asymmetry on the analysis of space geodetic data. J. Geophy. Res. 1997, 102, 20489–20502. [Google Scholar] [CrossRef]





| Radiosonde Lon (ºE), Lat (ºN), Hgt (m) | Ts-Tm Model (K) | GNSS Lon(ºE), Lat(ºN), Hgt (m) |
|---|---|---|
| XC (Xichang) 102.26, 27.90, 1599 | Tm = 0.58 Ts + 110.66 | YNZD 99.70, 27.82, 3296 |
| YNYS 100.75, 26.68, 2144 | ||
| TC (Tengchong) 98.48, 25.11, 1649 | Tm = 0.52 Ts + 130.75 | YNRL 97.85, 24.00, 723 |
| YNSD 99.19, 24.71, 1479 | ||
| YNYL 99.37, 25.88, 1696 | ||
| YNLC 100.08, 23.87, 1559 | ||
| SM (Simao) 100.98, 22.76, 1303 | Tm = 0.35 Ts + 181.68 | YNMH 100.45, 21.95, 1166 |
| YNMJ 101.67, 23.42, 1282 | ||
| MZ (Mengzi) 103.38, 23.38, 1302 | Tm = 0.49 Ts + 138.31 | YNWS 104.25, 23.41, 1452 |
| WN (Weining) 104.28, 26.86, 2236 | Tm = 0.62 Ts + 102.15 | YNHZ 103.29, 26.41, 2264 |
| KM (Kunming) 102.68, 25.01, 1892 | Tm = 0.45 Ts + 148.44 | KMIN 102.80, 25.03, 1986 |
| YNCX 101.49, 25.05, 1785 |
| Ephemeris | Orbit | CODE GPS satellite orbit final products |
| Clock | CODE GPS satellite clock offset final products | |
| Measurement models | Basic observables | GPS L1 + L2 |
| Modeled observables | Double differences | |
| Ionosphere-free linear combination | ||
| Satellite antenna center of mass offsets | igs14.atx | |
| GPS attitude model | Nominal (yaw-steering) attitude implemented | |
| Troposphere a priori model | ECMWF-based hydrostatic delay mapped with hydrostatic VMF1 | |
| Ionosphere | Second-order effect applied | |
| Estimated parameters | Adjustment method | Weighted least-squares algorithms |
| Station coordinates | Adjusted with minimum constraints | |
| Troposphere | Zenith tropospheric delay and two gradient parameters estimated every hour Loose relative constraints of 5 m are applied | |
| Gradient model | Chen–Herring model [46] | |
| Ambiguity | Partly fixed |
| Site | All-Season Ave. | Dry-Season Ave. | Wet-Season Ave. | |||
|---|---|---|---|---|---|---|
| Max | Min | Max | Min | Max | Min | |
| KMIN | 21 | 10 | 23 | 12 | 20 | 8 |
| YNCX | 17 | 8 | 18 | 8 | 17 | 8 |
| YNHZ | 18 | 9 | 21 | 10 | 17 | 9 |
| YNLC | 17 | 8 | 17 | 9 | 17 | 8 |
| YNMH | 18 | 9 | 18 | 9 | 20 | 8 |
| YNMJ | 23 | 8 | 21 | 8 | 23 | 8 |
| YNSD | 17 | 8 | 16 | 8 | 17 | 8 |
| YNWS | 19 | 8 | 20 | 9 | 18 | 8 |
| YNYL | 19 | 9 | 19 | 9 | 24 | 9 |
| YNYS | 18 | 9 | 18 | 9 | 18 | 9 |
| YNZD | 19 | 10 | 20 | 10 | 18 | 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Lv, Z.; Wu, W.; Li, D.; Zhang, R.; Sun, C. Multiscale Spatiotemporal Variations of GNSS-Derived Precipitable Water Vapor over Yunnan. Remote Sens. 2024, 16, 412. https://doi.org/10.3390/rs16020412
Wang M, Lv Z, Wu W, Li D, Zhang R, Sun C. Multiscale Spatiotemporal Variations of GNSS-Derived Precipitable Water Vapor over Yunnan. Remote Sensing. 2024; 16(2):412. https://doi.org/10.3390/rs16020412
Chicago/Turabian StyleWang, Minghua, Zhuochen Lv, Weiwei Wu, Du Li, Rui Zhang, and Chengzhi Sun. 2024. "Multiscale Spatiotemporal Variations of GNSS-Derived Precipitable Water Vapor over Yunnan" Remote Sensing 16, no. 2: 412. https://doi.org/10.3390/rs16020412
APA StyleWang, M., Lv, Z., Wu, W., Li, D., Zhang, R., & Sun, C. (2024). Multiscale Spatiotemporal Variations of GNSS-Derived Precipitable Water Vapor over Yunnan. Remote Sensing, 16(2), 412. https://doi.org/10.3390/rs16020412






