Assessment of FY-3E GNOS II Radio Occultation Data Using an Improved Three-Cornered Hat Method

Abstract

The spatial–temporal sampling errors arising from the differences in geographical locations and measurement times between co-located Global Navigation Satellite System (GNSS) radio occultation (RO) and radiosonde (RS) data represent systematic errors in the three-cornered hat (3CH) method. In this study, we propose a novel spatial–temporal sampling correction method to mitigate the sampling errors associated with both RO–RS and RS–model pairs. We analyze the 3CH processing chain with this new correction method in comparison to traditional approaches, utilizing Fengyun-3E (FY-3E) GNSS Occultation Sounder II (GNOS II) RO data, atmospheric models, and RS datasets from the Hailar and Xisha stations. Overall, the results demonstrate that the improved 3CH method performs better in terms of spatial–temporal sampling errors and the variances of atmospheric parameters, including refractivity, temperature, and specific humidity. Subsequently, we assess the error variances of the FY-3E GNOS II RO, RS and model atmospheric parameters in China, in particular the northern China and southern China regions, based on large ensemble datasets using the improved 3CH data processing chain. The results indicate that the FY-3E GNOS II BeiDou navigation satellite system (BDS) RO and Global Positioning System (GPS) RO show good consistency, with the average error variances of refractivity, temperature, and specific humidity being less than 1.12%², 0.13%², and 700%², respectively. A comparison of the datasets from northern and southern China reveals that the error variances for refractivity are smaller in northern China, while temperature and specific humidity exhibit smaller error variances in southern China, which is attributable to the differing climatic conditions.

1. Introduction

Global Navigation Satellite System (GNSS) radio occultation (RO) is a remote sensing technology that originated in the 1990s [1,2]. In recent decades, it has become one of the important technologies for monitoring the Earth’s atmosphere [3], providing a high vertical resolution, high accuracy, all-weather capability, global coverage, and long-term stability data for temperature, humidity, and pressure [4,5]. The GNSS RO observation data have important scientific research value and broad application prospects in numerical weather prediction (NWP) [6,7,8], global climate change [9,10,11,12] and extreme weather monitoring [13,14], ionospheric exploration [15], space science [16], and other fields.

Since the United States’ Global Positioning System/METeorology (GPS/MET) mission first demonstrated the feasibility of GNSS RO in 1995 [17], more than 30 GNSS RO missions have been undertaken, such as Constellation Observation System of Meteorology, Ionosphere and Climate -1/-2 (COSMIC -1/-2) [18,19], the Gravity Recovery and Climate Experiment (GRACE) [20,21], CHAllenging Minisatellite Payload (CHAMP) [22,23], and Meteorological Operational -A/-B/-C (MetOp -A/-B/-C) [24,25].

The development of China’s GNSS RO benefits from the construction of the BeiDou navigation satellite system (BDS) and the new generation of Fengyun (FY) meteorological satellites. The FY-3C was equipped with the first BDS/GPS dual-system-compatible GNSS Occultation Sounder (GNOS) [26,27]. The FY-3E was equipped with the upgraded GNSS Occultation Sounder II (GNOS II) payload [28], integrating GNSS RO and GNSS Reflectometry (GNSS-R) capabilities. FY-3E GNOS II provides BDS and GPS RO products. FY-3F/-3G, launched in 2023, is also equipped with GNOS II.

So far, FY-3E GNOS II has obtained a large amount of atmospheric, ionospheric, and wind field data products using BDS -2/-3 and GPS signals [29], and it has broad application prospects in ocean surface wind, soil moisture, and sea ice range [30]. Li et al. indicated that the accuracy of FY-3E data has surpassed that of FY-3D data [31]. He et al. and Liu et al. conducted in-depth analysis of the BDS and GPS occultation signal tracking capabilities and data quality of FY-3E, verifying the advantages of FY-3E GNOS II RO data in terms of global coverage, data quality, and penetration depth [32,33]. In earlier evaluations of FY-3E GNOS II RO, radiosonde (RS), or model data as reference data, researchers analyzed the error characteristics of FY-3E GNOS II RO by calculating the mean biases and standard deviations of the RO products relative to reference data. During the evaluation process, the observational errors caused by the errors in the reference data and the error covariance between the RO and the reference datasets were not considered [34]. Recently, the three-cornered hat (3CH) method has been applied to estimate the actual observational errors in RO.

Researchers use 3CH as a method for estimating the error variances of multiple datasets by comparing the differences between three different data sources to estimate their error variances. Grubbs derived the equations for the two-cornered hat (2CH) and 3CH methods under the assumption that there is no error correlation between datasets [35]. Compared with 2CH, 3CH is less sensitive to error correlation and sample size [36]. Originally used to evaluate random errors in atomic clocks [37], 3CH is currently used to evaluate geophysical data such as GNSS clock stability [38,39], geophysical load deformation [40], and sea surface temperatures [41]. Anthes and Rieckh initially applied the 3CH method to evaluate the error variances of GNSS RO, RS, European Centre for Medium-Range Weather Forecasts (ECMWF) and Global Forecast System (GFS) model datasets, demonstrating that the 3CH method can effectively compute the error variances between different datasets [42]. On this basis, the applicability and accuracy of this method have been demonstrated in complex weather systems, in areas with different latitudes, and at global scales [43,44,45]. Recent studies have utilized the 3CH method to analyze the error variances of the COSMIC -2 [46,47], MetOp -A/-B [48], and FY-3C RO [45]. However, no studies have yet employed this method to evaluate the error variances of the FY-3E GNOS II RO.

The 3CH method calculates the mean-square difference among three co-location pairs formed from different datasets, thereby providing independent linear estimates of the unknown error variances for these datasets. Due to variations in measurement times and locations, sampling errors occur among these co-located pairs [49]. To mitigate the impact of sampling errors, the spatial and temporal scope of co-location pairs can be constrained (typically within 3 to 6 h and 100 to 500 km) [50,51], and the “double-differencing” method can be applied for the spatial–temporal sampling correction of these co-located pairs [49,52,53]. Currently, spatial–temporal sampling corrections are applied to RO–RS pairs in studies utilizing the 3CH method [42,45]. However, the model data used in these studies are co-located with RO, and there are still spatial–temporal sampling errors when they are co-located with RS. Therefore, it is necessary to calibrate the RS–model co-located pairs to reduce the sampling errors between their corresponding variables.

Therefore, based on spatial–temporal sampling correction for both the RO–RS and RS–model pairs, this study proposes a new correction scheme to adjust the co-located pairs. We compare and analyze the error characteristics between different datasets and FY-3E GNOS II BDS and GPS RO datasets using the advanced 3CH method. The structure of this article is as follows: Section 2 provides a brief overview of the datasets used. Section 3 describes the specific algorithm used for spatial–temporal sampling correction and the 3CH method. In Section 4, the results are described and analyzed, and in Section 5 some conclusions and prospects are drawn.

2. Data Description

To estimate the error variances of the FY-3E GNOS II RO data product, this study utilizes the FY-3E GNOS II BDS RO, FY-3E GNOS II GPS RO, RS, the ECMWF reanalysis v5 (ERA5), and Final Operational Global Analysis (FNL) datasets. These datasets span from 1 September 2022 to 31 August 2023, covering the region of China.

2.1. Model Data

The ERA5 is a global atmospheric reanalysis produced by the ECMWF. It provides global atmospheric, land, and ocean climate data from 1979 to the present, such as temperature, humidity, wind speed, pressure, precipitation, and so on. It has a horizontal resolution of $0.25°\times 0.25°$, and 37 vertical levels (1000 hPa to 1 hPa). This study uses the pressure, temperature, and specific humidity data from ERA5. These can be downloaded from the website https://cds.climate.copernicus.eu (accessed on 13 October 2023).

In this study, ERA5 data are interpolated into the RO location and time in both spatial and temporal dimensions. The refractivity based on ERA5 is calculated using the Formula (1) by Smith and Weintraub [54]:

$$N=77.6{\displaystyle \frac{P}{T}}+3.73\times {10}^5{\displaystyle \frac{e}{T^2}}$$

(1)

where the symbol $N$ represents refractivity, while the symbols $T$, $P$, and $e$ represent temperature (K), dry atmospheric pressure (hPa), and the partial pressure of water vapor pressure (hPa), respectively.

Using the relationship between specific humidity and water vapor pressure ($e$), the water vapor can be calculated from Formula (2):

$$e={\displaystyle \frac{P\times q}{622+0.378q}}$$

(2)

where $P$ is the atmospheric pressure in hPa and $q$ is the specific humidity in g/kg.

The FNL data are provided by the National Centers for Environmental Prediction (NCEP) and the National Center for Atmospheric Research (NCAR), utilizing the most advanced global data assimilation system and comprehensive database. The FNL data used in this study have a spatial resolution of $1°\times 1°$ and a temporal resolution of 6 h, covering a vertical range from 1000 hPa to 10 hPa, and include global atmospheric parameters such as temperature, isobaric surface, and specific humidity. FNL data are spatially interpolated to the RO locations within a temporal window of ±3 h. The refractivity of FNL data can be calculated using Formulas (1) and (2). FNL data can be downloaded from the website https://rda.ucar.edu (accessed on 13 October 2023).

2.2. Radiosonde Data

The Integrated Global Radiosonde Archive (IGRA) integrates historical and near-real-time radiosonde and pilot balloon observation data from around the globe. These are distributed by the National Oceanic and Atmospheric Administration’s National Centers for Environmental Information (NCEI) [55]. This study utilizes data from 45 RS stations in China, covering the period from 1 September 2022 to 31 August 2023. This includes meteorological parameters such as station latitude and longitude, pressure, temperature, and dew point temperature. The IGRA2 RS data are provided in a text file format (txt) and can be downloaded from the website https://www.ncei.noaa.gov (accessed on 13 October 2023).

Due to the limited ascent height of RS and the difficulty in effectively recording humidity information above 200 hPa, RS data are primarily used to evaluate the atmospheric profile errors of FY-3E GNOS II RO within the pressure range of 1000 hPa to 200 hPa. For the co-location of RS and RO, the co-location criteria are set based on the observation time and geographic coordinates of the RS, with temporal and spatial windows of ±3 h and 300 km, respectively. The closest point in terms of distance is then selected.

To calculate the specific humidity from an RS, the water vapor pressure ($e$) is first calculated using the dew point temperature ($T_{dw}$) Formula (3), and then the specific humidity is calculated using the total atmospheric pressure and the water vapor pressure Formula (1). Given the water vapor pressure, the refractivity of the RS data can be calculated using Formula (2):

$$e=e_0\times \mathit{exp}\left[17.15\times {\displaystyle \frac{t_{dw}}{235+{ t}_{dw}}}\right]$$

(3)

where $t_{dw}$ represents the dew point temperature by °C and $e_0=6.112$ hPa is the saturation water vapor pressure at 0 °C. This formula is suitable for dew point temperatures ranging from −45 °C to 60 °C.

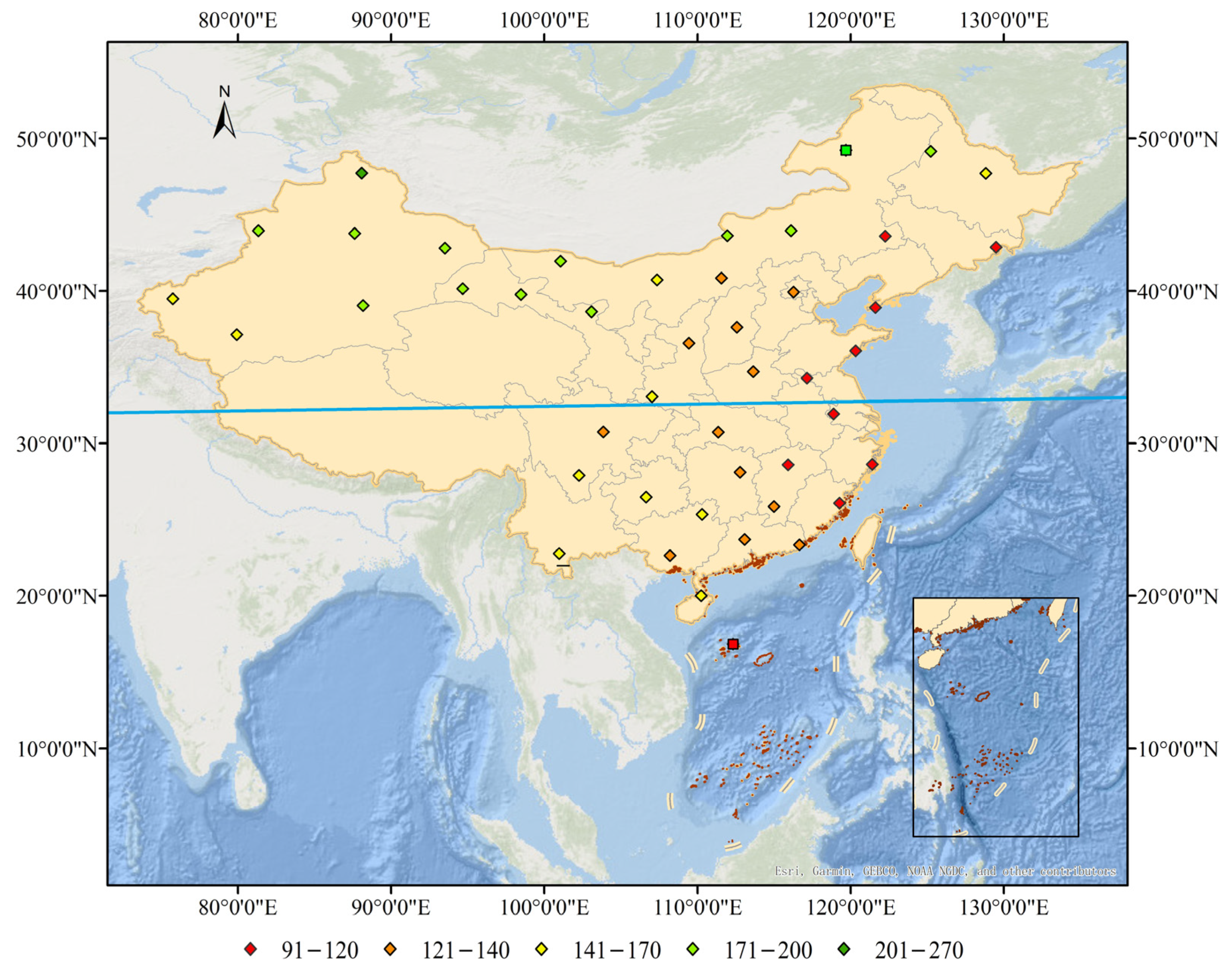
2.3. FY-3E GNOS II RO Data

The FY-3E GNOS II RO data utilized in this study are provided by the National Satellite Meteorological Centre (NSMC), China Meteorological Administration (CMA). Launched on 5 July 2021, FY-3E is the world’s first civil meteorological satellite in an early morning orbit. Using initial data provided by the CMA Global Forecast System (CMA-GFS), the temperature and specific humidity under moist air conditions are inverted through a one-dimensional variational process. The neutral atmospheric profiles from this satellite are primarily stored in the Dry Atmospheric Profile (ATP) and Wet Atmospheric Profile (WAP). This study analyzes the error variances of FY-3E GNOS II RO data using the RO event time and spatial information, temperature, pressure, and specific humidity data obtained from the WAP files, covering the period from 1 September 2022 to 31 August 2023. These data can be accessed via the website http://data.nsmc.org.cn (accessed on 13 October 2023).

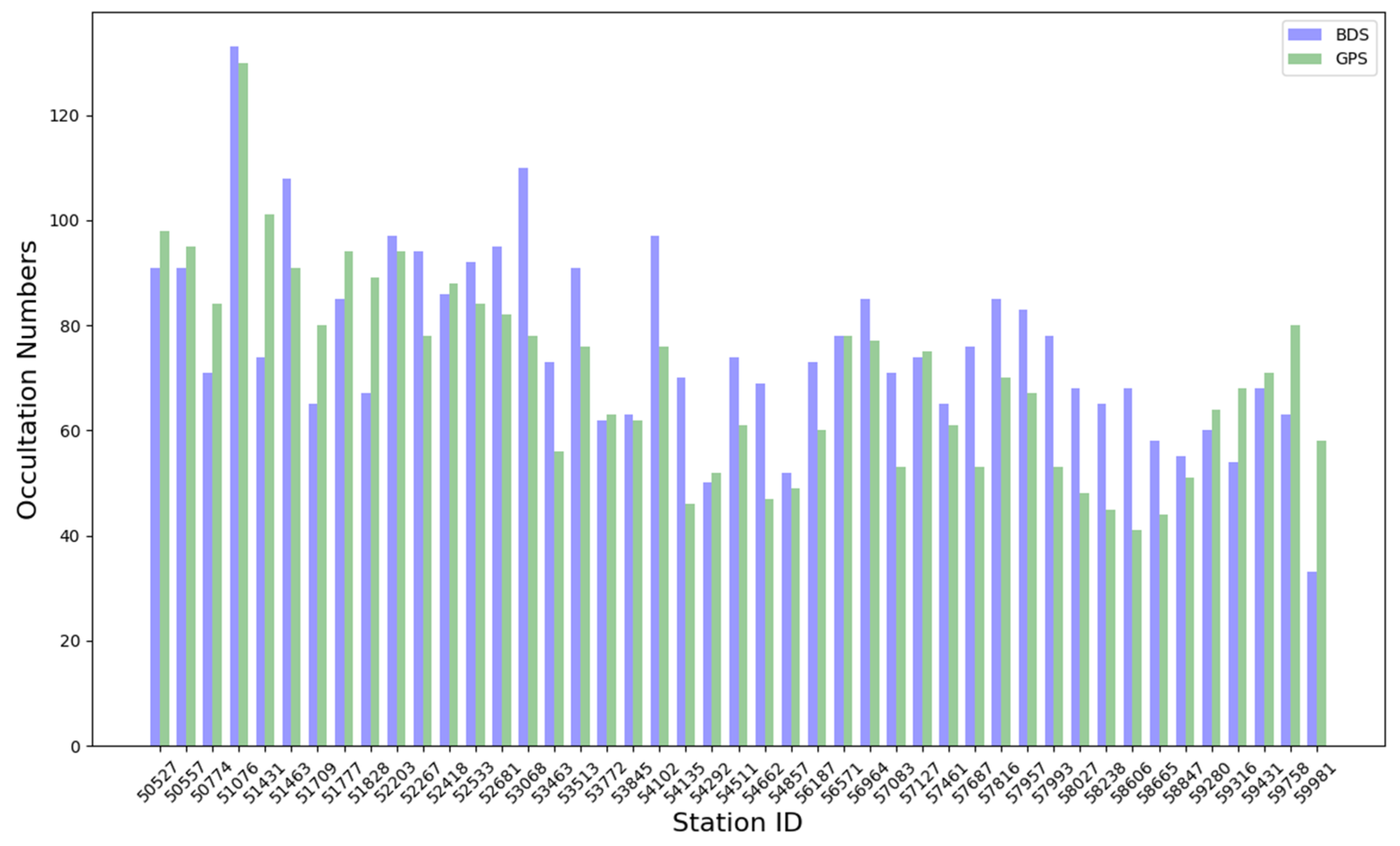
2.4. Co-Location of the Datasets

The Qinghai–Tibet Plateau is known as the “Roof of the World”. It features high altitudes and complex, variable terrain, significantly differentiating its atmospheric conditions from those of lower-altitude regions. The extreme environmental conditions of the plateau may impact the performance of RS instruments and the accuracy of their data; to ensure the accuracy and reliability of RS data, this study excludes RS stations from the Tibetan Plateau area.

Due to the significant variability in atmospheric parameters over small spatial scales, maintaining sufficient distances between RS stations is crucial to accurately capture the variations brought about by geographical and climatic differences. In China, the distribution of RS stations is uneven, with high density in some regions. To reduce data overlap and interference, this study stipulates that each RS station must be unique within a 300 km radius. Ultimately, 45 RS stations are selected for further research and analysis (Figure 1).

To thoroughly analyze the atmospheric characteristics of different climatic regions in China, this study divides China into northern and southern regions based on the approximate latitude of the Qinling–Huaihe River (32–34°N). This division helps to explore the climate conditions in different regions and the error characteristics of atmospheric observation data.

From Figure 1 and Figure 2, it is observed that the number of occultations co-located in the northern region of China is significantly greater than that in the southern region. This phenomenon is primarily determined by the orbital characteristics of the FY-3E satellite, namely, its higher revisit rates in mid- to high-latitude areas [33]. This attribute allows the northern region to produce more occultation data, thereby providing denser atmospheric parameter observations.

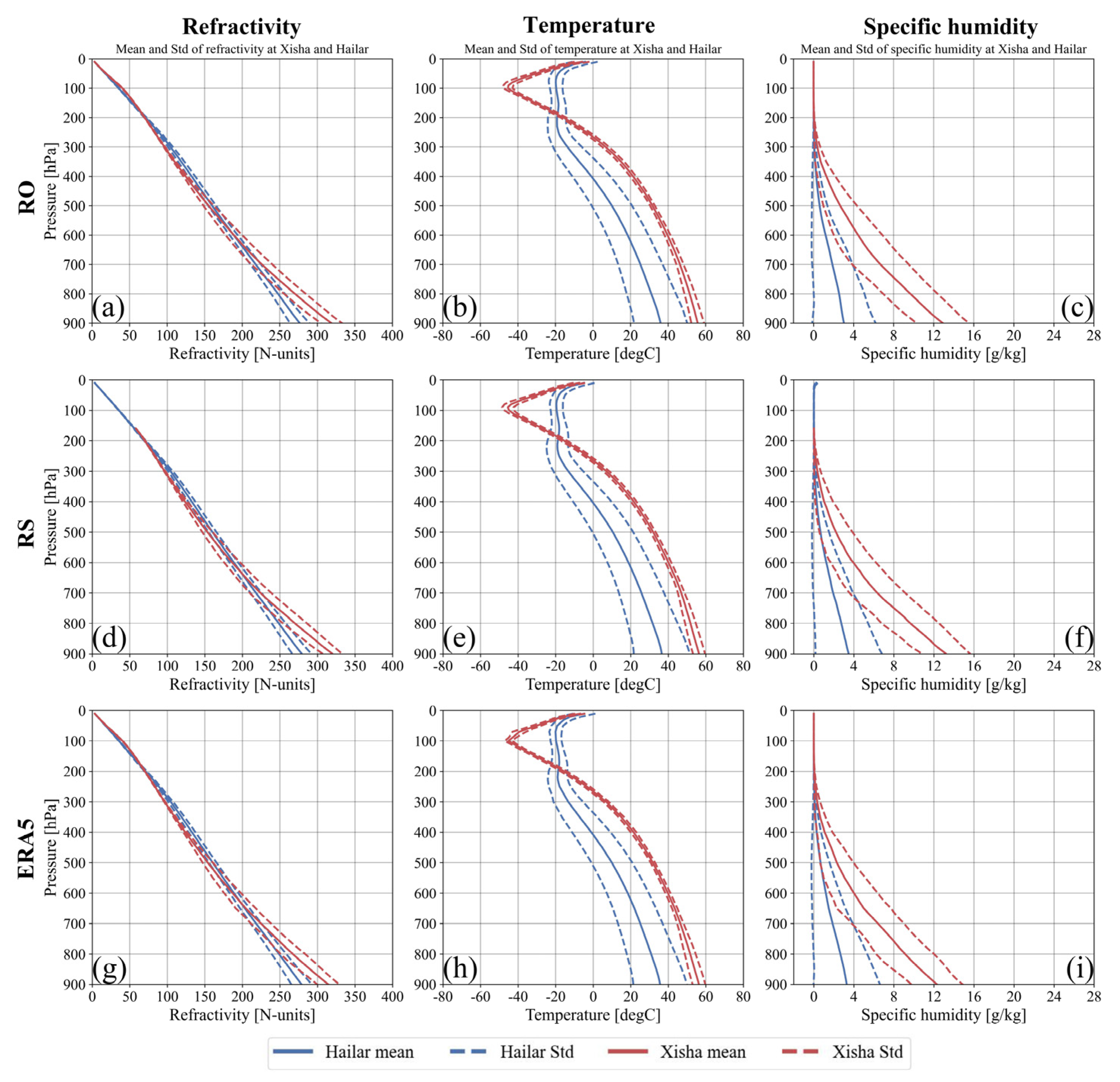
2.5. Mean Atmospheric Profiles

This subsection calculates the mean values and standard deviations of refractivity, temperature, and specific humidity data for the RO, RS, and ERA5 datasets at the southernmost Xisha station and the northernmost Hailar station. This demonstrates the data characteristics of different climatic conditions (Figure 3), where the Xisha station represents the tropical marine climate and the Hailar station represents the temperate continental climate. The Hailar station, located at an elevation of 653.3 m, cannot measure atmospheric conditions below 937.2 hPa, resulting in there being missing data for these pressure levels. Therefore, this section only analyzes the data from 900 hPa to 0 hPa.

Due to the high water vapor content in the lower atmosphere, the influence of water vapor on refractivity is significant, resulting in considerable differences in refractivity between the Xisha and Hailar stations (Figure 3a,d,g). However, in the middle and upper atmosphere, changes in water vapor, pressure and temperature cause the refractivity values at the Hailar station to approach those of the Xisha station.

The temperature profiles (Figure 3b,e,h) indicate that the average temperature at the Xisha station is higher than that at the Hailar station below 200 hPa. However, a notable temperature inversion phenomenon occurs between 0 hPa and 200 hPa, where the average temperature at the Xisha station is lower than that at the Hailar station, a characteristic of tropical climates.

From Figure 3c,f,i, it can be observed that in the lower atmosphere, the specific humidity at the Xisha station is significantly higher than at the Hailar station. In the middle and upper atmosphere, the difference in specific humidity between the two locations gradually decreases, but the specific humidity at the Xisha station remains slightly higher than that at the Hailar station. This is related to the differing climatic conditions of the two locations.

The comparison of the RO, RS, and ERA5 datasets shows that the three types of data exhibit good consistency.

3. Assessment Methods

To mitigate the sampling errors of both the RO–RS and RS–model pairs, we use a new spatial–temporal sampling correction method. Subsequently, the 3CH method is used to calculate the error variances of the RO, RS and ERA5 datasets, thereby facilitating a comprehensive statistical analysis of these datasets.

3.1. Spatial–Temporal Sampling Correction Algorithm

The spatial–temporal sampling errors of the co-located RO–RS pairs caused by the differences in the geographical location and measurement time of the RO and RS data. Meanwhile, the model data profiles used in this study are retrieved from the models of ERA5 and FNL by using GNSS RO event spatial and time information; thus, there are also spatial–temporal sampling errors between the RS–model pairs.

In order to mitigate the spatial–temporal sampling errors of the RO–RS pairs, we use the “double-difference” spatial–temporal sampling correction method, expressed in Formulas (4)–(6):

$$X^{SC}=\left(X_{RO}-X_{model\left(RO\right)}\right)-\left(X_{RS}-X_{model\left(RS\right)}\right)$$

(4)

$$X^{SC}=\left(X_{RO}-X_{RS}\right)-\left(X_{model\left(RO\right)}-X_{model\left(RS\right)}\right)$$

(5)

$$X^{SC}=X_{RO}-\left[X_{RS}+\left(X_{model\left(RO\right)}-X_{model\left(RS\right)}\right)\right]$$

(6)

where $X^{SC}$ represents the spatial–temporal sampling correction differences, $X_{model\left(RO\right)}$ represents the model values interpolated in time and space to the GNSS RO profile grids, $X_{model\left(RS\right)}$ represents the model grid values closest to the RS launch time, and the difference between them, $X_{model\left(RO\right)}-X_{model\left(RS\right)}$, is referred to as the model correction term.

The “double-difference” effectively isolates the true measurement differences from spatial and temporal sampling errors by referencing both datasets against a common baseline, thereby enhancing the accuracy of comparative analysis. To reinterpret the correction term, we modify the Formulas (4) to (5). This revised formula integrates the model correction term into the RS dataset, allowing it to better reflect the atmospheric conditions at the RO measurement location. Then, we modify the Formulas (5) to (6); the term in the square bracket represents the correction term for RS data. Therefore, the Formula (7) expresses the RS correction term $X_{RS}^{SC}$:

$$X_{RS}^{SC}=X_{RS}+\left(X_{model\left(RO\right)}-X_{model\left(RS\right)}\right)$$

(7)

In this way, the RS data corrected using the $X_{RS}^{SC}$ term can be used in the 3CH method to calculate the differences between RS and model (i.e., ERA5 and FNL) data easily. The application of the corrected RS data in the RS and model differencing process represents the improvement with our new spatial–temporal correction method.

3.2. Three-Cornered Hat Algorithm

The 3CH algorithm can simultaneously estimate the error variances of three or more datasets, and can effectively eliminate the bias between different data. Its accuracy is affected by factors such as error correlation, sample size, and random error [47]. When the error correlation between each data point is small, the error variance calculated using this method is accurate [36]. So far, the FY-3E GNOS II RO data have not been assimilated to the ERA5 and FNL data; therefore, the RO data used in this study are independent of the model data. While ERA5 and FNL models assimilate RS data, there should be a correlation between them. Currently, thanks to lots of other observations being assimilated into ERA5 and FNL models, the correlation between model data and RS data is small. Therefore, we assume that the datasets are independent of each other.

To effectively highlight the similarities and differences between different datasets, especially in the upper troposphere, the datasets are normalized based on ERA5 prior to the application of the 3CH method [42]. The derivation process of the 3CH method is described below.

When using datasets B ($X_B$) and C ($X_C$) as references to estimate the error variance of dataset A ($X_A$), we calculate the mean-square difference between A and B, denoted as ${\sigma }_{A-B}^2$; between A and C, denoted as ${\sigma }_{A-C}^2;$ and between B and C, denoted as ${\sigma }_{B-C}^2,$ respectively. Formulas (8)–(10) use $X_A$ and $X_B$ as an example:

$$X_{A-B}=X_A-X_B$$

(8)

$${\sigma }_{A-B}^2={\displaystyle \frac{1}{n}}\sum {(X_{A-B}-{ \mu }_{A-B})}^2$$

(9)

$${\sigma }_{A-B}^2={\sigma }_A^2+{\sigma }_B^2-2{COV}_{err}\left(A,B\right)$$

(10)

where $X$ represents the values of variables in these datasets, $\mu$ represents the mean value of the difference between the two datasets, and ${COV}_{err}$ represents the covariance between datasets.

Under the assumption that the errors in datasets A, B, and C are independent of each other, the covariance terms can be neglected. The following equation can be obtained:

$${\sigma }_{A-B}^2={\sigma }_A^2+{\sigma }_B^2$$

(11)

$${\sigma }_{A-C}^2={\sigma }_A^2+{\sigma }_C^2$$

(12)

$${\sigma }_{B-C}^2={\sigma }_B^2+{\sigma }_C^2$$

(13)

Therefore, combining Formulas (11)–(13), we can derive an independent linear equation to estimate the error variance of dataset A (${\sigma }_A^2$):

$${\sigma }_A^2={\displaystyle \frac{1}{2}}{\sigma }_{A-B}^2+{\displaystyle \frac{1}{2}}{\sigma }_{A-C}^2-{\displaystyle \frac{1}{2}}{\sigma }_{B-C}^2$$

(14)

This study estimates the observation error variances for various datasets using different combinations of RO, RS, ERA5, and FNL data. Utilizing Formula (14), we obtain three complete and precise linearly independent solutions for use estimating the error variance of RO data.

Combination of datasets, 1:

$${\sigma }_{RO}^2={\displaystyle \frac{1}{2}}{\sigma }_{RO-ERA5}^2+{\displaystyle \frac{1}{2}}{\sigma }_{RO-FNL}^2-{\displaystyle \frac{1}{2}}{\sigma }_{FNL-ERA5}^2$$

(15)

Combination of datasets, 2:

$${\sigma }_{RO}^2={\displaystyle \frac{1}{2}}{\sigma }_{RO-ERA5}^2+{\displaystyle \frac{1}{2}}{\sigma }_{RO-RS}^2-{\displaystyle \frac{1}{2}}{\sigma }_{RS-ERA5}^2$$

(16)

Combination of datasets, 3:

$${\sigma }_{RO}^2={\displaystyle \frac{1}{2}}{\sigma }_{RO-FNL}^2+{\displaystyle \frac{1}{2}}{\sigma }_{RO-RS}^2-{\displaystyle \frac{1}{2}}{\sigma }_{RS-FNL}^2$$

(17)

Using the three equations above, we can calculate the observational error variances of RO data. The same procedure can be employed to derive three equations for use estimating the error variances of other datasets (RS and ERA).

3.3. Experimental Programs

Firstly, we evaluate the impact of spatial–temporal sampling corrections on the estimation of 3CH error variance through a comparative analysis of three experimental groups. Then, based on an optimized 3CH method, we analyze the error variances of FY-3E GNOS II BDS and GPS RO refractivity, temperature, and specific humidity data in the China area. The specific experimental plans are as follows.

(1)

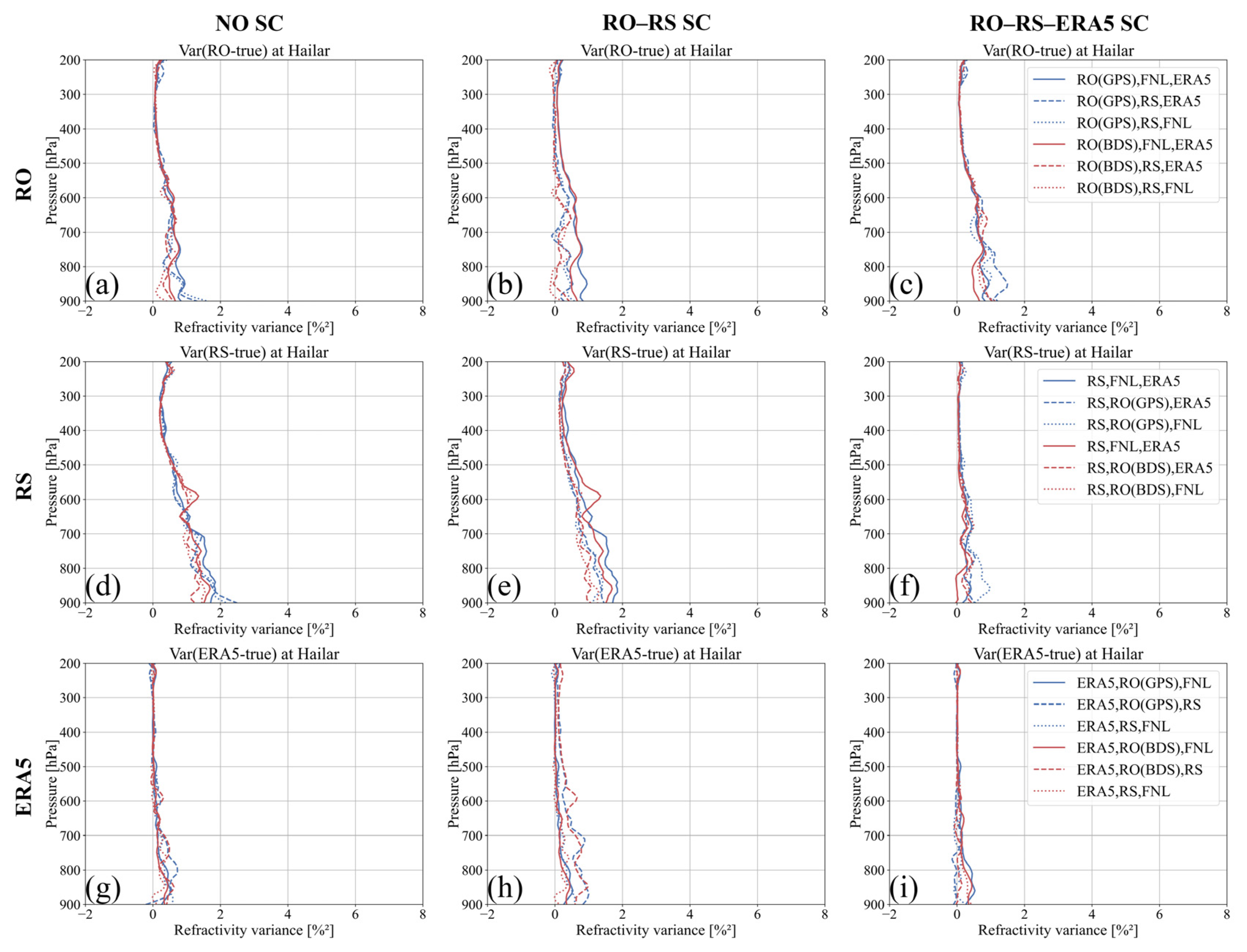
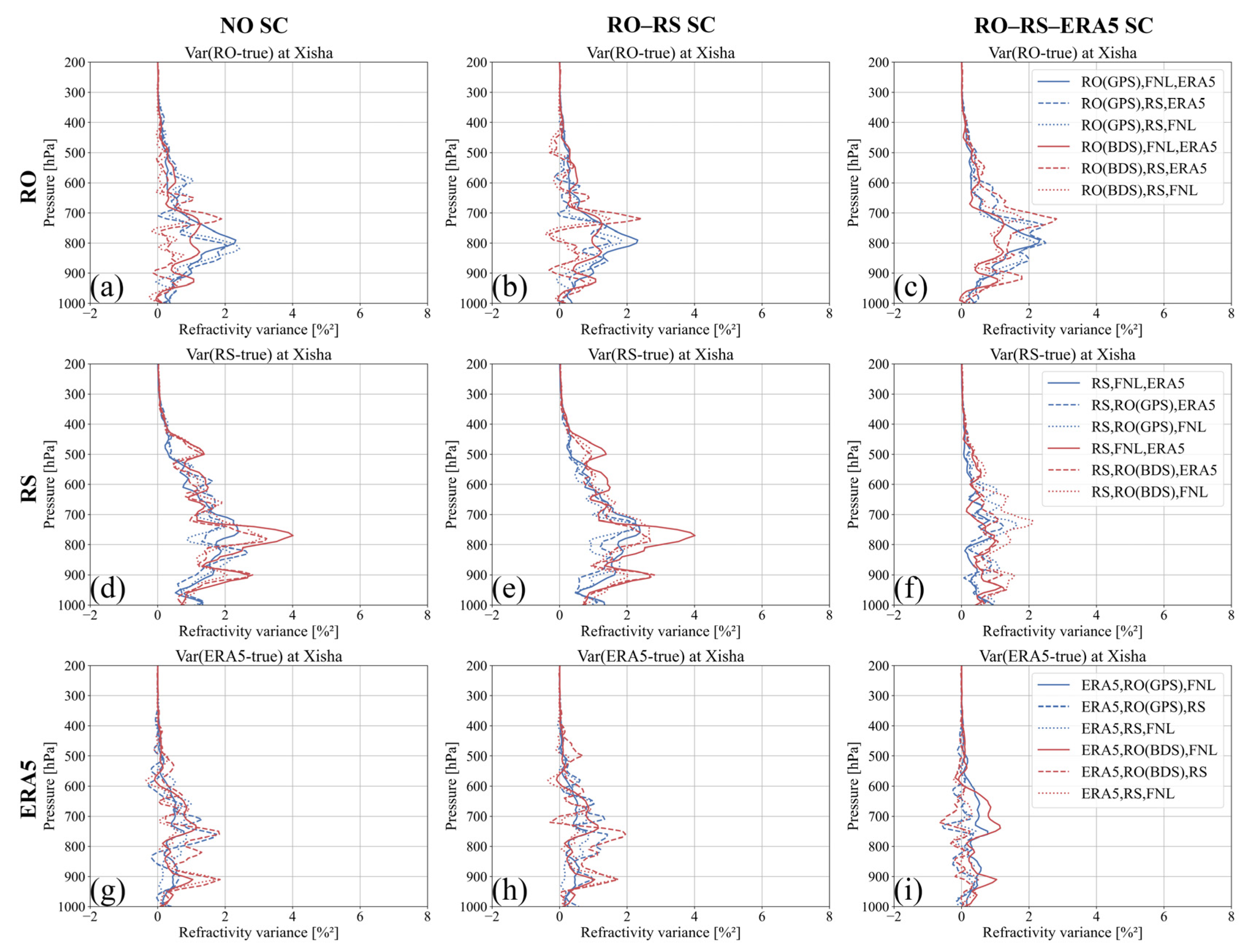
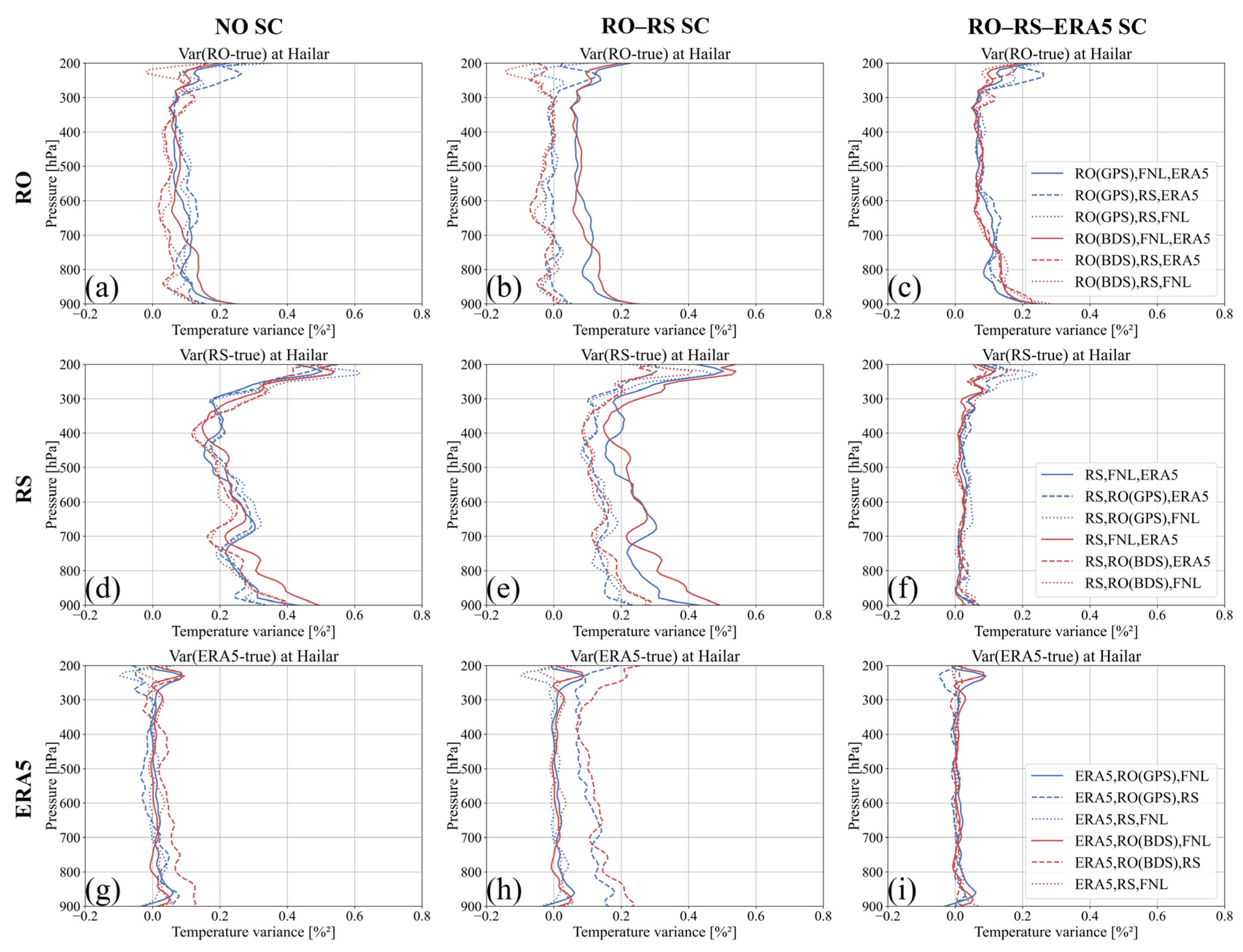
There were three experimental groups: no spatial–temporal sampling correction (NO SC), spatial–temporal sampling correction for RO–RS co-located pairs (RO–RS SC), and spatial–temporal sampling correction for both RO–RS and RS–model co-located pairs (RO–RS–ERA5 SC) data groups. These were calculated using the 3CH algorithm. We performed no sampling correction, only RO–RS sampling correction, and both RO–RS and RS–model sampling correction, respectively. In each data group, the error variances of refractivity, temperature, and specific humidity data for the RO, RS, and ERA5 datasets were computed using data from China’s northernmost RS station, Hailar, and the southernmost station, Xisha. Then, according to the results, we evaluated the impact of each correction scheme on the 3CH error variances and chose the best 3CH data processing chain.

(2)

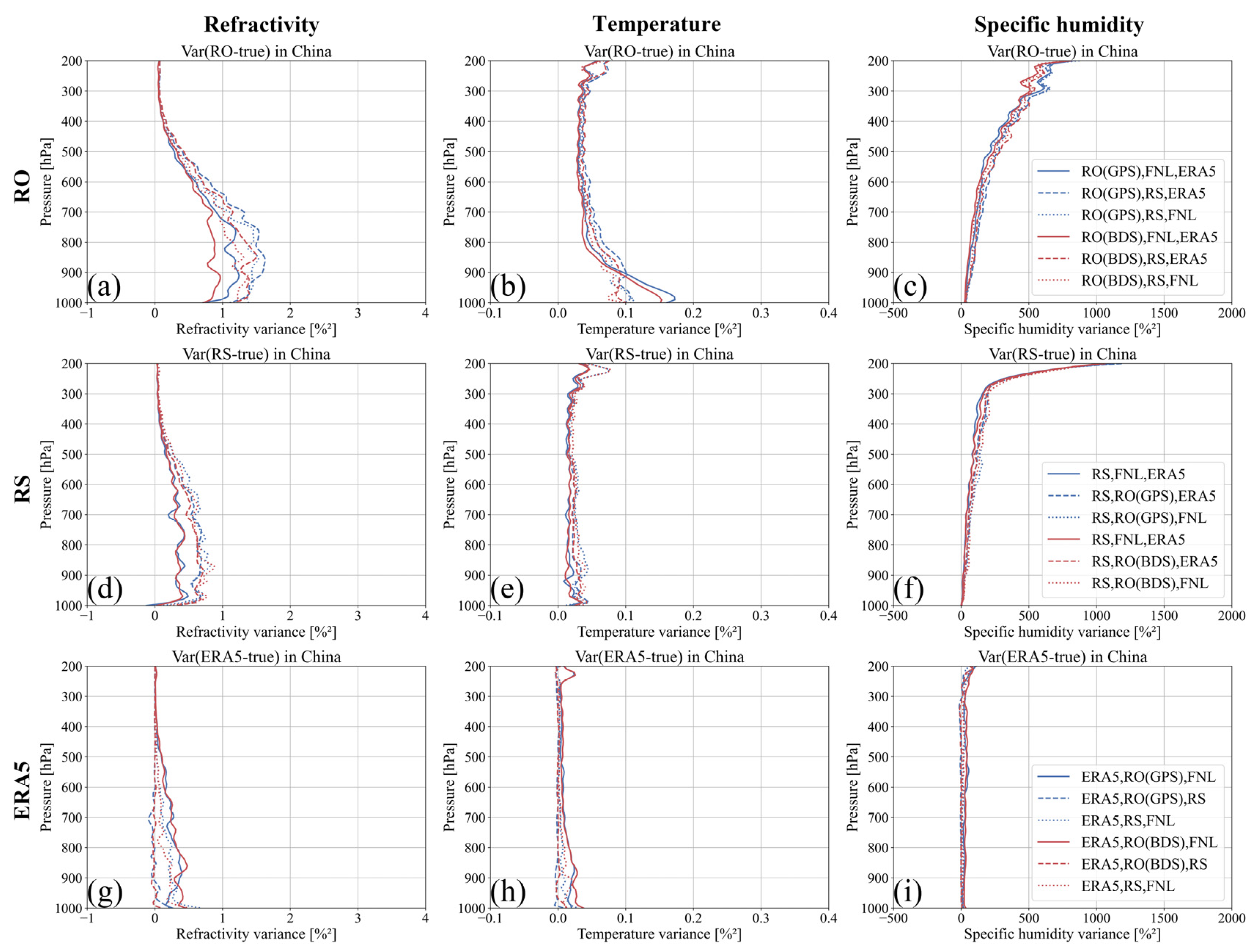
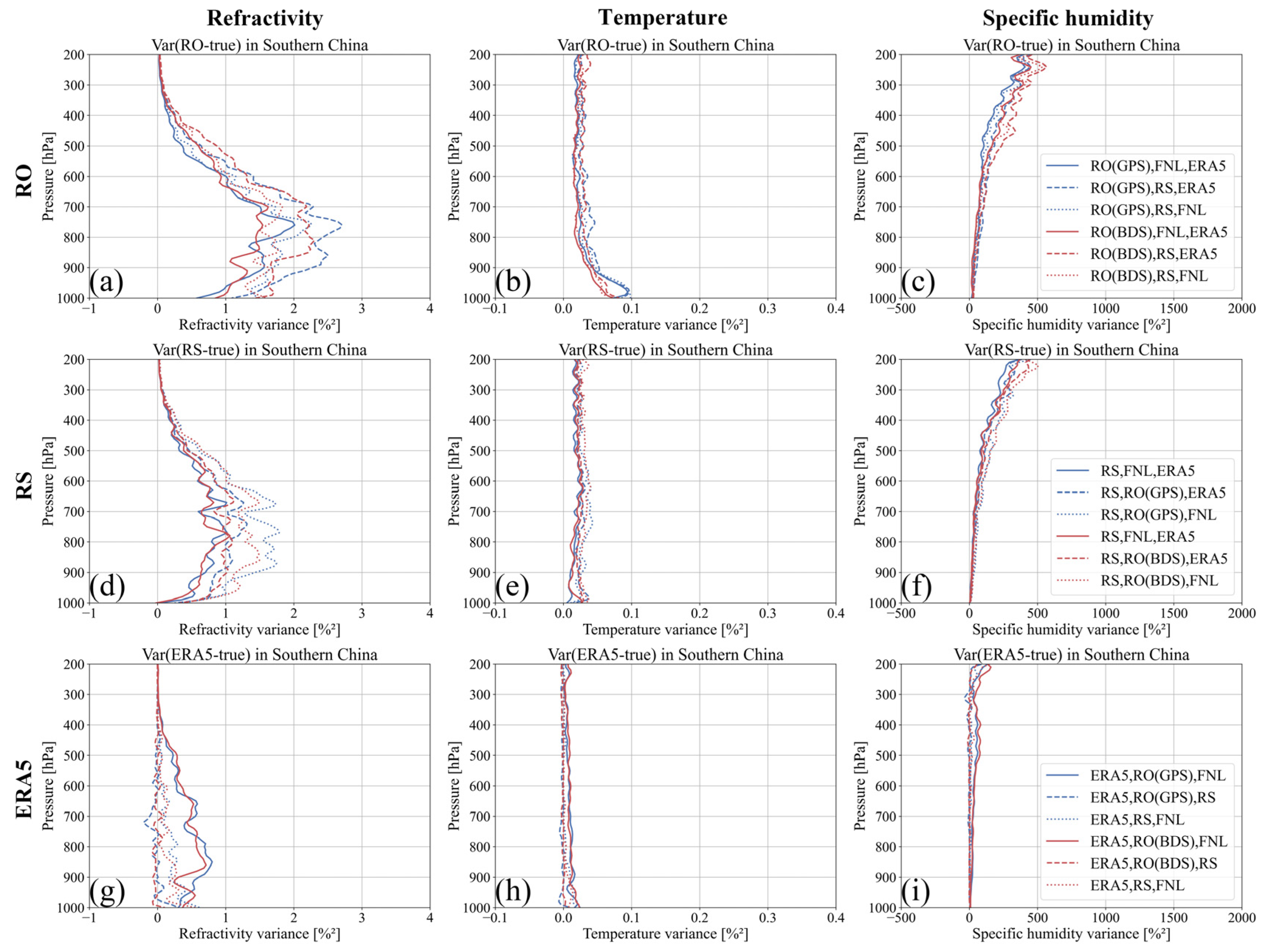
Using the optimized 3CH method, we calculated the error variances of refractivity, temperature, and specific humidity for the RO, RS, and ERA5 datasets at the 45 selected RS stations. Then, the data were divided into northern and southern China groups based on the locations of the RS stations. Finally, we conducted a comparative analysis of the 3CH error characteristics across different regions, GNSS systems, and datasets.

4. Results and Analysis

This section examines the effects of three spatial–temporal sampling correction schemes on the 3CH error variances across different datasets, utilizing data from the two individual RS stations. It then presents the 3CH error variances of the FY-3E GNOS II GPS and BDS RO data, comparing these with other datasets using large ensemble datasets from northern and southern China.

4.1. Comparison of Spatial–Temporal Sampling Correction Effects

This subsection presents the estimated error variances for refractivity, temperature, and specific humidity at the two selected individual stations, i.e., Hailar and Xisha. The analysis is based on the RO, RS, and ERA5 datasets, which are processed through the three different 3CH processing chains, illustrated in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9. To compare the performance of the three processing chains, the three columns represent the experimental groups: NO SC, RO–RS SC, and RO–RS–ERA5 SC. Meanwhile, to examine the error characteristics of the different datasets, the three rows display the RO, RS, and ERA5 datasets. In each subplot, the GPS and BDS RO datasets are depicted in blue and red, respectively, while different combinations of datasets used for computing the 3CH error variances are indicated by varying line styles.

4.1.1. Refractivity Error Variances

Figure 4 and Figure 5 illustrate the estimated refractivity error variances for the different datasets at the Hailar and Xisha stations, respectively. Overall, the GPS and BDS datasets exhibit consistent results, and the refractivity error variances of ERA5 data are relatively smaller than those of RO and RS datasets. The refractivity error variances increase with rising pressure, and the error variances at the Xisha station are greater than those at the Hailar station due to differences in the atmospheric conditions (e.g., temperature, pressure, and water vapor content) surrounding the two radiosonde stations.

Specifically, from the NO SC experimental group, one can find that the refractivity error variances of RS data are relatively larger than those of RO data. Due to the effects of spatial–temporal sampling errors, the refractivity error variances of RO and RS datasets exhibit relatively large fluctuations of around 1%² at the Hailar station (Figure 4a,d) and 2%² at the Xisha station (Figure 5a,d). Comparing the ERA5 datasets for the two stations, it is observed that the refractivity error variance at the Hailar station is smaller, varying by an amount near zero (Figure 4g and Figure 5g).

In the RO–RS SC experimental group, the refractivity error variances of RO and RS data at the Hailar station decreased, after using the RO–RS correction algorithm (Figure 4b,e), with a reduction magnitude of approximately 0.5%². However, the refractivity variances of RO and RS data at the Xisha station decreased slightly (Figure 5b,e), with a decrease of about 0.3%². Due to the elimination of the spatial–temporal sampling error for RO–RS pairs, these are used as a subtractive element in the ERA5, RO, and RS combination, leading to a slight increase in the error variance for this combination (Figure 4h and Figure 5h).

As shown in the RO–RS–ERA5 SC experimental group, the refractivity error variances of the RS and ERA5 data at both the Hailar and Xisha stations decreased significantly (see Figure 4f,i and Figure 5f,i), with error variances near 0.1%², 0%², 1%², and 0.3%², respectively. The refractivity error variances of the RO data at both stations exhibit only a slight decrease (see Figure 4c and Figure 5c), while the average of refractivity error variances for two stations show a maximum of 1.2%² and 2.1%², respectively. Overall, the RO–RS–ERA5 SC demonstrates better performance compared to the RO–RS SC.

4.1.2. Temperature Error Variances

Figure 6 and Figure 7 illustrate the estimated temperature error variances for the different datasets at the Hailar and Xisha stations, respectively. Overall, the temperature error variances of the ERA5 dataset are smaller compared to those in the RO and RS datasets. Except for slight differences in the temperature error variances between the BDS and GPS datasets below 600 hPa in the RS dataset at the Xisha station, the results from the other datasets are relatively consistent. Due to different climatic characteristics at the Hailar and Xisha stations, the temperature error variances also vary, with the Hailar station exhibiting larger variances.

The NO SC experimental group indicates that the temperature error variances of the RO and ERA5 datasets are both lower than those of the RS dataset. The error variances of the three datasets at the Hailar station are distributed at 0.1%², 0.2%², and nearly zero (Figure 6a,d,g). The temperature error variances of the RO and ERA5 datasets at the Xisha station exhibit relatively stable fluctuations (Figure 7a,g), whereas those of the RS dataset show slightly larger variations between 600 hPa and 1000 hPa (Figure 7d). This is primarily due to the inherent spatial and temporal discrepancies seen among the co-located pairs.

In the RO–RS SC experimental group, at the Hailar station, the error variances of the RO and RS data are significantly reduced in the RO, RS, and ERA5 (FNL) and RS, RO, ERA5 (FNL) combinations (Figure 6b,e), whereas the error variance of the ERA5, RO, and RS combination within the ERA5 dataset shows an increase (Figure 6h). Similar to the previously mentioned refractivity error variances, eliminating the spatial–temporal sampling errors in the RO–RS pairs results in positive (RO and RS) and negative (ERA5) effects on the error variances. The temperature error variances for these three combinations are, respectively, less than 0.22%², 0.56%², and 0.21%². At the Xisha station, the temperature error variances of the RO and ERA5 datasets are relatively stable (Figure 7b,h), primarily fluctuating near zero. However, the RS dataset that includes the GPS RO data combination exhibits larger variations in temperature error variances between 600 and 1000 hPa (Figure 7e), with a maximum error variance reaching 0.32%².

In the RO–RS–ERA5 SC experimental group, it was evident that the differences in temperature error variances among the RO, RS, and ERA5 data combinations at the Hailar station decreased (Figure 6c,f,i), with the average maximum error variances being 0.2%², 0.18%², and 0.1%², respectively. At the Xisha station, the temperature error variances of the RS data significantly decreased (Figure 7f), with most fluctuating near zero. Meanwhile, the temperature error variances for RO and ERA5 data oscillate around 0.05%² and near zero, respectively (Figure 7c,i).

Compared to the other two experimental groups, the RO–RS–ERA5 experimental group shows better convergence regarding error variances across different data combinations.

4.1.3. Specific Humidity Error Variances

Figure 8 and Figure 9 illustrate the estimated specific humidity error variances for the different datasets at the Hailar and Xisha stations, respectively. Overall, the RO and RS specific humidity error variances at the Hailar and Xisha stations gradually decreased with increasing pressure. Notably, significant fluctuations were observed between the 200 hPa and 700 hPa. The specific humidity error variances of BDS and GPS data were quite consistent. Compared to RO and RS, the specific humidity error variances of the ERA5 dataset were more stable.

In the NO SC experimental group, the specific humidity error variances of RO, RS, and ERA5 data at the Hailar station are primarily distributed at 0%²–1000%², 0%²–800%², and near zero, respectively (Figure 8a,d,g). Compared to the Hailar station, the specific humidity error variances of RO data at the Xisha station are relatively smaller below 400 hPa (Figure 9a), being primarily distributed between 0%² and 300%². And the specific humidity error variances of RS data above 500 hPa are more pronounced (Figure 9d), reaching up to 1700%². When comparing the ERA5 datasets at both stations, it is observed that the specific humidity error variances of both fluctuate near zero, indicating greater stability (Figure 9g).

In the RO–RS SC experimental group, the specific humidity error variances of the combinations of RO, RS, and ERA5 (FNL) and RS, RO, and ERA5 (FNL) at the Hailar and Xisha stations slightly decreased (Figure 8b,e and Figure 9b,e), with the maximum reduction in RO data at the Xisha station being about 300%². However, the error variance of the ERA5, RO, and RS combination within the ERA5 dataset slightly increased (Figure 8h and Figure 9h), with a maximum increase of about 200%². Compared to the NO SC experimental group, the differences among various data combinations of RO, RS, and ERA5 widened.

As evidenced in the RO–RS–ERA5 SC experimental group, the differences in specific humidity error variances among the various combinations of RO (Figure 8c and Figure 9c), RS (Figure 8f and Figure 9f), and ERA5 data (Figure 8i and Figure 9i) are smaller, demonstrating a more concentrated effect. The specific humidity error variances of RS data at the Hailar and Xisha stations significantly decreased, with variances ranging between 0%² and 500%² below 300 hPa (Figure 8f and Figure 9f). Therefore, the RO–RS–ERA5 experimental group demonstrated better correction effects. Between 200 and 300 hPa, the specific humidity error variances of RO and RS data at the Hailar station increased rapidly (Figure 8c,f).

In summary, due to the different climatic conditions at the Hailar and Xisha stations, there are differences in refractivity, temperature, and specific humidity error variances. Specifically, the Hailar station exhibits larger variations in temperature and specific humidity error variances, while the Xisha station shows greater changes in refractivity error variances. Additionally, a comparative analysis of three different 3CH processing chains reveals that the RO–RS–ERA5 experimental group effectively adjusts the spatial–temporal sampling errors between RO–RS and RS–model pairs, thereby more accurately reflecting the actual atmospheric conditions at each observation site.

Therefore, we employ the 3CH processing chain with the RO–RS–ERA5 spatial–temporal sampling correction scheme to evaluate the FY-3E GNOS II GPS RO, FY-3E GNOS II BDS RO, RS, and ERA5 datasets in China and its northern and southern regions.

4.2. Error Variances Based on Ensemble Datasets

This subsection presents the estimated error variances for refractivity, temperature, and specific humidity using large ensemble data from China. For this, we use the 3CH processing chain with the RO–RS–ERA5 spatial–temporal sampling correction scheme, which is illustrated in Figure 10, Figure 11 and Figure 12. The three columns represent the data variables, i.e., refractivity, temperature, and specific humidity. Meanwhile, to examine the error characteristics of the different datasets, the three rows display the RO, RS, and ERA5 datasets. In each subplot, similarly, the GPS and BDS RO datasets are depicted in blue and red, respectively, while different combinations of datasets used for computing the 3CH error variances are indicated by varying line styles.

4.2.1. Results for the Entire Region of China

In order to summarize the statistical error characteristics of the FY-3E GNOS II BDS RO, FY-3E GNOS II GPS RO, RS, and ERA5 data in China, Figure 10 shows the estimated values of the refractivity, temperature and specific humidity error variances for these datasets over the China region. The estimated error variances of FY-3E GNOS II BDS and FY-3E GNOS II GPS RO show minimal differences, demonstrating good consistency. Comparing RO, RS, and ERA5 datasets, the ERA5 dataset exhibits the smallest error variance.

The refractivity error variances of RO data range from 0%² to 1.8%² (Figure 10a). For RS data, the maximum refractivity error variance of approximately 0.9%² occurs at 900 hPa, with the RS, FNL, and ERA5 combination showing the smallest error variance (Figure 10d). ERA5 data exhibit the smallest refractivity error variances, all below 0.5%², particularly the ERA5, RO, and RS combination, which approaches zero (Figure 10g). The refractivity error variances of RO, RS, and ERA5 data exhibit large scattering in the lower atmosphere, primarily due to the negative bias in refractivity caused by super-refraction, which increases the refractivity error variances.

Figure 10b,e,h show the error variances of the temperature profiles of the RO, RS, and ERA5 datasets. Above 800 hPa, the error variances of the RO are mostly distributed within 0.05%², while those in the lower troposphere are larger and can reach a maximum of 0.18%². The estimated RS temperature error variances oscillate between 0%² and 0.04%². The ERA5 temperature error variances are slightly lower and on average close to zero. Due to the influence of temperature inversion layers in the lower troposphere and limitations of detection technology, the error variances of RO temperature data are larger near the ground.

As shown in Figure 10c,f, the distributions of specific humidity error variances for RO and RS data are similar, both exhibiting a trend of increasing with pressure. Below 300 hPa, the specific humidity error variances of RO data are less than 500%², while those of RS data are less than 300%². The specific humidity error variances of ERA5 data are relatively stable, mainly fluctuating near zero (Figure 10i).

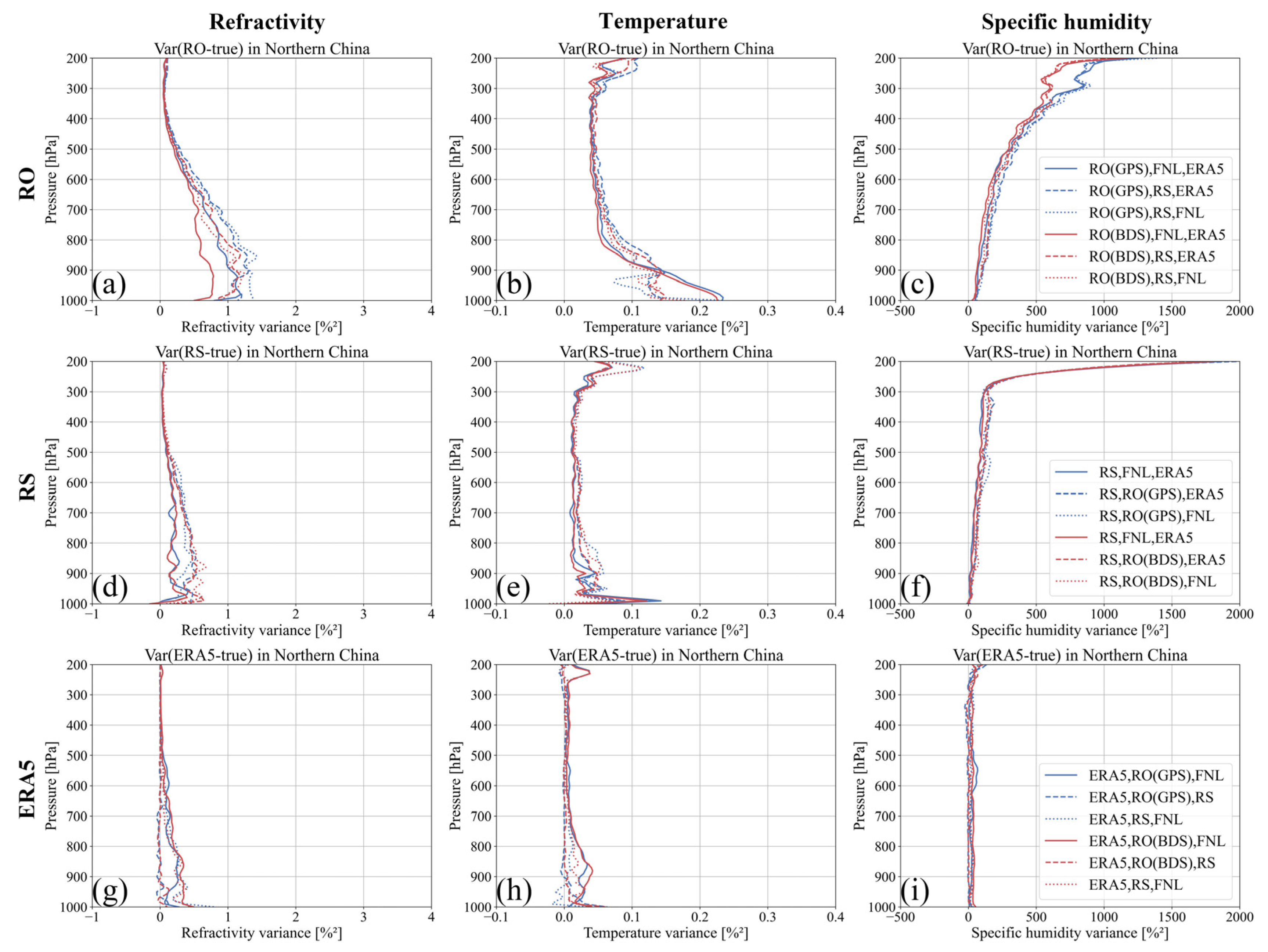
4.2.2. Comparison Results between the Northern and Southern Regions of China

In order to understand the impact of regional climate on the accuracy of atmospheric observation data, this section analyzes the atmospheric parameter error variances of FY-3E GNOS II BDS RO, FY-3E GNOS II GPS RO, RS, and ERA5 data in southern and northern China. Figure 11 and Figure 12, respectively, present the estimated values of refractivity, temperature, and specific humidity error variances for three datasets in the southern and northern regions of China.

In the northern and southern regions of China, the refractivity error variances increase with rising atmospheric pressure. The error variances of BDS and GPS RO refractivity show good consistency across these regions. In the southern region (Figure 11a), the distribution of RO refractivity error variances ranges from 0%² to 2.7%², while in the north (Figure 12a), it ranges from 0%² to 1.3%², with the RO, FNL, ERA5 combination exhibiting relatively smaller error variances.

For RS (Figure 11d and Figure 12d), the refractivity error variances of the south mainly range from 0%² to 1.8%², and in the north from 0%² to 0.7%², with the RS, FNL, ERA5 combination showing the smallest error variances.

Compared to RO and RS, the refractivity error variances of ERA5 are smaller (Figure 11g and Figure 12g), with the maximum error variance not exceeding 1%² in either region. Notably, the ERA5, RO, and RS combination has the smallest refractivity error variances, standing at almost zero.

Super-refraction phenomena frequently occur in tropical and subtropical regions [42], which is why the refractivity error variances of southern China are greater than those in the north.

Comparing the temperature error variances between the northern and southern regions of China, it is observed that the temperature error variances of BDS and GPS RO data show good consistency. In the lower atmosphere, the temperature error variances of RO data are significant in both regions, reaching a maximum of 0.1%² in the south (Figure 11b) and 0.22%² in the north (Figure 12b).

The RS and ERA5 results for temperature error variances of southern China are relatively small, with estimated temperature error variance profiles generally fluctuating near zero (Figure 11e,h). Compared with southern China, the temperature error variances for RS and ERA5 data in northern China (Figure 12e,h) fluctuate more near the surface, with maximum values of 0.14%² and 0.06%², respectively.

The temperature error variances for RO, RS, and ERA5 data in the southern region are smaller than those in the north, which is related to the climatic conditions of the two regions. The southern part of China, being subtropical and tropical, has a relatively stable temperature, whereas the north, with its significant seasonal and diurnal fluctuations, exhibits increased uncertainty in temperature measurements.

The specific humidity error variances among the datasets of different GNSS RO systems show good consistency across the northern and southern regions of China. In both regions, the specific humidity error variances of RO and RS data increase as atmospheric pressure decreases because specific humidity is a normalized variable. In the southern region (Figure 11c,f), the specific humidity error variances for RO and RS data are primarily within 500%²; while below 300 hPa in the northern region (Figure 12c,f), they are less than 600%² and 200%² for RO and RS, respectively. Compared to RS, RO data perform better in the upper troposphere, whereas RS data exhibit better results near the surface.

The specific humidity error variances for ERA5 data in both regions fluctuate near zero (Figure 11i and Figure 12i). A comparison of the specific humidity error variances between the northern and southern regions reveals that those in the south are generally lower than those in the north, a discrepancy closely related to the climatic characteristics of each region.

Overall, across different GNSS RO systems, the error variances of refractivity, temperature, and specific humidity exhibit good consistency in the northern and southern regions of China. Comparing the error variances of atmospheric parameters between the north and the south, the northern China has smaller refractivity error variances, while the southern China has smaller temperature and specific humidity error variances.

5. Summary and Conclusions

In this study, we propose a new spatial–temporal sampling correction method with which to mitigate the sampling errors associated with both RO–RS and RS–model pairs, and employ three different 3CH processing chains with NO SC, RO–RS SC, and RO–RS–ERA5 SC correction schemes to calculate the error variances of atmospheric parameters (i.e., refractivity, temperature, and specific humidity) for the FY-3E GNOS II BDS/GPS RO, RS, and ERA5 datasets at the Hailar and Xisha stations. We compare the impact of various 3CH processing chains on the error variances of atmospheric parameters within these datasets. Furthermore, by employing the improved 3CH processing chain with RO–RS–ERA5 spatial–temporal sampling correction scheme, we explore the consistency, accuracy, and differences in the error variances of atmospheric parameters across different GNSS RO systems and climatic regions in China, including the entire country, as well as southern and northern China. The main conclusions are as follows.

(1)

Comparing the NO SC, RO–RS SC, and RO–RS–ERA5 SC experimental groups, the 3CH processing chain with RO–RS–ERA5 SC effectively reduces the error variance of the RS dataset and minimizes the differences between the combinations of RO, RS, and ERA5 datasets. It effectively eliminates the impact of spatial–temporal sampling errors on RO–RS and RS–model pairs, and more accurately reflects the error variance of the atmospheric measurements.

(2)

In the entire China region, the average of error variances for atmospheric refractivity, temperature, and specific humidity from the FY-3E GNOS II RO are less than 1.12%², 0.13%², and 700%², respectively. The FY-3E GNOS II BDS RO and FY-3E GNOS II GPS RO have good error consistency.

(3)

Comparing the atmospheric parameter error variance between northern and southern China reveals that refractivity error variance is lower in the north, while temperature and specific humidity error variances are lower in the south. These differences are related to the different climatic conditions.

Overall, this study proposes a new 3CH processing chain that effectively reduces the impact of spatial–temporal sampling errors. It confirms the RO error consistency among different GNSS systems and the reliability of RO data in the FY-3E GNOS II mission. This approach provides new insights for atmospheric measurement data assessment methods, which supports the application of FY-3E GNOS II RO in fields such as climate change monitoring, numerical weather prediction, and data assimilation.