Weighted Fusion Method of Marine Gravity Field Model Based on Water Depth Segmentation

Abstract

Among the marine gravity field models derived from satellite altimetry, the Scripps Institution of Oceanography (SIO) series and Denmark Technical University (DTU) series models are the most representative and are often used to integrate global gravity field models, which were inverted by the deflection of vertical method and sea surface height method, respectively. The fusion method based on the offshore distance used in the EGM2008 model is just model stitching, which cannot realize the true fusion of the two types of marine gravity field models. In the paper, a new fusion method based on water depth segmentation is proposed, which established the Precision–Depth relationship of each model in each water depth segment in the investigated area, then constructed the FUSION model by weighted fusion based on the precision predicted from the Precision–Depth relationship at each grid in the whole region. The application in the South China Sea shows that the FUSION model built by the new fusion method has better accuracy than SIO28 and DTU17, especially in shallow water and offshore areas. Within 20 km offshore, the RMS of the FUSION model is 5.10 mGal, which is 8% and 4% better than original models, respectively. Within 100 m of shallow water, the accuracy of the FUSION model is 4.01 mGal, which is 14% and 12% higher than the original models, respectively. A further analysis shows that the fusion model is in better agreement with the seabed topography than original models. The new fusion method can blend the effective information of original models to provide a higher-precision marine gravity field.

1. Introduction

The marine gravity field has important application value in the fields of seabed depth prediction [1,2,3], plate tectonics and lithospheric structure research [4,5], and underwater navigation [6]. Thanks to the emergence of satellite altimeter geodetic mission (GM) data and the continuous improvement of inversion methods, scholars have published series of gravity field research results with high resolution and high precision [7,8,9,10,11,12]. The most representative of these are the series of ocean gravity field models constructed by the Scripps Institute of Oceanography (SIO) in the United States and the series of ocean gravity field models developed by the University of Technology in Denmark (DTU). The SIO series model is inverted by the deflection of vertical (DOV) method, while the DTU series model is based on the sea surface height (SSH) method [13,14].

The SIO and DTU series models have their own advantages due to different inversion methods, and scholars have compared and analyzed these two types of ocean gravity field models. The comparison of the gravity field models of SIO V29.1 and DTU21 in the Red Sea shows that the standard deviation of the difference between the gravity data of DTU21 and the ship is 17.5% smaller than that of the SIO V29.1 model in the range of a water depth less than 1000 m. In the sea area with a water depth greater than 1000 m, the accuracy of the SIO V29.1 model is better than that of the DTU21 model [15]. In the study, the RMS of the difference between shipborne and gravity anomaly models is significantly higher in the interval of water depth less than 100 m and gradually decreases with increasing water depth. The verification results of multiple ocean gravity field models using shipborne gravity data show that the DTU17 model has an accuracy advantage over the SIOV32.1 model within 40 km nearshore, while the accuracy of the two models is basically at the same level outside 40 km offshore [16]. In addition, the accuracy of the ocean gravity field model in the adjacent coastal areas is significantly lower than that in an open ocean, which is consistent with the results of Bao et al.’s work in the South China Sea [17]. Similarly, the accuracy evaluation of the NCEI ship survey data shows that the DTU17 has higher accuracy than the SIO V30.1 model in the nearshore range of 20 km [18,19]. From the above studies, it can be seen that the DTU model derived from SSH data is less affected by noise interference in nearshore and shallow water areas. The SIO model inverted by DOV data has good performance in an open ocean and deep sea, especially in areas with drastic changes in seabed topography. Therefore, it can be concluded that the two types of inversion methods have their own unique advantages in different types of sea areas. For the ocean gravity field model constructed by a single method, it is difficult to provide overall high-precision gravity field information in complex sea areas.

According to the evaluation of SIO29 and DTU21 in existing studies, there is a relationship between model precision and water depth [15]. In order to effectively integrate the advantages of the two types of inversion methods to construct an overall high-precision ocean gravity field model, this paper proposes a marine gravity field model fusion method based on water depth. Different from the model stitching based on the distance from the coastline used in the EGM2008 model [20], the new method does not need to rely on experience to set the boundary value, and can realize the true fusion of the two types of ocean gravity field models.

In this study, the marine gravity field model weighted fusion method is described in detail in the second section. In the third section, the South China Sea is taken as an application example, and the SIO28 and DTU17 models of the same period are selected for fusion. The results and analysis of model fusion are presented in Section 4. In the fifth section, further discussion is carried out based on the results of model fusion. The conclusion of this paper is given in Section 5.

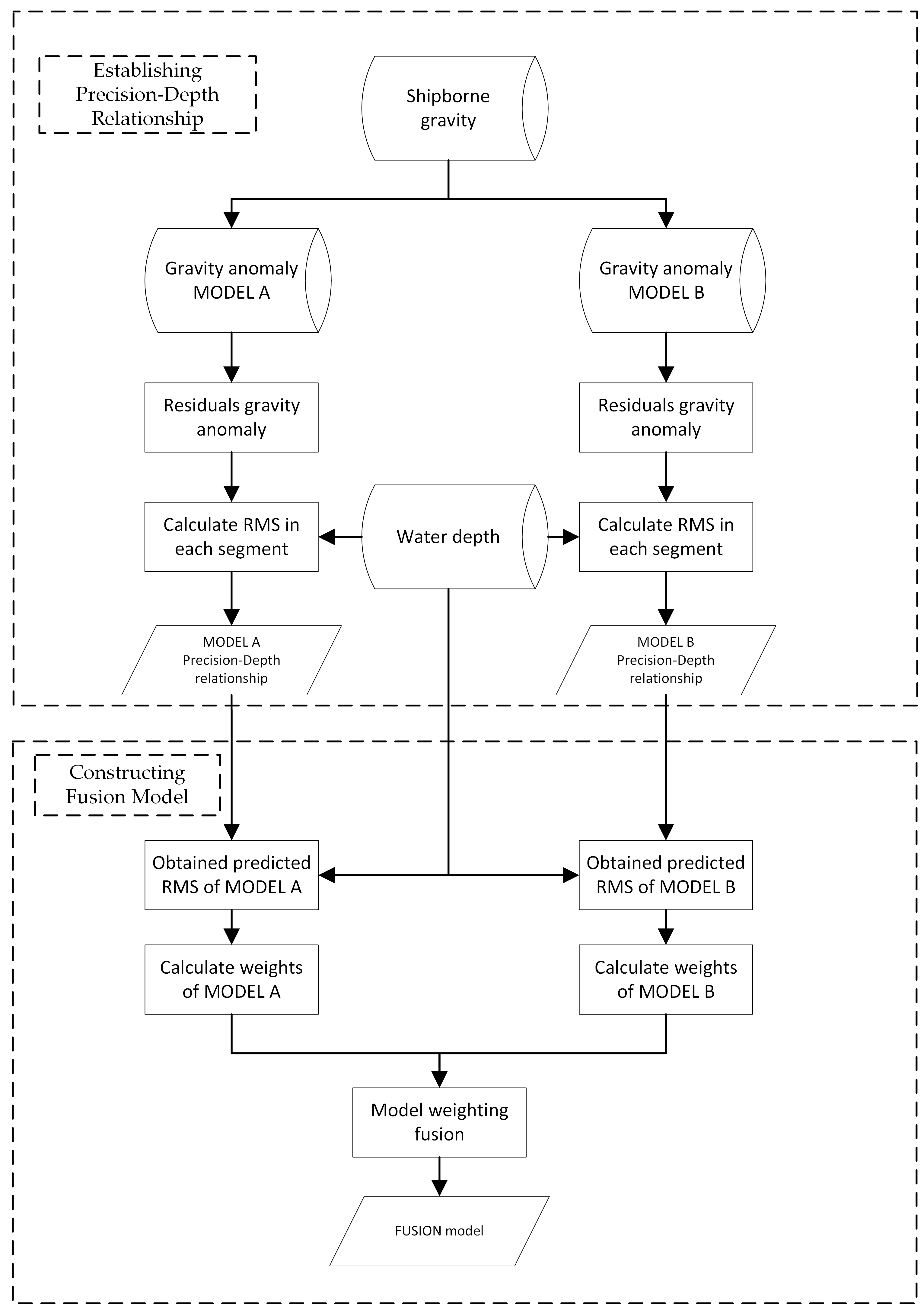
2. Methodology

This section presents a new fusion method to combine the advantages of gravity field models obtained using the two inversion methods. The complete process is shown in Figure 1: Firstly, the residuals of the gravity field models are calculated according to shipborne gravity data in the investigated area. The root mean square (RMS) of the residuals in each segment is calculated after the water depth has been segmented, then the Precision–Depth relationship is established. Secondly, according to the Precision–Depth relationship, the predicted precision at each grid point in the whole study area can be obtained based on the water depth. Then, the FUSION gravity anomaly model can be constructed by model weighted fusion.

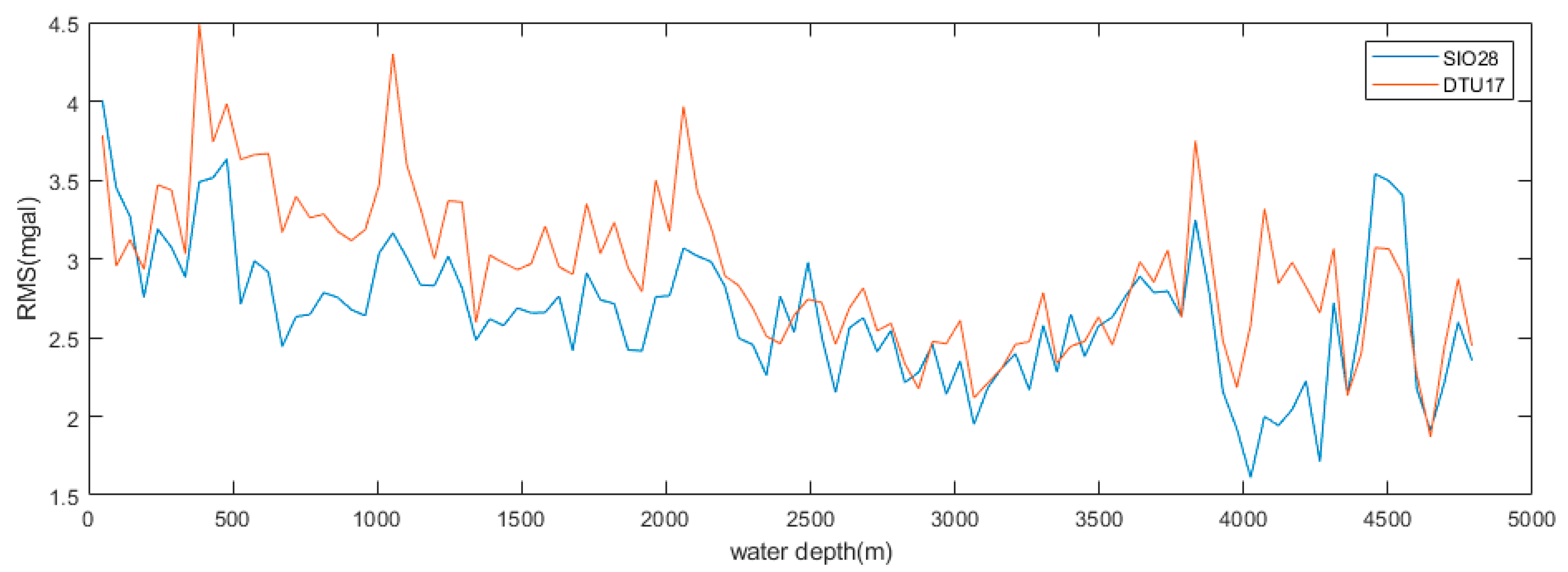
2.1. Establishing Precision–Depth Relationship

The two gravity field models used for fusion are named MODEL A and MODEL B. The gravity anomaly values of MODEL A and MODEL B at the ship data points are given by interpolation, so there are three values at ship data point $i$, namely the original gravity model values $GRA{V}_i^A$ and $GRA{V}_i^B$ and the water depth value $DEPT{H}_i^{SHIP}$. $Re{s}_{i,A}$ and $Re{s}_{i,B}$ are the residuals of each gravity field model according to the shipborne data at the ship point $i$:

$$\begin{array}{c}Re{s}_i^A=GRA{V}_i^A-GRA{V}_i^{SHIP}\\ Re{s}_i^B=GRA{V}_i^{B }-GRA{V}_i^{SHIP}\end{array}$$

(1)

We took the maximum and minimum values of depth in all the ship data points, and divided the water depth range into M segments as $SEGMEN{T}_j$ according to the specified segment step size. The residuals at each ship data point are counted by water depth segmentation. Each ship data point $i$ is counted into the corresponding water depth segment $SEGMEN{T}_j$ according to the depth of point $DEPT{H}_i^{SHIP}$; the number of points in each segment is denoted as $N_j$:

$$DEPT{H}_i^{SHIP}\in SEGMEN{T}_j,i=1,2\dots N_j,j=1,2\dots M$$

(2)

The RMS of residuals with a number of $N_j$ contained in the water depth segment $SEGMEN{T}_j$ is counted as precision according to Equation (3):

$$\begin{array}{c}RM{S}_j^A=\sqrt{{\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^{N_j}{\left|Re{s}_i^A\right|}^2}{N_j}}},j=1,2,\dots ,M.\\ RM{S}_j^B=\sqrt{{\displaystyle \frac{{{\displaystyle \sum }}_{i=1}^{N_j}{\left|Re{s}_i^B\right|}^2}{N_j}}},j=1,2,\dots ,M.\end{array}$$

(3)

The correspondence between $RM{S}_j^{MODEL}$ and $SEGMEN{T}_j$ is called the Precision–Depth relationship. The first part of Figure 1 illustrates the processing of establishing the Precision–Depth relationship.

2.2. Constructing Fusion Model

After establishing the Precision–Depth relationship, the predicted precision of gravity field models at grid points in study areas for fusion can be determined by the water depth. The predicted precision of the grid point is consistent with the RMS of the water depth segment at the point based on the Precision–Depth relationship. For instance, if the water depth $DEPT{H}_{grid}$ at each grid point is contained in the segment $SEGMEN{T}_j$,

$$DEPT{H}_{grid}\in SEGMEN{T}_j$$

(4)

Then, the predicted precision $RM{S}_j^{MODEL}$ of the corresponding model at this grid point could be obtained. Using the predicted precision, weights of both MODEL A and MODEL B at each grid point could be calculated:

$$\begin{array}{c}{P}_{grid}^A={\displaystyle \frac{{RM{S}_j^B}^2}{{RM{S}_j^A}^2+{RM{S}_j^B}^2}},j=1,2,\dots ,M\\ P_{grid}^B={\displaystyle \frac{{RM{S}_j^A}^2}{{RM{S}_j^A}^2+{RM{S}_j^B}^2}},j=1,2,\dots ,M\end{array}$$

(5)

Finally, the fusion model of each grid was obtained according to model weighted fusion given by Equation (5):

$$\begin{gathered} GRA{V}_{grid}^{FUSION}=GRA{V}_{grid}^A\times P_{grid}^A \\ +GRA{V}_{grid}^B\times P_{grid}^B \end{gathered}$$

(6)

The processing of model weighted fusion and constructing the fusion gravity field model FUSION are illustrated in the second part of Figure 1.

3. Application

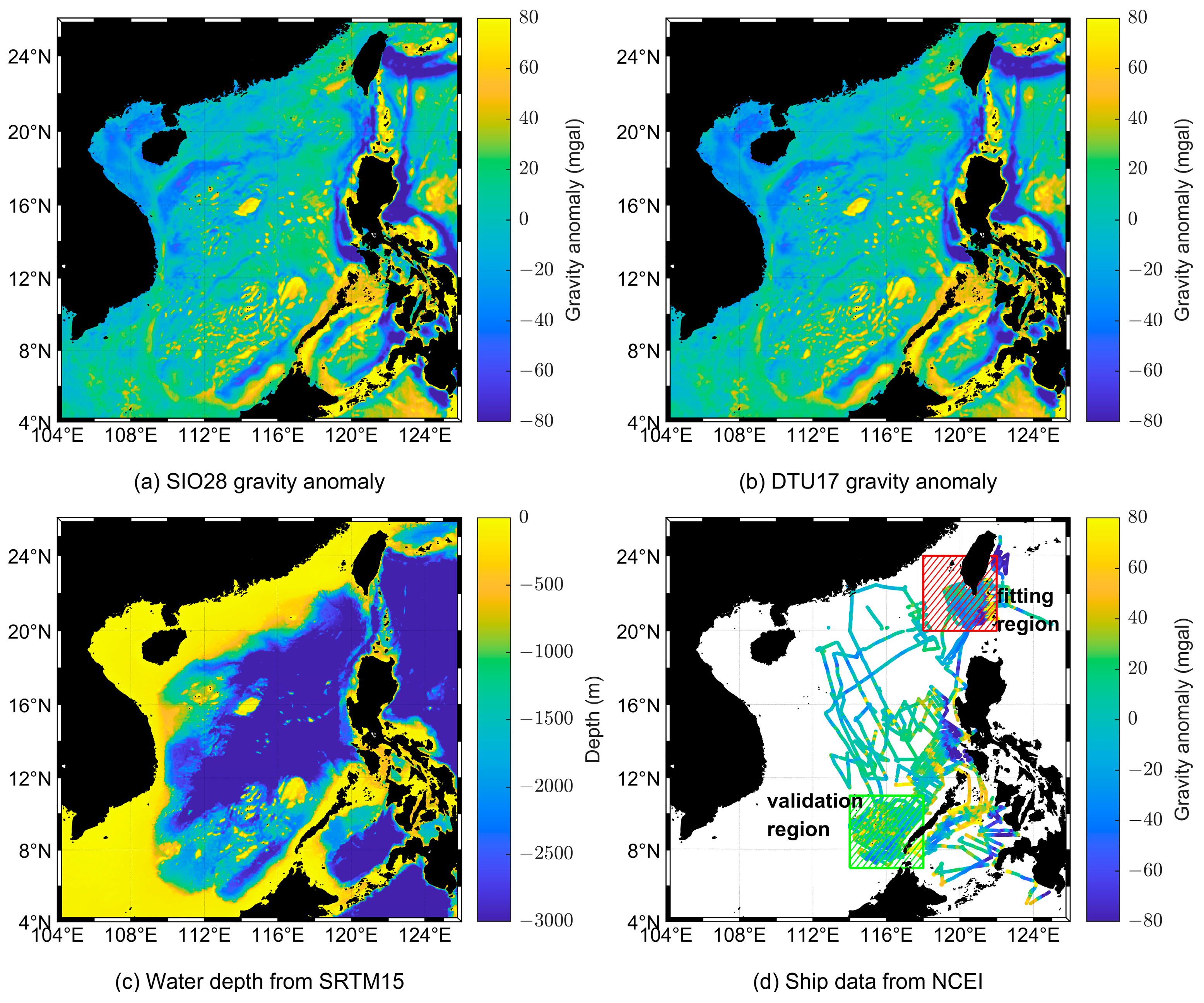
3.1. Study Area

In this study, the South China Sea (104~126°E, 4~26°N) has been chosen as the study area for the application of the new fusion method. The South China Sea (SCS) boasts abundant geological structures and encompasses various classic sea floor geologic features such as spreading ridges and continent-to-ocean transitional crust. The maximum depth of the Taiwan region is 5 km, which is representative of the maximum depth of 6 km in the South China Sea. At the same time, Taiwan contains complex geological structures such as the Southwest Taiwan Basin, the Penghu Islands, the northern Luzon Trough, the submarine canyon, and so on. Therefore, the Taiwan region is representative in the South China Sea. The Nansha region contains dense islands and shallow water depth, all of which provide a good natural test area for gravity anomaly research. In addition, the distribution of shipborne data in these two areas is relatively dense. In order for data distribution density, and regional representativeness, we chose the Taiwan region as the fitting region. After the model fusion was completed in the South China Sea, the Nansha region was investigated in detail.

3.2. Gravity Field and Bathymetric Model

The SIO series model and the DTU series model are two representative ocean gravity field models derived from satellite altimetry data, which are based on the DOV method and the SSH method, respectively. In order to better verify the performance of the new fusion method, two types of models published at the same time periods were used for model fusion. In view of the fact that DTU21 is not easily publicly available, the SIO V28.1 and DTU17 were selected as the original models for model fusion, which were publicly released in 2019 and contain similar satellite altimeter data (data request addresses: DTU17, https://ftp.space.dtu.dk/pub/, accessed on 22 February 2023; SIO V28.1, https://topex.ucsd.edu/pub/archive/, accessed on 4 May 2023). The geodetic mission (GM) data that dominate the construction of the ocean gravity field model in two models are shown in

Table 1. Altimeter GM data used for constructing marine gravity field models (unit: month).

	GEOSAT	ERS-1	JASON-1/2	CRYOSAT-2	SRIL
SIO28	18	12	14/12	~96	~32
DTU17	18	12	14/0	~84	~12

[11,19]. Figure 2a,b show the gravity anomaly in the South China Sea (SCS) from the SIO28 model and the DTU17 model, respectively.

The bathymetric model is also required in new fusion methods. The water depth data from version 2.4 of SRTM15 were used in this study, published by the Scripps Institute of Oceanography, which contain a large amount of multi-beam bathymetric data [1] (data request address: SRTM15, https://topex.ucsd.edu/pub/srtm15/, accessed on 4 May 2023). The water depth data from the SRTM15 bathymetric model in the South China Sea are shown in Figure 2c.

3.3. Shipborne Gravity Data and Preprocessing

The shipborne gravity data utilized in this study were obtained from the National Centers for Environmental Information (NCEI). There are more than 90 survey lines in the South China Sea, which come from different generations, different ships, and different measuring equipment. If it is used directly without pretreatment, its accuracy will be poor. In order to improve the accuracy of the ship gravity data, it is necessary to eliminate the survey lines that are obviously abnormal and the gross error inside the survey line of the shipboard gravity data. We deleted the data with a deviation of more than 20 mGal relative to the EGM2008 model, then remaining gross error data were eliminated according to the 3σ criterion [21]. After processing, the long-wavelength error model of each ship route was fitted and removed by the least squares method according to the difference between shipborne gravity and the EGM2008 model [22]. The error model is expressed as Equation (7).

$$\mathrm{\Delta }g=a_0+a_1\mathrm{\Delta }t+a_2\mathrm{\Delta }{t}^2$$

(7)

$\mathrm{\Delta }t$ is computed from the observation time minus the departure time.

As shown in

Table 2. Statistics of NCEI shipborne gravity data in South China Sea (unit: mGal).

	MAX	MIN	MEAN	STD	RMS
BEFORE	577.88	−518.44	−1.25	44.18	44.19
AFTER	11.39	−20.04	−0.21	3.88	3.88

, the statistics of the NCEI shipborne gravity data in the South China Sea show that the standard deviation (STD) of the discrepancies at the crossover points has decreased from 44.18 mGal to 3.88 mGal after preprocessing. The accuracy of shipborne gravity data has been significantly improved, which is sufficient for the verification and evaluation of marine gravity field models.

The distribution of the refined shipboard gravity data in the South China Sea is shown in Figure 2d. There is a total of 49,873 ship data points in the Taiwan region (red box), and the STD of the discrepancies at crossover points is 4.52 mGal. The STD of discrepancies at crossover points in the Nansha region (green box) is 3.54 mGal with 65,414 points. According to the distribution density of the ship’s gravity data, the area around Taiwan in the red box and the Nansha Islands in the green box were selected as the key investigations. The former was used to establish the Precision–Depth relationship as described in Section 2.1, and the latter was used to validate the fusion model established as described in Section 2.2.

3.4. The Fusion Gravity Field Model FUSION Built in SCS

In order to establish the Precision–Depth relationship between the gravity field model precision and water depth, the RMS of the residuals between the two gravity field models and the shipborne gravity in the waters near Taiwan Island (118~122°E, 20~24°N) was counted according to the depth segment. The deepest water depth of the region used to establish the relationship in this study is 4865 m. In this study, considering the range of water depth and data volume in each segment, the interval step was set to 48.65 m. Then, the RMS corresponding to the SIO28 and DTU17 gravity field models in each water depth segment was calculated by Equations (1)–(3). The Precision–Depth relationship of SIO28 and DTU17 models established in the Taiwan area is shown in Figure 3.

Next, the water depth from the SRTM15 model at all grid points in the South China Sea was divided into corresponding bathymetric segments according to Equation (4). Based on the above Precision–Depth relationship, the predicted RMS of the SIO28 model and DTU17 model in the whole SCS can be obtained, the distribution of which is shown in Figure 4a,b. Then, the weights of the two models in each water depth segment could be calculated by Equation (5), as shown in Figure 4c,d. Finally, the fusion model FUSION was built by model weighted fusion given by Equation (6).

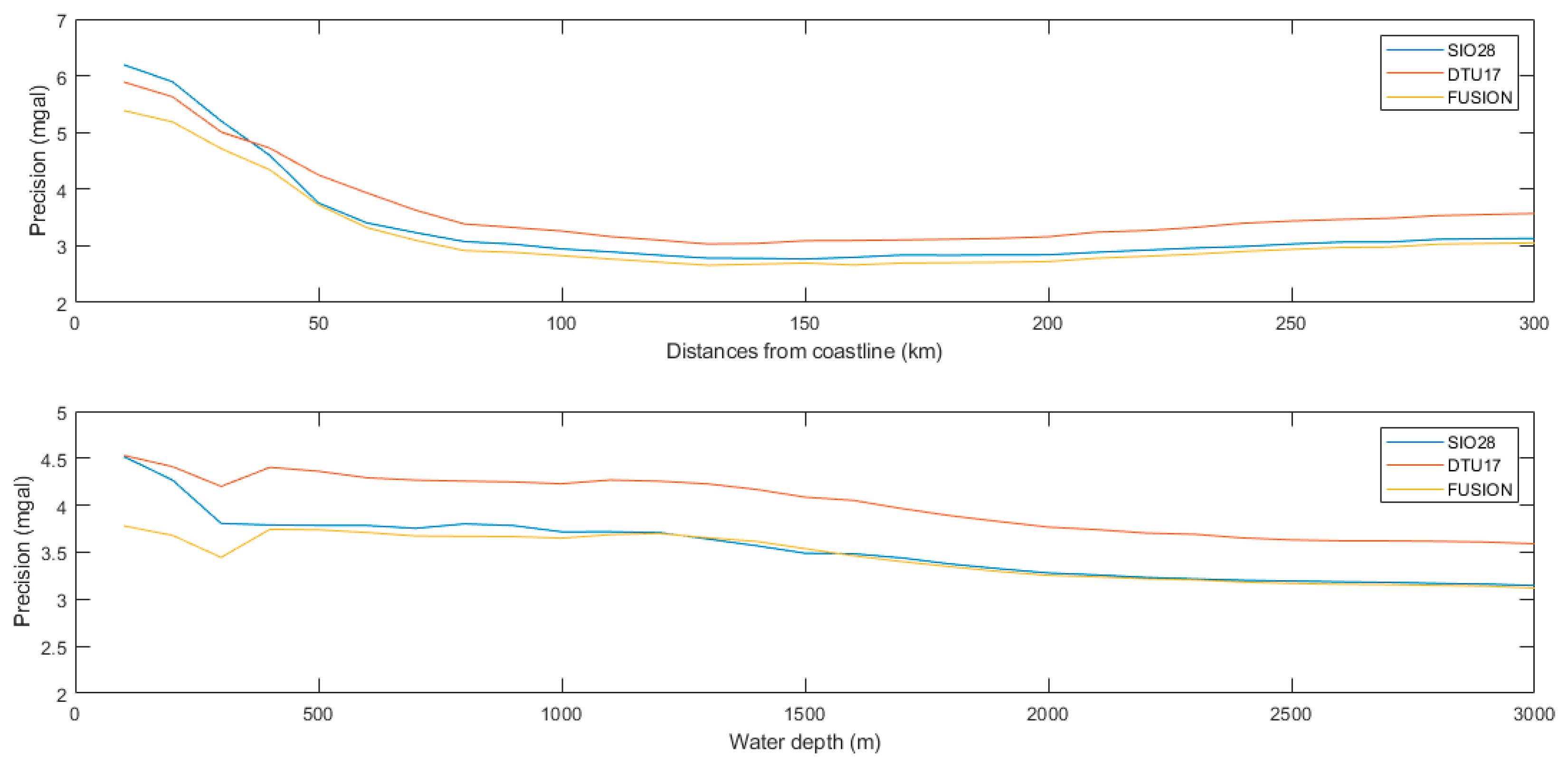
4. Results and Discussion

After the above series of processing, the marine gravity field fusion model in the South China Sea was constructed, as shown in Figure 5a. We analyzed original models SIO28 and DTU17 with the fusion model FUSION in the South China Sea using NCEI shipborne gravity anomaly data. We also analyzed SDUST2022 [11], released by the Shandong University of Science and Technology, and NSOAS24 [12], released by China’s Northeastern University, and XGM2019e [8], released by the Institute of Astronomical and Physical Geodesy, downloaded from the International Center for Global Earth Models (ICGEM, http://icgem.gfz-potsdam.de/calcgrid, accessed on 5 October 2024), for cross-comparison. The statistical results shown in

Table 3. Statistics of gravity field model validated by NCEI shipborne gravity data, overall South China Sea (unit: mGal).

	MODEL	MAX	MIN	MEAN	STD	RMS
Overall South China Sea	SIO28	22.13	−23.30	0.07	3.55	3.55
	DTU17	40.82	−27.59	0.20	4.02	4.02
	SDUST2022	23.64	−32.17	0.28	3.75	3.76
	NSOAS24	23.59	−27.48	0.01	3.71	3.71
	XGM2019	29.87	−42.30	0.23	4.67	4.68
	FUSION	23.18	−25.87	0.12	3.47	3.47
Nearshore (DIST ≤ 20 km)	SIO28	22.13	−23.30	0.35	6.48	6.49
	DTU17	40.82	−27.59	1.86	7.50	7.73
	SDUST2022	23.64	−32.17	1.86	6.99	7.23
	NSOAS24	23.59	−27.48	0.45	6.46	6.47
	XGM2019	29.71	−42.30	1.78	9.05	9.22
	FUSION	23.18	−25.87	1.06	5.67	5.77
Shallow Water (Depth ≤ 100 m)	SIO28	22.13	−20.80	0.88	5.29	5.37
	DTU17	21.80	−21.33	0.37	4.56	4.58
	SDUST2022	23.47	−18.10	1.07	5.05	5.16
	NSOAS24	22.27	−16.14	1.11	4.63	4.76
	XGM2019	25.41	−26.62	1.04	5.81	5.90
	FUSION	20.61	−16.17	0.63	4.01	4.06

reflect the relative precision of the predicted gravity anomalies. Overall for the South China Sea, the precision of each model is verified to be at the same level but FUSION has the highest precision in original models and existing models. Compared with the original models SIO28 and DTU17, the precision of the fusion model is improved by 2% and 13% in the whole sea area, by 12% and 24% in the nearshore 20 km, and by 24% and 12% in the shallow water 100 m. In the nearshore shallow waters, the precision of the gravity anomaly model becomes worse, while the precision improvement effect of the FUSION model is more obvious. The NSOAS24 model has better precision than the two original models within the nearshore range of 20 km, while FUSION has the best precision, proving the fusion method’s effectiveness.

In order to further reflect the performance of the new fusion method, the sea area around Nansha Islands, where the shipborne gravity data are densely distributed (green box of Figure 2d), was used further to investigate the quality of the new fusion model. The FUSION model around Nansha Islands is shown in Figure 5b and the statistics of the FUSION model validated by NCEI shipborne gravity data around Nansha Islands are shown in

Table 4. Statistics of the gravity field model validated by NCEI shipborne gravity data around Nansha islands (unit: mGal).

	MODEL	MAX	MIN	MEAN	STD	RMS
Overall Nansha Area	SIO28	17.29	−15.99	0.43	3.14	3.17
	DTU17	21.14	−20.25	0.40	3.58	3.60
	FUSION	16.56	−14.91	0.42	3.12	3.15
Nearshore (DIST ≤ 20 km)	SIO28	13.73	−8.94	1.89	5.20	5.53
	DTU17	21.14	−8.77	1.87	5.01	5.34
	FUSION	16.45	−7.54	1.95	4.71	5.10
Shallow Water (Depth ≤ 100 m)	SIO28	13.73	−11.47	1.19	4.52	4.67
	DTU17	21.14	−17.08	−0.32	4.53	4.54
	FUSION	16.77	−10.90	1.31	3.78	4.01

. As can be seen in Table 4, the precision of the FUSION model is better than that of the SIO28 and DTU17 models involved in the fusion in the whole SCS. In shallow water and nearshore areas, the FUSION gravity anomaly model outperforms the original models significantly. For nearshore areas with offshore distances of less than 20 km, the RMS of the difference between the SIO28 and DTU17 models and the shipboard gravity is 5.53 mGal and 5.34 mGal, respectively, while the RMS of the FUSION model is 5.10 mGal, which are 8% and 4% better than the original model, respectively. For shallow water with a depth of less than 100 m, the accuracy of the FUSION model is 4.01 mGal, which is 14% and 12% higher than that of the SIO28 model (4.67 mGal) and DTU17 model (4.54 mGal), respectively.

In order to further analyze the superiority of the FUSION model, the differences between original models and the fusion model are shown in Figure 6a,b. It can be seen that in Figure 6a, the regions where the FUSION is most similar to the SIO28 are mainly distributed around island–reef boundaries and seabed topography, while the FUSION being similar to DTU17 is more obvious in the area with rapid changes in shallow water or reef areas shown in Figure 6b. According to the precision improvement of the fusion model shown in Table 4, the difference in Figure 6a can reflect the precision advantage of the DOV method model in expressing the seafloor steep slope, and the difference in Figure 6b can reflect the precision advantage of the SSH method model in the nearshore and shallow water area. We took the differences between SIO28 and DTU17 in Figure 6a,b and the fusion model as absolute values, respectively, then used the latter subtracted from the former, and the difference is shown in Figure 6c. A positive value indicates that the fusion model is closer to DTU17, while a negative value suggests that it is closer to SIO28. By comparing the difference shown in Figure 6c with the SRTM15 seabed topographic model shown in Figure 6d, we can draw two conclusions:

(1)

The region where the fusion model is similar to DTU17’s gravity field model is concentrated in shallow reefs and nearshore areas. In these marine regions, gravity field model inversion with SSH is less affected by high-frequency noise on the sea surface to achieve higher weight.

(2)

The region where the fusion model is similar to the SIO28 gravity field model is mainly concentrated in deep-sea areas. Additionally, rapid changes at island–reef boundaries and seafloor topography are more pronounced in these areas. This represents that gravity field model inversion with DOV performs well in describing the details of undersea terrain changes in regions with low sea surface complexity.

According to these conclusions, FUSION preserves complete seafloor topography by assigning higher weights to each of the two original models in their dominant areas.

To analyze the spectral characteristics of the fusion model, a 2D Discrete Wavelet Transform (DWT) was used to separate and reconstruct information within specific frequency bands by selecting appropriate wavelet basis functions and decomposition levels. In gravity model analyses, previous research suggests that the ‘db3’ wavelet effectively separates gravity details [23,24]. Based on the relationship between wavelet decomposition and gravity anomaly wavelengths [25], the high-frequency components of the gravity field models SIO28, DTU17, and FUSION and water depth from SRTM15 with wavelengths less than 4’ (equivalent to 6.8 km) are shown in Figure 7. By comparing the difference in high-frequency components between different models in Figure 7 and associating with the Nansha regional characteristic landform labeled in Figure 6d, the following conclusions can be drawn:

(1)

The high-frequency component of the SIO28 model shows the change in the Nansha Trough in the southwest of the region and the west Palawan oblique thrust fault on the west side of Palawan Island, but there still exists high-frequency components in other flat areas, which are likely the noise amplified by DOV;

(2)

The DTU17 model has a high degree of agreement in the Reed Tablemount (at the northeast corner of the figure) and the Nansha Islands and reefs (at the upper left half of the figure) with the high-frequency component of the SRTM15 seabed terrain model shown in Figure 7d, which means that the DTU17 model retained the trusted detail changes in these areas;

(3)

Figure 7c shows that the fusion model retains the high-frequency detail of the shallow water area in the high-frequency component, while suppressing the high-frequency noise that appears in open waters, thereby integrating the advantages of both models.

The above analysis results are consistent with that the gravity anomaly model inversion from SSH has higher precision and less noise interference in shallow waters than inversion from DOV, and the model weighted fusion based on this method can combine the advantages of the two types of models. The high-frequency component of the FUSION model has the best consistency with the seabed topography, and can clearly reflect the features of the seabed geomorphology, which fully embodies the good performance of the fusion method in this study.

The EGM2008 gravity model used spatial mosaicking to fuse DNSC08 and SIOv18.1 gravity models based on the offshore distance [20]. The DNSC08 model was selected in the range of offshore distance less than 195 km, while the SIOv18.1 model was used for offshore distances beyond 280 km, with a tapered transition in the intermediate area. This method fundamentally involves the selective use of model data in different oceanic regions. The FUSION model built in this study truly combines the information contained in SIO28 and DTU17. The effective information of the original models is not limited to any particular region, and the FUSION model contains more effective information and achieves better model precision than single original gravity field models in the complex sea area around the Nansha Islands.

Figure 8 analyzes the precision of original and fusion gravity models according to shipborne gravity at different offshore distances and water depths around Nansha Islands. The SIO28 model using DOV inversion is more affected by high-frequency noise than the DTU17 model using SSH inversion. The precision of the DTU17 model is slightly better than that of the SIO28 model within 30 km offshore and a 100 m water depth due to the complex sea surface environment in the shoals and along the coast, which contains a lot of high-frequency noise, but is poor in other areas. The fusion model is superior to the two original models in most of the range of shore distances and water depths, and the advantage is more prominent in the area of 50 km near the shore and when the water depth is less than 400 m.

In the study of the marine gravity field, shipborne data are often considered to be more accurate than satellite survey data in presenting changes in sea surface details. Therefore, some scholars choose to introduce high-frequency components of high-precision shipborne data to improve the precision of the gravity anomaly model [24]. However, due to the high cost and low coverage of ship measurements, the gravity anomaly model can only be optimized in small areas with high-precision shipborne data. The fusion method proposed in this study can overcome the shortage of the small coverage of the current high-precision shipborne data, predict the precision of the gravity model with high-precision gravity anomaly data in a small area, and extrapolate the predicted precision to a larger coverage area and achieve model fusion. The water depth corresponding to the precision of the model in the method is used as a physical quantity to describe the seabed topography, and the information contained in it is strongly correlated with the gravity anomaly [16], which accords with the physical mechanism. At the same time, this method is convenient in calculation, and can effectively and quickly fuse gravity field models calculated using different methods or different data and fuse their advantages.

Predictably, this fusion method has certain requirements for the shipborne data and the similarity between the prior sea area and the fusion sea area. In this study, the model precision and water depth are correlated. First of all, the method requires ship data to be distributed in each water depth range. Secondly, the water depth of the target fusion sea area needs to be included in the water depth of the ship measurement point, so as to ensure that each point can obtain the model-predicted precision according to the Precision–Depth relationship. Future research will also be carried out based on these issues.

5. Conclusions

This study proposes a methodology for fusing multiple gravity field models based on establishing the Precision–Depth relationship. The SSH method and the DOV method for inverting the ocean gravity field have their own advantages. We evaluated the precision of SIO28 and DTU17 according to ship gravity data in the waters near Taiwan, and correlated the precision with water depth to establish the Precision–Depth relationship by water depth segmentation statistics. Based on this relationship, a weighted fusion method was applied to two models in the South China Sea. Cross-validation results using multiple representative models and NCEI ship gravity data in the South China Sea show that the precision of the FUSION model is slightly better than that of the original models with RMS of 3.47 mGal, and the advantages are obvious in the 20 km nearshore and 100 m shallow waters with RMS of 5.77 mGal and 4.06 mGal, which exhibit 12%~24% improvement compared to original models SIO28 and DTU17. In the Nansha validation region, within the 20 km offshore sea area, the RMS of the FUSION model is 5.10 mGal, which is 8% and 4% better than original models, respectively. Within 100 m of shallow water, the accuracy of the FUSION model is 4.01 mGal, which is 14% and 12% higher than the original models, respectively. The notable differences between original and fusion models are primarily concentrated in shallow reef zones. After analyzing the difference between the original and fusion gravity anomaly models, it can be concluded that the fusion model blends the effective information of the two original models and can provide a higher-precision marine gravity field than the original models in the complex sea area. It means that the fusion method proposed in this study can truly combine the unique advantages of different gravity models. According to the result of the wavelet analysis, the fusion model effectively reduces high-frequency noise components present in SIO28 while accentuating high-frequency variations pertaining to seabed characteristics and retaining valuable information from DTU17 within shallow water regions. According to these results, the FUSION model built in this study truly combines their advantages at the information content level. This model weighted fusion method overcomes the shortage of a low coverage of high-precision shipborne data, and optimizes and fuses the gravity model in large complex regions with small-area shipborne data.