Theoretical Analysis and Experimental Evaluation of Wide-Lane Combination for Single-Epoch Positioning with BeiDou-3 Observations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Theory of BDS-3 Multi-Frequency Observations Combination
2.2. Optimal Coefficients Selection for Multi-Frequency Combination Signals
2.3. Theoretical Analysis of Precision in BDS-3 Multi-Frequency Combination Signals
2.3.1. Ionosphere-Fixed Model
2.3.2. Ionosphere-Float Model
3. Results
3.1. Data Description and Processing Strategy
3.2. Results and Analyses of Two Baselines’ RTK Positioning
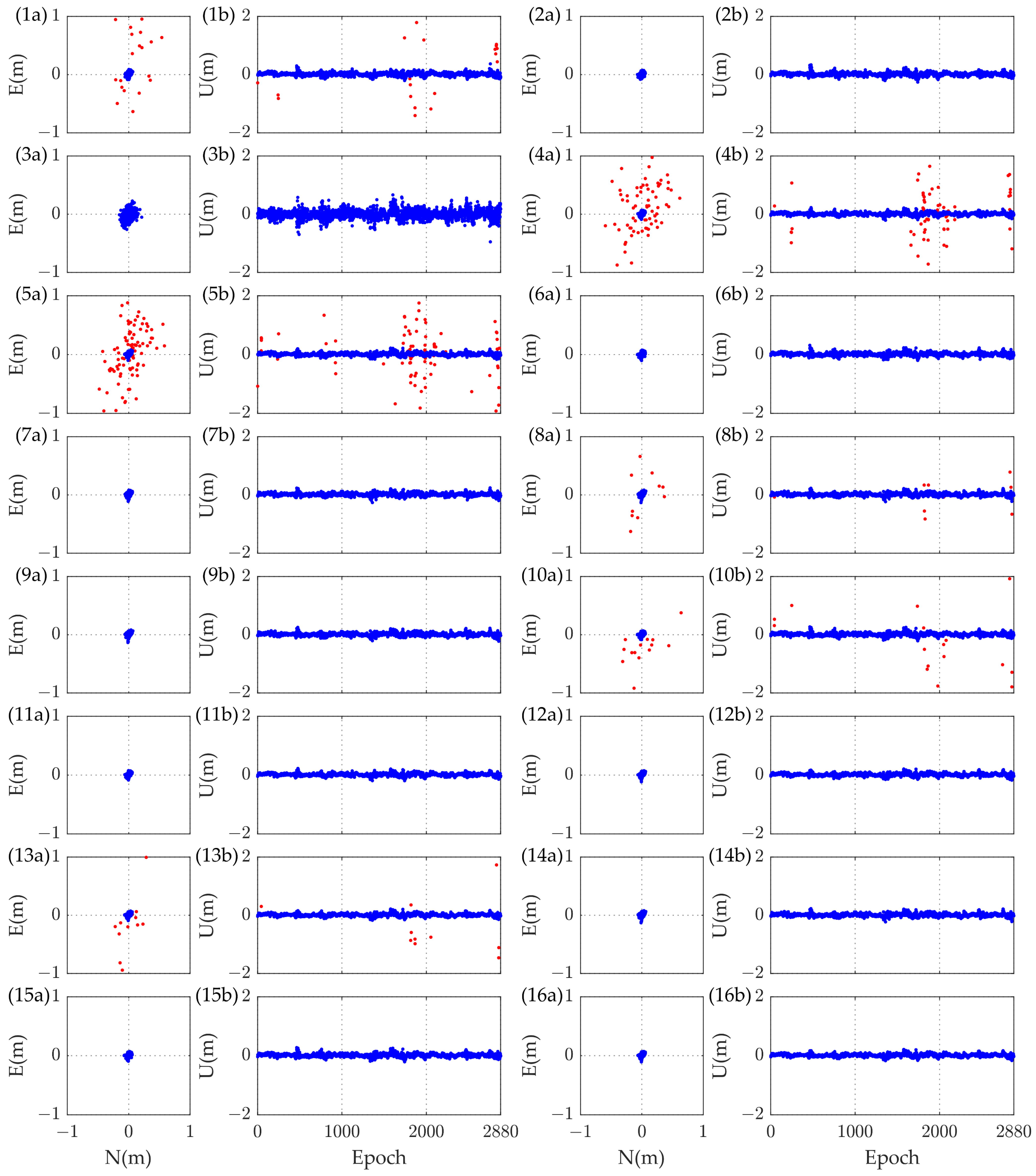
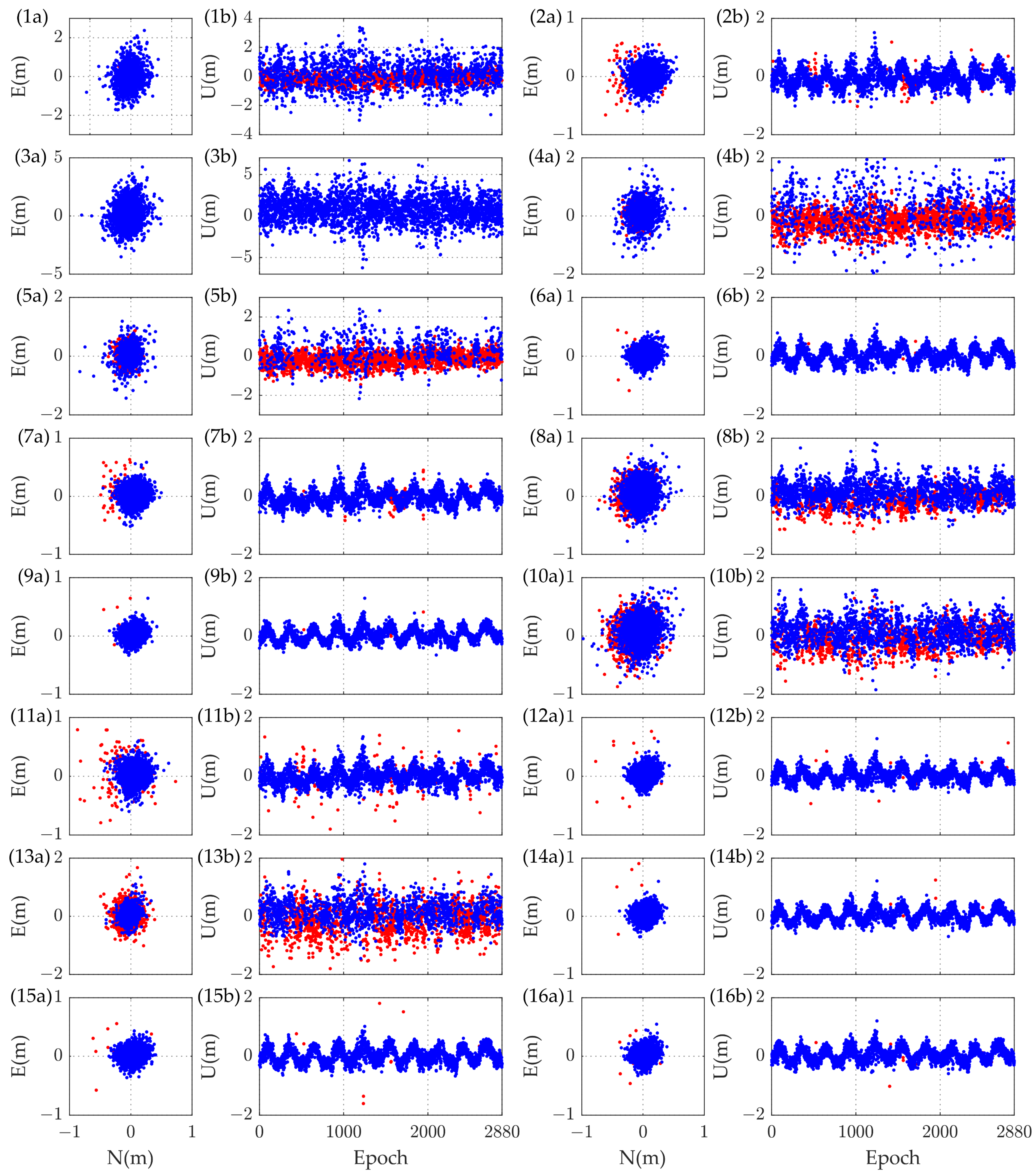
3.2.1. Positioning Performance of Baseline 1
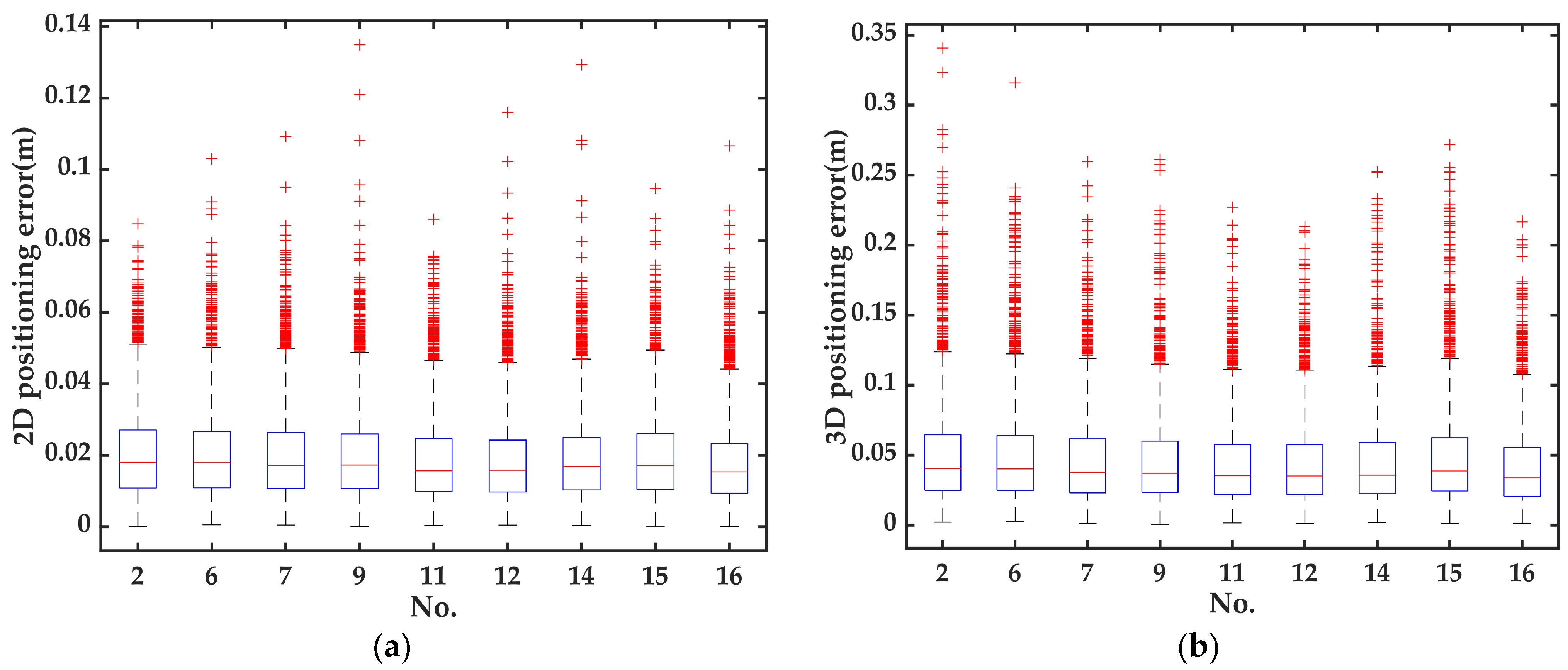
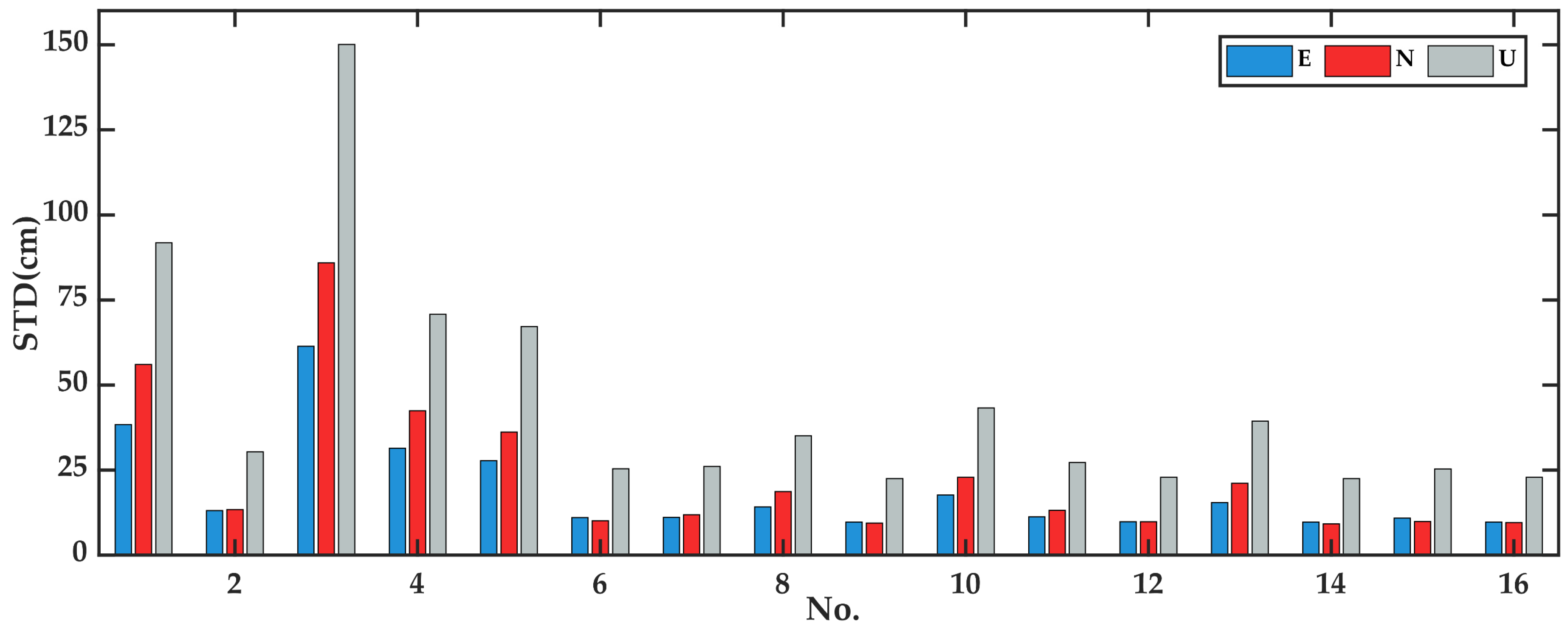
3.2.2. Positioning Performance of Baseline 2
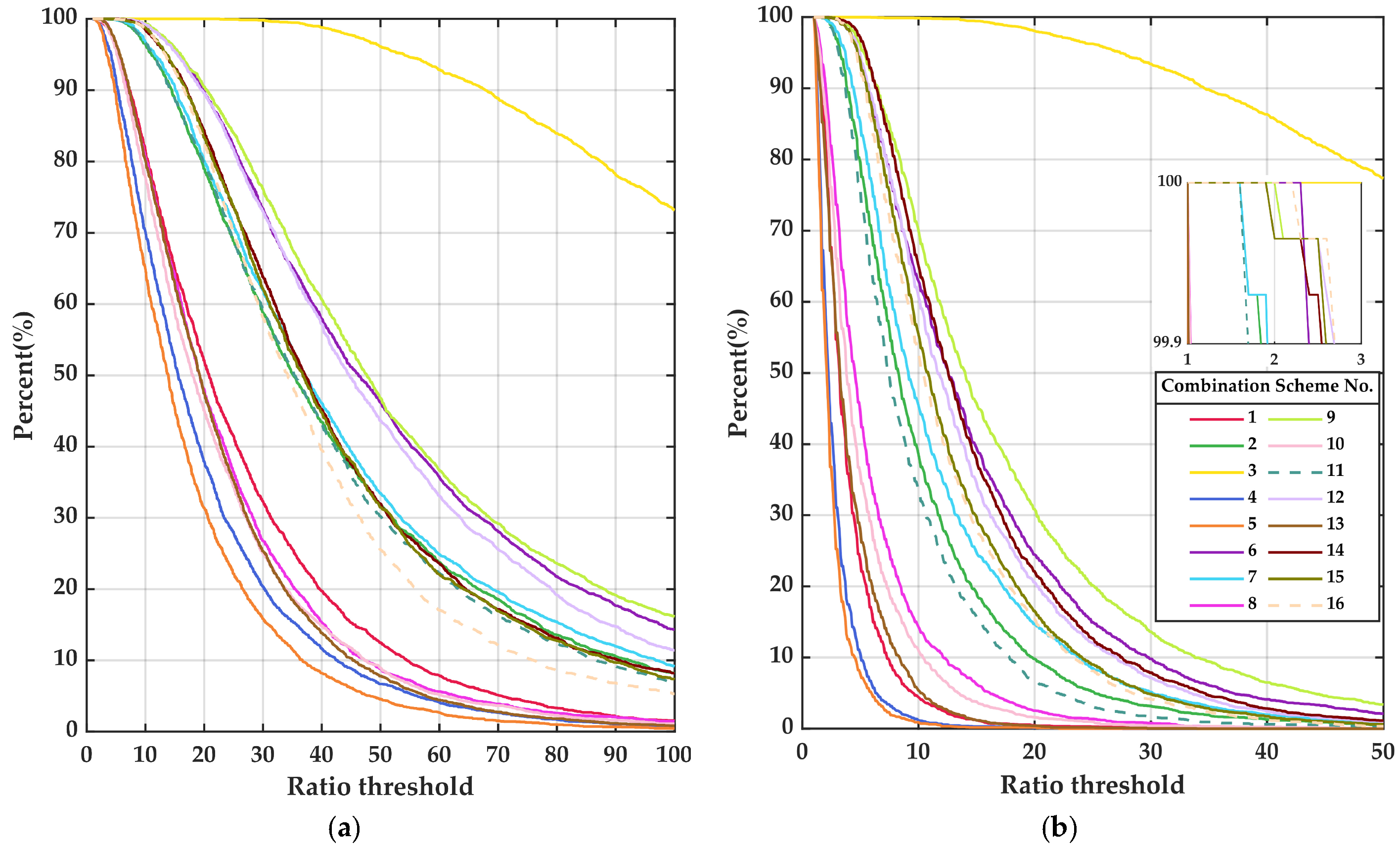
3.2.3. Performance of AR for Two Baselines
4. Discussion
5. Conclusions
- This study employs the LS method to derive the theoretical positioning precision for the single-epoch WL combination of 16 schemes, each with varying numbers of frequencies (three or more), under both the ionosphere-fixed and ionosphere-float models. These theoretical predictions are then validated using two baselines. The experimental results under both models show strong correlations with the theoretical derivations, with Pearson correlation coefficients of 0.997 and 0.968, respectively, demonstrating the validity of the theoretical derivations.
- In the ionosphere-fixed mode and the ionosphere-float mode, the triple-frequency scheme 9 (B1C, B1I, B2b) has excellent performance and high reliability. Although the positioning performance is slightly inferior to scheme 14 and scheme 16, the amount of data it uses is significantly smaller. The positioning performance of Scheme 9 under the ionosphere-fixed model is 100% FR, CEP (75%) is 2.6 cm, and SEP (75%) is 6.0 cm; the positioning performance under the ionosphere-float model is 99.7% FR, CEP (75%) is 16.2 cm, and SEP (75%) is 30.8 cm.
- This study shows that simply using multi-frequency data may not significantly improve positioning precision. Instead, it is more important to develop a reasonable frequency combination.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Teunissen, P.J.G.; Verhagen, S. GNSS Carrier Phase Ambiguity Resolution: Challenges and Open Problems. In Observing Our Changing Earth; Sideris, M.G., Ed.; International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2008; Volume 133, pp. 785–792. ISBN 978-3-540-85425-8. [Google Scholar]
- Xu, W.; Yan, C.; Chen, J. Performance Evaluation of BDS-2/BDS-3 Combined Precise Time Transfer with B1I/B2I/B3I/B1C/B2a Five-Frequency Observations. GPS Solut. 2022, 26, 80. [Google Scholar] [CrossRef]
- Li, X.; Liu, G.; Li, X.; Zhou, F.; Feng, G.; Yuan, Y.; Zhang, K. Galileo PPP Rapid Ambiguity Resolution with Five-Frequency Observations. GPS Solut. 2020, 24, 24. [Google Scholar] [CrossRef]
- Pan, L.; Zhang, X.; Liu, J. A comparison of three widely used GPS triple-frequency precise point positioning models. GPS Solut. 2019, 23, 121. [Google Scholar] [CrossRef]
- Fernández-Plazaola, U.; Martín-Guerrero, T.M.; Entrambasaguas, J.T. A New Method for Three-Carrier GNSS Ambiguity Resolution. J. Geod. 2008, 82, 269–278. [Google Scholar] [CrossRef]
- Li, B.; Li, Z.; Zhang, Z.; Tan, Y. ERTK: Extra-Wide-Lane RTK of Triple-Frequency GNSS Signals. J. Geod. 2017, 91, 1031–1047. [Google Scholar] [CrossRef]
- Cao, X.; Shen, F.; Zhang, S.; Li, J. Satellite Availability and Positioning Performance of Uncombined Precise Point Positioning Using BeiDou-2 and BeiDou-3 Multi-Frequency Signals. Adv. Space Res. 2021, 67, 1303–1316. [Google Scholar] [CrossRef]
- Tang, W.; Shen, M.; Deng, C.; Cui, J.; Yang, J. Network-Based Triple-Frequency Carrier Phase Ambiguity Resolution between Reference Stations Using BDS Data for Long Baselines. GPS Solut. 2018, 22, 73. [Google Scholar] [CrossRef]
- Tian, Y.; Zhao, D.; Chai, H.; Wang, S. BDS Ambiguity Resolution with the Modified TCAR Method for Medium-Long Baseline. Adv. Space Res. 2017, 59, 670–681. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Gao, W.; Li, Z. Real-Time Kinematic Positioning over Long Baselines Using Triple-Frequency BeiDou Signals. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 3254–3269. [Google Scholar] [CrossRef]
- Li, J.; Yang, Y.; Xu, J.; He, H.; Guo, H. GNSS Multi-Carrier Fast Partial Ambiguity Resolution Strategy Tested with Real BDS/GPS Dual- and Triple-Frequency Observations. GPS Solut. 2015, 19, 5–13. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Q.; Mao, Y.; Cui, X.; Cai, C.; Zhang, R. Comprehensive Performance Review of BDS-3 after One-Year Official Operation. Adv. Space Res. 2023, 71, 883–899. [Google Scholar] [CrossRef]
- Composition and Operational Status of the Beidou Navigation Satellite System Constellation. Available online: https://glonass-iac.ru/beidou/sostavOG/ (accessed on 17 September 2024).
- Zhang, Z.; Li, B.; He, X. Geometry-free single-epoch resolution of BDS-3 multi-frequency carrier ambiguities. Acta Geod. Cartogr. Sin. 2020, 49, 1139–1148. [Google Scholar]
- Li, B.; Zhang, Z.; Miao, W.; Chen, G. Improved Precise Positioning with BDS-3 Quad-Frequency Signals. Satell. Navig. 2020, 1, 30. [Google Scholar] [CrossRef]
- Liu, L.; Pan, S.; Gao, W.; Ma, C.; Tao, J.; Zhao, Q. Assessment of Quad-Frequency Long-Baseline Positioning with BeiDou-3 and Galileo Observations. Remote Sens. 2021, 13, 1551. [Google Scholar] [CrossRef]
- Nie, Z.; Wang, B.; Wang, Z.; He, K. An Offshore Real-Time Precise Point Positioning Technique Based on a Single Set of BeiDou Short-Message Communication Devices. J. Geod. 2020, 94, 78. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Z.; Zang, N.; Wang, S. High-Precision GNSS Ocean Positioning with BeiDou Short-Message Communication. J. Geod. 2019, 93, 125–139. [Google Scholar] [CrossRef]
- Gao, W.; Zhang, Z.; Pan, S.; Wang, C. Single Epoch Positioning Method Based on BDS Five-Frequency Extra-Wide-Lane Combination. J. Chin. Inert. Technol. 2023, 31, 918–924+931. [Google Scholar]
- Zhang, Z.; Li, B.; Gao, Y.; Zhang, Z.; Wang, S. Asynchronous and Time-Differenced RTK for Ocean Applications Using the BeiDou Short Message Service. J. Geod. 2023, 97, 7. [Google Scholar] [CrossRef]
- Lu, T.; Wang, X.; Lu, C. An improved GNSS high-dimensional ambiguity fast decorrelation algorithm. Geod. Geodyn. 2021, 41, 511–515. [Google Scholar]
- Liu, X.; Zhang, S.; Zhang, Q.; Ding, N.; Yang, W. A Fast Satellite Selection Algorithm with Floating High Cut-off Elevation Angle Based on ADOP for Instantaneous Multi-GNSS Single-Frequency Relative Positioning. Adv. Space Res. 2019, 63, 1234–1252. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, S.; Zhang, Q.; Zheng, N.; Zhang, W.; Ding, N. Theoretical Analysis of the Multi-GNSS Contribution to Partial Ambiguity Estimation and R-Ratio Test-Based Ambiguity Validation. GPS Solut. 2021, 25, 52. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; He, X.; Zhang, Z.; Miao, W. Models, Methods and Assessment of Four-Frequency Carrier Ambiguity Resolution for BeiDou-3 Observations. GPS Solut. 2020, 24, 96. [Google Scholar] [CrossRef]
- Feng, Y. GNSS Three Carrier Ambiguity Resolution Using Ionosphere-Reduced Virtual Signals. J. Geod. 2008, 82, 847–862. [Google Scholar] [CrossRef]
- Li, B.; Feng, Y.; Shen, Y. Three Carrier Ambiguity Resolution: Distance-Independent Performance Demonstrated Using Semi-Generated Triple Frequency GPS Signals. GPS Solut. 2010, 14, 177–184. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Q.; Zhang, S.; Wu, S. A New Efficient Fusion Positioning Method for Single-Epoch Multi-GNSS Based on the Theoretical Analysis of the Relationship between ADOP and PDOP. GPS Solut. 2022, 26, 139. [Google Scholar] [CrossRef]
- Bard, J.D.; Ham, F.M. Time difference of arrival dilution of precision and applications. IEEE Trans. Signal Process. 1999, 47, 521–523. [Google Scholar] [CrossRef]
- Teunissen, P.J.G. The Least-Squares Ambiguity Decorrelation Adjustment: A Method for Fast GPS Integer Ambiguity Esti-mation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Liu, X.; Chen, G.; Zhang, Q.; Zhang, S. Improved Single-epoch Single-frequency Par Lambda Algorithm with Baseline Constraints for the BeiDou Navigation Satellite System. IET Radar Sonar Navig. 2017, 11, 1549–1557. [Google Scholar] [CrossRef]
- Landskron, D.; Böhm, J. VMF3/GPT3: Refined Discrete and Empirical Troposphere Mapping Functions. J. Geod. 2018, 92, 349–360. [Google Scholar] [CrossRef]
- Teunissen, P.J. Influence of ambiguity precision on the success rate of GNSS integer ambiguity bootstrapping. J. Geod. 2007, 81, 351–358. [Google Scholar] [CrossRef]



| Signal | Frequency (MHz) | Wavelength (m) | Satellite |
|---|---|---|---|
| B1C | 1575.420 | 0.1903 | BDS-3 24MEO+3IGSO |
| B1I | 1561.098 | 0.1920 | |
| B3I | 1268.520 | 0.2363 | |
| B2b | 1207.140 | 0.2483 | |
| B2a | 1176.450 | 0.2548 |
| Item | Budget (≤100 km) |
|---|---|
| Phase noise | ≈1 |
| Orbit error | <0.5 |
| Tropospheric delay | <1 |
| 1st-order ionospheric delay | <10 |
| 2nd-order ionospheric delay | <0.5 |
| No. | i (B1C) | j (B1I) | k (B3I) | l (B2b) | m (B2a) | (m) | |||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.07 |
| 0 | 1 | −1 | 0 | 0 | 1.02 | −1.25 | 6.88 | 0.14 | |
| 2 | 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 |
| 0 | 1 | −2 | 1 | 0 | 1.30 | −1.16 | 13.90 | 0.14 | |
| 3 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 | |
| 4 | 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.07 |
| 0 | 1 | 0 | −1 | 0 | 0.85 | −1.32 | 5.58 | 0.17 | |
| 5 | 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.07 |
| 0 | 1 | 0 | 0 | −1 | 0.78 | −1.35 | 5.08 | 0.19 | |
| 6 | 0 | 0 | 1 | 0 | −1 | 3.26 | −1.66 | 18.79 | 0.08 |
| 0 | 1 | −2 | 0 | 1 | 1.50 | −1.07 | 15.97 | 0.13 | |
| 7 | 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 |
| 1 | 0 | −2 | 1 | 0 | 1.22 | −1.15 | 13.12 | 0.14 | |
| 8 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 1 | 0 | 0 | −1 | 0 | 0.81 | −1.31 | 5.39 | 0.18 | |
| 9 | 0 | 0 | 1 | 0 | −1 | 3.26 | −1.66 | 18.79 | 0.08 |
| 1 | 0 | −2 | 0 | 1 | 1.40 | −1.06 | 14.94 | 0.13 | |
| 10 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 0 | 1 | 0 | −1 | 0 | 0.85 | −1.32 | 5.58 | 0.17 | |
| 11 | 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 |
| 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.07 | |
| 0 | 1 | −2 | 1 | 0 | 1.30 | −1.16 | 13.90 | 0.14 | |
| 12 | 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.08 |
| 0 | 0 | 1 | 0 | −1 | 3.26 | −1.66 | 18.79 | 0.08 | |
| 0 | 1 | −2 | 0 | 1 | 1.40 | −1.06 | 14.94 | 0.13 | |
| 13 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.07 | |
| 0 | 1 | 0 | −1 | 0 | 0.85 | −1.32 | 5.58 | 0.17 | |
| 14 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 | |
| 1 | 0 | −2 | 0 | 1 | 1.40 | −1.06 | 14.94 | 0.13 | |
| 15 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 | |
| 0 | 1 | −2 | 0 | 1 | 1.50 | −1.07 | 15.97 | 0.13 | |
| 16 | 0 | 0 | 0 | 1 | −1 | 9.77 | −1.75 | 54.92 | 0.06 |
| 0 | 0 | 1 | −1 | 0 | 4.88 | −1.62 | 28.53 | 0.07 | |
| 1 | −1 | 0 | 0 | 0 | 20.93 | −1.01 | 154.86 | 0.07 | |
| 0 | 1 | −2 | 0 | 1 | 1.50 | −1.07 | 15.97 | 0.13 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 316.8 | 341.8 | 29.0 | 485.6 | 587.6 | 396.2 | 366.5 | 465.3 | 422.1 | 437.6 | 565.0 | 646.5 | 735.8 | 465.7 | 437.8 | 753.7 | |
| 5.6 | 5.4 | 18.6 | 4.5 | 4.1 | 5.0 | 5.2 | 4.6 | 4.9 | 4.7 | 4.2 | 3.9 | 3.7 | 4.6 | 4.8 | 3.6 | |
| 263.4 | 103.2 | 659.3 | 214.3 | 195.4 | 70.9 | 98.7 | 129.1 | 67.8 | 134.0 | 96.6 | 66.6 | 122.6 | 66.5 | 69.6 | 65.4 | |
| 810.8 | 114.4 | 958.8 | 672.8 | 620.0 | 74.6 | 109.2 | 172.3 | 71.2 | 179.1 | 109.2 | 70.9 | 168.9 | 71.2 | 74.5 | 70.9 |
| Items | Long Range | Short Range |
|---|---|---|
| Cutoff elevation | 10° | 20° |
| Sampling rate | 30 s | |
| Observation weighting | Elevation-dependent weighting [30] | |
| Satellite orbit | Broadcast ephemeris | |
| Satellite clock | DD eliminated | |
| Receiver clock | DD eliminated | |
| Ionospheric delay | Parameterization | DD eliminated |
| Tropospheric delay | Corrected by GPT3 model [31] | |
| Phase ambiguities | LAMBDA | |
| Ratio threshold | 3 | |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 1.5 | 1.5 | 3.7 | 1.3 | 1.3 | 1.4 | 1.4 | 1.3 | 1.3 | 1.4 | 1.3 | 1.3 | 1.3 | 1.3 | 1.4 | 1.2 |
| N | 2.0 | 1.9 | 5.0 | 1.7 | 1.7 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | 1.7 | 1.7 | 1.7 | 1.8 | 1.8 | 1.7 |
| U | 5.2 | 5.3 | 14.2 | 4.6 | 4.6 | 5.2 | 5.2 | 4.8 | 4.8 | 5.1 | 4.5 | 4.5 | 4.4 | 4.7 | 5.1 | 4.3 |
| 3D | 5.8 | 5.8 | 15.5 | 5.1 | 5.1 | 5.7 | 5.3 | 5.3 | 5.2 | 5.5 | 5.0 | 5.0 | 4.8 | 5.2 | 5.5 | 4.8 |
| FR | 89.2 | 100 | 100 | 77.3 | 68.7 | 100 | 100 | 97.5 | 100 | 95.4 | 100 | 100 | 99.6 | 100 | 100 | 100 |
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 38.4 | 13.1 | 61.4 | 31.4 | 27.8 | 11.0 | 11.1 | 14.2 | 9.7 | 17.7 | 11.3 | 9.8 | 15.5 | 9.7 | 10.9 | 9.7 |
| N | 56.0 | 13.4 | 85.9 | 42.4 | 36.2 | 10.1 | 11.9 | 18.7 | 9.4 | 22.9 | 13.2 | 9.8 | 21.1 | 9.2 | 9.9 | 9.6 |
| U | 91.8 | 30.4 | 150.1 | 70.8 | 67.2 | 25.4 | 26.1 | 35.1 | 22.5 | 43.3 | 27.2 | 22.9 | 39.4 | 22.5 | 25.3 | 22.9 |
| 3D | 114.2 | 35.7 | 183.6 | 88.3 | 81.3 | 29.5 | 30.7 | 42.3 | 26.2 | 52.0 | 32.3 | 26.7 | 47.3 | 26.2 | 29.3 | 26.6 |
| FR | 53.6 | 96.8 | 100 | 30.3 | 24.3 | 99.7 | 97.9 | 72.6 | 99.7 | 64.8 | 95.9 | 99.6 | 54.7 | 99.8 | 99.6 | 99.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Liu, X.; Zhang, S. Theoretical Analysis and Experimental Evaluation of Wide-Lane Combination for Single-Epoch Positioning with BeiDou-3 Observations. Remote Sens. 2024, 16, 4404. https://doi.org/10.3390/rs16234404
Wang Y, Liu X, Zhang S. Theoretical Analysis and Experimental Evaluation of Wide-Lane Combination for Single-Epoch Positioning with BeiDou-3 Observations. Remote Sensing. 2024; 16(23):4404. https://doi.org/10.3390/rs16234404
Chicago/Turabian StyleWang, Yulu, Xin Liu, and Shubi Zhang. 2024. "Theoretical Analysis and Experimental Evaluation of Wide-Lane Combination for Single-Epoch Positioning with BeiDou-3 Observations" Remote Sensing 16, no. 23: 4404. https://doi.org/10.3390/rs16234404
APA StyleWang, Y., Liu, X., & Zhang, S. (2024). Theoretical Analysis and Experimental Evaluation of Wide-Lane Combination for Single-Epoch Positioning with BeiDou-3 Observations. Remote Sensing, 16(23), 4404. https://doi.org/10.3390/rs16234404





