Optimizing the Vegetation Health Index for Agricultural Drought Monitoring: Evaluation and Application in the Yellow River Basin
Abstract
1. Introduction
2. Materials and Methods
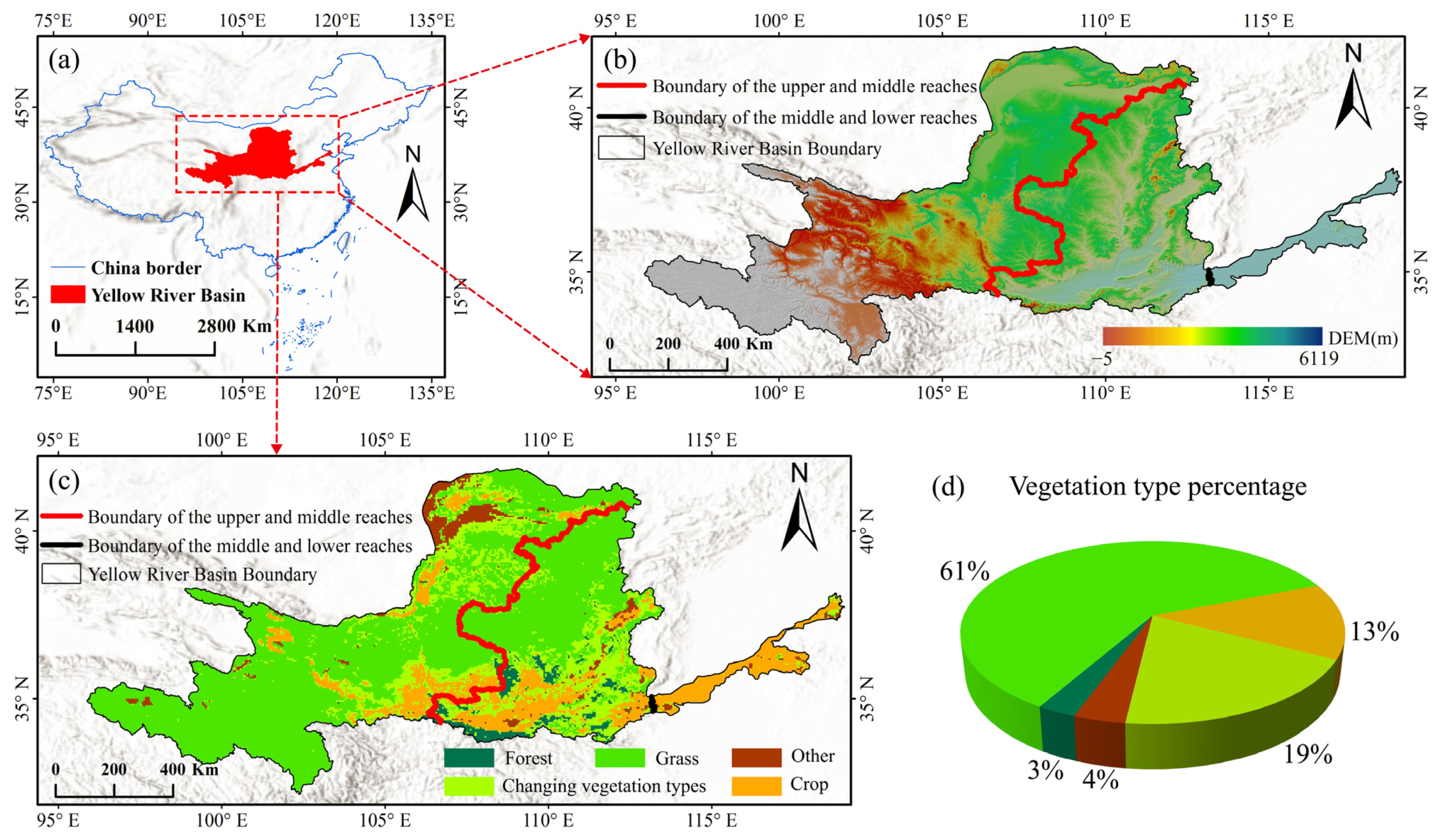
2.1. Study Area
2.2. Data
2.2.1. Meteorological Data
2.2.2. Vegetation Index
2.2.3. Land Use Data
2.3. Method
2.3.1. SPEI
2.3.2. VHI
2.3.3. SMA
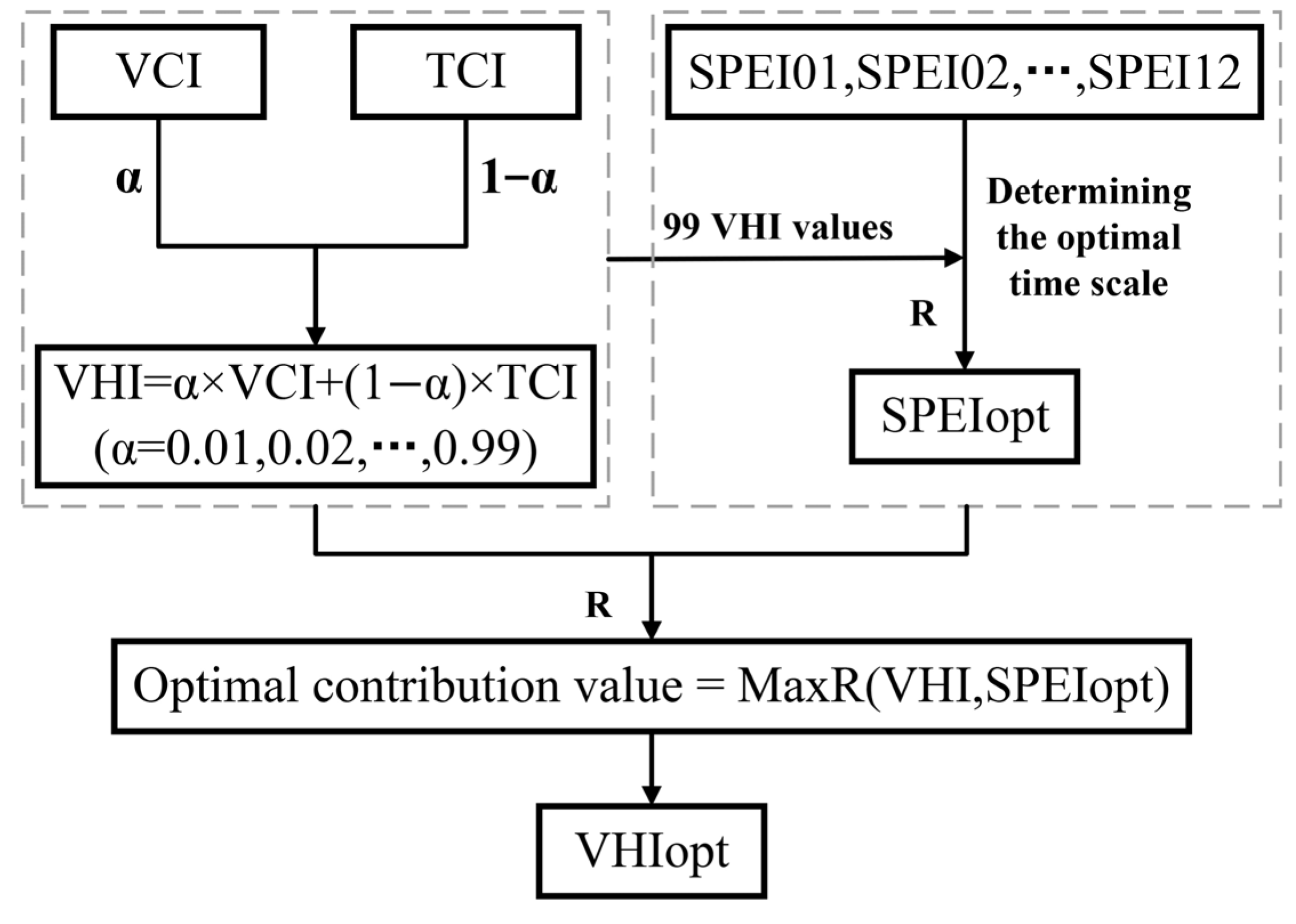
2.3.4. VHI Algorithm Optimization
2.3.5. Evaluation Indices
3. Results
3.1. Calculation of Optimal Weighting Factors
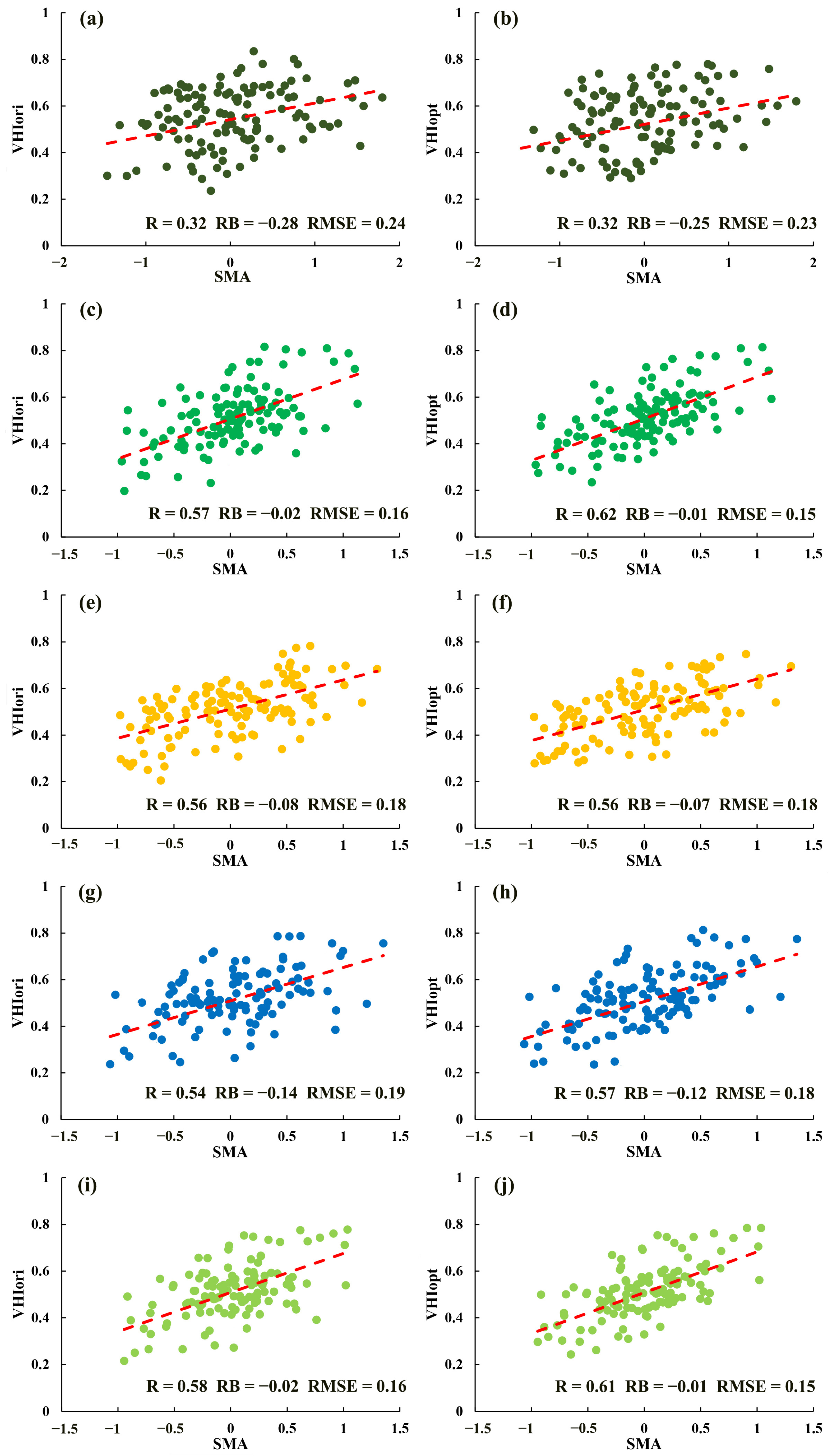
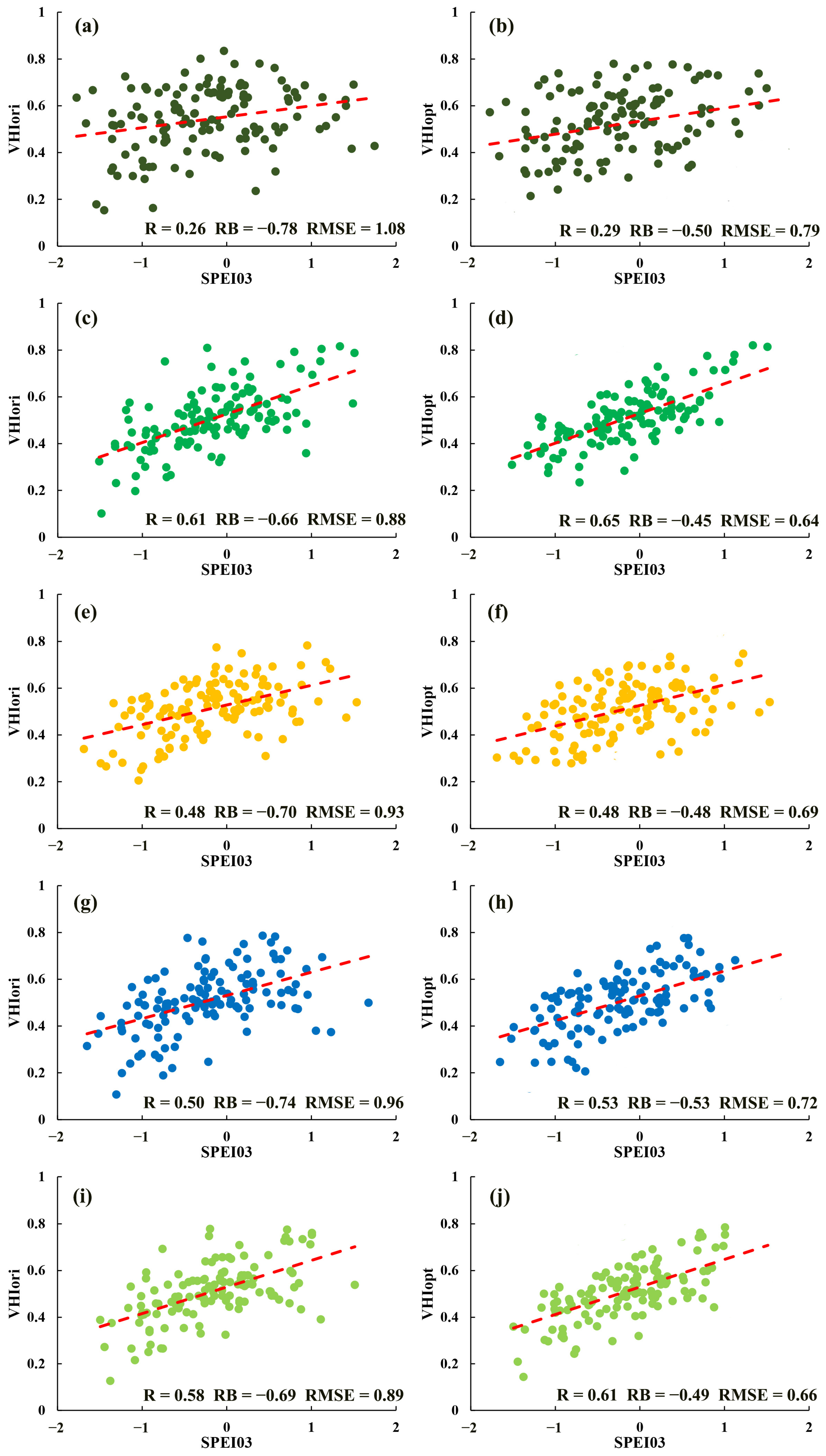
3.2. VHIopt Accuracy Evaluation
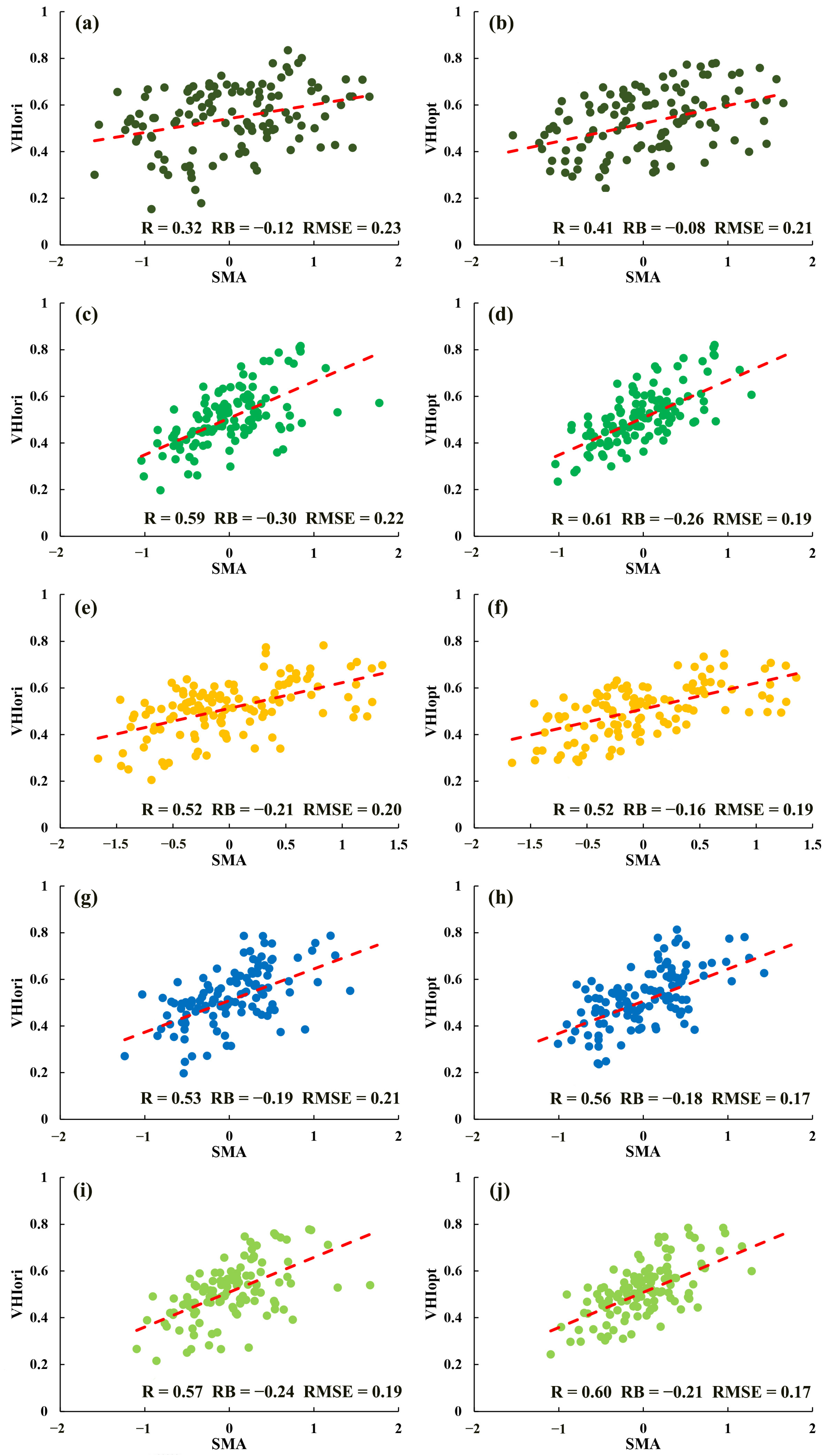
3.2.1. Evaluation Based on SMA
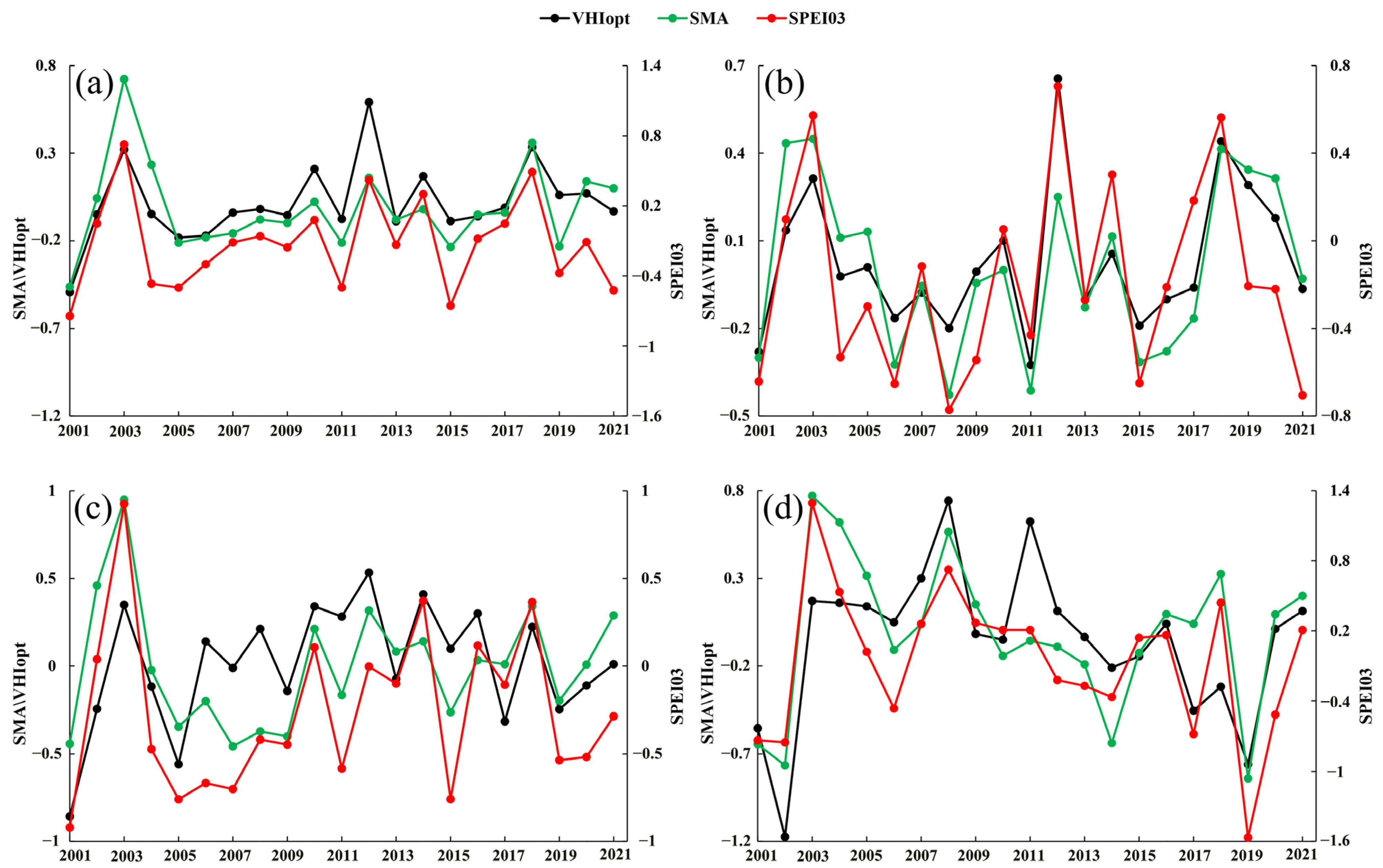
3.2.2. Evaluation Based on SPEI03
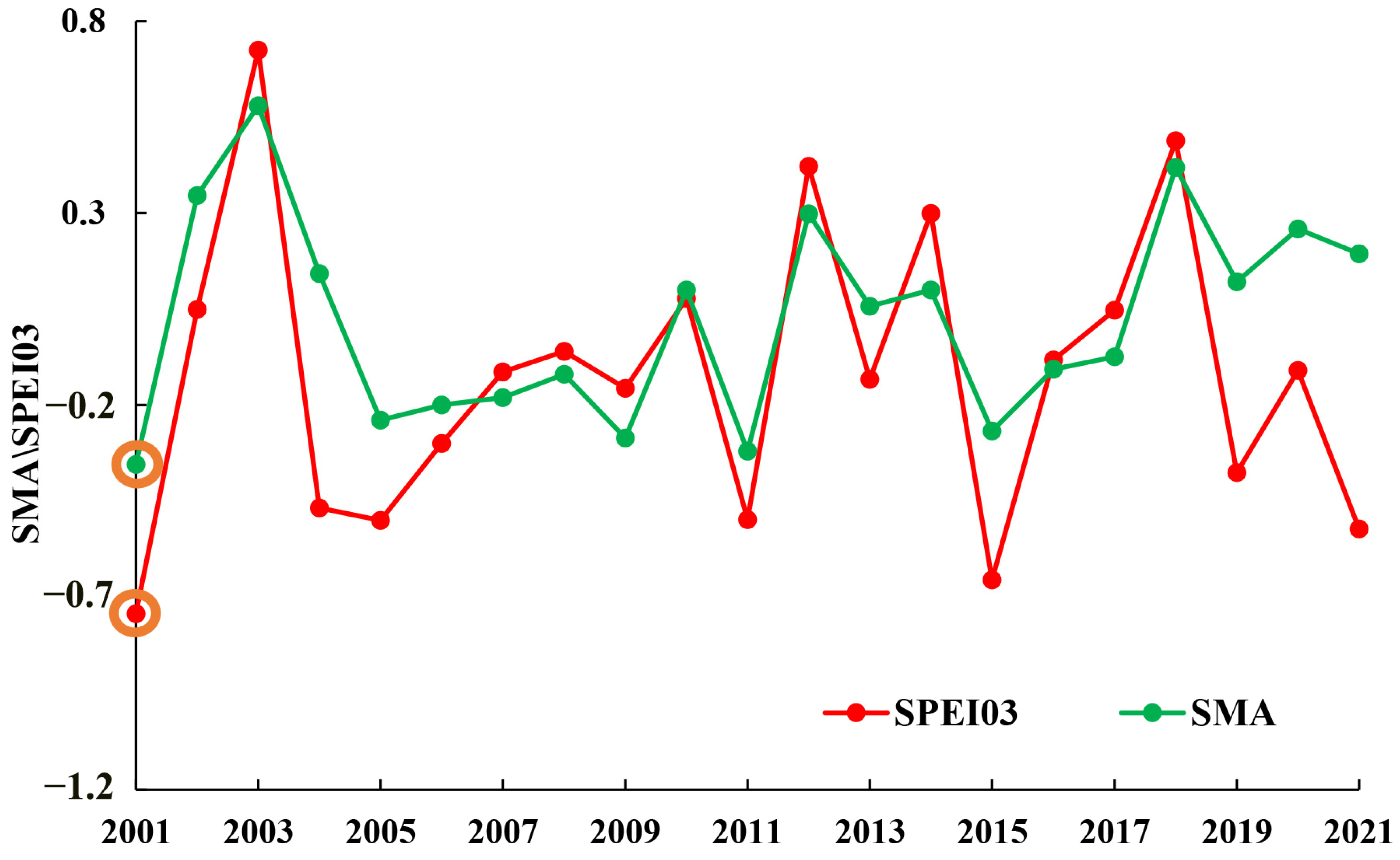
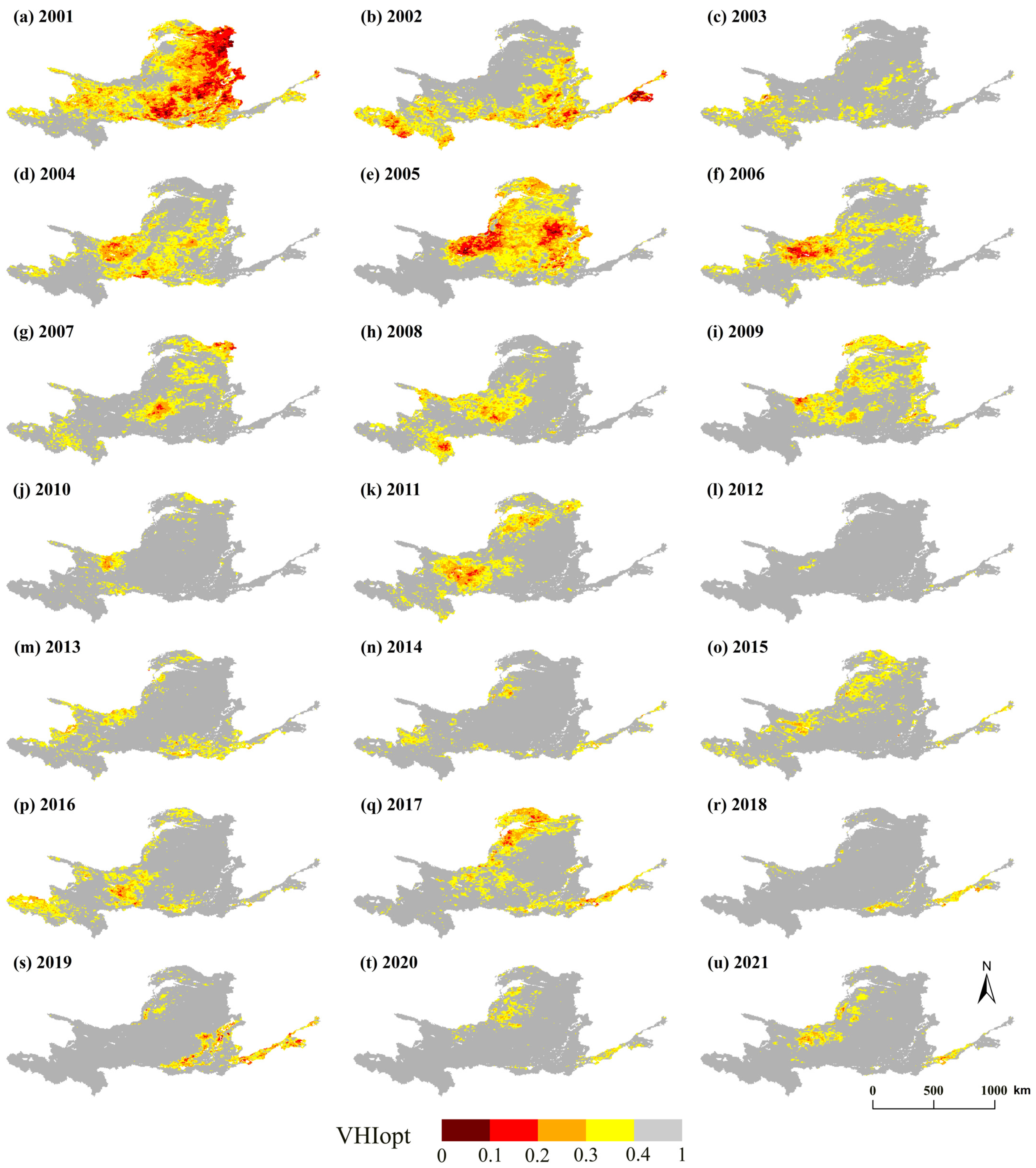
3.2.3. Verification of Typical Drought Years
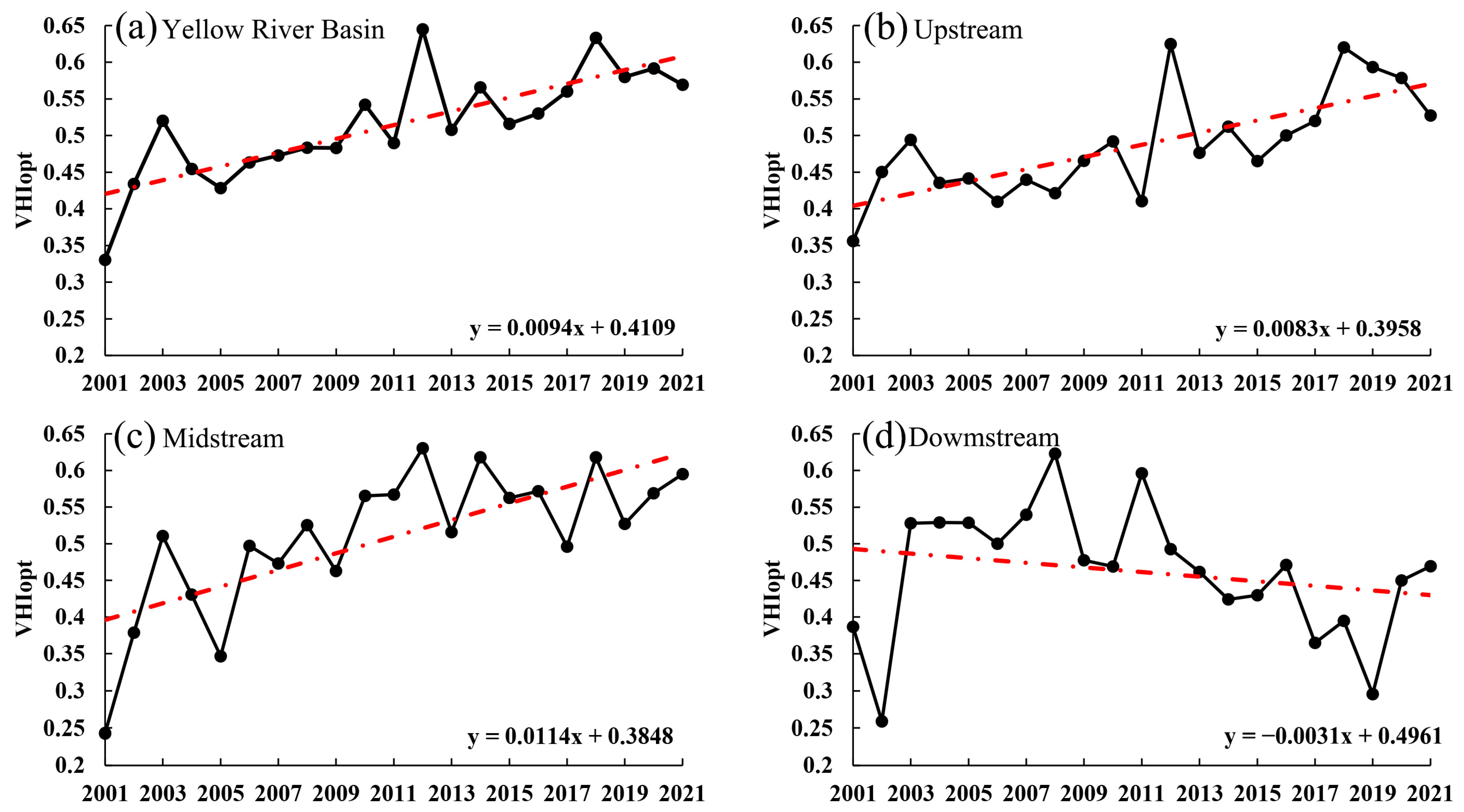
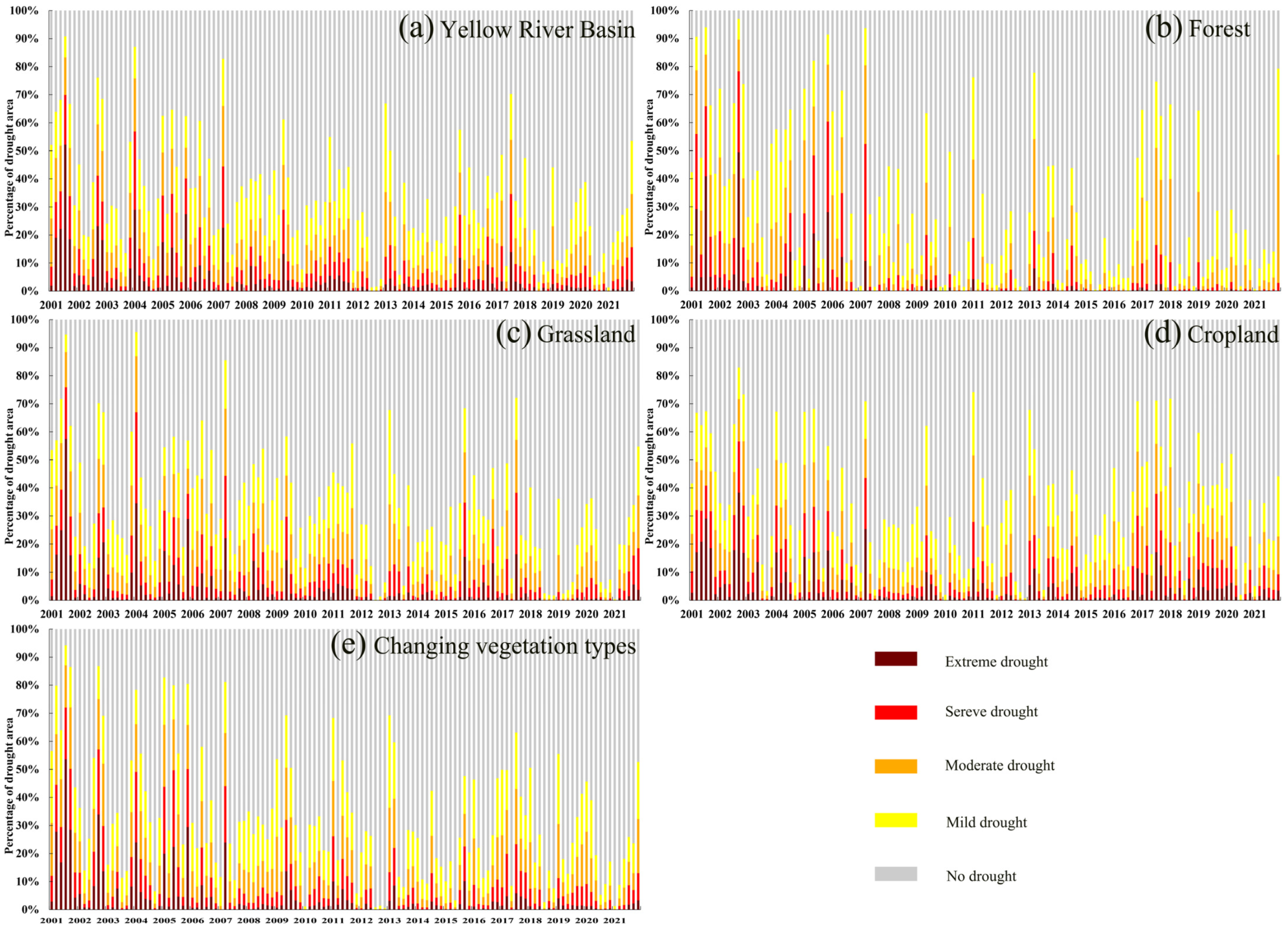
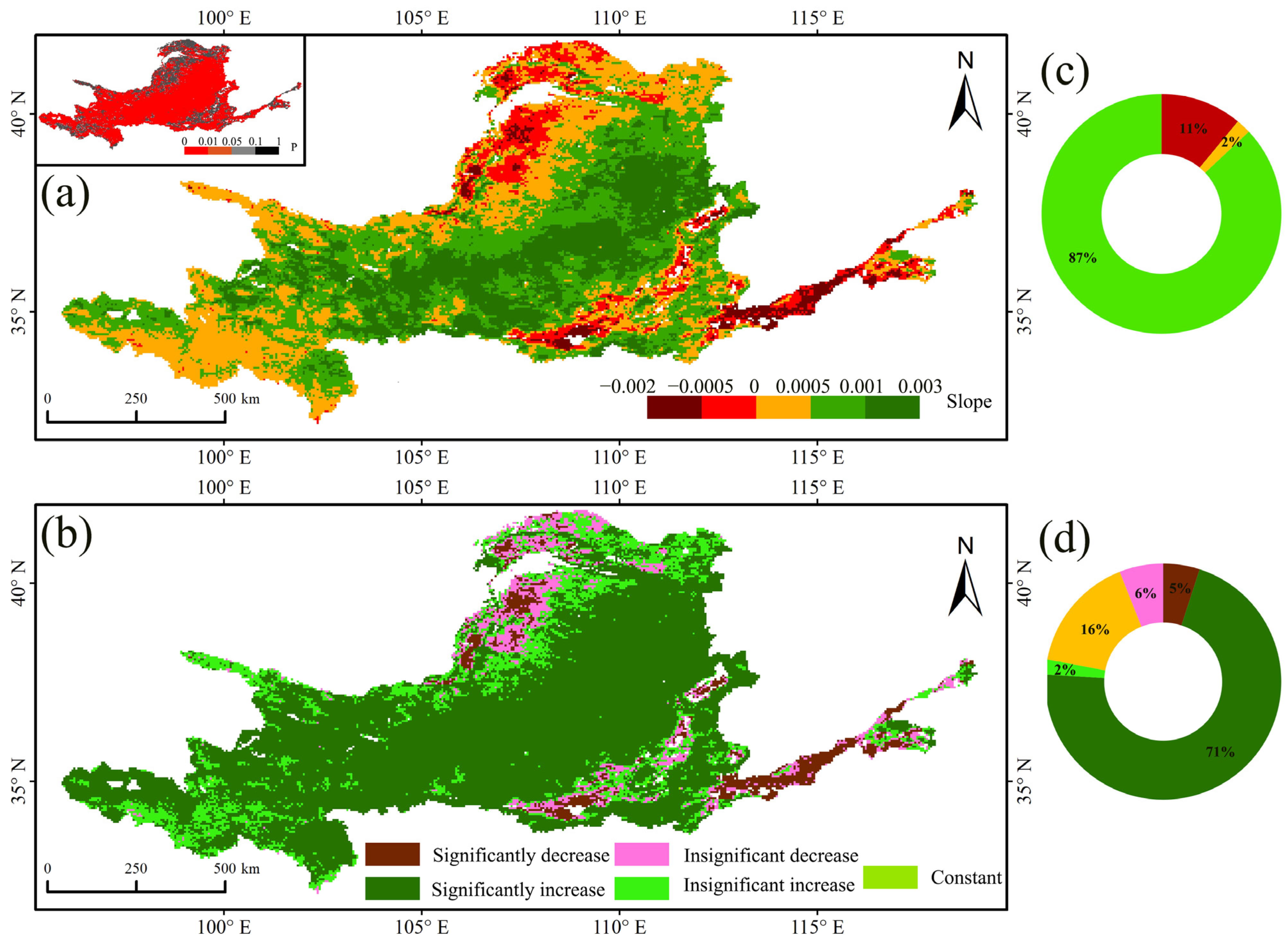
3.3. Spatial and Temporal Evolution Trend of Drought in YRB Based on VHIopt
3.3.1. Analysis of Drought Time Variation
3.3.2. Spatial Distribution Analysis of Drought
4. Discussion
4.1. Spatial Differences Between VHIopt and VHIori
4.2. Limitations and Uncertainties
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| IGBP Classification | Reclassification Results |
|---|---|
| Water Bodies | Other |
| Evergreen Needleleaf Forests | Forest |
| Evergreen Broadleaf Forests | Forest |
| Deciduous Needleleaf Forests | Forest |
| Deciduous Broadleaf Forests | Forest |
| Mixed Forests | Forest |
| Closed Shrublands | Forest |
| Open Shrublands | Forest |
| Woody Savannas | Grasslands |
| Savannas | Grasslands |
| Grasslands | Grasslands |
| Permanent Wetlands | Other |
| Croplands | Croplands |
| Urban and Built-Up Lands | Other |
| Cropland/Natural Vegetation Mosaics | Croplands |
| Snow and Ice | Other |
| Barren Sparse Vegetation | Other |
| Vegetation Type | Forest | Grass | Crop | Variable | All |
|---|---|---|---|---|---|
| Weight Value | 0.28 | 0.23 | 0.45 | 0.28 | 0.29 |

References
- Wu, J.; He, B.; Lv, A.; Zhou, L.; Liu, M.; Zhao, L. Quantitative assessment and spatial characteristics analysis of agricultural drought vulnerability in China. Nat. Hazards 2010, 56, 785–801. [Google Scholar] [CrossRef]
- Chen, L.; He, Z.; Zhang, Y.; Shan, P. Spatial-temporal Characteristics Analysis of Agricultural Drought Based on Vegetation Supply Water Index in Guizhou. China Rural. Water Hydropower 2023, 4, 158–166. [Google Scholar]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Haile, G.G.; Tang, Q.; Li, W.; Liu, X.; Zhang, X. Drought: Progress in broadening its understanding. Wiley Interdiscip. Rev. Water 2020, 7, e1407. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- Zeng, J.; Zhang, R.; Qu, Y.; Bento, V.A.; Zhou, T.; Lin, Y.; Wu, X.; Qi, J.; Shui, W.; Wang, Q. Improving the drought monitoring capability of VHI at the global scale via ensemble indices for various vegetation types from 2001 to 2018. Weather. Clim. Extrem. 2022, 35, 100412. [Google Scholar] [CrossRef]
- Liu, X.; Zhu, X.; Pan, Y.; Li, S.; Liu, Y. Agricultural drought monitor: Progress, challenges and prospect. Acta Geogr. Sin. 2015, 70, 1835–1848. [Google Scholar]
- Dilip, T.; Kumari, M.; Murthy, C.S.; Neelima, T.L.; Chakraborty, A.; Devi, M.U. Monitoring early-season agricultural drought using temporal Sentinel-1 SAR-based combined drought index. Environ. Monit. Assess. 2023, 195, 925. [Google Scholar] [CrossRef]
- Ciais, P.; Reichstein, M.; Viovy, N.; Granier, A.; Ogée, J.; Allard, V.; Aubinet, M.; Buchmann, N.; Bernhofer, C.; Carrara, A.; et al. Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 2005, 437, 529–533. [Google Scholar] [CrossRef]
- Gatti, L.V.; Gloor, M.; Miller, J.B.; Doughty, C.E.; Malhi, Y.; Domingues, L.G.; Basso, L.S.; Martinewski, A.; Correia, C.S.C.; Borges, V.F.; et al. Drought sensitivity of Amazonian carbon balance revealed by atmospheric measurements. Nature 2014, 506, 76–90. [Google Scholar] [CrossRef]
- Wang, G. Agricultural drought in a future climate: Results from 15 global climate models participating in the IPCC 4th assessment. Clim. Dyn. 2005, 25, 739–753. [Google Scholar] [CrossRef]
- Kogan, F.N. Operational space technology for global vegetation assessment. Bull. Am. Meteorol. Soc. 2001, 82, 1949–1964. [Google Scholar] [CrossRef]
- Pei, F.; Wu, C.; Liu, X.; Li, X.; Yang, K.; Zhou, Y.; Wang, K.; Xu, L.; Xia, G. Monitoring the vegetation activity in China using vegetation health indices. Agric. For. Meteorol. 2018, 248, 215–227. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, Z.; Zhang, W.; Lai, H.; Wang, F. Using Vegetation Health Index to Calculate Spatiotemporal Variation in Drought and Its Determinants in Inner Mongolia. J. Irrig. Drain. 2023, 42, 80–89+105. [Google Scholar]
- Hu, T.; van Dijk AI, J.M.; Renzullo, L.J.; Xu, Z.; He, J.; Tian, S.; Zhou, J.; Li, H. On agricultural drought monitoring in Australia using Himawari-8 geostationary thermal infrared observations. Int. J. Appl. Earth Obs. Geoinf. 2020, 91, 102153. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Z.; Lai, H.; Wang, F.; Li, Y.; Feng, K.; Qi, Q.; Di, D. Lag Time and Cumulative Effects of Climate Factors on Drought in North China Plain. Water 2023, 15, 3428. [Google Scholar] [CrossRef]
- Bento, V.A.; Gouveia, C.M.; DaCamara, C.C.; Libonati, R.; Trigo, I.F. The roles of NDVI and Land Surface Temperature when using the Vegetation Health Index over dry regions. Glob. Planet. Change 2020, 190, 103198. [Google Scholar] [CrossRef]
- Javed, T.; Li, Y.; Rashid, S.; Li, F.; Hu, Q.; Feng, H.; Chen, X.; Ahmad, S.; Liu, F.; Pulatov, B. Performance and relationship of four different agricultural drought indices for drought monitoring in China’s mainland using remote sensing data. Sci. Total Environ. 2021, 759, 143530. [Google Scholar] [CrossRef]
- Kogan, F.N. Global drought and flood-watch from NOAA polar-orbitting satellites. Adv. Space Res. 1998, 21, 477–480. [Google Scholar] [CrossRef]
- Kogan, N.F. Global Drought Watch from Space. Bull. Am. Meteorol. Soc. 1997, 78, 621–636. [Google Scholar]
- Rhee, J.; Im, J.; Carbone, G.J. Monitoring agricultural drought for arid and humid regions using multi-sensor remote sensing data. Remote Sens. Environ. 2010, 114, 2875–2887. [Google Scholar] [CrossRef]
- Bento, V.A.; Gouveia, C.M.; Dacamara, C.C.; Trigo, I.F. A climatological assessment of drought impact on vegetation health index. Agric. For. Meteorol. 2018, 259, 286–295. [Google Scholar] [CrossRef]
- Han, Y.; Li, Z.; Huang, C.; Zhou, Y.; Zong, S.; Hao, T.; Niu, H.; Yao, H. Monitoring Droughts in the Greater Changbai Mountains Using Multiple Remote Sensing-Based Drought Indices. Remote Sens. 2020, 12, 530. [Google Scholar] [CrossRef]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, L24406. [Google Scholar] [CrossRef]
- Sun, N.S.; Chen, Q.; Liu, F.G. Vegetation Health Index 1-km Grid Dataset in Yellow River–Huangshui River Valley (2000–2020). J. Glob. Change Data Discov. 2022, 4, 589–596. [Google Scholar]
- Li, W.; Wang, Y. An Analysis of the Spatial-Temporal Characteristics of Drought in Guangdong Based on Vegetation Condition Index from 2003 to 2017. J. South China Norm. Univ. (Nat. Sci. Ed.) 2020, 52, 85–91. [Google Scholar]
- Bento, V.A.; Trigo, I.F.; Gouveia, C.M.; DaCamara, C.C. Contribution of land surface temperature (TCI) to vegetation health index: A comparative study using clear sky and all-weather climate data records. Remote Sens. 2018, 10, 1324. [Google Scholar] [CrossRef]
- Yin, G.; Zhang, H. A new integrated index for drought stress monitoring based on decomposed vegetation response factors. J. Hydrol. 2023, 618, 129252. [Google Scholar] [CrossRef]
- Bouras, E.H.; Jarlan, L.; Er-Raki, S.; Albergel, C.; Richard, B.; Balaghi, R.; Khabba, S. Linkages between rainfed cereal production and agricultural drought through remote sensing indices and a land data assimilation system: A case study in Morocco. Remote Sens. 2020, 12, 4018. [Google Scholar] [CrossRef]
- Unganai, L.S.; Kogan, F.N. Drought monitoring and corn yield estimation in Southern Africa from AVHRR data. Remote Sens. Environ. 1998, 63, 219–232. [Google Scholar] [CrossRef]
- Yin, G.; Zhang, H.; Zhang, L. Remote Sensing Monitoring of Agricultural Drought and Vegetation Sensitivity Analysis in the Middle and Lower Reaches of the Yangtze River from 2001 to 2019. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1245–1256. [Google Scholar]
- Zeng, J.; Zhou, T.; Qu, Y.; Bento, V.A.; Qi, J.; Xu, Y.; Li, Y.; Wang, Q. An improved global vegetation health index dataset in detecting vegetation drought. Sci. Data 2023, 10, 338. [Google Scholar] [CrossRef] [PubMed]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Gao, X.; Zhao, Q.; Zhao, X.; Wu, P.; Pan, W.; Gao, X.; Sun, M. Temporal and spatial evolution of the standardized precipitation evapotranspiration index (SPEI) in the Loess Plateau under climate change from 2001 to 2050. Sci. Total Environ. 2017, 595, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zeng, J.; Qi, J.; Zhang, X.; Zeng, Y.; Shui, W.; Xu, Z.; Zhang, R.; Wu, X.; Cong, J. A multi-scale daily SPEI dataset for drought characterization at observation stations over mainland China from 1961 to 2018. Earth Syst. Sci. Data 2021, 13, 331–341. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Ndayisaba, F.; Jiang, L.; Zheng, G.; Chen, T.; De Maeyer, P. Determining variable weights for an optimal scaled drought condition index (OSDCI): Evaluation in central Asia. Remote Sens. Environ. 2019, 231, 111220. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente Serrano, S.M.; Reig-Gracia, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef]
- Li, L.; She, D.; Zheng, H.; Lin, P.; Yang, Z.L. Elucidating diverse drought characteristics from two meteorological drought indices (SPI and SPEI) in China. J. Hydrometeorol. 2020, 21, 1513–1530. [Google Scholar] [CrossRef]
- Um, M.J.; Kim, Y.; Park, D. Evaluation and modification of the drought severity index (DSI) in East Asia. Remote Sens. Environ. 2018, 209, 66–76. [Google Scholar] [CrossRef]
- Chen, J.; Sun, H.; Wang, J.; Liao, W.; Chen, H. Improvement of comprehensive meteorological drought index and its applicability analysis. Trans. Chin. Soc. Agric. Eng. 2020, 36, 71–77. [Google Scholar] [CrossRef]
- Liu, L.; Zeng, J.; Wu, X.; Qu, J.; Li, X.; Zhang, J.; Han, J. Review on ECO-environment research in the Yellow River Basin: A bibliometric perspective. Int. J. Environ. Res. Public Health 2022, 19, 11986. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chang, J.; Fan, J.; Yu, B. Agricultural drought evolution characteristics and driving mechanisms in the YRB under climate and land use changes. Trans. Chin. Soc. Agric. Eng. (Trans. CSAE) 2021, 37, 84–93. [Google Scholar]
- Huang, J.; Zhang, G.; Yu, H.; Wang, S.; Guan, X.; Ren, Y. Characteristics of climate change in the YRB during recent 40 years. J. Hydraul. Eng. 2020, 51, 1048–1058. [Google Scholar]
- Liu, H.; Jiang, L.L.; Liu, B.; Liu, R.; Xiao, Z.L. Characteristics of drought in China and its effect on vegetation change in recent 40 years. Acta Ecol. Sin. 2023, 43, 7936–7949. [Google Scholar]
- Yaning, C.; Yupeng, L.; Zhi, L.; Liu, Y.; Huang, W.; Liu, X.; Feng, M. Analysis of the impact of global climate change on dryland areas. Adv. Earth Sci. 2022, 37, 111. [Google Scholar]
- Han, L.; Zhang, Q.; Ma, P.; Wang, Y.; Huang, T.; Jia, Y.; Wang, X.; Wang, X.; Liu, W.; Li, D.; et al. Characteristics of drought disasters risk in the YRB under the climate warming. J. Desert Res. 2021, 41, 225. [Google Scholar]
- Xin’e Tao, H.C.; Xu, C. Characteristics of drought variations in Hanjiang Basin in 1961–2014 based on SPI/SPEI. J. Water Resour. Res. 2015, 4, 404–415. [Google Scholar]
- Zhang, A.; Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar] [CrossRef]
- Tian, F.; Liu, L.Z.; Yang, J.H.; Wu, J.J. Vegetation greening in more than 94% of the Yellow River Basin (YRB) region in China during the 21st century caused jointly by warming and anthropogenic activities. Ecol. Indic. 2021, 125, 107479. [Google Scholar] [CrossRef]
- Jin, L.; Chen, S.; Liu, M. Multiscale Spatiotemporal Dynamics of Drought within the Yellow River Basin (YRB): An Examination of Regional Variability and Trends. Water 2024, 16, 791. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Liu, J.-S.; Ma, T.-B. Dynamics and changes in spatial patterns of land use in YRB, China. Land Use Policy 2010, 27, 313–323. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, L.; He, Y.; Cao, S.; Wei, X.; Guo, Y.; Ran, L.; Filonchyk, M. Spatiotemporal evolution of agricultural drought and its attribution under different climate zones and vegetation types in the YRB of China. Sci. Total Environ. 2024, 914, 169687. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Si, W.; Du, Z.; Liang, H.; Lei, T.; Sun, B.; Wu, Z. Changes in GPP of China during the typical drought years from 1982 to 2017. Arid. Land Geogr. 2023, 46, 1577–1590. [Google Scholar]
- Yu, T.; Bao, A.; Zhang, J.; Tu, H.; Chen, B.; De Maeyer, P.; Van de Voorde, T. Evaluating surface soil moisture characteristics and the performance of remote sensing and analytical products in Central Asia. J. Hydrol. 2023, 617, 128921. [Google Scholar] [CrossRef]
- Lotfirad, M.; Esmaeili-Gisavandani, H.; Adib, A. Drought monitoring and prediction using SPI, SPEI, and random forest model in various climates of Iran. J. Water Clim. Change 2022, 13, 383–406. [Google Scholar] [CrossRef]
- Jiménez-Donaire, M.P.; Giráldez, J.V.; Vanwalleghem, T. Impact of climate change on agricultural droughts in Spain. Water 2020, 12, 3214. [Google Scholar] [CrossRef]
- Yu, X.; Pu, Y.; Kang, B. Spatial-temporal characteristics of drought in recent 50 years in Guangdong Province based on SPEI. J. Arid. Meteorol. 2022, 40, 1051. [Google Scholar]
- Li, Y. Effects of Multi-time Scale Meteorological Drought on Vegetation in the YRB from 1982 to 2020. J. Soil Water Conserv. 2024, 38, 187–196. [Google Scholar]
- Vicente-Serrano, S.M.; Gouveia, C.; Camarero, J.J.; Beguería, S.; Trigo, R.; López-Moreno, J.I.; Azorín-Molina, C.; Pasho, E.; Lorenzo-Lacruz, J.; Revuelto, J.; et al. Response of vegetation to drought time-scales across global land biomes. Proc. Natl. Acad. Sci. USA 2013, 110, 52–57. [Google Scholar] [CrossRef]
- Kogan, F.; Sullivan, J. Development of global drought-watch system using NOAA/AVHRR data. Adv. Space Res. 1993, 13, 219–222. [Google Scholar] [CrossRef]
- Jalayer, S.; Sharifi, A.; Abbasi-Moghadam, D.; Tariq, A.; Qin, S. Assessment of spatiotemporal characteristic of droughts using in situ and remote sensing-based drought indices. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1483–1502. [Google Scholar] [CrossRef]
- Zou, L.; Cao, S.; Sanchez-Azofeifa, A. Evaluating the utility of various drought indices to monitor meteorological drought in Tropical Dry Forests. Int. J. Biometeorol. 2020, 64, 701–711. [Google Scholar] [CrossRef] [PubMed]
- Qiao, L.; Zheng, Z.; Ma, X.; Zhang, X.; Ru, X.; Peng, J.; Zhao, X.; Xia, H. Monthly 1km resolution VCI and TCI drought index datasets in the YRB (2003–2021). China Sci. Data 2023, 8, 223–233. [Google Scholar]
- Xiao, D.; Wang, S. Comments on the progress and direction in soil water research. Ecol. Environ. Sci. 2009, 18, 1182–1188. [Google Scholar]
- Li, W.; Liu, S.; Hou, M.; Han, J.; Chen, X. Advance in the Study on Meteorological and Agricultural Drought Indices. Meteorol. Environ. Sci. 2021, 44, 76–82. [Google Scholar]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lrene, L.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture–climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Lai, E.N.; Wang-Erlandsson, L.; Virkki, V.; Porkka, M.; van der Ent, R.J. Root zone soil moisture in over 25% of global land permanently beyond pre-industrial variability as early as 2050 without climate policy. Hydrol. Earth Syst. Sci. 2023, 27, 3999–4018. [Google Scholar] [CrossRef]
- Farokhi, M.; Faridani, F.; Lasaponara, R.; Ansari, H.; Faridhosseini, A. Enhanced estimation of root zone soil moisture at 1 km resolution using SMAR model and MODIS-based downscaled AMSR2 soil moisture data. Sensors 2021, 21, 5211. [Google Scholar] [CrossRef]
- Carranza, C.; Nolet, C.; Pezij, M.; van der Ploeg, M. Root zone soil moisture estimation with Random Forest. J. Hydrol. 2021, 593, 125840. [Google Scholar] [CrossRef]
- Al Bitar, A.; Mahmoodi, A.; Kerr, Y.; Rodriguez-Fernandez, N.; Parrens, M.; Tarot, S. Global Assessment of Droughts in the Last Decade from SMOS Root Zone Soil Moisture. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8628–8631. [Google Scholar]
- Chen, C.C.; Dominguez, F. The location of large-scale soil moisture anomalies affects moisture transport and precipitation over southeastern South America. Geophys. Res. Lett. 2024, 51, e2023GL106777. [Google Scholar] [CrossRef]
- Cammalleri, C.; Vogt, J.V.; Bisselink, B.; de Roo, A. Comparing soil moisture anomalies from multiple independent sources over different regions across the globe. Hydrol. Earth Syst. Sci. 2017, 21, 6329–6343. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, B.; Shi, C.; Cui, W.; Zhao, C.; Liu, Y.; Ren, L.; Zhang, L.; Zhu, Y.; Chen, T.; et al. Evaluation of hydrological utility of IMERG Final run V05 and TMPA 3B42V7 satellite precipitation products in the Yellow River source region, China. J. Hydrol. 2018, 567, 696–711. [Google Scholar] [CrossRef]
- Zhou, L.; Tucker, C.J.; Kaufmann, R.K.; Slayback, D.; Shabanov, N.V.; Myneni, R.B. Variations in northern vegetation activity inferred from satellite data of vegetation index during 1981 to 1999. J. Geophys. Res. Atmos. 2001, 106, 20069–20083. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Assessing vegetation response to drought in the northern Great Plains using vegetation and drought indices. Remote Sens. Environ. 2003, 87, 85–98. [Google Scholar] [CrossRef]
- Vilonen, L.L.; Blair, J.; Trivedi, P.; Zeglin, L.; Smith, M.D. Limited legacy effects of extreme multiyear drought on carbon and nitrogen cycling in a mesic grassland. Elem. Sci. Anth. 2022, 10, 000093. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, J.; Li, X.; Zhou, H.; Yang, J.; Geng, G.; An, X.; Liu, L.; Tang, Z. A comprehensively quantitative method of evaluating the impact of drought on crop yield using daily multi-scale SPEI and crop growth process model. Int. J. Biometeorol. 2017, 61, 685–699. [Google Scholar] [CrossRef]
- Rojas, O.; Vrieling, A.; Rembold, F. Assessing drought probability for agricultural areas in Africa with coarse resolution remote sensing imagery. Remote Sens. Environ. 2011, 115, 343–352. [Google Scholar] [CrossRef]
- Quiring, S.M.; Ganesh, S. Evaluating the utility of the Vegetation Condition Index (VCI) for monitoring meteorological drought in Texas. Agric. For. Meteorol. 2010, 150, 330–339. [Google Scholar] [CrossRef]
- Huang, S.; Gan, Y.; Zhang, X.; Chen, N.; Wang, C.; Gu, X.; Ma, J.; Diyogi, D. Urbanization amplified asymmetrical changes of rainfall and exacerbated drought: Analysis over five urban agglomerations in the Yangtze River Basin, China. Earth’s Future 2023, 11, e2022EF003117. [Google Scholar] [CrossRef]
- Ault, T.R. On the essentials of drought in a changing climate. Science 2020, 368, 256–260. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, X.; Otkin, J.A.; Ji, P. Climate warming outweighs vegetation greening in intensifying flash droughts over China. Environ. Res. Lett. 2022, 17, 054041. [Google Scholar] [CrossRef]
- Zheng, F.; Wang, H.; Luo, H.; Yi, S. Decadal change in ENSO related seasonal precipitation over southern China under influences of ENSO and its combination mode. Clim. Dyn. 2020, 54, 1973–1986. [Google Scholar] [CrossRef]
- Chen, Y.; Fu, B.; Zhao, Y.; Wang, K.; Zhao, M.; Ma, J.; Wu, J.; Xu, C.; Liu, W.; Wang, H. Sustainable development in the YRB: Issues and strategies. J. Clean. Prod. 2020, 263, 121223. [Google Scholar] [CrossRef]
- Tang, Z.; Zhou, Z.; Wang, D.; Luo, F.; Bai, J.; Fu, Y. Impact of vegetation restoration on ecosystem services in the Loess plateau, a case study in the Jinghe Watershed, China. Ecol. Indic. 2022, 142, 109183. [Google Scholar] [CrossRef]
- Yuan, S.; Xing, X.L.; Ju, W.M. Temporal and spatial patterns of remote sensing drought indices and their responses to climate and land use changes in China. Acta Ecol. Sin. 2023, 43, 6691–6705. [Google Scholar]
- Jay, S.; Baret, F.; Dutartre, D.; Malatesta, G.; Héno, S.; Comar, A.; Weiss, M.; Maupas, F. Exploiting the centimeter resolution of UAV multispectral imagery to improve remote-sensing estimates of canopy structure and biochemistry in sugar beet crops. Remote Sens. Environ. 2019, 231, 110898. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, D.; Tian, W.; Zhao, H.; Geng, S.; Lu, H.; Ma, G.; Huang, J.; Choy Lim Kam Sian, K.T. Construction of an integrated drought monitoring model based on deep learning algorithms. Remote Sens. 2023, 15, 667. [Google Scholar] [CrossRef]
- Hazaymeh, K.; Hassan, Q.K. Remote sensing of agricultural drought monitoring: A state of art review. AIMS Environ. Sci. 2016, 3, 604–630. [Google Scholar] [CrossRef]
- Mullapudi, A.; Vibhute, A.D.; Mali, S.; Patil, C.H. A review of agricultural drought assessment with remote sensing data: Methods, issues, challenges and opportunities. Appl. Geomat. 2023, 15, 1–13. [Google Scholar] [CrossRef]
- An, Q.; He, H.; Gao, J.; Nie, Q.; Cui, Y.; Wei, C.; Xie, X. Analysis of temporal-spatial variation characteristics of drought: A case study from Xinjiang, China. Water 2020, 12, 741. [Google Scholar] [CrossRef]
- Guo, H.; Bao, A.; Liu, T.; Ndayisaba, F.; Jiang, L.; Kurban, A.; De Maeyer, P. Spatial and temporal characteristics of droughts in Central Asia during 1966–2015. Sci. Total Environ. 2018, 624, 1523–1538. [Google Scholar] [CrossRef] [PubMed]
- Zeng, J.; Zhang, R.; Lin, Y.; Wu, X.; Tang, J.; Guo, P.; Li, J.; Wang, Q. Drought frequency characteristics of China, 1981–2019, based on the vegetation health index. Clim. Res. 2020, 81, 131–147. [Google Scholar] [CrossRef]
- Moutia, S.; Sinan, M.; Lekhlif, B. Assessment of agricultural drought in Morocco based on a composite of the Vegetation Health Index (VHI) and Standardized Precipitation Evapotranspiration Index (SPEI)//E3S Web of Conferences. EDP Sci. 2021, 314, 04003. [Google Scholar] [CrossRef]
- Zhao, H.; Huang, Y.; Wang, X.; Li, X.; Lei, T. The performance of SPEI integrated remote sensing data for monitoring agricultural drought in the North China Plain. Field Crops Res. 2023, 302, 109041. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Chang, L.Y.; Minh, V.Q. Monitoring agricultural drought in the Lower Mekong Basin using MODIS NDVI and land surface temperature data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 417–427. [Google Scholar] [CrossRef]
- Kukunuri AN, J.; Murugan, D.; Singh, D. Variance based fusion of VCI and TCI for efficient classification of agriculture drought using MODIS data. Geocarto Int. 2022, 37, 2871–2892. [Google Scholar] [CrossRef]


| SPEI | SPEI ≤ −2.0 | −2.0 < SPEI ≤ −1.5 | −1.5 < SPEI ≤ −1.0 | −1.0 < SPEI ≤ −0.5 | −0.5 < SPEI |
|---|---|---|---|---|---|
| Drought Severity | Extreme Drought | Severe Drought | Moderate Drought | Mild Drought | No Drought |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hang, Q.; Guo, H.; Meng, X.; Wang, W.; Cao, Y.; Liu, R.; De Maeyer, P.; Wang, Y. Optimizing the Vegetation Health Index for Agricultural Drought Monitoring: Evaluation and Application in the Yellow River Basin. Remote Sens. 2024, 16, 4507. https://doi.org/10.3390/rs16234507
Hang Q, Guo H, Meng X, Wang W, Cao Y, Liu R, De Maeyer P, Wang Y. Optimizing the Vegetation Health Index for Agricultural Drought Monitoring: Evaluation and Application in the Yellow River Basin. Remote Sensing. 2024; 16(23):4507. https://doi.org/10.3390/rs16234507
Chicago/Turabian StyleHang, Qinghou, Hao Guo, Xiangchen Meng, Wei Wang, Ying Cao, Rui Liu, Philippe De Maeyer, and Yunqian Wang. 2024. "Optimizing the Vegetation Health Index for Agricultural Drought Monitoring: Evaluation and Application in the Yellow River Basin" Remote Sensing 16, no. 23: 4507. https://doi.org/10.3390/rs16234507
APA StyleHang, Q., Guo, H., Meng, X., Wang, W., Cao, Y., Liu, R., De Maeyer, P., & Wang, Y. (2024). Optimizing the Vegetation Health Index for Agricultural Drought Monitoring: Evaluation and Application in the Yellow River Basin. Remote Sensing, 16(23), 4507. https://doi.org/10.3390/rs16234507










