SAR-MINF: A Novel SAR Image Descriptor and Matching Method for Large-Scale Multidegree Overlapping Tie Point Automatic Extraction
Abstract
1. Introduction
- Differences in bands and resolution can lead to inconsistent noise distribution in images, necessitating a feature extraction method that can adapt to different levels of noise distribution;
- Differences in bands, polarization, and resolution can cause inconsistencies in the representation of terrain features, thus requiring matching algorithms to have the capability to match multimodal imagery;
- Differences in incidence angles and orbital directions, along with the layover issues encountered in high-resolution urban SAR imagery, necessitate the need for feature points to avoid layover areas;
- Differences in resolution can lead to scale discrepancies in images, requiring enhanced capability in extracting local information features;
- In extracting tie points, especially for multidegree overlapping, feature-based matching algorithms may struggle to extract common tie points stably.
- To overcome the varying noise distribution present in SAR images of different imaging modes and resolutions, a Gamma Modulation Filter (GMF) is proposed. Based on this, a SAR local energy model and an adaptive noise model are constructed, leading to the proposal of Gamma Modulation Phase Congruency (GMPC);
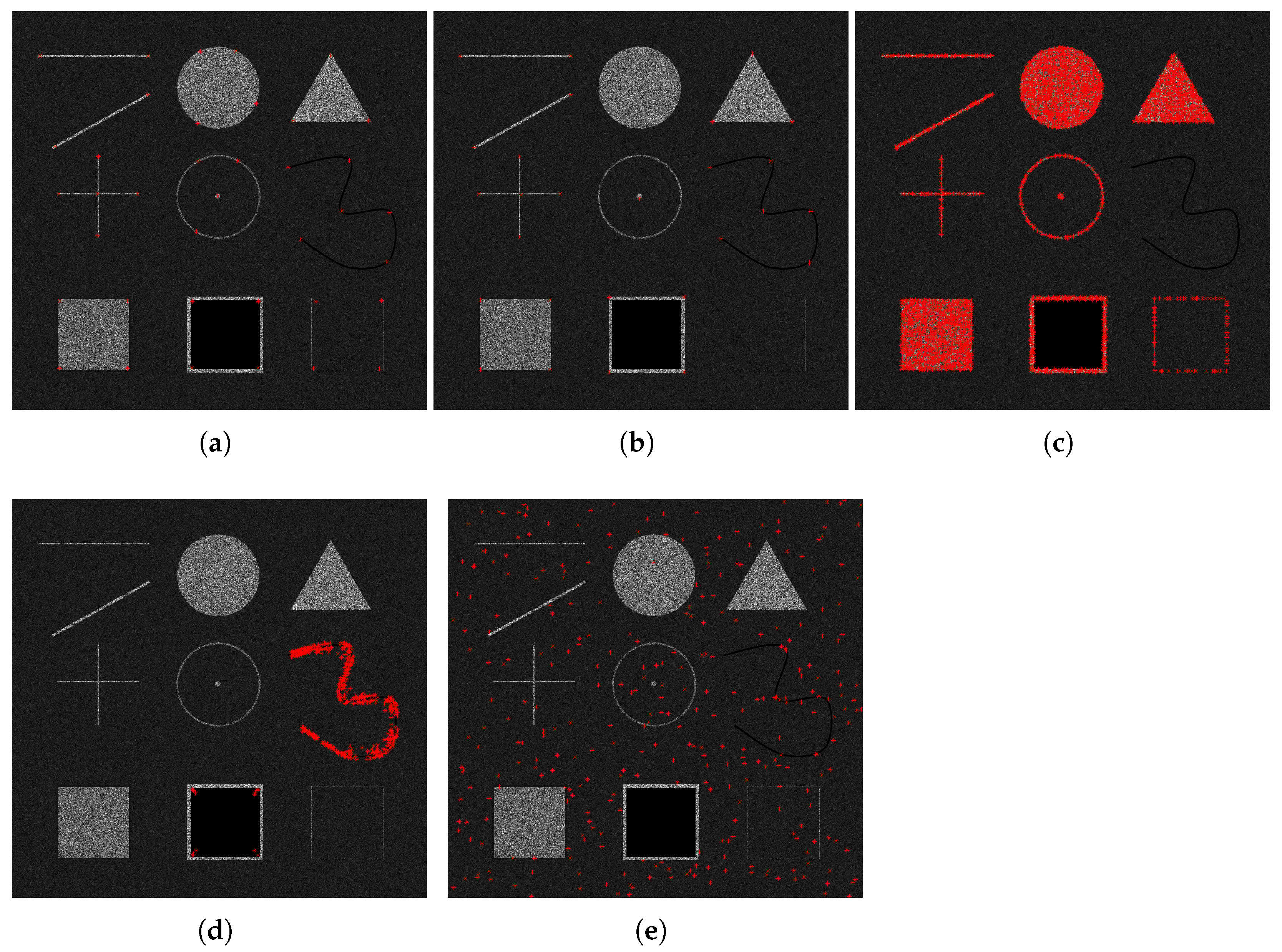
- The multiscale GMPC is used in place of the Laplacian of Gaussian (LoG) method in the Harris algorithm, leading to the introduction of the GMPC-Harris keypoint detection operator. This enhancement improves feature detection capabilities compared with both the traditional Harris and SAR-Harris methods;
- Based on GMPC, a layover perception algorithm is developed to eliminate pseudo-feature points in layover areas, thereby enhancing the matching performance of images in mountainous regions and different orbits;
- Based on GMPC, the maximum moment is improved, leading to the proposal of the Modality Independent Neighborhood Fusion (SAR-MINF) descriptor for SAR images. This aims to enhance the local feature information extraction capability for SAR images with radiometric differences, scale variations, and other discrepancies;
- A graph-based overlap extraction algorithm is proposed, and using the multidegree overlapping graph combined with a position-relationship-based fusion matching algorithm, a process for the automated extraction of large-scale SAR tie points was developed.
2. Materials and Methods
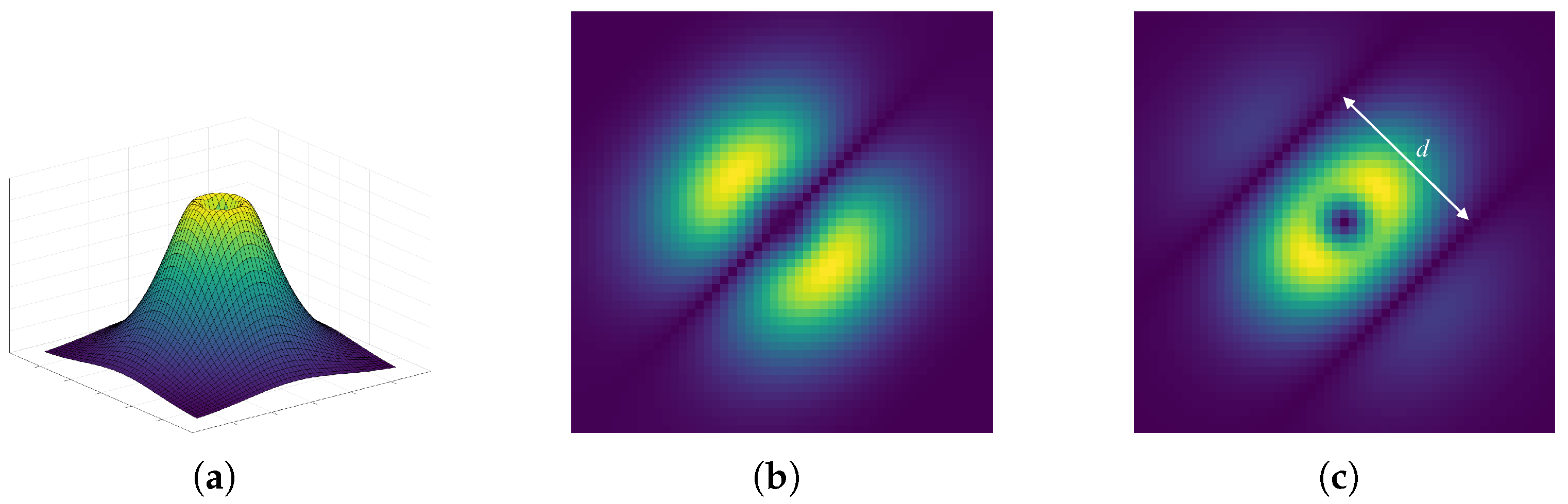
2.1. Gamma Modulation Phase Congruency (GMPC) Model
2.1.1. Original Phase Congruency (PC) Model
2.1.2. GMPC
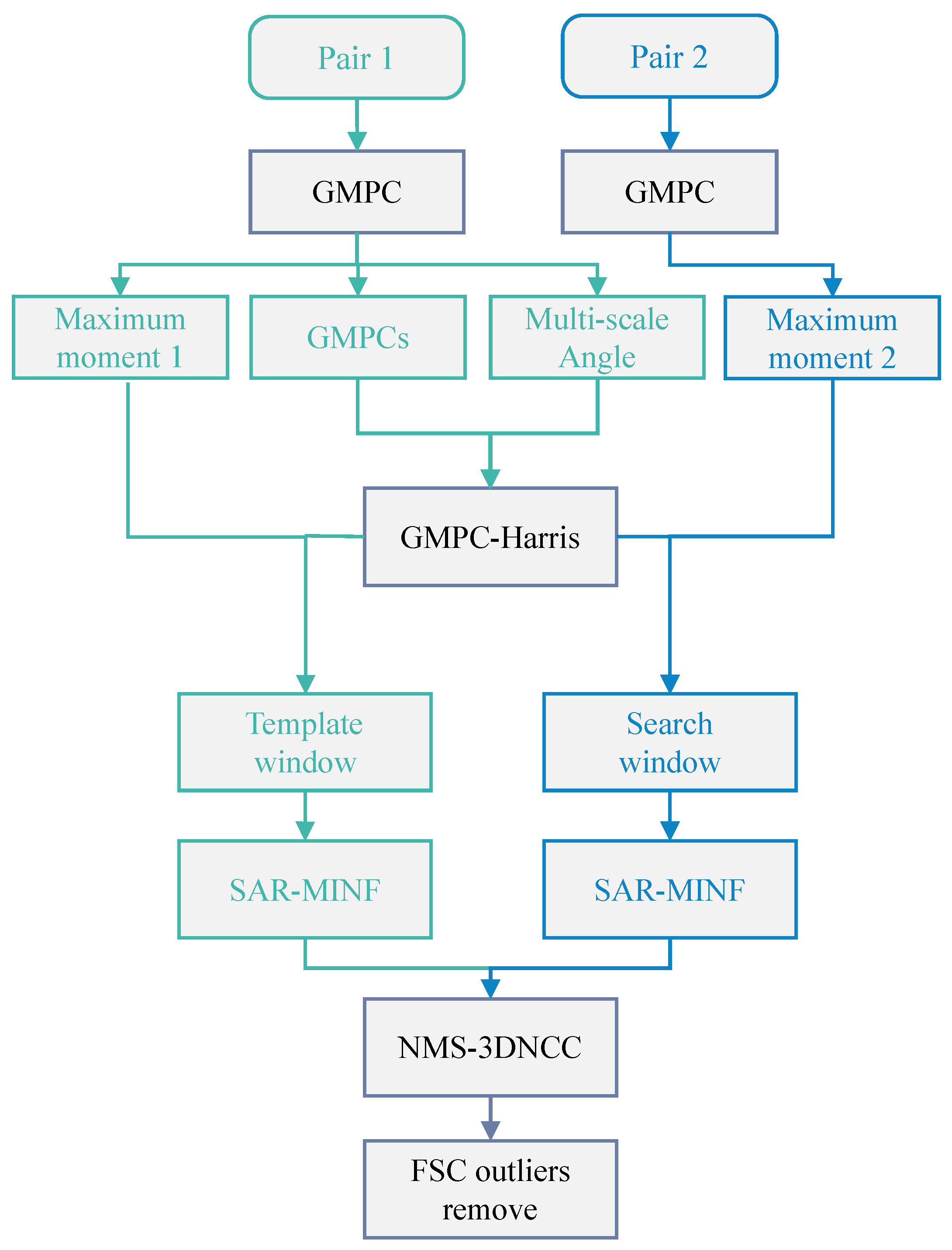
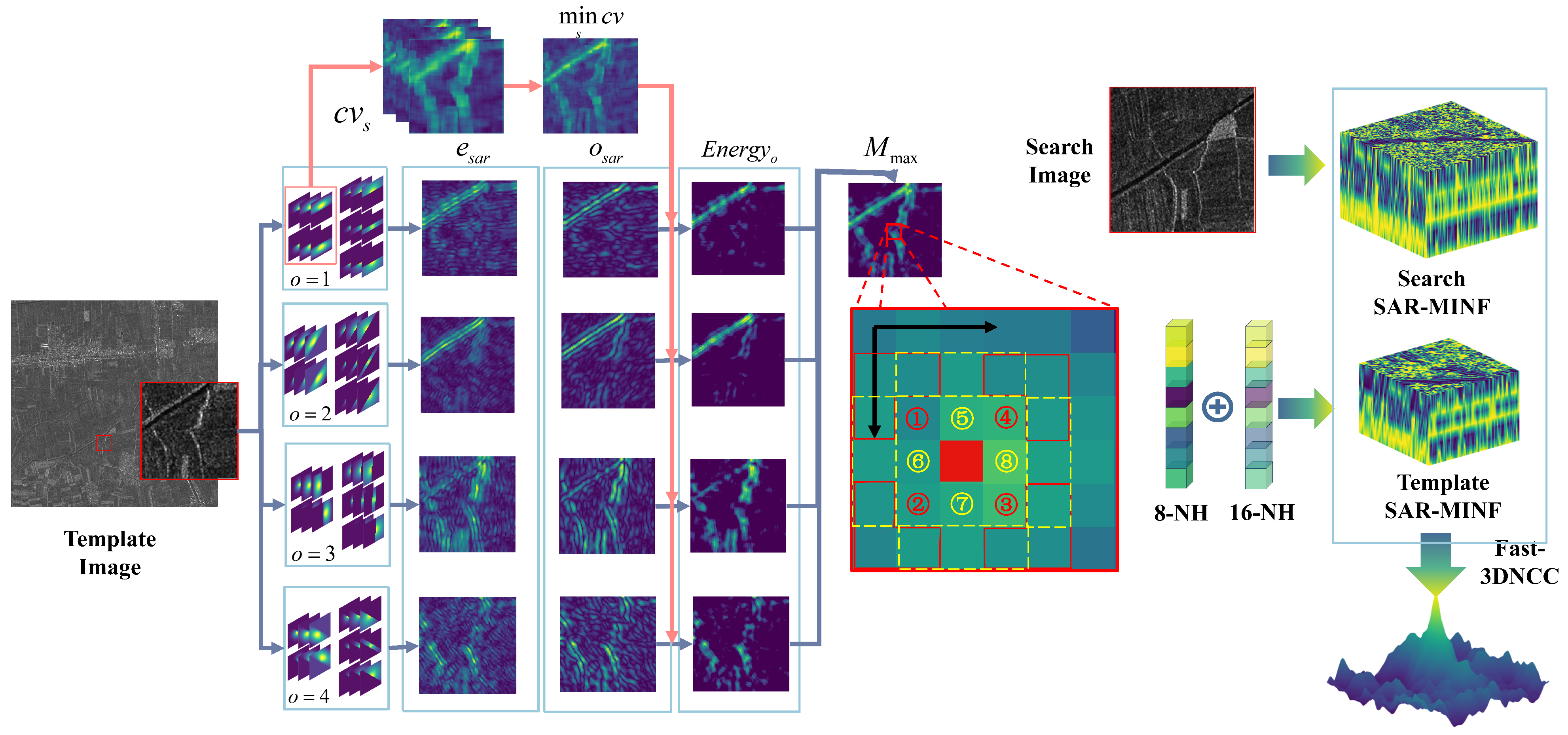
2.2. SAR Modality Independent Neighborhood Fusion (SAR-MINF) Matching Algorithm
2.2.1. GMPC-Harris Keypoint Detection Based on Layover Perception
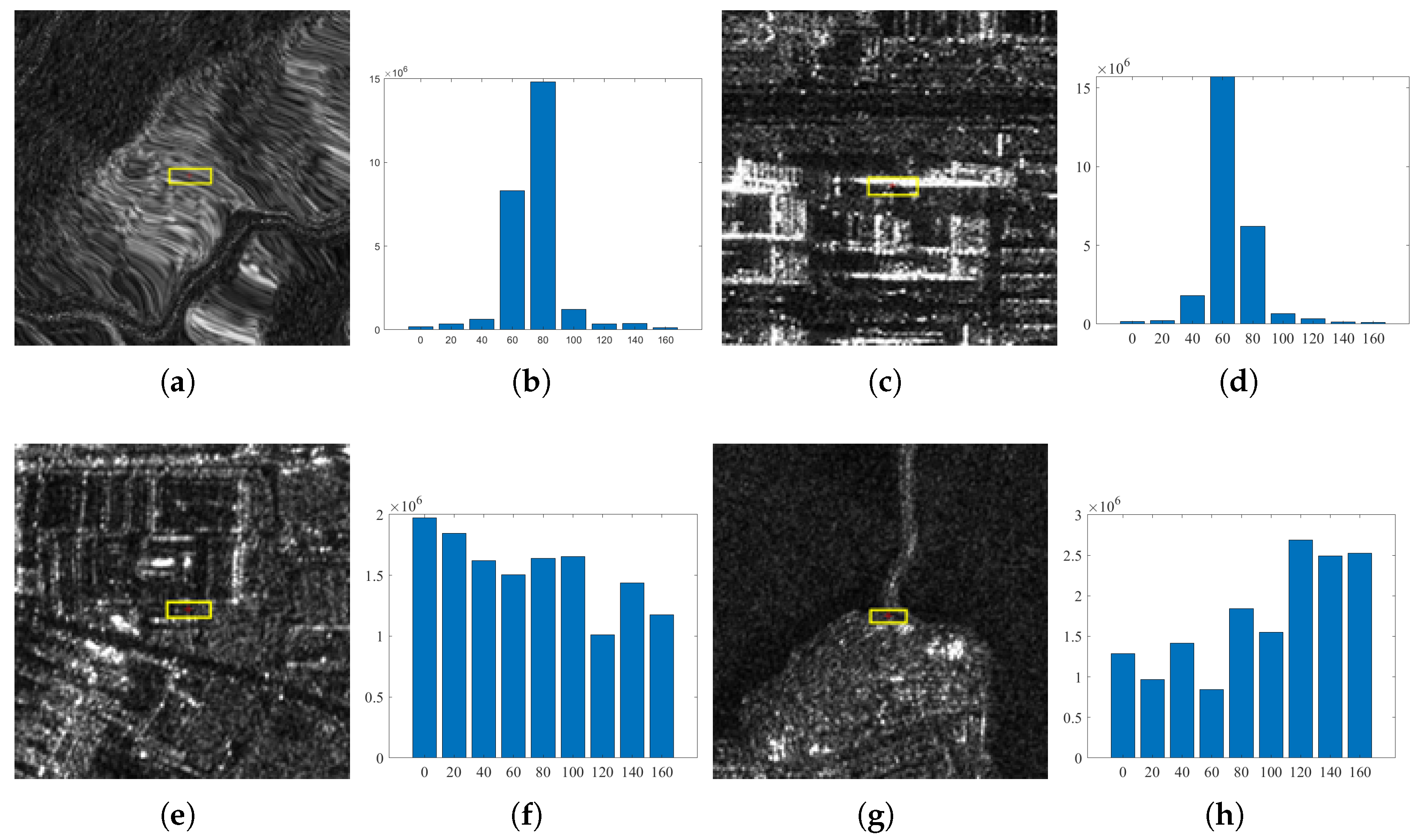
2.2.2. Feature Extraction Based on SAR-MINF
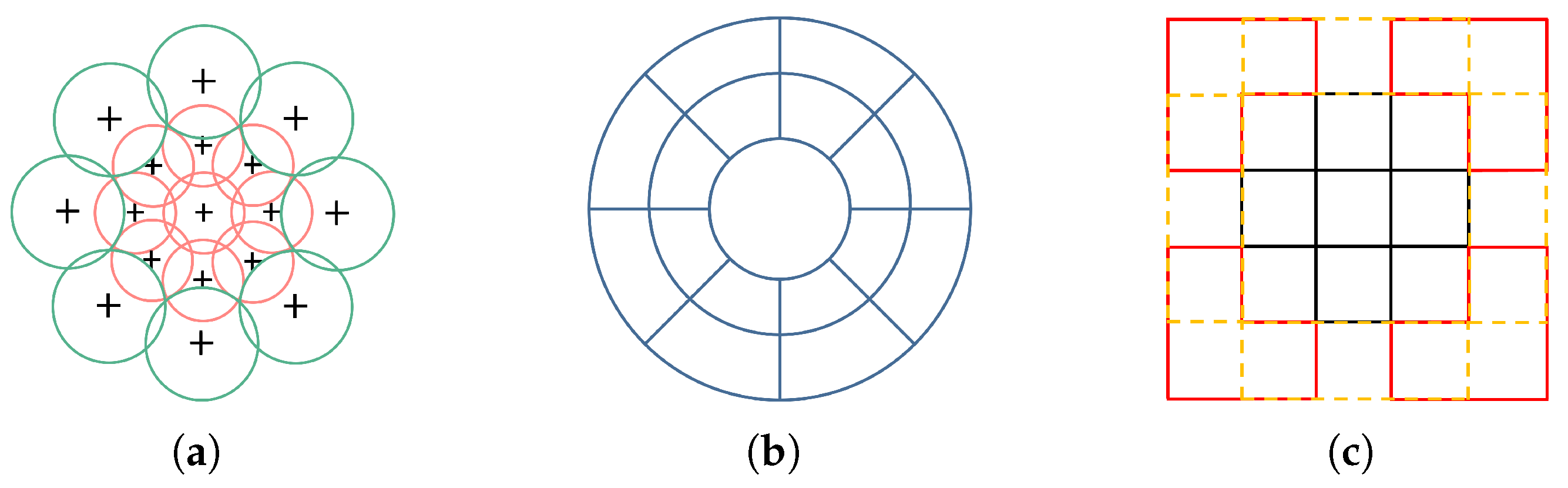
- For a pixel within a region, an 8-NH MIND descriptor is initially constructed for its eight-neighborhood to capture local structure;
- The descriptors are weighted by L2 normalization based on their distance to the central pixel and then fused with the 8-NH MIND to form an eight-dimensional descriptor for the central pixel;
- To further improve resilience against noise and local deformations, the SAR-MINF descriptor for pixel is obtained by convolving the descriptor with a Gaussian kernel along the Z-axis;
- The dense representation of the SAR-MINF feature descriptors for the region is achieved by aggregating the descriptors for each pixel within the area.
2.3. Large-Scale Tie Point Automatic Extraction Method
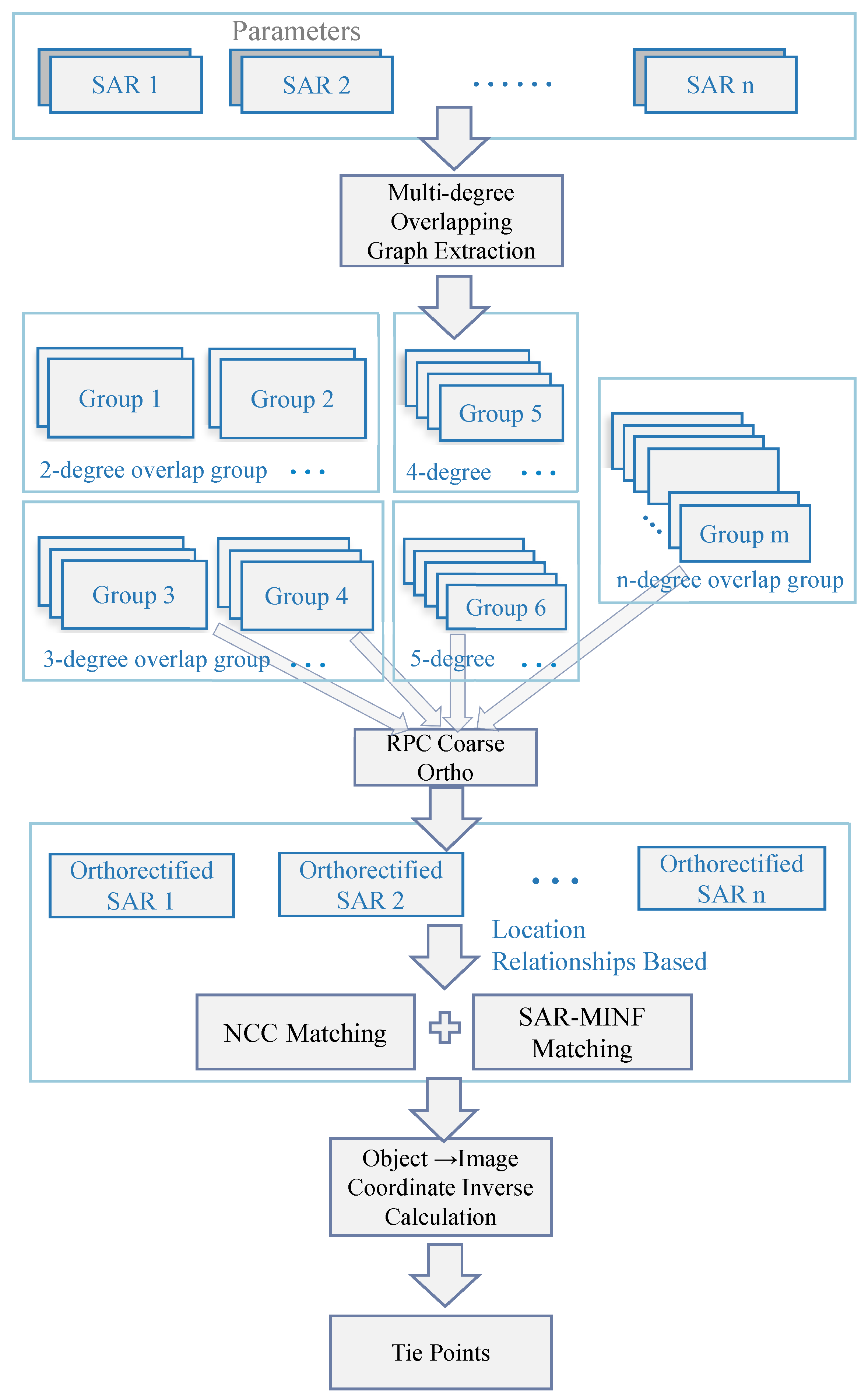
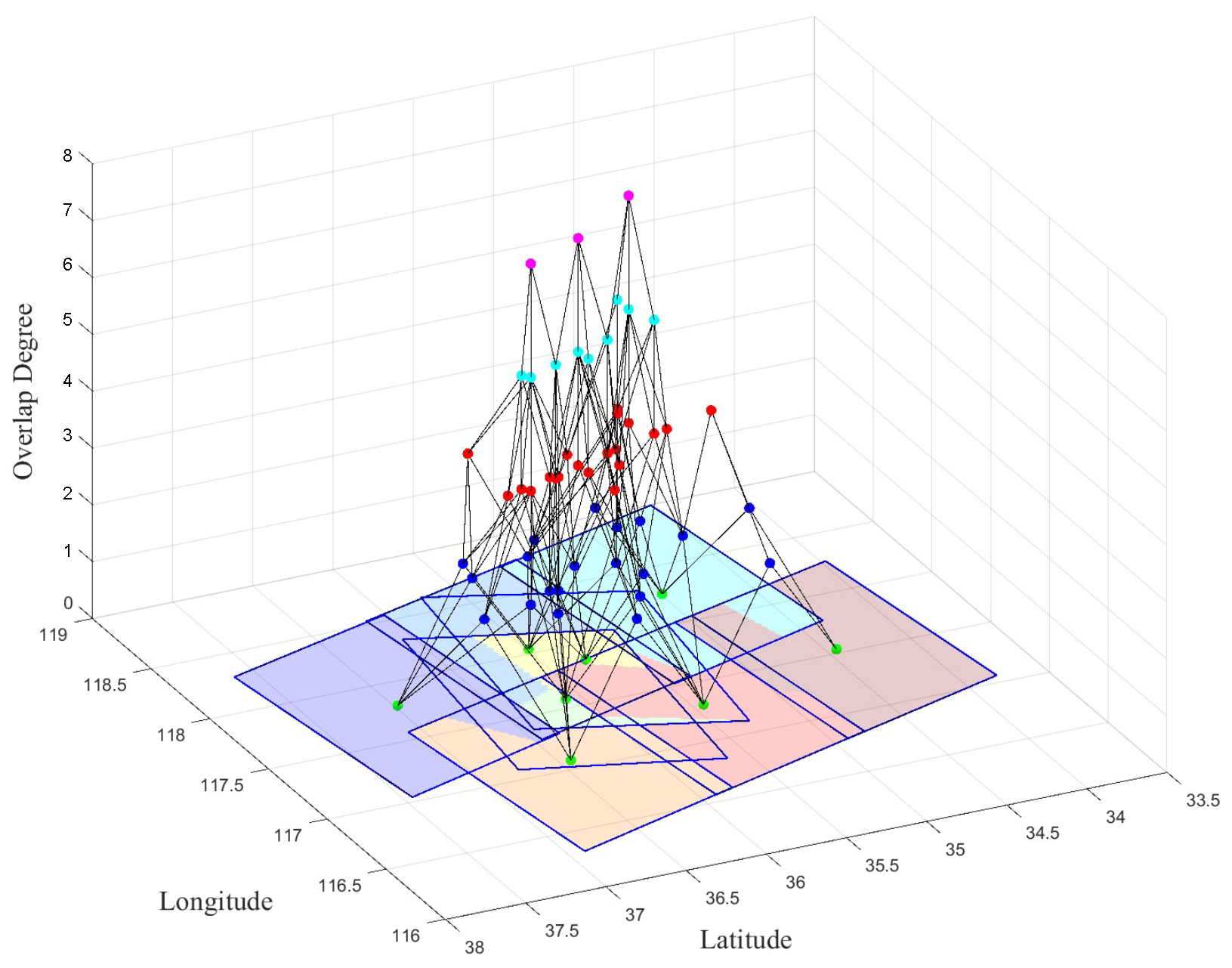
2.3.1. Graph-Based Extraction of Multidegree Overlapping Regions
| Algorithm 1: Algorithm of multidegree overlapping graph extraction. |
 |
- Input Image and Parameter Files: The input SAR images here is Level 1 products, so each data package contains the SAR image data file and the SAR parameter data file .
- Graph structure initialization: for each image , its quadrangle coordinates are obtained and polygonized to . The centroid of each polygon is used as the position of the image nodes in graph G, and the Node and NodeInfo are initialized with level 0, to denote that they represent separate images instead of overlapping regions.
- Construction of overlapping region nodes: the algorithm further examines all possible combinations from two to n images to identify and construct overlapping region nodes. For each combination C, the algorithm computes the intersection of the polygons in the combination. If this intersection is non-empty, it indicates the existence of an overlapping region. The geometric centroid of the overlap area is used as the position for the new node. Subsequently, Node and NodeInfo are updated, with the level d, which signifies the degree of overlap.
- Nodes Connections: Each overlap region node needs to be connected to the image nodes or other overlap region nodes that make up that overlap region.
- Output: The output of the algorithm is the graph G, which accurately represents the muiltdegree overlapping relationships between the input SAR images. Additionally, the output includes the nodeInfo structure, which contains detailed information about each node within the graph.
2.3.2. Fusion Matching Method Based on Location Relationships
3. Results and Discussion
3.1. SAR-MINF Matching Experiment
3.1.1. Data Sets and Parameter Settings
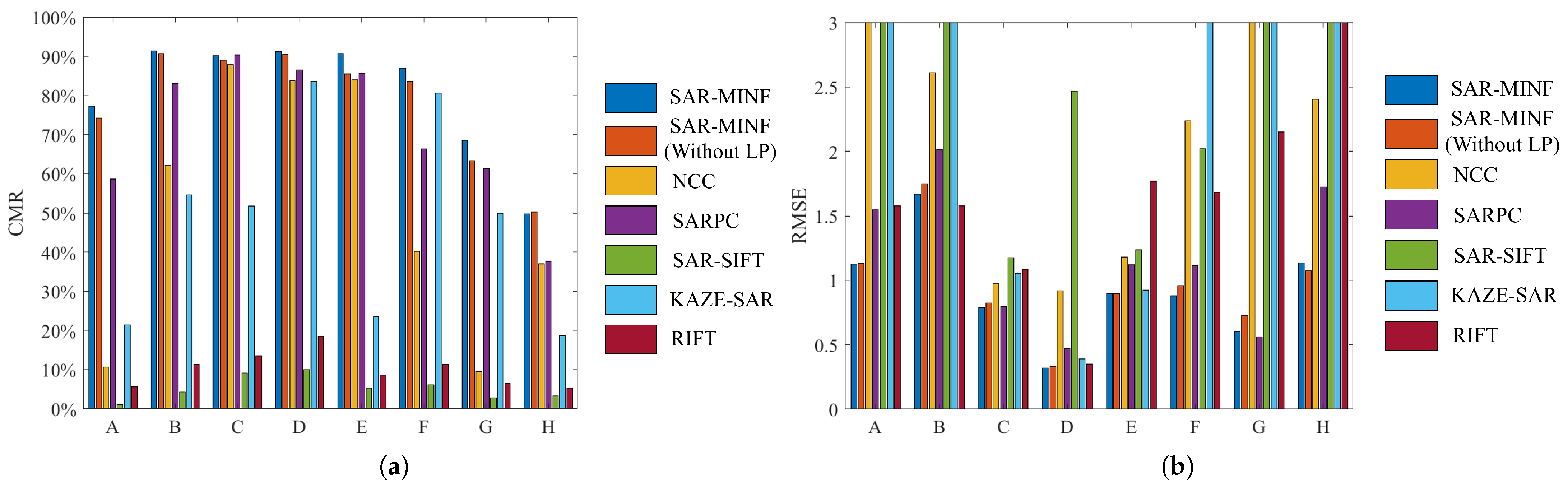
3.1.2. Evaluation Criteria
- Number of Correct Matches (NCM): The number of correct matches after the outlier removal step.
- Correct Matching Rate (CMR):is the number of keypoints, that is, the total number of points to be matched.
- Root Mean Squared Error (RMSE):We selected 10–20 pairs of corresponding points manually as the ground truth, including the keypoints of the template image and the matched points of the search image. , is the affine transformation matrix.
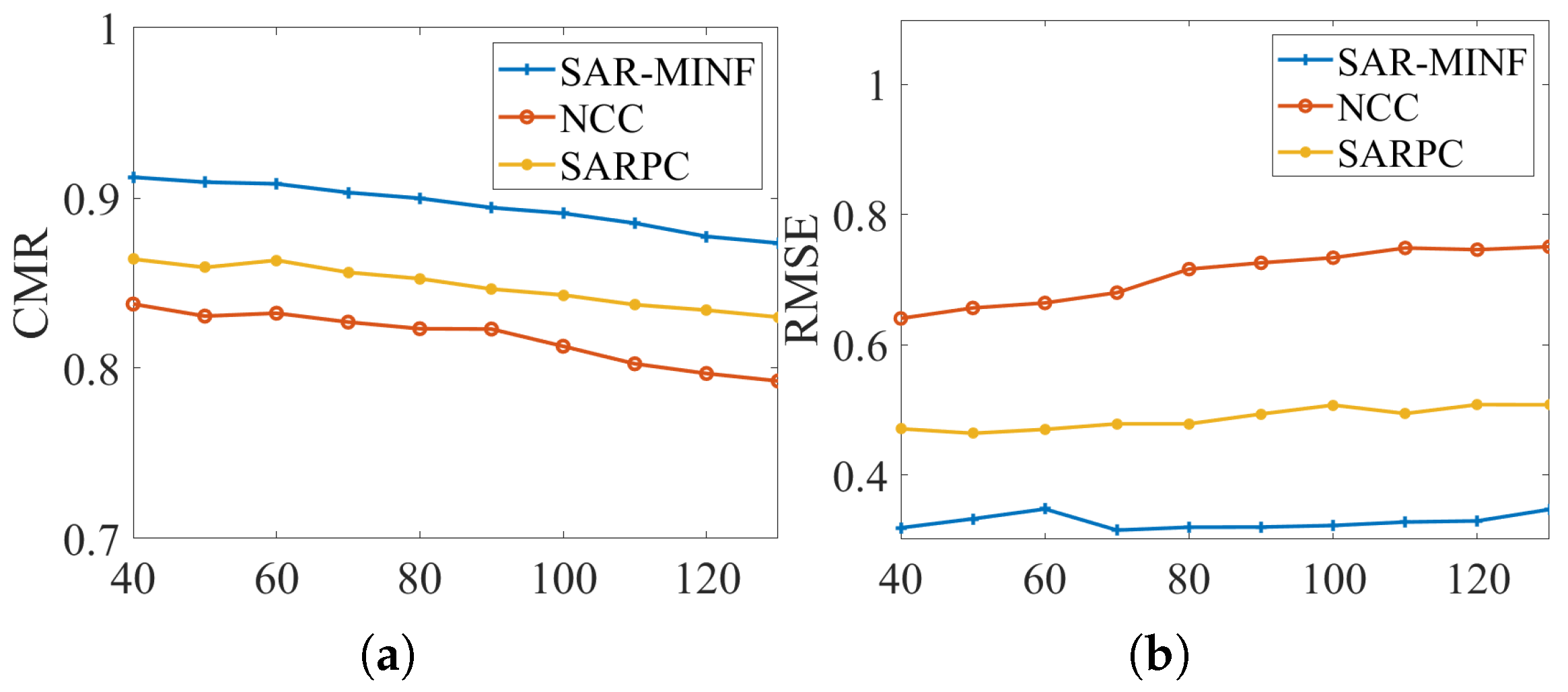
3.1.3. Results and Discussion
3.2. Tie Point Automatic Extraction Experiment
3.2.1. Data Sets and Parameter Settings
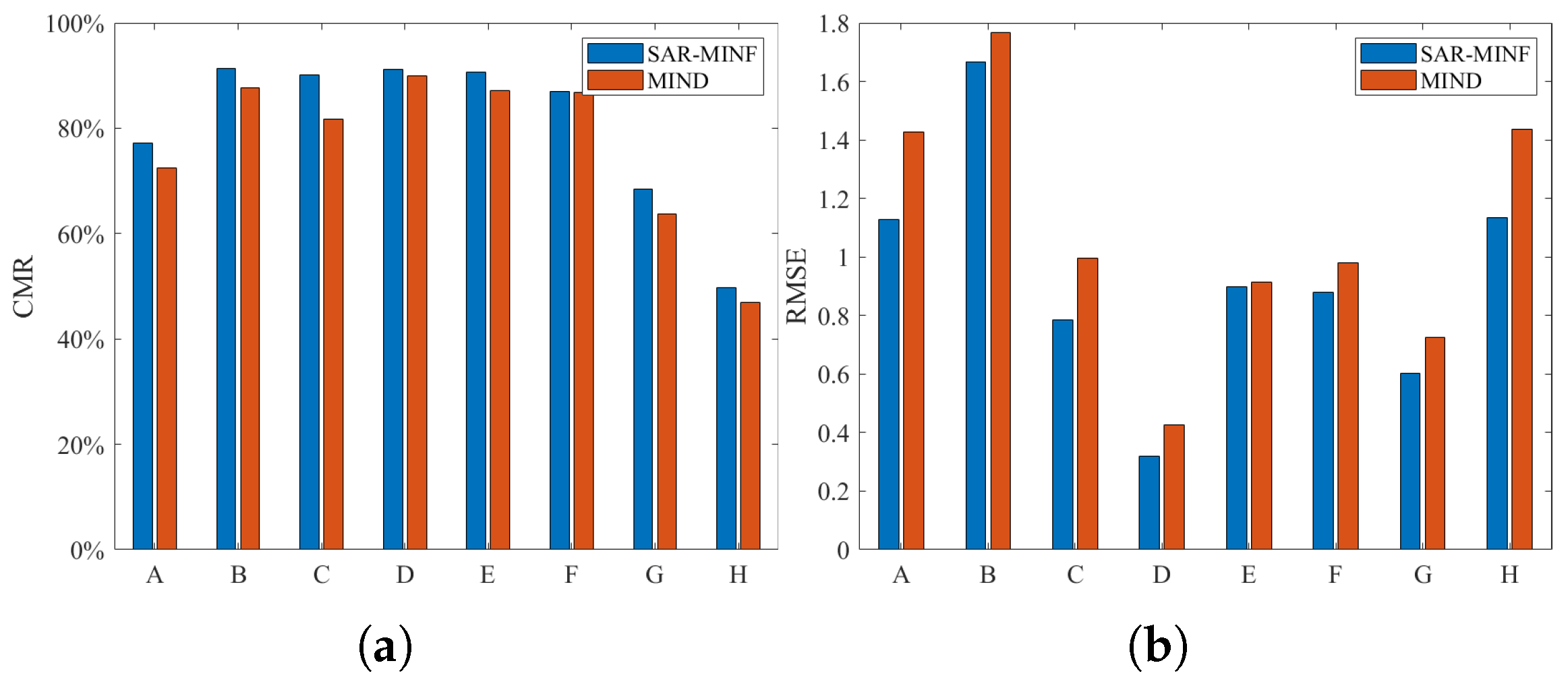
3.2.2. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Li, Y.; Wu, J.; Mao, Q.; Xiao, H.; Meng, F.; Gao, W.; Zhu, Y. A Novel Two-Dimensional Autofocusing Algorithm for Real Airborne Stripmap Terahertz Synthetic Aperture Radar Imaging. IEEE Geosci. Remote Sens. Lett. 2023, 20, 4012405. [Google Scholar] [CrossRef]
- Guo, L.; Wang, X.; Wang, Y.; Yue, M. A new approach of digital orthorectification map generation for GF3 satellite data. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Rignot, E.J.; Van Zyl, J.J. Change detection techniques for ERS-1 SAR data. IEEE Trans. Geosci. Remote Sens. 1993, 31, 896–906. [Google Scholar] [CrossRef]
- Marin, C.; Bovolo, F.; Bruzzone, L. Building change detection in multitemporal very high resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2664–2682. [Google Scholar] [CrossRef]
- Mao, Q.; Li, Y.; Zhu, Y. A hierarchical feature fusion and attention network for automatic ship detection from SAR images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 13981–13994. [Google Scholar] [CrossRef]
- Chanussot, J.; Mauris, G.; Lambert, P. Fuzzy fusion techniques for linear features detection in multitemporal SAR images. IEEE Trans. Geosci. Remote Sens. 1999, 37, 1292–1305. [Google Scholar] [CrossRef]
- Shakya, A.; Biswas, M.; Pal, M. Fusion and classification of multi-temporal SAR and optical imagery using convolutional neural network. Int. J. Image Data Fusion 2022, 13, 113–135. [Google Scholar] [CrossRef]
- Wang, J.; Lv, X.; Huang, Z.; Fu, X. An Epipolar HS-NCC Flow Algorithm for DSM Generation Using GaoFen-3 Stereo SAR Images. Remote Sens. 2022, 15, 129. [Google Scholar] [CrossRef]
- Kennedy, R.; Cohen, W. Automated designation of tie-points for image-to-image coregistration. Int. J. Remote Sens. 2003, 24, 3467–3490. [Google Scholar] [CrossRef]
- Liu, L.; Wang, Y.; Wang, Y. SIFT based automatic tie-point extraction for multitemporal SAR images. In Proceedings of the 2008 International Workshop on Education Technology and Training & 2008 International Workshop on Geoscience and Remote Sensing, Washington, DC, USA, 21–22 December 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 1, pp. 499–503. [Google Scholar]
- Zou, W.; Chen, L. Determination of optimum tie point interval for SAR image coregistration by decomposing autocorrelation coefficient. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5067–5084. [Google Scholar] [CrossRef]
- Shi, W.; Su, F.; Wang, R.; Fan, J. A visual circle based image registration algorithm for optical and SAR imagery. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2109–2112. [Google Scholar]
- Suri, S.; Reinartz, P. Mutual-information-based registration of TerraSAR-X and Ikonos imagery in urban areas. IEEE Trans. Geosci. Remote Sens. 2009, 48, 939–949. [Google Scholar] [CrossRef]
- Kuglin, C.D. The phase correlation image alignment methed. In Proceedings of the International Conference Cybernetics Society, San Francisco, CA, USA, 23–25 September 1975. [Google Scholar]
- Yu, L.; Zhang, D.; Holden, E.J. A fast and fully automatic registration approach based on point features for multi-source remote-sensing images. Comput. Geosci. 2008, 34, 838–848. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, J. Automatic registration method for optical remote sensing images with large background variations using line segments. Remote Sens. 2016, 8, 426. [Google Scholar] [CrossRef]
- Ying, X.; Yan, Z. Sar Image Registration Using a New Approach Based on the Region Feature. In Proceedings of the Foundations of Intelligent Systems: Proceedings of the Eighth International Conference on Intelligent Systems and Knowledge Engineering (ISKE 2013), Shenzhen, China, 20–23 November 2013; Springer: Berlin/Heidelberg, Germany, 2014; pp. 603–613. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Wang, S.; You, H.; Fu, K. BFSIFT: A novel method to find feature matches for SAR image registration. IEEE Geosci. Remote Sens. Lett. 2011, 9, 649–653. [Google Scholar] [CrossRef]
- Dellinger, F.; Delon, J.; Gousseau, Y.; Michel, J.; Tupin, F. SAR-SIFT: A SIFT-like algorithm for SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 453–466. [Google Scholar] [CrossRef]
- Pourfard, M.; Hosseinian, T.; Saeidi, R.; Motamedi, S.A.; Abdollahifard, M.J.; Mansoori, R.; Safabakhsh, R. KAZE-SAR: SAR image registration using KAZE detector and modified SURF descriptor for tackling speckle noise. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Ye, Y.; Bruzzone, L.; Shan, J.; Bovolo, F.; Zhu, Q. Fast and robust matching for multimodal remote sensing image registration. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9059–9070. [Google Scholar] [CrossRef]
- Xiang, Y.; Tao, R.; Wan, L.; Wang, F.; You, H. OS-PC: Combining feature representation and 3-D phase correlation for subpixel optical and SAR image registration. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6451–6466. [Google Scholar] [CrossRef]
- Zhongli, F.; Li, Z.; Qingdong, W.; Siting, L.; Yuanxin, Y. A fast matching method of SAR and optical images using angular weighted orientated gradients. Acta Geod. Cartogr. Sin. 2021, 50, 1390. [Google Scholar]
- Ye, Y.; Zhu, B.; Tang, T.; Yang, C.; Xu, Q.; Zhang, G. A robust multimodal remote sensing image registration method and system using steerable filters with first-and second-order gradients. ISPRS J. Photogramm. Remote Sens. 2022, 188, 331–350. [Google Scholar] [CrossRef]
- Xiong, B.; He, Z.; Hu, C.; Chen, Q.; Jiang, Y.; Kuang, G. A method of acquiring tie points based on closed regions in SAR images. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 2121–2124. [Google Scholar]
- Zhang, J.; Yang, S.; Zhao, Z.; Huang, G.; Lu, L.; Cheng, C. An Automatic Extraction Method for SAR Image Regional Network Adjustment Connection Points. 2015. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1v060px0gp610m80rs1d0jq06y335605&site=xueshu_se&hitarticle=1 (accessed on 1 November 2024).
- Yin, F.; Yu, H.; Lai, Y.; Liang, P. A Full Scale Connection Point Matching Method for High Overlap Remote Sensing Images Based on Phase Correlation. 2019. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=1s1a02m0rt2n0x60tc3e0jp0gj316563&site=xueshu_ses (accessed on 1 November 2024).
- Wang, T.; Cheng, Q.; Li, X. A Remote Sensing Image Fusion Method and Computer-Readable Medium that Takes into Account Image Distortion. 2023. Available online: https://www.zhangqiaokeyan.com/patent-detail/06120115594588.html (accessed on 1 November 2024).
- Morrone, M.C.; Owens, R.A. Feature detection from local energy. Pattern Recognit. Lett. 1987, 6, 303–313. [Google Scholar] [CrossRef]
- Venkatesh, S.; Owens, R.A. An energy feature detection scheme. In Proceedings of the International Conference on Image Processing, Singapore, 5–8 September 1989. [Google Scholar]
- Kovesi, P. Phase congruency detects corners and edges. In Proceedings of the Australian Pattern Recognition Society Conference: DICTA, Sydney, Australia, 10–12 December 2003; Volume 2003. [Google Scholar]
- Xiang, Y.; Wang, F.; Wan, L.; You, H. SAR-PC: Edge detection in SAR images via an advanced phase congruency model. Remote Sens. 2017, 9, 209. [Google Scholar] [CrossRef]
- Wei, Q.R.; Feng, D.Z.; Yuan, M.D. Automatic local thresholding algorithm for SAR image edge detection. In Proceedings of the IET International Radar Conference 2013, Xi’an, China, 14–16 April 2013. [Google Scholar]
- Li, S.; Lv, X.; Wang, H.; Li, J. A Novel Fast and Robust Multimodal Images Matching Method Based on Primary Structure-Weighted Orientation Consistency. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 9916–9927. [Google Scholar] [CrossRef]
- Chen, E. Study on Ortho-rectification Methodology of Space-borne Synthetic Aperture Radar Imagery. PhD Thesis, Chinese Academy of Forestry, Beijing, China, 2004. [Google Scholar]
- Tongtong, Z.; Honglei, Y.; Dongming, L.; Yongjie, L.; Junnan, L. Identification of layover and shadows regions in SAR images: Taking Badong as an example. Bull. Surv. Mapp. 2019, 85. [Google Scholar]
- Ren, Y. Research on Layover and Shadow Detecting in InSAR. PhD Thesis, Graduate School of National University of Defense Technology, Changsha, China, 2013. [Google Scholar]
- Heinrich, M.P.; Jenkinson, M.; Bhushan, M.; Matin, T.; Gleeson, F.V.; Brady, S.M.; Schnabel, J.A. MIND: Modality independent neighbourhood descriptor for multi-modal deformable registration. Med. Image Anal. 2012, 16, 1423–1435. [Google Scholar] [CrossRef]
- Mikolajczyk, K.; Schmid, C. A performance evaluation of local descriptors. IEEE Trans. Pattern Anal. Mach. Intell. 2005, 27, 1615–1630. [Google Scholar] [CrossRef]
- Tola, E.; Lepetit, V.; Fua, P. Daisy: An efficient dense descriptor applied to wide-baseline stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 815–830. [Google Scholar] [CrossRef]
- Wu, Y.; Ma, W.; Gong, M.; Su, L.; Jiao, L. A novel point-matching algorithm based on fast sample consensus for image registration. IEEE Geosci. Remote Sens. Lett. 2014, 12, 43–47. [Google Scholar] [CrossRef]
- Xiang, Y.; Peng, L.; Wang, F.; Qiu, X. Fast registration of multiview slant-range SAR images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Li, J.; Hu, Q.; Ai, M. RIFT: Multi-modal image matching based on radiation-variation insensitive feature transform. IEEE Trans. Image Process. 2019, 29, 3296–3310. [Google Scholar] [CrossRef] [PubMed]
- Umbra Lab Inc. Umbra Synthetic Aperture Radar (SAR) Open Data. 2023. Available online: https://registry.opendata.aws/umbra-open-data (accessed on 1 November 2024).
- GEOS Contributors. GEOS Coordinate Transformation Software Library; Open Source Geospatial Foundation: Beaverton, OR, USA, 2021. [Google Scholar]
- GDAL/OGR Contributors. GDAL/OGR Geospatial Data Abstraction Software Library. 2024. Available online: https://gdal.org (accessed on 1 November 2024).
- Bradski, G. The opencv library. Dr. Dobb’s J. Softw. Tools Prof. Program. 2000, 25, 120–123. [Google Scholar]
- Eigen: A C++ Template Library for Linear Algebra. Available online: https://eigen.tuxfamily.org (accessed on 10 April 2023).
- Frigo, M.; Johnson, S.G. The design and implementation of FFTW3. Proc. IEEE 2005, 93, 216–231. [Google Scholar] [CrossRef]











| Pair | Sensor | Resolution | Band | Polarization | Orbit | Size | Region |
|---|---|---|---|---|---|---|---|
| A | ALOS2 | 2.5 m | L | HH | DEC | Urban | |
| GF3 | 3 m | C | DH | ASC | |||
| B | GF3 | 10 m | C | HH | DEC | Urban | |
| Sentinal-1A | 10 m | C | VV | ASC | |||
| C | LT-1 | 3 m | L | HH | DEC | Urban, Mountain | |
| GF3 | 10 m | C | VV | ASC | |||
| D | GF3 | 10 m | C | HH | ASC | Airport | |
| GF3 | 10 m | C | HV | ASC | |||
| E | GF3 | 5 m | C | DH | DEC | Suburbs, Paddy | |
| GF3 | 3 m | C | DH | ASC | |||
| F | GF3 | 3 m | C | DH | ASC | Urban, Mountain | |
| GF3 | 3 m | C | DH | DEC | |||
| G | LT-1 | 3 m | L | HH | ASC | Urban | |
| GF3 | 3 m | C | VV | DEC | |||
| H | UMBRA | 0.5 m | X | VV | ASC | Airport Terminal | |
| UMBRA | 0.5 m | X | VV | ASC |
| Pair | Template Radius | Search Radius | Performance | SAR-MINF | SAR-MINF (Without LP) | NCC | SAR-PC | SAR-SIFT * | KAZE-SAR * | RIFT * |
|---|---|---|---|---|---|---|---|---|---|---|
| A | 105 | 75 | Keypoints | 382 | 440 | 440 | 440 | \ | \ | \ |
| NCM | 295 | 327 | 47 | 258 | 5 | 3 | 116 | |||
| CMR | 77.23% | 74.32% | 10.68% | 58.64% | \ | \ | \ | |||
| RMSE | 1.1274 | 1.1306 | 7.4491 | 1.5483 | 587.3138 | 1337.36 | 1.5794 | |||
| B | 65 | 35 | Keypoints | 209 | 278 | 278 | 278 | \ | \ | \ |
| NCM | 191 | 252 | 173 | 231 | 19 | 12 | 221 | |||
| CMR | 91.39% | 90.65% | 62.23% | 83.09% | \ | \ | \ | |||
| RMSE | 1.6674 | 1.7491 | 2.6119 | 2.014 | 3.1713 | 7.5040 | 1.9173 | |||
| C | 65 | 35 | Keypoints | 781 | 931 | 931 | 931 | \ | \ | \ |
| NCM | 704 | 829 | 817 | 841 | 330 | 267 | 326 | |||
| CMR | 90.14% | 89.04% | 87.76% | 90.33% | \ | \ | \ | |||
| RMSE | 0.7864 | 0.8232 | 0.9755 | 0.7967 | 1.1739 | 1.0559 | 1.0824 | |||
| D | 70 | 40 | Keypoints | 467 | 493 | 493 | 493 | \ | \ | \ |
| NCM | 426 | 446 | 413 | 426 | 222 | 414 | 369 | |||
| CMR | 91.22% | 90.47% | 83.77% | 86.41% | \ | \ | \ | |||
| RMSE | 0.3189 | 0.3274 | 0.9182 | 0.4710 | 2.4707 | 0.3902 | 0.3498 | |||
| E | 60 | 35 | Keypoints | 747 | 1081 | 1081 | 1081 | \ | \ | \ |
| NCM | 677 | 924 | 907 | 928 | 366 | 217 | 202 | |||
| CMR | 90.63% | 85.48% | 83.90% | 85.58% | \ | \ | \ | |||
| RMSE | 0.8973 | 0.8981 | 1.1818 | 1.1179 | 1.2343 | 0.9228 | 1.7696 | |||
| F | 55 | 15 | Keypoints | 239 | 276 | 276 | 276 | \ | \ | \ |
| NCM | 208 | 231 | 111 | 183 | 40 | 25 | 260 | |||
| CMR | 87.03% | 83.70% | 40.22% | 66.30% | \ | \ | \ | |||
| RMSE | 0.8782 | 0.9574 | 2.2352 | 1.1126 | 2.0194 | 4.264 | 1.6853 | |||
| G | 65 | 35 | Keypoints | 352 | 388 | 388 | 388 | \ | \ | \ |
| NCM | 241 | 246 | 37 | 238 | 9 | 1 | 137 | |||
| CMR | 68.47% | 63.40% | 9.54% | 61.34% | \ | \ | \ | |||
| RMSE | 0.6029 | 0.7298 | 7.7269 | 0.5596 | 38.6447 | 1218.50 | 2.0871 | |||
| H | 80 | 40 | Keypoints | 451 | 457 | 457 | 457 | \ | \ | \ |
| NCM | 225 | 230 | 169 | 172 | 24 | 64 | 110 | |||
| CMR | 49.81% | 50.33% | 36.98% | 37.64% | \ | \ | \ | |||
| RMSE | 1.1357 | 1.077 | 2.4045 | 1.7218 | 99.7471 | 34.3372 | 3.817 |
| Pair | SAR-MINF | NCC | SAR-PC | SAR-SIFT | KAZE-SAR | RIFT |
|---|---|---|---|---|---|---|
| B | 15.65 s | 5.06 s | 14.15 s | 98.48 s | 20.97 s | 6.10 s |
| C | 47.35 s | 15.23 s | 44.98 s | 708.86 s | 363.53 s | 20.71 s |
| Pair | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| GMPC-Harris | 2.851 s | 1.458 s | 7.375 s | 4.855 s | 7.384 s | 3.105 s | 1.822 s | 2.976 s |
| GMPC-Harris+LP | 2.97 s | 1.535 s | 7.587 s | 4.983 s | 7.615 s | 3.209 s | 1.931 s | 3.105 s |
| LP | 0.119 s | 0.077 s | 0.212 s | 0.128 s | 0.231 s | 0.104 s | 0.109 s | 0.129 s |
| Parameter | First Set of Images | Second Set of Images |
|---|---|---|
| Number of Images | 8 scenes | 34 scenes |
| Sensor | GF3 | GF3 |
| Imaging Mode | FSII | FSI |
| Nominal Resolution | 10 m | 5 m |
| Ortho Raster Resolution | 3.4 m × 4.2 m | 3.1 m × 3.8 m |
| Swath Width | About 110 km | About 50 km |
| Orbital Direction | 2 descending and 6 ascending | All descending |
| Polarization Direction | HH | HH |
| Incidence Angle Difference | ||
| Slant Range Dimension | About | About |
| Terrain Features | Plains, cities, mountains, etc. | Mountains, cities, plains, etc. |
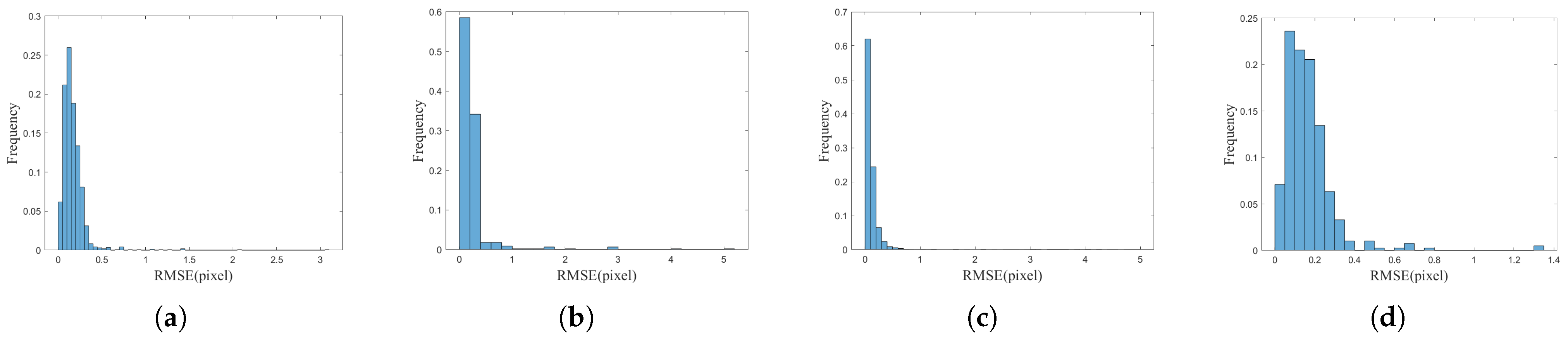
| Group | ID | 2-Degree Overlapping TPs | Multiple-Degree Overlapping TPs | RMSE | ||||
|---|---|---|---|---|---|---|---|---|
| Total Points | <0.5 ps Points | Percentage | Total Points | <0.5 ps Points | Percentage | |||
| 1 | 1 | 375 | 371 | 98.93% | 176 | 164 | 93.17% | 0.1998 |
| 2 | 791 | 777 | 98.23% | 318 | 313 | 98.42% | 0.1774 | |
| 3 | 751 | 739 | 98.40% | 143 | 141 | 98.60% | 0.1739 | |
| 4 | 548 | 538 | 98.17% | 175 | 172 | 98.28% | 0.1774 | |
| 5 | 550 | 542 | 98.55% | 121 | 119 | 98.35% | 0.1762 | |
| 6 | 238 | 233 | 97.89% | 113 | 106 | 93.80% | 0.1914 | |
| 7 | 491 | 487 | 99.18% | 137 | 133 | 97.08% | 0.1780 | |
| 8 | 517 | 511 | 98.83% | 124 | 117 | 94.35% | 0.1776 | |
| 2 | Total | 4992 | 4869 | 97.53% | 1183 | 1148 | 97.04% | 0.1702 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; Yang, X.; Lv, X.; Li, J. SAR-MINF: A Novel SAR Image Descriptor and Matching Method for Large-Scale Multidegree Overlapping Tie Point Automatic Extraction. Remote Sens. 2024, 16, 4696. https://doi.org/10.3390/rs16244696
Li S, Yang X, Lv X, Li J. SAR-MINF: A Novel SAR Image Descriptor and Matching Method for Large-Scale Multidegree Overlapping Tie Point Automatic Extraction. Remote Sensing. 2024; 16(24):4696. https://doi.org/10.3390/rs16244696
Chicago/Turabian StyleLi, Shuo, Xiongwen Yang, Xiaolei Lv, and Jian Li. 2024. "SAR-MINF: A Novel SAR Image Descriptor and Matching Method for Large-Scale Multidegree Overlapping Tie Point Automatic Extraction" Remote Sensing 16, no. 24: 4696. https://doi.org/10.3390/rs16244696
APA StyleLi, S., Yang, X., Lv, X., & Li, J. (2024). SAR-MINF: A Novel SAR Image Descriptor and Matching Method for Large-Scale Multidegree Overlapping Tie Point Automatic Extraction. Remote Sensing, 16(24), 4696. https://doi.org/10.3390/rs16244696






