High-Resolution Gravity Measurements on Board an Autonomous Underwater Vehicle: Data Reduction and Accuracy Assessment
Abstract
1. Introduction
- Utilizing prior knowledge concerning the accelerometer errors, such as those obtained from thermal calibration in the laboratory, to mitigate sensor bias and drift. A simple thermal calibration was carried out, in which the GraviMob gravimeter was subjected to varying temperatures at the gravity point in the GeF laboratory, and the outputs were compared with the available reference gravity value at this point to determine the temperature gradient. This calibrated temperature gradient was used to process data acquired during the GraviMob cruise, but the bias is still significant. This is probably due to the significant difference between the laboratory and actual underwater environments. This calibration method is highly recommended only when used with a climate chamber that subjects the GraviMob system to the actual temperature variations encountered underwater.
- Employing external reference data, such as those derived from available surface shipborne gravity or from Global Gravity field Models (GGMs), and/or redundant measurements like intersection points or repeated profiles to determine the accelerometer drift and bias present in gravity estimates. This method is often known as the correction technique. However, the availability and spatial resolution of such data are often limited, e.g., the spatial resolution of surface shipborne/GGM-derived gravity is usually lower than that of underwater gravimetry. The terrain effects derived from a high-resolution Digital Bathymetry Model (DBM) can be used to improve the spatial resolution of the surface/GGM-derived gravity data when these data are downward continued (DC) to the measurement depth to be employed as external reference data.
2. Methods
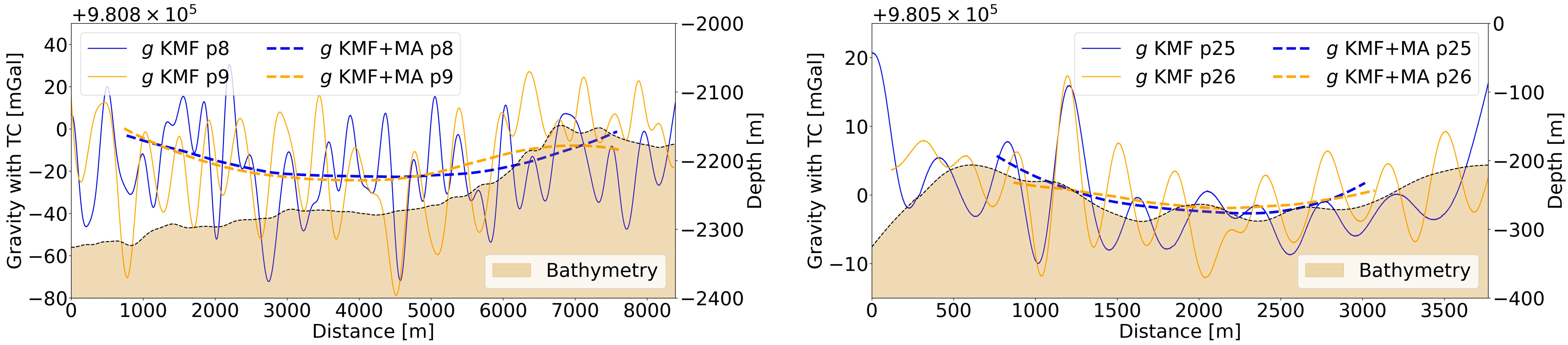
2.1. GraviMob-Measured Data Processing
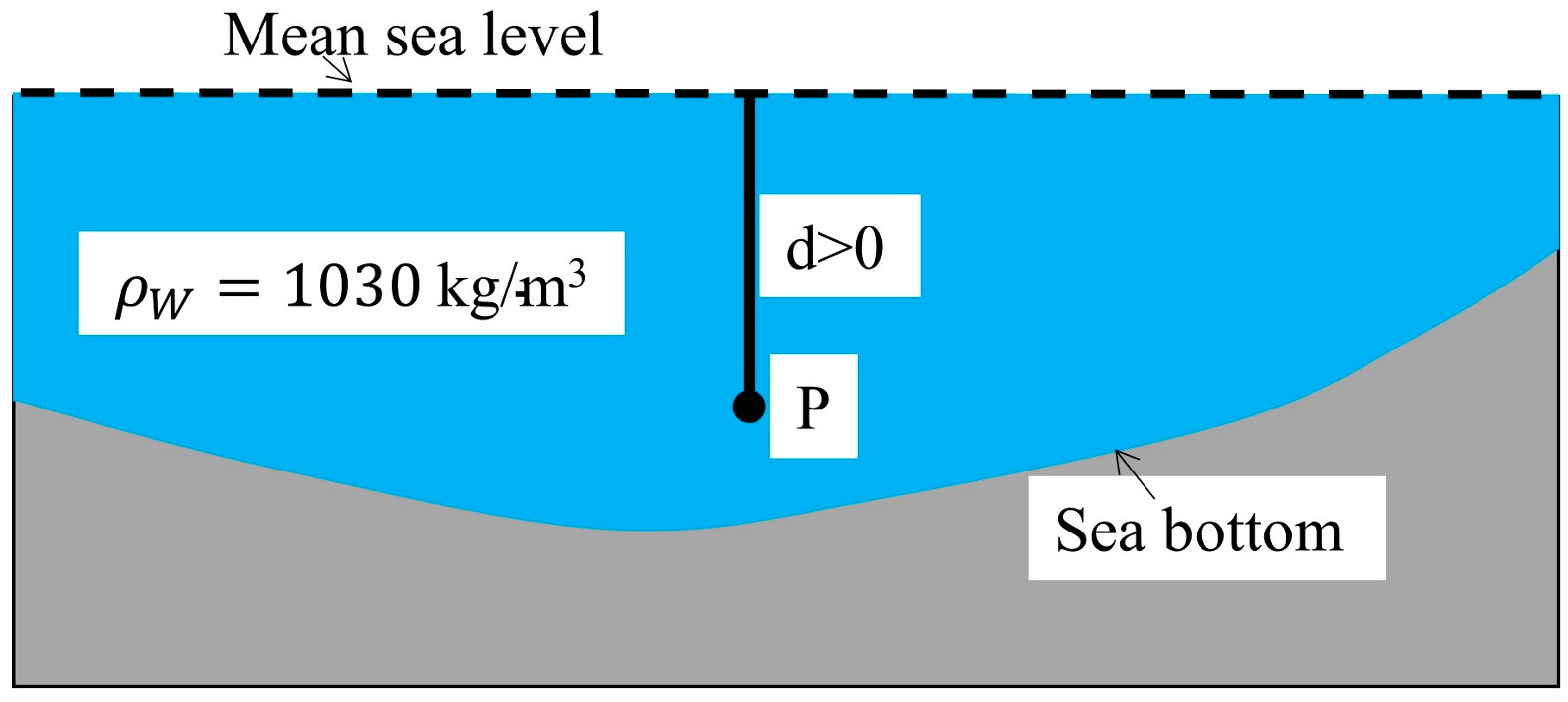
2.2. Free-Air Gravity Anomaly Computation at the Measurement Depth
2.3. Downward Continuation Model
2.4. Least-Squares Collocation Method
3. GraviMob Cruise and Data Processing
3.1. GraviMob Cruise
3.2. Data Processing
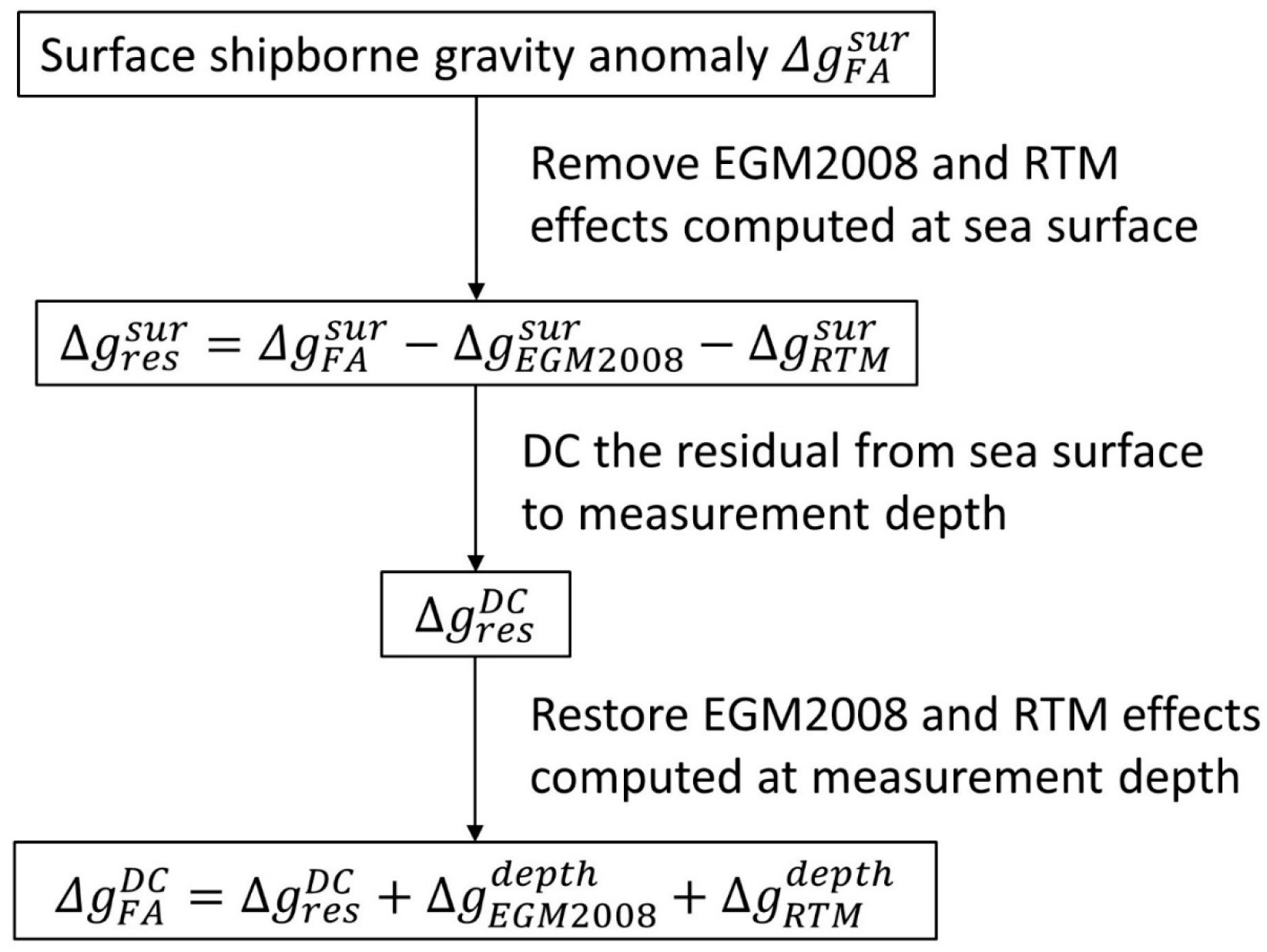
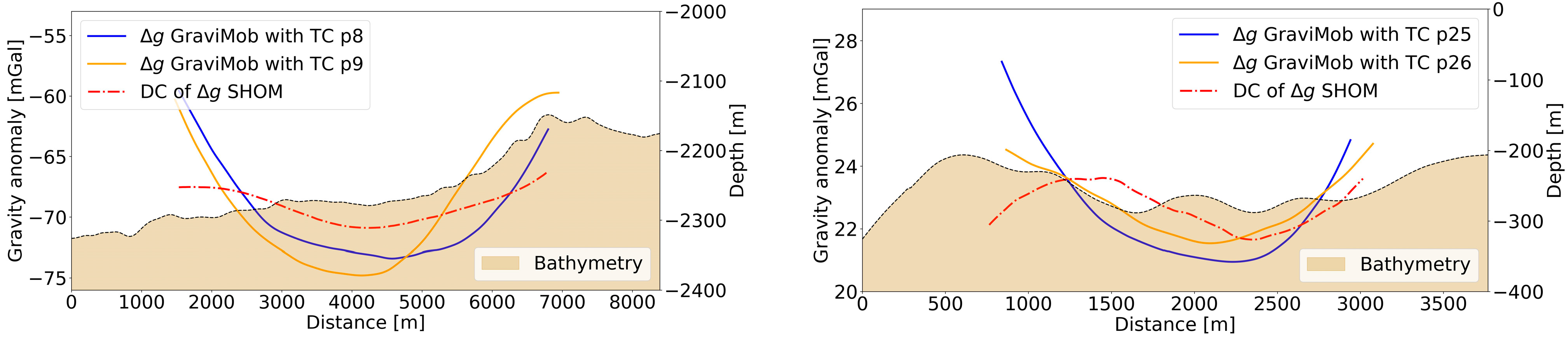
4. Downward Continuation of Shipborne Gravity Data
- -
- We employed a simple averaging to compute the coarse DBM grid (1′ × 1′ grid in the present study) from the detailed DBM grid (SRTM15arc_plus with the resolution of 15″).
- -
- A moving-average window was then employed to low-pass filter the coarse DBM grid (1′ × 1′) to the required resolution of the reference DBM grid; the required resolution is 9 km (equivalent to the spherical harmonic d/o 2190 of the EGM2008 employed) in the remove–restore procedure for DC shipborne gravity data in this study.
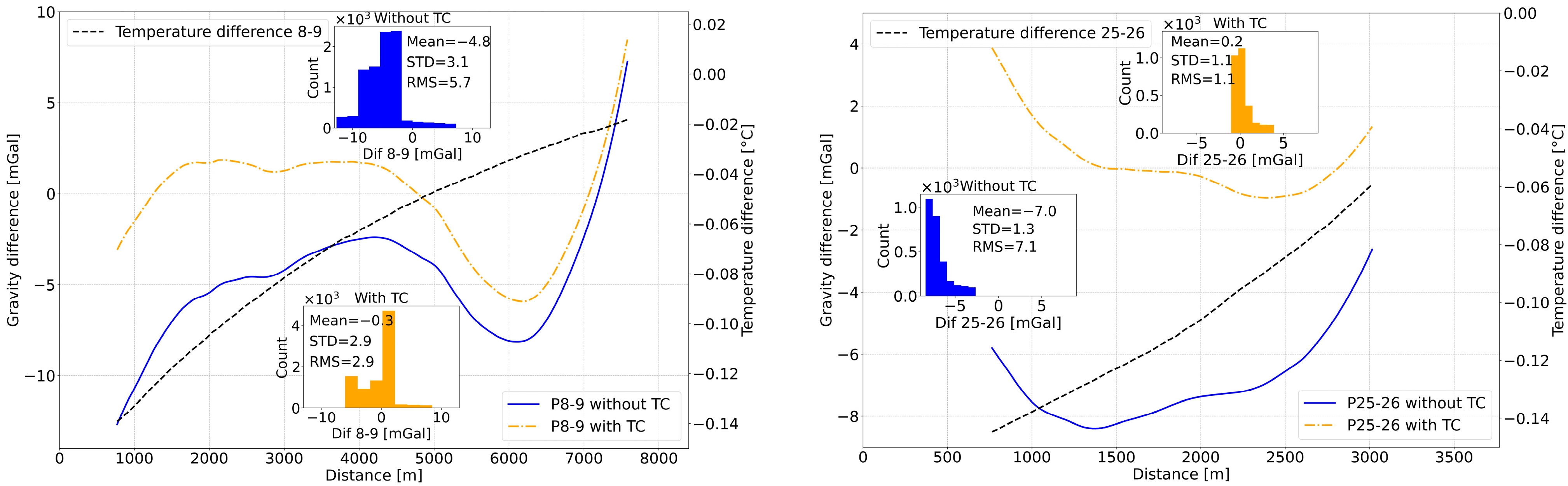
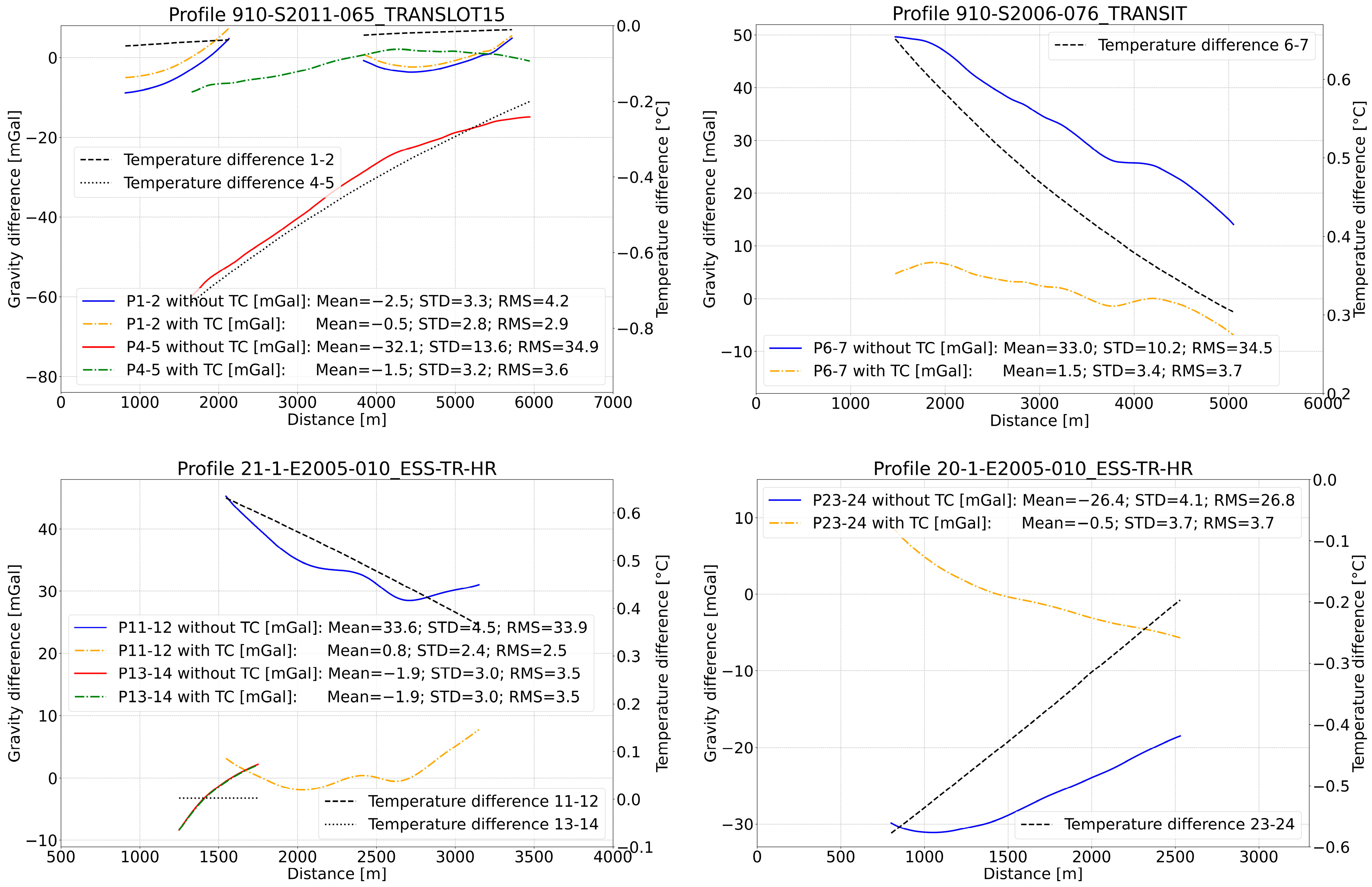
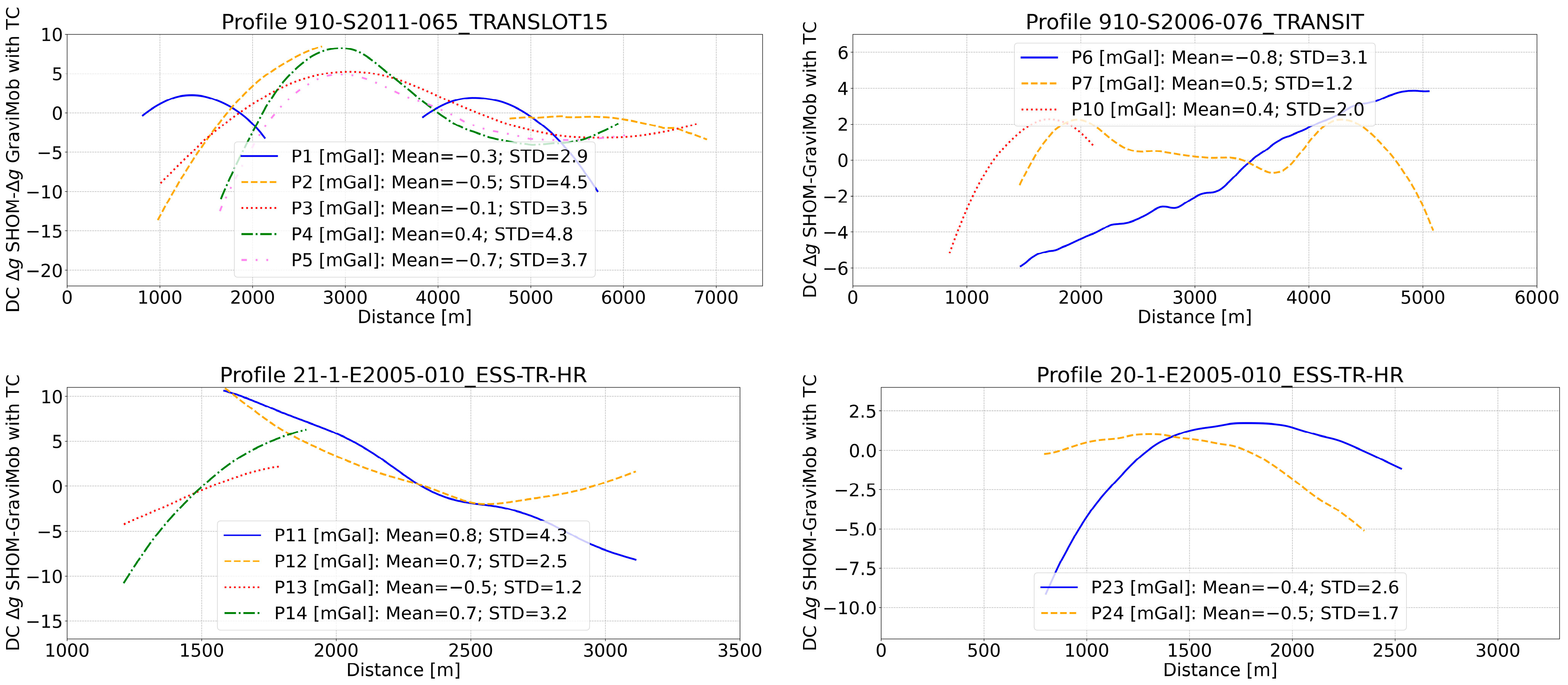
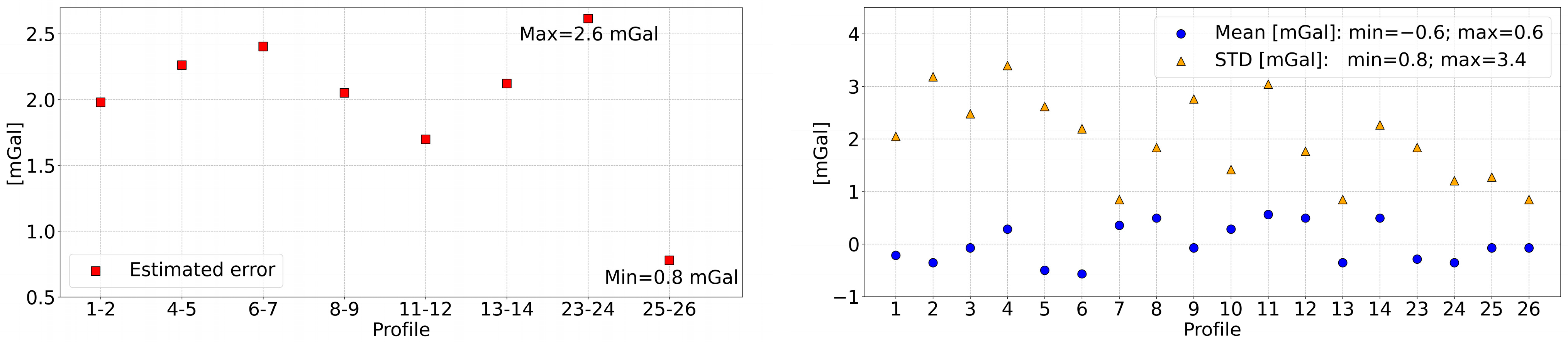
5. Temperature Correction: Results and Discussion
5.1. Temperature Correction Parameter Determination
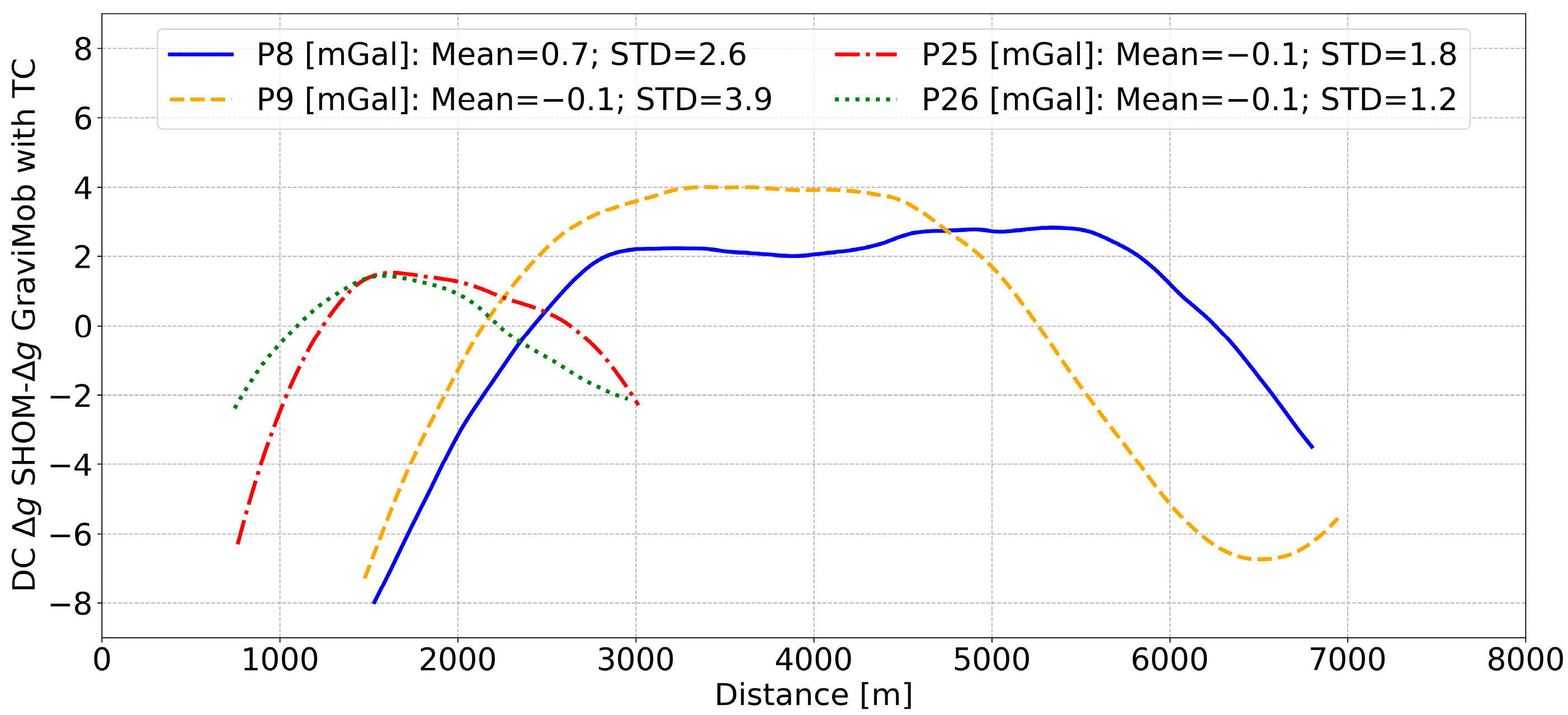
5.2. Validation Results for the Remaining Profiles
6. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sandwell, D.T.; Müller, R.D.; Smith, W.H.F.; Garcia, E.; Francis, R. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 2014, 346, 65–67. [Google Scholar] [CrossRef] [PubMed]
- Vu, D.T.; Bonvalot, S.; Bruinsma, S.; Bui, L.K. A local lithospheric structure model for Vietnam derived from a high-resolution gravimetric geoid. Earth Planets Space 2021, 73, 92. [Google Scholar] [CrossRef]
- Watts, A.B.; Talwani, M. Gravity Anomalies Seaward of Deep-Sea Trenches and their Tectonic Implications. Geophys. J. Int. 1974, 36, 57–90. [Google Scholar] [CrossRef]
- Hall, S.A.; Casey, J.F.; Elthon, D.L. A possible explanation of gravity anomalies over mid-ocean ridges. J. Geophys. Res. Solid Earth 1986, 91, 3724–3738. [Google Scholar] [CrossRef]
- Carbone, D.; Zuccarello, L.; Messina, A.; Scollo, S.; Rymer, H. Balancing bulk gas accumulation and gas output before and during lava fountaining episodes at Mt. Etna. Sci. Rep. 2015, 5, 18049. [Google Scholar] [CrossRef] [PubMed]
- Montagner, J.-P.; Juhel, K.; Barsuglia, M.; Ampuero, J.P.; Chassande-Mottin, E.; Harms, J.; Whiting, B.; Bernard, P.; Clévédé, E.; Lognonné, P. Prompt gravity signal induced by the 2011 Tohoku-Oki earthquake. Nat. Commun. 2016, 7, 13349. [Google Scholar] [CrossRef] [PubMed]
- Nabighian, M.N.; Ander, M.E.; Grauch, V.J.S.; Hansen, R.O.; LaFehr, T.R.; Li, Y.; Pearson, W.C.; Peirce, J.W.; Phillips, J.D.; Ruder, M.E. Historical development of the gravity method in exploration. Geophysics 2005, 70, 63ND–89ND. [Google Scholar] [CrossRef]
- Shinohara, M.; Yamada, T.; Ishihara, T.; Araya, A.; Kanazawa, T.; Fujimoto, H.; Uehira, K.; Tsukioka, S.; Omika, S.; Iizasa, K. Development of an underwater gravity measurement system using autonomous underwater vehicle for exploration of seafloor deposits. In Proceedings of the OCEANS 2015, Genova, Italy, 18–21 May 2015; pp. 1–7. [Google Scholar]
- National Research Council (NRC). Airborne Geophysics and Precise Positioning: Scientific Issues and Future Directions; National Academies Press: Washington, DC, USA, 1995; ISBN 978-0-309-05183-5. [Google Scholar]
- Sasagawa, G.S.; Crawford, W.; Eiken, O.; Nooner, S.; Stenvold, T.; Zumberge, M.A. A new sea-floor gravimeter. Geophysics 2003, 68, 544–553. [Google Scholar] [CrossRef]
- Kinsey, J.C.; Tivey, M.A.; Yoerger, D.R. Dynamics and navigation of autonomous underwater vehicles for submarine gravity surveying. Geophysics 2013, 78, G55–G68. [Google Scholar] [CrossRef]
- Ishihara, T.; Shinohara, M.; Fujimoto, H.; Kanazawa, T.; Araya, A.; Yamada, T.; Iizasa, K.; Tsukioka, S.; Omika, S.; Yoshiume, T.; et al. High-resolution gravity measurement aboard an autonomous underwater vehicle. Geophysics 2018, 83, G119–G135. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, J.; Zhang, K.; Yu, R. Experimental Study on Underwater Moving Gravity Measurement by Using Strapdown Gravimeter Based on AUV Platform. Mar. Geod. 2021, 44, 108–135. [Google Scholar] [CrossRef]
- Verdun, J.; Roussel, C.; Cali, J.; Maia, M.; D’Eu, J.-F.; Kharbou, O.; Poitou, C.; Ammann, J.; Durand, F.; Bouhier, M.-É. Development of a Lightweight Inertial Gravimeter for Use on Board an Autonomous Underwater Vehicle: Measurement Principle, System Design and Sea Trial Mission. Remote Sens. 2022, 14, 2513. [Google Scholar] [CrossRef]
- Jensen, T.E.; Olesen, A.V.; Forsberg, R.; Olsson, P.-A.; Josefsson, Ö. New Results from Strapdown Airborne Gravimetry Using Temperature Stabilisation. Remote Sens. 2019, 11, 2682. [Google Scholar] [CrossRef]
- Hofmann-Wellenhof, B.; Moritz, H. Physical Geodesy, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-211-33544-4. [Google Scholar]
- Roussel, C. Expérimentation d’un Gravimètre Mobile Léger et Novateur Pour la Mesure du Champ de Gravité en Fond de Mer. Ph.D. Thesis, Conservatoire National des Arts et Métiers, Paris, France, 2017. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation, 1st ed.; Wiley-Interscience: New York, NY, USA, 2001; ISBN 978-0-471-41655-5. [Google Scholar]
- Zumberge, M.A.; Ridgway, J.R.; Hildebrand, J.A. A towed marine gravity meter for near-bottom surveys. Geophysics 1997, 62, 1386–1393. [Google Scholar] [CrossRef]
- Forsberg, R. A new covariance model for inertial gravimetry and gradiometry. J. Geophys. Res. Solid Earth 1987, 92, 1305–1310. [Google Scholar] [CrossRef]
- Alberts, B.; Klees, R. A comparison of methods for the inversion of airborne gravity data. J. Geod. 2004, 78, 55–65. [Google Scholar] [CrossRef]
- Barzaghi, R.; Borghi, A.; Keller, K.; Forsberg, R.; Giori, I.; Loretti, I.; Olesen, A.V.; Stenseng, L. Airborne gravity tests in the Italian area to improve the geoid model of Italy. Geophys. Prospect. 2009, 57, 625–632. [Google Scholar] [CrossRef]
- Zhao, Q.; Xu, X.; Forsberg, R.; Strykowski, G. Improvement of Downward Continuation Values of Airborne Gravity Data in Taiwan. Remote Sens. 2018, 10, 1951. [Google Scholar] [CrossRef]
- Varga, M.; Pitoňák, M.; Novák, P.; Bašić, T. Contribution of GRAV-D airborne gravity to improvement of regional gravimetric geoid modelling in Colorado, USA. J. Geod. 2021, 95, 53. [Google Scholar] [CrossRef]
- Bidel, Y.; Zahzam, N.; Bresson, A.; Blanchard, C.; Bonnin, A.; Bernard, J.; Cadoret, M.; Jensen, T.E.; Forsberg, R.; Salaun, C.; et al. Airborne Absolute Gravimetry With a Quantum Sensor, Comparison With Classical Technologies. J. Geophys. Res. Solid Earth 2023, 128, e2022JB025921. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.R.; Wessel, P. Global Bathymetry and Topography at 15 Arc Sec: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Forsberg, R.; Tscherning, C.C. An Overview Manual for the GRAVSOFT Geodetic Gravity Field Modelling Programs; Technical University of Denmark (DTU): Kongens Lyngby, Denmark, 2008; Available online: https://ftp.space.dtu.dk/pub/RF/ (accessed on 21 January 2024).
- Forsberg, R. A Study of Terrain Reductions, Density Anomalies and Geophysical Inversion Methods in Gravity Field Modelling; Department of Geodetic Science and Surveying, Ohio State University: Columbus, OH, USA, 1984. [Google Scholar]
- Sansò, F.; Sideris, M.G. (Eds.) Geoid Determination: Theory and Methods; Lecture Notes in Earth System Sciences; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-540-74699-7. [Google Scholar]
- Torge, W.; Müller, J. Geodesy; De Gruyter: Berlin, Germany, 2012; ISBN 978-3-11-025000-8. [Google Scholar]
- Maia, M. GRAVIMOB Cruise, L’Europe R/V. 2016. SEANOE. Available online: https://campagnes.flotteoceanographique.fr/campagnes/16011200/ (accessed on 1 August 2023).
- Wessel, P.; Watts, A.B. On the accuracy of marine gravity measurements. J. Geophys. Res. Solid Earth 1988, 93, 393–413. [Google Scholar] [CrossRef]
- Hirt, C.; Featherstone, W.E.; Marti, U. Combining EGM2008 and SRTM/DTM2006.0 residual terrain model data to improve quasigeoid computations in mountainous areas devoid of gravity data. J. Geod. 2010, 84, 557–567. [Google Scholar] [CrossRef]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S. A high-resolution gravimetric quasigeoid model for Vietnam. Earth Planets Space 2019, 71, 65. [Google Scholar] [CrossRef]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S.; Bui, L.K.; Balmino, G. Determination of the geopotential value on the permanent GNSS stations in Vietnam based on the Geodetic Boundary Value Problem approach. Geophys. J. Int. 2021, 226, 1206–1219. [Google Scholar] [CrossRef]
- Vu, D.T.; Bruinsma, S.; Bonvalot, S.; Remy, D.; Vergos, G.S. A Quasigeoid-Derived Transformation Model Accounting for Land Subsidence in the Mekong Delta towards Height System Unification in Vietnam. Remote Sens. 2020, 12, 817. [Google Scholar] [CrossRef]
- Sánchez, L.; Ågren, J.; Huang, J.; Wang, Y.M.; Mäkinen, J.; Pail, R.; Barzaghi, R.; Vergos, G.S.; Ahlgren, K.; Liu, Q. Strategy for the realisation of the International Height Reference System (IHRS). J. Geod. 2021, 95, 33. [Google Scholar] [CrossRef]
- Forsberg, R.; Olesen, A.; Munkhtsetseg, D.; Amarzaya, B. Downward continuation and geoid determination in Mongolia from airborne and surface gravimetry and SRTM topography. In Proceedings of the 2007 International Forum on Strategic Technology, Ulaanbaatar, Mongolia, 3–6 October 2007; pp. 470–475. [Google Scholar]
- Hsiao, Y.; Hwang, C. Topography-assisted downward continuation of airborne gravity: An application for geoid determination in Taiwan. TAO Terr. Atmos. Ocean. Sci. 2010, 21, 6. [Google Scholar] [CrossRef]
- Wu, Y.; Abulaitijiang, A.; Featherstone, W.E.; McCubbine, J.C.; Andersen, O.B. Coastal gravity field refinement by combining airborne and ground-based data. J. Geod. 2019, 93, 2569–2584. [Google Scholar] [CrossRef]
- Hirt, C. RTM Gravity Forward-Modeling Using Topography/Bathymetry Data to Improve High-Degree Global Geopotential Models in the Coastal Zone. Mar. Geod. 2013, 36, 183–202. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Becker, J.J.; Sandwell, D.T.; Smith, W.H.F.; Braud, J.; Binder, B.; Depner, J.; Fabre, D.; Factor, J.; Ingalls, S.; Kim, S.-H.; et al. Global Bathymetry and Elevation Data at 30 Arc Seconds Resolution: SRTM30_PLUS. Mar. Geod. 2009, 32, 355–371. [Google Scholar] [CrossRef]
- Barzaghi, R.; Carrion, D.; Vergos, G.S.; Tziavos, I.N.; Grigoriadis, V.N.; Natsiopoulos, D.A.; Bruinsma, S.; Reinquin, F.; Seoane, L.; Bonvalot, S.; et al. GEOMED2: High-Resolution Geoid of the Mediterranean. In Proceedings of the International Symposium on Advancing Geodesy in a Changing World, Kobe, Japan, 30 July–4 August 2017; Freymueller, J.T., Sánchez, L., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 43–49. [Google Scholar]
- Abulaitijiang, A. Marine Gravity and Bathymetry Modelling from Recent Satellite Altimetry. Ph.D. Thesis, Technical University of Denmark, Kongens Lyngby, Denmark, 2019. [Google Scholar]
- Vu, D.T.; Verdun, J.; Cali, J.; Maia, M.; Poitou, C.; Ammann, J.; Roussel, C.; D’Eu, J.-F.; Bouhier, M.-É. GraviMob-1 campaign: Measurement data and processing results. SEANOE 2016. [Google Scholar] [CrossRef]
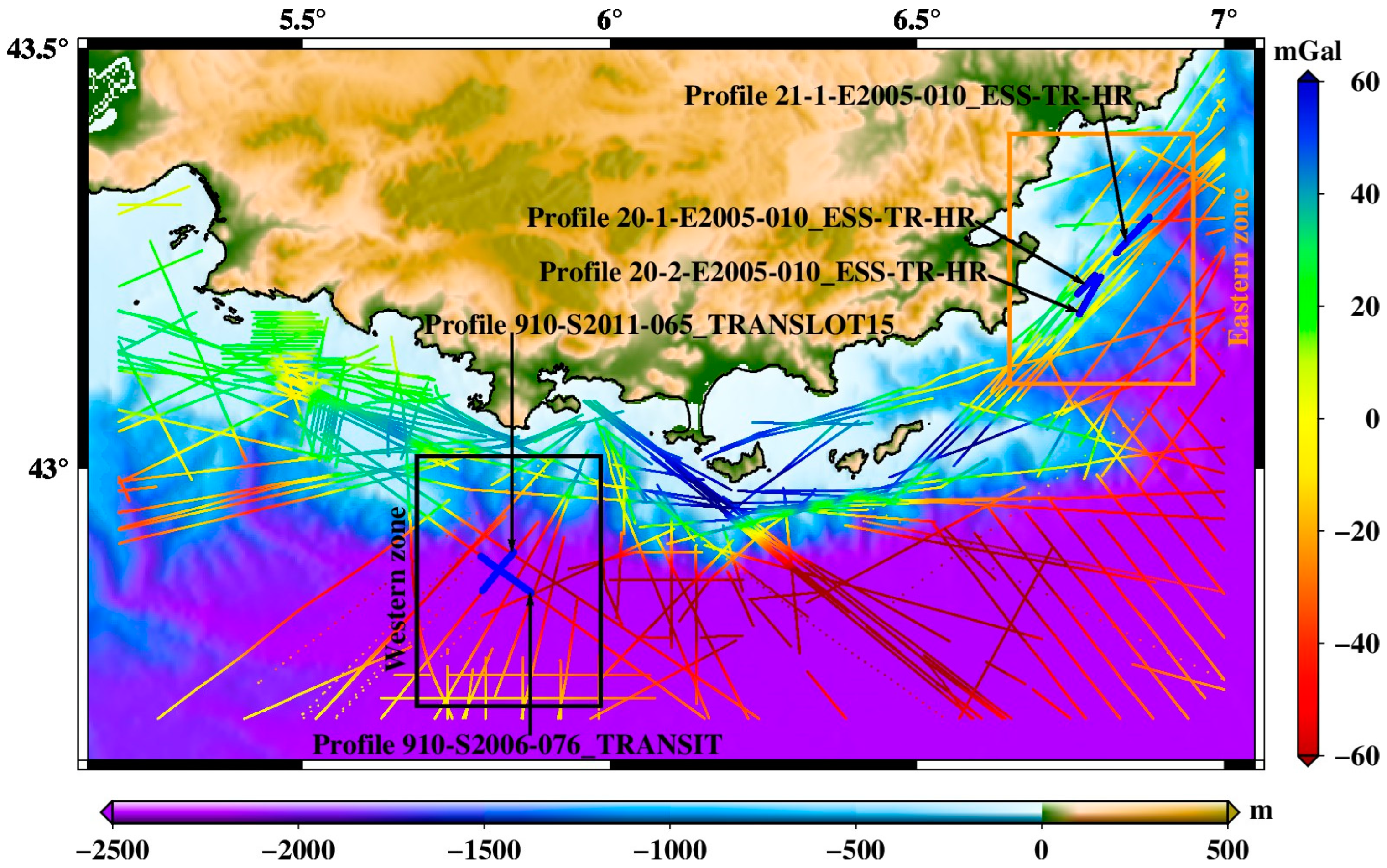
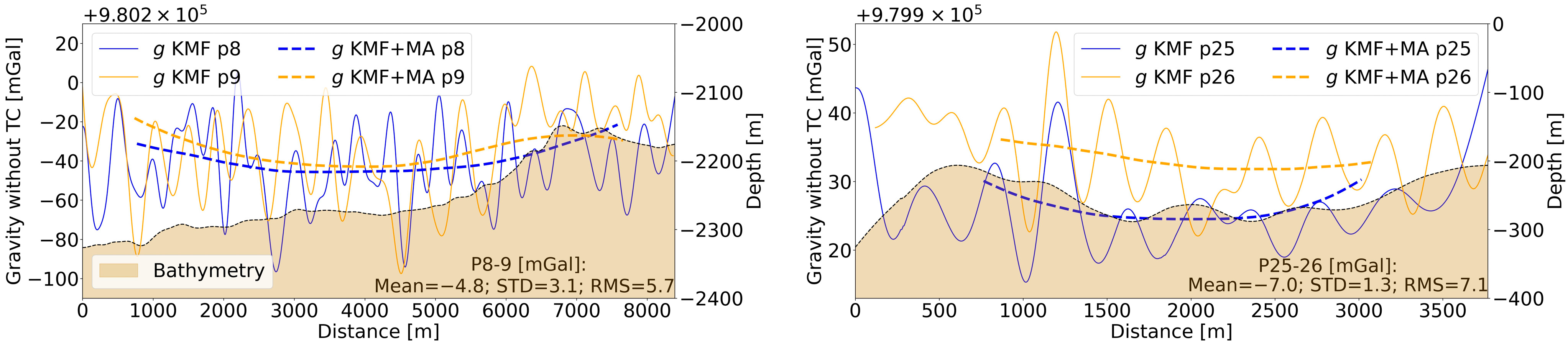
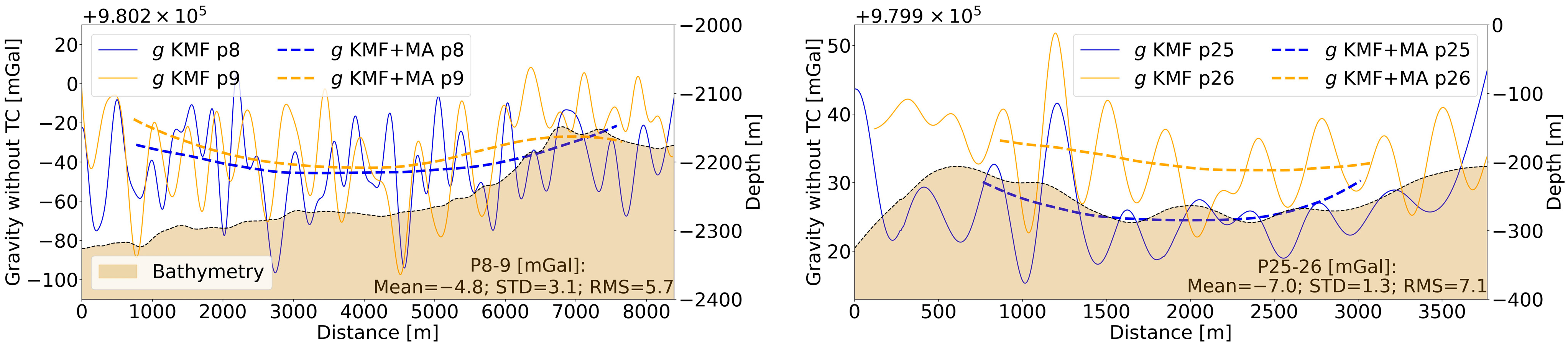

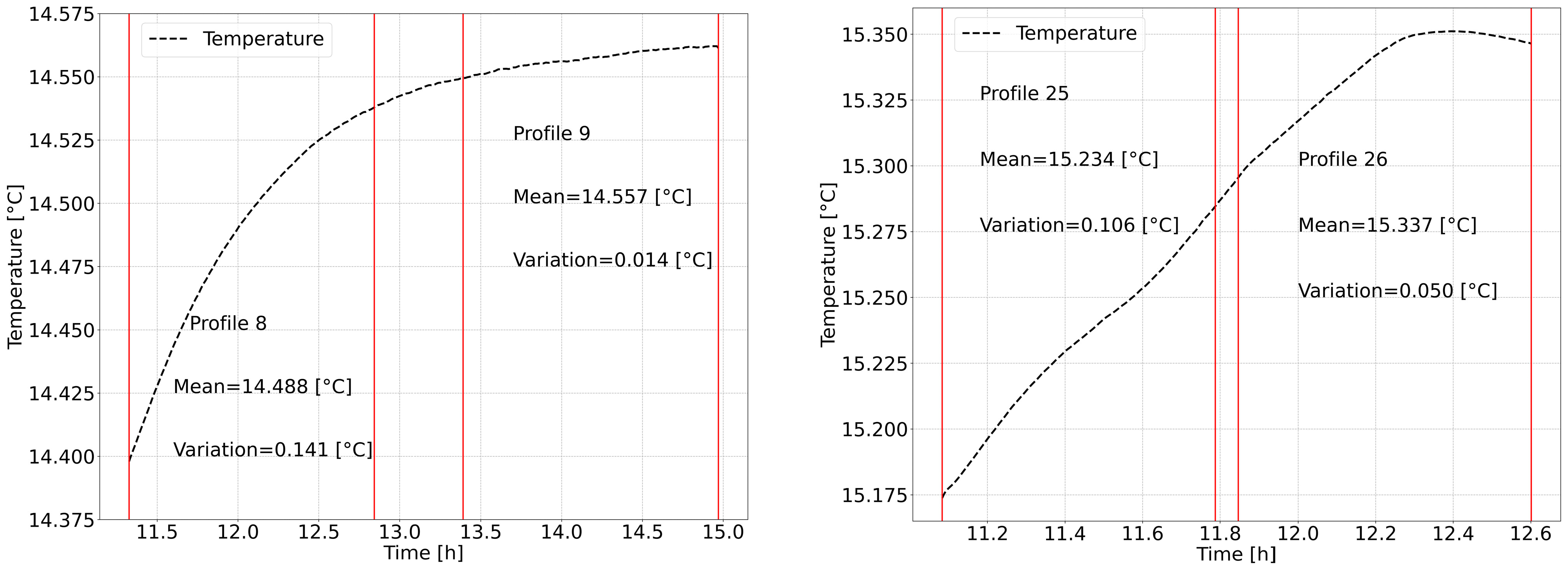

| N° | Date | Shipborne Profile Name | Navigation Mode | Depth or Distance to the Seafloor (m) | Distance (km) |
|---|---|---|---|---|---|
| 1 | 18 March 2016 | Profile 910-S2011-065_TRANSLOT15 | Constant depth | 1900 | 7 |
| 2 | Constant depth | 1900 | 8 | ||
| 3 | Constant depth | 1850 | 8 | ||
| 4 | 19 March 2016 | Terrain follow-up | 100 | 7.5 | |
| 5 | Terrain follow-up | 100 | 7.5 | ||
| 6 | Profile 910-S2006-076_TRANSIT | Terrain follow-up | 100 | 8 | |
| 7 | 20 March 2016 | Terrain follow-up | 100 | 8.5 | |
| 8 | Constant depth | 1900 | 9 | ||
| 9 | Constant depth | 1900 | 9 | ||
| 10 | Constant depth | 1850 | 3 | ||
| 11 | 22 March 2016 | Profile 21-1-E2005-010_ESS-TR-HR | Terrain follow-up | 100 | 7 |
| 12 | Terrain follow-up | 100 | 7 | ||
| 13 | Constant depth | 600 | 3 | ||
| 14 | Constant depth | 600 | 3 | ||
| 15 | 23 March 2016 | Profile 20-2-E2005-010_ESS-TR-HR | Terrain follow-up | 85 | 7 |
| 16 | Terrain follow-up | 85 | 7.5 | ||
| 17 | Constant depth | 100 | 8 | ||
| 18 | Constant depth | 100 | 8.5 | ||
| 19 | Constant depth | 80 | 7.5 | ||
| 20 | Constant depth | 80 | 8 | ||
| 21 | 24 March 2016 | Profile 20-1-E2005-010_ESS-TR-HR | Terrain follow-up | 100 | 4 |
| 22 | Terrain follow-up | 100 | 4 | ||
| 23 | Constant depth | 100 | 4 | ||
| 24 | Constant depth | 100 | 4 | ||
| 25 | Constant depth | 80 | 4 | ||
| 26 | Constant depth | 80 | 4 |
| Data | Min | Max | Mean | STD | Zone |
|---|---|---|---|---|---|
| −80.4 | 63.5 | −4.7 | 36.9 | All | |
| −38.5 | 34.4 | −3.4 | 9.5 | ||
| −13.1 | 19.2 | 0.3 | 4.1 | ||
| −28.9 | 21.2 | −3.6 | 6.8 | ||
| −67.7 | 44.5 | −29.3 | 22.7 | Western (black rectangle) | |
| −25.9 | 34.4 | −1.7 | 8.4 | ||
| −10.9 | 19.2 | −0.3 | 4.0 | ||
| −25.6 | 18.0 | −1.3 | 5.1 | ||
| −51.8 | 33.8 | −12.7 | 22.0 | Eastern (orange rectangle) | |
| −33.9 | 22.3 | −1.4 | 10.0 | ||
| −13.1 | 11.1 | −0.2 | 5.0 | ||
| −22.2 | 15.7 | −1.1 | 6.7 |
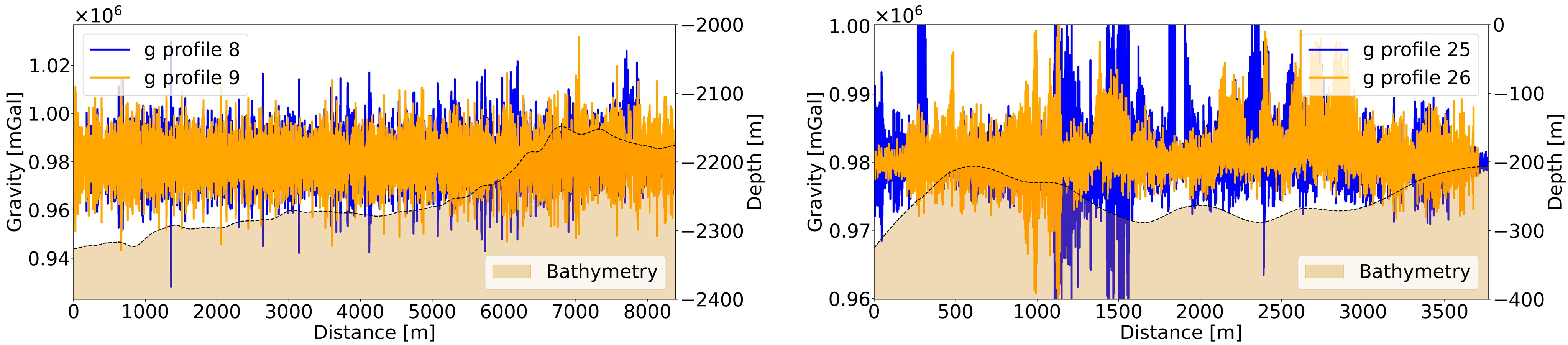
| Profile 8 | Profile 9 | Profile 25 | Profile 26 | |
|---|---|---|---|---|
| Mean value of gravity anomaly differences between DC shipborne (SHOM) and GraviMob (mGal) measurements [1] | 623.8 | 618.5 | 573.3 | 566.2 |
| Mean value of differences between sensor temperature and T0 (°C) [2] | 9.312 | 9.243 | 8.566 | 8.463 |
| [1]/[2] (mGal/°C) | 66.989 | 66.916 | 66.927 | 66.903 |
| Mean value of [1]/[2] (mGal/°C) | 66.934 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, D.T.; Verdun, J.; Cali, J.; Maia, M.; Poitou, C.; Ammann, J.; Roussel, C.; D’Eu, J.-F.; Bouhier, M.-É. High-Resolution Gravity Measurements on Board an Autonomous Underwater Vehicle: Data Reduction and Accuracy Assessment. Remote Sens. 2024, 16, 461. https://doi.org/10.3390/rs16030461
Vu DT, Verdun J, Cali J, Maia M, Poitou C, Ammann J, Roussel C, D’Eu J-F, Bouhier M-É. High-Resolution Gravity Measurements on Board an Autonomous Underwater Vehicle: Data Reduction and Accuracy Assessment. Remote Sensing. 2024; 16(3):461. https://doi.org/10.3390/rs16030461
Chicago/Turabian StyleVu, Dinh Toan, Jérôme Verdun, José Cali, Marcia Maia, Charles Poitou, Jérôme Ammann, Clément Roussel, Jean-François D’Eu, and Marie-Édith Bouhier. 2024. "High-Resolution Gravity Measurements on Board an Autonomous Underwater Vehicle: Data Reduction and Accuracy Assessment" Remote Sensing 16, no. 3: 461. https://doi.org/10.3390/rs16030461
APA StyleVu, D. T., Verdun, J., Cali, J., Maia, M., Poitou, C., Ammann, J., Roussel, C., D’Eu, J.-F., & Bouhier, M.-É. (2024). High-Resolution Gravity Measurements on Board an Autonomous Underwater Vehicle: Data Reduction and Accuracy Assessment. Remote Sensing, 16(3), 461. https://doi.org/10.3390/rs16030461








