Research on the Ionospheric Delay of Long-Range Short-Wave Propagation Based on a Regression Analysis
Abstract
1. Introduction
2. Theory Description
3. Results and Discussion
3.1. The Quasi-Parabolic (QP) Ionosphere Model
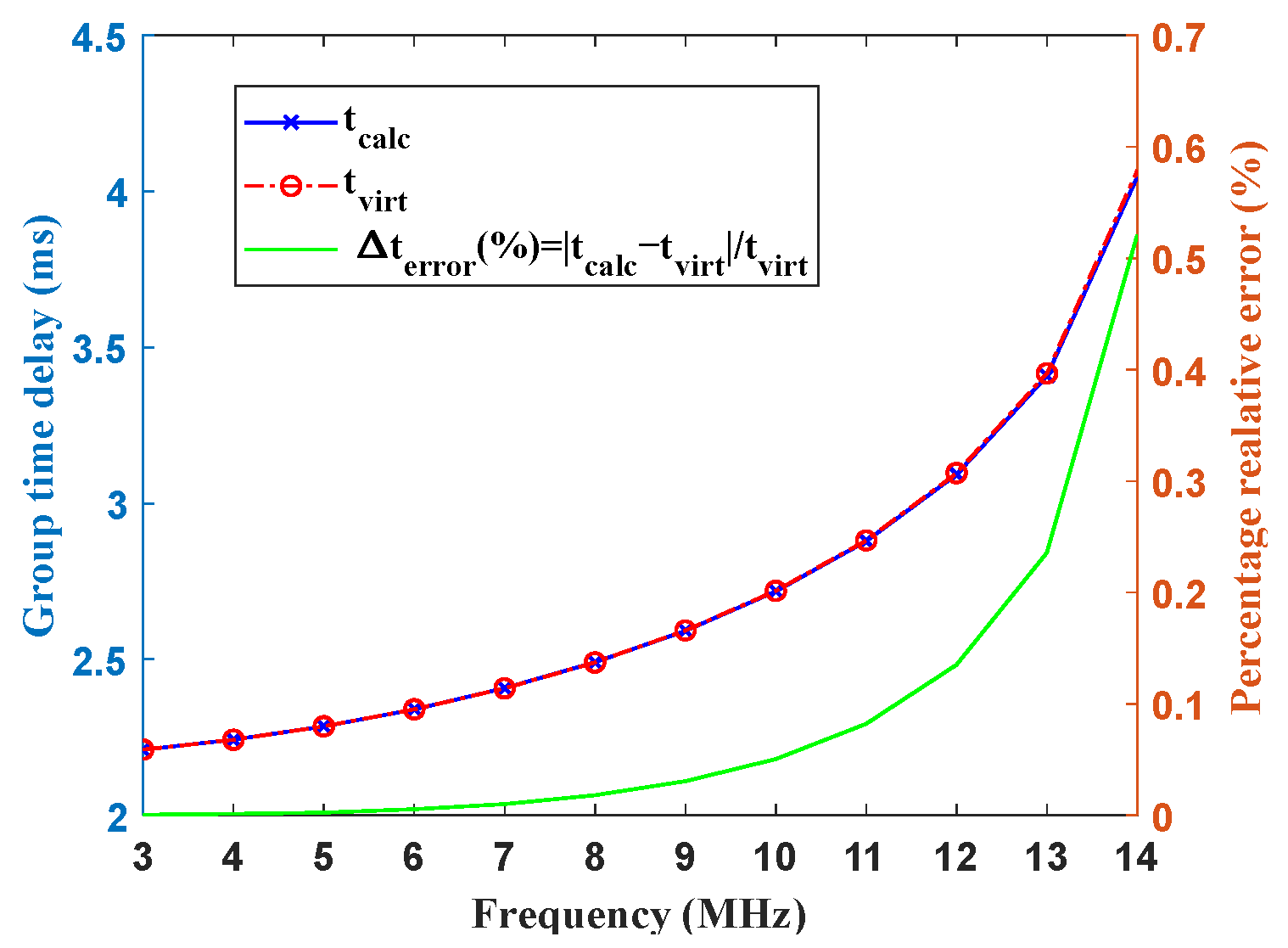
3.2. Validation of the Performance of the Ray-Tracing Algorithm
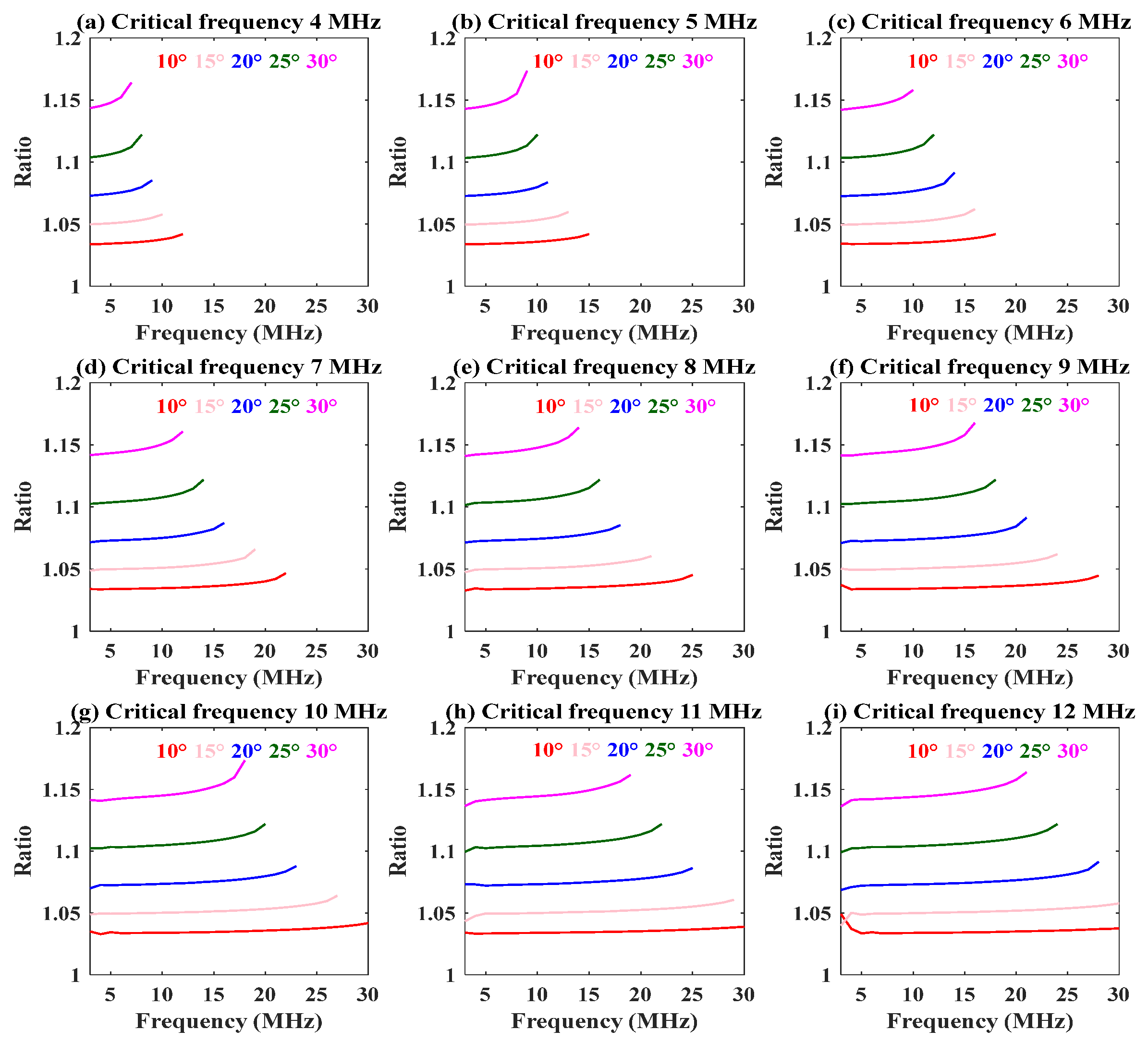
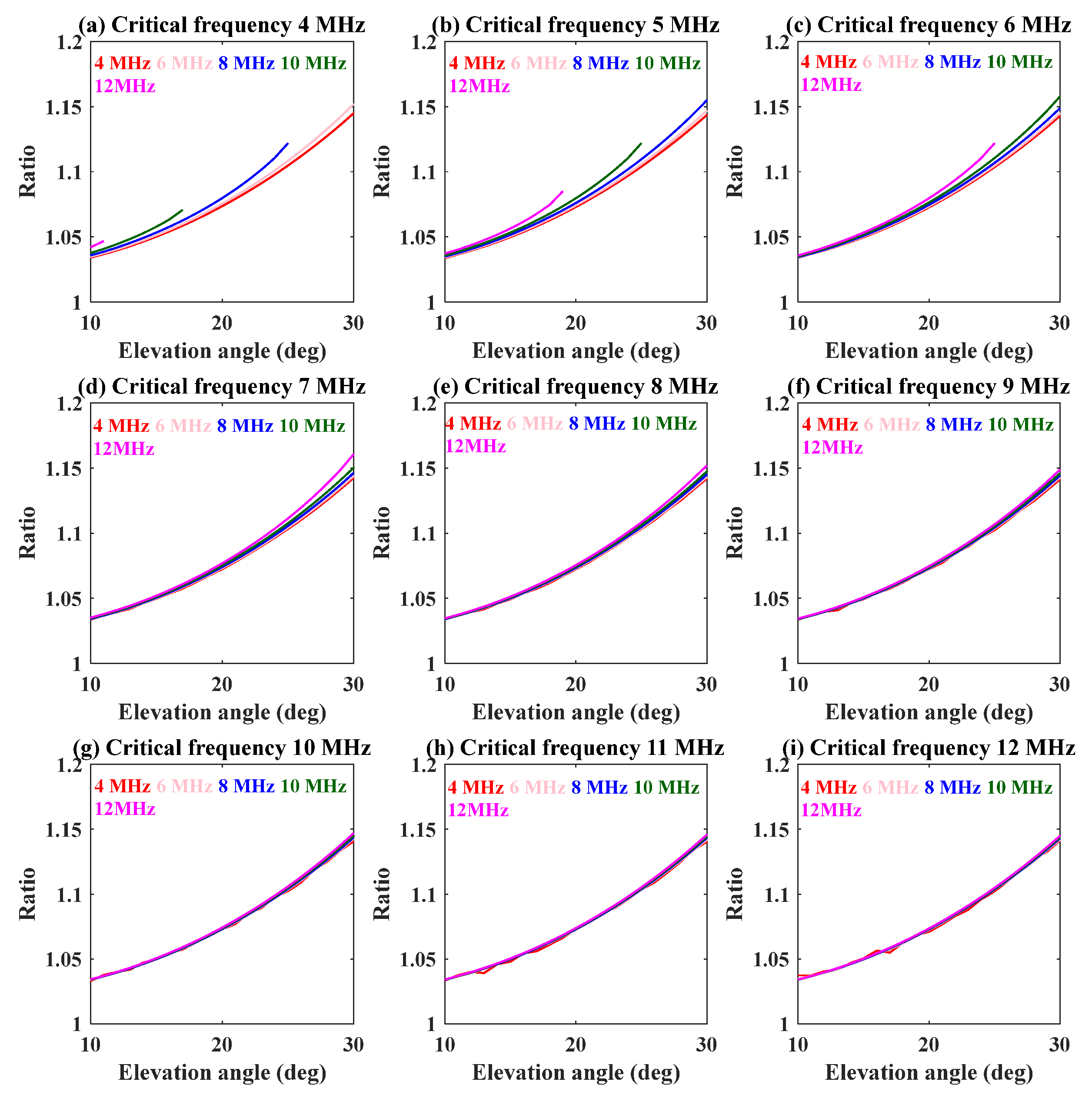
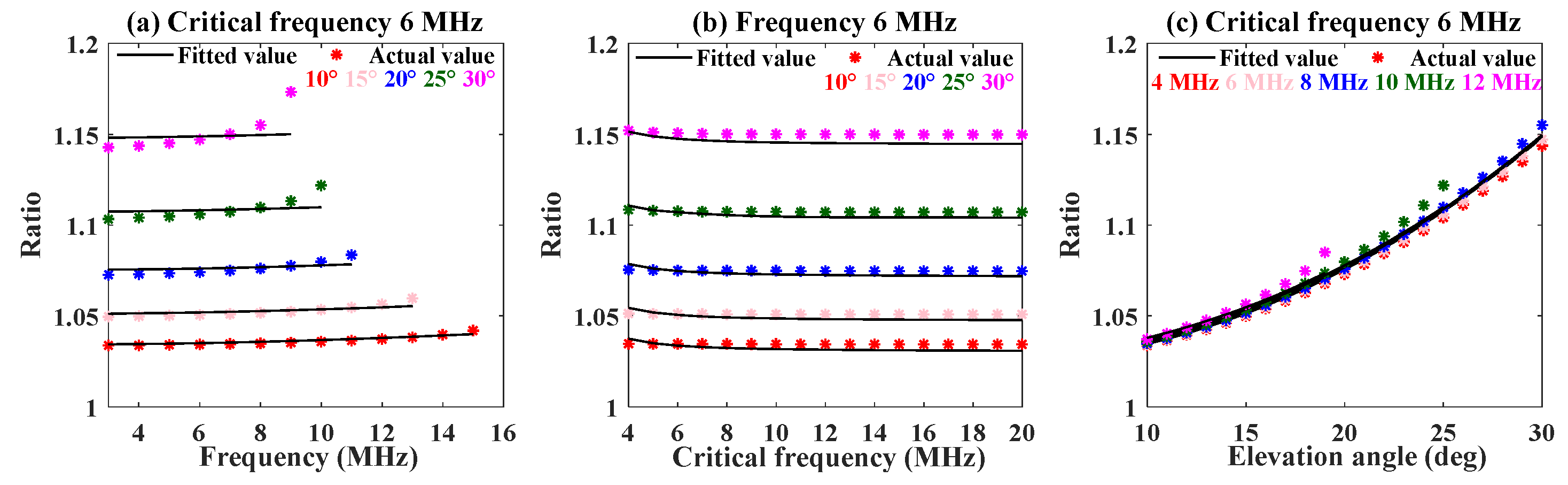
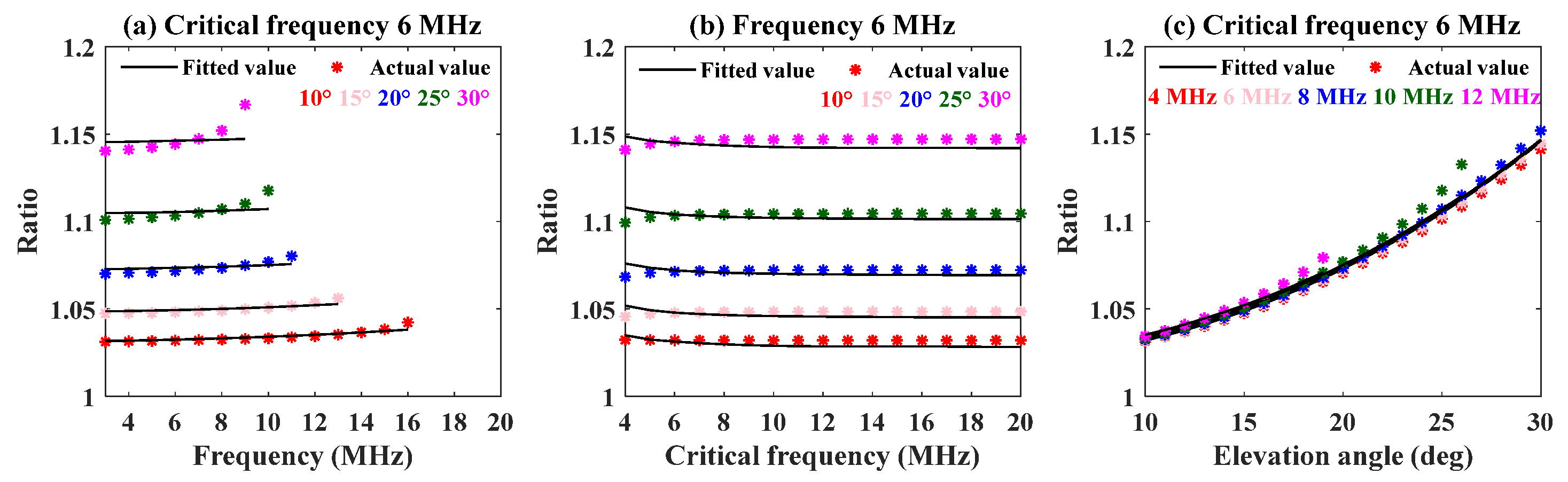
3.3. The Mapping Model between the Numerical Ratio and the Three Factors of Frequency, Critical Frequency, and Elevation Angle
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Xiong, N.L.; Tang, C.C.; Li, X.J. Introduction to Ionospheric Physics; Wuhan University Press: Wuhan, China, 1999; ISBN 7-307-02672-4. (In Chinese) [Google Scholar]
- Wen, D.B. Investigation of GPS-Based Ionospheric Tomographic Algorithms and Their Applications. Ph.D. Thesis, Institute of Geodesy and Geophysics Chinese Academy of Sciences, Wuhan, China, 2007. [Google Scholar]
- Heelis, R.A.; Maute, A. Challenges to Understanding the Earth’s Ionosphere and Thermosphere. JGR Space Phys. 2020, 125, e2019JA027497. [Google Scholar] [CrossRef]
- Klobuchar, J.A. Ionospheric Effects on GPS. Glob. Position. Syst. Theory Appl. 1991, 1, 517–546. [Google Scholar] [CrossRef]
- Xiao, Z.B.; Liu, Z.Y.; Tang, X.M.; Wang, F.X. Effect of ionosphere dispersion on the navigation signal receiving. J. Natl. Univ. Def. Technol. 2014, 36, 146–149. [Google Scholar] [CrossRef]
- Klobuchar, J. Ionospheric Time-Delay Algorithm for Single-Frequency GPS Users. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 325–331. [Google Scholar] [CrossRef]
- Prieto-Cerdeira, R.; Orús Pérez, R.; Breeuwer, E.; Lucas-Rodriguez, R.; Falcone, M. Performance of the Galileo Single-Frequency Ionospheric Correction During In-Orbit Validation. GPSworld 2014, 25, 53–58. [Google Scholar]
- Yuan, Y.; Wang, N.; Li, Z.; Huo, X. The BeiDou Global Broadcast Ionospheric Delay Correction Model (BDGIM) and Its Preliminary Performance Evaluation Results. Navigation 2019, 66, 55–69. [Google Scholar] [CrossRef]
- Pang, J.; Liu, Z.Y.; Tang, X.M.; Ou, G. Ionosphere dispersion effects simulation for high order BOC modulated signals. J. Natl. Univ. Def. Technol. 2015, 37, 74–77. [Google Scholar] [CrossRef]
- Liu, X.; Yuan, Y.; Huo, X.; Li, Z.; Li, W. Model Analysis Method (MAM) on the Effect of the Second-Order Ionospheric Delay on GPS Positioning Solution. Chin. Sci. Bull. 2010, 55, 1529–1534. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, J.; Yu, B.; Sheng, C.; Gan, X. Research on Remote GPS Common-View Precise Time Transfer Based on Different Ionosphere Disturbances. Sensors 2020, 20, 2290. [Google Scholar] [CrossRef] [PubMed]
- Petrie, E.J.; Hernández-Pajares, M.; Spalla, P.; Moore, P.; King, M.A. A Review of Higher Order Ionospheric Refraction Effects on Dual Frequency GPS. Surv. Geophys. 2011, 32, 197–253. [Google Scholar] [CrossRef]
- Hernández-Pajares, M.; Aragón-Ángel, À.; Defraigne, P.; Bergeot, N.; Prieto-Cerdeira, R.; García-Rigo, A. Distribution and Mitigation of Higher-order Ionospheric Effects on Precise GNSS Processing. JGR Solid Earth 2014, 119, 3823–3837. [Google Scholar] [CrossRef]
- Zhang, X.; Ren, X.; Guo, F. Influence of Higher-Order Ionospheric Delay Correction on Static Precise Point Positioning. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 883–887. [Google Scholar] [CrossRef]
- Cai, C.; Liu, G.; Yi, Z.; Cui, X.; Kuang, C. Effect Analysis of Higher-Order Ionospheric Corrections on Quad-Constellation GNSS PPP. Meas. Sci. Technol. 2019, 30, 024001. [Google Scholar] [CrossRef]
- Hadas, T.; Krypiak-Gregorczyk, A.; Hernández-Pajares, M.; Kaplon, J.; Paziewski, J.; Wielgosz, P.; Garcia-Rigo, A.; Kazmierski, K.; Sosnica, K.; Kwasniak, D.; et al. Impact and Implementation of Higher-Order Ionospheric Effects on Precise GNSS Applications. JGR Solid Earth 2017, 122, 9420–9436. [Google Scholar] [CrossRef]
- Jin, S.; Jin, R.; Kutoglu, H. Positive and Negative Ionospheric Responses to the March 2015 Geomagnetic Storm from BDS Observations. J. Geod. 2017, 91, 613–626. [Google Scholar] [CrossRef]
- Chen, L.; Yi, W.; Song, W.; Shi, C.; Lou, Y.; Cao, C. Evaluation of Three Ionospheric Delay Computation Methods for Ground-Based GNSS Receivers. GPS Solut. 2018, 22, 125. [Google Scholar] [CrossRef]
- Hartmann, G.K.; Leitinger, R. Range Errors Due to Ionospheric and Tropospheric Effects for Signal Frequencies above 100 MHz. Bull. Geod. 1984, 58, 109–136. [Google Scholar] [CrossRef]
- Brunner, F.K.; Gu, M. An Improved Model for the Dual Frequency Ionospheric Correction of GPS Observations. Manuscripta Geod. 1991, 16, 205–214. [Google Scholar]
- Bassiri, S.; Hajj, G.A. Higher-Order Ionospheric Effects on the GPS Observables and Means of Modeling Them. Manuscripta Geod. 1993, 18, 280–289. [Google Scholar]
- Strangeways, H.J.; Ioannides, R.T. Rigorous Calculation of Ionospheric Effects on GPS Earth-Satellite Paths Using a Precise Path Determination Method. AGeod 2002, 37, 281–292. [Google Scholar] [CrossRef]
- Wang, K.N.; Fu, H.Y. Simulation of the ionospheric higher-order effect and Doppler effect during TID based on ray tracing. Chin. J. Radio Sci. 2022, 37, 1032–1038. [Google Scholar] [CrossRef]
- Su, K.; Jin, S.; Hoque, M. Evaluation of Ionospheric Delay Effects on Multi-GNSS Positioning Performance. Remote Sens. 2019, 11, 171. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Z. Anomalies in Broadcast Ionospheric Coefficients Recorded by GPS Receivers over the Past Two Solar Cycles (1992–2013); Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Wang, A.; Chen, J.; Zhang, Y.; Meng, L.; Wang, J. Performance of Selected Ionospheric Models in Multi-Global Navigation Satellite System Single-Frequency Positioning over China. Remote Sens. 2019, 11, 2070. [Google Scholar] [CrossRef]
- Bianchi, C.; Settimi, A.; Scotto, C.; Azzarone, A.; Lozito, A. A Method to Test HF Ray Tracing Algorithm in the Ionosphere by Means of the Virtual Time Delay. Adv. Space Res. 2011, 48, 1600–1605. [Google Scholar] [CrossRef]
- Budden, K.G. The Propagation of Radio Waves: The Theory of Radio Waves of Low Power in the Ionosphere and Magnetosphere, 1st ed.; Cambridge University Press: Cambridge, UK, 1985; ISBN 978-0-521-25461-8. [Google Scholar]
- Davies, K. Ionospheric Radio; The Institution of Engineering and Technology: London, UK, 1990. [Google Scholar]
- Rawer, K. Wave Propagation in the Ionosphere; Springer: Dordrecht, The Netherlands, 1993; ISBN 978-90-481-4069-5. [Google Scholar]
- De Voogt, A. The Calculation of the Path of a Radio-Ray in a Given Ionosphere. Proc. IRE 1953, 41, 1183–1186. [Google Scholar] [CrossRef]
- Pietrella, M.; Pezzopane, M.; Pignatelli, A.; Pignalberi, A.; Settimi, A. An Updating of the IONORT Tool to Perform a High-Frequency Ionospheric Ray Tracing. Remote Sens. 2023, 15, 5111. [Google Scholar] [CrossRef]
- Croft, T.A.; Hoogansian, H. Exact Ray Calculations in a Quasi-Parabolic Ionosphere with No Magnetic Field. Radio Sci. 1968, 3, 69–74. [Google Scholar] [CrossRef]




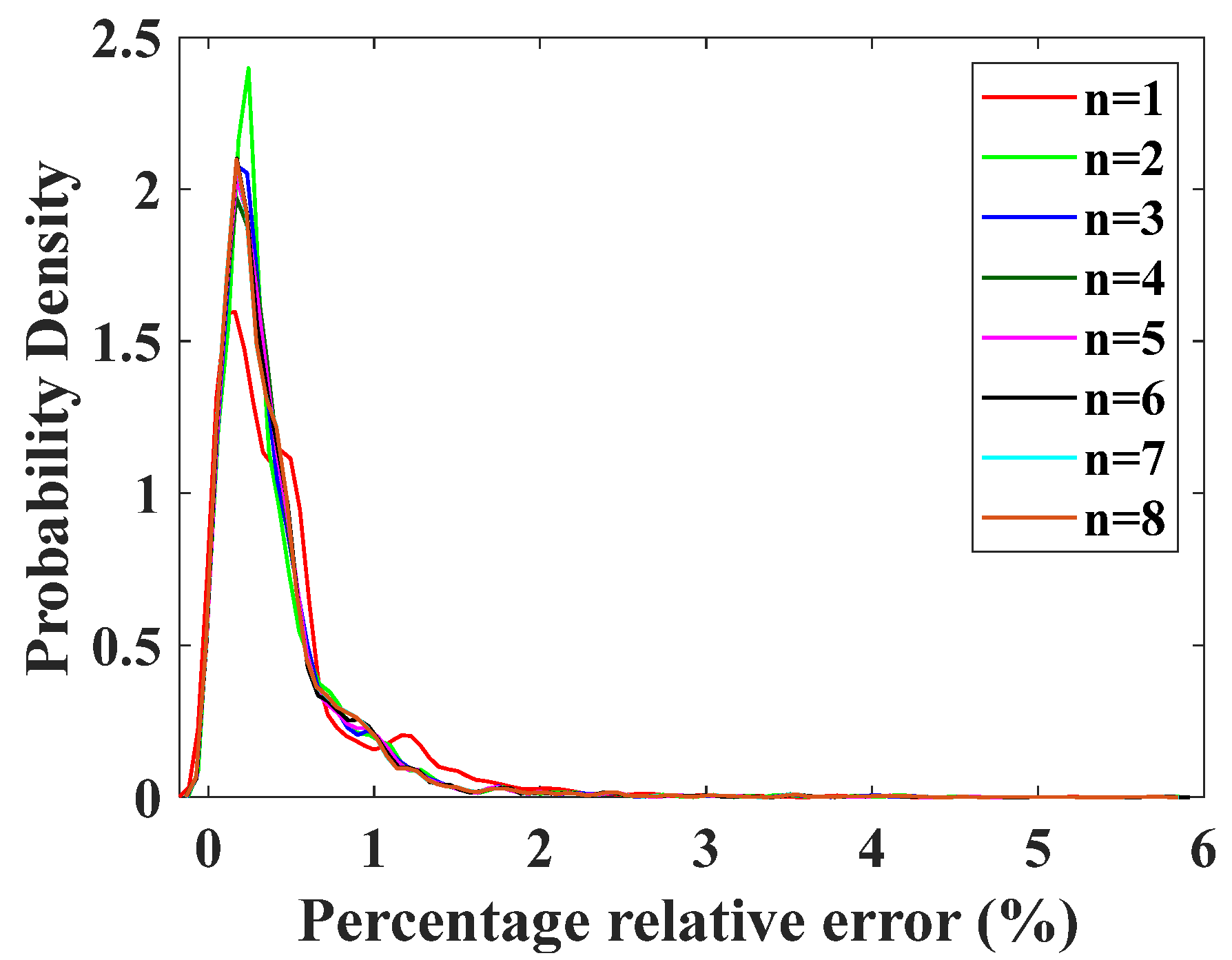
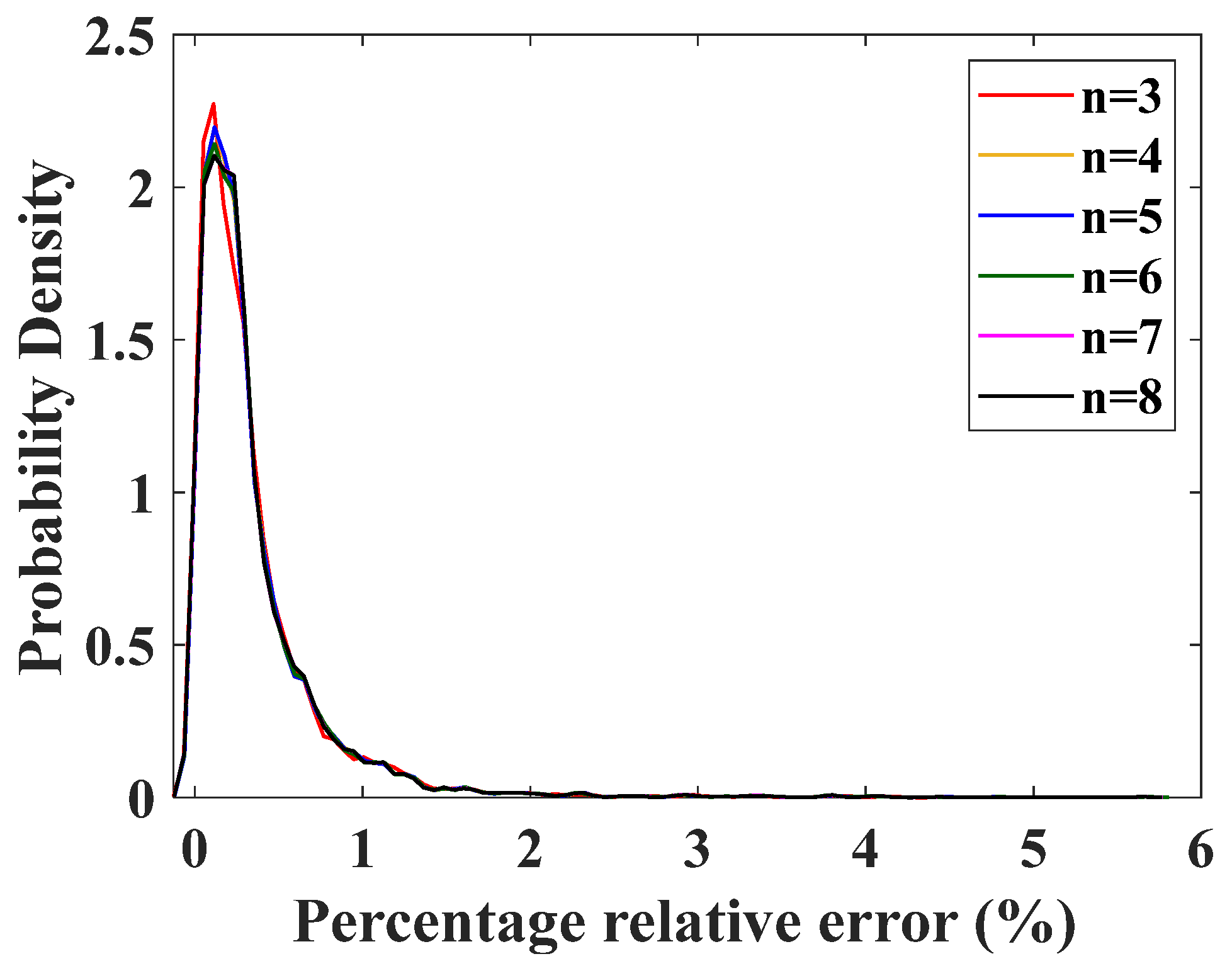
| The Order of the Polynomial (n) | Root Mean Square Errors () |
|---|---|
| 3 | 6.89594 |
| 4 | 6.88583 |
| 5 | 6.88579 |
| 6 | 6.88434 |
| 7 | 6.88202 |
| 8 | 6.88187 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Li, H.; Guo, L.; Ye, D.; Yang, K.; Li, J. Research on the Ionospheric Delay of Long-Range Short-Wave Propagation Based on a Regression Analysis. Remote Sens. 2024, 16, 553. https://doi.org/10.3390/rs16030553
Jiang X, Li H, Guo L, Ye D, Yang K, Li J. Research on the Ionospheric Delay of Long-Range Short-Wave Propagation Based on a Regression Analysis. Remote Sensing. 2024; 16(3):553. https://doi.org/10.3390/rs16030553
Chicago/Turabian StyleJiang, Xiaoli, Huimin Li, Lixin Guo, Dalin Ye, Kehu Yang, and Jiawen Li. 2024. "Research on the Ionospheric Delay of Long-Range Short-Wave Propagation Based on a Regression Analysis" Remote Sensing 16, no. 3: 553. https://doi.org/10.3390/rs16030553
APA StyleJiang, X., Li, H., Guo, L., Ye, D., Yang, K., & Li, J. (2024). Research on the Ionospheric Delay of Long-Range Short-Wave Propagation Based on a Regression Analysis. Remote Sensing, 16(3), 553. https://doi.org/10.3390/rs16030553






