A Robust Track Estimation Method for Airborne SAR Based on Weak Navigation Information and Additional Envelope Errors
Abstract
:1. Introduction
- Using weak navigation information to perform preliminary motion compensation, which ensures that only residual errors remain in the signal, preventing complete image defocusing and enhancing the algorithm’s broad applicability;
- Initial track estimation is carried out utilizing the additional envelope errors introduced by the EOK algorithm, aimed at further reducing the residual errors. This results in a straighter envelope, which provides a solid foundation for subsequent estimations;
- The article presents the calculation method of the compensated component for each target and analyzes the accuracy from both theoretical and simulation perspectives.
2. Materials and Methods
2.1. Basic Methodologies
2.1.1. Principle of Motion Compensation (MoCo)
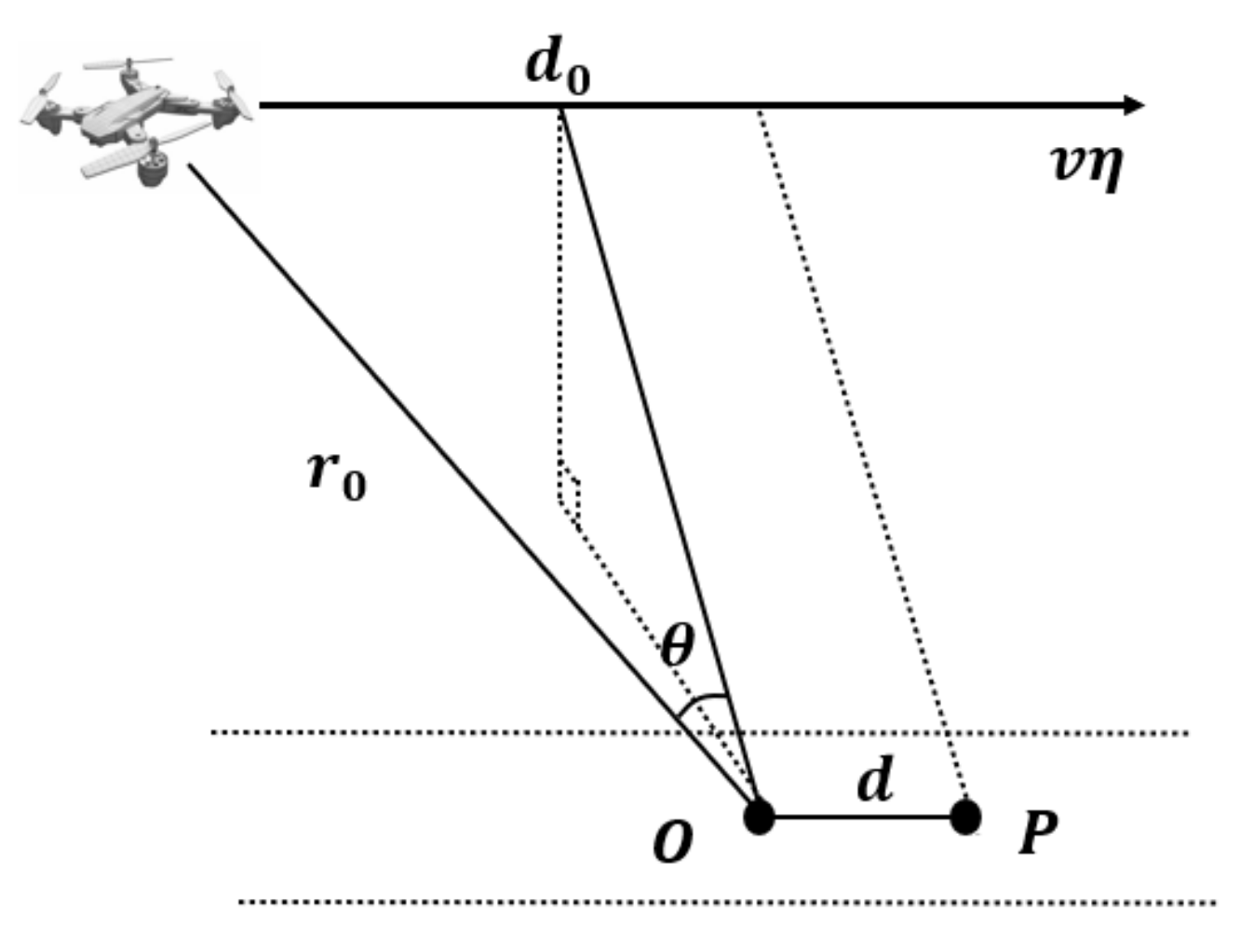
2.1.2. EOK Algorithm and Additional Envelope Errors
2.1.3. Principle of WTA Algorithm
- (1)
- Estimating the double gradients of phase errors
- (2)
- Performing the polynomial fitting
- (3)
- Solving the track error with the WTLS method
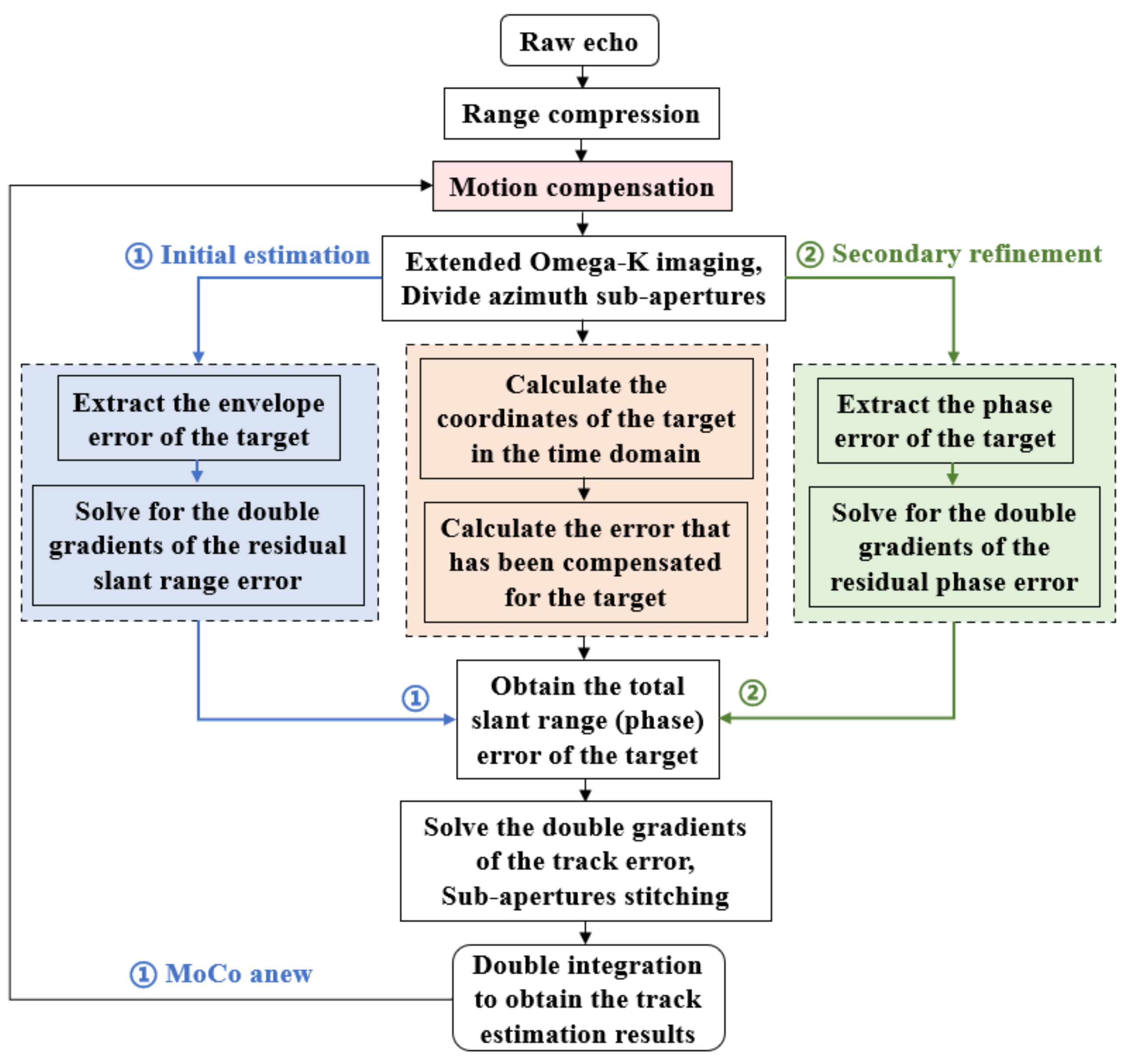
2.2. Novel Algorithm Methodology
2.2.1. Pre-Processing of Raw Data
2.2.2. The Initial Track Estimation Based on Additional Envelope Errors
- (1)
- Solving the residual range errors
- (2)
- Calculating the compensated range errors
- (3)
- Estimating the track initially
2.2.3. The Track Refinement Based on Phase Errors
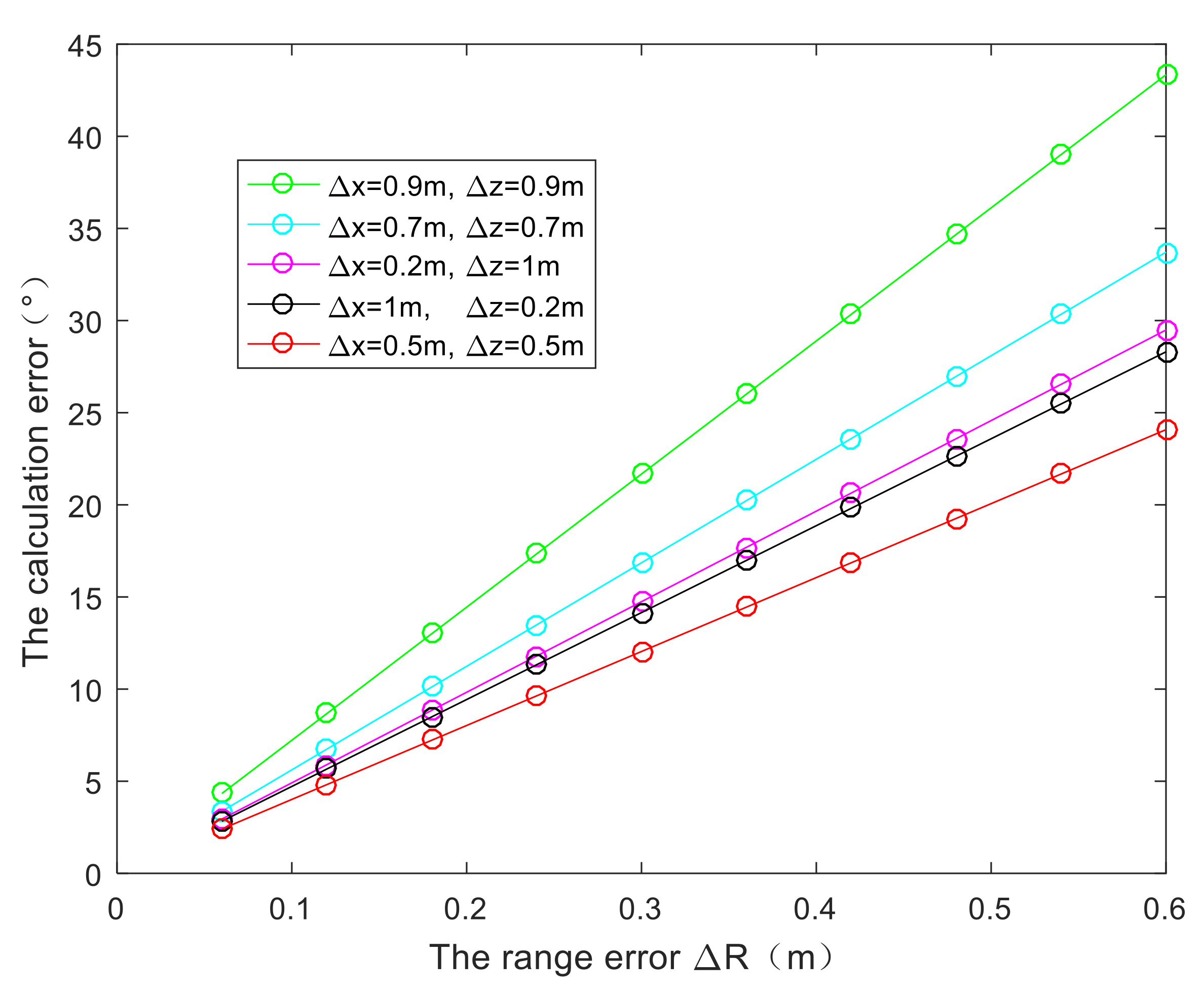
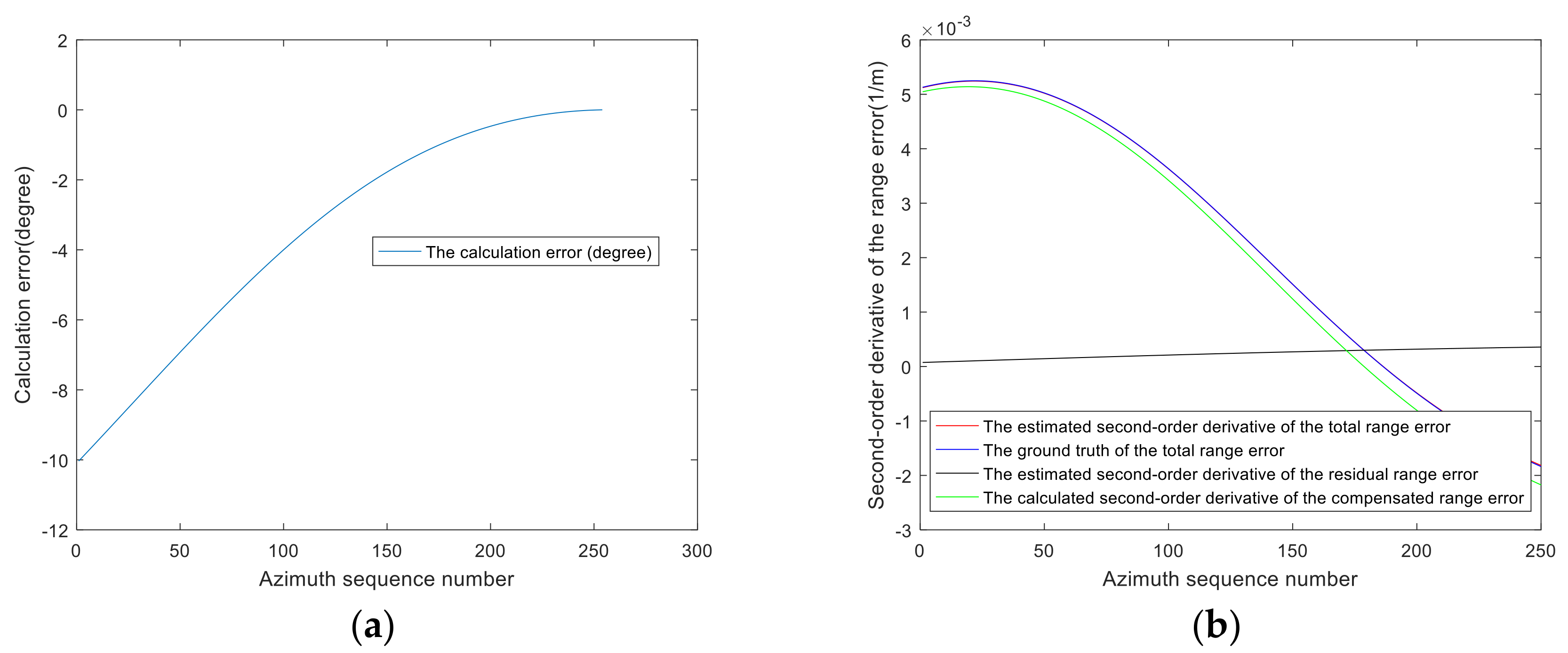
2.2.4. Analysis of Calculation Accuracy of Compensated Range Error
- The shorter the wavelength, , the larger the calculation error, ;
- The larger the reference height, , the larger the calculation error, ;
- The smaller the range history, , the larger the calculation error, ;
- The larger the range error, , the larger the calculation error, ;
- The larger the measurement values (or estimation values) of the motion error, and , the larger the calculation error, . The impact of and on the outcome is contingent upon their coefficients. The coefficient of is , and the coefficient of is . Consequently, exerts a greater influence on when exceeds 1; conversely, has a more pronounced effect on when is less than 1.
3. Results
3.1. Results of Simulations
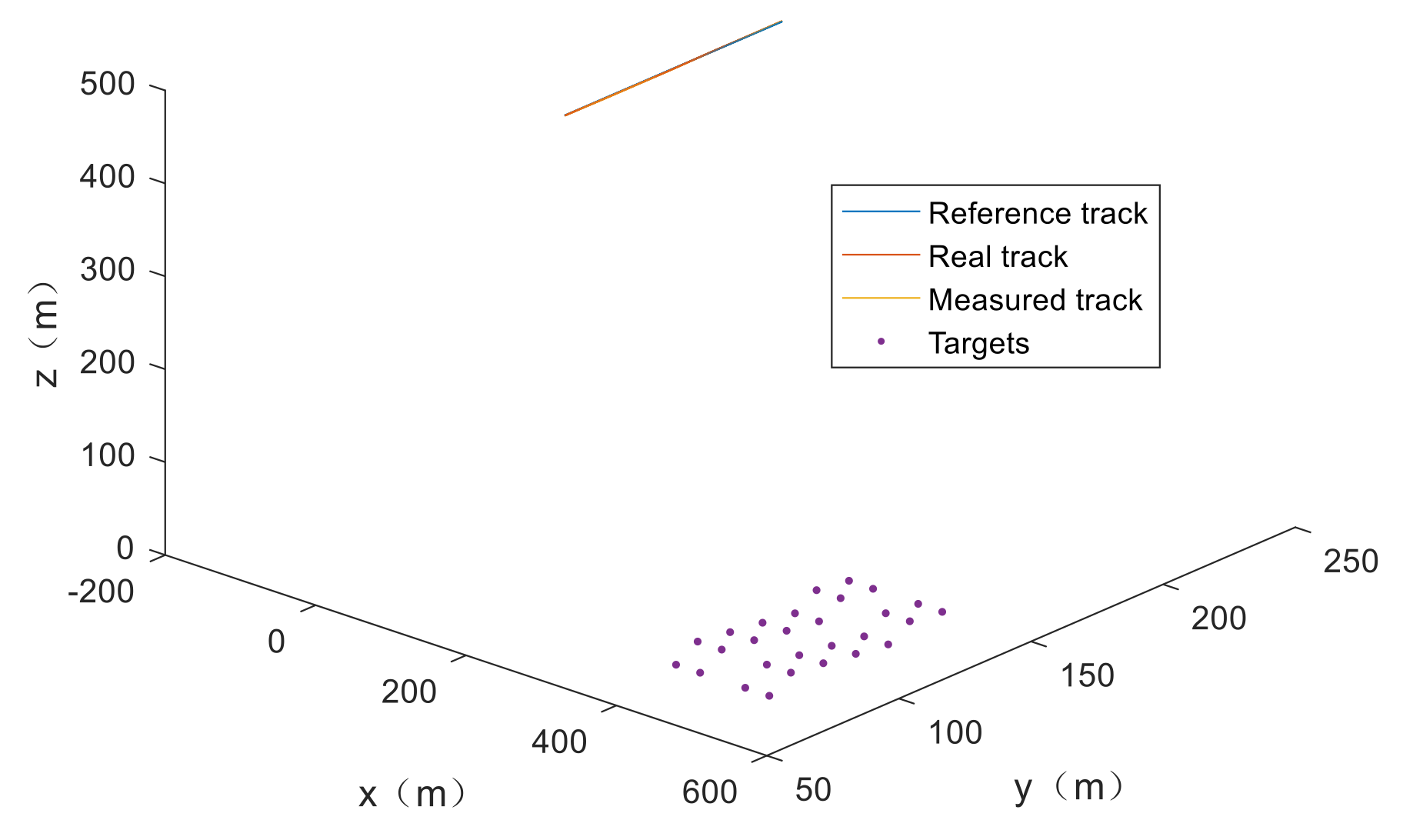
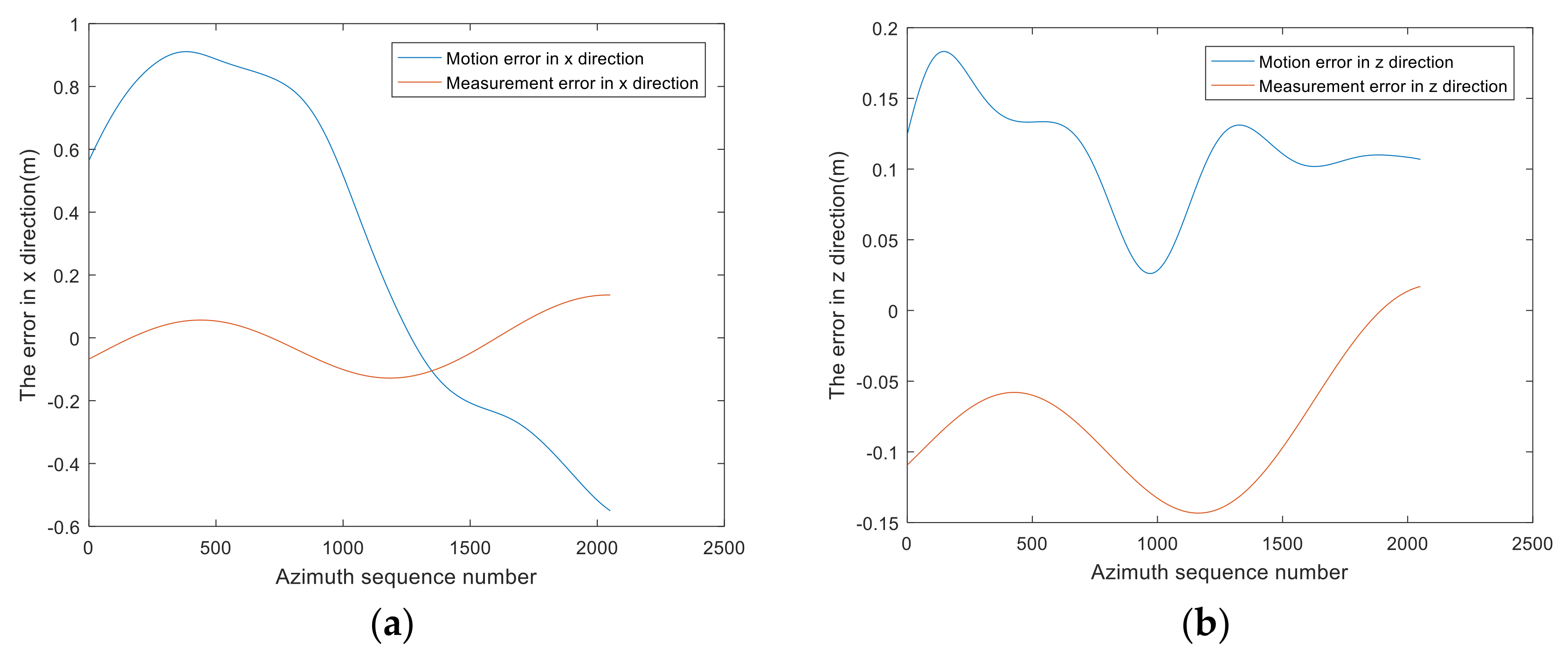
3.1.1. Pre-Processing of Raw Data
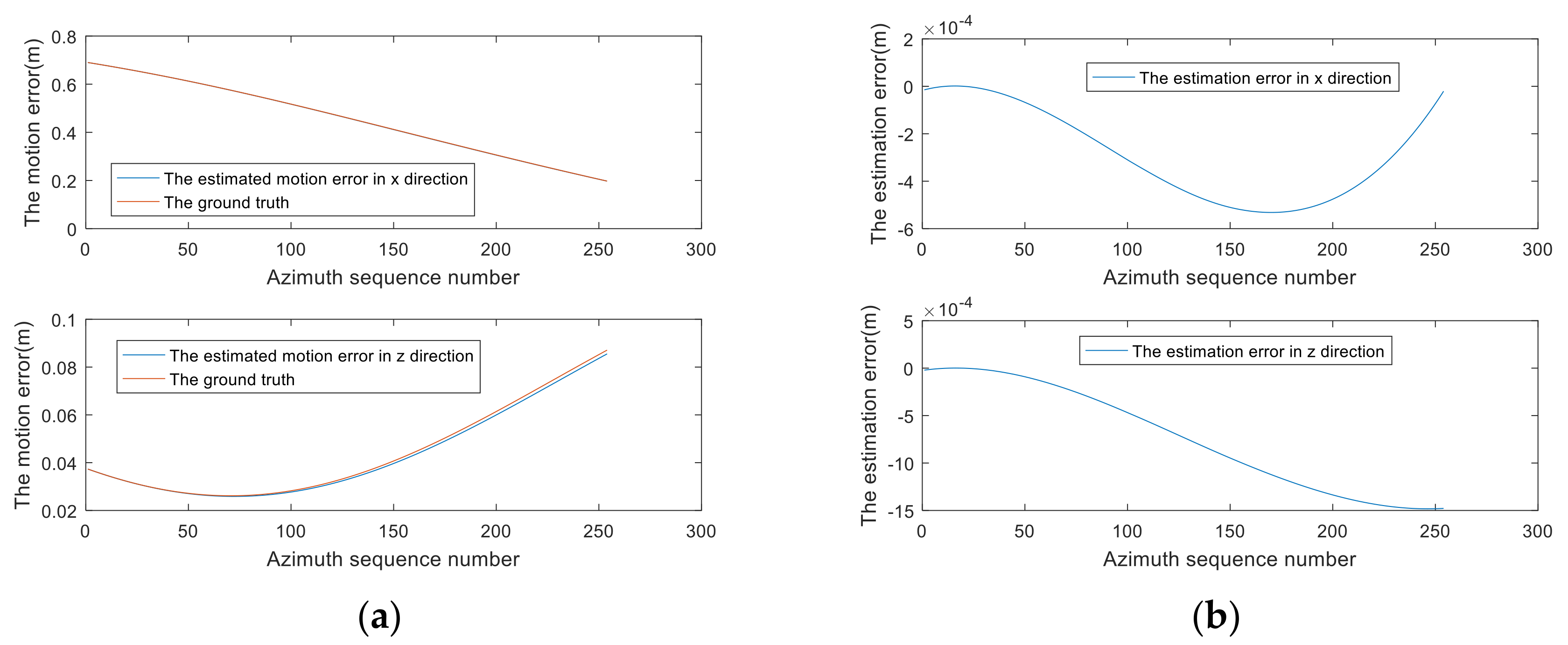
3.1.2. Validating the Calculation Accuracy of Compensated Component
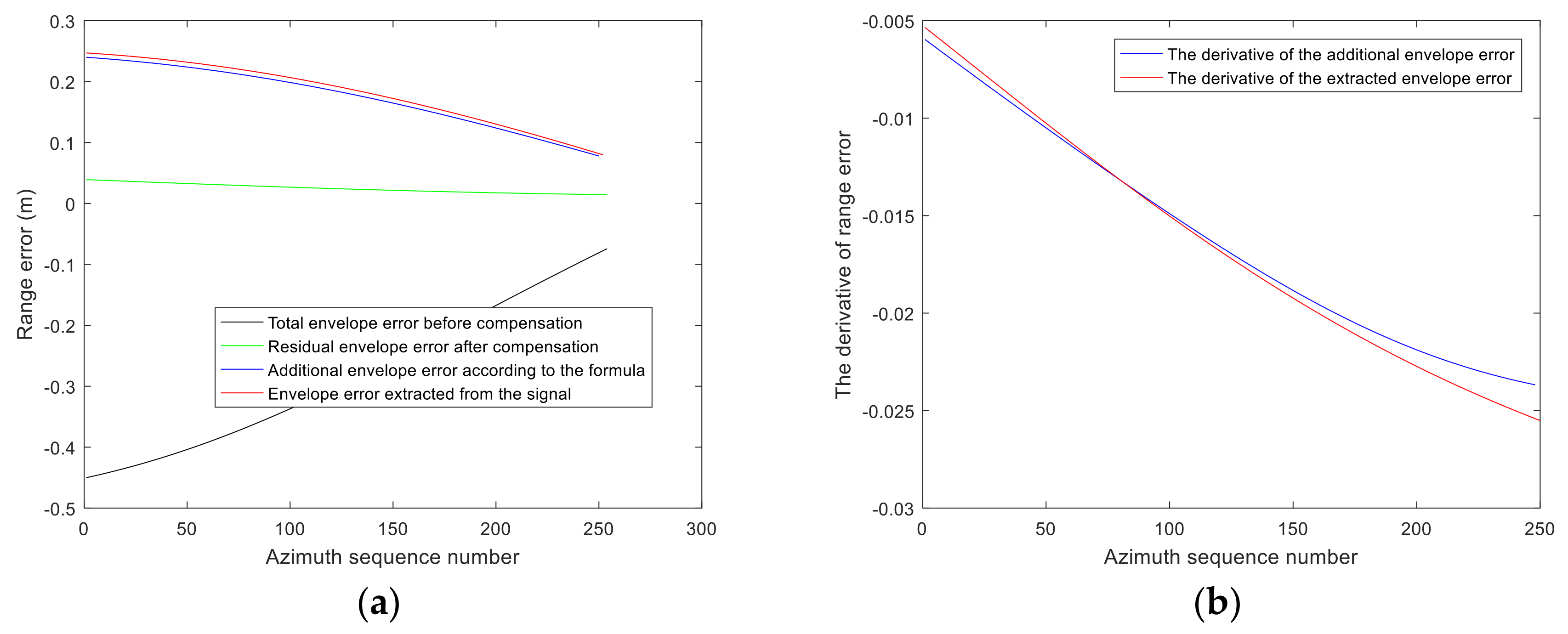
3.1.3. Validating the Feasibility of Utilizing the Additional Envelope Errors
3.1.4. The Track Estimation and the Imaging Results
- (1)
- The signal after initial motion compensation
- (2)
- The initially estimated track based on additional envelope errors
- (3)
- The signal after using the initially estimated track for compensation
- (4)
- The refined track using the phase-based estimation
- (5)
- The signal after using the refined track for compensation
- (6)
- The focused image and imaging quality test
3.1.5. The Comparison Experiment
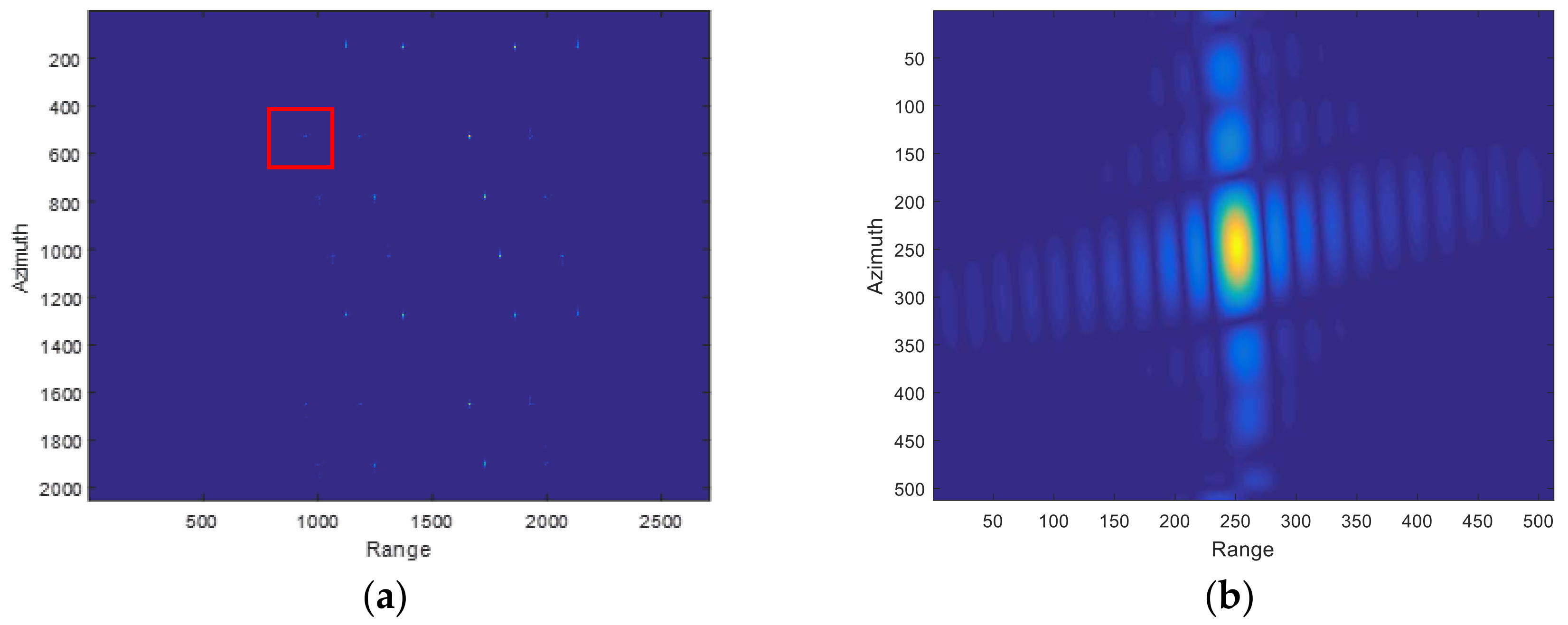
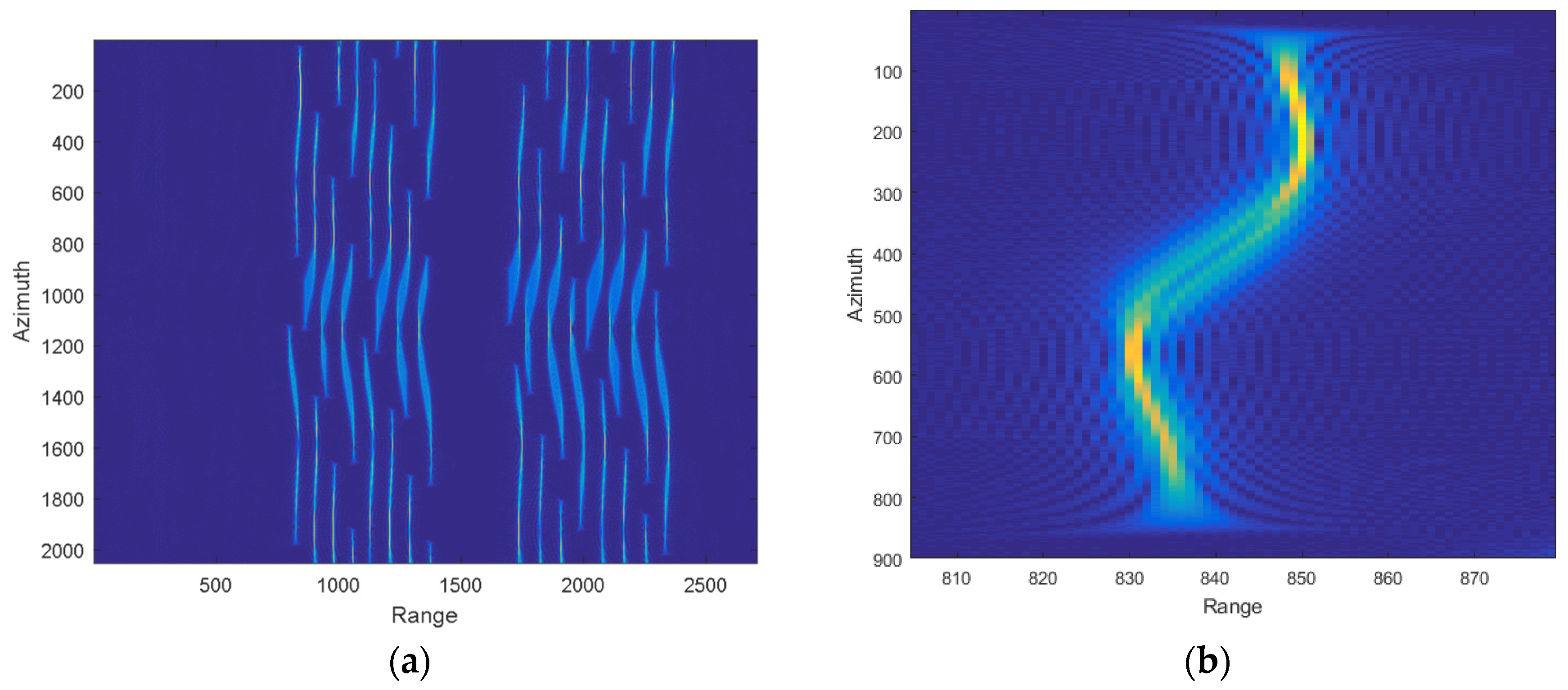
3.2. Results of Real Data Experiments
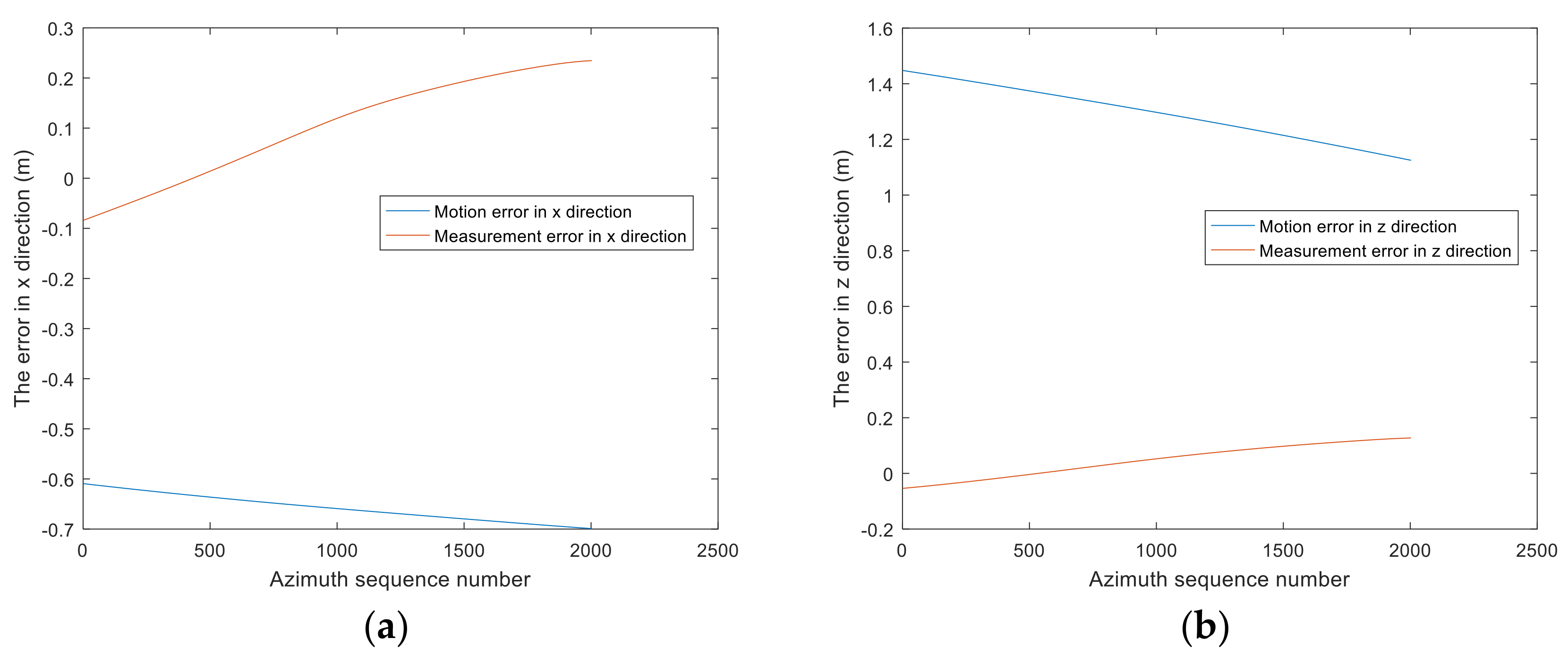
3.2.1. Parameters
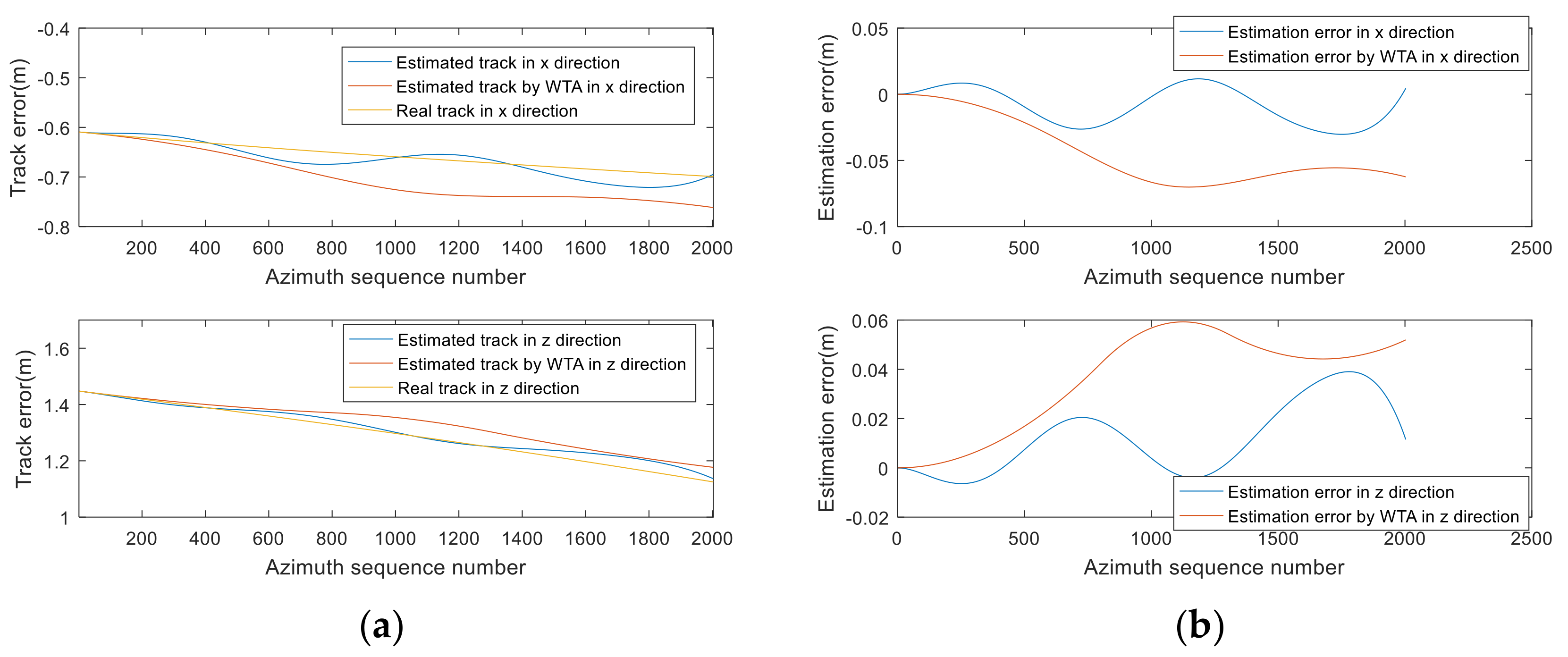
3.2.2. The Estimated Track and Comparison Results
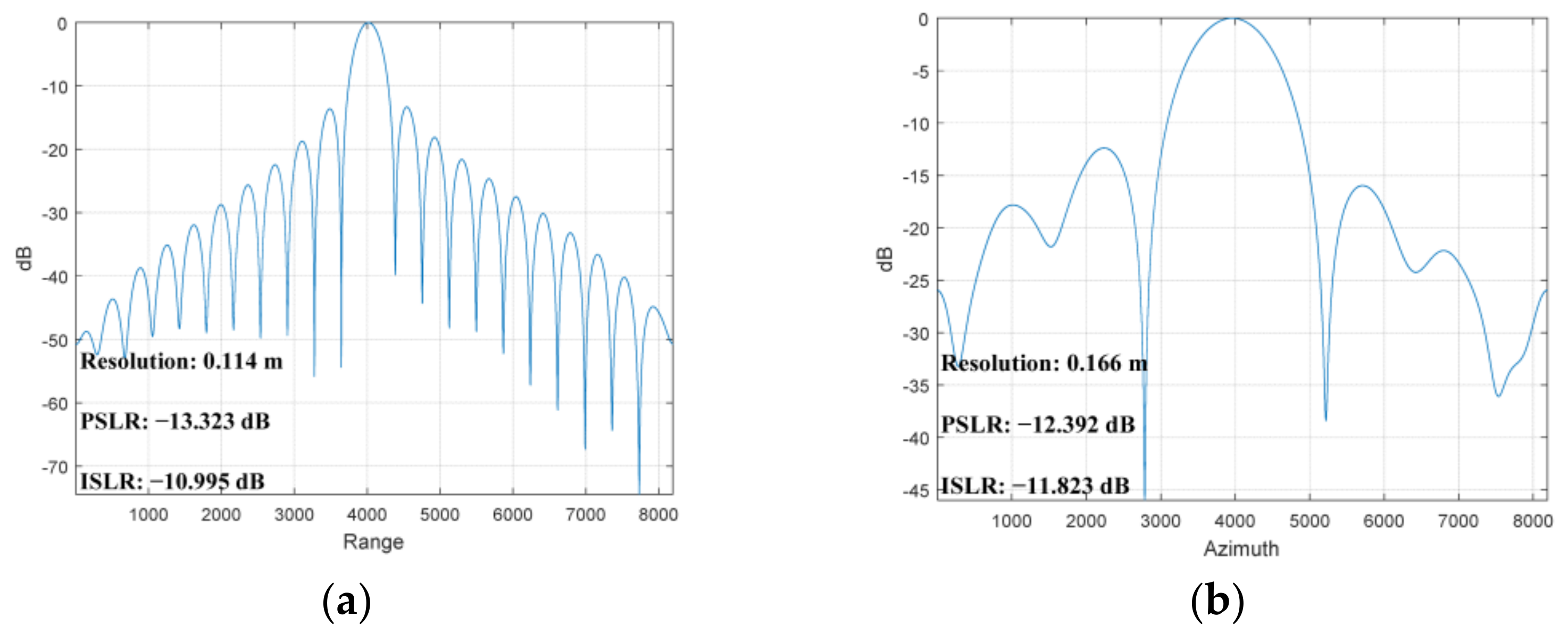
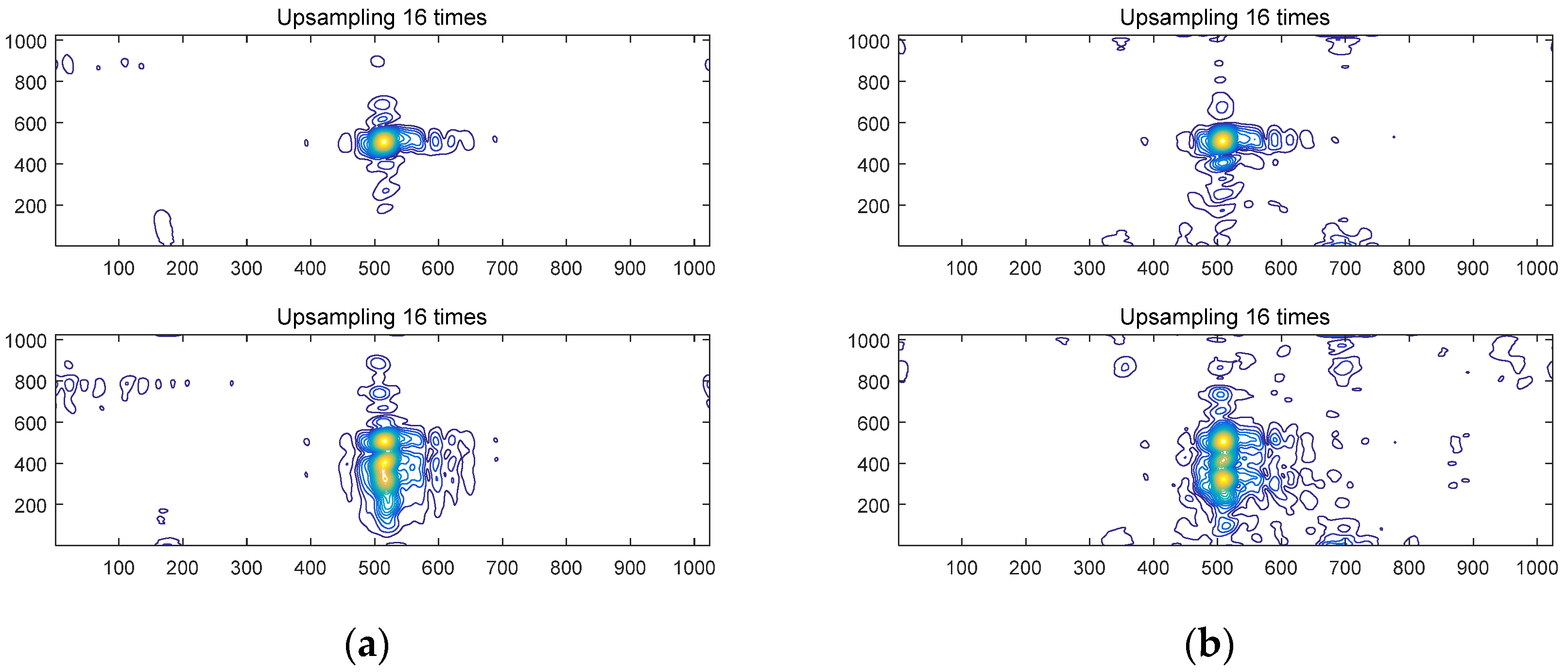
3.2.3. The Imaging Results and Quality Test
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Edwards, M.; Madsen, D.; Stringham, C.; Margulis, A.; Wicks, B.; Long, D.G. microASAR: A small, robust LFM-CW SAR for operation on UAVs and small aircraft. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008. [Google Scholar]
- Otten, M.; van Rossum, W.; van der Graaf, M.; Vlothuizen, W.; Tan, R. Multichannel imaging with the AMBER FMCW SAR. In Proceedings of the EUSAR 2014, 10th European Conference on Synthetic Aperture Radar, Berlin, Germany, 3–5 June 2014. [Google Scholar]
- Gromek, D.; Samczynski, P.; Kulpa, K.; Cruz, G.C.S.; Oliveira, T.M.M.; Felix, L.F.S.; Goncalves, P.A.V.; Silva, C.M.B.P.; Santos, A.L.C.; Morgado, J.A.P. C-band SAR radar trials using UAV platform: Experimental results of SAR system integration on a UAV carrier. In Proceedings of the 2016 17th International Radar Symposium (IRS), Krakow, Poland, 10–12 May 2016. [Google Scholar]
- Ding, M.; Wang, X.; Tang, L.; Qu, J.; Wang, Y.; Zhou, L.; Wang, B. A W-Band Active Phased Array Miniaturized Scan-SAR with High Resolution on Multi-Rotor UAVs. Remote Sens. 2022, 14, 5840. [Google Scholar] [CrossRef]
- Ye, W.; Yeo, T.S.; Bao, Z. Weighted least-squares estimation of phase errors for SAR/ISAR autofocus. IEEE Trans. Geosci. Remote Sens. 1999, 37, 2487–2494. [Google Scholar] [CrossRef]
- Zhu, D.; Jiang, R.; Mao, X.; Zhu, Z. Multi-Subaperture PGA for SAR Autofocusing. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 468–488. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, M.; Wang, G.; Wang, H. Range-Dependent Map-Drift Algorithm for Focusing UAV SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2016, 13, 1158–1162. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Z.; Zhou, Y.; Wang, P.; Qiu, J. A Novel Motion Compensation Scheme for Airborne Very High Resolution SAR. Remote Sens. 2021, 13, 2729. [Google Scholar] [CrossRef]
- Tong, X.; Bao, M.; Sun, G.; Han, L.; Zhang, Y.; Xing, M. Refocusing of Moving Ships in Squint SAR Images Based on Spectrum Orthogonalization. Remote Sens. 2021, 13, 2807. [Google Scholar] [CrossRef]
- Chen, M.; Qiu, X.; Li, R.; Li, W.; Fu, K. Analysis and Compensation for Systematical Errors in Airborne Microwave Photonic SAR Imaging by 2-D Autofocus. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 2221–2236. [Google Scholar] [CrossRef]
- Wahl, D.; Eichel, P.; Ghiglia, D.; Jakowatz, C. Phase gradient autofocus-a robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 827–835. [Google Scholar] [CrossRef]
- Thompson, D.G.; Bates, J.S.; Arnold, D.V. Extending the phase gradient autofocus algorithm for low-altitude stripmap mode SAR. In Proceedings of the 1999 IEEE Radar Conference, Radar into the Next Millennium (Cat. No. 99CH36249), Waltham, MA, USA, 22 April 1999. [Google Scholar]
- Zhang, L.; Qiao, Z.; Xing, M.; Yang, L.; Bao, Z. A robust motion compensation approach for UAV SAR imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Evers, A.; Jackson, J.A. A Generalized Phase Gradient Autofocus Algorithm. IEEE Trans. Comput. Imaging 2019, 5, 606–619. [Google Scholar] [CrossRef]
- Franceschetti, G.; Lanari, R. Synthetic Aperture Radar Processing; CRC Press: Boca Raton, FL, USA, 1999. [Google Scholar]
- Samczynski, P.; Kulpa, K.S. Coherent mapdrift technique. IEEE Trans. Geosci. Remote Sens. 2009, 48, 1505–1517. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, B.; Xing, M.; Bao, Z.; Guo, L. The space-variant phase-error matching map-drift algorithm for highly squinted SAR. IEEE Geosci. Remote Sens. Lett. 2012, 10, 845–849. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, F.; Chen, Z.; Li, J.; Hong, W. An improved map-drift algorithm for unmanned aerial vehicle SAR imaging. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1966–1970. [Google Scholar]
- Liu, M.; Li, C.; Shi, X. A back-projection fast autofocus algorithm based on minimum entropy for SAR imaging. In Proceedings of the 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Republic of Korea, 26–30 September 2011. [Google Scholar]
- Yang, L.; Xing, M.; Zhang, L.; Sheng, J.; Bao, Z. Entropy-based motion error correction for high-resolution spotlight SAR imagery. IET Radar Sonar Navig. 2012, 6, 627–637. [Google Scholar] [CrossRef]
- Xiong, T.; Xing, M.; Wang, Y.; Wang, S.; Sheng, J.; Guo, L. Minimum-entropy-based autofocus algorithm for SAR data using chebyshev approximation and method of series reversion, and its implementation in a data processor. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1719–1728. [Google Scholar] [CrossRef]
- Fienup, J.R.; Miller, J.J. Aberration correction by maximizing generalized sharpness metrics. J. Opt. Soc. Am. A 2003, 20, 609–620. [Google Scholar] [CrossRef] [PubMed]
- Schulz, T.J. Optimal sharpness function for SAR autofocus. IEEE Signal Process. Lett. 2006, 14, 27–30. [Google Scholar] [CrossRef]
- Ash, J.N. An autofocus method for backprojection imagery in synthetic aperture radar. IEEE Geosci. Remote Sens. Lett. 2011, 9, 104–108. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Pu, W.; Li, Z.; Yang, J. An effective autofocus method for fast factorized back-projection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6145–6154. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X.; Jin, T.; Xue, G.; Zhou, Z. An interpolated phase adjustment by contrast enhancement algorithm for SAR. IEEE Geosci. Remote Sens. Lett. 2010, 8, 211–215. [Google Scholar]
- Zhang, T.; Liao, G.; Li, Y.; Gu, T.; Zhang, T.; Liu, Y. A two-stage time-domain autofocus method based on generalized sharpness metrics and AFBP. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–13. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Sun, G.-C.; Li, Z. A 2-D space-variant motion estimation and compensation method for ultrahigh-resolution airborne stepped-frequency SAR with long integration time. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6390–6401. [Google Scholar] [CrossRef]
- Chen, J.; Xing, M.; Yu, H.; Liang, B.; Peng, J.; Sun, G.-C. Motion compensation/autofocus in airborne synthetic aperture radar: A review. IEEE Geosci. Remote Sens. Mag. 2022, 10, 185–206. [Google Scholar] [CrossRef]
- Xing, M.; Jiang, X.; Wu, R.; Zhou, F.; Bao, Z. Motion compensation for UAV SAR based on raw radar data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2870–2883. [Google Scholar] [CrossRef]
- Bezvesilniy, O.O.; Gorovyi, I.M.; Vavriv, D.M. Autofocusing SAR images via local estimates of flight trajectory. Int. J. Microw. Wirel. Technol. 2016, 8, 881–889. [Google Scholar] [CrossRef]
- Liang, Y.; Li, G.; Wen, J.; Zhang, G.; Dang, Y.; Xing, M. A Fast Time-Domain SAR Imaging and Corresponding Autofocus Method Based on Hybrid Coordinate System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8627–8640. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Wang, Y.; Wang, Q. A robust motion error estimation method based on raw data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2780–2790. [Google Scholar] [CrossRef]
- Li, J.; Chen, J.; Wang, P.; Loffeld, O. A coarse-to-fine autofocus approach for very high-resolution airborne stripmap SAR imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 3814–3829. [Google Scholar] [CrossRef]
- Ding, Z.; Li, L.; Wang, Y.; Zhang, T.; Gao, W.; Zhu, K.; Zeng, T.; Yao, D. An autofocus approach for UAV-based ultrawideband ultrawidebeam SAR data with frequency-dependent and 2-D space-variant motion errors. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–18. [Google Scholar] [CrossRef]
- Sjanic, Z.; Gustafsson, F. Simultaneous navigation and SAR auto-focusing. In Proceedings of the 2010 13th International Conference on Information Fusion, Edinburgh, UK, 26–29 July 2010. [Google Scholar]
- Pu, W.; Wu, J.; Huang, Y.; Yang, J.; Yang, H. Fast Factorized Backprojection Imaging Algorithm Integrated With Motion Trajectory Estimation for Bistatic Forward-Looking SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3949–3965. [Google Scholar] [CrossRef]
- Ran, L.; Liu, Z.; Zhang, L.; Li, T.; Xie, R. An Autofocus Algorithm for Estimating Residual Trajectory Deviations in Synthetic Aperture Radar. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3408–3425. [Google Scholar] [CrossRef]
- Zhang, T.; Liao, G.; Li, Y.; Gu, T.; Zhang, T.; Liu, Y. An Improved Time-Domain Autofocus Method Based on 3-D Motion Errors Estimation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Torgrimsson, J.; Dammert, P.; Hellsten, H.; Ulander, L.M.H. Factorized Geometrical Autofocus for Synthetic Aperture Radar Processing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6674–6687. [Google Scholar] [CrossRef]
- Torgrimsson, J.; Dammert, P.; Hellsten, H.; Ulander, L.M.H. An Efficient Solution to the Factorized Geometrical Autofocus Problem. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4732–4748. [Google Scholar] [CrossRef]
- Torgrimsson, J.; Dammert, P.; Hellsten, H.; Ulander, L.M.H. SAR Processing Without a Motion Measurement System. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1025–1039. [Google Scholar] [CrossRef]
- Li, J.; Wang, P.; Li, C.; Chen, J.; Yang, W. Precise estimation of flight path for airborne SAR motion compensation. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014. [Google Scholar]
- Dadi, M.; Donghui, H.U.; Chibiao, D. A new approach to airborne high Resolution SAR motion compensation for large trajectory deviations. Chin. J. Electron. 2012, 21, 764–769. [Google Scholar]
- Yang, M.; Zhu, D.; Song, W. Comparison of two-step and one-step motion compensation algorithms for airborne synthetic aperture radar. Electron. Lett. 2015, 51, 1108–1110. [Google Scholar] [CrossRef]
- Zhang, L.; Sheng, J.; Xing, M.; Qiao, Z.; Xiong, T.; Bao, Z. Wavenumber-Domain Autofocusing for Highly Squinted UAV SAR Imagery. IEEE Sens. J. 2012, 12, 1574–1588. [Google Scholar] [CrossRef]
- Reigber, A.; Alivizatos, E.; Potsis, A.; Moreira, A. Extended wavenumber-domain synthetic aperture radar focusing with integrated motion compensation. IEE Proc.-Radar Sonar Navig. 2006, 153, 301–310. [Google Scholar] [CrossRef]
- Xing, M.; Wu, Y.; Zhang, Y.D.; Sun, G.C.; Bao, Z. Azimuth Resampling Processing for Highly Squinted Synthetic Aperture Radar Imaging With Several Modes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4339–4352. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture Radar Data: Algorithms and Implementation; Artech House: Norwood, MA, USA, 2005. [Google Scholar]

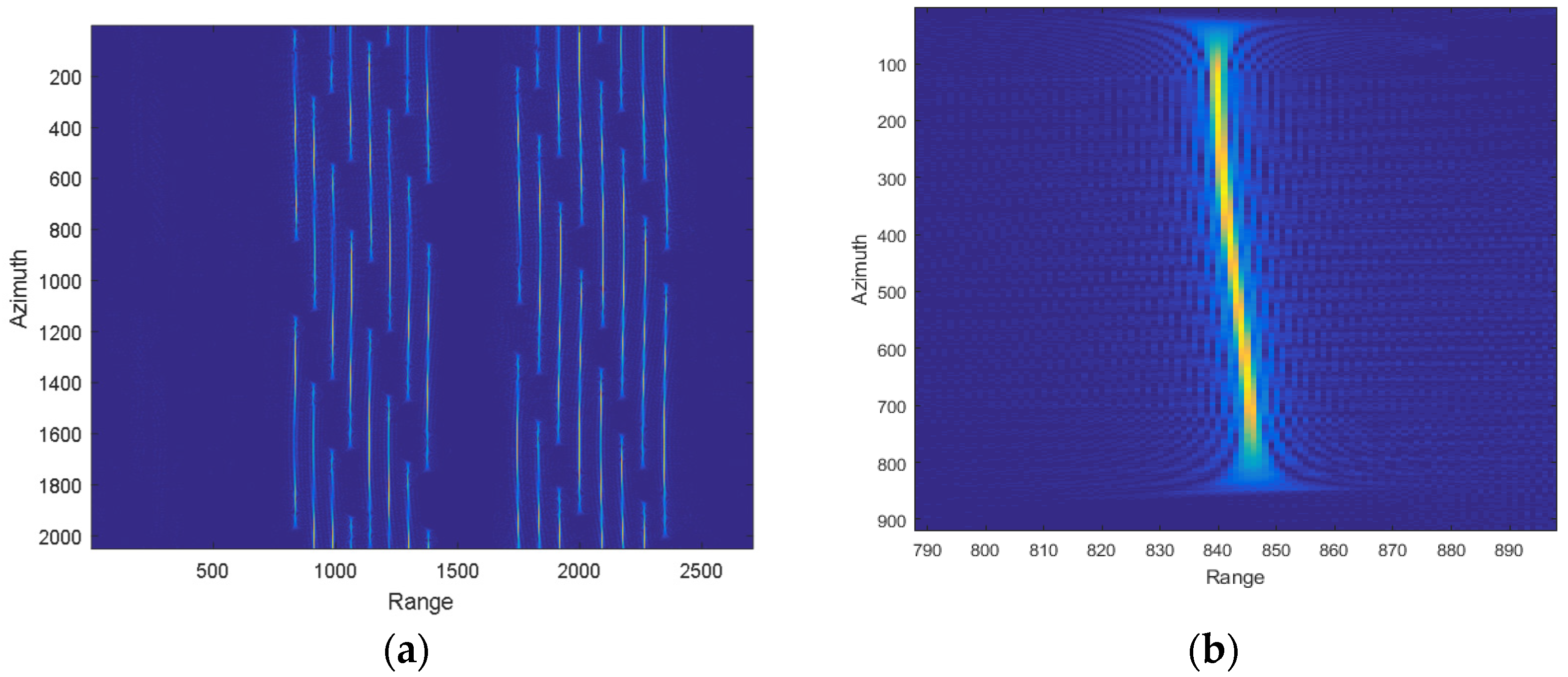
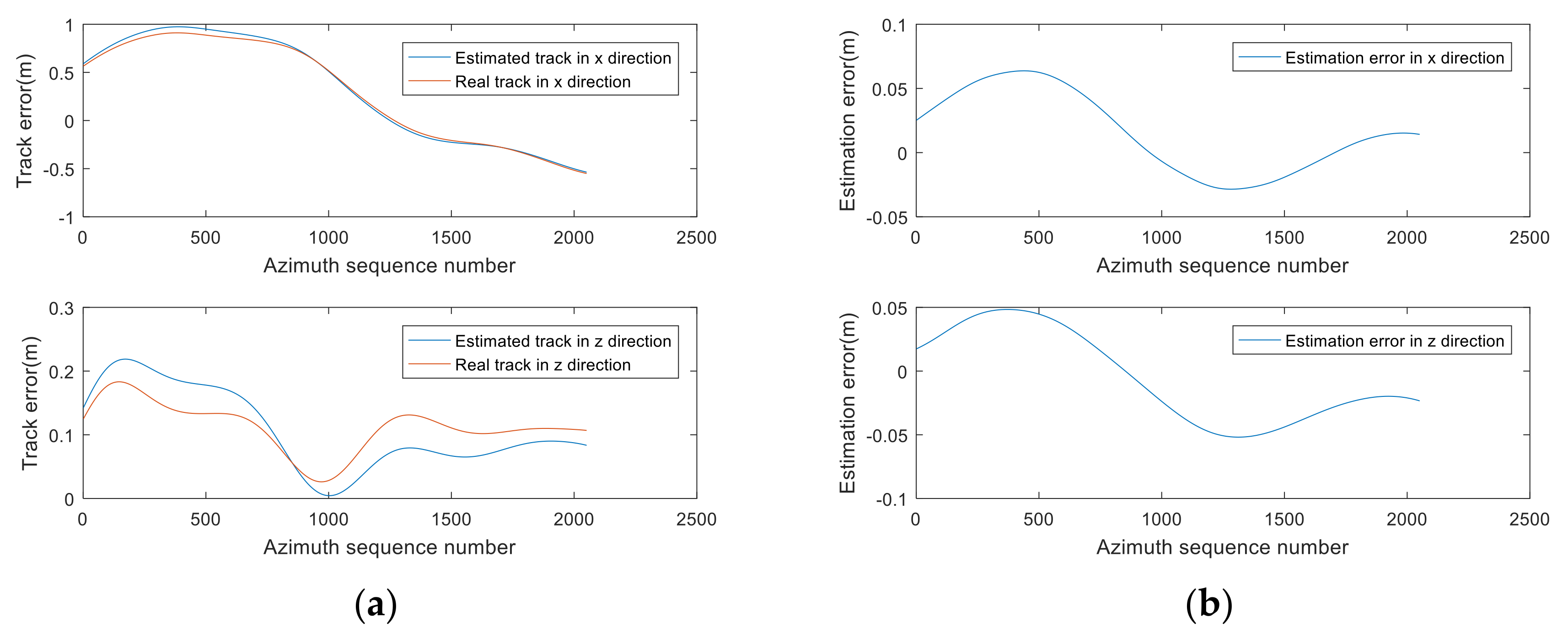
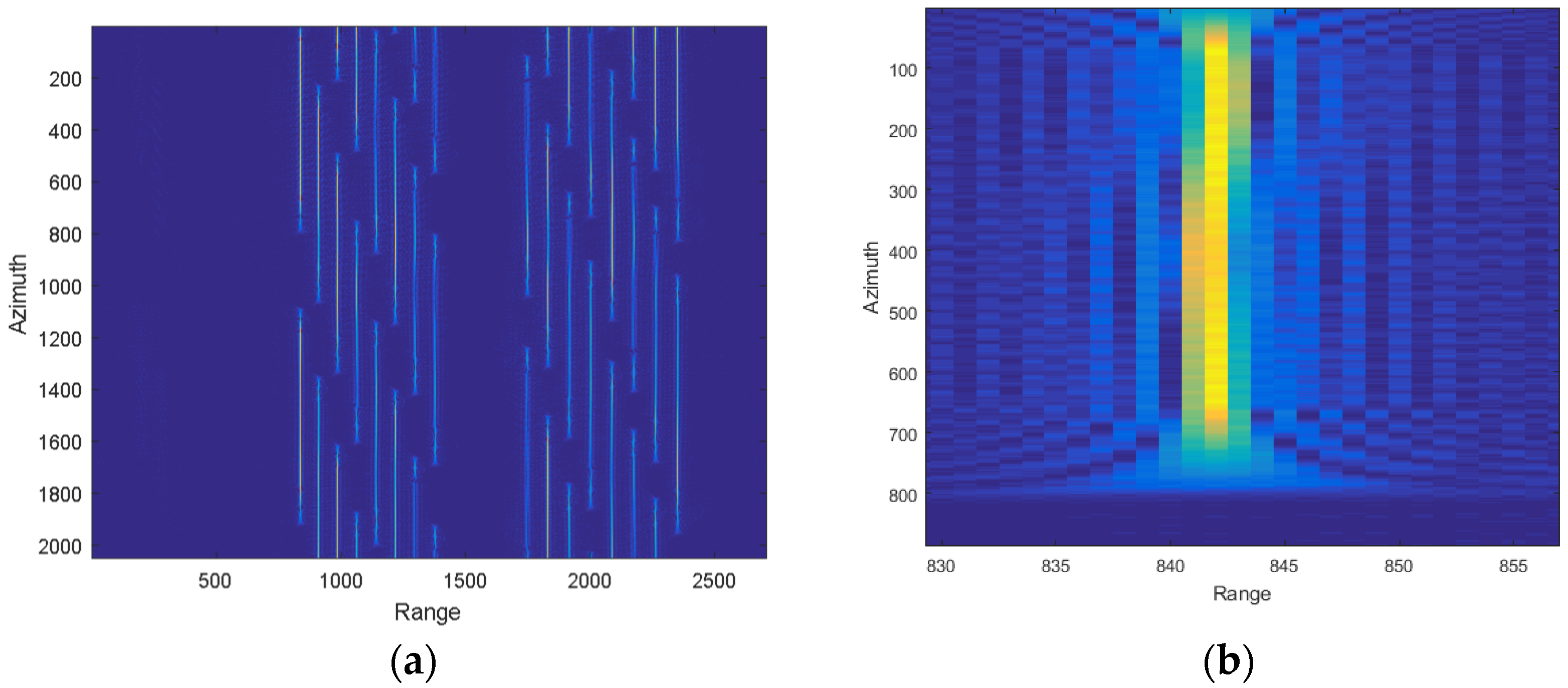
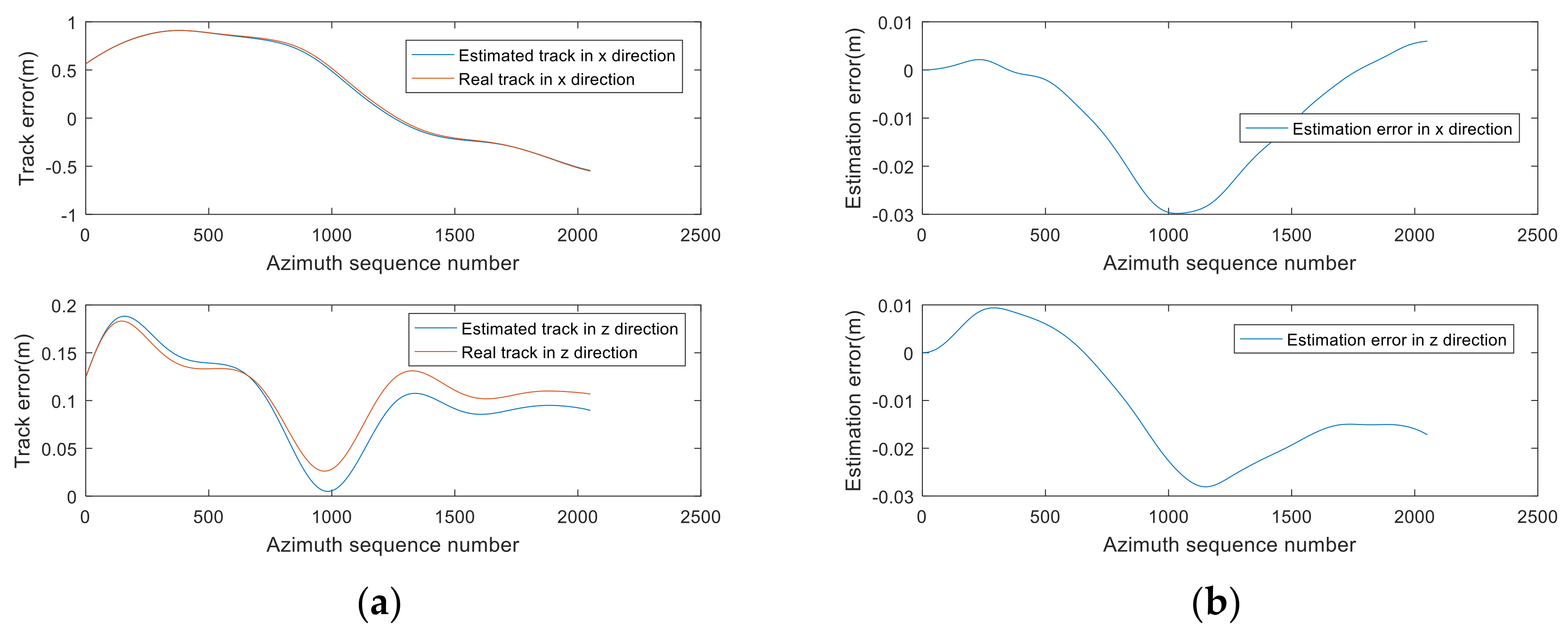




| Parameter | Value |
|---|---|
| carrier frequency | 15.2 GHz |
| wavelength | 0.0197 m |
| bandwidth | 1.2 GHz |
| velocity | 10.034 m/s |
| height | 411.024 m |
| squint angle | −7° |
| PRF | 250 Hz |
| Parameter | Value |
|---|---|
| carrier frequency | 9.6 GHz |
| wavelength | 0.0312 m |
| bandwidth | 810 MHz |
| velocity | 98.187 m/s |
| height | 4288.56 m |
| squint angle | 1.71° |
| PRF | 1000 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, M.; Qiu, X.; Cheng, Y.; Chen, M.; Ding, C. A Robust Track Estimation Method for Airborne SAR Based on Weak Navigation Information and Additional Envelope Errors. Remote Sens. 2024, 16, 625. https://doi.org/10.3390/rs16040625
Gao M, Qiu X, Cheng Y, Chen M, Ding C. A Robust Track Estimation Method for Airborne SAR Based on Weak Navigation Information and Additional Envelope Errors. Remote Sensing. 2024; 16(4):625. https://doi.org/10.3390/rs16040625
Chicago/Turabian StyleGao, Ming, Xiaolan Qiu, Yao Cheng, Min Chen, and Chibiao Ding. 2024. "A Robust Track Estimation Method for Airborne SAR Based on Weak Navigation Information and Additional Envelope Errors" Remote Sensing 16, no. 4: 625. https://doi.org/10.3390/rs16040625
APA StyleGao, M., Qiu, X., Cheng, Y., Chen, M., & Ding, C. (2024). A Robust Track Estimation Method for Airborne SAR Based on Weak Navigation Information and Additional Envelope Errors. Remote Sensing, 16(4), 625. https://doi.org/10.3390/rs16040625






