Gridless Underdetermined DOA Estimation for Mobile Agents with Limited Snapshots Based on Deep Convolutional Generative Adversarial Network
Abstract
:1. Introduction
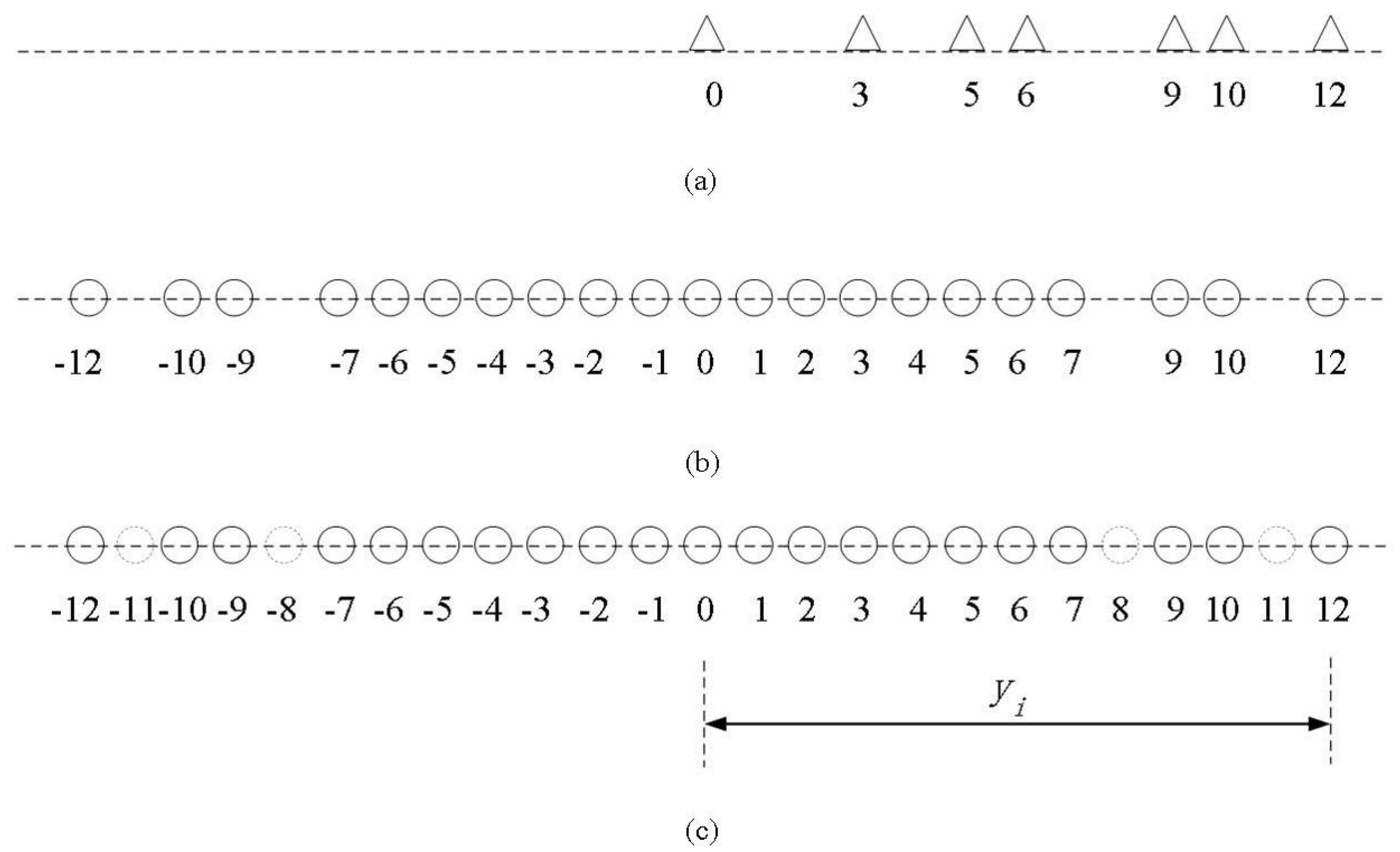
2. Signal Model
3. The Proposed Method
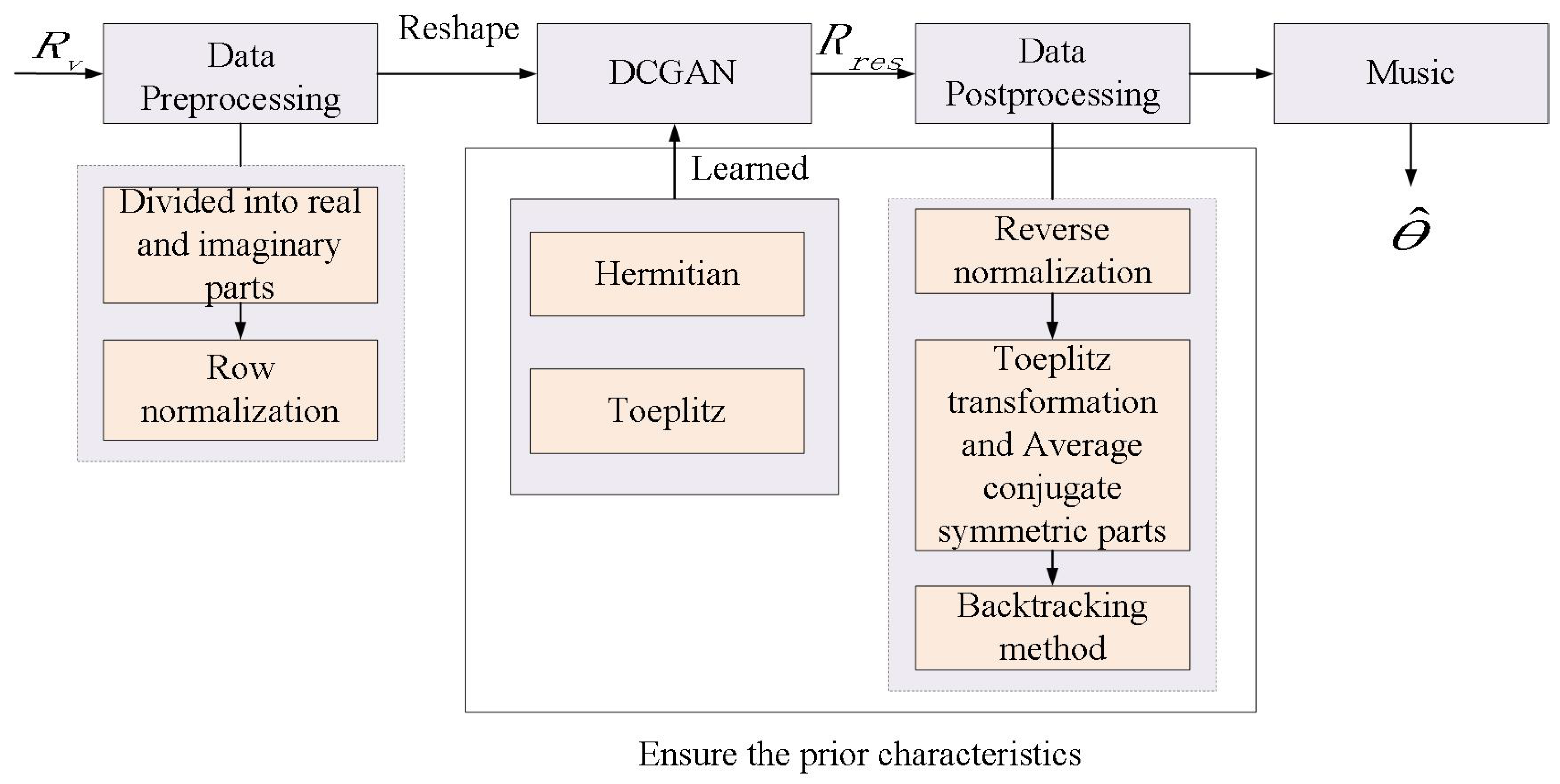
3.1. Data Preprocessing
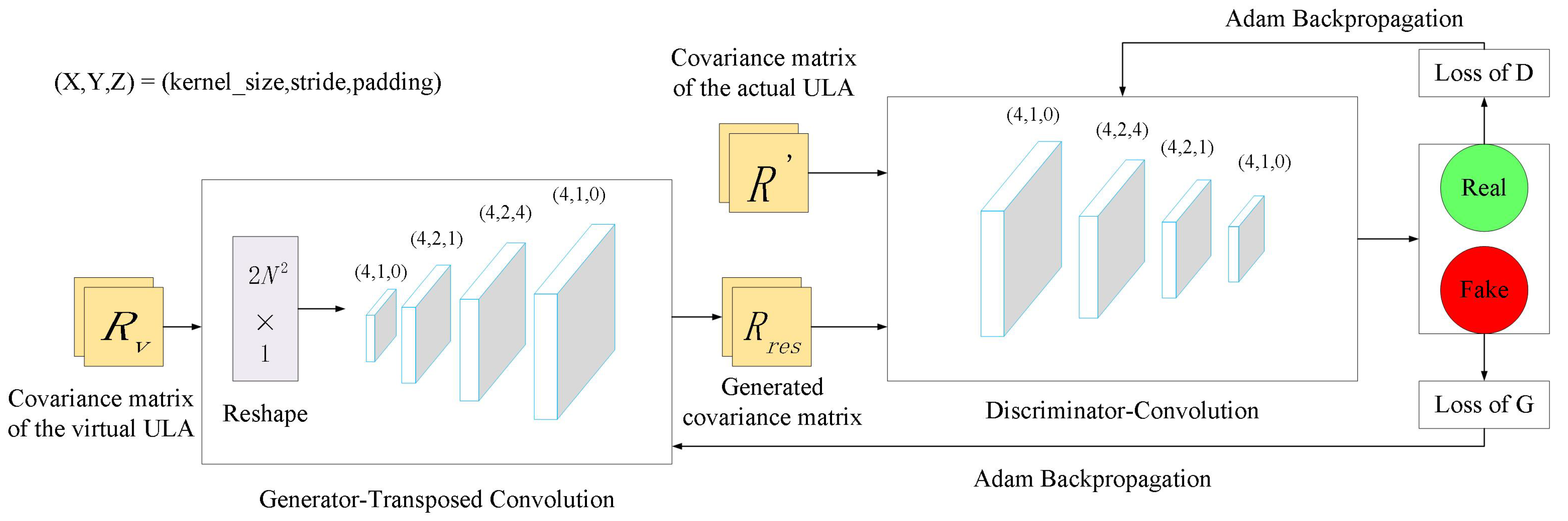
3.2. DCGAN Structure
3.3. Data Post-Processing
4. Training Approach
4.1. Loss Function
4.2. DCGAN Training
5. Simulation Results
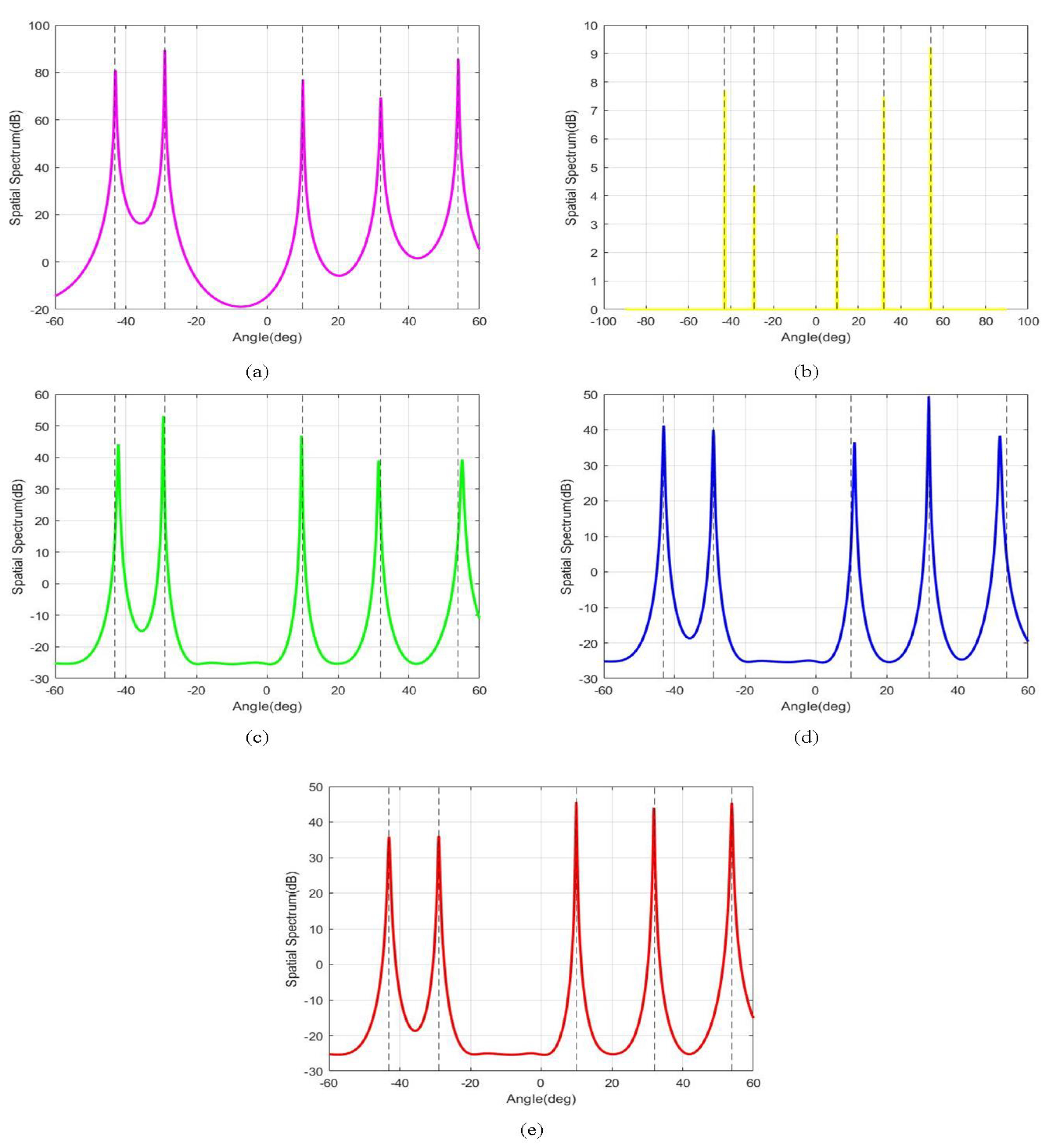
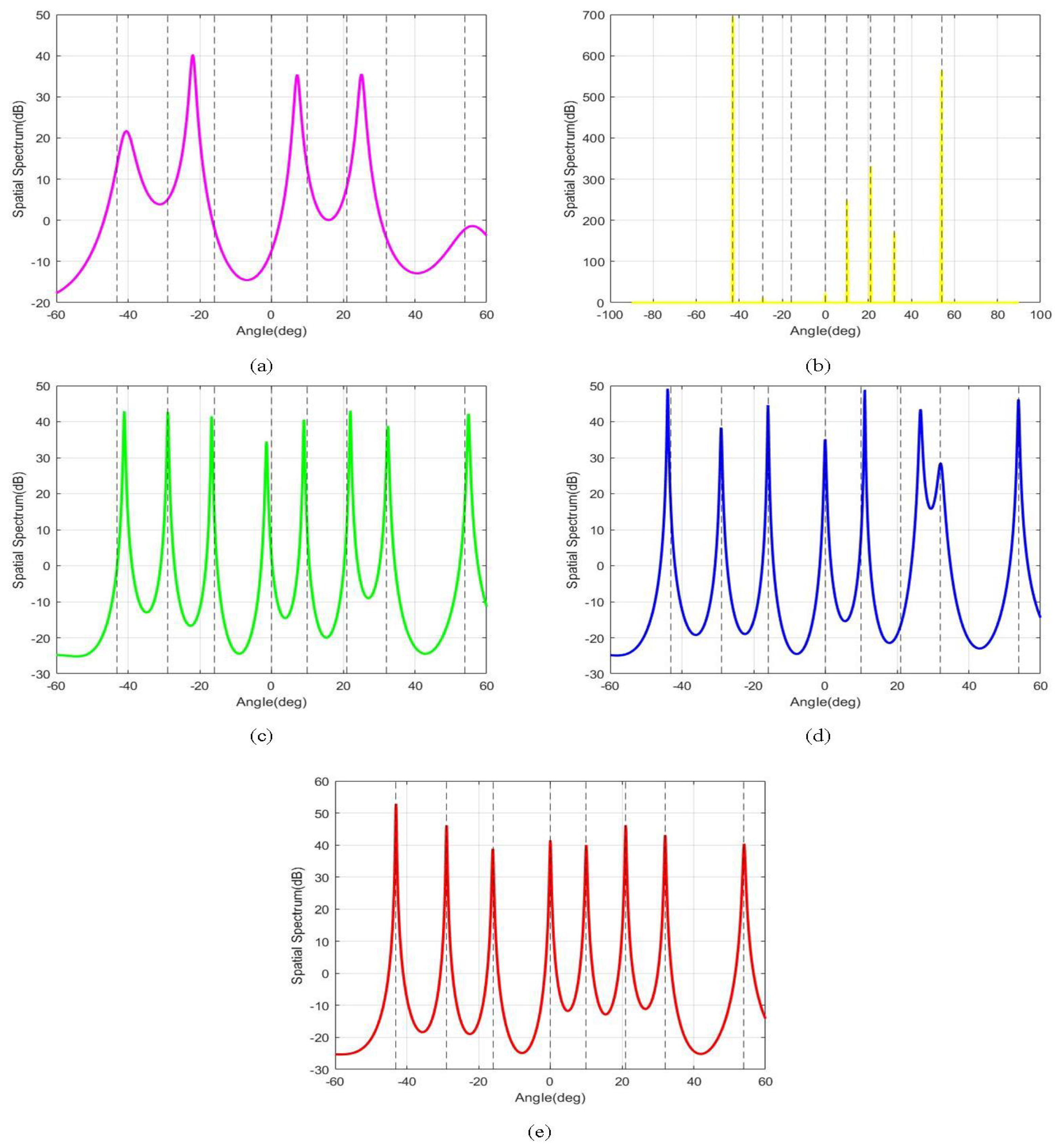
5.1. Single Experiment Results
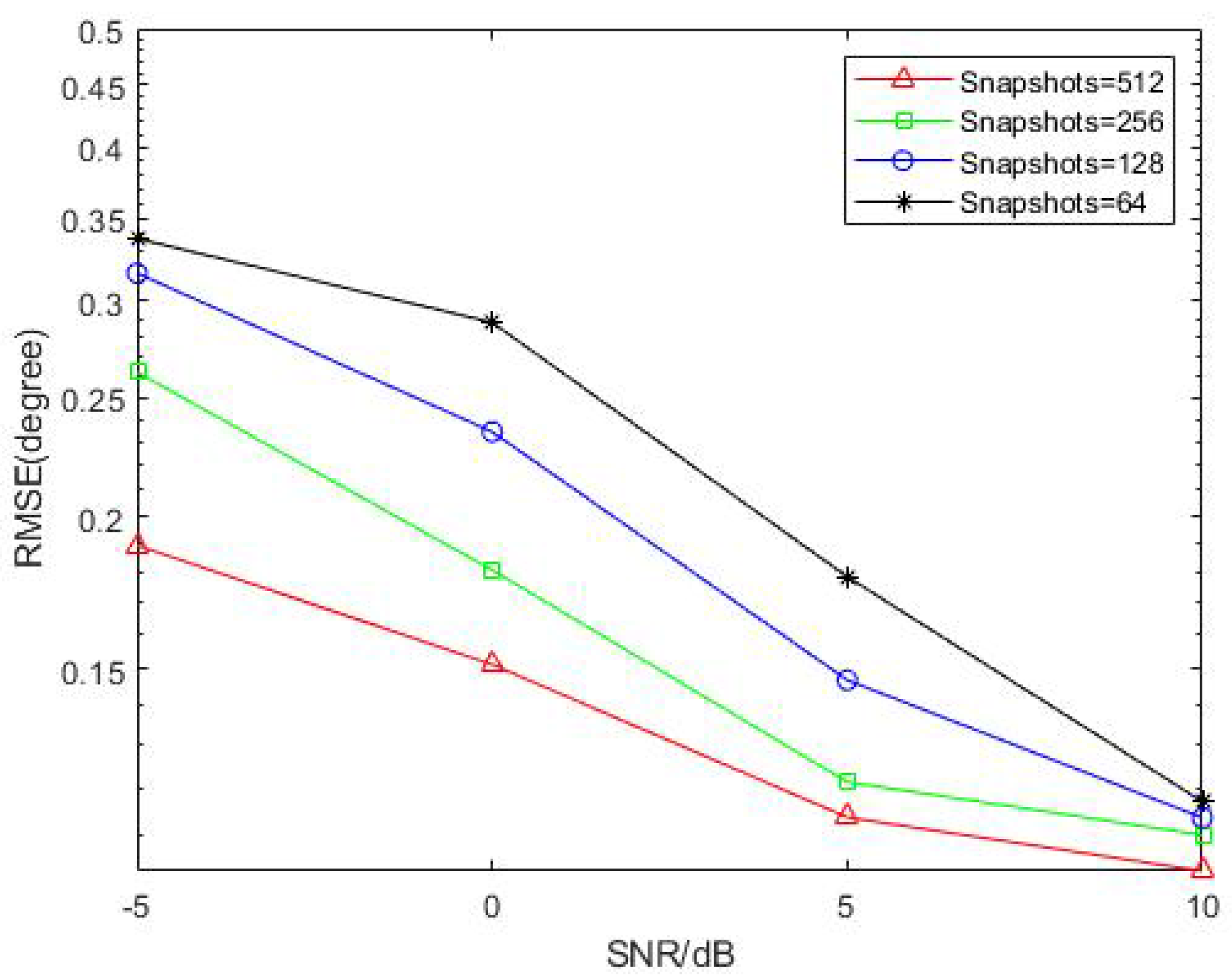
5.2. Quantitative Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Florio, A.; Avitabile, G.; Talarico, C.; Coviello, G. A Reconfigurable Full-Digital Architecture for Angle of Arrival Estimation. IEEE Trans. Circuits Syst. Regul. Pap. 2023, in press. [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Ye, Z.; Xu, X. DOA Estimation by Exploiting the Symmetric Configuration of Uniform Linear Array. IEEE Trans. Antennas Propag. 2007, 55, 3716–3720. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, K.; Wang, J. Direction-of-arrival estimation for coherent GPS signals based on oblique projection. Signal Process. 2012, 92, 294–299. [Google Scholar] [CrossRef]
- El Zooghby, A.H.; Christodoulou, C.G.; Georgiopoulos, M. Performance of radial-basis function networks for direction of arrival estimation with antenna arrays. IEEE Trans. Antennas Propag. 1997, 45, 1611–1617. [Google Scholar] [CrossRef]
- Shieh, C.; Lin, C. Direction of arrival estimation based on phase differences using neural fuzzy network. IEEE Trans. Antennas Propag. 2000, 48, 1115–1124. [Google Scholar] [CrossRef]
- Liu, Z.-M.; Zhang, C.; Yu, P.S. Direction-of-Arrival Estimation Based on Deep Neural Networks with Robustness to Array Imperfections. IEEE Trans. Antennas Propag. 2018, 66, 7315–7327. [Google Scholar] [CrossRef]
- Papageorgiou, G.K.; Sellathurai, M.; Eldar, Y.C. Deep Networks for Direction-of-Arrival Estimation in Low SNR. IEEE Trans. Signal Process. 2021, 69, 3714–3729. [Google Scholar] [CrossRef]
- Wu, L.; Liu, Z.-M.; Huang, Z.-T. Deep Convolution Network for Direction of Arrival Estimation with Sparse Prior. IEEE Signal Process. Lett. 2019, 26, 1688–1692. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, B.; Yang, T.; Liu, D. Phase enhancement model based on supervised convolutional neural network for coherent DOA estimation. Appl. Intell. 2020, 50, 2411–2422. [Google Scholar] [CrossRef]
- Lima de Oliveira, M.L.; Bekooij, M.J.G. ResNet Applied for a Single-Snapshot DOA Estimation. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar]
- Peng, J.; Nie, W.; Li, T.; Xu, J. An end-to-end DOA estimation method based on deep learning for underwater acoustic array. In Proceedings of the OCEANS 2022, Hampton Roads, VA, USA, 17–20 October 2022; pp. 1–6. [Google Scholar]
- Cao, Y.; Lv, T.; Lin, Z.; Huang, P.; Lin, F. Complex ResNet Aided DoA Estimation for Near-Field MIMO Systems. IEEE Trans. Veh. Technol. 2020, 69, 11139–11151. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, G.; Zhan, C.; Zhang, Y. DOA Estimation Method Based on Improved Deep Convolutional Neural Network. Sensors 2022, 22, 1305. [Google Scholar] [CrossRef]
- Xiang, H.; Chen, B.; Yang, M.; Xu, S. Angle Separation Learning for Coherent DOA Estimation with Deep Sparse Prior. IEEE Commun. Lett. 2021, 25, 465–469. [Google Scholar] [CrossRef]
- Fang, W.; Cao, Z.; Yu, D.; Wang, X.; Ma, Z.; Lan, B.; Xu, Z. A Lightweight Deep Learning-Based Algorithm for Array Imperfection Correction and DOA Estimation. J. Commun. Inf. Netw. 2022, 7, 296–308. [Google Scholar] [CrossRef]
- Yao, Y.; Lei, H.; He, W. Wideband DOA Estimation Based on Deep Residual Learning with Lyapunov Stability Analysis. IEEE Geosci. Remote. Sens. Lett. 2022, 19, 8014505. [Google Scholar] [CrossRef]
- Gao, S.; Ma, H.; Liu, H.; Yang, J.; Yang, Y. A Gridless DOA Estimation Method for Sparse Sensor Array. Remote Sens. 2023, 15, 5281. [Google Scholar] [CrossRef]
- Wu, X.; Yang, X.; Jia, X.; Tian, F. A Gridless DOA Estimation Method Based on Convolutional Neural Network with Toeplitz Prior. IEEE Signal Process. Lett. 2022, 29, 1247–1251. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Liu, L.; Rao, Z. An Adaptive Lp Norm Minimization Algorithm for Direction of Arrival Estimation. Remote Sens. 2022, 14, 766. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Shi, Z.; Zhang, Y.D. Off-Grid Direction-of-Arrival Estimation Using Coprime Array Interpolation. IEEE Signal Process. Lett. 2018, 25, 1710–1714. [Google Scholar] [CrossRef]



| Method | −5 dB | 0 dB | 5 dB | 10 dB |
|---|---|---|---|---|
| SR-D | 5890 s | 5290 s | 5720 s | 5810 s |
| CNN-D | 216.5672 s | 209.0678 s | 184.01 s | 171.723 s |
| Proposed | 192.8996 s | 179.845 s | 172.8436 s | 171.667 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Yang, F.; Zhou, M.; Hao, L.; Wang, J.; Sun, H.; Kong, A.; Qi, J. Gridless Underdetermined DOA Estimation for Mobile Agents with Limited Snapshots Based on Deep Convolutional Generative Adversarial Network. Remote Sens. 2024, 16, 626. https://doi.org/10.3390/rs16040626
Cui Y, Yang F, Zhou M, Hao L, Wang J, Sun H, Kong A, Qi J. Gridless Underdetermined DOA Estimation for Mobile Agents with Limited Snapshots Based on Deep Convolutional Generative Adversarial Network. Remote Sensing. 2024; 16(4):626. https://doi.org/10.3390/rs16040626
Chicago/Turabian StyleCui, Yue, Feiyu Yang, Mingzhang Zhou, Lianxiu Hao, Junfeng Wang, Haixin Sun, Aokun Kong, and Jiajie Qi. 2024. "Gridless Underdetermined DOA Estimation for Mobile Agents with Limited Snapshots Based on Deep Convolutional Generative Adversarial Network" Remote Sensing 16, no. 4: 626. https://doi.org/10.3390/rs16040626
APA StyleCui, Y., Yang, F., Zhou, M., Hao, L., Wang, J., Sun, H., Kong, A., & Qi, J. (2024). Gridless Underdetermined DOA Estimation for Mobile Agents with Limited Snapshots Based on Deep Convolutional Generative Adversarial Network. Remote Sensing, 16(4), 626. https://doi.org/10.3390/rs16040626







