A Novel Fully Convolutional Auto-Encoder Based on Dual Clustering and Latent Feature Adversarial Consistency for Hyperspectral Anomaly Detection
Abstract
:1. Introduction
- (1)
- The deep network for hyperspectral anomaly detection lacks a clear learning direction and merely relies on the assumption of high reconstruction errors to identify anomalies that fail to meet the requirements of diverse hyperspectral anomaly detection scenarios. It is urgent for us to develop a method that provides a learning approach for a hyperspectral anomaly-detection deep network that includes guidance for its training phase.
- (2)
- The current state-of-the-art methods of hyperspectral anomaly detection primarily rely on pixel-level spectral reconstruction for deep learning-based methods, which inappropriately comes to terms with the spatial structure of HSI and interferes with the deep network’s ability to learn any spatial features. In reality, spatial information plays a crucial role in hyperspectral anomaly detection. The lack of spatial structure analysis brings limitations to the detection performance of certain existing approaches.
- (3)
- The background of HSI is inherently multivariate and complex. However, most traditional and deep learning-based methods still assume a multivariate normal distribution for the hyperspectral background. This assumption does not always hold true for the real-world complex background of HSI, in which existing algorithms are inadequate for adapting to such scenes. As a result, applications of these hyperspectral anomaly detection methods are mostly limited to simple scenarios.
- (1)
- A novel fully convolutional auto-encoder is proposed to make full use of spatial information to assist hyperspectral anomaly detection tasks to achieve a joint anomaly detection process with a spatial structure.
- (2)
- A novel module for extracting prior knowledge that combines the DBSCAN and connected component analysis clustering is designed to guide deep network learning by extracting background and anomaly samples. This ensures that the proposed deep network has a clear learning direction. Additionally, the induction of triplet loss helps separate the distance between the background and anomaly. Hence, it enhances the separability between the background and anomaly.
- (3)
- To overcome the limitations of assuming a specific distribution for the background and achieve a more accurate reconstruction for the pure background, we propose a latent feature adversarial consistency network. This network aims to learn the true distribution of the real background and employs an adversarial consistency enhancement loss to strengthen the constraints for reconstructing a purer background.
2. Proposed Method
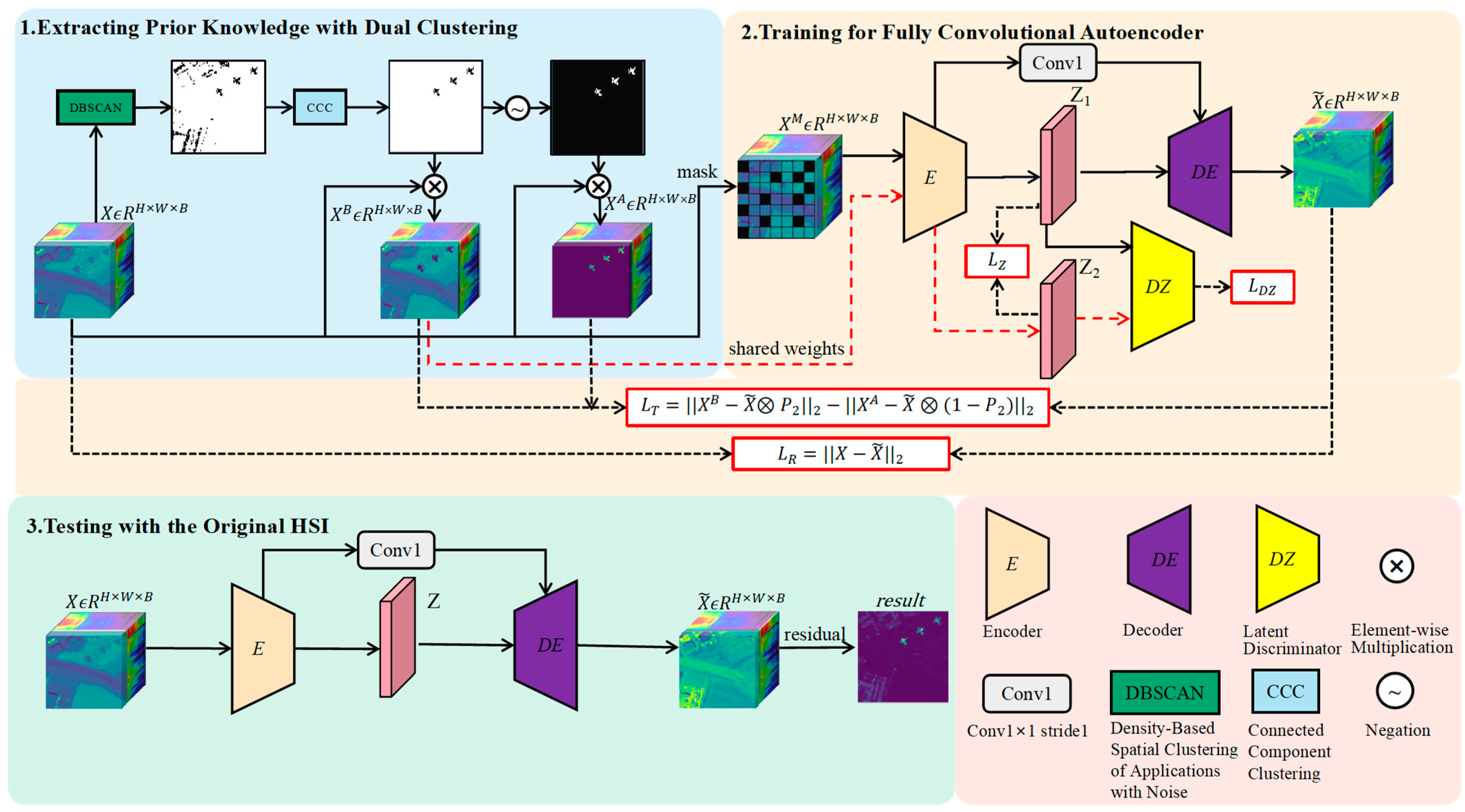
2.1. Overview
- (1)
- Extracting Prior Knowledge with Dual Clustering: The purpose of dual clustering is to obtain coarse labels for supervised network learning and provide the network with a clear learning direction to enhance its performance. Dual clustering (i.e., unsupervised DBSCAN and connected domain analysis clustering) techniques can be employed to cluster the HSI from the spectral domain to the spatial domain, which yields preliminary separation results between the background and anomaly regions. Subsequently, prior samples representing the background and anomaly regions are obtained through this processing, which effectively purifies the supervision information provided to the deep network by conveying more background-related information as well as anomaly related information. These anomaly features are then utilized to suppress anomaly generation while the background features contribute toward reconstructing most of the background.
- (2)
- Training for the Fully Convolutional Auto-Encoder: The prior background and anomaly samples extracted in the first stage are used as training data for the training of a fully convolutional auto-encoder model. During the training phase, the original hyperspectral information is input into a fully convolutional deep network using a mask strategy while an adversarial consistency network is employed to learn the true background distribution and suppress anomaly generation. Finally, by leveraging self-supervision learning as a foundation, the whole deep network is guided to learn by incorporating triplet loss and adversarial consistency loss. Additionally, a spatial and spectral joint attention mechanism is utilized in both the encoder and decoder stages to enable adaptive learning for spatial and spectral focus.
- (3)
- Testing with the Original Hyperspectral Imagery: The parameters of the proposed deep network are fixed, and the original hyperspectral imagery is fed into the trained network for reconstructing the expected background for hyperspectral imagery. At this stage, the deep network only consists of an encoder and a decoder. The reconstruction error serves as the final detection result of the proposed hyperspectral anomaly detection method.
2.2. Extracting Prior Knowledge with Dual Clustering
2.3. Training for Fully Convolutional Auto-Encoder
2.3.1. Data Augmentation
2.3.2. Network Architecture
- (1)
- Fully Convolutional Auto-Encoder (FCAE): Previous deep learning-based hyperspectral anomaly detection methods, such as GAED [45], employ fully connected layers for pixel-wise self-supervised learning of HSI on the spectral dimension. However, these methods result in the degradation of the spatial structure within HSI, which leads to a significant loss of spatial information and underutilization of the spatial characteristics of the original HSI. Additionally, dealing with input hyperspectral images in pixel-by-pixel mode prevents the deep network from capturing spectral correlations between adjacent pixels, which results in isolated features and limited information acquisition. A straightforward improvement can be observed in Auto-AD [48], in which a convolutional auto-encoder (CAE) is utilized for the self-supervised learning of the HSI cube. By incorporating convolution operations, pooling operations, and sampling operations into AE architecture, the CAE not only extracts spatial features effectively but also enhances spectral feature correlation.
- (2)
- Latent Feature Adversarial Consistency Network (LFACN): The latent feature adversarial consistency network, as illustrated in Figure 4a, comprises an encoder and a discriminator for the latent features. The input samples and the prior background samples are mapped to latent features and , respectively, through an encoder with shared weights. In order to ensure that the latent features of the background exhibit similar distributions, we employ a latent feature discriminator to oppose the encoder, which makes the latent feature of the input resemble the hyperspectral image as closely as possible to the latent feature in adversarial situations. This approach directly results in the true distribution of the background. All the inputs can then be effectively mapped to similar background latent features. Thereby, this approach enables accurate decoding of the corresponding pure background. Moreover, the latent feature , which is obtained by mapping the reconstructed background through the encoder , could also exhibit more similarity to the latent feature of the prior background samples . However, due to the deep network’s inability to guarantee this point, a latent feature consistency loss is employed in order to strengthen the constraint.
2.3.3. Learning Procedure
| Algorithm 1 Algorithm Flow Diagram of the FCAE-DCAC |
| Input: The original HSI Parameters: Epoch, learning rate , (eps, mints), D, , and Output: Final detection result: Stage 1: Extracting Prior Knowledge with Dual Clustering Obtain the prior anomaly samples , the prior background sample , and the coarse label by (Equations (1)–(3)) Stage 2: Training for Fully Convolutional Auto-Encoder Acquire training samples by (Equation (4)) Initialize the network with random weights for each epoch perform the following: FCAE update: by Latent Feature Adversarial Consistency Network update: by back-propagate and to change end Stage 3: Testing with the Original HSI Obtain the reconstructed HSI using the Original HSI as input by (Equation (12)) Calculate the degree of anomaly for each pixel in by (Equation (13)) |
2.4. Testing with the Original HSI
3. Experiments and Analysis
3.1. Data Description
- (1)
- San Diego Dataset: This dataset was acquired by the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) hyperspectral sensor over the San Diego airport area, CA, USA. The spatial resolution is 3.5 m. Its original size was 400 × 400 as depicted in Figure 5a. The image consists of a total of 224 spectral bands within the range of 370–2510 nm with 189 remaining after excluding bands that were affected by water absorption and low signal-to-noise ratio. Within this dataset, three regions named San Diego-1, San Diego-2, and San Diego-3 were selected. Figure 5b–d display the pseudocolor images and the ground-truth maps of these datasets. The image size of San Diego-1 is 100 × 100 and it contains three aircraft with different sizes that are considered anomaly targets. These anomaly targets comprise a total of 58 pixels, which account for 0.58% of the entire image. The image size of San Diego-2 is 60 × 60. Tarp, building, and shadow are the background land covers. Within this image, there are 22 densely distributed targets identified as anomalies. These anomaly targets comprise a total of 214 pixels, which account for 5.94% of the entire image. Similarly, the image size of San Diego-3 is 40 × 90 with a tarp, building, and shadow as background. In this image, there are 21 densely distributed targets identified as anomaly targets. These anomaly targets comprise a total of 423 pixels, which account for 11.75% of the entire image. It should be noted that the spectral curves of the building in the upper right corner significantly differ from other background features in the San Diego-2 image. Furthermore, the proportion occupied by this building is not as substantial as the other two types of background. Consequently, there are some challenges and difficulties in modeling and analyzing the background features in these datasets.
- (2)
- Hyperspectral Digital Imagery Collection Experiment (HYDICE) Dataset: This dataset was acquired by the HYDICE sensor over a suburban residential area in Michigan, USA. The spatial resolution is 3 m, and the image size is 80 × 100. There are 210 spectral bands within the range of 400–2500 nm, with 175 remaining after eliminating noise and water vapor absorption bands. This hyperspectral dataset includes background land covers such as parking lots, soil, water bodies, and roads. Figure 5e displays the pseudocolor image and the ground-truth map of this dataset. Ten vehicles are considered anomaly targets and they comprise 17 pixels, which account for 0.21% of the entire image.
- (3)
- Pavia Dataset: This dataset was acquired by the Reflective Optics System Imaging Spectrometer (ROSIS) in the center of Pavia, northern Italy. The spatial resolution is 1.3 m and the image size is 150 × 150. This dataset consists of 102 spectral bands within the range of 430–860 nm. Figure 5f displays the pseudocolor image and the ground-truth map of this dataset. The background land covers captured in this dataset include bridges, water bodies, and bare soil, while the anomaly targets are vehicles on the bridge. These anomaly targets comprise a total of 63 pixels, which account for 0.28% of the entire image.
- (4)
- Los Angeles-1 (LA-1) Dataset: This dataset was acquired by the AVIRIS sensor over the Los Angeles area. The spatial resolution is 7.5 m and the image size is 100 × 100. It encompasses a total of 205 spectral bands within the range of 430–860 nm. Figure 5g displays the pseudocolor image and the ground-truth map of this dataset. Notably, there are a few houses that are considered anomaly targets in these images, which comprise a total of 232 pixels, accounting for 2.32% of the entire image.
- (5)
- Gulfport Dataset: This dataset was acquired by the AVIRIS sensor over Gulfport, Southern, MS, USA, in 2010. The spatial resolution is 3.4 m and the image size is 100 × 100. After eliminating bands with a low signal-to-noise ratio (SNR), a total of 191 bands remained. The spectral coverage spans from 400 to 2500 nm. Figure 5h displays the pseudocolor image and the ground-truth map of this dataset. Three airplanes of various sizes are identified as anomaly targets comprising a total of 60 pixels and accounting for 0.60% of the entire image.
3.2. Evaluation Metrics
3.3. Detection Performance
3.4. Parametric Analysis
3.5. Ablation Study
3.6. Comparison of Inference Times
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| The original HSI. | |
| The reconstructed HSI. | |
| The coarse classified anomaly sample (i.e., the prior anomaly samples). | |
| The coarse classified background sample (i.e., the prior background sample). | |
| The input training samples. | |
| The multiplication of corresponding elements. | |
| The binary classification map. | |
| The coarse labels. | |
| The connected components labeling map. | |
| The category label graph. | |
| The mask map. | |
| The inverse mask map of . | |
| The final detection map. |
References
- Su, H.; Wu, Z.; Zhang, H.; Du, Q. Hyperspectral anomaly detection: A survey. IEEE Geosci. Remote Sens. Mag. 2021, 10, 64–90. [Google Scholar] [CrossRef]
- Shah, N.R.; Maud, A.R.M.; Bhatti, F.A.; Ali, M.K.; Khurshid, K.; Maqsood, M.; Amin, M. Hyperspectral anomaly detection: A performance comparison of existing techniques. Int. J. Digit. Earth 2022, 15, 2078–2125. [Google Scholar] [CrossRef]
- Li, J.; Hong, D.; Gao, L.; Yao, J.; Zheng, K.; Zhang, B.; Chanussot, J. Deep learning in multimodal remote sensing data fusion: A comprehensive review. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102926. [Google Scholar] [CrossRef]
- Chang, C.-I. Hyperspectral anomaly detection: A dual theory of hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5511720. [Google Scholar] [CrossRef]
- Bioucas-Dias, J.M.; Plaza, A.; Camps-Valls, G.; Scheunders, P.; Nasrabadi, N.; Chanussot, J. Hyperspectral remote sensing data analysis and future challenges. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–36. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Liu, W.; Li, Z.; Yu, H.; Ni, L. Model-Guided Coarse-to-Fine Fusion Network for Unsupervised Hyperspectral Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2023, 20, 5508605. [Google Scholar] [CrossRef]
- Zhu, D.; Du, B.; Zhang, L. Two-stream convolutional networks for hyperspectral target detection. IEEE Trans. Geosci. Remote Sens. 2020, 59, 6907–6921. [Google Scholar] [CrossRef]
- Zhang, S.; Meng, X.; Liu, Q.; Yang, G.; Sun, W. Feature-Decision Level Collaborative Fusion Network for Hyperspectral and LiDAR Classification. Remote Sens. 2023, 15, 4148. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A review of change detection in multitemporal hyperspectral images: Current techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Manolakis, D.; Truslow, E.; Pieper, M.; Cooley, T.; Brueggeman, M. Detection algorithms in hyperspectral imaging systems: An overview of practical algorithms. IEEE Signal Process. Mag. 2013, 31, 24–33. [Google Scholar] [CrossRef]
- Gao, L.; Sun, X.; Sun, X.; Zhuang, L.; Du, Q.; Zhang, B. Hyperspectral anomaly detection based on chessboard topology. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5505016. [Google Scholar] [CrossRef]
- Chang, C.-I.; Chiang, S.-S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef]
- Theiler, J.; Ziemann, A.; Matteoli, S.; Diani, M. Spectral variability of remotely sensed target materials: Causes, models, and strategies for mitigation and robust exploitation. IEEE Geosci. Remote Sens. Mag. 2019, 7, 8–30. [Google Scholar] [CrossRef]
- Xiang, P.; Song, J.; Qin, H.; Tan, W.; Li, H.; Zhou, H. Visual attention and background subtraction with adaptive weight for hyperspectral anomaly detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2270–2283. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Theiler, J. An overview of background modeling for detection of targets and anomalies in hyperspectral remotely sensed imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2317–2336. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzon, E.M.; Garcia, I.; Plaza, A. Analysis and optimizations of global and local versions of the RX algorithm for anomaly detection in hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 801–814. [Google Scholar] [CrossRef]
- Schaum, A. Joint subspace detection of hyperspectral targets. In Proceedings of the 2004 IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2004; Volume 3, p. 1824. [Google Scholar]
- Guo, Q.; Zhang, B.; Ran, Q.; Gao, L.; Li, J.; Plaza, A. Weighted-RXD and linear filter-based RXD: Improving background statistics estimation for anomaly detection in hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2351–2366. [Google Scholar] [CrossRef]
- Du, B.; Zhang, L. A discriminative metric learning based anomaly detection method. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6844–6857. [Google Scholar]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Zhou, J.; Kwan, C.; Ayhan, B.; Eismann, M.T. A novel cluster kernel RX algorithm for anomaly and change detection using hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6497–6504. [Google Scholar] [CrossRef]
- Zhao, R.; Du, B.; Zhang, L. A robust nonlinear hyperspectral anomaly detection approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1227–1234. [Google Scholar] [CrossRef]
- Tao, R.; Zhao, X.; Li, W.; Li, H.-C.; Du, Q. Hyperspectral anomaly detection by fractional Fourier entropy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4920–4929. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1463–1474. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A low-rank and sparse matrix decomposition-based Mahalanobis distance method for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1376–1389. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, W.; Guo, R.; Ayhan, B.; Kwan, C.; Vance, S.; Qi, H. Hyperspectral anomaly detection through spectral unmixing and dictionary-based low-rank decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4391–4405. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1990–2000. [Google Scholar] [CrossRef]
- Galatsanos, N.P.; Katsaggelos, A.K. Methods for choosing the regularization parameter and estimating the noise variance in image restoration and their relation. IEEE Trans. Image Process. 1992, 1, 322–336. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, X.; Li, S.; Li, K.; Li, J.; Benediktsson, J.A. Hyperspectral anomaly detection with attribute and edge-preserving filters. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5600–5611. [Google Scholar] [CrossRef]
- Xie, W.; Jiang, T.; Li, Y.; Jia, X.; Lei, J. Structure tensor and guided filtering-based algorithm for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4218–4230. [Google Scholar] [CrossRef]
- Liu, Q.; Meng, X.; Shao, F.; Li, S. Supervised-unsupervised combined deep convolutional neural networks for high-fidelity pansharpening. Inf. Fusion 2023, 89, 292–304. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Yao, J.; Gao, L.; Hong, D. Deep unsupervised blind hyperspectral and multispectral data fusion. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6007305. [Google Scholar] [CrossRef]
- Liu, Q.; Chen, X.; Meng, X.; Chen, H.; Shao, F.; Sun, W. Dual-Task Interactive Learning for Unsupervised Spatio-Temporal-Spectral Fusion of Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5402015. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Li, Z.; Gao, L.; Jia, X. X-shaped interactive autoencoders with cross-modality mutual learning for unsupervised hyperspectral image super-resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5518317. [Google Scholar] [CrossRef]
- Hu, X.; Xie, C.; Fan, Z.; Duan, Q.; Zhang, D.; Jiang, L.; Wei, X.; Hong, D.; Li, G.; Zeng, X. Hyperspectral anomaly detection using deep learning: A review. Remote Sens. 2022, 14, 1973. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Du, Q. Transferred deep learning for anomaly detection in hyperspectral imagery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 597–601. [Google Scholar] [CrossRef]
- Rao, W.; Qu, Y.; Gao, L.; Sun, X.; Wu, Y.; Zhang, B. Transferable network with Siamese architecture for anomaly detection in hyperspectral images. Int. J. Appl. Earth Obs. Geoinf. 2022, 106, 102669. [Google Scholar] [CrossRef]
- Song, S.; Zhou, H.; Yang, Y.; Song, J. Hyperspectral anomaly detection via convolutional neural network and low rank with density-based clustering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 3637–3649. [Google Scholar] [CrossRef]
- Gao, L.; Li, J.; Zheng, K.; Jia, X. Enhanced Autoencoders with Attention-Embedded Degradation Learning for Unsupervised Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5509417. [Google Scholar] [CrossRef]
- Bati, E.; Çalışkan, A.; Koz, A.; Alatan, A.A. Hyperspectral anomaly detection method based on auto-encoder. In Proceedings of the Image and Signal Processing for Remote Sensing XXI, Toulouse, France, 21–24 September 2015; Volume 9643, pp. 220–226. [Google Scholar]
- Arisoy, S.; Nasrabadi, N.M.; Kayabol, K. GAN-based hyperspectral anomaly detection. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021; pp. 1891–1895. [Google Scholar]
- Racetin, I.; Krtalić, A. Systematic review of anomaly detection in hyperspectral remote sensing applications. Appl. Sci. 2021, 11, 4878. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y.; Xie, W.; Du, Q. Discriminative reconstruction constrained generative adversarial network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4666–4679. [Google Scholar] [CrossRef]
- Xiang, P.; Ali, S.; Jung, S.K.; Zhou, H. Hyperspectral anomaly detection with guided autoencoder. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5538818. [Google Scholar] [CrossRef]
- Fan, G.; Ma, Y.; Mei, X.; Fan, F.; Huang, J.; Ma, J. Hyperspectral anomaly detection with robust graph autoencoders. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5511314. [Google Scholar]
- Wang, L.; Wang, X.; Vizziello, A.; Gamba, P. RSAAE: Residual Self-Attention-Based Autoencoder for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5510614. [Google Scholar] [CrossRef]
- Wang, S.; Wang, X.; Zhang, L.; Zhong, Y. Auto-AD: Autonomous hyperspectral anomaly detection network based on fully convolutional autoencoder. IEEE Trans. Geosci. Remote Sens. 2021, 60, 5503314. [Google Scholar] [CrossRef]
- Wang, D.; Zhuang, L.; Gao, L.; Sun, X.; Huang, M.; Plaza, A. PDBSNet: Pixel-shuffle Down-sampling Blind-Spot Reconstruction Network for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5511914. [Google Scholar] [CrossRef]
- Gao, L.; Wang, D.; Zhuang, L.; Sun, X.; Huang, M.; Plaza, A. BS 3 LNet: A new blind-spot self-supervised learning network for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5504218. [Google Scholar]
- He, K.; Chen, X.; Xie, S.; Li, Y.; Dollár, P.; Girshick, R. Masked autoencoders are scalable vision learners. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 21–24 June 2022; pp. 16000–16009. [Google Scholar]
- Li, Z.; Wang, Y.; Xiao, C.; Ling, Q.; Lin, Z.; An, W. You Only Train Once: Learning a General Anomaly Enhancement Network With Random Masks for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5506718. [Google Scholar] [CrossRef]
- Manolakis, D.; Shaw, G. Detection algorithms for hyperspectral imaging applications. IEEE Signal Process. Mag. 2002, 19, 29–43. [Google Scholar] [CrossRef]
- Bradley, A.P. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern Recognit. 1997, 30, 1145–1159. [Google Scholar] [CrossRef]
- Ferri, C.; Hernández-Orallo, J.; Flach, P.A. A coherent interpretation of AUC as a measure of aggregated classification performance. In Proceedings of the 28th International Conference on Machine Learning (ICML-11), Bellevue, WA, USA, 28 June–2 July 2011; pp. 657–664. [Google Scholar]


























| Dataset | of Different Methods | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GRX | LRX | FRFE | CRD | AED | LRASR | GAED | RGAE | Auto-AD | Ours | |
| Sandiego-1 | 0.8736 | 0.8570 | 0.9787 | 0.9768 | 0.9900 2 | 0.9824 | 0.9861 | 0.9854 | 0.9895 | 0.9994 1 |
| Sandiego-2 | 0.7499 | 0.7211 | 0.7821 | 0.9290 | 0.9399 | 0.8065 | 0.8905 | 0.8819 | 0.9466 2 | 0.9773 1 |
| Sandiego-3 | 0.7125 | 0.7540 | 0.7694 | 0.9485 2 | 0.9659 | 0.7214 | 0.7811 | 0.8341 | 0.9163 | 0.9815 1 |
| HYDICE | 0.9857 | 0.9911 | 0.9933 | 0.9976 | 0.9951 2 | 0.9744 | 0.9843 | 0.9646 | 0.9951 2 | 0.9980 1 |
| Pavia | 0.9538 | 0.9525 | 0.9457 | 0.9510 | 0.9793 | 0.9380 | 0.9398 | 0.9688 | 0.9914 2 | 0.9979 1 |
| LA-1 | 0.9692 | 0.9492 | 0.9655 | 0.9229 | 0.9780 2 | 0.9440 | 0.9424 | 0.9569 | 0.9406 | 0.9808 1 |
| Gulfport | 0.9526 | 0.9532 | 0.9722 | 0.9342 | 0.9953 | 0.9120 | 0.9705 | 0.9842 | 0.9968 2 | 0.9975 1 |
| Average | 0.8853 | 0.8826 | 0.9153 | 0.9514 | 0.9777 2 | 0.8970 | 0.9278 | 0.9394 | 0.9680 | 0.9903 1 |
| Component | of Different Cases | ||||||
|---|---|---|---|---|---|---|---|
| Sandiego-1 | Sandiego-2 | Sandiego-3 | HYDICE | Pavia | LA-1 | Gulfport | |
| FCAE without SSJA | 0.9732 | 0.8785 | 0.8567 | 0.9887 | 0.9600 | 0.9168 | 0.9679 |
| FCAE | 0.9786 | 0.8864 | 0.8630 | 0.9920 | 0.9686 | 0.9229 | 0.9763 |
| 0.9975 2 | 0.9221 2 | 0.9336 2 | 0.9961 2 | 0.9881 2 | 0.9669 2 | 0.9822 2 | |
| FCAE + + LFACN | 0.9996 1 | 0.9763 1 | 0.9722 1 | 0.9979 1 | 0.9932 1 | 0.9791 1 | 0.9957 1 |
| Dataset | Inference Time of Different Detectors | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GRX | LRX | FRFE | CRD | AED | LRASR | GAED | RGAE | Auto-AD | Ours | |
| Sandiego-1 | 0.2146 | 9.1735 | 9.8865 | 3.9145 | 0.2107 | 46.3339 | 0.0305 2 | 0.0335 | 0.0210 1 | 0.0390 |
| Sandiego-2 | 0.3168 | 25.6535 | 14.9289 | 5.0192 | 0.2456 | 57.3001 | 0.0394 | 0.0570 | 0.0275 2 | 0.0185 1 |
| Sandiego-3 | 0.0998 | 18.2074 | 5.4494 | 2.1902 | 0.1884 | 19.2353 | 0.0150 1 | 0.0157 2 | 0.0160 | 0.0210 |
| HYDICE | 0.2146 | 9.1735 | 9.8865 | 3.9145 | 0.2107 | 46.3339 | 0.0305 | 0.0335 | 0.0210 1 | 0.0235 2 |
| Pavia | 0.9823 | 16.8106 | 33.5833 | 5.3146 | 0.3625 | 61.1938 | 0.1072 | 0.0476 | 0.0305 1 | 0.0355 2 |
| LA-1 | 0.3173 | 14.2751 | 21.3859 | 5.3762 | 0.2242 | 72.0277 | 0.0345 | 0.0459 | 0.0240 1 | 0.0330 2 |
| Gulfport | 0.5988 | 13.7447 | 13.6096 | 5.0287 | 0.2652 | 63.4349 | 0.0620 | 0.0373 | 0.0220 1 | 0.0275 2 |
| Average | 0.3771 | 14.6755 | 14.9511 | 4.1165 | 0.2563 | 48.4835 | 0.0436 | 0.0366 | 0.0229 1 | 0.0283 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, R.; Yang, Z.; Meng, X.; Shao, F. A Novel Fully Convolutional Auto-Encoder Based on Dual Clustering and Latent Feature Adversarial Consistency for Hyperspectral Anomaly Detection. Remote Sens. 2024, 16, 717. https://doi.org/10.3390/rs16040717
Zhao R, Yang Z, Meng X, Shao F. A Novel Fully Convolutional Auto-Encoder Based on Dual Clustering and Latent Feature Adversarial Consistency for Hyperspectral Anomaly Detection. Remote Sensing. 2024; 16(4):717. https://doi.org/10.3390/rs16040717
Chicago/Turabian StyleZhao, Rui, Zhiwei Yang, Xiangchao Meng, and Feng Shao. 2024. "A Novel Fully Convolutional Auto-Encoder Based on Dual Clustering and Latent Feature Adversarial Consistency for Hyperspectral Anomaly Detection" Remote Sensing 16, no. 4: 717. https://doi.org/10.3390/rs16040717
APA StyleZhao, R., Yang, Z., Meng, X., & Shao, F. (2024). A Novel Fully Convolutional Auto-Encoder Based on Dual Clustering and Latent Feature Adversarial Consistency for Hyperspectral Anomaly Detection. Remote Sensing, 16(4), 717. https://doi.org/10.3390/rs16040717






