On the Use of Ultra-WideBand-Based Augmentation for Precision Maneuvering
Abstract
:1. Introduction
2. Materials and Methods
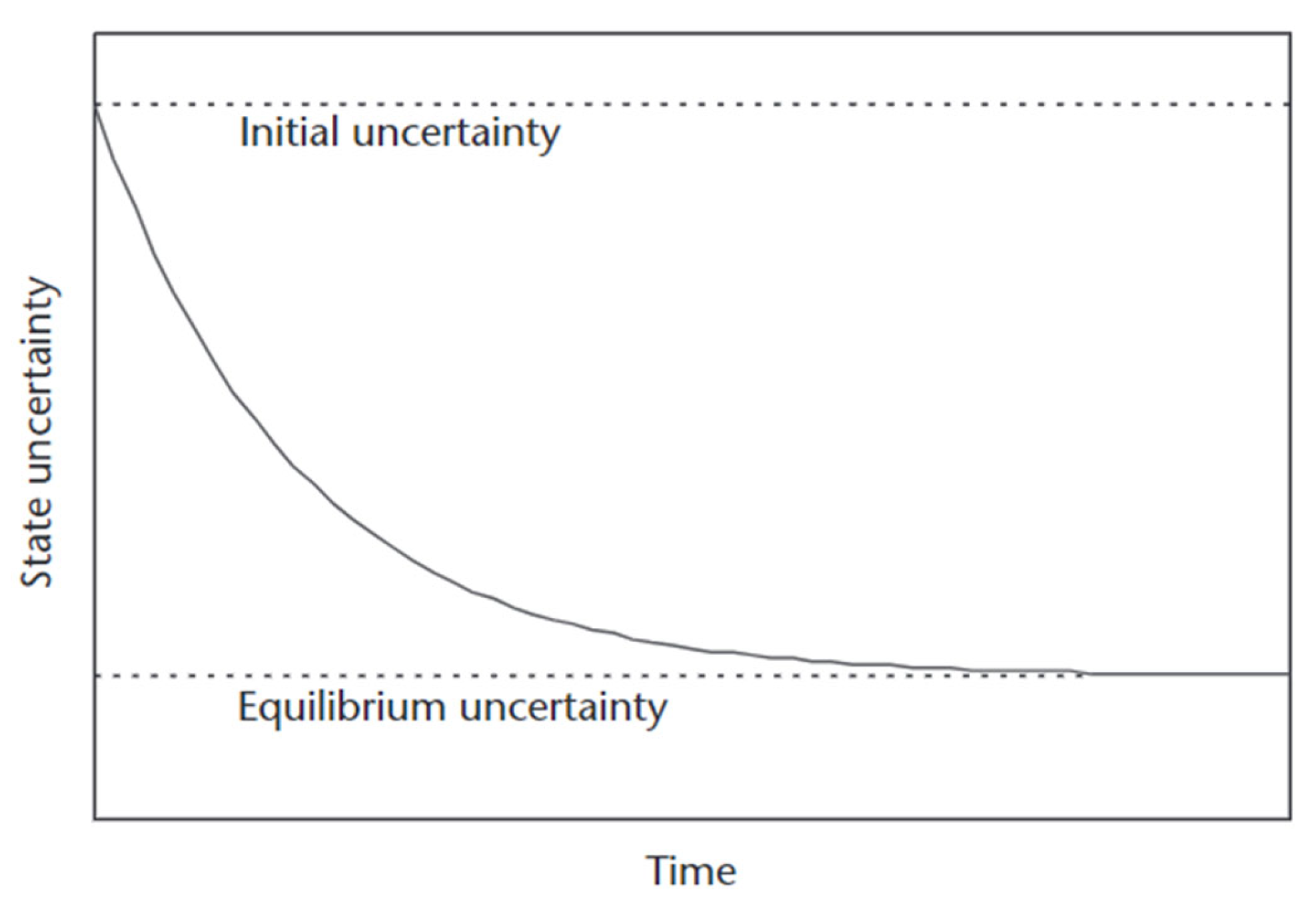
2.1. The Kalman Filter
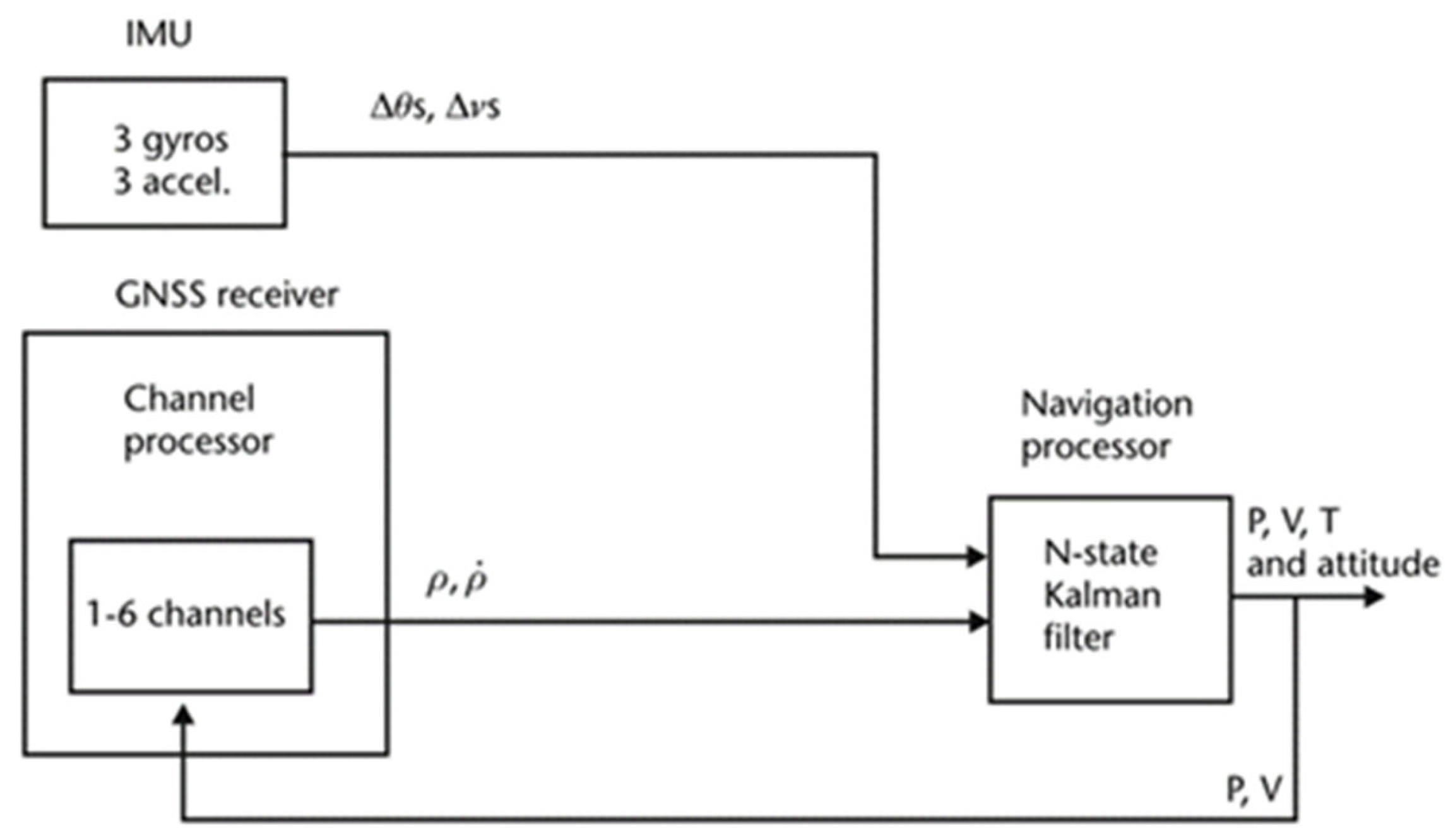
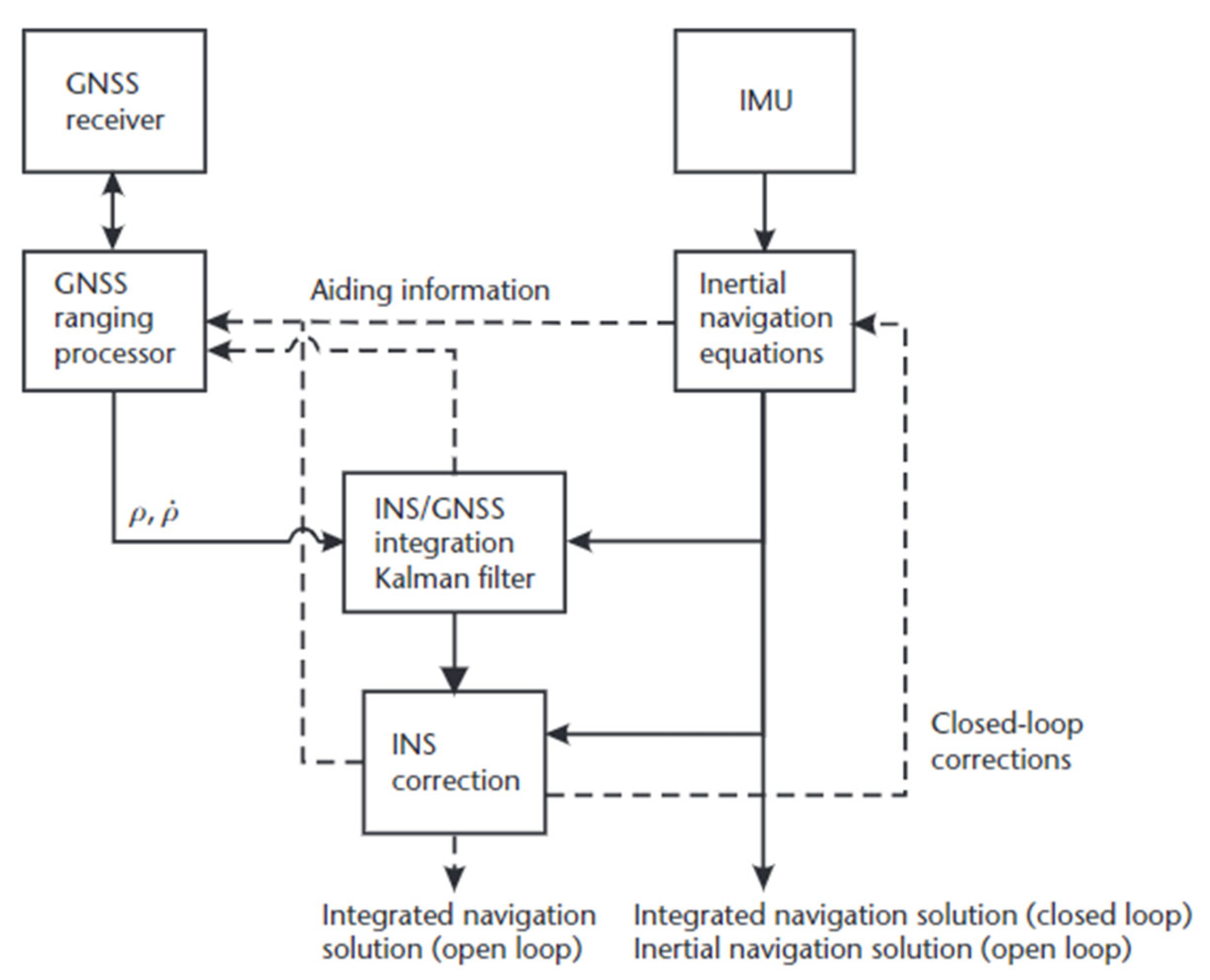
2.2. Tightly Coupled Sensor Fusion: GNSS, IMU, and UWB
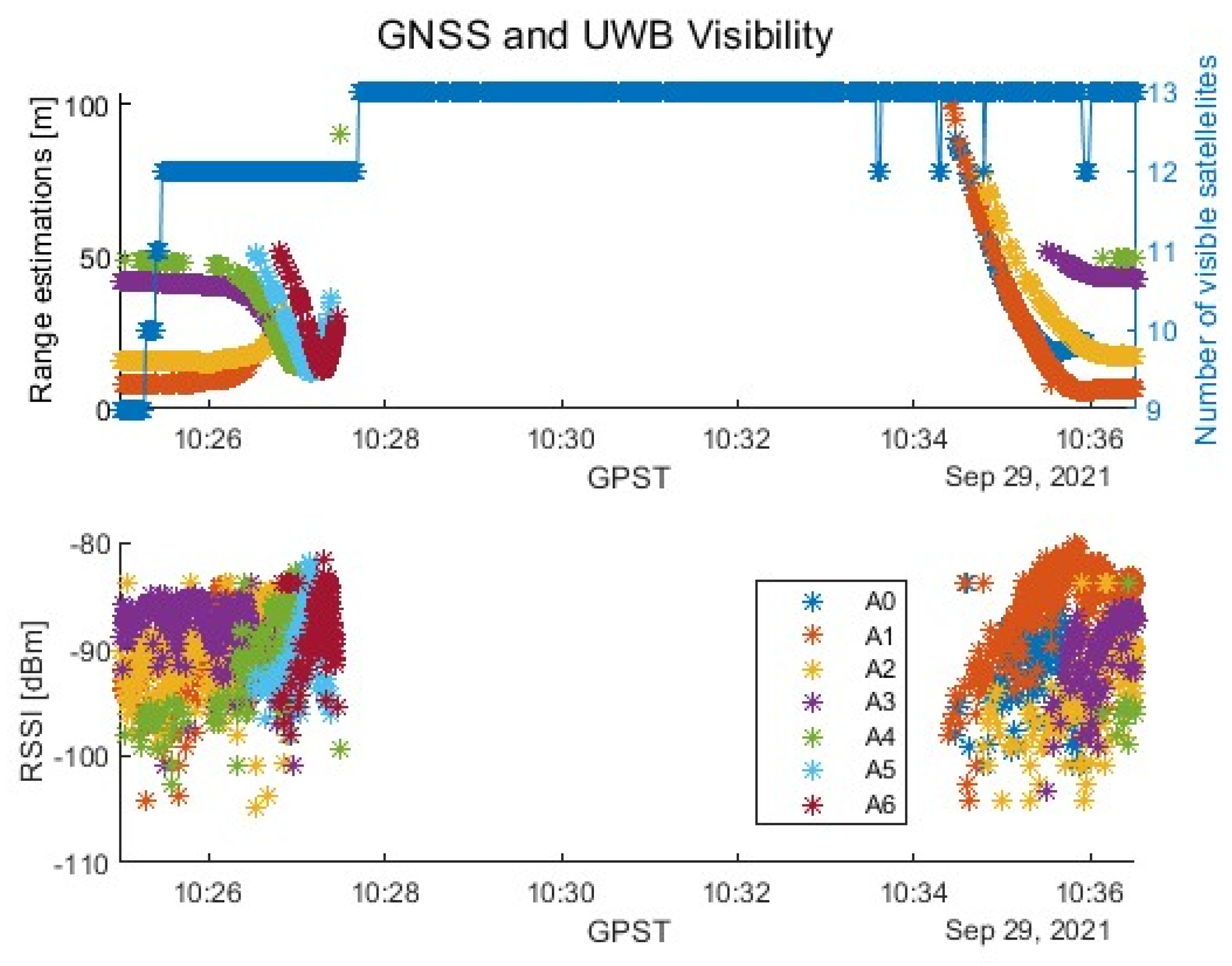
3. Results
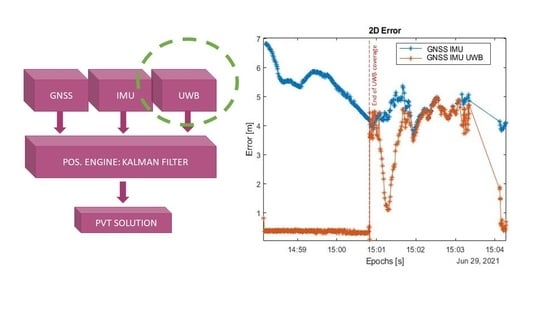
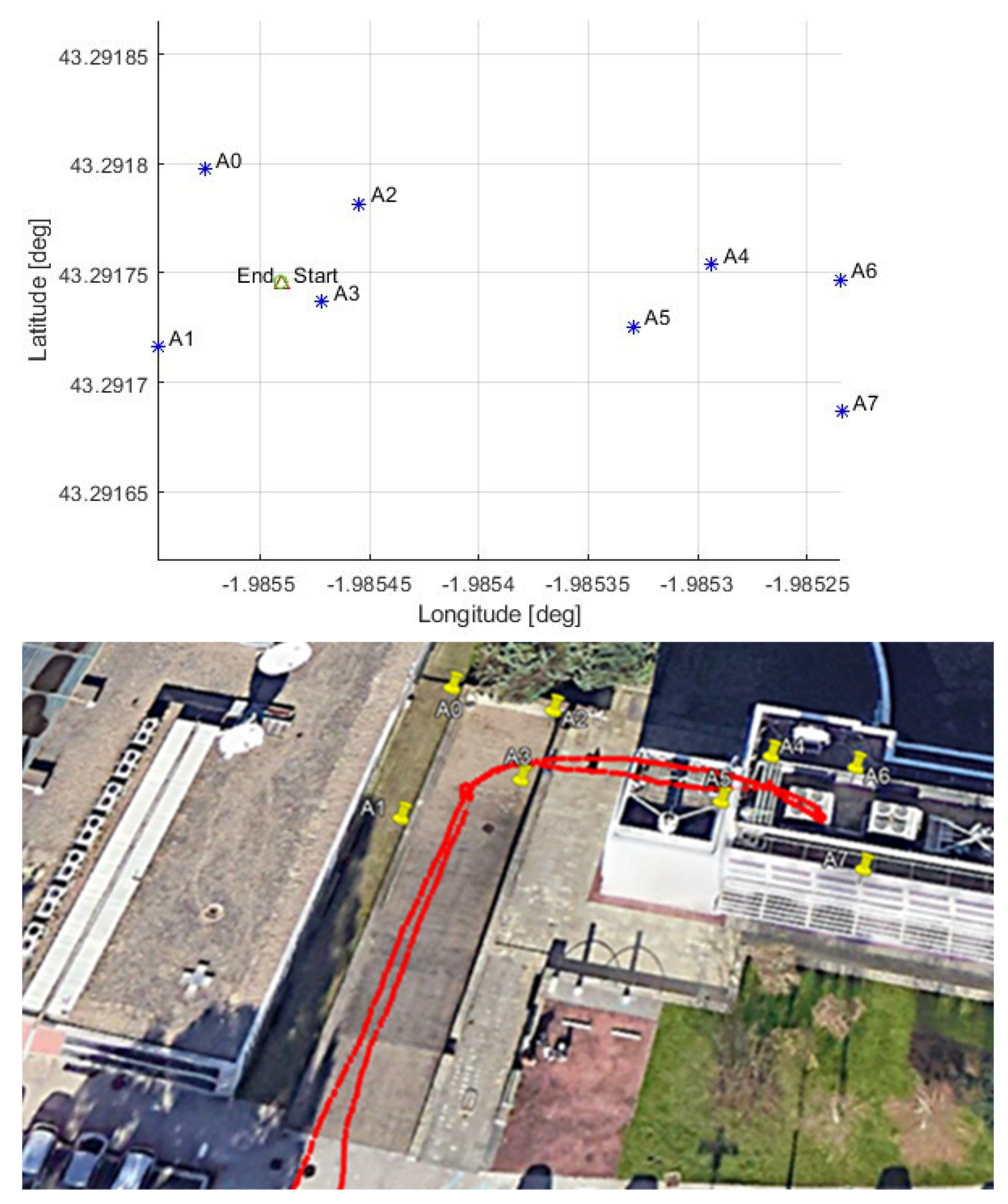
3.1. Automotive
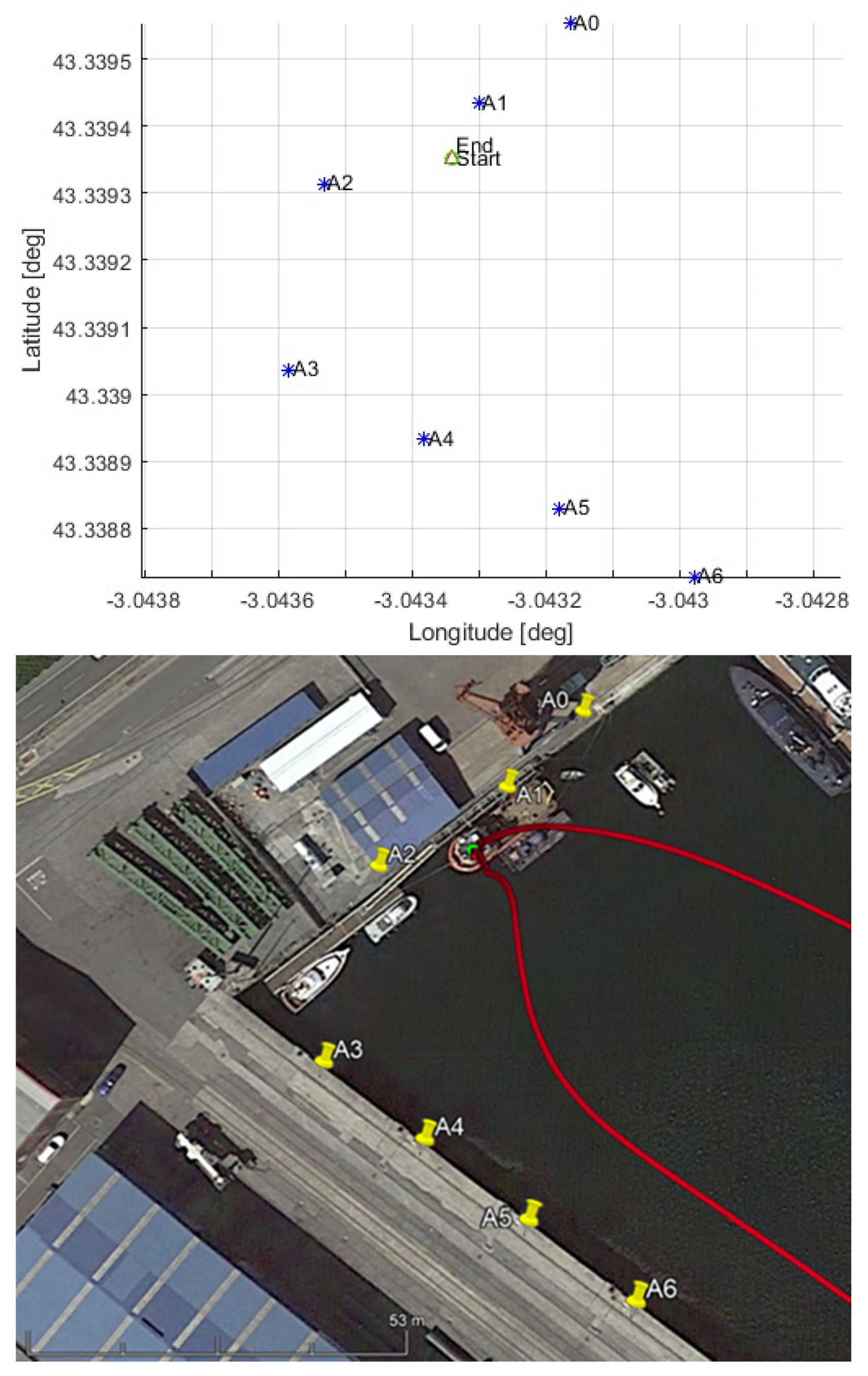
3.2. Maritime
4. Discussion
4.1. Automotive
4.2. Maritime
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Novak, A.; Skultety, F.; Bugaj, M.; Jun, F. Safety Studies on GNSS Instrument Approach at Žilina Airport. In Proceedings of the MOSATT 2019—Modern Safety Technologies in Transportation International Scientific Conference, Piscataway, NJ, USA, 28–29 November 2019; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2019; pp. 122–125. [Google Scholar] [CrossRef]
- Manz, H. Safety relevant application of satellite based localisation in transportation with the focus on railways. In Proceedings of the 2015 International Association of Institutes of Navigation World Congress, IAIN 2015, Prague, Czech Republic, 20–23 October 2015; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2015. [Google Scholar] [CrossRef]
- Zhang, Q.; Niu, X.; Shi, C. Impact Assessment of Various IMU Error Sources on the Relative Accuracy of the GNSS/INS Systems. IEEE Sens. J. 2020, 20, 5026–5038. [Google Scholar] [CrossRef]
- Amami, M.; Amami, M.M. The Advantages and Limitations of Low-Cost Single Frequency GPS/MEMS-Based INS Integration. Glob. J. Eng. Technol. Adv. 2022, 2022, 018–031. [Google Scholar] [CrossRef]
- Groves, P.D.; Wang, L.; Walter, D.; Martin, H.; Voutsis, K.; Jiang, Z. The four key challenges of advanced multisensor navigation and positioning. In Record—IEEE PLANS, Position Location and Navigation Symposium; IEEE: Piscataway, NJ, USA, 2014; pp. 773–792. [Google Scholar] [CrossRef]
- Grejner-Brzezinska, D.A.; Toth, C.K.; Moore, T.; Raquet, J.F.; Miller, M.M.; Kealy, A. Multisensor Navigation Systems: A Remedy for GNSS Vulnerabilities? Proc. IEEE 2016, 104, 1339–1353. [Google Scholar] [CrossRef]
- Ubisense—Ultra-Wideband Real-Time Location System (RTLS). Available online: https://ubisense.com/ (accessed on 30 November 2020).
- Lee, Y.; Kim, J.; Lee, H.; Moon, K. IoT-based data transmitting system using a UWB and RFID system in smart warehouse. In Proceedings of the International Conference on Ubiquitous and Future Networks, ICUFN, Milan, Italy, 4–7 July 2017; IEEE Computer Society: Washington, DC, USA, 2017; pp. 545–547. [Google Scholar] [CrossRef]
- Pochanin, G. Application of the Industry 4.0 Paradigm to the Design of a UWB Radiolocation System for Humanitarian Demining. In Proceedings of the UWBUSIS 2018—2018 9th International Conference on Ultrawideband and Ultrashort Impulse Signals, Odessa, Ukraine, 4–7 September 2018; Institute of Electrical and Electronics Engineers Inc.: Piscataway, NJ, USA, 2018; pp. 50–56. [Google Scholar] [CrossRef]
- Gao, Y.; Meng, X.; Hancock, C.M.; Stephenson, S.; Zhang, Q. UWB/GNSS-based Cooperative Positioning Method for V2X Applications. 2014. Available online: https://nottingham-repository.worktribe.com/output/733331 (accessed on 30 September 2020).
- Cheng, L.; Chang, H.; Wang, K.; Wu, Z. Real Time Indoor Positioning System for Smart Grid based on UWB and Artificial Intelligence Techniques. In Proceedings of the 2020 IEEE Conference on Technologies for Sustainability, Oklahoma City, OK, USA, 2020; SusTech: Shenzhen, China, 2020. [Google Scholar] [CrossRef]
- Corrales, J.A.; Candelas, F.A.; Torres, F. Hybrid tracking of human operators using IMU/UWB data fusion by a Kalman filte. In Proceedings of the HRI 2008—3rd ACM/IEEE International Conference on Human-Robot Interaction: Living with Robots, Amsterdam, The Netherlands, 12–15 March 2008; pp. 193–200. [Google Scholar] [CrossRef]
- Tiemann, J.; Schweikowski, F.; Wietfeld, C. Design of an UWB indoor-positioning system for UAV navigation in GNSS-denied environments. In Proceedings of the 2015 International Conference on Indoor Positioning and Indoor Navigation, IPIN 2015, Banff, AB, Canada, 13–16 October 2015. [Google Scholar] [CrossRef]
- Macgougan, G.; O’Keefe, K.; Klukas, R. Tightly-coupled GPS/UWB positioning: First test results from a difficult urban environment. In Proceedings of the 2009 IEEE International Conference on Ultra-Wideband, ICUWB 2009, Vancouver, BC, Canada, 9–11 September 2009; pp. 381–385. [Google Scholar] [CrossRef]
- MacGougan, G.; O’Keefe, K.; Klukas, R. Accuracy and reliability of tightly coupled GPS/ultra-wideband positioning for surveying in urban environments. GPS Solut. 2010, 14, 351–364. [Google Scholar] [CrossRef]
- MacGougan, G.; O’Keefe, K.; Chiu, D.S. Multiple UWB Range Assisted GPS RTK in Hostile Environments. In Proceedings of the 21st International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2008), Savannah, Georgia, 16–19 September 2008; Available online: https://www.ion.org/publications/abstract.cfm?articleID=8208 (accessed on 30 January 2024).
- Zhang, R.G.; Shen, F.; Li, Q.H. A Hybrid Indoor/Outdoor Positioning and Orientation Solution Based on INS, UWB and Dual-Antenna RTK-GNSS. In Proceedings of the 27th Saint Petersburg International Conference on Integrated Navigation Systems, ICINS 2020—Proceedings, St. Petersburg, Russia, 25–27 May 2020. [Google Scholar] [CrossRef]
- Di Pietra, V.; Dabove, P.; Piras, M. Loosely Coupled GNSS and UWB with INS Integration for Indoor/Outdoor Pedestrian Navigation. Sensors 2020, 20, 6292. [Google Scholar] [CrossRef]
- Li, Z.; Chang, G.; Gao, J.; Wang, J. Hernandez. GPS/UWB/MEMS-IMU tightly coupled navigation with improved robust Kalman filter. Adv. Space Res. 2016, 58, 2424–2434. [Google Scholar] [CrossRef]
- Wang, C.; Xu, A.; Sui, X.; Hao, Y.; Shi, Z.; Chen, Z. A seamless navigation system and applications for autonomous vehicles using a tightly coupled GNSS/UWB/INS/map integration scheme. Remote Sens. 2022, 14, 27. [Google Scholar] [CrossRef]
- Li, Z.; Wang, R.; Gao, J.; Wang, J. An Approach to Improve the Positioning Performance of GPS/INS/UWB Integrated System with Two-Step Filter. Remote Sens. 2017, 10, 19. [Google Scholar] [CrossRef]
- Zhang, R.; Shen, F.; Liang, Y.; Zhao, D. Using UWB Aided GNSS/INS Integrated Navigation to Bridge GNSS Outages Based on Optimal Anchor Distribution Strategy. In Proceedings of the 2020 IEEE/ION Position, Location and Navigation Symposium, PLANS 2020, Portland, OR, USA, 20–23 April 2020; pp. 1405–1411. [Google Scholar] [CrossRef]
- Jiménez, F.; Naranjo, J.E.; García, F.; Armingol, J.M. Can Low-Cost Road Vehicles Positioning Systems Fulfil Accuracy Specifications of New ADAS Applications? J. Navig. 2011, 64, 251–264. [Google Scholar] [CrossRef]
- I.M.O. (IMO). Resolution A.915(22) Adopted on 29 November 2001 (Agenda item 9) Revised Maritime Policy and Requirements for a Future Global Navigation Satellite System (GNSS); IMO: London, UK, 2001. [Google Scholar]
- European Comission. White Paper on Transport Roadmap to A Single European Transport Area-towards A Competitive and Resource-Efficient Transport System; Publications Office of the European Union: Luxembourg, 2011. [Google Scholar] [CrossRef]
- Groves, P.D. Principles of GNSS, Inertial, and Multisensor Integrated; Artech House: Boston, MA, USA, 2008. [Google Scholar]
- Kaplan, E.; Hegarty, C. Understanding GPS/GNSS: Principles and Applications, 3rd ed.; Artech: Morristown, NJ, USA, 2017; ISBN 9781630814427. [Google Scholar]
- Herrera, A.M.; Suhandri, H.F.; Realini, E.; Reguzzoni, M.; de Lacy, M.C. goGPS: Open-source MATLAB software. GPS Solut. 2016, 20, 595–603. [Google Scholar] [CrossRef]
- Losada, M.; Zamora-Cadenas, L.; Jiménez-Irastorza, A.; Arrue, N.; Vélez, I. UWB-based time-of-arrival ranging system for multipath indoor environments. In Proceedings of the 3rd International Conference on Advances in Circuits, Electronics and Micro-Electronics, CENICS 2010, Venice, Italy, 18–25 July 2010; pp. 17–22. [Google Scholar] [CrossRef]
- Arrue, N.; Losada, M.; Zamora-Cadenas, L.; Jiménez-Irastorza, A.; Vélez, I. Design of an IR-UWB indoor localization system based on a novel RTT ranging estimator. In Proceedings of the 1st International Conference on Sensor Device Technologies and Applications, SENSORDEVICES 2010, Venice, Italy, 18–25 July 2010; pp. 52–57. [Google Scholar] [CrossRef]
- Monica, S.; Ferrari, G. UWB-based localization in large indoor scenarios: Optimized placement of anchor nodes. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 987–999. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Huang, S.P.; Wu, T.W.; Tsai, W.T.; Liou, C.Y.; Mao, S.G. UWB System for Indoor Positioning and Tracking with Arbitrary Target Orientation, Optimal Anchor Location, and Adaptive NLOS Mitigation. IEEE Trans. Veh. Technol. 2020, 69, 9304–9314. [Google Scholar] [CrossRef]
- Ferrigno, L.; Miele, G.; Milano, F.; Pingerna, V.; Cerro, G.; Laracca, M. A UWB-based localization system: Analysis of the effect of anchor positions and robustness enhancement in indoor environments. In Proceedings of the Conference Record—IEEE Instrumentation and Measurement Technology Conference, Glasgow, UK, 17–20 May 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Suwatthikul, C.; Chantaweesomboon, W.; Manatrinon, S.; Athikulwongse, K.; Kaemarungsi, K. Implication of anchor placement on performance of UWB real-time locating system. In Proceedings of the 2017 8th International Conference on Information and Communication Technology for Embedded Systems, IC-ICTES 2017, Chonburi, Thailand, 7–9 May 2017. [Google Scholar] [CrossRef]
- Cerro, G.; Ferrigno, L.; Laracca, M.; Miele, G.; Milano, F.; Pingerna, V. UWB-Based Indoor Localization: How to Optimally Design the Operating Setup? IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- European GNSS Agency (GSA). Report on Maritime and Inland Waterways User Needs and Requirements. 2018. Available online: https://www.gsc-europa.eu/system/files/galileo_documents/Maritime-Report-on-User-Needs-and-Requirements-v1.0.pdf (accessed on 31 September 2022).




| Subsystem | Model and Specifications |
|---|---|
| GNSS antenna | Septentrio—PolaNt-x (triple frequency, multi-constellation) (Leuven, Belgium) |
| Low-cost GNSS receiver | Ublox—ZED-F9P mPCIE (dual frequency, multi-constellation) (Thalwil, Switzerland) |
| Low-cost IMU | Advanced Navigation—Orientus (Sydney, Australia) |
| Low-cost UWB receiver | Proprietary hardware |
| Reference system | Septentrio—AsteRx Full (triple frequency, multi-constellation) (Leuven, Belgium) |
| Processing unit | Novatronic—VBox 3611 4L i5-6300U/8 GB RA (Madrid, Spain) |
| Scenario Name | Horizontal Error (HPE) [m] | # of Solutions | ||||
|---|---|---|---|---|---|---|
| Min. | Mean | Max. | Variance | 95% | ||
| GNSS_IMU—Round 1 | 3.29 | 7.4 | 10.6 | 0.98 | 8.48 | 328 |
| GNSS_IMU_UWB—Round 1 | 0.26 | 0.3 | 0.51 | 0.05 | 0.34 | 328 |
| GNSS_IMU—Round 2 | 6.32 | 6.66 | 7.5 | 0.09 | 7.33 | 61 |
| GNSS_IMU_UWB—Round 2 | 0.29 | 0.33 | 0.56 | 0.002 | 0.45 | 61 |
| GNSS_IMU—Round 3 | 3.24 | 5.88 | 8.71 | 0.8 | 7.58 | 308 |
| GNSS_IMU_UWB—Round 3 | 0.26 | 0.43 | 0.52 | 0.003 | 0.47 | 308 |
| GNSS_IMU—Round 4 | 3.95 | 6.01 | 7.52 | 0.62 | 7.31 | 219 |
| GNSS_IMU_UWB—Round 4 | 0.24 | 0.27 | 0.39 | 0.0004 | 0.3 | 219 |
| GNSS_IMU—Round 5 | 3.4 | 5.91 | 10.39 | 1.84 | 8.87 | 435 |
| GNSS_IMU_UWB— Round 5 | 0.27 | 0.36 | 0.8 | 0.001 | 0.39 | 435 |
| GNSS_IMU—Round 6 | 3.87 | 5.37 | 7.06 | 0.56 | 6.8 | 213 |
| GNSS_IMU_UWB—Round 6 | 3.87 | 4.7 | 8.2 | 0.3 | 5.49 | 213 |
| GNSS_IMU—Round 7 | 4.35 | 7.74 | 16.7 | 8.22 | 12.34 | 106 |
| GNSS_IMU_UWB—Round 7 | 0.39 | 1.56 | 1.93 | 0.11 | 1.81 | 106 |
| Improvement due to UWB | Horizontal Error (HPE) [m] | # of solutions | ||||
| Min. | Mean | Max. | Variance | 95% | ||
| Round 1 | 92% | 96% | 95% | 95% | 96% | 0% |
| Round 2 | 95% | 95% | 93% | 98% | 94% | 0% |
| Round 3 | 92% | 93% | 94% | 100% | 94% | 0% |
| Round 4 | 94% | 96% | 95% | 100% | 96% | 0% |
| Round 5 | 92% | 94% | 92% | 100% | 96% | 0% |
| Round 6 | 0% | 12% | −16% | 46% | 19% | 0% |
| Round 7 | 91% | 80% | 88% | 99% | 85% | 0% |
| Scenario Name | Horizontal Error (HPE) [m] | # of Solutions | ||||
|---|---|---|---|---|---|---|
| Min. | Mean | Max. | Variance | 95% | ||
| GNSS_IMU—Round 1 | 1.82 | 11.11 | 13.76 | 8.46 | 13.53 | 1090 |
| GNSS_IMU_UWB—Round 1 | 0.05 | 3.22 | 6.58 | 4.5 | 6.22 | 1090 |
| GNSS_IMU—Round 2 | 6.9 | 8.02 | 10.99 | 0.79 | 10.09 | 999 |
| GNSS_IMU_UWB—Round 2 | 0.14 | 0.97 | 7.57 | 0.78 | 2.12 | 999 |
| GNSS_IMU—Round 3 | 1.76 | 3.3 | 8.79 | 2.97 | 7.51 | 699 |
| GNSS_IMU_UWB—Round 3 | 0.21 | 1.11 | 6.62 | 0.39 | 1.73 | 699 |
| GNSS_IMU—Round 4 | 0.35 | 1.9 | 4.25 | 0.66 | 3.63 | 1094 |
| GNSS_IMU_UWB—Round 4 | 0.17 | 0.68 | 4.25 | 0.14 | 1.23 | 1094 |
| GNSS_IMU—Round 5 | 0.37 | 2.47 | 4.31 | 0.33 | 3.36 | 3998 |
| GNSS_IMU_UWB—Round 5 | 0.03 | 0.67 | 3.69 | 0.1 | 1.08 | 3998 |
| Improvement Due to UWB | Horizontal Error (HPE) [m] | # of Solutions | ||||
| Min. | Mean | Max. | Variance | 95% | ||
| Round 1 | 97% | 71% | 52% | 47% | 54% | 0% |
| Round 2 | 98% | 88% | 31% | 1% | 79% | 0% |
| Round 3 | 88% | 66% | 25% | 87% | 77% | 0% |
| Round 4 | 51% | 64% | 0% | 79% | 66% | 0% |
| Round 5 | 93% | 73% | 14% | 70% | 68% | 0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabalegui, P.; De Miguel, G.; Fernández-Berrueta, N.; Aizpuru, J.; Mendizabal, J.; Adín, I. On the Use of Ultra-WideBand-Based Augmentation for Precision Maneuvering. Remote Sens. 2024, 16, 911. https://doi.org/10.3390/rs16050911
Zabalegui P, De Miguel G, Fernández-Berrueta N, Aizpuru J, Mendizabal J, Adín I. On the Use of Ultra-WideBand-Based Augmentation for Precision Maneuvering. Remote Sensing. 2024; 16(5):911. https://doi.org/10.3390/rs16050911
Chicago/Turabian StyleZabalegui, Paul, Gorka De Miguel, Nerea Fernández-Berrueta, Joanes Aizpuru, Jaizki Mendizabal, and Iñigo Adín. 2024. "On the Use of Ultra-WideBand-Based Augmentation for Precision Maneuvering" Remote Sensing 16, no. 5: 911. https://doi.org/10.3390/rs16050911
APA StyleZabalegui, P., De Miguel, G., Fernández-Berrueta, N., Aizpuru, J., Mendizabal, J., & Adín, I. (2024). On the Use of Ultra-WideBand-Based Augmentation for Precision Maneuvering. Remote Sensing, 16(5), 911. https://doi.org/10.3390/rs16050911