An Adaptive Polarimetric Target Decomposition Algorithm Based on the Anisotropic Degree
Abstract
1. Introduction
2. Methodology
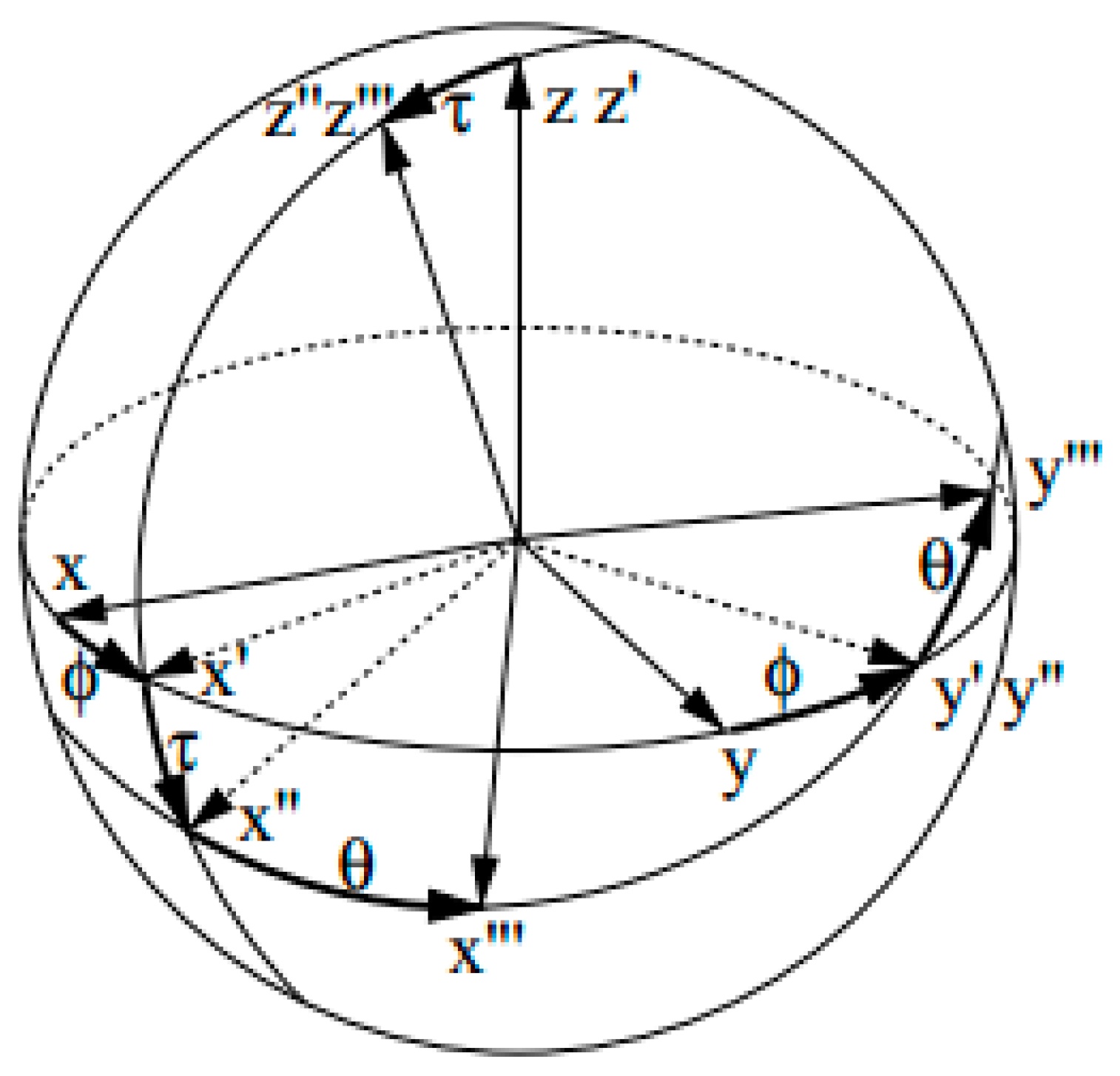
2.1. Orientation Angle Compensation
2.2. Construction of Polarimetric Target Decomposition Algorithm
2.2.1. Random Particle Model
2.2.2. Volume Scattering Model
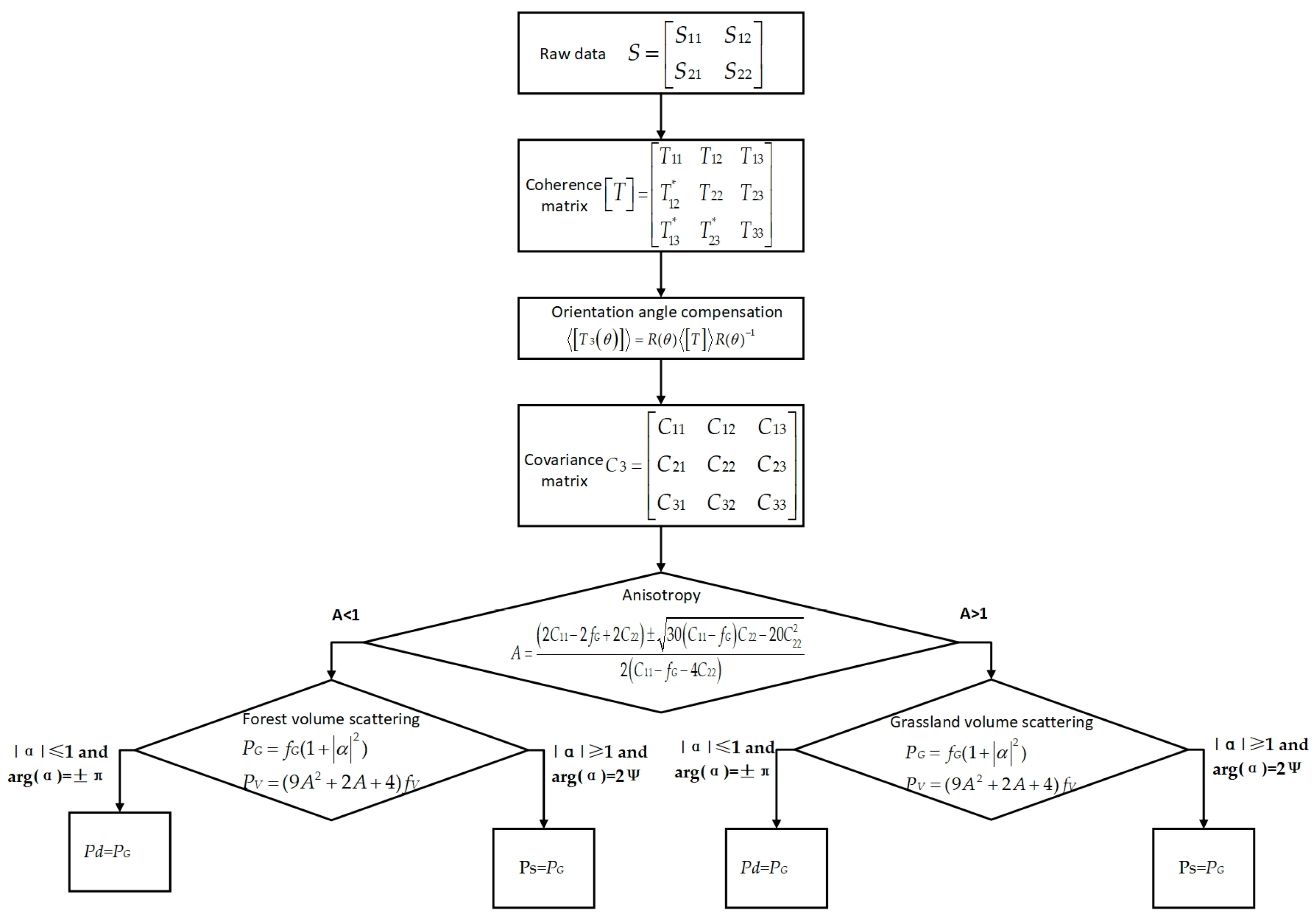
2.3. Polarimetric Target Decomposition Algorithm
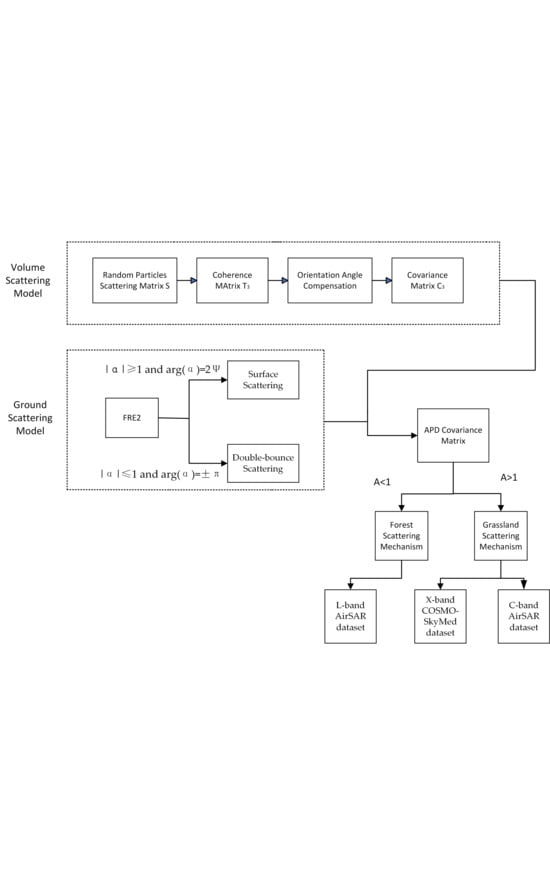
2.4. Flowchart and Specific Steps of the Algorithm
3. Experimental Results and Analysis
3.1. Experiments on L-Band AirSAR Dataset
3.2. Experiments on C-Band AirSAR Dataset
3.3. Experiments on X-Band COSMO-SkyMed Dataset
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ali, I.; Cawkwell, F.; Dwyer, E.; Barrett, B.; Green, S. Satellite remote sensing of grasslands: From observation to management. J. Plant Ecol. 2016, 9, 649–671. [Google Scholar] [CrossRef]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of Estimating Soil Moisture Under Vegetation Cover by Means of PolSAR. IEEE Trans. Geosci. Remote Sens. 2009, 47, 442–454. [Google Scholar] [CrossRef]
- Sun, Y.; Montazeri, S.; Wang, Y.; Zhu, X.X. Automatic registration of a single SAR image and GIS building footprints in a large-scale urban area. ISPRS J. Photogramm. Remote Sens. 2020, 170, 1–14. [Google Scholar] [CrossRef]
- Chen, G.; Wang, L.; Kamruzzaman, M.M. Spectral Classification of Ecological Spatial Polarization SAR Image Based on Target Decomposition Algorithm and Machine Learning. Neural. Comput. Appl. 2020, 32, 5449–5460. [Google Scholar] [CrossRef]
- Alvarez-Perez, J.L. Coherence, Polarization, and Statistical Independence in Cloude–Pottier’s Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 2011, 49, 426–441. [Google Scholar] [CrossRef]
- Song, Q.; Xu, F. Polarimetric SAR Target Decomposition based on sparse NMF. In Proceedings of the 2016 Progress in Electromagnetic Research Symposium (PIERS), Shanghai, China, 8–11 August 2016. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Xiao, S. Urban Damage Level Mapping Based on Co-Polarization Coherence Pattern Using Multitemporal Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2657–2667. [Google Scholar] [CrossRef]
- Chen, S.; Wang, X.; Sato, M. Urban Damage Level Mapping Based on Scattering Mechanism Investigation Using Fully Polarimetric SAR Data for the 3.11 East Japan Earthquake. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6919–6929. [Google Scholar] [CrossRef]
- Musthafa, M.; Khati, U.; Singh, G. Sensitivity of PolSAR decomposition to forest disturbance and regrowth dynamics in a managed forest. Adv. Space Res. 2020, 66, 1863–1875. [Google Scholar] [CrossRef]
- Varghese, A.O.; Suryavanshi, A.; Joshi, A.K. Analysis of different polarimetric target decomposition methods in forest density classification using C band SAR data. Int. J. Remote Sens. 2016, 37, 694–709. [Google Scholar] [CrossRef]
- Acar, H.; Ozerdem, M.S.; Acar, E. Soil Moisture Inversion Via Semiempirical and Machine Learning Methods with Full-Polarization Radarsat-2 and Polarimetric Target Decomposition Data: A Comparative Study. IEEE Access 2020, 8, 197896–197907. [Google Scholar] [CrossRef]
- Zhang, L.; Meng, Q.; Zeng, J.; Wei, X.; Shi, H. Evaluation of Gaofen-3 C-Band SAR for Soil Moisture Retrieval Using Different Polarimetric Decomposition Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 5707–5719. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, J.; Chen, Y.; Xu, K.; Wang, D. Coastal Wetland Classification with GF-3 Polarimetric SAR Imagery by Using Object-Oriented Random Forest Algorithm. Sensors 2021, 21, 3395. [Google Scholar] [CrossRef] [PubMed]
- Cloude, S.R.; Pottier, E. A Review of Target Decomposition Theorems in Radar Polarimetry. IEEE Trans. Geosci. Remote Sens. 1996, 34, 498–518. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, W.; Wang, C.; Liu, X. A Modified Four-Component Decomposition Method With Refined Volume Scattering Models. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1946–1958. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Yajima, Y.; Yamada, H. A Four-Component Decomposition of POLSAR Images Based on the Coherency Matrix. IEEE Geosci. Remote Sens. Lett. 2006, 3, 292–296. [Google Scholar] [CrossRef]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.-E. Four-Component Scattering Power Decomposition with Extended Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2012, 9, 166–170. [Google Scholar] [CrossRef]
- Kumar, A.; Maurya, H.; Misra, A.R.; Panigrahi, R.K. An Improved Decomposition as a Trade-Off Between Utilizing Unitary Matrix Rotations and New Scattering Models. IEEE Access 2021, 9, 77482–77492. [Google Scholar] [CrossRef]
- Freeman, A.; Durden, S.L. Three-component scattering model to describe polarimetric SAR data. In Proceedings of the International Society for Optics and Photonics, San Diego, CA, USA, 12 February 1993. [Google Scholar] [CrossRef]
- Jagdhuber, T.; Hajnsek, I.; Papathanassiou, K.P. An Iterative Generalized Hybrid Decomposition for Soil Moisture Retrieval Under Vegetation Cover Using Fully Polarimetric SAR. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3911–3922. [Google Scholar] [CrossRef]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Requirements for Model-Based Polarimetric Decompositions. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 8–11 July 2008; IEEE: New York, NY, USA, 2008; Volume 5, pp. 417–420. [Google Scholar]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-based Decomposition of Polarimetric SAR Covariance Matrices Constrained for Nonnegative Eigenvalues. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3452–3459. [Google Scholar] [CrossRef]
- Lee, J.S.; Ainsworth, T.L. The Effect of Orientation Angle Compensation on Coherency Matrix and Polarimetric Target Decompositions. IEEE Trans. Geosci. Remote Sens. 2011, 49, 53–64. [Google Scholar] [CrossRef]
- Yin, J.; Yang, J. Target Decomposition Based on Symmetric Scattering Model for Hybrid Polarization SAR Imagery. IEEE Geosci. Remote Sens. Lett. 2021, 18, 494–498. [Google Scholar] [CrossRef]
- Chen, S.-W.; Li, Y.-Z.; Wang, X.-S.; Xiao, S.-P.; Sato, M. Modeling and Interpretation of Scattering Mechanisms in Polarimetric Synthetic Aperture Radar: Advances and perspectives. IEEE Signal Process. Mag. 2014, 31, 79–89. [Google Scholar] [CrossRef]
- Cloude, S.R. Polarisation: Applications in Remote Sensing; Oxford University Press: New York, NY, USA, 2010. [Google Scholar]
- Singh, G.; Yamaguchi, Y.; Park, S.; Cui, Y.; Kobayashi, H. Hybrid Freeman/Eigenvalue Decomposition Method with Extended Volume Scattering Model. IEEE Geosci. Remote Sens. Lett. 2013, 10, 81–85. [Google Scholar] [CrossRef]
- Maurya, H.; Bhattacharya, A.; Mishra, A.K.; Panigrahi, R.K. Hybrid Three-Component Scattering Power Characterization From Polarimetric SAR Data Isolating Dominant Scattering Mechanisms. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Chen, S.-W.; Sato, M. Tsunami Damage Investigation of Built-Up Areas Using Multitemporal Spaceborne Full Polarimetric SAR Images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1985–1997. [Google Scholar] [CrossRef]
- Yamaguchi, Y.; Sato, A.; Boerner, W.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2251–2258. [Google Scholar] [CrossRef]
- Xiang, D.; Ban, Y.; Su, Y. Model-Based Decomposition with Cross Scattering for Polarimetric SAR Urban Areas. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2496–2500. [Google Scholar] [CrossRef]
- Hu, C.; Wang, Y.; Sun, X.; Quan, S.; Xiang, D. Model-Based Polarimetric Target Decomposition with Power Redistribution for Urban Areas. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 8795–8808. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, W.; Liu, X.; Wang, C. Seven-Component Decomposition Using Refined Volume Scattering Models and New Configurations of Mixed Dipoles. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4339–4351. [Google Scholar] [CrossRef]
- Zhang, S.; Yu, X.; Wang, L. Modified version of three-component model-based decomposition for polarimetric SAR data. J. Syst. Eng. Electron. 2019, 30, 270–277. [Google Scholar] [CrossRef]
- Han, W.; Fu, H.; Zhu, J.; Wang, C.; Xie, Q. Polarimetric SAR Decomposition by Incorporating a Rotated Dihedral Scattering Model. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Yue, X.; Teng, F.; Lin, Y.; Hong, W. Target Scattering Feature Extraction Based on Parametric Model Using Multi-Aspect SAR Data. Remote Sens. 2023, 15, 1883. [Google Scholar] [CrossRef]
- Arii, M.; van Zyl, J.J.; Kim, Y. Adaptive Model-Based Decomposition of Polarimetric SAR Covariance Matrices. IEEE Trans. Geosci. Remote Sens. 2010, 49, 1104–1113. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Xiao, S.-P.; Sato, M. General Polarimetric Model-Based Decomposition for Coherency Matrix. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1843–1855. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Singh, G.; Manickam, S.; Yamaguchi, Y. An adaptive general four-component scattering power decomposition with unitary transformation of coherency matrix (AG4U). IEEE Geosci. Remote Sens. Lett. 2015, 12, 2110–2114. [Google Scholar] [CrossRef]
- Cui, Y.; Yamaguchi, Y.; Yang, J.; Park, S.-E.; Kobayashi, H.; Singh, G. Three-Component Power Decomposition for Polarimetric SAR Data Based on Adaptive Volume Scatter Modeling. Remote Sens. 2012, 4, 1559–1572. [Google Scholar] [CrossRef]
- Chen, S.-W.; Wang, X.-S.; Li, Y.-Z.; Sato, M. Adaptive Model-Based Polarimetric Decomposition Using PolInSAR Coherence. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1705–1718. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, W.; Liu, X.; Wang, C.; Kuijper, A.; Guthe, S. Demonstration and Analysis of an Extended Adaptive General Four-Component Decomposition. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 2573–2586. [Google Scholar] [CrossRef]
- Wang, T.; Suo, Z.; Jiang, P.; Ti, J.; Ding, Z.; Qin, T. An Optimal Polarization SAR Three-Component Target Decomposition Based on Semi-Definite Programming. Remote Sens. 2023, 15, 5292. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, Q.; Jiao, J. An Adaptive Decomposition Approach with Dipole Aggregation Model for Polarimetric SAR Data. Remote Sens. 2021, 13, 2583. [Google Scholar] [CrossRef]
- Freeman, A. Fitting a Two-Component Scattering Model to Polarimetric SAR Data from Forests. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2583–2592. [Google Scholar] [CrossRef]
- Dey, S.; Bhattacharya, A.; Frery, A.C.; Lopez-Martinez, C.; Rao, Y.S. A Model-Free Four Component Scattering Power Decomposition for Polarimetric SAR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 3887–3902. [Google Scholar] [CrossRef]
- Maurya, H.; Panigrahi, R.K. Non-negative scattering power decomposition for PolSAR data interpretation. IET Radar Sonar Navig. 2018, 12, 593–602. [Google Scholar] [CrossRef]
- Li, X.; Liu, Y.; Huang, P.; Liu, X.; Tan, W.; Fu, W.; Li, C. A Hybrid Polarimetric Target Decomposition Algorithm with Adaptive Volume Scattering Model. Remote Sens. 2022, 14, 2441. [Google Scholar] [CrossRef]
- Maurya, H.; Panigrahi, R.K. PolSAR Coherency Matrix Optimization Through Selective Unitary Rotations for Model-Based Decomposition Scheme. IEEE Geosci. Remote Sens. Lett. 2018, 16, 658–662. [Google Scholar] [CrossRef]
- Manuel, L. Analysis and Estimation of Biophysical Parameters of Vegetation by Radar Polarimetry. Ph.D. Thesis, Universidad Politecnica de Valencia, Valencia, Spain, 2000. [Google Scholar]
- Liu, L. Research on Composite Electromagnetic Scattering from Grass-Containing Rough Surfaces and Targets; Xidian University: Xi’an, China, 2020. [Google Scholar] [CrossRef]



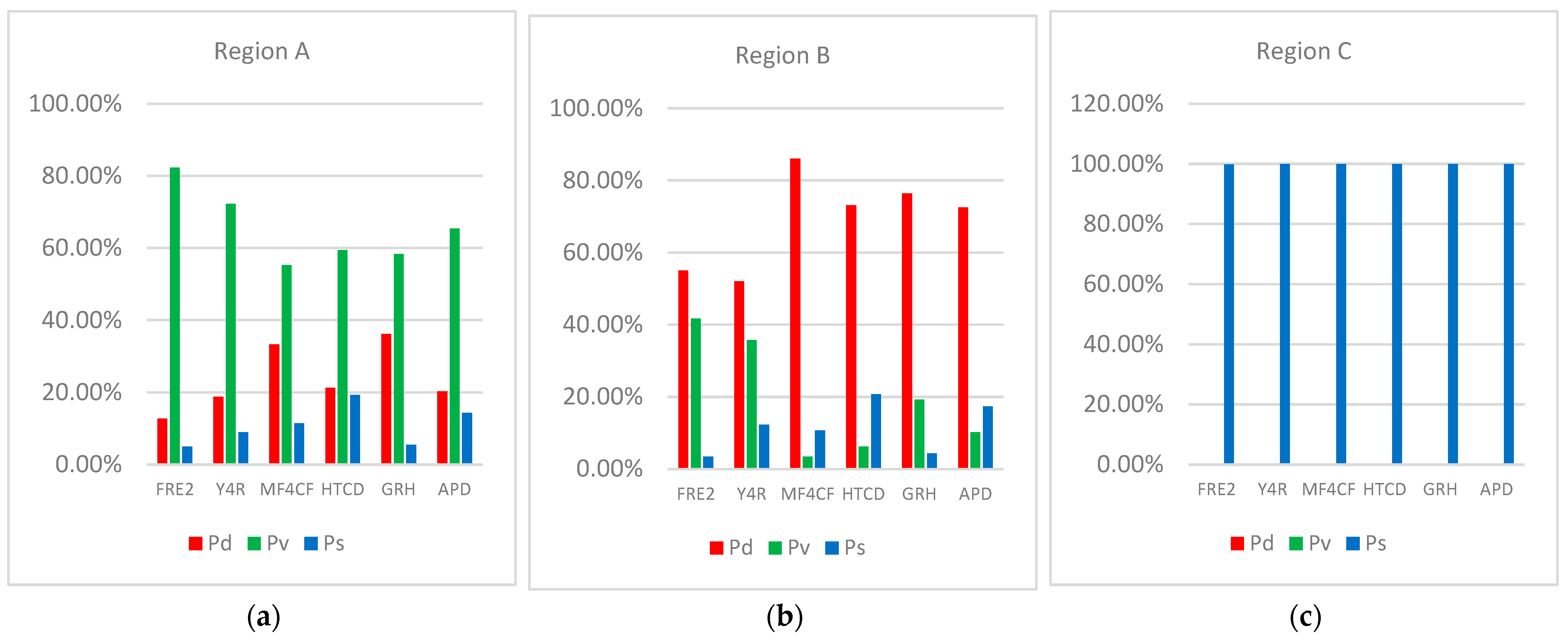




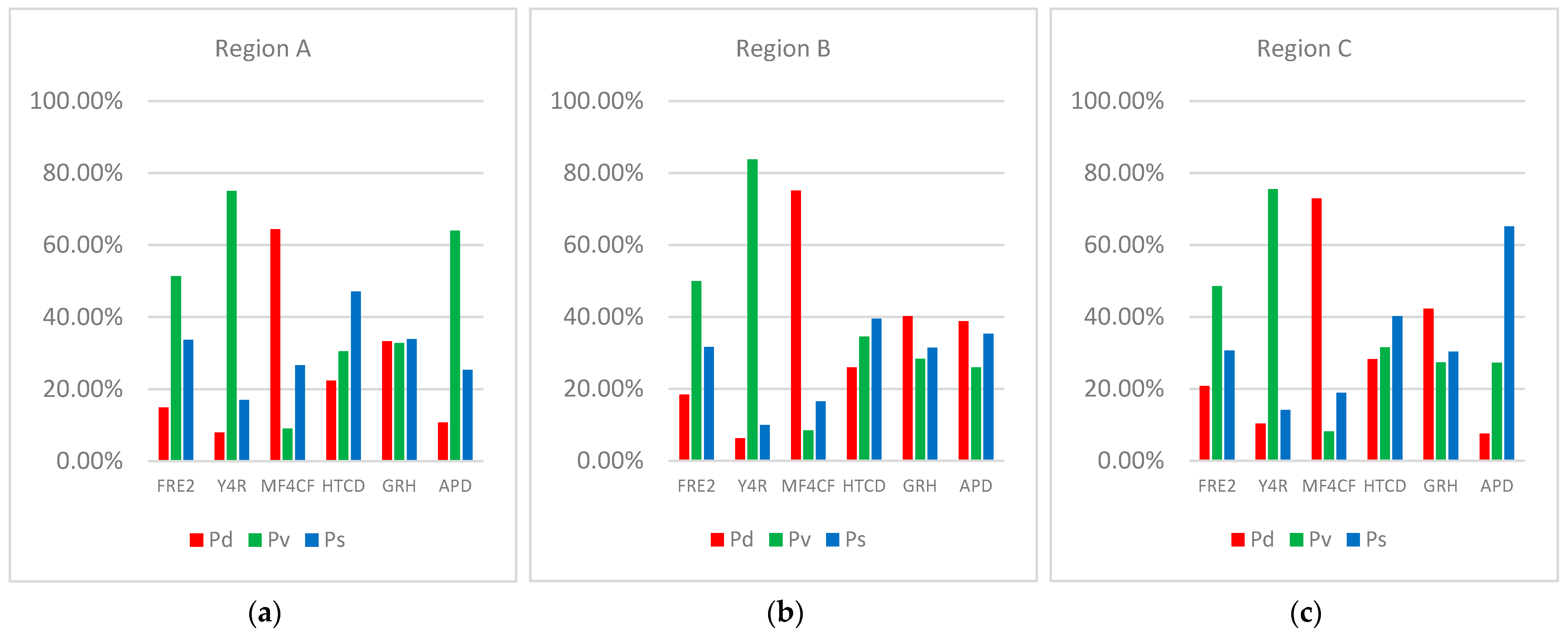

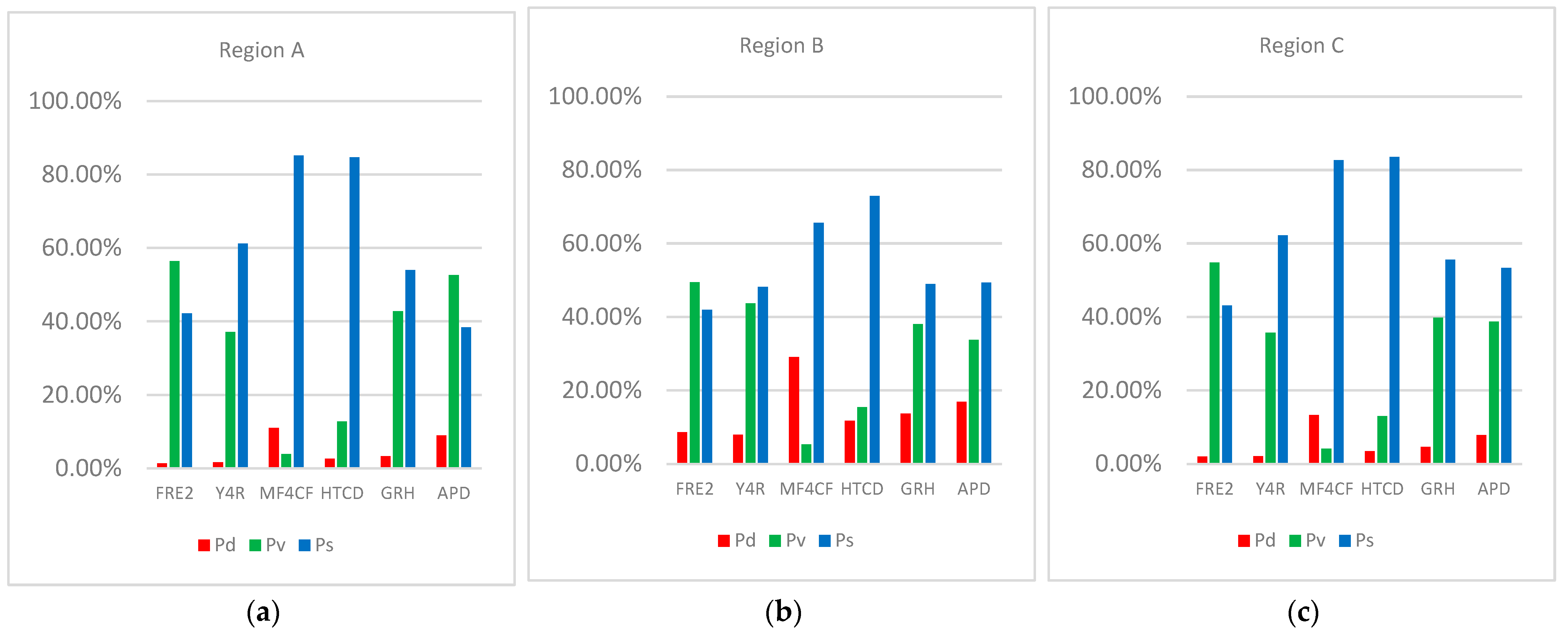
| Region | Component | FRE2 | Y4R | MF4CF | HTCD | GRH | APD |
|---|---|---|---|---|---|---|---|
| A | Pd | 12.75 | 18.80 | 33.25 | 21.29 | 36.15 | 20.30 |
| Pv | 82.31 | 72.27 | 55.28 | 59.45 | 58.38 | 65.42 | |
| Ps | 4.94 | 8.93 | 11.47 | 19.26 | 5.47 | 14.28 | |
| B | Pd | 54.97 | 51.99 | 86.00 | 73.11 | 76.43 | 72.53 |
| Pv | 41.66 | 35.77 | 3.36 | 6.15 | 19.24 | 10.13 | |
| Ps | 3.37 | 12.24 | 10.64 | 20.74 | 4.33 | 17.34 | |
| C | Pd | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Pv | 0.21 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | |
| Ps | 99.79 | 100.00 | 100.00 | 100.00 | 99.99 | 100.00 |
| Region | Component | FRE2 | Y4R | MF4CF | HTCD | GRH | APD |
|---|---|---|---|---|---|---|---|
| A | Pd | 14.86 | 7.93 | 64.34 | 22.38 | 33.33 | 10.70 |
| Pv | 51.41 | 75.04 | 9.02 | 30.54 | 32.77 | 64.00 | |
| Ps | 33.73 | 17.03 | 26.64 | 47.08 | 33.90 | 25.30 | |
| B | Pd | 18.44 | 6.30 | 75.07 | 26.01 | 40.24 | 38.76 |
| Pv | 49.92 | 83.76 | 8.44 | 34.51 | 28.36 | 25.97 | |
| Ps | 31.64 | 9.94 | 16.49 | 39.48 | 31.40 | 35.27 | |
| C | Pd | 20.77 | 10.38 | 72.94 | 28.25 | 42.30 | 7.57 |
| Pv | 48.59 | 75.49 | 8.16 | 31.55 | 27.32 | 27.31 | |
| Ps | 30.64 | 14.13 | 18.90 | 40.20 | 30.38 | 65.12 |
| Region | Component | FRE2 | Y4R | MF4CF | HTCD | GRH | APD |
|---|---|---|---|---|---|---|---|
| A | Pd | 1.38 | 1.66 | 10.97 | 2.63 | 3.28 | 8.97 |
| Pv | 56.41 | 37.16 | 3.92 | 12.71 | 42.77 | 52.66 | |
| Ps | 42.21 | 61.18 | 85.11 | 84.66 | 53.95 | 38.37 | |
| B | Pd | 8.62 | 7.92 | 29.08 | 11.73 | 13.69 | 16.89 |
| Pv | 49.45 | 43.68 | 5.31 | 15.39 | 38.03 | 33.73 | |
| Ps | 41.93 | 48.4 | 65.61 | 72.88 | 48.28 | 49.38 | |
| C | Pd | 2.00 | 2.07 | 13.26 | 3.49 | 4.57 | 7.88 |
| Pv | 54.86 | 35.69 | 4.09 | 13.03 | 39.82 | 38.77 | |
| Ps | 43.14 | 62.24 | 82.65 | 83.48 | 55.61 | 53.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, P.; Li, B.; Li, X.; Tan, W.; Xu, W.; Chen, Y. An Adaptive Polarimetric Target Decomposition Algorithm Based on the Anisotropic Degree. Remote Sens. 2024, 16, 1015. https://doi.org/10.3390/rs16061015
Huang P, Li B, Li X, Tan W, Xu W, Chen Y. An Adaptive Polarimetric Target Decomposition Algorithm Based on the Anisotropic Degree. Remote Sensing. 2024; 16(6):1015. https://doi.org/10.3390/rs16061015
Chicago/Turabian StyleHuang, Pingping, Baoyu Li, Xiujuan Li, Weixian Tan, Wei Xu, and Yuejuan Chen. 2024. "An Adaptive Polarimetric Target Decomposition Algorithm Based on the Anisotropic Degree" Remote Sensing 16, no. 6: 1015. https://doi.org/10.3390/rs16061015
APA StyleHuang, P., Li, B., Li, X., Tan, W., Xu, W., & Chen, Y. (2024). An Adaptive Polarimetric Target Decomposition Algorithm Based on the Anisotropic Degree. Remote Sensing, 16(6), 1015. https://doi.org/10.3390/rs16061015