Analysing the Relationship between Spatial Resolution, Sharpness and Signal-to-Noise Ratio of Very High Resolution Satellite Imagery Using an Automatic Edge Method
Abstract
:1. Introduction
1.1. The Concepts of Spatial Resolution and Image Sharpness
1.2. The Automatic Edge Method
1.3. Objectives
2. Materials and Methods
2.1. Using the AEM to Estimate the Image SNR
- The edge should be linear;
- The edge should mark the transition between two strongly contrasted areas;
- The transition between these two areas should be sudden;
- The areas around the edge, if considered individually, should be as homogeneous as possible.
2.2. Sharpness Classification Methodology
- Aliased Product: FWHM values lower than 1.0 pixel (the lower the FWHM value, the stronger the aliasing effects in the image);
- Balanced Product: FWHM values between 1.0 and 2.0 pixels (images with a FWHM value closer to 1.5 will have more “balanced” sharpness performance). This range was also confirmed by [29];
- Blurry Product: FWHM values higher than 2.0 pixels (the greater the FWHM, the stronger the blurring effects in the image).
2.3. The SNR Threshold Problem
2.4. Materials
- Landsat-7/8/9 L1T terrain-corrected products: https://earthexplorer.usgs.gov/ (accessed on 14 March 2024);
- Sentinel-2A/B L1C products: https://scihub.copernicus.eu/dhus/ (accessed on 14 March 2024);
- VHR_IMAGE_2021 Level-3 products: https://panda.copernicus.eu/web/cds-catalogue/panda (accessed on 14 March 2024).
3. Results
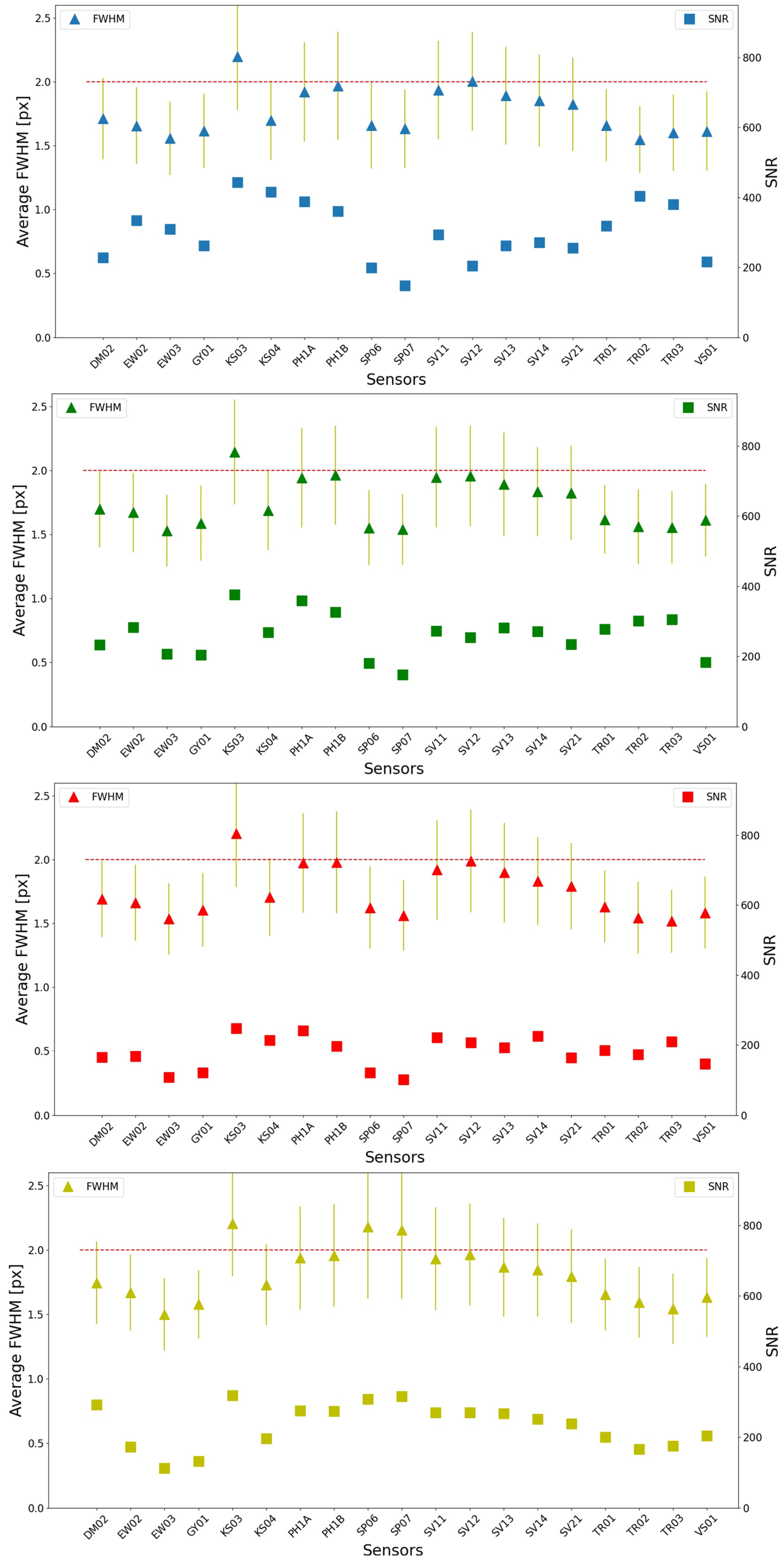
3.1. FWHM and SNR Estimation
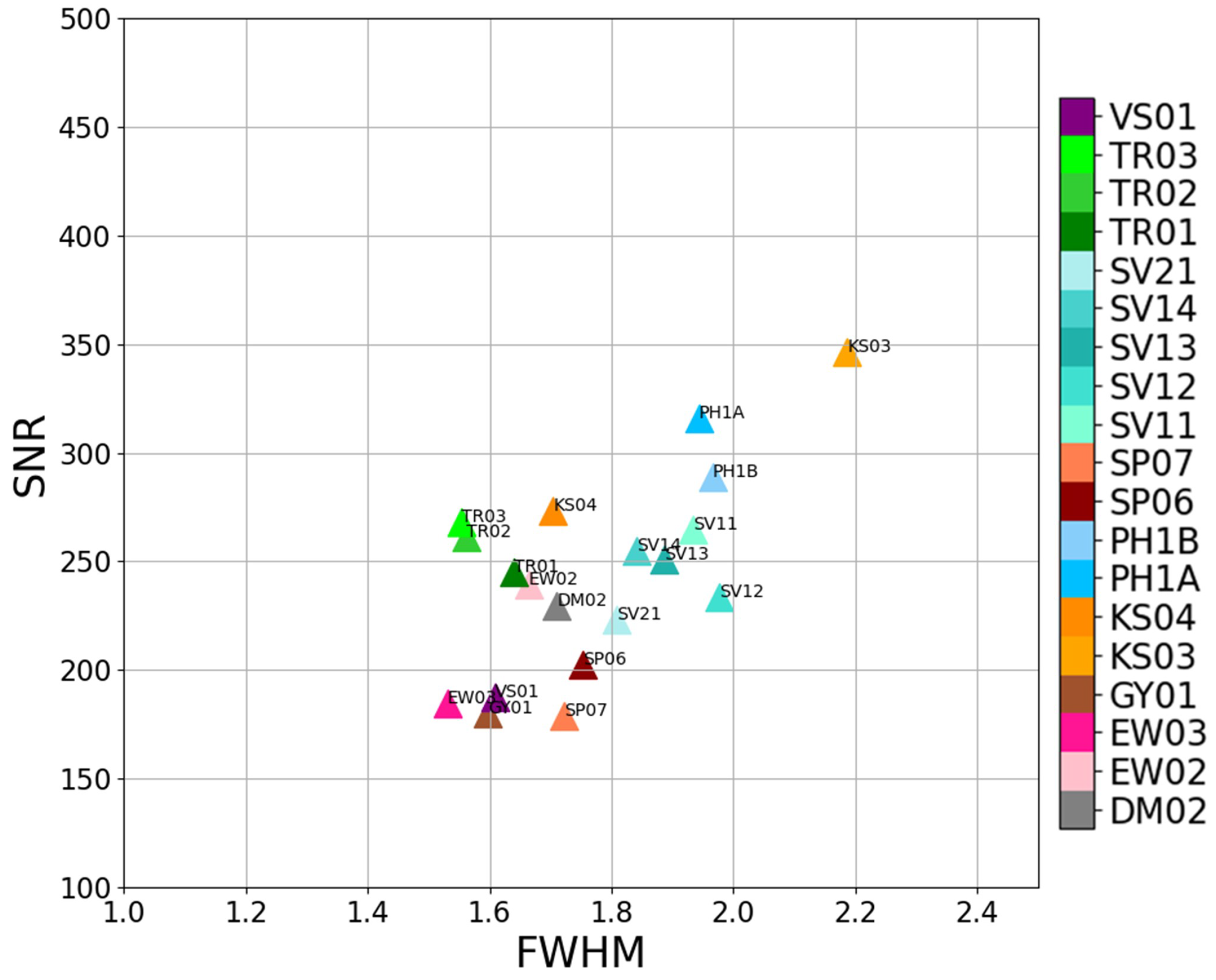
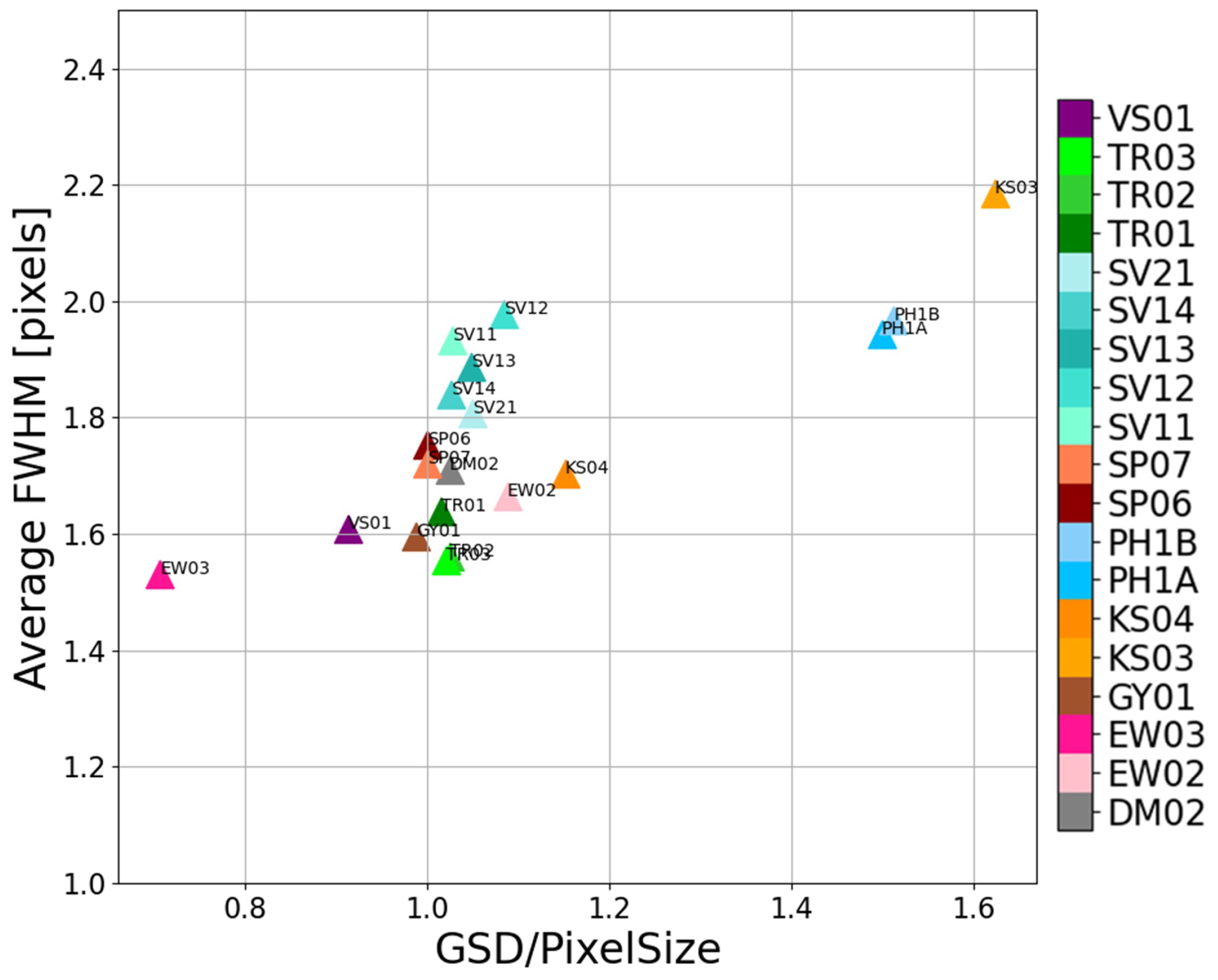
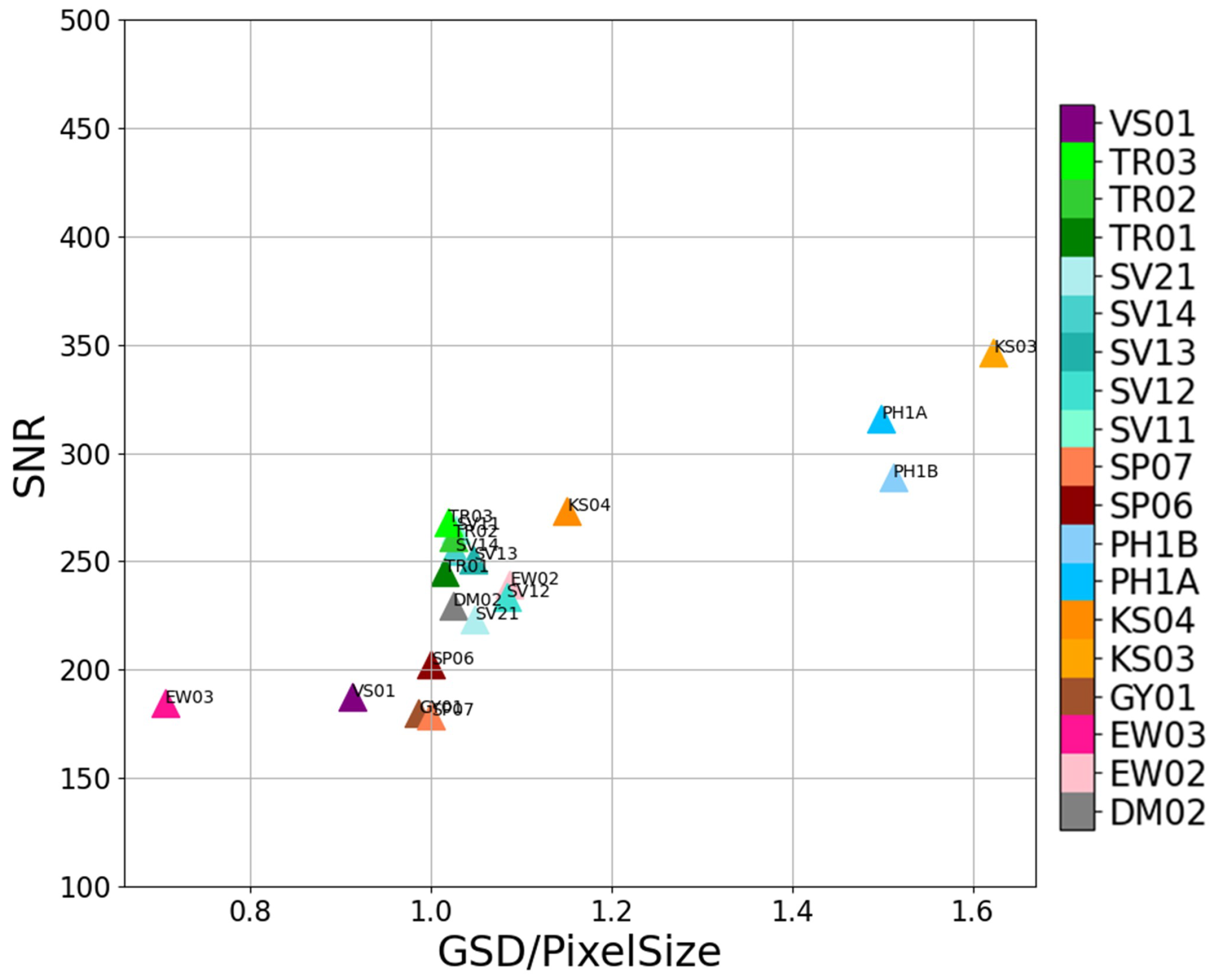
3.2. FWHM and SNR Assessment against GSD/PS Ratio
4. Discussion
4.1. FWHM and SNR Generic Assessment
4.2. Image Quality Assessment: FWHM, SNR and GSD/PS Ratio
- Platform motion, causing jitter and smear;
- Imperfections in the manufacturing of the optical system;
- Finite slit size;
- Random noise;
- Atmospheric effects.
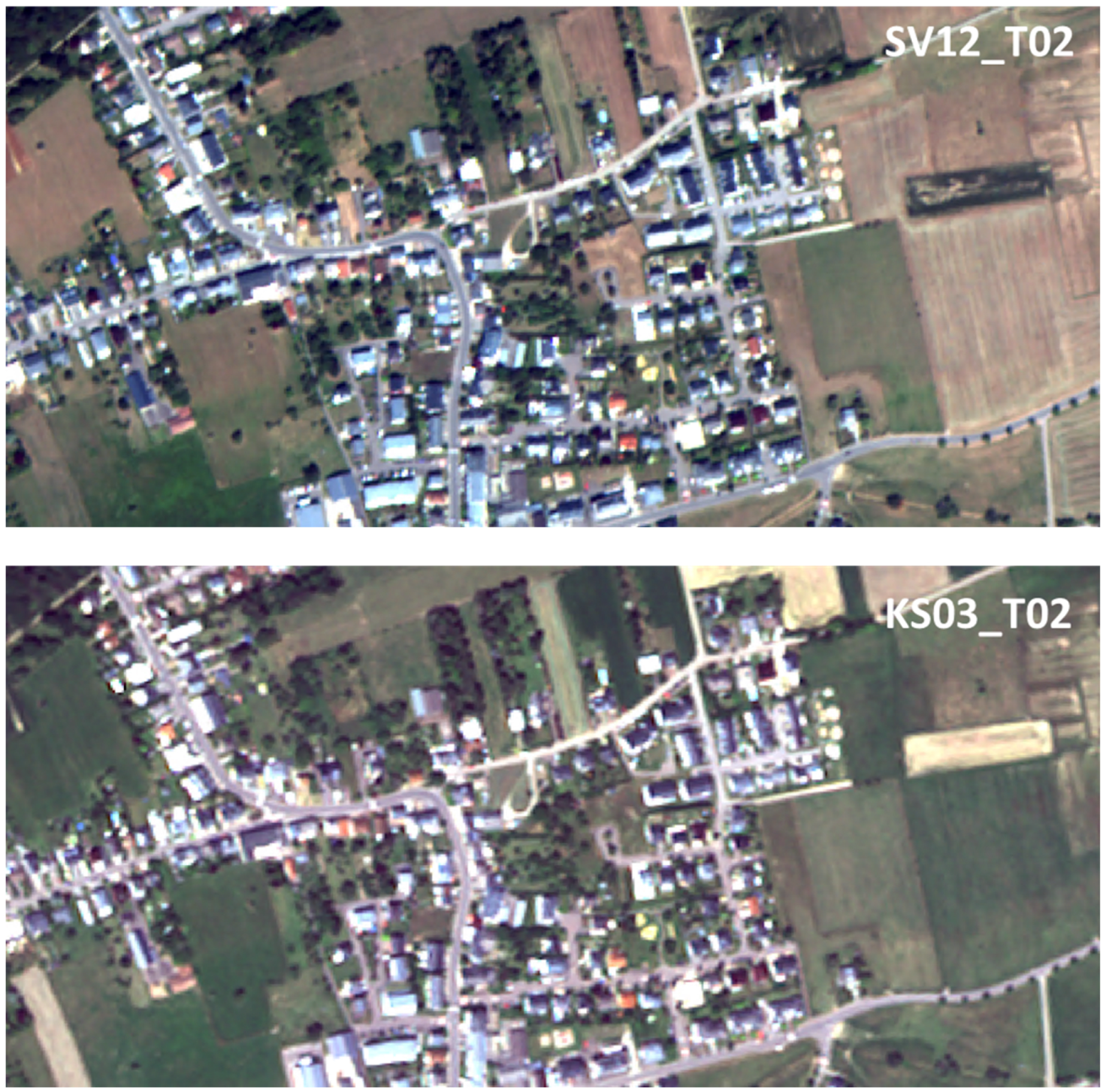
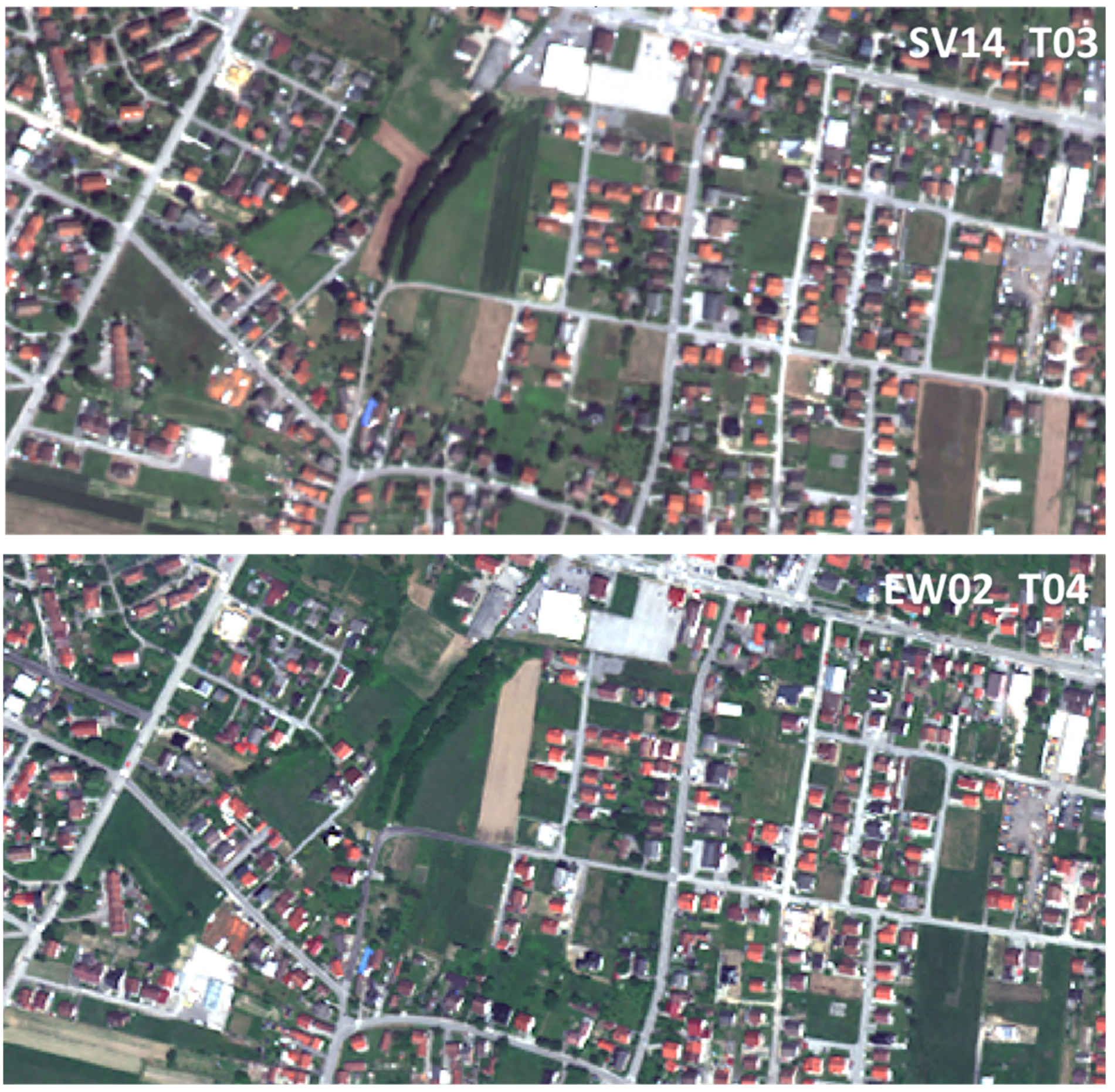
4.3. Investigating the SuperView-1 Outliers
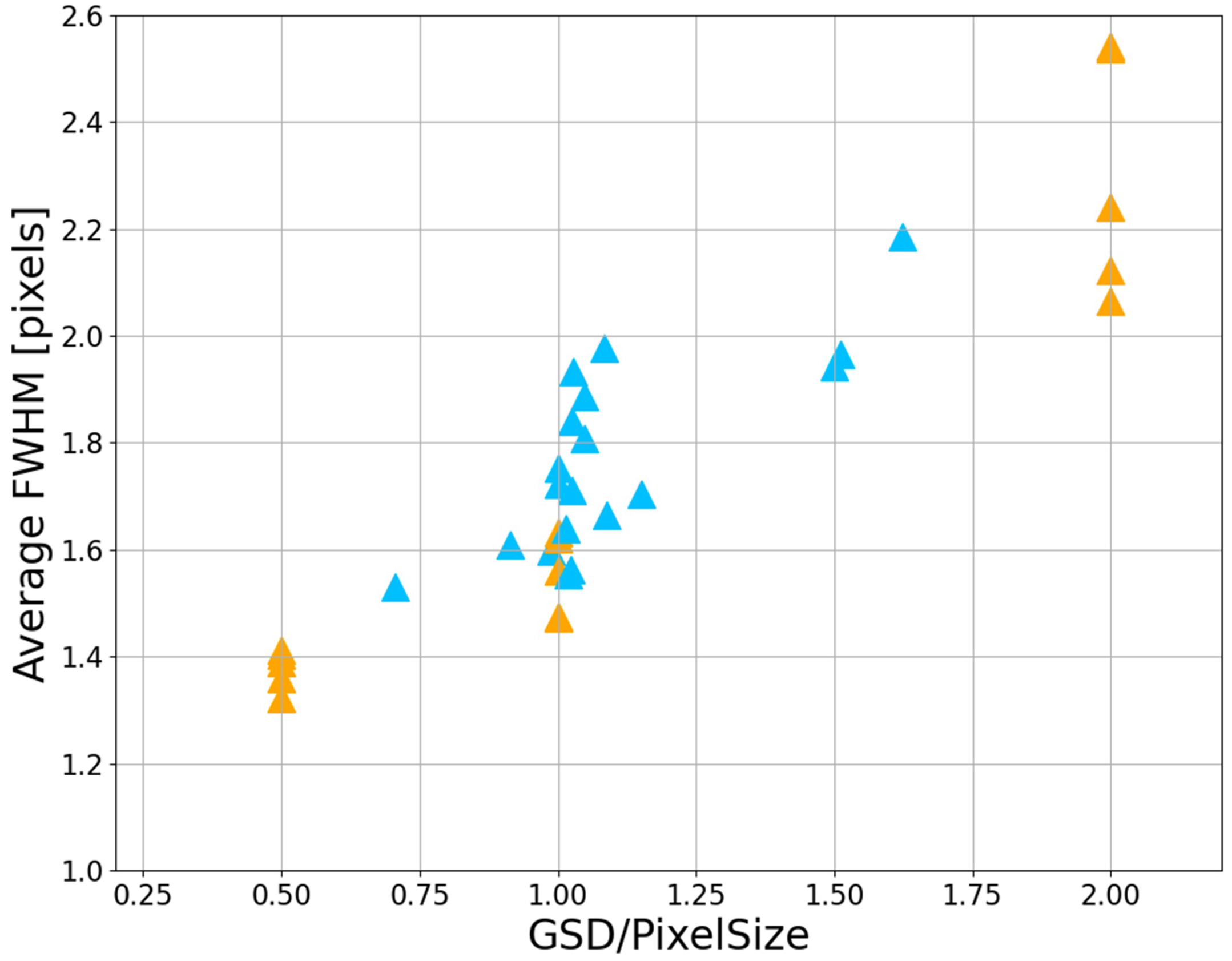
4.4. Expanding the GSD/PS Range: A Synthetic Experiment with Landsat and Sentinel Products
- Landsat-7/8/9 products: original PS of 30 m (i.e., GSD/PS = 1.00), up-sampled to 15 m (i.e., GSD/PS = 2.00) and down-sampled to 60 m (i.e., GSD/PS = 0.50);
- Sentinel-2 products: original PS of 10 m (i.e., GSD/PS = 1.00), up-sampled to 5 m (i.e., GSD/PS = 2.00) and down-sampled to 20 m (i.e., GSD/PS = 0.5).
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AEM | Automatic Edge Method |
| CCM | Copernicus Contributing Missions |
| CQC | Coordinated Quality Control |
| DN | Digital Number |
| EEA | European Economic Area |
| EM | Edge Method |
| EO | Earth Observation |
| ESF | Edge Spread Function |
| FWHM | Full-Width at Half-Maximum |
| GIQE | Generalized Image-Quality Equation |
| GSD | Ground Sampling Distance |
| HA | Homogeneous Area |
| IFOV | Instantaneous Field Of View |
| LSF | Line Spread Function |
| MTF | Modulation Transfer Function |
| NIIRS | National Imagery Interpretability Rating Scale |
| NIR | Near-Infrared |
| ONA | Off-Nadir Angle |
| PS | Pixel Size |
| PSF | Point Spread Function |
| RER | Relative Edge Response |
| RGB | Red, Green and Blue |
| SNR | Signal-to-Noise Ratio |
| USGS | United States Geological Survey |
| VC | Virtual Constellation |
| VHR | Very High Resolution |
Appendix A
| Mission | Product ID | Product Name | GSD [m] | PS [m] |
|---|---|---|---|---|
| DEIMOS-2 | DM02_01 | DM02_HRS_MS4_1C_20210616T101753_20210616T101755_TOU_1234_6ad4 | 4.19 | 4.00 |
| DM02_02 | DM02_HRS_MS4_1C_20210617T085910_20210617T085912_TOU_1234_9a36 | 4.00 | 4.00 | |
| DM02_03 | DM02_HRS_MS4_1C_20210717T083735_20210717T083737_TOU_1234_7e80 | 4.06 | 4.00 | |
| DM02_04 | DM02_HRS_MS4_1C_20210730T084952_20210730T084955_TOU_1234_b629 | 4.01 | 4.00 | |
| DM02_05 | DM02_HRS_MS4_1C_20210731T072451_20210731T072454_TOU_1234_1aa9 | 4.23 | 4.00 | |
| WORLDVIEW | EW02_01 | EW02_WV1_MS4_OR_20200609T084534_20200609T084540_TOU_1234_873f | 2.43 | 2.00 |
| EW02_02 | EW02_WV1_MS4_OR_20210610T103006_20210610T103017_TOU_1234_5940 | 2.06 | 2.00 | |
| EW02_03 | EW02_WV1_MS4_OR_20210704T104516_20210704T104524_TOU_1234_46fd | 2.31 | 2.00 | |
| EW02_04 | EW02_WV1_MS4_OR_20210807T095542_20210807T095545_TOU_1234_c0bf | 1.90 | 2.00 | |
| EW03_01 | EW03_WV3_MS4_OR_20200818T102631_20200818T102654_TOU_1234_5c88 | 1.24 | 2.00 | |
| EW03_02 | EW03_WV3_MS4_OR_20210719T101306_20210719T101336_TOU_1234_79d9 | 1.36 | 2.00 | |
| EW03_03 | EW03_WV3_MS4_OR_20210721T090836_20210721T090847_TOU_1234_140e | 1.34 | 2.00 | |
| EW03_04 | EW03_WV3_MS4_OR_20210925T112632_20210925T112644_TOU_1234_2f52 | 1.71 | 2.00 | |
| GEOEYE | GY01_01 | GY01_GIS_MS4_OR_20200606T100416_20200606T100423_TOU_1234_dc9d | 2.18 | 2.00 |
| GY01_02 | GY01_GIS_MS4_OR_20200629T104347_20200629T104355_TOU_1234_469f | 1.91 | 2.00 | |
| GY01_03 | GY01_GIS_MS4_OR_20200908T090225_20200908T090228_TOU_1234_c95f | 1.95 | 2.00 | |
| GY01_04 | GY01_GIS_MS4_OR_20210703T102536_20210703T102553_TOU_1234_7326 | 1.95 | 2.00 | |
| GY01_05 | GY01_GIS_MS4_OR_20210903T095209_20210903T095215_TOU_1234_f694 | 1.88 | 2.00 | |
| KOMPSAT | KS03_01 | KS03_AIS_MSP_1G_20200609T114244_20200609T114246_TOU_1234_82ef | 3.00 | 2.00 |
| KS03_02 | KS03_AIS_MSP_1G_20200625T120729_20200625T120731_TOU_1234_46e4 | 2.87 | 2.00 | |
| KS03_03 | KS03_AIS_MSP_1G_20200801T125053_20200801T125055_TOU_1234_2069 | 3.77 | 2.00 | |
| KS03_04 | KS03_AIS_MSP_1G_20200914T130815_20200914T130817_TOU_1234_2cc3 | 3.76 | 2.00 | |
| KS03_05 | KS03_AIS_MSP_1G_20210715T111238_20210715T111240_TOU_1234_cb09 | 2.83 | 2.00 | |
| KS04_01 | KS04_AIS_MSP_1G_20200813T121309_20200813T121311_TOU_1234_3281 | 2.21 | 2.00 | |
| KS04_02 | KS04_AIS_MSP_1G_20200912T130938_20200912T130939_TOU_1234_d250 | 2.31 | 2.00 | |
| KS04_03 | KS04_AIS_MSP_1G_20210624T112153_20210624T112155_TOU_1234_e7a2 | 2.22 | 2.00 | |
| KS04_04 | KS04_AIS_MSP_1G_20210624T112409_20210624T112410_TOU_1234_fc8b | 2.47 | 2.00 | |
| PLEIADES | PH1A_01 | PH1A_PHR_MS___3_20200523T090432_20200523T090432_TOU_1234_82cf | 2.81 | 2.00 |
| PH1A_02 | PH1A_PHR_MS___3_20200813T083340_20200813T083346_TOU_1234_52ca | 3.06 | 2.00 | |
| PH1A_03 | PH1A_PHR_MS___3_20200901T101529_20200901T101535_TOU_1234_3ebf | 3.03 | 2.00 | |
| PH1A_04 | PH1A_PHR_MS___3_20200914T110429_20200914T110429_TOU_1234_6017 | 2.87 | 2.00 | |
| PH1A_05 | PH1A_PHR_MS___3_20210906T110647_20210906T110652_TOU_1234_8047 | 3.22 | 2.00 | |
| PH1B_01 | PH1B_PHR_MS___3_20210709T102247_20210709T102251_TOU_1234_57d4 | 2.80 | 2.00 | |
| PH1B_02 | PH1B_PHR_MS___3_20210718T082612_20210718T082618_TOU_1234_9135 | 2.81 | 2.00 | |
| PH1B_03 | PH1B_PHR_MS___3_20210727T112528_20210727T112534_TOU_1234_0c30 | 2.82 | 2.00 | |
| PH1B_04 | PH1B_PHR_MS___3_20210818T101425_20210818T101433_TOU_1234_20e3 | 3.19 | 2.00 | |
| PH1B_05 | PH1B_PHR_MS___3_20210921T105222_20210921T105230_TOU_1234_bf1e | 3.50 | 2.00 | |
| SPOT | SP06_01 | SP06_NAO_MS4__3_20210616T102257_20210616T102307_TOU_1234_fe33 | 4.00 | 4.00 |
| SP06_02 | SP06_NAO_MS4__3_20210624T110229_20210624T110301_TOU_1234_d272 | 4.00 | 4.00 | |
| SP06_03 | SP06_NAO_MS4__3_20210714T083035_20210714T083045_TOU_1234_1c5e | 4.00 | 4.00 | |
| SP06_04 | SP06_NAO_MS4__3_20210814T101933_20210814T101942_TOU_1234_918d | 4.00 | 4.00 | |
| SP07_01 | SP07_NAO_MS4__3_20200630T102323_20200630T102323_TOU_1234_fbdc | 4.00 | 4.00 | |
| SP07_02 | SP07_NAO_MS4__3_20210610T101730_20210610T101738_TOU_1234_071c | 4.00 | 4.00 | |
| SP07_03 | SP07_NAO_MS4__3_20210611T110012_20210611T110045_TOU_1234_86cf | 4.00 | 4.00 | |
| SP07_04 | SP07_NAO_MS4__3_20210727T082941_20210727T082959_TOU_1234_1fc8 | 4.00 | 4.00 | |
| SUPERVIEW-1 | SV11_01 | SW00_OPT_MS4_1C_20200725T112833_20200725T112835_TOU_1234_1333 | 2.00 | 2.00 |
| SV11_02 | SW00_OPT_MS4_1C_20210622T081606_20210622T081608_TOU_1234_3ebc | 2.06 | 2.00 | |
| SV11_03 | SW00_OPT_MS4_1C_20210907T092821_20210907T092823_TOU_1234_8d84 | 2.07 | 2.00 | |
| SV11_04 | SW00_OPT_MS4_1C_20210923T103134_20210923T103136_TOU_1234_99d5 | 2.09 | 2.00 | |
| SV12_01 | SW00_OPT_MS4_1C_20200721T112528_20200721T112530_TOU_1234_5bb0 | 2.08 | 2.00 | |
| SV12_02 | SW00_OPT_MS4_1C_20200810T114626_20200810T114628_TOU_1234_135d | 2.19 | 2.00 | |
| SV12_03 | SW00_OPT_MS4_1C_20210705T090341_20210705T090343_TOU_1234_a963 | 2.01 | 2.00 | |
| SV12_04 | SW00_OPT_MS4_1C_20211003T115354_20211003T115356_TOU_1234_acd7 | 2.39 | 2.00 | |
| SV13_01 | SW00_OPT_MS4_1C_20200709T095313_20200709T095315_TOU_1234_5b57 | 2.00 | 2.00 | |
| SV13_02 | SW00_OPT_MS4_1C_20210602T104919_20210602T104922_TOU_1234_7d74 | 2.24 | 2.00 | |
| SV13_03 | SW00_OPT_MS4_1C_20210624T103220_20210624T103222_TOU_1234_88de | 2.01 | 2.00 | |
| SV13_04 | SW00_OPT_MS4_1C_20210909T100805_20210909T100807_TOU_1234_525f | 2.13 | 2.00 | |
| SV14_01 | SW00_OPT_MS4_1C_20200710T102057_20200710T102059_TOU_1234_d720 | 2.05 | 2.00 | |
| SV14_02 | SW00_OPT_MS4_1C_20210629T114234_20210629T114236_TOU_1234_8530 | 2.06 | 2.00 | |
| SV14_03 | SW00_OPT_MS4_1C_20210706T100258_20210706T100301_TOU_1234_3cf5 | 2.09 | 2.00 | |
| SV14_04 | SW00_OPT_MS4_1C_20210803T082311_20210803T082313_TOU_1234_b5eb | 2.01 | 2.00 | |
| SUPERVIEW-2 | SV21_01 | SW00_OPT_MS4_1C_20210707T100020_20210707T100023_TOU_1234_be4a | 2.04 | 2.00 |
| SV21_02 | SW00_OPT_MS4_1C_20210731T094046_20210731T094049_TOU_1234_1f36 | 2.07 | 2.00 | |
| SV21_03 | SW00_OPT_MS4_1C_20210804T080013_20210804T080016_TOU_1234_98e4 | 2.13 | 2.00 | |
| SV21_04 | SW00_OPT_MS4_1C_20210907T113148_20210907T113151_TOU_1234_0833 | 2.12 | 2.00 | |
| SV21_05 | SW00_OPT_MS4_1C_20210910T093006_20210910T093009_TOU_1234_8a03 | 2.13 | 2.00 | |
| TRIPLESAT | TR01_01 | TR00_VHI_MS4_1C_20200704T071337_20200704T071340_TOU_1234_731f | 4.15 | 4.00 |
| TR01_02 | TR00_VHI_MS4_1C_20210606T081823_20210606T081826_TOU_1234_4fde | 4.04 | 4.00 | |
| TR01_03 | TR00_VHI_MS4_1C_20210606T081826_20210606T081830_TOU_1234_9911 | 4.03 | 4.00 | |
| TR01_04 | TR00_VHI_MS4_1C_20210920T094216_20210920T094220_TOU_1234_0392 | 4.02 | 4.00 | |
| TR02_01 | TR00_VHI_MS4_1C_20210605T082416_20210605T082420_TOU_1234_3e9c | 4.00 | 4.00 | |
| TR02_02 | TR00_VHI_MS4_1C_20210630T080542_20210630T080546_TOU_1234_b8e8 | 4.08 | 4.00 | |
| TR02_03 | TR00_VHI_MS4_1C_20210630T080552_20210630T080556_TOU_1234_28c7 | 4.09 | 4.00 | |
| TR02_04 | TR00_VHI_MS4_1C_20210711T080456_20210711T080459_TOU_1234_a1c2 | 4.22 | 4.00 | |
| TRIPLESAT | TR03_01 | TR00_VHI_MS4_1C_20210622T082010_20210622T082014_TOU_1234_8f50 | 4.05 | 4.00 |
| TR03_02 | TR00_VHI_MS4_1C_20210629T081102_20210629T081105_TOU_1234_5dd1 | 4.01 | 4.00 | |
| TR03_03 | TR00_VHI_MS4_1C_20210713T075220_20210713T075224_TOU_1234_a50b | 4.19 | 4.00 | |
| TR03_04 | TR00_VHI_MS4_1C_20210808T075943_20210808T075947_TOU_1234_a808 | 4.07 | 4.00 | |
| VISION-1 | VS01_01 | VS01_S14_MS4__3_20200901T095846_20200901T095858_TOU_1234_1708 | 3.73 | 4.00 |
| VS01_02 | VS01_S14_MS4__3_20210603T091123_20210603T091144_TOU_1234_6caa | 3.83 | 4.00 | |
| VS01_03 | VS01_S14_MS4__3_20210709T075029_20210709T075050_TOU_1234_71e2 | 3.56 | 4.00 | |
| VS01_04 | VS01_S14_MS4__3_20210801T082843_20210801T082934_TOU_1234_95fa | 3.59 | 4.00 | |
| VS01_05 | VS01_S14_MS4__3_20210805T071433_20210805T071448_TOU_1234_bb17 | 3.55 | 4.00 | |
| LANDSAT-7 | LE07_01 | LE07_L1TP_192029_20000706_20200918_02_T1 | 30 | 30 |
| LE07_02 | LE07_L1TP_199026_20000824_20200917_02_T1 | 30 | 30 | |
| LE07_03 | LE07_L1TP_200033_20000831_20211120_02_T1 | 30 | 30 | |
| LE07_04 | LE07_L1TP_201023_20000619_20200918_02_T1 | 30 | 30 | |
| LANDSAT-8 | LC08_01 | LC08_L1TP_192029_20140806_20200911_02_T1 | 30 | 30 |
| LC08_02 | LC08_L1TP_199026_20140519_20200911_02_T1 | 30 | 30 | |
| LC08_03 | LC08_L1TP_200033_20140713_20200911_02_T1 | 30 | 30 | |
| LC08_04 | LC08_L1TP_201023_20140517_20200911_02_T1 | 30 | 30 | |
| LANDSAT-9 | LC09_01 | LC09_L1TP_192029_20220703_20230408_02_T1 | 30 | 30 |
| LC09_02 | LC09_L1TP_199026_20220517_20230416_02_T1 | 30 | 30 | |
| LC09_03 | LC09_L1TP_200033_20220828_20230331_02_T1 | 30 | 30 | |
| LC09_04 | LC09_L1TP_201023_20220718_20230407_02_T1 | 30 | 30 | |
| SENTINEL-2A | S2A_01 | S2A_MSIL1C_20160504T105622_N0202_R094_T31UDP_20160504T105917 | 10 | 10 |
| S2A_02 | S2A_MSIL1C_20160606T110622_N0202_R137_T30UYD_20160606T110624 | 10 | 10 | |
| S2A_03 | S2A_MSIL1C_20160613T105622_N0202_R094_T30SVJ_20160613T110559 | 10 | 10 | |
| S2A_04 | S2A_MSIL1C_20160718T101032_N0204_R022_T32TQQ_20160718T101028 | 10 | 10 | |
| SENTINEL-2B | S2B_01 | S2B_MSIL1C_20180506T105029_N0206_R051_T31UDP_20180509T155709 | 10 | 10 |
| S2B_02 | S2B_MSIL1C_20180519T105619_N0206_R094_T30UYD_20180519T132003 | 10 | 10 | |
| S2B_03 | S2B_MSIL1C_20180708T105619_N0206_R094_T30SVJ_20180708T134424 | 10 | 10 | |
| S2B_04 | S2B_MSIL1C_20180822T101019_N0206_R022_T32TQQ_20180822T142412 | 10 | 10 |
| Product ID | Product Name |
|---|---|
| SV11_T01 | SW00_OPT_MS4_1C_20210923T103134_20210923T103136_TOU_1234_99d5 |
| GY11_T01 | GY01_GIS_MS4_OR_20220617T105537_20220617T105555_TOU_1234_4955 |
| SV12_T02 | SW00_OPT_MS4_1C_20200721T112528_20200721T112530_TOU_1234_5bb0 |
| KS03_T02 | KS03_AIS_MSP_1G_20200623T123121_20200623T123123_TOU_1234_ba37 |
| SV14_T03 | SW00_OPT_MS4_1C_20200710T102057_20200710T102059_TOU_1234_d720 |
| EW02_T03 | EW02_WV1_MS4_OR_20210526T094717_20210526T094729_TOU_1234_7650 |
References
- Fiete, R.D. Image chain analysis for space imaging systems. J. Imaging Sci. Technol. 2007, 51, 103–109. [Google Scholar] [CrossRef]
- Joseph, G. How to Specify an Electro-optical Earth Observation Camera? A Review of the Terminologies Used and its Interpretation. J. Indian Soc. Remote Sens. 2020, 48, 171–180. [Google Scholar] [CrossRef]
- Holst, G.C. Electro-Optical Imaging System Performance; SPIE-International Society for Optical Engineering: Bellingham, WA, USA, 2008. [Google Scholar]
- Cenci, L.; Pampanoni, V.; Laneve, G.; Santella, C.; Boccia, V. Presenting a Semi-Automatic, Statistically-Based Approach to Assess the Sharpness Level of Optical Images from Natural Targets via the Edge Method. Case Study: The Landsat 8 OLI–L1T Data. Remote Sens. 2021, 13, 1593. [Google Scholar] [CrossRef]
- Crespi, M.; De Vendictis, L. A procedure for high resolution satellite imagery quality assessment. Sensors 2009, 9, 3289–3313. [Google Scholar] [CrossRef] [PubMed]
- Elachi, C.; Van Zyl, J.J. Introduction to the Physics and Techniques of Remote Sensing; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Joseph, G. Building Earth Observation Cameras; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Townshend, J.R. The spatial resolving power of earth resources satellites. Prog. Phys. Geogr. 1981, 5, 32–55. [Google Scholar] [CrossRef]
- Valenzuela, A.Q.; Reyes, J.C.G. Basic spatial resolution metrics for satellite imagers. IEEE Sens. J. 2019, 19, 4914–4922. [Google Scholar] [CrossRef]
- Lee, D.; Helder, D.; Christopherson, J.; Stensaas, G. Spatial Quality for Satellite Image Data and Landsat8 OLI Lunar Data. In Proceedings of the 38th CEOS Working Group Calibration Validation Plenary, College Park, MD, USA, 30 September–2 October 2014; Volume 30. [Google Scholar]
- Bakken, S.; Henriksen, M.B.; Birkeland, R.; Langer, D.D.; Oudijk, A.E.; Berg, S.; Pursley, Y.; Garrett, J.L.; Gran-Jansen, F.; Honoré-Livermore, E.; et al. Hypso-1 cubesat: First images and in-orbit characterization. Remote Sens. 2023, 15, 755. [Google Scholar] [CrossRef]
- Gallés, P.; Takáts, K.; Hernández-Cabronero, M.; Berga, D.; Pega, L.; Riordan-Chen, L.; Garcia, C.; Becker, G.; Garriga, A.; Bukva, A.; et al. A New Framework for Evaluating Image Quality Including Deep Learning Task Performances as a Proxy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 17, 3285–3296. [Google Scholar] [CrossRef]
- Innovative Imaging and Research (I2R), Spatial Resolution Digital Imagery Guideline. 2023. Available online: https://www.i2rcorp.com/main-business-lines/sensor-hardware-design-support-services/spatial-resolution-digital-imagery-guideline (accessed on 14 March 2024).
- Schowengerdt, R.A. Remote Sensing: Models and Methods for Image Processing; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Pampanoni, V.; Cenci, L.; Laneve, G.; Santella, C.; Boccia, V. On-orbit image sharpness assessment using the edge method: Methodological improvements for automatic edge identification and selection from natural targets. In Proceedings of the IGARSS 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 6010–6013. [Google Scholar]
- Pampanoni, V.; Cenci, L.; Laneve, G.; Santella, C.; Boccia, V. A Fully Automatic Method for on-Orbit Sharpness Assessment: A Case Study Using Prisma Hyperspectral Satellite Images. In Proceedings of the IGARSS 2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 7226–7229. [Google Scholar]
- Pagnutti, M.; Blonski, S.; Cramer, M.; Helder, D.; Holekamp, K.; Honkavaara, E.; Ryan, R. Targets, methods, and sites for assessing the in-flight spatial resolution of electro-optical data products. Can. J. Remote Sens. 2010, 36, 583–601. [Google Scholar] [CrossRef]
- Boreman, G.D. Modulation Transfer Function in Optical and Electro-Optical Systems; SPIE Press: Bellingham, WA, USA, 2001; Volume 4. [Google Scholar]
- Viallefont-Robinet, F.; Helder, D.; Fraisse, R.; Newbury, A.; van den Bergh, F.; Lee, D.; Saunier, S. Comparison of MTF measurements using edge method: Towards reference data set. Opt. Express 2018, 26, 33625–33648. [Google Scholar] [CrossRef]
- Fascetti, F.; Santella, C. Copernicus Coordinated Data Quality Control: Definition of an Automatic Methodology to Evaluate Signal-To-Noise Ratio on Optical Data. 2023. Available online: https://spacedata.copernicus.eu/documents/20123/212613/D-077_BGD_CQC_T7_PR19_AutomaticSNRMethodology_v1.0.pdf (accessed on 14 March 2024).
- Vescovi, F.D.; Haskell, L. Copernicus Data Quality Control—Technical Note Harmonisation of Optical Product Types—Geometric Corrections. 2016. Available online: https://spacedata.copernicus.eu/documents/20123/121286/CQC_TechnicalNote+(1).pdf (accessed on 14 March 2024).
- Cenci, L.; Galli, M.; Palumbo, G.; Sapia, L.; Santella, C.; Albinet, C. Describing the quality assessment workflow designed for DEM products distributed via the Copernicus Programme. Case study: The absolute vertical accuracy of the Copernicus DEM dataset in Spain. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 6143–6146. [Google Scholar]
- Optical VHR Coverage over Europe. 2022. Available online: https://spacedata.copernicus.eu/optical-vhr-coverage-over-europe-vhr_image_2021- (accessed on 14 March 2024).
- Choi, T.; Helder, D.L. Generic sensor modeling for modulation transfer function (MTF) estimation. In Proceedings of the Pecora 16, Global Priorities in Land Remote Sensing, Falls, South Dakota, 23–27 October 2005; Volume 16, pp. 23–27. [Google Scholar]
- Kabir, S.; Leigh, L.; Helder, D. Vicarious methodologies to assess and improve the quality of the optical remote sensing images: A critical review. Remote Sens. 2020, 12, 4029. [Google Scholar] [CrossRef]
- Duggin, M.; Sakhavat, H.; Lindsay, J. Systematic and random variations in thematic mapper digital radiance data. Photogramm. Eng. Remote Sens. 1985, 51, 1427–1434. [Google Scholar]
- Ren, H.; Du, C.; Liu, R.; Qin, Q.; Yan, G.; Li, Z.L.; Meng, J. Noise evaluation of early images for Landsat 8 Operational Land Imager. Opt. Express 2014, 22, 27270–27280. [Google Scholar] [CrossRef] [PubMed]
- Helder, D.; Choi, T.; Rangaswamy, M. In-flight characterization of spatial quality using point spread functions. Post-Launch Calibration Satell. Sens. 2004, 2, 151–170. [Google Scholar]
- Valenzuela, A.; Reyes, J. Comparative study of the different versions of the general image quality equation. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 4, 493–500. [Google Scholar] [CrossRef]
- Qi, L.; Lee, Z.; Hu, C.; Wang, M. Requirement of minimal signal-to-noise ratios of ocean color sensors and uncertainties of ocean color products. J. Geophys. Res. Ocean. 2017, 122, 2595–2611. [Google Scholar] [CrossRef]
- Schott, J.R.; Gerace, A.; Woodcock, C.E.; Wang, S.; Zhu, Z.; Wynne, R.H.; Blinn, C.E. The impact of improved signal-to-noise ratios on algorithm performance: Case studies for Landsat class instruments. Remote Sens. Environ. 2016, 185, 37–45. [Google Scholar] [CrossRef]
- Cenci, L.; Galli, M.; Santella, C.; Boccia, V.; Albinet, C. Analyzing the Impact of the Different Instances of the Copernicus DEM Dataset on the Orthorectification of VHR Optical Data. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 6001–6004. [Google Scholar]
- SPOT 6 and SPOT 7. Available online: https://spacedata.copernicus.eu/web/guest/spot-6-and-spot-7 (accessed on 14 March 2024).
- Aastrand, P.; Lemajic, S.; Wirnhardt, C. SPOT TrueSharp 4m; Comparison with Sentinel-2, PlanetScope, SPOT, and Pleiades—A Preliminary QUALITY Assessment; Publications Office of the European Union: Luxembourg, 2021. [Google Scholar] [CrossRef]
- Jacquemoud, S. Inversion of the PROSPECT+SAIL canopy reflectance model from AVIRIS equivalent spectra: Theoretical study. Remote Sens. Environ. 1993, 44, 281–292. [Google Scholar] [CrossRef]
- Landsat Science. Available online: https://landsat.gsfc.nasa.gov/ (accessed on 14 March 2024).
- Sentinel-2 Mission Guide. Available online: https://sentinels.copernicus.eu/web/sentinel/missions/sentinel-2 (accessed on 14 March 2024).
- Chuvieco, E. Fundamentals of Satellite Remote Sensing: An Environmental Approach; CRC Press: Boca Raton, FL, USA, 2020. [Google Scholar]
- Rees, G. Physical Principles of Remote Sensing; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Superview-2 Satellite. Available online: http://en.spacewillinfo.com/uploads/soft/220425/1-220425132913.pdf (accessed on 14 March 2024).
- Superview-1 Satellite Imagery Product Guide. Available online: http://en.spacewillinfo.com/uploads/soft/210106/8-210106153503.pdf (accessed on 14 March 2024).
- Leachtenauer, J.C.; Malila, W.; Irvine, J.; Colburn, L.; Salvaggio, N. General image-quality equation: GIQE. Appl. Opt. 1997, 36, 8322–8328. [Google Scholar] [CrossRef]
- Irvine, J.M. National imagery interpretability rating scales (NIIRS): Overview and methodology. Airborne Reconnaiss. XXI 1997, 3128, 93–103. [Google Scholar]
- Li, L.; Luo, H.; Zhu, H. Estimation of the image interpretability of ZY-3 sensor corrected panchromatic nadir data. Remote Sens. 2014, 6, 4409–4429. [Google Scholar] [CrossRef]
- Thurman, S.T.; Fienup, J.R. Analysis of the general image quality equation. In Proceedings of the Visual Information Processing XVII, SPIE, Orlando, FL, USA, 18–19 March 2008; Volume 6978, pp. 102–114. [Google Scholar]
- Khetkeeree, S.; Liangrocapart, S. Satellite image restoration using adaptive high boost filter based on in-flight point spread function. Asian J. Geoinformat. 2018, 18, 15–17. [Google Scholar]
- GeoEye-1 Instruments. Available online: https://earth.esa.int/eogateway/missions/geoeye-1#instruments-section (accessed on 14 March 2024).
- WorldView-2 Instruments. Available online: https://earth.esa.int/eogateway/missions/worldview-2#instruments-section (accessed on 14 March 2024).
- Saunier, S.; Pflug, B.; Lobos, I.M.; Franch, B.; Louis, J.; De Los Reyes, R.; Debaecker, V.; Cadau, E.G.; Boccia, V.; Gascon, F.; et al. Sen2Like: Paving the way towards harmonization and fusion of optical data. Remote Sens. 2022, 14, 3855. [Google Scholar] [CrossRef]

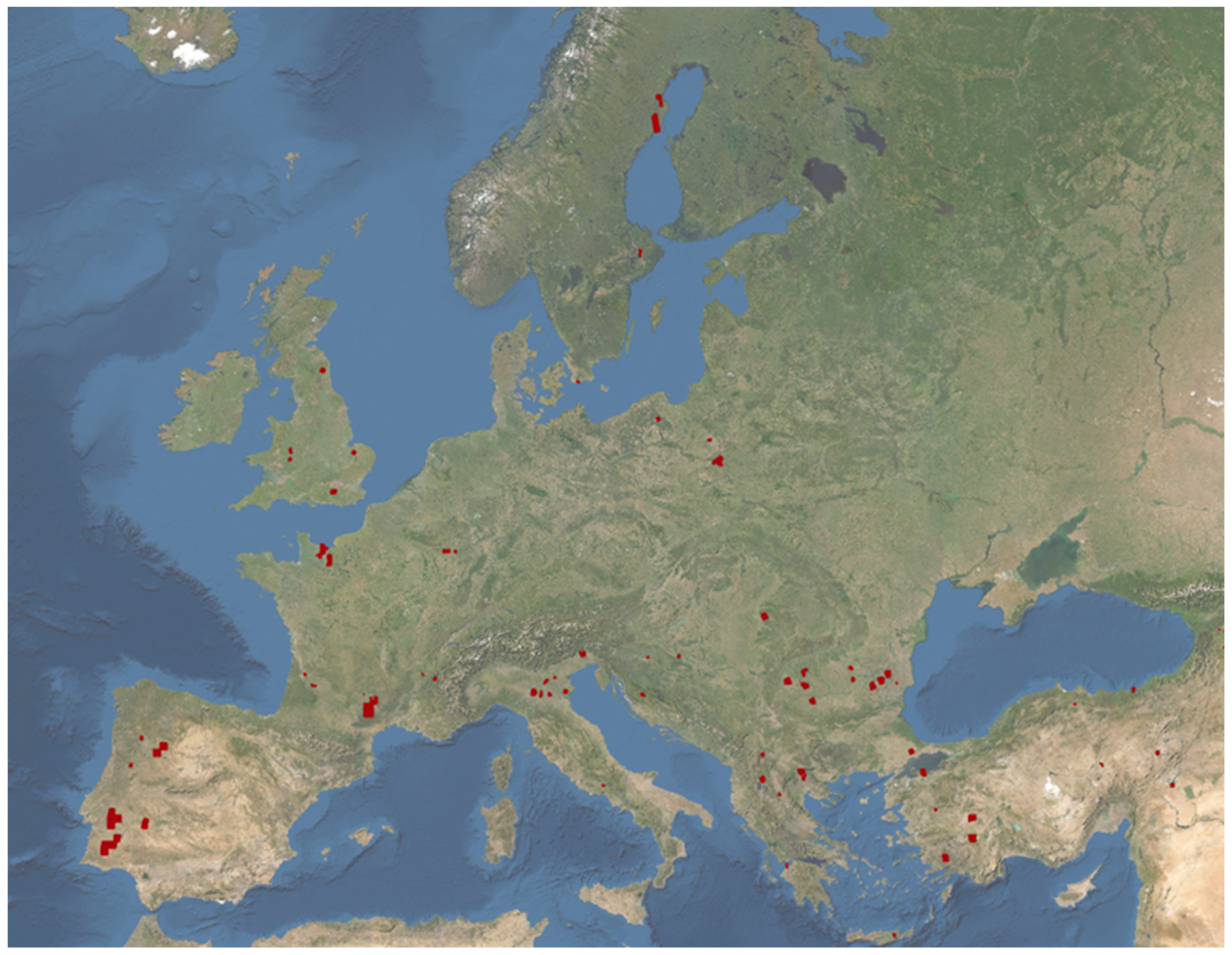




| Mission | Satellite ID | Satellite Product Count | Mission Product Count |
|---|---|---|---|
| DEIMOS-2 | DM02 | 5 | 5 |
| WORLDVIEW | EW02 | 4 | 8 |
| EW03 | 4 | ||
| GEOEYE-1 | GY01 | 5 | 5 |
| KOMPSAT | KS03 | 5 | 9 |
| KS04 | 4 | ||
| PLEIADES | PH1A | 5 | 10 |
| PH1B | 5 | ||
| SPOT | SP06 | 4 | 8 |
| SP07 | 4 | ||
| SUPERVIEW-1 | SV11 | 4 | 16 |
| SV12 | 4 | ||
| SV13 | 4 | ||
| SV14 | 4 | ||
| SUPERVIEW-2 | SV21 | 5 | 5 |
| TRIPLESAT | TR01 | 4 | 12 |
| TR02 | 4 | ||
| TR03 | 4 | ||
| VISION-1 | VS01 | 5 | 5 |
| Mission | Satellite ID | Blue | Green | Red | NIR |
|---|---|---|---|---|---|
| LANDSAT-7 | LE07 | 0.45–0.52 | 0.52–0.60 | 0.63-0.69 | 0.77–0.90 |
| LANDSAT-8 | LC08 | 0.45–0.51 | 0.53–0.59 | 0.64-0.67 | 0.85–0.88 |
| LANDSAT-9 | LC09 | 0.45–0.51 | 0.53–0.59 | 0.64-0.67 | 0.85–0.88 |
| SENTINEL-2A | S2A | 0.46–0.52 | 0.54–0.58 | 0.65-0.68 | 0.78–0.89 |
| SENTINEL-2B | S2B | 0.46–0.52 | 0.54–0.58 | 0.65-0.68 | 0.78–0.89 |
| Mission | Satellite ID | Satellite Product Count | Mission Product Count |
|---|---|---|---|
| LANDSAT-7 | LE07 | 4 | 4 |
| LANDSAT-8 | LC08 | 4 | 4 |
| LANDSAT-9 | LC09 | 4 | 4 |
| SENTINEL-2A | S2A | 4 | 4 |
| SENTINEL-2B | S2B | 4 | 4 |
| Satellite ID | Total Edge Count | FWHM | SNR | |
|---|---|---|---|---|
| μ | σ | |||
| DM02 | 979 | 1.71 | 0.32 | 228.13 |
| EW02 | 1342 | 1.66 | 0.30 | 334.33 |
| EW03 | 901 | 1.56 | 0.29 | 309.86 |
| GY01 | 1419 | 1.62 | 0.29 | 262.37 |
| KS03 | 2659 | 2.20 | 0.42 | 442.76 |
| KS04 | 872 | 1.70 | 0.32 | 416.02 |
| PH1A | 3295 | 1.92 | 0.39 | 387.65 |
| PH1B | 3710 | 1.97 | 0.42 | 359.82 |
| SP06 | 2011 | 1.66 | 0.34 | 199.48 |
| SP07 | 2622 | 1.63 | 0.31 | 148.44 |
| SV11 | 1949 | 1.94 | 0.38 | 293.55 |
| SV12 | 2027 | 2.00 | 0.39 | 204.67 |
| SV13 | 1542 | 1.89 | 0.38 | 261.55 |
| SV14 | 1176 | 1.85 | 0.36 | 271.52 |
| SV21 | 1934 | 1.82 | 0.37 | 255.38 |
| TR01 | 468 | 1.66 | 0.28 | 318.30 |
| TR02 | 634 | 1.55 | 0.26 | 403.83 |
| TR03 | 1857 | 1.56 | 0.30 | 380.04 |
| VS01 | 1028 | 1.61 | 0.31 | 215.78 |
| Satellite ID | Total Edge Count | FWHM | SNR | |
|---|---|---|---|---|
| μ | σ | |||
| DM02 | 1639 | 1.70 | 0.30 | 232.72 |
| EW02 | 1263 | 1.67 | 0.31 | 283.44 |
| EW03 | 782 | 1.53 | 0.28 | 206.29 |
| GY01 | 1180 | 1.59 | 0.29 | 203.86 |
| KS03 | 3420 | 2.14 | 0.41 | 376.33 |
| KS04 | 778 | 1.69 | 0.31 | 268.11 |
| PH1A | 3615 | 1.94 | 0.39 | 359.47 |
| PH1B | 4805 | 1.96 | 0.39 | 326.42 |
| SP06 | 1297 | 1.55 | 0.29 | 180.41 |
| SP07 | 2502 | 1.54 | 0.28 | 147.55 |
| SV11 | 1915 | 1.95 | 0.39 | 272.53 |
| SV12 | 1896 | 1.96 | 0.39 | 254.43 |
| SV13 | 1471 | 1.89 | 0.40 | 281.84 |
| SV14 | 1304 | 1.83 | 0.35 | 270.56 |
| SV21 | 2027 | 1.82 | 0.37 | 233.88 |
| TR01 | 540 | 1.62 | 0.27 | 277.27 |
| TR02 | 1032 | 1.56 | 0.29 | 302.00 |
| TR03 | 1640 | 1.56 | 0.28 | 305.64 |
| VS01 | 958 | 1.61 | 0.28 | 183.33 |
| Satellite ID | Total Edge Count | FWHM | SNR | |
|---|---|---|---|---|
| μ | σ | |||
| DM02 | 2575 | 1.69 | 0.30 | 164.21 |
| EW02 | 1546 | 1.66 | 0.30 | 167.16 |
| EW03 | 1060 | 1.54 | 0.28 | 108.56 |
| GY01 | 1453 | 1.60 | 0.29 | 121.22 |
| KS03 | 3658 | 2.20 | 0.48 | 247.18 |
| KS04 | 1247 | 1.70 | 0.31 | 213.52 |
| PH1A | 4520 | 1.97 | 0.39 | 241.10 |
| PH1B | 5193 | 1.98 | 0.40 | 196.61 |
| SP06 | 2045 | 1.62 | 0.32 | 121.60 |
| SP07 | 2629 | 1.56 | 0.28 | 102.26 |
| SV11 | 2534 | 1.92 | 0.39 | 221.74 |
| SV12 | 2082 | 1.99 | 0.40 | 206.50 |
| SV13 | 1836 | 1.90 | 0.39 | 192.98 |
| SV14 | 1510 | 1.83 | 0.35 | 225.53 |
| SV21 | 2378 | 1.79 | 0.34 | 164.08 |
| TR01 | 895 | 1.63 | 0.28 | 184.43 |
| TR02 | 2274 | 1.54 | 0.28 | 172.51 |
| TR03 | 2458 | 1.51 | 0.25 | 209.93 |
| VS01 | 1555 | 1.58 | 0.28 | 146.36 |
| Satellite ID | Total Edge Count | FWHM | SNR | |
|---|---|---|---|---|
| μ | σ | |||
| DM02 | 1709 | 1.74 | 0.32 | 292.61 |
| EW02 | 1249 | 1.67 | 0.30 | 172.28 |
| EW03 | 556 | 1.50 | 0.28 | 112.79 |
| GY01 | 1003 | 1.58 | 0.26 | 131.78 |
| KS03 | 2622 | 2.20 | 0.41 | 318.23 |
| KS04 | 1100 | 1.73 | 0.32 | 195.82 |
| PH1A | 3360 | 1.94 | 0.40 | 274.73 |
| PH1B | 4646 | 1.96 | 0.40 | 273.16 |
| SP06 | 2236 | 2.18 | 0.56 | 308.29 |
| SP07 | 1607 | 2.15 | 0.54 | 316.41 |
| SV11 | 1920 | 1.93 | 0.40 | 269.88 |
| SV12 | 1721 | 1.96 | 0.40 | 269.24 |
| SV13 | 1495 | 1.87 | 0.38 | 267.18 |
| SV14 | 1128 | 1.84 | 0.36 | 251.43 |
| SV21 | 2103 | 1.80 | 0.36 | 238.00 |
| TR01 | 576 | 1.65 | 0.28 | 200.17 |
| TR02 | 1886 | 1.60 | 0.27 | 166.38 |
| TR03 | 1890 | 1.54 | 0.27 | 175.86 |
| VS01 | 1277 | 1.63 | 0.31 | 204.51 |
| Satellite ID | Total Edge Count | FWHM | SNR | GSD/PS | |
|---|---|---|---|---|---|
| μ | σ | ||||
| DM02 | 6902 | 1.71 | 0.31 | 229.42 | 1.02 |
| EW02 | 5400 | 1.66 | 0.30 | 239.30 | 1.09 |
| EW03 | 3299 | 1.53 | 0.28 | 184.37 | 0.71 |
| GY01 | 5055 | 1.60 | 0.28 | 179.81 | 0.99 |
| KS03 | 12359 | 2.19 | 0.41 | 346.12 | 1.68 |
| KS04 | 3997 | 1.70 | 0.31 | 273.37 | 1.15 |
| PH1A | 14790 | 1.94 | 0.39 | 315.74 | 1.50 |
| PH1B | 18354 | 1.97 | 0.40 | 289.00 | 1.51 |
| SP06 | 7589 | 1.75 | 0.38 | 202.45 | 1.00 |
| SP07 | 9360 | 1.72 | 0.35 | 178.67 | 1.00 |
| SV11 | 8318 | 1.93 | 0.39 | 264.43 | 1.03 |
| SV12 | 7726 | 1.98 | 0.39 | 233.71 | 1.08 |
| SV13 | 6344 | 1.89 | 0.40 | 250.89 | 1.05 |
| SV14 | 5118 | 1.84 | 0.35 | 254.76 | 1.03 |
| SV21 | 8442 | 1.81 | 0.36 | 222.84 | 1.05 |
| TR01 | 2479 | 1.64 | 0.28 | 245.04 | 1.01 |
| TR02 | 5826 | 1.56 | 0.28 | 261.18 | 1.03 |
| TR03 | 7845 | 1.55 | 0.28 | 267.87 | 1.02 |
| VS01 | 4818 | 1.61 | 0.30 | 187.49 | 0.91 |
| Satellite ID | Total Edge Count | FWHM (Subset) | FWHM (Product) |
|---|---|---|---|
| SV11_T01 | 67 | 1.99 | 1.93 |
| GY01_T01 | 29 | 1.55 | 1.60 |
| SV12_T02 | 346 | 1.91 | 1.98 |
| KS03_T02 | 404 | 2.08 | 2.19 |
| SV14_T03 | 134 | 1.87 | 1.84 |
| EW02_T03 | 73 | 1.65 | 1.66 |
| Satellite ID | PS | Total Edge Count | FWHM | SNR | GSD/PS | |
|---|---|---|---|---|---|---|
| μ | σ | |||||
| LE07 | 30 m | 9385 | 1.56 | 0.23 | 276.67 | 1.00 |
| LE07 | 15 m | 8128 | 2.24 | 0.44 | 360.13 | 2.00 |
| LE07 | 60 m | 488 | 1.39 | 0.20 | 208.87 | 0.50 |
| LC08 | 30 m | 10354 | 1.48 | 0.22 | 190.70 | 1.00 |
| LC08 | 15 m | 7702 | 2.12 | 0.46 | 470.05 | 2.00 |
| LC08 | 60 m | 457 | 1.36 | 0.21 | 130.26 | 0.50 |
| LC09 | 30 m | 9380 | 1.47 | 0.23 | 186.53 | 1.00 |
| LC09 | 15 m | 9743 | 2.06 | 0.46 | 335.70 | 2.00 |
| LC09 | 60 m | 454 | 1.32 | 0.22 | 118.65 | 0.50 |
| S2A | 10 m | 65513 | 1.63 | 0.28 | 212.60 | 1.00 |
| S2A | 5 m | 15569 | 2.54 | 0.48 | 224.30 | 2.00 |
| S2A | 20 m | 12917 | 1.40 | 0.23 | 144.78 | 0.50 |
| S2B | 10 m | 57867 | 1.62 | 0.27 | 216.06 | 1.00 |
| S2B | 5 m | 13823 | 2.53 | 0.48 | 228.05 | 2.00 |
| S2B | 20 m | 11721 | 1.41 | 0.22 | 150.34 | 0.50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pampanoni, V.; Fascetti, F.; Cenci, L.; Laneve, G.; Santella, C.; Boccia, V. Analysing the Relationship between Spatial Resolution, Sharpness and Signal-to-Noise Ratio of Very High Resolution Satellite Imagery Using an Automatic Edge Method. Remote Sens. 2024, 16, 1041. https://doi.org/10.3390/rs16061041
Pampanoni V, Fascetti F, Cenci L, Laneve G, Santella C, Boccia V. Analysing the Relationship between Spatial Resolution, Sharpness and Signal-to-Noise Ratio of Very High Resolution Satellite Imagery Using an Automatic Edge Method. Remote Sensing. 2024; 16(6):1041. https://doi.org/10.3390/rs16061041
Chicago/Turabian StylePampanoni, Valerio, Fabio Fascetti, Luca Cenci, Giovanni Laneve, Carla Santella, and Valentina Boccia. 2024. "Analysing the Relationship between Spatial Resolution, Sharpness and Signal-to-Noise Ratio of Very High Resolution Satellite Imagery Using an Automatic Edge Method" Remote Sensing 16, no. 6: 1041. https://doi.org/10.3390/rs16061041
APA StylePampanoni, V., Fascetti, F., Cenci, L., Laneve, G., Santella, C., & Boccia, V. (2024). Analysing the Relationship between Spatial Resolution, Sharpness and Signal-to-Noise Ratio of Very High Resolution Satellite Imagery Using an Automatic Edge Method. Remote Sensing, 16(6), 1041. https://doi.org/10.3390/rs16061041






