Reweighted Extreme Learning Machine-Based Clutter Suppression and Range Compensation Algorithm for Non-Side-Looking Airborne Radar
Abstract
:1. Introduction
2. Signal Model
3. The Proposed Algorithm
3.1. Design of Pre-Processing and Initial Reweighted Network Training
3.2. Design of Objectives-Driven Reverse Feedback Framework
3.3. Design of Special Processes and Theoretical Derivations for Estimating Compensation Matrix
| Algorithm 1 The main procedures of the proposed algorithm. |
|
4. Simulation Results
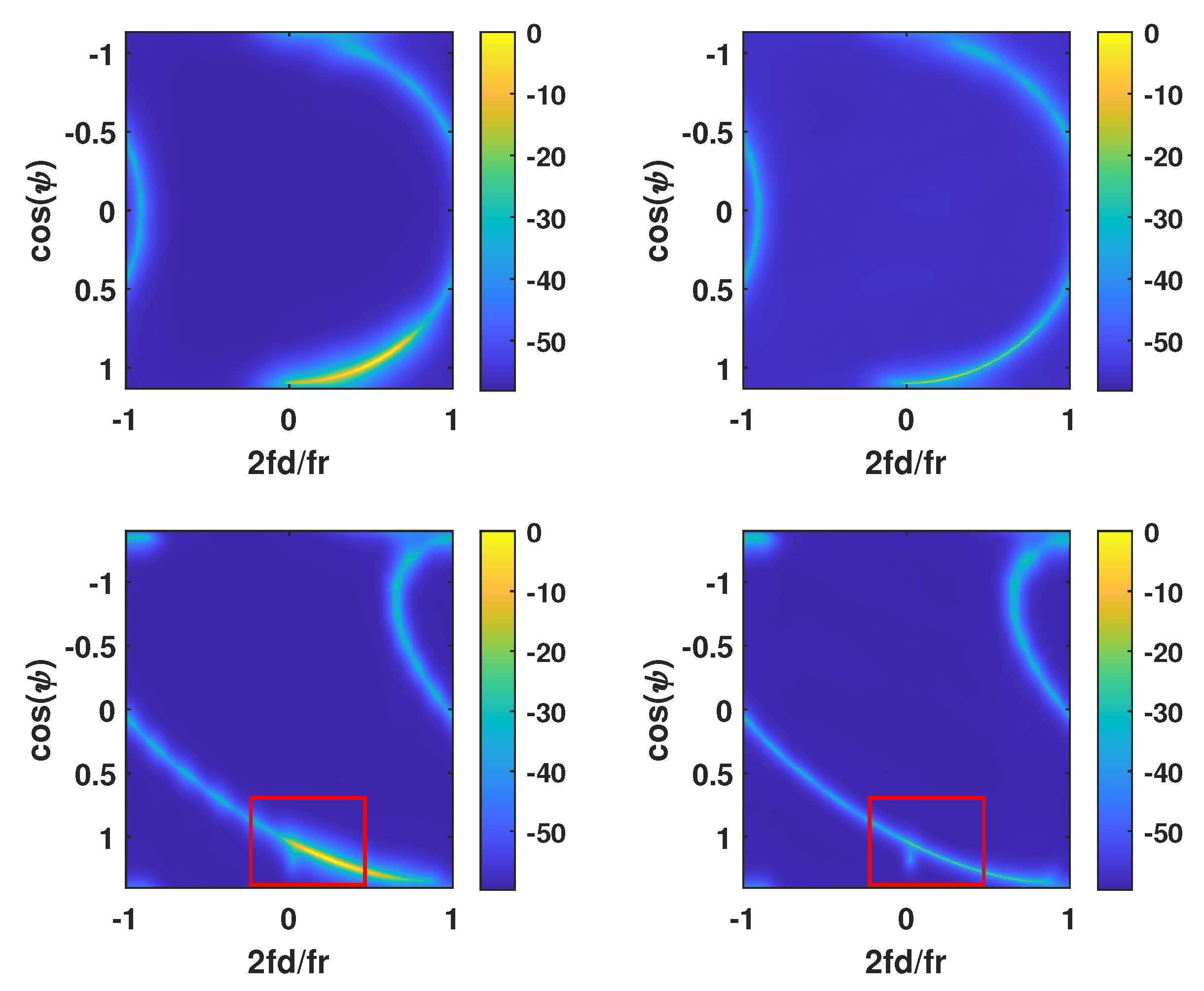
4.1. Space–Time Distribution of the Clutter Spectrum
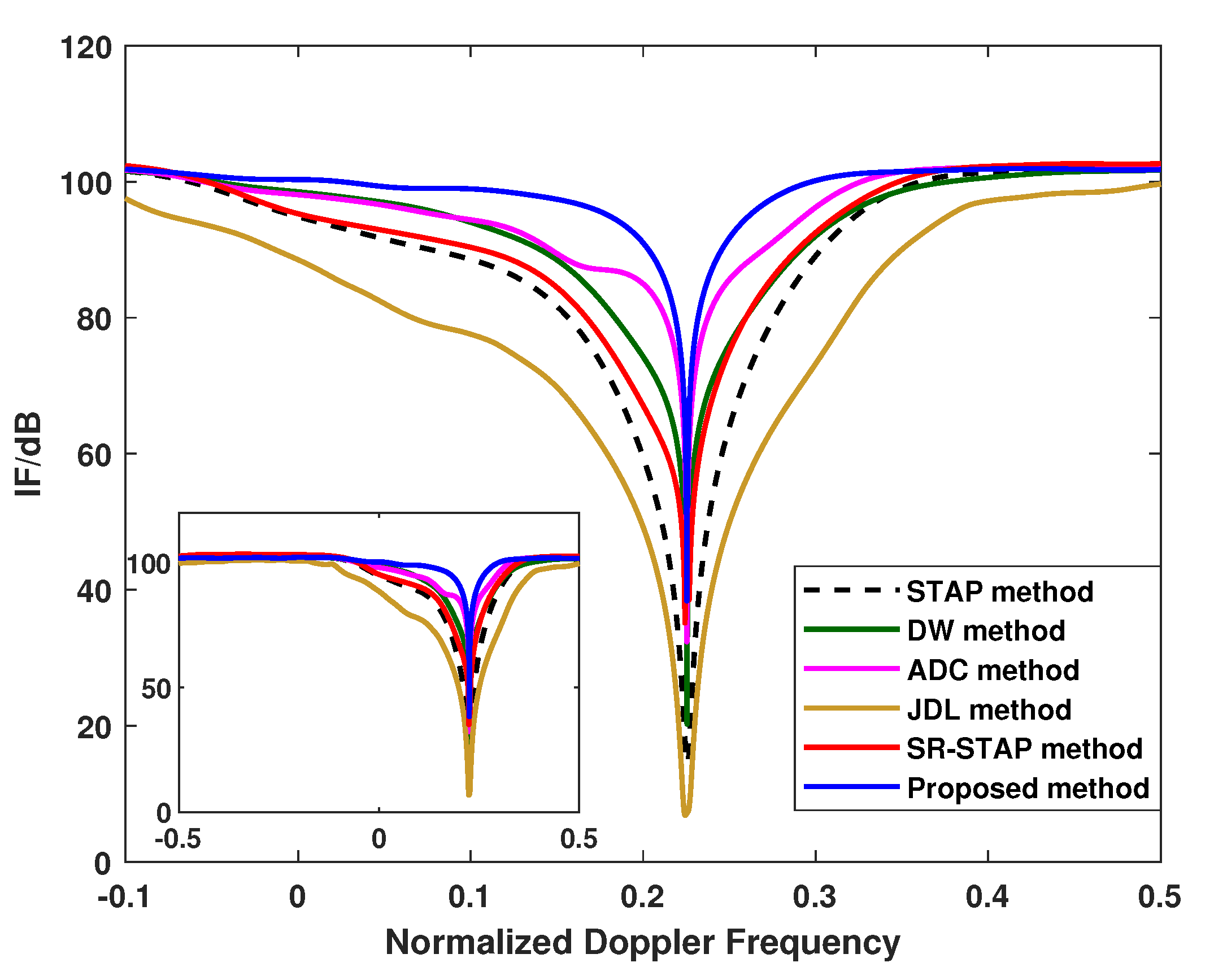
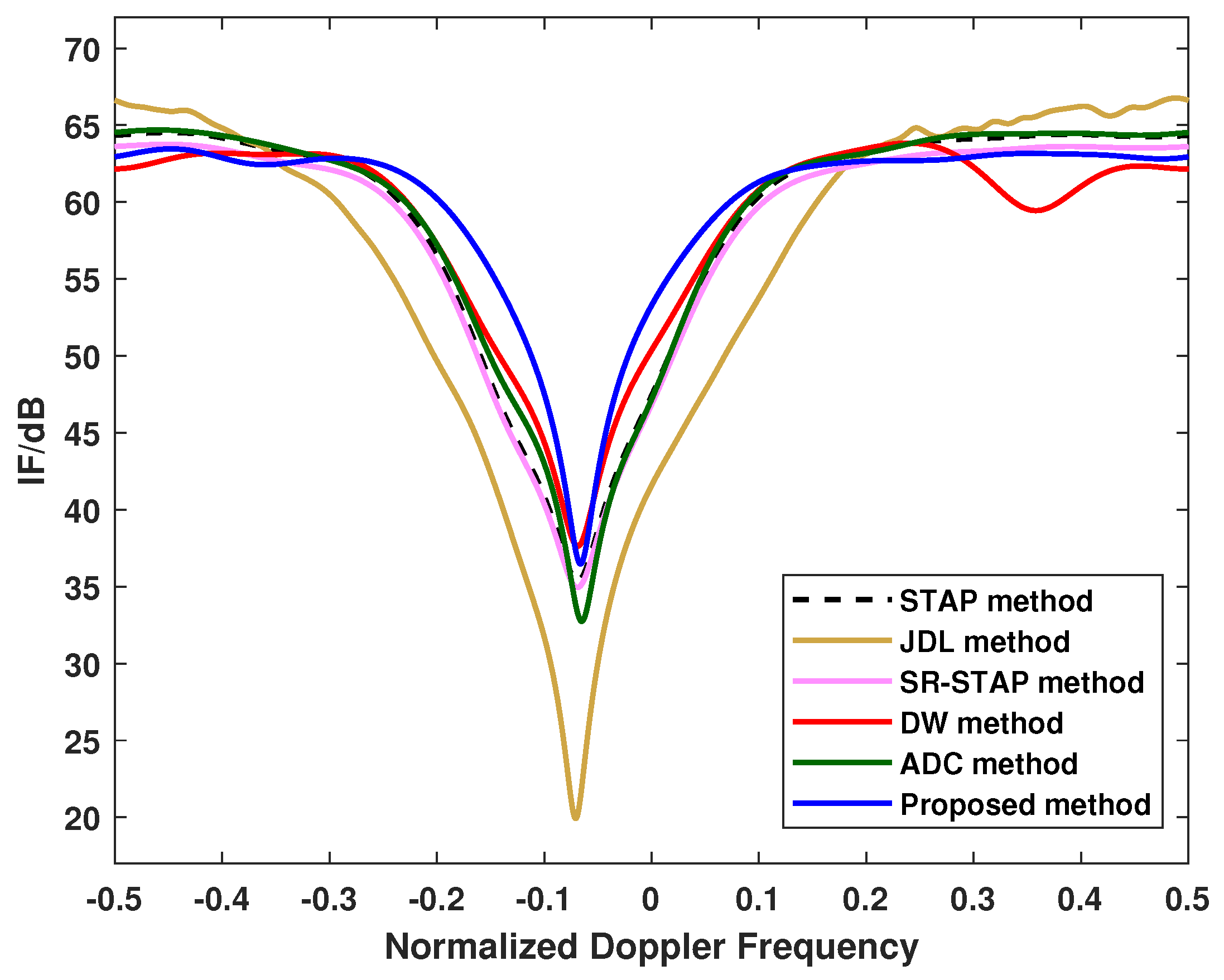
4.2. Results of the Improvement Factor
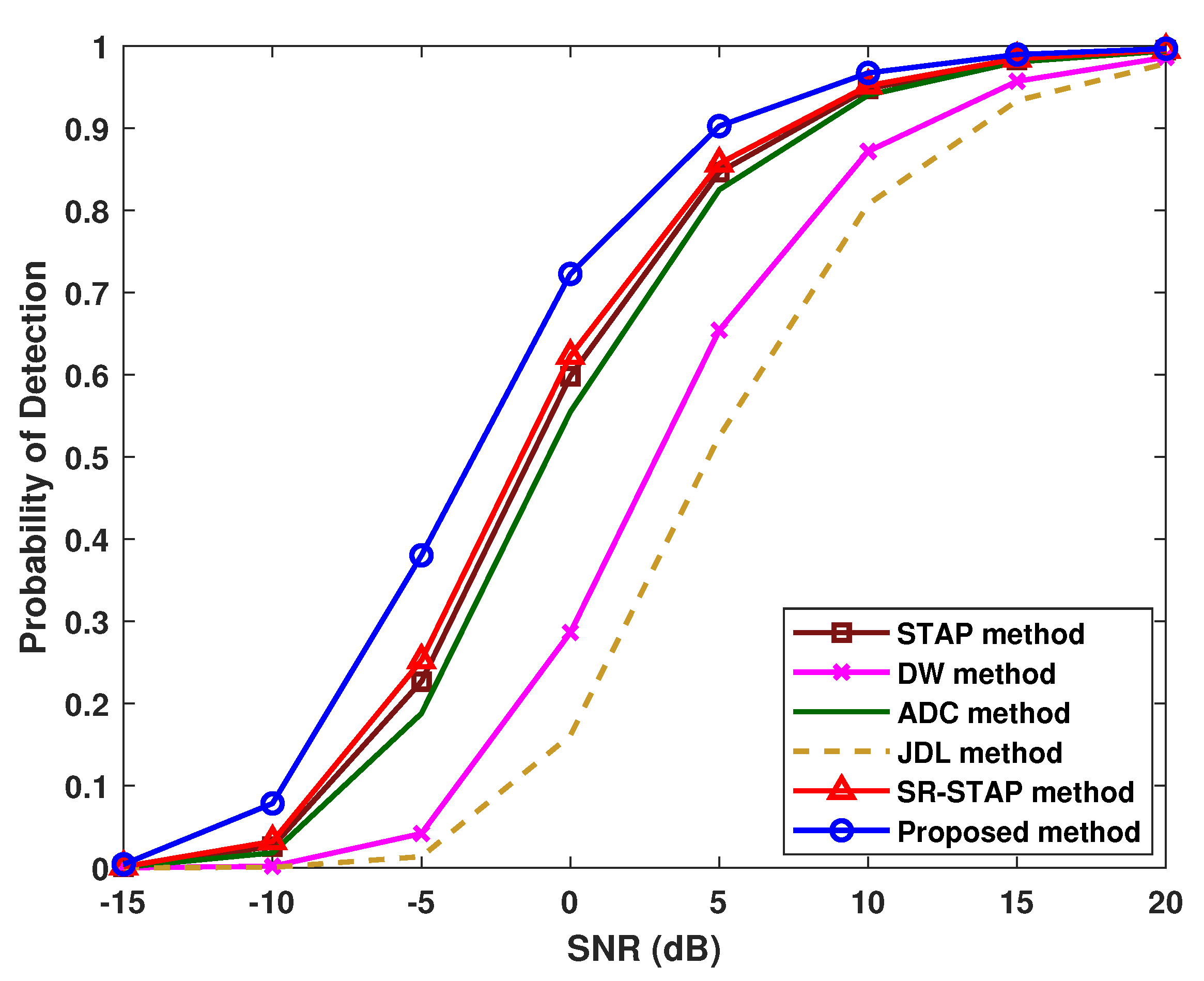
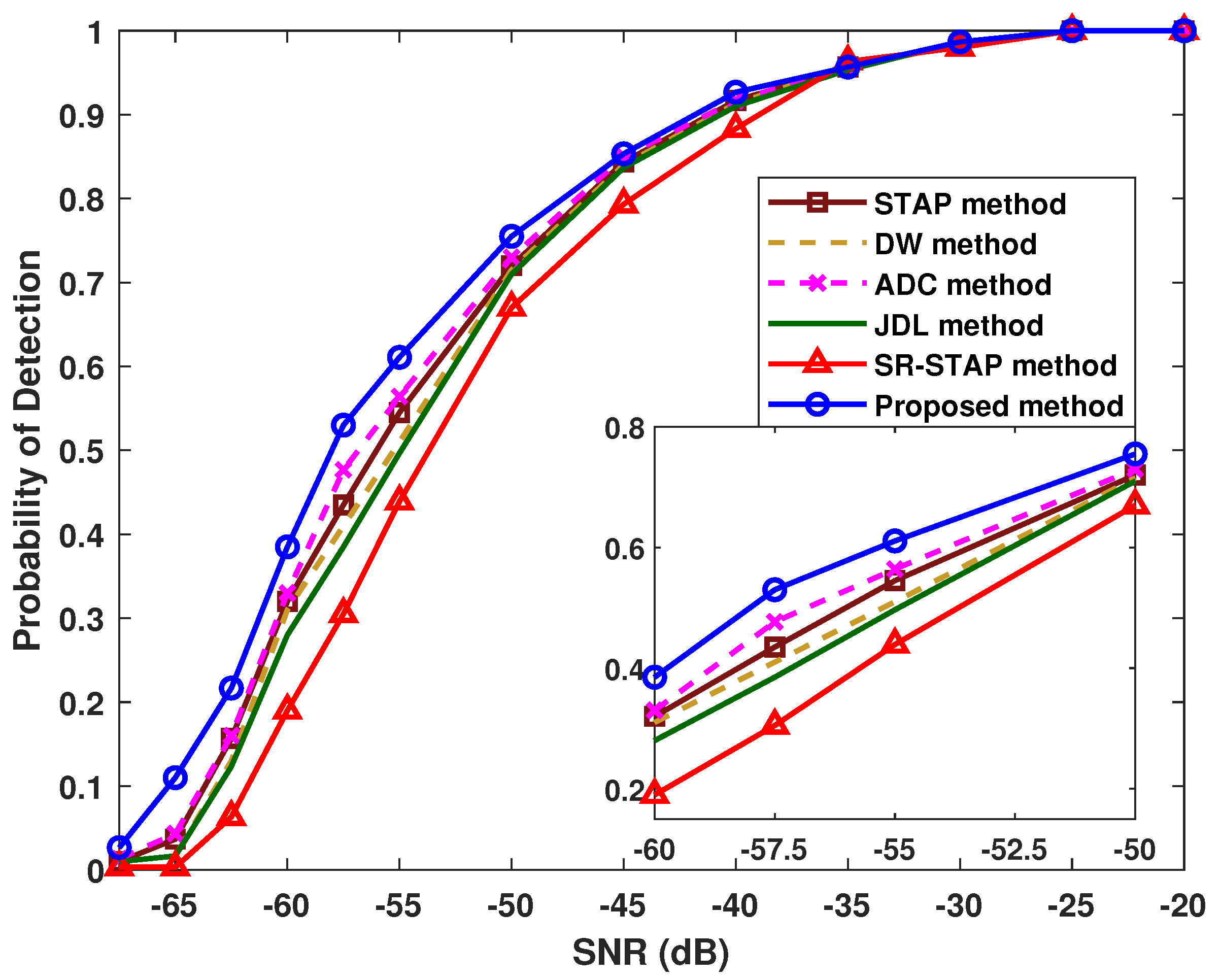
4.3. Results of the Probability of Detection
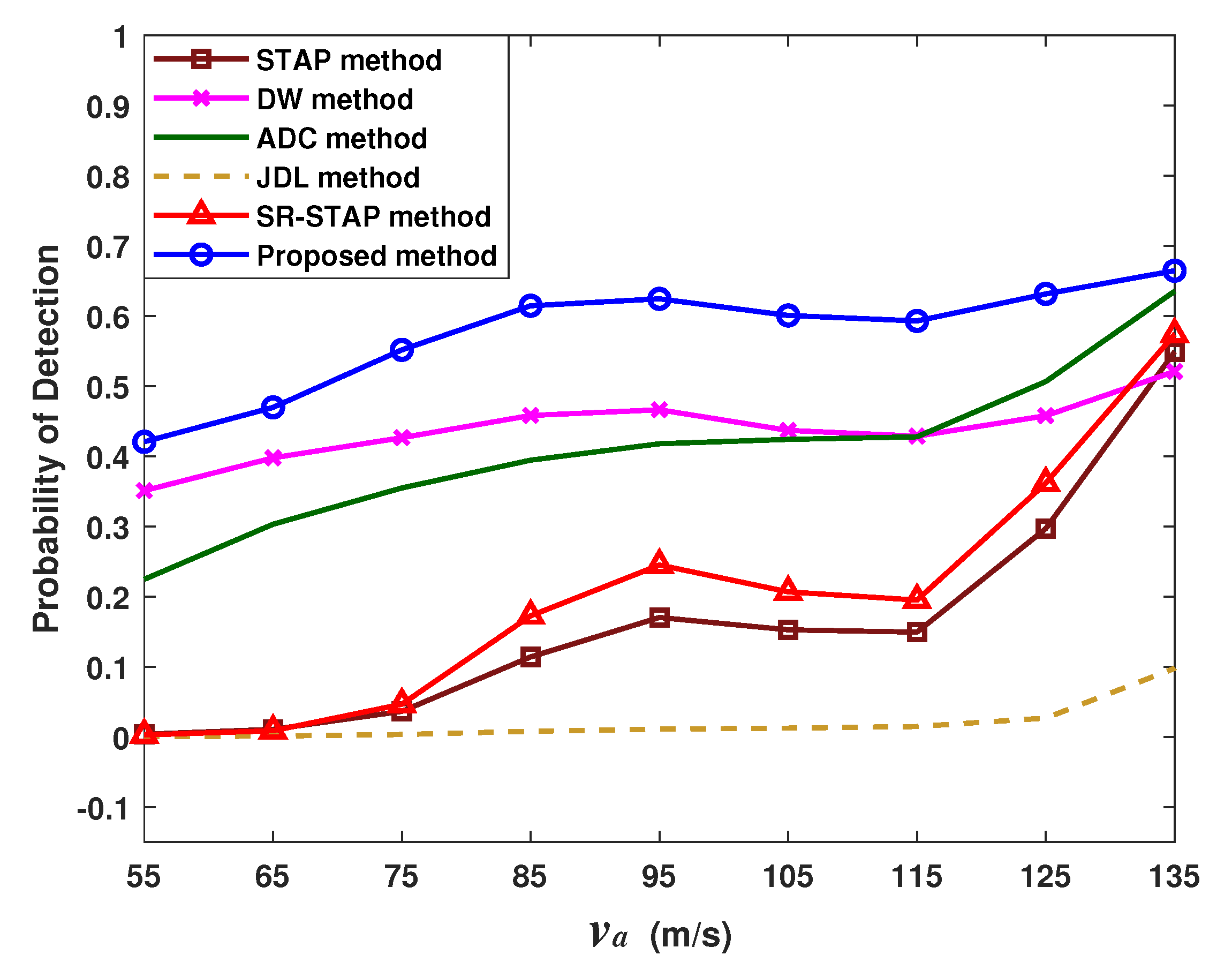
4.4. Influence of Different Radar Circumstances
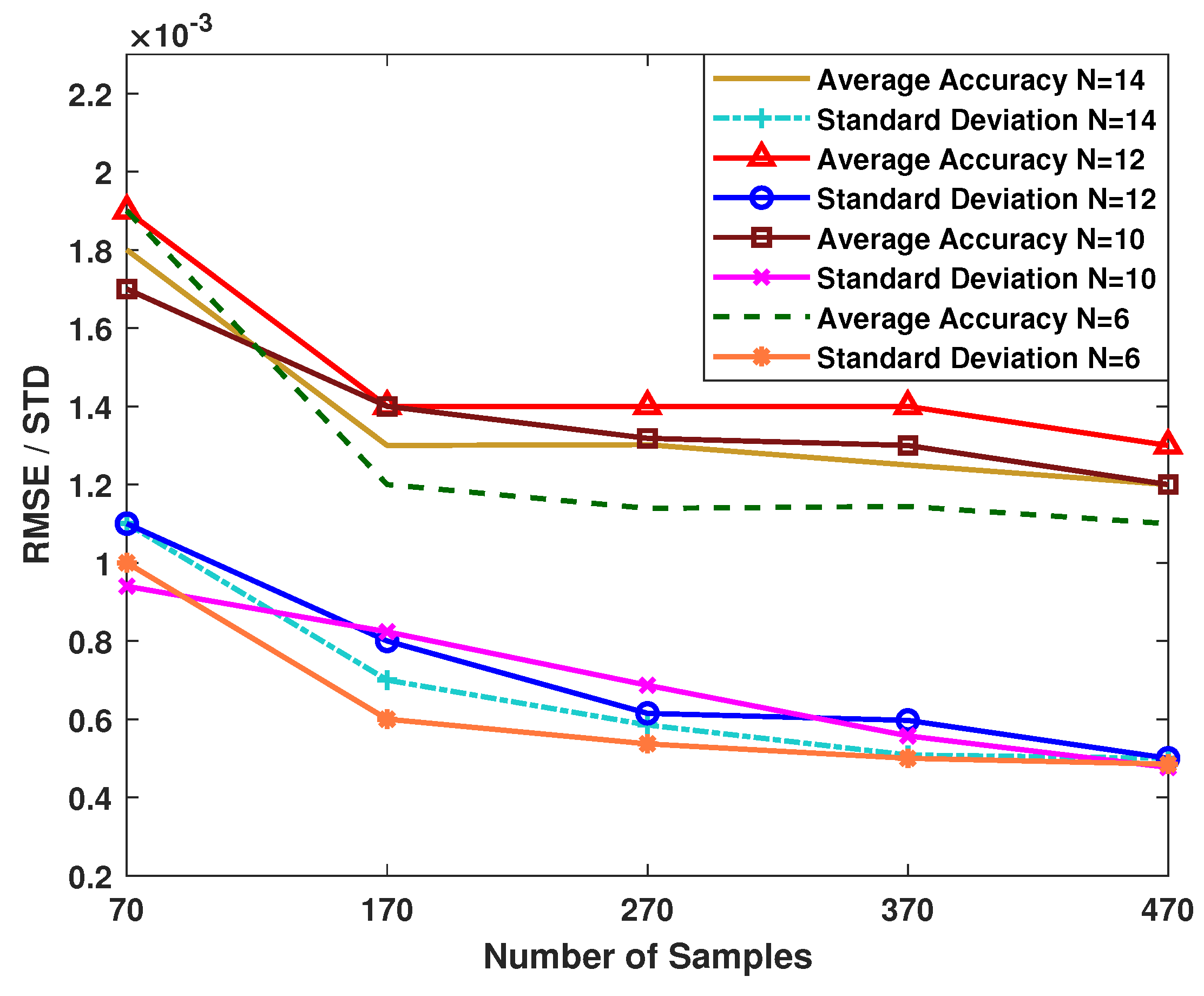
4.5. Test Errors of the Proposed Network
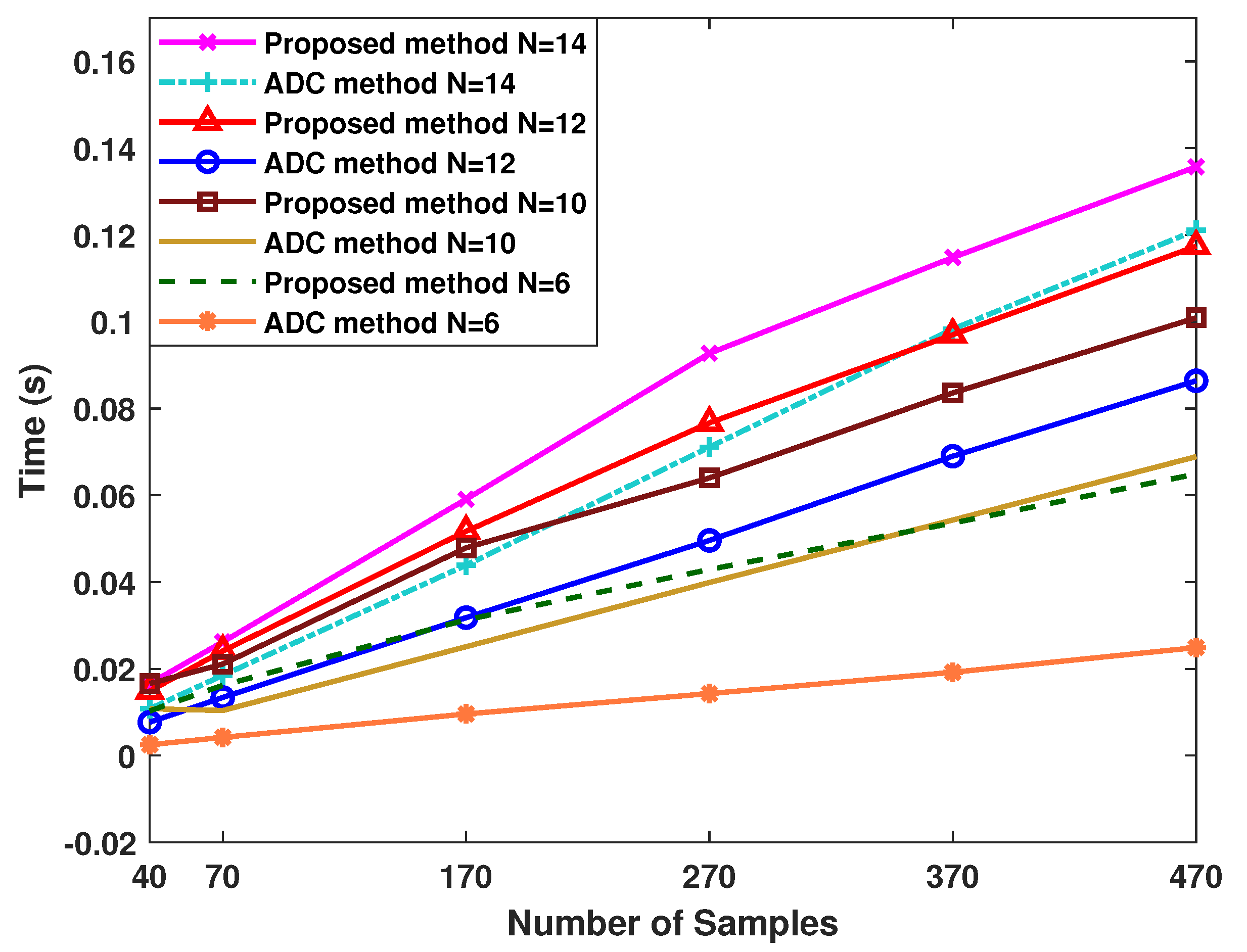
4.6. Comparison of the Computation Time
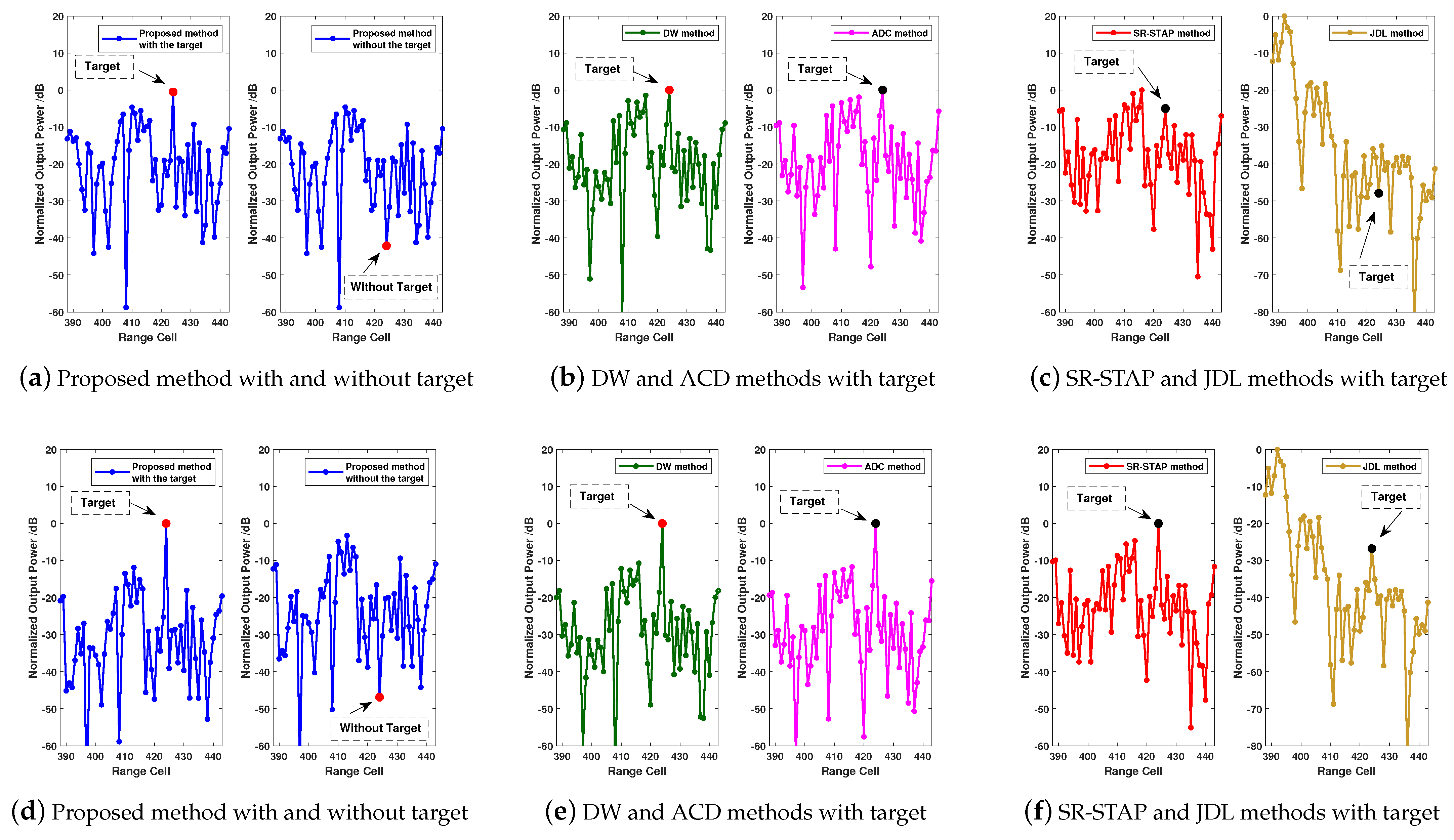
4.7. Results with Experimental Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Klemm, R. Principles of Space-Time Adaptive Processing; The Institution of Electrical Engineers: London, UK, 2002. [Google Scholar]
- Lapierre, F.; Droogenbroeck, M.V.; Verly, J.G. New methods for handling the dependence of the clutter spectrum in non-sidelooking monostatic STAP radars. In Proceedings of the 2003 IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 6–10 April 2003; pp. 73–76. [Google Scholar]
- Lapierre, F.D.; Ries, P.; Verly, J.G. Foundation for mitigating range dependence in radar space-time adaptive processing. IET Radar Sonar Navig. 2009, 3, 18–29. [Google Scholar] [CrossRef]
- Lapierre, F.; Verly, J.G. Computationally-efficient range dependence compensation method for bistatic radar STAP. In Proceedings of the IEEE International Radar Conference, Arlington, VA, USA, 9–12 May 2005; pp. 714–719. [Google Scholar]
- Kreyenkamp, O.; Klemm, R. Doppler compensation in forward-looking STAP radar. IEE Proc. Radar Sonar Navig. 2001, 148, 253–258. [Google Scholar] [CrossRef]
- Borsari, G.K. Mitigating effects on STAP processing caused by an inclined array. In Proceedings of the 1998 IEEE Radar Conference, Dallas, TX, USA, 14 May 1998; pp. 135–140. [Google Scholar]
- Himed, B.; Zhang, Y.; Hajjari, A. STAP with angle-Doppler compensation for bistatic airborne radars. In Proceedings of the IEEE Radar Conference, Long Beach, CA, USA, 25 April 2002; pp. 311–317. [Google Scholar]
- Lapierre, F.D.; Verly, J.G. Registration-based range-dependence compensation for bistatic STAP radars. EURASIP J. Appl. Signal Process. 2005, 1, 85–98. [Google Scholar] [CrossRef]
- Wang, Y.; Peng, Y. Space-time joint processing method for simultaneous clutter and jamming rejection in airborne radar. Electron. Lett. 1996, 32, 258. [Google Scholar] [CrossRef]
- Dipietro, R.C. Extended factored space-time processing for airborne radar systems. In Proceedings of the 26th Asilomar Conference, Pacific Grove, CA, USA, 26–28 October 1992; pp. 425–430. [Google Scholar]
- Wang, Y.L.; Chen, J.W.; Bao, Z.; Peng, Y.N. Robust space-time adaptive processing for airborne radar in nonhomogeneous clutter environments. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 70–81. [Google Scholar] [CrossRef]
- Brown, R.D.; Schneible, R.A.; Wicks, M.C.; Wang, H.; Zhang, Y.H. STAP for clutter suppression with sum and difference beams. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 634–646. [Google Scholar] [CrossRef]
- Goldstein, J.S. Reduced rank adaptive filtering. IEEE Trans. Signal Process. 1997, 45, 492–496. [Google Scholar] [CrossRef]
- Goldstein, J.S.; Reed, I.S.; Scharf, L.L. A multistage representation of the Wiener filter based on orthogonal projections. IEEE Trans. Inf. Theor. 1998, 44, 2943–2959. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, A.X.; Li, J.X. Fast and accurate rank selection methods for multistage Wiener filter. IEEE Trans. Signal Process. 2016, 64, 973–984. [Google Scholar] [CrossRef]
- Cotter, S.F.; Rao, B.D.; Engan, K.; Delgado, K.K. Sparse solutions to linear inverseproblems with multiple measurement vectors. IEEE Trans. Signal Process. 2005, 53, 2477–2488. [Google Scholar]
- Bai, G.; Tao, R.; Zhao, J.; Bai, X. Parameter-searched OMP method for eliminating basis mismatch in space-time spectrum estimation. Signal Process. 2017, 138, 11–15. [Google Scholar] [CrossRef]
- Ji, S.; Xue, Y.; Carin, L. Bayesian compressive sensing. IEEE Trans. Signal Process. 2008, 56, 2346–2356. [Google Scholar] [CrossRef]
- Li, Z.H.; Zhang, Y.S.; He, X.Y.; Guo, Y.D. Low-complexity off-grid STAP algorithm based on local search clutter subspace estimation. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1862–1866. [Google Scholar] [CrossRef]
- Han, S.D.; Fan, C.Y.; Huang, X.T. A novel STAP based on spectrum-aided reduced-dimension clutter sparse recovery. IEEE Geosci. Remote Sens. Lett. 2017, 14, 213–217. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, W.D.; Juwono, F.H.; Huang, D.F. Reweighted smoothed l0-norm based DOA estimation for MIMO radar. Signal Process. 2017, 137, 44–51. [Google Scholar] [CrossRef]
- Yang, Z.; Lamare, R.C.D.; Li, X.; Wang, H. Knowledge-aided stap using low rank and geometry properties. Int. J. Antennas Propag. 2014, 2014, 196507. [Google Scholar] [CrossRef]
- Chen, W.C.; Chen, B.; Liu, Y.C.; Wang, C.J.; Peng, X.J.; Liu, H.W.; Zhou, M.Y. Infinite switching dynamic probabilistic network with Bayesian nonparametric learning. IEEE Trans. Signal Process. 2022, 70, 2224–2238. [Google Scholar] [CrossRef]
- Duan, K.; Chen, H.; Xie, W.; Wang, Y. Deep learning for high-resolution estimation of clutter angle-Doppler spectrum in STAP. IET Radar Sonar Navig. 2022, 16, 193–207. [Google Scholar] [CrossRef]
- Li, H.; Zhuang, L.; Guan, Y.; Wang, J. A machine learning approach for clutter suppression in airborne radar based on multitask learning. IEEE Access 2020, 8, 22541–22552. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.; Song, S.; Gupta, J.N.; Wu, C. Semi-supervised and unsupervised extreme learning machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the IEEE International Joint Conference on Neural Network, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Zou, B.; Wang, X.; Feng, W.; Zhu, H.; Lu, F. DU-CG-STAP method based on sparse recovery and unsupervised learning for airborne radar clutter suppression. Remote Sens. 2022, 14, 3472. [Google Scholar] [CrossRef]
- Mou, X.; Chen, X.; Guan, J.; Dong, Y.; Liu, N. Sea clutter suppression for radar PPI images based on SCS-GAN. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1886–1890. [Google Scholar] [CrossRef]
- Li, G.Q.; Song, Z.Y.; Guan, J.; Fu, Q. A convolutional neural network based approach to sea clutter suppression for small boat detection. Front. Informa. Technol. Electron. Eng. 2020, 21, 1504–1520. [Google Scholar] [CrossRef]
- Liu, J.; Liao, G.S.; Xu, J.W.; Zhu, S.Q.; Juwono, F.J.; Zeng, C. Autoencoder neural network-based STAP algorithm for airborne radar with inadequate training samples. Remote Sens. 2022, 14, 6021. [Google Scholar] [CrossRef]
- Liu, J.; Liao, G.S.; Xu, J.W.; Zhu, S.Q.; Zeng, C.; Juwono, F.J. Unsupervised affinity propagation clustering based clutter suppression and target detection algorithm for non-side-looking airborne radar. Remote Sens. 2023, 15, 2077. [Google Scholar] [CrossRef]
- Zaimbashi, A. An adaptive cell averaging-based CFAR detector for interfering targets and clutter-edge situations. Digit. Signal Process. 2014, 31, 59–68. [Google Scholar] [CrossRef]
- Liu, W.J.; Liu, J.; Hao, C.P.; Gao, Y.C.; Wang, Y.L. Multichannel adaptive signal detection: Basic theory and literature review. Sci. China Inf. Sci. 2022, 65, 121301. [Google Scholar] [CrossRef]
- Xu, J.W.; Liao, G.S.; Huang, L.; Zhu, S.Q. Joint magnitude and phase constrained STAP approach. Digit. Signal Process. 2015, 46, 32–40. [Google Scholar] [CrossRef]
- Ottersten, B.; Stoica, P.; Roy, R. Covariance matching estimation techniques for array signal processing applications. Digit. Signal Process. 1998, 8, 185–210. [Google Scholar] [CrossRef]
- Gini, F.; Greco, M. Covariance matrix estimation for CFAR detection in correlated heavy tailed clutter. Signal Process. 2002, 82, 1847–1859. [Google Scholar] [CrossRef]
- Sarkar, T.K.; Wang, H.; Park, S.; Adve, R.; Koh, J.; Kim, K.; Zhang, Y.; Wicks, M.C.; Brown, R.D. A deterministic least-squares approach to space-time adaptive processing. IEEE Trans. Antennas Propag. 2001, 49, 91–103. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liao, G.; Zeng, C.; Tao, H.; Xu, J.; Zhu, S.; Juwono, F.H. Reweighted Extreme Learning Machine-Based Clutter Suppression and Range Compensation Algorithm for Non-Side-Looking Airborne Radar. Remote Sens. 2024, 16, 1093. https://doi.org/10.3390/rs16061093
Liu J, Liao G, Zeng C, Tao H, Xu J, Zhu S, Juwono FH. Reweighted Extreme Learning Machine-Based Clutter Suppression and Range Compensation Algorithm for Non-Side-Looking Airborne Radar. Remote Sensing. 2024; 16(6):1093. https://doi.org/10.3390/rs16061093
Chicago/Turabian StyleLiu, Jing, Guisheng Liao, Cao Zeng, Haihong Tao, Jingwei Xu, Shengqi Zhu, and Filbert H. Juwono. 2024. "Reweighted Extreme Learning Machine-Based Clutter Suppression and Range Compensation Algorithm for Non-Side-Looking Airborne Radar" Remote Sensing 16, no. 6: 1093. https://doi.org/10.3390/rs16061093
APA StyleLiu, J., Liao, G., Zeng, C., Tao, H., Xu, J., Zhu, S., & Juwono, F. H. (2024). Reweighted Extreme Learning Machine-Based Clutter Suppression and Range Compensation Algorithm for Non-Side-Looking Airborne Radar. Remote Sensing, 16(6), 1093. https://doi.org/10.3390/rs16061093








