A Coherent Integration Method for Moving Target Detection in Frequency Agile Signal-Based Passive Bistatic Radar
Abstract
1. Introduction
- (1)
- An observation model that describes the received signals in terms of the FAPBR system is established and analyzed. Subsequently, a novel target detection algorithm with FA signal coherent integration for passive bistatic radar is proposed for realizing long-range detection and obtaining finer range resolution. In particular, this paper gives a detailed scheme process and algorithm steps, thereby extending the application of PBR.
- (2)
- This paper develops the phase quadratic difference to effectively eliminate the Doppler phase hopping induced by agile carrier frequency. In comparison with the existing methods, the proposed method can mitigate the Doppler migration without the assistance of prior information on the target velocity. Moreover, the method is suitable for multi-target scenarios, and, therefore, has wider applicability and convenience.
- (3)
- This paper adopts frequency reordering, i.e., pulse signal reordering, to generate the HRRPs of a target while suppressing the random range phase fluctuation caused by randomized stepped frequencies. Additionally, to address range ambiguity resulting from the HPRF during FA signal coherent integration, this paper introduces the S-RAD method to extend the system’s detection range.
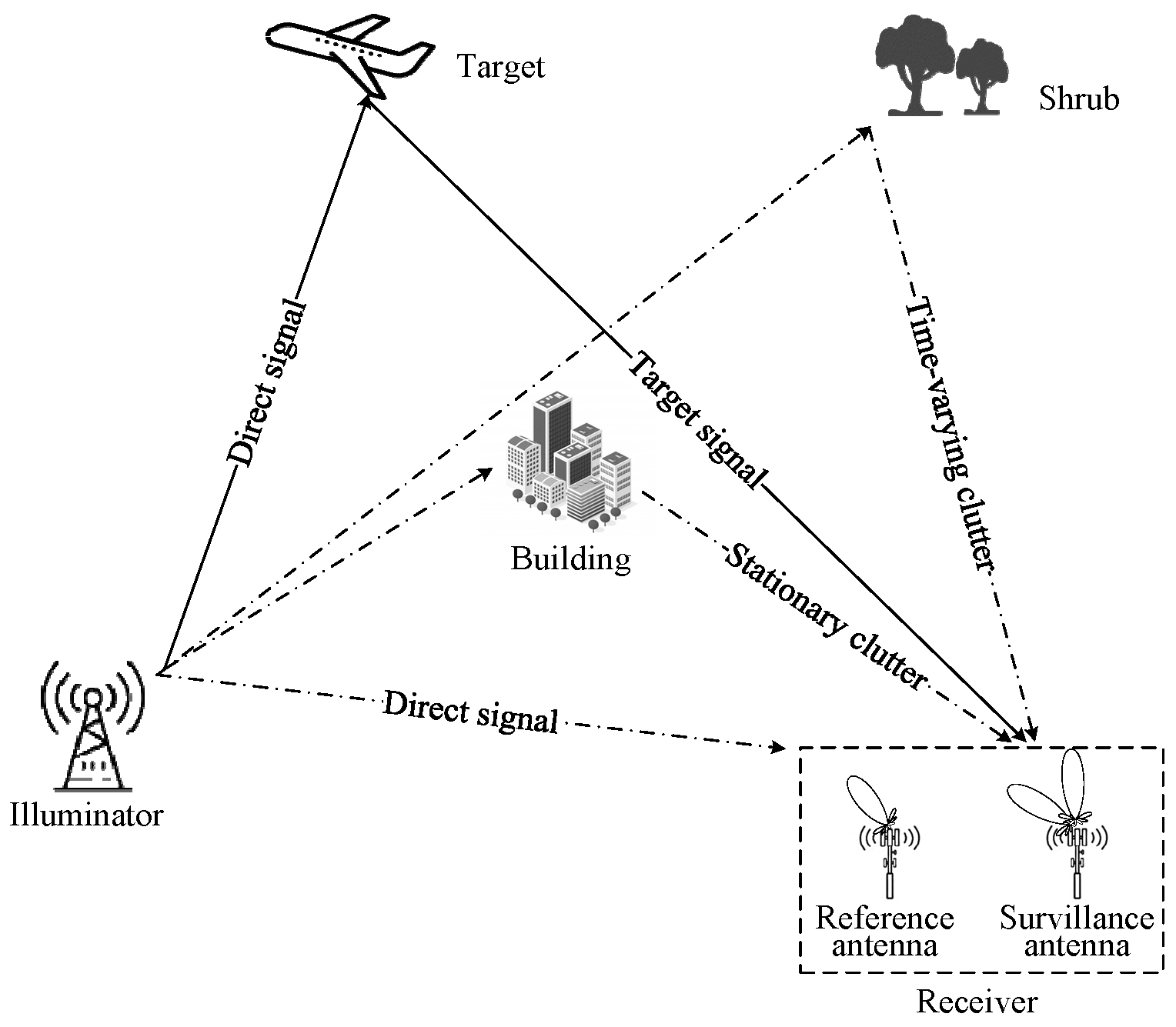
2. Signal Model and Problem Analysis
2.1. Signal Model
2.2. Problem Analysis
3. Proposed FAPBR Coherent Integration Scheme
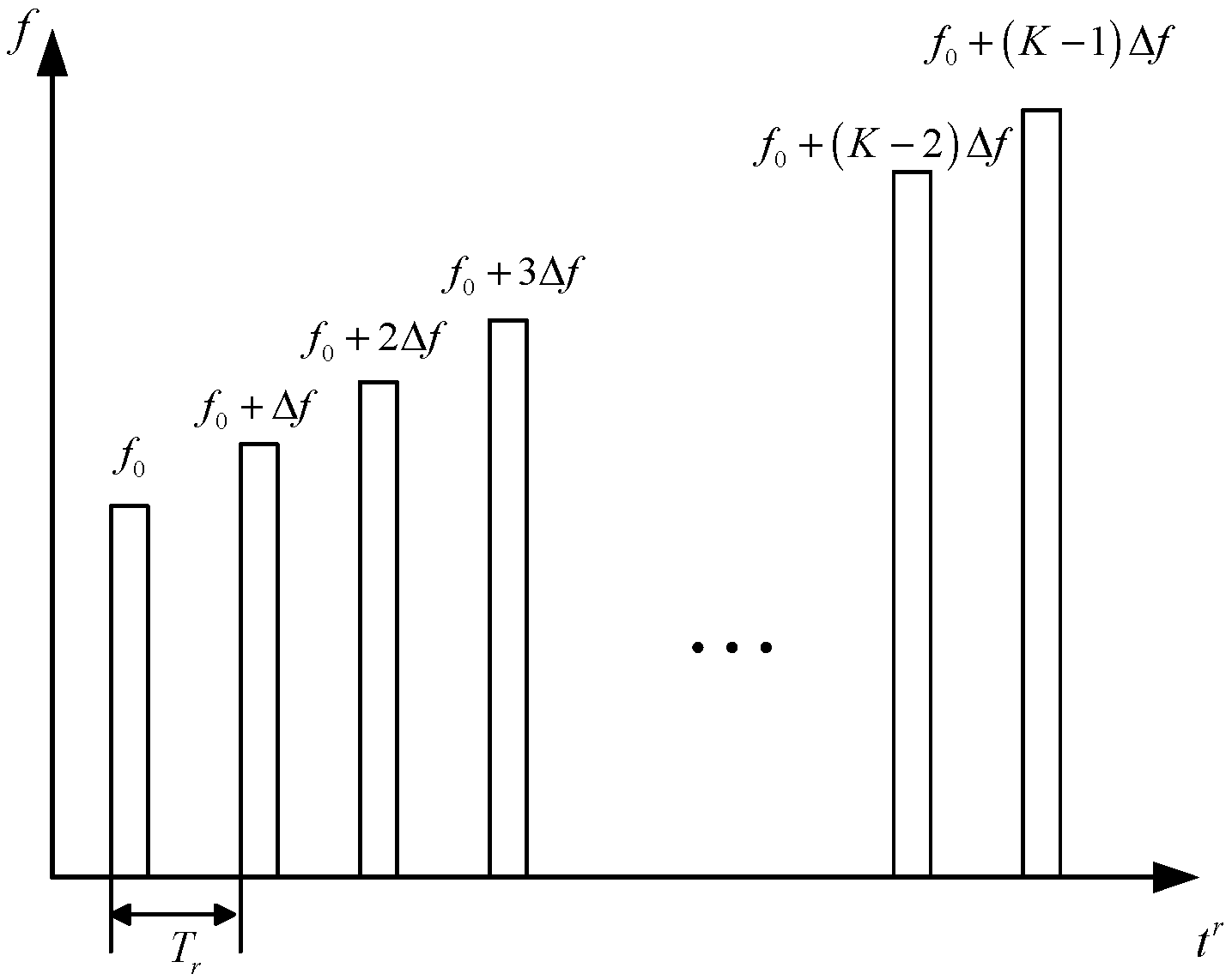
3.1. Doppler Migration Correction
3.2. HRRP Generation
3.3. Sliding Range Ambiguity Decoupling
4. Simulation and Performance Analysis
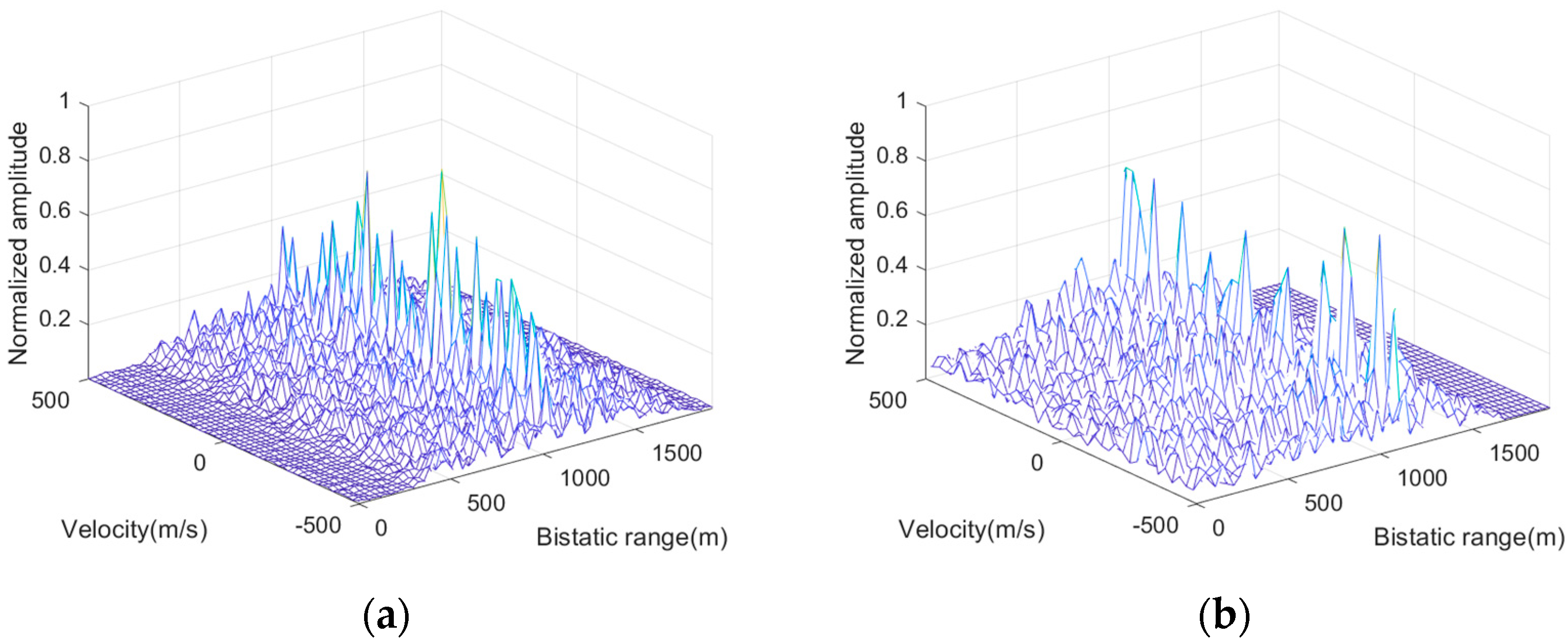
4.1. Coherent Integration for Multiple Target
4.2. Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malanowski, M. Signal Processing for Passive Bistatic Radar; Artech House: London, UK, 2019. [Google Scholar]
- Blázquez-García, R.; Cristallini, D.; Ummenhofer, M.; Seidel, V.; Heckenbach, J.; O’Hagan, D. Capabilities and challenges of passive radar systems based on broadband low-Earth orbit communication satellites. IET Radar Sonar Navig. 2024, 18, 78–92. [Google Scholar] [CrossRef]
- Kuschel, H.; Cristallini, D.; Olsen, K.E. Tutorial: Passive radar tutorial. IEEE Aerosp. Electron. Syst. Mag. 2019, 34, 2–19. [Google Scholar] [CrossRef]
- Abratkiewicz, K.; Księżyk, A.; Płotka, M.; Samczyński, P.; Wszołek, J.; Zieliński, T.P. SSB-Based Signal Processing for Passive Radar Using a 5G Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3469–3484. [Google Scholar] [CrossRef]
- Almodóvar-Hernández, A.; Mata-Moya, D.; Jarabo-Amores, M.-P.; Rey-Maestre, N.; Benito-Ortiz, M. Motion Compensation for Long Integration Times and DoA Processing in Passive Radars. Remote Sens. 2023, 15, 1031. [Google Scholar] [CrossRef]
- Griffiths, H.D.; Baker, C.J. An Introduction to Passive Radar; Artech House: London, UK, 2022. [Google Scholar]
- Ma, J.; Li, H.; Gan, L. Order-Statistic Based Target Detection with Compressive Measurements in Single-Frequency Multistatic Passive Radar. Signal Process. 2023, 203, 108785. [Google Scholar] [CrossRef]
- Blasone, G.P.; Colone, F.; Lombardo, P. Forward-Looking Passive Radar with Non-Uniform Linear Array for automotive applications. IEEE Trans. Veh. Technol. 2023, 72, 11132–11146. [Google Scholar] [CrossRef]
- Zhang, C.; Shi, S.; Yan, S.; Gong, J. Moving Target Detection and Parameter Estimation Using BeiDou GEO Satellites-Based Passive Radar with Short-Time Integration. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 3959–3972. [Google Scholar] [CrossRef]
- Wang, Y.; Bao, Q.; Wang, D.; Chen, Z. An experimental study of passive bistatic radar using uncooperative radar as a transmitter. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1868–1872. [Google Scholar] [CrossRef]
- Howland, P.E.; Maksimiuk, D.; Reitsma, G. FM radio based bistatic radar. IEE Proc. Radar Sonar Navig. 2005, 152, 107–115. [Google Scholar] [CrossRef]
- Lü, M.; Yi, J.; Wan, X.; Zhan, W. Cochannel interference in DTMB-based passive radar. IEEE Trans. Aerosp. Electron. Syst. 2018, 55, 2138–2149. [Google Scholar] [CrossRef]
- Zuo, L.; Wang, J.; Zhao, T.; Cheng, Z. A Joint Low-Rank and Sparse Method for Reference Signal Purification in DTMB-Based Passive Bistatic Radar. Sensors 2021, 21, 3607. [Google Scholar] [CrossRef] [PubMed]
- Geng, Z.; Xu, R.; Deng, H. LTE-based multistatic passive radar system for UAV detection. IET Radar Sonar Navig. 2020, 14, 1088–1097. [Google Scholar] [CrossRef]
- Gui, L.; Yuan, W.; Xiao, F. CSI-based passive intrusion detection bound estimation in indoor NLoS scenario. Fundam. Res. 2023, 3, 988–996. [Google Scholar] [CrossRef]
- Ma, H.; Antoniou, M.; Stove, A.G.; Winkel, J.; Cherniakov, M. Maritime moving target localization using passive GNSS-based multistatic radar. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4808–4819. [Google Scholar] [CrossRef]
- Wang, B.; Cha, H.; Zhou, Z.; Tian, B. Clutter cancellation and long time integration for GNSS-based passive bistatic radar. Remote Sens. 2021, 13, 701. [Google Scholar] [CrossRef]
- Huang, C.; Li, Z.; An, H.; Sun, Z.; Wu, J.; Yang, J. Passive multistatic radar imaging of vessel target using GNSS satellites of opportunity. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Wang, H.; Kuang, J.; Wang, Z.; Xu, H. Transmission performance evaluation of JTIDS. In Proceedings of the MILCOM 2005–2005 IEEE Military Communications Conference, Atlantic City, NJ, USA, 17–20 October 2005; pp. 2264–2268. [Google Scholar]
- Bai, L.; Wang, J.; Chen, X. Ambiguity function analysis and side peaks suppression of Link16 signal based passive radar. J. Syst. Eng. Electron. 2023, 34, 1526–1536. [Google Scholar] [CrossRef]
- Liu, L.; Fu, Y.; Li, Q.; Lu, Y.; Cao, Z.; Chen, Y. Anti-jamming Research of UAV Communication Based on Link-16 Datalink. In Proceedings of the 2023 6th International Conference on Computer Network, Electronic and Automation (ICCNEA), Xi’an, China, 22–24 September 2023; pp. 157–161. [Google Scholar]
- Huang, T.; Liu, Y.; Xu, X.; Eldar, Y.C.; Wang, X. Analysis of frequency agile radar via compressed sensing. IEEE Trans. Signal Process. 2018, 66, 6228–6240. [Google Scholar] [CrossRef]
- Axelsson, S.R. Analysis of random step frequency radar and comparison with experiments. IEEE Trans. Geosci. Remote Sens. 2007, 45, 890–904. [Google Scholar] [CrossRef]
- Zuo, L.; Wang, J.; Wang, J.; Chen, G. UAV detection via long-time coherent integration for passive bistatic radar. Digit. Signal Process. 2021, 112, 102997. [Google Scholar] [CrossRef]
- Huang, C.; Li, Z.; Lou, M.; Qiu, X.; An, H.; Wu, J.; Yang, J.; Huang, W. BeiDou-based passive radar vessel target detection: Method and experiment via long-time optimized integration. Remote Sens. 2021, 13, 3933. [Google Scholar] [CrossRef]
- Wang, H.; Huang, W.; Jiang, Y.; Ba, T. Moving target coherent integration method for non-coherent short pulse radar. IET Radar Sonar Navig. 2019, 13, 953–960. [Google Scholar] [CrossRef]
- Jędrzejewski, K.; Malanowski, M.; Kulpa, K.; Pożoga, M. Experimental verification of passive radar space object detection with a single low-frequency array radio telescope. IET Radar Sonar Navig. 2024, 18, 68–77. [Google Scholar] [CrossRef]
- Colone, F.; Lombardo, P. Non-coherent adaptive detection in passive radar exploiting polarimetric and frequency diversity. IET Radar Sonar Navig. 2016, 10, 15–23. [Google Scholar] [CrossRef]
- Martelli, T.; Colone, F.; Tilli, E.; Di Lallo, A. Multi-frequency target detection techniques for DVB-T based passive radar sensors. Sensors 2016, 16, 1594. [Google Scholar] [CrossRef] [PubMed]
- Huang, P.; Dong, S.; Liu, X.; Jiang, X.; Liao, G.; Xu, H.; Sun, S. A coherent integration method for moving target detection using frequency agile radar. IEEE Geosci. Remote Sens. Lett. 2018, 16, 206–210. [Google Scholar] [CrossRef]
- Olsen, K.E.; Christiansen, J.M. Multiband passive bistatic radar coherent range and Doppler-walk compensation. In Proceedings of the 2015 IEEE Radar Conference (RadarCon), Arlington, VA, USA, 10–15 May 2015; pp. 0123–0126. [Google Scholar]
- Lin, C.; Tian, R.; Bao, Q.; Chen, Z. Coherent integration method of frequency agile radar for target detection. In Proceedings of the 2017 Sixth Asia-Pacific Conference on Antennas and Propagation (APCAP), Xi’an, China, 16–19 October 2017; pp. 1–3. [Google Scholar]
- Chen, G.; Wang, J.; Zuo, L.; Zhao, D. Long-Time Coherent Integration for Frequency Hopping Pulse Signal via Phase Compensation. IEEE Access 2020, 8, 30458–30466. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.; Cai, C.; Liu, X. An improved algorithm for compatibility of pulse-to-pulse frequency agility and MTD. Comput. Simul. 2011, 28, 5–8. [Google Scholar]
- Quan, Y.; Li, Y.; Wu, Y.; Ran, L.; Xing, M.; Liu, M. Moving target detection for frequency agility radar by sparse reconstruction. Rev. Sci. Instrum. 2016, 87, 094703. [Google Scholar] [CrossRef]
- Li, Y.; Huang, T.; Xu, X.; Liu, Y.; Wang, L.; Eldar, Y.C. Phase transitions in frequency agile radar using compressed sensing. IEEE Trans. Signal Process. 2021, 69, 4801–4818. [Google Scholar] [CrossRef]
- Lellouch, G.; Pribic, R.; van Genderen, P. Merging frequency agile ofdm waveforms and compressive sensing into a novel radar concept. In Proceedings of the 2009 European Radar Conference (EuRAD), Rome, Italy, 30 September–2 October 2009; pp. 137–140. [Google Scholar]
- Liao, Z.; Lu, D.; Hu, J.; Zhang, J. Computationally efficient range profile synthesis method based on zero-padding inverse discrete Fourier transform for random stepped frequency radar. J. Appl. Remote Sens. 2019, 13, 016505. [Google Scholar] [CrossRef]
- Liu, S.; Cao, Y.; Yeo, T.-S.; Wang, F.; Han, J. Range sidelobe suppression for randomized stepped-frequency chirp radar. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 3874–3885. [Google Scholar] [CrossRef]
- Malanowski, M. Detection and parameter estimation of manoeuvring targets with passive bistatic radar. IET Radar Sonar Navig. 2012, 6, 739–745. [Google Scholar] [CrossRef]
- Colone, F.; O’hagan, D.; Lombardo, P.; Baker, C. A multistage processing algorithm for disturbance removal and target detection in passive bistatic radar. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 698–722. [Google Scholar] [CrossRef]
- Harris, F.J.; Dick, C.; Rice, M. Digital receivers and transmitters using polyphase filter banks for wireless communications. IEEE Trans. Microw. Theory Tech. 2003, 51, 1395–1412. [Google Scholar] [CrossRef]
- Feixing, W.; Hongzhong, Z.; Jianxiong, Z.; Qiang, F. Range ambiguity resolution based on phase difference for high PRF stepped-frequency radar. Chin. J. Electron. 2008, 17, 751–755. [Google Scholar]
- Chen, J.; Zheng, X.; Zhang, C.; Xu, Z.; Li, A. The Capacity Analysis of the Orthogonal Frequency Hopping Stacked Nets in the Data Link. J. Phys. Conf. Ser. 2019, 1302, 022060. [Google Scholar] [CrossRef]
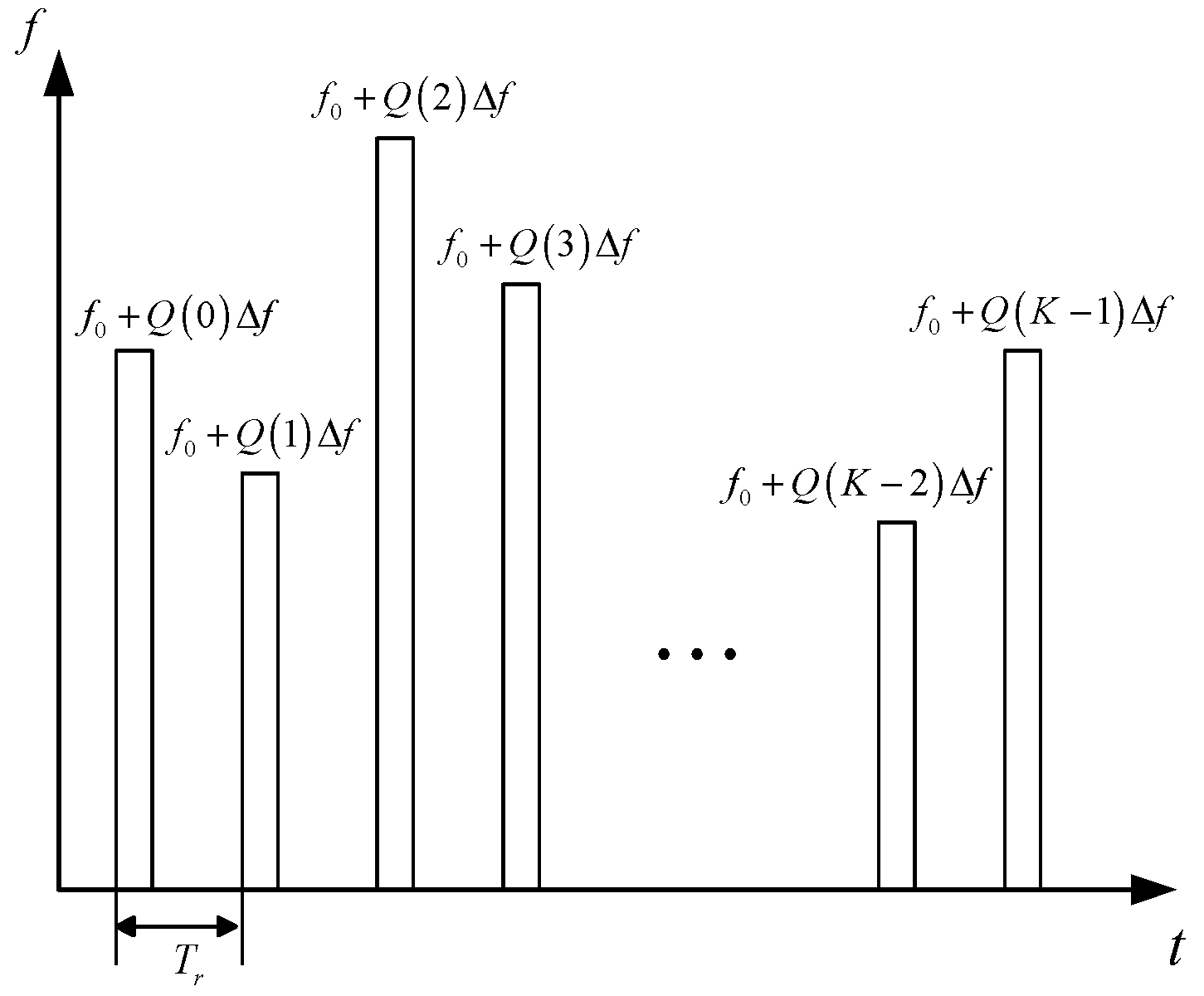








| Parameters | Symbol | Values |
|---|---|---|
| Initial carrier frequency (MHz) | f0 | 875 |
| Bandwidth (MHz) | B | 5 |
| Frequency step interval (MHz) | ∆f | 5 |
| Available frequencies number | G | 50 |
| Pulse duration time (μs) | - | 6.4 |
| Pulse repeat interval (μs) | Tr | 13 |
| CPI (ms) | T | 50 |
| Signal | SNR (dB) | Bistatic Range (m) | Velocity (m/s) |
|---|---|---|---|
| Target 1 | −10 | 1066 | −51 |
| Target 2 | −15 | 18,555 | 129 |
| Target 3 | −20 | 22,577 | 77 |
| Methods | CMs |
|---|---|
| HI&S-RAD | NsGKlog2(K)/2 |
| JZP-VS&S-RAD | NsNvGlog2(G)/2 + 2KNsNv |
| Proposed method | NsGlog2(G)/2 + (2K − 3)NsNv + 2GNs |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, L.; Li, N.; Tan, J.; Peng, X.; Cao, Y.; Zhou, Z.; Han, J. A Coherent Integration Method for Moving Target Detection in Frequency Agile Signal-Based Passive Bistatic Radar. Remote Sens. 2024, 16, 1148. https://doi.org/10.3390/rs16071148
Zuo L, Li N, Tan J, Peng X, Cao Y, Zhou Z, Han J. A Coherent Integration Method for Moving Target Detection in Frequency Agile Signal-Based Passive Bistatic Radar. Remote Sensing. 2024; 16(7):1148. https://doi.org/10.3390/rs16071148
Chicago/Turabian StyleZuo, Luo, Nan Li, Jie Tan, Xiangyu Peng, Yunhe Cao, Zuobang Zhou, and Jiusheng Han. 2024. "A Coherent Integration Method for Moving Target Detection in Frequency Agile Signal-Based Passive Bistatic Radar" Remote Sensing 16, no. 7: 1148. https://doi.org/10.3390/rs16071148
APA StyleZuo, L., Li, N., Tan, J., Peng, X., Cao, Y., Zhou, Z., & Han, J. (2024). A Coherent Integration Method for Moving Target Detection in Frequency Agile Signal-Based Passive Bistatic Radar. Remote Sensing, 16(7), 1148. https://doi.org/10.3390/rs16071148







