Iterative Signal Detection and Channel Estimation with Superimposed Training Sequences for Underwater Acoustic Information Transmission in Time-Varying Environments
Abstract
:1. Introduction
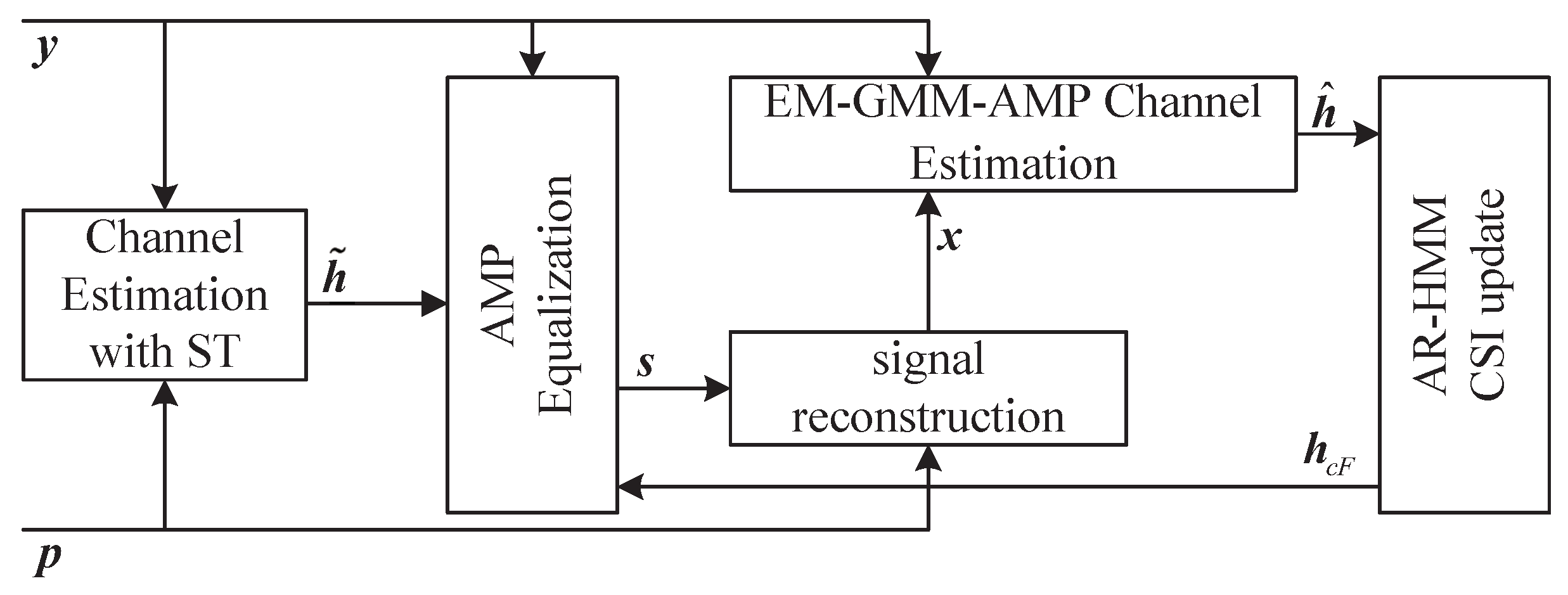
- We propose a communication scheme that uses coarse channel estimation based on superimposed training, AMP equalization, and EM-GMM-AMP channel estimation. Based on the factor graph of the underwater acoustic channel model, an approximate message passing underwater acoustic channel estimation method based on Gaussian mixture distribution is derived.
- We combine the EM-GMM-AMP algorithm with the AR-HMM model for CSI updating based on time correlation, further improving the accuracy of channel estimation.
- The effectiveness of the algorithm proposed in this paper is verified through pool experiments and field experiments.
2. System Model
2.1. Time-Varying Channel System Model
2.2. Superimposed Training Model
2.3. Soft Iteration UAC Receiver
3. Channel Estimation and Equalization Based on Superimposed Training Sequences
3.1. Coarse Channel Estimation Based on Superimposed Training Sequences
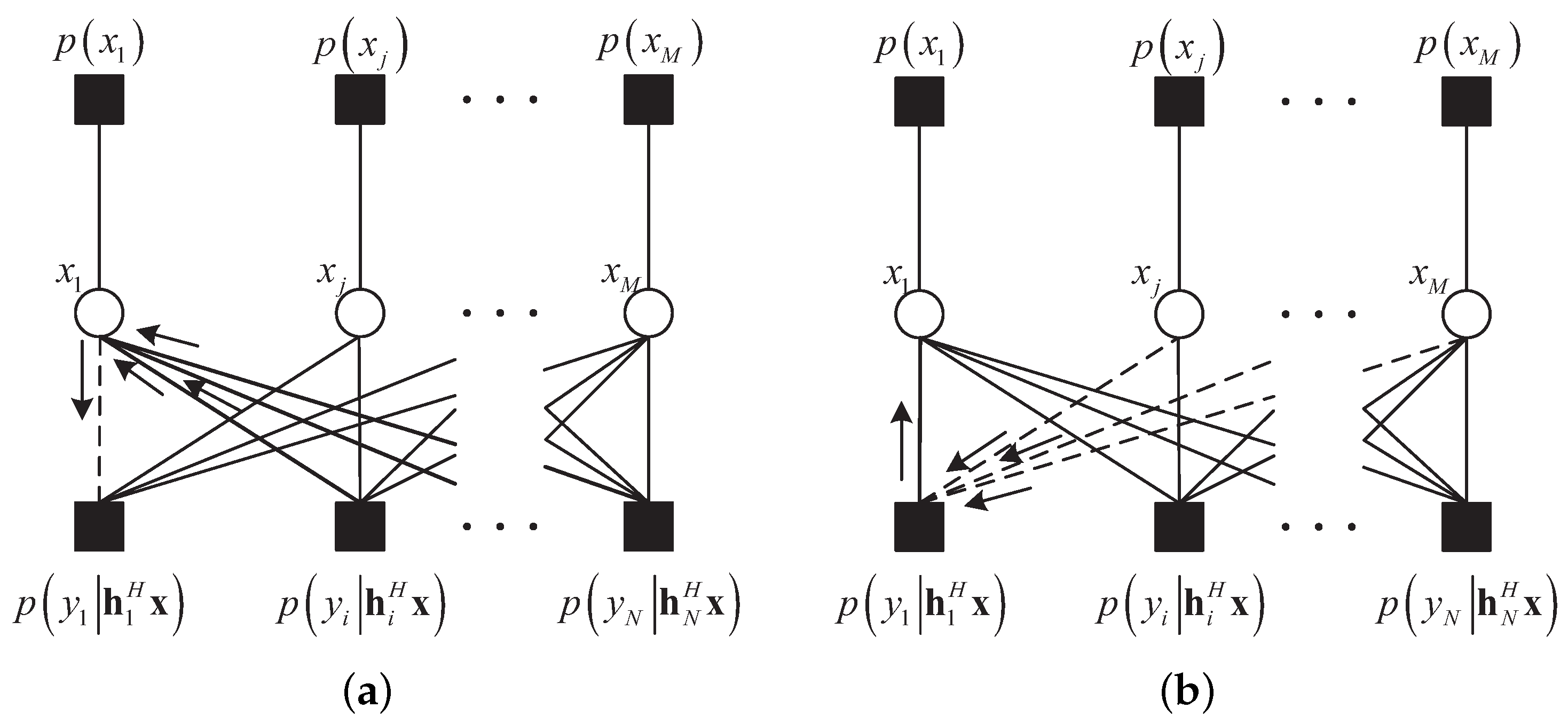
3.2. Equalization Based on Approximate Message Passing
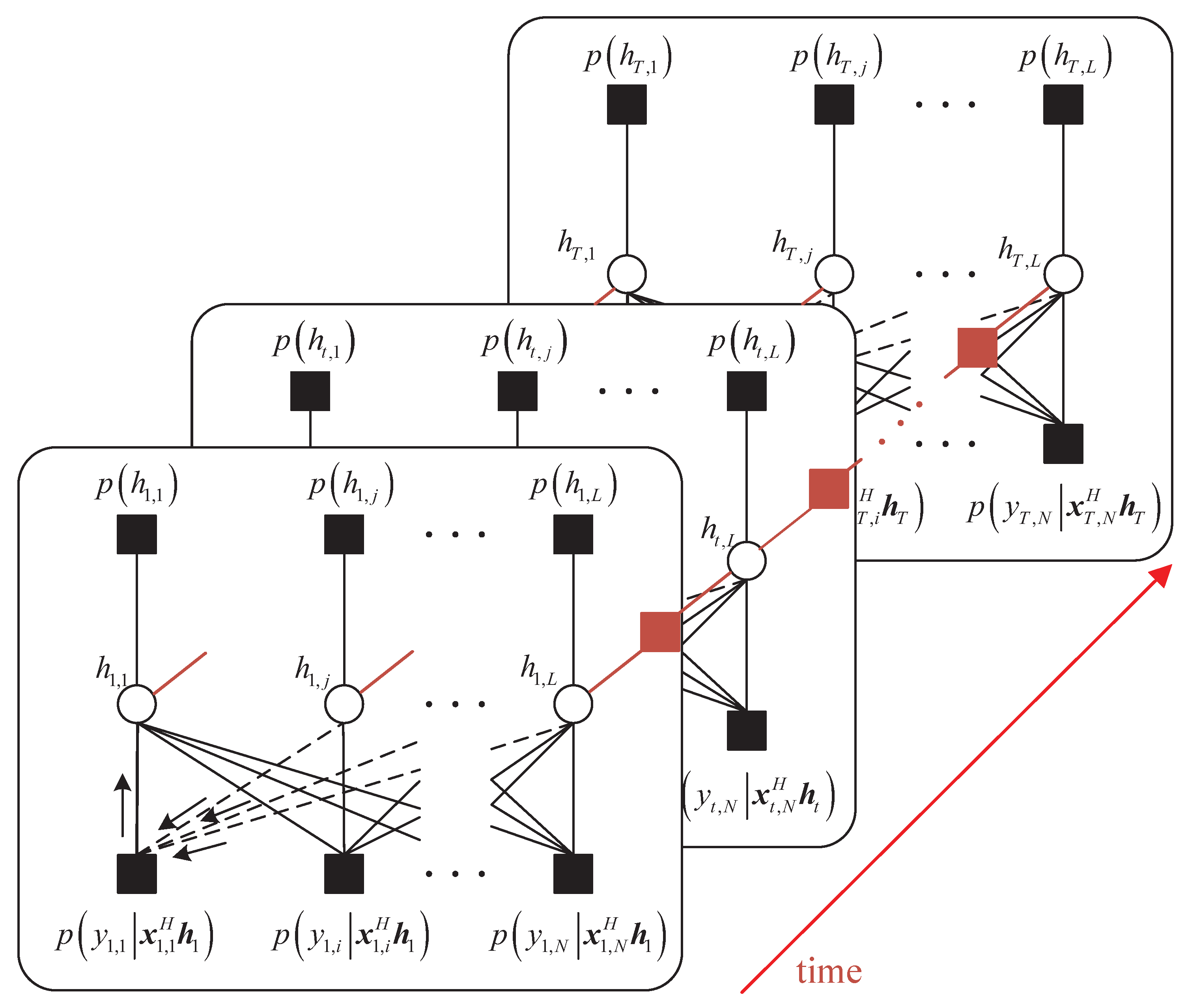
3.3. GMM Time-Varying Channel Estimation Based on AR-HMM Model
4. Numerical Results
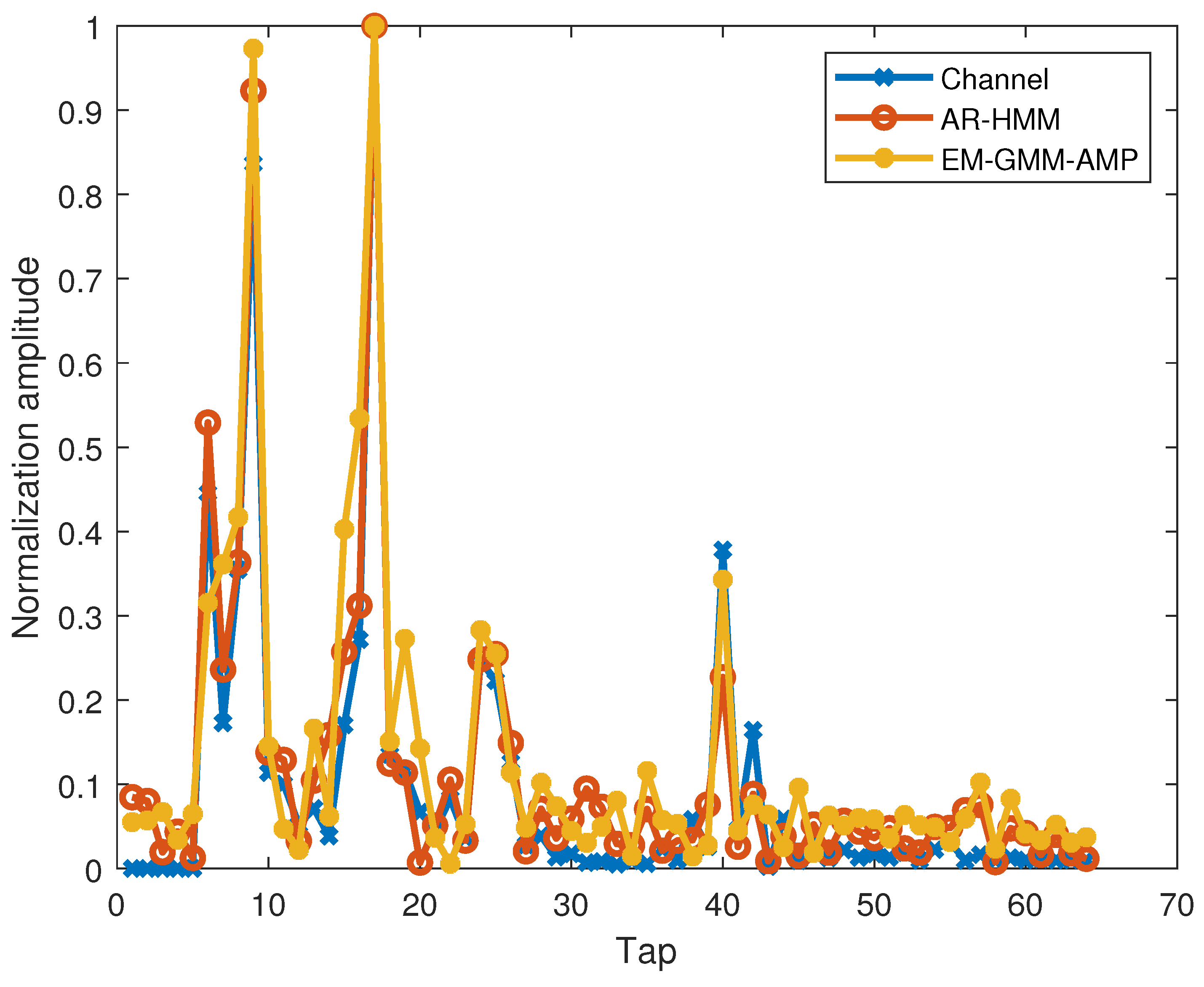
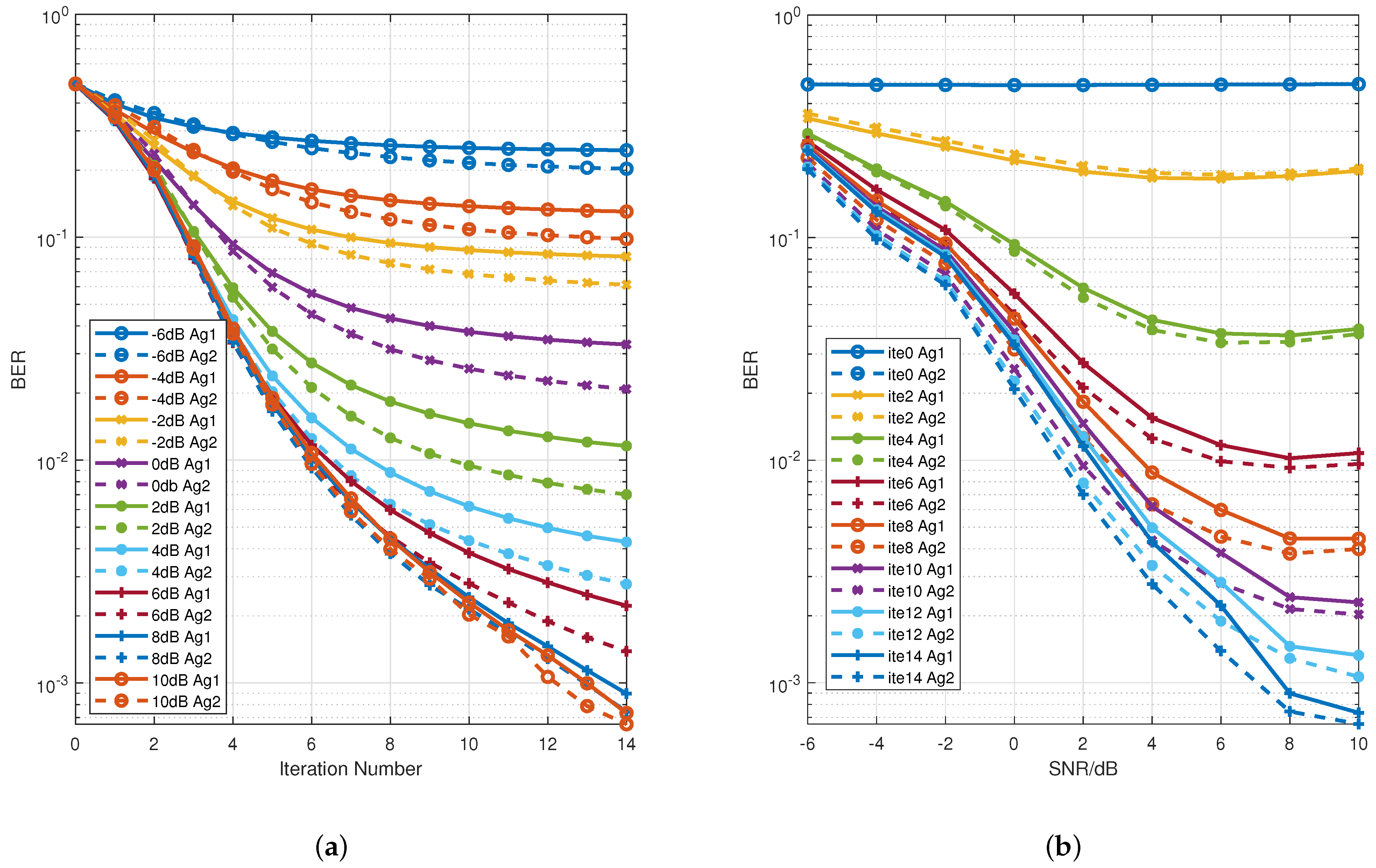
4.1. Simulation
4.2. Field Experiments
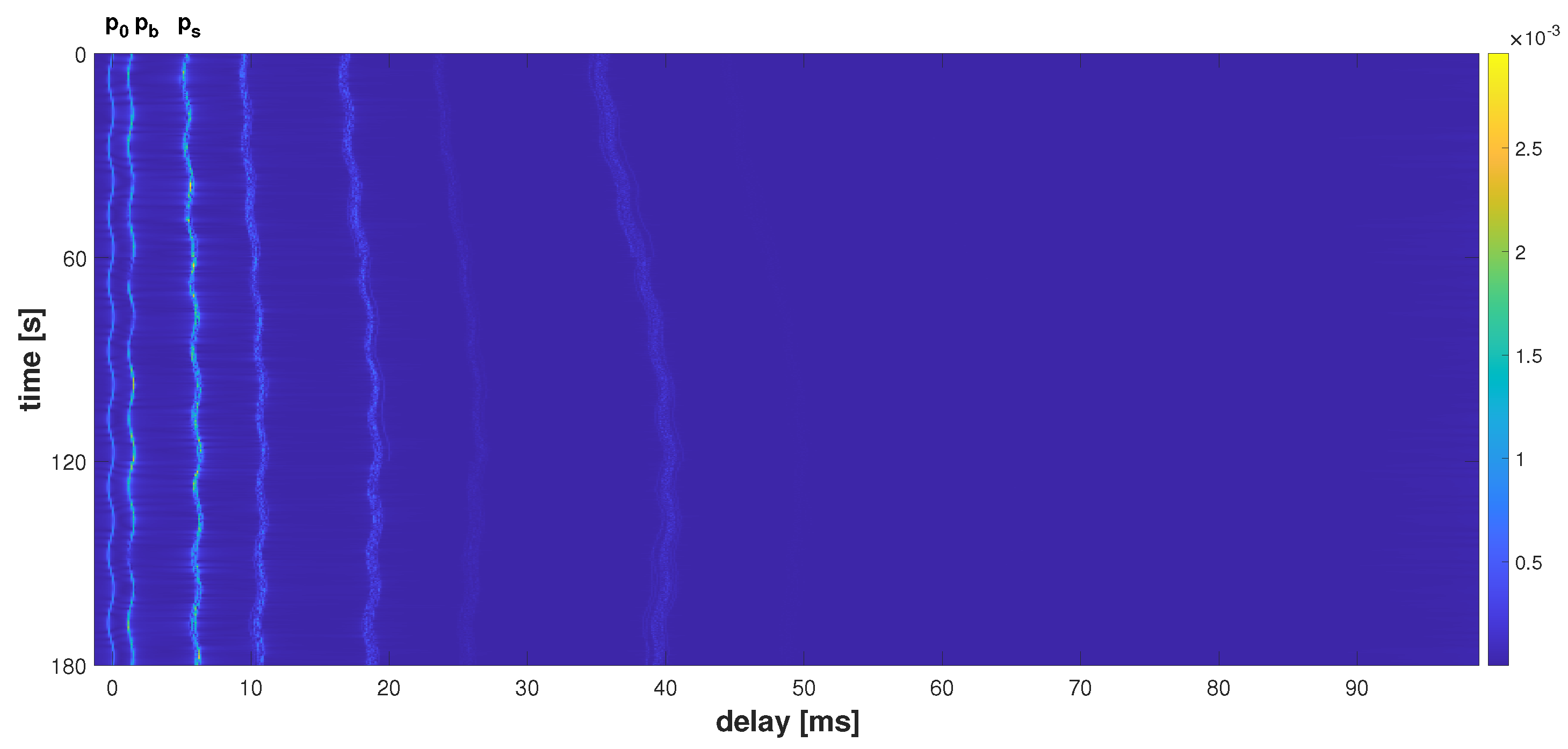
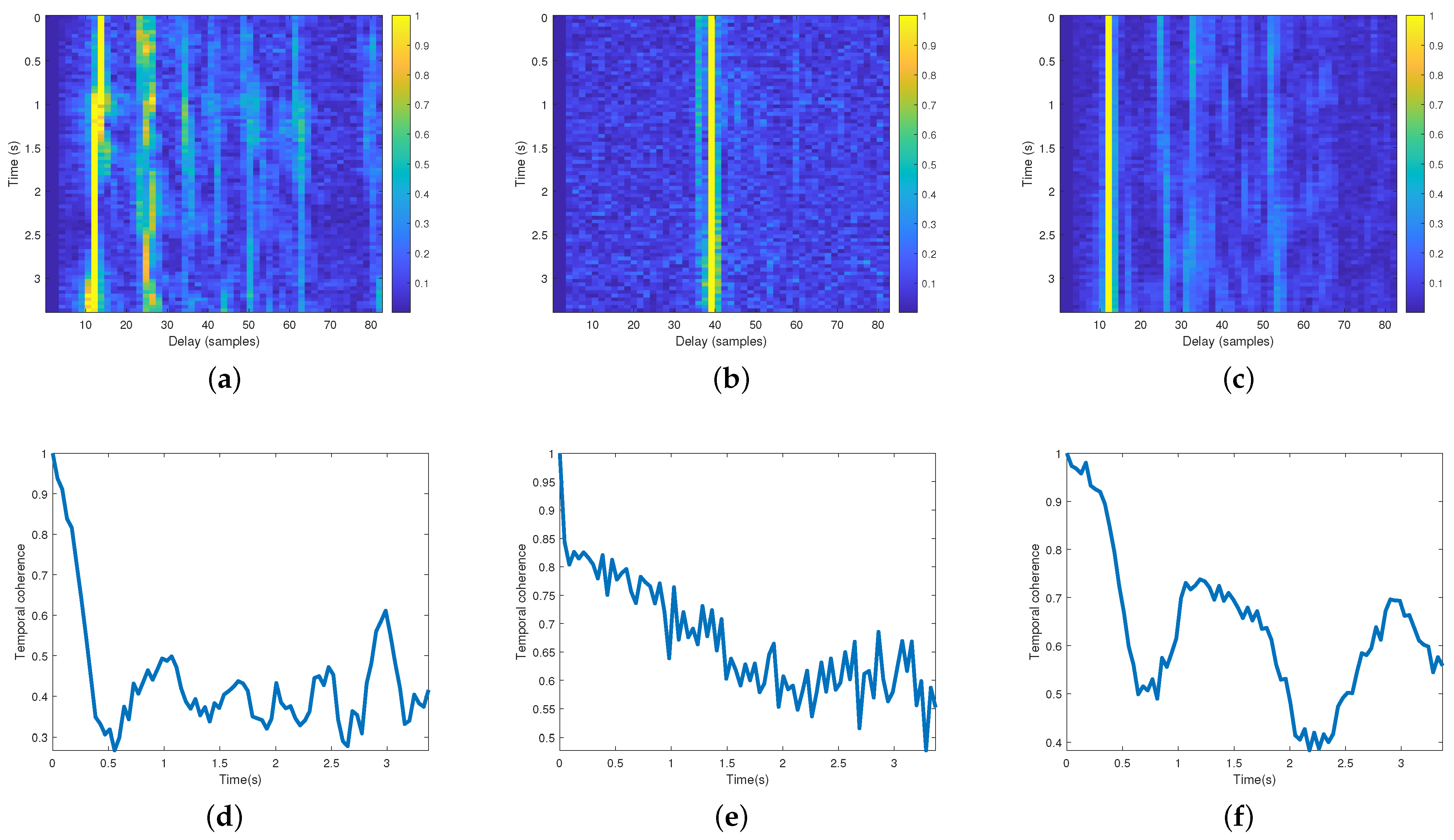
4.2.1. Movement Experiment in Pool at Harbin Engineering University
4.2.2. Songhua Lake Mobile Communication Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Derivation of Denoising Function η(·,·) and κ(·,·) in GMM-AMP Channel Estimation
References
- Dao, N.-N.; Tu, N.H.; Thanh, T.T.; Bao, V.N.Q.; Na, W.; Cho, S. Neglected infrastructures for 6G—Underwater communications: How mature are they? J. Netw. Comput. Appl. 2023, 213, 103595. [Google Scholar] [CrossRef]
- Song, A.; Stojanovic, M.; Chitre, M. Editorial underwater acoustic communications: Where we stand and what is next? IEEE J. Ocean. Eng. 2019, 44, 1–6. [Google Scholar]
- Yang, T. Properties of underwater acoustic communication channels in shallow water. J. Acoust. Soc. Am. 2012, 131, 129–145. [Google Scholar] [CrossRef] [PubMed]
- Molisch, A.F. Wideband and Directional Channel Characterization. In Wireless Communications; John Wiley & Sons: New York, NY, USA, 2011; pp. 101–123. [Google Scholar] [CrossRef]
- Zhang, X.; Yang, P.; Wang, Y.; Shen, W.; Yang, J.; Wang, J.; Ye, K.; Zhou, M.; Sun, H. A Novel Multireceiver SAS RD Processor. IEEE Trans. Geosci. Remote. Sens. 2024, 62, 1–11. [Google Scholar] [CrossRef]
- Yang, P. An imaging algorithm for high-resolution imaging sonar system. Multimed. Tools Appl. 2023, 83, 31957–31973. [Google Scholar] [CrossRef]
- Efron, B. Large-Scale Inference: Empirical Bayes Methods for Estimation, Testing, and Prediction; Cambridge University Press: Cambridge, UK, 2012; Volume 1. [Google Scholar]
- Minka, T.P. A Family of Algorithms for Approximate Bayesian Inference. Ph.D Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2001. [Google Scholar]
- Bernardo, J.; Girón, F. A Bayesian analysis of simple mixture problems. Bayesian Stat. 1988, 3, 67–78. [Google Scholar]
- Donoho, D.L.; Maleki, A.; Montanari, A. Message-passing algorithms for compressed sensing. Proc. Natl. Acad. Sci. USA 2009, 106, 18914–18919. [Google Scholar] [CrossRef] [PubMed]
- Zou, Q.; Yang, H. A Concise Tutorial on Approximate Message Passing. arXiv 2022, arXiv:2201.07487. [Google Scholar]
- Rangan, S. Generalized approximate message passing for estimation with random linear mixing. In Proceedings of the 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; pp. 2168–2172. [Google Scholar]
- Rangan, S.; Schniter, P.; Fletcher, A.K. Vector approximate message passing. IEEE Trans. Inf. Theory 2019, 65, 6664–6684. [Google Scholar] [CrossRef]
- Ma, J.; Ping, L. Orthogonal amp. IEEE Access 2017, 5, 2020–2033. [Google Scholar] [CrossRef]
- Takeuchi, K. Convolutional approximate message-passing. IEEE Signal Process. Lett. 2020, 27, 416–420. [Google Scholar] [CrossRef]
- Liu, L.; Huang, S.; Kurkoski, B.M. Memory approximate message passing. In Proceedings of the 2021 IEEE International Symposium on Information Theory (ISIT), Melbourne, Australia, 12–20 July 2021; pp. 1379–1384. [Google Scholar]
- Luo, M.; Guo, Q.; Jin, M.; Eldar, Y.C.; Huang, D.; Meng, X. Unitary approximate message passing for sparse Bayesian learning. IEEE Trans. Signal Process. 2021, 69, 6023–6039. [Google Scholar] [CrossRef]
- Tian, Y.N.; Han, X.; Yin, J.W.; Liu, Q.Y.; Li, L. Group sparse underwater acoustic channel estimation with impulsive noise: Simulation results based on Arctic ice cracking noise. J. Acoust. Soc. Am. 2019, 146, 2482–2491. [Google Scholar] [CrossRef] [PubMed]
- Bello, P. Characterization of Randomly Time-Variant Linear Channels. IEEE Trans. Commun. Syst. 1963, 11, 360–393. [Google Scholar] [CrossRef]
- Qarabaqi, P.; Stojanovic, M. Statistical characterization and computationally efficient modeling of a class of underwater acoustic communication channels. IEEE Journal of Oceanic Engineering 2013, 38, 701–717. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J.; Wang, H.; Shen, X.; Wang, B.; Dong, Y. Deep reinforcement learning-based adaptive modulation for underwater acoustic communication with outdated channel state information. Remote. Sens. 2022, 14, 3947. [Google Scholar] [CrossRef]
- Wan, L.; Zhou, H.; Xu, X.; Huang, Y.; Zhou, S.; Shi, Z.; Cui, J.H. Adaptive modulation and coding for underwater acoustic OFDM. IEEE J. Ocean. Eng. 2014, 40, 327–336. [Google Scholar] [CrossRef]
- Sun, D.; Wu, J.; Hong, X.; Liu, C.; Cui, H.; Si, B. Iterative double-differential direct-sequence spread spectrum reception in underwater acoustic channel with time-varying Doppler shifts. J. Acoust. Soc. Am. 2023, 153, 1027–1041. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhao, Y.; Gerstoft, P.; Zhou, F.; Qiao, G.; Yin, J. Deep transfer learning-based variable Doppler underwater acoustic communications. J. Acoust. Soc. Am. 2023, 154, 232–244. [Google Scholar] [CrossRef] [PubMed]
- Guo, Q.; Ping, L.; Huang, D. A low-complexity iterative channel estimation and detection technique for doubly selective channels. IEEE Trans. Wirel. Commun. 2009, 8, 4340–4349. [Google Scholar]
- Yang, G.; Guo, Q.; Ding, H.; Yan, Q.; Huang, D.D. Joint message-passing-based bidirectional channel estimation and equalization with superimposed training for underwater acoustic communications. IEEE J. Ocean. Eng. 2021, 46, 1463–1476. [Google Scholar] [CrossRef]
- Yang, G.; Guo, Q.; Qin, Z.; Huang, D.; Yan, Q. Belief-Propagation-Based Low-Complexity Channel Estimation and Detection for Underwater Acoustic Communications With Moving Transceivers. IEEE J. Ocean. Eng. 2022, 47, 1246–1263. [Google Scholar] [CrossRef]
- Zhang, Z.; Rao, B.D. Sparse signal recovery with temporally correlated source vectors using sparse Bayesian learning. IEEE J. Sel. Top. Signal Process. 2011, 5, 912–926. [Google Scholar] [CrossRef]
- Zhou, Y.; Tong, F.; Yang, X. Research on co-channel interference cancellation for underwater acoustic mimo communications. Remote. Sens. 2022, 14, 5049. [Google Scholar] [CrossRef]
- Yin, J.; Zhu, G.; Han, X.; Guo, L.; Li, L.; Ge, W. Temporal Correlation and Message-Passing-Based Sparse Bayesian Learning Channel Estimation for Underwater Acoustic Communications. IEEE J. Ocean. Eng. 2024, 1–20. [Google Scholar] [CrossRef]
- Orozco-Lugo, A.G.; Lara, M.M.; McLernon, D.C. Channel estimation using implicit training. IEEE Trans. Signal Process. 2004, 52, 240–254. [Google Scholar] [CrossRef]
- Yuan, W.; Li, S.; Wei, Z.; Yuan, J.; Ng, D.W.K. Data-aided channel estimation for OTFS systems with a superimposed pilot and data transmission scheme. IEEE Wirel. Commun. Lett. 2021, 10, 1954–1958. [Google Scholar] [CrossRef]
- Lyu, S.; Ling, C. Hybrid vector perturbation precoding: The blessing of approximate message passing. IEEE Trans. Signal Process. 2018, 67, 178–193. [Google Scholar] [CrossRef]
- Vila, J.P.; Schniter, P. Expectation-maximization Gaussian-mixture approximate message passing. IEEE Trans. Signal Process. 2013, 61, 4658–4672. [Google Scholar] [CrossRef]
- Panhuber, R. Fast, Efficient, and Viable Compressed Sensing, Low-Rank, and Robust Principle Component Analysis Algorithms for Radar Signal Processing. Remote. Sens. 2023, 15, 2216. [Google Scholar] [CrossRef]







| Simulations | Pool | Songhua Lake | |
|---|---|---|---|
| Code rate | 1/2 | 1/2 | 1/2 |
| Mapping | QPSK | QPSK | QPSK |
| Power TrainSeq/Data | 0.2:0.8 | 0.2:0.8 | 0.2:0.8 |
| Block length | 1024 symbols | 1024 symbols | 1024 symbols |
| Sub-block length | 64 symbols | 64/128/256/512 symbols | 64/128/256/512 symbols |
| CP | 128 symbols | 128 symbols | 128 symbols |
| System | SC-FDE | SC-FDE | SC-FDE |
| Center frequency | - | 12 kHz | 12 kHz |
| Bandwidth | 2 kHz | 6 kHz | 6 kHz |
| fs | - | 96 kHz | 96 kHz |
| Communication range | - | 4 m–9 m | 400 m–1400 m |
| Tx/Rx depth | - | Tx (2/3 m) Rx 4 m | Tx (5/10 m) Rx (15:35) m |
| Relative speed | 4 m/s | 0.2 m/s−1 m/s | 0.5 m/s−1 m/s |
| SNR | −6 dB to 12 dB | 25 dB | 6 dB to 18 dB |
| Horizontal Movement | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Block Number | Soft Iteration Algorithm Based on GMP [26] | Soft Iteration Algorithm Based on EM-GMM-AMP | ||||||||
| Iteration Number | Iteration Number | |||||||||
| 0 | 2 | 4 | 6 | 8 | 0 | 2 | 4 | 6 | 8 | |
| 1 | 32.68% | 10.47% | 0 | 0 | 0 | 32.68% | 5.48% | 0 | 0 | 0 |
| 2 | 32.39% | 1.08% | 0 | 0 | 0 | 32.39% | 0.49% | 0 | 0 | 0 |
| 3 | 39.82% | 30.33% | 24.36% | 15.75% | 6.36% | 39.82% | 13.21% | 0.98% | 0 | 0 |
| 4 | 34.83% | 22.80% | 18.00% | 7.53% | 0 | 34.83% | 17.71% | 1.08% | 0 | 0 |
| 5 | 34.74% | 4.01% | 0 | 0 | 0 | 34.74% | 2.25% | 0 | 0 | 0 |
| 6 | 40.70% | 28.77% | 14.77% | 0.29% | 0 | 40.70% | 14.38% | 1.08% | 0 | 0 |
| 7 | 44.03% | 22.21% | 12.33% | 0.59% | 0 | 44.03% | 3.03% | 0 | 0 | 0 |
| 8 | 33.07% | 18.20% | 1.66% | 0.00% | 0 | 33.07% | 8.22% | 0 | 0 | 0 |
| 9 | 27.01% | 1.57% | 0.00% | 0 | 0 | 27.01% | 0.98% | 0 | 0 | 0 |
| 10 | 36.20% | 21.33% | 2.94% | 1.37% | 0 | 36.20% | 14.68% | 4.40% | 0.07% | 0 |
| mean | 35.55% | 16.08% | 7.41% | 2.55% | 0.64% | 35.55% | 8.04% | 0.75% | 0.01% | 0.00% |
| Vertical Movement | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Block Number | Soft Iteration Algorithm Based on GMP [26] | Soft Iteration Algorithm Based on EM-GMM-AMP | ||||||||
| Iteration Number | Iteration Number | |||||||||
| 0 | 1 | 2 | 4 | 6 | 0 | 1 | 2 | 4 | 6 | |
| 1 | 19.86% | 6.36% | 0.78% | 0.20% | 0.20% | 19.86% | 4.60% | 0.10% | 0 | 0 |
| 2 | 16.83% | 3.42% | 0.68% | 0 | 0 | 16.83% | 4.60% | 1.57% | 0 | 0 |
| 3 | 14.09% | 1.27% | 0 | 0 | 0 | 14.09% | 1.08% | 0.00% | 0 | 0 |
| 4 | 25.34% | 9.49% | 1.37% | 0.10% | 0 | 25.34% | 9.39% | 1.86% | 0.10% | 0 |
| 5 | 22.80% | 9.20% | 3.33% | 0.29% | 0.10% | 22.80% | 8.51% | 3.13% | 0.29% | 0 |
| 6 | 11.84% | 2.64% | 0.29% | 0 | 0 | 11.84% | 1.76% | 0.29% | 0 | 0 |
| 7 | 20.16% | 5.97% | 2.05% | 0 | 0 | 20.16% | 6.07% | 1.08% | 0 | 0 |
| 8 | 14.58% | 2.94% | 0 | 0 | 0 | 14.58% | 2.25% | 0.20% | 0 | 0 |
| 9 | 30.92% | 17.51% | 11.45% | 2.54% | 0 | 30.92% | 16.73% | 9.39% | 1.47% | 0 |
| 10 | 15.26% | 5.58% | 2.05% | 0.00% | 0 | 15.26% | 5.19% | 1.47% | 0 | 0 |
| mean | 19.17% | 6.44% | 2.20% | 0.31% | 0.03% | 19.17% | 6.02% | 1.91% | 0.19% | 0.00% |
| Block Number | Sub-Block Length | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 64 Symbols | 128 Symbols | 256 Symbols | 512 Symbols | No Sub-Block | ||||||
| 6.88 dB | 11.16 dB | 6.69 dB | 15.6 dB | 6.59 dB | 15.52 dB | 6.71 dB | 15.56 dB | 8.84 dB | 16.7 dB | |
| = 0.7 | = 0.8 | = 0.85 | = 0.93 | = 0.8 | = 0.78 | = 0.85 | = 0.93 | = 0.95 | = 1 | |
| 1 | 0 | 0 | 0.00% | 0 | 0 | 0.10% | 0.68% | 0.49% | 0 | 0 |
| 2 | 0.10% | 0 | 0.78% | 0 | 0.88% | 0.10% | 5.38% | 2.64% | 0.10% | 0 |
| 3 | 0.10% | 0.18% | 0.68% | 0 | 0.39% | 0.10% | 3.03% | 1.86% | 0 | 0 |
| 4 | 0 | 0 | 2.45% | 0.59% | 0.20% | 0.59% | 5.48% | 1.57% | 0 | 0 |
| 5 | 0 | 0 | 0.68% | 0 | 0.68% | 0.29% | 2.35% | 0 | 0 | 0 |
| 6 | 0 | 0 | 6.95% | 0 | 2.15% | 0.49% | 1.47% | 0.98% | 0 | 0 |
| 7 | 0 | 0 | 0.10% | 0 | 0.29% | 0.29% | 0.98% | 0.98% | 0 | 0 |
| 8 | 0 | 0 | 1.37% | 0 | 0.49% | 0.29% | 3.03% | 0 | 0 | 0 |
| 9 | 0 | 0 | 0.29% | 0 | 0.10% | 0.49% | 2.25% | 0 | 0 | 0 |
| 10 | 0.39% | 0.09% | 0.10% | 1.27% | 6.85% | 0 | 2.25% | 0.59% | 0 | 0 |
| 11 | 0 | 0 | 0.98% | 0 | 0.20% | 0.29% | 4.50% | 3.91% | 0 | 0 |
| 12 | 0 | 0 | 1.27% | 0.39% | 0 | 0 | 1.08% | 0.10% | 0 | 0 |
| 13 | 0 | 0 | 0.35% | 0 | 11.45% | 2.54% | 1.96% | 1.66% | 0 | 0 |
| 14 | 0.09% | 0 | 0.10% | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.10% | 0 | 0 |
| 16 | 0 | 0.19% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| mean | 0.04% | 0.03% | 1.01% | 0.14% | 1.48% | 0.35% | 2.15% | 0.93% | 0.01% | 0.00% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, L.; Han, X.; Ge, W. Iterative Signal Detection and Channel Estimation with Superimposed Training Sequences for Underwater Acoustic Information Transmission in Time-Varying Environments. Remote Sens. 2024, 16, 1209. https://doi.org/10.3390/rs16071209
Li L, Han X, Ge W. Iterative Signal Detection and Channel Estimation with Superimposed Training Sequences for Underwater Acoustic Information Transmission in Time-Varying Environments. Remote Sensing. 2024; 16(7):1209. https://doi.org/10.3390/rs16071209
Chicago/Turabian StyleLi, Lin, Xiao Han, and Wei Ge. 2024. "Iterative Signal Detection and Channel Estimation with Superimposed Training Sequences for Underwater Acoustic Information Transmission in Time-Varying Environments" Remote Sensing 16, no. 7: 1209. https://doi.org/10.3390/rs16071209
APA StyleLi, L., Han, X., & Ge, W. (2024). Iterative Signal Detection and Channel Estimation with Superimposed Training Sequences for Underwater Acoustic Information Transmission in Time-Varying Environments. Remote Sensing, 16(7), 1209. https://doi.org/10.3390/rs16071209








