Sentinel-1-Based Soil Freeze–Thaw Detection in Agro-Forested Areas: A Case Study in Southern Québec, Canada
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Sites
2.2. In-Situ Data
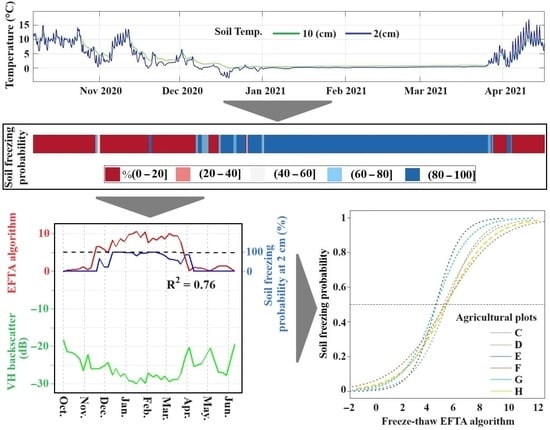
2.3. Deriving Soil Freezing Probability
2.4. Satellite Data Acquisition
2.4.1. Speckle Filtering
2.4.2. Local Incidence Angle (LIA) Corrections
2.5. FT Algorithms
2.6. Probabilistic Statistical Analysis
- Soil freezing probability ~ 1 + VHEFTA;
- Soil freezing probability ~ 1 + VHEFTA + (1|Plot);
- Soil freezing probability ~ 1 + VHEFTA × Soil types + (1|Plot);
- Soil freezing probability ~ 1 + VHEFTA × Crop types + (1|Plot);
- Soil freezing probability ~ 1 + VHEFTA × Soil types + VHEFTA × Crop types + (1|Plot);
- Soil freezing probability ~ 1 + VHEFTA × Soil types + VHEFTA × Crop types + VHEFTA × Crop residues + (1|Plot).
2.7. Model Calibration and Validation
3. Results
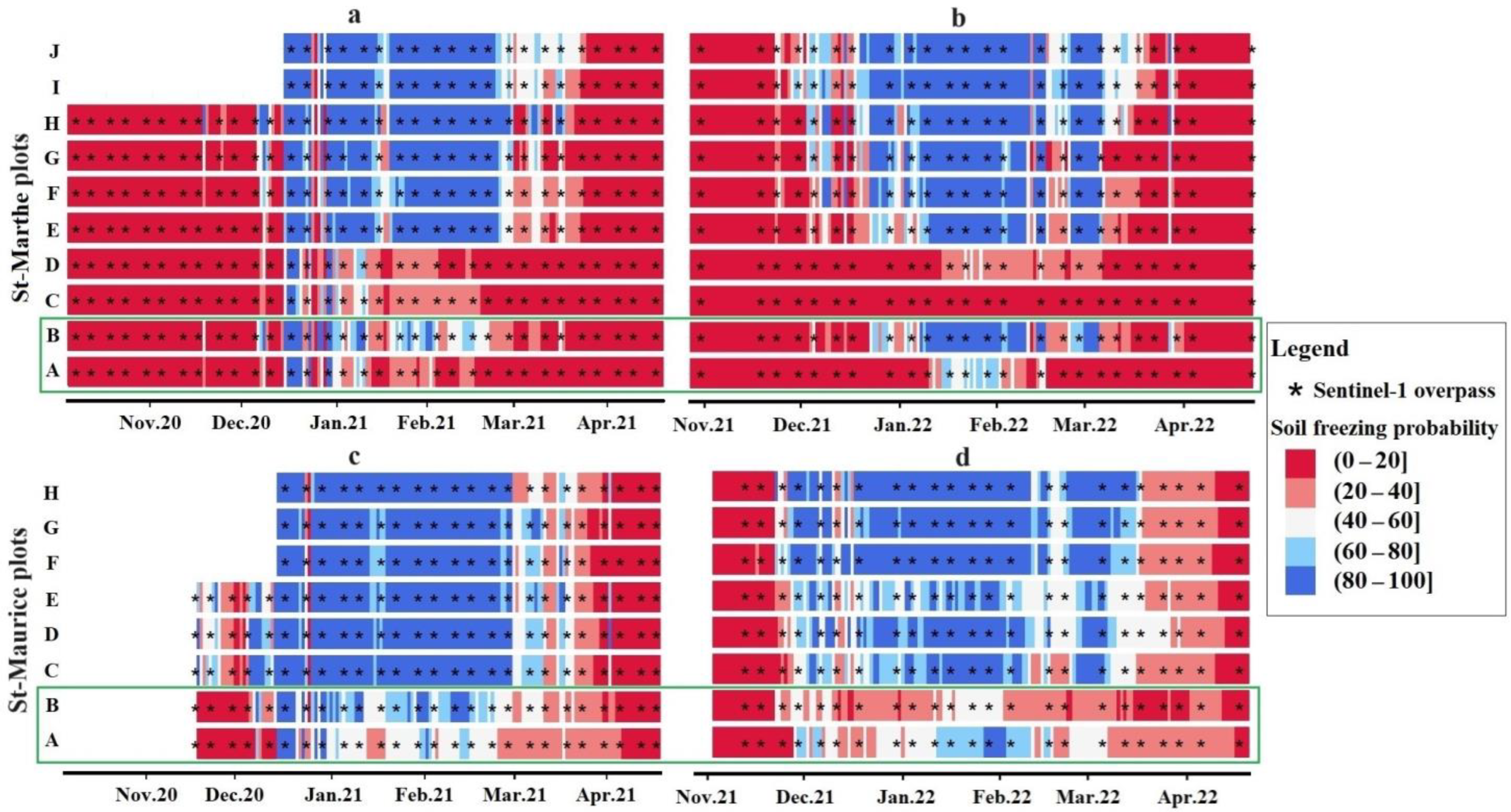
3.1. Observed FT Spatiotemporal Variability
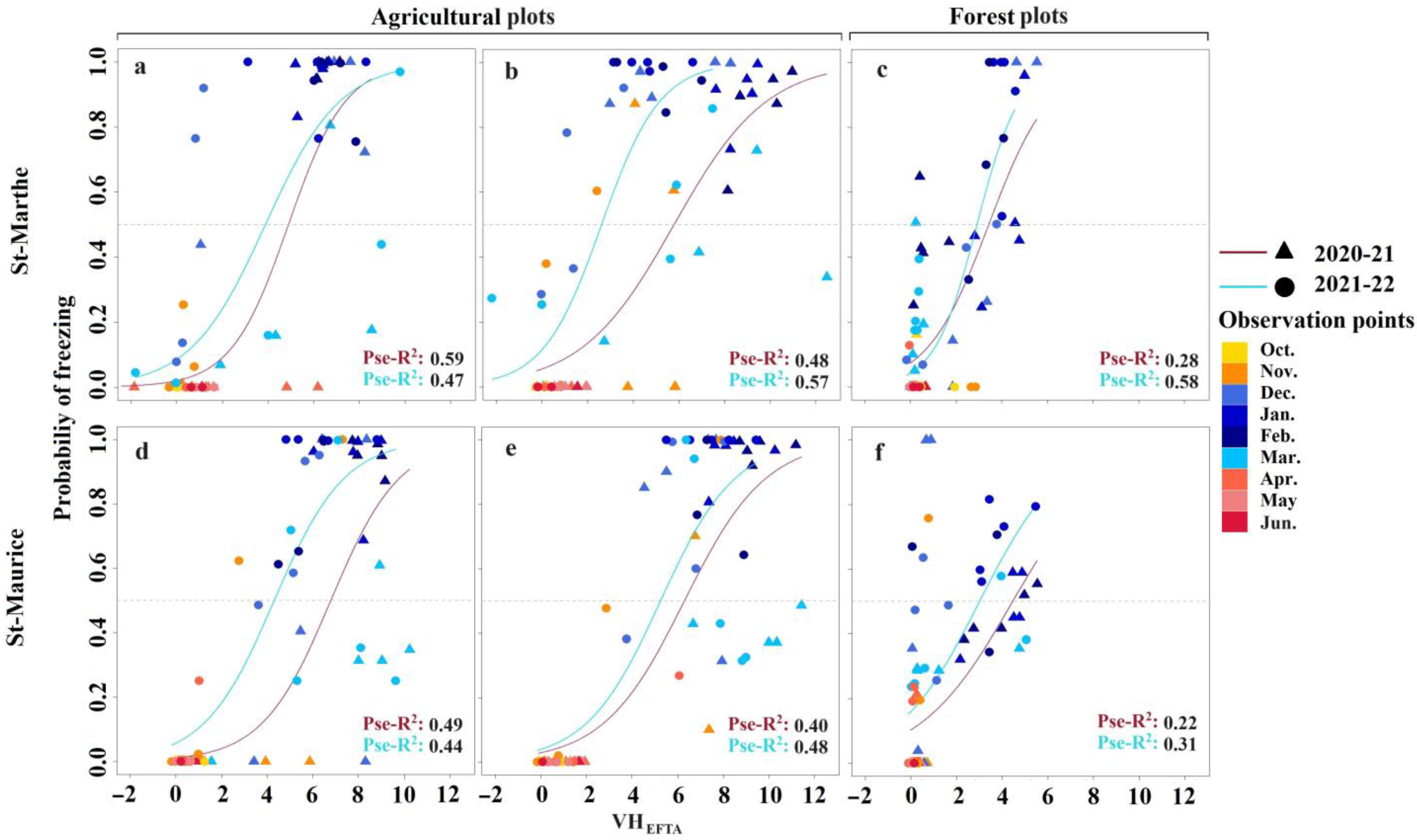
3.2. Comparisons of Predictors for Modelling Freezing Probability
3.3. Spatially Variable Probabilistic Modelling of FT Detection
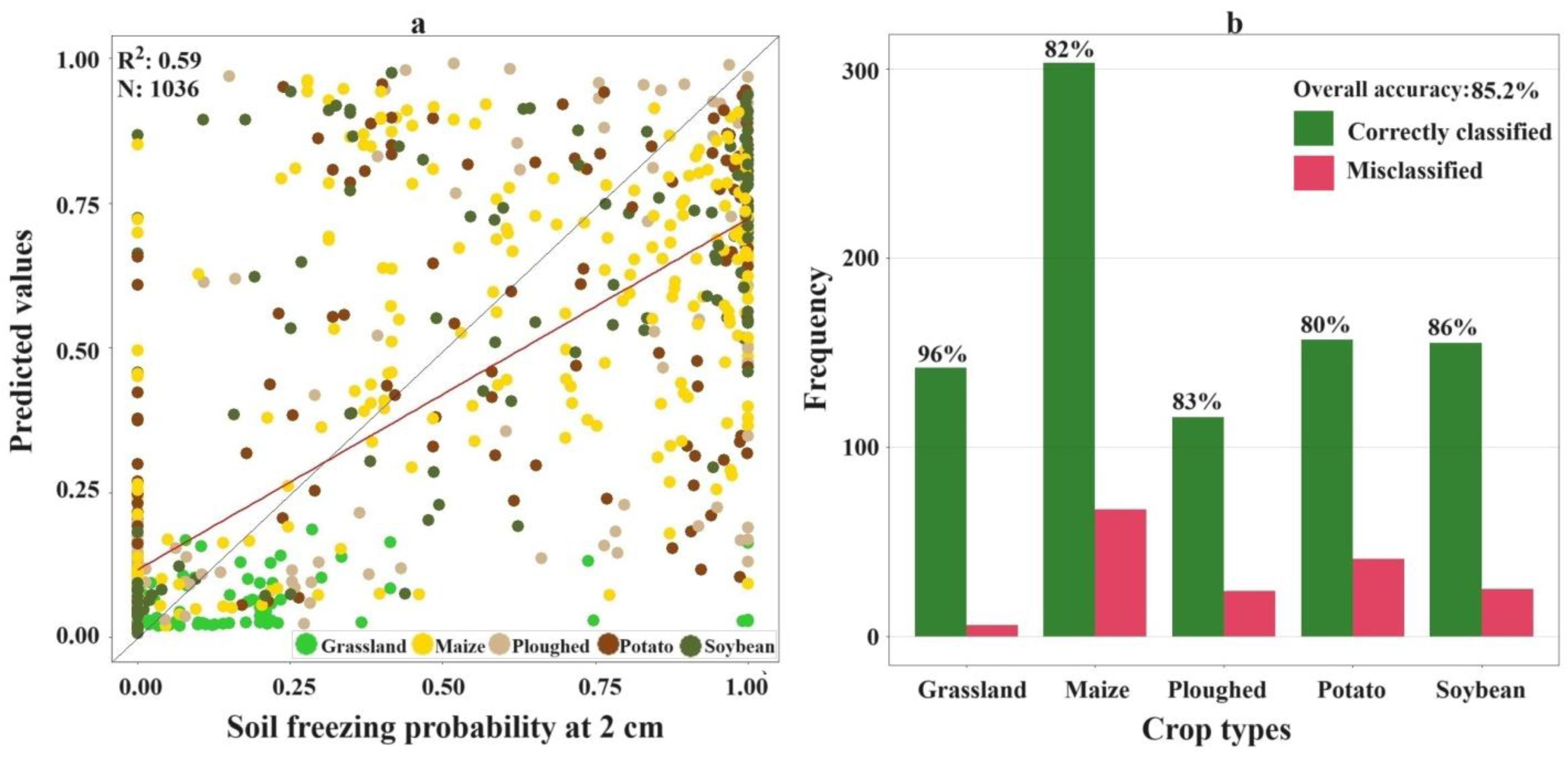
3.4. Model Validation
4. Discussion
4.1. FT Spatial and Temporal Variability
4.2. Retrieving Ground Frozen State from VH Backscatter
4.3. GLM Prediction and Influencing Variables on Radar Signals
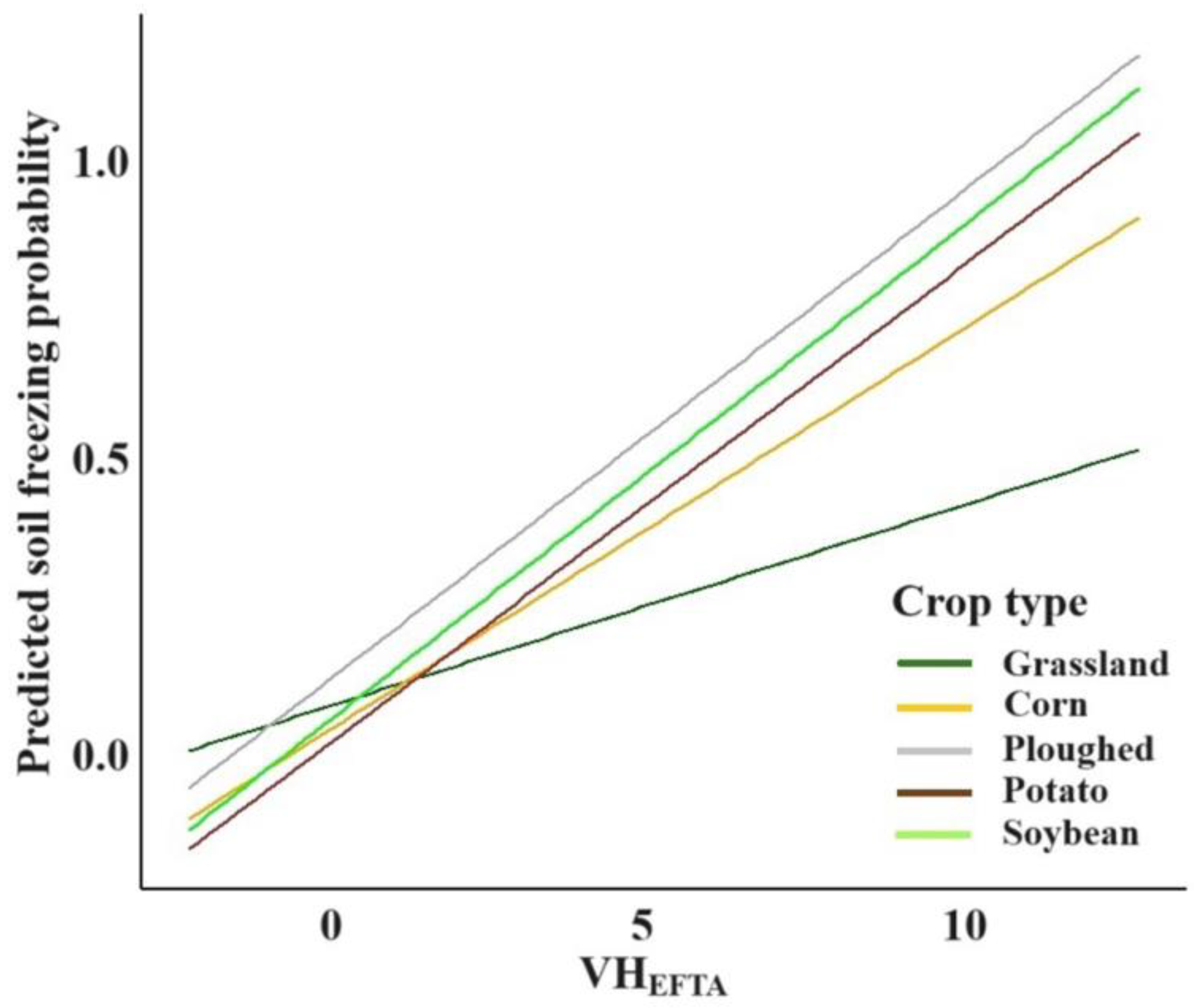
4.4. Crop-Mixed Model and Predictor Effects
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Henry, H.A.L. Soil Freeze–Thaw Cycle Experiments: Trends, Methodological Weaknesses and Suggested Improvements. Soil. Biol. Biochem. 2007, 39, 977–986. [Google Scholar] [CrossRef]
- Zhang, T.; Armstrong, R.L.; Smith, J. Investigation of the Near-surface Soil Freeze-thaw Cycle in the Contiguous United States: Algorithm Development and Validation. J. Geophys. Res. Atmos. 2003, 108, D22. [Google Scholar] [CrossRef]
- McDonald, K.C.; Kimball, J.S.; Zhao, M.; Njoku, E.; Zimmermann, R.; Running, S.W. Spaceborne Microwave Remote Sensing of Seasonal Freeze-Thaw Processes in the Terrestrial High Latitudes: Relationships with Land-Atmosphere CO2 Exchange. In Microwave Remote Sensing of the Atmosphere and Environment IV; International Society for Optics and Photonics: Bellingham, WA, USA, 2004; Volume 5654, pp. 167–178. [Google Scholar]
- Gao, C.; Bai, W.; Wang, Z.; Wu, X.; Liu, L.; Deng, N.; Xia, J. Simulations and Analysis of GNSS Multipath Observables for Frozen and Thawed Soil under Complex Surface Conditions. Water 2021, 13, 1986. [Google Scholar] [CrossRef]
- Walvoord, M.A.; Kurylyk, B.L. Hydrologic Impacts of Thawing Permafrost—A Review. Vadose Zone J. 2016, 15, vzj2016- 01. [Google Scholar] [CrossRef]
- Wang, J.; Luo, S.; Li, Z.; Wang, S.; Li, Z. The Freeze/Thaw Process and the Surface Energy Budget of the Seasonally Frozen Ground in the Source Region of the Yellow River. Theor. Appl. Clim. 2019, 138, 1631–1646. [Google Scholar] [CrossRef]
- Krogstad, K. Impact of Winter Soil Processes on Nutrient Leaching in Cold Region Agroecosystems. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2021. [Google Scholar]
- Cober, J.R.; Macrae, M.L.; Van Eerd, L.L. Nutrient Release from Living and Terminated Cover Crops under Variable Freeze–Thaw Cycles. Agron. J. 2018, 110, 1036–1045. [Google Scholar] [CrossRef]
- Edwards, L.M. The Effects of Soil Freeze–Thaw on Soil Aggregate Breakdown and Concomitant Sediment Flow in Prince Edward Island: A Review. Can. J. Soil. Sci. 2013, 93, 459–472. [Google Scholar] [CrossRef]
- Leuther, F.; Schlüter, S. Impact of Freeze–Thaw Cycles on Soil Structure and Soil Hydraulic Properties. Soil 2021, 7, 179–191. [Google Scholar] [CrossRef]
- Wang, K.; Zhang, T.; Zhong, X. Changes in the Timing and Duration of the Near-Surface Soil Freeze/Thaw Status from 1956 to 2006 across China. Cryosphere 2015, 9, 1321–1331. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. Simulated Change in the Near-Surface Soil Freeze/Thaw Cycle on the Tibetan Plateau from 1981 to 2010. Chin. Sci. Bull. 2014, 59, 2439–2448. [Google Scholar] [CrossRef]
- Peng, X.; Frauenfeld, O.W.; Cao, B.; Wang, K.; Wang, H.; Su, H.; Huang, Z.; Yue, D.; Zhang, T. Response of Changes in Seasonal Soil Freeze/Thaw State to Climate Change from 1950 to 2010 across China. J. Geophys. Res. Earth Surf. 2016, 121, 1984–2000. [Google Scholar] [CrossRef]
- Wang, R.; Zhu, Q.; Ma, H.; Ai, N. Spatial-Temporal Variations in near-Surface Soil Freeze-Thaw Cycles in the Source Region of the Yellow River during the Period 2002–2011 Based on the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR-E) Data. J. Arid Land 2017, 9, 850–864. [Google Scholar] [CrossRef]
- Luo, S.; Wang, J.; Pomeroy, J.W.; Lyu, S. Freeze–Thaw Changes of Seasonally Frozen Ground on the Tibetan Plateau from 1960 to 2014. J. Clim. 2020, 33, 9427–9446. [Google Scholar] [CrossRef]
- Xu, G.; Huang, M.; Li, P.; Li, Z.; Wang, Y. Effects of Land Use on Spatial and Temporal Distribution of Soil Moisture within Profiles. Environ. Earth Sci. 2021, 80, 80. [Google Scholar] [CrossRef]
- Qin, Y.; Bai, Y.; Chen, G.; Liang, Y.; Li, X.; Wen, B.; Lu, X.; Li, X. The Effects of Soil Freeze–Thaw Processes on Water and Salt Migrations in the Western Songnen Plain, China. Sci. Rep. 2021, 11, 3888. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Fu, Q.; Li, T.; Liu, D.; Hou, R.; Li, Q.; Yi, J.; Li, M.; Meng, F. Snow Melting Water Infiltration Mechanism of Farmland Freezing-Thawing Soil and Determination of Meltwater Infiltration Parameter in Seasonal Frozen Soil Areas. Agric. Water Manag. 2021, 258, 107165. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, P.; Xu, G.; Li, Z.; Wang, T.; Cheng, S.; Zhang, H.; Ma, T. The Effect of Soil Water Content and Erodibility on Losses of Available Nitrogen and Phosphorus in Simulated Freeze-Thaw Conditions. Catena 2018, 166, 21–33. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, Y.; Yang, F. Critical Review on Soil Phosphorus Migration and Transformation under Freezing-Thawing Cycles and Typical Regulatory Measurements. Sci. Total Environ. 2020, 751, 141614. [Google Scholar] [CrossRef] [PubMed]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Berg, A.A.; Lemmetyinen, J.; Arnold, L. Response of L-Band Brightness Temperatures to Freeze/Thaw and Snow Dynamics in a Prairie Environment from Ground-Based Radiometer Measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Shao, W.; Zhang, T. Assessment of Four Near-Surface Soil Freeze/Thaw Detection Algorithms Based on Calibrated Passive Microwave Remote Sensing Data Over China. Earth Space Sci. 2020, 7, e2019EA000807. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Pulliainen, J.; Vehvilainen, J.; Drusch, M.; Kontu, A.; Kainulainen, J.; Seppanen, J. L-Band Radiometer Observations of Soil Processes in Boreal and Subarctic Environments. IEEE Trans. Geosci. Remote Sens. 2011, 50, 1483–1497. [Google Scholar] [CrossRef]
- Derksen, C.; Xu, X.; Dunbar, R.S.; Colliander, A.; Kim, Y.; Kimball, J.S.; Black, T.A.; Euskirchen, E.; Langlois, A.; Loranty, M.M. Retrieving Landscape Freeze/Thaw State from Soil Moisture Active Passive (SMAP) Radar and Radiometer Measurements. Remote Sens. Environ. 2017, 194, 48–62. [Google Scholar] [CrossRef]
- Jin, R.; Zhang, T.; Li, X.; Yang, X.; Ran Antarctic, Y. Mapping Surface Soil Freeze-Thaw Cycles in China Based on SMMR and SSM/I Brightness Temperatures from 1978 to 2008. Arct. Antarct. Alp. Res. 2015, 47, 213–229. [Google Scholar] [CrossRef]
- Zhao, T.; Zhang, L.; Jiang, L.; Zhao, S.; Chai, L.; Jin, R. A new soil freeze/thaw discriminant algorithm using AMSR-E passive microwave imagery. Hydrol. Process. 2011, 25, 1704–1716. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Derksen, C.; Rowlandson, T.; Berg, A.; Lemmetyinen, J.; Royer, A.; Tetlock, E.; Helgason, W.; Sonnentag, O. Spatial Variability of L-Band Brightness Temperature during Freeze/Thaw Events over a Prairie Environment. Remote Sens. 2017, 9, 894. [Google Scholar] [CrossRef]
- Park, S.-E.; Bartsch, A.; Sabel, D.; Wagner, W.; Naeimi, V.; Yamaguchi, Y. Monitoring Freeze/Thaw Cycles Using ENVISAT ASAR Global Mode. Remote Sens. Environ. 2011, 115, 3457–3467. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.S.; Azarderakhsh, M.; Dunbar, R.S.; Moghaddam, M.; McDonald, K.C. Classification of Alaska Spring Thaw Characteristics Using Satellite L-Band Radar Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2014, 53, 542–556. [Google Scholar]
- Dunbar, S.; Xu, X.; Colliander, A.; Derksen, C.; Kimball, J.; Kim, Y. Algorithm Theoretical Basis Document (ATBD) SMAP Level 3 Radiometer Freeze/Thaw Data Products (L3_FT_P and L3_FT_P_E); NASA Jet Propulsion Laboratory (JPL): Pasadena, CA, USA, 2016. [Google Scholar]
- Rodionova, N.V. Identification of Frozen/Thawed Soils in the Areas of Anadyr (Chukotka) and Belaya Gora (Sakha) from the Sentinel 1 Radar Data. Atmos. Ocean. Phys. 2019, 55, 1314–1321. [Google Scholar] [CrossRef]
- Fayad, I.; Baghdadi, N.; Bazzi, H.; Zribi, M. Near Real-Time Freeze Detection over Agricultural Plots Using Sentinel-1 Data. Remote Sens. 2020, 12, 1976. [Google Scholar] [CrossRef]
- Baghdadi, N.; Bazzi, H.; El Hajj, M.; Zribi, M. Detection of Frozen Soil Using Sentinel-1 SAR Data. Remote Sens. 2018, 10, 1182. [Google Scholar] [CrossRef]
- de Aguirre Escobar, A.M. Analysis of Surface Roughness in Agricultural Soils Using In-Situ Measurements and Remote Sensing Techniques. Ph.D. Thesis, Public University of Navarre, Universidad Pública de Navarra, Navarre, Spain, 2017. [Google Scholar]
- Hudier, E.; Gosseli, J.-S. Impact of Daily Melt and Freeze Patterns on Sea Ice Large Scale Roughness Features Extraction. In Geoscience and Remote Sensing New Achievements; IntechOpen: London, UK, 2010. [Google Scholar]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the Characterization of Soil Surface Parameters over Bare Agricultural Fields. Remote Sens. Environ. 2005, 96, 78–86. [Google Scholar] [CrossRef]
- Khaldoune, J.; Van Bochove, E.; Bernier, M.; Nolin, M.C. Mapping Agricultural Frozen Soil on the Watershed Scale Using Remote Sensing Data. Appl. Environ. Soil. Sci. 2011, 2011, 193237. [Google Scholar] [CrossRef]
- Rodionova, N.V. Correlation of the Sentinel 1 Radar Data with Ground-Based Measurements of the Soil Temperature and Moisture. Izv. Atmos. Ocean. Phys. 2019, 55, 939–948. [Google Scholar] [CrossRef]
- Dharmadasa, V.; Kinnard, C.; Baraër, M. An Accuracy Assessment of Snow Depth Measurements in Agro-Forested Environments by UAV Lidar. Remote Sens. 2022, 14, 1649. [Google Scholar] [CrossRef]
- Wackerly, D.D. Mathematical Statistics with Applications, 7th ed.; Thomson Brooks/Cole: Belmont, CA, USA, 2008. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Torres, R.; Snoeij, P.; Geudtner, D.; Bibby, D.; Davidson, M.; Attema, E.; Potin, P.; Rommen, B.; Floury, N.; Brown, M. GMES Sentinel-1 Mission. Remote Sens. Environ. 2012, 120, 9–24. [Google Scholar] [CrossRef]
- Filipponi, F. Sentinel-1 GRD Preprocessing Workflow. In Proceedings of the International Electronic Conference on Remote Sensing, Vitrul, 22 May–5 June 2019; MDPI: Basel, Switzerland, 2019; p. 11. [Google Scholar]
- Domg, Y.; Milne, A.K. Toward edge sharpening: A SAR speckle filtering algorithm. IEEE Trans. Geosci. Remote Sens. 2001, 39, 851–863. [Google Scholar] [CrossRef]
- Lee, J.-S.; Wen, J.-H.; Ainsworth, T.L.; Chen, K.-S.; Chen, A.J. Improved Sigma Filter for Speckle Filtering of SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2008, 47, 202–213. [Google Scholar]
- Amani, M.; Brisco, B.; Afshar, M.; Mirmazloumi, S.M.; Mahdavi, S.; Mirzadeh, S.M.J.; Huang, W.; Granger, J. A Generalized Supervised Classification Scheme to Produce Provincial Wetland Inventory Maps: An Application of Google Earth Engine for Big Geo Data Processing. Big Earth Data 2019, 3, 378–394. [Google Scholar] [CrossRef]
- Fuhrmann, T.; Garthwaite, M.C. Resolving Three-Dimensional Surface Motion with InSAR: Constraints from Multi-Geometry Data Fusion. Remote Sens. 2019, 11, 241. [Google Scholar] [CrossRef]
- Schaufler, S.; Bauer-Marschallinger, B.; Hochstöger, S.; Wagner, W. Modelling and Correcting Azimuthal Anisotropy in Sentinel-1 Backscatter Data. Remote Sens. Lett. 2018, 9, 799–808. [Google Scholar] [CrossRef]
- Rautiainen, K.; Lemmetyinen, J.; Schwank, M.; Kontu, A.; Ménard, C.B.; Mätzler, C.; Drusch, M.; Wiesmann, A.; Ikonen, J.; Pulliainen, J. Detection of Soil Freezing from L-Band Passive Microwave Observations. Remote Sens. Environ. 2014, 147, 206–218. [Google Scholar] [CrossRef]
- Touati, C.; Ratsimbazafy, T.; Poulin, J.; Bernier, M.; Homayouni, S.; Ludwig, R. Landscape Freeze/Thaw Mapping from Active and Passive Microwave Earth Observations over the Tursujuq National Park, Quebec, Canada. Écoscience 2021, 28, 421–433. [Google Scholar] [CrossRef]
- Zribi, M.; Sahnoun, M.; Baghdadi, N.; Le Toan, T.; Hamida, A.B. Analysis of the Relationship between Backscattered P-Band Radar Signals and Soil Roughness. Remote Sens. Environ. 2016, 186, 13–21. [Google Scholar] [CrossRef]
- Baghdadi, N.; King, C.; Bourguignon, A.; Remond, A. Potential of ERS and RADARSAT Data for Surface Roughness Monitoring over Bare Agricultural Fields: Application to Catchments in Northern France. Int. J. Remote Sens. 2002, 23, 3427–3442. [Google Scholar] [CrossRef]
- Brier, G.W. Verification of Forecasts Expressed in Terms of Probability. Mon. Weather. Rev. 1950, 78, 1–3. [Google Scholar] [CrossRef]
- Smith, M.W. Microclimatic Influences on Ground Temperatures and Permafrost Distribution, Mackenzie Delta, Northwest Territories. Can. J. Earth Sci. 1975, 12, 1421–1438. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Marks, D.; Link, T.; Ellis, C.; Hardy, J.; Rowlands, A.; Granger, R. The Impact of Coniferous Forest Temperature on Incoming Longwave Radiation to Melting Snow. Int. J. 2009, 23, 2513–2525. [Google Scholar] [CrossRef]
- Jagtar Bhatti, V.B.; Mark Castonguay, R.E.; Arp, P.A. Modeling Snowpack and Soil Temperature and Moisture Conditions in a Jack Pine, Black Spruce and Aspen Forest Stand in Central Saskatchewan (BOREAS SSA). Can. J. Soil. Sci. 2006, 86, 203–217. [Google Scholar] [CrossRef]
- Decker, K.L.M.; Wang, D.; Waite, C.; Scherbatskoy, T. Snow Removal and Ambient Air Temperature Effects on Forest Soil Temperatures in Northern Vermont. Soil. Sci. Soc. Am. J. 2003, 67, 1234–1242. [Google Scholar] [CrossRef]
- Bauer-Marschallinger, B.; Cao, S.; Navacchi, C.; Freeman, V.; Reuß, F.; Geudtner, D.; Rommen, B.; Vega, F.C.; Snoeij, P.; Attema, E. The Normalised Sentinel-1 Global Backscatter Model, Mapping Earth’s Land Surface with C-Band Microwaves. Sci. Data 2021, 8, 277. [Google Scholar] [CrossRef] [PubMed]
- Soudani, K.; Delpierre, N.; Berveiller, D.; Hmimina, G.; Vincent, G.; Morfin, A.; Dufrêne, É. Potential of Synthetic Aperture Radar Sentinel-1 Time Series for the Monitoring of Phenological Cycles in a Deciduous Forest. bioRxiv 2021. [Google Scholar] [CrossRef]
- Asmuß, T.; Bechtold, M.; Tiemeyer, B. On the Potential of Sentinel-1 for High Resolution Monitoring of Water Table Dynamics in Grasslands on Organic Soils. Remote Sens. 2019, 11, 1659. [Google Scholar] [CrossRef]
- Rowlandson, T.L.; Berg, A.A.; Roy, A.; Kim, E.; Lara, R.P.; Powers, J.; Lewis, K.; Houser, P.; McDonald, K.; Toose, P. Capturing Agricultural Soil Freeze/Thaw State through Remote Sensing and Ground Observations: A Soil Freeze/Thaw Validation Campaign. Remote Sens. Environ. 2018, 211, 59–70. [Google Scholar] [CrossRef]
- Behari, J. Microwave Remote Sensing Techniques in Soil Moisture Estimation. In Microwave Dielectric Behavior of Wet Soils; Springer: Dordrecht, The Netherlands, 2005; pp. 66–91. [Google Scholar]
- Dharmadasa, V.; Kinnard, C.; Baraër, M. Topographic and Vegetation Controls of the Spatial Distribution of Snow Depth in Agro-Forested Environments by UAV Lidar. Cryosphere 2023, 17, 1225–1246. [Google Scholar] [CrossRef]
- Huang, S.; Ding, J.; Zou, J.; Liu, B.; Zhang, J.; Chen, W. Soil Moisture Retrival Based on Sentinel-1 Imagery under Sparse Vegetation Coverage. Sensors 2019, 19, 589. [Google Scholar] [CrossRef] [PubMed]



| Plot | Soil Type | Land Cover/Crop Type | Residues | |||
|---|---|---|---|---|---|---|
| 2020–21 | 2021–22 | 2020–21 | 2021–22 | |||
| St-Maurice | A | Fine sand | Forest | Forest | Forest litter | Forest litter |
| B | Fine sand | Forest | Forest | Forest litter | Forest litter | |
| C | Silty clay | Potato | Corn | Bare field | Corn stalks | |
| D | Silty clay | Potato | Corn | Bare field | Corn stalks | |
| E | Loamy sand | Potato | Corn | Bare field | Corn stalks | |
| F | Silty clay | Corn | Soybean | Corn stalks | Soybean debris | |
| G | Silty clay | Corn | Soybean | Corn stalks | Soybean debris | |
| H | Silty clay | Corn | Soybean | Corn stalks | Soybean debris | |
| St-Marthe | A | Loam | Forest | Forest | Forest litter | Forest litter |
| B | Fine loamy sand | Forest | Forest | Forest litter | Forest litter | |
| C | Fine loamy sand | Grassland | Grassland | Grass | Grass | |
| D | Fine loamy sand | Grassland | Grassland | Grass | Grass | |
| E | Clay | Potato | Corn | Grass | Grass | |
| F | Clay | Potato | Corn | Grass | Grass | |
| G | Clay | Soybean | Ploughed | Soybean debris | Bare field | |
| H | Clay | Soybean | Ploughed | Soybean debris | Bare field | |
| I | Clay | Corn | Ploughed | Corn stalks | Scattered debris | |
| J | Clay | Corn | Ploughed | Corn stalks | Scattered debris | |
| Algorithms | Soil Depth (cm) | Polarization | Pseudo-R2 | AIC |
|---|---|---|---|---|
| EFTA | 2 | VH | 0.54 | 199 |
| VV | 0.36 | 623 | ||
| 10 | VH | 0.49 | 115 | |
| VV | 0.36 | 194 | ||
| Delta | 2 | VH | 0.32 | 706 |
| VV | 0.22 | 879 | ||
| 10 | VH | 0.27 | 333 | |
| VV | 0.21 | 468 | ||
| FTI | 2 | VH | 0.31 | 714 |
| VV | 0.20 | 918 | ||
| 10 | VH | 0.22 | 445 | |
| VV | 0.16 | 546 |
| Models | R2 | Pseudo-R2 | AIC | |
|---|---|---|---|---|
| Marginal | Conditional | |||
| 1 | 0.54 | 241 | ||
| 2 | 0.56 | 0.57 | 239 | |
| 3 | 0.55 | 0.58 | 231 | |
| 4 | 0.59 | 0.61 | 232 | |
| 5 | 0.59 | 0.60 | 252 | |
| 6 | 0.59 | 0.60 | 271 | |
| Predictors | Estimates | CI | p |
|---|---|---|---|
| (Intercept) | 0.04 | −0.06–0.14 | 0.441 |
| VHEFTA | 0.04 | 0.02–0.06 | <0.001 |
| Crop type | |||
| Grassland | Reference | ||
| Maize | −0.03 | −0.14–0.08 | 0.593 |
| Ploughed | 0.09 | −0.03–0.21 | 0.142 |
| Potato | −0.05 | −0.17–0.07 | 0.398 |
| Soybean | 0.00 | −0.12–0.12 | 0.989 |
| Crop type and VHFFTA interactions | |||
| VHEFTA: Maize | 0.04 | 0.02–0.07 | 0.001 |
| VHEFTA: Ploughed | 0.06 | 0.03–0.09 | <0.001 |
| VHEFTA: Potato | 0.06 | 0.03–0.08 | <0.001 |
| VHEFTA: Soybean | 0.06 | 0.03–0.09 | <0.001 |
| Random Effects | |||
| σ2 | 0.07 | ||
| τ00 Plot | 0.00 | ||
| ICC | 0.05 | ||
| N Plot | 14 | ||
| Observations | 1036 | ||
| Marginal R2/Conditional R2 | 0.586/0.608 |
| State | R2 | MAE | Brier Score |
|---|---|---|---|
| Calibration 2020–21, validation 2021–22 | 0.60 | 0.18 | 0.19 |
| Calibration 2021–22, validation 2020–21 | 0.56 | 0.18 | 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taghipourjavi, S.; Kinnard, C.; Roy, A. Sentinel-1-Based Soil Freeze–Thaw Detection in Agro-Forested Areas: A Case Study in Southern Québec, Canada. Remote Sens. 2024, 16, 1294. https://doi.org/10.3390/rs16071294
Taghipourjavi S, Kinnard C, Roy A. Sentinel-1-Based Soil Freeze–Thaw Detection in Agro-Forested Areas: A Case Study in Southern Québec, Canada. Remote Sensing. 2024; 16(7):1294. https://doi.org/10.3390/rs16071294
Chicago/Turabian StyleTaghipourjavi, Shahabeddin, Christophe Kinnard, and Alexandre Roy. 2024. "Sentinel-1-Based Soil Freeze–Thaw Detection in Agro-Forested Areas: A Case Study in Southern Québec, Canada" Remote Sensing 16, no. 7: 1294. https://doi.org/10.3390/rs16071294
APA StyleTaghipourjavi, S., Kinnard, C., & Roy, A. (2024). Sentinel-1-Based Soil Freeze–Thaw Detection in Agro-Forested Areas: A Case Study in Southern Québec, Canada. Remote Sensing, 16(7), 1294. https://doi.org/10.3390/rs16071294