Impact of Pseudo-Stochastic Pulse and Phase Center Variation on Precision Orbit Determination of Haiyang-2A from Experimental HY2 Receiver GPS Data
Abstract
1. Introduction
2. Model and Strategies
2.1. Pseudo-Stochastic Pulse Model
2.2. Reduced-Dynamic Method
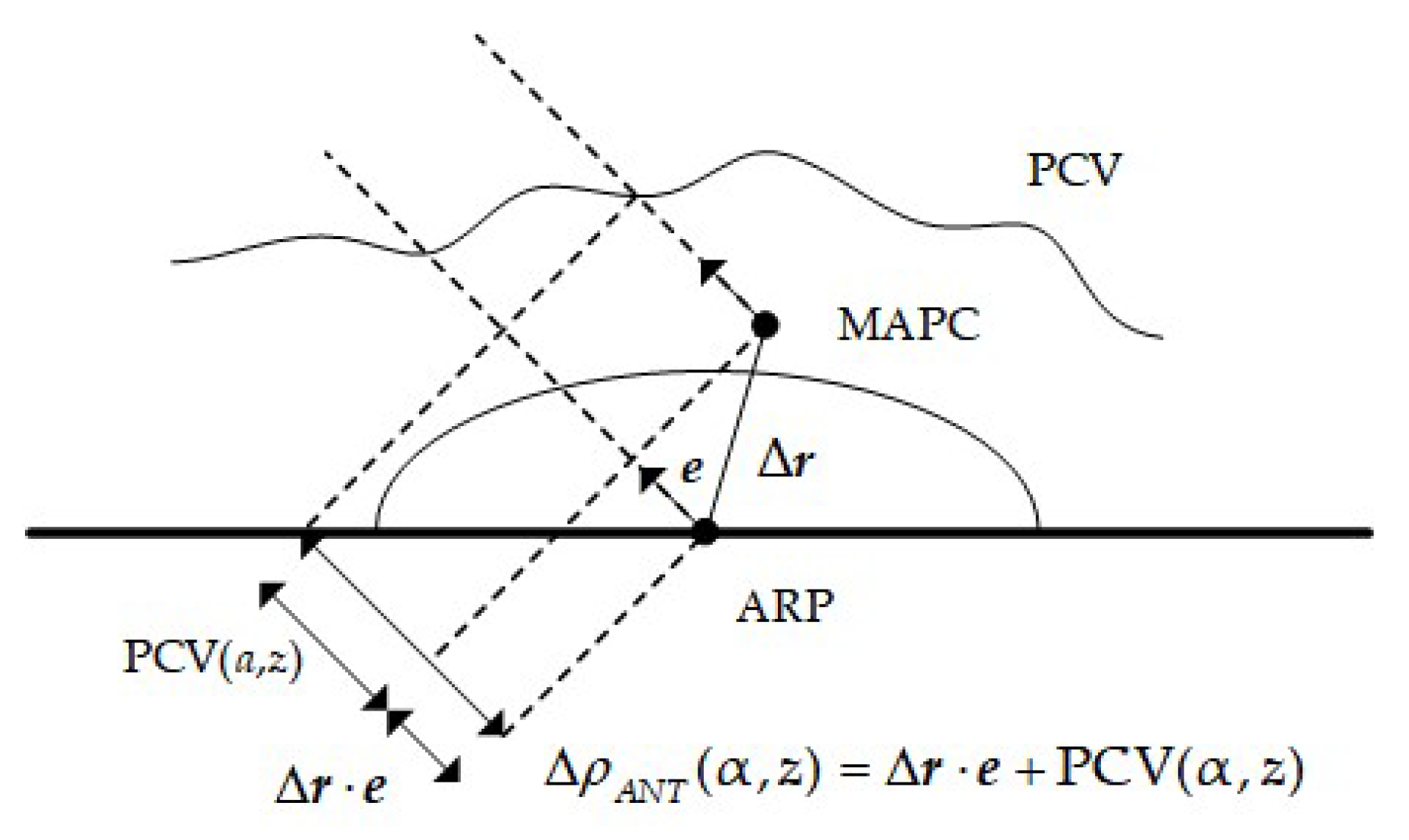
2.3. Antenna Phase Center Variation Model
2.4. Methods for Estimating the Phase Center Variation Model
2.5. Reduced-Dynamic Orbit Determination Strategies of HY-2A
3. Result and Analysis
3.1. Quality Analysis of Satellite-Borne GPS Observations
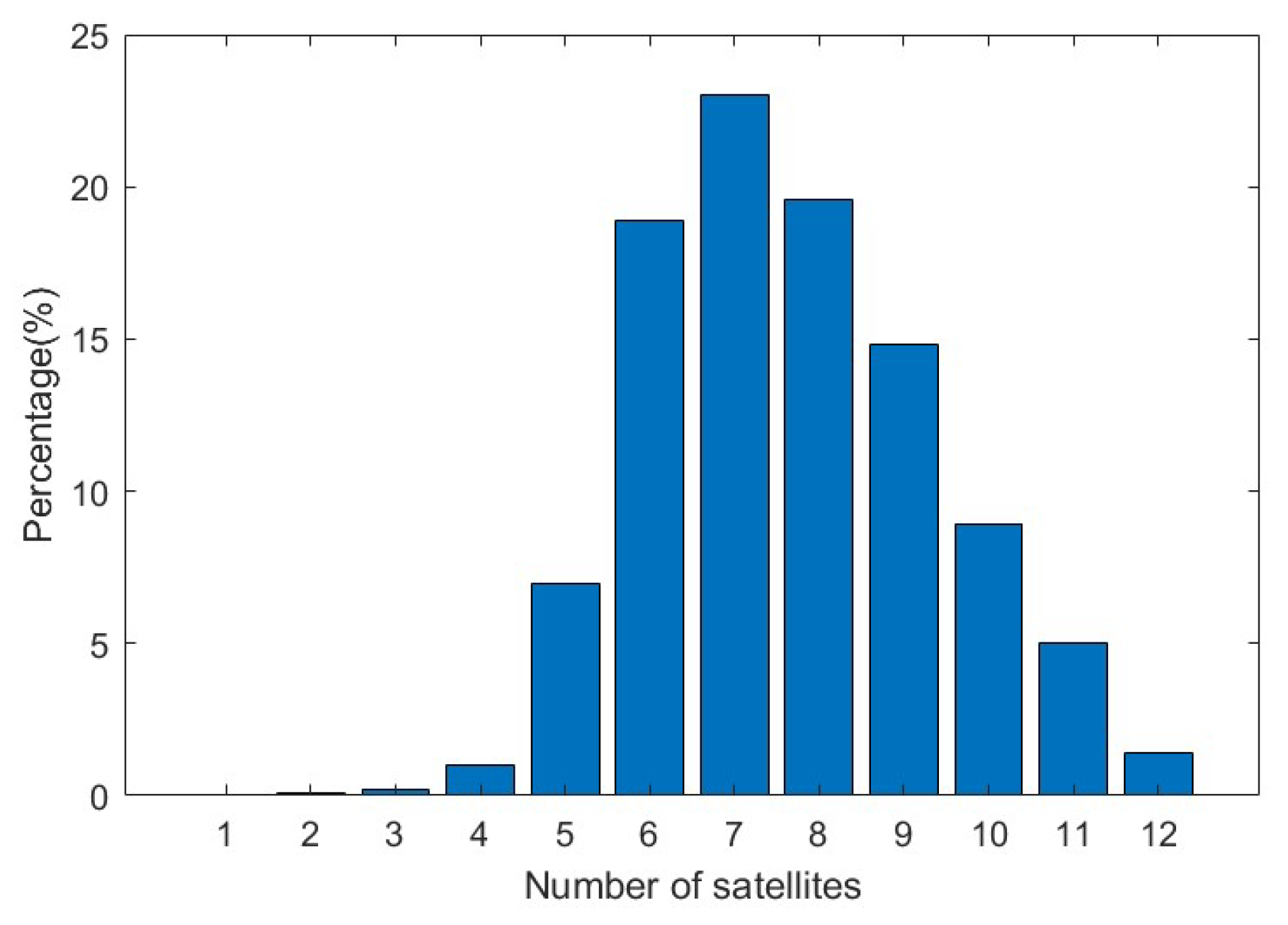
3.1.1. Satellite Visibility
3.1.2. Multipath Effect
3.1.3. Ionospheric Delay and Rate of Change of Ionospheric Delay
3.2. Impact of Pseudo-Stochastic Pulse on Reduced-Dynamic Orbit Determination
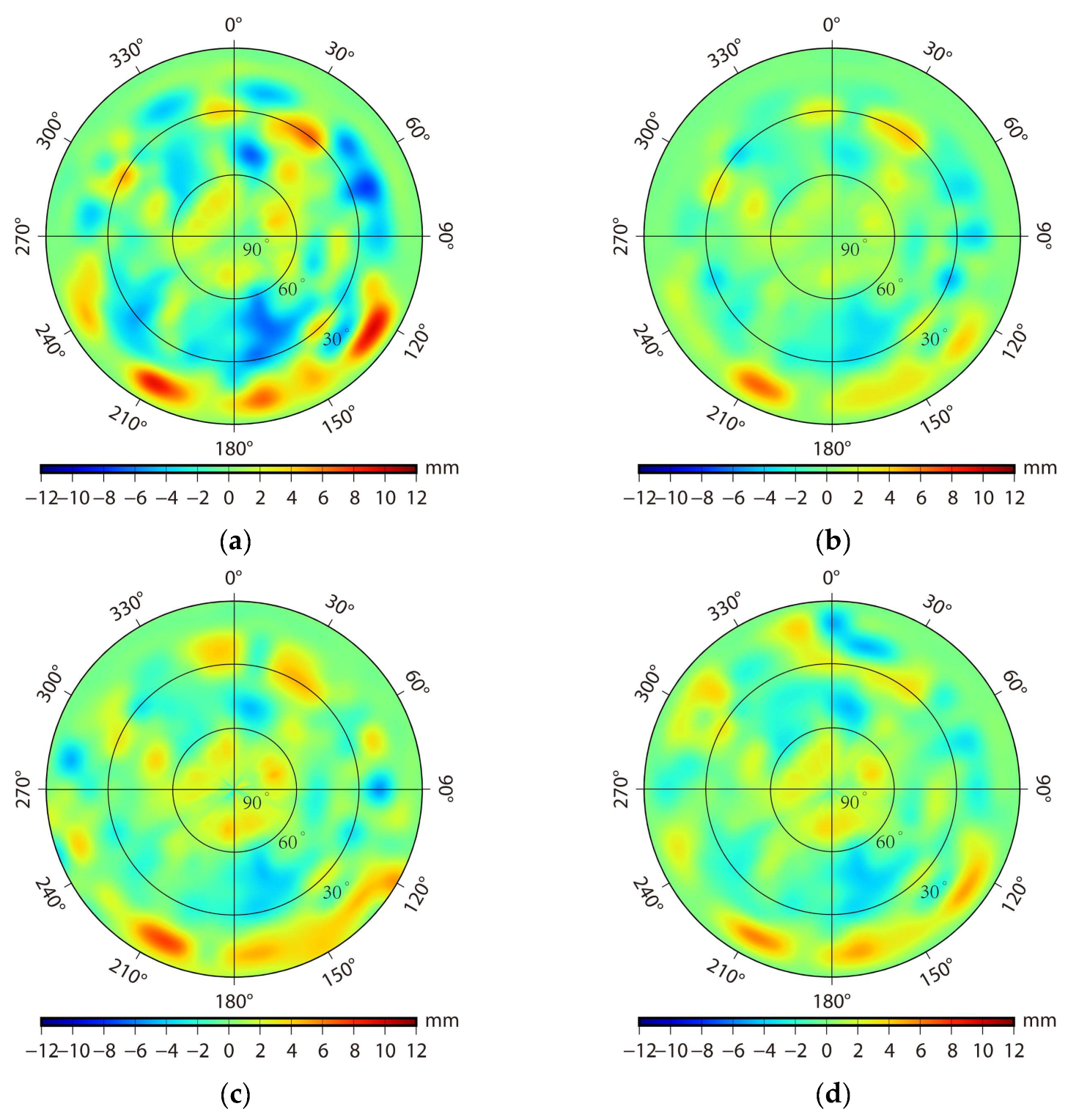
3.3. Estimation of the PCV Model
- (1)
- The direct method treats the PCV of grid points as an unknown parameter to be solved in the observation equation, resulting in a more detailed PCV estimation, and thus the estimated PCV map shows a spotted distribution. The residual method estimates the PCV by averaging the carrier phase residuals within the grid interval, resulting in similar PCV values for adjacent grid points and a mostly striped distribution in the PCV map.
- (2)
- The larger PCV values of the PCV model estimated using the direct method and residual method are all distributed within the low elevation grid space. This is mainly because the observation data are affected by the multipath effect at low altitude angles, which leads to poor observation data quality.
- (3)
- There is a significant decrease in the PCV value when the resolution of the PCV model estimated using the direct method is increased from 10° to 5°. This is because the increase in parameters makes the PCV model more refined; on the contrary, the improvement of resolution has relatively little effect on the residual method to estimate the PCV model.
3.4. Analysis of Orbit Precision for HY-2A
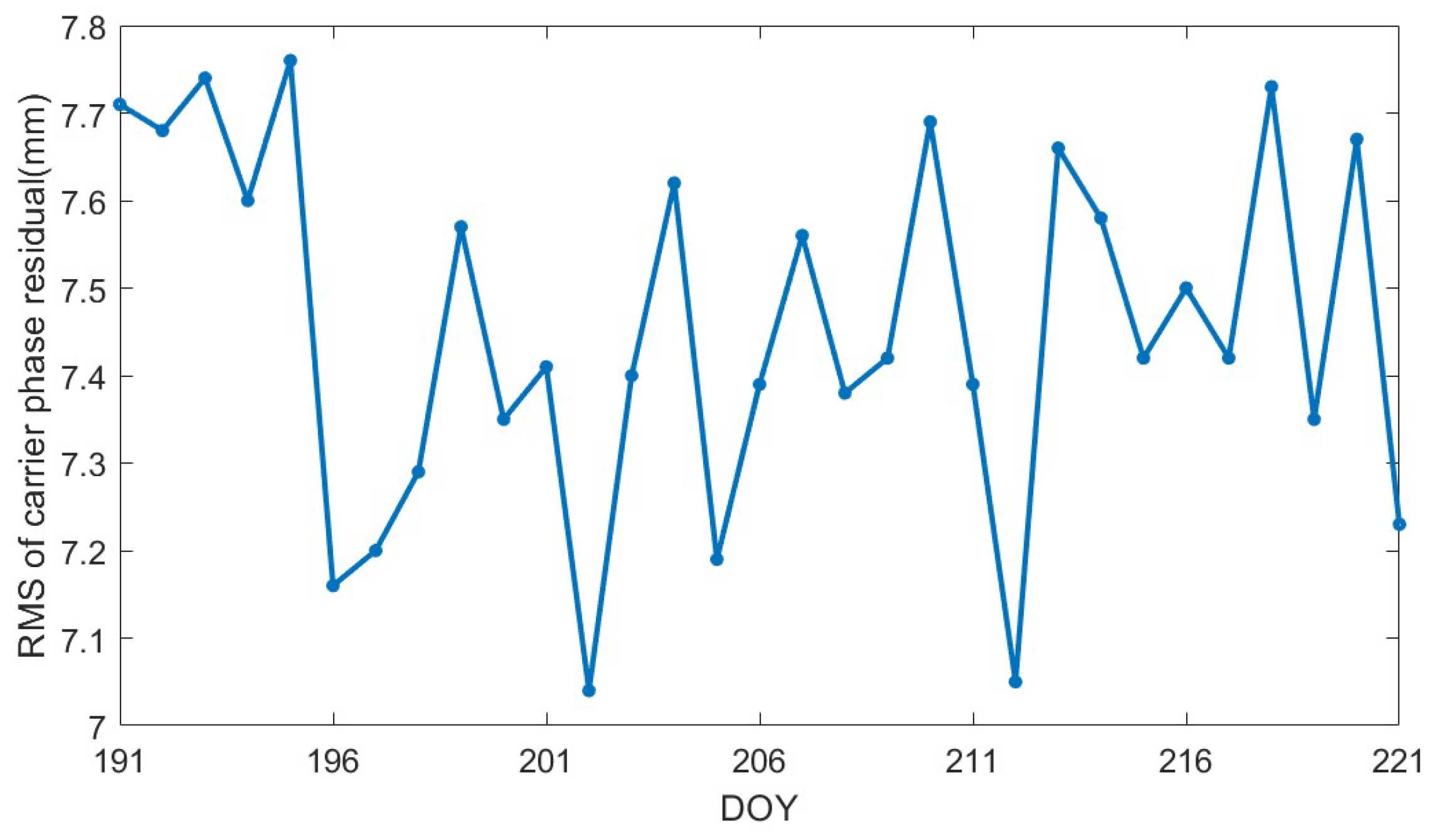
3.4.1. Carrier Phase Residuals Analysis
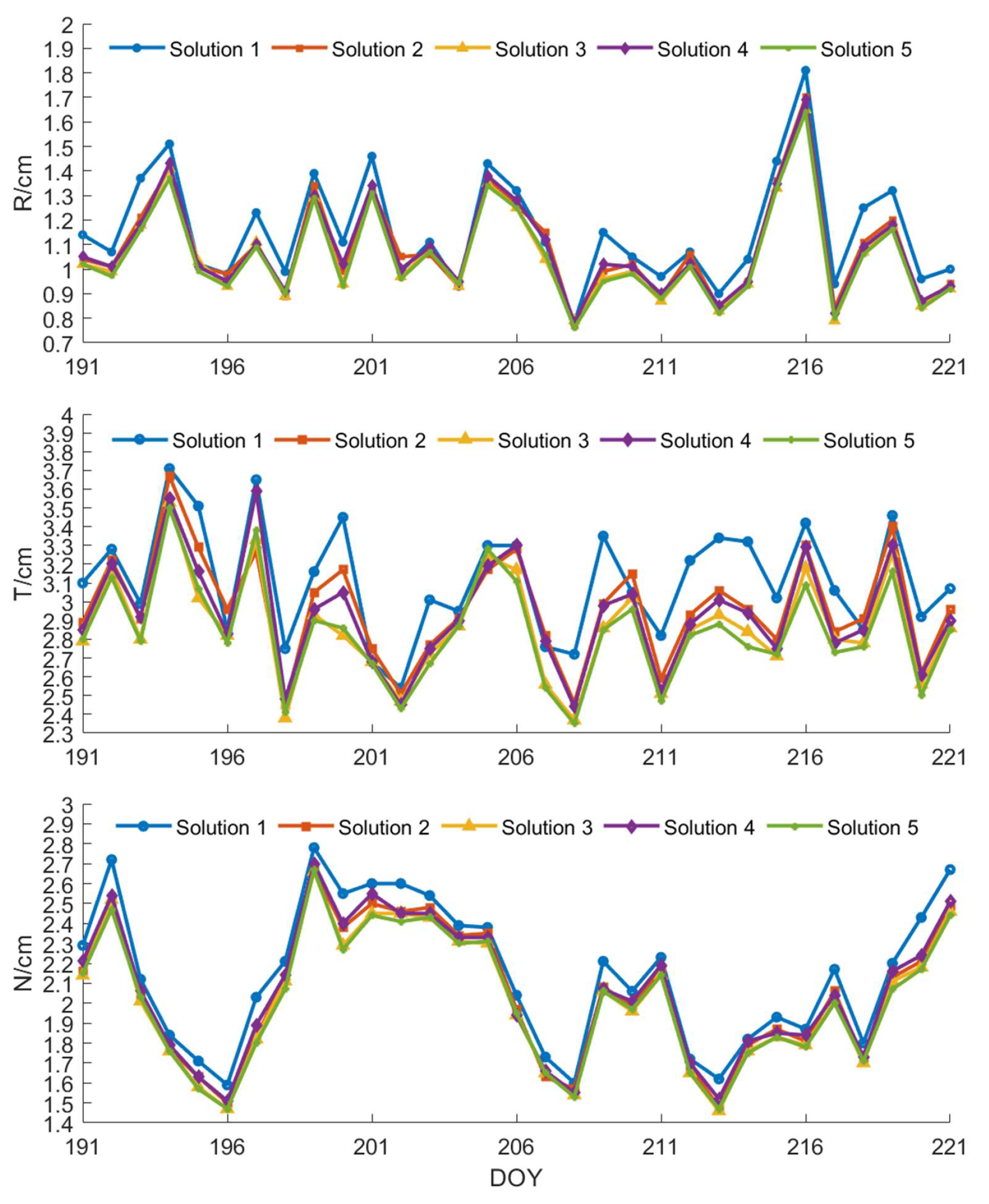
3.4.2. Comparison with Precision Science Orbits
3.4.3. SLR 3D Validation
- (1)
- Convert the PSO provided by CNES to the Bernese standard orbit format and convert it to a 1s sampling interval.
- (2)
- Calculate the station coordinates to the current epoch and transform the position and velocity of the HY-2A, along with the current epoch station coordinates, to the J2000 inertial system.
- (3)
- According to the time corresponding to each residual in the SLR residual file, the position and velocity of the HY-2A in the J2000 inertial system at that time and the station coordinates of that day are extracted.
- (4)
- The position and velocity of the HY-2A and the position of the station are converted from the J2000 inertial system to the position in the RTN coordinate system, and then the unit vector of the three directions of RTN is calculated according to Equation (16). Finally, the RTN residual component can be obtained by multiplying each SLR residual.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, B.H. Constructing China’s ocean satellite system to the capability of ocean environment and disaster enhance monitoring. Chinese Space Sci. Technol. 2011, 31, 8. [Google Scholar]
- Zhang, Q.; Zhang, J.; Zhang, H.; Wang, R.; Jia, H. The study of HY2A satellite engineering development and in-orbit movement. Eng. Sci. 2013, 80, 12–18. [Google Scholar]
- Lin, M.S.; Zhang, Y.G.; Yuan, X.Z. The development course and trend of ocean remote sensing satellite. Haiyan Xuebao 2015, 37, 1–10. [Google Scholar]
- Cerri, L.; Berthias, J.; Bertiger, W.; Haines, B.; Lemoine, F.; Mercier, F.; Ries, J.C.; Willis, P.; Zelensky, N.; Ziebart, M. Precision orbit determination standards for the Jason series of altimeter missions. Mar. Geod. 2010, 33, 379–418. [Google Scholar] [CrossRef]
- Cazenave, A.; Hamlington, B.; Horwath, M.; Barletta, V.R.; Benveniste, J.; Chambers, D.; Döll, P.; Hogg, A.E.; Legeais, J.F.; Merrifield, M.; et al. Observational requirements for long-term monitoring of the global mean sea level and its components over the altimetry era. Front. Mar. Sci. 2019, 6, 582. [Google Scholar] [CrossRef]
- Guo, J.Y.; Wang, Y.C.; Shen, Y.; Liu, X.; Sun, Y.; Kong, Q.L. Estimation of SLR station coordinates by means of SLR measurements to kinematic orbit of LEO satellites. Earth Planets Space 2018, 70, 201. [Google Scholar] [CrossRef]
- Zhou, C.C.; Zhong, S.M.; Peng, B.B.; Ou, J.K.; Zhang, J.; Chen, R.J. Real-time orbit determination of Low Earth orbit satellite based on RINEX/DORIS 3.0 phase data and spaceborne GPS data. Adv. Space Res. 2020, 66, 1700–1712. [Google Scholar] [CrossRef]
- Kong, Q.L.; Guo, J.Y.; Sun, Y.; Zhao, C.M.; Chen, C.F. Centimeter-level precise orbit determination for the HY-2A satellite using DORIS and SLR tracking data. Acta Geophys. 2017, 65, 1–12. [Google Scholar] [CrossRef]
- Zhou, X.H.; Wang, X.H.; Zhao, G.; Zhao, G.; Peng, H.L.; Wu, B. The precise orbit determination for HY2A satellite using GPS, DORIS and SLR data. Geomat. Inf. Sci. Wuhan Univ. 2015, 40, 1000–1005. [Google Scholar]
- Zhu, J.; Wang, J.; Chen, J.; He, Y. Centimeter precise orbit determination for HY-2 via DORIS. J. Astronaut. 2013, 34, 163–169. [Google Scholar]
- Zhao, X.L.; Zhou, S.S.; Ci, Y.; Hu, X.G.; Cao, J.F.; Chang, Z.Q.; Tang, C.P.; Guo, D.N.; Guo, K.; Liao, M. High-precision orbit determination for a LEO nanosatellite using BDS-3. GPS Solut. 2020, 24, 102. [Google Scholar] [CrossRef]
- Kang, Z.; Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Nagel, P.; Pastor, R. Precise orbit determination for the GRACE mission using only GPS data. J. Geod. 2006, 80, 322–331. [Google Scholar] [CrossRef]
- Švehla, D.; Rothacher, M. Kinematic positioning of LEO and GPS satellites and IGS stations on the ground. Adv. Space Res. 2005, 36, 376–381. [Google Scholar] [CrossRef]
- Mao, X.Y.; Arnold, D.; Girardin, V.; Villiger, A.; Jäggi, A. Dynamic GPS-based LEO orbit determination with 1 cm precision using the Bernese GNSS Software. Adv. Space Res. 2020, 67, 788–805. [Google Scholar] [CrossRef]
- Zhang, B.B.; Wang, Z.; Zhou, L.; Feng, J.; Qiu, Y.; Li, F. Precise orbit solution for swarm using space-borne GPS data and optimized pseudo-stochastic pulses. Sensors 2017, 17, 635. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.; Tseng, T.-P.; Lin, T.; Švehla, D.; Schreiner, B. Precise orbit determination for the FORMOSAT-3/COSMIC satellite mission using GPS. J. Geod. 2009, 83, 477–489. [Google Scholar] [CrossRef]
- Ijssel, J.; Visser, P.; Rodriguez, P. Champ precise orbit determination using GPS data. Adv. Space Res. 2003, 31, 1889–1895. [Google Scholar] [CrossRef]
- Xia, Y.W.; Liu, X.; Guo, J.Y.; Yang, Z.M.; Qi, L.H.; Ji, B.; Chang, X.T. On GPS data quality of GRACE-FO and GRACE satellites: Effects of phase center variation and satellite attitude on precise orbit determination. Acta Geod. Geophys. 2020, 56, 93–111. [Google Scholar] [CrossRef]
- Jäggi, A.; Dahle, C.; Arnold, D.; Bock, H.; Meyer, U.; Beutler, G.; van Den Ijssel, J. Swarm kinematic orbits and gravity fields from 18 months of GPS data. Adv. Space Res. 2016, 57, 218–233. [Google Scholar] [CrossRef]
- Guo, J.; Zhao, Q.; Guo, X.; Liu, X.; Liu, J.; Zhou, Q. Quality assessment of onboard GPS receiver and its combination with DORIS and SLR for Haiyang 2A precise orbit determination. Sci. China Earth Sci. 2015, 58, 138–150. [Google Scholar] [CrossRef]
- Lin, M.S.; Wang, X.H.; Peng, H.L.; Zhao, Q.L.; Li, M. Precise orbit determination technology based on dual-frequency GPS solution for HY-2 satellite. Eng. Sci. 2014, 16, 97–101. [Google Scholar]
- Guo, J.; Zhao, Q.L.; Li, M.; Hu, Z.G. Centimeter level orbit determination for HY2A using GPS data. Geomat. Inf. Sci. Wuhan Univ. 2013, 38, 52–55. [Google Scholar]
- Guo, J.Y.; Qi, L.H.; Liu, X.; Chang, X.T.; Ji, B.; Zhang, F.Z. High-order ionospheric delay correction of GNSS data for precise reduced-dynamic determination of LEO satellite orbits: Cases of GOCE, GRACE, and SWARM. GPS Solut. 2023, 27, 13. [Google Scholar] [CrossRef]
- Montenbruck, O.; Garcia-Fernandez, M.; Yoon, Y.; Schön, S.; Jäggi, A. Antenna phase center calibration for precise positioning of LEO satellites. GPS Solut. 2009, 13, 23–34. [Google Scholar] [CrossRef]
- Beutler, G.; Brockmann, E. Extended orbit modeling techniques at the CODE processing center of the international GPS service for geodynamics (IGS): Theory and initial results. Manuscr. Geod. 1994, 19, 367–386. [Google Scholar]
- Vaclavovic, P.; Dousa, J. G-Nut/Anubis: Open-Source Tool for Multi-GNSS Data Monitoring with a Multipath Detection for New Signals, Frequencies and Constellations. In Gravity, Geoid and Earth Observation; Springer: Cham, Switzerland, 2015; Volume 143, pp. 775–782. [Google Scholar]
- Liu, M.M.; Yuan, Y.B.; Ou, J.K.; Chai, Y.J. Research on attitude models and antenna phase center correction for Jason-3 Satellite orbit determination. Sensors 2019, 19, 2408. [Google Scholar] [CrossRef] [PubMed]
- Schmid, R.; Rothacher, M.; Thaller, D.; Steigenberger, P. Absolute phase center corrections of satellite and receiver antennas. GPS Solut. 2005, 9, 283–293. [Google Scholar] [CrossRef]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Bock, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef]
- Tian, Y.G.; Hao, J.M. Swarm satellite antenna phase center correction and its influence on the precision orbit determination. Acta Geod. Cartogr. Sin. 2016, 45, 1406–1412. [Google Scholar]
- Gu, D.; Lai, Y.; Liu, J.; Ju, B.; Tu, J. Spaceborne GPS receiver antenna phase center offset and variation estimation for the Shiyan 3 satellite. Chin. J. Aeronaut. 2016, 29, 1335–1344. [Google Scholar] [CrossRef]
- Mao, X.; Visser, P.N.A.M.; van den IJssel, J. Impact of GPS antenna phase center and code residual variation maps on orbit and baseline determination of GRACE. Adv. Space Res. 2017, 59, 2987–3002. [Google Scholar] [CrossRef]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. Solid Earth 2012, 117, B04406. [Google Scholar] [CrossRef]
- Ivantsov, A.V. Dynamical model of motion for asteroids based on the DE405 theory. Kinemat. Phys. Celest. Bodies 2007, 23, 65–69. [Google Scholar] [CrossRef]
- Luzum, B.; Petit, G. The IERS conventions (2010): Reference systems and new models. Proc. Int. Astron. Union 2012, 10, 227–228. [Google Scholar] [CrossRef]
- Rim, H.J. TOPEX Orbit Determination Using GPS Tracking System. Ph.D. Thesis, University of Texas at Austin, Austin, TX, USA, 1992. [Google Scholar]
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 global ocean tide atlas: Design and performance. Ocean Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
- Schreiter, L.; Montenbruck, O.; Zangerl, F.; Siemes, C.; Arnold, D.; Jäggi, A. Bandwidth correction of Swarm GPS carrier phase observations for improved orbit and gravity field determination. GPS Solut. 2021, 25, 70. [Google Scholar] [CrossRef] [PubMed]
- Estey, L.H.; Meertens, C.M. TEQC: The Multi-Purpose Toolkit for GPS/GLONASS Data. GPS Solut. 1999, 3, 42–49. [Google Scholar] [CrossRef]
- Hwang, C.; Tseng, T.-P.; Lin, T.-J.; Švehla, D.; Hugentobler, U.; Chao, B.F. Quality assessment of FORMOSAT-3/COSMIC and GRACE GPS observables: Analysis of multipath, ionospheric delay and phase residual in orbit determination. GPS Solut. 2009, 14, 121–131. [Google Scholar] [CrossRef]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: Orbit and network validation. J. Geod. 2018, 93, 2315–2334. [Google Scholar] [CrossRef]
- Männel, B.; Rothacher, M. Geocenter variations derived from a combined processing of LEO- and ground-based GPS observations. J. Geod. 2017, 91, 933–944. [Google Scholar] [CrossRef]
- Guo, J.Y.; Wang, G.Z.; Guo, H.Y.; Lin, M.S.; Peng, H.L.; Chang, X.T.; Jiang, Y.M. Validating precise orbit determination from Satellite-Borne GPS data of Haiyang-2D. Remote Sens. 2022, 14, 2477. [Google Scholar] [CrossRef]
- Guo, H.Y.; Guo, J.Y.; Yang, Z.M.; Wang, G.Z.; Qi, L.H.; Lin, M.S.; Peng, H.L.; Ji, B. On Satellite-Borne GPS data quality and reduced-dynamic precise orbit determination of HY-2C: A case of orbit validation with onboard DORIS data. Remote Sens. 2021, 13, 4329. [Google Scholar] [CrossRef]
- Hu, Z.G.; Zhao, Q.L.; Guo, J.; Liu, J.N. Research on Impact of GPS phase center variation on precise orbit determination of low earth orbit satellite. Acta Geod. Cartogr. Sin. 2011, 40, 34–38. [Google Scholar]
- Pearlman, M.; Degnan, J.; Bosworth, J. The international laser ranging service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Yuan, J.; Zhao, C.; Wu, Q. Phase center offset and phase center variation estimation in-flight for ZY-3 01 and ZY-3 02 space-borne GPS antennas and the influence on precision orbit determination. Acta Geod. Cartogr. Sin. 2018, 47, 672–682. [Google Scholar]





| Model/Parameters | Description | |
|---|---|---|
| Mechanical model | Global gravity feld model | EGM2008 [33], 120 × 120 |
| N-body | JPL DE405 [34] | |
| Solid earth tides | IERS2010 [35] | |
| Solar radiation pressure | Box-Wing [36] | |
| Ocean tides | FES2004 [37] | |
| Observation model | GPS data | Undifferenced ionosphere-free phase and code (interval 1 s) |
| GPS orbits | Post-processed precise orbit provided by CODE | |
| GPS clock | Post-processed precise clock corrections provided by CODE (time interval 30 s) | |
| POD arc length | 24 h | |
| SLR | Normal Point (NP) data provided by ILRS | |
| Attitude model | Provided by the NSOAS | |
| GPS Satellite antenna phase model | PCV.I08 | |
| HY-2A PCV | Calibrations in orbit | |
| Elevation cutoff | 5° | |
| Estimated parameters | Initial state of orbit segment | 3-D inertial system position and velocity |
| Receiver clock offset | Epoch estimation | |
| Ambiguity | Each satellite, each observation arc, float solution | |
| R, T, N empirical force | Estimated every 240 min | |
| Pseudo-stochastic pulse priori sigma | 1 × 10−4 m/s2, 1 × 10−5 m/s2, 1 × 10−6 m/s2, 1 × 10−7 m/s2, 1 × 10−8 m/s2, 1 × 10−9 m/s2 | |
| Pseudo-stochastic pulse time interval | 6 min, 15 min, 30 min, 60 min |
| DOY | MP1 RMS (cm) | MP1 RMS (cm) | O/slip | Completeness Rate | Utilization Rate |
|---|---|---|---|---|---|
| 203 | 41.0 | 31.1 | 41 | 95.40% | 94.12% |
| 204 | 38.9 | 31.0 | 45 | 99.55% | 93.97% |
| 205 | 44.3 | 32.1 | 39 | 98.31% | 93.02% |
| 206 | 44.5 | 34.0 | 46 | 99.25% | 93.51% |
| 207 | 41.3 | 32.5 | 42 | 95.05% | 93.58% |
| 208 | 41.7 | 30.8 | 44 | 99.84% | 93.70% |
| 209 | 40.9 | 32.0 | 49 | 99.95% | 93.02% |
| Mean | 42.4 | 32.7 | 45 | 98.19% | 93.56% |
| Priori Sigma (m/s2) | Direction of Orbit Comparison | Time Interval/min | |||
|---|---|---|---|---|---|
| 6 | 15 | 30 | 60 | ||
| 1 × 10−4 | R | 0.96 | 0.96 | 0.96 | 0.97 |
| T | 3.01 | 2.99 | 2.99 | 3.04 | |
| N | 2.43 | 2.43 | 2.44 | 2.42 | |
| 3D | 3.99 | 3.97 | 3.97 | 4.00 | |
| 1 × 10−5 | R | 0.97 | 0.97 | 0.96 | 0.96 |
| T | 2.96 | 2.98 | 2.97 | 3.02 | |
| N | 2.44 | 2.42 | 2.43 | 2.41 | |
| 3D | 3.96 | 3.96 | 3.96 | 3.98 | |
| 1 × 10−6 | R | 0.96 | 0.96 | 0.97 | 0.97 |
| T | 3.02 | 3.00 | 2.99 | 3.01 | |
| N | 2.42 | 2.41 | 2.41 | 2.42 | |
| 3D | 3.99 | 3.96 | 3.97 | 3.98 | |
| 1 × 10−7 | R | 0.95 | 0.95 | 0.96 | 0.96 |
| T | 2.98 | 2.96 | 2.98 | 2.98 | |
| N | 2.43 | 2.42 | 2.41 | 2.41 | |
| 3D | 3.95 | 3.94 | 3.96 | 3.96 | |
| 1 × 10−8 | R | 0.93 | 0.93 | 0.94 | 0.94 |
| T | 3.01 | 2.95 | 2.95 | 2.97 | |
| N | 2.39 | 2.39 | 2.41 | 2.43 | |
| 3D | 3.94 | 3.91 | 3.93 | 3.95 | |
| 1 × 10−9 | R | 0.95 | 0.94 | 0.95 | 0.95 |
| T | 3.02 | 3.01 | 3.00 | 3.01 | |
| N | 2.42 | 2.40 | 2.43 | 2.43 | |
| 3D | 3.99 | 3.96 | 3.98 | 3.99 | |
| Solutions | R | T | N | 3D |
|---|---|---|---|---|
| Solution 1 | 1.15 | 3.12 | 2.14 | 3.96 |
| Solution 2 | 1.09 | 2.96 | 2.04 | 3.76 |
| Solution 3 | 1.06 | 2.88 | 2.01 | 3.67 |
| Solution 4 | 1.07 | 2.95 | 2.05 | 3.73 |
| Solution 5 | 1.06 | 2.85 | 2.00 | 3.64 |
| Solutions | R | T | N | Res |
|---|---|---|---|---|
| Solution 1 | 1.12 | 1.88 | 1.29 | 2.54 |
| Solution 2 | 1.08 | 1.78 | 1.23 | 2.41 |
| Solution 3 | 1.05 | 1.74 | 1.20 | 2.35 |
| Solution 4 | 1.07 | 1.74 | 1.22 | 2.38 |
| Solution 5 | 1.05 | 1.69 | 1.19 | 2.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Guo, J.; Ya, S.; Jia, Y.; Guo, H.; Chang, X.; Liu, X. Impact of Pseudo-Stochastic Pulse and Phase Center Variation on Precision Orbit Determination of Haiyang-2A from Experimental HY2 Receiver GPS Data. Remote Sens. 2024, 16, 1336. https://doi.org/10.3390/rs16081336
Wang Y, Guo J, Ya S, Jia Y, Guo H, Chang X, Liu X. Impact of Pseudo-Stochastic Pulse and Phase Center Variation on Precision Orbit Determination of Haiyang-2A from Experimental HY2 Receiver GPS Data. Remote Sensing. 2024; 16(8):1336. https://doi.org/10.3390/rs16081336
Chicago/Turabian StyleWang, Youyuan, Jinyun Guo, Shaoshuai Ya, Yongjun Jia, Hengyang Guo, Xiaotao Chang, and Xin Liu. 2024. "Impact of Pseudo-Stochastic Pulse and Phase Center Variation on Precision Orbit Determination of Haiyang-2A from Experimental HY2 Receiver GPS Data" Remote Sensing 16, no. 8: 1336. https://doi.org/10.3390/rs16081336
APA StyleWang, Y., Guo, J., Ya, S., Jia, Y., Guo, H., Chang, X., & Liu, X. (2024). Impact of Pseudo-Stochastic Pulse and Phase Center Variation on Precision Orbit Determination of Haiyang-2A from Experimental HY2 Receiver GPS Data. Remote Sensing, 16(8), 1336. https://doi.org/10.3390/rs16081336








