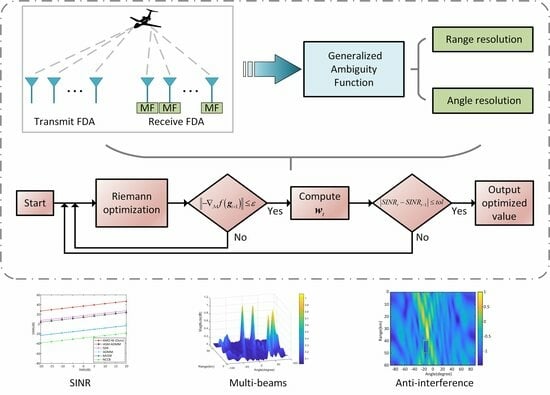
Efficiently Refining Beampattern in FDA-MIMO Radar via Alternating Manifold Optimization for Maximizing Signal-to-Interference-Noise Ratio
Abstract
1. Introduction
- •
- We derive the generalized ambiguity function of the FDA-MIMO radar for studying the key parameters that impact the range–angle resolution, and introduce a direct solution framework that avoids convex relaxation.
- •
- Under constant modulus conditions, the problem of jointly designing transmit waveforms and receive filter weights in the FDA-MIMO radar is transformed into a nonconvex bivariate quadratic programming problem (NBQP) for the simplicity of the subsequent solution.
- •
- A nested iterative alternating manifold optimization (AMO-NI) algorithm is proposed for efficiently solving the NBQP and obtaining the optimal transmit waveforms and receive filter weights after a finite number of iterations.
- •
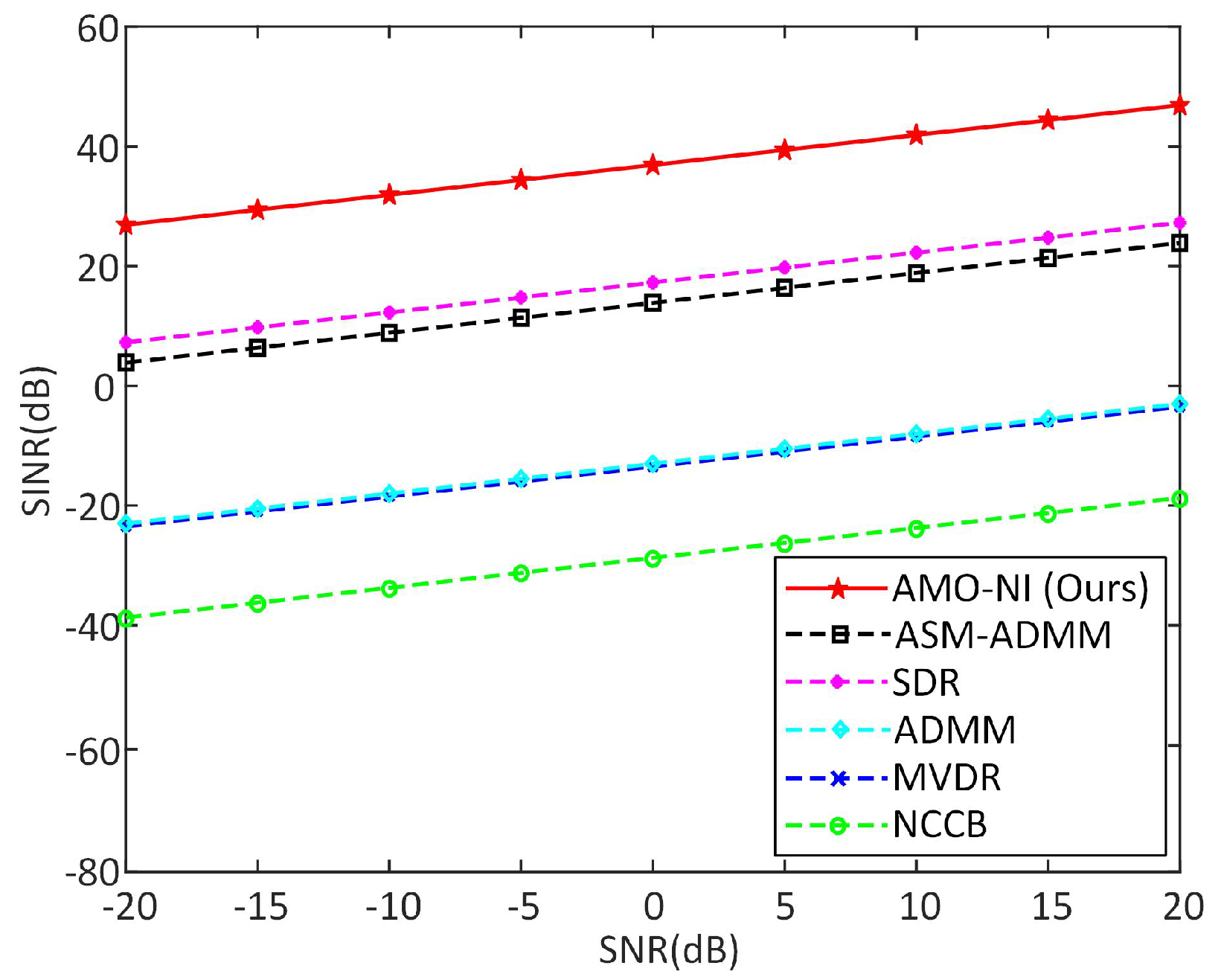
- Extensive experiments are conducted, and our method demonstrates a higher SINR while outperforming other methods in range–angle decoupling and computational efficiency.
2. Problem Formulation and Analysis
2.1. Signal Model
2.2. Generalized Ambiguity Function for FDA-MIMO Radar
- •
- The range resolution is related to the frequency offsets and bandwidth.
- •
- If choosing a nonlinear frequency offset, it is necessary to ensure that the maximum frequency offset is smaller than the bandwidth.
- •
- Optimizing the transmit and receive beamforming patterns can help lower the bandwidth, thereby improving the range resolution.
2.3. Optimization Problem of Joint Beamforming
- (1)
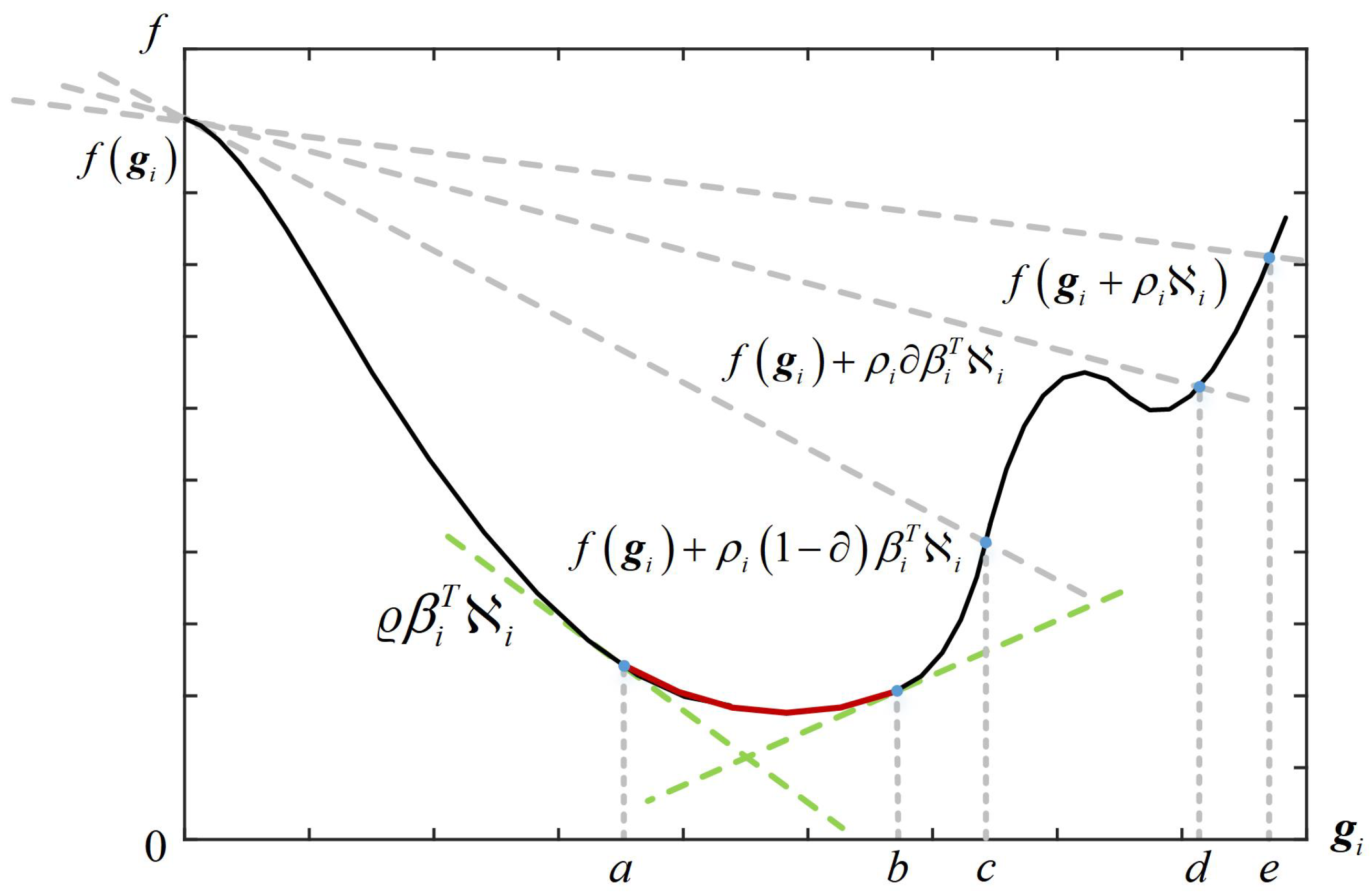
- The optimization of the transmit sequence in fixing the receive filter weights is nonconvex and NP-hard. Traditional convex optimization methods [50] are no longer applicable in this context, and their solution space may contain multiple local optimal solutions.
- (2)
- (3)
- During the optimization process, the coupling terms can easily lead to the degradation of the 2D resolution [32].
3. Solution to the Optimization Problem
- (A)
- Solution of
- (B)
- Solution of
| Algorithm 1 AMO-NI. |
|
4. Numerical Simulations
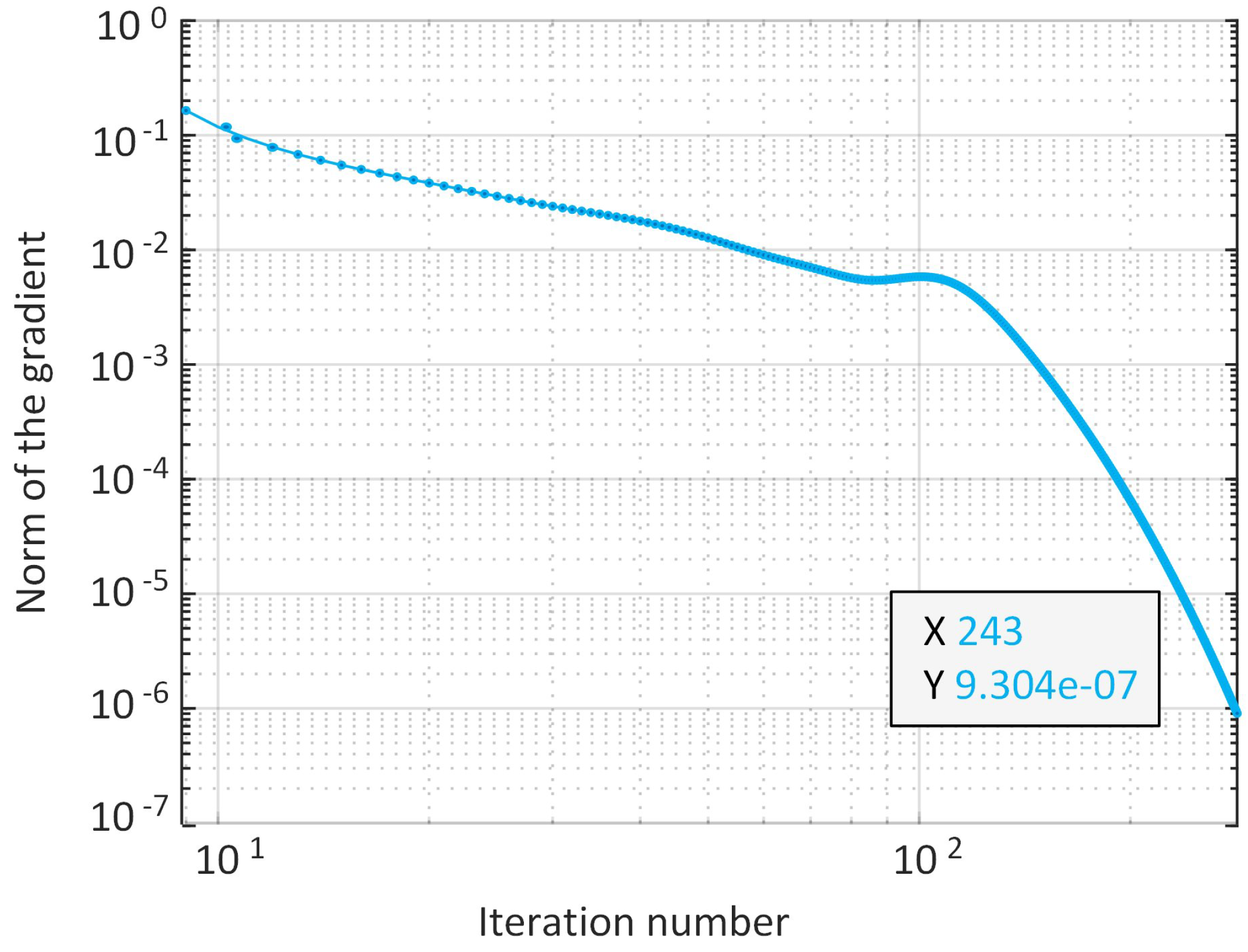
4.1. The Convergence Evaluation and Complexity Analysis
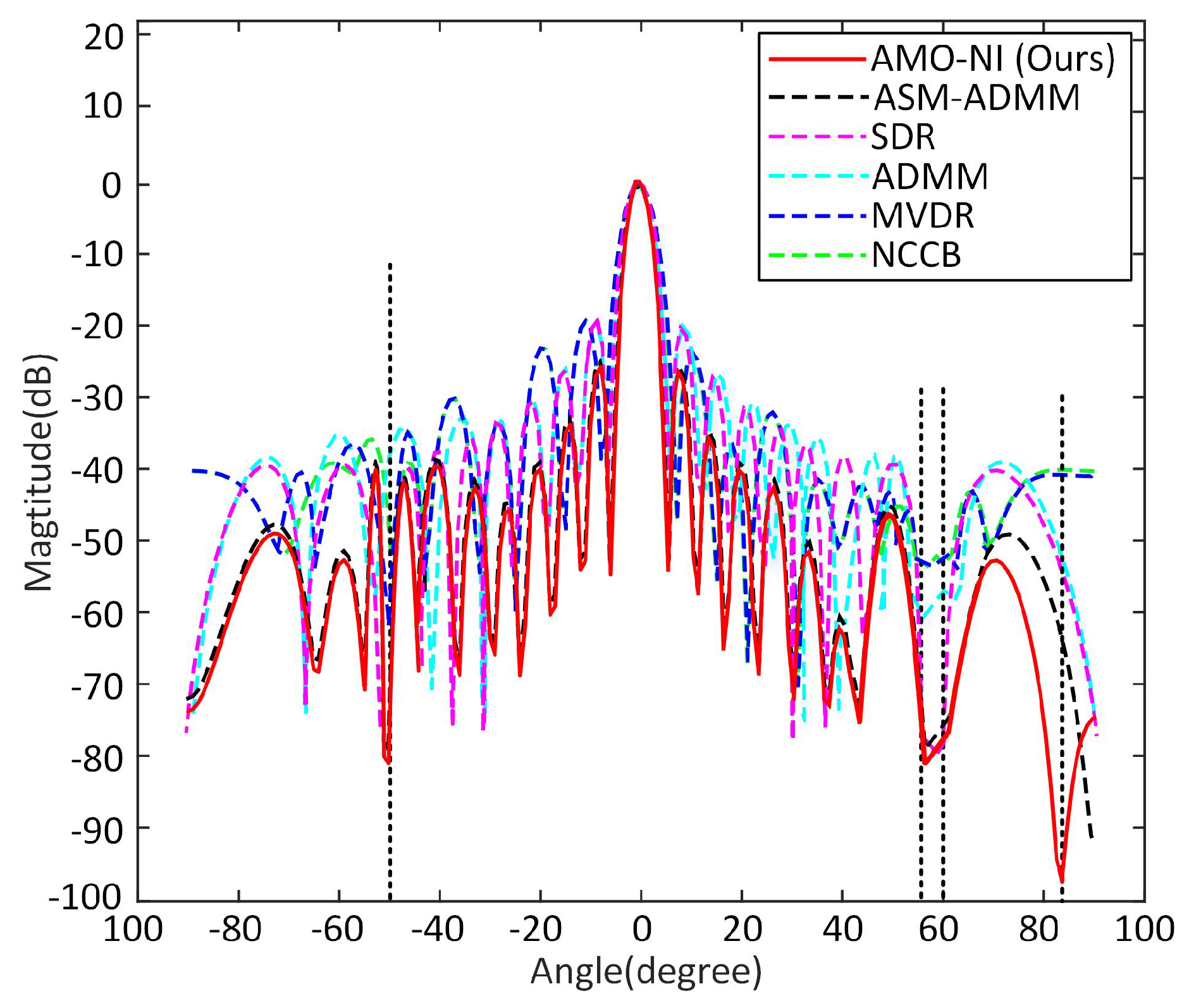
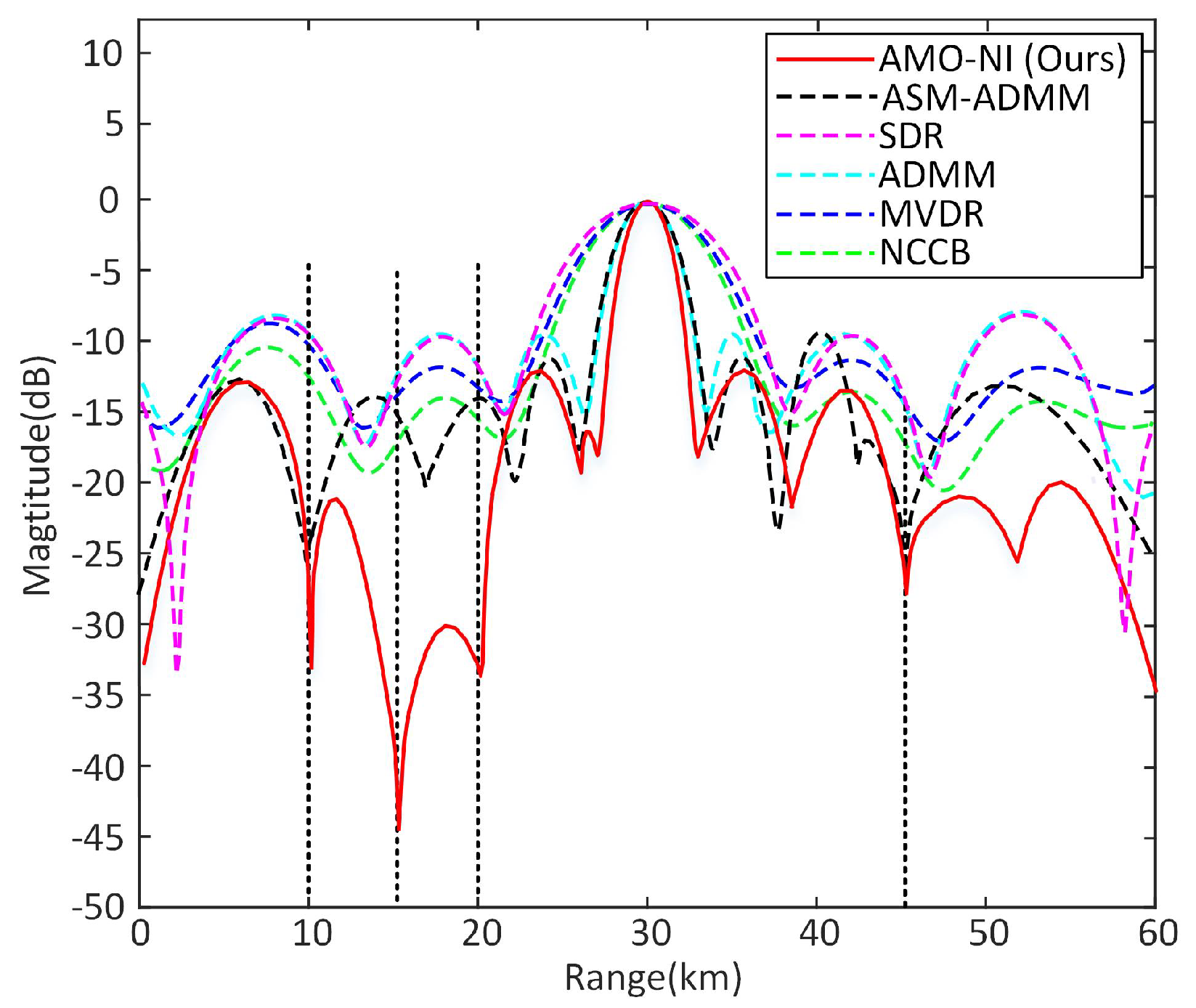
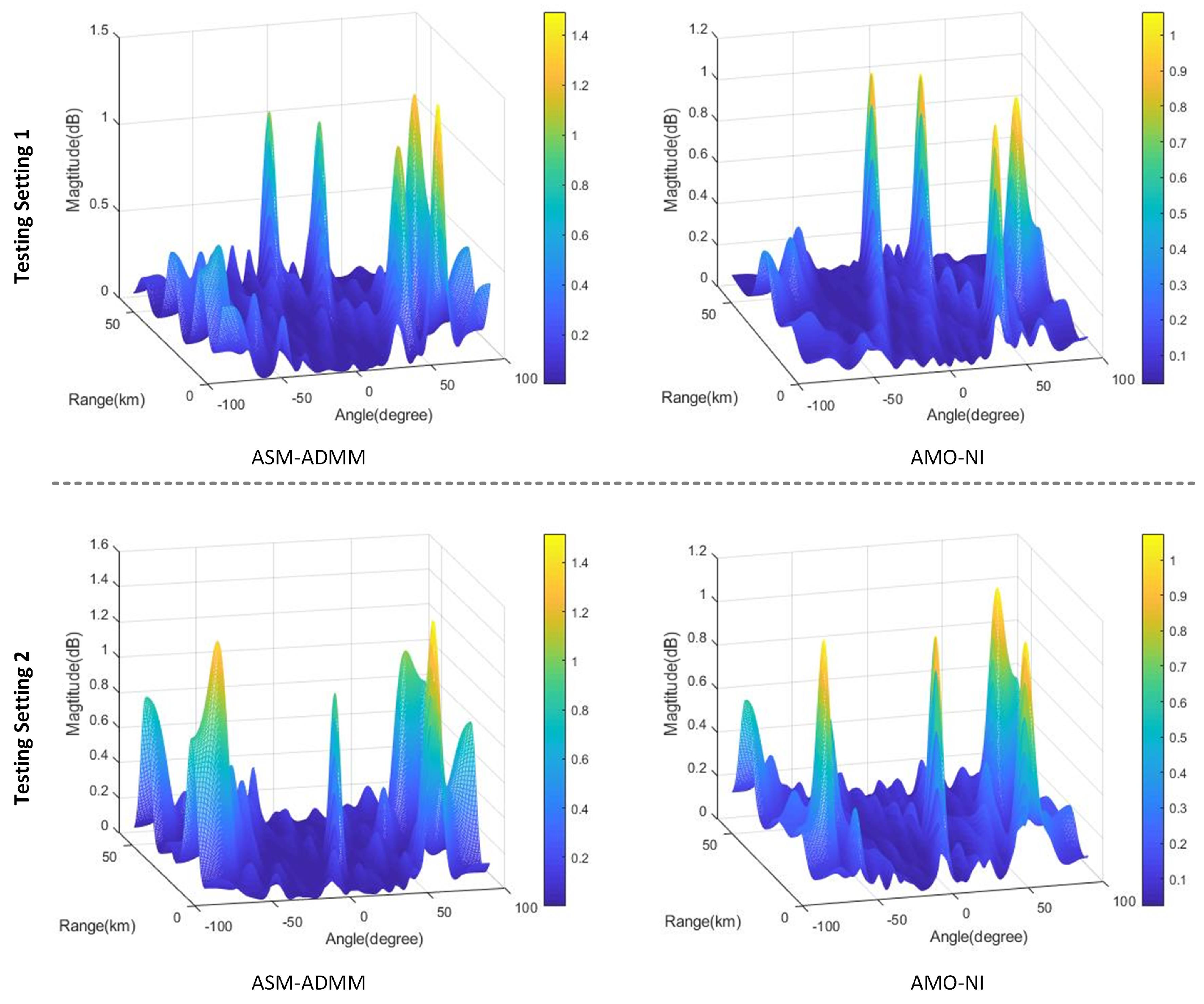
4.2. Results of Transceiver Beampattern
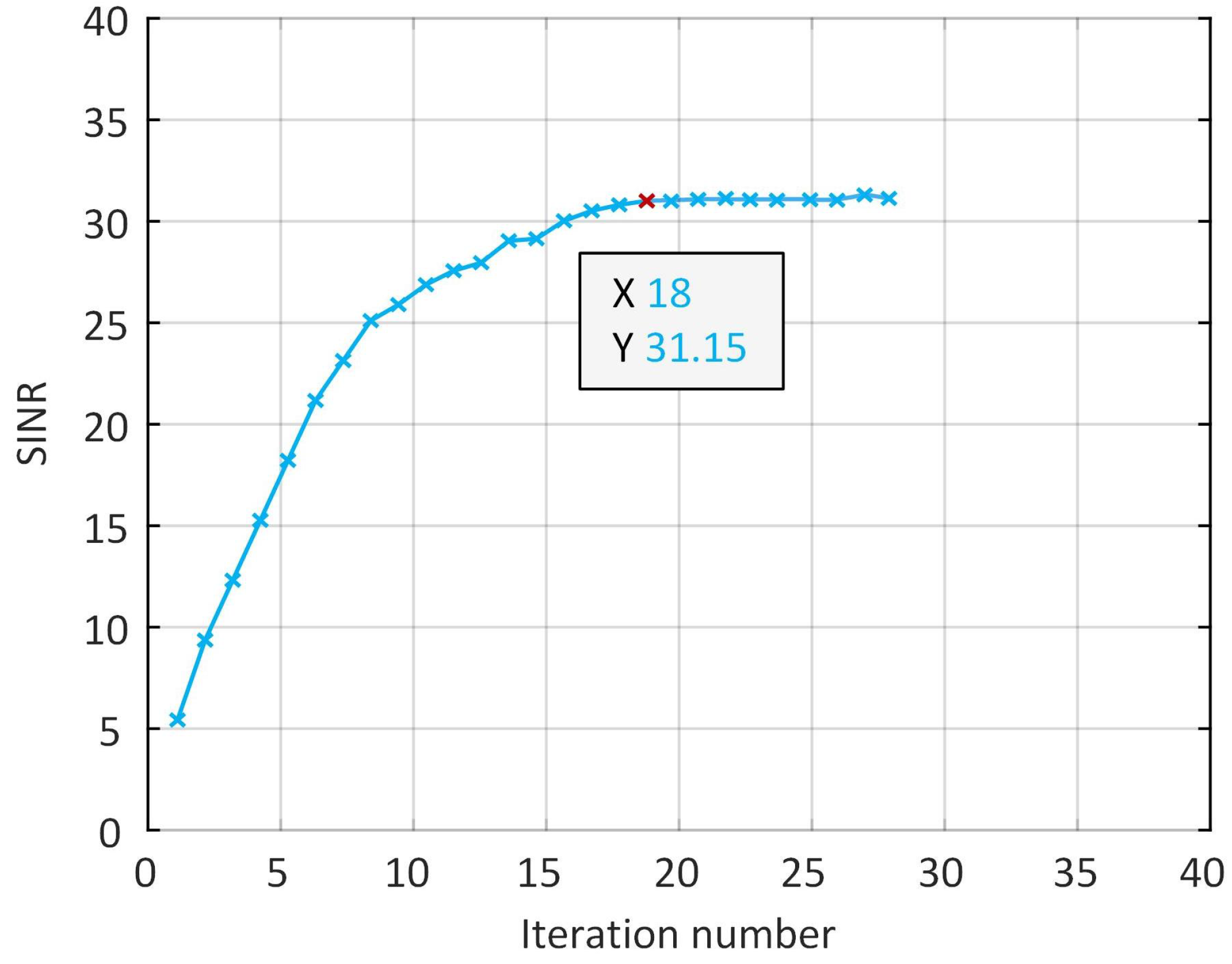
4.3. Results of SINR
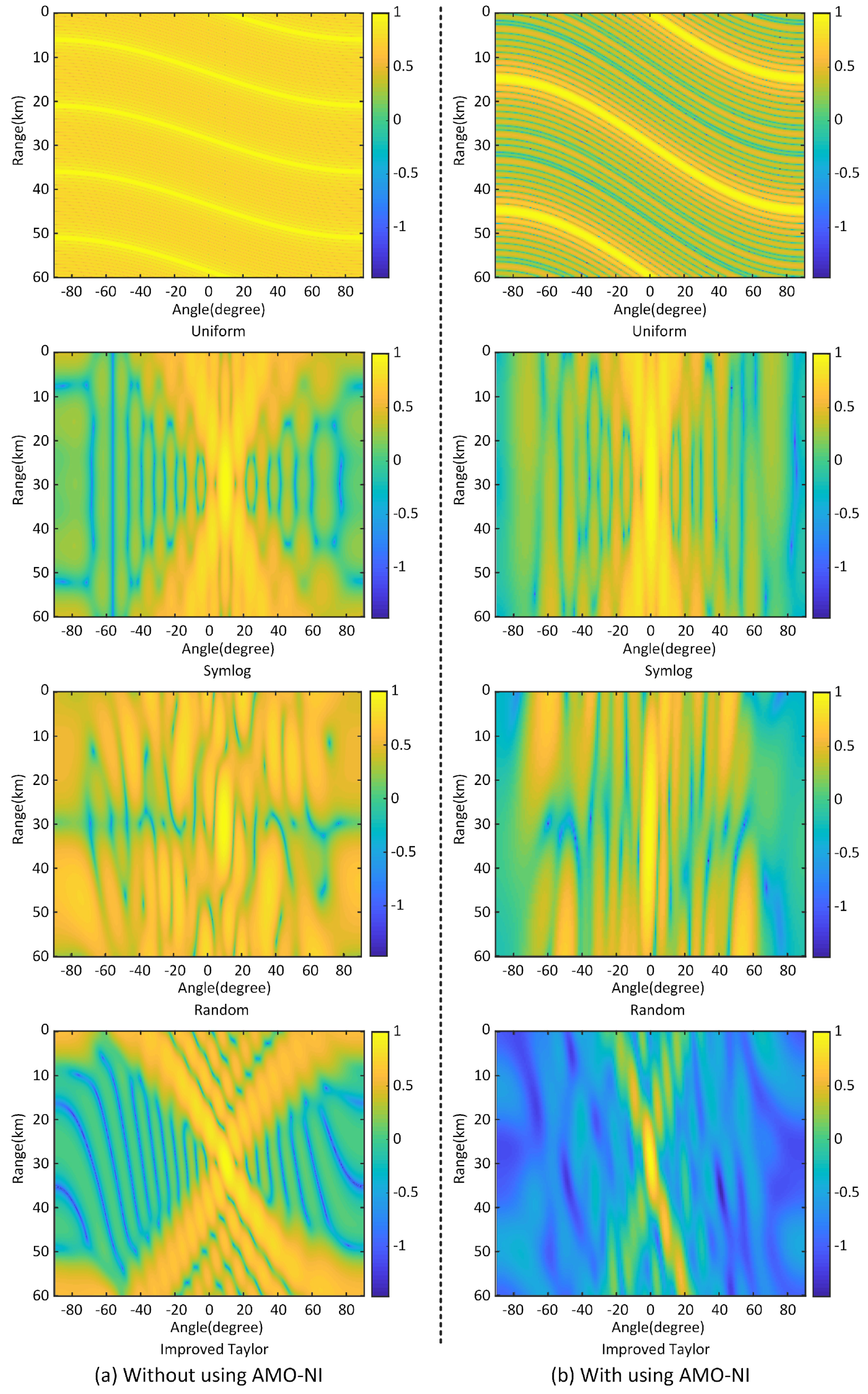
4.4. Effects of Frequency Offset Configuration on Beamforming
4.5. Extended Experiments
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ding, Z.; Xie, J.; Xu, J. A Joint Array Parameters Design Method Based on FDA-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2909–2919. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, X.; Huang, M.; Lan, X.; Sun, L. DOA and Range Estimation for FDA-MIMO Radar with Sparse Bayesian Learning. Remote Sens. 2021, 13, 2553. [Google Scholar] [CrossRef]
- Huang, B.; Wang, W.; Basit, A.; Gui, R. Bayesian Detection in Gaussian Clutter for FDA-MIMO Radar. IEEE Trans. Veh. Technol. 2022, 71, 2655–2667. [Google Scholar] [CrossRef]
- Tian, X.; Chen, H.; Huang, B.; Wang, W.Q. Fast Parameter Estimation Algorithms for Conformal FDA-MIMO Radar. IEEE Sens. J. 2023, 23, 30633–30641. [Google Scholar] [CrossRef]
- Lan, L.; Xu, J.; Liao, G.; Zhang, Y.; Fioranelli, F.; So, H.C. Suppression of Mainbeam Deceptive Jammer With FDA-MIMO Radar. IEEE Trans. Veh. Technol. 2020, 69, 11584–11598. [Google Scholar] [CrossRef]
- Wu, Z.; Zhu, S.; Xu, J.; Lan, L.; Zhang, M. Interference Suppression Method With MR-FDA-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 6250–6264. [Google Scholar] [CrossRef]
- Wang, K.; Liao, G.; Xu, J.; Zhang, Y.; Lan, L.; Wang, W. Multi-scale moving target detection with FDA-MIMO radar. Signal Process. 2024, 216, 109301. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.; Xu, J.; Zhu, S.; Zhang, Y. Range-angle-dependent beamforming for FDA-MIMO radar using oblique projection. Sci. China Inf. Sci. 2022, 65, 152305. [Google Scholar] [CrossRef]
- Yu, L.; He, F.; Zhang, Y.; Su, Y. Low-PSL Mismatched Filter Design for Coherent FDA Radar Using Phase-Coded Waveform. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3507405. [Google Scholar] [CrossRef]
- Akkoc, A.; Korkmaz, N.A.; Genc, Y.; Afacan, E.; Yazgan, E. Time-Invariant and Localized Secure Reception With Sequential Multicarrier Receive-FDA. IEEE Trans. Antennas Propag. 2023, 71, 7064–7072. [Google Scholar] [CrossRef]
- Jia, W.; Jakobsson, A.; Wang, W.Q. Optimal Frequency Offset Selection for FDA-MIMO Beampattern Design in the Range-Angle Plane. IEEE Signal Process. Lett 2023, 31, 316–320. [Google Scholar] [CrossRef]
- Chen, G.; Wang, C.; Gong, J.; Tan, M.; Liu, Y. Data-Independent Phase-Only Beamforming of FDA-MIMO Radar for Swarm Interference Suppression. Remote Sens. 2023, 15, 1159. [Google Scholar] [CrossRef]
- Li, J.; Liao, G.; Huang, Y.; Zhang, Z.; Nehorai, A. Riemannian Geometric Optimization Methods for Joint Design of Transmit Sequence and Receive Filter on MIMO Radar. IEEE Trans. Signal Process. 2020, 68, 5602–5616. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, F.; Shi, J.; He, J.; Truong, T.K. 2D-DOA Estimation for Coherent Signals via a Polarized Uniform Rectangular Array. IEEE Signal Process. Lett. 2023, 30, 893–897. [Google Scholar] [CrossRef]
- Zhang, Z.; Shi, J.; Wen, F. Phase Compensation-based 2D-DOA Estimation for EMVS-MIMO Radar. IEEE Trans. Aerosp. Electron. Syst. 2023; 1–10. [Google Scholar]
- Chalise, B.K.; Amin, M.G.; Martone, A.; Kirk, B.; Sherbondy, K. Optimum Hybrid MVDR Beamformer With Sparse Signal Recovery Approach. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar]
- He, Q.; He, Z.; Wang, Z.; Peng, W. Co-Design of Transmit-Receive Weights for MIMO System With LPI and Multi-Targets. IEEE Commun. Lett. 2022, 26, 1863–1867. [Google Scholar] [CrossRef]
- Zhai, Y.; Li, X.; Hu, J.; Zhong, K. The Transmit Beampattern Design in MIMO Radar System: A Manifold Optimization based Method. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–5. [Google Scholar]
- Xiong, J.; Wang, W.Q.; Gao, K. FDA-MIMO Radar Range–Angle Estimation: CRLB, MSE, and Resolution Analysis. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 284–294. [Google Scholar] [CrossRef]
- Johnston, J.; Venturino, L.; Grossi, E.; Lops, M.; Wang, X. Waveform and Filter Design in MIMO OFDM Dual-Function Radar-Communication. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar]
- Zhang, R.; Chen, Y.; Gu, M.; Sheng, W. Synthesis of Directional Modulation LFM Radar Waveform for Sidelobe Jamming Suppression. IEEE Sens. J. 2023, 23, 28055–28066. [Google Scholar] [CrossRef]
- Ding, Z.; Xie, J. Joint Transmit and Receive Beamforming for Cognitive FDA-MIMO Radar With Moving Target. IEEE Sens. J. 2021, 21, 20878–20885. [Google Scholar] [CrossRef]
- Dong, F.; Wang, W.; Li, X.; Liu, F.; Chen, S.; Hanzo, L. Joint Beamforming Design for Dual-Functional MIMO Radar and Communication Systems Guaranteeing Physical Layer Security. IEEE Trans. Green Commun. Netw. 2023, 7, 537–549. [Google Scholar] [CrossRef]
- Nishihara, R.; Lessard, L.; Recht, B.; Packard, A.; Jordan, M. A general analysis of the convergence of ADMM. In Proceedings of the ICML’15: Proceedings of the 32nd International Conference on International Conference on Machine Learning, PMLR, Lille, France, 6–11 July 2015; pp. 343–352.
- Yu, X.; Qiu, H.; Yang, J.; Wei, W.; Cui, G.; Kong, L. Multispectrally Constrained MIMO Radar Beampattern Design via Sequential Convex Approximation. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2935–2949. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Zhang, J.A.; Di Renzo, M.; Quek, T.Q.S. Joint Beamforming for RIS-Assisted Integrated Sensing and Communication Systems. IEEE Trans. Commun. 2023; 1–14. [Google Scholar]
- Basit, A.; Wang, W.Q.; Wali, S.; Yaw Nusenu, S. Transmit beamspace design for FDA–MIMO radar with alternating direction method of multipliers. Signal Process. 2021, 180, 107832. [Google Scholar] [CrossRef]
- Gong, P.; Zhang, Z.; Wu, Y.; Wang, W.Q. Joint Design of Transmit Waveform and Receive Beamforming for LPI FDA-MIMO Radar. IEEE Signal Process. Lett. 2022, 29, 1938–1942. [Google Scholar] [CrossRef]
- Lan, L.; Liao, G.; Xu, J.; Zhang, Y.; Liao, B. Transceive Beamforming With Accurate Nulling in FDA-MIMO Radar for Imaging. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4145–4159. [Google Scholar] [CrossRef]
- Wang, W.Q.; Dai, M.; Zheng, Z. FDA Radar Ambiguity Function Characteristics Analysis and Optimization. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1368–1380. [Google Scholar] [CrossRef]
- Ma, Y.; Wei, P.; Zhang, H. General Focusing Beamformer for FDA: Mathematical Model and Resolution Analysis. IEEE Trans. Antennas Propag. 2019, 67, 3089–3100. [Google Scholar] [CrossRef]
- Gui, R.; Huang, B.; Wang, W.Q.; Sun, Y. Generalized Ambiguity Function for FDA Radar Joint Range, Angle and Doppler Resolution Evaluation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 3502305. [Google Scholar] [CrossRef]
- Bang, H.; Wang, W.Q.; Zhang, S.; Liao, Y. FDA-Based Space–Time–Frequency Deceptive Jamming Against SAR Imaging. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2127–2140. [Google Scholar] [CrossRef]
- Liao, Y.; Tang, H.; Chen, X.; Wang, W.Q. Frequency Diverse Array Beampattern Synthesis with Taylor Windowed Frequency Offsets. IEEE Antennas Wirel. Propag. Lett. 2020, 19, 1901–1905. [Google Scholar] [CrossRef]
- Langhuan, G.; Youg, L.; Wei, C.; Limeng, D.; Yumei, T. Highly focussed beampattern synthesis in FDA-MIMO radar with multicarrier transmission. IET Radar Sonar Navig. 2023, 17, 665–682. [Google Scholar]
- Tan, M.; Gong, J.; Wang, C. Range Dimensional Monopulse Approach With FDA-MIMO Radar for Mainlobe Deceptive Jamming Suppression. IEEE Antenn. Wirel. Propag. Lett. 2024, 23, 643–647. [Google Scholar] [CrossRef]
- Xu, J.; Liao, G.; Zhang, Y.; Ji, H.; Huang, L. An Adaptive Range-Angle-Doppler Processing Approach for FDA-MIMO Radar Using Three-Dimensional Localization. IEEE J. Sel. Top. Signal Process. 2017, 11, 309–320. [Google Scholar] [CrossRef]
- Huang, B.; Jian, J.; Basit, A.; Gui, R.; Wang, W.Q. Adaptive Distributed Target Detection for FDA-MIMO Radar in Gaussian Clutter Without Training Data. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 2961–2972. [Google Scholar] [CrossRef]
- Tan, M.; Wang, C.; Li, Z. Correction Analysis of Frequency Diverse Array Radar about Time. IEEE Trans. Antennas Propag. 2021, 69, 834–847. [Google Scholar] [CrossRef]
- Zhou, C.; Wang, C.; Gong, J.; Tan, M.; Bao, L.; Liu, M. Ambiguity Function Evaluation and Optimization of the Transmitting Beamspace-Based FDA Radar. Signal Process. 2023, 203, 108810. [Google Scholar] [CrossRef]
- Wen, H.; Gu, P.; He, Z.; Lian, J.; Wang, J.; Song, D.; Ding, D.z. Optimal Function-based Frequency Offset Design Based on Polynomial Fitting for Frequency Diverse Array Beampattern Synthesis. IEEE Antenn. Wirel. Propag. Lett. 2023, 23, 149–153. [Google Scholar] [CrossRef]
- Jian, J.; Wang, W.; Huang, B.; Zhang, L.; Imran, M.A.; Huang, Q. MIMO-FDA Communications with Frequency Offsets Index Modulation. IEEE Trans. Wireless Commun. 2023; 1–15. [Google Scholar]
- Zhu, Z.; Chen, W.; Yang, Y.; Shu, Q. Frequency Diverse Array Beampattern Synthesis with Random Permutated Power Increasing Frequency Offset. IEEE Antennas Wirel. Propagat. Lett. 2022, 21, 1975–1979. [Google Scholar] [CrossRef]
- Cheng, X.; Wu, L.; Ciuonzo, D.; Wang, W. Joint Design of Horizontal and Vertical Polarization Waveforms for Polarimetric Radar via SINR Maximization. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 3313–3328. [Google Scholar] [CrossRef]
- Yao, Y.; Li, Z.; Liu, H.; Miao, P.; Wu, L. Robust Transceiver Optimization Against Echo Eclipsing via Majorization-Minimization. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 2464–2479. [Google Scholar] [CrossRef]
- Aghashahi, S.; Zeinalpour-Yazdi, Z.; Tadaion, A.; Mashhadi, M.B.; Elzanaty, A. MU-Massive MIMO with Multiple RISs: SINR Maximization and Asymptotic Analysis. IEEE Wirel. Commun. Lett. 2023, 12, 997–1001. [Google Scholar] [CrossRef]
- Chu, C.; Chen, Y.; Luo, Y.; Zhang, Q. Wideband MIMO Radar Waveform Design under Multiple Criteria. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3506305. [Google Scholar] [CrossRef]
- Raei, E.; Sedighi, S.; Alaee-Kerahroodi, M.; Bhavani Shankar, M.R. MIMO Radar Transmit Beampattern Shaping for Spectrally Dense Environments. IEEE Trans. Aerosp. Electron. Syst. 2023, 59, 1007–1020. [Google Scholar] [CrossRef]
- Alhujaili, K.; Yu, X.; Cui, G.; Monga, V. Spectrally Compatible MIMO Radar Beampattern Design under Constant Modulus Constraints. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4749–4766. [Google Scholar] [CrossRef]
- Liu, R.; Zhang, W.; Yu, X.; Lu, Q.; Wei, W.; Kong, L.; Cui, G. Transmit-Receive Beamforming for Distributed Phased-MIMO Radar System. IEEE Trans. Veh. Technol. 2022, 71, 1439–1453. [Google Scholar] [CrossRef]
- Fan, W.; Liang, J.; Lu, G.; Fan, X.; So, H.C. Spectrally-Agile Waveform Design for Wideband MIMO Radar Transmit Beampattern Synthesis via Majorization-ADMM. IEEE Trans. Signal Process. 2021, 69, 1563–1578. [Google Scholar] [CrossRef]
- Yuan, G.; Wei, Z.; Lu, X. Global convergence of BFGS and PRP methods under a modified weak Wolfe–Powell line search. Appl. Math. Model. 2017, 47, 811–825. [Google Scholar] [CrossRef]
- Zhuang, J.; Ni, L.; Guo, J.; Tan, T. Robust adaptive beamforming with null-pattern constraints. Signal Process. 2020, 169, 107420. [Google Scholar] [CrossRef]
- Liu, Y.; Ruan, H.; Wang, L.; Nehorai, A. The Random Frequency Diverse Array: A New Antenna Structure for Uncoupled Direction-Range Indication in Active Sensing. IEEE J. Sel. Top. Signal Process. 2017, 11, 295–308. [Google Scholar] [CrossRef]
- Su, Y.; Cheng, T.; He, Z.; Li, X. Adaptive simultaneous multibeam resource management for colocated MIMO radar in multiple targets tracking. Signal Process. 2020, 172, 107543. [Google Scholar] [CrossRef]





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| transmitting sensors | range grid | 181 | |
| receiving sensors | angle vector | [−90°,90°] | |
| snapshot number | angle grid | 301 | |
| frequency offset | target location | ||
| carrier frequency | interference 1 | ||
| speed of light | interference 2 | ||
| inter-element spacing | interference 3 | ||
| complex coefficient | interference 4 | ||
| range vector | [0 km, 60 km] |
| Method | Complexity (Single Iteration) | Time (s) |
|---|---|---|
| NCCB [53] | 1.51 | |
| MVDR [16] | 1.29 | |
| ADMM [51] | 25.20 | |
| SDR [50] | 0.37 | |
| ASM-ADMM [28] | 543 | |
| AMO-NI (Ours) | 0.20 |
| Method | Half-Power Width | |
|---|---|---|
| Angle (Degree) ↓ | Range (km) ↓ | |
| NCCB [53] | 6.0 | 14.2 |
| MVDR [16] | 10.0 | 35.0 |
| ADMM [51] | 4.0 | 9.4 |
| SDR [50] | 87.0 | 16.9 |
| ASM-ADMM [28] | 5.7 | 10.8 |
| AMO-NI (Ours) | 3.6 | 8.9 |
| Frequency Offsets | Half-Power Width without AMO-NI | Half-Power Width with AMO-NI | ||
|---|---|---|---|---|
| Angle (Degree) | Range (km) | Angle (Degree) | Range (km) | |
| Uniform [39] | 22 | 1.2 | 3.6 | 0.3 |
| Symlog [34] | 22 | 24.8 | 3.6 | 22 |
| Random [54] | 22 | 26.8 | 3.6 | 22 |
| Improved Taylor [35] | 22 | 11.2 | 3.6 | 8.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, L.; Li, Y.; Dong, L.; Tan, Y.; Cheng, W. Efficiently Refining Beampattern in FDA-MIMO Radar via Alternating Manifold Optimization for Maximizing Signal-to-Interference-Noise Ratio. Remote Sens. 2024, 16, 1364. https://doi.org/10.3390/rs16081364
Geng L, Li Y, Dong L, Tan Y, Cheng W. Efficiently Refining Beampattern in FDA-MIMO Radar via Alternating Manifold Optimization for Maximizing Signal-to-Interference-Noise Ratio. Remote Sensing. 2024; 16(8):1364. https://doi.org/10.3390/rs16081364
Chicago/Turabian StyleGeng, Langhuan, Yong Li, Limeng Dong, Yumei Tan, and Wei Cheng. 2024. "Efficiently Refining Beampattern in FDA-MIMO Radar via Alternating Manifold Optimization for Maximizing Signal-to-Interference-Noise Ratio" Remote Sensing 16, no. 8: 1364. https://doi.org/10.3390/rs16081364
APA StyleGeng, L., Li, Y., Dong, L., Tan, Y., & Cheng, W. (2024). Efficiently Refining Beampattern in FDA-MIMO Radar via Alternating Manifold Optimization for Maximizing Signal-to-Interference-Noise Ratio. Remote Sensing, 16(8), 1364. https://doi.org/10.3390/rs16081364