Application of Artificial Intelligence in Landslide Susceptibility Assessment: Review of Recent Progress
Abstract
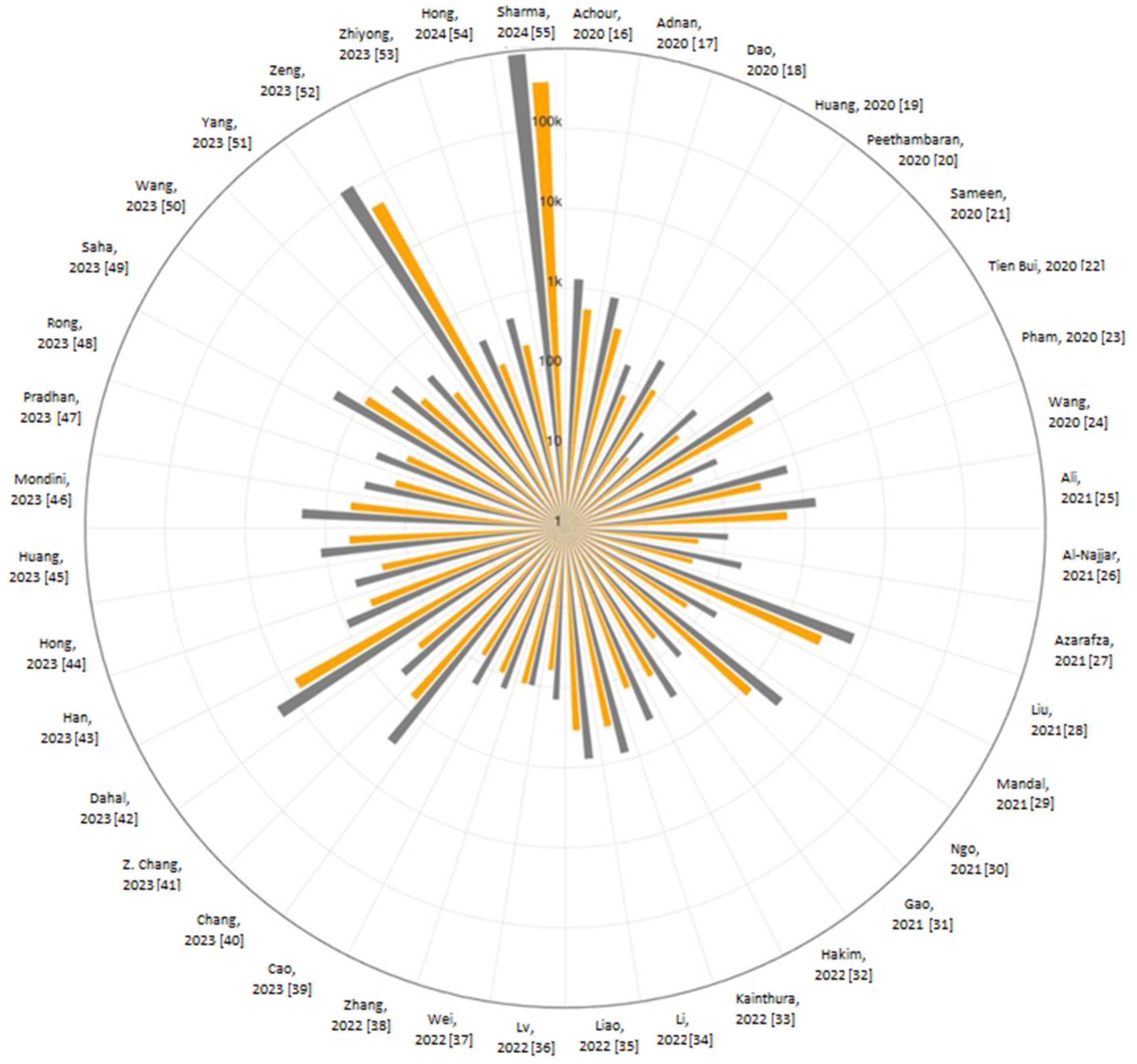
1. Introduction
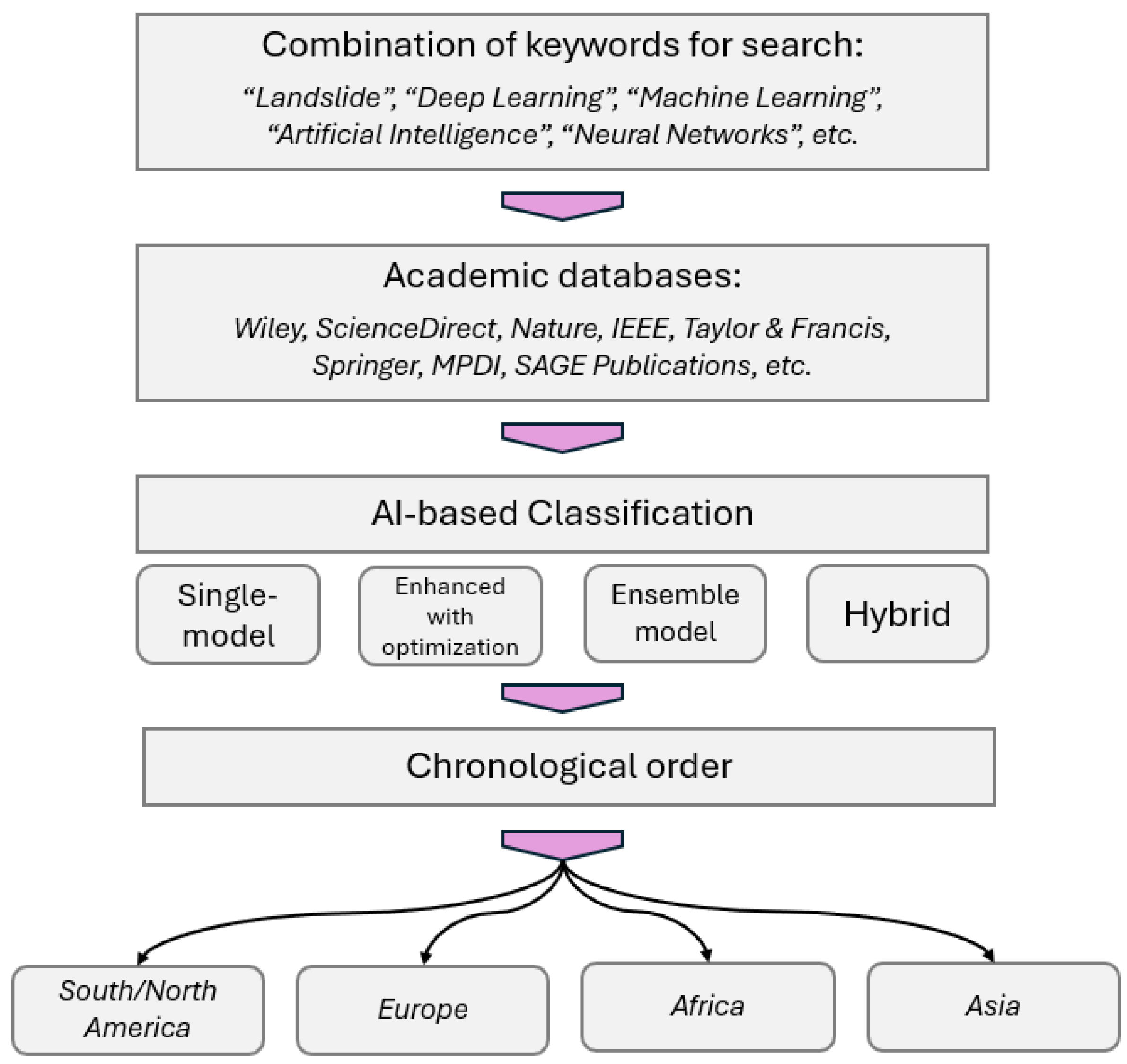
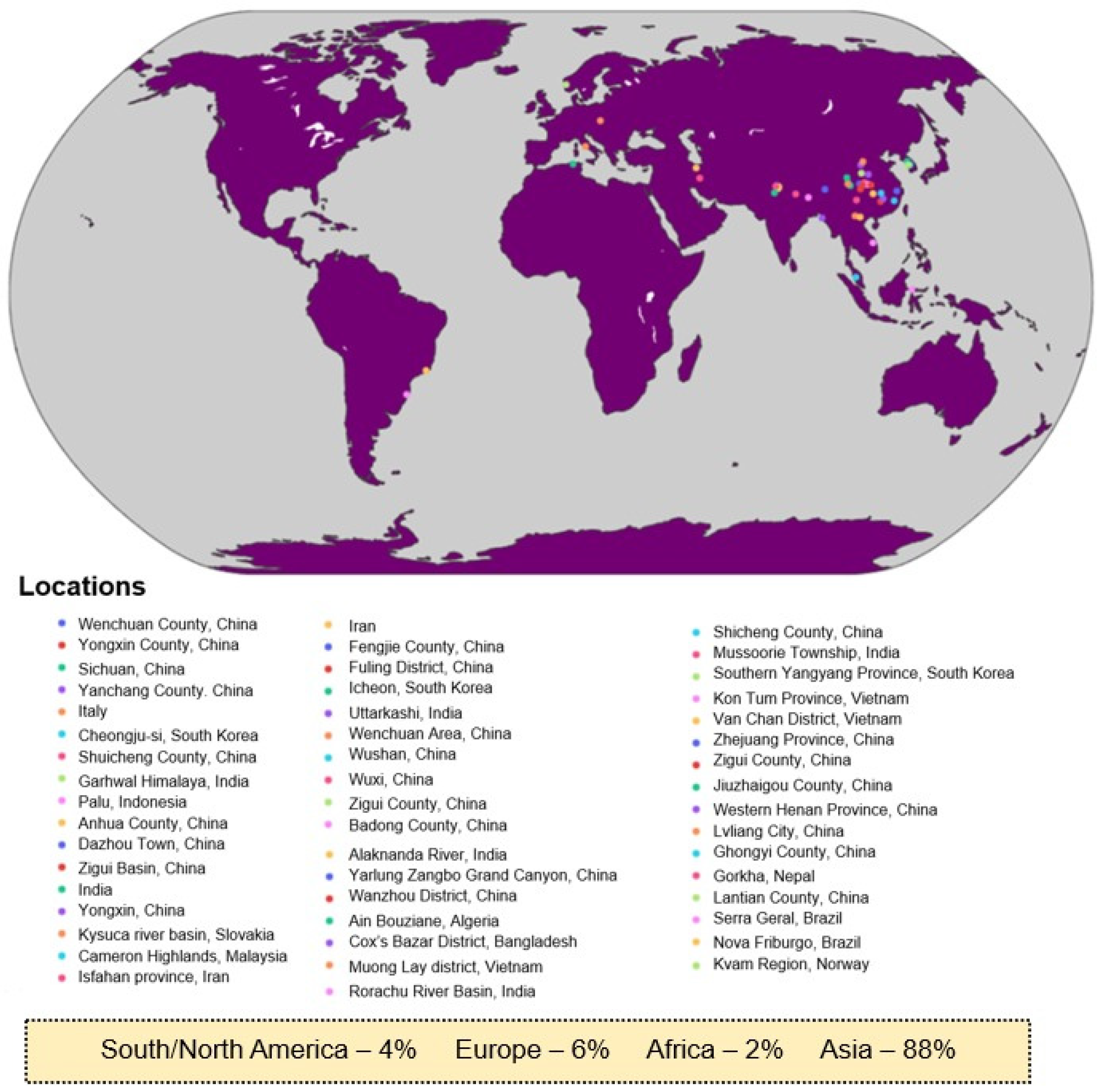
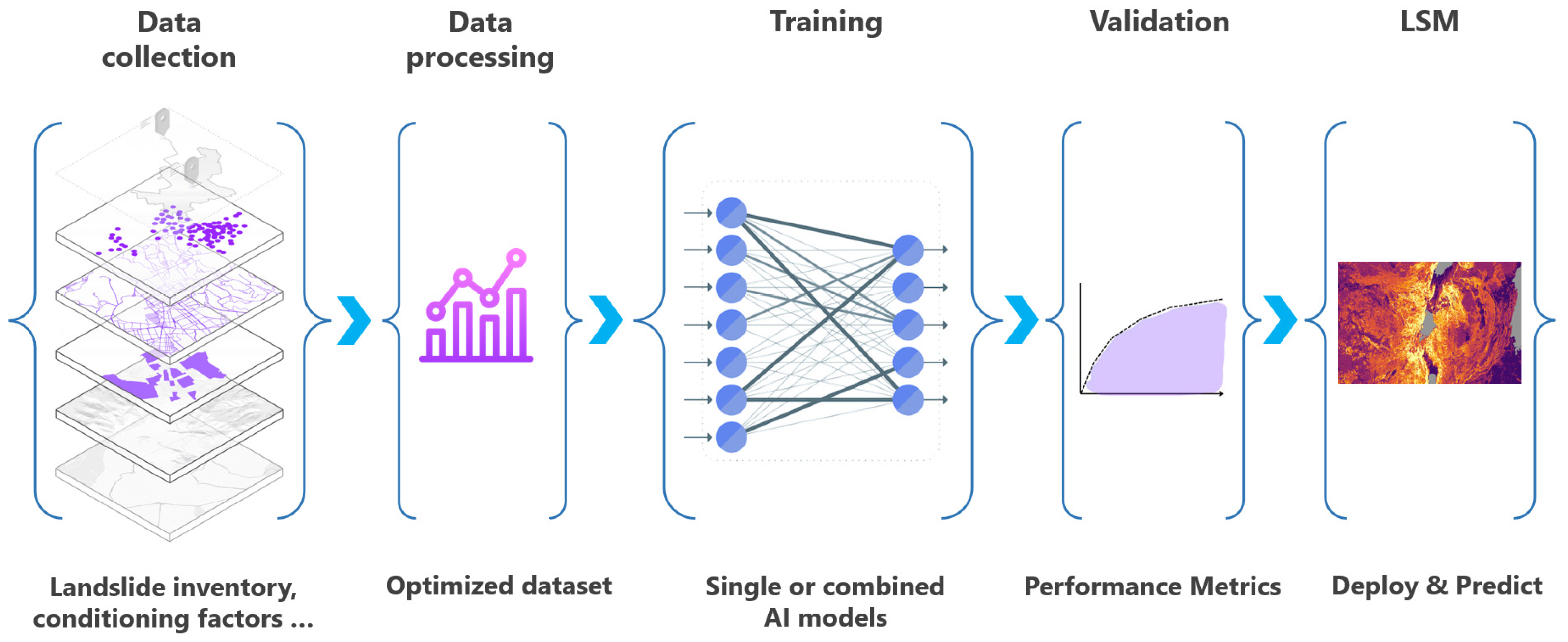
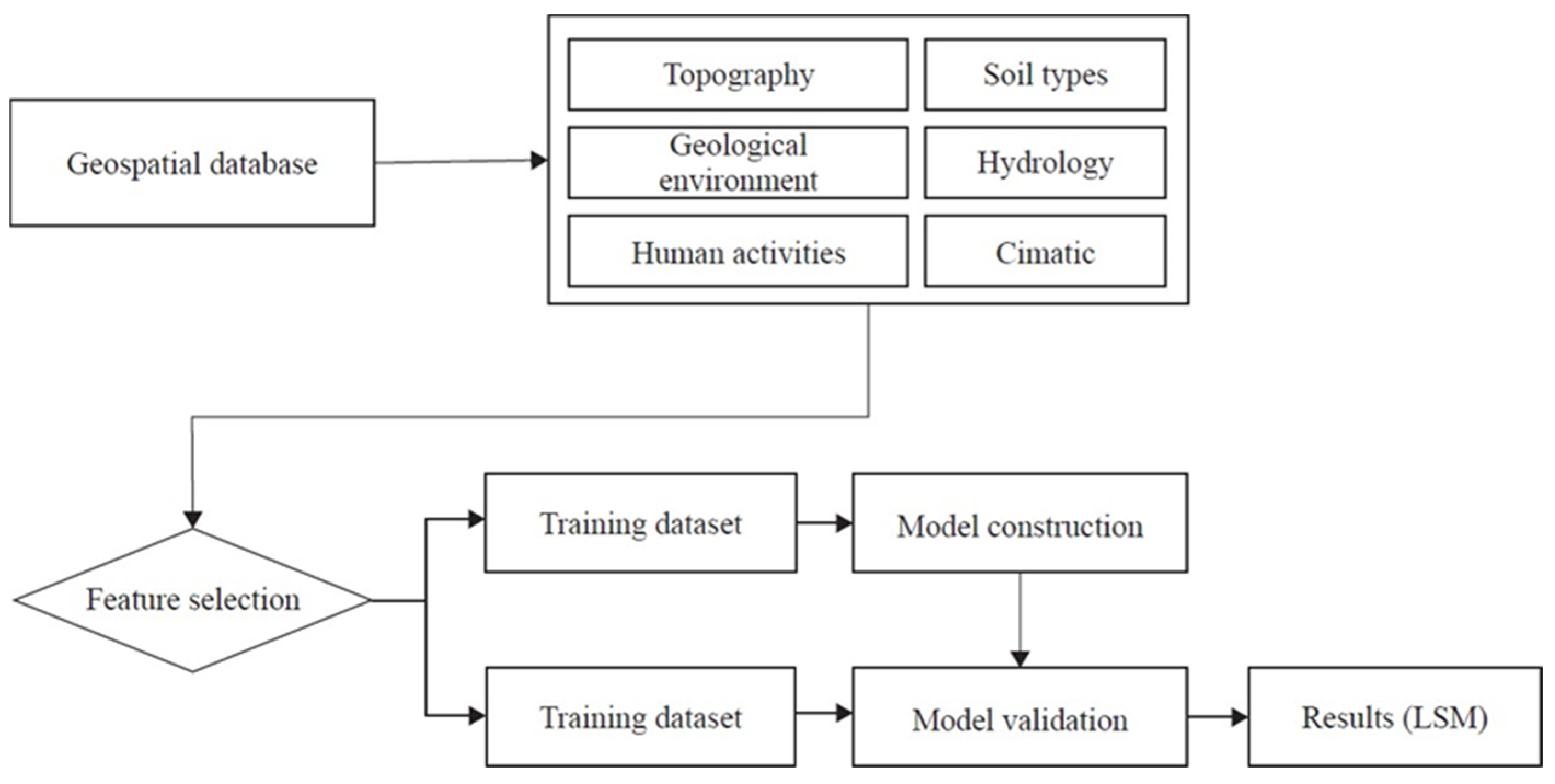
2. Methodology
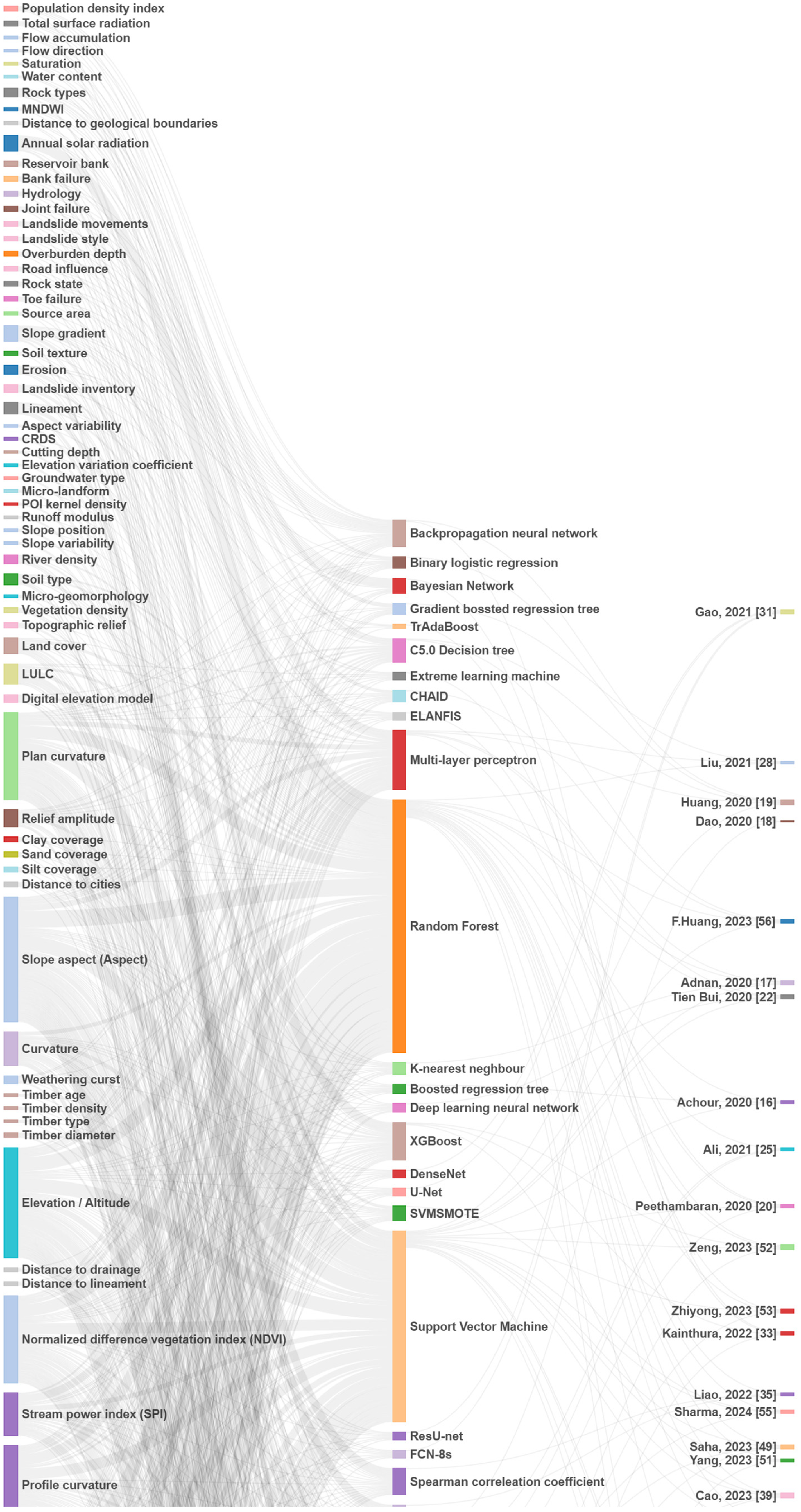
3. Overview of Al Techniques in LSM
4. Complexity-Based Classification of AI Models in LSM
- Single-model approaches focus on individual ML or DL models without additional modifications, providing a baseline for landslide prediction and highlighting the potential of each model in isolation. This category illustrates the strengths and limitations of popular algorithms such as RF, SVM, and CNN when used independently in LSM;
- Enhanced models with optimization introduces advanced optimization techniques to improve the performance of single models, particularly in challenging terrains or data-limited environments. Techniques like Bayesian optimization, class weighting, and transfer learning are utilized to tackle issues such as sample imbalance, hyperparameter tuning, and data scarcity, yielding more accurate and adaptable LSM models;
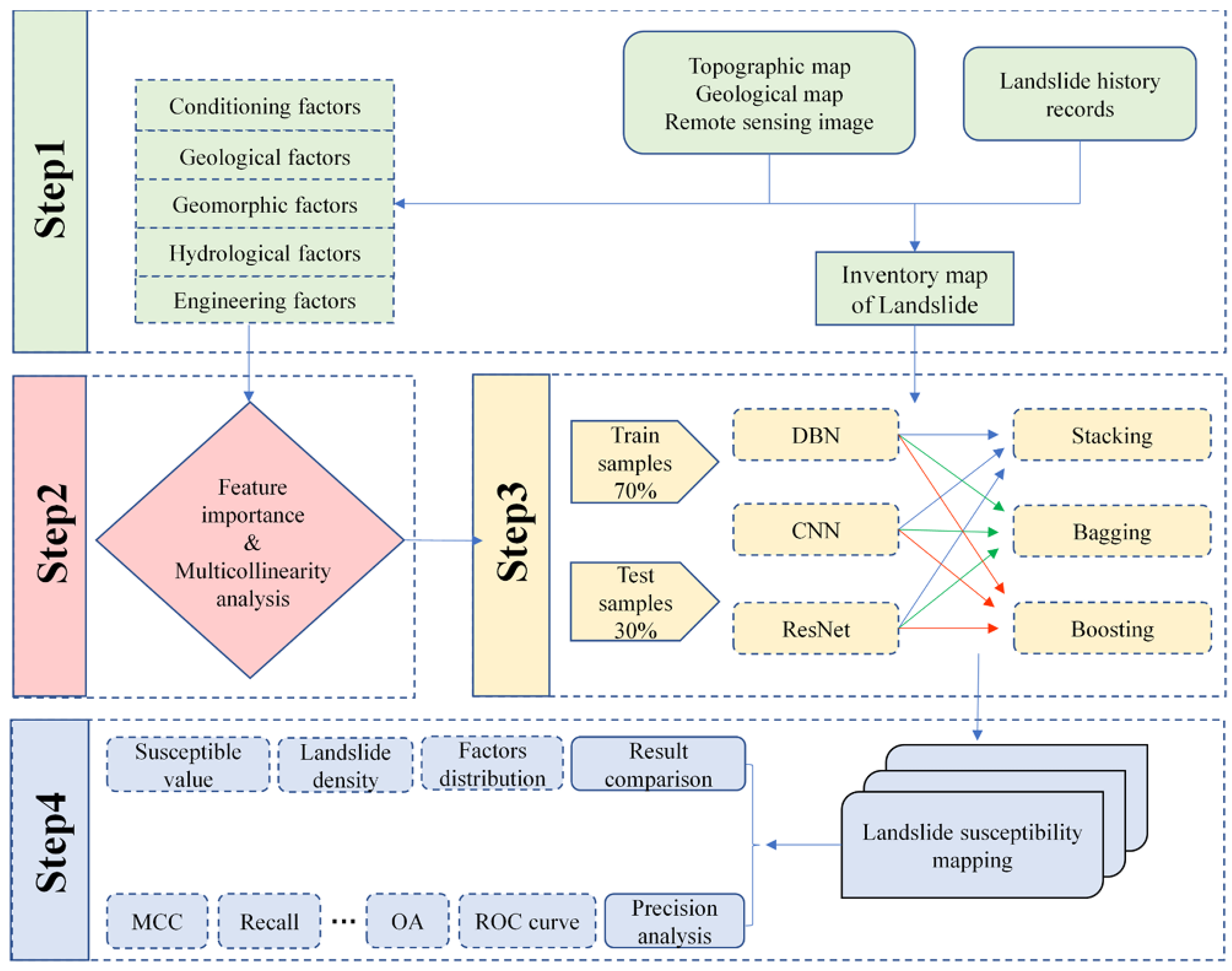
- Ensemble models combine multiple base models to improve predictive accuracy and robustness across diverse terrains. Techniques such as stacking, bagging, and blending enhance model performance by aggregating strengths from different algorithms, with separate strategies for ML and DL ensembles to address specific environmental complexities in LSM;
- Hybrid models integrate multiple AI techniques within a single framework, combining ML and DL methods or blending optimization and ensemble techniques. These models are particularly suited for high-dimensional or complex terrains, where capturing interactions between diverse conditioning factors is critical for accurate LSM.
4.1. Single-Model Approaches
4.1.1. Traditional ML Models
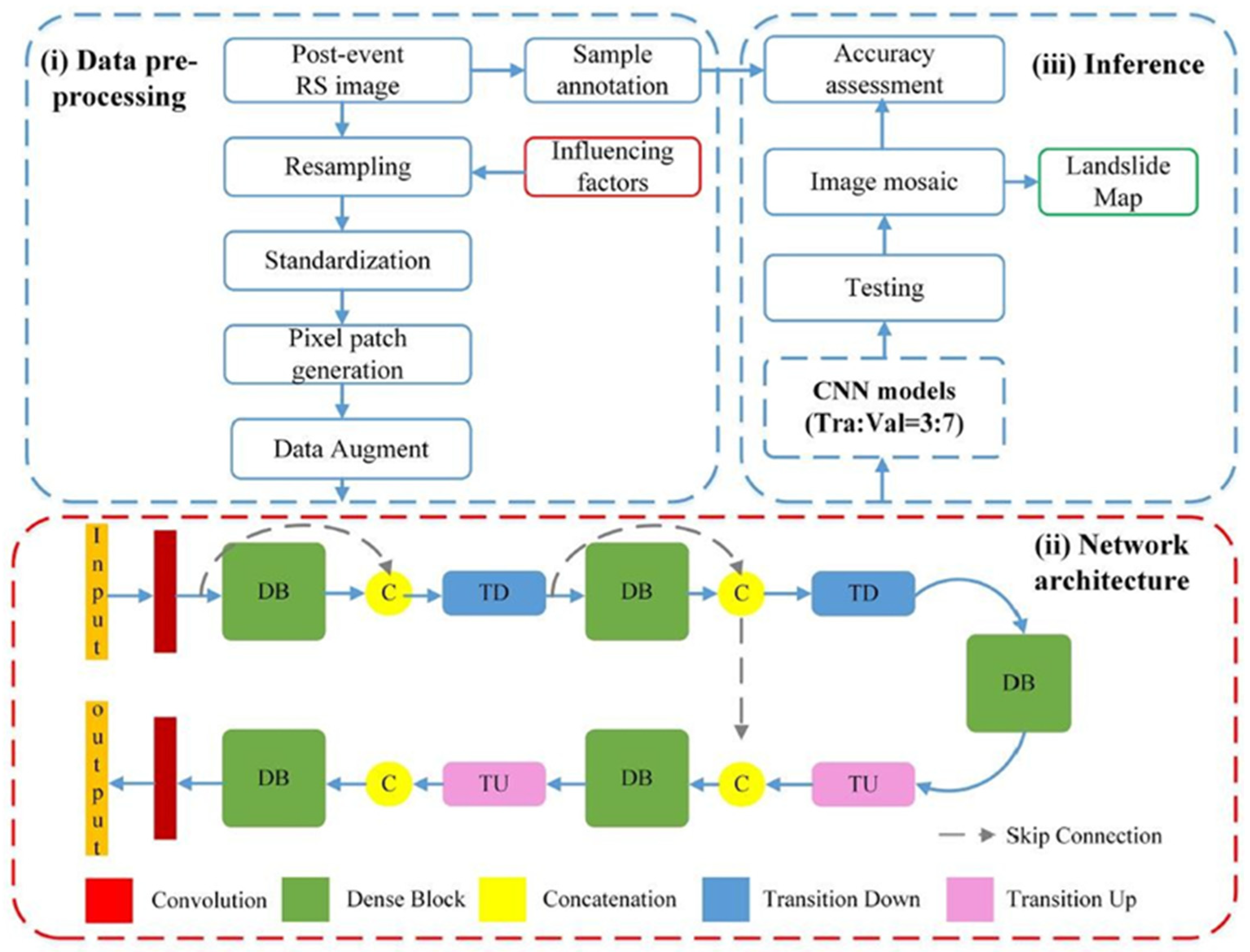
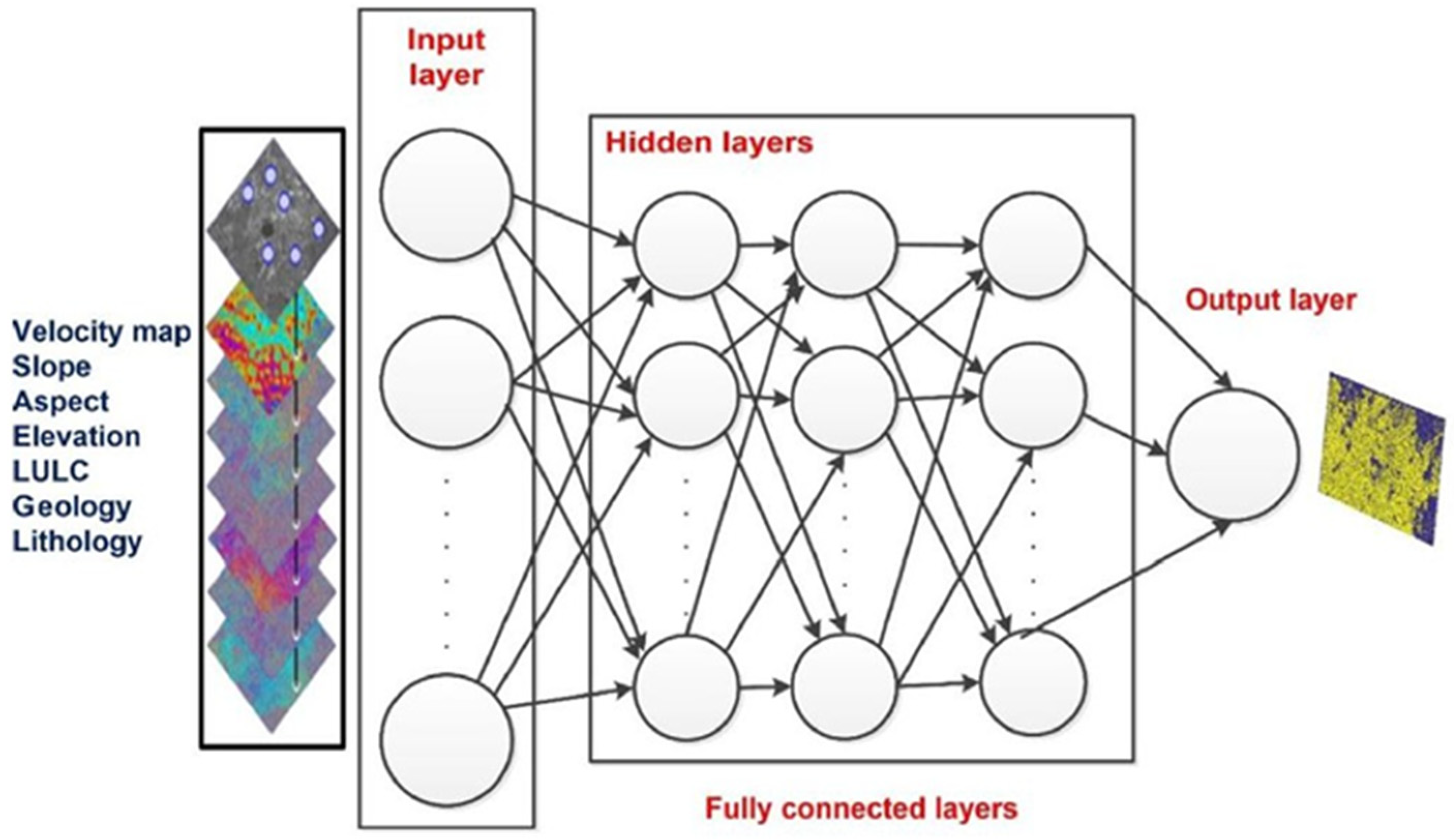
4.1.2. DL Models
4.2. Enhanced Models with Optimization
4.2.1. Traditional ML Models with Optimization
4.2.2. DL Models with Optimization
4.3. Ensemble Models
4.3.1. Traditional ML Ensemble Models
4.3.2. DL Ensemble Models
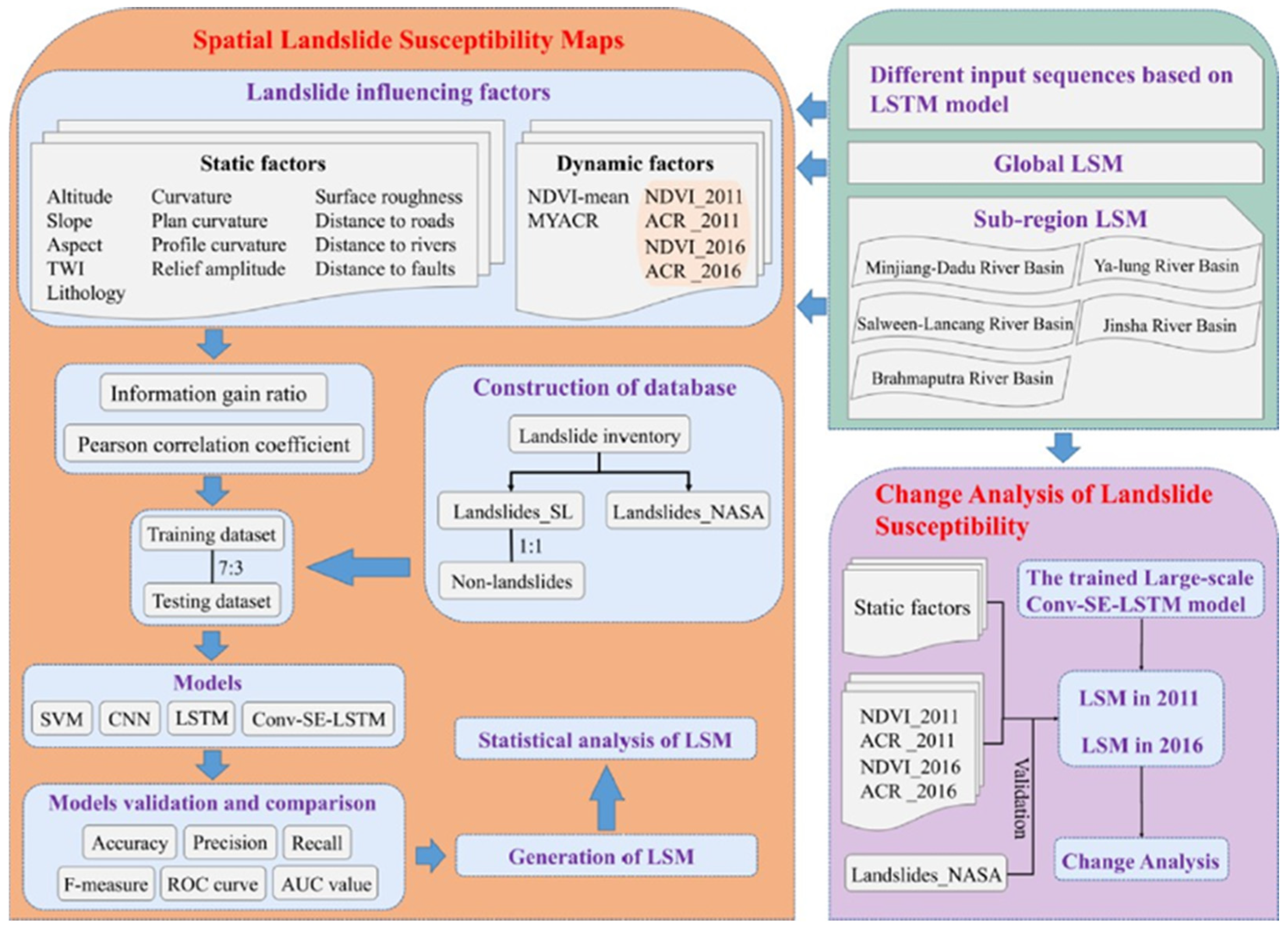
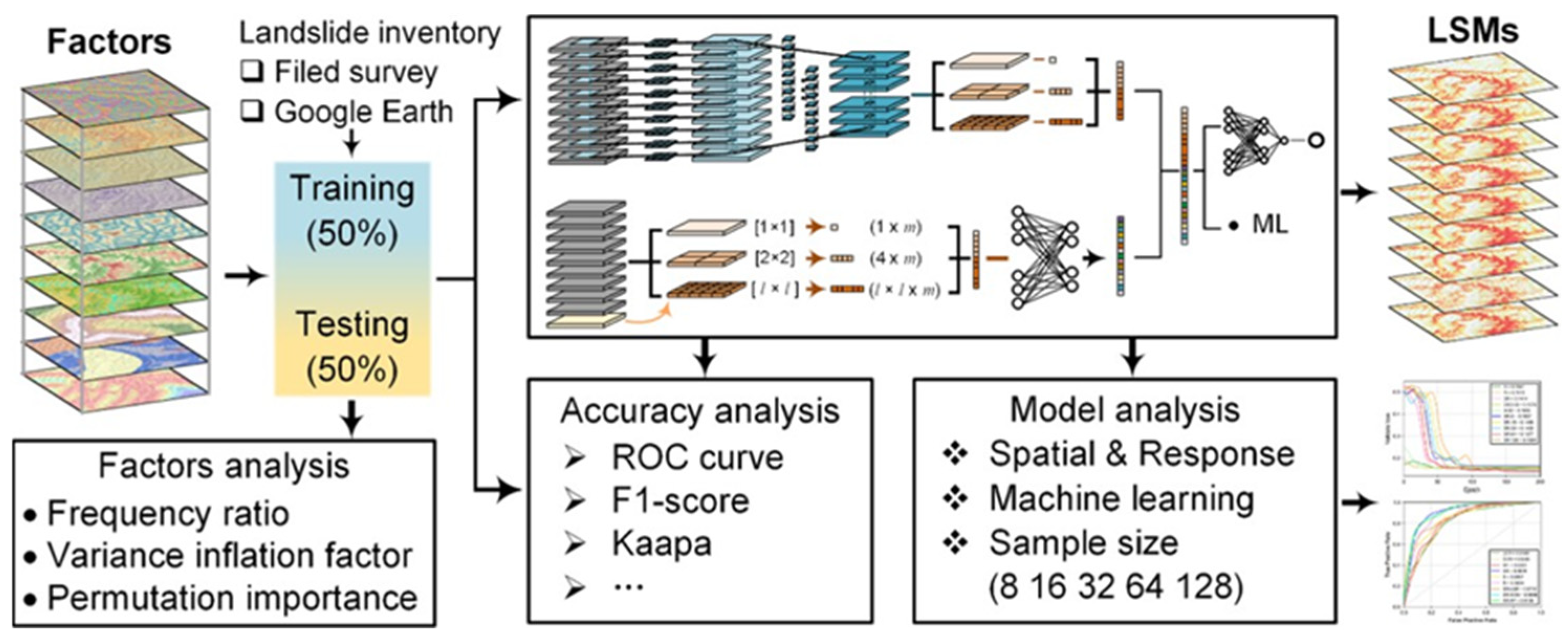
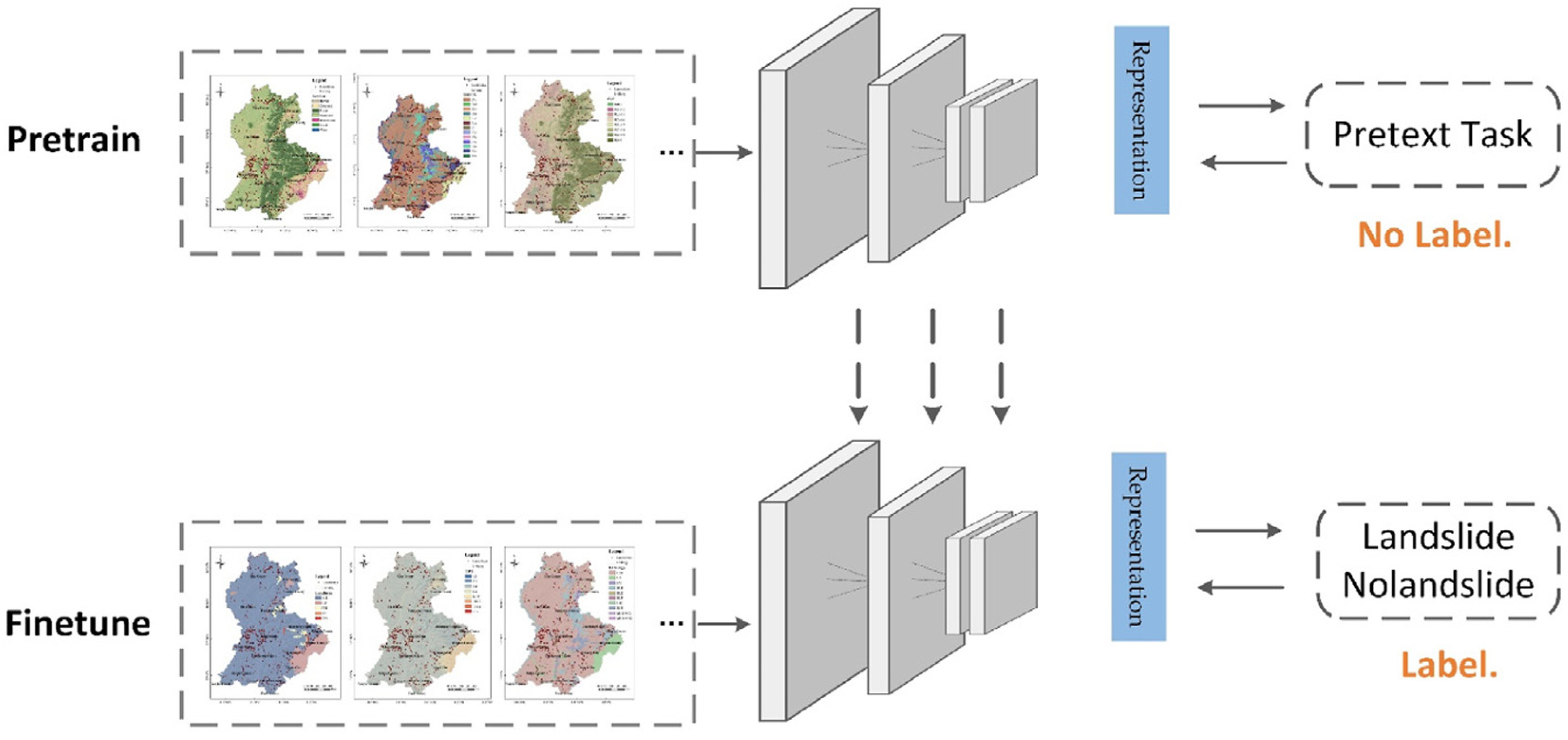
4.4. Hybrid Models
- Data-Scarce Regions: GAN-based hybrids and UATL frameworks show effectiveness in regions with limited data, with GANs enhancing data representation and UATL providing adaptive learning capabilities.
- Complex Spatial–Temporal Patterns: DL-based hybrids such as HEL and Conv-SE-LSTM excel in capturing intricate spatial and temporal dependencies, making them highly effective for dynamic landscapes influenced by variable factors like rainfall and vegetation cover.
- High-Dimensional Data: Hybrid models with convolutional layers (e.g., SR-ML) or feature selection (e.g., SCC-RFE) efficiently manage high-dimensional datasets, enhancing predictive power in terrains with a broad range of conditioning factors.
- Region-Specific Models: Models like FDEMATEL-ANP and KDE-MDBN are effective for region-specific analyses, providing tailored insights that capture local environmental factors or post-disaster conditions, especially useful in targeted or unique geographic settings.
5. Conclusions
- Single-model approaches provide essential baseline insights into landslide susceptibility patterns using models such as RF, SVM, and CNN. These models are highly accessible, offering a straightforward approach for initial assessments in LSM. However, their predictive power is often limited in complex terrains or when handling imbalanced datasets, underscoring the need for more advanced methods in challenging environments.
- Enhanced models with optimization improve upon single models by addressing specific limitations through techniques like Bayesian optimization, class weighting, and transfer learning. Such models excel in scenarios with data imbalance or data scarcity, offering greater adaptability and precision. In areas with uneven data distributions or where new data collection is limited, these optimized models deliver substantial improvements in predictive reliability, making them valuable tools for LSM in structured and data-limited regions.
- Ensemble models aggregate the strengths of multiple algorithms to capture complex spatial patterns that single models may overlook. Techniques such as stacking, bagging, and blending create robust predictive frameworks that perform well across diverse and variable terrains. These ensemble methods excel in large-scale assessments, where achieving high stability and consistency is essential for accurate, broad-area LSM. By combining different models, ensemble methods increase resilience against environmental variability, establishing themselves as reliable choices for both national and regional assessments.
- Hybrid models represent the most flexible and powerful approach, integrating ML and DL techniques or combining ensemble and optimization strategies to achieve high adaptability. These models are especially effective in high-dimensional and data-rich environments, where capturing intricate relationships between conditioning factors is essential. Hybrid models address the limitations of single, optimized, and ensemble models by blending multiple approaches, providing a balanced combination of predictive power and robustness. This versatility makes hybrid models particularly suited for high-stakes applications where precision is paramount, such as in regions prone to frequent landslides or complex geomorphological features.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Publication Year, Authors | Geographic Location | Combined AI Model? (Y/N) | AI Models | Geological/Weather Information | Selected Parameters for Models | Software Used to Develop Models | Data Size | Accuracy | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Altitude Range (Sea Level) | Slope Angle | Mean Annual Precipitation | Mean or Max/Min Temperature | |||||||||||
| Achour et al., 2020 [16] | A1 highway at Ain Bouziane, North-East of Algeria | No |
| 226 to 718 m | 0° to 46° | 556 mm | 7 °C and 37 °C, max/min |
| R software; ArcGIS | 1871 landslide pixels: 70% training; 30% testing. | AUC of models: RF: 0.972 SVM: 0.856 BRT: 0.760 | |||
| Adnan et al., 2020 [17] | Cox’s Bazar district, South-East of Bangladesh | Yes |
| 18 m | 0° to 59° | 4288 mm | - |
| - | 1262 sample locations (670 landslide and 592 non-landslide): 60% training; 40% testing. | RF: 96.63% MLP: 95.45% SVM: 94.06% KNN: 90.69% Combined method: 97% | |||
| Dao et al., 2020 [18] | Muong Lay district, Dien Bien province, Vietnam. | No |
| 125 to 1778 m | 0° to 73° | 1483 mm | 22–23 °C, mean |
| Open-source WEKA software | 217 landslides: 70% training; 30% testing. | AUC and accuracy of training: QDA: 0.881 and 81.67% FLDA: 0.867 and 81.46 MLP: 0.901 and 86.42% DL: 0.899 and 81.85% AUC and accuracy of validation: QDA: 0.806 and 72.31% FLDA: 0.860 and 79.21% MLP: 0.841 and 76.15% DL: 0.887 and 82.31% MLP: 0.841 and 76.15% DL: 0.887 & 82.31% | |||
| Huang et al., 2020 [19] | Shicheng County, China | No |
| 0 to 1320 m | 3.9° to 19.1° | 1885 mm | - |
| - | 369 landslides: 70% training; 30% testing | AUC of models:
| |||
| Peethambaran et al., 2020 [20] | Mussoorie Township, Dehradun, India | No |
| 654 to 2253 m | 0° to 72.5° | 155 mm | - |
| MATLAB | 49 landslides: 70% training; 30% testing. | AUC of models:
| |||
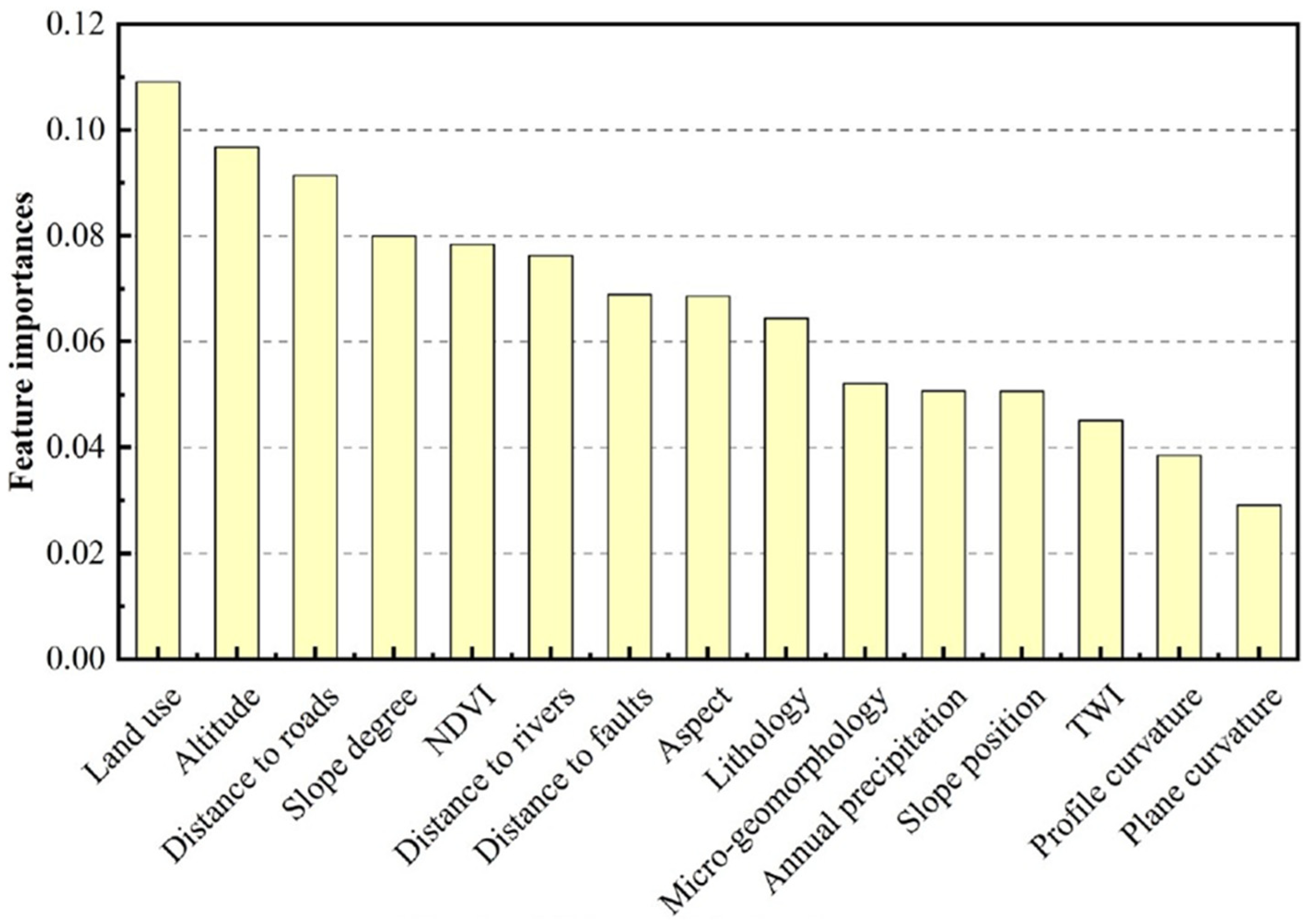
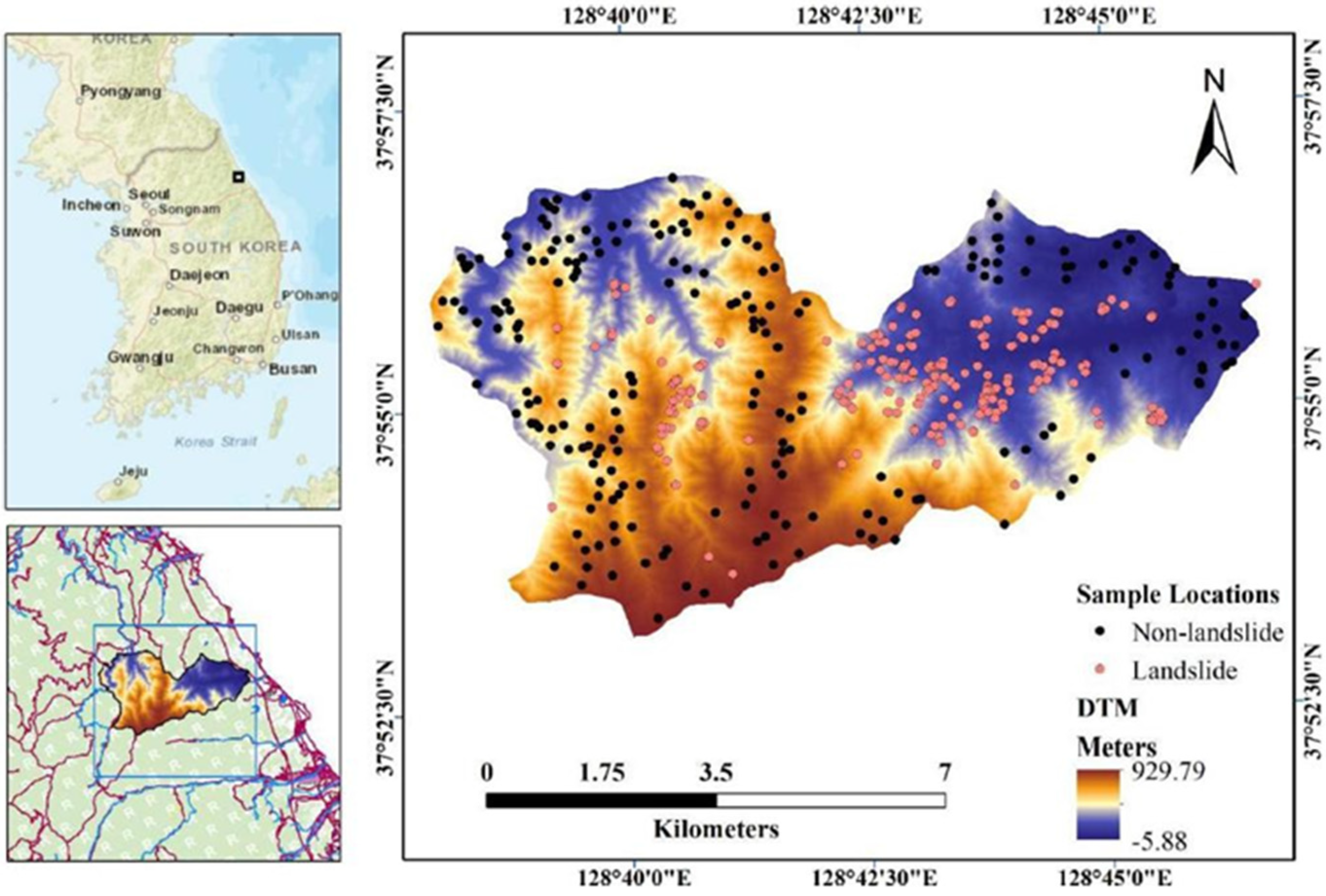
| Sameen et al., 2020 [21] | Southern Yangyang Province, South Korea | No |
| −5.88 to 929.79 m | 0° to 79° | - | - |
| Python using Scikit-Learn and Keras | 219 landslides: 70% training; 30% testing. | Accuracy and AUC of training:
| |||
| Tien Bui et al., 2020 [22] | Kon Tum Province, Vietnam | No |
| 136.8 to 2580.2 | 0° to 72.5° | 1700–3000 mm | - |
| WEKA software, Python, ArcGIS | 1657 landslides: | Accuracy (%) of training:
| |||
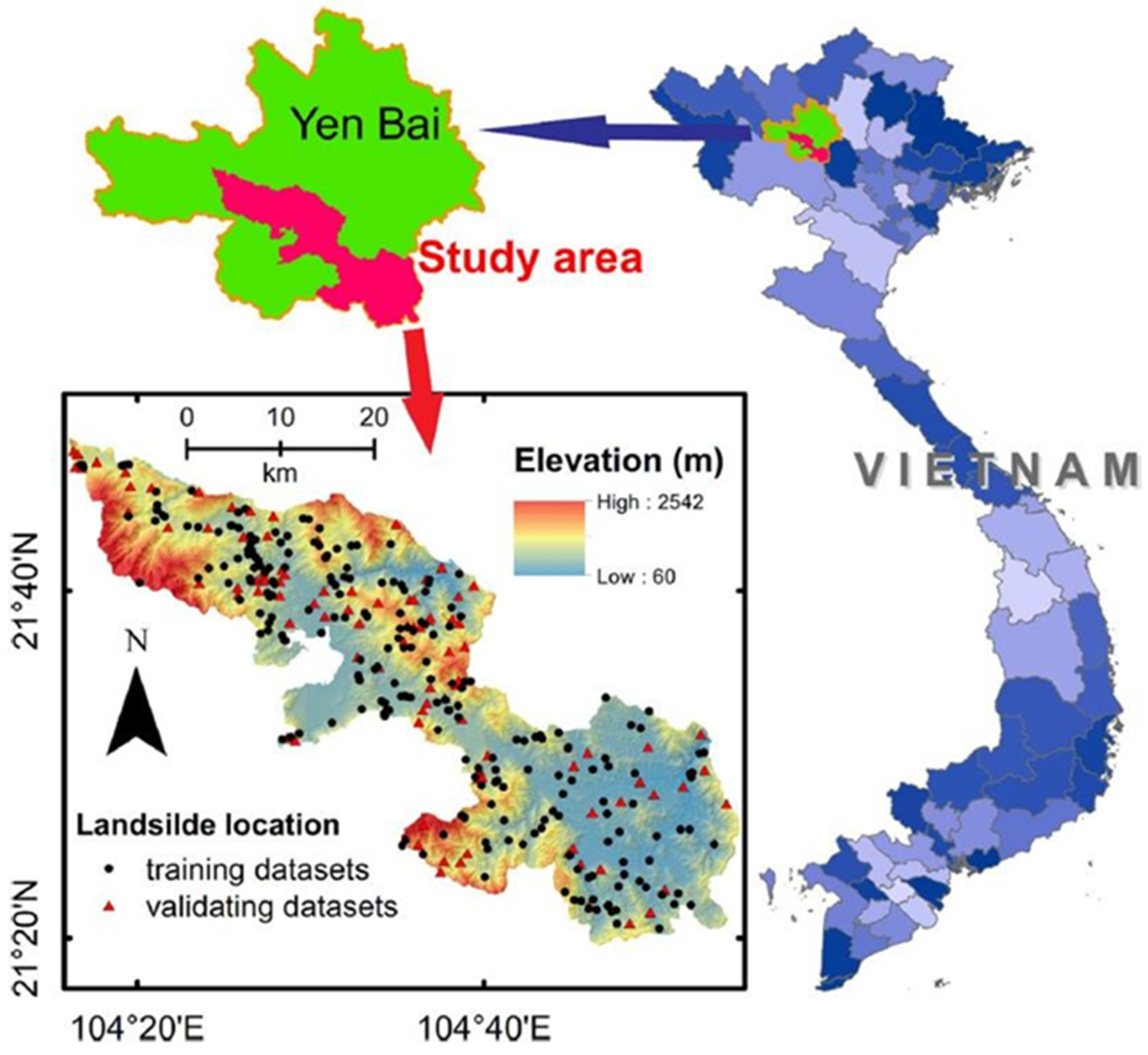
| Pham et al., 2020 [23] | Van Chan district, Yen Yen Bai Province, Vietnam | No |
| 60 m to 2542 m | 0° to 84.2° | - | - |
| WEKA software ArcGIS 10.3 | 167 landslides: 70% training; 30% testing. | AUC of Training:
| |||
| Wang et al., 2020 [24] | Zhejiang Province, China | Yes |
| −58 to 1879 m | 0° to 52.4° | 1100—2000 mm | 15 °C to 18 °C |
| GeoSOM, scikitlearn Python | 1051 landslide samples: 70% training; 30% testing. | Training accuracy:
| |||
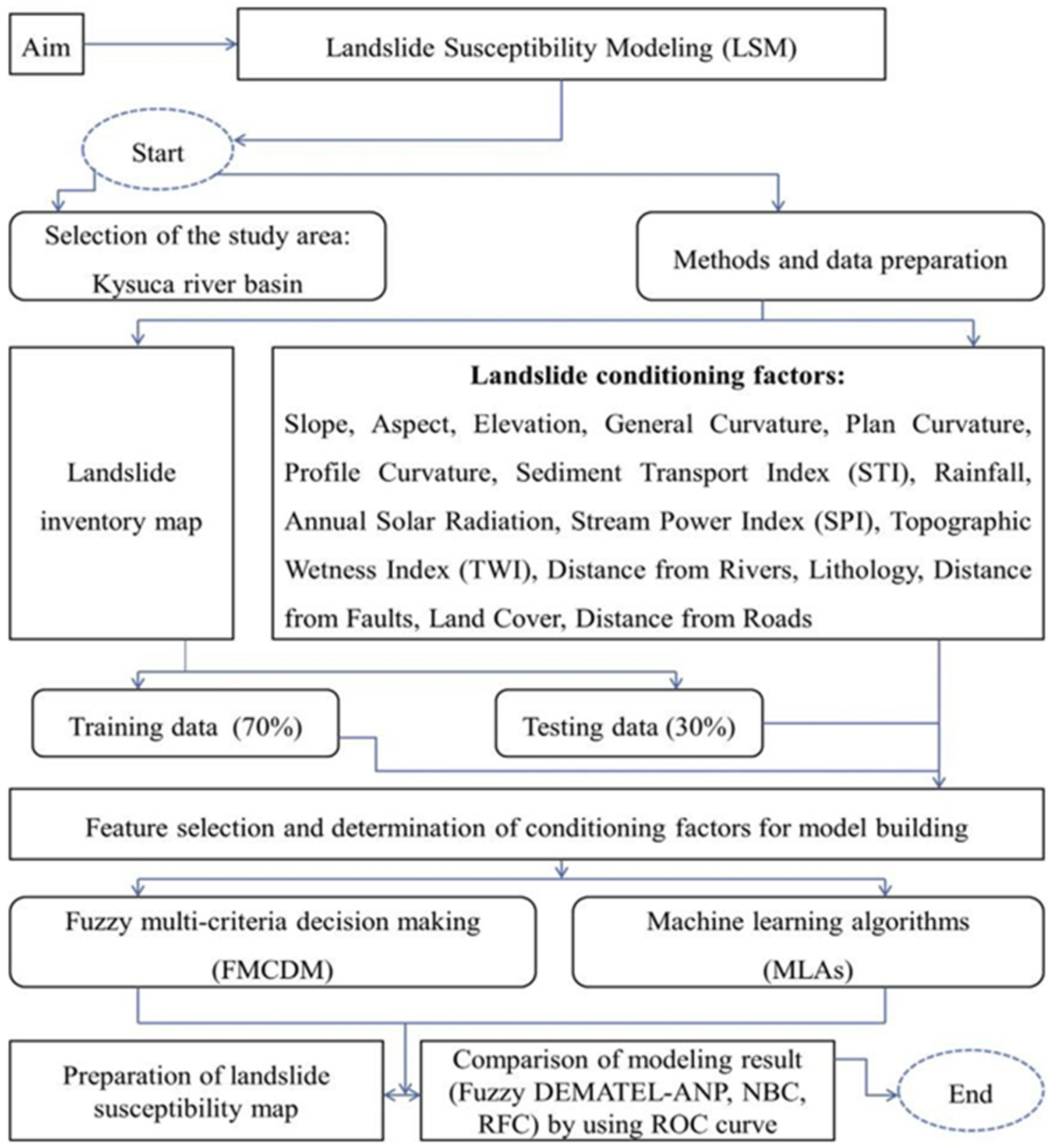
| Ali et al., 2021 [25] | Kysuca river basin, Slovakia | No |
| 326 to 1226 m | 0° to 63.14° | 800 to 1500 mm | - |
| 2000 landslide and non-landslide 70% training, 30% testing | AUC: Fuzzy DEMATEL-ANP = 0.924 RF = 0.954 NB = 0.909 | ||||
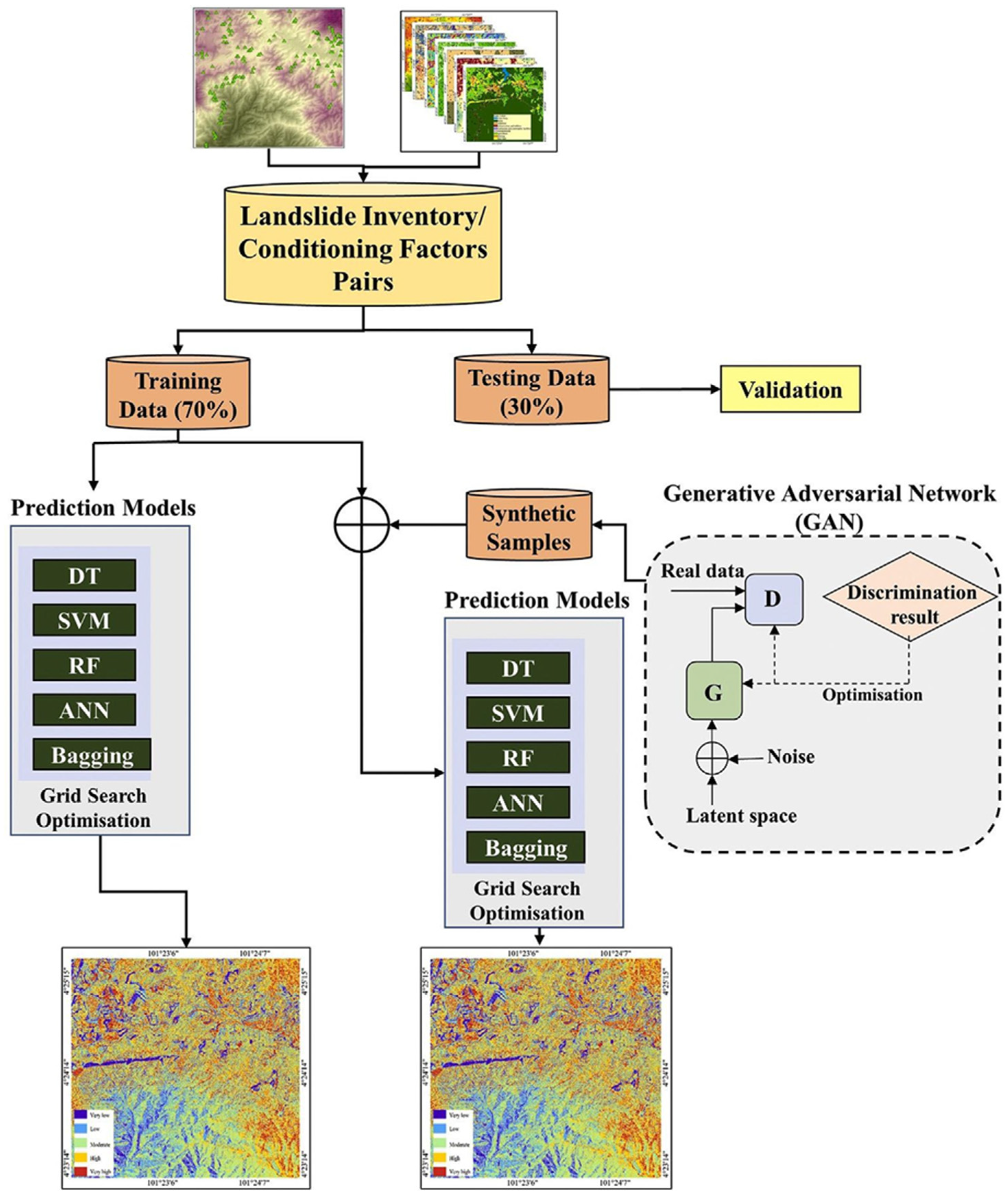
| Al-Najjar, 2021 [26] | Cameron Highlands, Pahang state, Malaysia | GAN is usedto createadditionaldata |
| 840 to 2110 m | 0° to 78.88° | - | 14 °C at night, 24 °C during the day |
| 156 landslides, 70% training, 30% testing 222 landslides 80% training, 20% testing | Before GAN method, AUROC values for training/test were: DT: 0.90/0.76 RF: 0.94/0.81 SVM: 0.86/0.85 ANN: 0.69/0.72 Bagging ensemble: 0.82/0.75 After GAN method: DT: 0.92/0.78 RF: 0.94/0.82 SVM: 0.88/0.82 ANN: 0.75/0.78 Bagging ensemble: 0.84/0.8 | ||||
| Azarafza et al., 2021 [27] | Isfahan province, Iran | Yes |
| 1211 to 2560 m | 116.9 mm on average | Min and max: 10.6 °C and 40.6 °C Average: 16.7 °C |
| ArcGIS 10.4 to produce landslide susceptibility maps | 90.9% AUC; 84.8% IRs; 0.17 MSE 0.40 RMSE 0.42 MAPE | |||||
| Liu et al., 2021 [28] | Kvam region, Norway | Yes |
| 250 to 1190 m | 500 mm | Mean temperature 3.3 °C |
| 10,197 location points 70% training, 30% testing | AUC values: RF = 0.99 GBRT = 0.99 MLP = 0.97 | |||||
| Mandal et al., 2021 [29] | Rorachu river basin of Sikkim Himalaya, India | No |
| 786 to 4062 m | 75.24° | From 510 to 2240 mm | Mean temperature 22 °C—summer, 4 °C—winter |
| - | 214 landslides 70% training, 30% testing | AUC values for training: CNN = 0.903 RF = 0.9 ANN = 0.897 Bagging = 0.881 For testing: CNN = 0.939 RF = 0.925 ANN = 0.925 Bagging = 0.915 | |||
| Ngo et al., 2021 [30] | Iran | No |
| −10 to 4500 m | 0° to 60° | 450–1800 mm in West, North 100–300 mm in East, South | - |
| ArcGIS 10.2 to generate non-landslide locations for training and testing | 4069 Landslides 70% training, 30% testing | RNN: 85% AUC CNN: 88% AUC | |||
| Gao et al., 2021 [31] | Zigui County Yichang, Hubei, China Jiuzhaigou County, Sichuan Province, China | No |
| Site-1: 80 to 1220 m Site-2: 2268 to 4114 m | Site-1: 0° to 62.69° Site-2: 0° to 67.57° | - | - |
| Python: TensorFlow | Site-1: 74 landslides Site-2: 124 landslides. Data augmentation was used to increase data amount | Site-1:
| |||
| Gameiro et al., 2021 [57] | Serra Geral, southern Brazil. | No |
| Up to 1400 m | - | - | - |
| Matlab | 1638 landslide and 1638 non- landslide data points:
| Single model global accuracy:
| |||
| Soares et al., 2022 [58] | Nova Fribugo (Train area [TA]1) and Teresopolis (TA2) in Rio de Janeiro (RJ); and Rolante (TA3) in Rio Grande do Sul (RS), Brazil | No |
| RJ: 1100 and 2000 m RS: 19 to 997 m | RJ: 1585.62 mm RS: 1700 and 2000 mm | - |
| Tensorflow 2.0 Python Deep learning framework | TA1: 497 landslides TA2: 117 landslides TA3: 110 landslides | Precision: TA1 = 0.47 TA2 = 0.5 TA3 = 0.56 | ||||
| Chen et al., 2022 [61] | 1) Fengjie County (FJ) 2) Fuling District (FL) Both in Chongqing City, China |
| 0° to 88.32° | - | - |
| Accuracy: For FJ: RF = 74.8% RL = 74.9% MAML = 72.6% For FL: RF = 77.8% RL = 81.6% MAML = 76.4% | |||||||
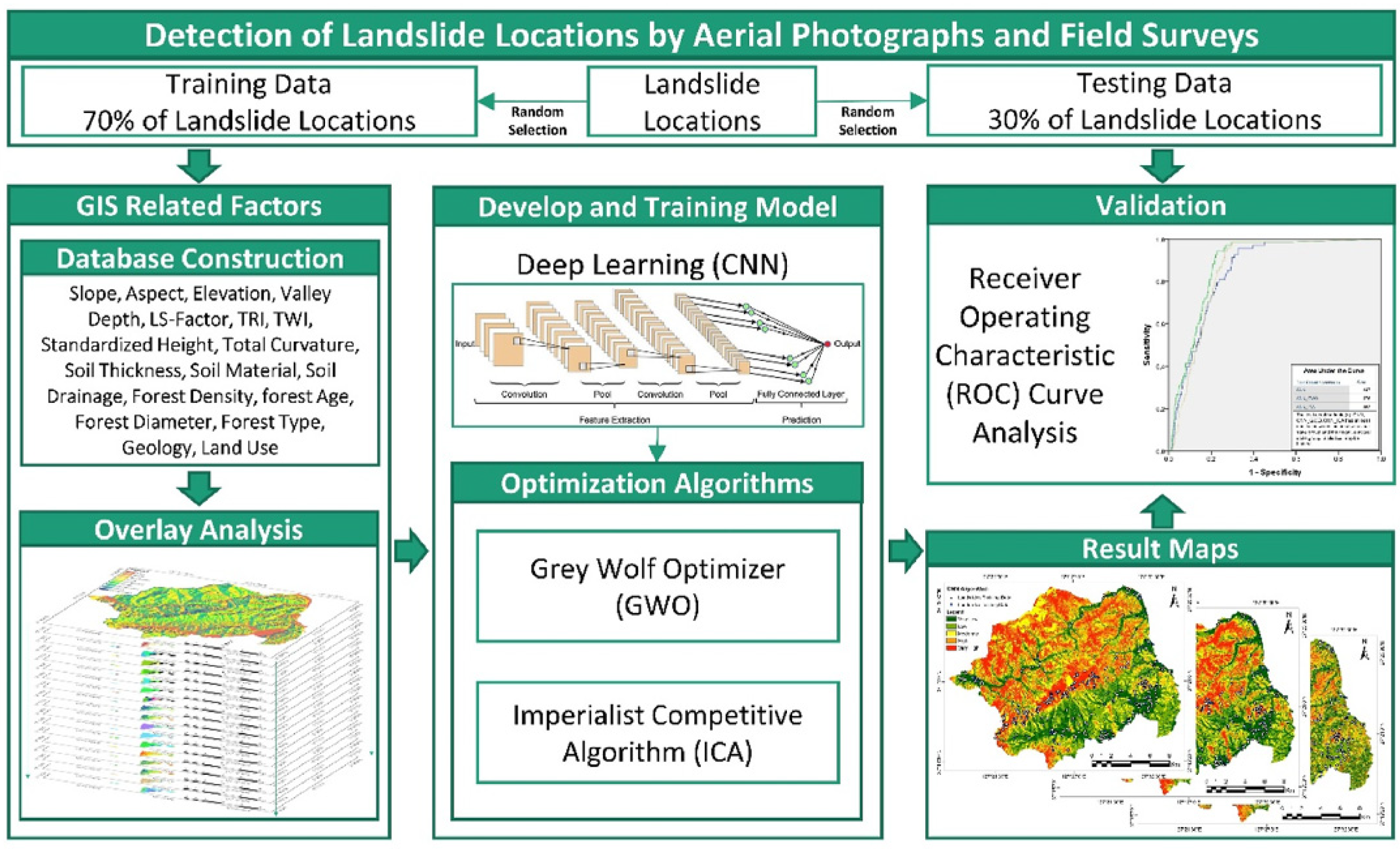
| Hakim et al., 2022 [32] | Icheon City, South Korea | Yes |
| 25 to 710 m | 0° to 76° | 1234 mm | 24 °C and 7 °C |
| 456 landslides 70% training, 30% testing | Only CNN: AUC = 0.847 RMSE = 0.12 CNN-GWO: AUC = 0.876 RMSE = 0.08 CNN-ICA: AUC = 0.852 RMSE = 0.09 | ||||
| Kainthura, 2022 [33] | Uttarkashi, India | Yes |
| 920 to 3830 m | 0° to >35° | 1902 mm | - |
| ArcGis to generate study area | 373 landslide and 181 non- landslide 75% training; 25% testing | AUC for training: HBNRS = 0.897 HBPNNRS = 0.977 HBRS = 0.995 HXGBRS = 0.996 HRFRS = 0.989 AUC for testing: HBNRS = 0.883 HBPNNRS = 0.924 HBRS = 0.894 HXGBRS = 0.937 HRFRS = 0.904 | |||
| Li et al., 2023 [34] | Wenchuan area, China | Yes |
| 763 to 5827 m | 0° to >40° | Annual rainfall ranging from 528.7–1332.2 mm | Average annual temperature: 13.5 °C–14.1 °C |
| 1147 landslides 70% training, 30% testing | AUC for training: GL-ResNet = 0.98 Res-Net = 0.97 SVM = 0.95 DBN = 0.95 GRU = 0.94 LR = 0.92 AUC for testing GL-ResNet = 0.96 Res-Net = 0.95 SVM = 0.94 DBN = 0.95 GRU = 0.94 LR = 0.92 | ||||
| Liao et al., 2022 [35] | Wushan and Wuxi, Chongqing, China | Yes |
| 0 to >2500 m | 0° to 41.54° | - | - |
| ArcGIS | 1137 landslides 70% training; 30% testing | AUC for grid size of 2000 m: RF = 0.98 SCC-RF = 0.94 RFE-RF = 0.92 SCC-RFE-RF = 0.96 | |||
| Lv et al., 2022 [36] | Zigui and Badong county, Hubei province, China | Yes |
| 80 to 2000 m | 0° to 78.419° | 1100 mm | - |
| 202 landslides 70% training, 30% testing | AUC: DBN = 0.956 CNN = 0.976 ResNet = 0.981 Stacking = 0.984 SA = 0.979 WA = 0.979 Boosting = 0.982 | ||||
| Meghanadh et al., 2022 [59] | Alaknanda river, Srinagar- Rudraprayag area, Uttarakhand state, India |
| 634 to 1764 m | 21° to 70° | - | - |
| ROC_AUC: Proposed model = 0.9072 Random forest = 0.9099 Support vector machine = 0.8992 | ||||||
| Wei et al., 2022 [37] | Yarlung Zangbo Grand Canyon region, Nyingchi, Tibet Autonomous Region | No |
| 324 to 7782 m | 0° to 89° | 605 to 1903 mm | - |
| ArcGIS, Python | 203 landslides 50% training, 50% testing | AUC: SR = 0.92 SR-ML = 0.91 | |||
| Zhang et al., 2022 [38] | Wanzhou District, Chongqing Municipality, Three Gorges Reservoir | No |
| 26 to 1006 m | 0° to 65.125° | 1132.39 to 1192.74 mm | - |
| 233 landslides 60% training, 40% testing | AUC: LR = 0.835 LightGBM = 0.89 RF = 0.844 | ||||
| Cao et al., 2023 [39] | Western Henan Province, China | No |
| 12–2387 m | 0° to 76° | 700–900 mm | 13.8°C |
| - | 256 landslides: 70% training; 30% testing. | Training AUC: RF: 1.00 XGBoost: 1.00 SVM: 0.98 LDA: 0.89 LR: 0.87 Testing AUC: XGBoost: 0.8759 RF: 0.8743 LDA: 0.8685 LR: 0.8624 SVM: 0.7666 | |||
| Chang et al., 2023 [40] | Lvliang City, Western Shanxi, China | No |
| 552–2768 m | 0° to 35° | 450–510 mm | - |
| TabNet, ArcGIS | 3476 landslides: 80% training; 20% testing. | Accuracy (%):
| |||
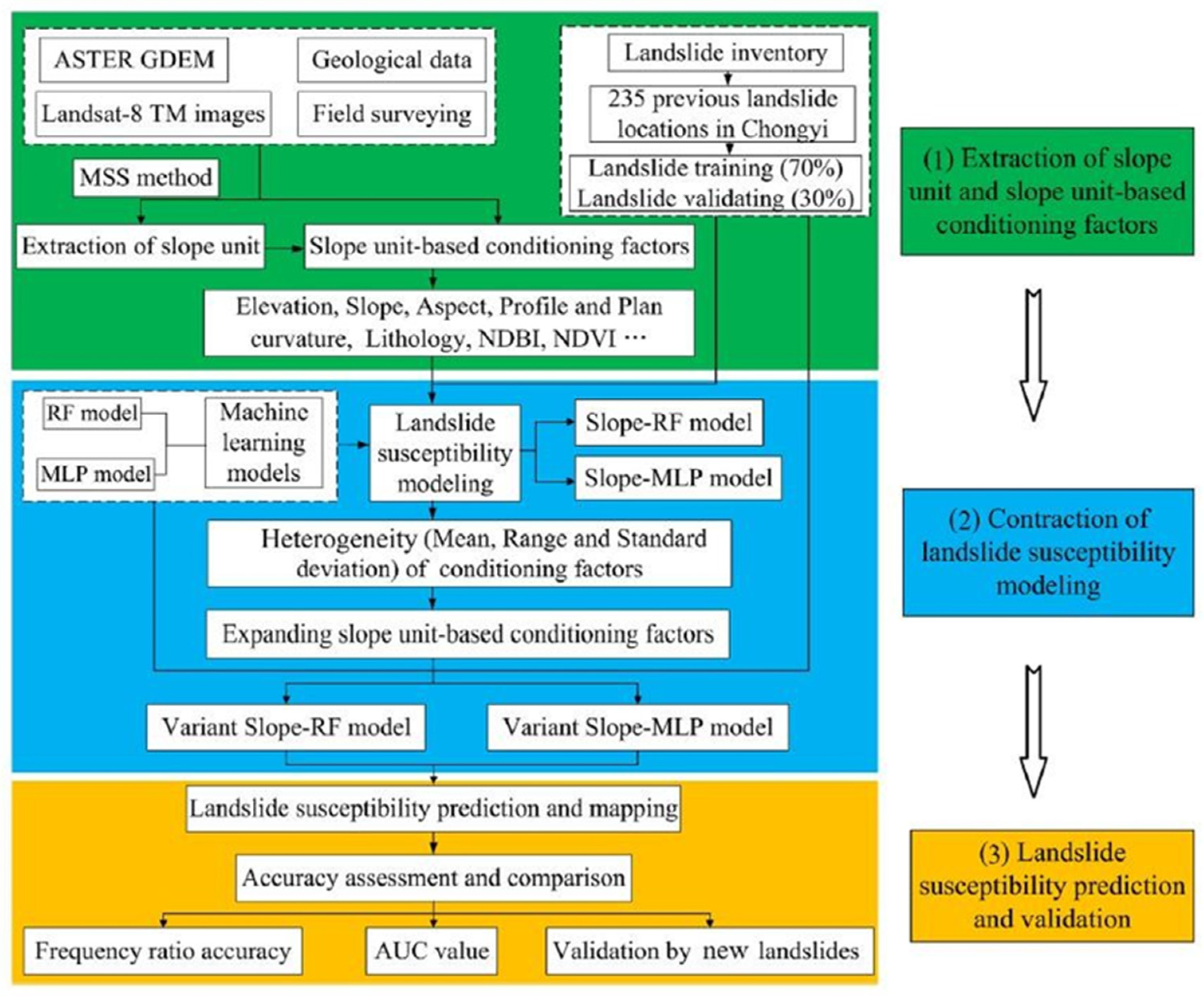
| Zhilu Chang et al., 2023 [41] | Chongyi County, China | No |
| 142–1998 m | 0°–47.8° | 1615.2 mm | - |
| - | 744 landslides: 70% training; 30% testing. | AUC of models:
| |||
| Dahal and Lombardo, 2023 [42] | Gorkha, Nepal | No |
| 500–7000 m | - | - |
| r.slopeunits; Python | 24,903 coseismic landslides: 70% training; 30% testing. | AUC performance:
| ||||
| Han et al., 2023 [43] | Wenchuan county, China | No |
| 490–5600 m | - | - | - |
| ArcGIS, Python | 1336 sample points (668 landslide, 668 non- landslide): 70% training; 30% testing. | AUC of training: KDE-MDBN: 0.978AUC of testing:
| |||
| Hong, 2023 [44] | Yongxin County, China | Yes |
| 41–1389 m | 0°–67.6° | Average—1530.7 mm | Mean—18.2 °C |
| ArcGIS, SPSS, Matlab | 728 sample points (364 landslide, 364 non- landslide): 70% training; 30% testing. | AUC of training:
| |||
| Wubiao Huang et al., 2023 [45] | Sichuan-Tibet, China | No |
| 200 to 8589 m | 0°–89.4° | Annual cumulative rainfall: 288.49 to 2288.1 mm | - |
| Python: Scikit- learn and PaddlePaddle2.0 | 1669 landslide events: 70% training; 30% testing. | AUC of models:
| |||
| Faming Huang et al., 2023 [56] | Yanchang County, China | No |
| 473–1369 m | 0°–50° | 564 mm | - |
| ArcGIS, SPSS, R | Grids size/special resolution, m:
| AUC of models with training portion of dataset:
| |||
| Mondini et al., 2023 [46] | Italy | No |
| - | - | Cumulated rainfall: 1 mm ≤ E ≤ 2070 mm | - |
| CTRL–T; Tensorflow; Python. | 2472 rainfall- induced landslides: 80% training; 20% testing. | Training and validation accuracy:
| |||
| Pradhan et al., 2023 [47] | CheongJu region, South Korea | No |
| 20–655 m | 0° to 78° | >1200 mm | - |
| - | 519 landslides: 70% training; 30% testing. | Accuracy:
| |||
| Rong, 2023 [48] | Shuicheng County, China | Yes |
| 633–2863 m | 940–1450 mm | - |
| Python, keras, scikit | 480 | AUC and accuracy of the best integrated model:
| ||||
| Saha et al., 2023 [49] | Garhwal Himalaya, India | No |
| 1500–2500 m | - | - | - |
| ArcGIS | >3000 landslide points | AUC of testing: SVM: 0.845 RF: 0.874 Bagging: 0.906 ANN: 0.887 DLNN: 0.925 | |||
| Wang and Brenning, 2023 [50] | Source: Reuleut, Indonesia Target: Palu, Indonesia. | Yes |
| Source: up to 1851 m Target: 202 to 2331 m | Mean slope: Source: 13.2°. Target: 24.6° | - |
| R software | 507 landslides samples in source area 320 landslides in target area | pAUROC: 0.096 | ||||
| Yang et al., 2023 [51] | Anhua County, China | No |
| 202–2331 m | 0° to 71.7° | 986–2440 mm | Mean—16.2 °C |
| ArcGIS | 492 landslide samples | AUC of models:
| |||
| Zeng et al., 2023 [52] | Dazhou Town, China | Yes |
| >146 m <660 m | 0° to 74° | 1188.7 mm | - |
| ArcGIS Python | 78,529 landslide units. 78,529 non-landslide units. 70% training; 30% testing. | Stacking based RF- XGBoost—AUC 0.955 (the best model) | |||
| Zhiyong, 2023 [53] | Zigui Basin, China | Yes |
| <2008 m | 0° to 86° | 1250 mm | 13 °C |
| Python | 520 training set, 113 test set | AUC of models:
| |||
| Hong, 2024 [54] | Yongxin, China | Yes |
| 41–1389 m | 79% of area has slope less than 24° | 1530.7 mm | 18.2 °C |
| Matlab Weka ArcGIS | 364 landslide point data 364 non- landslide point data | AUC of training:
| |||
| Sharma et al., 2024 [55] | Political boundary of India | Yes |
| - | - |
| The final dataset had 1,282,908 data points with 641,454 of landslide and non-landslide points. The testing data contains 15,000 landslide points and 300,000 non- landslide points. | Ensemble—ROC AUC—0.989 | ||||||
References
- Li, B.V.; Jenkins, C.N.; Xu, W. Strategic Protection of Landslide Vulnerable Mountains for Biodiversity Conservation under Land-Cover and Climate Change Impacts. Proc. Natl. Acad. Sci. USA 2022, 119, e2113416118. [Google Scholar] [CrossRef] [PubMed]
- Ozturk, U.; Bozzolan, E.; Holcombe, E.A.; Shukla, R.; Pianosi, F.; Wagener, T. How Climate Change and Unplanned Urban Sprawl Bring More Landslides. Nature 2022, 608, 262–265. [Google Scholar] [CrossRef] [PubMed]
- Pánek, T. Landslides and Quaternary Climate Changes—The State of the Art. Earth-Sci. Rev. 2019, 196, 102871. [Google Scholar] [CrossRef]
- Jakob, M. Landslides in a Changing Climate. In Landslide Hazards, Risks, and Disasters; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Palmer, J. A Slippery Slope: Could Climate Change Lead to More Landslides? Eos 2020, 101. [Google Scholar] [CrossRef]
- Guzzetti, F.; Gariano, S.L.; Peruccacci, S.; Brunetti, M.T.; Melillo, M. Rainfall and Landslide Initiation. In Rainfall: Modeling, Measurement and Applications; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
- Ravanel, L.; Magnin, F.; Deline, P. Impacts of the 2003 and 2015 Summer Heatwaves on Permafrost-Affected Rock-Walls in the Mont Blanc Massif. Sci. Total Environ. 2017, 609, 132–143. [Google Scholar] [CrossRef]
- Rohan, T.; Shelef, E.; Mirus, B.; Coleman, T. Prolonged Influence of Urbanization on Landslide Susceptibility. Landslides 2023, 20, 1433–1447. [Google Scholar] [CrossRef]
- Li, G.; Lei, Y.; Yao, H.; Wu, S.; Ge, J. The Influence of Land Urbanization on Landslides: An Empirical Estimation Based on Chinese Provincial Panel Data. Sci. Total Environ. 2017, 595, 681–690. [Google Scholar] [CrossRef] [PubMed]
- Dille, A.; Dewitte, O.; Handwerger, A.L.; d’Oreye, N.; Derauw, D.; Ganza Bamulezi, G.; Ilombe Mawe, G.; Michellier, C.; Moeyersons, J.; Monsieurs, E.; et al. Acceleration of a Large Deep-Seated Tropical Landslide Due to Urbanization Feedbacks. Nat. Geosci. 2022, 15, 1048–1055. [Google Scholar] [CrossRef]
- Strom, A.; Abdrakhmatov, K. Bedrock Landslide Types and Classification Systems. In Rockslides and Rock Avalanches of Central Asia; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar]
- Highland, L.M.; Bobrowsky, P. The Landslide Handbook—A Guide to Understanding Landslides; US Geological Survey: Reston, VI, USA, 2008. [Google Scholar]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine Learning Methods for Landslide Susceptibility Studies: A Comparative Overview of Algorithm Performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Adam Voiland, T.S. Dalia Kirschbaum A Global View of Landslide Susceptibility. Available online: https://earthobservatory.nasa.gov/images/89937/a-global-view-of-landslide-susceptibility (accessed on 6 August 2024).
- Pourghasemi, H.R.; Teimoori Yansari, Z.; Panagos, P.; Pradhan, B. Analysis and Evaluation of Landslide Susceptibility: A Review on Articles Published during 2005–2016 (Periods of 2005–2012 and 2013–2016). Arab. J. Geosci. 2018, 11, 193. [Google Scholar] [CrossRef]
- Achour, Y.; Pourghasemi, H.R. How Do Machine Learning Techniques Help in Increasing Accuracy of Landslide Susceptibility Maps? Geosci. Front. 2020, 11, 871–883. [Google Scholar] [CrossRef]
- Adnan, M.S.G.; Rahman, M.S.; Ahmed, N.; Ahmed, B.; Rabbi, M.F.; Rahman, R.M. Improving Spatial Agreement in Machine Learning-Based Landslide Susceptibility Mapping. Remote Sens. 2020, 12, 3347. [Google Scholar] [CrossRef]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Phong, T.V.; Ly, H.B.; Le, T.T.; Trinh, P.T.; et al. A Spatially Explicit Deep Learning Neural Network Model for the Prediction of Landslide Susceptibility. Catena 2020, 188, 104451. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.H.; Li, S.; Guo, Z. Comparisons of Heuristic, General Statistical and Machine Learning Models for Landslide Susceptibility Prediction and Mapping. Catena 2020, 191, 104580. [Google Scholar] [CrossRef]
- Peethambaran, B.; Anbalagan, R.; Kanungo, D.P.; Goswami, A.; Shihabudheen, K.V. A Comparative Evaluation of Supervised Machine Learning Algorithms for Township Level Landslide Susceptibility Zonation in Parts of Indian Himalayas. Catena 2020, 195, 104751. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Lee, S. Application of Convolutional Neural Networks Featuring Bayesian Optimization for Landslide Susceptibility Assessment. Catena 2020, 186, 104249. [Google Scholar] [CrossRef]
- Bui, D.T.; Tsangaratos, P.; Nguyen, V.T.; Liem, N.V.; Trinh, P.T. Comparing the Prediction Performance of a Deep Learning Neural Network Model with Conventional Machine Learning Models in Landslide Susceptibility Assessment. Catena 2020, 188, 104426. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Qi, C.; Phong, T.V.; Dou, J.; Ho, L.S.; Le, H.V.; Prakash, I. Coupling RBF Neural Network with Ensemble Learning Techniques for Landslide Susceptibility Mapping. Catena 2020, 195, 104805. [Google Scholar] [CrossRef]
- Wang, Y.; Feng, L.; Li, S.; Ren, F.; Du, Q. A Hybrid Model Considering Spatial Heterogeneity for Landslide Susceptibility Mapping in Zhejiang Province, China. Catena 2020, 188, 104425. [Google Scholar] [CrossRef]
- Ali, S.A.; Parvin, F.; Vojteková, J.; Costache, R.; Linh, N.T.T.; Pham, Q.B.; Vojtek, M.; Gigović, L.; Ahmad, A.; Ghorbani, M.A. GIS-Based Landslide Susceptibility Modeling: A Comparison between Fuzzy Multi-Criteria and Machine Learning Algorithms. Geosci. Front. 2021, 12, 857–876. [Google Scholar] [CrossRef]
- Al-Najjar, H.A.H.; Pradhan, B. Spatial Landslide Susceptibility Assessment Using Machine Learning Techniques Assisted by Additional Data Created with Generative Adversarial Networks. Geosci. Front. 2021, 12, 625–637. [Google Scholar] [CrossRef]
- Azarafza, M.; Azarafza, M.; Akgün, H.; Atkinson, P.M.; Derakhshani, R. Deep Learning-Based Landslide Susceptibility Mapping. Sci. Rep. 2021, 11, 24112. [Google Scholar] [CrossRef]
- Liu, Z.; Gilbert, G.; Cepeda, J.M.; Lysdahl, A.O.K.; Piciullo, L.; Hefre, H.; Lacasse, S. Modelling of Shallow Landslides with Machine Learning Algorithms. Geosci. Front. 2021, 12, 385–393. [Google Scholar] [CrossRef]
- Mandal, K.; Saha, S.; Mandal, S. Applying Deep Learning and Benchmark Machine Learning Algorithms for Landslide Susceptibility Modelling in Rorachu River Basin of Sikkim Himalaya, India. Geosci. Front. 2021, 12, 101203. [Google Scholar] [CrossRef]
- Thi Ngo, P.T.; Panahi, M.; Khosravi, K.; Ghorbanzadeh, O.; Kariminejad, N.; Cerda, A.; Lee, S. Evaluation of Deep Learning Algorithms for National Scale Landslide Susceptibility Mapping of Iran. Geosci. Front. 2021, 12, 505–519. [Google Scholar] [CrossRef]
- Gao, X.; Chen, T.; Niu, R.; Plaza, A. Recognition and Mapping of Landslide Using a Fully Convolutional DenseNet and Influencing Factors. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7881–7894. [Google Scholar] [CrossRef]
- Hakim, W.L.; Rezaie, F.; Nur, A.S.; Panahi, M.; Khosravi, K.; Lee, C.W.; Lee, S. Convolutional Neural Network (CNN) with Metaheuristic Optimization Algorithms for Landslide Susceptibility Mapping in Icheon, South Korea. J. Environ. Manag. 2022, 305, 114367. [Google Scholar] [CrossRef]
- Kainthura, P.; Sharma, N. Hybrid Machine Learning Approach for Landslide Prediction, Uttarakhand, India. Sci. Rep. 2022, 12, 20101. [Google Scholar] [CrossRef]
- Li, Y.; Yang, J.; Han, Z.; Li, J.; Wang, W.; Chen, N.; Hu, G.; Huang, J. An Ensemble Deep-Learning Framework for Landslide Susceptibility Assessment Using Multiple Blocks: A Case Study of Wenchuan Area, China. Geomat. Nat. Hazards Risk 2023, 14, 2221771. [Google Scholar] [CrossRef]
- Liao, M.; Wen, H.; Yang, L. Identifying the Essential Conditioning Factors of Landslide Susceptibility Models under Different Grid Resolutions Using Hybrid Machine Learning: A Case of Wushan and Wuxi Counties, China. Catena 2022, 217, 106428. [Google Scholar] [CrossRef]
- Lv, L.; Chen, T.; Dou, J.; Plaza, A. A Hybrid Ensemble-Based Deep-Learning Framework for Landslide Susceptibility Mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 108, 102713. [Google Scholar] [CrossRef]
- Wei, R.; Ye, C.; Sui, T.; Ge, Y.; Li, Y.; Li, J. Combining Spatial Response Features and Machine Learning Classifiers for Landslide Susceptibility Mapping. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102681. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Y.; Xu, S.; He, Y.; Li, Z.; Yu, X.; Liang, Y.; Wu, W.; Wang, Y. Combining a Class-Weighted Algorithm and Machine Learning Models in Landslide Susceptibility Mapping: A Case Study of Wanzhou Section of the Three Gorges Reservoir, China. Comput. Geosci. 2022, 158, 104966. [Google Scholar] [CrossRef]
- Cao, W.; Fu, Y.; Dong, Q.; Wang, H.; Ren, Y.; Li, Z.; Du, Y. Landslide Susceptibility Assessment in Western Henan Province Based on a Comparison of Conventional and Ensemble Machine Learning. China Geol. 2023, 6, 409–419. [Google Scholar] [CrossRef]
- Chang, L.; Xing, G.; Yin, H.; Fan, L.; Zhang, R.; Zhao, N.; Huang, F.; Ma, J. Landslide Susceptibility Evaluation and Interpretability Analysis of Typical Loess Areas Based on Deep Learning. Nat. Hazards Res. 2023, 3, 155–169. [Google Scholar] [CrossRef]
- Chang, Z.; Catani, F.; Huang, F.; Liu, G.; Meena, S.R.; Huang, J.; Zhou, C. Landslide Susceptibility Prediction Using Slope Unit-Based Machine Learning Models Considering the Heterogeneity of Conditioning Factors. J. Rock Mech. Geotech. Eng. 2023, 15, 1127–1143. [Google Scholar] [CrossRef]
- Dahal, A.; Lombardo, L. Explainable Artificial Intelligence in Geoscience: A Glimpse into the Future of Landslide Susceptibility Modeling. Comput. Geosci. 2023, 176, 105364. [Google Scholar] [CrossRef]
- Han, S.; Liu, B.; Fan, X.; Feng, T.; Yang, J.J.; Zhou, Z.; Gong, H.; Luo, J. A New Approach for Landslide Susceptibility Assessments Based on KDE-MDBN: A Case Study from Mountainous Regions Impacted by the Wenchuan Earthquake, China. Environ. Model. Softw. 2023, 167, 105759. [Google Scholar] [CrossRef]
- Hong, H. Assessing Landslide Susceptibility Based on Hybrid Best-First Decision Tree with Ensemble Learning Model. Ecol. Indic. 2023, 147, 109968. [Google Scholar] [CrossRef]
- Huang, W.; Ding, M.; Li, Z.; Yu, J.; Ge, D.; Liu, Q.; Yang, J. Landslide Susceptibility Mapping and Dynamic Response along the Sichuan-Tibet Transportation Corridor Using Deep Learning Algorithms. Catena 2023, 222, 106866. [Google Scholar] [CrossRef]
- Mondini, A.C.; Guzzetti, F.; Melillo, M. Deep Learning Forecast of Rainfall-Induced Shallow Landslides. Nat. Commun. 2023, 14, 2466. [Google Scholar] [CrossRef]
- Pradhan, B.; Dikshit, A.; Lee, S.; Kim, H. An Explainable AI (XAI) Model for Landslide Susceptibility Modeling. Appl. Soft Comput. 2023, 142, 110324. [Google Scholar] [CrossRef]
- Rong, G.; Li, K.; Tong, Z.; Liu, X.; Zhang, J.; Zhang, Y.; Li, T. Population Amount Risk Assessment of Extreme Precipitation-Induced Landslides Based on Integrated Machine Learning Model and Scenario Simulation. Geosci. Front. 2023, 14, 101541. [Google Scholar] [CrossRef]
- Saha, S.; Majumdar, P.; Bera, B. Deep Learning and Benchmark Machine Learning Based Landslide Susceptibility Investigation, Garhwal Himalaya (India). Quat. Sci. Adv. 2023, 10, 100075. [Google Scholar] [CrossRef]
- Wang, Z.; Brenning, A. Unsupervised Active–Transfer Learning for Automated Landslide Mapping. Comput. Geosci. 2023, 181, 105457. [Google Scholar] [CrossRef]
- Yang, C.; Liu, L.L.; Huang, F.; Huang, L.; Wang, X.M. Machine Learning-Based Landslide Susceptibility Assessment with Optimized Ratio of Landslide to Non-Landslide Samples. Gondwana Res. 2023, 123, 198–216. [Google Scholar] [CrossRef]
- Zeng, T.; Wu, L.; Peduto, D.; Glade, T.; Hayakawa, Y.S.; Yin, K. Ensemble Learning Framework for Landslide Susceptibility Mapping: Different Basic Classifier and Ensemble Strategy. Geosci. Front. 2023, 14, 101645. [Google Scholar] [CrossRef]
- Zhiyong, F.; Changdong, L.; Wenmin, Y. Landslide Susceptibility Assessment through TrAdaBoost Transfer Learning Models Using Two Landslide Inventories. Catena 2023, 222, 106799. [Google Scholar] [CrossRef]
- Hong, H. Landslide Susceptibility Assessment Using Locally Weighted Learning Integrated with Machine Learning Algorithms. Expert Syst. Appl. 2024, 237, 121678. [Google Scholar] [CrossRef]
- Sharma, N.; Saharia, M.; Ramana, G.V. High Resolution Landslide Susceptibility Mapping Using Ensemble Machine Learning and Geospatial Big Data. Catena 2024, 235, 107653. [Google Scholar] [CrossRef]
- Huang, F.; Teng, Z.; Guo, Z.; Catani, F.; Huang, J. Uncertainties of Landslide Susceptibility Prediction: Influences of Different Spatial Resolutions, Machine Learning Models and Proportions of Training and Testing Dataset. Rock Mech. Bull. 2023, 2, 100028. [Google Scholar] [CrossRef]
- Gameiro, S.; de Oliveira, G.G.; Guasselli, L.A. The Influence of Sampling on Landslide Susceptibility Mapping Using Artificial Neural Networks. Geocarto Int. 2022, 38, 1–23. [Google Scholar] [CrossRef]
- Soares, L.P.; Dias, H.C.; Garcia, G.P.B.; Grohmann, C.H. Landslide Segmentation with Deep Learning: Evaluating Model Generalization in Rainfall-Induced Landslides in Brazil. Remote Sens. 2022, 14, 2237. [Google Scholar] [CrossRef]
- Meghanadh, D.; Kumar Maurya, V.; Tiwari, A.; Dwivedi, R. A Multi-Criteria Landslide Susceptibility Mapping Using Deep Multi-Layer Perceptron Network: A Case Study of Srinagar-Rudraprayag Region (India). Adv. Space Res. 2022, 69, 1883–1893. [Google Scholar] [CrossRef]
- Roback, K.; Clark, M.K.; West, A.J.; Zekkos, D.; Li, G.; Gallen, S.F.; Champlain, D.; W, G.J. Map Data of Landslides Triggered by the 25 April 2015 Mw 7.8 Gorkha, Nepal Earthquake: US Geological Survey Data Release. ScienceBase-Catalog 2017. [Google Scholar]
- Chen, L.; Ding, Y.; Pirasteh, S.; Hu, H.; Zhu, Q.; Ge, X.; Zeng, H.; Yu, H.; Shang, Q.; Song, Y. Meta-Learning an Intermediate Representation for Few-Shot Prediction of Landslide Susceptibility in Large Areas. Int. J. Appl. Earth Obs. Geoinf. 2022, 110, 102807. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kudaibergenov, M.; Nurakynov, S.; Iskakov, B.; Iskaliyeva, G.; Maksum, Y.; Orynbassarova, E.; Akhmetov, B.; Sydyk, N. Application of Artificial Intelligence in Landslide Susceptibility Assessment: Review of Recent Progress. Remote Sens. 2025, 17, 34. https://doi.org/10.3390/rs17010034
Kudaibergenov M, Nurakynov S, Iskakov B, Iskaliyeva G, Maksum Y, Orynbassarova E, Akhmetov B, Sydyk N. Application of Artificial Intelligence in Landslide Susceptibility Assessment: Review of Recent Progress. Remote Sensing. 2025; 17(1):34. https://doi.org/10.3390/rs17010034
Chicago/Turabian StyleKudaibergenov, Muratbek, Serik Nurakynov, Berik Iskakov, Gulnara Iskaliyeva, Yelaman Maksum, Elmira Orynbassarova, Bakytzhan Akhmetov, and Nurmakhambet Sydyk. 2025. "Application of Artificial Intelligence in Landslide Susceptibility Assessment: Review of Recent Progress" Remote Sensing 17, no. 1: 34. https://doi.org/10.3390/rs17010034
APA StyleKudaibergenov, M., Nurakynov, S., Iskakov, B., Iskaliyeva, G., Maksum, Y., Orynbassarova, E., Akhmetov, B., & Sydyk, N. (2025). Application of Artificial Intelligence in Landslide Susceptibility Assessment: Review of Recent Progress. Remote Sensing, 17(1), 34. https://doi.org/10.3390/rs17010034







