Dynamic Calibration Method of Multichannel Amplitude and Phase Consistency in Meteor Radar
Abstract
:1. Introduction
2. Methods
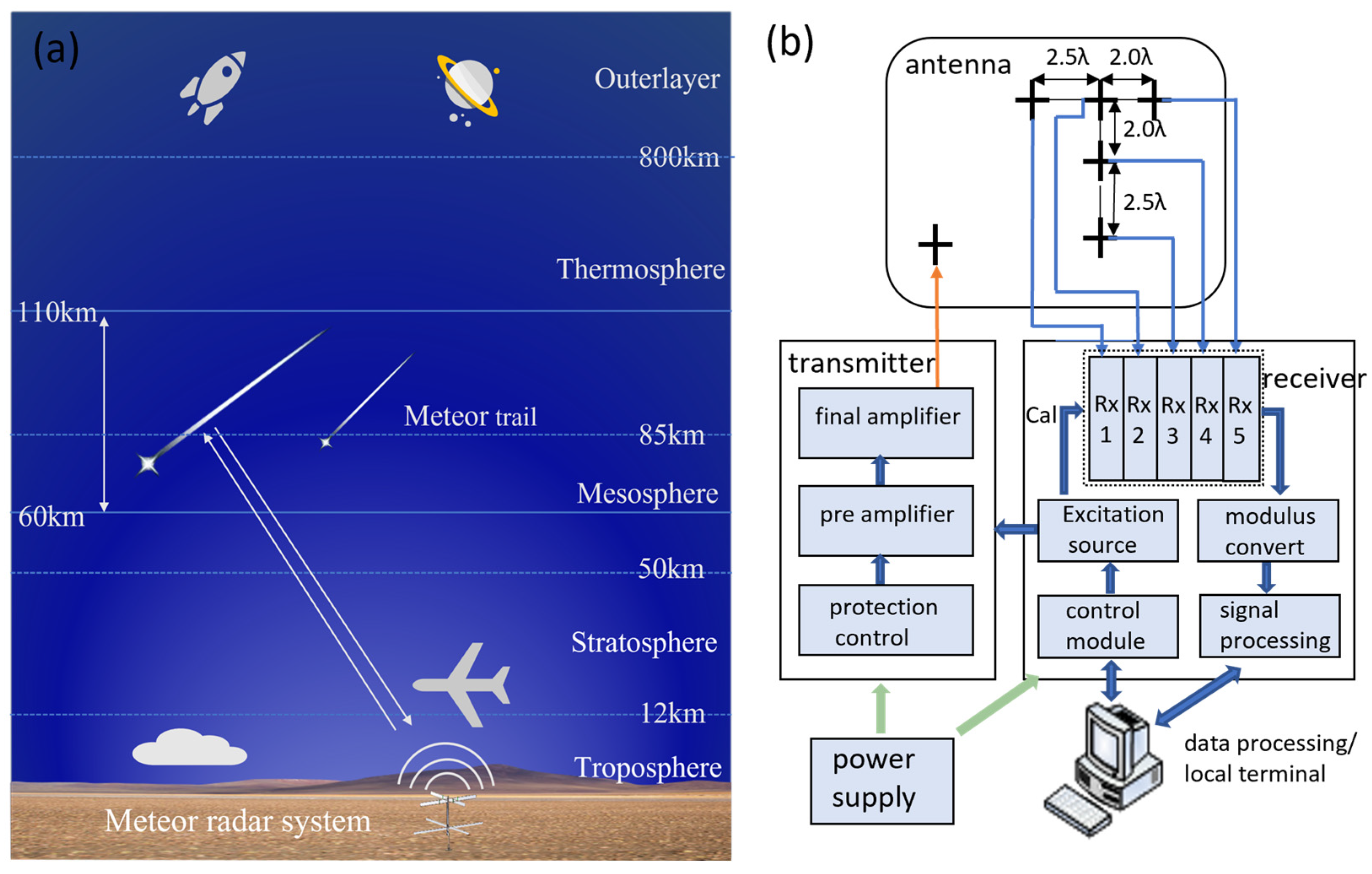
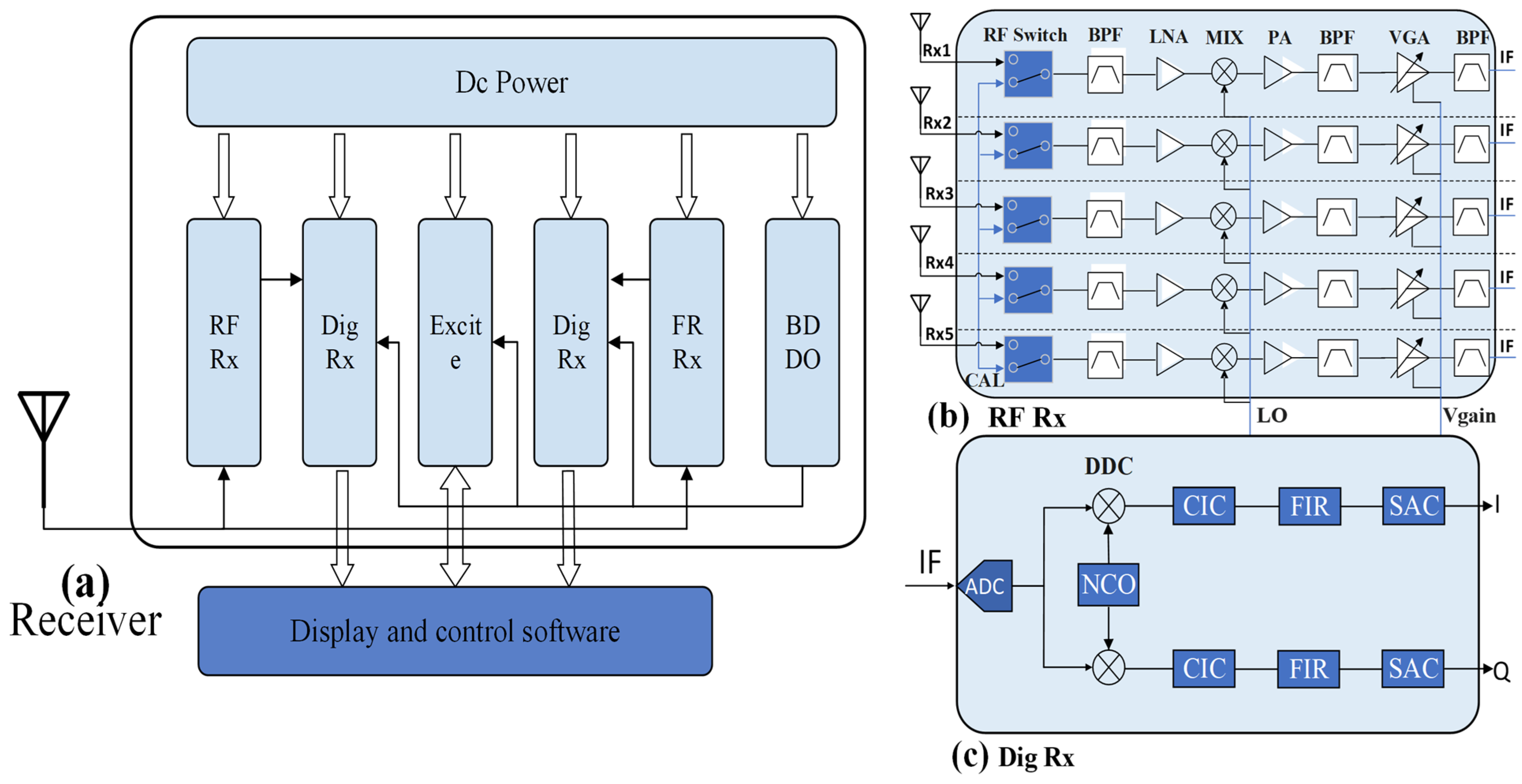
2.1. System Composition
2.2. Calibration Hardware Circuit Design
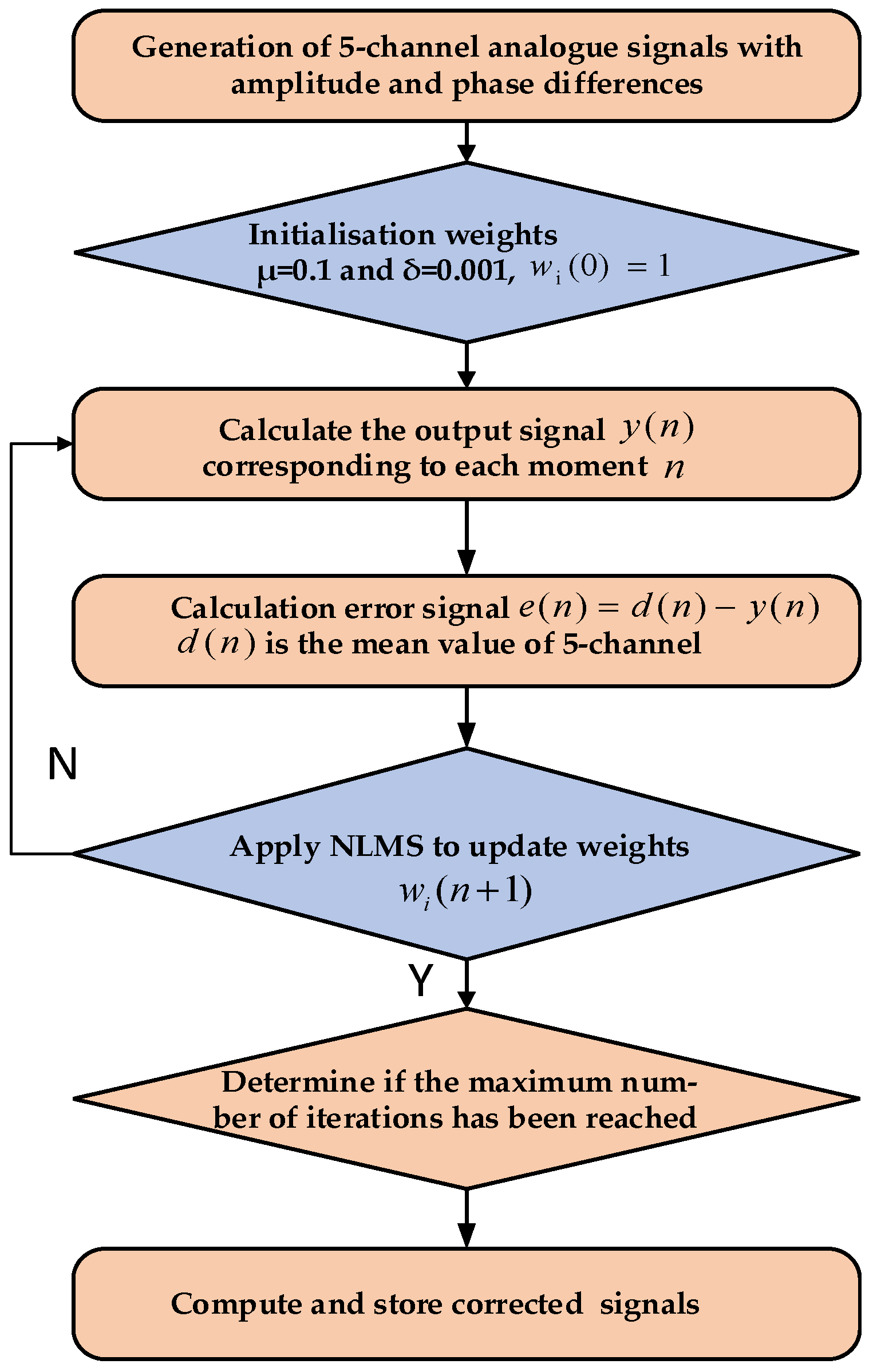
2.3. NLMS and Correlation Calibration Algorithms
- Collect one second of echo data to obtain the raw I/Q waveform data of the A and B codes (complementary code sequences) for the five channels;
- Under the condition of a pulse repetition frequency of 430 Hz, extract 6000 data points;
- Perform a sliding correlation algorithm on the extracted data. The sliding window and sliding correlation calculation formula is as follows:
- 4.
- Calculate the amplitude and phase values of the echo signals corresponding to each channel point index ;
- 5.
- Use the mean value of five channels as the calibration reference and calculate the initial amplitude and phase calibration coefficient for each channel at ;
- 6.
- Set the initial value of step-size and ;
- 7.
- Obtain the current input signal ;
- 8.
- Compute the filter output as Formula (3);
- 9.
- Calculate the error as Formula (4), the target value is ;
- 10.
- Update the weights of each channel according to the NLMS algorithm as Formula (6);
- 11.
- Set the maximum number of iterations to 1000;
- 12.
- Repeat steps 7 to 10 until the error criterion is met or the maximum number of iterations is reached;
- 13.
- For the received five channels of meteor data, perform the calibration by multiplying the complex calibration coefficients, and separately calculate the I and Q signals for each channel. The formula below shows the calibration coefficients obtained through the NLMS algorithm for each channel;
3. Simulation
4. Application in Meteor Radar
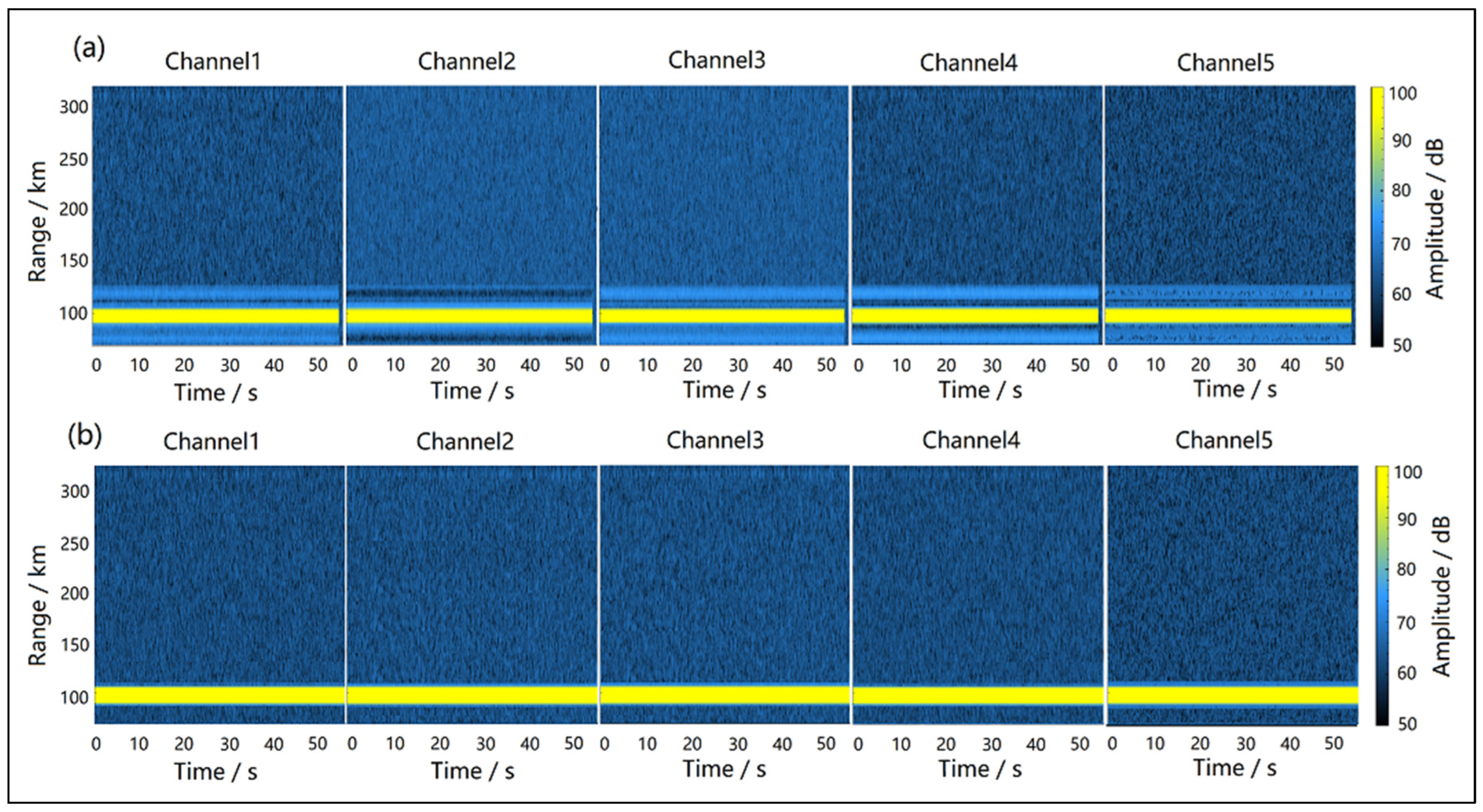
4.1. Calibration Effect on Meteor Echo Image
4.2. Calibration Effect on Pulse Compression
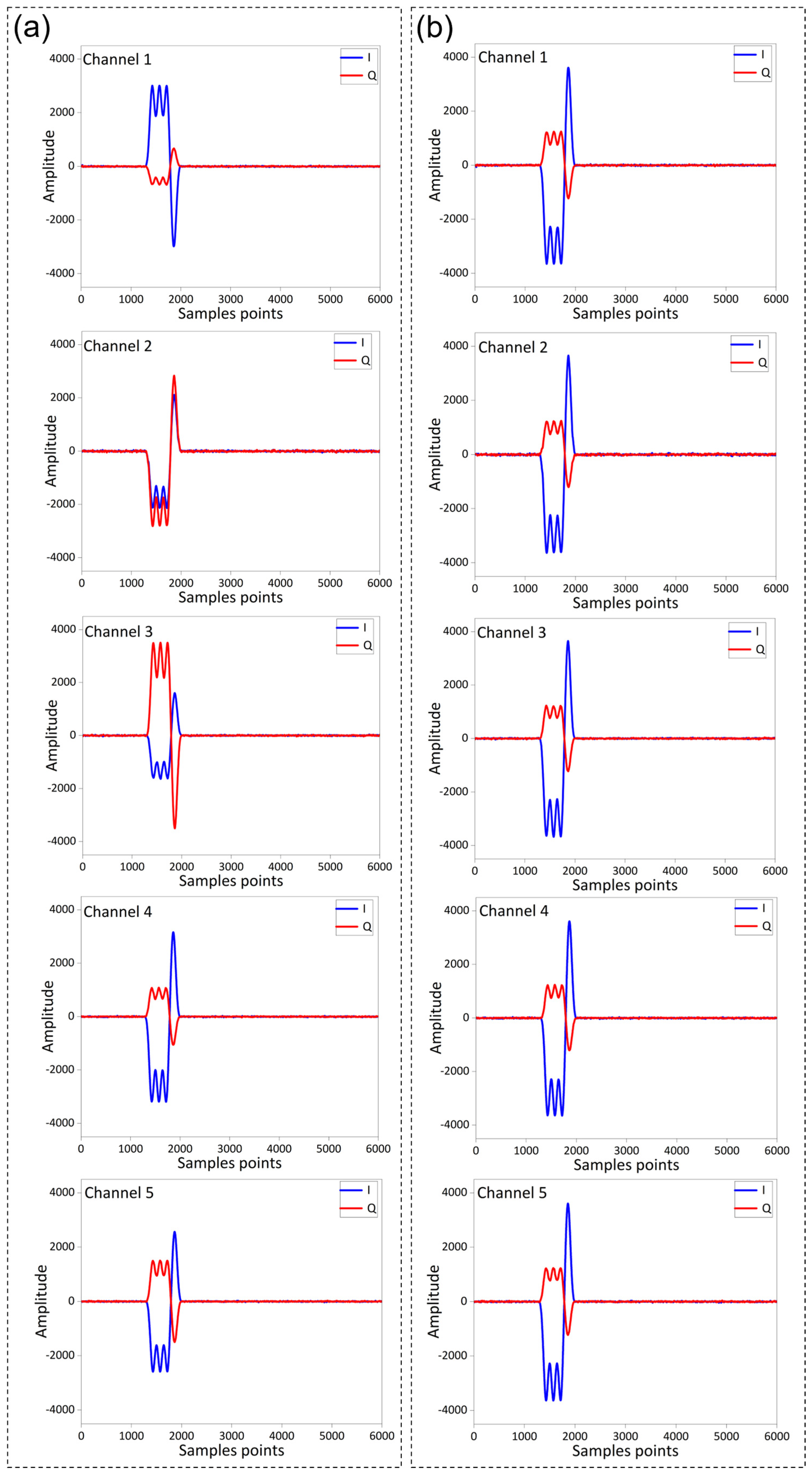
4.3. Calibration Effect on Signal Waveforms
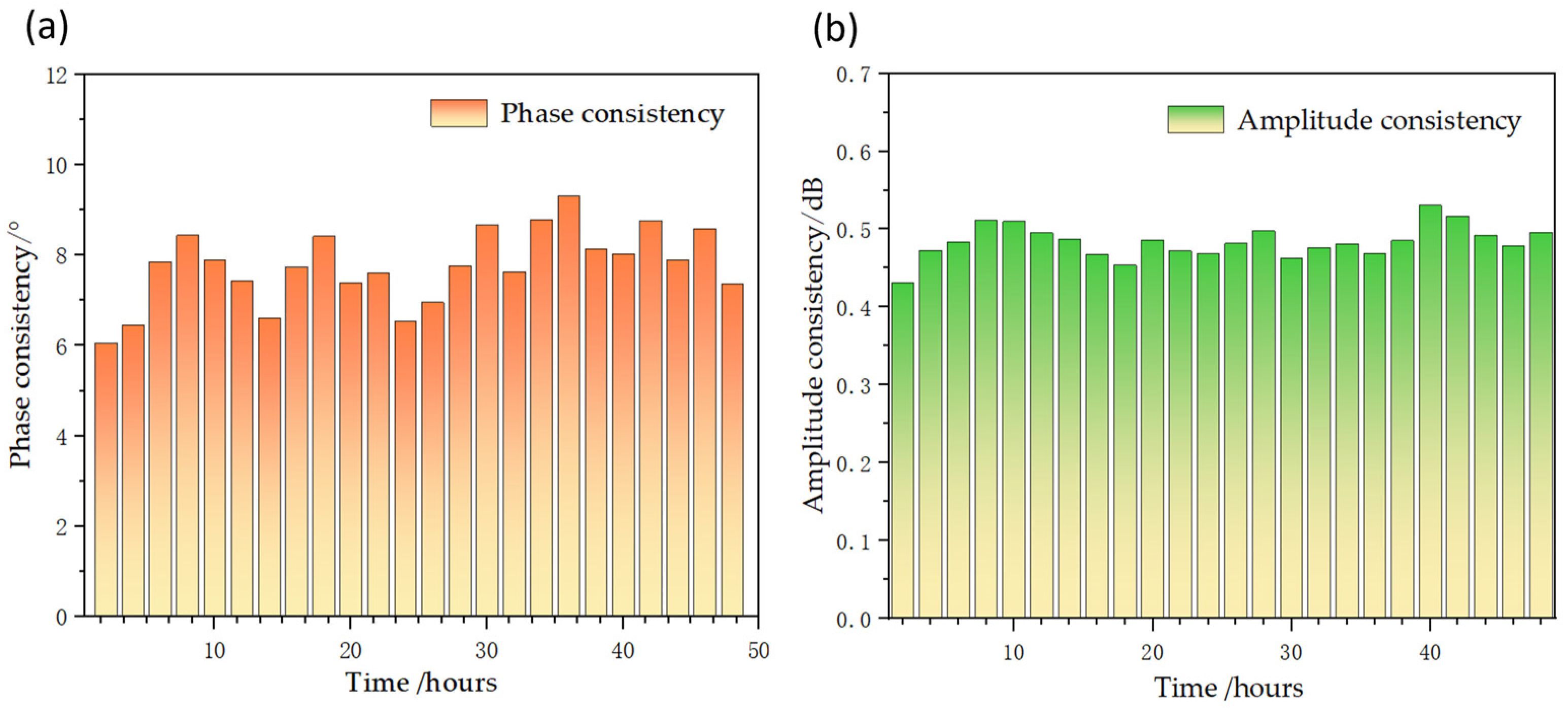
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hao, X.; Ma, Y.; Ding, Z.; Wang, L.; Li, N.; Chen, J. Influence of Meteor Count on Wind Field Retrieved by All-Sky Meteor Radar. Atmosphere 2023, 14, 519. [Google Scholar] [CrossRef]
- Younger, J.P.; Reid, I.M.; Vincent, R.A.; Murphy, D.J. A Method for Estimating the Height of a Mesospheric Density Level using Meteor radar. Geophys. Res. Lett. 2015, 42, 6106–6111. [Google Scholar] [CrossRef]
- Zhou, B.Z.; Xue, X.H.; Yi, W.; Ye, H.L.; Zeng, J.; Chen, J.S.; Wu, J.F.; Chen, T.D.; Dou, X.K. A Comparison of MLT Wind between Meteor Radar Chain Data and SD-WACCM Results. Earth Planet. Phys. 2022, 6, 451–464. [Google Scholar] [CrossRef]
- Reid, I.M. Meteor Radar for Investigation of the MLT Region: A Review. Atmosphere 2024, 15, 505. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Chen, J.; Chen, T.; Li, N. Quasi-90-day Oscillation Observed in the MLT Region at Low Latitudes from the Kunming Meteor Radar and SABER. Earth Planet. Phys. 2019, 3, 136–146. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.H.; Lu, M.L.; Zeng, J.; Ye, H.L.; Wu, J.F.; Wang, C.; Chen, T.D. Mesopause temperatures and relative densities at midlatitudes observed by the Mengcheng meteor radar. Earth Planet. Phys. 2023, 7, 665–674. [Google Scholar] [CrossRef]
- Ceplecha, Z.; Borovicka, J.Í.; Elford, W.G.; ReVelle, D.O.; Hawkes, R.L.; Porubcan, V.Í.; Šimek, M. Meteor Phenomena and Bodies. Space Sci. Rev. 1998, 84, 327–471. [Google Scholar] [CrossRef]
- Jones, J.; Campbell Brown, M. The Initial Train Radius of Sporadic Meteors. Mon. Not. R. Astro. Soc. 2005, 359, 1131–1136. [Google Scholar] [CrossRef]
- Wang, J.; Yi, W.; Wu, J.; Chen, T.; Xue, X.; Zeng, J.; Vincent, R.A.; Reid, I.M.; Batista, P.P.; Buriti, R.A.; et al. Coordinated observations of migrating tides by multiple meteor radars in the equatorial mesosphere and lower thermosphere. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030678. [Google Scholar] [CrossRef]
- Hall, C.; Dyrland, M.; Tsutsumi, M.; Mulligan, F. Temperature trends at 90 km over Svalbard, Norway (78°N l6°E), seen in one decade of meteor radar observations. J. Geophys. Res. 2012, 117, D08104. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Chen, J.; Dou, X.; Chen, T.; Li, N. Estimation of Mesopause Temperatures at Low Latitudes using the Kunming Meteor radar. Radio Sci. 2016, 51, 130–141. [Google Scholar] [CrossRef]
- Stober, G.; Vadas, S.L.; Becker, E.; Liu, A.; Kozlovsky, A.; Janches, D.; Qiao, Z.; Krochin, W.; Shi, G.; Yi, W.; et al. Gravity waves generated by the Hunga Tonga–Hunga Ha′apai volcanic eruption and their global propagation in the mesosphere/lower thermosphere observed by meteor radars and modeled with the High-Altitude general Mechanistic Circulation Model. Atmos. Chem. Phys. 2024, 24, 4851–4873. [Google Scholar] [CrossRef]
- He, M.; Forbes, J.M. Rossby wave second harmonic generation observed in the middle atmosphere. Nat. Commun. 2022, 13, 7544. [Google Scholar] [CrossRef] [PubMed]
- Kam, H.; Kim, Y.H.; Mitchell, N.; Kim, J.-H.; Lee, C. Evaluation of Estimated Mesospheric Temperatures from 11-year Meteor Radar Datasets of King Sejong Station (62°S, 59°W) and Esrange (68°N, 21°E). J. Atmos. Sol.-Terr. Phys. 2019, 196, 105148. [Google Scholar] [CrossRef]
- Yang, C.; Lai, D.; Yi, W.; Wu, J.; Xue, X.; Li, T.; Chen, T.; Dou, X. Observed Quasi 16-Day Wave by Meteor Radar over 9 Years at Mengcheng (33.4°N, 116.5°E) and Comparison with the Whole Atmosphere Community Climate Model Simulation. Remote Sens. 2023, 15, 830. [Google Scholar] [CrossRef]
- Batubara, M.; Yamamoto, M.-Y.; Madkour, W.; Manik, T. Long-term distribution of meteors in a solar cycle period observed by VHF meteor radars at near-equatorial latitudes. J. Geophys. Res. Space Phys. 2018, 123, 10403–10415. [Google Scholar] [CrossRef]
- Holdsworth, D.A.; Reid, I.M.; Cervera, M.A. Buckland Park All-Sky Interferometric Meteor Radar. Radio Sci. 2004, 39, RS5009. [Google Scholar] [CrossRef]
- Zeng, J.; Stober, G.; Yi, W.; Xue, X.; Zhong, W.; Reid, I.; Adami, C.; Ning, B.; Li, G.; Dou, X. Mesosphere/Lower Thermosphere 3-Dimensional Spatially Resolved Winds observed by Chinese Multistatic Meteor Radar Network using the Newly developed VVP Method. J. Geophys. Res. Atmos. 2024, 129, e2023JD040642. [Google Scholar] [CrossRef]
- Hocking, W.; Fuller, B.; Vandepeer, B. Real-Time Determination of Meteor-correlation Parameters Utilizing Modern Digital Technology. J. Atmos. Sol.-Terr. Phys. 2001, 63, 155–169. [Google Scholar] [CrossRef]
- Wang, D.; Zhang, F.; Chen, L.; Li, Z.; Yang, L. The Calibration Method of Multi-Channel Spatially Varying Amplitude-Phase Consistency Errors in Airborne Array TomoSAR. Remote Sens. 2023, 15, 3032. [Google Scholar] [CrossRef]
- Maghraby, A.K.S.E.; Park, H.; Camps, A.; Grubii, A.; Colombo, C.; Tatnall, A. Phase and baseline calibration for microwave interferometric radiometers using beacons. IEEE Trans. Geosci. Remote Sens. Lett. 2020, 58, 5242–5253. [Google Scholar] [CrossRef]
- Yi, W.; Xue, X.; Reid, I.; Younger, J.; Chen, J.; Chen, T.; Li, N. Estimation of Mesospheric Densities at Low Latitudes using the Kunming Meteor Radar together with SABER Temperatures. J. Geophys. Res. Space Physics. 2018, 123, 3183–3195. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, W.; Chen, Z.; Wang, P.; Zhang, H.; Qiu, J.; Zhao, Q.; Deng, Y.; Zhang, Z.; Yu, W. Digital beamforming synthetic aperture radar (DBSAR): Experiments and performance analysis in support of 16-channel airborne X-band SAR data. IEEE Trans. Geosci. Remote Sens.Lett. 2020, 59, 6784–6798. [Google Scholar] [CrossRef]
- Meng, Z.; Li, Y.; Song, X.; Xing, M.; Bao, Z. Amplitude-phase Discontinuity Calibration for Phased Array Radar in Varying Gamming Environment. IET Signal Process. 2014, 8, 729–737. [Google Scholar] [CrossRef]
- Chen, H.; Ming, F.; Li, L.; Liu, G. Elevation Multi-Channel Imbalance Calibration Method of Digital Beamforming Synthetic Aperture Radar. Remote Sens. 2022, 14, 4350. [Google Scholar] [CrossRef]
- Deng, X.; Lan, A.L.; Yan, J.Y.; Wu, L.; Wu, J.; Zhang, J.J. Calibrating the amplitude and phase imbalances in agiledarn hf radar. Radio Sci. 2021, 56, e2020RS007138. [Google Scholar] [CrossRef]
- Zhou, Y.; Li, J.; Zhang, H.; Chen, Z.; Zhang, L.; Wang, P. Internal Calibration for Airborne X-Band DBF-SAR Imaging. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Rousta, B.; Naser-Moghadasi, M.; Arand, B.A.; Sadeghzadeh, R.A. An Efficient Scheduling for Fast Calibration of Digital Beamforming Active Phased Array Radar. IETE J. Res. 2019, 68, 449–455. [Google Scholar] [CrossRef]
- Kim, H.; Kim, J.; Kim, J.; Choi, J.; Hong, S.; Kim, N.; Kim, B. Calibration of Wideband LFM Radars Based on Sliding Window Algorithm. Electronics 2023, 12, 3564. [Google Scholar] [CrossRef]
- Fu, W.; Liu, H.; Chen, Z.; Yang, S.; Hu, Y.; Wen, F. Improved Amplitude-Phase Calibration Method of Nonlinear Array for Wide-Beam High-Frequency Surface Wave Radar. Remote Sens. 2023, 15, 4405. [Google Scholar] [CrossRef]
- Zhao, X.; Deng, Y.; Zhang, H.; Liu, X. A Channel Imbalance Calibration Scheme with Distributed Targets for Circular Quad-Polarization SAR with Reciprocal Crosstalk. Remote Sens. 2023, 15, 1365. [Google Scholar] [CrossRef]
- D’Emilia, G.; Gaspari, A.; Natale, E. Amplitude–Phase Calibration of Tri-axial Accelerometers in the Low-Frequency Range by a LDV. J. Sens. Sens. Syst. 2019, 8, 223–231. [Google Scholar] [CrossRef]
- Guo, X.; Camps, A.; Park, H.; Liu, H.; Zhang, C.; Wu, J. Phase and Amplitude Calibration of Rotating Equispaced Circular Array for Geostationary Microwave Interferometric Radiometers—Simulation Results and Discussion. IEEE Trans. Geosci. Remote Sens. Lett. 2021, 60, 1–19. [Google Scholar] [CrossRef]
- Zhang, L.; Xing, M.-D.; Qiu, C.-W.; Bao, Z. Adaptive two-step calibration for high-resolution and wide-swath SAR imaging. IET Radar Sonar Navig. 2010, 4, 548–559. [Google Scholar] [CrossRef]
- Graetz, J. Auto-Calibration of Cone Beam Geometries from Arbitrary Rotating Markers using a Vector Geometry Formulation of Projection Matrices. Phys. Med. Biol. 2021, 66, 075013. [Google Scholar] [CrossRef]
- Jones, W. Theory of the Initial Radius of Meteor Trains. Mon. Not. R. Astro. Soc. 1995, 275, 812–818. [Google Scholar] [CrossRef]
- Jones, J.; Webster, A.R.; Hocking, W.K. An Improved Interferometer Design for Use with Meteor Radars. Radio Sci. 1998, 33, 55–65. [Google Scholar] [CrossRef]
- Jing, Y.; Lu, X.; Li, X. Research on a Low-Complexity Multi-channel High-Precision Amplitude and Phase Calibration Algorithm. In Proceedings of the 13th International Conference on Communication Software and Networks (ICCSN), Chongqing, China, 25 June 2021; pp. 113–118. [Google Scholar] [CrossRef]
- Vanwynsberghe, C.; Bouley, S.; Antoni, J. Gain and phase calibration of sensor arrays from ambient noise by cross-spectral measurements fitting. J. Acoust. Soc. Am. 2023, 153, 1319–1330. [Google Scholar] [CrossRef]
- Pawlik, P.; Grecki, M.; Simrock, S. New method for RF Field Amplitude and Phase Calibration in Flash Accelerator. In Proceedings of the International Conference Mixed Design of Integrated Circuits and System(MIXDES), Gdynia, Poland, 22–24 June 2006. [Google Scholar] [CrossRef]
- Joy, A.; Chakka, V. Performance comparison of LMS/NLMS based transceiver filters for MIMO two-way relaying scheme. In Proceedings of the 2011 International Conference on Communications & Signal Processing (ICCSP), Kerala, India, 10–12 February 2011; pp. 105–107. [Google Scholar] [CrossRef]
- Nagal, R.; Kumar, P.; Bansal, P. A Survey with Emphasis on Adaptive filter, Structure, LMS and NLMS Adaptive Algorithm for Adaptive Noise Cancellation System. J. Eng. Sci. Technol. Rev. 2017, 10, 150–160. [Google Scholar] [CrossRef]
- Yang, X.W.; Wu, C.Z.; He, Y.; Lu, X.Y.; Chen, T. A Dynamic Rollover Prediction Index of Heavy-Duty Vehicles With a Real-Time Parameter Estimation Algorithm Using NLMS Method. IEEE Trans. Veh. Technol. 2022, 71, 2734–2748. [Google Scholar] [CrossRef]
- Borisagar, K.R.; Sedani, B.S.; Kulkarni, G.R. Simulation and Performance Analysis of LMS and NLMS Adaptive Filters in Non-stationary Noisy Environment. In Proceedings of the 2011 International Conference on Computational Intelligence and Communication Networks, Gwalior, India, 7–9 October 2011; pp. 682–686. [Google Scholar] [CrossRef]


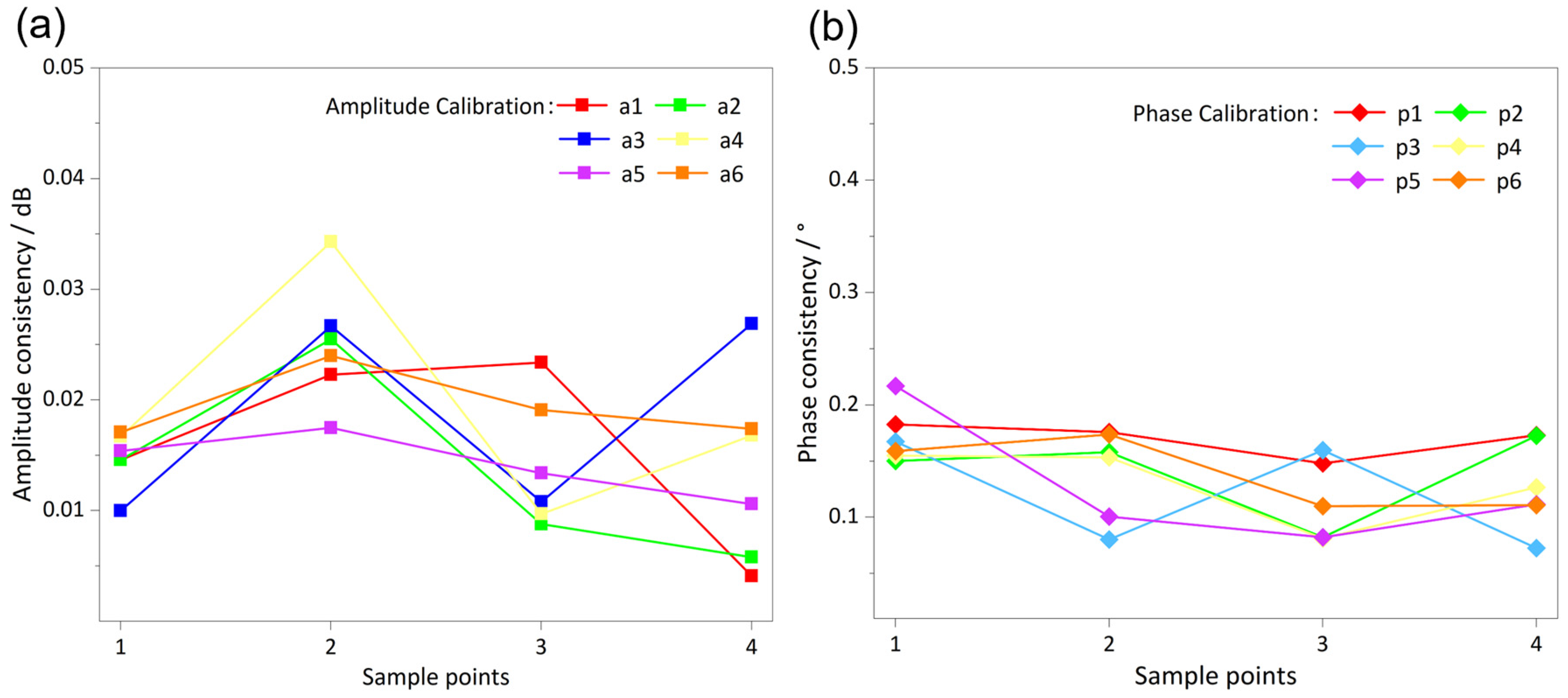
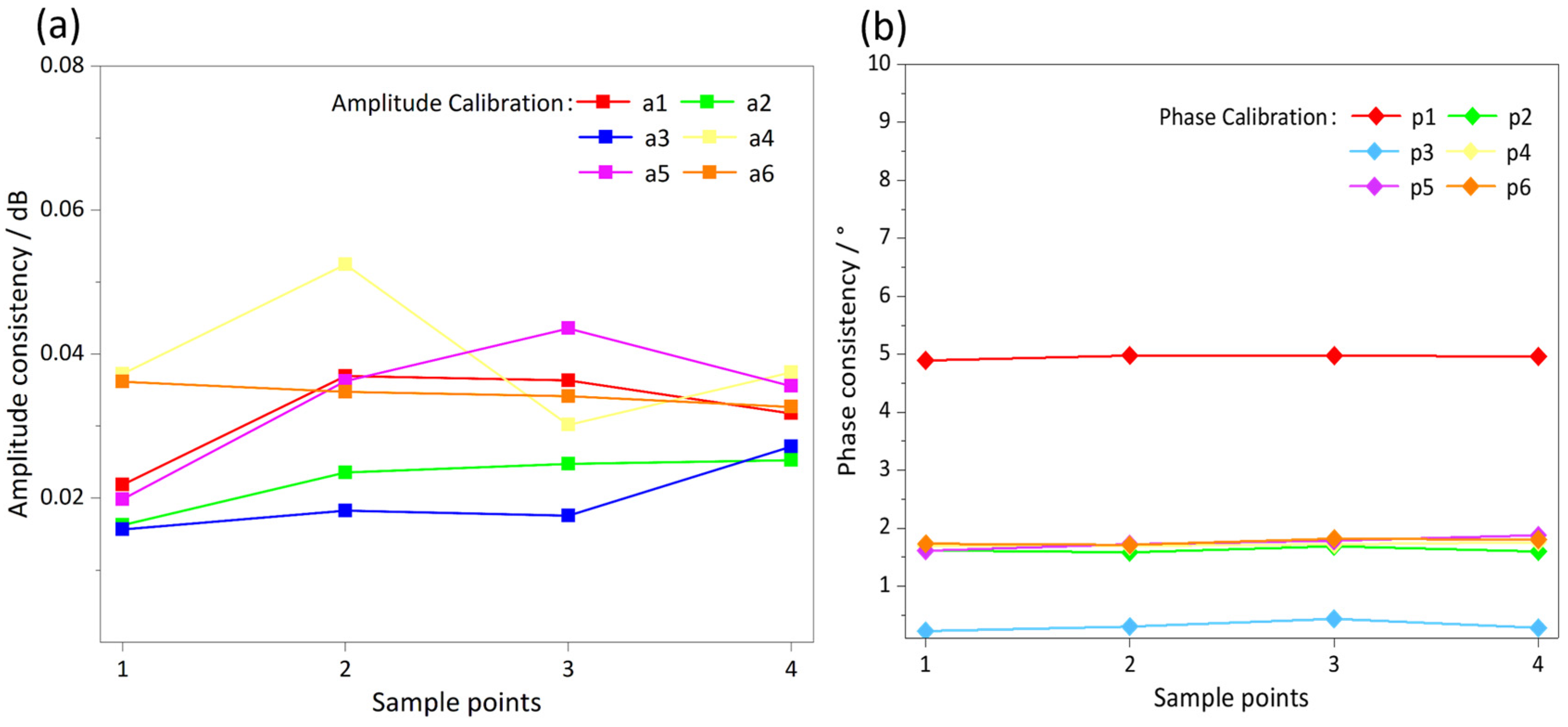
| Channel | Amplitude (dB) | Phase (o) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Point1 | Point 2 | Point 3 | Point 4 | Point 1 | Point 2 | Point 3 | Point 4 | ||
| Original | CH1 | −0.9784 | −0.9932 | −1.0822 | −1.0515 | −86.9761 | −91.5301 | 91.7915 | −86.6542 |
| CH2 | −1.8672 | −1.8479 | −1.9218 | −1.9057 | −90.3839 | −94.9626 | 88.1729 | −90.4200 | |
| CH3 | −0.8439 | −0.7950 | −0.9011 | −0.8842 | −88.7715 | −93.1451 | 89.9926 | −88.6469 | |
| CH4 | −1.2654 | −1.2765 | −1.3215 | −1.3042 | −77.7208 | −82.4398 | 100.8693 | −77.5637 | |
| CH5 | −0.3864 | −0.3812 | −0.4660 | −0.4582 | −73.5094 | −77.8493 | 105.2076 | −73.3297 | |
| Consistency | 0.4900 | 0.4905 | 0.4815 | 0.4795 | 6.6403 | 6.6538 | 6.6394 | 6.6760 | |
| Calibrated | CH1 | −2.7473 | −2.7621 | 2.8512 | −2.8205 | −90.4151 | −94.9691 | 88.3525 | −90.0932 |
| CH2 | −2.7823 | −2.763 | −2.8369 | −2.8208 | −90.3839 | −94.9626 | 88.1729 | −90.4200 | |
| CH3 | −2.7701 | −2.7212 | −2.8273 | −2.8104 | −90.7171 | −95.0908 | 88.0470 | −90.5926 | |
| CH4 | −2.7610 | −2.7721 | −2.8171 | −2.7998 | −90.2123 | −94.9312 | 88.3779 | −90.0552 | |
| CH5 | −2.7499 | −2.7448 | −2.8295 | −2.8217 | −90.3544 | −94.6943 | 88.3626 | −90.1747 | |
| Consistency | 0.0141 | 0.0173 | 0.0113 | 0.0085 | 0.1655 | 0.1296 | 0.1311 | 0.2064 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Chen, X.; Huang, S.; Chen, Z.; Li, J.; Hao, W. Dynamic Calibration Method of Multichannel Amplitude and Phase Consistency in Meteor Radar. Remote Sens. 2025, 17, 331. https://doi.org/10.3390/rs17020331
Jin Y, Chen X, Huang S, Chen Z, Li J, Hao W. Dynamic Calibration Method of Multichannel Amplitude and Phase Consistency in Meteor Radar. Remote Sensing. 2025; 17(2):331. https://doi.org/10.3390/rs17020331
Chicago/Turabian StyleJin, Yujian, Xiaolong Chen, Songtao Huang, Zhuo Chen, Jing Li, and Wenhui Hao. 2025. "Dynamic Calibration Method of Multichannel Amplitude and Phase Consistency in Meteor Radar" Remote Sensing 17, no. 2: 331. https://doi.org/10.3390/rs17020331
APA StyleJin, Y., Chen, X., Huang, S., Chen, Z., Li, J., & Hao, W. (2025). Dynamic Calibration Method of Multichannel Amplitude and Phase Consistency in Meteor Radar. Remote Sensing, 17(2), 331. https://doi.org/10.3390/rs17020331








