Abstract
The INterpolated FLOod Surface (INFLOS) tool was developed to meet the operational needs of the Copernicus Emergency Management Service (CEMS) Rapid Mapping (RM) component, which delivers critical crisis information within hours during and after disasters. With increasing demand for accurate and real-time flood depth estimates, INFLOS provides a rapid, adaptable solution for estimating floodwater depth across diverse flood scenarios, using remotely sensed data and high-resolution Digital Terrain Models (DTMs). INFLOS calculates flood depth by interpolating water surface elevation from sample points along flooded area boundaries, derived from satellite imagery. This tool is capable of delivering flood depth estimates in a rapid mapping context, leveraging a multistep interpolation and filtering process for improved accuracy. Tested across fourteen regions in Europe and South America, INFLOS has been successfully integrated into CEMS RM operations. The tool’s computational optimisations further enhance efficiency, improving computation times by up to 15-fold, compared to similar techniques. Indeed, it is able to process areas of up to 6000 ha in a median time of 5.2 min, and up to 30 min at most. In conclusion, INFLOS is currently operational and consistently generates flood depth products quickly, supporting real-time emergency management and reinforcing the CEMS RM portfolio.
1. Introduction
1.1. Context
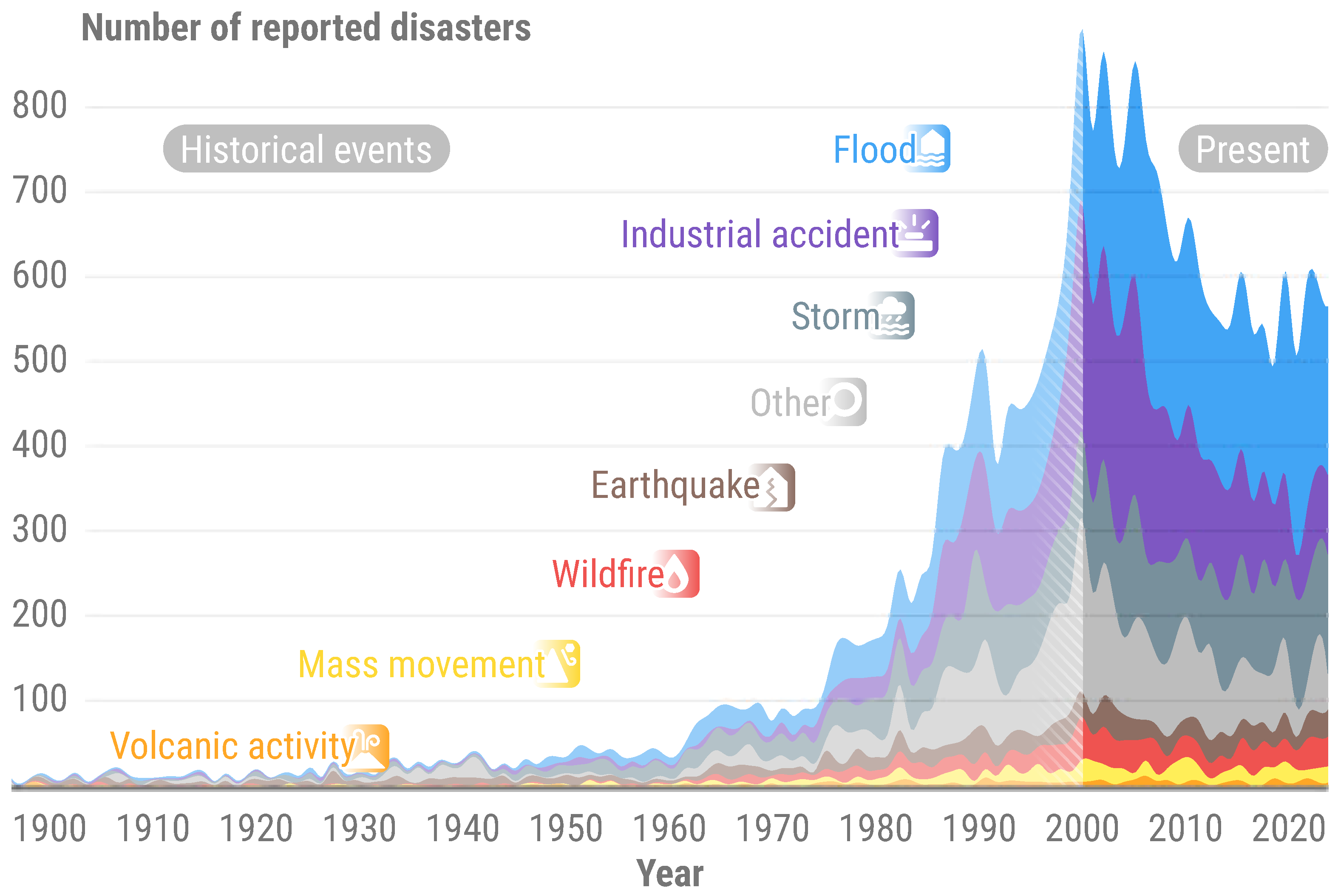
Floods are among the most destructive natural disasters worldwide, affecting millions of people and causing significant economic and environmental damage. Climate change and its complex feedback mechanisms have made monitoring the hydrological cycle, including flood events, increasingly challenging. Research indicates that precipitation patterns, flood frequency, and intensity are experiencing anomalies [1], with a notable increase in reported floods since 1950, according to the Emergency Events Database (EM-DAT) repository [2], as illustrated in Figure 1. Moreover, flood-related events accounted for more than 33% of all reported disasters in 2023. This surge highlights the inadequacy of current flood prevention, management, and monitoring systems, owing to the erratic and changing climate and weather patterns [3].
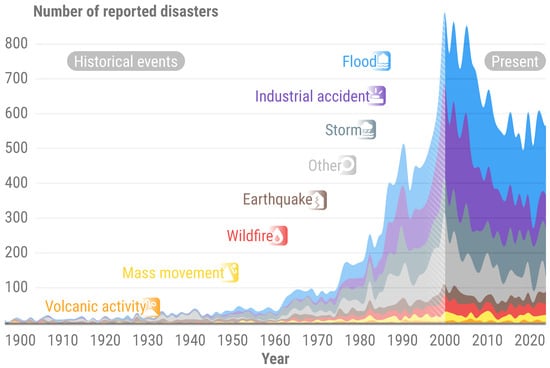
Figure 1.
Number of reported natural and technological disasters, between 1900 and 2023, according to EM-DAT [2]. The EM-DAT classification scheme was changed to better align with CEMS RM main disaster classes. The CEMS RM “Other” class includes the following EM-DATA classes: “Epidemic”, “Humanitarian”, “Algae bloom”, “Collapse of a dumping site”, “Heavy snowfall”, and “Iceberg”. Historical events, prior to 2000, are subject to biases. The year 2024 is omitted, for data validation is still pending.
As a result, approximately 1.47 billion people worldwide face a high risk of severe flooding [4]. Urban areas pose a significant concern, due to their high population density and proximity to large watercourses and coastlines, resulting from economic drivers [5]. In Europe, for example, 51% of the population lives in coastal regions [6], and the median distance between people and the nearest water body is 3 km [7]. This emphasises the need for robust flood management strategies to protect these densely populated areas. The rapid pace of urbanisation, which is expected to add 2.5 billion people to urban centres by 2050 [8], will further exacerbate flood risks.
As urban expansion continues, it is essential for policymakers, urban planners, and civil security services to have access to reliable data to support flood management, mitigation efforts, and recovery strategies. Traditional monitoring methods, such as ground-based surveys and aerial photography, provide precise information, but may not offer real-time data during crises. Remotely sensed satellite imagery and advanced computer vision techniques offer a more efficient, timely, and comprehensive solution for flood monitoring and damage assessment [9]. This approach has become the leading solution for crisis data collection and provision, especially due to the increased frequency of major disasters [10]. The growing availability of high-resolution satellite images has significantly improved the accuracy and timeliness of flood mapping. Typical workflows include the use of optical imagery and Synthetic Aperture Radar (SAR) [11]. Optical sensors capture images in the visible and infrared spectra, which can help identify water bodies, flood traces, mudflows, and other flood-related features. However, their effectiveness may be limited by the time of acquisition and atmospheric conditions. On the other hand, SAR systems use microwaves that can penetrate clouds and capture data both day and night. This makes them particularly valuable for mapping flood extents, especially during high-precipitation events with dense cloud cover.
Numerous global services utilise remotely sensed data to provide information on floods and their impact, including the Copernicus Emergency Management Service (CEMS), an integral component of the European Union’s Copernicus Programme. The CEMS is dedicated to delivering timely and accurate geospatial information to support disaster management and civil protection authorities globally. Authorised users, such as national civil protection authorities, European Commission services, and the European External Action Service, can access crisis information by triggering the service. The CEMS operates 24/7/365, with the rapid mapping (RM) framework serving as its core. This framework delivers geospatial information within hours or days following a disaster [12] for various events, including floods, wildfires, earthquakes, and landslides. Examples of provided information include delineation maps that outline the geographical extent of a disaster and grading maps that assess the impact on populations and assets, such as buildings or transportation networks. From satellite imagery reception to crisis product delivery, operators have up to 7 and 10 h, respectively, for delineation and grading product delivery, highlighting the importance of efficient and reliable workflows.
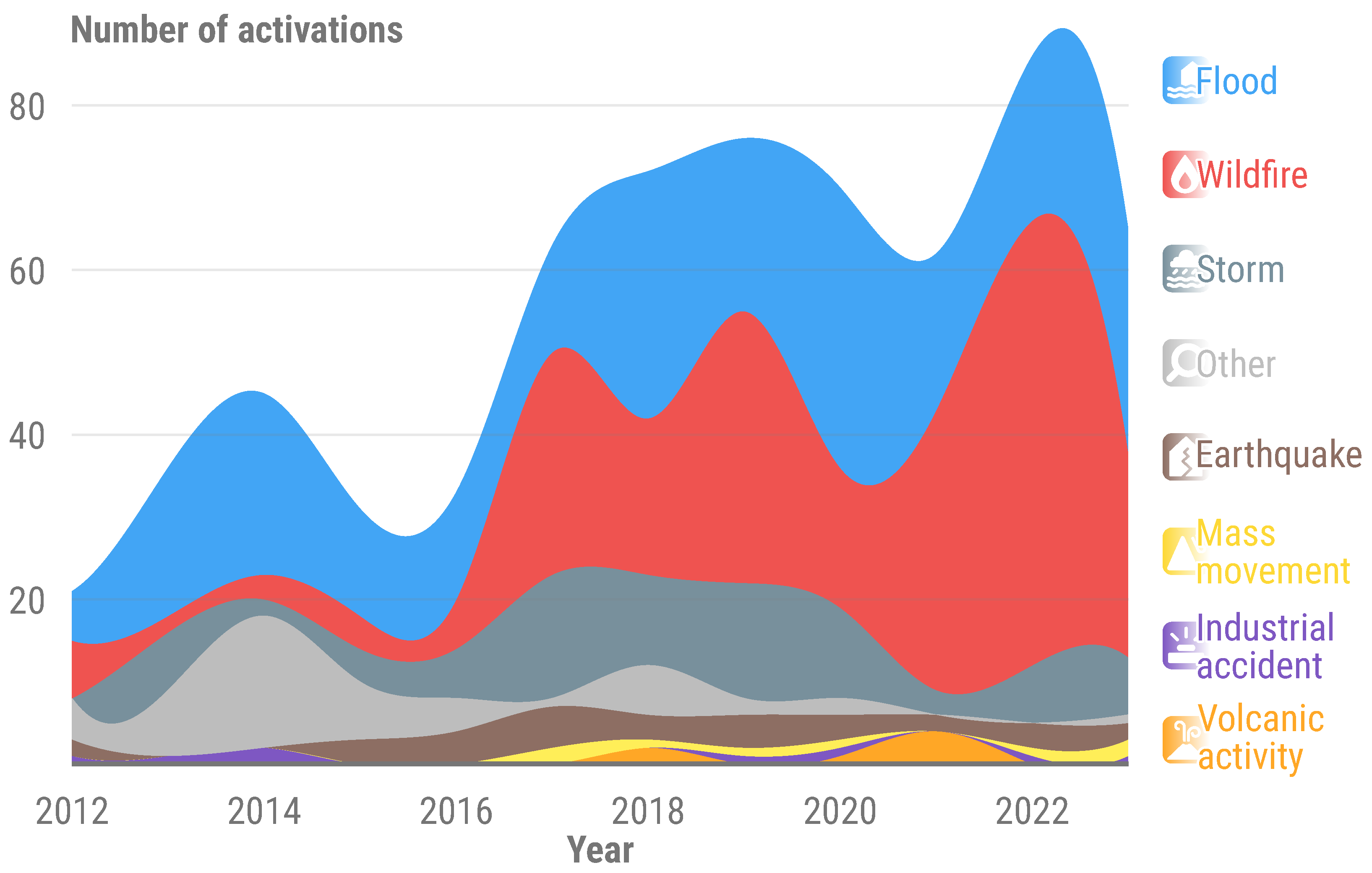
More specifically, floods and related events, such as tsunamis, storms, and mudflows, depending on the context, are the most common disasters for which the CEMS is activated, accounting for over 46% of the total (Figure 2). CEMS RM users, including EU Directorate Generals and Member State Civil Protection agencies, have requested information on flood depths to enhance emergency relief and impact assessment. This demand requires the development of a rapid and operational methodology that can adapt to various scenarios and integrate into CEMS RM tools. Furthermore, the methodology must be compatible with flood extents derived from different satellite sources, including high-resolution (HR), and Very High-Resolution (VHR) imagery, as well as optical and radar sensors.
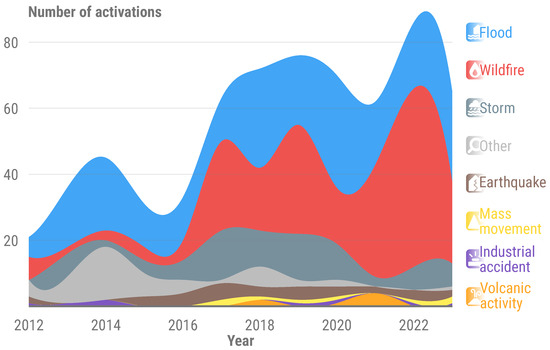
Figure 2.
Number of Copernicus Emergency Management Service—Rapid Mapping activations between 2012 and 2023. When applicable, flood activations may also include tsunamis, storms, and mudflows, depending on the context of a given event.
1.2. State of the Art
Several methodologies have been developed to estimate flood depth. The most common techniques involve hydrological and hydraulic modelling. These models integrate various inputs, such as meteorological data, land use information, and elevation, to simulate water flow and forecast flood behaviour. However, before integrating these inputs into a modelling solution, several pre-processing steps are required. Furthermore, benchmarks of solutions like HEC-RAS [13], LISFLOOD-FP [14], or FLO-2d [15] suggest simulations that can last for several hours, contingent upon the anticipated precision and spatial resolution relevant for CEMS RM activities [16]. This is particularly true for VHR elevation data, crucial in the context of urban flood mapping [17].
Techniques such as cellular automata (CA) can simplify the physical principles of these models by employing rule sets that describe the behaviour of floodwater in a discrete space, based on topography, adjacent water cells, and other ancillary data if required. This simplification allows CA-based solutions, such as CA-ffé, to run up to 95% faster than conventional methods like HEC-RAS, while producing comparable flood depth results to hydraulic modelling [18]. Further optimisations, such as parallelisation, Graphic Processing Unit (GPU) computing, or memorisation, can further reduce computation times [19], as demonstrated by the Cellular Automata Dual-DraInagE Simulation (CADDIES) project [20]. However, a limitation of CA in rapid mapping is the requirement of an initial state, such as a water volume distribution across the Area Of Interest (AOI), flow rate, or rain gauge readings [21]. These data can be challenging for operators to acquire, given their time constraints and the need for knowledge of local platforms for accessing such information. Typically, CEMS users provide these data when available during an activation, without any guarantee of delivery time, data quality, or compatibility with the CA-based model’s expected input.
Alternatively, machine learning-based techniques demonstrate promising results, characterised by rapid inference times and minimal ancillary data or initial state requirements [22]. These methods primarily rely on the flood extent extracted from remotely sensed imagery and a Digital Terrain Model (DTM), from which various topographic indexes can be derived [23]. However, feature engineering can become time-consuming, depending on AOI size, DTM resolution, and necessary topographic information. Moreover, these models require an extensive training dataset and are susceptible to over-fitting, among other drawbacks [24], which can lead to inaccurate flood depth patterns.
To reduce the requirement for large computational resources and ancillary data, techniques have been developed that rely solely on remotely sensed information and DTMs to estimate water depths across various flood scenarios [25,26]. FwDET [27] is an example of such a method, which leverages delineated flooded polygons to extract elevations from a DTM along the flood boundary. After filtering out samples based on terrain slope, this information is propagated across the flood area using the Nearest Neighbour interpolation technique to compute floodwater elevations. The final flood depth is determined by subtracting the DTM from the flood surface, with an optional iterative smoothing procedure. This tool has applications in both riverine and coastal flooding, with the updated FwDET v2.0 addressing coastal complexities and improving computational efficiency [28]. FwDET is widely used in emergency response and disaster resilience research, providing generally accurate and timely flood management support. Although the underlying strategy is promising, testing in the context of CEMS RM activations has proven unsuccessful. Firstly, the iterative Nearest Neighbour interpolation of elevations results in tessellated artefacts, leading to a discrete spatial distribution of depth values despite using a low-pass filter to smooth the associated flood surface. Moreover, sample refinement with terrain slope is insufficient to account for artefacts in the DTMs and their variability, which has proven to be a recurrent issue in an operational setting.
Considering this context, the INterpolated FLOod Surface (INFLOS) tool was developed to fulfil CEMS RM requirements. It utilises an existing flood extent polygon layer derived from remotely sensed imagery combined with the best available DTM. To ensure consistency and robustness across a wide range of applications, several key steps have been implemented, taking reference data and topographic context into consideration. As a result, the proposed approach was operationally tested on more than 180 products worldwide. This paper aims at illustrating the different steps involved in rapidly estimating flood depths from satellite imagery and elevation data, and provides key considerations for both operators and stakeholders when using the generated products.
2. Materials and Methods
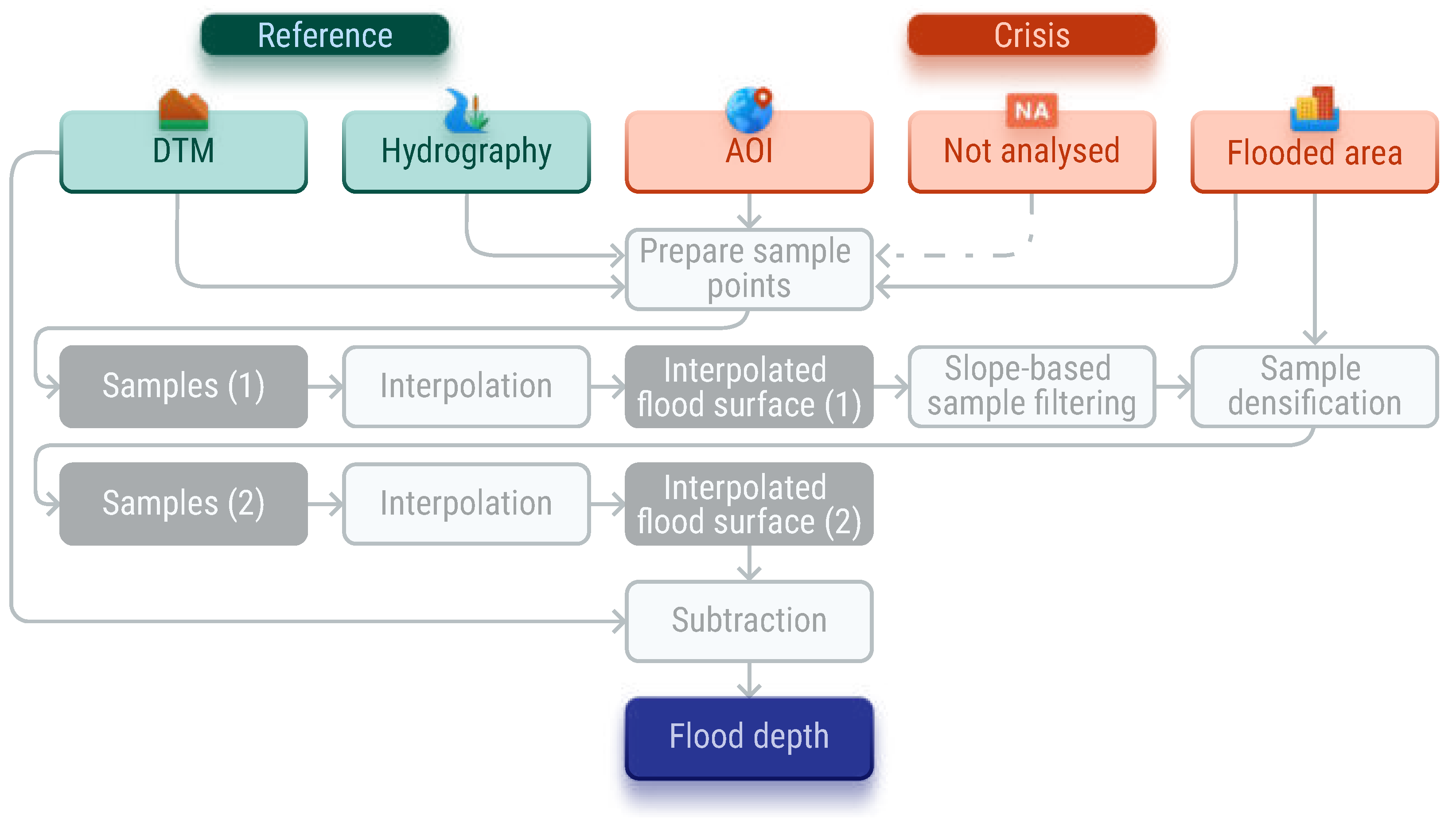
The INterpolated FLOod Surface (INFLOS) technique integrates reference and crisis information gathered, processed, or generated by operators during CEMS RM activations for floods and associated events. The main dependencies of the proposed methodology include data on flooded areas, hydrography, and elevation, as illustrated in Figure 3. Reference information describes the baseline, pre-event conditions, encompassing hydrography and elevation data. Crisis information refers to dynamic data that specifically characterise changes induced by the event, such as newly formed or expanded water bodies. This category also includes any updates to hydrographic features and alterations in terrain or assets caused by the event. The crisis information is obtained through the analysis of Synthetic Aperture Radar (SAR) images—including Sentinel 1, COSMO-SkyMed, PAZ, and RADARSAT-2— optical images—including Pléiades, Pléiades Neo, GeoEye, WorldView-2, and Sentinel-2—or aerial photographs, supported by remote sensing software and libraries such as eoreader [29].
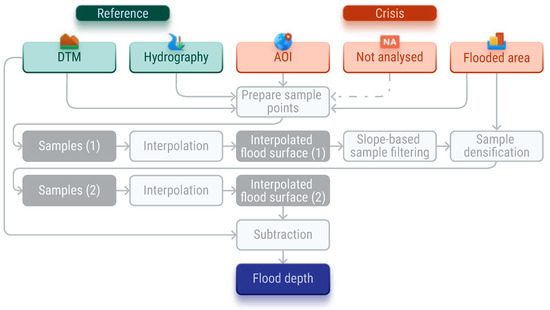
Figure 3.
Simplified workflow and data model for INFLOS.
Table 1 presents the required and optional datasets for INFLOS. The combination of flooded area data and hydrographic information indicates the full water extent. Hydrography data are typically sourced from open-source spatial databases, such as OpenStreetMap [30], or national topographic repositories. Consequently, flooded areas are derived by subtracting hydrography from the overall water extent. In addition to these mandatory datasets, operators can provide ancillary features that define the domain inside which flood depths are estimated. These include the AOI and any areas within the AOI that were not analysed due to incomplete crisis imagery coverage. They are essential for reducing computation time and removing edge samples.

Table 1.
List of required and optional input datasets for INFLOS.
Reference and crisis data were collected and generated for 14 activations, representing a total of 69 areas of interest and over 180 products (Table 2). Spanning several European countries and Europe, these activations cover a wide range of landscapes, from coastal to mountainous areas.

Table 2.
List of CEMS RM activations processed with INFLOS from September 2023 to May 2024. The number of areas of interest and generated flood depth products are indicated for each activation. All related products are accessible through the CEMS RM portal: https://emergency.copernicus.eu/mapping/list-of-activations-rapid (accessed on 12 January 2025).
To estimate flood depth, INFLOS is based upon four assumptions, three of which are illustrated in Figure 4:
- (A)
- Flood depth, referred to as , can be determined by initially estimating a flood surface, denoted as . This is achieved by subtracting elevation data e from the flood surface. Consequently, . Negative values of correspond to areas unaffected by the flood and located outside the boundaries of the observed event layer.
- (B)
- Flood depth at the edges of flooded areas can be approximated as zero, as described by the formula for edge vertices.
- (C)
- Considering the large analysis scales of CEMS RM, cross-sections of a flooded area should approximate a flat water surface, with slopes of a dozen centimetres per kilometre at most [32]. Indeed, INFLOS does not take local hydrodynamic processes into account, but rather focusses on the effects of gravity on water. As a result, processes such as water surface bulging in the concave bank of a meandering river are not accounted for [33].
- (D)
- It is not possible to consistently infer the bathymetry of hydrological features or the corresponding water depth from the various DTM specifications made available during flood activations.
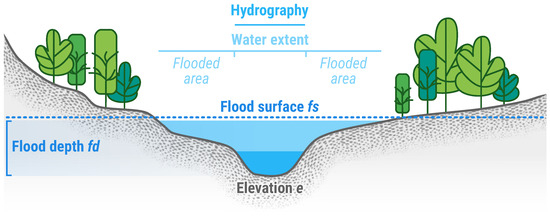
Figure 4.
Cross-section of a watercourse, illustrating terminology and concepts used for describing flood depth. It includes hydrography and elevation (e), available to the operator as inputs. INFLOS generates a flood surface estimate (), used to derive flood depth ().
Figure 4.
Cross-section of a watercourse, illustrating terminology and concepts used for describing flood depth. It includes hydrography and elevation (e), available to the operator as inputs. INFLOS generates a flood surface estimate (), used to derive flood depth ().
The proposed methodology involves a two-stage interpolation process, consisting of the following steps: (1) preparation of sample points and outlier filtering, (2) first-pass interpolation to generate a preliminary flood surface, (3) removal of additional outliers and densification of robust samples, (4) second-pass interpolation, where the final flood surface is estimated, and (5) flood depth computation.
2.1. Preparation of Sample Points
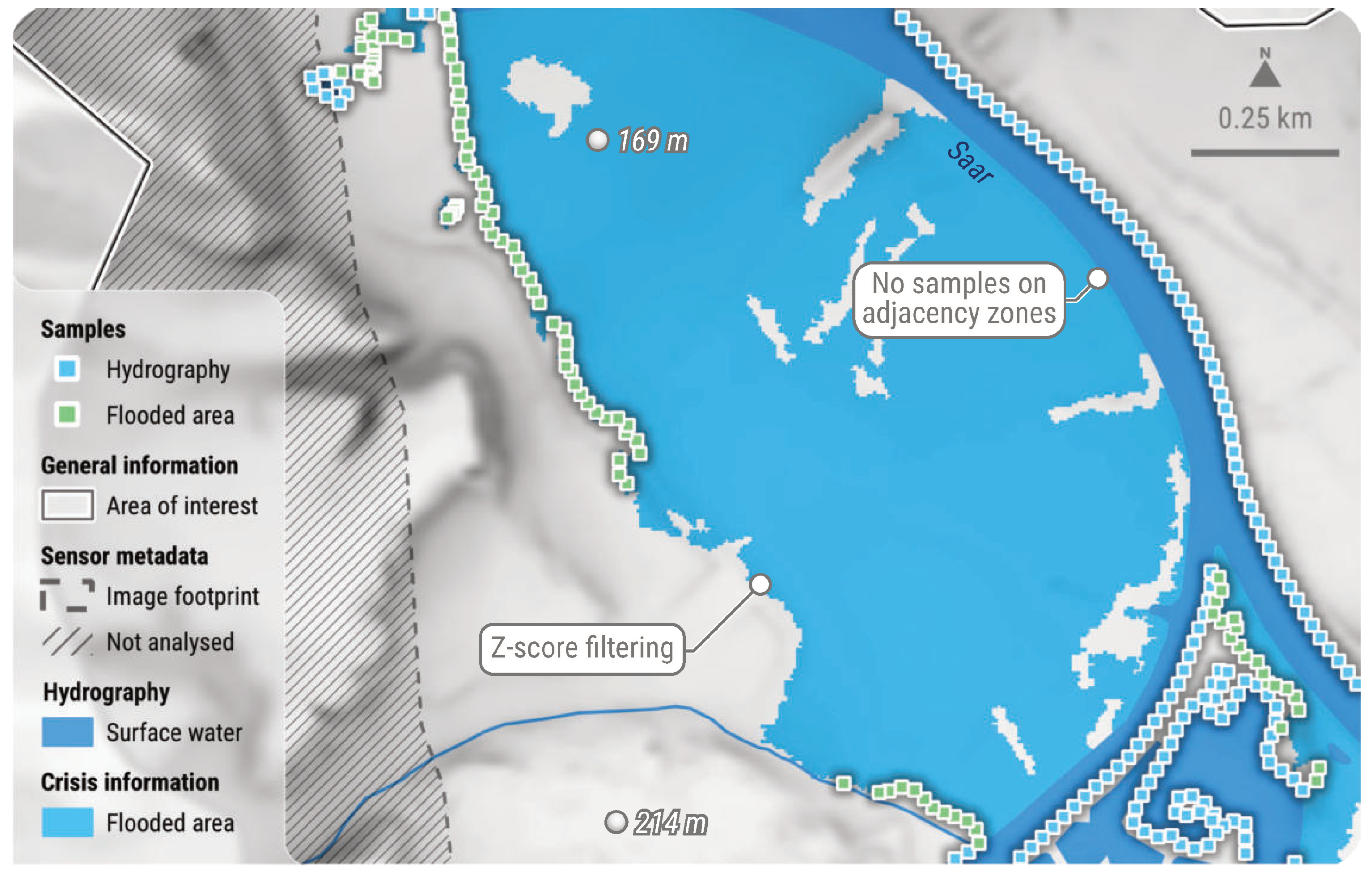
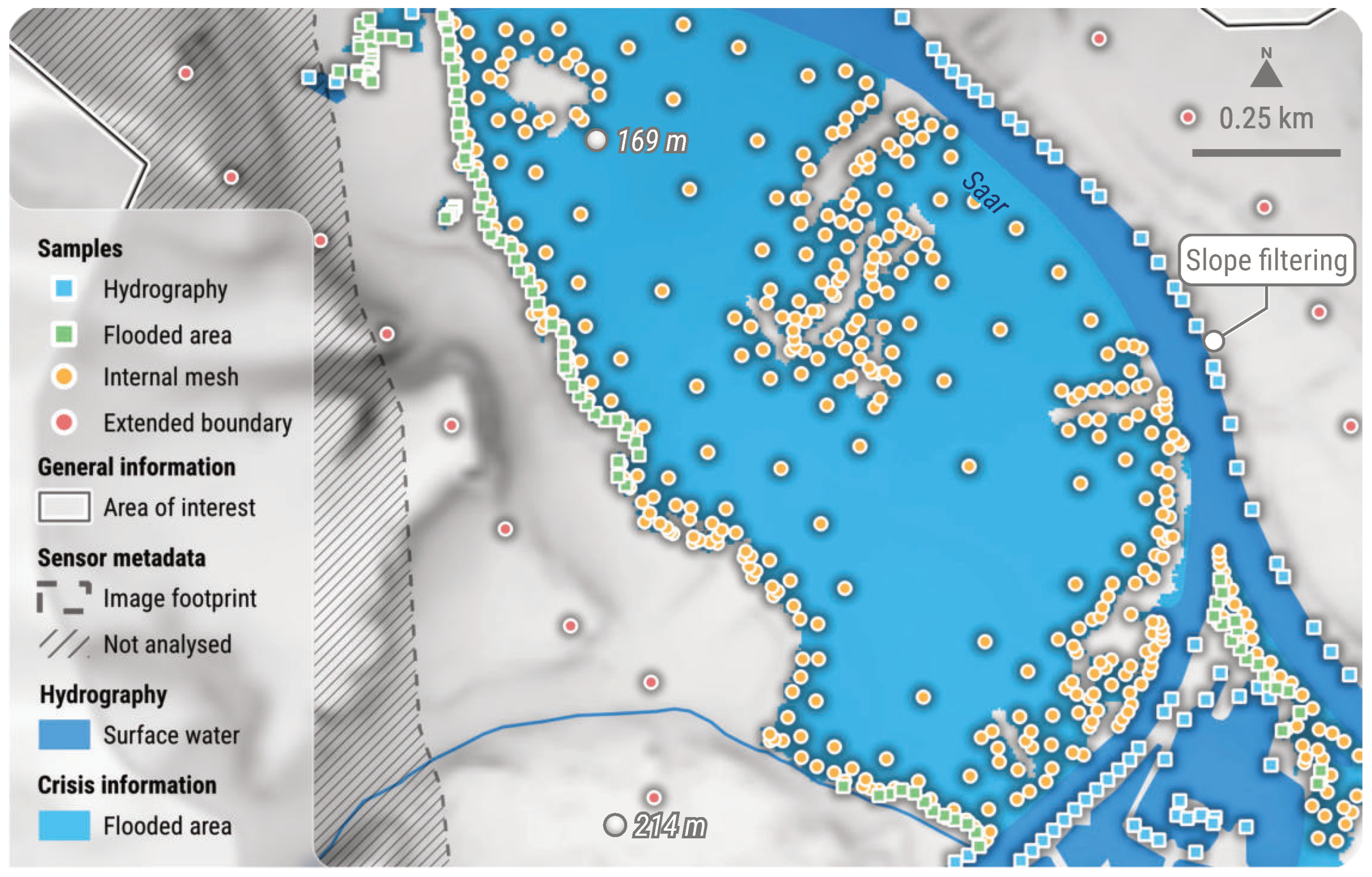
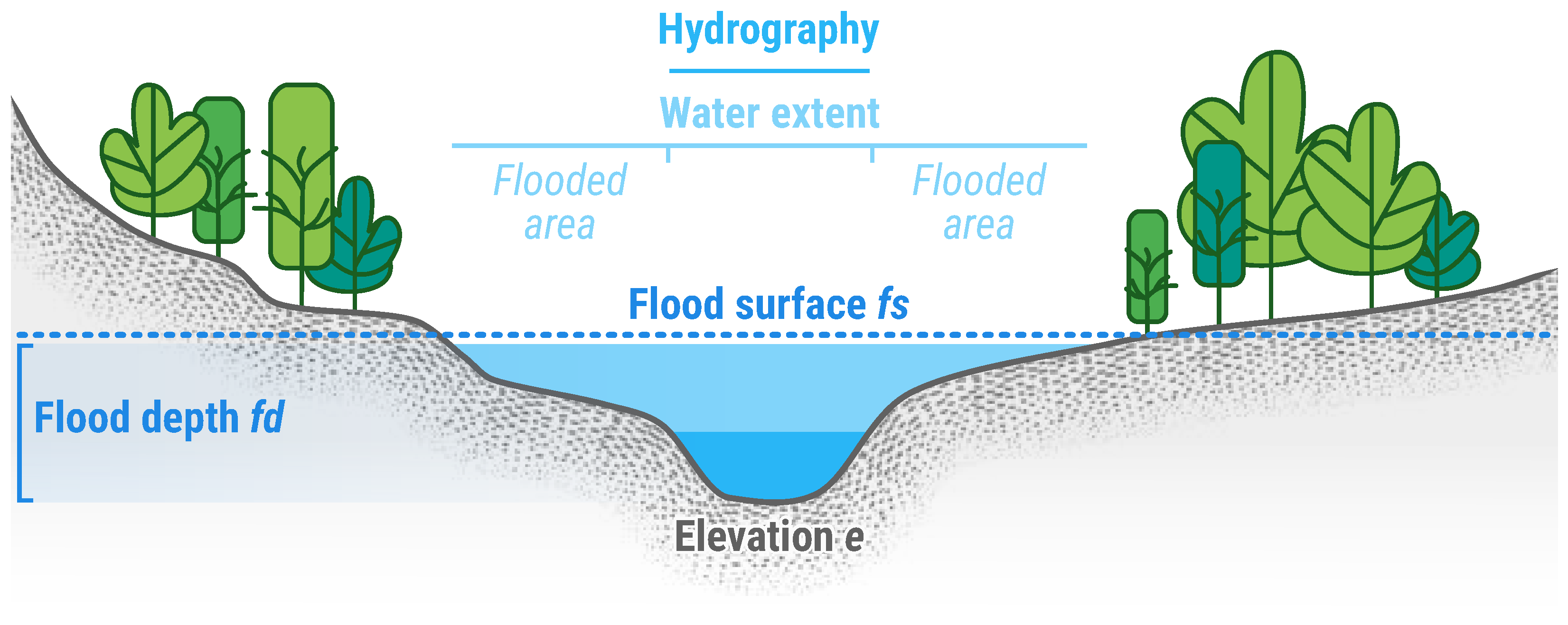
INFLOS operates on the basis of interpolating a flood surface using a set of sample points located along the edges of flooded areas, where the water depth can be approximated to zero, as per assumptions (A) and (B). The distance between samples is contingent upon the resolution of the crisis image, allowing for an adaptive technique that is applicable across a wide range of sensors. To ensure statistical significance for subsequent statistical filtering, at least 30 samples are drawn [34]. The result of this sampling process is illustrated in Figure 5.
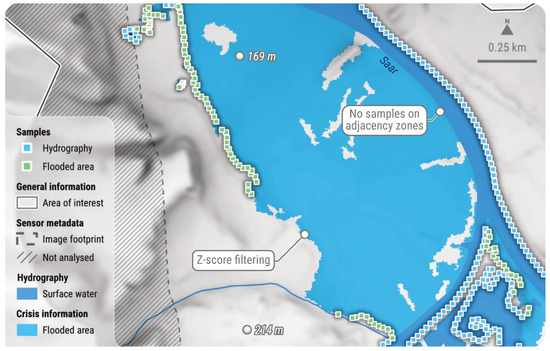
Figure 5.
Spatial distribution of sample points, prior to the initial interpolation phase. Each point draws its elevation value directly from a DTM. This example is based on an on-demand CEMS RM delineation product delivered for EMSR722 AOI02 Saar (Germany). DTM (10 m) courtesy of GeoBasis-DE/BKG (2018). All related products can be accessed through the official viewer for EMSR722: https://rapidmapping.emergency.copernicus.eu/EMSR722/ (accessed on 12 January 2025).
Furthermore, the same principle can be extended to include hydrography features adjacent to flooded areas, leading to a more accurate representation of the flood domain. This could potentially enable bathymetry estimation from suitable elevation data.
In line with assumption (B), it is recommended to select only samples located on the periphery of the full water extent for analysis. It can be reasonably assumed that samples situated within this domain will have non-zero positive depth values. Consequently, INFLOS excludes all samples situated along the boundaries where both the flooded areas and hydrography are adjacent. Furthermore, samples extracted from flooded areas and positioned near or beyond the limits of the AOI or image footprint are also removed, as they do not align with the actual limits of the observed water extent (Figure 5). This selective sampling methodology ensures a faithful representation of the actual event.
After completing the sampling process, the elevation of each point is calculated using the DTM. In the context of rapid mapping, the reliability of elevation data may not be guaranteed entirely, even with the utmost operator expertise. As a result, the accuracy of mapped water boundaries could be locally inconsistent. This issue is particularly prevalent in Synthetic Aperture Radar (SAR) imagery, where radar shadows from features like hedges can be misleading, as they may resemble water due to similar amplitude values.
As a result, significant inaccuracies must be rectified by the operator before proceeding with the rest of the workflow, to guarantee the accuracy and reliability of flood depth values. However, to address these challenges, INFLOS has been developed to handle minor inconsistencies in both elevation data and flood delineation. Indeed, pre-processing steps are implemented to remove potential height value outliers among the sampling points. To achieve this, a filtering technique based on the standard score is employed. For each flood polygon, the distribution of its samples’ height is used to compute the standard score, as per Formula (1), where x corresponds to a sample’s height, to the mean height for samples belonging to a given polygon, and to the standard deviation of heights.
Any sample where is considered an outlier and is removed, retaining only the most optimal 68% of the initial set of sample points. Optionally, the standard score threshold can be adjusted to account for data quality and specific hydro-geomorphological features of the landscape. Such features include entrenchment, gullies, or abrupt terrain changes, common in highly dissected landscapes or floodplains with braided rivers. These geomorphological features lead to rapid local variations in elevation, and require flexible thresholds to minimise discarding valid values. Incorporating this adaptability ensures that INFLOS remains robust across diverse terrain types, from steep mountainous regions to low-gradient coastal plains. This also does not account for georeferencing and orthorectification issues that can result in misalignments between satellite imagery and elevation data. Nonetheless, manipulating the standard score threshold would require extensive testing for each use case, which is unfeasible during production. This explains the rationale behind proposing a default value.
2.2. First-Pass Interpolation
The sample set obtained from the previous step is used to interpolate a flood surface. This interpolation process involves propagating elevation data from the sample points to a broader domain of interpolation, which is typically defined by the convex hull of all sample points. Various interpolation techniques are available, each with specific trade-offs in terms of accuracy, smoothing, parameterisation, and processing speed, among other factors [35,36]. Several spatial interpolation techniques were explored during development, with three main criteria guiding selection:
- Exact spatial interpolation is mandatory to ensure border samples have a flood depth of 0, satisfying assumption (B), which states .
- Given the time constraints of CEMS RM, the interpolation technique must produce results as fast as possible.
- The interpolation method should operate without requiring fine-tuning of parameters, as it requires expertise and time to test multiple configurations. Preferably, only sample locations and heights should be needed as input. Indeed, an important objective of this development for rapid mapping is that the operator does not intervene.
The Nearest Neighbour interpolation method is the simplest and fastest, making it suitable for rapid mapping. This technique is notably used for FwDET [27]. It assigns the elevation of the nearest sample point to each unsampled location in the interpolation domain [37]. While computationally efficient, this approach frequently results in a stepped surface appearance, particularly evident in complex landscapes like entrenched valleys. Furthermore, the reliance on the nearest sample renders it particularly susceptible to outliers. To address these issues, FwDET employs a modified version of this algorithm, where the average elevations of neighbouring samples are iteratively assigned to unsampled areas within a moving window.
Alternative methods were also explored, such as Inverse Distance Weighting (IDW) [38] and kriging [39]. However, both of the above-mentioned methods require the user to set some input parameters (e.g., the value of the power parameter for IDW or the semi-variogram model for kriging) [40], making the results operator-dependent and potentially less replicable. With IDW, the power hyperparameter p is influenced by the density of sample points. Indeed, higher values of p give greater influence to closer points, whereas lower values of p tend to produce smoother results by increasing the priority of more distant points [41]. With regard to INFLOS, the density is highly dependent on the crisis image’s spatial resolution and the filtering strength of the standard score threshold. To mitigate this issue, alternative techniques can be used, such as kriging, which accounts for spatial autocorrelation and ensures accurate and unbiased interpolation results [42,43]. Unfortunately, kriging is computationally intensive in both time and memory [44], making it impractical for large AOIs under tight time constraints and varying workstation specifications across the CEMS RM consortium.
As a result, INFLOS uses the natural neighbour algorithm, representing the best trade-off between all the requirements for CEMS RM. It is based on the principles of Voronoi tessellation [45,46,47] and does not require any input parameter to be set by the operator. This method identifies the nearest subset of samples to an unsampled point and calculates interpolated values by weighting the elevations based on their proportional areas, as well as the overlap between the Voronoi polygon for a given data point and that of neighbouring samples [48]. These concepts are formalised in Formulas (2) and (3), where
- is the interpolated value at point x.
- are the values of neighbouring data points.
- N is the number of neighbouring data points contributing to the interpolation.
- is the weight assigned to a neighbour i.
- is the area of the overlap between the Voronoi polygon of neighbour i and that of the interpolated point.
- is the total area of the Voronoi polygon for the interpolated point.
This ensures that the interpolated surface is smooth and continuous. Another advantage of natural neighbour interpolation is its ability to adapt to irregularly spaced data without fine-tuning parameters. However, this technique has more computational requirements than Nearest Neighbour interpolation or IDW, due to the complexity of working with Voronoi polygons. Nevertheless, the natural neighbour algorithm is a more robust option for the timely and accurate mapping of flood depths, due to answering all three criteria enumerated earlier.
The trade-offs between interpolation techniques considered in this study are summarised in Table 3.

Table 3.
Comparison of exact interpolation techniques analysed for INFLOS. The listed pros and cons consider CEMS RM requirements specifically, mostly processing speed and required hyperparameter tuning.
2.3. Sample Refinement and Densification
After the initial interpolation of the flood surface, the sampling set undergoes further refinement to guarantee accuracy and robustness. As stated in assumption (C), the cross-sections of the interpolated flood surface should approximate a flat profile. To achieve this, samples that introduce excessive slope in the flood surface, defined by a threshold of 0.5°, are identified and removed. This step is crucial, because slope within the flood surface may indicate anomalous data points, which could lead to inaccurate flood depths.
Subsequently, this curated dataset is densified to improve the robustness and smoothness of the interpolated flood surface. This is achieved by meshing flooded areas and extracting vertices from this mesh (Figure 6). Vertex density is proportional to the spatial resolution of the crisis image, thus enabling an adaptive process. Additional points are added along the buffered geometry of the water extend to maintain a flat flood surface plane and prevent edge effects. All these points are assigned an elevation value based on the 10 closest border sample points and a weighted-distance approach, before being integrated back into the full sample set. This step not only helps generate a smooth flood surface, but also minimises the influence of remaining outliers by increasing the density of data points.
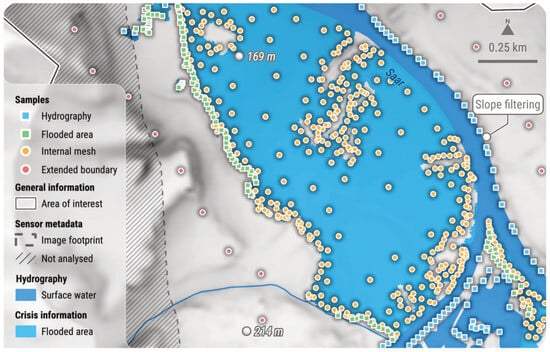
Figure 6.
Spatial distribution of sample points, following the application of outlier filtering and densification techniques, represents the dataset before the second-pass interpolation. Elevations derived from internal meshing and boundary extension are obtained directly from their nearest hydrography and flooded area neighbour samples. This example is based on an on-demand CEMS RM delineation product delivered for EMSR722 AOI02 Saar (Germany). DTM (10 m) courtesy of GeoBasis-DE/BKG (2018). All related products can be accessed through the official viewer for EMSR722: https://rapidmapping.emergency.copernicus.eu/EMSR722/ (accessed on 12 January 2025).
2.4. Second-Pass Interpolation and Flood Depth Computation
The final flood surface is obtained by applying the same interpolation algorithm as the first pass a second time—natural neighbour in this case—to the curated sample set as an input. The interpolated elevation values from the DTM are then subtracted from the flood surface, resulting in the depth values associated with the flooding. These depth values are only calculated for flooded areas, excluding the hydrographic data, as previously stated in assumption (D). Minor discrepancies between the crisis image and the elevation data could result in negative or zero depth values. To address this, a minimum threshold of 0.15 m is applied, ensuring that areas identified as flooded have a non-zero depth.
Next, a series of formatting procedures are undertaken to produce a layer that adheres to the standards and guidelines of CEMS RM. The flood depth values are distributed as a continuous raster file. To obtain vector layers, the data are then discretised into the following classes: below 0.50 m, 0.50 m to 1.00 m, 1.00 to 2.00 m, 2.00 m to 4.00 m, 4.00 m to 6.00 m, and above 6.00 m. This discrete representation is then converted and shared in vector format.
2.5. Validation and Quality Assessment
A significant challenge in the validation process for INFLOS is the absence of robust in situ data, which are crucial for validating flood depth values. This gap arises from the scarcity of validated, precise in situ measurements that can accurately represent flood extents and depths at specific moments, corresponding to the acquisition date and time of crisis satellite imagery.
Regarding the validation of results through the use of traditional flood modelling techniques, although hydraulic simulations offer a potential avenue for assessing INFLOS interpolation results, this approach requires considerable effort and reduces the number of flood products that can be verified. This may compromise the validity of the results, considering the variety and number of CEMS RM activations. Furthermore, hydraulic models have inherent limitations and depend on input data quality, which may not consistently capture the nuances of observed flood events or align with the CEMS RM data model.
Alternative data sources, such as traditional and social media, alongside water gauge readings, offer supplementary validation avenues. However, when available to the operator during production, these sources often lack precise timestamps and geolocations, reducing their reliability in matching the exact conditions and timing of satellite image acquisitions during a crisis. Nevertheless, they can indicate whether an area was flooded and to what extent.
Given these limitations, it is unrealistic to expect highly precise flood depths from INFLOS, as the system is primarily designed for rapid mapping to provide a situational overview for emergency management. Therefore, the primary metric for quality assessment during the validation process is the flatness of the interpolated flood surface, as well as the coherence of the inferred values when compared to elevation data. This criterion aligns with assumption (C), suggesting that a flatter surface indicates higher confidence in the result. Consequently, the quality assessment of INFLOS involves analysing cross-sections where both the DTM and the interpolated flood surface are compared. Figure 4 demonstrates this approach, illustrating how the flood surface and elevation e would be overlaid in a Geographical Information System (GIS) suite for analysis.
Additionally, a sensitivity analysis is also performed on key parameters, namely the interpolation technique and the standard score threshold used for filtering samples.
The interpolation technique and its potential hyperparameters are tested across all experiments, using the same sample set obtained at the end of the process described in Section 2.3. The objective is to determine the contribution of the proposed interpolation technique specifically. This analysis focuses on natural neighbour, IDW, and kriging, as outlined in Section 2.2.
The sensitivity of the standard score threshold used for filtering outliers in Section 2.3 is tested across values ranging from to , with an increment of . This results in 30 experiments per product referenced in Table 2. It employs an independent set of samples for testing, drawn randomly along the edge of the observed flood event. The sensitivity analysis is performed by sampling the reference elevation of the DTM and comparing it against interpolated values at the same location for the proposed range of standard scores. The size of the sample set during test time is calculated for each product using Formula (4), where
- n is the sample size.
- Z is the critical value of the standard normal distribution for a given confidence level. In this case, it ensures that the sample size is sufficient to verify that reference and interpolated elevations are not significantly different from one another. With the desired confidence interval of , the critical value is equal to .
- is the standard deviation of differences between reference and interpolated elevations, estimated from a pilot dataset.
- e is the acceptable margin of error, set to be within m of the mean reference elevation.
The number of samples for each product is then adjusted using the finite population correction, described in Formula (5), where
- is the adjusted sample size.
- n is the sample size, calculated using Formula (4).
- N is the total population size, corresponding to the total number of vertices for a given flood product.
Finally, INFLOS is benchmarked against FwDET [27], a comparable solution for flood mapping, to evaluate processing speed, a critical factor for rapid mapping. Products described in Table 2 are leveraged to assess the performance trade-offs between INFLOS and FwDET. The tests are conducted on a desktop computer equipped with an 8-core 3.60 GHz CPU and 32 GB of RAM. To ensure a fair comparison, INFLOS is evaluated against two configurations of FwDET: one without any post-processing and another incorporating FwDET’s optional iterative low-pass smoothing filter applied over 150 iterations.
3. Implementing the Algorithm and Results
3.1. Development Stage Overview
The development of INFLOS has been structured through multiple stages, categorised by the Technological Readiness Level (TRL) framework [52]. In a period of six months, INFLOS progressed from a proof of concept at TRL 3 to a mature solution for flood depth estimation at TRL 9. This progression involved rigorous testing across diverse landscapes, using a large range of flooded case studies derived from satellite images and elevation datasets.
Initial testing focused on single-date flood depth estimations within a constrained set of use cases. As development progressed, the scope expanded to include monitoring phases that accounted for fluctuating water extents and levels across the same AOIs at first. This process gradually incorporated a broader spectrum of use cases into the evaluation process.
These development stages led to the operational deployment of INFLOS into the CEMS RM toolkit. All partners within the CEMS RM consortium successfully used INFLOS to generate numerous flood depth products in real-world operational settings. This phased approach not only validated the performance of INFLOS across different scenarios, but also ensured its adaptability and robustness, reinforcing its value as a critical tool in flood response and management strategies.
3.2. Proof of Concept
Initially, INFLOS was tested on single-date flood products to validate the accuracy of the interpolated flood surfaces, ensuring they maintained near-flat profiles across various configurations. This testing was essential to confirm that the computed flood depths aligned with the elevations indicated by DTMs, regardless of the geographical features present within the event area. Consequently, the testing encompassed a diverse range of geographical settings, from narrow, deep valleys to large open plains, as detailed in Table 4. This comprehensive approach aimed to reflect the diversity of flood activations and related events within the CEMS RM framework.

Table 4.
List of CEMS RM activations used for conceptualising, developing, and testing INFLOS in an experimental setting. All related products are accessible through the CEMS RM portal: https://emergency.copernicus.eu/mapping/list-of-activations-rapid (accessed on 12 January 2025).
During this stage, a sensitivity analysis was carried out, leveraging testing sites described in Table 4. First, interpolation techniques were compared to validate insights from the available literature, regarding robustness to outliers, hyperparameter tuning, and compute time. A subset of these tests is showcased in Figure 7.
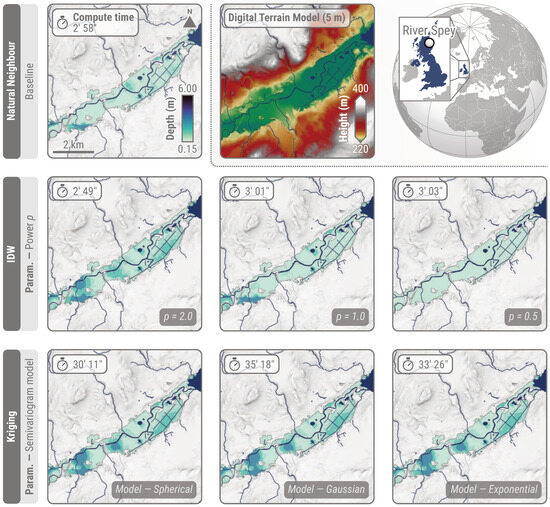
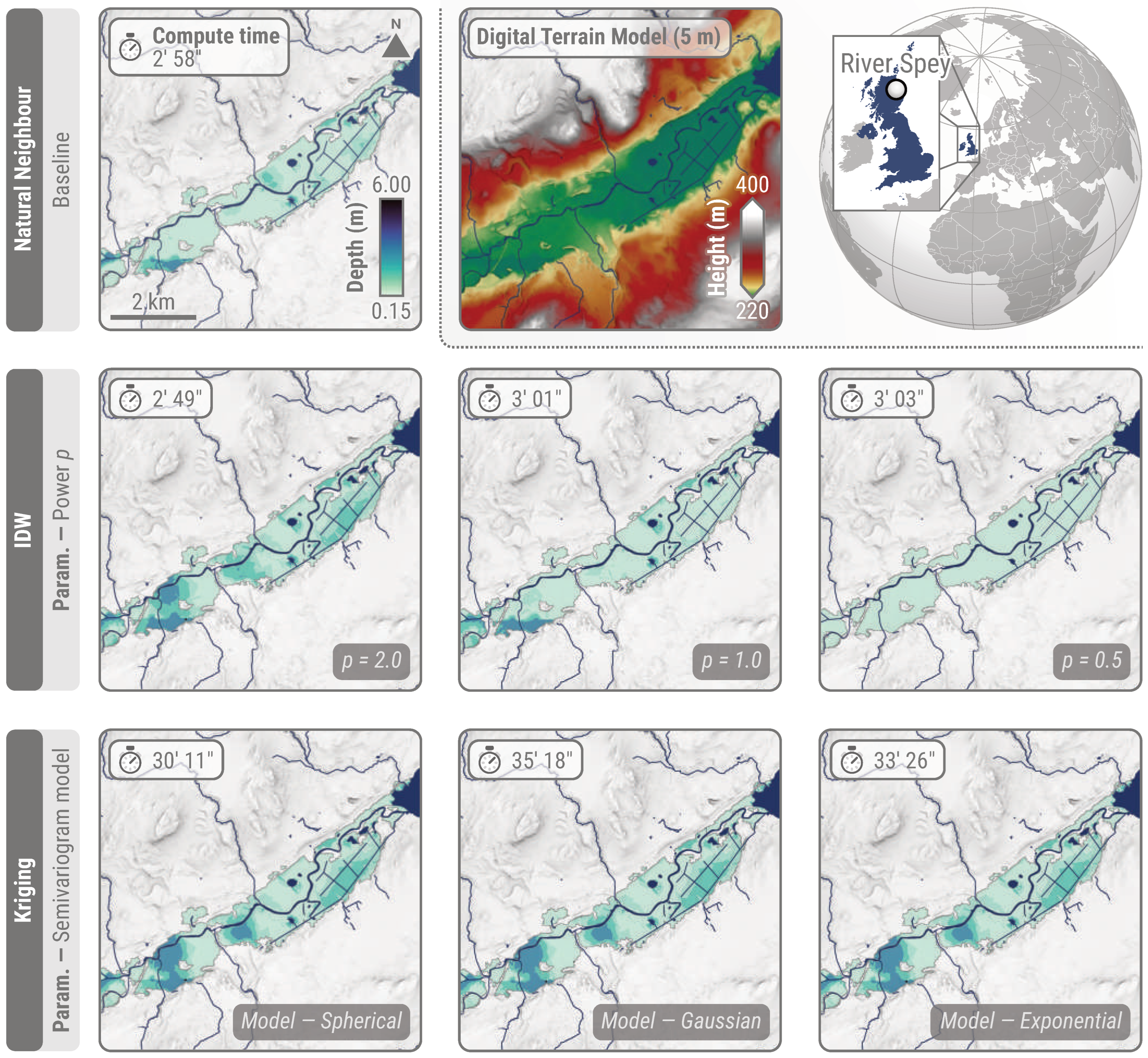
Figure 7.
Comparison of interpolation techniques—natural neighbour, IDW, and kriging—with flood depth estimates for EMSR698 AOI01 River Spey (Scotland, UK)—DEL MONIT01 (10 October 2023). The natural neighbour algorithm corresponds to the baseline used in this analysis. Both of the other techniques require hyperparameter tuning, with comparisons performed when conceptualising INFLOS. Examples of hyperparameter values are showcased, including the power value for IDW and the semivariogram model for kriging. Considering CEMS RM’s tight production schedule, compute time is also indicated. DTM (5 m) courtesy of Scottish Government, SEPA, and Scottish Water (2012).
While INFLOS yields compute times close to 3 min for EMSR698 AOI01 River Spey (Scotland, UK) with the natural neighbour and IDW algorithms, kriging ranges from 30.2 min to 35.3 min. Overall, this represents an increase of in compute time. Consequently, kriging already exceeds the target of a 30 min time frame for an AOI and event size that are below average compared to other events. Tuning the semivariogram model does not result in significant changes in flood depth, as exhibited in the last row of Figure 7, which is an important factor to minimise operator input by providing a sensible default value. Despite this perk, the compute time makes it unsuitable for the requirements of CEMS RM. In comparison, while IDW generates results promptly, the spatial patterns of flood depths vary greatly depending on p, the power value. Indeed, the higher the value of p, the more important the nearby samples. Conversely, the lower the p, the greater the importance of distant samples. This explains the increase in flood depth smoothness when decreasing the p value. As a result, IDW is also unsuitable for CEMS RM, due to reasons opposite to that of kriging, with the operator being required to fine-tune p. This analysis highlights the reasons why natural neighbour was selected, namely for the fast compute time and non-existent operator input.
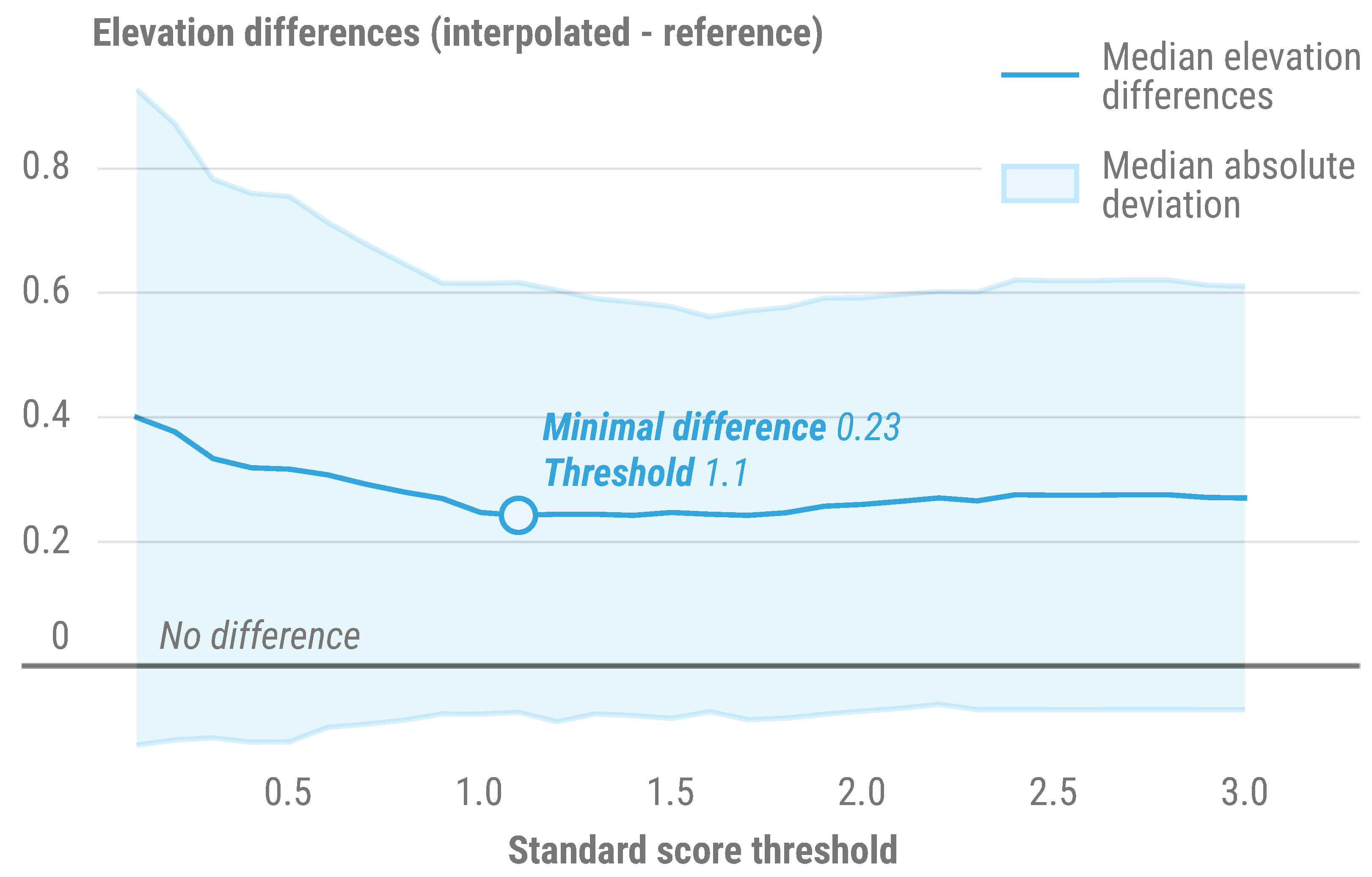
In addition to interpolation techniques, the impact of the standard score threshold used for filtering samples was also subject to a sensitivity analysis (Figure 8). Median elevation differences between interpolated and reference values were computed from an independent test set, based on values drawn at the location of 296,295 samples across all 183 evaluated products. Elevation differences reach an optimal minimum value of . This corresponds to a standard score threshold of , rounded down to as the default threshold value for INFLOS, due to simplicity and interpretability purposes. Overall, median elevation differences are systematically positive, without ever reaching a difference of 0, which would indicate no differences between interpolated and reference elevations. This shows a tendency to the overestimation of interpolated values, likely explained by delineation errors pulling the interpolation plane upwards along high slopes delimiting floodplains. Moreover, the median absolute deviation initially highlights a high dispersion of values, which taper down past a threshold of ∼1.0. This could indicate that the more intense the filtering, the less the interpolation adapts to local variations, which is especially problematic in large catchments where elevations vary greatly between upstream and downstream.
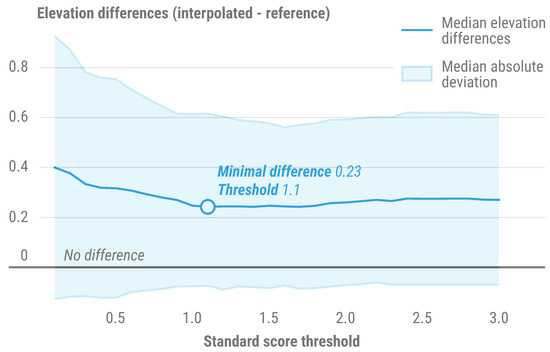
Figure 8.
Impact of the standard score threshold on elevation differences between interpolated and reference values across the test sample set. Elevation differences correspond to . To represent the central tendency, the median of differences was computed for each threshold i, as a robust metric to account for outliers. The median absolute deviation (MAD) measures dispersion around median elevation differences, and is also a metric robust to outliers. The lower boundary is computed as . The upper boundary is computed as [53].
Once INFLOS demonstrated sufficient stability for broader applications, the testing phase expanded to include monitoring cycles for all products in Table 4. This phase was critical to validate that INFLOS could accurately account for dynamic flood events. Specifically, the algorithm was required to demonstrate that the interpolated flood depths logically increased with the expansion of flood extents and decreased as the flooding receded.
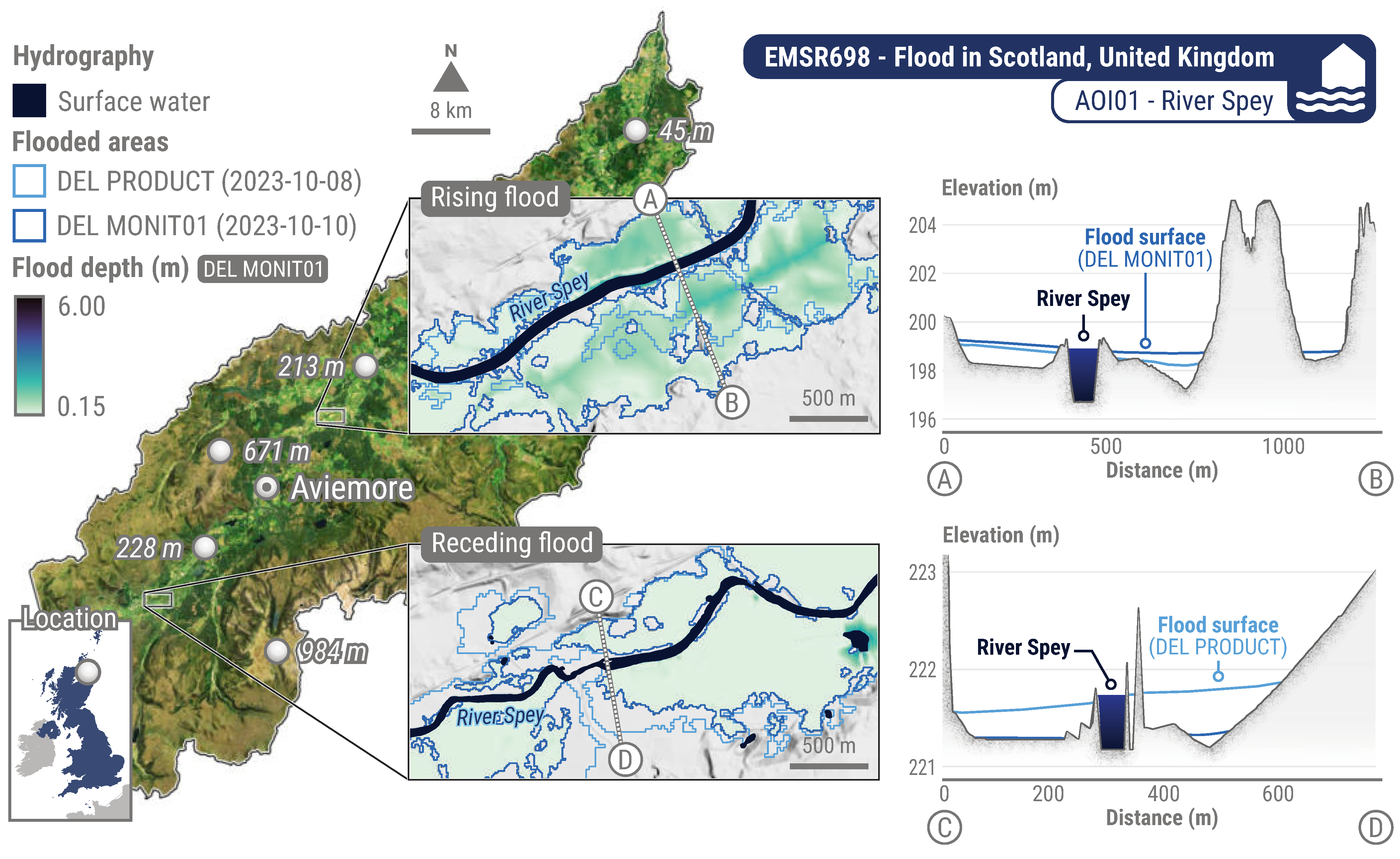
To illustrate these capabilities, Figure 9 displays upstream and downstream cross-sections that were generated for the River Spey in Scotland, as part of the EMSR698 activation. Upriver, the reduction in the flooded area results in a lower flood surface in the DEL MONIT01 generated on 10 October 2023, compared to the initial DEL PRODUCT from 8 October 2023. As per assumption (C), these interpolated flood surfaces are expected to be nearly flat, exhibiting slopes close or equal to . Despite vertical exaggerations in the profile visualisations in Figure 9, the slopes for flood surfaces in DEL PRODUCT and DEL MONIT01 are measured at and , respectively. This minimal variation across each profile supports the assumption of flat flood surfaces. Downriver, as the inundation extends, flooded areas in DEL MONIT01 display a broader extent, resulting in increased flood depth estimates compared to the earlier DEL PRODUCT. The profiles remain nearly uniform and consistent with the flatness criterion, showing flood surface slopes of for DEL PRODUCT and for DEL MONIT01.
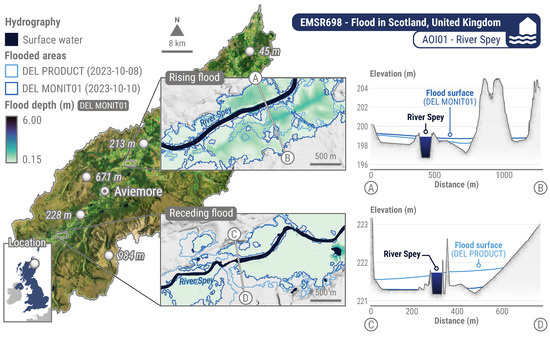
Figure 9.
Upstream and downstream cross-sections with rising and receding floodwater along the River Spey in Scotland. The DEL PRODUCT (8 October 2023) and DEL MONIT01 (10 October 2023) flooded areas were delineated from Sentinel-1 (20 m) imagery. They illustrate how the inundation progressed downstream between satellite acquisitions. The flood surface is a sum of elevation data and interpolated flood depth. Most artefacts in the flood depth layer are due to DTM quality. This example draws from on-demand CEMS RM products delivered for EMSR698 AOI01 River Spey (Scotland, UK). Pre-event imagery is a Sentinel-2 (10 m) product acquired on 7 September 2024. DTM (5 m) courtesy of Scottish Government, SEPA, and Scottish Water (2012). All related products can be accessed through the official viewer for EMSR698: https://rapidmapping.emergency.copernicus.eu/EMSR698/ (accessed on 12 January 2025).
The validation process was applied across all use cases listed in Table 4, yielding consistent results regardless of the geographical or hydrological context. This preliminary assessment, conducted under conditions similar to those in the CEMS RM framework, facilitated INFLOS’ progress towards a TRL of 5. At this stage, the proposed methodology demonstrated its effectiveness in a relevant environment, providing a solid basis for further enhancements and optimisations necessary for full operational deployment.
3.3. Pre-Operational Environment
The transition of INFLOS to a pre-operational stage involved an update in employed technologies. Initially, the proof of concept was conducted using ArcGIS Pro model builders, enabling rapid iteration across various use cases. After validating the methodology, the workflow was transferred to Jupyter Notebooks [54] and subsequently refined into standalone Python scripts, accommodating both ESRI and open-source platforms, notably incorporating WhiteboxTools [55] for its implementation of the natural neighbour algorithm, as well as geopandas [56], xarray [57] and sertit-utils [58]. This adaptability facilitated the integration of INFLOS into diverse technical environments, making it accessible via command line for advanced users, or through an ArcGIS Pro tool for a more user-friendly use.
Following this adaptation, INFLOS was shared among CEMS RM partners, initiating an extensive testing phase that involved processing over 180 flood products (Table 2). This was crucial not only for operational benchmarking, but also for ensuring compatibility across the varied IT infrastructures within the CEMS RM consortium. Feedback from partners played a vital role in this phase, identifying areas for improvement, which were addressed in subsequent updates.
This approach not only strengthened the tool’s robustness but also enabled an assessment of INFLOS’ performance in terms of execution time, a critical metric for its suitability in rapid mapping scenarios. Initial benchmarking was conducted internally at SERTIT, using a standard desktop computer setup equipped with an 8-core 3.60 GHz CPU and 32 GB of RAM. This configuration aimed to simulate a typical user environment, providing realistic performance insights. The median processing time using INFLOS was recorded at 5.2 min, highlighting its efficiency in managing datasets under typical CEMS RM operational conditions. Processing times varied significantly depending on the AOI, data complexity, and output size. The longest was 30.4 min for EMSR723 AOI01 Grand Est (France), which involved a large area of 527,668 ha, resulting in a raster size of 30,469 × 17,676 pixels. This scenario tested the tool’s capacity to handle extensive data volumes under demanding conditions. The quickest processing time was notably brief, at approximately 0.4 min for EMSR720 AOI03 Roca Sales (Brazil), with a small raster size of pixels for an area of 4633 ha.
The collaborative testing and refinement of INFLOS underscored its potential to meet end-user requirements in emergency mapping operations, with a TRL of 7, paving the way for full-scale production deployment.
3.4. Benchmarking
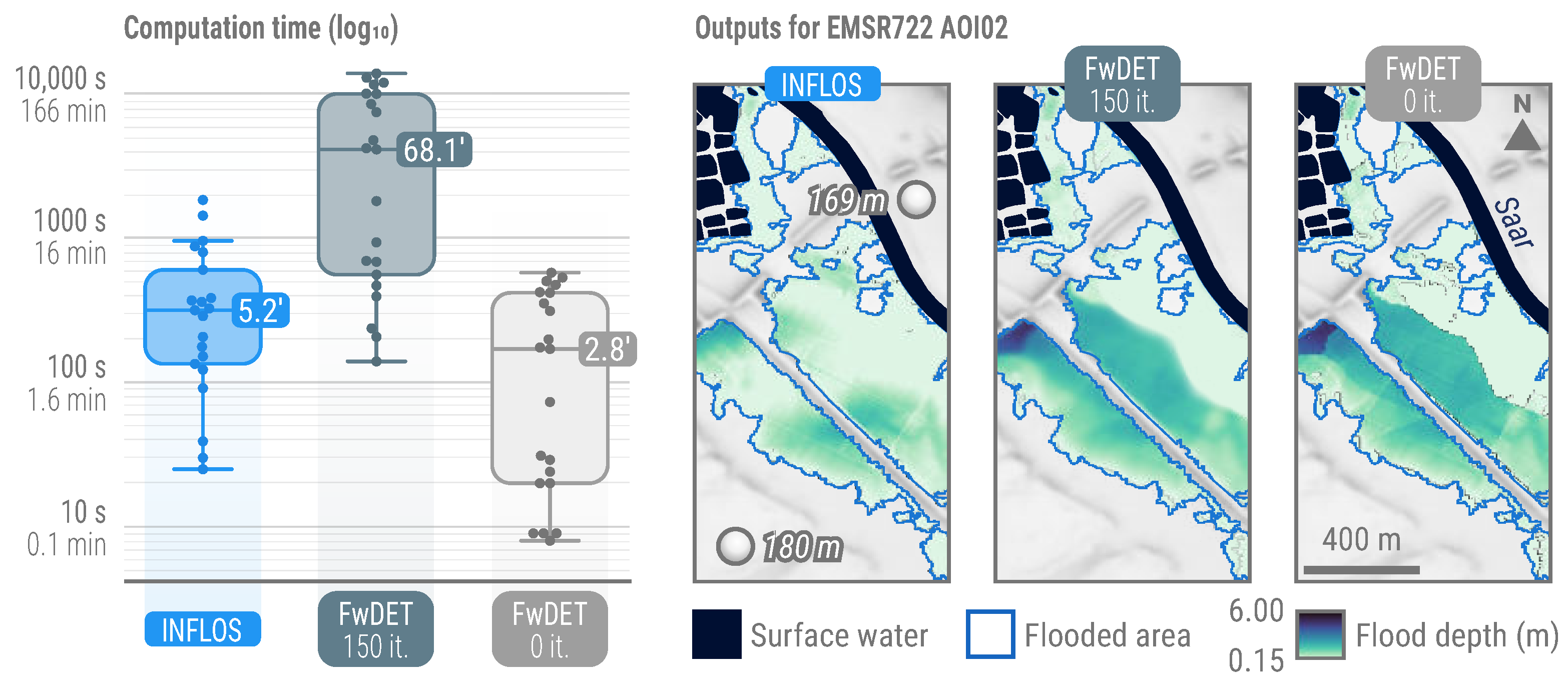
The analysis of INFLOS computation times indicates that it complies with the rapid processing requirements of CEMS RM, achieving a median computation time of 5.2 min (Figure 10). In comparison, FwDET demonstrates faster median computation times of 2.8 min when its optional smoothing post-process is omitted, with zero iterations. However, this comes at the cost of reduced output quality. Indeed, FwDET’s low-pass filter, typically requiring from 100 to 200 iterations for optimal results [27], significantly enhances the smoothness and flatness of the flood surface, but also increases computational requirements. This trade-off is illustrated in Figure 10.
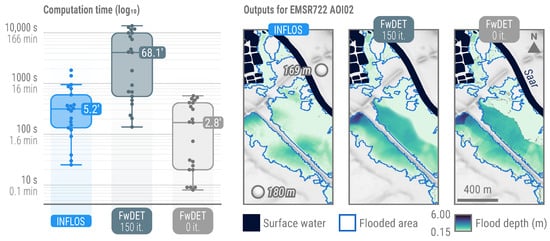
Figure 10.
Benchmarking of INFLOS compared to FwDET with 0 and 150 iterations. For enhanced visual clarity, computation times are presented on a logarithmic scale. Snapshots from EMSR722 AOI01 Blies (Germany)—DEL PRODUCT (19 May 2024) illustrate typical flood depth estimates when using these techniques. Other displayed layers include hydrography downloaded from OpenStreetMap and flooded areas delineated from RADARSAT-2 imagery (18 May 2024). DTM (10 m) courtesy of GeoBasis-DE/BKG (2018). All related products can be accessed through the official viewer for EMSR722: https://rapidmapping.emergency.copernicus.eu/EMSR722/ (accessed on 12 January 2025).
Simultaneously, INFLOS exhibits a broader range of computation times, spanning from 0.4 to 30.4 min, reflecting variability due to AOI size and terrain complexity. By contrast, FwDET without post-processing maintains a narrower range of 0.1 to 9.5 min, indicating better scalability than INFLOS. However, applying FwDET’s low-pass filter substantially impacts performance, with a median computation time of 68.1 min after 150 iterations, exceeding INFLOS’ maximum processing time, even for the largest AOIs and flood event sizes.
3.5. Operational Production
The integration of INFLOS into the CEMS RM portfolio required adhering to data models, symbology, and processing protocol requirements. This ensures that the outputs from INFLOS are not only thematically accurate, but also seamlessly fit into the existing operational framework. Flood depth is distributed in the Crisis Information Package (CIP) as a continuous raster layer and a classified vector file. This dual-format delivery ensures versatility in usage, catering to different user needs and technical environments. The raster format enables detailed quantitative analyses, while the vector format facilitates integration and visualisation within various GIS platforms. Moreover, a standardised symbology has been developed, enhancing the readability and usability of flood maps. This includes defining colour scales that accurately represent water depth, making it intuitive for end-users to interpret the severity and extent of flooding directly from the map. Figure 11 demonstrates the finalised integration of INFLOS into the CEMS RM portfolio, showcasing a flood delineation monitoring product for EMSR720 in Brazil.
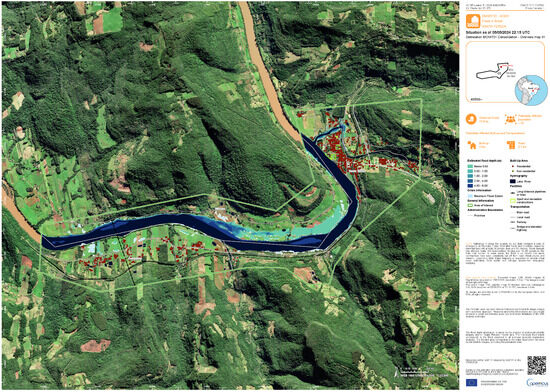
Figure 11.
Example of an on-demand CEMS RM delineation monitoring product. This ready-to-print map was generated for EMSR720 AOI05 Santa Tereza (Brazil, State of Rio Grande do Sul) on 6 May 2024, as part of an activation triggered by inundations. It shows the current and maximum extent of the flood, as well as an estimate of flood depth. WorldDEM Neo (5 m) courtesy of Airbus (2024). All related products can be accessed through the official viewer for EMSR720: https://rapidmapping.emergency.copernicus.eu/EMSR720/ (accessed on 12 January 2025).
As a result of the comprehensive development phase, INFLOS has evolved into a fully operational system (TRL 9), being utilised for all delineation products within CEMS RM, and effectively tracking fluctuations in flood events over time.
4. Discussion
INFLOS has demonstrated its efficiency in deriving flood depths from flood extents delineated using remote sensing imagery and elevation data within the context of CEMS RM. Following extensive testing across over 180 products, INFLOS has proven its adaptability to a diverse range of input data and terrain configurations, showcasing its operational viability. The tool effectively processes imagery with varying resolutions, sourced from both optical and Synthetic Aperture Radar (SAR) sensors. While INFLOS is compatible with medium-resolution Digital Terrain Models (DTMs), such as FABDEM (30 m resolution), finer grid cell sizes and authoritative sources are generally preferred. In particular, high-resolution (HR) or Very High-Resolution (VHR) DTMs can significantly enhance the accuracy of flood depth estimates by capturing intricate topographical variations often found in flood-prone areas [59]. However, the quality of the DTM also plays a crucial role, as poor-quality data can lead to inaccurate interpolations. In such cases, operators must weigh the trade-offs. When authoritative or high-resolution data are compromised due to defects such as those listed in Table 5, it is often preferable to use FABDEM as a fallback solution. This strategy minimises potential errors in flood depth values resulting from input elevation data.

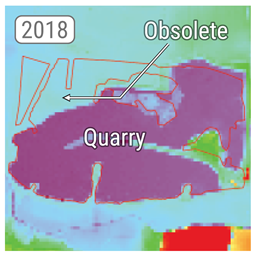
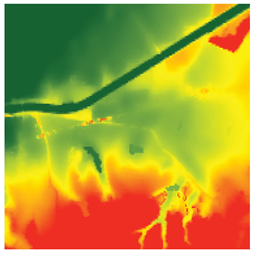
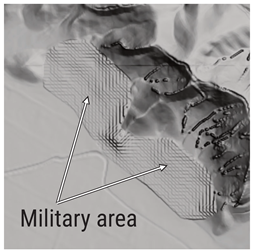
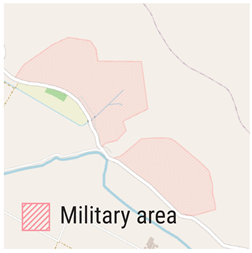
Table 5.
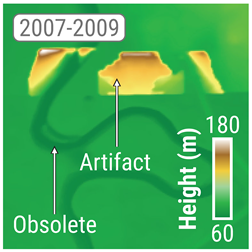
During CEMS RM activations, issues pertaining to elevation data were encountered when generating flood depth products. The example of outdated data illustrates discrepancies with current imagery, with the expansion of a quarry indicating land cover and land use changes that cannot be accounted for during production. The example of product quality shows that there are stark differences between the authoritative DTM and FABDEM data, the latter being more representative of actual topography. The authoritative DTM was generated using TIN interpolation, likely from a sparse point cloud, thereby explaining the low-detail and low-quality product. The example of confidential areas showcases one of the several techniques used to mask areas such as military bases or airports. In these situations, placeholder data are used in place of the actual elevation. These placeholder data can be fully masked out, inferred from nearby pixels, or set to a specific value. The combination of variables that results in a terrain model that is not representative of the current topography is demonstrated by the example of compounding errors. In this instance, improper processing of the available DTM led to artefacts up to 120 m above the floodplain. Additionally, there are differences in the current imagery that show how a stream was channelled between 2009 and 2023, along with changes in land use and cover.
While this study and the rapid mapping process do not assess the suitability of specific Digital Terrain Models (DTMs) for flood mapping, such an evaluation is crucial for end-users to gauge the reliability and limitations of the delivered products. In addition to scrutinising potential flaws in the input data, it is essential to consider parameters such as spatial resolution and vertical accuracy, which can significantly impact flood depth estimations. Notably, FABDEM achieves a median absolute difference of 1.04 m compared to reference data in flood-prone areas [60], but this level of vertical accuracy may still be insufficient for certain use cases, such as EMSR708 AOI01 (Westhoek, Belgium), where floodplain elevations range between 4.0 and 5.0 m. Although some existing studies have explored the importance of vertical accuracy in the context of flooding [61], none have addressed the specific challenges and requirements of rapid mapping, highlighting a notable gap in the academic literature.
Even though INFLOS meets the original operational requirement of processing within a 30-min time frame, the increasing scale and frequency of major disasters [62] suggests a potential rise in the size of AOIs and flooded areas needing analysis. In this regard, the lower processing times of FwDET without post-processing suggest areas for improvement. One potential avenue could be exploring alternative interpolation techniques that maintain the quality of flood surface representation while reducing computational overhead. Currently, both interpolation passes account for over 80 % of INFLOS’ runtime, making such a change crucial for improving its operational capabilities.
As illustrated in Figure 10, INFLOS generates smooth flood surfaces, verifying assumption (C) proposed in Section 2. This result is achieved by leveraging the natural neighbour interpolation algorithm, which considers the surrounding samples for each interpolated point, effectively integrating a built-in smoothing pass [48]. In comparison, FwDET relies on the Nearest Neighbour algorithm [27], producing tessellated surfaces that do not convincingly depict water surfaces, especially in complex terrain, such as meandering entrenched valleys. As a result, this approach does not meet our initial assumptions and requirements as well as INFLOS. This is reflected in Figure 10 by significant changes in flood depths. Although the low-pass filter mitigates this issue to some extent, its impact on computation time reduces FwDET’s usability in rapid mapping contexts. In addition, the comparison between interpolation techniques in Figure 7 highlights the benefits of using the natural neighbour algorithm, with a fast processing time and no parameter fine-tuning from operators.
Nonetheless, alternative interpolation techniques could be investigated to potentially yield improvements in computational efficiency, interpolated elevations, and, ultimately, operational flood depth products. However, the interpolation technique employed by INFLOS should preserve an exact nature to ensure that elevations at sample locations are the same between interpolated and references values. One promising example is the Radial Basis Function (RBF) method [63], which can effectively balance accuracy and computational efficiency. Furthermore, the robust handling of outliers and incorporation of spatial autocorrelation analysis would likely provide additional enhancements to the results.
Operators with advanced knowledge of INFLOS may still want to fine-tune this threshold in specific circumstances to account for pronounced elevation amplitudes and possibly improve depth estimates. Although the proposed methodology incorporates outlier removal procedures, it remains vulnerable to the precision and quality of input data, not just the Digital Terrain Models (DTMs). In particular, over- and under-estimations of flooded areas can significantly impact results. Thorough data cleaning is crucial to maintaining output accuracy. While the methodology is quick and reliable at the statistical distribution level, it lacks sensitivity to local context, particularly when dealing with large flood polygons spanning several kilometres. In complex and heterogeneous terrains, the standard score threshold may inadvertently eliminate locally meaningful and valid points. Moreover, despite the fact that the sensitivity analysis produced the default standard score threshold used for outlier filtering,
Since spatial autocorrelation highlights patterns and relationships in the planimetric domain by measuring a variable’s degree of correlation with itself across space, it could be used to address problems with standard score filtering [64]. Indeed, nearby points tend to be more similar to each other than to distant points in the context of elevation data. While robust kriging [65] or empirical Bayesian kriging [66] directly account for spatial autocorrelation in the interpolation technique, these algorithms have been shown to be too time-consuming for rapid mapping requirements in an operational setting. An alternative would be to quantify the spatial autocorrelation for each sample, using metrics like the Local Moran’s I or Getis-Ord [67]. Indeed, they show negative autocorrelation when high and low elevations are scattered, and positive autocorrelation when similar values cluster spatially.
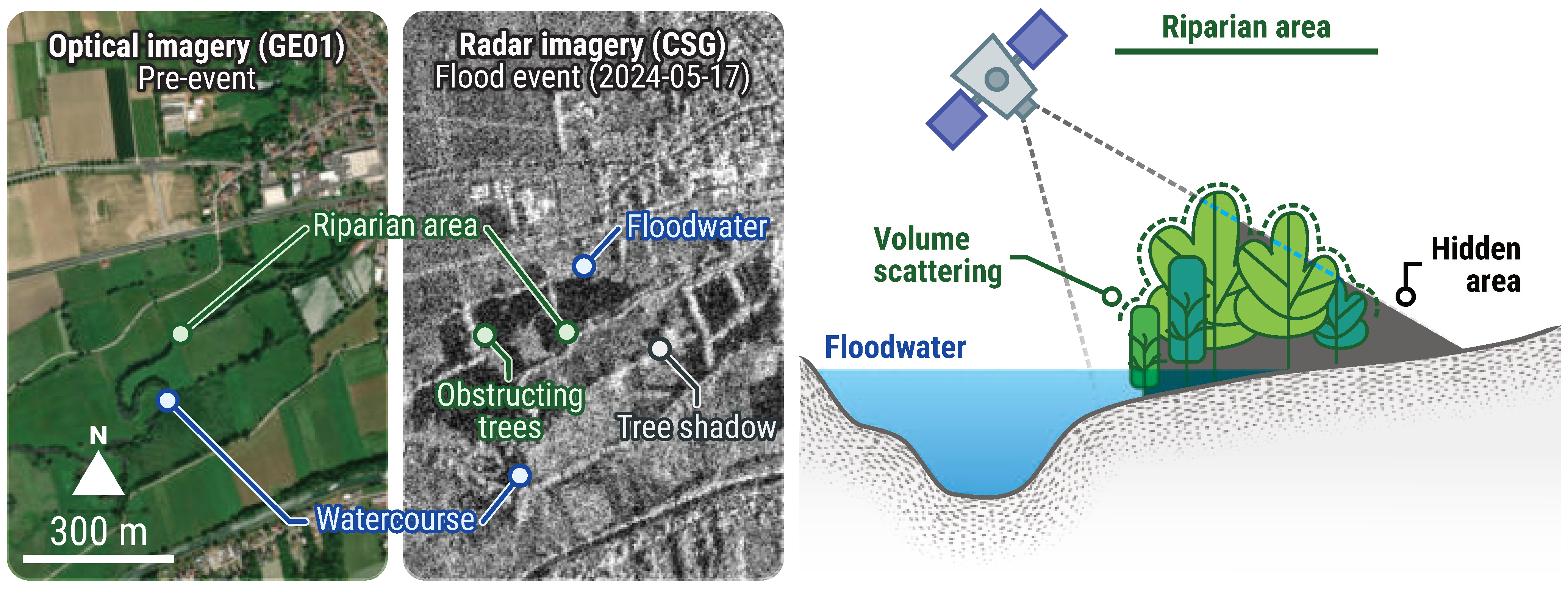
Regardless of the filtering technique employed, satellite- and aerial-based water extractions remain a significant challenge in natural landscapes, particularly in riparian and forested areas (Figure 12). Dense vegetation can obscure water bodies, leading to substantial under-detection. Standard outlier filtering techniques often struggle to capture these submerged areas, as they can be invisible in optical imagery and difficult to distinguish in SAR imagery due to canopy backscatter. Furthermore, SAR imagery poses an additional challenge, as shadows cast by topography and trees can exhibit similar amplitude characteristics to water surfaces, which typically display low values due to specular reflection. This can result in inaccurate flood depth estimations, particularly when false positives occur upslope of flood-prone areas, causing the interpolation plane to be artificially elevated.
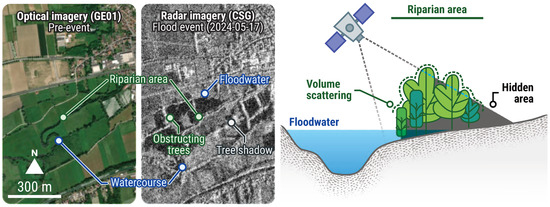
Figure 12.
Limits to flood mapping using remote sensing in semi-natural and forested areas. Floods can be hidden by a canopy, with the sensors available as part of crisis activities. In addition, tall vegetation can block incident signal, causing shadows whose backscatter or lack thereof is similar to that of water. The example here is based on EMSR722 AOI01 Blies (Germany), following an activation triggered on 17 May 2024. The pre-event optical image (GeoEye01 © Maxar), acquired on 29 May 2023, shows an open-field agricultural system with riparian vegetation situated in a broad, level floodplain. The crisis radar image (COSMO-SkyMed Second Generation © e-GEOS), acquired on 21 May 2024, displays flooded areas in dark colour, resulting from low backscattering signals from water surfaces. It is also evident how tall vegetation affects backscatter. The radar sensors used for rapid mapping carry C- or X-band sensors, which are unable to penetrate tree crowns and capture floodwater beneath the canopy. Areas that are susceptible to flooding, such as riparian corridors, exhibit high backscatter. Furthermore, owing to the angle of radar sensors, tall vegetation emits shadows without any backscatter, resulting in dark areas akin to those of flooded fields. All related products can be accessed through the official viewer for EMSR722: https://rapidmapping.emergency.copernicus.eu/EMSR722/ (accessed on 12 January 2025).
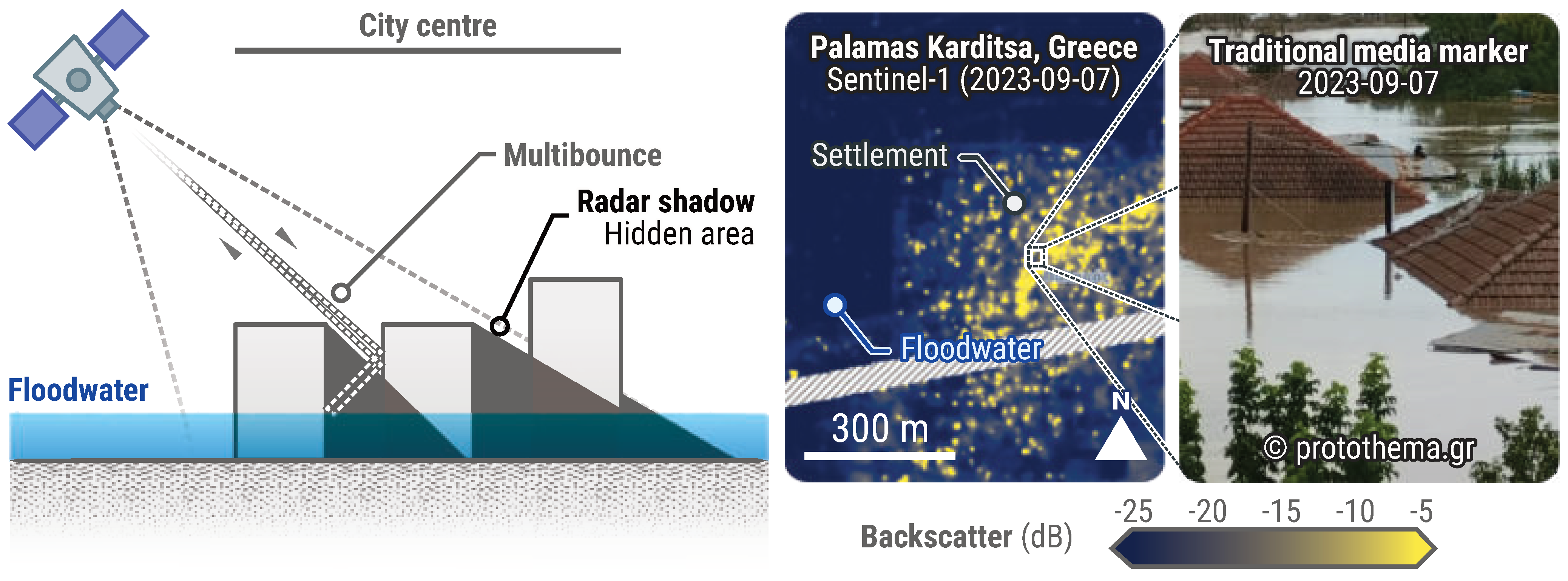
Urban environments present challenges for flood mapping as well, due to their complex geometry and dense structures. Optimal flood mapping in these areas requires the use of VHR imagery, captured at a nadir angle, to improve visibility in street corridors. However, SAR sensors are inherently side-looking and often face difficulties in this setting. Street geometry can lead to multiple backscatter rebounds off angular surfaces like buildings, causing strong return signals that may mask the presence of floodwater (Figure 13). Additionally, less dense settlements experience radar shadowing from buildings and other tall features.
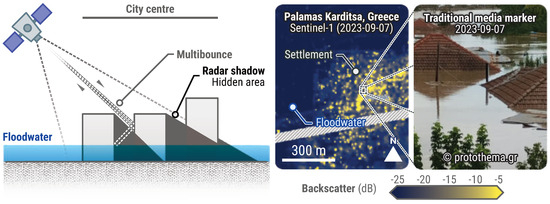
Figure 13.
Limits to flood mapping using remote sensing in an urban context. This example pertains to EMSR692 (Greece, Thessaly Region), an activation triggered on the 5 September 2023 following heavy rainfall. The Sentinel−1 radar image (7 September 2023) shows a high backscatter in the municipality of Palamas Karditsa (AOI02), even though it was entirely flooded as per various sources, including water gauges and media data. Floodwater should result in low backscatter, as water surfaces reflect the radar signal incidentally, a phenomenon visible in the fields around Palamas Karditsa. High backscatter in the flooded city is the result of multibounce scattering, caused by buildings and narrow streets. Media data were collected and made available by Hensoldt AG. All related products can be accessed through the official viewer for EMSR692: https://rapidmapping.emergency.copernicus.eu/EMSR692/ (accessed on 12 January 2025).
Recent techniques proposed by Chini et al. (2019) [68] leverage Sentinel-1 interferometry to mitigate these issues, demonstrating the potential of interferometry in urban flood mapping. Radar interferometry can discern subtle elevation changes by analysing the phase differences between SAR images acquired at different times [69], potentially indicating the presence of water in settlements. However, incorporating interferometry into rapid mapping workflows would require additional effort to assess repeatability, performance, and timeliness. To address some of the limitations of remote sensing and INFLOS, SERTIT has initiated the development of an extrapolation tool called EXFLOS (EXtrapolated FLood Surfaces) within the framework of CEMS RM. The purpose of EXFLOS is to support the parametric flooding of various landscapes, including urban settlements or vegetated areas, while still leveraging the original layers mentioned in Table 1. The EXFLOS tool is still in the development and validation phase, and will be presented in a separate publication.
Although shadows and obstructions caused by above-ground features, such as buildings and trees, can lead to both under- and over-estimations of actual flooded areas, their impact on rapid mapping and flood depth estimation has yet to be explored. While over-estimations can be partially addressed through operator training in computer-aided image interpretation, under-estimations remain a significant challenge with no readily available solution in the context of rapid mapping. EXFLOS offers potential as a faster alternative to time-intensive hydraulic modelling, but a better understanding of how flood delineation quality impacts flood depth estimation is critical for both consortium members and end-users. Nonetheless, addressing this matter would require an important collaborative effort at the consortium level, rather than by an individual entity, to accommodate variations in image interpretation and processing across operators and production sites.
5. Conclusions
INFLOS is a novel methodology developed for estimating flood depth within the context of the Copernicus Emergency Management Service’s Rapid Mapping (CEMS RM) framework. Conceptualised independently of similar solutions, INFLOS has undergone a rigorous development process, evolving from a proof of concept to a mature and operational tool. This progression involved thorough testing across diverse landscapes, crisis imagery from optical and Synthetic Aperture Radar (SAR) sensors, and various Digital Terrain Model (DTM) datasets. The phased approach validated INFLOS’ performance across different scenarios, ensuring its adaptability and robustness. This reinforced its value as a critical tool in flood response and management strategies. Initially, the proof of concept focused on single-date flood product testing, verifying the consistency of the interpolated flood surfaces with DTM elevations. Subsequent testing expanded to include monitoring cycles, which demonstrated INFLOS’ ability to account for dynamic flood events. The transition to a pre-operational stage involved adapting the system to diverse technical environments, making it accessible through both command-line and graphical user interfaces. Extensive testing and refinement in this phase enhanced the tool’s robustness and allowed for performance evaluation against comparable solutions, such as FwDET. Execution time, a critical metric for rapid mapping scenarios, was also extensively tested and optimised. The results highlight INFLOS’ key strengths, as it balances scalability and computational efficiency while delivering flood surface outputs suitable for operational rapid mapping. The system’s final integration into CEMS RM demonstrates its maturity, making it an operational tool used for all delineation products, including monitoring phases. In summary, INFLOS has undergone a comprehensive development process, resulting in a robust and effective tool for flood depth estimation. Its validated performance and adaptability make it a valuable asset in flood response and management strategies. Moreover, INFLOS flood depth outputs will enhance the accuracy and information content of emergency mapping products, providing valuable insights for the flood risk management community. The information has potential for assessing potential damage resulting from flood events and estimating economic impact [70].
Author Contributions
Conceptualisation, A.C.; methodology, A.C., R.B., Q.P. and S.C.; software, R.B. and Q.P.; validation, P.C., C.H., A.C., Q.P. and R.B.; writing—original draft preparation, Q.P., S.C. and A.C.; writing—review and editing, Q.P., S.C., P.C. and A.C.; visualisation, Q.P.; supervision, S.C. and P.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original data presented in the study are openly available either using CEMS RM’s official OpenAPI, or manually via the portal: https://emergency.copernicus.eu/mapping/list-of-activations-rapid (accessed on 12 January 2025).
Acknowledgments
We would like to express our gratitude to the Joint Research Centre for their support and guidance in the development of this methodology, more specifically Pietro Ceccato, Jean-François Pekel, Alan Steel, Paolo Pasquali, Simone Dalmasso, Inès Joubert-Boitat, and Oliva Martin Sanchez. Their expertise and insights have been invaluable, as this work would not have been possible without their contribution. We are also grateful to our CEMS RM partners, with a special mention for e-GEOS, the project’s prime contractor, as well as team members CLS, GAF AG, GMV, IABG, Ithaca, Planetek Hellas, TPZ Iberica, and SERTIT, for their active engagement and operational use of INFLOS. Their practical application of the tool has provided us with invaluable insights, which have led to significantly enhancing the robustness and relevance of our work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tarasova, L.; Lun, D.; Merz, R.; Blöschl, G.; Basso, S.; Bertola, M.; Miniussi, A.; Rakovec, O.; Samaniego, L.; Thober, S.; et al. Shifts in flood generation processes exacerbate regional flood anomalies in Europe. Commun. Earth Environ. 2023, 4, 49. [Google Scholar] [CrossRef] [PubMed]
- Delforge, D.; Wathelet, V.; Below, R.; Sofia, C.L.; Tonnelier, M.; Loenhout, J.v.; Speybroeck, N. EM-DAT: The Emergency Events Database. Res. Sq. 2024; preprint. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Viglione, A.; Perdigão, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Rentschler, J.; Salhab, M. People in Harm’s Way: Flood Exposure and Poverty in 189 Countries; Technical Report; World Bank: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Makhnovsky, D. The Coastal Regions of Europe: Economic Development at the Turn of the 20th Century. Balt. Reg. 2014, 4, 50–66. [Google Scholar] [CrossRef]
- European Commission; Eurostat. Eurostat Regional Yearbook 2011; Publications Office: Luxembourg, 2011. [Google Scholar]
- Kummu, M.; De Moel, H.; Ward, P.J.; Varis, O. How Close Do We Live to Water? A Global Analysis of Population Distance to Freshwater Bodies. PLoS ONE 2011, 6, e20578. [Google Scholar] [CrossRef] [PubMed]
- United Nations. World Urbanization Prospects: The 2018 Revision; United Nations: New York, NY, USA, 2019; OCLC: 1120698127. [Google Scholar]
- Notti, D.; Giordan, D.; Caló, F.; Pepe, A.; Zucca, F.; Galve, J.P. Potential and Limitations of Open Satellite Data for Flood Mapping. Remote Sens. 2018, 10, 1673. [Google Scholar] [CrossRef]
- Boccardo, P.; Giulio Tonolo, F. Remote Sensing Role in Emergency Mapping for Disaster Response. In Engineering Geology for Society and Territory—Volume 5; Lollino, G., Manconi, A., Guzzetti, F., Culshaw, M., Bobrowsky, P., Luino, F., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 17–24. [Google Scholar] [CrossRef]
- Munawar, H.S.; Hammad, A.W.A.; Waller, S.T. Remote Sensing Methods for Flood Prediction: A Review. Sensors 2022, 22, 960. [Google Scholar] [CrossRef]
- Ajmar, A.; Boccardo, P.; Broglia, M.; Kucera, J.; Giulio-Tonolo, F.; Wania, A. Response to Flood Events: The Role of Satellite-based Emergency Mapping and the Experience of the Copernicus Emergency Management Service. In Flood Damage Survey and Assessment: New Insights from Research and Practice, 1st ed.; Geophysical Monograph Series; Molinari, D., Menoni, S., Ballio, F., Eds.; Wiley: Hoboken, NJ, USA, 2017; pp. 211–228. [Google Scholar] [CrossRef]
- Brunner, G.W. HEC-RAS River Analysis System. Hydraulic Reference Manual. Version 1.0; Technical Report; Hydrologic Engineering Center: Davis, CA, USA, 1997. [Google Scholar]
- Van Der Knijff, J.M.; Younis, J.; De Roo, A.P.J. LISFLOOD: A GIS-based distributed model for river basin scale water balance and flood simulation. Int. J. Geogr. Inf. Sci. 2010, 24, 189–212. [Google Scholar] [CrossRef]
- Erena, S.H.; Worku, H.; De Paola, F. Flood hazard mapping using FLO-2D and local management strategies of Dire Dawa city, Ethiopia. J. Hydrol. Reg. Stud. 2018, 19, 224–239. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.G.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S.; et al. Benchmarking 2D hydraulic models for urban flooding. Proc. Inst. Civ.-Eng.—Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Jamali, B.; Bach, P.M.; Cunningham, L.; Deletic, A. A Cellular Automata Fast Flood Evaluation (CA-ffé) Model. Water Resour. Res. 2019, 55, 4936–4953. [Google Scholar] [CrossRef]
- Kleyko, D.; Frady, E.P.; Sommer, F.T. Cellular Automata Can Reduce Memory Requirements of Collective-State Computing. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 2701–2713. [Google Scholar] [CrossRef]
- Gibson, M.J.; Savic, D.A.; Djordjevic, S.; Chen, A.S.; Fraser, S.; Watson, T. Accuracy and Computational Efficiency of 2D Urban Surface Flood Modelling Based on Cellular Automata. Procedia Eng. 2016, 154, 801–810. [Google Scholar] [CrossRef]
- Liu, L.; Liu, Y.; Wang, X.; Yu, D.; Liu, K.; Huang, H.; Hu, G. Developing an effective 2-D urban flood inundation model for city emergency management based on cellular automata. Nat. Hazards Earth Syst. Sci. 2015, 15, 381–391. [Google Scholar] [CrossRef]
- Hosseiny, H.; Nazari, F.; Smith, V.; Nataraj, C. A Framework for Modeling Flood Depth Using a Hybrid of Hydraulics and Machine Learning. Sci. Rep. 2020, 10, 8222. [Google Scholar] [CrossRef] [PubMed]
- Elkhrachy, I. Flash Flood Water Depth Estimation Using SAR Images, Digital Elevation Models, and Machine Learning Algorithms. Remote Sens. 2022, 14, 440. [Google Scholar] [CrossRef]
- Karpatne, A.; Ebert-Uphoff, I.; Ravela, S.; Babaie, H.A.; Kumar, V. Machine Learning for the Geosciences: Challenges and Opportunities. arXiv 2017, arXiv:1711.04708. [Google Scholar] [CrossRef]
- Cian, F.; Marconcini, M.; Ceccato, P.; Giupponi, C. Flood depth estimation by means of high-resolution SAR images and lidar data. Nat. Hazards Earth Syst. Sci. 2018, 18, 3063–3084. [Google Scholar] [CrossRef]
- Betterle, A.; Salamon, P. Water depth estimate and flood extent enhancement for satellite-based inundation maps. Nat. Hazards Earth Syst. Sci. 2024. [Google Scholar] [CrossRef]
- Cohen, S.; Brakenridge, G.R.; Kettner, A.; Bates, B.; Nelson, J.; McDonald, R.; Huang, Y.; Munasinghe, D.; Zhang, J. Estimating Floodwater Depths from Flood Inundation Maps and Topography. J. Am. Water Resour. Assoc. 2018, 54, 847–858. [Google Scholar] [CrossRef]
- Cohen, S.; Raney, A.; Munasinghe, D.; Loftis, J.D.; Molthan, A.; Bell, J.; Rogers, L.; Galantowicz, J.; Brakenridge, G.R.; Kettner, A.J.; et al. The Floodwater Depth Estimation Tool (FwDET v2.0) for improved remote sensing analysis of coastal flooding. Nat. Hazards Earth Syst. Sci. 2019, 19, 2053–2065. [Google Scholar] [CrossRef]
- Maxant, J.; Braun, R.; Caspard, M.; Clandillon, S. ExtractEO, a Pipeline for Disaster Extent Mapping in the Context of Emergency Management. Remote Sens. 2022, 14, 5253. [Google Scholar] [CrossRef]
- OpenStreetMap Contributors. Planet Dump. 2017. Available online: https://www.openstreetmap.org (accessed on 14 August 2024).
- Hawker, L.; Uhe, P.; Paulo, L.; Sosa, J.; Savage, J.; Sampson, C.; Neal, J. A 30 m global map of elevation with forests and buildings removed. Environ. Res. Lett. 2022, 17, 024016. [Google Scholar] [CrossRef]
- Denbina, M.; Simard, M.; Rodriguez, E.; Wu, X.; Chen, A.; Pavelsky, T. Mapping Water Surface Elevation and Slope in the Mississippi River Delta Using the AirSWOT Ka-Band Interferometric Synthetic Aperture Radar. Remote Sens. 2019, 11, 2739. [Google Scholar] [CrossRef]
- Rahman, P.; Ali, M.S. Change in Transverse Slope of Water Surface at River Bend: A Numerical Study. J. Eng. Sci. 2021, 12, 93–101. [Google Scholar] [CrossRef]
- Mascha, E.J.; Vetter, T.R. Significance, Errors, Power, and Sample Size: The Blocking and Tackling of Statistics. Anesth. Analg. 2018, 126, 691–698. [Google Scholar] [CrossRef]
- Shyamala, G.; Arun Kumar, B.; Manvitha, S.; Vinay Raj, T. Assessment of Spatial Interpolation Techniques on Groundwater Contamination. In International Conference on Emerging Trends in Engineering (ICETE); Satapathy, S.C., Raju, K.S., Molugaram, K., Krishnaiah, A., Tsihrintzis, G.A., Eds.; Series Title: Learning and Analytics in Intelligent Systems; Springer International Publishing: Cham, Switzerland, 2020; Volume 2, pp. 262–269. [Google Scholar] [CrossRef]
- Xu, W.; Zou, Y.; Zhang, G.; Linderman, M. A comparison among spatial interpolation techniques for daily rainfall data in Sichuan Province, China. Int. J. Climatol. 2015, 35, 2898–2907. [Google Scholar] [CrossRef]
- Xing, Y.; Song, Q.; Cheng, G. Benefit of Interpolation in Nearest Neighbor Algorithms. SIAM J. Math. Data Sci. 2022, 4, 935–956. [Google Scholar] [CrossRef]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci. 2008, 34, 1044–1055. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. Kriging: A method of interpolation for geographical information systems. Int. J. Geogr. Inf. Syst. 1990, 4, 313–332. [Google Scholar] [CrossRef]
- Lam, N.S.N. Spatial Interpolation Methods: A Review. Am. Cartogr. 1983, 10, 129–150. [Google Scholar] [CrossRef]
- Roberts, E.A.; Sheley, R.L.; Lawrence, R.L. Using sampling and inverse distance weighted modeling for mapping invasive plants. West. N. Am. Nat. 2004, 64, 312–323. [Google Scholar]
- Chu, H.J.; Wang, C.K.; Huang, M.L.; Lee, C.C.; Liu, C.Y.; Lin, C.C. Effect of point density and interpolation of LiDAR-derived high-resolution DEMs on landscape scarp identification. GISci. Remote Sens. 2014, 51, 731–747. [Google Scholar] [CrossRef]
- Zhang, H.; Lu, L.; Liu, Y.; Liu, W. Spatial Sampling Strategies for the Effect of Interpolation Accuracy. ISPRS Int. J. Geo-Inf. 2015, 4, 2742–2768. [Google Scholar] [CrossRef]
- van Stein, B.; Wang, H.; Kowalczyk, W.; Emmerich, M.; Bäck, T. Cluster-based Kriging approximation algorithms for complexity reduction. Appl. Intell. 2019, 50, 778–791. [Google Scholar] [CrossRef]
- Sibson, R. A vector identity for the Dirichlet tessellation. Math. Proc. Camb. Philos. Soc. 1980, 87, 151–155. [Google Scholar] [CrossRef]
- Sibson, R. A brief description of natural neighbour interpolation. In Interpreting Multivariate Data; Barnett, V., Ed.; John Wiley and Sons: New York, NY, USA, 1981; pp. 21–36. [Google Scholar]
- Watson, D.F. Contouring: A Guide to the Analysis and Display of Spatial Data/Book and Disk; Computer Methods in the Geosciences; Pergamon: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Ledoux, H.; Gold, C. An Efficient Natural Neighbour Interpolation Algorithm for Geoscientific Modelling. In Developments in Spatial Data Handling; Springer: Berlin/Heidelberg, Germany, 2005; pp. 97–108. [Google Scholar] [CrossRef]
- Kim, S.; Rhee, S.; Kim, T. Digital surface model interpolation based on 3D mesh models. Remote Sens. 2018, 11, 24. [Google Scholar] [CrossRef]
- Oliver, M.A.; Webster, R. A tutorial guide to geostatistics: Computing and modelling variograms and kriging. Catena 2014, 113, 56–69. [Google Scholar] [CrossRef]
- Zhu, Q.; Feng, J.; Huang, J. Natural neighbor: A self-adaptive neighborhood method without parameter K. Pattern Recognit. Lett. 2016, 80, 30–36. [Google Scholar] [CrossRef]
- Mankins, J.C. Technology Readiness Levels—A White Paper; Advanced Concepts Office, Office of Space Access and Technology, National Aeronautics and Space Administration (NASA): Washington, DC, USA, 1995; Volume 6, p. 5.
- Wilcox, R.R. Summarizing Data. In Applying Contemporary Statistical Techniques; Elsevier: Amsterdam, The Netherlands, 2003; pp. 55–91. [Google Scholar]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A publishing format for reproducible computational workflows. In Positioning and Power in Academic Publishing: Players, Agents and Agendas; Loizides, F., Schmidt, B., Eds.; IOS Press: Amsterdam, The Netherlands, 2016; pp. 87–90. [Google Scholar]
- Lindsay, J. The whitebox geospatial analysis tools project and open-access GIS. In Proceedings of the GIS Research UK 22nd Annual Conference, Glasgow, UK, 16–18 April 2014; pp. 16–18. [Google Scholar]
- Jordahl, K.; den Bossche, J.V.; Fleischmann, M.; Wasserman, J.; McBride, J.; Gerard, J.; Tratner, J.; Perry, M.; Badaracco, A.G.; Farmer, C.; et al. geopandas/geopandas: v0.8.1. 2020. Available online: https://zenodo.org/records/3946761 (accessed on 31 July 2024).
- Hoyer, S.; Hamman, J. xarray: N-D labeled arrays and datasets in Python. J. Open Res. Softw. 2017, 5, 10. [Google Scholar] [CrossRef]
- Braun, R. sertit-utils: v1.39.1. 2024. Available online: https://zenodo.org/records/14640090 (accessed on 31 July 2024).
- Scown, M.W.; Thoms, M.C.; De Jager, N.R. Floodplain complexity and surface metrics: Influences of scale and geomorphology. Geomorphology 2015, 245, 102–116. [Google Scholar] [CrossRef]
- Meadows, M.; Jones, S.; Reinke, K. Vertical accuracy assessment of freely available global DEMs (FABDEM, Copernicus DEM, NASADEM, AW3D30 and SRTM) in flood-prone environments. Int. J. Digit. Earth 2024, 17, 2308734. [Google Scholar] [CrossRef]
- Alho, P.; Hyyppä, H.; Hyyppä, J. Consequence of DTM precision for flood hazard mapping: A case study in SW Finland. Nord. J. Surv. Real Estate Res. 2009, 6, 21–39. [Google Scholar]
- Etkin, D. Risk transference and related trends: Driving forces towards more mega-disasters. Environ. Hazards 1999, 1, 69–75. [Google Scholar] [CrossRef]
- Tao, K. A closer look at the radial basis function (RBF) networks. In Proceedings of the 27th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–3 November 1993; pp. 401–405. [Google Scholar] [CrossRef]
- Legendre, P. Spatial Autocorrelation: Trouble or New Paradigm? Ecology 1993, 74, 1659–1673. [Google Scholar] [CrossRef]
- Hawkins, D.M.; Cressie, N. Robust Kriging—A Proposal. J. Int. Assoc. Math. Geol. 1984, 16, 3–18. [Google Scholar] [CrossRef]
- Krivoruchko, K.; Gribov, A. Evaluation of empirical Bayesian kriging. Spat. Stat. 2019, 32, 100368. [Google Scholar] [CrossRef]
- Ord, J.K.; Getis, A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. Geogr. Anal. 1995, 27, 286–306. [Google Scholar] [CrossRef]
- Chini, M.; Pelich, R.; Pulvirenti, L.; Pierdicca, N.; Hostache, R.; Matgen, P. Sentinel-1 InSAR coherence to detect floodwater in urban areas: Houston and Hurricane Harvey as a test case. Remote Sens. 2019, 11, 107. [Google Scholar] [CrossRef]
- Gens, R.; Van Genderen, J.L. Review Article SAR interferometry—issues, techniques, applications. Int. J. Remote Sens. 1996, 17, 1803–1835. [Google Scholar] [CrossRef]
- European Commission Joint Research Centre. Global Flood Depth-Damage Functions: Methodology and the Database with Guidelines; Publications Office: Luxembourg, 2016. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).