A Global-Scale Overlapping Pixels Calculation Method for Whisk-Broom Payloads with Multi-Module-Staggered Longlinear-Array Detectors
Abstract
:1. Introduction
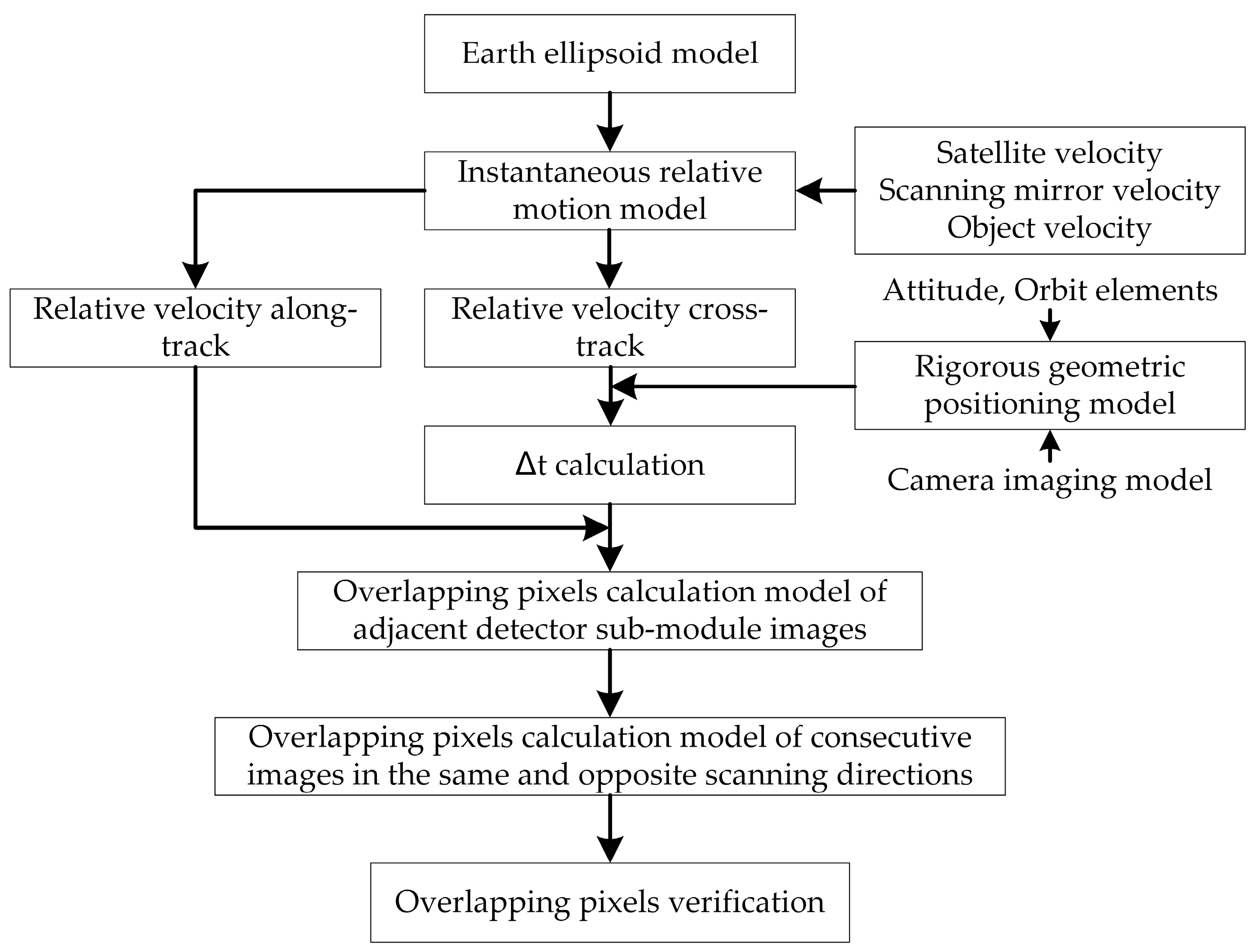
2. Materials and Methods
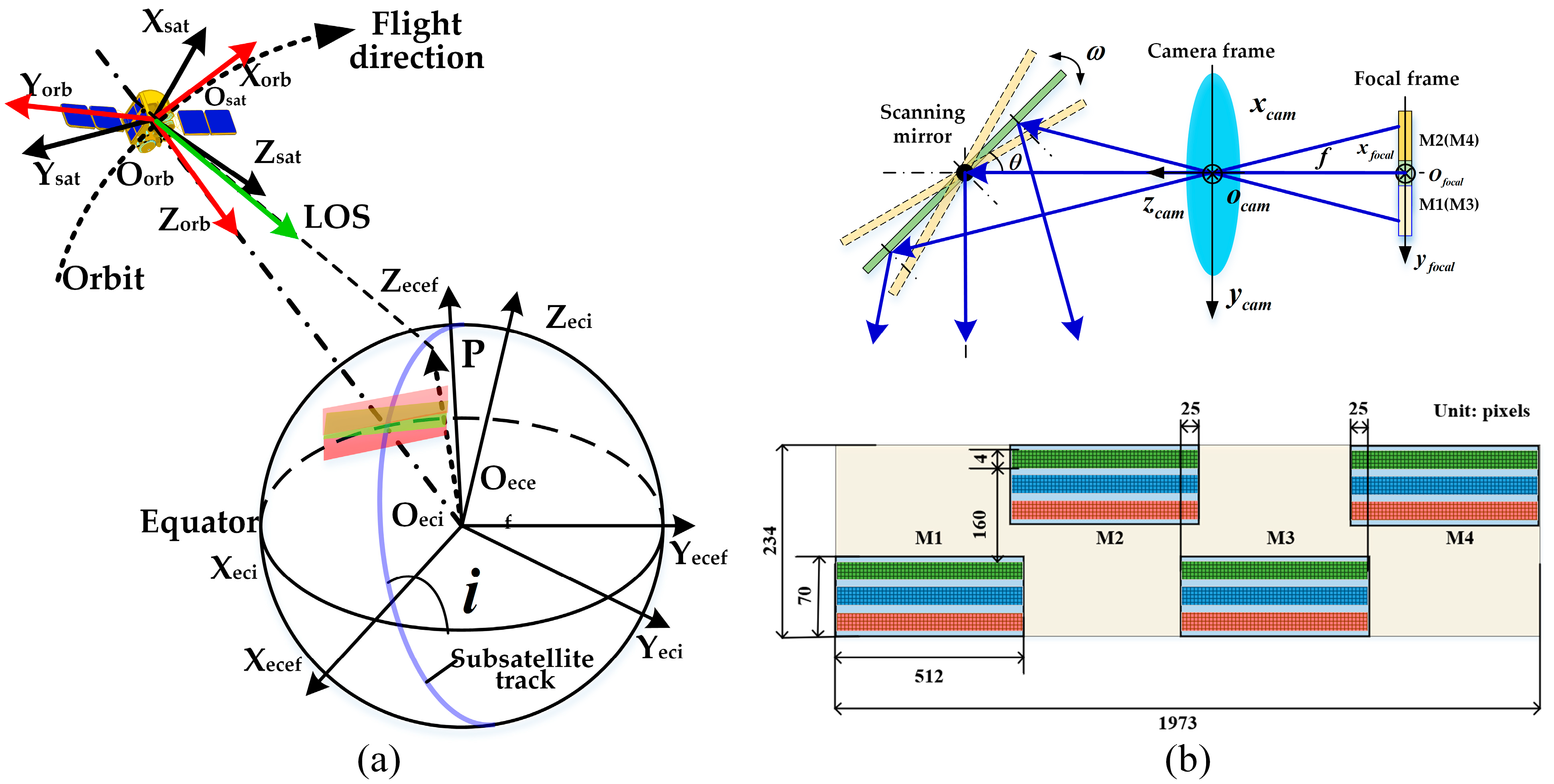
2.1. Rigorous Geometric Positioning Model (RGPM)
2.2. Overlapping Pixels Calculation Method of Adjacent Detector Sub-Module Images
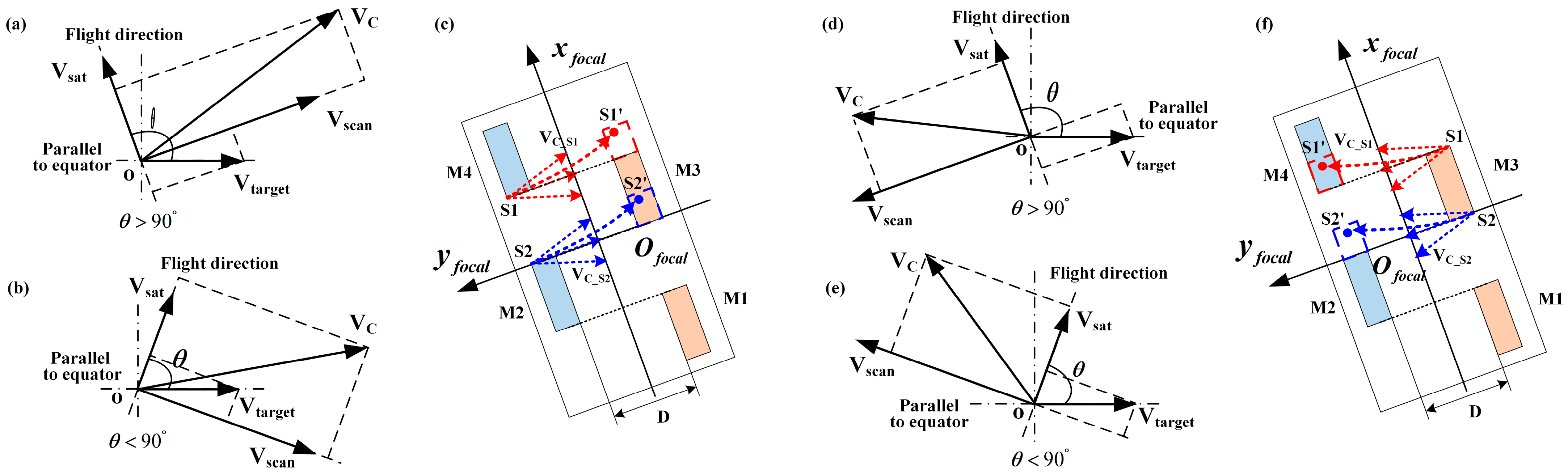
2.2.1. Overlapping Pixels Analysis of Adjacent Detector Sub-Module Images
- If > 0, the stitching seam between M4 and M3 (an odd stitching seam number) will result in information missing after a time interval of . On the contrary, the stitching seam between M3 and M2 (an even stitching seam number) will result in information overlapping.
- If < 0, the stitching seam between M4 and M3 (an odd stitching seam number) will result in information overlapping after a time interval of . On the contrary, the stitching seam between M3 and M2 (an even stitching seam number) will result in missing information.
- If, namely, the along-track velocity equals zero, there is neither information overlapping nor information missing in the stitching seam between M4 and M3 (an odd stitching seam number) or M3 and M2 (an even stitching seam number). But in practice, it is almost impossible for the along-track velocity to equal zero.
2.2.2. Overlapping Pixels Calculation Model of Adjacent Detector Sub-Module Images
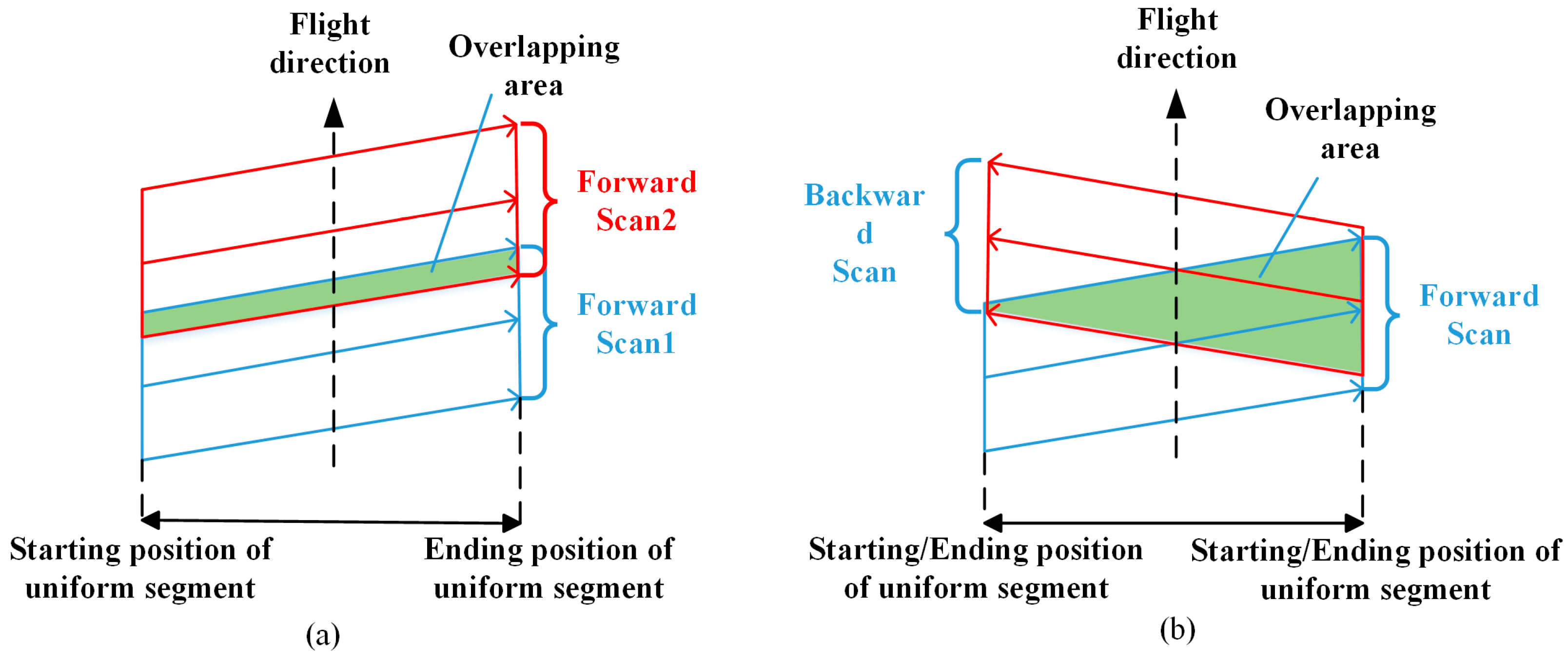
2.3. Overlapping Pixels Calculation Method of Consecutive Scanning Images
3. Experimental Results and Discussion
3.1. Simulation Results and Analysis
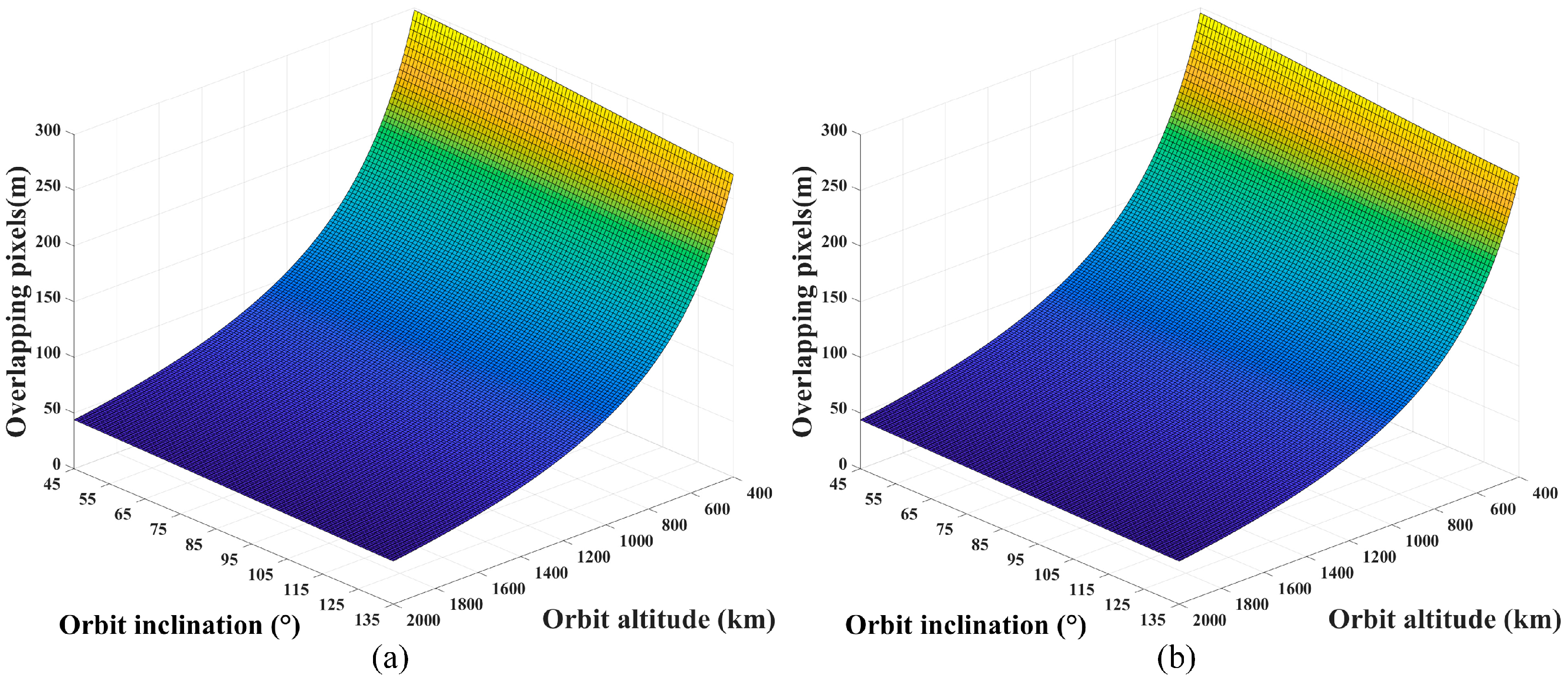
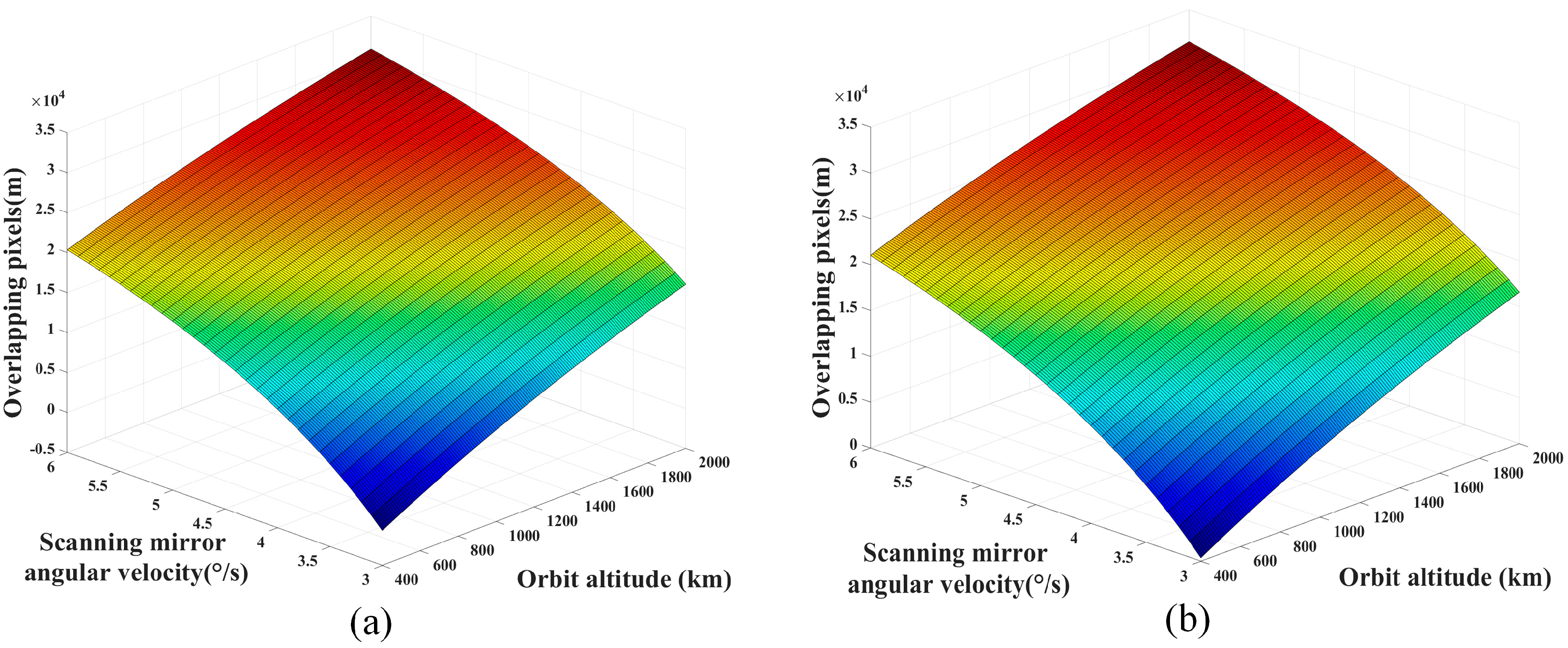
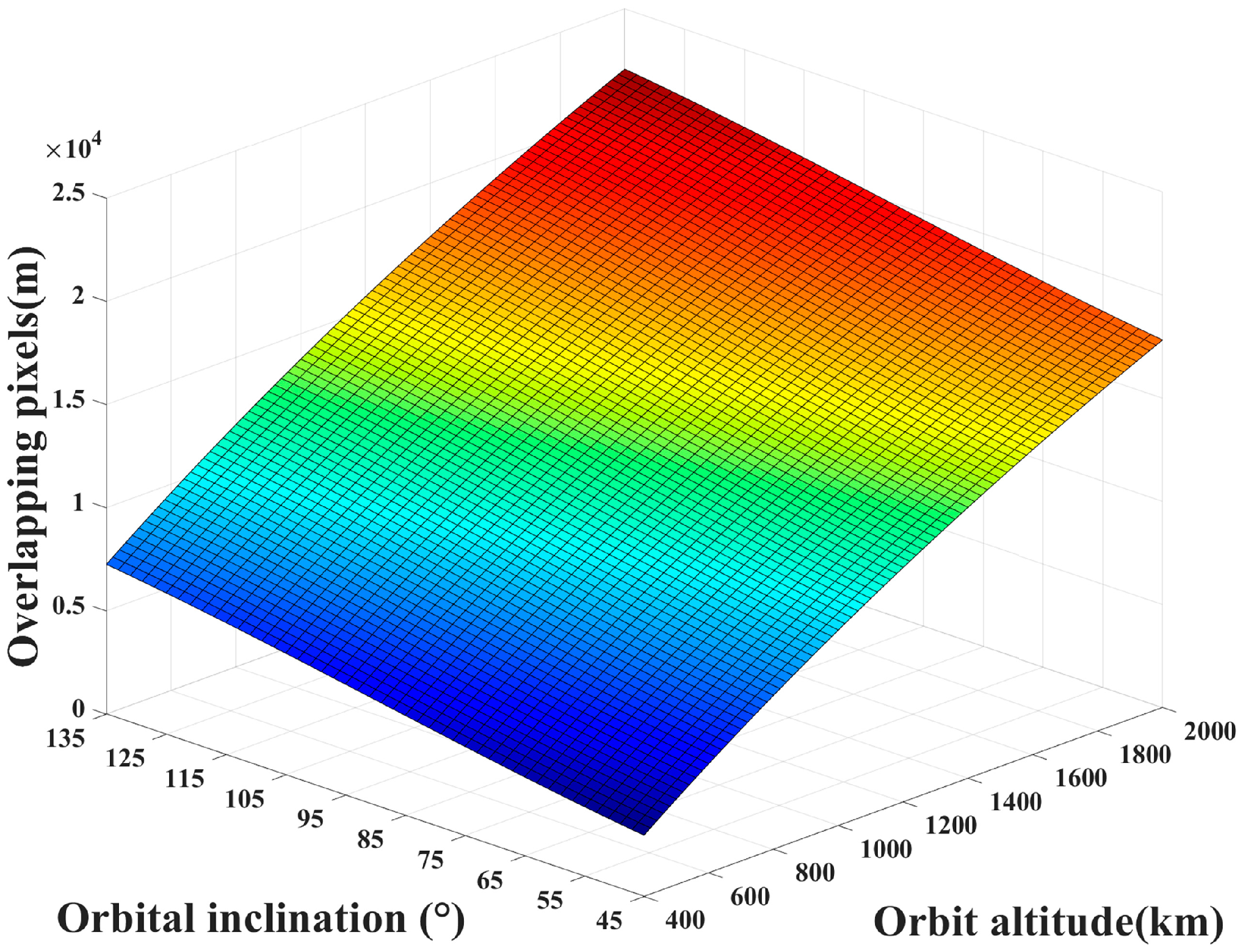
3.1.1. Overlapping Pixels Calculation of Adjacent Detector Sub-Module Images
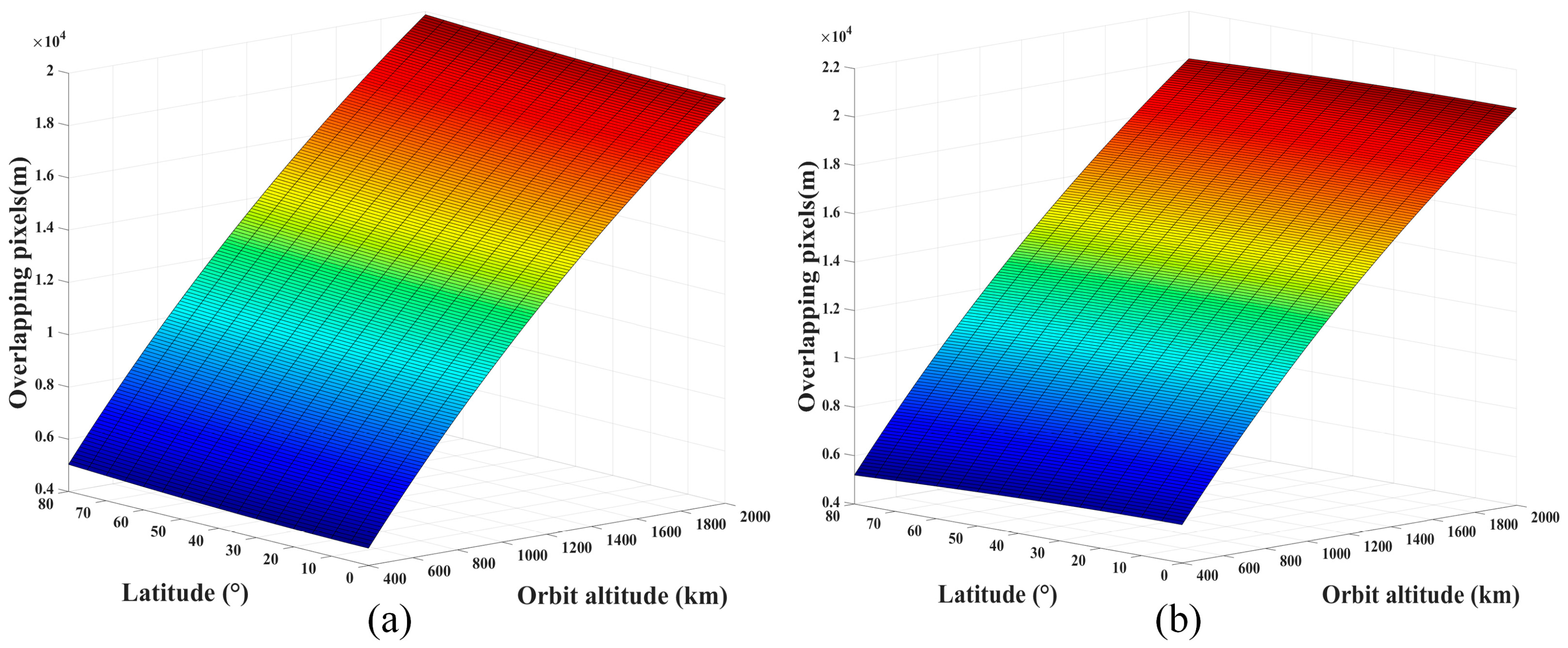
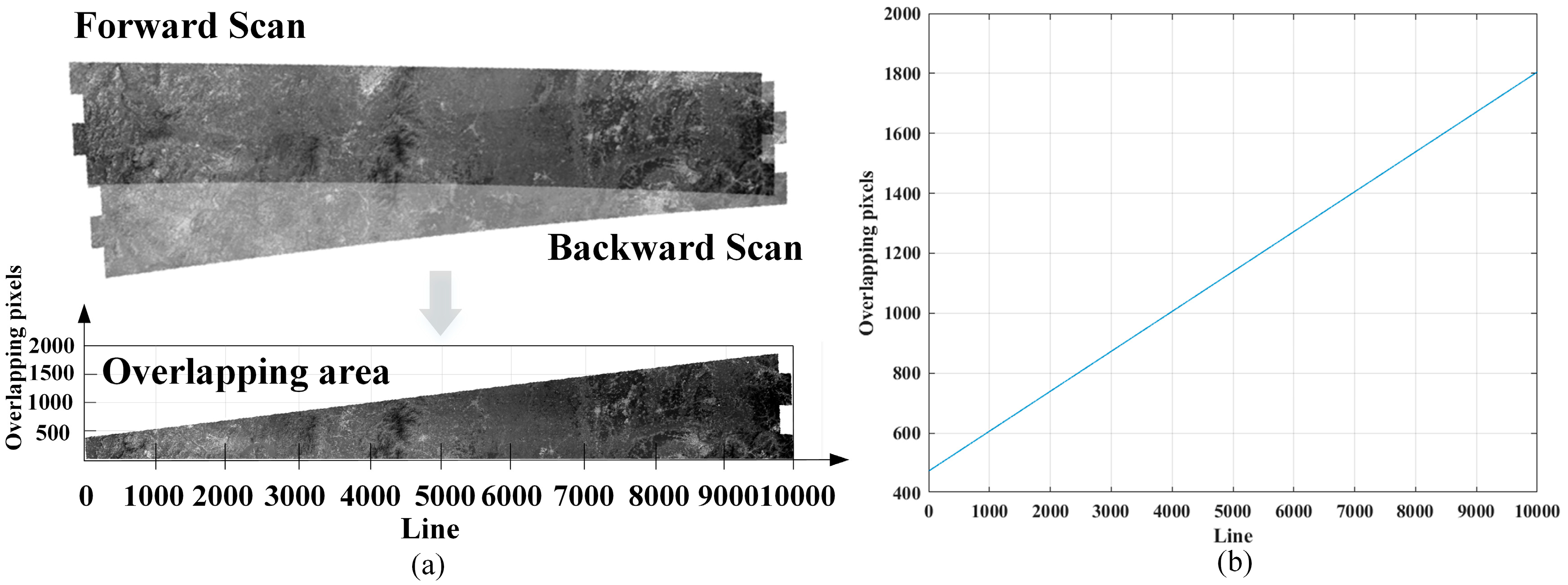
3.1.2. Overlapping Pixels Calculation of the Same Scanning Direction Images
3.1.3. Overlapping Pixels Calculation of the Opposite Scanning Direction Images
3.2. In-Orbit Experimental Results and Discussion
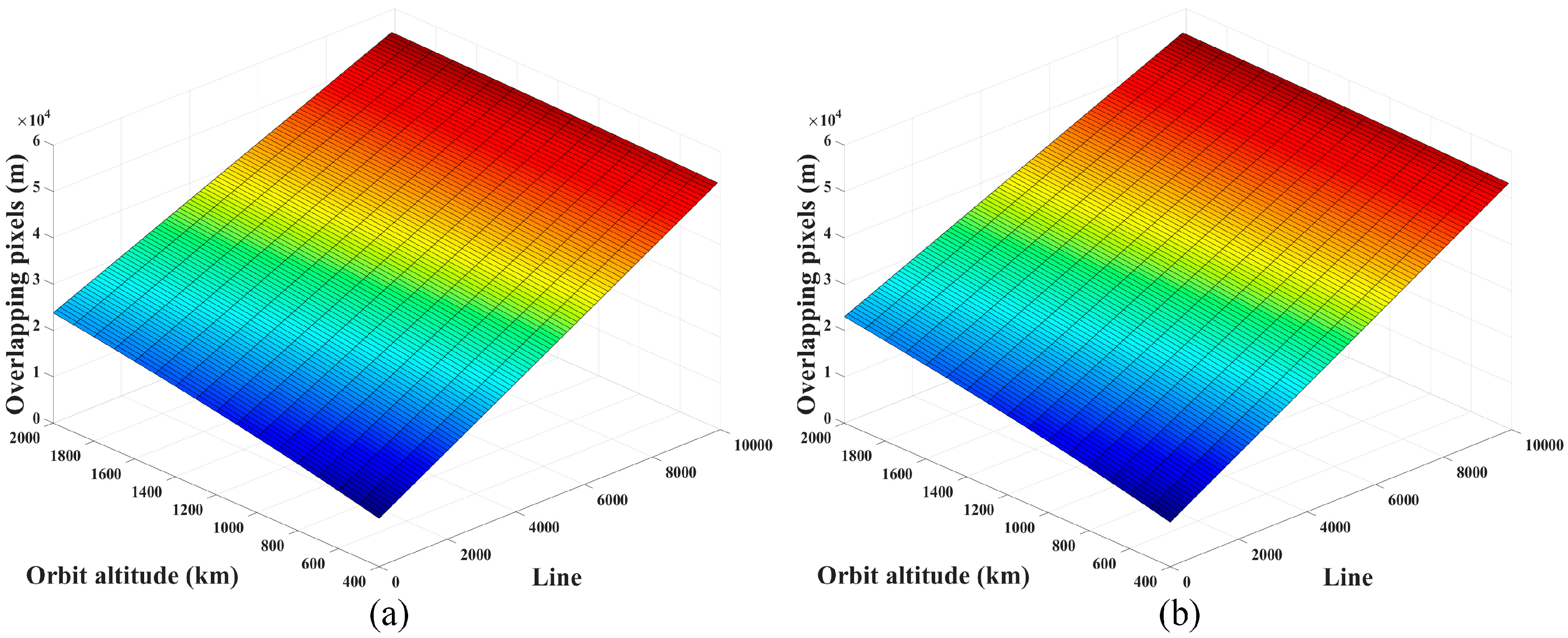
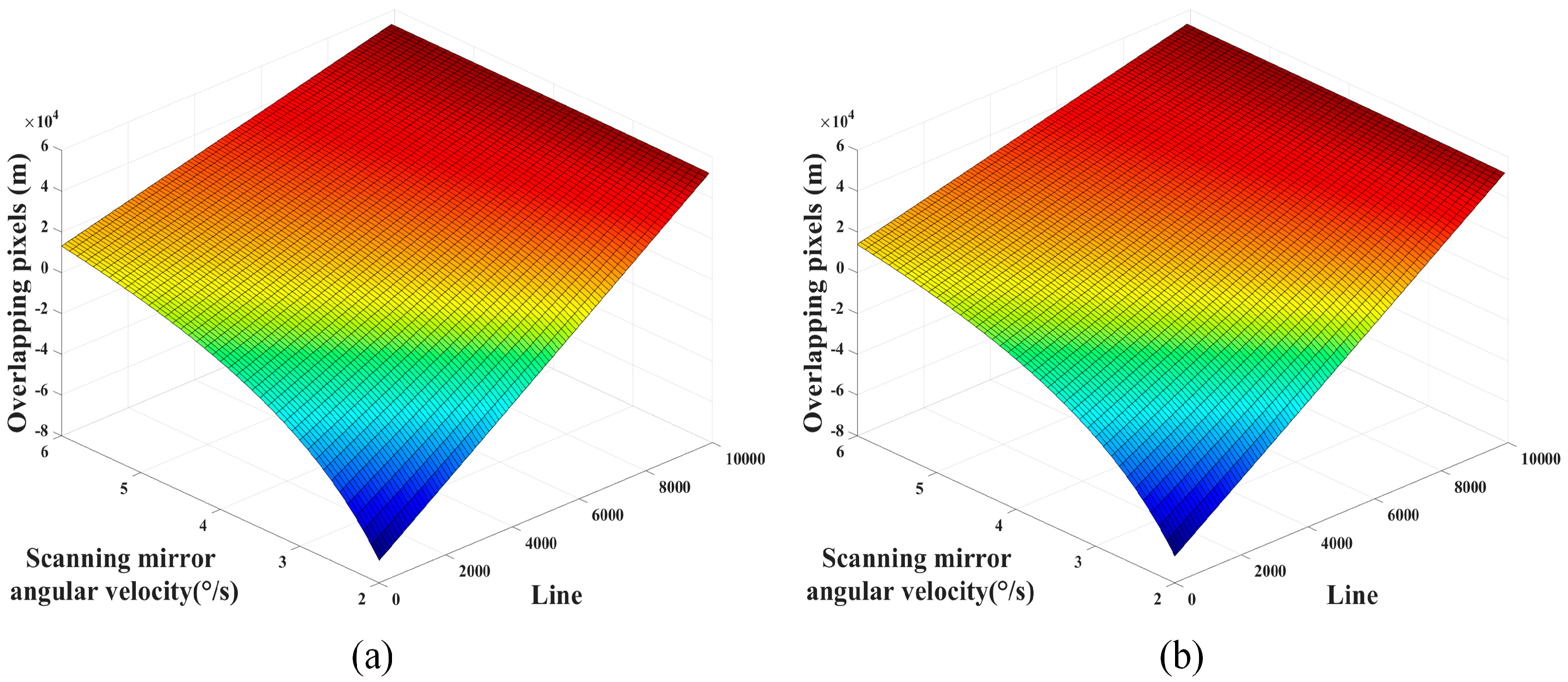
3.2.1. Overlapping Pixels Calculation of Adjacent Detector Sub-Module Images
3.2.2. Overlapping Pixels Calculation of the Same Scanning Direction Images
3.2.3. Overlapping Pixels Calculation of the Opposite Scanning Direction Images
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, Z.; Li, X.; Li, L.; Su, X.; Yang, L.; Zhang, Y.; Hu, X.; Lin, C.; Tang, Y.; Hao, J.; et al. Wide-Swath and High-Resolution Whisk-Broom Imaging and on-Orbit Performance of SDGSAT-1 Thermal Infrared Spectrometer. Remote Sens. Environ. 2024, 300, 113887. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, Y.; Zhang, Y.; Zhang, Z.; Xiao, X.; Yu, Y.; Wang, L. A Spliced Satellite Optical Camera Geometric Calibration Method Based on Inter-Chip Geometry Constraints. Remote Sens. 2021, 13, 2832. [Google Scholar] [CrossRef]
- Zhang, S.; Jin, S. In-orbit calibration method based on empirical model for non-collinear TDI CCD camera. Int. J. Comput. Sci. Issues 2013, 10, 114. [Google Scholar]
- Bo, Y.; Mi, W. On-Orbit Geometric Calibration Method of ZY-1 02C Panchromatic Camera. Natl. Remote Sens. Bull. 2013, 17, 1175–1190. [Google Scholar] [CrossRef]
- Weser, T.; Rottensteiner, F.; Willneff, J.; Poon, J.; Fraser, C.S. Development and Testing of a Generic Sensor Model for Pushbroom Satellite Imagery. Photogramm. Rec. 2008, 23, 255–274. [Google Scholar] [CrossRef]
- Zhong, H.; Long, X.; Wang, X. Analysis of imaging quality and processing methods of spaceborne focal plane field stitching TDI CCD camera. Sci. Sin. Informationis 2011, 41, 19–31. [Google Scholar] [CrossRef]
- Zhang, L.; Li, S.; Jin, G.; Yang, X. Modeling of Satellite Borne TDI CCD Pitching Imaging Image Motion Velocity Vector. In Proceedings of the 2009 IEEE International Conference on Automation and Logistics, Shenyang, China, 5–7 August 2009; pp. 1587–1591. [Google Scholar]
- Chen, F.; Hu, Z.; Li, X.; Yang, L.; Hu, X.; Zhang, Y. Research on wide-width and high-resolution thermal infrared remote sensing imaging technology. Chin. J. Lasers 2021, 48, 1210002. [Google Scholar] [CrossRef]
- Poli, D.; Toutin, T. Review of Developments in Geometric Modelling for High Resolution Satellite Pushbroom Sensors. Photogramm. Rec. 2012, 27, 58–73. [Google Scholar] [CrossRef]
- Tang, X.; Hu, F.; Wang, M.; Pan, J.; Jin, S.; Lu, G. Inner FoV Stitching of Spaceborne TDI CCD Images Based on Sensor Geometry and Projection Plane in Object Space. Remote Sens. 2014, 6, 6386–6406. [Google Scholar] [CrossRef]
- Wang, H. GF-5 VIMI On-Orbit Calibration Instrument and Performance. J. Comput. Commun. 2019, 7, 293–300. [Google Scholar] [CrossRef]
- Teng, Y.; Ren, H.; Hu, Y.; Dou, C. Land Surface Temperature Retrieval from SDGSAT-1 Thermal Infrared Spectrometer Images: Algorithm and Validation. Remote Sens. Environ. 2024, 315, 114412. [Google Scholar] [CrossRef]
- Robinson, D.; Tonn, S. Mechanical Aspects of the Thermal InfraRed System (TIRS) on Landsat 8. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015; pp. 1–10. [Google Scholar]
- Hair, J.H.; Reuter, D.C.; Tonn, S.L.; McCorkel, J.; Simon, A.A.; Djam, M.; Alexander, D.; Ballou, K.; Barclay, R.; Coulter, P.; et al. Landsat 9 Thermal Infrared Sensor 2 Architecture and Design. In Proceedings of the IGARSS 2018–2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8841–8844. [Google Scholar]
- Lv, H.; Liu, Y.; Guo, Y. Computation of overlapping pixels of mechanical assembly CCD focal planes in remote sensing cameras. Opt. Precis. Eng. 2012, 20, 1041–1050. [Google Scholar] [CrossRef]
- Guo, J.; Gong, D.; Zhu, L.; Sun, J.; Shao, M. Calculation of overlapping pixels in interleaving assembly of CCD focal plane of mapping camera. Opt. Precis. Eng. 2013, 21, 1251–1257. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Lin, C. Calculation of Overlapping Pixels of Staggered Linear Array Detectors for Space Camera. Acta Opt. Sin. 2014, 34, 0128003. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, X.; Wang, Y.; Su, C. Matching Design About Pixel Number of Interleaving Assembly Time Delay Integration CCD for Lateral Swing Imaging. Laser Optoelectron. Prog. 2016, 53, 051104. [Google Scholar] [CrossRef]
- Farrier, M.G.; Dyck, R.H. A Large Area TDI Image Sensor for Low Light Level Imaging. IEEE J. Solid State Circuits 1980, 15, 753–758. [Google Scholar] [CrossRef]
- Yan, D.; Wu, W.; Sun, T. Analysis and Calculation of Overlapping Pixels of Assembly CCD Image Plane in Space Camera. Comput. Meas. Control 2016, 24, 193–194+198. [Google Scholar] [CrossRef]
- Hu, Y.; Jin, G.; Chang, L.; Yang, X. Image motion matching calculation and imaging validation of TDI CCD camera on elliptical orbit. Opt. Precis. Eng. 2014, 22, 2274–2284. [Google Scholar]
- Wu, Y.; Li, G.; Zhang, Y. Calculation of overlapping pixels in interleaving assembly for CCD focal plane of space camera. Opt. Precis. Eng. 2016, 24, 422–429. [Google Scholar] [CrossRef]
- Pan, J.; Hu, F.; Wang, M.; Jin, S.; Li, G. An Inner FOV Stitching Method for Non-Gcollinear TDI CCD Images. Acta Geod. Cartogr. Sin. 2014, 43, 1165–1173. [Google Scholar] [CrossRef]
- Xu, Y.; Feng, H.; Xu, Z.; Li, Q.; Chen, Y. Analysis on stitching overlap pixel threshold of one-orbit multi-strip agile remote sensing imaging. Opto-Electron. Eng. 2017, 44, 1066–1074+1124. [Google Scholar]
- Li, X.; Hu, Z.; Jiang, L.; Yang, L.; Chen, F. GCPs Extraction with Geometric Texture Pattern for Thermal Infrared Remote Sensing Images. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Chen, X.; Xing, F.; You, Z.; Zhong, X.; Qi, K. On-Orbit High-Accuracy Geometric Calibration for Remote Sensing Camera Based on Star Sources Observation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–11. [Google Scholar] [CrossRef]
- Smith, S.M.; Brady, J.M. SUSAN—A new approach to low level image processing. Int. J. Comput. Vis. 1997, 23, 45–78. [Google Scholar] [CrossRef]
- Kim, H.; Kim, E.; Chung, D.-W.; Seo, D.-C. Geometric Calibration Using Stellar Sources in Earth Observation Satellite. Trans. Jpn. Soc. Aeronaut. SPACE Sci. 2009, 52, 104–107. [Google Scholar] [CrossRef]
- Cole-Rhodes, A.A.; Johnson, K.L.; LeMoigne, J.; Zavorin, I. Multiresolution Registration of Remote Sensing Imagery by Optimization of Mutual Information Using a Stochastic Gradient. IEEE Trans. Image Process. 2003, 12, 1495–1511. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, L.; Zhao, L.; Jiao, J.; Jiang, L.; Yang, L.; Chen, F.; Sun, S. In-Orbit Geometric Calibration for Long-Linear-Array and Wide-Swath Whisk-Broom TIS of SDGSAT-1. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar] [CrossRef]
- Maral, G.; De Ridder, J.; Evans, B.G.; Richharia, M. Low Earth Orbit Satellite Systems for Communications. Int. J. Satell. Commun. 1991, 9, 209–225. [Google Scholar] [CrossRef]







| Item | Index |
|---|---|
| Orbit altitude/km | 505 |
| Orbit inclination/(°) | 97.5 |
| Imaging width/km | 300 |
| Resolution/m | 30 |
| Bands/μm | 8–10.5 10.3–11.3 11.5–12.5 |
| Scanning FOV/(°) | ≥33.1 |
| Scanning cycle/(s) | 7.54 |
| Region | Direction of Movement | Scan Direction | Overlapping Position | Calculation Results (Pixels) | Actual Results (Pixels) | Error (Pixels) |
|---|---|---|---|---|---|---|
| (32°27′N, 111°12′E) (31°55′N, 111°25′E) (33°14′N, 114°26′E) (32°42′N, 114°37′E) | Ascending | Forward | M1-M2 | 13.15 | 13.18 | 0.03 |
| M2-M3 | 36.85 | 36.82 | 0.03 | |||
| M3-M4 | 13.15 | 12.98 | 0.17 | |||
| (32°53′N, 111°9′E) (32°21′N, 111°22′E) (33°17′N, 114°29′E) (32°45′N, 114°40′E) | Ascending | Backward | M1-M2 | 36.95 | 36.98 | 0.03 |
| M2-M3 | 13.05 | 13.07 | 0.02 | |||
| M3-M4 | 36.95 | 36.90 | 0.05 | |||
| (48°36′N, 129°50′E) (48°3′N, 129°44′E) (48°8′N, 133°57′E) (47°35′N, 133°48′E) | Descending | Forward | M1-M2 | 13.04 | 12.89 | 0.15 |
| M2-M3 | 36.96 | 36.99 | 0.03 | |||
| M3-M4 | 13.04 | 12.90 | 0.14 | |||
| (49°2′N, 129°53′E) (48°29′N, 129°47′E) (48°11′N, 133°53′E) (47°38′N, 133°45′E) | Descending | Backward | M1-M2 | 36.88 | 36.98 | 0.10 |
| M2-M3 | 13.12 | 12.87 | 0.25 | |||
| M3-M4 | 36.88 | 36.89 | 0.01 |
| Region | Direction of Movement | Scan Direction | Calculation Results/Pixels | Actual Results/Pixels | Error/Pixels |
|---|---|---|---|---|---|
| (32°55′N, 111°6′E) (31°55′N, 111°25′E) (33°42′N, 114°19′E) (32°42′N, 114°37′E) | Ascending | Forward | 224.47 | 224.06 | 0.41 |
| (33°21′N, 111°2′E) (32°21′N, 111°22′E) (33°45′N, 114°22′E) (32°45′N, 114°40′E) | Ascending | Backward | 201.20 | 201.42 | 0.22 |
| (48°36′N, 129°50′E) (47°36′N, 129°35′E) (48°8′N, 133°57′E) (47°8′N, 133°37′E) | Descending | Forward | 222.62 | 222.82 | 0.20 |
| (49°2′N, 129°53′E) (48°2′N, 129°38′E) (48°11′N, 133°53′E) (47°11′N, 133°34′E) | Descending | Backward | 198.50 | 198.08 | 0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Wu, C.; Liang, Q.; Zhao, L.; Xu, Y.; Guo, J.; Li, X.; Chen, F. A Global-Scale Overlapping Pixels Calculation Method for Whisk-Broom Payloads with Multi-Module-Staggered Longlinear-Array Detectors. Remote Sens. 2025, 17, 433. https://doi.org/10.3390/rs17030433
Du X, Wu C, Liang Q, Zhao L, Xu Y, Guo J, Li X, Chen F. A Global-Scale Overlapping Pixels Calculation Method for Whisk-Broom Payloads with Multi-Module-Staggered Longlinear-Array Detectors. Remote Sensing. 2025; 17(3):433. https://doi.org/10.3390/rs17030433
Chicago/Turabian StyleDu, Xinwang, Chao Wu, Quan Liang, Lixing Zhao, Yixuan Xu, Junhong Guo, Xiaoyan Li, and Fansheng Chen. 2025. "A Global-Scale Overlapping Pixels Calculation Method for Whisk-Broom Payloads with Multi-Module-Staggered Longlinear-Array Detectors" Remote Sensing 17, no. 3: 433. https://doi.org/10.3390/rs17030433
APA StyleDu, X., Wu, C., Liang, Q., Zhao, L., Xu, Y., Guo, J., Li, X., & Chen, F. (2025). A Global-Scale Overlapping Pixels Calculation Method for Whisk-Broom Payloads with Multi-Module-Staggered Longlinear-Array Detectors. Remote Sensing, 17(3), 433. https://doi.org/10.3390/rs17030433









