MoonLIGHT and MPAc: The European Space Agency’s Next-Generation Lunar Laser Retroreflector for NASA’s CLPS/PRISM1A (CP-11) Mission

Abstract

Since 1969, 55 years ago, Lunar Laser Ranging (LLR) has provided accurate and precise (down to ~1 cm RMS) measurements of the Moon’s orbit thanks to the Apollo and Lunokhod Cube Corner Retroreflector (CCR) Laser Retroreflector Arrays (LRAs) deployed on the Moon. Nowadays, the current level of precision of these measurements is largely limited by the lunar librations affecting the old generation of LRAs. To improve this situation, next-generation libration-free retroreflectors are necessary. To this end, the Satellite/lunar/GNSS laser ranging/altimetry and cube/microsat Characterization Facilities Laboratory (SCF_Lab) at the Istituto Nazionale di Fisica Nucleare—Laboratori Nazionali di Frascati (INFN-LNF), in collaboration with the University of Maryland (UMD) and supported by the Italian Space Agency (ASI), developed MoonLIGHT (Moon Laser Instrumentation for General relativity High-accuracy Tests), a single large CCR with a front face diameter of 100 mm, nominally unaffected by librations, and with optical performances comparable to the Apollo/Lunokhod LRAs of CCRs. Such a big CCR (hereafter, ML100) is mounted into a specifically devised, designed, and manufactured robotic actuator, funded by the European Space Agency (ESA), the so-called MoonLIGHT Pointing Actuator (MPAc), which, once its host craft has landed on the Moon, will finely align the front face of the ML100 towards the Earth. The (optical) performances of such a piece of hardware, MoonLIGHT+MPAc, were tested in/by the SCF_Lab in order to ensure that it was space flight ready before its integration onto the deck of the host craft. After its successful deployment on the Moon, additional and better-quality LLR data (down to ~ 1 mm RMS or better for the contribution of the laser retroreflector instrument, MoonLIGHT, to the total LLR error budget) will be available to the community for future and enhanced tests of gravitational theories.

1. Introduction

Lunar Laser Ranging (LLR) technique consists of Time-of-Flight (ToF) measurements performed through laser pulses fired from terrestrial ground stations to orbiting payloads equipped with Cube Corner Retroreflectors (CCRs), eventually deployed on the Moon. Such passive, lightweight, and maintenance-free optical devices are trihedral prisms composed of three adjacent, mutually orthogonal plane-reflecting surfaces, which are able to reflect back incident rays, independently, on the prism and beam orientations, yet within an acceptance light-cone for the incident light. Measurements from the CCR light return provide a long-term stable time history of station positions; support maintenance of the terrestrial reference frame (TRF), Earth rotation parameters, and gravity field; precision orbit determination; and lunar and space science.

LLR provides accurate measurements of the Moon’s orbit through high-precision data collected for decades by ground stations and retroreflected by the Apollo 11, 14, and 15 CCR Laser Retroreflector Arrays (LRAs) (hereafter, AP11, AP14, and AP15), as well as the Lunokhod 1 and 2 CCR LRAs deployed on the Moon’s surface. The current level of range precision is limited by the effect of the lunar librations due to the eccentricity of the Moon’s orbit around the Earth. The effect of the librations on current LRAs is explained in detail in [1,2]; here, we provide only a summary. Because of this, at any given time, a corner of either the AP11, AP14, and AP15 LRA is several centimeters more distant from the Earth with respect to the opposite corner. This effect causes a broadening of the returning pulse depending upon the array’s physical dimensions and the beam angle of incidence. Nowadays this effect is estimated to be as large as ~15–50 mm [3], but by averaging over N lunar returns to a laser ground station, the range of uncertainty reduces by a factor that, with medium–long-term improvements in statistics and an understanding of systematics, is expected to approach N^1/2 the declared level of accuracy of ~1 cm [4], down to ~few-mm [5].

Since, in recent years, great efforts have been made to upgrade the ground segment (laser stations) to further improve the level of accuracy, a corresponding upgrade of the space segment (lunar retroreflectors) is now needed.

To this end, since its foundation in 2003, the Satellite/lunar/GNSS laser ranging/altimetry and cube/microsat Characterization Facilities Laboratory (SCF_Lab), an infrastructure built, owned, and run by Istituto Nazionale di Fisica Nucleare—Laboratori Nazionali di Frascati (INFN-LNF), in collaboration with the University of Maryland (UMD), has started its activity devoted to develop, design, manufacture, and space qualify innovative payloads intended for laser ranging operations in the Earth–Moon system. The SCF_Lab Team, supported by the Italian Space Agency (ASI), intends to reach the aforementioned goals by deploying the Moon Laser Instrumentation for General relativity High-accuracy Tests (MoonLIGHT) CCR on the Moon in 2025, more than 50 years after the last deployment of devices of the same kind [6,7].

MoonLIGHT (dubbed ML100) is a single, 100 mm large CCR for LLR from terrestrial ground stations, designed to accomplish the following:

• To compensate for the detrimental effect of lunar librations through single, short reflected pulses with shorter temporal spreading;
• To provide returning signal intensities comparable to those from the Apollo arrays;
• To obtain a final precision better than ~ few mm range, which is required for precision tests of General Relativity (GR) [1,2].

This paper is organized as follows: in Section 2, we list the main characteristics of ML100; in Section 3, we describe MPAc, the space qualified and flight ready double gimbal for finely aligning the front face of the ML100 towards the Earth, once and forever after landing; in Section 4, we show the scientific case behind such a hardware deployment on the Moon; finally, Section 5 wraps up and concludes this work.

2. The MoonLIGHT CCR

2.1. Characteristics

ML100, like the Apollo retroreflectors, is an uncoated CCR of Suprasil 311, a radiation-resistant grade of Fused Silica, which has a very low thermal expansion that minimizes thermal effects that could detrimentally affect the optical performance of the CCR. ML100 has a circular front face with an aperture of 100 mm in diameter, and it is optimized for a laser beam wavelength of λ = 532 nm, which is the wavelength most frequently used by the majority of existing laser ranging stations. Its three Dihedral Angle Offsets (DAOs) are 0° each, within an error of 0.2” for all three edges, and the planarity of the front face surface is λ/10 RMS.

Concerning its performances, from the optical point of view, the intensity I of the return signal is proportional to the fourth power of the CCR diameter. The AP11 (or, equivalently, the AP14) and AP15 LRAs are composed of 100 and 300 CCRs, respectively. Each retroreflector has a diameter d_AP = 38 mm. Therefore, the ratio between returning signal intensities from the Apollo LRAs and ML100 gives the following:

$${\displaystyle \frac{I_{AP11}}{I_{ML}}}=100\eta {\left({\displaystyle \frac{d_{AP}}{d_{ML}}}\right)}^4\approx 0.21,$$

(1)

$${\displaystyle \frac{I_{AP15}}{I_{ML}}}=300\eta {\left({\displaystyle \frac{d_{AP}}{d_{ML}}}\right)}^4\approx 0.63,$$

(2)

where the parameter η = 0.1 takes into account the degradation in signal strength due to lunar dust on the CCR’s front face over the years [8]. Thus, we expect that during the early years of its activity the returning signal intensity from ML100 will be a sensible fraction of AP11, AP14, and AP15 intensities.

In addition, in support of the choice of the ML100 CCR dimensions, the Moon Velo-city Aberration (VA) (i.e., the relative motion between the Moon and the operating LLR ground stations) falls inside the angular size of the main peak of the Far Field Diffraction Pattern (FFDP) of ML100, which is θ ≈ 1.22 λ/d_ML = 6.49 μrad.

In fact, the VA of the Moon is defined as follows:

$${\theta }_{ME}={\displaystyle \frac{2}{c}}\left({∆v}_M-v_E\cos \varphi \right),$$

(3)

where c is the speed of light; Δv_M is the difference between the Moon orbital velocity and rotational velocity at its equator; v_E is the Earth’s rotational velocity at the equator; and ϕ is the ground station latitude [9]. For the operating LLR stations, such as McDonald (ϕ = 30°.68 N), APOLLO (ϕ = 32°.78 N), Matera (ϕ = 40°.65 N), and Grasse (ϕ = 43°.75 N), the Moon VA stays in the range of 4.12–4.55 μrad, well inside θ. For this reason, in our data analysis, when applicable, we evaluate the optical response in the range 4.0–4.5 μrad in the FFDP domain. More refined analyses on the VA are discussed in the recent literature [10].

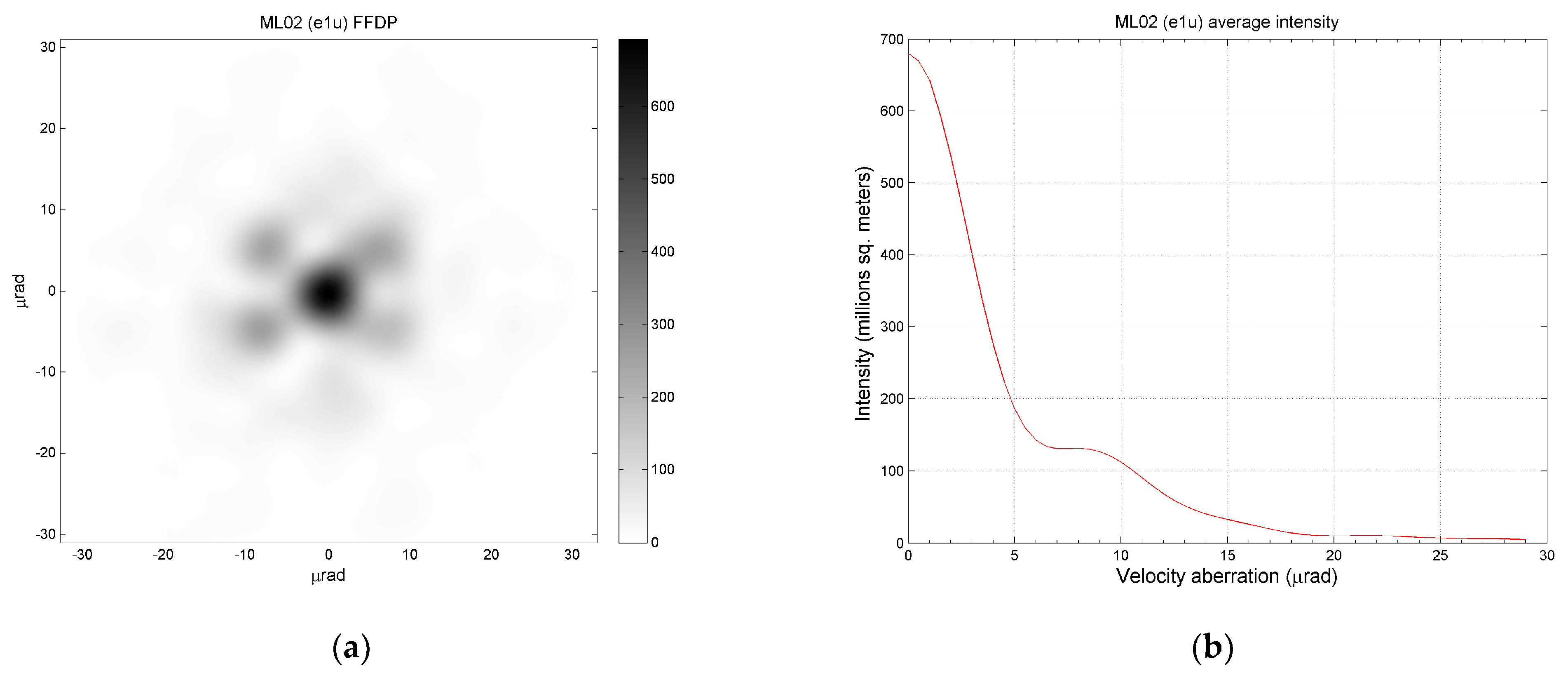
2.2. Optical Analysis

To test and approve the optical performances of ML100, it is mandatory to reconstruct its FFDP (i.e., the return laser intensity distribution on the image plane), its Optical Cross Section (OCS, i.e., the laser return intensity distribution averaged over the azimuthal angle in the image plane vs. VA), and, most important, the average value of the OCS at the desired VA range 4.0–4.5 μrad for Moon exploration.

The SCF_Lab optical bench is equipped with a linearly polarized continuous wave laser, and it is designed to separate the horizontal and vertical polarization components (and corresponding FFDPs) to be acquired by two CCD cameras through a dedicated computer. The recording of the two polarizations is mandatory for uncoated CCRs like ML100 because the FFDP is evenly split into the two components and has a strong dependency on the orientation of the input linear polarization [2,11].

Reference FFDPs and return intensities of ML100, simulated by using the CODEV software and measured in the SCF_Lab optical bench, are shown in Figure 1 and Figure 2, respectively. The simulated and measured OCSs are comparable within the above-mentioned range of VA and provide optimal values for LLR, as compared with those from the Apollo LRAs.

Finally, we mention that one of the new LLR trends to be exploited in the future will be the use of different states of the polarizations of the interrogating laser. Since MoonLIGHT is an uncoated CCR, its laser return changes the incoming polarization and, therefore, its response will be different, and potentially higher, in a polarization state different from the interrogating one. The capability of sending but also receiving/analysing different polarizations will allow the LLR station to maximise data accumulated from MoonLIGHT. The ASI-Matera Laser Ranging Observatory in Italy has such a capability thanks to specialized instrumentation developed by the University/INFN of Padua.

3. MPAc, the MoonLIGHT Pointing Actuator

3.1. Features

The MoonLIGHT CCR field of view, in far-field conditions, is quite narrow (a cone with an opening angle of about 34°, whose apex is geometrically located in the vertex of the CCR), and it must be pointed accurately to the Earth (within 3° maximum). Taking into account that the industry of landers could not guarantee such an accurate pointing of the device, INFN-LNF proposed the MoonLIGHT Pointing Actuator (MPAc) hardware to the ESA in 2018. In 2019, MPAc was chosen by the ESA, which issued a specifically tailored manufacturing contract in favor of INFN-LNF. In 2021, the ESA agreed with NASA to launch MPAc to the Reiner Gamma swirl on the Moon, with a Commercial Lunar Payload Service (CLPS), which is part of the Artemis program; and at the same time, NASA chose Intuitive Machines (IM) as the company that would develop and manufacture the commercial lander where MPAc would be integrated, confirming its flight for Q4 2025 (as per official NASA communication) [12].

Once on the Moon, MPAc will be able to perform two continuous perpendicular rotations to accurately point the front face of MoonLIGHT towards the Earth; the device will operate in ultra-high-vacuum space conditions and in a wide temperature range [13,14]. The final integration of the MoonLIGHT+MPAc payload took place in 2023, and the Proto Flight Model 1 (PFM1) hardware space qualification tests were successfully passed in late 2023. The MoonLIGHT+MPAc payload was finally delivered to the ESA, NASA, and IM; it has been in storage since 6^th December 2023, following acceptance, and is waiting for final integration on board IM’s CP-11 lander.

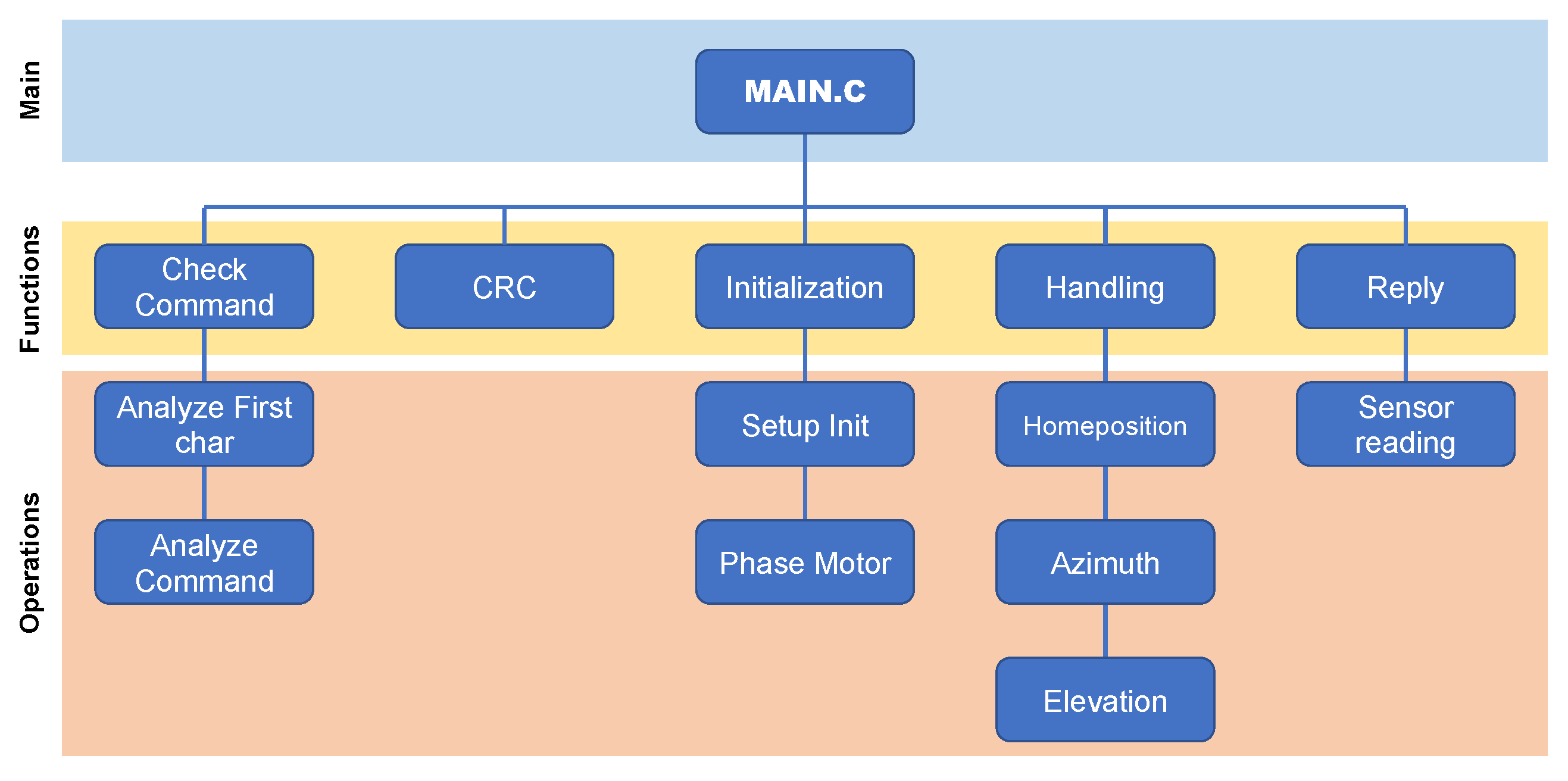
3.2. MPAc PFM1 Functionality

The MPAc payload (Figure 3) is a double-axis pointing actuator payload that aims to accurately orientate in azimuth and elevation the front face of the MoonLIGHT CCR towards the Earth’s mean direction after landing on the lunar surface and to keep this position for the rest of the mission.

The MPAc design implements a modular configuration that isolates the CCR from the electronics and moving elements. MPAc is divided into three main blocks with different functions and characteristics:

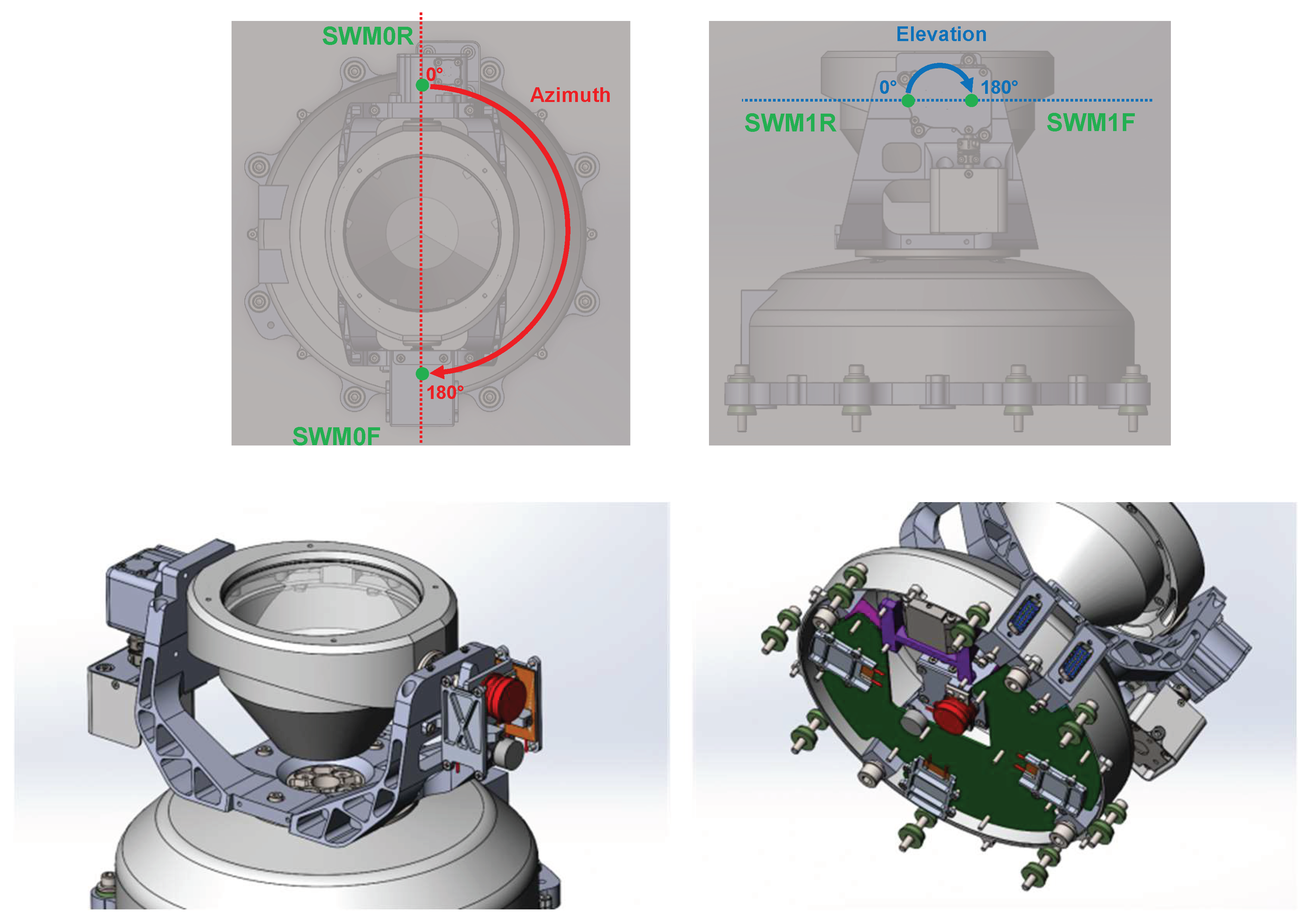
• The azimuth frame is the interface with the lander and contains most of the electronics and the motor responsible for azimuth rotations from 0° to 180° around an axis perpendicular to the lander deck. These rotations are transmitted to the elevation frame (Figure 4).
• The elevation frame contains the motor responsible for elevation rotations from 0° to 180° around an axis parallel to the lander deck (Figure 4). This frame also holds the CCR housing.
• The CCR housing is a completely passive block that holds and protects the CCR through its integration structure.

The ranges of rotations displayed in Figure 4 for Motor 0 (M0) and Motor 1 (M1), respectively, for azimuth and elevation, are determined by two limit switches (SW) per motor:

• Forward, at the end of clockwise rotations, SWM0F and SWM1F, for M0 and M1, respectively;
• Rewind, at the end of counterclockwise rotations, SWM0R and SWM1R.

Analogously, the two potentiometers are named POTM0 and POTM1.

The MPAc software is written in C, and it is divided into main and five block functions (Check Command, Cyclic Redundancy Check (CRC), Initialization, Handling and Reply), which, in turn, are divided into sub-routines (Figure 5). The software is designed to perform operations only triggered from Earth, and the serial communication follows the RS-422 protocol with the following features: the data format uses 8 data bits, no parity, and 1 stop bit with a Baud rate of 115.2 kbps.

The MPAc payload will be integrated onto the IM-3 Nova-C lander. The landing site will be near Reiner Gamma at RN = (7.585°N, 58.725°W) within a declared landing accuracy given by a 100 m diameter landing ellipse centered at RN. The azimuth accuracy will be 180° ± 10° w.r.t. the +Y-axis pointed at local South. The elevation accuracy will be within ±3° w.r.t. the Earth direction (IM communication). The average local slope of the landing site is currently not known/available.

MPAc will be mounted as already pointing to the NED (Nominal Earth Direction) with a guaranteed conical Field-of-View (FoV) of a semi-aperture of 45°. The NED (Figure 6) is the center of the Earth libration pattern as seen from the Moon (azimuth and elevation in the MPAc reference system) and is computed by INFN, knowing the nominal landing site on the Moon given in the lander reference system.

IM will inform INFN and the ESA about the potential misalignment of the lander between the nominal landing and the actual landing w.r.t. the lander reference system (azimuth and elevation). Knowing the actual position of the lander and its misalignment, INFN can compute the numerical values, azimuth, and elevation of the actual NED in the MPAc reference system (A₀ and E₀, respectively).

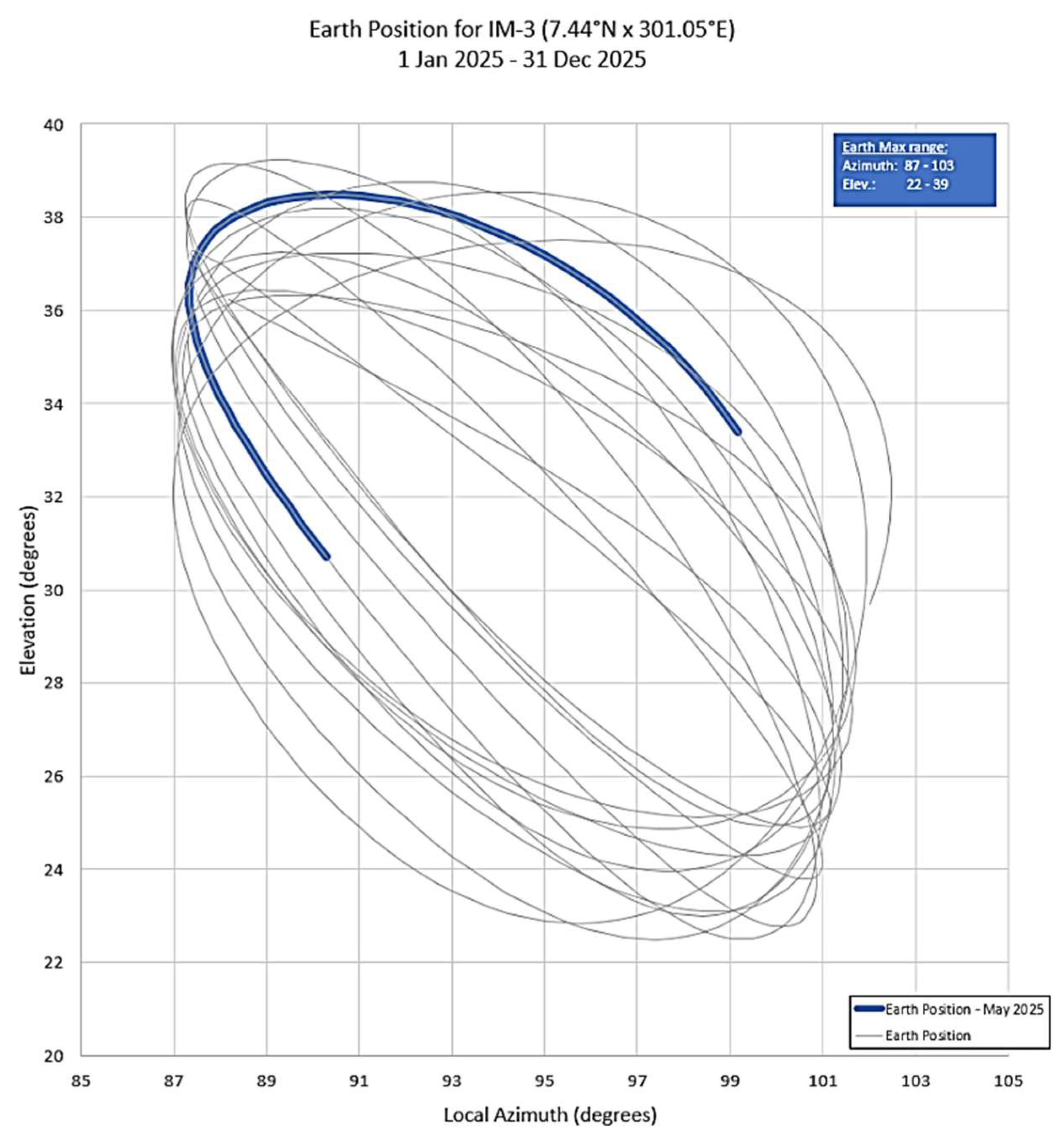
4. Impact of the LLR Measurements and Expected Science Products

We have shown that MoonLIGHT will provide laser returns (in OCS units) comparable to those from the Apollo arrays currently deployed on the surface of the Moon. The returns will be comparable even after taking into account the new pointing accuracy as the misalignment between MoonLIGHT and the NED. Therefore, in the following, we describe the data collection and analysis performed by the APOLLO station on the laser return photons from the Apollo arrays and apply the same considerations and conclusions to the case of MoonLIGHT. The only and important difference with respect to the case of the arrays is that MoonLIGHT is a single CCR, so the range determination from it will be significantly unaffected by the temporal spread caused by the lunar librations.

In the case of the APOLLO station, powerful laser pulses (~115 mJ, ~90 ps FWHM at 20 Hz, 532 nm) are fired to Apollo arrays. The APOLLO data consist of photon collection periods spanning 3–10 min (3000–10000 laser shots) on a single lunar array. A run typically contains a few hundred lunar range photons and a single observing session, spanning 1–1.5 h, typically containing 5–10 runs [15].

The data acquired during a run is processed into a final product called a normal point. A normal point provides a representative measurement of the Round-trip Travel Time (RTT) from the station to the CCR(s) and back at some specific epoch and is the fundamental observable used in the LLR-based analysis described below.

Lunar photon timing residuals are obtained by subtracting the predicted return time on a shot-by-shot basis from the calculated RTTs, resulting in a strongly peaked signal similar to the aggregate fiducial (Figure 7). A line is fit to the residuals versus time within the run to capture the offset and slope. Lunar returns that fall within a windowed region of the fitted line are tagged as registered lunar returns, indicating that they are candidate lunar range photons (red points in Figure 7, top panel), and a refined linear fit is performed on these registered photons (blue line in Figure 7, top panel). A representative time is formed for the run by finding the mean of the registered lunar return times.

The fitted line is subtracted from the residual signal to result in a new residual histogram. In order to fit this latest residual histogram, we assert that the lunar signal should be a combination of the fiducial signal profile (Figure 7, middle panel) with a trapezoidal array profile, which describes the array orientation at the time of ranging. A one-parameter fit is performed on the latest residual histogram by sliding the aggregate fiducial signal fit (red curve) horizontally, convolved with the trapezoidal array tilt profile at the time of ranging (magenta lines), to optimally align with the lunar histogram (Figure 7, bottom panel). During the fit:

• A constraint is imposed such that the area under the fit function shall match to the area under a windowed region of the lunar histogram;
• A constant is added to match the measured background.

When laser return photons will be collected from MoonLIGHT to establish normal points, there will be no convolution of the fiducial signal fit with any tilt profile at the time of ranging, with MoonLIGHT being a single CCR, and the tilt profile is applicable only to arrays of CCR.

The science products expected from MoonLIGHT are reported in the following for astrophysical/gravitational sciences and for the lunar science [1,13,14]:

• Astrophysical Sciences:
  • Deployment of MoonLIGHT will support, on the LLR space segment, an improvement up to a factor 100 of several tests of GR and relativistic gravity (Table 1). In fact, LLR currently provides the best, or among the best, constraints on the following:
    • Weak equivalence principle (WEP) at a level of 10⁻¹³.
    • Strong equivalence principle (SEP) at a level of 4 × 10⁻⁴.
    • Time-rate-of-change of Newton’s gravitational constant, G, to better than a part in 10⁻¹² per year.
    • Geodetic precession at a level of 0.1%.
    • Yukawa deviations from 1/r² gravity at 10⁻¹⁰ times the strength of gravity.
  • In addition, LLR currently allows us to set stringent constraints on the following new theories of fundamental gravity:
    • Spacetime torsion [16].
    • f(R) gravity [17].
    • Non-minimally coupled gravity [18,19,20].
    • Lorentz invariance violations [21].
    • Gravitational waves of deci-Hertz (or lower) frequency that act on, and may be detected with, the Moon by means of laser-based experiments on the lunar surface [22].
• Lunar Science [23]:
  • Moments of inertia, elastic tides, tidal dissipation, dissipation at the CMB (Core Mantle Boundary), fluid core oblateness, inner core, free librations.
  • Establishing a global lunar geophysical network (LGN) [24].

Concerning LLR data analysis, INFN-LNF authors make use of the PEP (Planetary Ephemeris Program) software package, developed and maintained since the 1960s by the Harvard–Smithsonian Center for Astrophysics (CfA), MA, USA. See [25] for a description of the PEP given in the first and historical measurement of the Geodetic Precession in GR.

Table 1. Compilation of GR tests with LLR from S. Turyshev et al., the NASA BPS Division’s “Lunar Surface Science Workshop Fundamental and Applied Lunar Surface Research in Physical Sciences”, August 2021, and from [26]. Credit: [14].

Fundamental Physics Measurement	Current LLR Accuracy of ~1 cm, Supported by Apollo/Lunokhod LRAs	LLR Accuracy of ~1mm (Contribution of Next-Generation CCRs)	Ultimate LLR Accuracy ~0.1mm (Contribution of Next-Generation CCRs)
WEP	|Δa/a| < 2.4 × 10−14	<10−14	10−15
SEP	|η| < 3.4 × 10−4	3 × 10−5	3 × 10−6
PPN β	|β − 1| < 7.2 × 10−5	<10−5	10−6
Time variation of G	$|{\displaystyle \frac{\dot{G}}{G}}$| < 9.5 × 10−15 yr−1	5 × 10−15	<1 × 10−15
Inverse Square Law	|α| < 3 × 10−12	10−12	10−13
Geodetic precession	|KGP − 1| < 6.4 × 10−3	<6 × 10−4	<6 × 10−5

Table 1. Compilation of GR tests with LLR from S. Turyshev et al., the NASA BPS Division’s “Lunar Surface Science Workshop Fundamental and Applied Lunar Surface Research in Physical Sciences”, August 2021, and from [26]. Credit: [14].

Fundamental Physics Measurement	Current LLR Accuracy of ~1 cm, Supported by Apollo/Lunokhod LRAs	LLR Accuracy of ~1mm (Contribution of Next-Generation CCRs)	Ultimate LLR Accuracy ~0.1mm (Contribution of Next-Generation CCRs)
WEP	|Δa/a| < 2.4 × 10−14	<10−14	10−15
SEP	|η| < 3.4 × 10−4	3 × 10−5	3 × 10−6
PPN β	|β − 1| < 7.2 × 10−5	<10−5	10−6
Time variation of G	$|{\displaystyle \frac{\dot{G}}{G}}$| < 9.5 × 10−15 yr−1	5 × 10−15	<1 × 10−15
Inverse Square Law	|α| < 3 × 10−12	10−12	10−13
Geodetic precession	|KGP − 1| < 6.4 × 10−3	<6 × 10−4	<6 × 10−5

5. Summary

A recent, general review of the lunar laser ranging discipline can be found in [27].

The first MoonLIGHT (equipped with MPAc) will soon be launched with the NASA-CLPS/PRISM1A (CP-11) mission, and the landing site will be the Reiner Gamma swirl region. MoonLIGHT (equipped with MPAc) will be among the first next-generation single, large-diameter CCRs deployed by means of NASA-CLPS missions, the EL3 lunar program, and the LGN during the decade 2023–2032. The scientific return, concerning lunar science and fundamental physics, will continue for decades because CCRs are passive, long-lived instruments, as demonstrated during the past 55 years by Apollo and Lunokhod LRAs.

Concerning fundamental physics, thanks to the use of the lunar ephemeris and orbit determination software package PEP, it will be possible, exploiting the newer LLR normal points, to more accurately estimate the orbit of the Moon and hence to test the GR in the Solar System. LLR is also a powerful tool with which to test gravity theories beyond GR, as shown in [16,17,18,19,20].

The role of MoonLIGHT+MPAc in the framework of a European roadmap for fundamental physics in space is discussed in [28].