Temporal Upscaling of Agricultural Evapotranspiration with an Improved Evaporative Fraction Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experiment and Data Collection
2.1.1. Eddy Flux and Micrometeorological Measurements
2.1.2. Remote Sensing Data Collection
2.2. Data Preprocessing
2.3. Improved Evaporative Fraction Method
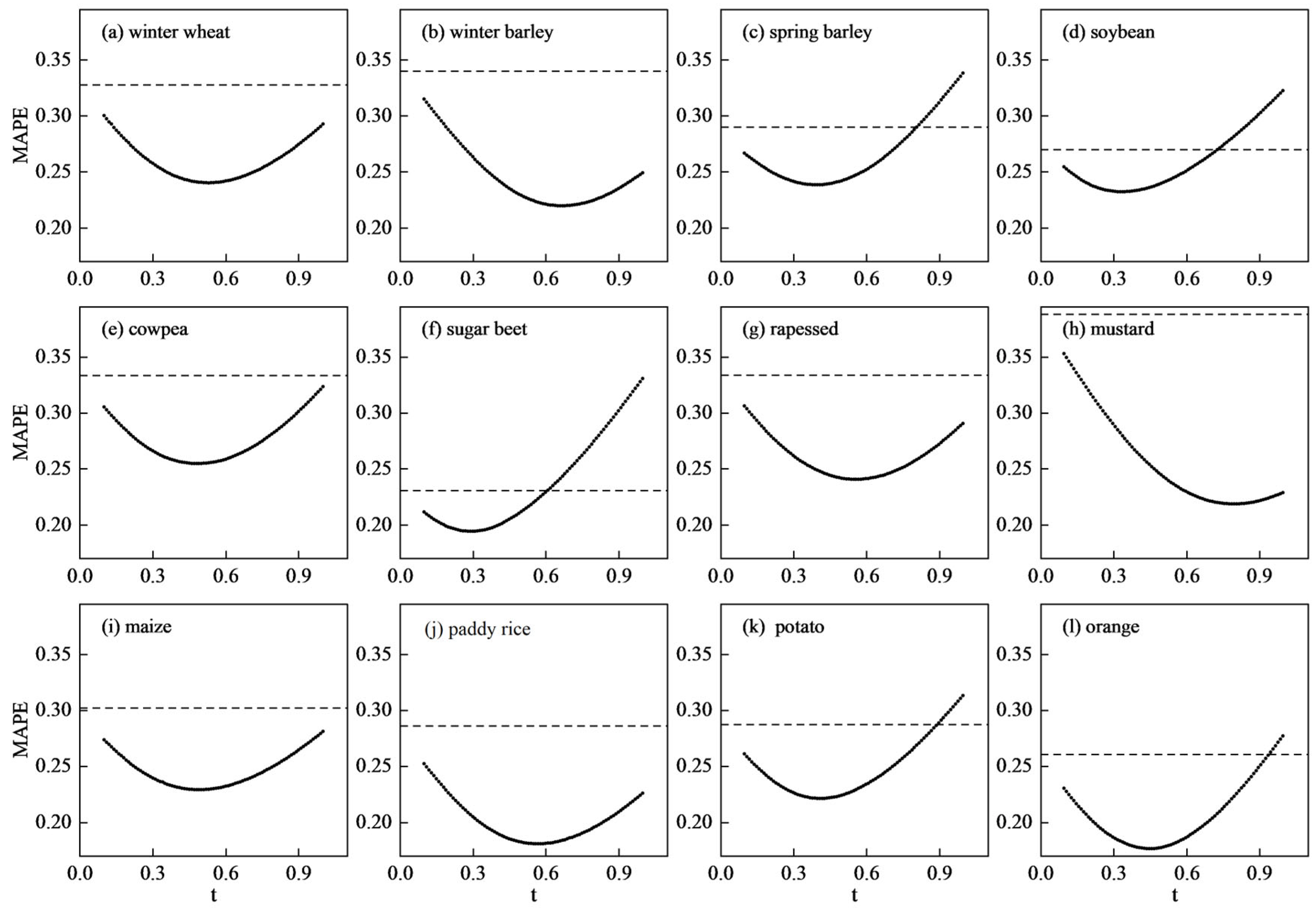
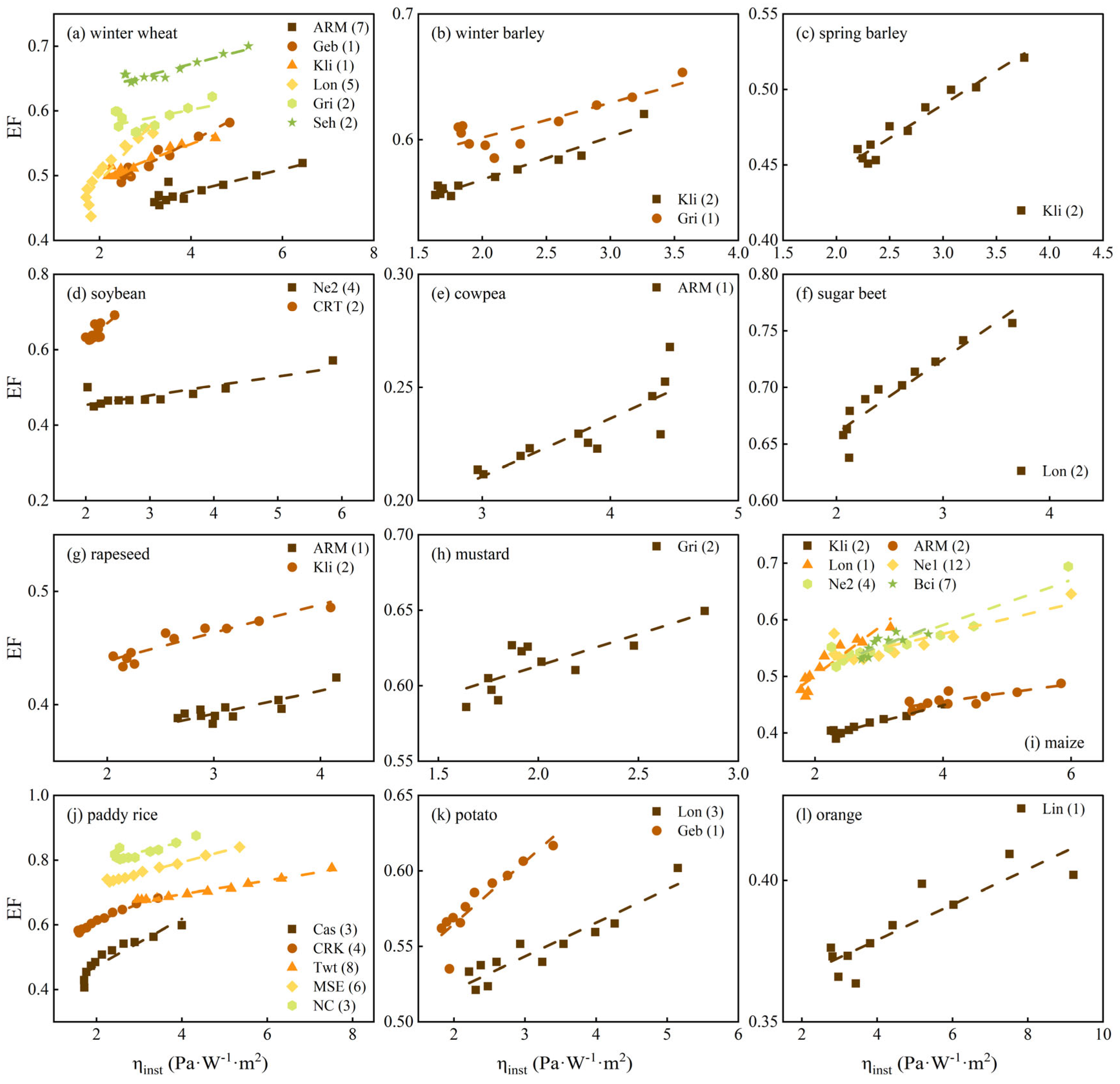
2.3.1. The Deviation Coefficient Between EFday and EFst
2.3.2. The Potential Deviation Between EFday and EFst
2.3.3. Daily EF
2.4. Validation Methods
3. Results
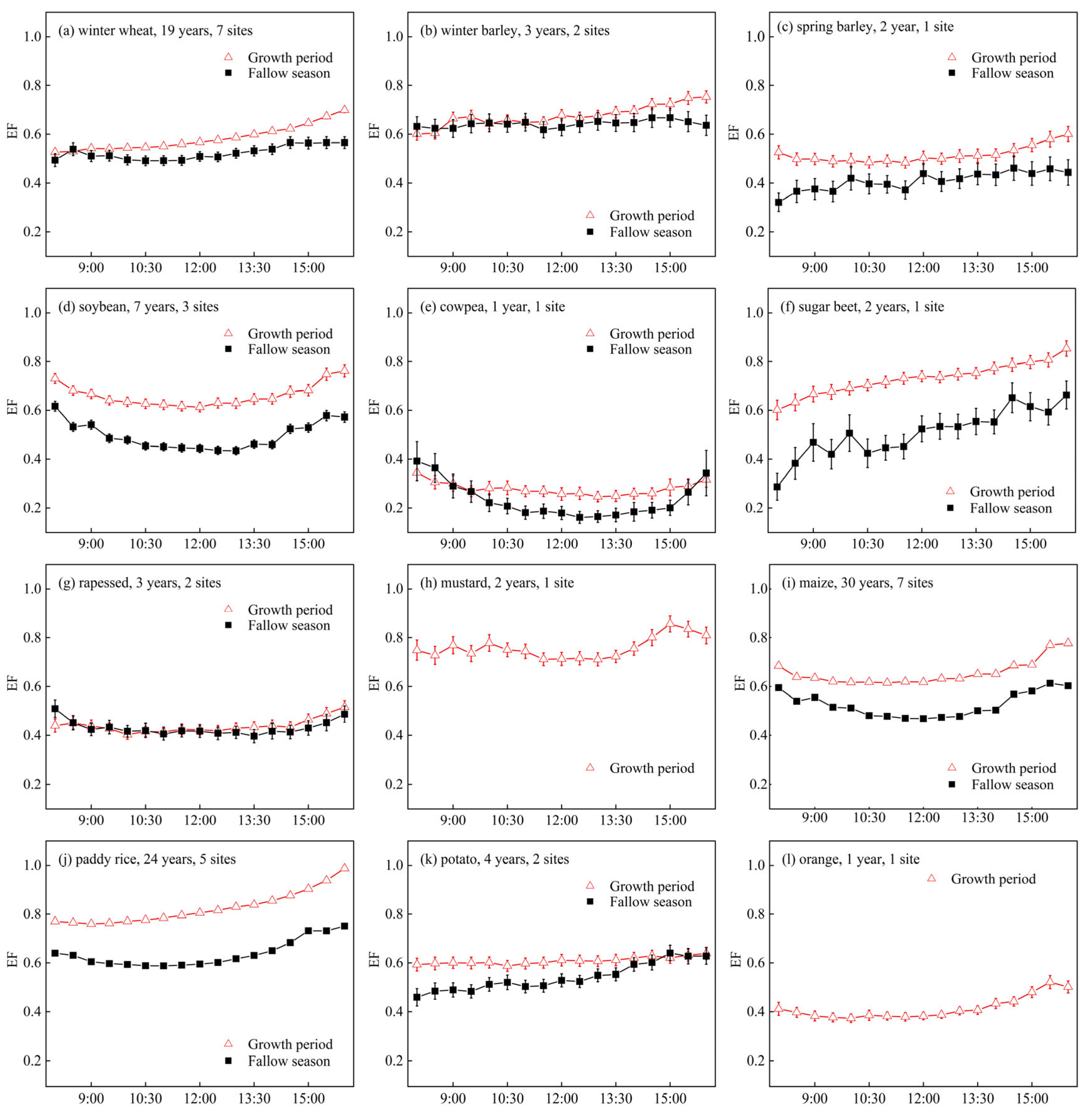
3.1. Measured Diurnal Evaporative Fraction for Agricultural Systems
3.2. Daily EF from the Improved Evaporative Fraction Method
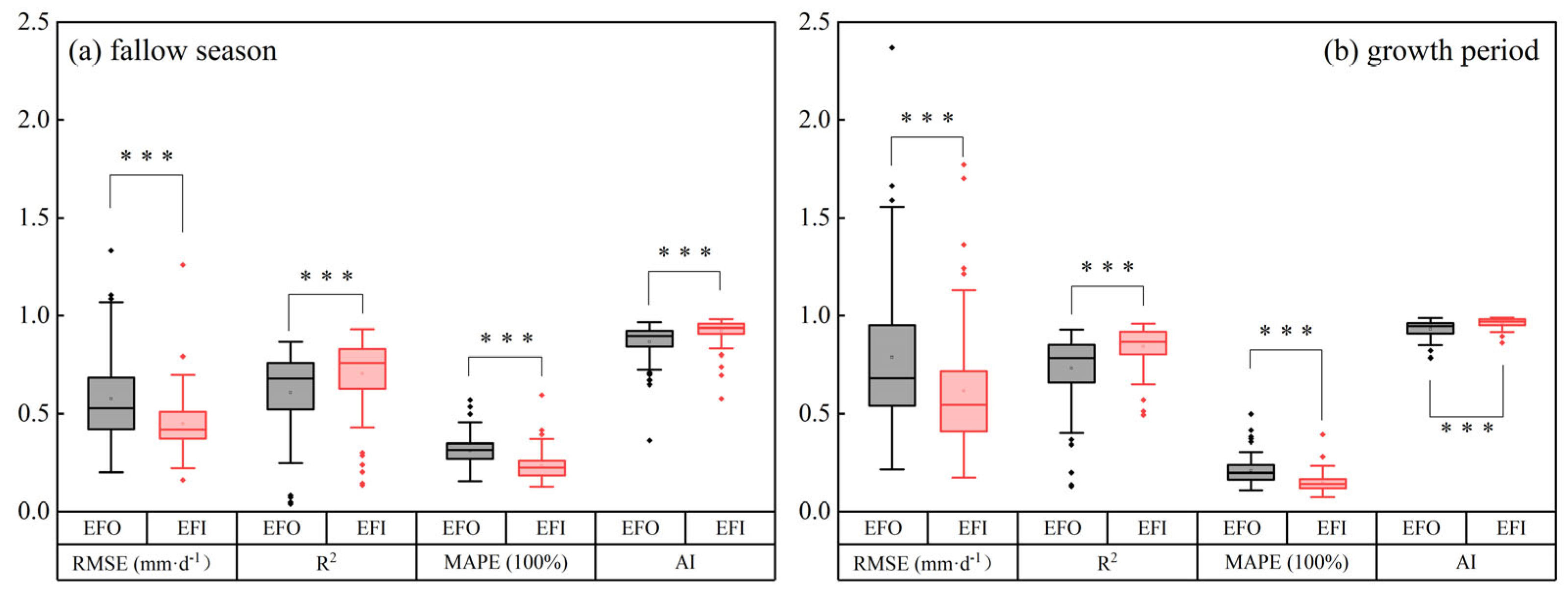
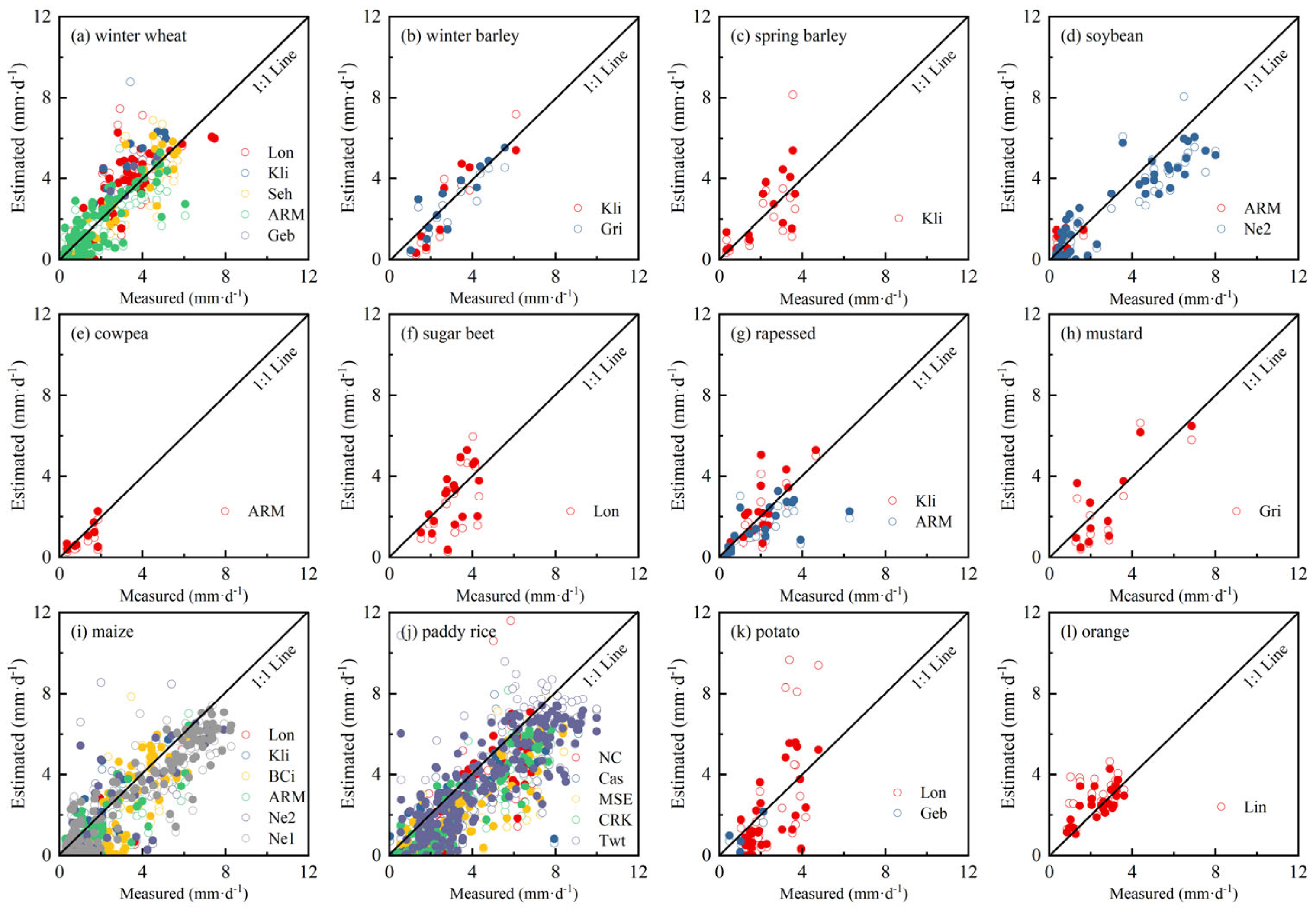
3.3. Daily ET from Daily Evaporative Fraction
3.3.1. Daily ET with the EFI When Short-Time EF from Ground-Measured Data
3.3.2. Daily ET from EFI When EFst from Remote Sensing Model
4. Discussion
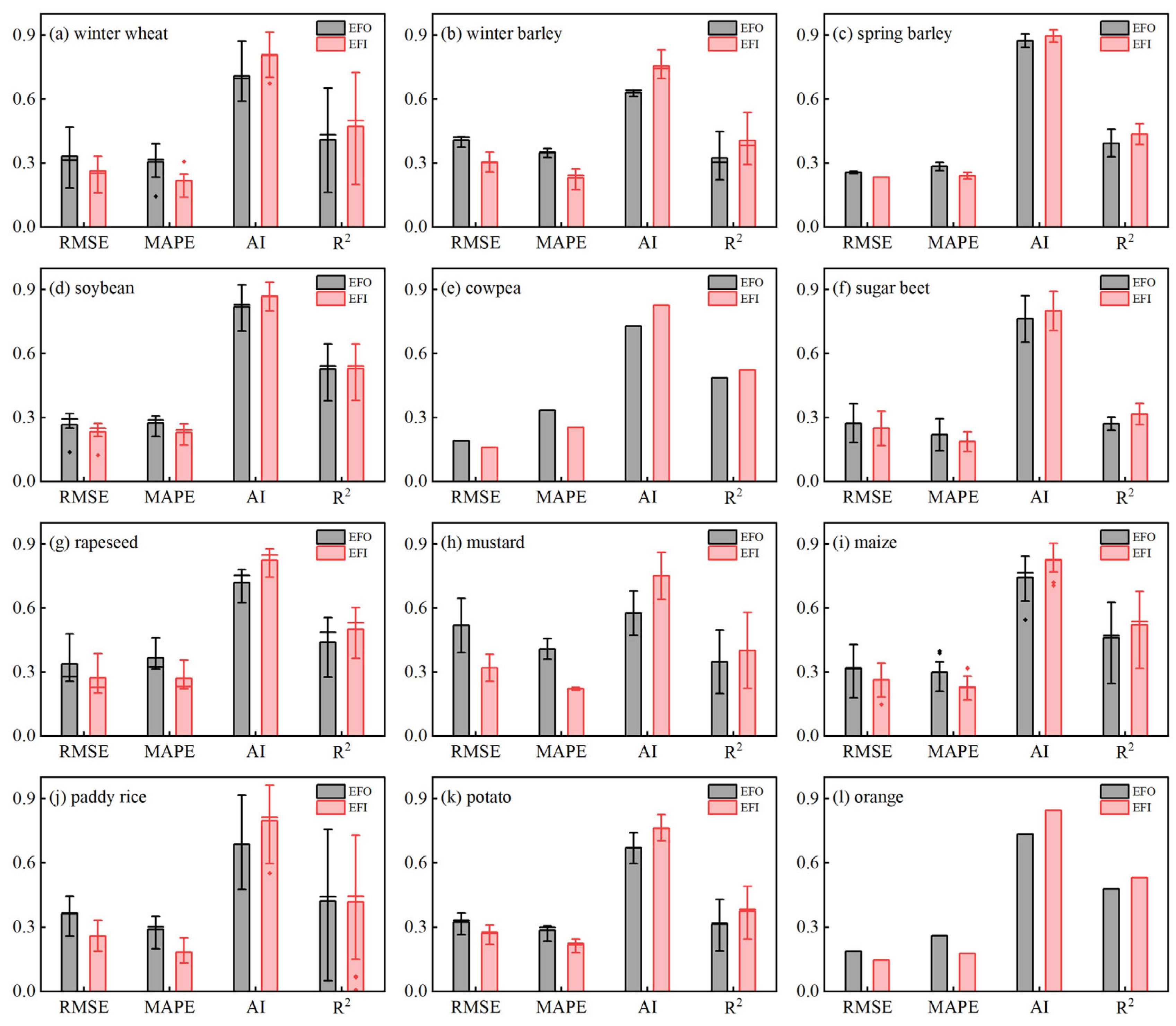
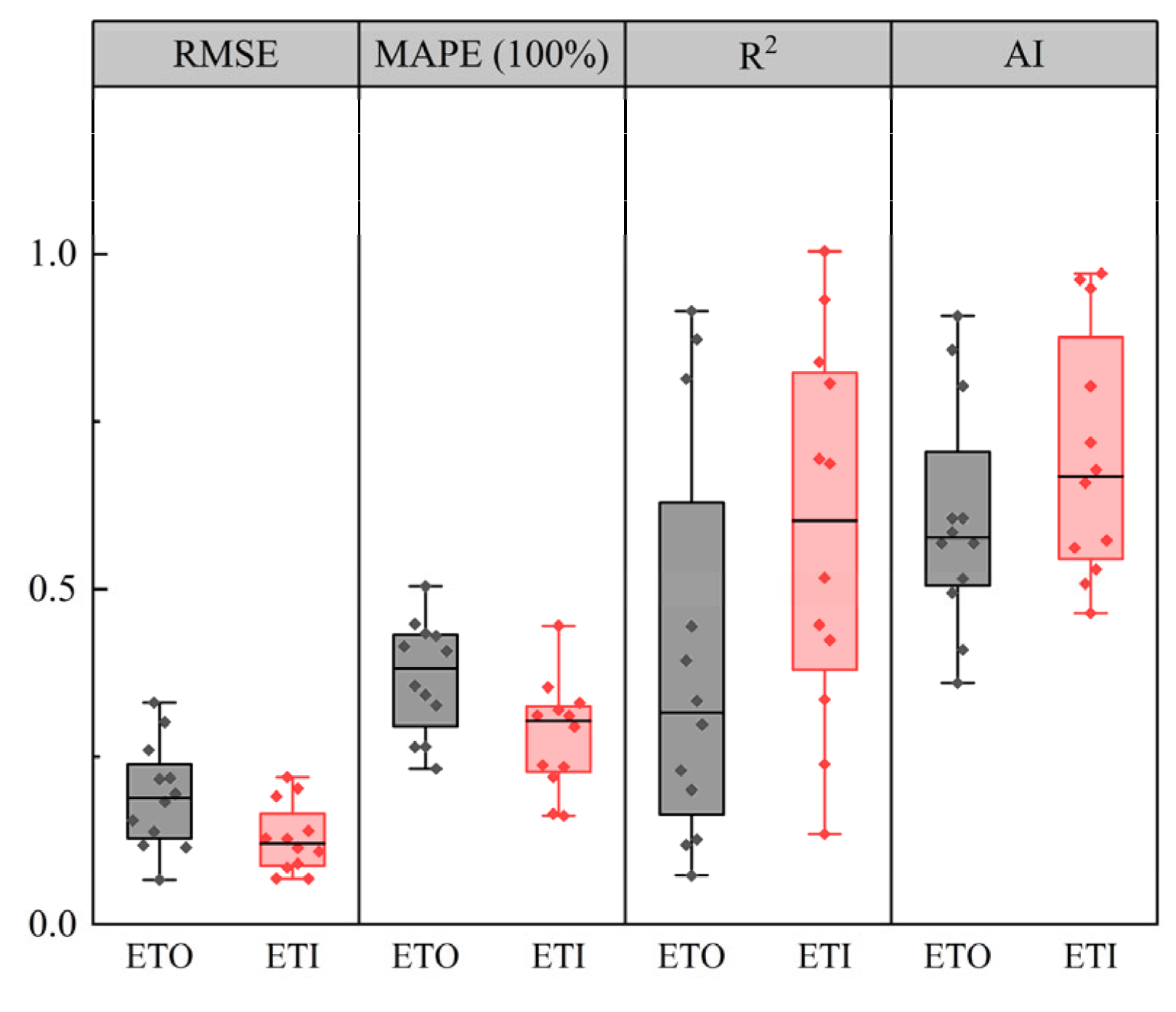
4.1. Performance of the Improved Evaporative Method
4.2. Comparision with Other Upscaling Methods
4.3. The Correctness of the Hypothesis of EFI
4.4. Uncertainty of the ETday Estimation with EFI
4.4.1. Uncertainty About Short-Time EF Calculation and Daily Rn
4.4.2. Uncertainty About the EFI Structure
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Site ID | Abbreviation | Latitude | Longitude | Filed Area | Fetch c | Time Resolution | Crop Type | Time Span | Reference |
|---|---|---|---|---|---|---|---|---|---|
| CHN_NC | NC | 28.45°N | 116.01°E | 1.2 ha b | 90 m | HH | PR | 2017–2019 | - |
| US_Twt | Twt | 38.11°N | 121.65°W | 240 ha | 500 m | HH | PR | 2009–2016 | Baldocchi et al. [71] |
| KR_CRK | CRK | 38.20°N | 127.25°E | 0.4 ha b | 300 m | HH | PR | 2015–2018 | Huang et al. [72] |
| JP_MSE | MSE | 36.05°N | 140.03°E | 0.5 ha b | 140 m | HH | PR | 2001–2006 | and Ono et al. [73] |
| IT_Cas | Cas | 45.07°N | 8.72°E | 28.0 ha | 105 m | HH | PR | 2007–2010 | Meijide et al. [74] |
| BE_Lon | Lon | 50.55°N | 4.74°E | 12.0 ha | 240 m | HH | MA SB WW PO | 2004–2014 | Buysse et al. [75] |
| DE_Geb | Geb | 51.10°N | 10.91°E | 63.8 ha | * | HH | WW PO | 2001–2002 | Anthoni et al. [76] |
| DE_Kli | Kli | 50.89°N | 13.52°E | 20.2 ha | * | HH | SB RA WW MA WBA | 2005–2014 | Prescher et al. [77] |
| DE_Seh | Seh | 50.87°N | 6.45°E | 6.6 ha | 135 m | HH | WW | 2007–2009 | Schmidt et al. [78] |
| FR_Gri | Gri | 48.84°N | 1.95°E | 20.0 ha | 400 m | HH | MU WBA | 2004–2009 | Loubet et al. [79] |
| IT_BCi | BCi | 40.52°N | 14.96°E | 10.0 ha | 182 m | HH | MA | 2004–2010 | Bai et al. [80] |
| US_ARM | ARM | 36.60°N | 82.51°W | 12.0 ha a | 400 m | HH | WW MA RA CO | 2003–2012 | Raz-Yaseef et al. [81] |
| US_CRT | CRT | 41.63°N | 96.65°W | 50.0 ha | 400 m | HH | SO WW | 2011–2013 | Chu et al. [82] |
| US_Lin | Lin | 36.35°N | 119.09°W | 4.0 ha | * | HH | OR | 2010 | Fares et al. [83] |
| US_Ne1 | Ne1 | 41.17°N | 83.52°W | 49.0 ha | * | HR | MA | 2001–2012 | Nguy-Robertson et al. [84] |
| US_Ne2 | Ne2 | 41.16°N | 83.53°W | 52.0 ha | * | HR | MA SO | 2001–2008 |
Appendix B
Bowen Ratio Method
Appendix C
The Variation in Daytime Wind Speed and ra
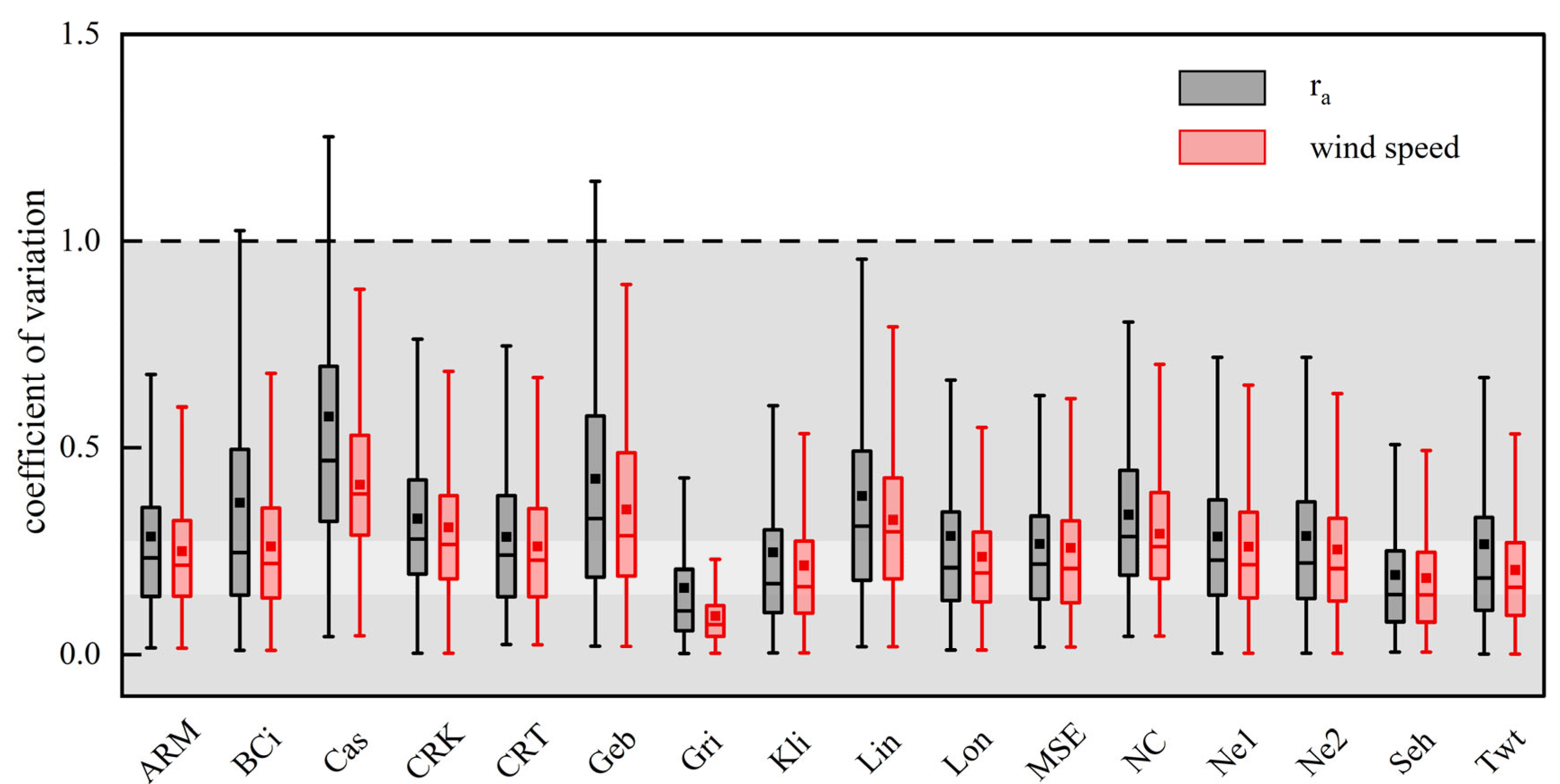
Appendix D
Appendix D.1. Latent Heat Flux (LE)
Appendix D.2. Net Radiation (Rn)
Appendix D.3. Soil Heat Flux (G)
Appendix D.4. Sensible Heat Flux (H)
Appendix D.5. Evaporation Fraction
Appendix E
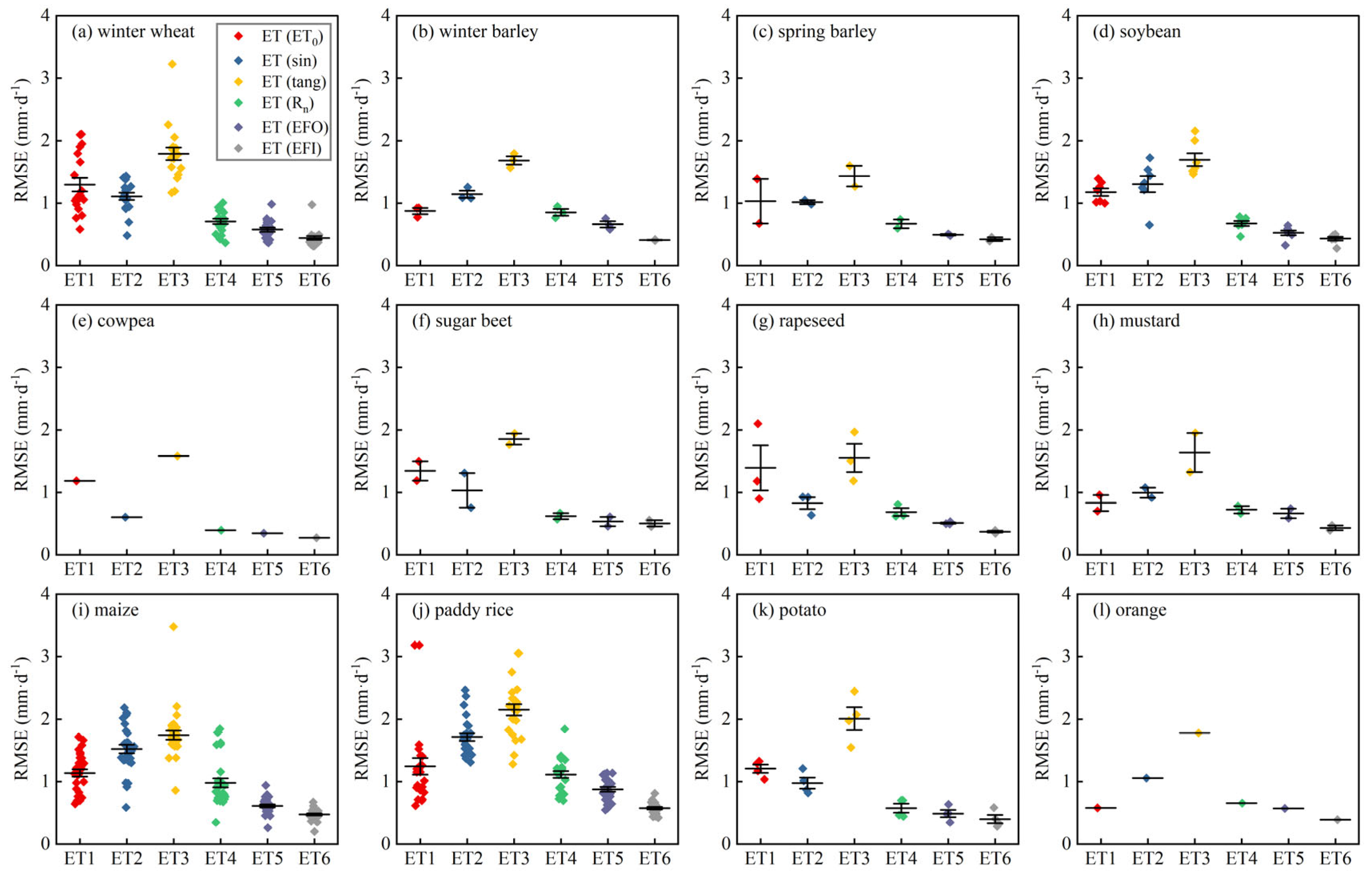
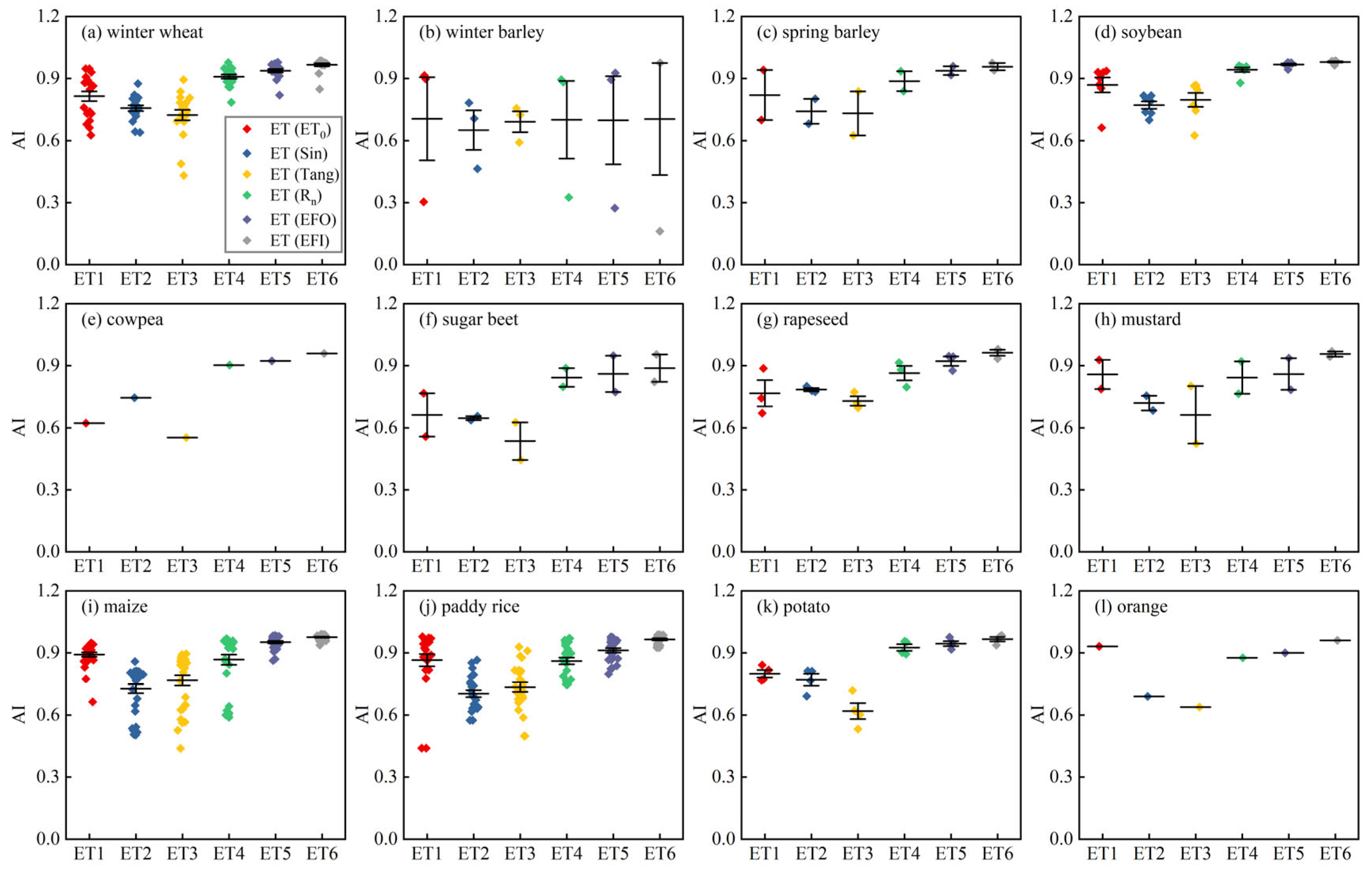
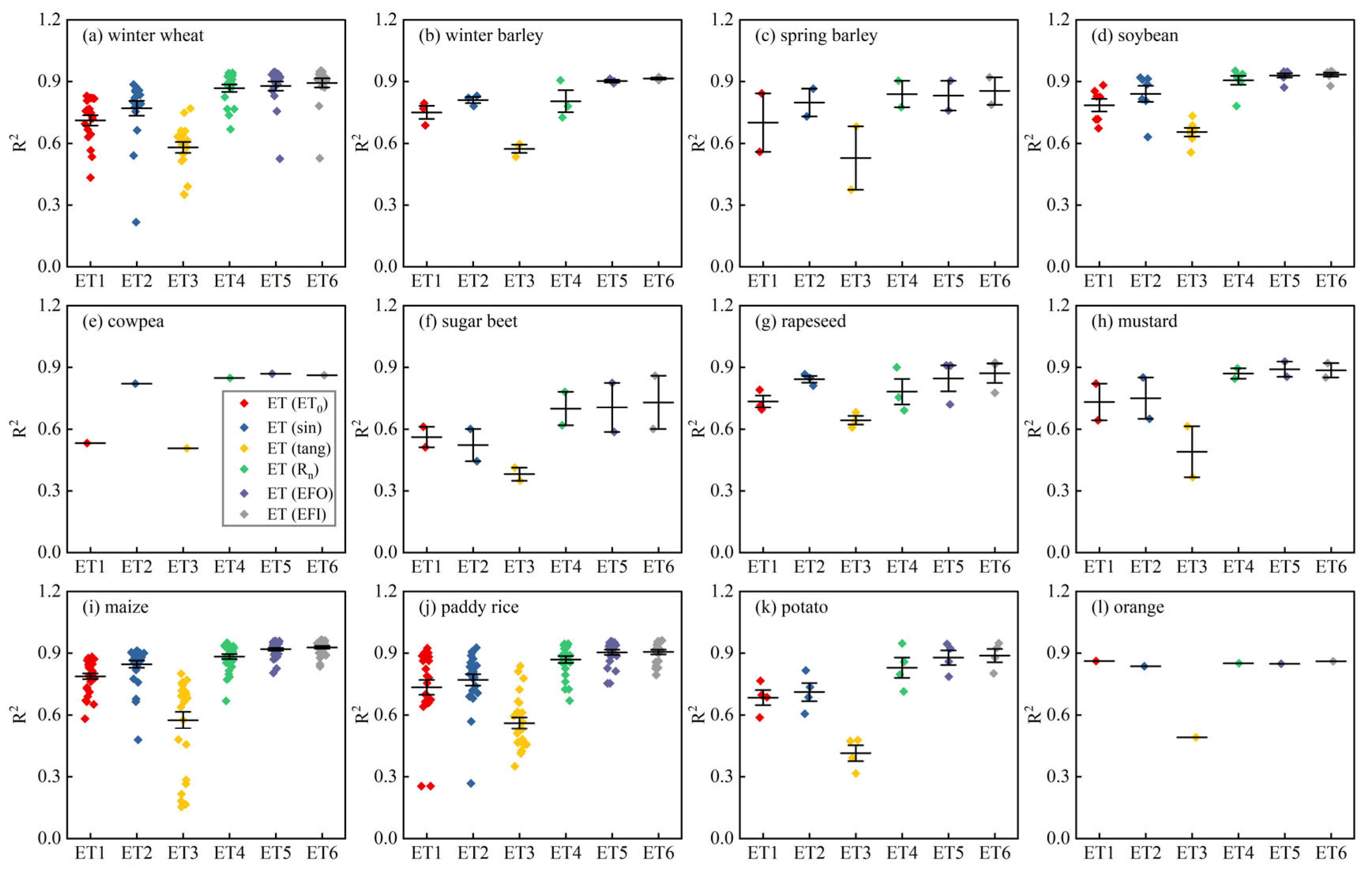
Appendix F
| Acronym | Meaning | Unit |
| EC | Eddy covariance | - |
| EF | Evaporative fraction: the ratio between latent heat flux and available energy | - |
| EFday | Daily evaporative fraction | - |
| EFI | Improved evaporative fraction method | - |
| EFO | Constant evaporative fraction method | - |
| EFst | Short-time evaporative fraction | - |
| ERA5 | European Centre for Medium-Range Weather Forecasts Reanalysis v5, a raster climate dataset | - |
| ET | Evapotranspiration | Mm·d−1 |
| ETday | Daily evapotranspiration | mm·d−1 |
| ETIG | ETday estimated with EFI when EFst and daily Rn-G come from SEBAL and ERA5, respectively | mm·d−1 |
| ETIS | ETday estimated with EFI when EFst and daily Rn-G come from EC system and ground-measured data, respectively | mm·d−1 |
| ETOG | ETday estimated with EFO when EFst and daily Rn-G come from SEBAL and ERA5, respectively | mm·d−1 |
| ETOS | ETday estimated with EFO when EFst and daily Rn-G come from EC system and ground-measured data, respectively | mm·d−1 |
| ETst | Short-time evapotranspiration | mm·d−1 |
| FS | Fallow season | - |
| G | Soil heat flux | W·m−2 |
| GP | Growth period | - |
| H | Sensible heat flux | W·m−2 |
| LE | Latent heat flux | W·m−2 |
| Rn | Net heat radiation | W·m−2 |
| SEBAL | A Surface Energy Balance Algorithm for Land model used to estimate energy flux | - |
| t | Adjustment coefficient of Ω | - |
| VPD | Vapor pressure deficit | kPa |
| δ | Deviation coefficient between EFst and EFday | - |
| η | Ratio between VPD and available energy | kPa·W−1·m2 |
| τ | Available energy | W·m−2 |
| Ω | Potential deviation between EFst and EFday | - |
References
- Jackson, R.D.; Reginato, R.J.; Idso, S.B. Wheat canopy temperature: A practical tool for evaluating water requirements. Water Resour. Res. 1977, 13, 651–656. [Google Scholar] [CrossRef]
- Price, J.C. Estimation of Regional Scale Evapotranspiration Through Analysis of Satellite Thermal-infrared Data. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 286–292. [Google Scholar] [CrossRef]
- Price, J.C. The potential of remotely sensed thermal infrared data to infer surface soil moisture and evaporation. Water Resour. Res. 1980, 16, 787–795. [Google Scholar] [CrossRef]
- Seguin, B.; Itier, B. Using midday surface temperature to estimate daily evaporation from satellite thermal IR data. Int. J. Remote Sens. 1983, 4, 371–383. [Google Scholar] [CrossRef]
- Carlson, T.N.; Capehart, W.J.; Gillies, R.R. A new look at the simplified method for remote sensing of daily evapotranspiration. Remote Sens. Environ. 1995, 54, 161–167. [Google Scholar] [CrossRef]
- Sugita, M.; Brutsaert, W. Daily evaporation over a region from lower boundary layer profiles measured with radiosondes. Water Resour. Res. 1991, 27, 747–752. [Google Scholar] [CrossRef]
- Jackson, R.D.; Hatfield, J.L.; Reginato, R.J.; Idso, S.B.; Pinter, P.J. Estimation of daily evapotranspiration from one time-of-day measurements. Agr. Water Manag. 1983, 7, 351–362. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-Based Energy Balance for Mapping Evapotranspiration with Internalized Calibration (METRIC)—Model. J. Irrig. Drain Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Tasumi, M.; Allen, R.G.; Trezza, R.; Wright, J.L. Satellite-Based Energy Balance to Assess Within-Population Variance of Crop Coefficient Curves. J. Irrig. Drain Eng. 2005, 29, 94–109. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Y.; Xu, D. Comparison of evapotranspiration temporal scaling methods based on lysimeter measurements. J. Remote Sens. 2011, 15, 270–280. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J.; Hsu, A.Y.; Ormsby, J.P. FIFE: The Variation in ENERGY partition at Surface at Surfacae Flux Sites; IAHS Publisher: Wallingford, UK, 1989. [Google Scholar]
- Gomez, M.; Olioso, A.; Sobrino, J.; Jacob, F. Retrieval of evapotranspiration over the Alpilles/ReSeDA experimental site using airborne POLDER sensor and a thermal camera. Remote Sens. Environ. 2005, 96, 399–408. [Google Scholar] [CrossRef]
- Li, F.; Xin, X.; Peng, Z.; Liu, Q. Estimating daily evapotranspiration based on a model of evaporative fraction (EF) for mixed pixels. Hydrol. Earth Syst. Sci. 2019, 23, 949–969. [Google Scholar] [CrossRef]
- Lian, X.; Piao, S.; Huntingford, C.; Li, Y.; Zeng, Z.; Wang, X.; Ciais, P.; McVicar, T.R.; Peng, S.; Ottlé, C.; et al. Partitioning global land evapotranspiration using CMIP5 models constrained by observations. Nat. Clim. Change 2018, 8, 640–646. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Gómez, M.; Jiménez-Muñoz, J.C.; Olioso, A. Application of a simple algorithm to estimate daily evapotranspiration from NOAA–AVHRR images for the Iberian Peninsula. Remote Sens. Environ. 2007, 110, 139–148. [Google Scholar] [CrossRef]
- Zhang, L.; Lemeur, R. Evaluation of daily evapotranspiration estimates from instantaneous measurements. Agr. Forest. Meteorol. 1995, 74, 139–154. [Google Scholar] [CrossRef]
- Laipelt, L.; Henrique Bloedow Kayser, R.; Santos Fleischmann, A.; Ruhoff, A.; Bastiaanssen, W.; Erickson, T.A.; Melton, F. Long-term monitoring of evapotranspiration using the SEBAL algorithm and Google Earth Engine cloud computing. ISPRS. J. Photogramm. 2021, 178, 81–96. [Google Scholar] [CrossRef]
- Peng, J.; Borsche, M.; Liu, Y.; Loew, A. How representative are instantaneous evaporative fraction measurements of daytime fluxes? Hydrol. Earth Syst. Sci. 2013, 17, 3913–3919. [Google Scholar] [CrossRef]
- Liu, Z. The accuracy of temporal upscaling of instantaneous evapotranspiration to daily values with seven upscaling methods. Hydrol. Earth Syst. Sci. 2021, 25, 4417–4433. [Google Scholar] [CrossRef]
- Van Niel, T.G.; McVicar, T.R.; Roderick, M.L.; van Dijk, A.I.; Beringer, J.; Hutley, L.B.; van Gorsel, E. Upscaling latent heat flux for thermal remote sensing studies: Comparison of alternative approaches and correction of bias. J. Hydrol. 2012, 468–469, 35–46. [Google Scholar] [CrossRef]
- Xu, T.; Liu, S.; Xu, L.; Chen, Y.; Jia, Z.; Xu, Z.; Nielson, J. Temporal Upscaling and Reconstruction of Thermal Remotely Sensed Instantaneous Evapotranspiration. Remote Sens. 2015, 7, 3400–3425. [Google Scholar] [CrossRef]
- Nichols, W.E.; Cuenca, R.H. Evaluation of the evaporative fraction for parameterization of the surface energy balance. Water Resour. Res. 1993, 29, 3681–3690. [Google Scholar] [CrossRef]
- Hoedjes, J.; Chehbouni, A.; Jacob, F.; Ezzahar, J.; Boulet, G. Deriving daily evapotranspiration from remotely sensed instantaneous evaporative fraction over olive orchard in semi-arid Morocco. J. Hydrol. 2008, 354, 53–64. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z. An improved constant evaporative fraction method for estimating daily evapotranspiration from remotely sensed instantaneous observations. Geophys. Res. Lett. 2017, 44, 2319–2326. [Google Scholar] [CrossRef]
- Liu, X.; Xu, J.; Zhou, X.; Wang, W.; Yang, S. Evaporative fraction and its application in estimating daily evapotranspiration of water-saving irrigated rice field. J. Hydrol. 2020, 584, 124317. [Google Scholar] [CrossRef]
- Suleiman, A.; Crago, R. Hourly and Daytime Evapotranspiration from Grassland Using Radiometric Surface Temperatures. Agron. J. 2004, 96, 384–390. [Google Scholar] [CrossRef]
- Wei, J.; Cui, Y.; Luo, Y. Rice growth period detection and paddy field evapotranspiration estimation based on an improved SEBAL model: Considering the applicable conditions of the advection equation. Agr. Water Manag. 2023, 278, 108141. [Google Scholar] [CrossRef]
- Amani, S.; Shafizadeh-Moghadam, H. A review of machine learning models and influential factors for estimating evapotranspiration using remote sensing and ground-based data. Agr. Water Manag. 2023, 284, 108324. [Google Scholar] [CrossRef]
- Blatchford, M.L.; Mannaerts, C.M.; Zeng, Y.; Nouri, H.; Karimi, P. Status of accuracy in remotely sensed and in-situ agricultural water productivity estimates: A review. Remote Sens. Environ. 2019, 234, 111413. [Google Scholar] [CrossRef]
- Wei, J.; Cui, Y.; Luo, W.; Luo, Y. Mapping Paddy Rice Distribution and Cropping Intensity in China from 2014 to 2019 with Landsat Images, Effective Flood Signals, and Google Earth Engine. Remote Sens. 2022, 14, 759. [Google Scholar] [CrossRef]
- Hollinger, D.Y.; Goltz, S.M.; Davidson, E.A.; Lee, J.T.; Tu, K.; Valentine, H.T. Seasonal patterns and environmental control of carbon dioxide and water vapour exchange in an ecotonal boreal forest. Glob. Change Biol. 1999, 5, 891–902. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agr. Forest. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agr. Forest. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; ISBN 9251042195. [Google Scholar]
- Yan, H.; Zhang, C.; Coenders Gerrits, M.; Acquah, S.J.; Zhang, H.; Wu, H.; Zhao, B.; Huang, S.; Fu, H. Parametrization of aerodynamic and canopy resistances for modeling evapotranspiration of greenhouse cucumber. Agr. Forest. Meteorol. 2018, 262, 370–378. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N.; Mastrorilli, M.; El Moujabber, M. Evapotranspiration and canopy resistance of grass in a Mediterranean region. Theor Appl Climatol 1994, 50, 61–71. [Google Scholar] [CrossRef]
- Rouphael, Y.; Colla, G. Modelling the transpiration of a greenhouse zucchini crop grown under a Mediterranean climate using the Penman-Monteith equation and its simplified version. Aust. J. Agric. Res. 2004, 55, 931. [Google Scholar] [CrossRef]
- Bailey, B.J.; Montero, J.I.; Biel, C.; Wilkinson, D.J.; Anton, A.; Jolliet, O. Transpiration of Ficus benjamina: Comparison of measurements with predictions of the Penman-Monteith model and a simplified version. Agr. Forest. Meteorol. 1993, 65, 229–243. [Google Scholar] [CrossRef]
- Montero, J.I.; Antón, A.; Muñoz, P.; Lorenzo, P. Transpiration from geranium grown under high temperatures and low humidities in greenhouses. Agr. Forest. Meteorol. 2001, 107, 323–332. [Google Scholar] [CrossRef]
- Malek, E.; Bingham, G.E.; McCurdy, G.D. Continuous measurement of aerodynamic and alfalfa canopy resistances using the Bowen ratio-energy balance and Penman-Monteith methods. Bound. Lay. Meteorol. 1992, 59, 187–194. [Google Scholar] [CrossRef]
- Rana, G.; Ferrara, R.M.; Cona, F.; de Lorenzi, F. Actual transpiration and canopy resistance in a Mediterranean vineyard irrigated with saline water. Irrig. Sci. 2021, 39, 469–481. [Google Scholar] [CrossRef]
- Bailey, W.G.; Davies, J.A. The effect of uncertainty in aerodynamic resistance on evaporation estimates from the combination model. Bound. Lay. Meteorol. 1981, 20, 187–199. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Sun, S.; Fiifi Tawia Hagan, D.; Chen, T.; Dolman, H.; Liu, Y. Long-term changes in evapotranspiration over China and attribution to climatic drivers during 1980–2010. J. Hydrol. 2021, 595, 126037. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Zhu, C.; Lu, J.; Ullah, W.; Hagan, D.F.T.; Kattel, G.; Peng, J. Attribution of global evapotranspiration trends based on the Budyko framework. Hydrol. Earth Syst. Sci. 2022, 26, 3691–3707. [Google Scholar] [CrossRef]
- Yao, Y.; Liao, X.; Xiao, J.; He, Q.; Shi, W. The sensitivity of maize evapotranspiration to vapor pressure deficit and soil moisture with lagged effects under extreme drought in Southwest China. Agr. Water Manag. 2023, 277, 108101. [Google Scholar] [CrossRef]
- Cheng, M.; Shi, L.; Jiao, X.; Nie, C.; Liu, S.; Yu, X.; Bai, Y.; Liu, Y.; Liu, Y.; Song, N.; et al. Up-scaling the latent heat flux from instantaneous to daily-scale: A comparison of three methods. J. Hydrol. Reg. Stud. 2022, 40, 101057. [Google Scholar] [CrossRef]
- Cheng, M.; Jiao, X.; Li, B.; Yu, X.; Shao, M.; Jin, X. Long time series of daily evapotranspiration in China based on the SEBAL model and multisource images and validation. Earth Syst. Sci. Data 2021, 13, 3995–4017. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. 1985, 90, 8995. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Li, F.; Zhang, L.; Zhang, B. Vineyard evaporative fraction based on eddy covariance in an arid desert region of Northwest China. Agr. Water Manag. 2008, 95, 937–948. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Change Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Farah, H.O.; Bastiaanssen, W.; Feddes, R.A. Evaluation of the temporal variability of the evaporative fraction in a tropical watershed. Int. J. Appl. Earth Obs. 2004, 5, 129–140. [Google Scholar] [CrossRef]
- Pérez-Delgado, M.-L.; Günen, M.A. A comparative study of evolutionary computation and swarm-based methods applied to color quantization. Expert Syst. Appl. 2023, 231, 120666. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Bastiaanssen, W.; Menenti, M.; Feddes, R.A.; Holtslag, A. A remote sensing surface energy balance algorithm for land (SEBAL). 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar] [CrossRef]
- Charter, R.A. Study samples are too small to produce sufficiently precise reliability coefficients. J. Gen. Psychol. 2003, 130, 117–129. [Google Scholar] [CrossRef]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Comparison of Five Models to Scale Daily Evapotranspiration from One-Time-of-Day Measurements. Trans. ASABE 2006, 49, 1409–1417. [Google Scholar] [CrossRef]
- Brutsaert, W.; Sugita, M. Application of self-preservation in the diurnal evolution of the surface energy budget to determine daily evaporation. J. Geophys. Res. Atmos. 1992, 97, 18377–18382. [Google Scholar] [CrossRef]
- Cammalleri, C.; Anderson, M.C.; Kustas, W.P. Upscaling of evapotranspiration fluxes from instantaneous to daytime scales for thermal remote sensing applications. Hydrol. Earth Syst. Sci. 2014, 18, 1885–1894. [Google Scholar] [CrossRef]
- Su, Z. The Surface Energy Balance System (SEBS) for estimation of turbulent heat fluxes. Hydrol. Earth Syst. Sci. 2002, 6, 85–100. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Han, Z.; Scanlon, B.R.; Sun, Z.; Han, P.; Hou, A. Evapotranspiration Estimation for Tibetan Plateau Headwaters Using Conjoint Terrestrial and Atmospheric Water Balances and Multisource Remote Sensing. Water Resour. Res. 2019, 55, 8608–8630. [Google Scholar] [CrossRef]
- Herman, M.R.; Nejadhashemi, A.P.; Abouali, M.; Hernandez-Suarez, J.S.; Daneshvar, F.; Zhang, Z.; Anderson, M.C.; Sadeghi, A.M.; Hain, C.R.; Sharifi, A. Evaluating the role of evapotranspiration remote sensing data in improving hydrological modeling predictability. J. Hydrol. 2018, 556, 39–49. [Google Scholar] [CrossRef]
- Shamloo, N.; Taghi Sattari, M.; Apaydin, H.; Valizadeh Kamran, K.; Prasad, R. Evapotranspiration estimation using SEBAL algorithm integrated with remote sensing and experimental methods. Int. J. Digit. Earth 2021, 14, 1638–1658. [Google Scholar] [CrossRef]
- Kiptala, J.K.; Mohamed, Y.; Mul, M.L.; van der Zaag, P. Mapping evapotranspiration trends using MODIS and SEBAL model in a data scarce and heterogeneous landscape in Eastern Africa. Water Resour. Res. 2013, 49, 8495–8510. [Google Scholar] [CrossRef]
- Ochege, F.U.; Luo, G.; Obeta, M.C.; Owusu, G.; Duulatov, E.; Cao, L.; Nsengiyumva, J.B. Mapping evapotranspiration variability over a complex oasis-desert ecosystem based on automated calibration of Landsat 7 ETM+ data in SEBAL. GISci. Remote Sens. 2019, 49, 1305–1332. [Google Scholar] [CrossRef]
- Jaafar, H.H.; Sujud, L.H. High-resolution satellite imagery reveals a recent accelerating rate of increase in land evapotranspiration. Remote Sens. Environ. 2024, 315, 114489. [Google Scholar] [CrossRef]
- Ippolito, M.; de Caro, D.; Cannarozzo, M.; Provenzano, G.; Ciraolo, G. Evaluation of daily crop reference evapotranspiration and sensitivity analysis of FAO Penman-Monteith equation using ERA5-Land reanalysis database in Sicily, Italy. Agr. Water Manag. 2024, 295, 108732. [Google Scholar] [CrossRef]
- Yang, C.; Ma, Y.; Yuan, Y. Terrestrial and Atmospheric Controls on Surface Energy Partitioning and Evaporative Fraction Regimes Over the Tibetan Plateau in the Growing Season. JGR Atmos. 2021, 126, e2021JD035011. [Google Scholar] [CrossRef]
- Baldocchi, D.; Knox, S.; Dronova, I.; Verfaillie, J.; Oikawa, P.; Sturtevant, C.; Matthes, J.H.; Detto, M. The impact of expanding flooded land area on the annual evaporation of rice. Agr. For. Meteorol. 2016, 223, 181–193. [Google Scholar] [CrossRef]
- Huang, Y.; Ryu, Y.; Jiang, C.; Kimm, H.; Kim, S.; Kang, M.; Shim, K. BESS-Rice: A remote sensing derived and biophysical process-based rice productivity simulation model. Agr. For. Meteorol. 2018, 256–257, 253–269. [Google Scholar] [CrossRef]
- Ono, K.; Maruyama, A.; Kuwagata, T.; Mano, M.; Takimoto, T.; Hayashi, K.; Hasegawa, T.; Miyata, A. Canopy-scale relationships between stomatal conductance and photosynthesis in irrigated rice. Glob. Change Biol. 2013, 19, 2209–2220. [Google Scholar] [CrossRef]
- Meijide, A.; Manca, G.; Goded, I.; Magliulo, V.; Di Tommasi, P.; Seufert, G.; Cescatti, A. Seasonal trends and environmental controls of methane emissions in a rice paddy field in Northern Italy. Biogeosciences 2011, 8, 3809–3821. [Google Scholar] [CrossRef]
- Buysse, P.; Bodson, B.; Debacq, A.; de Ligne, A.; Heinesch, B.; Manise, T.; Moureaux, C.; Aubinet, M. Carbon budget measurement over 12 years at a crop production site in the silty-loam region in Belgium. Agr. For. Meteorol. 2017, 246, 241–255. [Google Scholar] [CrossRef]
- Anthoni, P.M.; Knohl, A.; Rebmann, C.; Freibauer, A.; Mund, M.; Ziegler, W.; Kolle, O.; Schulze, E.-D. Forest and agricultural land-use-dependent CO2 exchange in Thuringia, Germany. Glob. Change Biol. 2004, 10, 2005–2019. [Google Scholar] [CrossRef]
- Prescher, A.-K.; Grünwald, T.; Bernhofer, C. Land use regulates carbon budgets in eastern Germany: From NEE to NBP. Agr. For. Meteorol. 2010, 150, 1016–1025. [Google Scholar] [CrossRef]
- Schmidt, M.; Reichenau, T.G.; Fiener, P.; Schneider, K. The carbon budget of a winter wheat field: An eddy covariance analysis of seasonal and inter-annual variability. Agr. For. Meteorol. 2012, 165, 114–126. [Google Scholar] [CrossRef]
- Loubet, B.; Laville, P.; Lehuger, S.; Larmanou, E.; Fléchard, C.; Mascher, N.; Genermont, S.; Roche, R.; Ferrara, R.M.; Stella, P.; et al. Carbon, nitrogen and Greenhouse gases budgets over a four years crop rotation in northern France. Plant Soil 2011, 343, 109–137. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.; Zhang, S.; Yao, F.; Magliulo, V. A remote sensing-based two-leaf canopy conductance model: Global optimization and applications in modeling gross primary productivity and evapotranspiration of crops. Remote Sens. Environ. 2018, 215, 411–437. [Google Scholar] [CrossRef]
- Raz-Yaseef, N.; Billesbach, D.P.; Fischer, M.L.; Biraud, S.C.; Gunter, S.A.; Bradford, J.A.; Torn, M.S. Vulnerability of crops and native grasses to summer drying in the U.S. Southern Great Plains. Agric. Ecosyst. Environ. 2015, 213, 209–218. [Google Scholar] [CrossRef]
- Chu, H.; Chen, J.; Gottgens, J.F.; Ouyang, Z.; John, R.; Czajkowski, K.; Becker, R. Net ecosystem methane and carbon dioxide exchanges in a Lake Erie coastal marsh and a nearby cropland. J. Geophys. Res. Biogeosci. 2014, 119, 722–740. [Google Scholar] [CrossRef]
- Fares, S.; Weber, R.; Park, J.-H.; Gentner, D.; Karlik, J.; Goldstein, A.H. Ozone deposition to an orange orchard: Partitioning between stomatal and non-stomatal sinks. Environ. Pollut. 2012, 169, 258–266. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Suyker, A.; Xiao, X. Modeling gross primary production of maize and soybean croplands using light quality, temperature, water stress, and phenology. Agr. For. Meteorol. 2015, 213, 160–172. [Google Scholar] [CrossRef]
- Obisesan, O.E.; Jegede, O.O. Evaluation of selected parameterizations of aerodynamic resistance to heat transfer for the estimation of sensible heat flux at a tropical site in Ile-Ife, Nigeria. Ife J. Sci. 2022, 24, 95–108. [Google Scholar]
- Allen, R.G.; Burnett, B.; Kramber, W.; Huntington, J.; Kjaersgaard, J.; Kilic, A.; Kelly, C.; Trezza, R. Automated Calibration of the METRIC—Landsat Evapotranspiration Process. JAWRA J. Am. Water Resour. Assoc. 2013, 49, 563–576. [Google Scholar] [CrossRef]







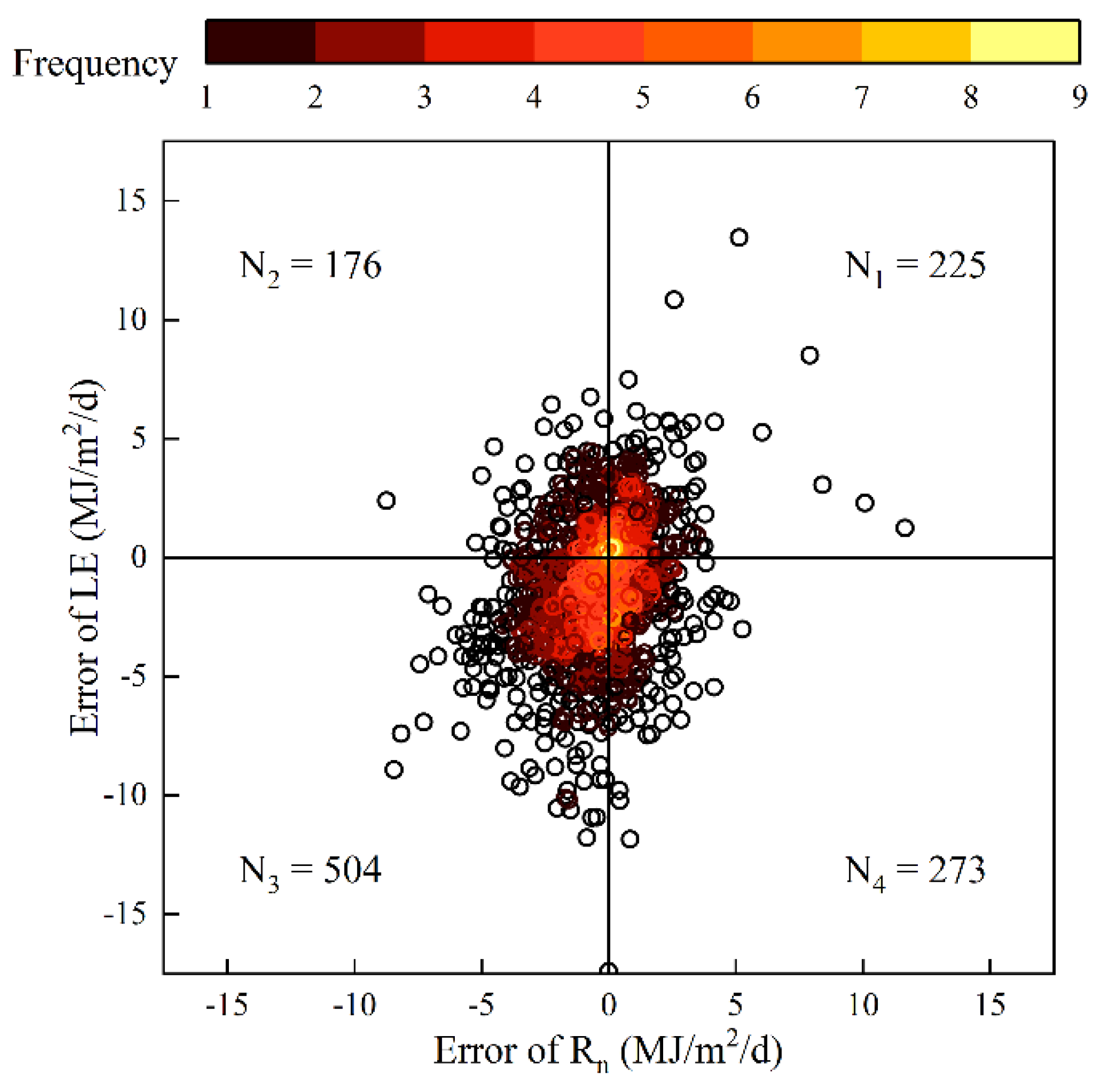

| Case | ETday Symbol | Upscaling Methods | Sources of Daily Rn-G | Sources Short-Time EF |
|---|---|---|---|---|
| Case Ⅰ | ETOS | EFO | ERA5 | SEBAL |
| Case Ⅱ | ETIS | EFI | ERA5 | SEBAL |
| Case Ⅲ | ETOG | EFO | Ground-measured | EC system |
| Case Ⅳ | ETIG | EFI | Ground-measured | EC system |
| Providers | Assumptions | Inputs | Core Equations | Accuracy Improvement Compared to EFO |
|---|---|---|---|---|
| Hoedjes et al. [23] | The linear relationship between Rs, RH and EF; the scaling factor was the ratio of EFmea,st and EFest,st. | Rs, RH, and EFmea,st | MAPE: 8% vs. 0.5% | |
| Liu et al. [25] | VPD controls the simulated error between estimated ETday with EFO and measured ETday. | A, B, and VPD | RMSE: 0.24 vs. 0.21 mm·d−1 | |
| Liu [19] | The ratio of LE to Rn is a constant. | EFst | MAPE 20% vs. 18% | |
| Tang and Li [24] | The decoupling factor is constant for one day. | Ta, ra, rs, and r * | MAPE: 22.8% vs. 11.7% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Luo, Y.; Liu, B.; Cui, Y. Temporal Upscaling of Agricultural Evapotranspiration with an Improved Evaporative Fraction Method. Remote Sens. 2025, 17, 1016. https://doi.org/10.3390/rs17061016
Wei J, Luo Y, Liu B, Cui Y. Temporal Upscaling of Agricultural Evapotranspiration with an Improved Evaporative Fraction Method. Remote Sensing. 2025; 17(6):1016. https://doi.org/10.3390/rs17061016
Chicago/Turabian StyleWei, Jun, Yufeng Luo, Bo Liu, and Yuanlai Cui. 2025. "Temporal Upscaling of Agricultural Evapotranspiration with an Improved Evaporative Fraction Method" Remote Sensing 17, no. 6: 1016. https://doi.org/10.3390/rs17061016
APA StyleWei, J., Luo, Y., Liu, B., & Cui, Y. (2025). Temporal Upscaling of Agricultural Evapotranspiration with an Improved Evaporative Fraction Method. Remote Sensing, 17(6), 1016. https://doi.org/10.3390/rs17061016








