An Improved Knowledge-Based Ground Moving Target Relocation Algorithm for a Lightweight Unmanned Aerial Vehicle-Borne Radar System
Abstract
1. Introduction
- We introduce the moving target relocation model with undesired phase errors for dual-channel GMTI radar system.
- We evaluate the strengths and limitations of the LS algorithm and median filter algorithm in estimating the clutter’s interferometric phase of MA2DC algorithm and KB algorithm.
- We propose an improved KB target relocation algorithm to maintain high accuracy while reducing sensitivity to the undesired phase errors. In the algorithm, we first employ the RANSAC algorithm to eliminate the outliers and then utilize the remaining accurate interferometric phase for relocating moving targets. The experimental results demonstrate that the proposed algorithm can indeed improve the accuracy of moving target relocation.
2. Relocation Signal Model Analysis
2.1. Moving Target Relocation Model
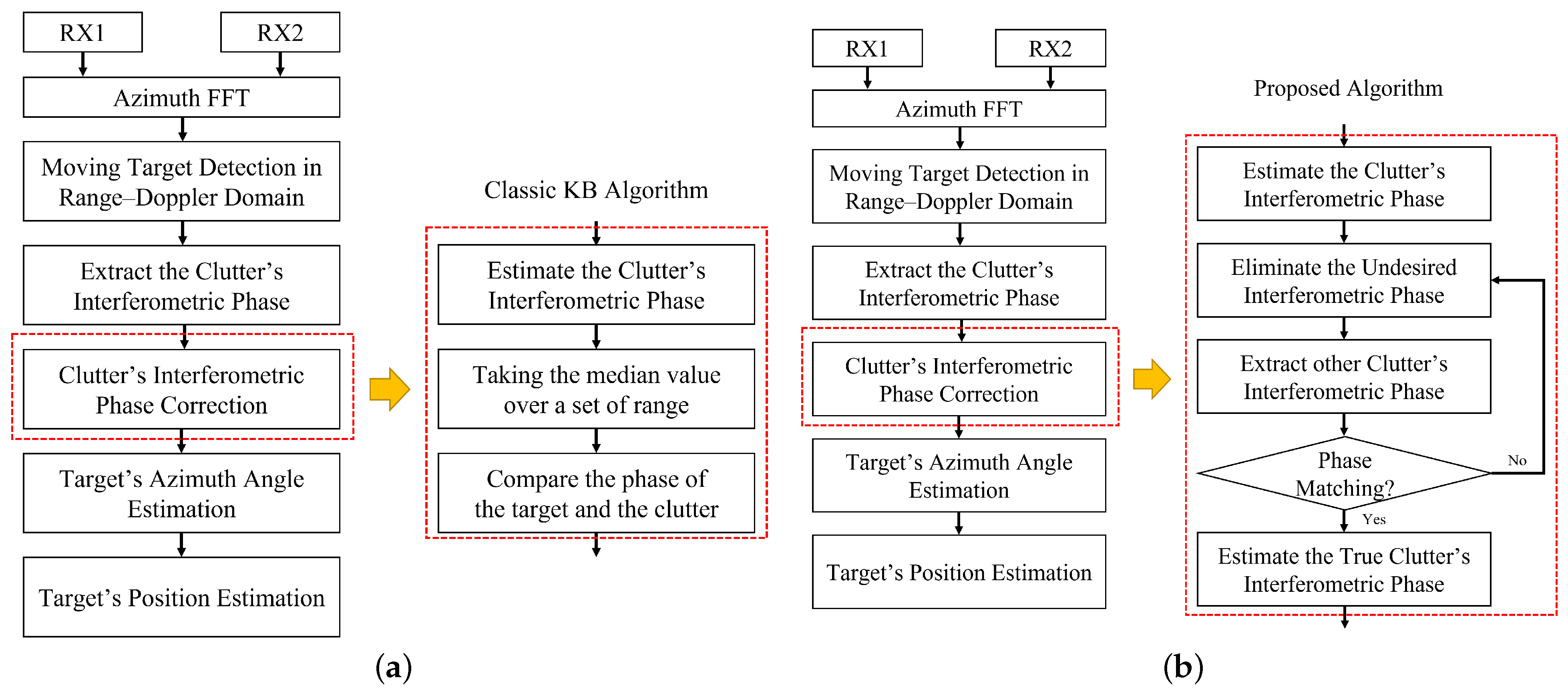
2.2. The Classic Knowledge-Based Target Relocation Algorithm
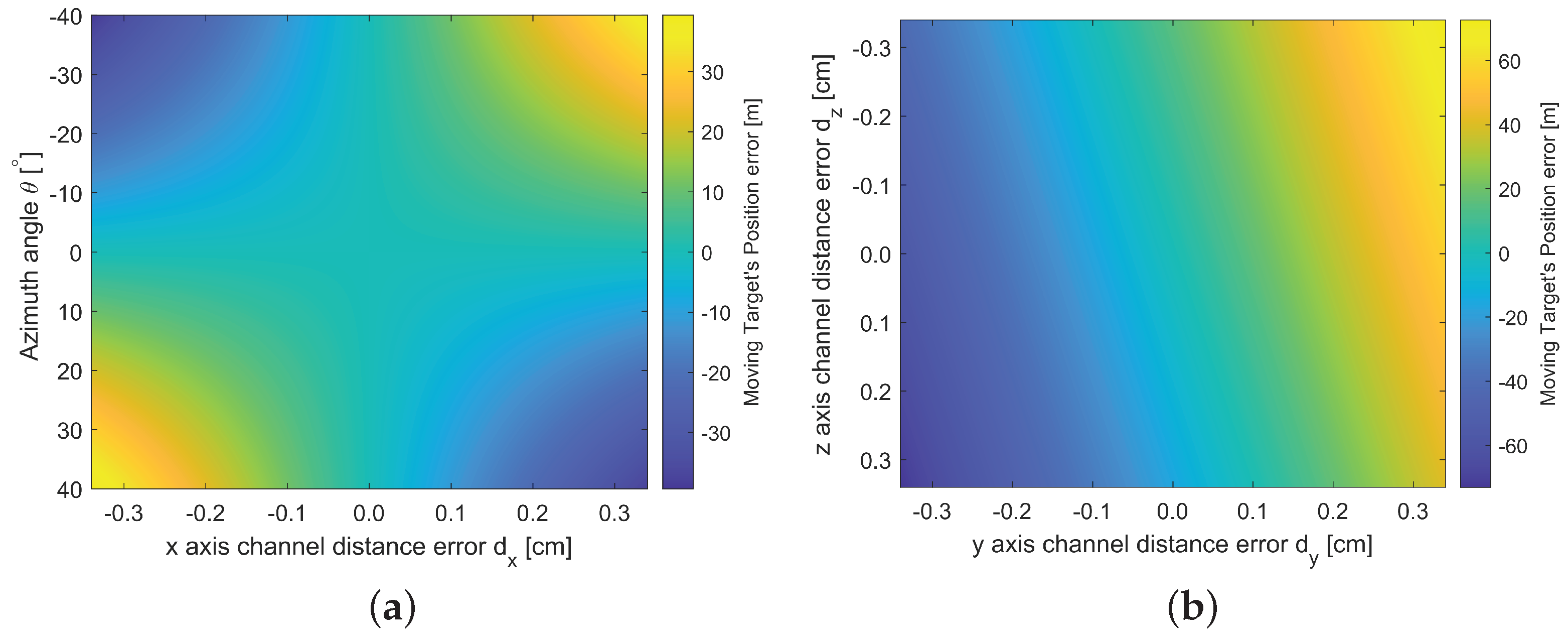
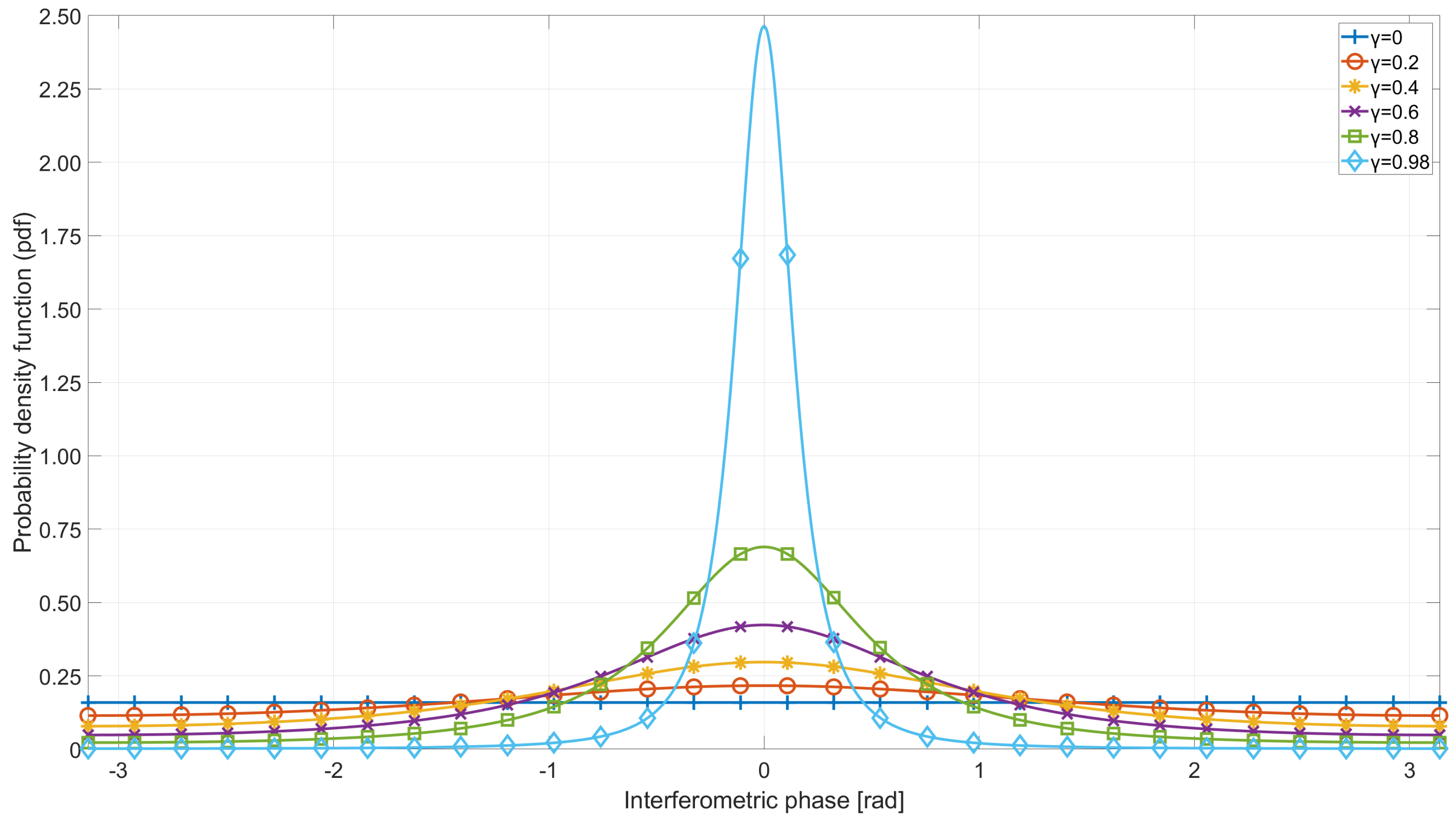
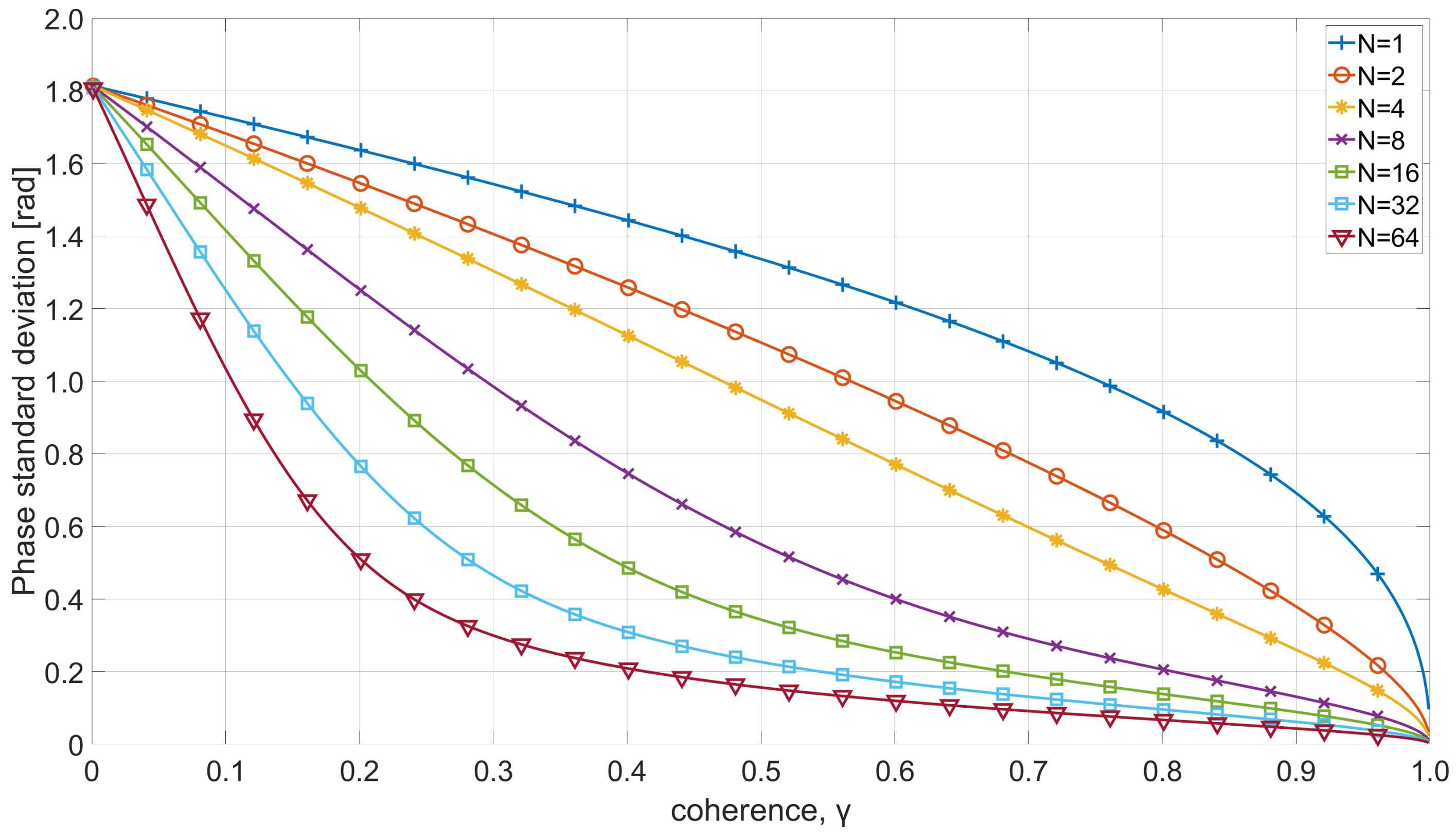
3. Moving Target Relocation with Undesired Phase Error
3.1. Undesired Phase Error Signal Model
3.2. Proposed Improved Algorithm That Eliminates the Undesired Phase Error
- First, we randomly select Q cells among the K azimuth Doppler frequency cells of the clutter’s interferometric phase. Then, the clutter’s interferometric phase can be estimated using the LS algorithm.
- Next, we calculate the difference between the residual K-Q cells and the estimation and compare it with a threshold . If the difference is smaller than the threshold , then it is considered as a compatible cell and included in a set.
- We repeat steps 1 and 2 for some predetermined number of iterations. Finally, we have the set that includes the most effective compatible cells, and we employ the LS algorithm to compute an improved estimation of the clutter’s interferometric phase.
4. Experimental Results
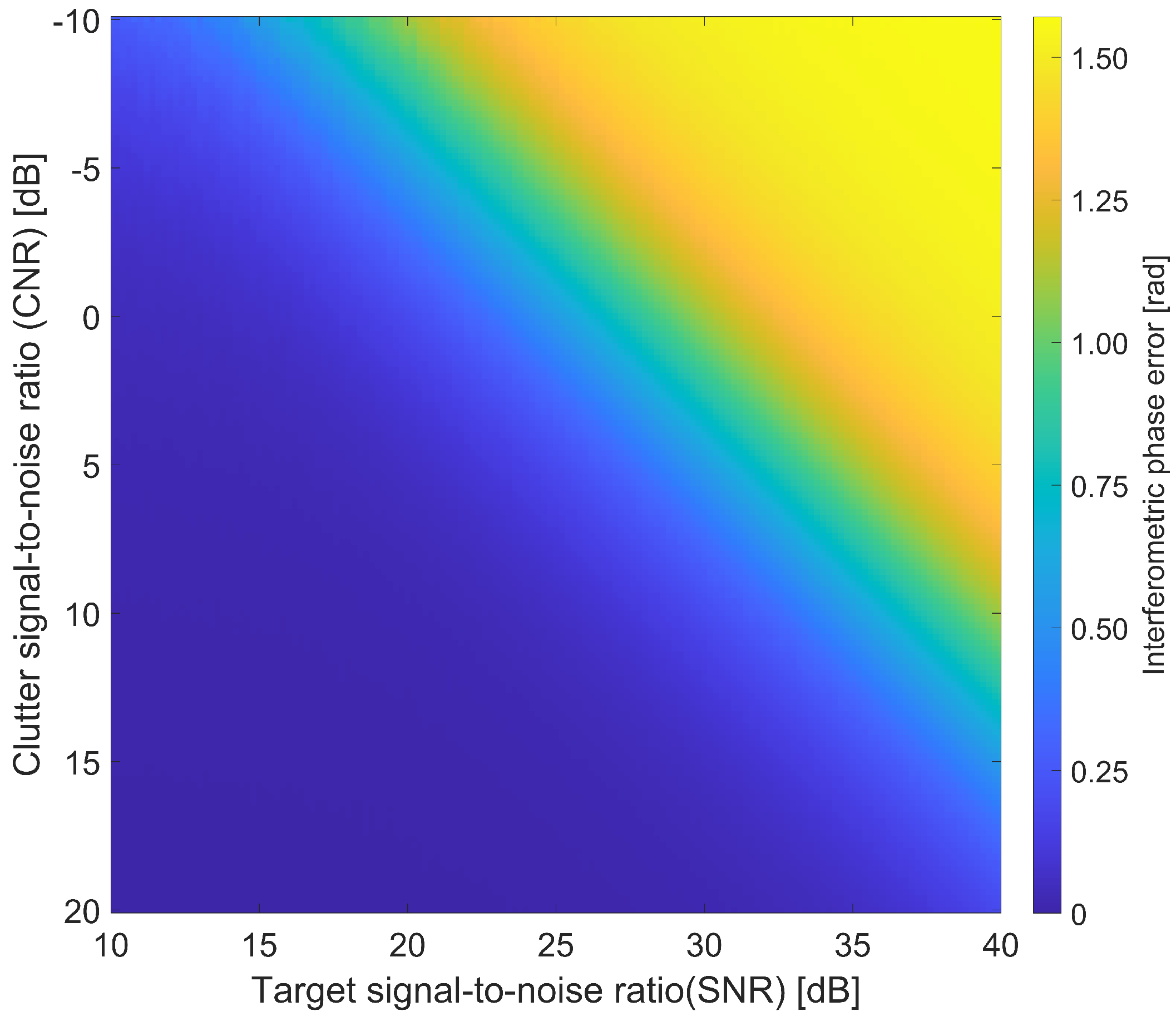
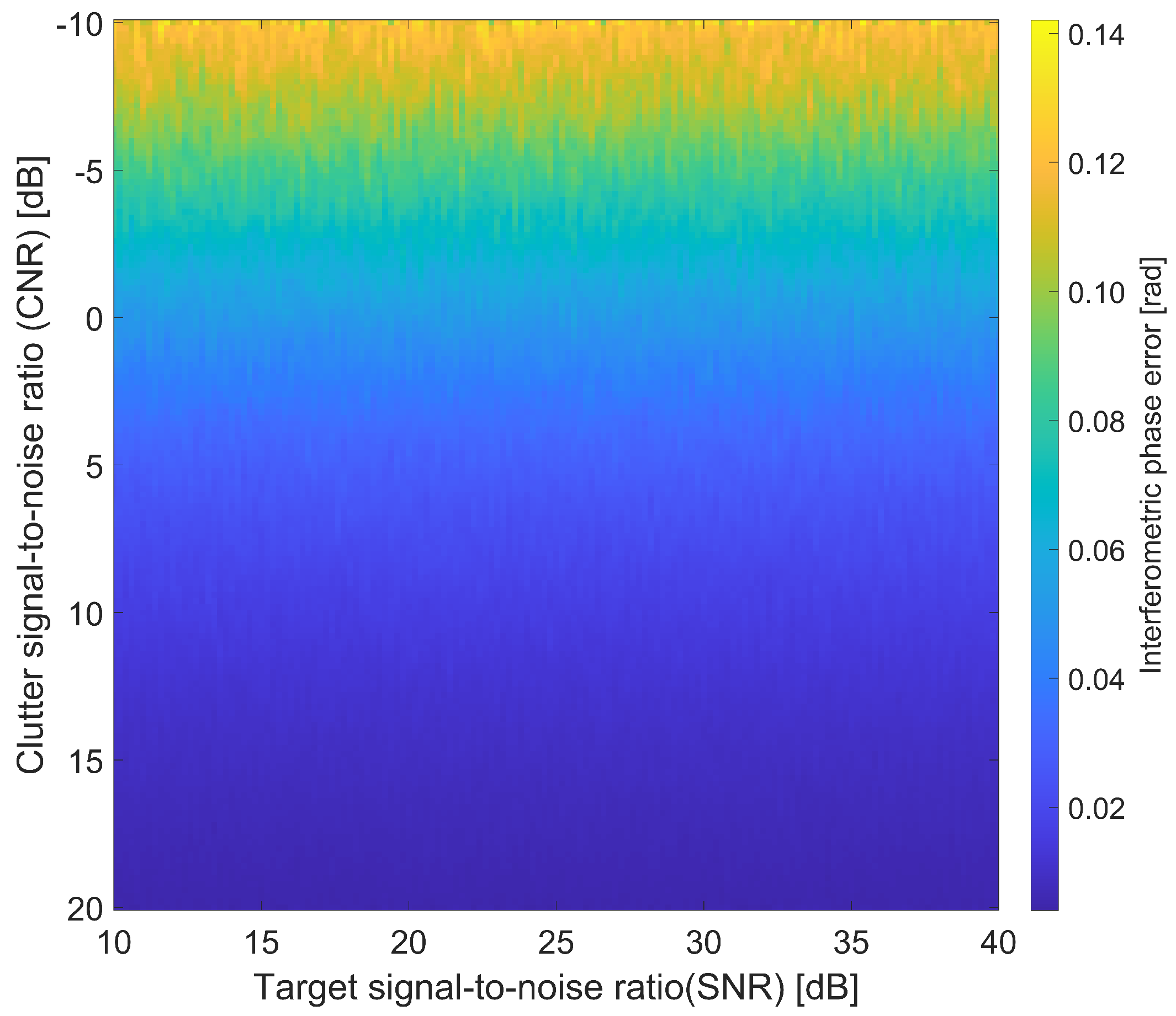
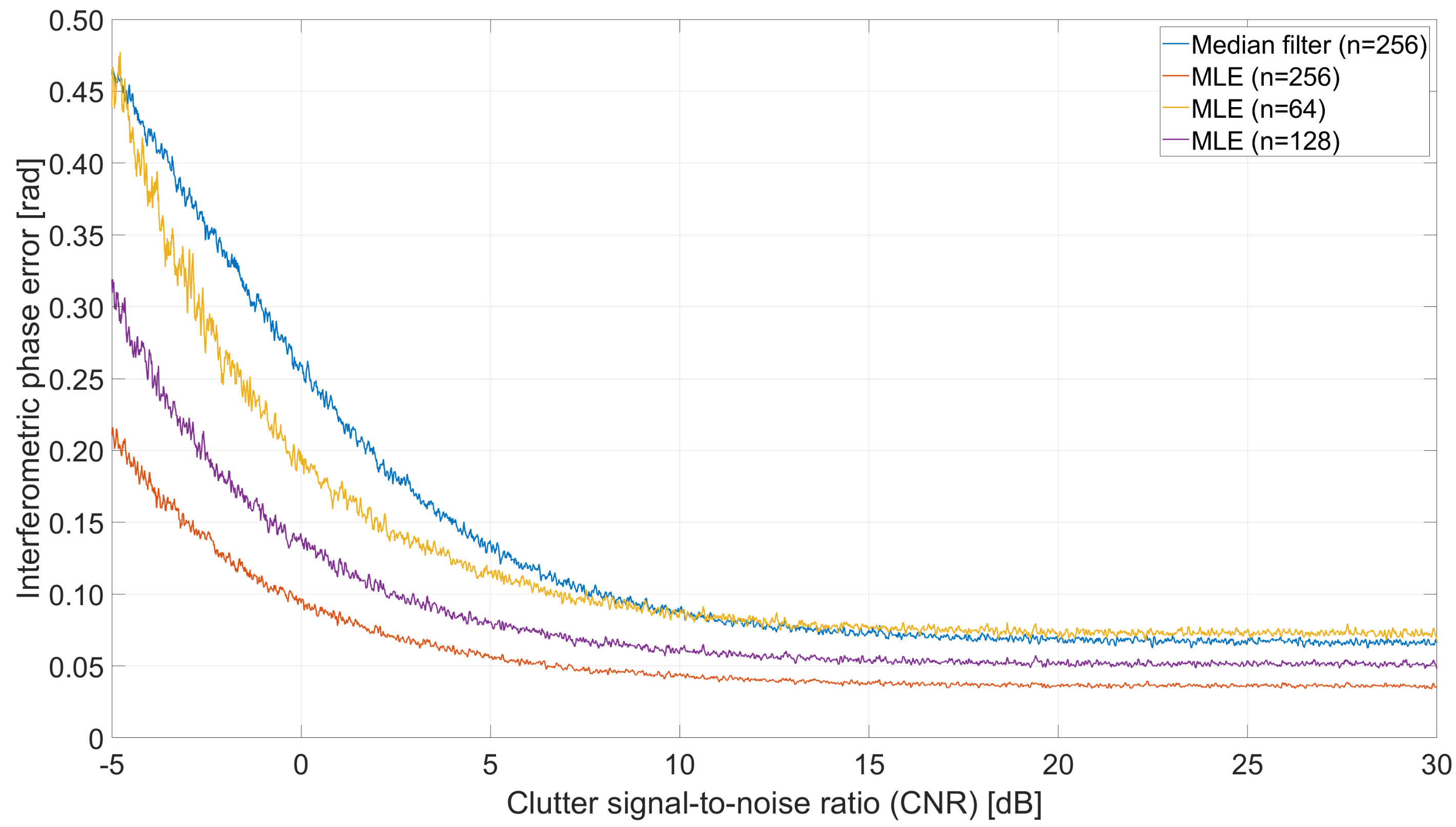
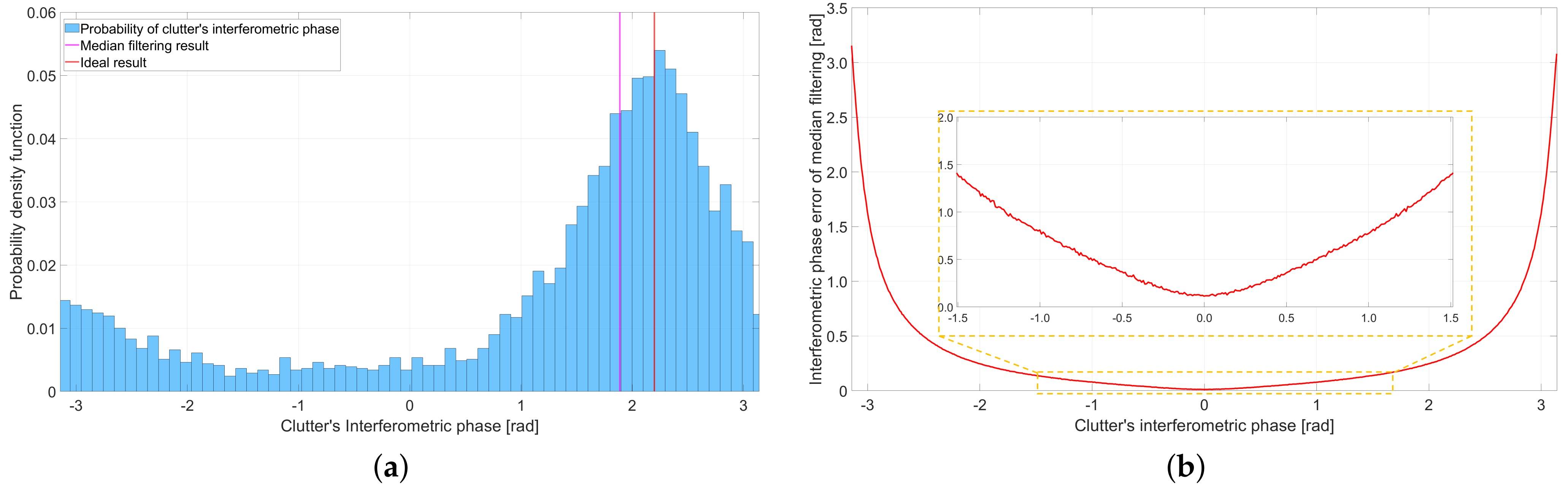
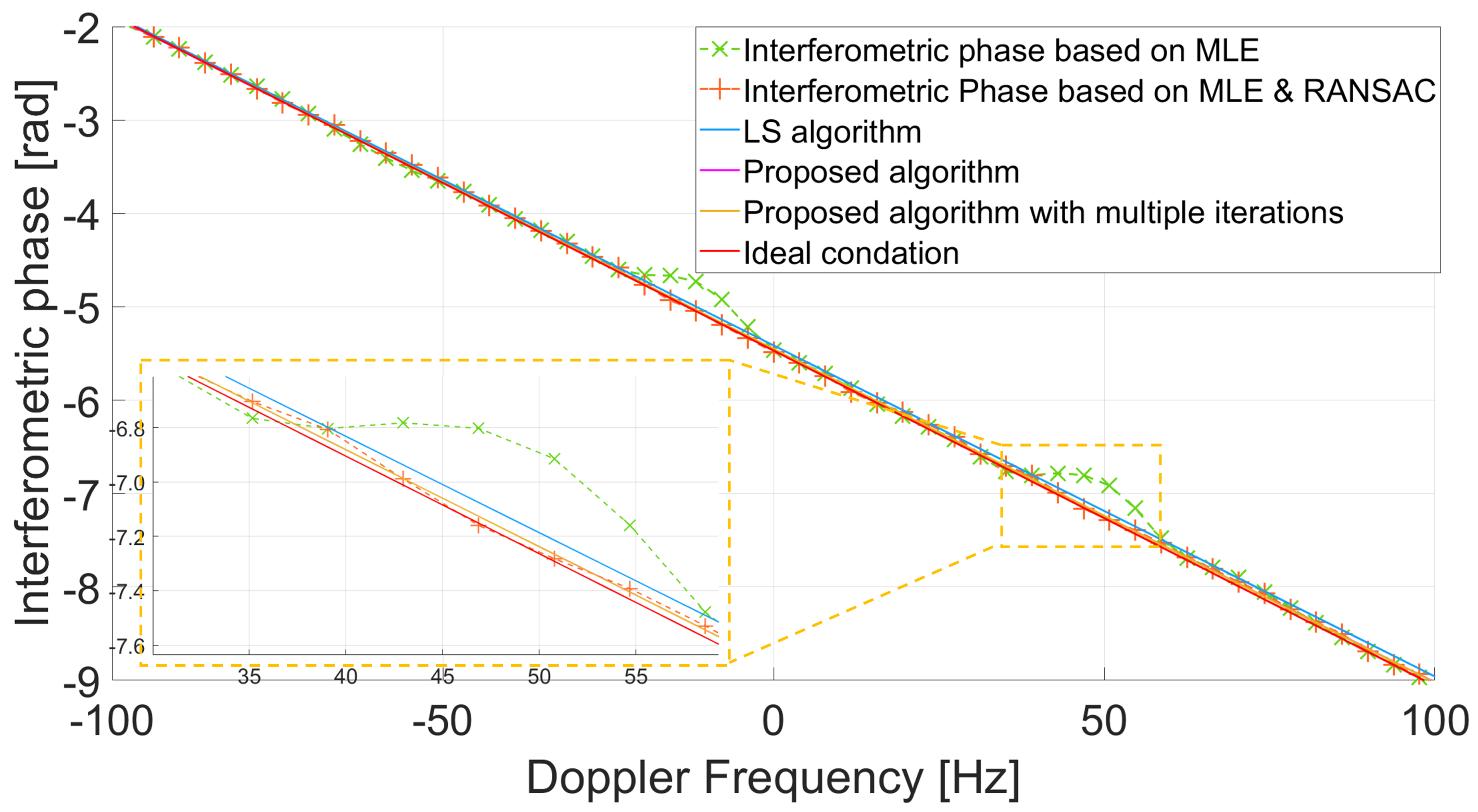
4.1. Comparison in the Simulated Experiment
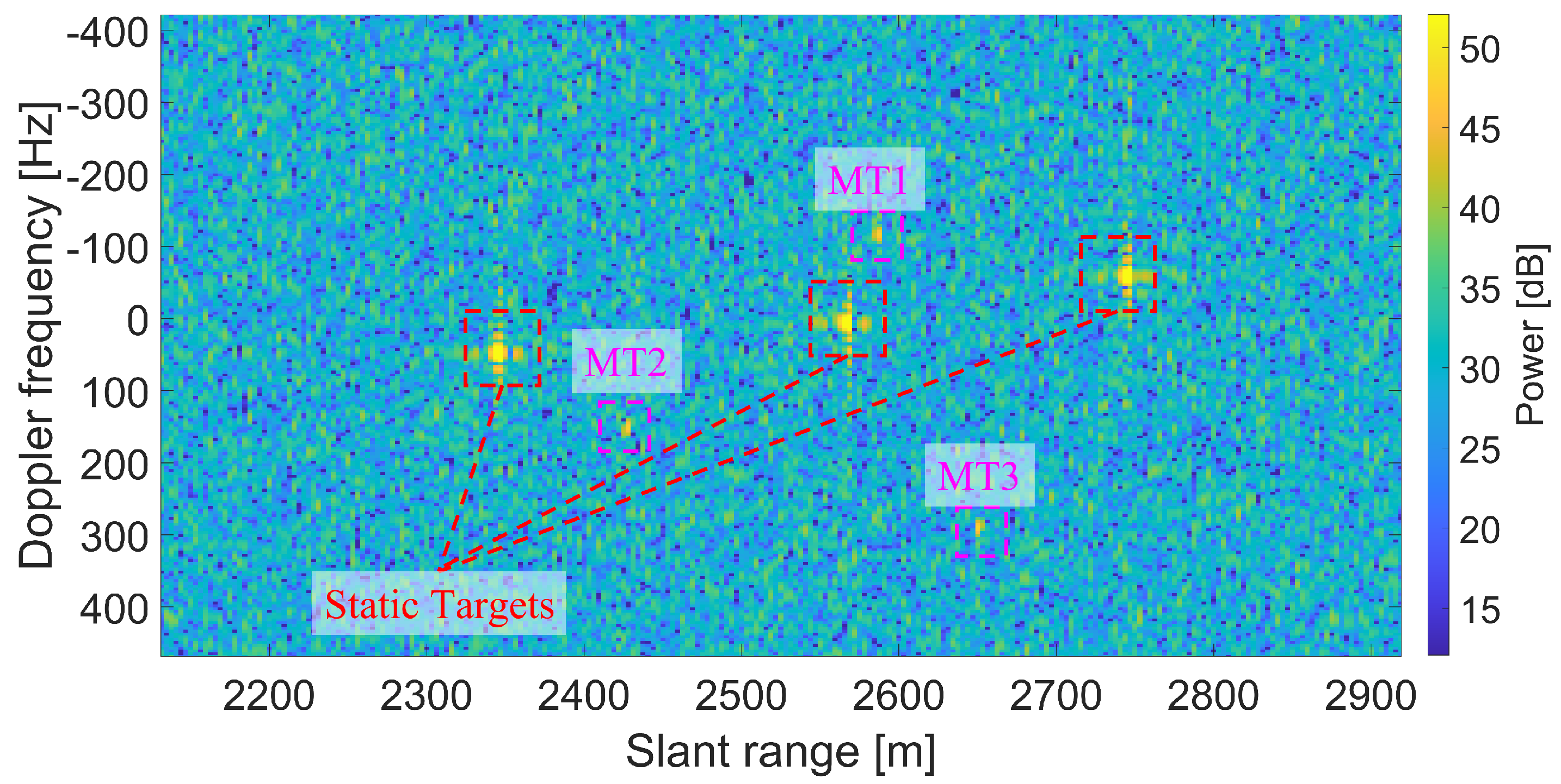
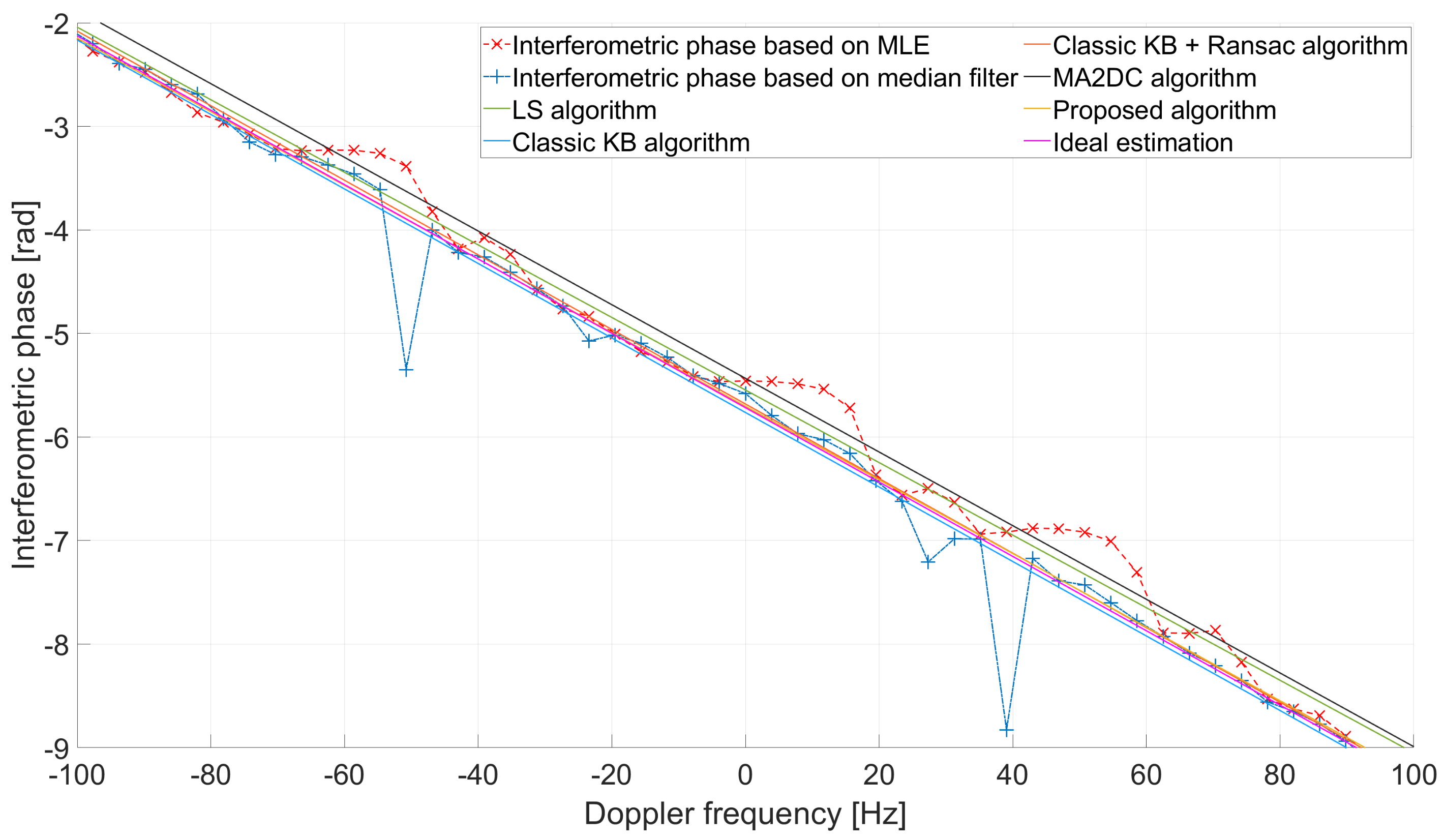
4.2. Comparison in a Real Experiment
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GMTI | Ground moving target indication |
| UAV | Unmanned aerial vehicle |
| KB | Knowledge-based |
| RANSAC | Random sample sonsensus |
| INS | Inertial navigational systems |
| DCB | Digital channel balancing |
| SNR | Signal-to-noise ratio |
| KA-GMTR | Knowledge-aided ground moving target relocation |
| A2DC | Adaptive 2-D calibration |
| MA2DC | Modified adaptive 2-D calibration |
| LS | Least squares |
| MLE | Maximum likelihood estimator |
| LFM | Linear frequency modulation |
| DOA | Direction of arrival |
| CNR | Clutter-to-noise ratio |
| FFT | Fast Fourier transform |
| Probability density function | |
| CRB | Cramér–Rao bound |
| RD | Range–Doppler |
| CSI | Clutter suppression interference |
| CA-CFAR | Cell-averaging constant false alarm rate |
| ROI | Region of interest |
References
- Entzminger, J.N.; Fowler, C.A.; Kenneally, W.J. JointSTARS and GMTI: Past, present and future. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 748–761. [Google Scholar] [CrossRef]
- Chang, C.Y.; Woo, A.; Forry, H.; Sherman, J.; Recht, M.; Clark, R.; Levin, R. HISAR-300: An Advanced Airborne Multi-Mission Surveillance Radar. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar]
- Greenspan, M. Joint STARS—The Start of 50 Years of All Speed Surface Moving Target Detection and Tracking. IEEE Aerosp. Electron. Syst. Mag. 2023, 38, 32–37. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Klare, J.; Brenner, A.R.; Ender, J.H.G. Wide-Area Traffic Monitoring with the SAR/GMTI System PAMIR. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3019–3030. [Google Scholar] [CrossRef]
- Wang, B.; Song, C.; Liu, N.; Liu, Z.; Zhou, L.; Xiang, M. An Advanced Lightweight Dual-Band Digital Array SAR System: Earth Observation Imaging and Moving Target Detection. IEEE Sens. J. 2023, 23, 21776–21786. [Google Scholar] [CrossRef]
- Mosito, K.E.; Nel, W.A.J.; Blaauw, C.; Gaffar, Y.A.; de Witt, J.J. Detection, Tracking and Geo-location of Moving Targets in Airborne Radar Data using a DPCA GMTI Technique. In Proceedings of the 2022 IEEE Radar Conference (RadarConf22), New York, NY, USA, 21–25 March 2022; pp. 1–6. [Google Scholar]
- Li, X.; Wang, R.; Liang, G.; Yang, Z. A Multi-Objective Intelligent Optimization Method for Sensor Array Optimization in Distributed SAR-GMTI Radar Systems. Remote Sens. 2024, 16, 3041. [Google Scholar] [CrossRef]
- Kanistras, K.; Martins, G.; Rutherford, M.J.; Valavanis, K.P. A survey of unmanned aerial vehicles (UAVs) for traffic monitoring. In Proceedings of the 2013 International Conference on Unmanned Aircraft Systems (ICUAS), Atlanta, GA, USA, 28–31 May 2013; pp. 221–234. [Google Scholar]
- Otten, M.; Maas, N.; Bolt, R.; Caro-Cuenca, M.; Medenblik, H. Circular Micro-SAR for mini-UAV. In Proceedings of the 2018 15th European Radar Conference (EuRAD), Madrid, Spain, 26–28 September 2018; pp. 321–324. [Google Scholar]
- Jiang, S.; Cao, Y.; Luo, Y.; Guo, S.; Zhou, X.; Wang, X.; Zhang, S. Realization of dual-channel GMTI real-time processing technology based on FPGA. IET Conf. Proc. 2024, 2023, 1284–1289. [Google Scholar] [CrossRef]
- Criollo, L.; Mena-Arciniega, C.; Xing, S. Classification, military applications, and opportunities of unmanned aerial vehicles. Aviation 2024, 28, 115–127. [Google Scholar] [CrossRef]
- Cerutti-Maori, D.; Sikaneta, I. A Generalization of DPCA Processing for Multichannel SAR/GMTI Radars. IEEE Trans. Geosci. Remote Sens. 2013, 51, 560–572. [Google Scholar] [CrossRef]
- Chapin, E.; Chen, C.W. Airborne along-track interferometry for GMTI. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 13–18. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Wang, W.; An, D. Moving Target Indication for Dual-Channel Circular SAR/GMTI Systems. Sensors 2019, 20, 158. [Google Scholar] [CrossRef]
- Melvin, W.L. A STAP overview. IEEE Aerosp. Electron. Syst. Mag. 2004, 19, 19–35. [Google Scholar] [CrossRef]
- Yang, D.; Yang, X.; Liao, G.; Zhu, S. Strong Clutter Suppression via RPCA in Multichannel SAR/GMTI System. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2237–2241. [Google Scholar] [CrossRef]
- Melvin, W.L.; Guerci, J.R. Knowledge-aided signal processing: A new paradigm for radar and other advanced sensors. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 983–996. [Google Scholar] [CrossRef]
- Riedl, M.; Potter, L.C. Knowledge-Aided Bayesian Space-Time Adaptive Processing. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1850–1861. [Google Scholar] [CrossRef]
- Li, X.; Yang, Z.; Tan, X.; Liao, G.; Shu, Y. A Novel Knowledge-Aided Training Samples Selection Method for Terrain Clutter Suppression in Hybrid Baseline Radar Systems. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Budillon, A.; Pascazio, V.; Schirinzi, G. Estimation of Radial Velocity of Moving Targets by Along-Track Interferometric SAR Systems. IEEE Geosci. Remote Sens. Lett. 2008, 5, 349–353. [Google Scholar] [CrossRef]
- Wang, C.; Liao, G.; Zhang, Q. First Spaceborne SAR-GMTI Experimental Results for the Chinese Gaofen-3 Dual-Channel SAR Sensor. Sensors 2017, 17, 2683. [Google Scholar] [CrossRef]
- Huang, P.; Xia, X.-G.; Wang, L.; Xu, H.; Liu, X.; Liao, G.; Jiang, X. Imaging and Relocation for Extended Ground Moving Targets in Multichannel SAR-GMTI Systems. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–24. [Google Scholar] [CrossRef]
- Li, X.; Gao, W.; Han, X. Doppler beam sharpening/ground moving target indication techniques based on space–time adaptive processing for airborne active phased array fire-control radar. J. Eng. 2019, 2019, 6048–6051. [Google Scholar] [CrossRef]
- Jia, X.; Song, H. Clutter suppression for multichannel wide area surveillance system via a combination of STAP and RPCA. In Proceedings of the 2019 6th Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Xiamen, China, 26–29 November 2019; pp. 1–4. [Google Scholar]
- Zhao, Y.; Wang, J.; Song, F.; Wang, J.; Xu, J.; Zhou, M. Single-Channel SAR Moving Target Detection Method Based on RPCA. In Proceedings of the 2023 6th International Conference on Information Communication and Signal Processing (ICICSP), Xi’an, China, 23–25 September 2023; pp. 85–89. [Google Scholar]
- Deming, R.W.; MacIntosh, S.; Best, M. Three-channel processing for improved geo-location performance in SAR-based GMTI interferometry. In Proceedings of the Algorithms for Synthetic Aperture Radar Imagery XIX, Baltimore, MD, USA, 25–26 April 2012; p. 83940F-83940F-17. [Google Scholar]
- Ruixian, H.; Baochang, L.; Tong, W.; Dongdong, L.; Zheng, B. A Knowledge-Based Target Relocation Method for Wide-Area GMTI Mode. IEEE Geosci. Remote Sens. Lett. 2014, 11, 748–752. [Google Scholar] [CrossRef]
- Chen, H.; Wang, Z.; Gao, W.; Sun, H.; Lu, Y.; Li, Y. Knowledge-Aided Ground Moving Target Relocation for Airborne Dual-Channel Wide-Area Radar by Exploiting the Antenna Pattern Information. Remote Sens. 2021, 13, 4724. [Google Scholar] [CrossRef]
- Liu, K.; He, X.; Liao, G.; Zhu, S.; Tan, H.; Qiu, J. Multichannel SAR-GMTI Algorithm Based on Adaptive Data Reconstruction and Improved RPCA. IEEE Trans. Geosci. Remote Sens. 2025, 63, 1–16. [Google Scholar] [CrossRef]
- Klemm, R. Principles of Space-Time Adaptive Processing; IET: London, UK, 2006. [Google Scholar]
- Zhang, L.; Qiao, Z.; Xing, M.-d.; Yang, L.; Bao, Z. A Robust Motion Compensation Approach for UAV SAR Imagery. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3202–3218. [Google Scholar] [CrossRef]
- Lei, Y.; Tong, W.; Zheng, B. Ground Moving Target Indication Using an InSAR System with a Hybrid Baseline. IEEE Geosci. Remote Sens. Lett. 2008, 5, 373–377. [Google Scholar] [CrossRef]
- Nickel, U. Overview of generalized monopulse estimation. IEEE Aerosp. Electron. Syst. Mag. 2006, 21, 27–56. [Google Scholar] [CrossRef]
- Gierull, C.H. Digital Channel Balancing of Along-Track Interferometric SAR Data; Defence R & D Canada-Ottawa: Ottawa, ON, Canada, 2003. [Google Scholar]
- Jäger, M.; Scheiber, R.; Reigber, A. Robust, Model-Based External Calibration of Multi-Channel Airborne SAR Sensors Using Range Compressed Raw Data. Remote Sens. 2019, 11, 2674. [Google Scholar] [CrossRef]
- Barros Cardoso da Silva, A.; Baumgartner, S.V.; de Almeida, F.Q.; Krieger, G. In-Flight Multichannel Calibration for Along-Track Interferometric Airborne Radar. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3104–3121. [Google Scholar] [CrossRef]
- Han, S.; De Maio, A.; Carotenuto, V.; Pallotta, L.; Huang, X. Censoring Outliers in Radar Data: An Approximate ML Approach and its Analysis. IEEE Trans. Aerosp. Electron. Syst. 2019, 55, 534–546. [Google Scholar] [CrossRef]
- Chen, X.; Cheng, Y.; Wu, H.; Wang, H. Heterogeneous Clutter Suppression for Airborne Radar STAP Based on Matrix Manifolds. Remote Sens. 2021, 13, 3195. [Google Scholar] [CrossRef]
- Ge, B.; An, D.; Liu, J.; Feng, D.; Chen, L.; Zhou, Z. Modified Adaptive 2-D Calibration Algorithm for Airborne Multichannel SAR-GMTI. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Wang, Q.; Xue, B.; Hu, X.; Wu, G.; Zhao, W. Robust Space–Time Joint Sparse Processing Method with Airborne Active Array for Severely Inhomogeneous Clutter Suppression. Remote Sens. 2022, 14, 2647. [Google Scholar] [CrossRef]
- Barros Cardoso da Silva, A.; Joshi, S.K.; Baumgartner, S.V.; de Almeida, F.Q.; Krieger, G. Phase Correction for Accurate DOA Angle and Position Estimation of Ground-Moving Targets Using Multi-Channel Airborne Radar. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Seymour, M.S.; Cumming, I.G. Maximum likelihood estimation for SAR interferometry. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 2274, pp. 2272–2275. [Google Scholar]
- Candeias, A.L.B.; Mura, J.C.; Dutra, L.V.; Moreira, J.R. Interferogram phase noise reduction using morphological and modified median filters. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS ’95. Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 161, pp. 166–168. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Rosen, P.A.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R.M. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar] [CrossRef]
- Rodriguez, E.; Martin, J.M. Theory and design of interferometric synthetic aperture radars. IEE Proc. F (Radar Signal Process.) 1992, 139, 147–159. [Google Scholar]
- Yan, H.; Zheng, M.J.; Zhu, D.Y.; Wang, H.T.; Chang, W.S. A new approach to increase the two-dimensional detection probability of CSI algorithm for WAS-GMTI mode. Adv. Space Res. 2015, 56, 325–332. [Google Scholar] [CrossRef]






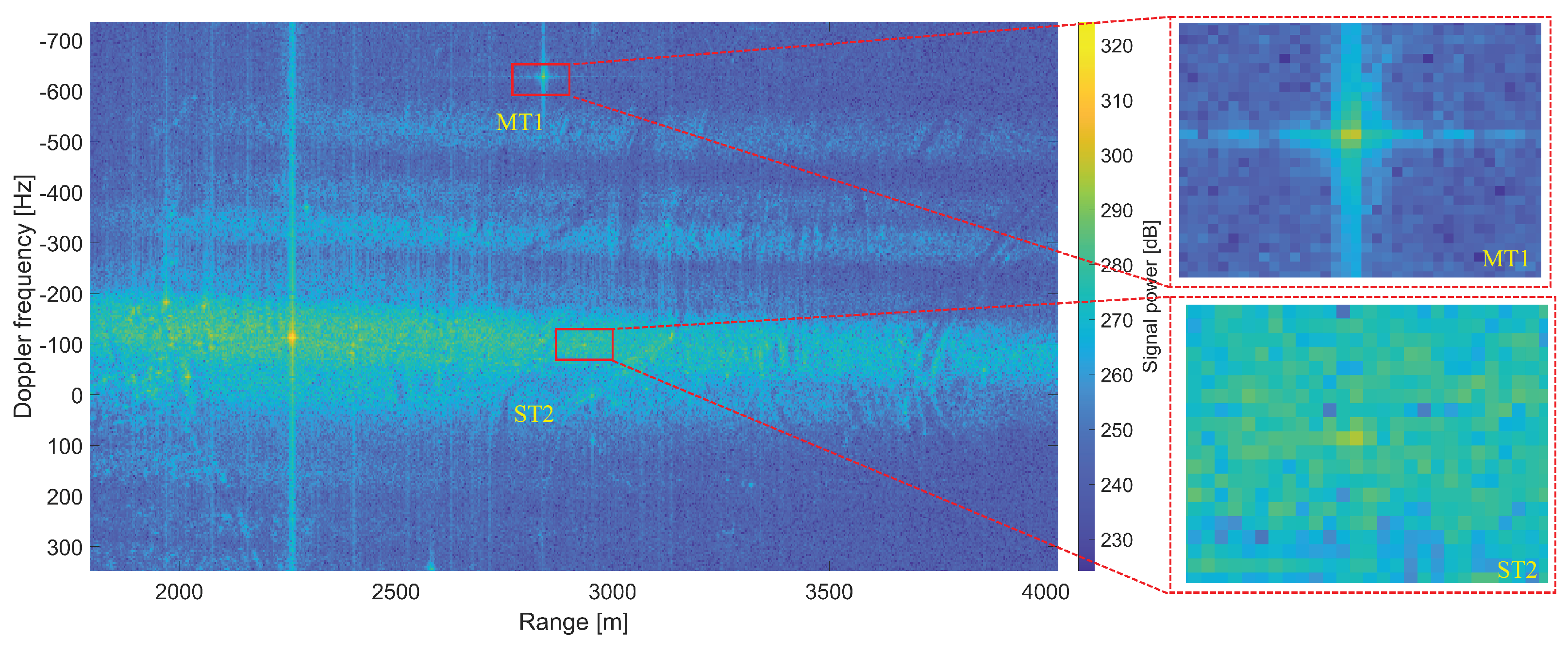
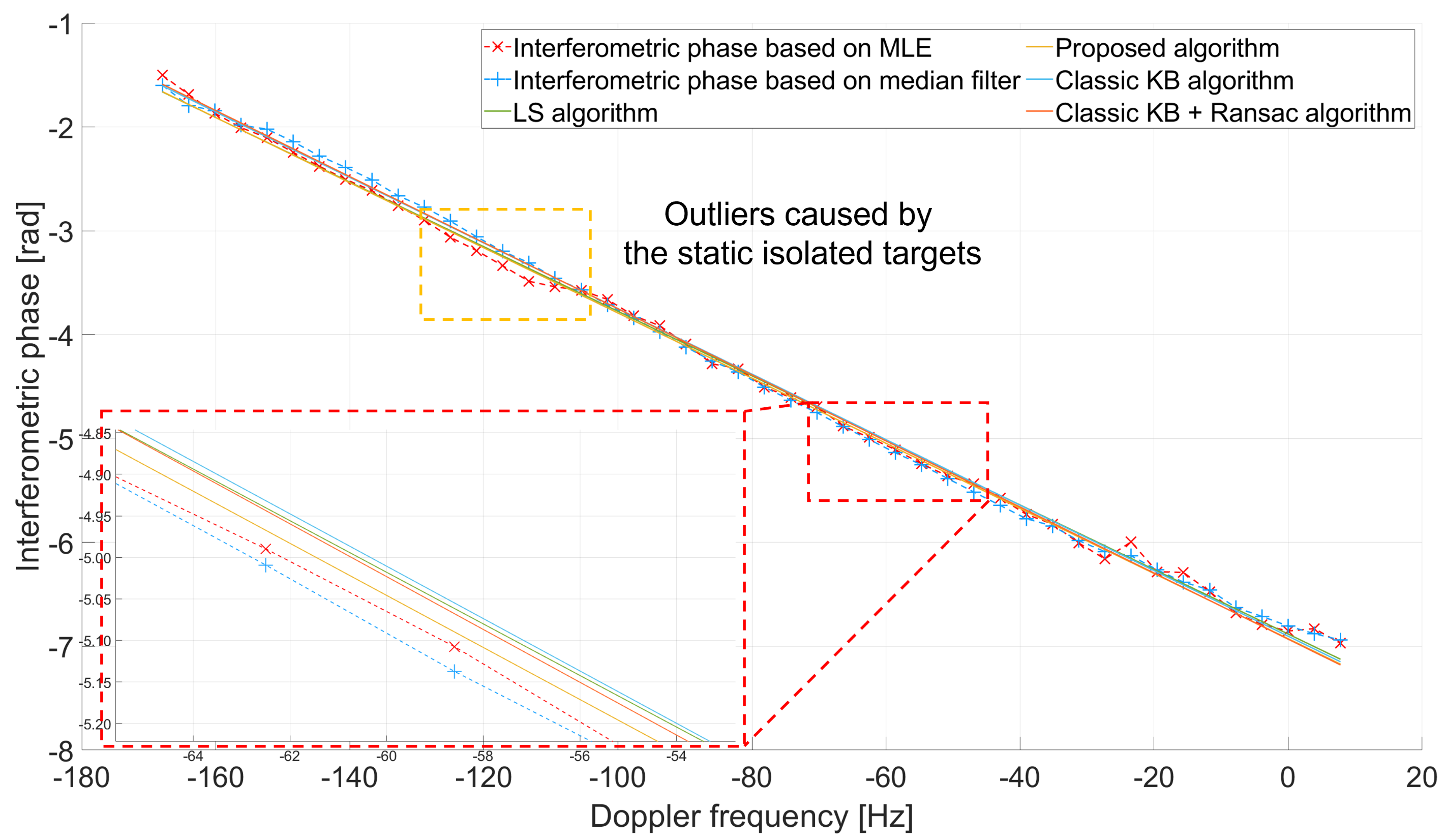



| Quantity | Symbol | Value |
|---|---|---|
| Velocity of the platform | v | 14 m/s |
| Number of Tx/Rx channels | 1/2 | |
| Pulse repetition frequency | PRF | 2000 Hz |
| Range bandwidth | BW | 40 MHz |
| Channel distance | 0.17 m | |
| Carrier frequency | 17 GHz | |
| Altitude of the platform | 800 m |
| Algorithm | MT1 | MT2 | MT3 |
|---|---|---|---|
| LS algorithm | 10.1225 m | 9.3559 m | 9.5544 m |
| Classic KB algorithm | 2.7080 m | 1.6274 m | 1.7954 m |
| Classic KB + RANSAC algorithm | 1.1675 m | 1.1638 m | 1.2321 m |
| MA2DC algorithm | 19.3282 m | 18.0241 m | 17.9821 m |
| Proposed algorithm | 0.5886 m | 0.5467 m | 0.6041 m |
| Method | Mean Position Error |
|---|---|
| LS algorithm in MLE | 17.4308 m |
| Classic KB algorithm | 14.9256 m |
| Classic KB + RANSAC algorithm | 6.0884 m |
| MA2DC algorithm | 12.9502 m |
| Proposed algorithm | 4.1860 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhang, Y.; Ge, X.; Li, Y.; Liu, Y.; Bu, X.; Liang, X. An Improved Knowledge-Based Ground Moving Target Relocation Algorithm for a Lightweight Unmanned Aerial Vehicle-Borne Radar System. Remote Sens. 2025, 17, 1182. https://doi.org/10.3390/rs17071182
Liu W, Zhang Y, Ge X, Li Y, Liu Y, Bu X, Liang X. An Improved Knowledge-Based Ground Moving Target Relocation Algorithm for a Lightweight Unmanned Aerial Vehicle-Borne Radar System. Remote Sensing. 2025; 17(7):1182. https://doi.org/10.3390/rs17071182
Chicago/Turabian StyleLiu, Wencheng, Yuan Zhang, Xuyang Ge, Yanlei Li, Yunlong Liu, Xiangxi Bu, and Xingdong Liang. 2025. "An Improved Knowledge-Based Ground Moving Target Relocation Algorithm for a Lightweight Unmanned Aerial Vehicle-Borne Radar System" Remote Sensing 17, no. 7: 1182. https://doi.org/10.3390/rs17071182
APA StyleLiu, W., Zhang, Y., Ge, X., Li, Y., Liu, Y., Bu, X., & Liang, X. (2025). An Improved Knowledge-Based Ground Moving Target Relocation Algorithm for a Lightweight Unmanned Aerial Vehicle-Borne Radar System. Remote Sensing, 17(7), 1182. https://doi.org/10.3390/rs17071182