Retrospective Spectrum-Conversion Method Based on Time-Modulated Van Atta Array
Abstract
:1. Introduction
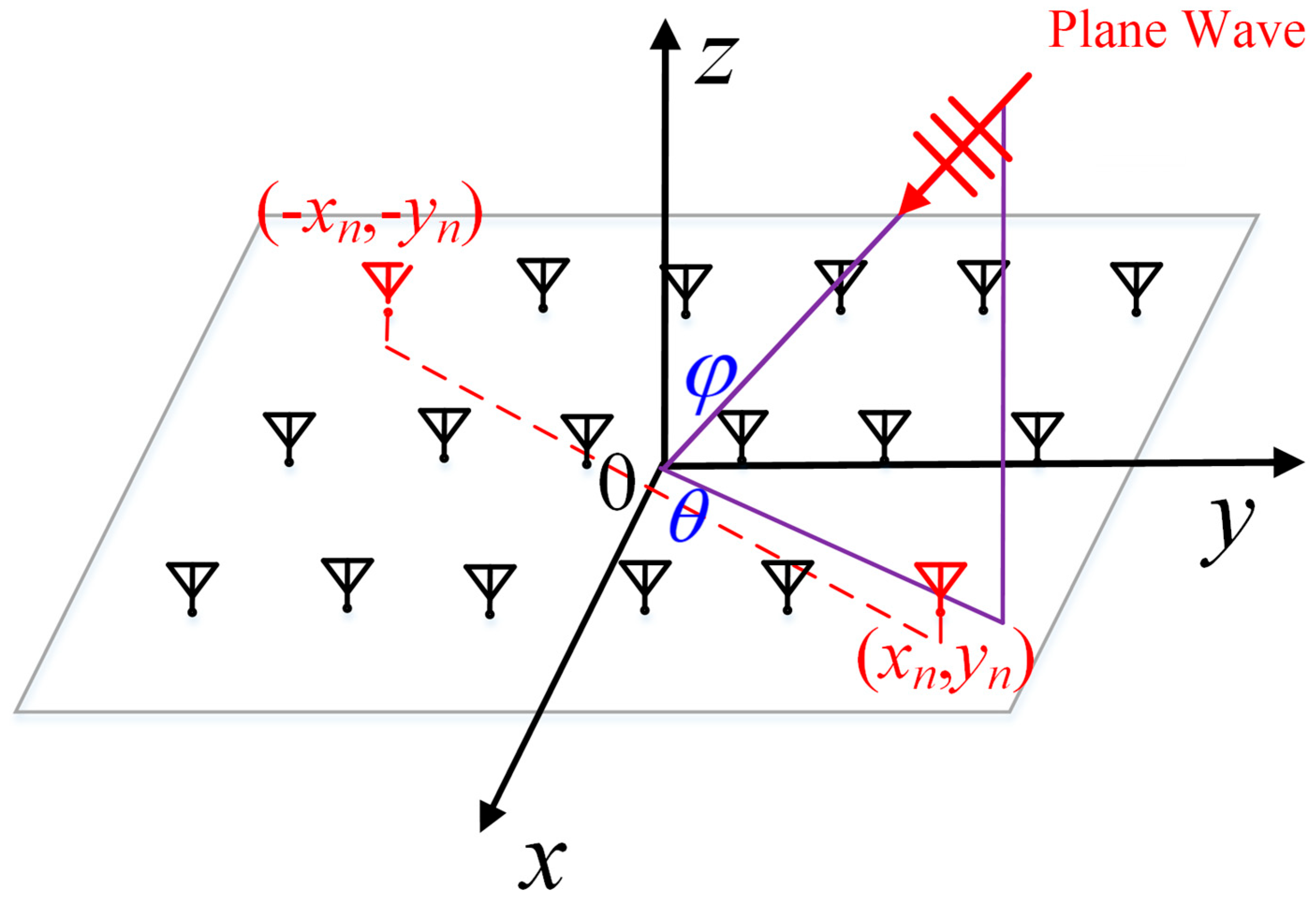
2. Van Atta Array Backtracking Principle
3. Van Atta Array Design
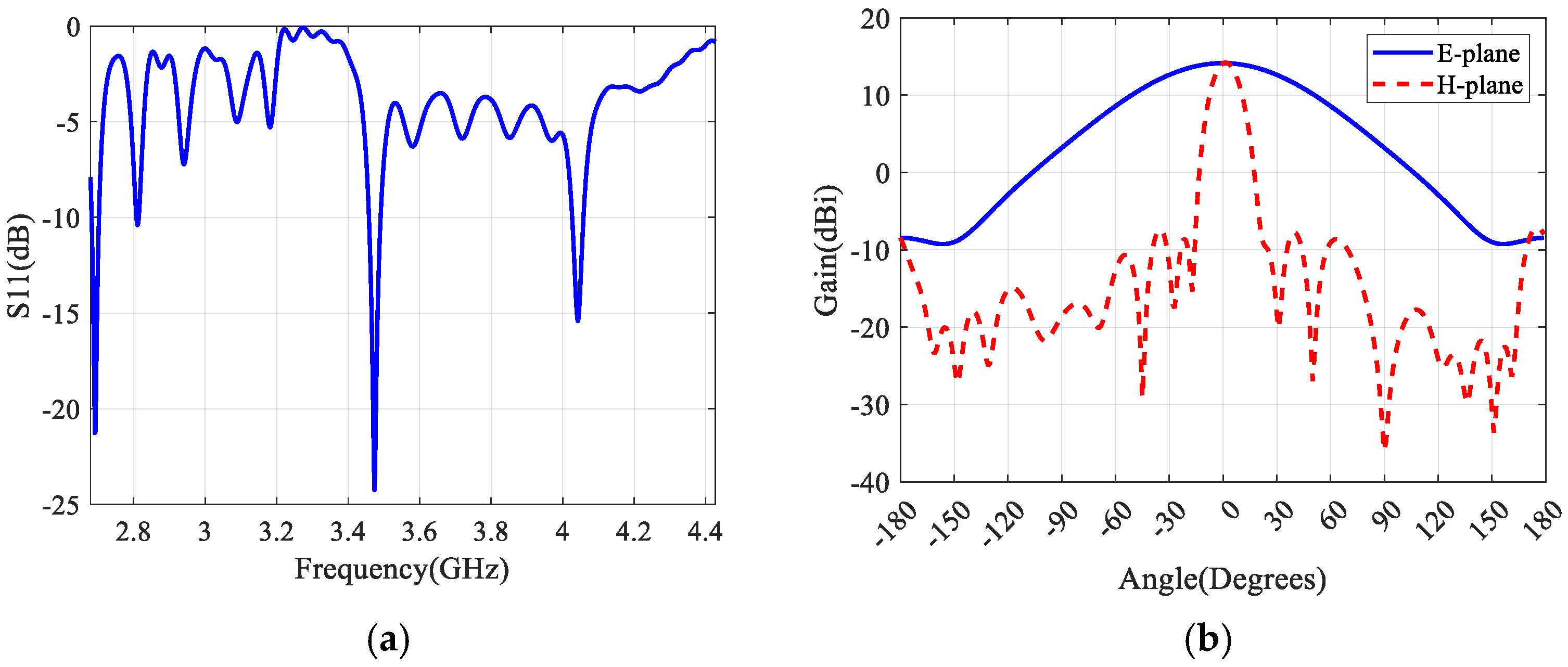
3.1. The Design of Antenna
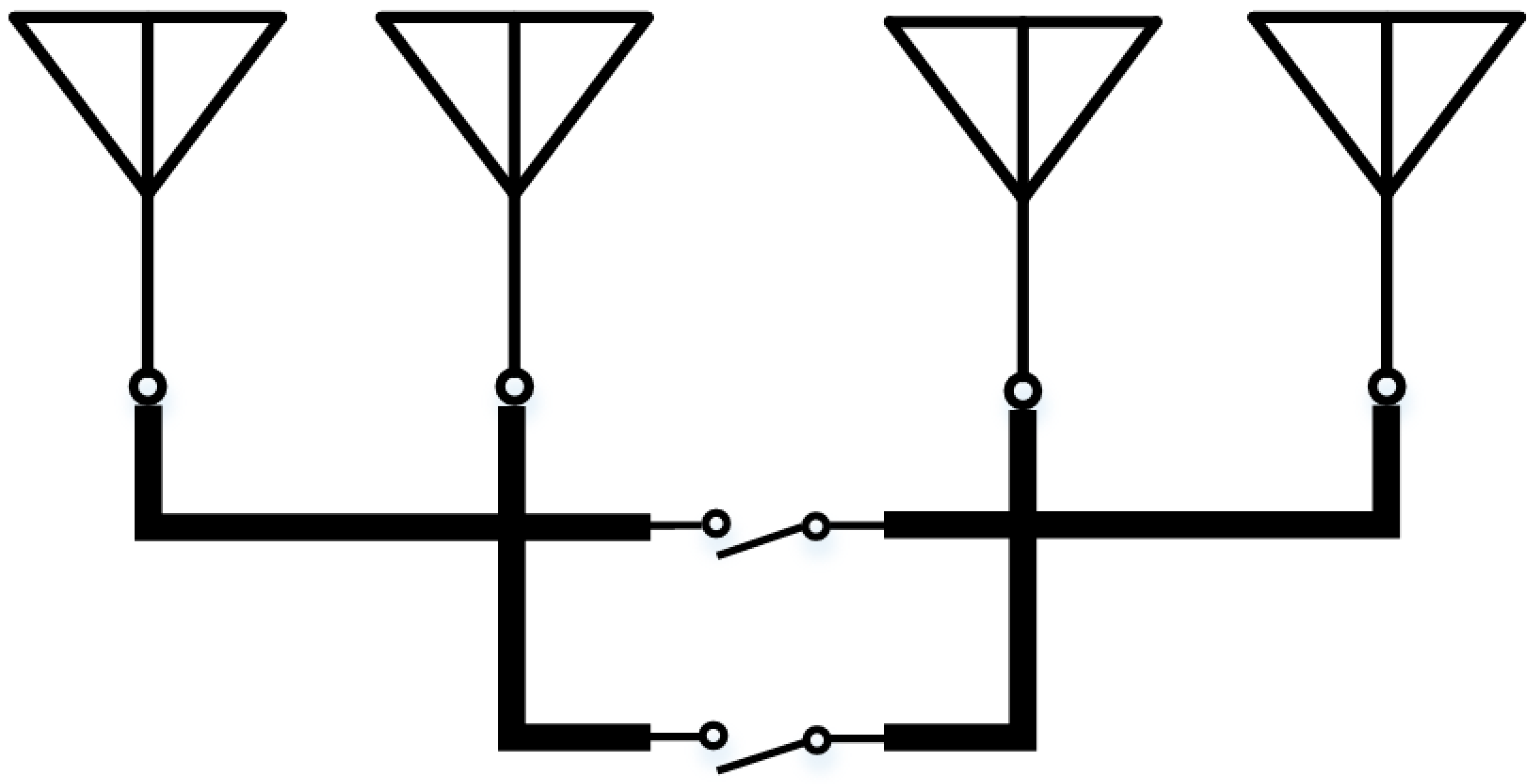
3.2. The Design of Transmission Line Network
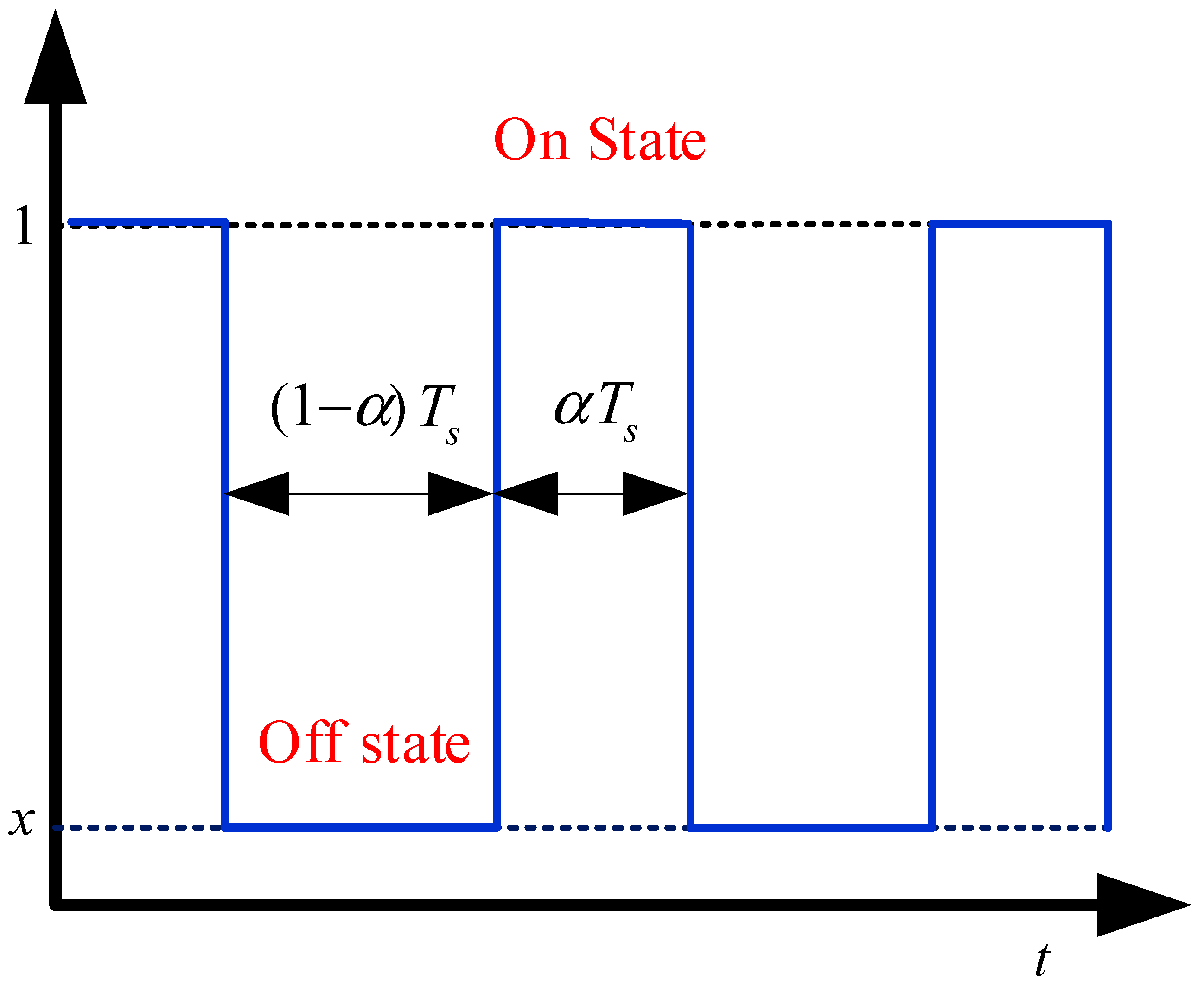
3.3. Establishment of the On–Off Model of the Van Atta Array
3.4. The Design of the SPST Switch
4. Time-Modulated Van Atta Array Testing
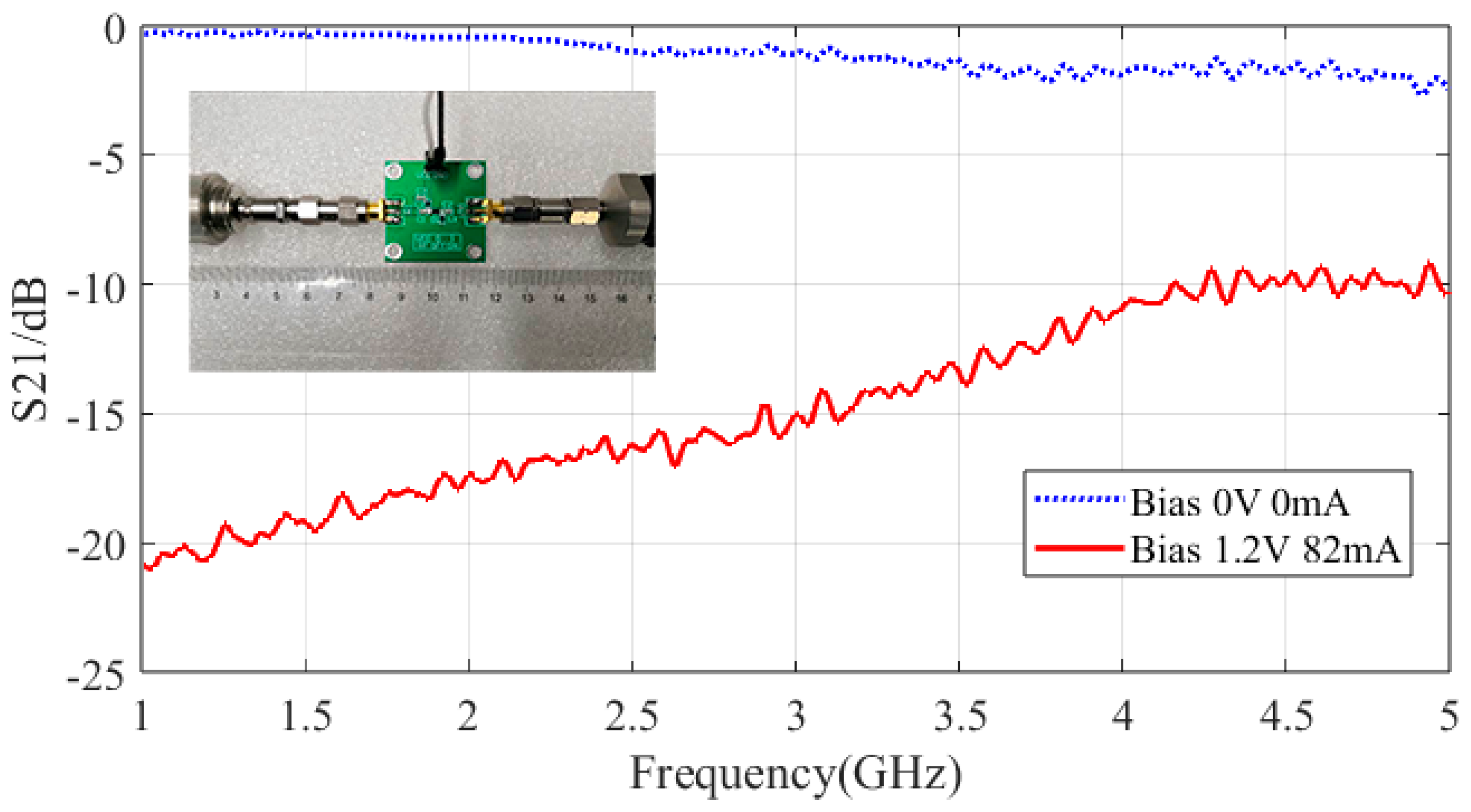
4.1. The SPST Switch Test
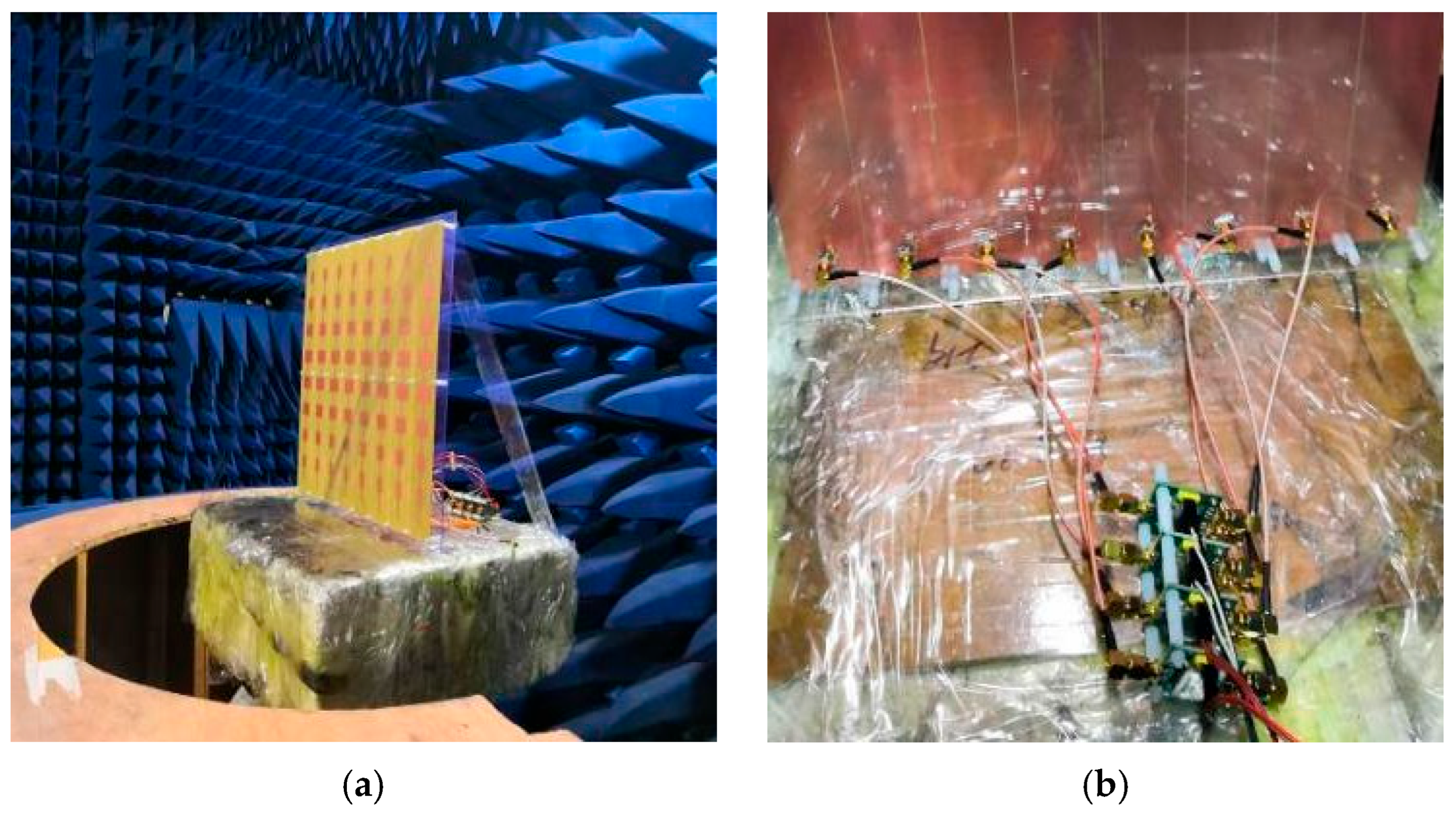
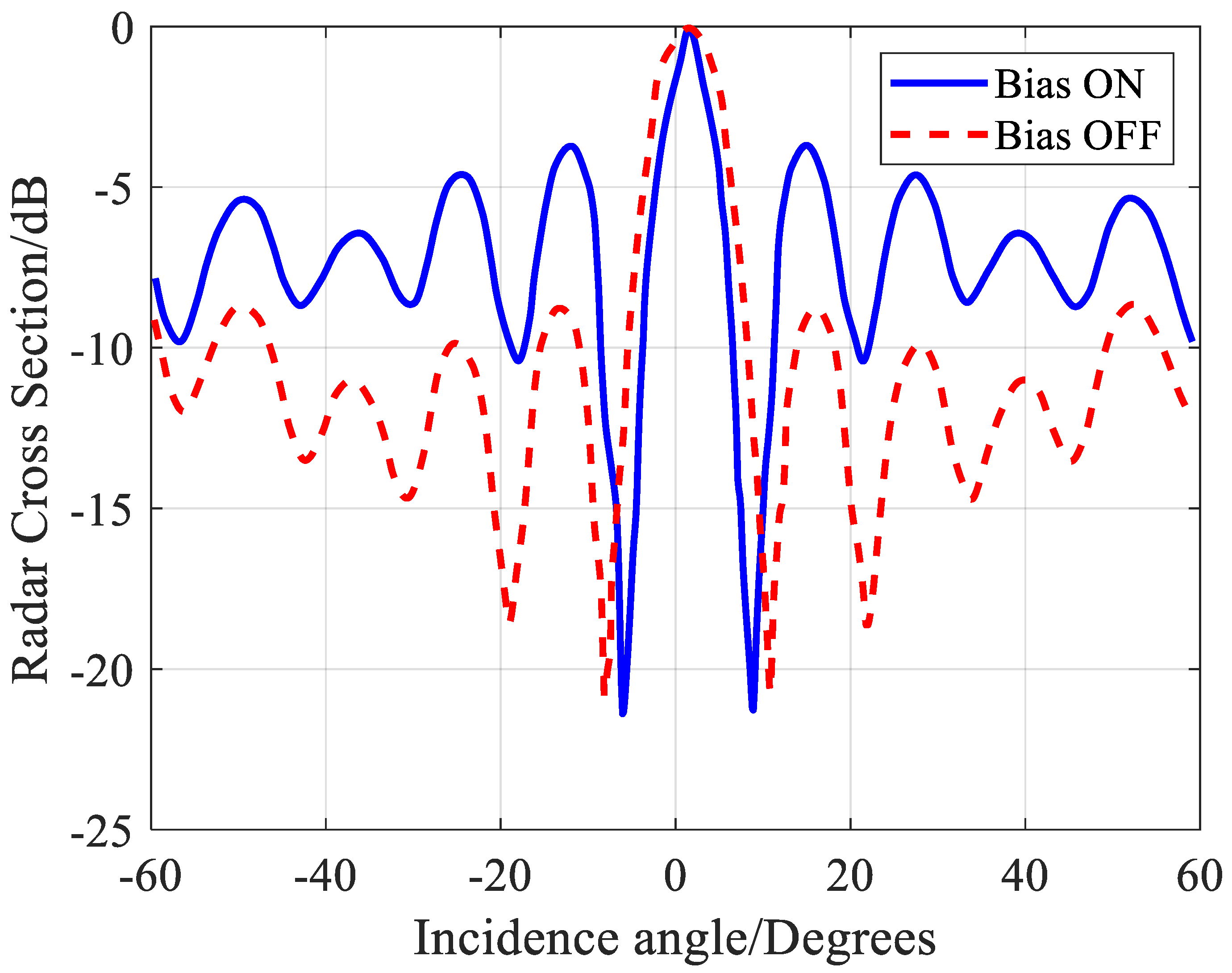
4.2. On–Off Van Atta Array Test
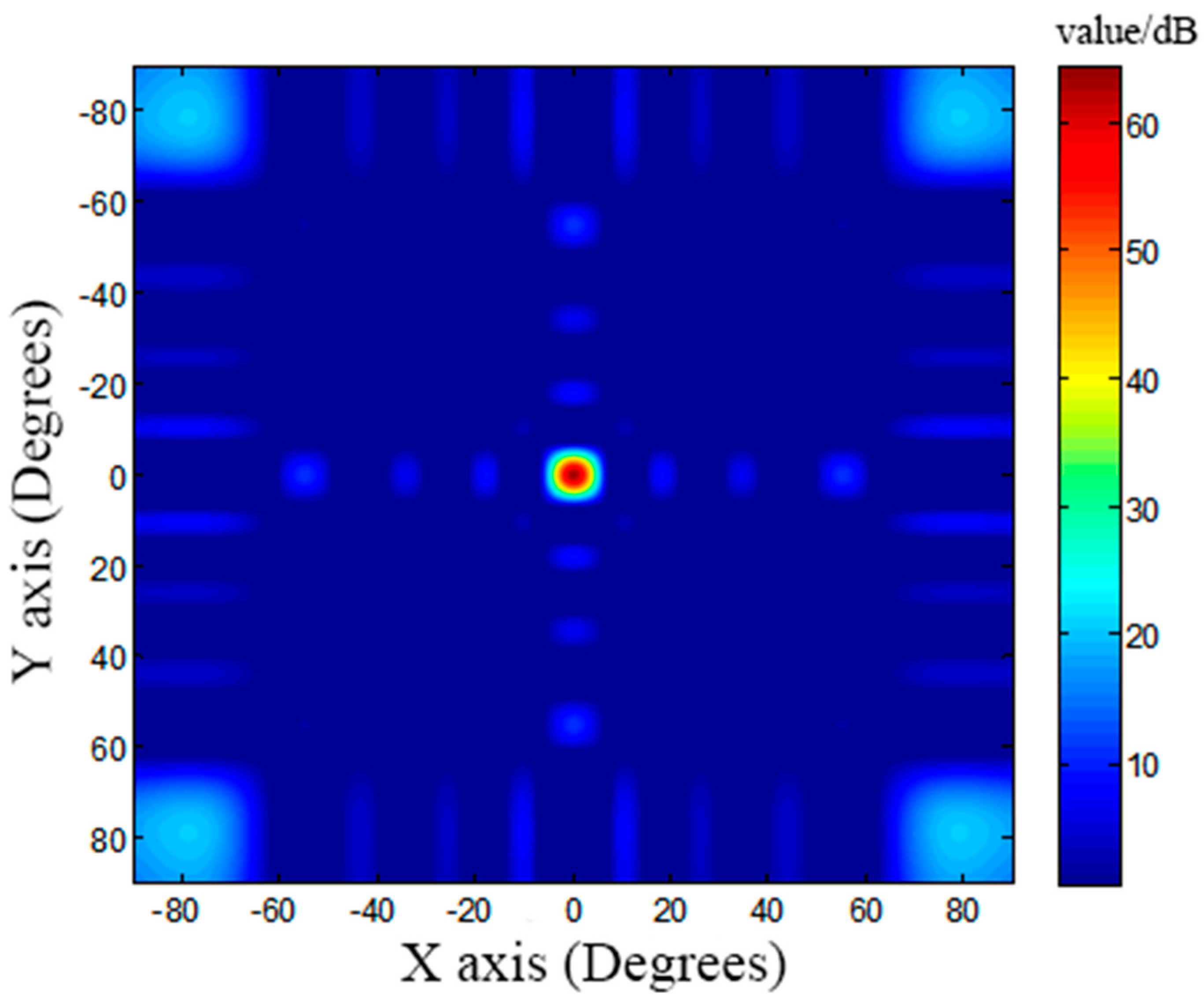
5. Spectrum-Conversion Method
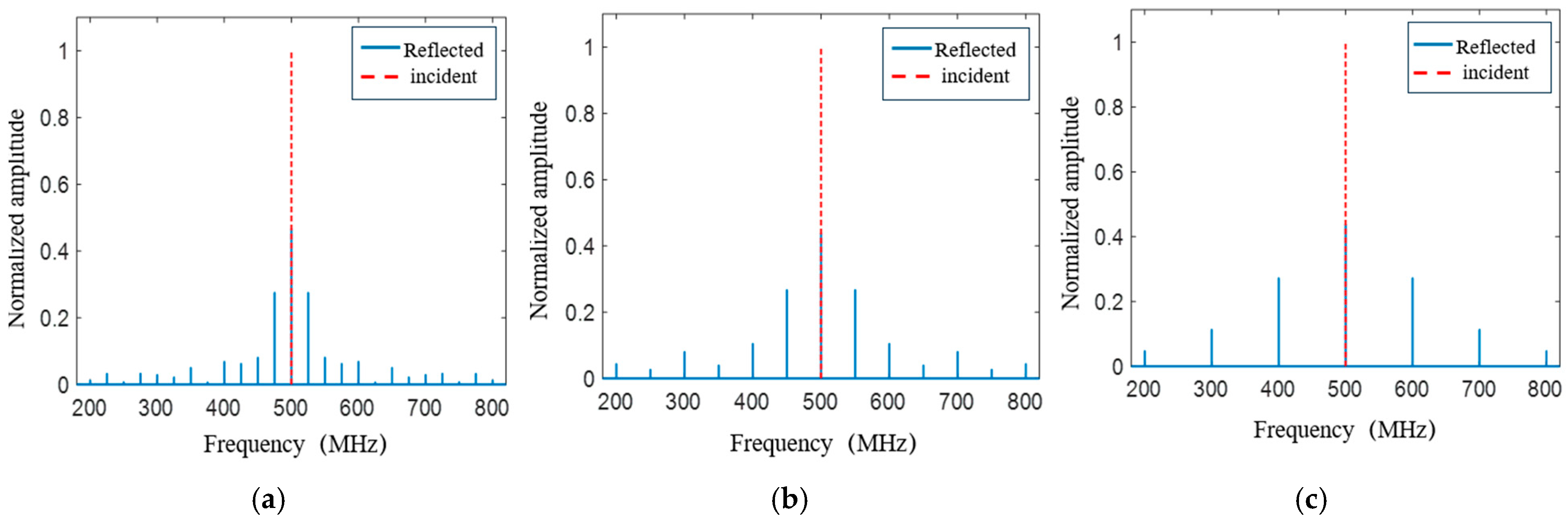
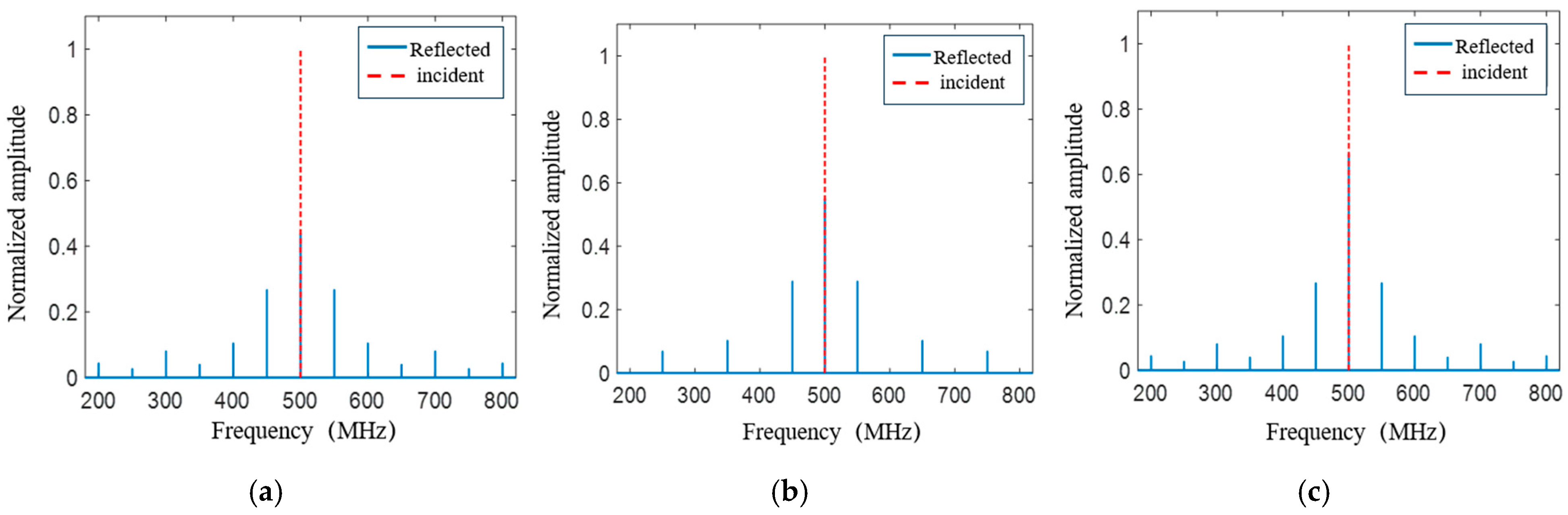
5.1. Modulation Frequency fs
5.2. Duty Cycle α
5.3. Amplitude Coefficient x
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EM | Electromagnetic |
| RCS | Radar cross section |
| PSS | Phase-switched surface |
| AFSS | Active frequency selective surface |
| TMRA | Time-modulated reflector array |
| SPST | Single-pole single-throw |
| GCPW | Grounded coplanar waveguide |
| CPW | Coplanar waveguide |
References
- Ettorre, M.; Alomar, W.A.; Grbic, A. 2-D van atta array of wideband, wideangle slots for radiative wireless power transfer systems. IEEE Trans. Antennas Propag. 2018, 66, 4577–4585. [Google Scholar] [CrossRef]
- Henry, D.; Hester, J.G.D.; Aubert, H.; Pons, P.; Tentzeris, M.M. Long-range wireless interrogation of passive humidity sensors using van-atta cross-polarization effect and different beam scanning techniques. IEEE Trans. Microw. Theory Tech. 2017, 65, 5345–5354. [Google Scholar] [CrossRef]
- Chen, G.; Su, X.; He, L.; Guan, D.; Liu, Z. Coherent signal DOA estimation method based on space–time–coding metasurface. Remote Sens. 2025, 17, 218. [Google Scholar] [CrossRef]
- Li, H.; Li, Z.; Liu, K.; Xu, K.; Luo, C.; Lv, Y.; Deng, Y. A Broadband information metasurface-assisted target jamming system for synthetic aperture radar. Remote Sens. 2024, 16, 1499. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Q.; Pan, X.; Wang, J.; Zhao, F. SAR image transform based on amplitude and frequency shifting joint modulation. IEEE Sens. J. 2025, 25, 7043–7052. [Google Scholar] [CrossRef]
- Yu, L.; Liu, J.; Liang, M.; Yu, X.; Xie, X.; Bi, H.; Hong, W. A structurally flexible occupancy network for 3-d target reconstruction using 2-d SAR images. Remote Sens. 2025, 17, 347. [Google Scholar] [CrossRef]
- Yang, Z.; Wang, Y.; Zhang, C.; Zhan, X.; Sun, G.; Liu, Y.; Mao, Y. Array three-dimensional SAR imaging via composite low-rank and sparse prior. Remote Sens. 2025, 17, 321. [Google Scholar] [CrossRef]
- Li, H.; Ma, C.; Zhou, T.; Wang, J.; Ye, D.; Sun, Y.; Zhu, W.; Denidni, T.A.; Ran, L. Reconfigurable Fresnel Lens Based on an Active Second-Order Bandpass Frequency-Selective Surface. IEEE Trans. Antennas Propag. 2020, 68, 4054–4059. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, J.; Feng, D. An Approach for SAR feature reconfiguring based on periodic phase modulation with inter-pulse time bias. Remote Sens. 2025, 17, 991. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, Q.; Sun, B.; Cao, Y.; Xu, Y. Asymmetric angular selected transmission in phase gradient metagratings and zero index metamaterials. J. Appl. Phys. 2023, 133, 223103. [Google Scholar] [CrossRef]
- Sui, R.; Wang, J.; Sun, G.; Xu, Z.; Feng, D. A dual-polarimetric high range resolution profile modulation method based on time-modulated APCM. IEEE Trans. Antennas Propag. 2025, 73, 1007–1017. [Google Scholar] [CrossRef]
- Chang, Y.; Wang, L.; Li, B.; Jiao, W. Phase switched screen for radar cloaking based on reconfigurable artificial magnetic conductor. IEEE Trans. Electromagn. Compat. 2021, 63, 1417–1422. [Google Scholar] [CrossRef]
- Chambers, B.; Tennant, A. The phase-switched screen. IEEE Antennas Propag. Mag. 2004, 46, 23–37. [Google Scholar] [CrossRef]
- Fang, X.; Li, M.; Ramaccia, D.; Toscano, A.; Bilotti, F.; Ding, D. Self-adaptive retro-reflective doppler cloak based on planar space-time modulated metasurfaces. Appl. Phys. Lett. 2023, 122, 021702. [Google Scholar] [CrossRef]
- Xu, L.; Feng, D.; Wang, X. Matched-filter properties of linear-frequency-modulation radar signal reflected from a phase-switched screen. IET Radar Sonar Navig. 2016, 10, 318–324. [Google Scholar] [CrossRef]
- Zhao, F.; Zhao, F.; Wang, J.; Wang, J.; Feng, D.; Feng, D.; Wu, Q.; Wu, Q.; Liu, X.; Liu, X. Time-modulated active frequency selective surface absorber/reflector for spectrum conversion. J. Appl. Phys. 2022, 131, 035101. [Google Scholar] [CrossRef]
- Zhang, H.; Hu, C.; Yang, J.; Tang, L.; Huang, D.; Shao, L.; Piao, M.; Li, C.; Shi, H. Graphene-based active frequency selective surface in microwave frequency. J. Appl. Phys. 2019, 125, 094501. [Google Scholar] [CrossRef]
- Rahmani-Shams, Y.; Mohammd-Ali-Nezhad, S.; Yeganeh, A.N.; Sedighy, S.H. Dual band, low profile and compact tunable frequency selective surface with wide tuning range. J. Appl. Phys. 2018, 123, 235301. [Google Scholar] [CrossRef]
- Xu, Y.; Feng, D.; Wang, J.; Sui, R. A method for transforming 2D imaging features with the AFSS-loaded rotating Luneberg lens reflector. IET Microw. Antennas Propag. 2022, 16, 860–868. [Google Scholar] [CrossRef]
- Valle, C.L.; Carranza, G.T.; Rumpf, R.C. conformal frequency selective surfaces for arbitrary curvature. IEEE Trans. Antennas Propag. 2023, 71, 612–620. [Google Scholar] [CrossRef]
- Saikia, M.; Srivastava, K.V.; Ramakrishna, S.A. A polarization-insensitive time-modulated frequency-selective surface for broad frequency range. IET Microw. Antennas Propag. 2022, 16, 37–45. [Google Scholar] [CrossRef]
- Saha, S.; Begam, N.; Chatterjee, A.; Biswas, S.; Sarkar, P.P. Reconfigurable frequency selective surface with tunable characteristics depending on intensity of atmospheric light. IET Microw. Antennas Propag. 2019, 13, 2336–2341. [Google Scholar] [CrossRef]
- Sun, G.; Wang, J.; Xing, S.; Huang, D.; Feng, D.; Wang, X. A flexible conformal multifunctional time-modulated metasurface for radar characteristics manipulation. IEEE Trans. Microw. Theory Tech. 2024, 72, 4294–4308. [Google Scholar] [CrossRef]
- Wang, J.; Feng, D.; Xu, Z.; Wu, Q.; Hu, W. Time-domain digital-coding active frequency selective surface absorber/reflector and its imaging characteristics. IEEE Trans. Antennas Propag. 2021, 69, 3322–3331. [Google Scholar] [CrossRef]
- Wang, J.; Feng, D.; Kong, Y.; Quan, S.; Xing, S. Imaging properties of nonperiodic time-varying active frequency selective surface. IEEE Trans. Antennas Propag. 2022, 70, 5884–5891. [Google Scholar] [CrossRef]
- Wang, Y.; Tennant, A. Experimental time-modulated reflector array. IEEE Trans. Antennas Propag. 2014, 62, 6533–6536. [Google Scholar] [CrossRef]
- Song, G.Y.; Cheng, Q.; Cui, T.J.; Jing, Y. Acoustic planar surface retroreflector. Phys. Rev. Mater. 2018, 2, 065201. [Google Scholar] [CrossRef]
- Feng, M.; Li, Y.; Zhang, J.; Han, Y.; Wang, J.; Ma, H.; Qu, S. Wide-angle flat metasurface corner reflector. Appl. Phys. Lett. 2018, 113, 143504. [Google Scholar] [CrossRef]
- Cui, T.J.; Liu, S.; Zhang, L. Information metamaterials and metasurfaces. J. Mater. Chem. C. 2017, 5, 3644–3668. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, X.Q.; Liu, S.; Zhang, Q.; Zhao, J.; Dai, J.Y.; Bai, G.D.; Wan, X.; Cheng, Q.; Castaldi, G.; et al. Space-time-coding digital metasurfaces. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, X.; Dai, J.Y.; Cheng, Q.; Li, X.; Qi, N.H.; Ke, J.C.; Bai, G.D.; Liu, S.; Jin, S.; et al. Programmable time-domain digital-coding metasurface for non-linear harmonic manipulation and new wireless communication systems. Natl. Sci. Rev. 2019, 6, 231–238. [Google Scholar] [CrossRef]
- Dai, J.Y.; Tang, W.; Yang, L.X.; Li, X.; Chen, M.Z.; Ke, J.C.; Cheng, Q.; Jin, S.; Cui, T.J. Realization of multi-modulation schemes for wireless communication by time-domain digital coding metasurface. IEEE Trans. Antennas Propag. 2020, 68, 1618–1627. [Google Scholar] [CrossRef]
- Li, X.-F.; Ban, Y.-L.; Sun, Q.; Che, Y.-X.; Hu, J.; Nie, Z. A compact dual-band van atta array based on the single-port single-band/dual-band antennas. IEEE Antennas Wirel. Propag. Lett. 2023, 22, 888–892. [Google Scholar] [CrossRef]
- Meng, Z.K.; Shi, Y. Antenna array design with self-adaptive in-band radar-cross-section reduction and beam scanning. IEEE Trans. Antennas Propag. 2023, 71, 1820–1831. [Google Scholar] [CrossRef]
- Wang, Y.; Piao, D.; Zuo, J. A wide-angle and fully polarimetric retrodirective array based on tri-polarized antennas with pattern complementation. IEEE Trans. Antennas Propag. 2022, 70, 4518–4525. [Google Scholar] [CrossRef]
- Huang, G.; Purushothama, J.M.; Ding, Y.; Li, X.; Gong, W. Synthesis-free backscatter directional modulation communication using Van-Atta arrays. IET Microw. Antennas Propag. 2022, 16, 654–659. [Google Scholar] [CrossRef]
- Trzebiatowski, K.; Rzymowski, M.; Kulas, L.; Nyka, K. Simple millimeter wave identification system based on 60 GHz van atta Arrays. Sensors 2022, 22, 9809. [Google Scholar] [CrossRef]
- Miao, Z.-W.; Hao, Z.-C.; Yuan, Q. A passive circularly polarized van atta reflector for vehicle radar applications. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 2254–2257. [Google Scholar] [CrossRef]
- Song, K.; Feng, D.; Wang, J.; Xie, Q.; Liu, L. Phase modulation of retro-reflected radar echo signal using a microstrip van-atta array. IEEE Access 2019, 7, 96011–96018. [Google Scholar] [CrossRef]
- Ramaccia, D.; Tobia, A.; Toscano, A.; Bilotti, F. Antenna-based carpet device for extremely large obstacles: Experimental verification. In Proceedings of the 2018 IEEE International Symposium on Antennas and Propagation & USNC/URSI National Radio Science Meeting, Boston, MA, USA, 8–13 July 2018; pp. 2283–2284. [Google Scholar]
- Tobia, A.; Ramaccia, D.; Toscano, A.; Bilotti, F. Antenna-based carpet cloak: A possible frequency and angular broadband cloaking technique. In Proceedings of the 2016 10th International Congress on Advanced Electromagnetic Materials in Microwaves and Optics (METAMATERIALS), Marseille, France, 28 August–2 September 2017; pp. 358–360. [Google Scholar]
- Leong, K.; Miyamoto, R.; Itoh, T. Moving forward in retrodirective antenna arrays. IEEE Potentials 2003, 22, 16–21. [Google Scholar] [CrossRef]
- Miyamoto, R.; Itoh, T. Retrodirective arrays for wireless communications. IEEE Microw. Mag. 2002, 3, 71–79. [Google Scholar] [CrossRef]
- Jorgensen, D.; Loadman, C. Retrodirective Antenna Systems for Wireless Communications. CNSR. Available online: https://cnsr.cs.unb.ca/Download/PDF/a3b.pdf (accessed on 13 January 2024).
- Shiroma, W.; Miyamoto, R.; Shiroma, G.; Tuovinen, J.; Forsyth, W.; Murakami, B.; Tamamoto, M.; Ohta, A. Progress in retrodirective arrays for wireless communications. In Proceedings of the 2003 IEEE Topical Conference on Wireless Communication Technology, Honolulu, Hl, USA, 15–17 October 2003; pp. 80–81. [Google Scholar]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Wang, J.; Wang, J.; Hu, W.; Feng, D.; Song, K. Retrospective Spectrum-Conversion Method Based on Time-Modulated Van Atta Array. Remote Sens. 2025, 17, 1257. https://doi.org/10.3390/rs17071257
Zhao F, Wang J, Wang J, Hu W, Feng D, Song K. Retrospective Spectrum-Conversion Method Based on Time-Modulated Van Atta Array. Remote Sensing. 2025; 17(7):1257. https://doi.org/10.3390/rs17071257
Chicago/Turabian StyleZhao, Feng, Junjie Wang, Jinrong Wang, Weihong Hu, Dejun Feng, and Kunpeng Song. 2025. "Retrospective Spectrum-Conversion Method Based on Time-Modulated Van Atta Array" Remote Sensing 17, no. 7: 1257. https://doi.org/10.3390/rs17071257
APA StyleZhao, F., Wang, J., Wang, J., Hu, W., Feng, D., & Song, K. (2025). Retrospective Spectrum-Conversion Method Based on Time-Modulated Van Atta Array. Remote Sensing, 17(7), 1257. https://doi.org/10.3390/rs17071257





