Absolute Vicarious Calibration, Extended PICS (EPICS) Based De-Trending and Validation of Hyperspectral Hyperion, DESIS, and EMIT
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sensors and Sites Overview
2.1.1. Sensor Overview
DESIS
- Mission Specification and Product Used:
- Previous works and their potential limitations:
EMIT
- Mission Specification and Product Used:
- Previous works and their potential limitations:
Hyperion
- Mission Specification and Product Used:
- Previous works and their potential limitations:
Landsat Sensors
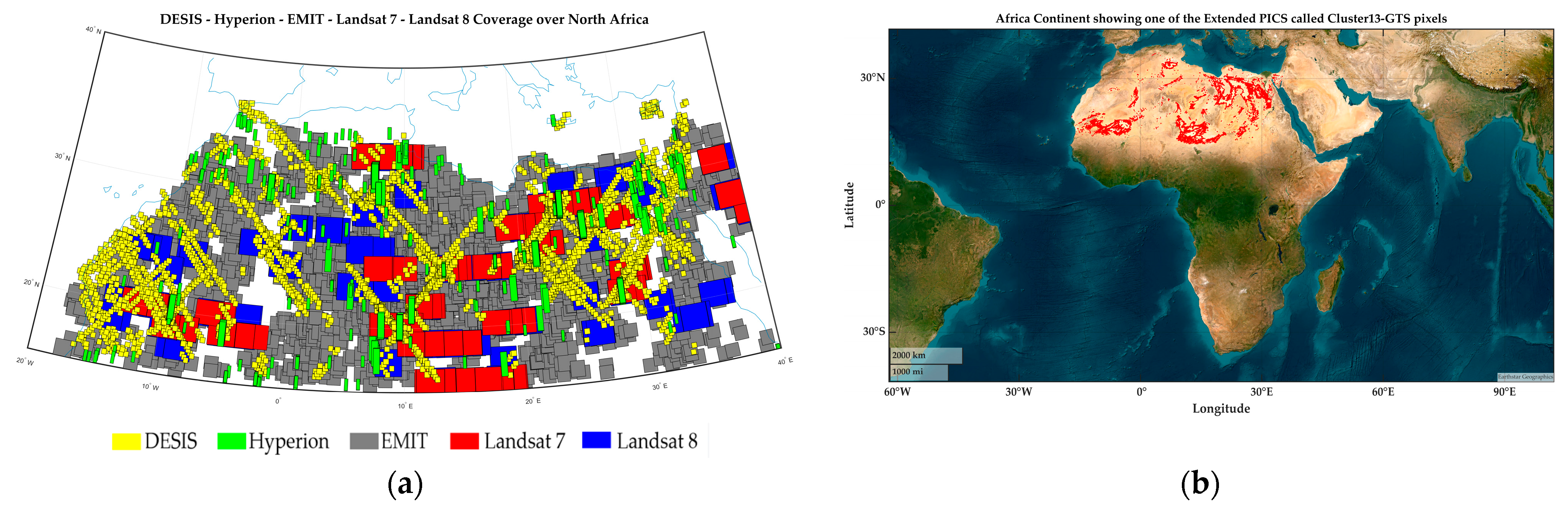
2.1.2. Study Area
Cluster13–GTS over North Africa
RCN Sites
Other Ground Truth Targets
Libya4
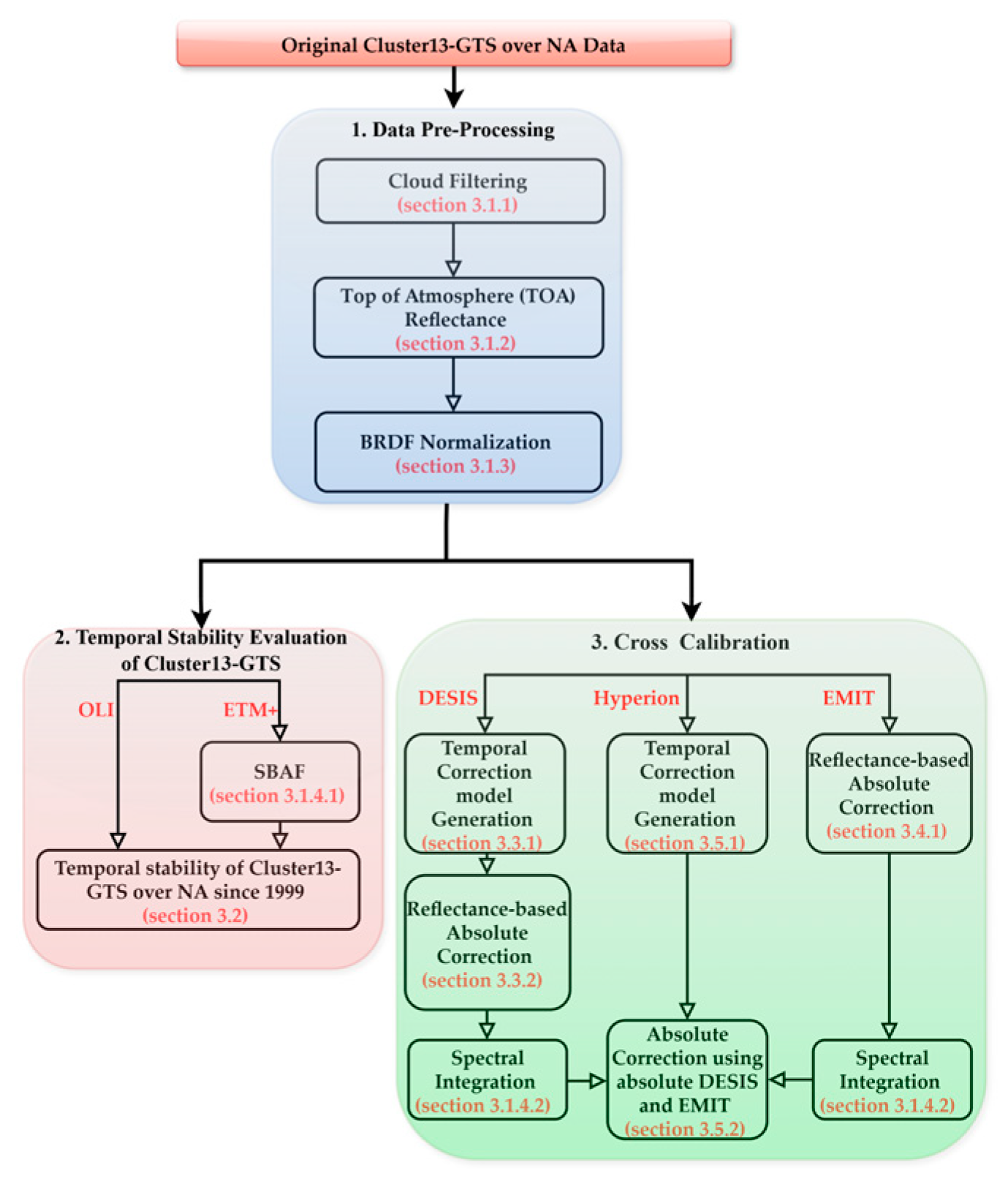
2.2. Methods
- Data Pre-processing
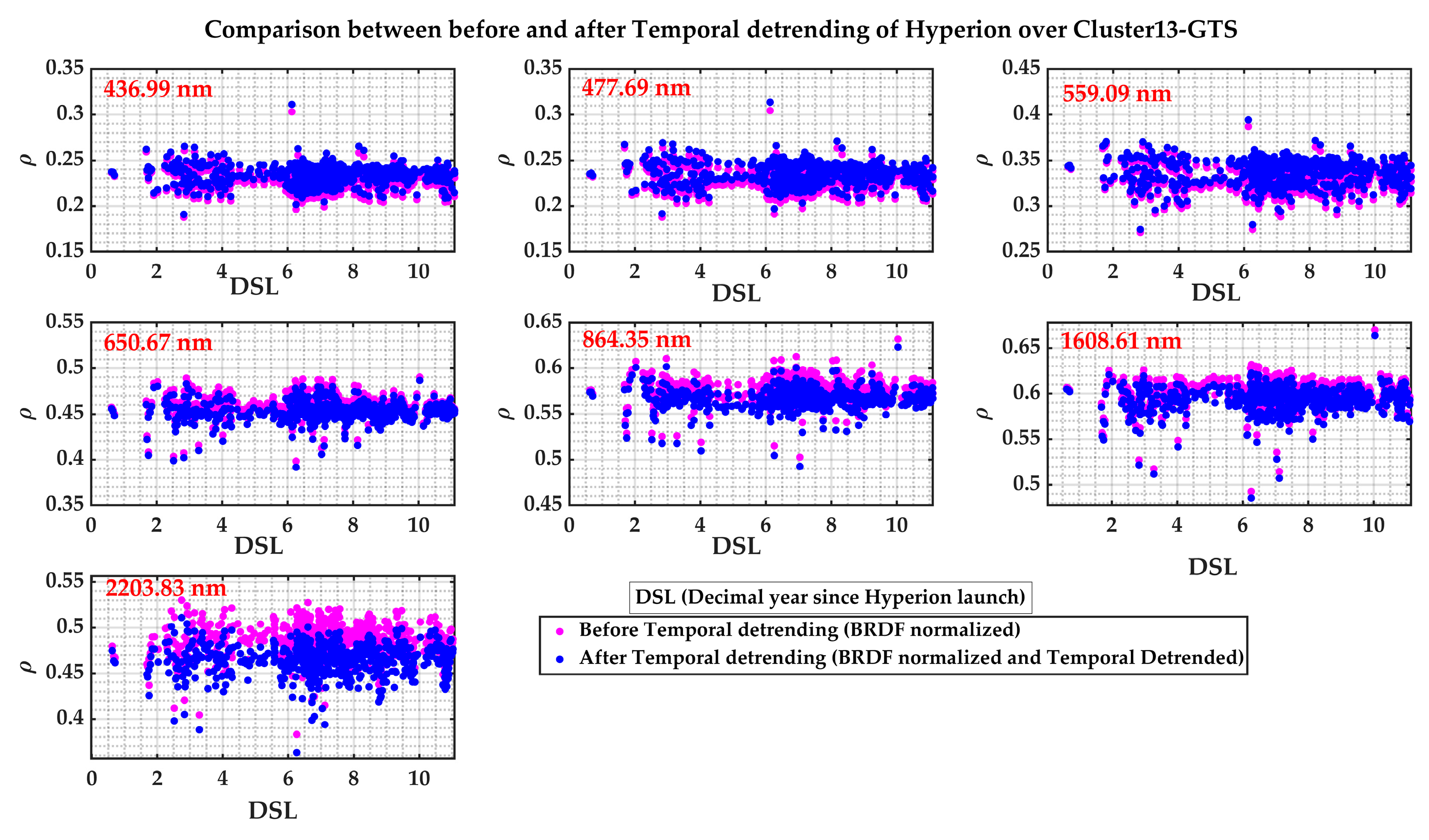
- Temporal Stability Evaluation of Cluster13–GTS since 1999
- Vicarious Calibration of DESIS
- Vicarious Calibration of EMIT
- Cross-Calibration of Hyperion using Absolute DESIS and EMIT
- Validation of Calibration Coefficients
- Uncertainty Analysis
- Statistical Tests
2.2.1. Data Pre–Processing
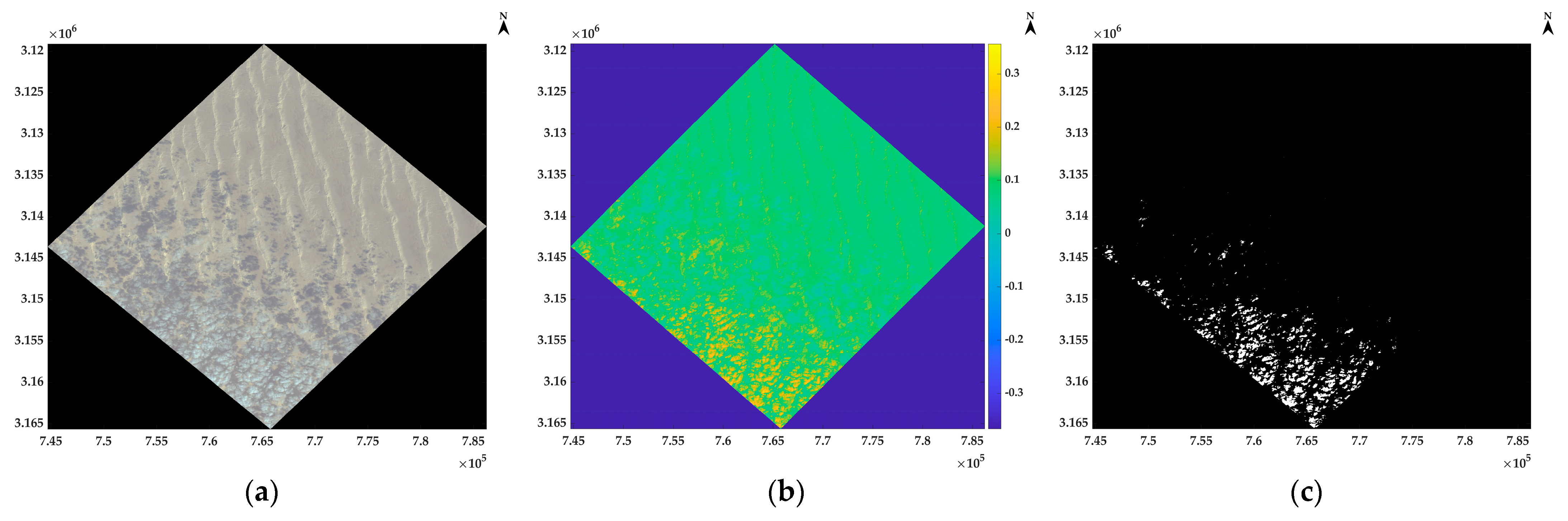
Cloud Filtering
- DESIS
- 2.
- Hyperion
- 3.
- EMIT
- 4.
- Landsat series
TOA Reflectance Computation
- DESIS
- 2.
- Hyperion
- 3.
- EMIT
- 4.
- Landsat series
BRDF Normalization
Normalization of Spectral Difference
- SBAF
- 2.
- Spectral Integration
2.2.2. Temporal Stability Evaluation of Cluster13–GTS Since 1999
2.2.3. Vicarious Absolute Calibration of DESIS
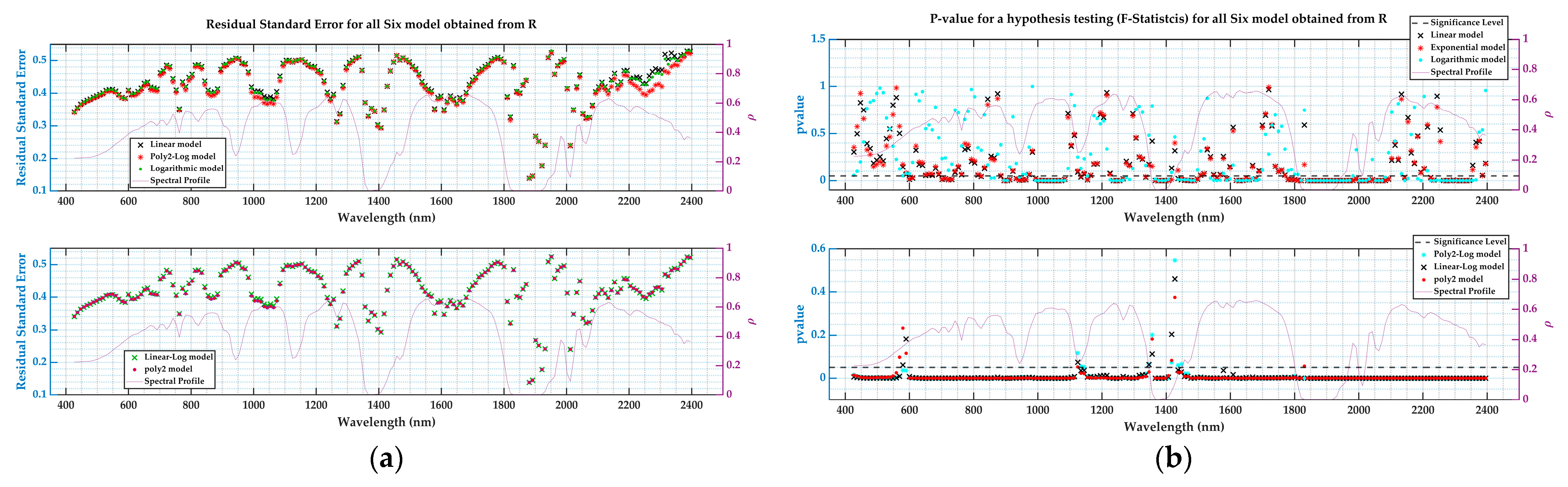
DESIS Temporal Correction Model Generation
- Residual standard error (RSE): The smaller the residual standard error, the better the regression model fits the underlying data, meaning the error in the model’s prediction is minimum.
- F–Statistics and p–value: The F–score indicates how well the regression model describes the underlying data, in other words, how significant the model is. Suppose the p–value that corresponds to the F–score is less than 0.05. In that case, the regression model fits better, meaning the p–value tells how well the predictor variables are statistically worthy in predicting the output. So, overall, an f–score with a p–value of less than the selected significance (in this case 0.05) confirms that the regression model fits the underlying data well.
- Significance of the coefficients: This is calculated through the t–distribution on each coefficient in the model. This answers the question of which coefficient/predictor is statistically different than zero. If the p–value corresponding to the t–distribution is less than the 0.05 significance level, then the predictor variable is said to be significant to the model.
DESIS Reflectance–Based Absolute Correction Using RCN
- DESIS data selection and filtering
- 2.
- TOA Reflectance Extraction
- DESIS ROI TOA Reflectance Extraction:
- RCN TOA Reflectance Extraction for DESIS Comparison:
- 3.
- DESIS Gain Calculation
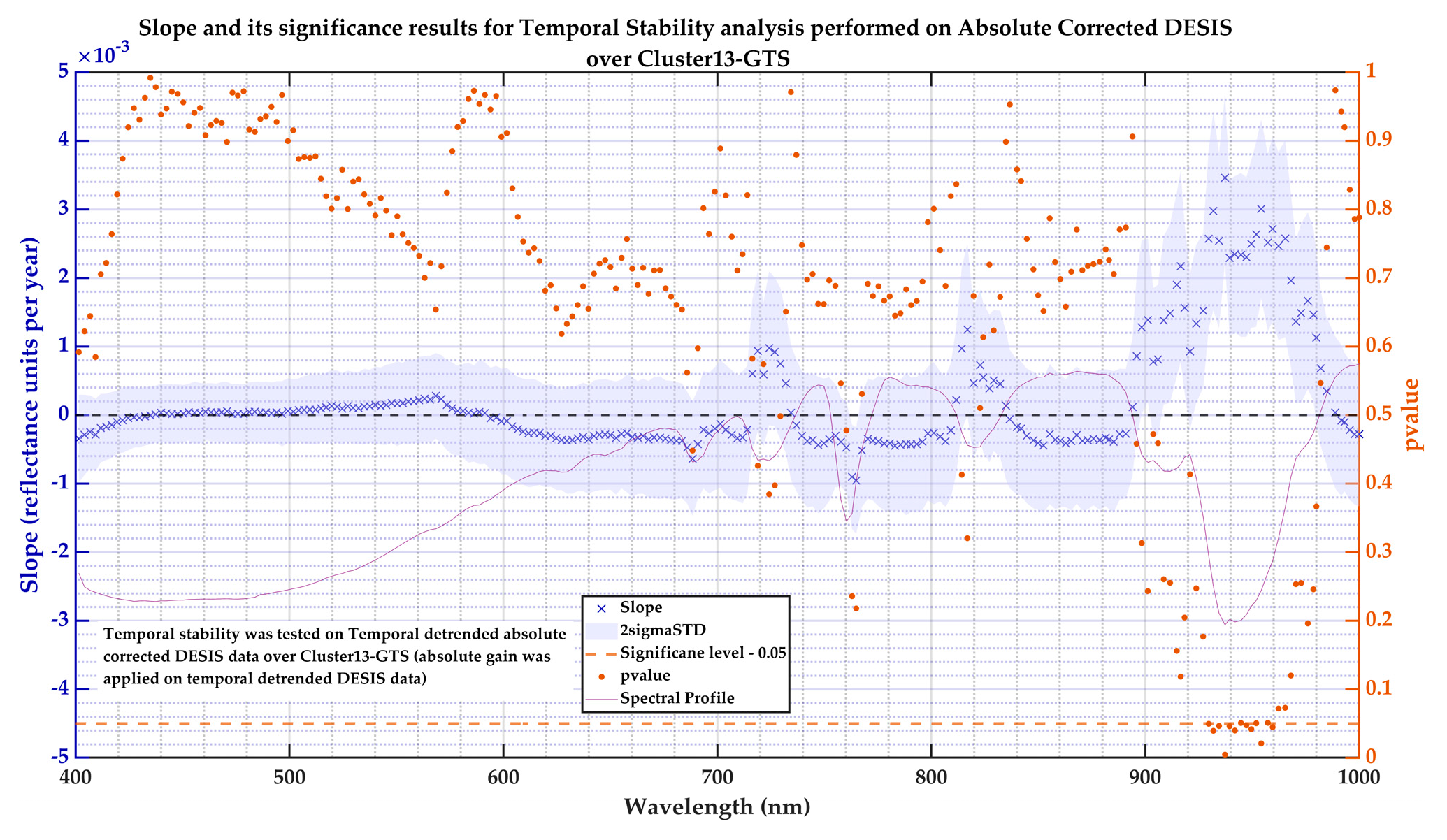
DESIS Statistical Test for Linearity Check After Temporal De–Trending
2.2.4. Vicarious Absolute Calibration of EMIT
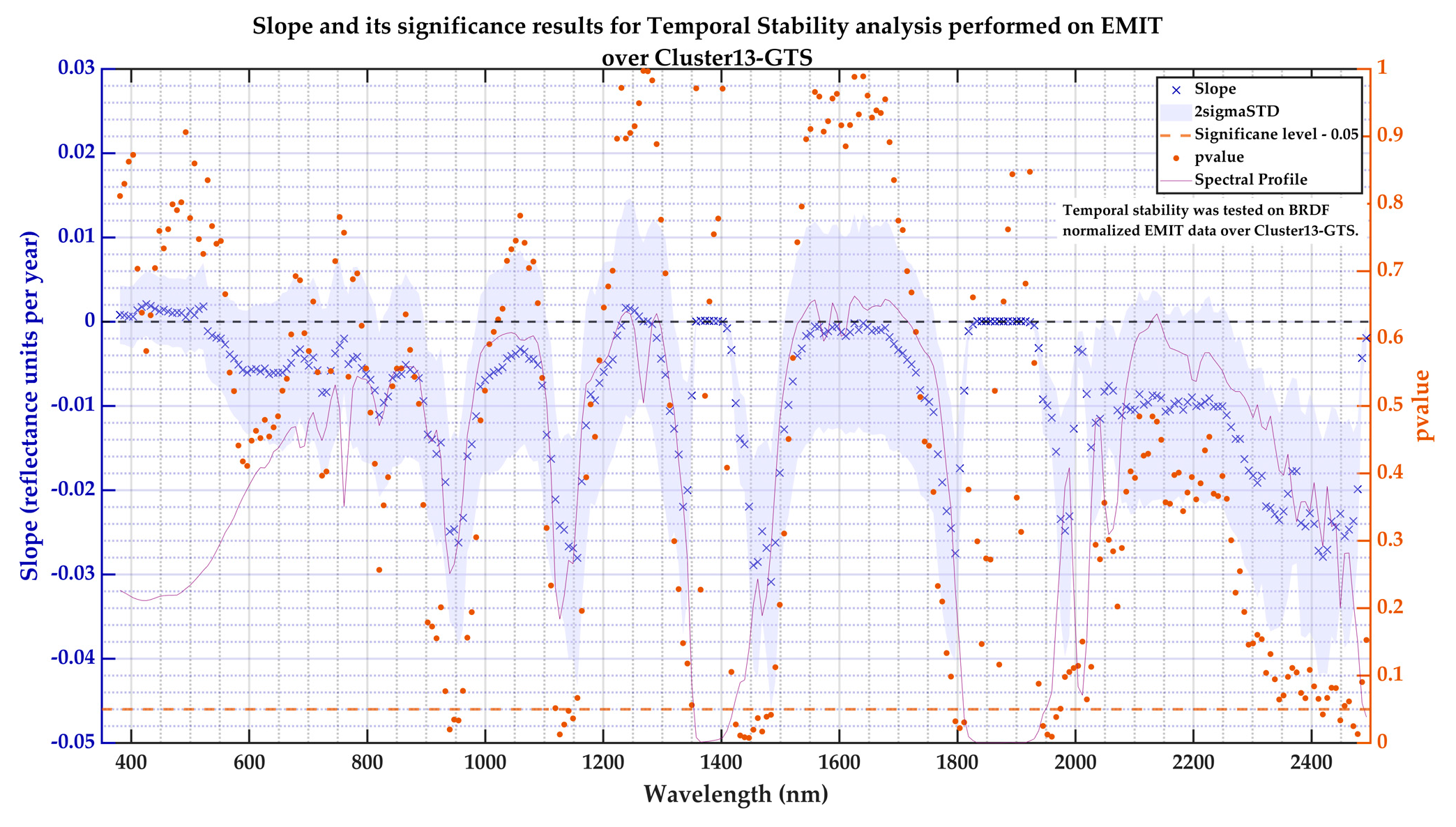
Temporal Stability Evaluation of EMIT
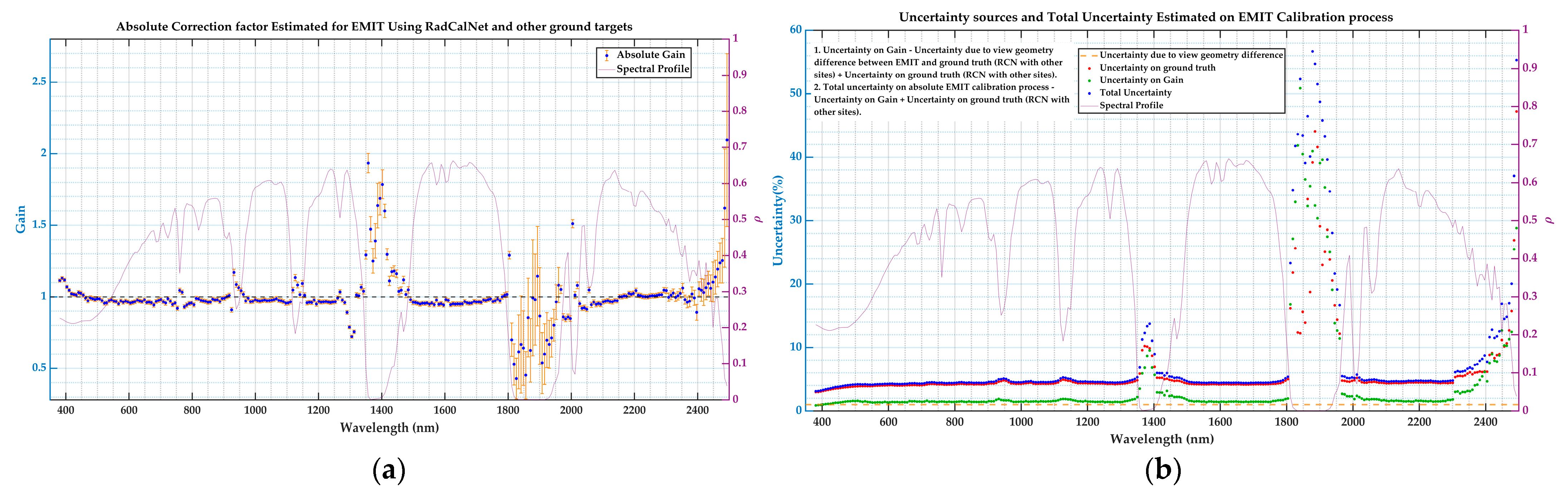
EMIT Reflectance–Based Absolute Correction Using RCN and In–Situ Measurements
- EMIT Data selection and filtering
- 2.
- TOA Reflectance Extraction
- EMIT ROI TOA Reflectance Extraction:
- Reference TOA Reflectance Extraction:
- 3.
- EMIT Gain Calculation
2.2.5. Cross–Calibration of Hyperion Using Absolute DESIS and EMIT
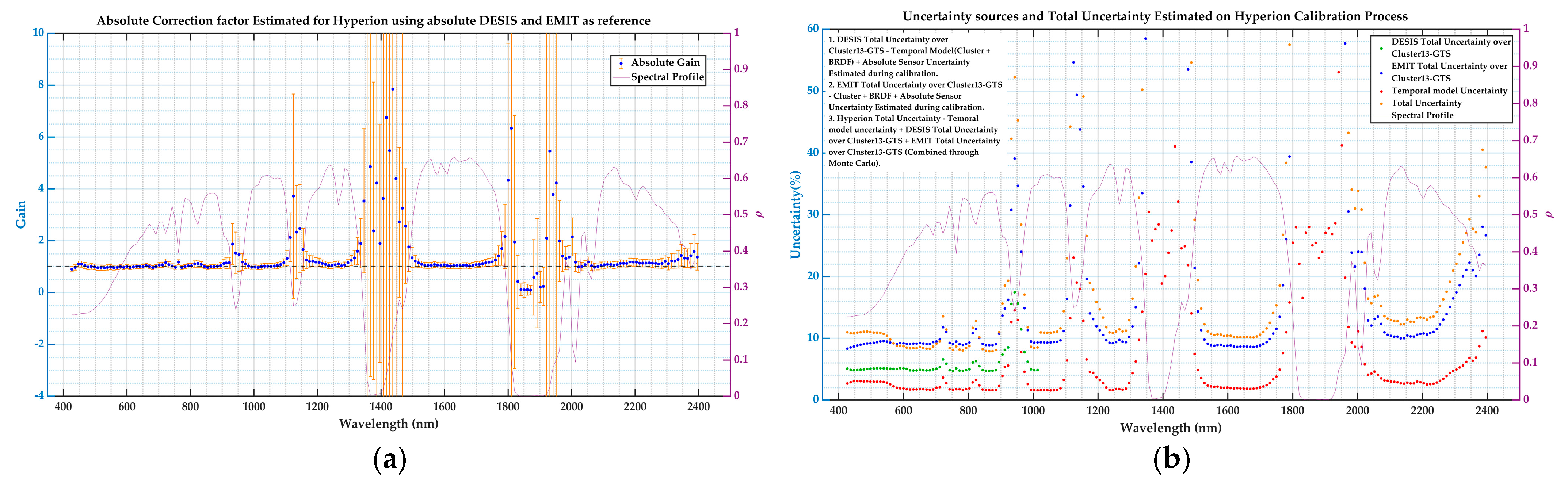
Hyperion Temporal Correction Model Generation
Hyperion Absolute Correction Factor Estimation Using DESIS and EMIT
Hyperion Statistical Test for Linearity Check After Temporal De–Trending
2.2.6. Validation of Calibration Coefficients
Validation of DESIS, EMIT, and Hyperion Calibration Coefficients
Comparison of Old and New Calibration Techniques for Hyperion
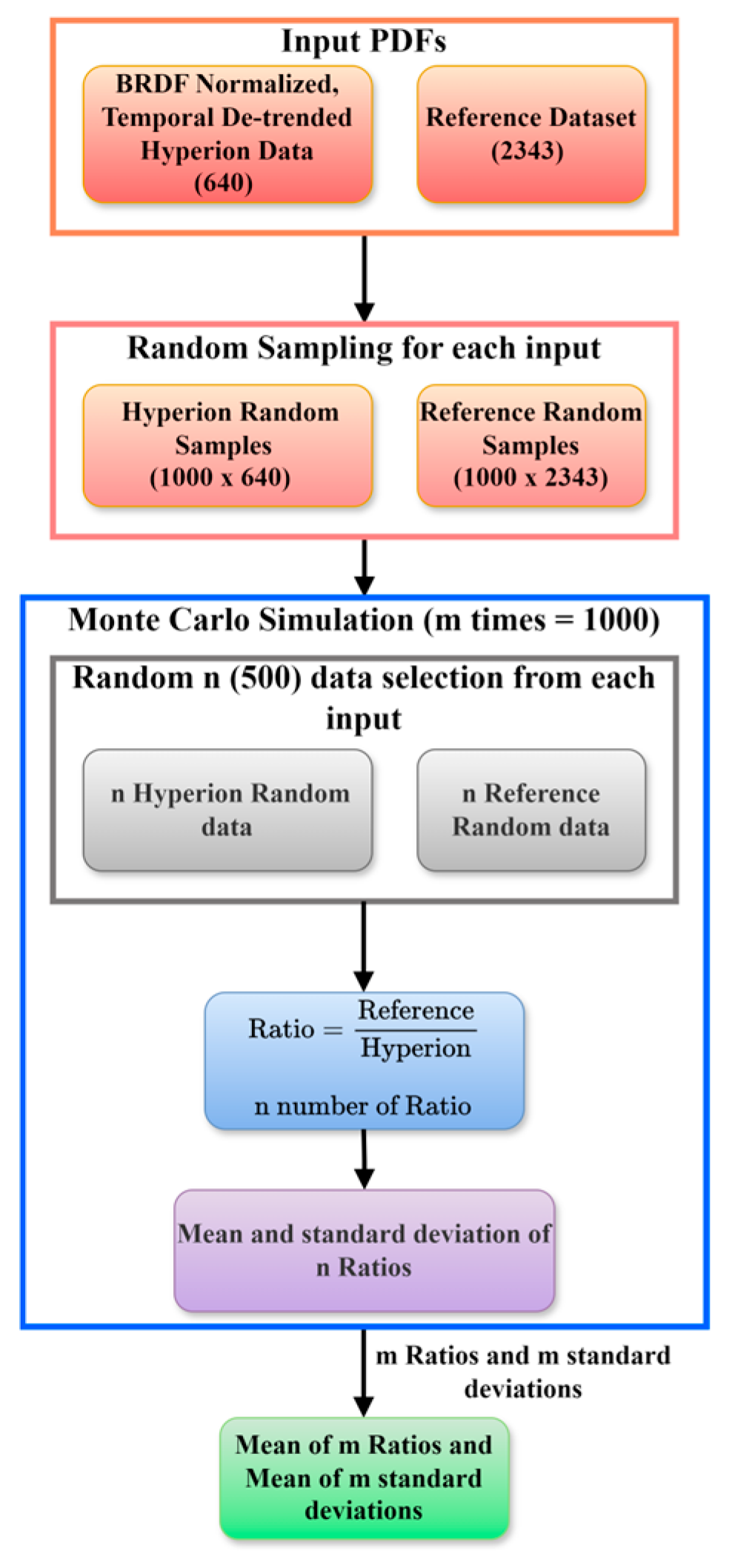
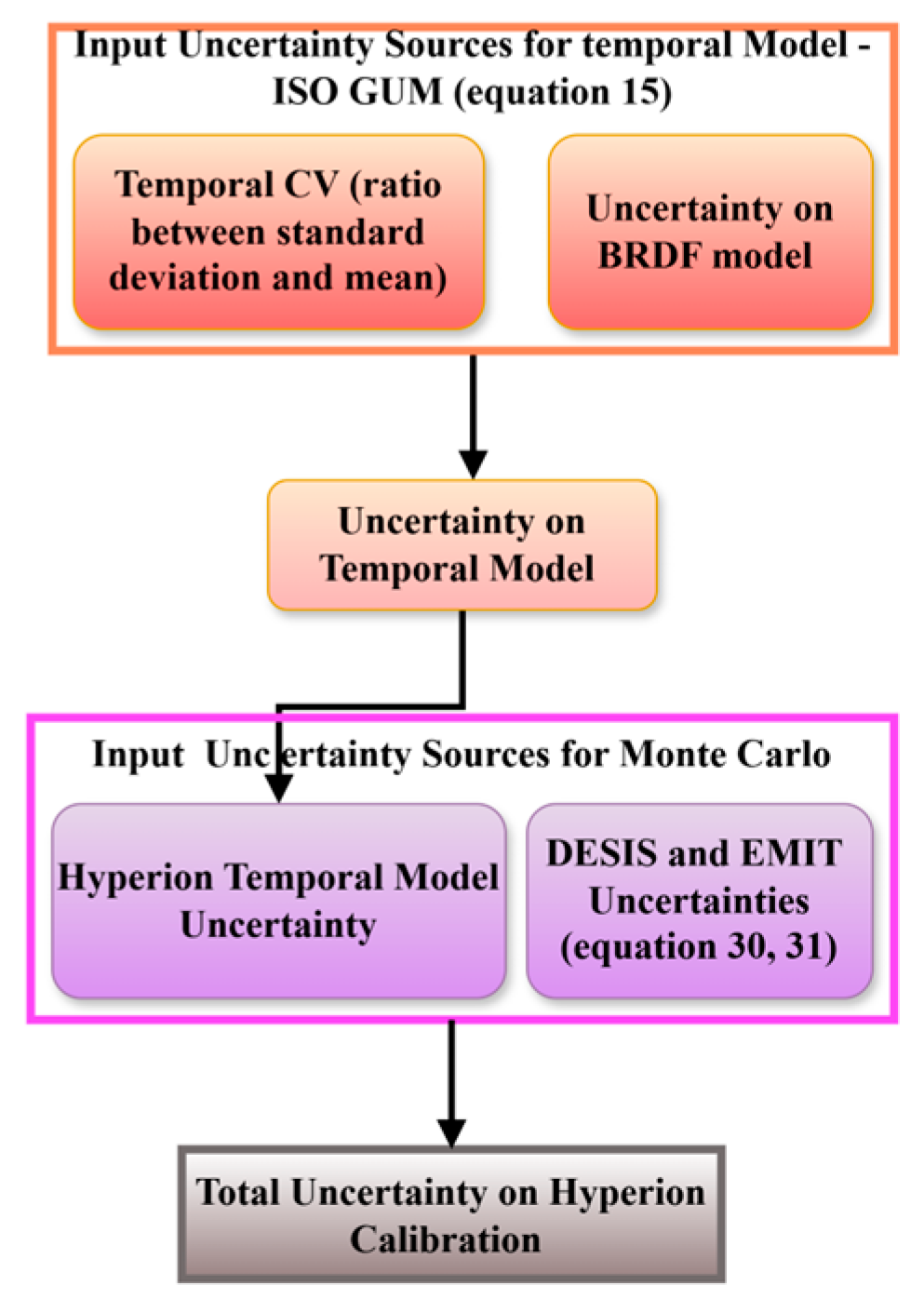
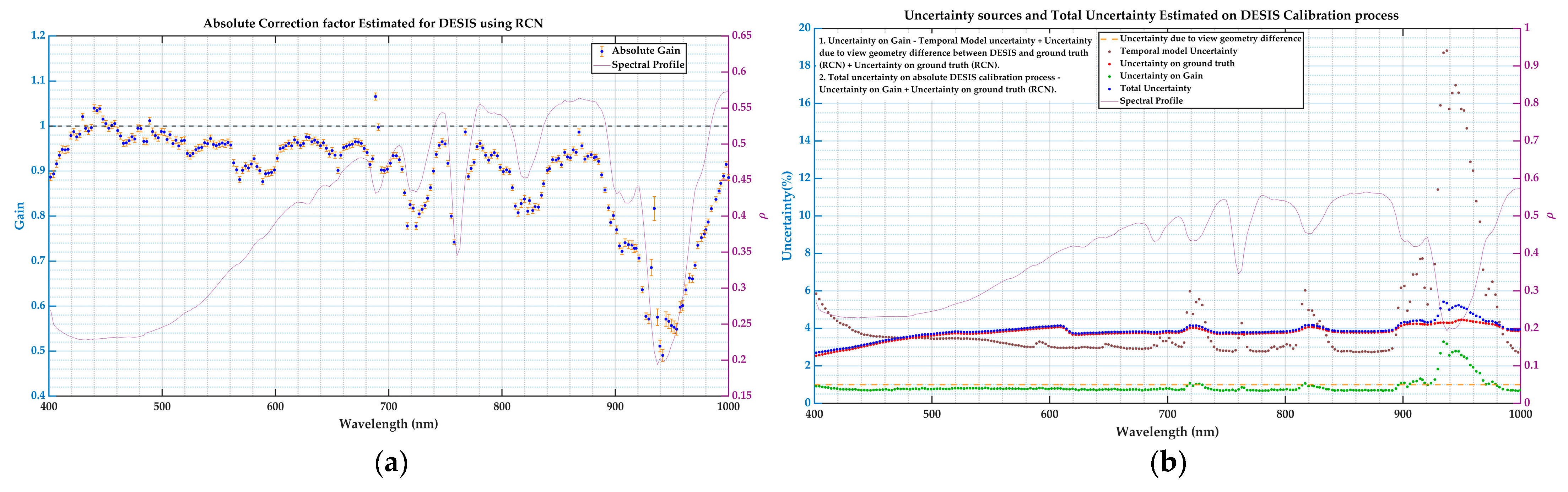
2.2.7. Uncertainty Analysis
DESIS and EMIT
Hyperion
2.2.8. Statistical Tests
Slope Test
Welch’s t–Test or Mean Test
3. Results and Analysis
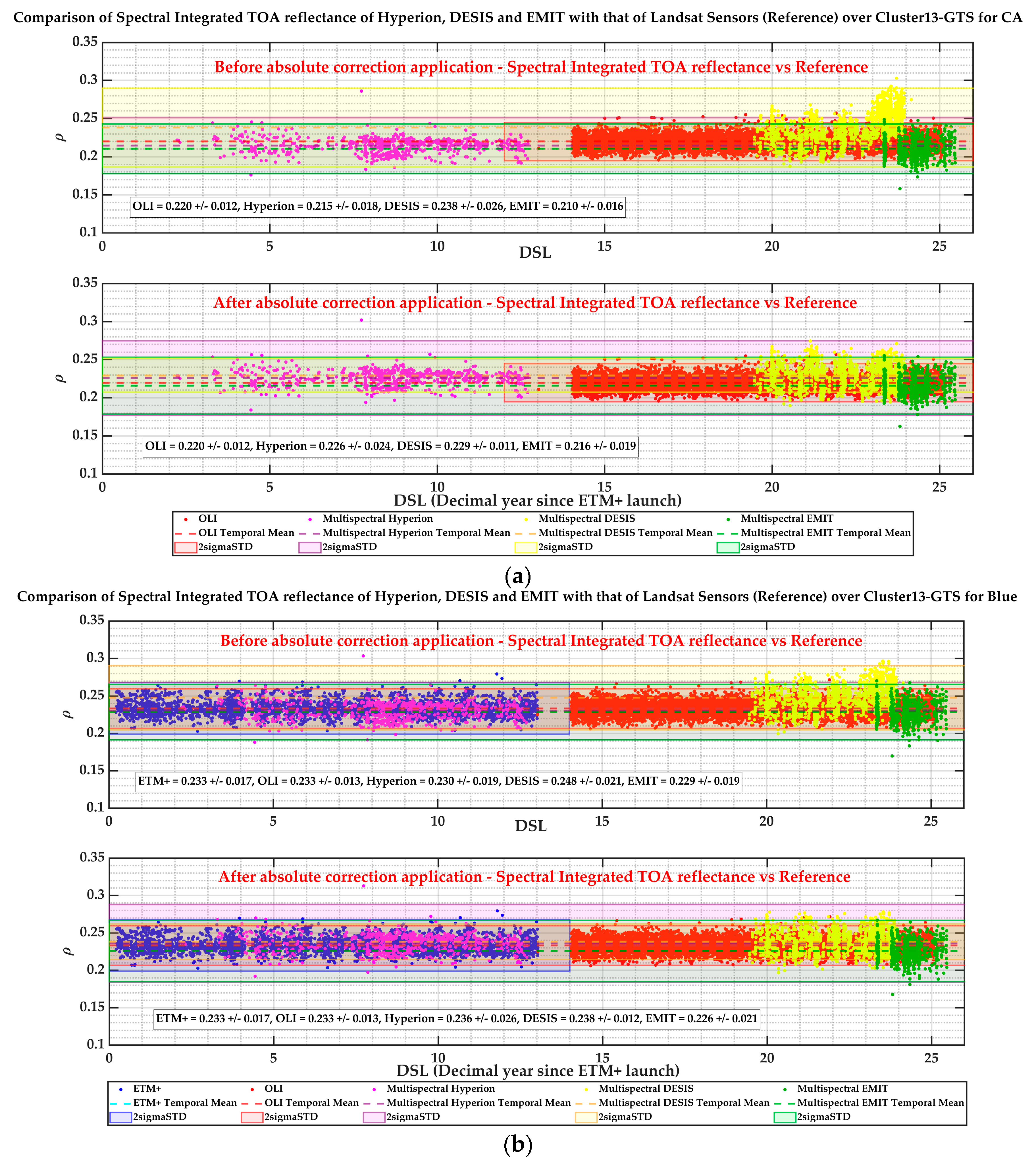
3.1. Data Processing
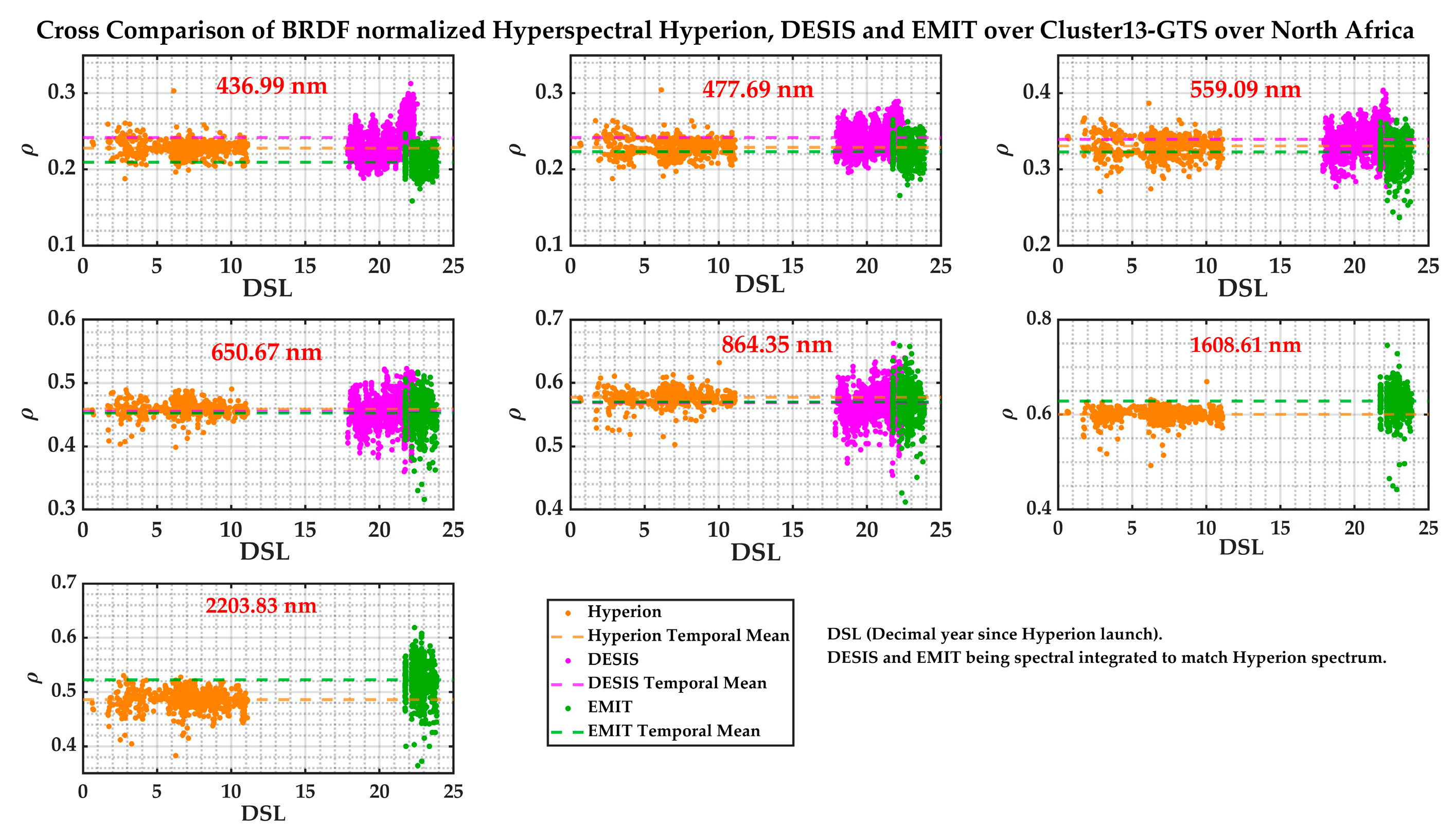
BRDF Normalization
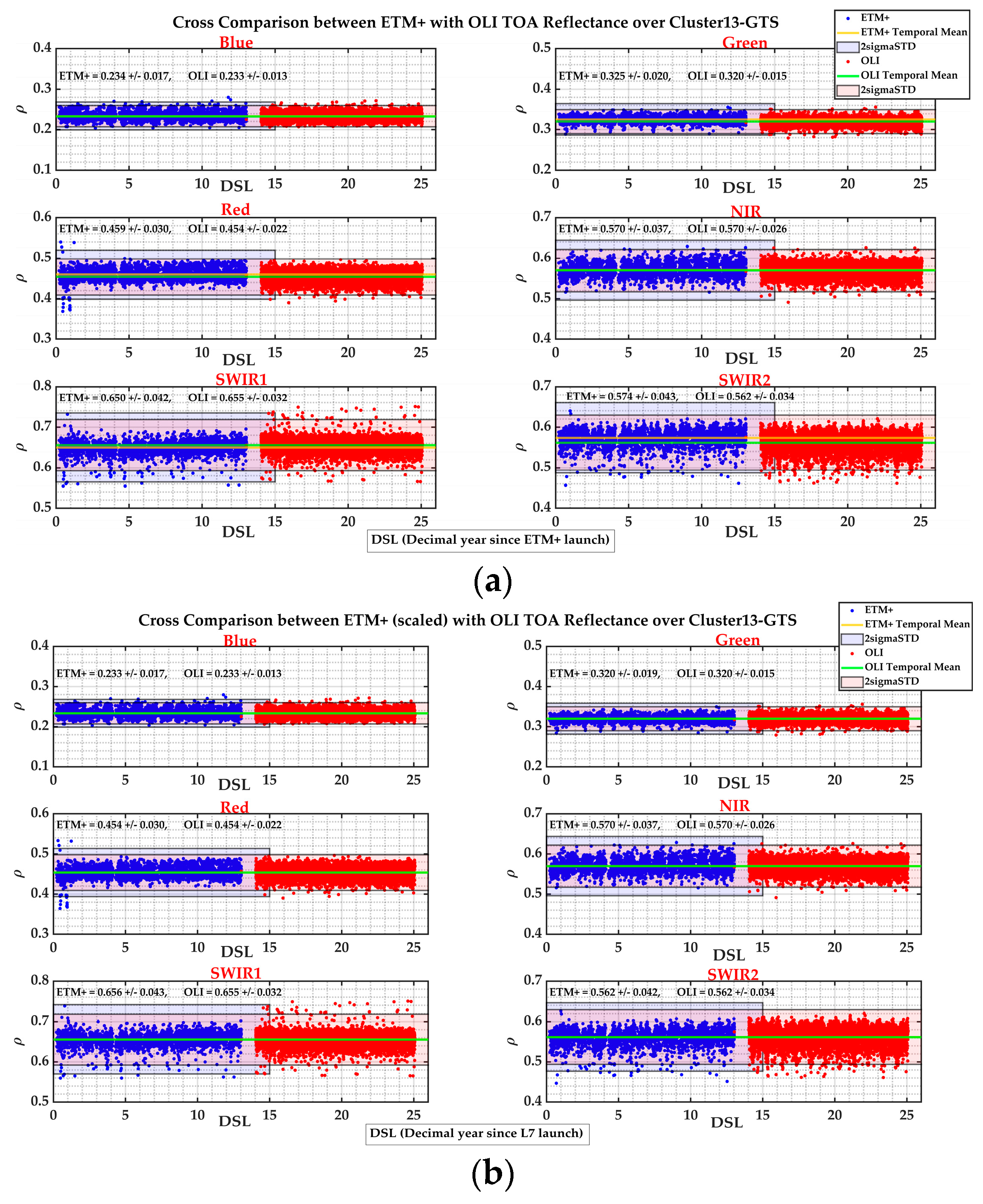
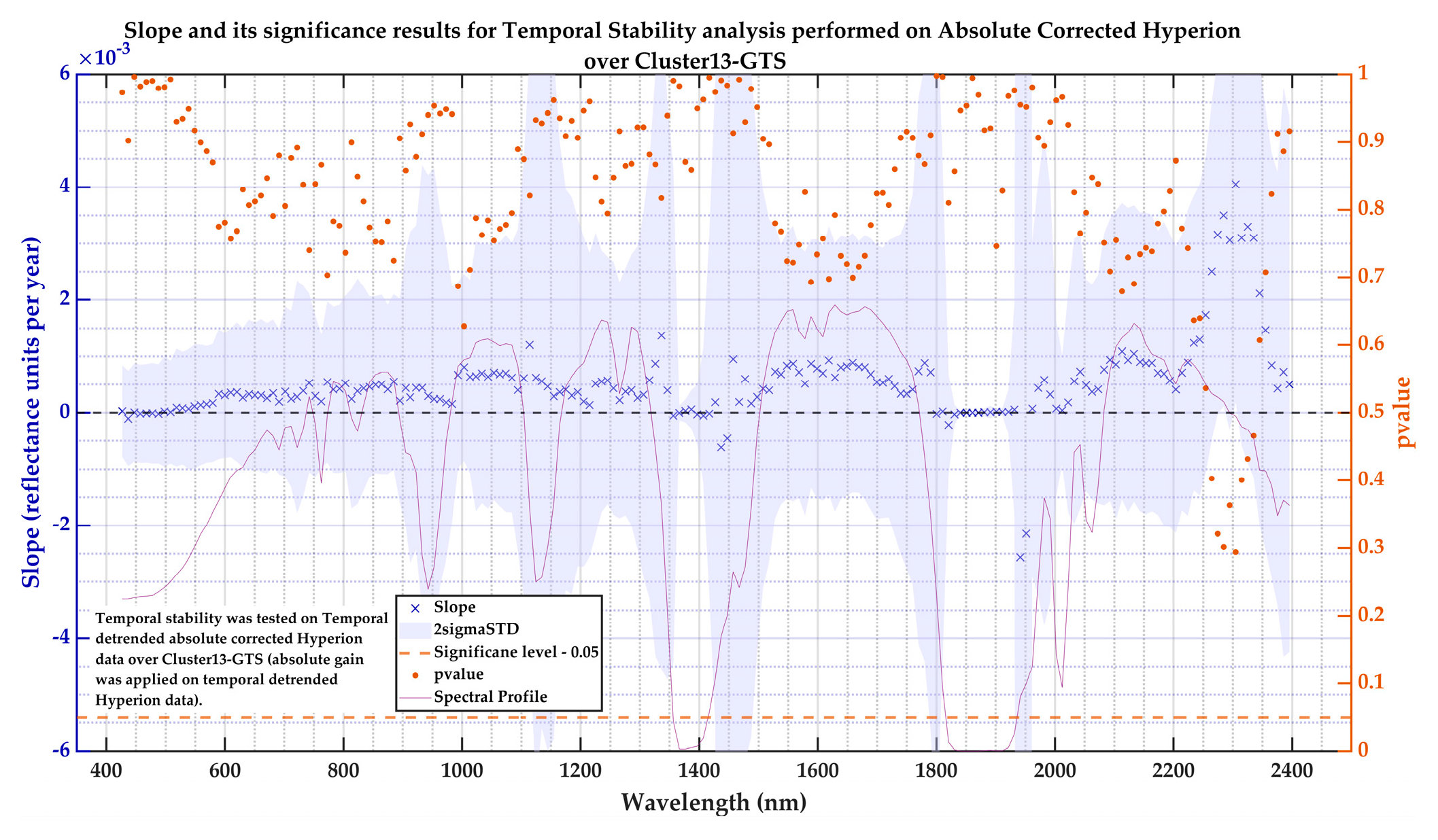
3.2. Temporal Stability Evaluation of Cluster13–GTS Since 1999 Results
3.3. Vicarious Absolute Calibration of DESIS Results
3.3.1. DESIS Temporal Correction Model Generation
3.3.2. DESIS Reflectance–Based Absolute Correction Using RCN Results
3.4. Vicarious Absolute Calibration of EMIT Results
3.5. Vicarious Absolute Cross–Calibration of Hyperion Using DESIS and EMIT Results
3.5.1. Hyperion Temporal Correction Model Generation
3.5.2. Hyperion Absolute Correction Factor Using Absolute DESIS and EMIT
3.6. Validation Results
3.6.1. Validation of DESIS, EMIT, and Hyperion Calibration Coefficients
3.6.2. Comparison of Old and New Calibration Techniques for Hyperion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Wavelengths | Temporal Coefficients | Absolute Gain | Total Uncertainty (%) | ||||
|---|---|---|---|---|---|---|---|
| 401.53 | 0.2995 | −0.0104 | −0.0266 | 0.0115 | −0.0009 | 0.8866 | 2.70 |
| 404.20 | 0.2751 | 0.0057 | −0.0377 | 0.0145 | −0.0013 | 0.8937 | 2.74 |
| 406.82 | 0.2632 | 0.0082 | −0.0337 | 0.0128 | −0.0011 | 0.9161 | 2.76 |
| 409.33 | 0.2551 | 0.0098 | −0.0316 | 0.0118 | −0.0010 | 0.9352 | 2.78 |
| 411.81 | 0.2491 | 0.0125 | −0.0320 | 0.0118 | −0.0010 | 0.9479 | 2.81 |
| 414.34 | 0.2470 | 0.0137 | −0.0314 | 0.0115 | −0.0010 | 0.9469 | 2.83 |
| 416.91 | 0.2443 | 0.0193 | −0.0338 | 0.0120 | −0.0011 | 0.9483 | 2.86 |
| 419.44 | 0.2353 | 0.0222 | −0.0334 | 0.0116 | −0.0010 | 0.9789 | 2.89 |
| 422.01 | 0.2317 | 0.0231 | −0.0325 | 0.0112 | −0.0010 | 0.9874 | 2.91 |
| 424.64 | 0.2334 | 0.0213 | −0.0300 | 0.0103 | −0.0009 | 0.9759 | 2.93 |
| 427.29 | 0.2304 | 0.0124 | −0.0219 | 0.0078 | −0.0007 | 0.9819 | 2.95 |
| 429.86 | 0.2223 | 0.0239 | −0.0290 | 0.0099 | −0.0009 | 1.0209 | 2.97 |
| 432.45 | 0.2285 | 0.0224 | −0.0262 | 0.0091 | −0.0009 | 0.9948 | 3.00 |
| 434.98 | 0.2293 | 0.0193 | −0.0237 | 0.0082 | −0.0008 | 0.9887 | 3.04 |
| 437.49 | 0.2271 | 0.0185 | −0.0226 | 0.0078 | −0.0007 | 0.9964 | 3.06 |
| 439.95 | 0.2187 | 0.0245 | −0.0255 | 0.0085 | −0.0008 | 1.0397 | 3.10 |
| 442.49 | 0.2199 | 0.0174 | −0.0200 | 0.0069 | −0.0007 | 1.0341 | 3.13 |
| 445.02 | 0.2196 | 0.0118 | −0.0154 | 0.0057 | −0.0006 | 1.0383 | 3.16 |
| 447.76 | 0.2250 | 0.0170 | −0.0192 | 0.0067 | −0.0007 | 1.0153 | 3.19 |
| 450.34 | 0.2273 | 0.0106 | −0.0143 | 0.0053 | −0.0005 | 1.0052 | 3.23 |
| 452.89 | 0.2305 | 0.0056 | −0.0105 | 0.0043 | −0.0005 | 0.9952 | 3.27 |
| 455.57 | 0.2292 | 0.0048 | −0.0094 | 0.0039 | −0.0004 | 1.0014 | 3.31 |
| 458.18 | 0.2286 | −0.0002 | −0.0055 | 0.0028 | −0.0003 | 1.0054 | 3.34 |
| 460.75 | 0.2324 | 0.0025 | −0.0074 | 0.0033 | −0.0004 | 0.9900 | 3.38 |
| 463.28 | 0.2351 | −0.0011 | −0.0044 | 0.0024 | −0.0003 | 0.9780 | 3.39 |
| 465.82 | 0.2393 | 0.0008 | −0.0052 | 0.0026 | −0.0003 | 0.9615 | 3.42 |
| 468.30 | 0.2392 | 0.0024 | −0.0055 | 0.0025 | −0.0003 | 0.9625 | 3.45 |
| 470.77 | 0.2383 | 0.0033 | −0.0054 | 0.0024 | −0.0003 | 0.9674 | 3.48 |
| 473.36 | 0.2357 | 0.0032 | −0.0058 | 0.0025 | −0.0003 | 0.9761 | 3.50 |
| 475.87 | 0.2368 | 0.0009 | −0.0046 | 0.0022 | −0.0002 | 0.9713 | 3.52 |
| 478.57 | 0.2315 | 0.0002 | −0.0034 | 0.0018 | −0.0002 | 0.9950 | 3.55 |
| 481.24 | 0.2328 | 0.0012 | −0.0037 | 0.0018 | −0.0002 | 0.9943 | 3.57 |
| 483.80 | 0.2408 | −0.0057 | 0.0013 | 0.0003 | −0.0001 | 0.9660 | 3.60 |
| 486.39 | 0.2447 | −0.0075 | 0.0044 | −0.0005 | 0.0000 | 0.9656 | 3.62 |
| 488.99 | 0.2345 | 0.0037 | −0.0027 | 0.0011 | −0.0001 | 1.0117 | 3.64 |
| 491.55 | 0.2417 | 0.0039 | −0.0032 | 0.0013 | −0.0001 | 0.9876 | 3.67 |
| 493.97 | 0.2455 | 0.0057 | −0.0041 | 0.0015 | −0.0002 | 0.9788 | 3.67 |
| 496.50 | 0.2480 | 0.0005 | −0.0005 | 0.0005 | −0.0001 | 0.9739 | 3.68 |
| 499.24 | 0.2464 | −0.0040 | 0.0029 | −0.0005 | 0.0000 | 0.9878 | 3.70 |
| 501.75 | 0.2485 | −0.0029 | 0.0015 | 0.0000 | 0.0000 | 0.9867 | 3.71 |
| 504.32 | 0.2544 | −0.0052 | 0.0024 | −0.0002 | 0.0000 | 0.9701 | 3.73 |
| 506.92 | 0.2536 | −0.0079 | 0.0047 | −0.0009 | 0.0001 | 0.9807 | 3.75 |
| 509.54 | 0.2616 | −0.0064 | 0.0050 | −0.0011 | 0.0001 | 0.9608 | 3.77 |
| 512.15 | 0.2623 | −0.0084 | 0.0071 | −0.0018 | 0.0002 | 0.9685 | 3.78 |
| 514.69 | 0.2692 | −0.0147 | 0.0120 | −0.0032 | 0.0003 | 0.9556 | 3.80 |
| 517.17 | 0.2698 | −0.0162 | 0.0136 | −0.0035 | 0.0003 | 0.9671 | 3.82 |
| 519.66 | 0.2720 | −0.0050 | 0.0071 | −0.0020 | 0.0002 | 0.9680 | 3.83 |
| 522.19 | 0.2831 | −0.0088 | 0.0100 | −0.0028 | 0.0003 | 0.9389 | 3.83 |
| 524.69 | 0.2863 | −0.0145 | 0.0133 | −0.0036 | 0.0003 | 0.9340 | 3.82 |
| 527.22 | 0.2881 | −0.0124 | 0.0115 | −0.0029 | 0.0002 | 0.9390 | 3.80 |
| 529.76 | 0.2872 | −0.0105 | 0.0093 | −0.0024 | 0.0002 | 0.9473 | 3.80 |
| 532.33 | 0.2896 | −0.0157 | 0.0123 | −0.0031 | 0.0003 | 0.9513 | 3.81 |
| 534.93 | 0.2932 | −0.0134 | 0.0113 | −0.0029 | 0.0002 | 0.9524 | 3.81 |
| 537.56 | 0.2944 | −0.0185 | 0.0162 | −0.0044 | 0.0004 | 0.9627 | 3.82 |
| 540.15 | 0.2993 | −0.0168 | 0.0145 | −0.0039 | 0.0003 | 0.9609 | 3.82 |
| 542.69 | 0.3004 | −0.0168 | 0.0148 | −0.0040 | 0.0003 | 0.9722 | 3.83 |
| 545.21 | 0.3091 | −0.0201 | 0.0166 | −0.0044 | 0.0004 | 0.9591 | 3.85 |
| 547.76 | 0.3153 | −0.0197 | 0.0163 | −0.0043 | 0.0004 | 0.9564 | 3.85 |
| 550.38 | 0.3196 | −0.0193 | 0.0165 | −0.0044 | 0.0004 | 0.9595 | 3.86 |
| 552.91 | 0.3239 | −0.0192 | 0.0171 | −0.0046 | 0.0004 | 0.9624 | 3.87 |
| 555.56 | 0.3300 | −0.0242 | 0.0206 | −0.0056 | 0.0005 | 0.9599 | 3.89 |
| 558.08 | 0.3336 | −0.0266 | 0.0222 | −0.0059 | 0.0005 | 0.9633 | 3.91 |
| 560.62 | 0.3405 | −0.0240 | 0.0201 | −0.0053 | 0.0005 | 0.9577 | 3.92 |
| 563.18 | 0.3589 | −0.0351 | 0.0258 | −0.0066 | 0.0006 | 0.9181 | 3.93 |
| 565.79 | 0.3684 | −0.0428 | 0.0306 | −0.0078 | 0.0007 | 0.9027 | 3.94 |
| 568.41 | 0.3793 | −0.0637 | 0.0424 | −0.0106 | 0.0009 | 0.8811 | 3.95 |
| 571.00 | 0.3752 | −0.0624 | 0.0420 | −0.0105 | 0.0009 | 0.9016 | 3.96 |
| 573.58 | 0.3762 | −0.0570 | 0.0380 | −0.0095 | 0.0008 | 0.9115 | 3.98 |
| 576.10 | 0.3836 | −0.0571 | 0.0377 | −0.0093 | 0.0008 | 0.9068 | 3.99 |
| 578.60 | 0.3864 | −0.0464 | 0.0310 | −0.0076 | 0.0006 | 0.9157 | 4.01 |
| 581.13 | 0.3882 | −0.0400 | 0.0274 | −0.0068 | 0.0006 | 0.9273 | 4.02 |
| 583.66 | 0.4006 | −0.0461 | 0.0301 | −0.0073 | 0.0006 | 0.9101 | 4.04 |
| 586.23 | 0.4089 | −0.0570 | 0.0394 | −0.0102 | 0.0009 | 0.9007 | 4.05 |
| 588.78 | 0.4204 | −0.0904 | 0.0597 | −0.0153 | 0.0014 | 0.8765 | 4.06 |
| 591.34 | 0.4171 | −0.0837 | 0.0563 | −0.0147 | 0.0013 | 0.8941 | 4.08 |
| 593.96 | 0.4205 | −0.0814 | 0.0547 | −0.0143 | 0.0013 | 0.8955 | 4.09 |
| 596.58 | 0.4269 | −0.0757 | 0.0503 | −0.0130 | 0.0012 | 0.8970 | 4.10 |
| 599.04 | 0.4304 | −0.0634 | 0.0420 | −0.0106 | 0.0009 | 0.9024 | 4.10 |
| 601.61 | 0.4247 | −0.0432 | 0.0287 | −0.0070 | 0.0006 | 0.9283 | 4.12 |
| 604.19 | 0.4205 | −0.0309 | 0.0202 | −0.0048 | 0.0004 | 0.9496 | 4.13 |
| 606.75 | 0.4238 | −0.0308 | 0.0204 | −0.0049 | 0.0004 | 0.9517 | 4.15 |
| 609.26 | 0.4264 | −0.0267 | 0.0178 | −0.0042 | 0.0003 | 0.9559 | 4.15 |
| 611.80 | 0.4275 | −0.0223 | 0.0149 | −0.0035 | 0.0003 | 0.9615 | 4.11 |
| 614.34 | 0.4330 | −0.0229 | 0.0148 | −0.0033 | 0.0003 | 0.9560 | 3.98 |
| 616.90 | 0.4306 | −0.0170 | 0.0114 | −0.0024 | 0.0002 | 0.9693 | 3.84 |
| 619.52 | 0.4350 | −0.0145 | 0.0082 | −0.0015 | 0.0001 | 0.9633 | 3.76 |
| 622.11 | 0.4373 | −0.0215 | 0.0135 | −0.0029 | 0.0002 | 0.9571 | 3.73 |
| 624.71 | 0.4352 | −0.0219 | 0.0142 | −0.0032 | 0.0002 | 0.9612 | 3.73 |
| 627.18 | 0.4266 | −0.0291 | 0.0179 | −0.0040 | 0.0003 | 0.9759 | 3.74 |
| 629.66 | 0.4275 | −0.0264 | 0.0160 | −0.0034 | 0.0003 | 0.9744 | 3.75 |
| 632.22 | 0.4366 | −0.0194 | 0.0121 | −0.0025 | 0.0002 | 0.9650 | 3.76 |
| 634.72 | 0.4417 | −0.0143 | 0.0084 | −0.0015 | 0.0001 | 0.9687 | 3.77 |
| 637.24 | 0.4512 | −0.0165 | 0.0090 | −0.0016 | 0.0001 | 0.9638 | 3.77 |
| 639.76 | 0.4591 | −0.0220 | 0.0118 | −0.0022 | 0.0001 | 0.9563 | 3.76 |
| 642.32 | 0.4595 | −0.0202 | 0.0113 | −0.0021 | 0.0001 | 0.9627 | 3.78 |
| 644.95 | 0.4652 | −0.0366 | 0.0223 | −0.0052 | 0.0004 | 0.9507 | 3.79 |
| 647.57 | 0.4689 | −0.0590 | 0.0363 | −0.0089 | 0.0008 | 0.9379 | 3.80 |
| 650.02 | 0.4691 | −0.0573 | 0.0359 | −0.0087 | 0.0007 | 0.9455 | 3.80 |
| 652.59 | 0.4780 | −0.0525 | 0.0329 | −0.0081 | 0.0007 | 0.9354 | 3.81 |
| 655.24 | 0.4992 | −0.0677 | 0.0421 | −0.0101 | 0.0008 | 0.9014 | 3.82 |
| 657.72 | 0.4902 | −0.0404 | 0.0245 | −0.0054 | 0.0004 | 0.9352 | 3.81 |
| 660.22 | 0.4867 | −0.0282 | 0.0147 | −0.0027 | 0.0002 | 0.9521 | 3.81 |
| 662.76 | 0.4897 | −0.0234 | 0.0109 | −0.0015 | 0.0000 | 0.9550 | 3.81 |
| 665.30 | 0.4913 | −0.0216 | 0.0099 | −0.0013 | 0.0000 | 0.9579 | 3.82 |
| 667.85 | 0.4945 | −0.0213 | 0.0095 | −0.0011 | 0.0000 | 0.9598 | 3.82 |
| 670.48 | 0.4944 | −0.0191 | 0.0083 | −0.0008 | 0.0000 | 0.9651 | 3.83 |
| 673.16 | 0.4976 | −0.0151 | 0.0057 | −0.0001 | −0.0001 | 0.9644 | 3.83 |
| 675.80 | 0.4999 | −0.0121 | 0.0039 | 0.0003 | −0.0001 | 0.9615 | 3.83 |
| 678.36 | 0.5044 | −0.0130 | 0.0040 | 0.0003 | −0.0001 | 0.9502 | 3.82 |
| 680.91 | 0.5078 | −0.0115 | 0.0021 | 0.0011 | −0.0002 | 0.9410 | 3.83 |
| 683.47 | 0.5112 | −0.0227 | 0.0126 | −0.0023 | 0.0001 | 0.9144 | 3.82 |
| 685.87 | 0.4804 | −0.0494 | 0.0289 | −0.0064 | 0.0005 | 0.9273 | 3.80 |
| 688.42 | 0.4045 | −0.0078 | −0.0036 | 0.0030 | −0.0004 | 1.0655 | 3.79 |
| 690.88 | 0.4343 | −0.0219 | 0.0120 | −0.0022 | 0.0001 | 0.9974 | 3.79 |
| 693.47 | 0.4878 | −0.0734 | 0.0463 | −0.0115 | 0.0010 | 0.9023 | 3.81 |
| 696.11 | 0.5087 | −0.0702 | 0.0429 | −0.0104 | 0.0009 | 0.9013 | 3.83 |
| 698.82 | 0.5216 | −0.0960 | 0.0593 | −0.0146 | 0.0013 | 0.9040 | 3.86 |
| 701.41 | 0.5216 | −0.1041 | 0.0643 | −0.0158 | 0.0014 | 0.9175 | 3.86 |
| 703.92 | 0.5215 | −0.0815 | 0.0505 | −0.0122 | 0.0010 | 0.9342 | 3.85 |
| 706.74 | 0.5296 | −0.0714 | 0.0437 | −0.0104 | 0.0009 | 0.9339 | 3.83 |
| 709.37 | 0.5377 | −0.0641 | 0.0385 | −0.0089 | 0.0007 | 0.9251 | 3.84 |
| 711.78 | 0.5451 | −0.0680 | 0.0416 | −0.0096 | 0.0008 | 0.9039 | 3.88 |
| 714.02 | 0.5603 | −0.1224 | 0.0842 | −0.0220 | 0.0020 | 0.8518 | 3.94 |
| 716.36 | 0.5745 | −0.2431 | 0.1689 | −0.0452 | 0.0042 | 0.7780 | 4.05 |
| 718.89 | 0.5190 | −0.2327 | 0.1573 | −0.0414 | 0.0038 | 0.8253 | 4.15 |
| 721.55 | 0.5290 | −0.1944 | 0.1251 | −0.0325 | 0.0029 | 0.8177 | 4.14 |
| 724.21 | 0.5518 | −0.2512 | 0.1657 | −0.0432 | 0.0039 | 0.7776 | 4.15 |
| 726.85 | 0.5408 | −0.2377 | 0.1563 | −0.0409 | 0.0037 | 0.8049 | 4.12 |
| 729.45 | 0.5488 | −0.2241 | 0.1469 | −0.0381 | 0.0034 | 0.8149 | 4.06 |
| 732.03 | 0.5664 | −0.1985 | 0.1280 | −0.0325 | 0.0029 | 0.8237 | 3.98 |
| 734.37 | 0.5765 | −0.1522 | 0.0952 | −0.0236 | 0.0020 | 0.8396 | 3.92 |
| 736.90 | 0.5809 | −0.1305 | 0.0807 | −0.0196 | 0.0017 | 0.8632 | 3.86 |
| 739.50 | 0.5770 | −0.0814 | 0.0487 | −0.0111 | 0.0009 | 0.9000 | 3.81 |
| 741.99 | 0.5680 | −0.0437 | 0.0240 | −0.0046 | 0.0003 | 0.9369 | 3.78 |
| 744.52 | 0.5643 | −0.0339 | 0.0176 | −0.0028 | 0.0001 | 0.9573 | 3.77 |
| 747.13 | 0.5634 | −0.0325 | 0.0162 | −0.0024 | 0.0001 | 0.9650 | 3.77 |
| 749.74 | 0.5647 | −0.0261 | 0.0128 | −0.0016 | 0.0000 | 0.9603 | 3.78 |
| 752.27 | 0.5628 | −0.0216 | 0.0114 | −0.0015 | 0.0000 | 0.9173 | 3.78 |
| 755.17 | 0.5571 | −0.0230 | 0.0117 | −0.0013 | 0.0000 | 0.7999 | 3.78 |
| 757.74 | 0.5069 | −0.0664 | 0.0509 | −0.0145 | 0.0014 | 0.7423 | 3.77 |
| 760.33 | 0.2609 | −0.0485 | 0.0397 | −0.0104 | 0.0009 | 1.3166 | 3.78 |
| 762.96 | 0.1943 | 0.0355 | −0.0327 | 0.0106 | −0.0011 | 1.8235 | 3.80 |
| 764.91 | 0.2797 | 0.0314 | −0.0341 | 0.0115 | −0.0012 | 1.4397 | 3.80 |
| 767.57 | 0.4569 | 0.0046 | −0.0119 | 0.0053 | −0.0006 | 0.9868 | 3.78 |
| 770.33 | 0.5432 | −0.0289 | 0.0168 | −0.0027 | 0.0001 | 0.8879 | 3.79 |
| 772.71 | 0.5575 | −0.0230 | 0.0122 | −0.0016 | 0.0000 | 0.9058 | 3.79 |
| 775.34 | 0.5769 | −0.0200 | 0.0104 | −0.0012 | 0.0000 | 0.9196 | 3.79 |
| 778.00 | 0.5770 | −0.0148 | 0.0083 | −0.0008 | −0.0001 | 0.9543 | 3.79 |
| 780.59 | 0.5776 | −0.0154 | 0.0088 | −0.0010 | 0.0000 | 0.9612 | 3.80 |
| 783.08 | 0.5811 | −0.0209 | 0.0112 | −0.0015 | 0.0000 | 0.9512 | 3.81 |
| 785.58 | 0.5862 | −0.0401 | 0.0244 | −0.0052 | 0.0004 | 0.9351 | 3.81 |
| 788.26 | 0.5876 | −0.0667 | 0.0427 | −0.0103 | 0.0009 | 0.9243 | 3.83 |
| 790.57 | 0.5792 | −0.0643 | 0.0411 | −0.0099 | 0.0008 | 0.9353 | 3.83 |
| 793.17 | 0.5774 | −0.0481 | 0.0312 | −0.0073 | 0.0006 | 0.9408 | 3.83 |
| 795.90 | 0.5788 | −0.0562 | 0.0355 | −0.0085 | 0.0007 | 0.9338 | 3.83 |
| 798.37 | 0.5953 | −0.0925 | 0.0596 | −0.0146 | 0.0012 | 0.9082 | 3.83 |
| 801.16 | 0.5978 | −0.1045 | 0.0679 | −0.0169 | 0.0015 | 0.8987 | 3.85 |
| 804.08 | 0.5913 | −0.0896 | 0.0585 | −0.0144 | 0.0012 | 0.9026 | 3.86 |
| 806.67 | 0.5863 | −0.0657 | 0.0432 | −0.0106 | 0.0009 | 0.8986 | 3.89 |
| 809.15 | 0.5980 | −0.1054 | 0.0687 | −0.0173 | 0.0015 | 0.8631 | 3.92 |
| 811.70 | 0.6075 | −0.1971 | 0.1300 | −0.0338 | 0.0030 | 0.8221 | 3.98 |
| 814.26 | 0.5824 | −0.2663 | 0.1760 | −0.0463 | 0.0042 | 0.8074 | 4.07 |
| 816.88 | 0.5435 | −0.2432 | 0.1604 | −0.0422 | 0.0039 | 0.8276 | 4.16 |
| 819.76 | 0.5358 | −0.1798 | 0.1203 | −0.0320 | 0.0030 | 0.8379 | 4.17 |
| 822.81 | 0.5548 | −0.2153 | 0.1359 | −0.0348 | 0.0031 | 0.8108 | 4.18 |
| 824.26 | 0.5494 | −0.1858 | 0.1200 | −0.0310 | 0.0028 | 0.8344 | 4.17 |
| 827.17 | 0.5786 | −0.1975 | 0.1265 | −0.0325 | 0.0029 | 0.8126 | 4.12 |
| 829.18 | 0.5823 | −0.2091 | 0.1345 | −0.0345 | 0.0031 | 0.8208 | 4.10 |
| 832.20 | 0.6028 | −0.2077 | 0.1343 | −0.0344 | 0.0031 | 0.8199 | 4.04 |
| 834.88 | 0.6060 | −0.1705 | 0.1118 | −0.0286 | 0.0025 | 0.8460 | 3.98 |
| 836.69 | 0.6019 | −0.1426 | 0.0916 | −0.0230 | 0.0020 | 0.8719 | 3.94 |
| 840.07 | 0.5974 | −0.1097 | 0.0714 | −0.0178 | 0.0015 | 0.9014 | 3.89 |
| 841.97 | 0.5997 | −0.0935 | 0.0581 | −0.0139 | 0.0012 | 0.9053 | 3.88 |
| 844.66 | 0.5928 | −0.0639 | 0.0364 | −0.0079 | 0.0006 | 0.9253 | 3.87 |
| 847.73 | 0.5979 | −0.0662 | 0.0388 | −0.0086 | 0.0007 | 0.9245 | 3.85 |
| 849.93 | 0.5986 | −0.0669 | 0.0426 | −0.0100 | 0.0008 | 0.9282 | 3.85 |
| 852.46 | 0.6081 | −0.0722 | 0.0459 | −0.0109 | 0.0009 | 0.9141 | 3.85 |
| 855.37 | 0.5963 | −0.0575 | 0.0386 | −0.0088 | 0.0007 | 0.9415 | 3.85 |
| 857.88 | 0.5998 | −0.0498 | 0.0283 | −0.0059 | 0.0004 | 0.9313 | 3.85 |
| 860.30 | 0.6017 | −0.0627 | 0.0336 | −0.0066 | 0.0004 | 0.9295 | 3.85 |
| 862.87 | 0.5912 | −0.0613 | 0.0354 | −0.0077 | 0.0006 | 0.9469 | 3.85 |
| 865.44 | 0.5964 | −0.0800 | 0.0499 | −0.0113 | 0.0009 | 0.9417 | 3.85 |
| 867.97 | 0.5720 | −0.0495 | 0.0320 | −0.0070 | 0.0005 | 0.9866 | 3.85 |
| 870.59 | 0.5893 | −0.0494 | 0.0286 | −0.0059 | 0.0004 | 0.9559 | 3.84 |
| 873.18 | 0.6064 | −0.0622 | 0.0342 | −0.0069 | 0.0005 | 0.9265 | 3.85 |
| 875.77 | 0.6015 | −0.0757 | 0.0418 | −0.0087 | 0.0006 | 0.9331 | 3.85 |
| 878.76 | 0.5981 | −0.0761 | 0.0432 | −0.0093 | 0.0007 | 0.9362 | 3.85 |
| 881.52 | 0.6019 | −0.0779 | 0.0462 | −0.0103 | 0.0008 | 0.9299 | 3.86 |
| 883.08 | 0.5997 | −0.0768 | 0.0476 | −0.0111 | 0.0009 | 0.9313 | 3.86 |
| 885.31 | 0.6001 | −0.0824 | 0.0515 | −0.0121 | 0.0010 | 0.9215 | 3.87 |
| 888.08 | 0.6133 | −0.1057 | 0.0652 | −0.0154 | 0.0013 | 0.8915 | 3.89 |
| 890.92 | 0.6213 | −0.1385 | 0.0869 | −0.0212 | 0.0018 | 0.8579 | 3.91 |
| 894.05 | 0.6100 | −0.2180 | 0.1454 | −0.0380 | 0.0034 | 0.8184 | 4.03 |
| 895.97 | 0.5935 | −0.2908 | 0.1963 | −0.0519 | 0.0047 | 0.7858 | 4.15 |
| 898.36 | 0.5432 | −0.2848 | 0.1892 | −0.0501 | 0.0046 | 0.8011 | 4.28 |
| 901.20 | 0.5517 | −0.2782 | 0.1769 | −0.0454 | 0.0041 | 0.7698 | 4.34 |
| 903.76 | 0.5868 | −0.2594 | 0.1671 | −0.0433 | 0.0039 | 0.7337 | 4.32 |
| 905.98 | 0.5865 | −0.2785 | 0.1895 | −0.0505 | 0.0047 | 0.7217 | 4.37 |
| 908.63 | 0.5544 | −0.3012 | 0.2018 | −0.0536 | 0.0049 | 0.7407 | 4.40 |
| 911.62 | 0.5571 | −0.3114 | 0.2047 | −0.0543 | 0.0050 | 0.7365 | 4.41 |
| 914.77 | 0.5613 | −0.3403 | 0.2252 | −0.0599 | 0.0055 | 0.7355 | 4.44 |
| 916.56 | 0.5745 | −0.3508 | 0.2291 | −0.0603 | 0.0055 | 0.7280 | 4.41 |
| 918.38 | 0.5941 | −0.3205 | 0.2030 | −0.0523 | 0.0047 | 0.7284 | 4.35 |
| 920.93 | 0.6202 | −0.2992 | 0.1942 | −0.0505 | 0.0046 | 0.7066 | 4.32 |
| 923.84 | 0.6337 | −0.3429 | 0.2266 | −0.0594 | 0.0054 | 0.6364 | 4.36 |
| 927.07 | 0.5970 | −0.3719 | 0.2481 | −0.0664 | 0.0062 | 0.5775 | 4.45 |
| 929.66 | 0.4887 | −0.4049 | 0.2719 | −0.0736 | 0.0069 | 0.5713 | 4.67 |
| 931.85 | 0.3246 | −0.2972 | 0.1989 | −0.0543 | 0.0052 | 0.6856 | 5.07 |
| 934.49 | 0.2162 | −0.1970 | 0.1254 | −0.0339 | 0.0033 | 0.8168 | 5.42 |
| 937.29 | 0.2872 | −0.2884 | 0.1764 | −0.0457 | 0.0042 | 0.5754 | 5.35 |
| 939.40 | 0.3556 | −0.2932 | 0.1831 | −0.0487 | 0.0046 | 0.5113 | 5.00 |
| 941.92 | 0.3603 | −0.3077 | 0.2000 | −0.0541 | 0.0052 | 0.4907 | 5.10 |
| 944.74 | 0.3091 | −0.2624 | 0.1683 | −0.0453 | 0.0043 | 0.5713 | 5.19 |
| 947.28 | 0.3269 | −0.2782 | 0.1788 | −0.0481 | 0.0046 | 0.5663 | 5.24 |
| 949.58 | 0.3565 | −0.3057 | 0.1978 | −0.0532 | 0.0051 | 0.5570 | 5.15 |
| 951.90 | 0.3733 | −0.3268 | 0.2121 | −0.0570 | 0.0054 | 0.5532 | 5.10 |
| 954.22 | 0.4069 | −0.3600 | 0.2303 | −0.0612 | 0.0057 | 0.5488 | 5.04 |
| 957.31 | 0.4204 | −0.3346 | 0.2177 | −0.0584 | 0.0055 | 0.5977 | 4.84 |
| 959.57 | 0.4470 | −0.3566 | 0.2311 | −0.0615 | 0.0057 | 0.6012 | 4.78 |
| 962.30 | 0.4801 | −0.3512 | 0.2274 | −0.0604 | 0.0056 | 0.6360 | 4.67 |
| 965.42 | 0.5301 | −0.3647 | 0.2376 | −0.0628 | 0.0058 | 0.6623 | 4.61 |
| 968.10 | 0.6089 | −0.3677 | 0.2388 | −0.0623 | 0.0057 | 0.6605 | 4.46 |
| 970.43 | 0.6244 | −0.3255 | 0.2155 | −0.0566 | 0.0052 | 0.6908 | 4.39 |
| 972.90 | 0.6014 | −0.3180 | 0.2110 | −0.0556 | 0.0051 | 0.7353 | 4.38 |
| 976.03 | 0.6011 | −0.3265 | 0.2152 | −0.0566 | 0.0052 | 0.7522 | 4.38 |
| 978.62 | 0.6165 | −0.3111 | 0.2030 | −0.0528 | 0.0048 | 0.7603 | 4.32 |
| 980.00 | 0.6275 | −0.2962 | 0.1878 | −0.0479 | 0.0043 | 0.7696 | 4.27 |
| 981.99 | 0.6385 | −0.2650 | 0.1666 | −0.0419 | 0.0037 | 0.7868 | 4.19 |
| 984.84 | 0.6482 | −0.2318 | 0.1468 | −0.0367 | 0.0032 | 0.8164 | 4.08 |
| 988.87 | 0.6626 | −0.1984 | 0.1271 | −0.0316 | 0.0027 | 0.8371 | 3.97 |
| 991.66 | 0.6588 | −0.1781 | 0.1128 | −0.0277 | 0.0024 | 0.8557 | 3.95 |
| 993.15 | 0.6513 | −0.1646 | 0.1052 | −0.0257 | 0.0022 | 0.8727 | 3.94 |
| 995.64 | 0.6434 | −0.1397 | 0.0877 | −0.0210 | 0.0017 | 0.8888 | 3.92 |
| 997.92 | 0.6256 | −0.1129 | 0.0710 | −0.0168 | 0.0014 | 0.9148 | 3.92 |
| 1000.08 | 0.6494 | −0.1316 | 0.0740 | −0.0166 | 0.0013 | 0.8855 | 3.94 |
| Wavelengths | Absolute Gain | Total Uncertainty (%) |
|---|---|---|
| 381.01 | 1.1139 | 3.10 |
| 388.41 | 1.1297 | 3.13 |
| 395.82 | 1.1178 | 3.20 |
| 403.23 | 1.0697 | 3.30 |
| 410.64 | 1.0465 | 3.41 |
| 418.05 | 1.0214 | 3.49 |
| 425.47 | 1.0169 | 3.56 |
| 432.89 | 1.0133 | 3.67 |
| 440.32 | 1.0300 | 3.76 |
| 447.74 | 1.0252 | 3.79 |
| 455.17 | 1.0117 | 3.85 |
| 462.60 | 0.9915 | 3.93 |
| 470.03 | 0.9718 | 4.00 |
| 477.46 | 0.9926 | 4.05 |
| 484.90 | 0.9873 | 4.09 |
| 492.33 | 0.9815 | 4.14 |
| 499.77 | 0.9865 | 4.16 |
| 507.21 | 0.9861 | 4.20 |
| 514.65 | 0.9725 | 4.19 |
| 522.09 | 0.9545 | 4.16 |
| 529.53 | 0.9568 | 4.20 |
| 536.98 | 0.9727 | 4.15 |
| 544.42 | 0.9791 | 4.14 |
| 551.87 | 0.9689 | 4.13 |
| 559.31 | 0.9668 | 4.18 |
| 566.76 | 0.9503 | 4.20 |
| 574.21 | 0.9713 | 4.22 |
| 581.66 | 0.9608 | 4.22 |
| 589.11 | 0.9701 | 4.26 |
| 596.56 | 0.9643 | 4.25 |
| 604.01 | 0.9553 | 4.28 |
| 611.46 | 0.9603 | 4.30 |
| 618.91 | 0.9657 | 4.24 |
| 626.37 | 0.9769 | 4.24 |
| 633.82 | 0.9705 | 4.23 |
| 641.28 | 0.9665 | 4.24 |
| 648.73 | 0.9787 | 4.26 |
| 656.19 | 0.9598 | 4.27 |
| 663.64 | 0.9625 | 4.34 |
| 671.10 | 0.9577 | 4.34 |
| 678.55 | 0.9419 | 4.36 |
| 686.01 | 0.9678 | 4.31 |
| 693.47 | 0.9748 | 4.30 |
| 700.93 | 0.9811 | 4.30 |
| 708.38 | 0.9656 | 4.35 |
| 715.84 | 0.9558 | 4.46 |
| 723.30 | 0.9866 | 4.48 |
| 730.76 | 0.9695 | 4.51 |
| 738.22 | 0.9451 | 4.49 |
| 745.68 | 0.9559 | 4.42 |
| 753.14 | 0.9195 | 4.44 |
| 760.60 | 1.0457 | 4.45 |
| 768.06 | 1.0324 | 4.39 |
| 775.52 | 0.9291 | 4.37 |
| 782.98 | 0.9418 | 4.41 |
| 790.44 | 0.9527 | 4.39 |
| 797.90 | 0.9560 | 4.41 |
| 805.36 | 0.9433 | 4.44 |
| 812.82 | 0.9892 | 4.50 |
| 820.28 | 0.9862 | 4.53 |
| 827.75 | 0.9738 | 4.47 |
| 835.21 | 0.9708 | 4.42 |
| 842.67 | 0.9683 | 4.47 |
| 850.13 | 0.9612 | 4.46 |
| 857.59 | 0.9631 | 4.41 |
| 865.06 | 0.9840 | 4.43 |
| 872.52 | 0.9775 | 4.43 |
| 879.98 | 0.9790 | 4.42 |
| 887.44 | 0.9666 | 4.42 |
| 894.90 | 0.9885 | 4.46 |
| 902.37 | 0.9904 | 4.57 |
| 909.83 | 1.0015 | 4.58 |
| 917.29 | 1.0099 | 4.58 |
| 924.75 | 0.9084 | 4.73 |
| 932.22 | 1.1700 | 4.98 |
| 939.68 | 1.0863 | 5.00 |
| 947.14 | 1.0641 | 5.10 |
| 954.60 | 1.0435 | 5.02 |
| 962.06 | 1.0177 | 4.83 |
| 969.53 | 0.9707 | 4.60 |
| 976.99 | 0.9906 | 4.54 |
| 984.45 | 0.9656 | 4.49 |
| 991.91 | 0.9676 | 4.52 |
| 999.37 | 0.9794 | 4.50 |
| 1006.83 | 0.9725 | 4.55 |
| 1014.29 | 0.9699 | 4.62 |
| 1021.76 | 0.9728 | 4.63 |
| 1029.22 | 0.9774 | 4.69 |
| 1036.68 | 0.9721 | 4.55 |
| 1044.14 | 0.9730 | 4.52 |
| 1051.60 | 0.9757 | 4.51 |
| 1059.06 | 0.9796 | 4.54 |
| 1066.52 | 0.9875 | 4.54 |
| 1073.98 | 0.9741 | 4.52 |
| 1081.44 | 0.9719 | 4.53 |
| 1088.90 | 0.9661 | 4.55 |
| 1096.36 | 0.9545 | 4.59 |
| 1103.82 | 0.9563 | 4.66 |
| 1111.28 | 0.9645 | 4.78 |
| 1118.74 | 1.0477 | 5.11 |
| 1126.20 | 1.1340 | 5.28 |
| 1133.66 | 1.0833 | 5.21 |
| 1141.11 | 1.0156 | 5.09 |
| 1148.57 | 1.0938 | 5.06 |
| 1156.03 | 1.0115 | 4.85 |
| 1163.49 | 0.9573 | 4.74 |
| 1170.95 | 0.9612 | 4.61 |
| 1178.40 | 0.9595 | 4.63 |
| 1185.86 | 0.9769 | 4.60 |
| 1193.32 | 0.9487 | 4.64 |
| 1200.78 | 0.9674 | 4.58 |
| 1208.23 | 0.9627 | 4.58 |
| 1215.69 | 0.9645 | 4.59 |
| 1223.15 | 0.9664 | 4.55 |
| 1230.60 | 0.9631 | 4.56 |
| 1238.06 | 0.9594 | 4.55 |
| 1245.52 | 0.9637 | 4.57 |
| 1252.97 | 0.9652 | 4.51 |
| 1260.43 | 0.9922 | 4.48 |
| 1267.88 | 1.0344 | 4.49 |
| 1275.34 | 0.9766 | 4.48 |
| 1282.79 | 0.9587 | 4.45 |
| 1290.25 | 0.8907 | 4.48 |
| 1297.71 | 0.7874 | 4.49 |
| 1305.16 | 0.7223 | 4.52 |
| 1312.61 | 0.7557 | 4.58 |
| 1320.07 | 1.0137 | 4.66 |
| 1327.52 | 1.0077 | 4.78 |
| 1334.98 | 1.0674 | 4.88 |
| 1342.43 | 1.0397 | 5.03 |
| 1349.88 | 1.2917 | 5.31 |
| 1357.34 | 1.9340 | 6.85 |
| 1364.79 | 1.4728 | 11.27 |
| 1372.24 | 1.2496 | 12.29 |
| 1379.69 | 1.3908 | 13.35 |
| 1387.14 | 1.6373 | 13.74 |
| 1394.59 | 1.6862 | 11.06 |
| 1402.04 | 1.7857 | 8.96 |
| 1409.49 | 1.5997 | 5.99 |
| 1416.94 | 1.2959 | 5.96 |
| 1424.39 | 1.1113 | 5.95 |
| 1431.84 | 1.1751 | 5.58 |
| 1439.29 | 1.1797 | 5.96 |
| 1446.74 | 1.1609 | 5.44 |
| 1454.19 | 1.0386 | 5.39 |
| 1461.64 | 1.0472 | 5.20 |
| 1469.08 | 1.1185 | 5.26 |
| 1476.53 | 1.0167 | 5.22 |
| 1483.98 | 1.0495 | 5.07 |
| 1491.43 | 0.9797 | 4.86 |
| 1498.87 | 0.9608 | 4.71 |
| 1506.32 | 0.9592 | 4.56 |
| 1513.76 | 0.9554 | 4.53 |
| 1521.21 | 0.9483 | 4.47 |
| 1528.66 | 0.9542 | 4.47 |
| 1536.10 | 0.9535 | 4.47 |
| 1543.55 | 0.9564 | 4.43 |
| 1550.99 | 0.9468 | 4.44 |
| 1558.43 | 0.9562 | 4.40 |
| 1565.88 | 0.9439 | 4.45 |
| 1573.32 | 0.9771 | 4.47 |
| 1580.76 | 0.9465 | 4.46 |
| 1588.20 | 0.9513 | 4.45 |
| 1595.65 | 0.9413 | 4.40 |
| 1603.09 | 0.9806 | 4.43 |
| 1610.53 | 0.9746 | 4.45 |
| 1617.97 | 0.9435 | 4.44 |
| 1625.41 | 0.9503 | 4.44 |
| 1632.85 | 0.9478 | 4.43 |
| 1640.29 | 0.9494 | 4.44 |
| 1647.73 | 0.9489 | 4.45 |
| 1655.17 | 0.9501 | 4.45 |
| 1662.61 | 0.9664 | 4.42 |
| 1670.05 | 0.9568 | 4.40 |
| 1677.48 | 0.9542 | 4.41 |
| 1684.92 | 0.9559 | 4.39 |
| 1692.36 | 0.9675 | 4.43 |
| 1699.80 | 0.9635 | 4.42 |
| 1707.23 | 0.9639 | 4.44 |
| 1714.67 | 0.9607 | 4.45 |
| 1722.10 | 0.9769 | 4.44 |
| 1729.54 | 0.9739 | 4.43 |
| 1736.97 | 0.9813 | 4.45 |
| 1744.41 | 0.9855 | 4.45 |
| 1751.84 | 0.9671 | 4.47 |
| 1759.27 | 0.9718 | 4.54 |
| 1766.71 | 0.9855 | 4.56 |
| 1774.14 | 0.9719 | 4.65 |
| 1781.57 | 1.0004 | 4.69 |
| 1789.01 | 1.0121 | 4.84 |
| 1796.44 | 1.0168 | 5.13 |
| 1803.87 | 1.2899 | 5.37 |
| 1811.30 | 0.6995 | 23.31 |
| 1818.73 | 0.5283 | 34.82 |
| 1826.16 | 0.4283 | 41.75 |
| 1833.59 | 0.6156 | 43.63 |
| 1841.02 | 0.6672 | 52.31 |
| 1848.45 | 0.6421 | 43.39 |
| 1855.88 | 0.4524 | 39.08 |
| 1863.31 | 0.8536 | 46.46 |
| 1870.73 | 0.6256 | 40.11 |
| 1878.16 | 0.9925 | 56.68 |
| 1885.59 | 0.9802 | 54.71 |
| 1893.01 | 1.1437 | 51.50 |
| 1900.44 | 0.8652 | 48.73 |
| 1907.86 | 0.5373 | 45.81 |
| 1915.29 | 0.5999 | 43.25 |
| 1922.71 | 0.6973 | 39.63 |
| 1930.14 | 0.6677 | 34.60 |
| 1937.56 | 0.7135 | 28.08 |
| 1944.98 | 0.8013 | 21.66 |
| 1952.41 | 0.9634 | 19.16 |
| 1959.83 | 1.0819 | 16.69 |
| 1967.25 | 1.0520 | 5.48 |
| 1974.67 | 0.8590 | 5.41 |
| 1982.09 | 0.8446 | 5.20 |
| 1989.52 | 0.8592 | 5.15 |
| 1996.94 | 0.8476 | 5.27 |
| 2004.35 | 1.5108 | 5.19 |
| 2011.77 | 1.0128 | 5.72 |
| 2019.19 | 1.0805 | 5.24 |
| 2026.61 | 0.9508 | 4.93 |
| 2034.03 | 0.9193 | 4.78 |
| 2041.45 | 0.9232 | 4.82 |
| 2048.86 | 0.9125 | 4.89 |
| 2056.28 | 1.0483 | 4.91 |
| 2063.70 | 0.9436 | 4.95 |
| 2071.11 | 0.9615 | 4.88 |
| 2078.53 | 0.9459 | 4.78 |
| 2085.94 | 0.9522 | 4.74 |
| 2093.36 | 0.9465 | 4.72 |
| 2100.77 | 0.9644 | 4.64 |
| 2108.18 | 0.9691 | 4.61 |
| 2115.59 | 0.9725 | 4.66 |
| 2123.01 | 0.9663 | 4.66 |
| 2130.42 | 0.9647 | 4.69 |
| 2137.83 | 0.9734 | 4.64 |
| 2145.24 | 0.9717 | 4.65 |
| 2152.65 | 1.0009 | 4.66 |
| 2160.06 | 1.0010 | 4.67 |
| 2167.47 | 1.0068 | 4.75 |
| 2174.88 | 1.0045 | 4.71 |
| 2182.28 | 1.0239 | 4.71 |
| 2189.69 | 1.0179 | 4.77 |
| 2197.10 | 1.0245 | 4.74 |
| 2204.50 | 1.0438 | 4.77 |
| 2211.91 | 1.0118 | 4.72 |
| 2219.31 | 1.0090 | 4.73 |
| 2226.72 | 1.0024 | 4.73 |
| 2234.12 | 1.0015 | 4.78 |
| 2241.53 | 1.0003 | 4.69 |
| 2248.93 | 1.0055 | 4.68 |
| 2256.33 | 1.0080 | 4.64 |
| 2263.73 | 1.0070 | 4.62 |
| 2271.14 | 1.0099 | 4.68 |
| 2278.54 | 1.0143 | 4.67 |
| 2285.94 | 1.0153 | 4.70 |
| 2293.34 | 1.0471 | 4.75 |
| 2300.74 | 1.0443 | 4.78 |
| 2308.14 | 0.9974 | 6.11 |
| 2315.53 | 1.0117 | 6.28 |
| 2322.93 | 1.0268 | 6.17 |
| 2330.33 | 0.9967 | 6.23 |
| 2337.73 | 1.0082 | 6.33 |
| 2345.12 | 1.0249 | 6.66 |
| 2352.52 | 1.0618 | 6.83 |
| 2359.91 | 0.9802 | 6.66 |
| 2367.31 | 0.9613 | 7.25 |
| 2374.70 | 0.9693 | 7.36 |
| 2382.09 | 1.0200 | 7.90 |
| 2389.49 | 0.9929 | 8.21 |
| 2396.88 | 0.8909 | 8.75 |
| 2404.27 | 1.0569 | 7.74 |
| 2411.66 | 1.0466 | 11.63 |
| 2419.05 | 1.0307 | 12.80 |
| 2426.44 | 1.0644 | 11.50 |
| 2433.83 | 1.0936 | 11.76 |
| 2441.22 | 1.0601 | 12.54 |
| 2448.61 | 1.1034 | 16.90 |
| 2455.99 | 1.1379 | 14.50 |
| 2463.38 | 1.1933 | 14.82 |
| 2470.77 | 1.2369 | 17.00 |
| 2478.15 | 1.2531 | 20.05 |
| 2485.54 | 1.6195 | 37.06 |
| 2492.92 | 2.0945 | 55.31 |
| Wavelengths | Temporal Coefficients | Absolute Gain | Total Uncertainty (%) | ||
|---|---|---|---|---|---|
| 426.82 | 0.2510 | −0.0015 | 0.0001 | 0.8954 | 10.99 |
| 436.99 | 0.2335 | −0.0018 | 0.0001 | 0.9625 | 10.82 |
| 447.17 | 0.2076 | −0.0018 | 0.0001 | 1.0911 | 10.80 |
| 457.34 | 0.2092 | −0.0020 | 0.0001 | 1.0889 | 10.92 |
| 467.52 | 0.2202 | −0.0020 | 0.0002 | 1.0364 | 10.99 |
| 477.69 | 0.2342 | −0.0022 | 0.0002 | 0.9782 | 11.06 |
| 487.87 | 0.2348 | −0.0020 | 0.0002 | 0.9984 | 11.09 |
| 498.04 | 0.2453 | −0.0021 | 0.0002 | 0.9830 | 11.03 |
| 508.22 | 0.2620 | −0.0021 | 0.0002 | 0.9516 | 10.93 |
| 518.39 | 0.2729 | −0.0021 | 0.0002 | 0.9528 | 10.92 |
| 528.57 | 0.2863 | −0.0024 | 0.0002 | 0.9438 | 10.88 |
| 538.74 | 0.2952 | −0.0023 | 0.0002 | 0.9621 | 10.71 |
| 548.92 | 0.3100 | −0.0021 | 0.0002 | 0.9730 | 10.39 |
| 559.09 | 0.3363 | −0.0017 | 0.0001 | 0.9517 | 9.81 |
| 569.27 | 0.3476 | −0.0010 | 0.0001 | 0.9627 | 9.21 |
| 579.45 | 0.3571 | −0.0003 | 0.0000 | 0.9891 | 8.78 |
| 589.62 | 0.3843 | 0.0005 | −0.0001 | 0.9643 | 8.79 |
| 599.8 | 0.3900 | 0.0013 | −0.0001 | 0.9966 | 8.73 |
| 609.97 | 0.4220 | 0.0013 | −0.0001 | 0.9617 | 8.50 |
| 620.15 | 0.4237 | 0.0018 | −0.0002 | 0.9798 | 8.38 |
| 630.32 | 0.4183 | 0.0019 | −0.0002 | 1.0030 | 8.40 |
| 640.5 | 0.4327 | 0.0021 | −0.0002 | 1.0071 | 8.41 |
| 650.67 | 0.4523 | 0.0027 | −0.0002 | 0.9839 | 8.59 |
| 660.85 | 0.4469 | 0.0026 | −0.0002 | 1.0324 | 8.45 |
| 671.02 | 0.4759 | 0.0022 | −0.0002 | 0.9956 | 8.30 |
| 681.2 | 0.4873 | 0.0021 | −0.0002 | 0.9543 | 8.31 |
| 691.37 | 0.4503 | 0.0019 | −0.0002 | 0.9868 | 8.66 |
| 701.55 | 0.4548 | 0.0033 | −0.0003 | 1.0519 | 9.15 |
| 711.72 | 0.4519 | 0.0041 | −0.0004 | 1.0623 | 9.54 |
| 721.9 | 0.3888 | 0.0061 | −0.0005 | 1.1489 | 13.56 |
| 732.07 | 0.4450 | 0.0051 | −0.0005 | 1.0669 | 11.42 |
| 742.25 | 0.5155 | 0.0030 | −0.0003 | 1.0169 | 8.42 |
| 752.43 | 0.4993 | 0.0019 | −0.0002 | 0.9676 | 8.14 |
| 762.6 | 0.3373 | 0.0009 | −0.0001 | 1.1699 | 8.68 |
| 772.78 | 0.5170 | 0.0021 | −0.0002 | 0.9619 | 8.18 |
| 782.95 | 0.5513 | 0.0028 | −0.0002 | 0.9898 | 8.04 |
| 793.13 | 0.5285 | 0.0038 | −0.0003 | 1.0267 | 8.43 |
| 803.3 | 0.5182 | 0.0043 | −0.0004 | 1.0259 | 8.75 |
| 813.48 | 0.4474 | 0.0061 | −0.0005 | 1.0985 | 11.69 |
| 823.65 | 0.4231 | 0.0065 | −0.0006 | 1.1136 | 12.78 |
| 833.83 | 0.4735 | 0.0054 | −0.0004 | 1.0781 | 10.15 |
| 844 | 0.5479 | 0.0040 | −0.0003 | 0.9957 | 8.24 |
| 854.18 | 0.5800 | 0.0040 | −0.0003 | 0.9609 | 7.96 |
| 864.35 | 0.5681 | 0.0037 | −0.0003 | 0.9868 | 7.91 |
| 874.53 | 0.5596 | 0.0035 | −0.0003 | 1.0023 | 7.94 |
| 884.7 | 0.5462 | 0.0034 | −0.0003 | 1.0079 | 8.11 |
| 894.88 | 0.4735 | 0.0045 | −0.0004 | 1.0359 | 10.98 |
| 905.05 | 0.3928 | 0.0057 | −0.0006 | 1.1171 | 15.63 |
| 912.45 | 0.3826 | 0.0106 | −0.0009 | 1.1346 | 18.54 |
| 922.54 | 0.3557 | 0.0121 | −0.0010 | 1.1474 | 19.33 |
| 932.64 | 0.1446 | 0.0106 | −0.0009 | 1.8698 | 42.30 |
| 942.73 | 0.1444 | 0.0106 | −0.0010 | 1.5324 | 52.30 |
| 952.82 | 0.1740 | 0.0110 | −0.0010 | 1.4757 | 45.29 |
| 962.91 | 0.2976 | 0.0100 | −0.0009 | 1.1743 | 28.40 |
| 972.99 | 0.4110 | 0.0092 | −0.0008 | 1.1028 | 17.08 |
| 983.08 | 0.5059 | 0.0070 | −0.0006 | 1.0195 | 11.80 |
| 993.17 | 0.5852 | 0.0050 | −0.0004 | 0.9729 | 8.64 |
| 1003.3 | 0.5935 | 0.0048 | −0.0004 | 0.9760 | 8.42 |
| 1013.3 | 0.6034 | 0.0049 | −0.0004 | 0.9643 | 8.53 |
| 1023.4 | 0.6076 | 0.0051 | −0.0004 | 0.9942 | 10.95 |
| 1033.49 | 0.6020 | 0.0053 | −0.0004 | 1.0099 | 10.92 |
| 1043.59 | 0.6030 | 0.0053 | −0.0004 | 1.0108 | 10.90 |
| 1053.69 | 0.6000 | 0.0047 | −0.0003 | 1.0078 | 10.91 |
| 1063.79 | 0.5897 | 0.0048 | −0.0003 | 1.0161 | 10.98 |
| 1073.89 | 0.5820 | 0.0056 | −0.0004 | 1.0348 | 11.08 |
| 1083.99 | 0.5595 | 0.0079 | −0.0006 | 1.0720 | 11.63 |
| 1094.09 | 0.4959 | 0.0107 | −0.0008 | 1.1453 | 14.38 |
| 1104.19 | 0.3708 | 0.0136 | −0.0011 | 1.3268 | 22.97 |
| 1114.19 | 0.1562 | 0.0130 | −0.0010 | 2.1281 | 44.27 |
| 1124.28 | 0.0539 | 0.0079 | −0.0007 | 3.7216 | 105.99 |
| 1134.38 | 0.0959 | 0.0092 | −0.0008 | 2.3328 | 76.74 |
| 1144.48 | 0.1077 | 0.0104 | −0.0009 | 2.4675 | 68.67 |
| 1154.58 | 0.2076 | 0.0109 | −0.0010 | 1.6601 | 49.15 |
| 1164.68 | 0.3792 | 0.0115 | −0.0010 | 1.2565 | 26.58 |
| 1174.77 | 0.4439 | 0.0106 | −0.0009 | 1.2035 | 19.00 |
| 1184.87 | 0.4550 | 0.0102 | −0.0008 | 1.2105 | 17.87 |
| 1194.97 | 0.4814 | 0.0098 | −0.0007 | 1.1696 | 15.87 |
| 1205.07 | 0.4915 | 0.0088 | −0.0007 | 1.1633 | 14.71 |
| 1215.17 | 0.5320 | 0.0083 | −0.0006 | 1.1185 | 13.36 |
| 1225.17 | 0.5752 | 0.0072 | −0.0005 | 1.0780 | 11.80 |
| 1235.27 | 0.6143 | 0.0059 | −0.0004 | 1.0374 | 10.96 |
| 1245.36 | 0.6132 | 0.0055 | −0.0003 | 1.0342 | 10.86 |
| 1255.46 | 0.5579 | 0.0052 | −0.0003 | 1.0615 | 11.09 |
| 1265.56 | 0.4804 | 0.0030 | −0.0002 | 1.0980 | 11.45 |
| 1275.66 | 0.5511 | 0.0044 | −0.0003 | 1.0273 | 11.12 |
| 1285.76 | 0.5944 | 0.0064 | −0.0005 | 1.0550 | 11.23 |
| 1295.86 | 0.5418 | 0.0093 | −0.0007 | 1.1442 | 12.94 |
| 1305.96 | 0.4604 | 0.0115 | −0.0009 | 1.2389 | 16.41 |
| 1316.05 | 0.3815 | 0.0119 | −0.0010 | 1.3429 | 21.63 |
| 1326.05 | 0.2713 | 0.0135 | −0.0011 | 1.5998 | 32.76 |
| 1336.15 | 0.1795 | 0.0115 | −0.0010 | 1.8936 | 50.27 |
| 1346.25 | 0.0484 | 0.0058 | −0.0005 | 3.5385 | 78.73 |
| 1356.35 | 0.0010 | 0.0000 | 0.0000 | 23.6373 | 506.22 |
| 1366.45 | 0.0004 | 0.0000 | 0.0000 | 4.8508 | 166.85 |
| 1376.55 | 0.0010 | 0.0001 | 0.0000 | 2.3777 | 241.53 |
| 1386.65 | 0.0009 | 0.0001 | 0.0000 | 4.2248 | 274.85 |
| 1396.74 | 0.0031 | 0.0000 | 0.0000 | 1.8948 | 241.81 |
| 1406.84 | 0.0039 | 0.0001 | 0.0000 | 3.6334 | 226.23 |
| 1416.94 | 0.0050 | 0.0005 | 0.0000 | 6.7435 | 239.28 |
| 1426.94 | 0.0122 | 0.0017 | −0.0001 | 5.4785 | 229.91 |
| 1437.04 | 0.0113 | 0.0018 | −0.0002 | 7.8495 | 1552.27 |
| 1447.14 | 0.0320 | 0.0046 | −0.0004 | 4.3911 | 416.67 |
| 1457.23 | 0.0797 | 0.0081 | −0.0008 | 2.7167 | 106.63 |
| 1467.33 | 0.0591 | 0.0064 | −0.0006 | 3.2464 | 274.82 |
| 1477.43 | 0.0902 | 0.0082 | −0.0008 | 2.5597 | 86.14 |
| 1487.53 | 0.1901 | 0.0097 | −0.0009 | 1.7591 | 54.61 |
| 1497.63 | 0.3416 | 0.0108 | −0.0009 | 1.3460 | 29.18 |
| 1507.73 | 0.4422 | 0.0097 | −0.0008 | 1.2133 | 19.44 |
| 1517.83 | 0.5135 | 0.0086 | −0.0007 | 1.1409 | 14.82 |
| 1527.92 | 0.5722 | 0.0072 | −0.0006 | 1.0830 | 12.29 |
| 1537.92 | 0.6056 | 0.0062 | −0.0005 | 1.0505 | 11.11 |
| 1548.02 | 0.6262 | 0.0056 | −0.0004 | 1.0394 | 10.72 |
| 1558.12 | 0.6269 | 0.0048 | −0.0004 | 1.0433 | 10.53 |
| 1568.22 | 0.5792 | 0.0047 | −0.0003 | 1.0740 | 10.64 |
| 1578.32 | 0.5790 | 0.0033 | −0.0002 | 1.0532 | 10.61 |
| 1588.42 | 0.6198 | 0.0037 | −0.0003 | 1.0387 | 10.38 |
| 1598.51 | 0.5910 | 0.0038 | −0.0003 | 1.0594 | 10.43 |
| 1608.61 | 0.5943 | 0.0028 | −0.0002 | 1.0313 | 10.42 |
| 1618.71 | 0.6390 | 0.0034 | −0.0002 | 1.0164 | 10.22 |
| 1628.81 | 0.6417 | 0.0038 | −0.0003 | 1.0303 | 10.16 |
| 1638.81 | 0.6304 | 0.0036 | −0.0002 | 1.0329 | 10.18 |
| 1648.9 | 0.6286 | 0.0030 | −0.0002 | 1.0275 | 10.21 |
| 1659 | 0.6242 | 0.0035 | −0.0003 | 1.0407 | 10.18 |
| 1669.1 | 0.6259 | 0.0034 | −0.0003 | 1.0405 | 10.15 |
| 1679.2 | 0.6447 | 0.0035 | −0.0003 | 1.0210 | 10.13 |
| 1689.3 | 0.6253 | 0.0045 | −0.0003 | 1.0451 | 10.29 |
| 1699.4 | 0.6035 | 0.0053 | −0.0004 | 1.0666 | 10.59 |
| 1709.5 | 0.5855 | 0.0061 | −0.0005 | 1.0809 | 11.02 |
| 1719.6 | 0.5608 | 0.0069 | −0.0005 | 1.1091 | 11.61 |
| 1729.7 | 0.5326 | 0.0077 | −0.0006 | 1.1383 | 12.52 |
| 1739.7 | 0.5049 | 0.0086 | −0.0007 | 1.1666 | 14.10 |
| 1749.79 | 0.4852 | 0.0092 | −0.0008 | 1.1876 | 15.35 |
| 1759.89 | 0.4399 | 0.0112 | −0.0009 | 1.2597 | 18.55 |
| 1769.99 | 0.3518 | 0.0129 | −0.0011 | 1.4235 | 26.76 |
| 1780.09 | 0.2463 | 0.0126 | −0.0011 | 1.6964 | 38.41 |
| 1790.19 | 0.1465 | 0.0120 | −0.0011 | 2.1630 | 57.49 |
| 1800.29 | 0.0411 | 0.0071 | −0.0006 | 4.3316 | 121.91 |
| 1810.38 | 0.0083 | 0.0020 | −0.0002 | 6.3369 | 223.71 |
| 1820.48 | 0.0054 | 0.0007 | −0.0001 | 1.9486 | 249.95 |
| 1830.58 | 0.0050 | 0.0001 | 0.0000 | 0.4253 | 239.59 |
| 1840.58 | 0.0025 | −0.0001 | 0.0000 | 0.1081 | 210.60 |
| 1850.68 | 0.0021 | −0.0001 | 0.0000 | 0.1036 | 286.98 |
| 1860.78 | 0.0031 | 0.0000 | 0.0000 | 0.1108 | 189.35 |
| 1870.87 | 0.0035 | 0.0000 | 0.0000 | 0.0938 | 193.94 |
| 1880.98 | 0.0014 | −0.0001 | 0.0000 | 0.5886 | 246.64 |
| 1891.07 | 0.0015 | −0.0001 | 0.0000 | 0.7407 | 284.45 |
| 1901.17 | 0.0025 | −0.0002 | 0.0000 | 0.2107 | 283.86 |
| 1911.27 | 0.0025 | −0.0002 | 0.0000 | 0.2382 | 307.22 |
| 1921.37 | 0.0012 | 0.0000 | 0.0000 | 2.0990 | 383.78 |
| 1931.47 | 0.0013 | 0.0000 | 0.0000 | 5.4532 | 566.30 |
| 1941.57 | 0.0096 | 0.0013 | −0.0002 | 3.7841 | 3115.84 |
| 1951.57 | 0.0156 | 0.0024 | −0.0003 | 4.2268 | 1460.41 |
| 1961.66 | 0.0543 | 0.0025 | −0.0003 | 1.9907 | 78.09 |
| 1971.76 | 0.1704 | 0.0076 | −0.0007 | 1.4135 | 43.27 |
| 1981.86 | 0.2764 | 0.0137 | −0.0012 | 1.3216 | 34.09 |
| 1991.96 | 0.2449 | 0.0135 | −0.0011 | 1.3782 | 31.02 |
| 2002.06 | 0.0650 | 0.0011 | −0.0001 | 2.1474 | 33.88 |
| 2012.15 | 0.0793 | −0.0011 | 0.0000 | 1.1616 | 30.83 |
| 2022.25 | 0.2458 | 0.0022 | −0.0003 | 0.9806 | 22.23 |
| 2032.35 | 0.4428 | 0.0068 | −0.0006 | 0.9966 | 16.43 |
| 2042.45 | 0.4253 | 0.0074 | −0.0006 | 1.0666 | 15.68 |
| 2052.45 | 0.2896 | 0.0028 | −0.0003 | 1.1822 | 16.74 |
| 2062.55 | 0.3140 | 0.0033 | −0.0003 | 1.0272 | 16.92 |
| 2072.65 | 0.4009 | 0.0028 | −0.0003 | 0.9735 | 15.22 |
| 2082.75 | 0.5065 | 0.0040 | −0.0004 | 0.9979 | 13.59 |
| 2092.84 | 0.5463 | 0.0054 | −0.0005 | 1.0325 | 13.19 |
| 2102.94 | 0.5635 | 0.0071 | −0.0006 | 1.0630 | 12.96 |
| 2113.04 | 0.5688 | 0.0076 | −0.0006 | 1.0767 | 12.79 |
| 2123.14 | 0.5770 | 0.0067 | −0.0005 | 1.0742 | 12.78 |
| 2133.24 | 0.6030 | 0.0062 | −0.0005 | 1.0513 | 12.27 |
| 2143.34 | 0.5875 | 0.0086 | −0.0006 | 1.0666 | 12.29 |
| 2153.34 | 0.5375 | 0.0095 | −0.0007 | 1.1204 | 13.01 |
| 2163.43 | 0.5246 | 0.0074 | −0.0006 | 1.1212 | 12.69 |
| 2173.53 | 0.5222 | 0.0074 | −0.0006 | 1.1182 | 12.67 |
| 2183.63 | 0.4918 | 0.0110 | −0.0008 | 1.1778 | 13.30 |
| 2193.73 | 0.4769 | 0.0113 | −0.0008 | 1.1703 | 13.37 |
| 2203.83 | 0.4651 | 0.0081 | −0.0006 | 1.1671 | 13.27 |
| 2213.93 | 0.5062 | 0.0092 | −0.0007 | 1.1264 | 13.02 |
| 2224.03 | 0.5144 | 0.0098 | −0.0007 | 1.1296 | 13.39 |
| 2234.12 | 0.5064 | 0.0095 | −0.0007 | 1.1306 | 13.52 |
| 2244.22 | 0.4940 | 0.0079 | −0.0006 | 1.1352 | 14.27 |
| 2254.22 | 0.4818 | 0.0072 | −0.0006 | 1.1289 | 15.26 |
| 2264.32 | 0.4728 | 0.0076 | −0.0006 | 1.1223 | 16.31 |
| 2274.42 | 0.4817 | 0.0061 | −0.0005 | 1.0932 | 17.52 |
| 2284.52 | 0.4642 | 0.0065 | −0.0006 | 1.1194 | 19.15 |
| 2294.61 | 0.4159 | 0.0093 | −0.0008 | 1.2069 | 20.96 |
| 2304.71 | 0.4497 | 0.0082 | −0.0007 | 1.1081 | 22.06 |
| 2314.81 | 0.3951 | 0.0145 | −0.0011 | 1.2189 | 23.62 |
| 2324.91 | 0.3932 | 0.0164 | −0.0012 | 1.2132 | 25.53 |
| 2335.01 | 0.3610 | 0.0189 | −0.0013 | 1.2831 | 27.03 |
| 2345.11 | 0.2877 | 0.0192 | −0.0014 | 1.4367 | 29.30 |
| 2355.21 | 0.3086 | 0.0173 | −0.0013 | 1.3362 | 27.73 |
| 2365.2 | 0.2937 | 0.0192 | −0.0014 | 1.3239 | 27.18 |
| 2375.3 | 0.2392 | 0.0166 | −0.0013 | 1.4274 | 33.02 |
| 2385.4 | 0.2247 | 0.0177 | −0.0014 | 1.5928 | 40.53 |
| 2395.5 | 0.2569 | 0.0196 | −0.0015 | 1.3768 | 37.70 |
References
- Tatem, J. Andrew Fifty Years of Earth–Observation Satellites. Available online: https://www.americanscientist.org/article/fifty-years-of-earth-observation-satellites (accessed on 4 September 2024).
- Envisat and Some Principles of Earth–Observing Satellites. Available online: https://www.esa.int/Applications/Observing_the_Earth/Envisat_and_some_principles_of_Earth-observing_satellites (accessed on 9 September 2024).
- Sentinels Helping to Map Minerals. Available online: https://www.esa.int/Applications/Observing_the_Earth/Sentinels_helping_to_map_minerals (accessed on 4 September 2024).
- Wu, Z.; Snyder, G.; Vadnais, C.; Arora, R.; Babcock, M.; Stensaas, G.; Doucette, P.; Newman, T. User Needs for Future Landsat Missions. Remote Sens. Environ. 2019, 231, 111214. [Google Scholar] [CrossRef]
- Lu, B.; Dao, P.D.; Liu, J.; He, Y.; Shang, J. Recent Advances of Hyperspectral Imaging Technology and Applications in Agriculture. Remote Sens. 2020, 12, 2659. [Google Scholar] [CrossRef]
- Thenkabail, S.P. Hyperspectral Remote Sensing of Vegetation; CRC Press: Boca Raton, FL, USA, 2016; ISBN 9781439845387. [Google Scholar]
- The Power of Temporal Resolution in Satellite Earth Observation: Understanding and Applications. Available online: https://ongeo-intelligence.com/blog/temporal-resolution-in-satellite-earth-observation (accessed on 14 December 2024).
- Kogut, P. Multispectral vs. Hyperspectral: Choose The Right Tech. Available online: https://eos.com/blog/multispectral-vs-hyperspectral-imaging/ (accessed on 7 November 2024).
- Hyperspectral Imaging from Space. Available online: https://gisgeography.com/hyperspectral-imaging/ (accessed on 22 May 2023).
- Kabir, S.; Leigh, L.; Helder, D. Vicarious Methodologies to Assess and Improve the Quality of the Optical Remote Sensing Images: A Critical Review. Remote Sens. 2020, 12, 4029. [Google Scholar] [CrossRef]
- Pinto, C.; Ponzoni, F.; Castro, R.; Leigh, L.; Mishra, N.; Aaron, D.; Helder, D. First In–Flight Radiometric Calibration of MUX and WFI on–Board CBERS–4. Remote Sens. 2016, 8, 405. [Google Scholar] [CrossRef]
- Bouvet, M.; Thome, K.; Berthelot, B.; Bialek, A.; Czapla–Myers, J.; Fox, N.P.; Goryl, P.; Henry, P.; Ma, L.; Marcq, S.; et al. RadCalNet: A Radiometric Calibration Network for Earth Observing Imagers Operating in the Visible to Shortwave Infrared Spectral Range. Remote Sens. 2019, 11, 2401. [Google Scholar] [CrossRef]
- Czapla–Myers, J.S.; Thome, K.J.; Anderson, N.J.; Leigh, L.M.; Pinto, C.T.; Wenny, B.N. The Ground–Based Absolute Radiometric Calibration of the Landsat 9 Operational Land Imager. Remote Sens. 2024, 16, 1101. [Google Scholar] [CrossRef]
- Fan, L.; Jiang, Z.; Yu, S.; Liu, Y.; Wang, D.; Chen, M. A General On–Orbit Absolute Radiometric Calibration Method Compatible with Multiple Imaging Conditions. Remote Sens. 2024, 16, 3503. [Google Scholar] [CrossRef]
- Pinto, C.T.; Ponzoni, F.J.; Castro, R.M.; Leigh, L.; Kaewmanee, M.; Aaron, D.; Helder, D. Evaluation of the Uncertainty in the Spectral Band Adjustment Factor (SBAF) for Cross–Calibration Using Monte Carlo Simulation. Remote Sens. Lett. 2016, 7, 837–846. [Google Scholar] [CrossRef]
- Mishra, N.; Haque, M.O.; Leigh, L.; Aaron, D.; Helder, D.; Markham, B. Radiometric Cross Calibration of Landsat 8 Operational Land Imager (OLI) and Landsat 7 Enhanced Thematic Mapper plus (ETM+). Remote Sens. 2014, 6, 12619–12638. [Google Scholar] [CrossRef]
- Farhad, M.M.; Kaewmanee, M.; Leigh, L.; Helder, D. Radiometric Cross Calibration and Validation Using 4 Angle BRDF Model between Landsat 8 and Sentinel 2A. Remote Sens. 2020, 12, 806. [Google Scholar] [CrossRef]
- EO–1. Available online: https://www.eoportal.org/satellite-missions/eo-1#hyperion (accessed on 8 August 2023).
- Earth Observing 1: General Questions and Answers. Available online: https://www.usgs.gov/centers/eros/earth-observing-1-general-questions-and-answers (accessed on 8 August 2023).
- Middleton, E.M.; Ungar, S.G.; Mandl, D.J.; Ong, L.; Frye, S.W.; Campbell, P.E.; Landis, D.R.; Young, J.P.; Pollack, N.H. The Earth Observing One (EO–1) Satellite Mission: Over a Decade in Space. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 243–256. [Google Scholar] [CrossRef]
- Franks, S.; Neigh, C.S.R.; Campbell, P.K.; Sun, G.; Yao, T.; Zhang, Q.; Huemmrich, K.F.; Middleton, E.M.; Ungar, S.G.; Frye, S.W. EO–1 Data Quality and Sensor Stability with Changing Orbital Precession at the End of a 16 Year Mission. Remote Sens. 2017, 9, 412. [Google Scholar] [CrossRef] [PubMed]
- Czapla–Myers, J.; Ong, L.; Thome, K.; McCorkel, J. Validation of EO–1 Hyperion and Advanced Land Imager Using the Radiometric Calibration Test Site at Railroad Valley, Nevada. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 816–826. [Google Scholar] [CrossRef]
- Jing, X.; Leigh, L.; Helder, D.; Teixeira Pinto, C.; Aaron, D. Lifetime Absolute Calibration of the EO–1 Hyperion Sensor and Its Validation. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9466–9475. [Google Scholar] [CrossRef]
- Khadka, N.; Pinto, C.T.; Leigh, L. Detection of Change Points in Pseudo–Invariant Calibration Sites Time Series Using Multi–Sensor Satellite Imagery. Remote Sens. 2021, 13, 2079. [Google Scholar] [CrossRef]
- ISS: MUSES (Multi–User System for Earth Sensing). Available online: https://www.eoportal.org/satellite-missions/iss-muses (accessed on 24 April 2024).
- ISS: EMIT (Earth Surface Mineral Dust Source InvesTigation). Available online: https://www.eoportal.org/satellite-missions/iss-emit#mission-capabilities (accessed on 24 April 2024).
- Satellite Missions Catalogue. Available online: https://www.eoportal.org/satellite-missions (accessed on 4 January 2024).
- DESIS. Available online: https://www.tbe.com/what-we-do/markets/space/geospatial-solutions/desis (accessed on 14 February 2024).
- EMIT. Available online: https://earth.jpl.nasa.gov/emit/instrument/specifications/ (accessed on 24 April 2024).
- Fajardo Rueda, J.; Leigh, L.; Teixeira Pinto, C. Identification of Global Extended Pseudo Invariant Calibration Sites (EPICS) and Their Validation Using Radiometric Calibration Network (RadCalNet). Remote Sens. 2024, 16, 4129. [Google Scholar] [CrossRef]
- Alonso, K.; Bachmann, M.; Burch, K.; Carmona, E.; Cerra, D.; de los Reyes, R.; Dietrich, D.; Heiden, U.; Hölderlin, A.; Ickes, J.; et al. Data Products, Quality and Validation of the DLR Earth Sensing Imaging Spectrometer (DESIS). Sensors 2019, 19, 4471. [Google Scholar] [CrossRef]
- Shrestha, M.; Helder, D.; Christopherson, J. Dlr Earth Sensing Imaging Spectrometer (Desis) Level 1 Product Evaluation Using Radcalnet Measurements. Remote Sens. 2021, 13, 2420. [Google Scholar] [CrossRef]
- Calcon. Cross Comparison of DESIS with Landsat 8 OLI and Sentinel 2A MSI; Calcon: Logan, UT, USA, 2020. [Google Scholar]
- Shrestha, M.; Sampath, A.; Ramaseri Chandra, S.N.; Christopherson, J.B.; Shaw, J.; Anderson, C. Open–File System Characterization Report on the German Aerospace Center (DLR) Earth Sensing Imaging Spectrometer (DESIS); System Characterization of Earth Observation Sensors; U.S. Geological Survey: Reston, VA, USA, 2021.
- Carmona, E.; Alonso, K.; Bachmann, M.; Burch, K.; Cerra, D.; De Los, R.; Lopez, R.; Heiden, U.; Knodt, U.; Krutz, D.; et al. Vicarious Calibration of the DESIS Imaging Spectrometer. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021. [Google Scholar]
- Thompson, D.R.; Green, R.O.; Bradley, C.; Brodrick, P.G.; Mahowald, N.; Ben Dor, E.; Bennett, M.; Bernas, M.; Carmon, N.; Chadwick, K.D.; et al. On–Orbit Calibration and Performance of the EMIT Imaging Spectrometer. Remote Sens. Environ. 2024, 303, 113986. [Google Scholar] [CrossRef]
- Green, R.O.; Mahowald, N.; Thompson, D.R.; Ung, C.; Brodrick, P.; Pollock, R.; Bennett, M.; Lundeen, S.; Joyce, M.; Olson–Duvall, W.; et al. Performance and Early Results from the Earth Surface Mineral Dust Source Investigation (EMIT) Imaging Spectroscopy Mission. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2023; IEEE Computer Society: Washington, DC, USA, 2023. [Google Scholar]
- McCorkel, J.; Thome, K.; Ong, L. Vicarious Calibration of Eo–1 Hyperion. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 400–407. [Google Scholar] [CrossRef]
- Landsat Satellite Missions. Available online: https://www.usgs.gov/landsat-missions/landsat-satellite-missions (accessed on 28 November 2024).
- Landsat 7. Available online: https://www.usgs.gov/landsat-missions/landsat-7 (accessed on 19 February 2024).
- Landsat 8. Available online: https://www.usgs.gov/landsat-missions/landsat-8 (accessed on 19 February 2024).
- Landsat 7 Maneuvers. Available online: https://www.usgs.gov/landsat-missions/landsat-7-maneuvers (accessed on 18 February 2024).
- Fajardo Rueda, J.; Leigh, L.; Pinto, C.T. A Global Mosaic of Temporally Stable Pixels for Radiometric Calibration of Optical Satellite Sensors Using Landsat 8. Remote Sens. 2024, 16, 2437. [Google Scholar] [CrossRef]
- Czapla–Myers. RadCalNet Site Description: CEOS Reference: QA4EO–WGCV–RadCalNet–RVUS–Q–V2; Tucson, AZ, USA, 2022. [Google Scholar]
- Landier, L. RadCalNet Site Description: CEOS Reference: QA4EO–WGCV–RadCalNet–LCFR–Q–V3; Beijing, China, 2022. [Google Scholar]
- Ma, L. RadCalNet Site Description: CEOS Reference: QA4EO–WGCV–RadCalNet–BSCN–Q–V3; Toulouse, France, 2022. [Google Scholar]
- Bialek, A.; Sinclair, M. RadCalNet Site Description: CEOS Reference: QA4EO–WGCV–RadCalNet–GONA–Q–V2; Teddington, UK, 2022. [Google Scholar]
- Radiometric Calibration Network Portal. Available online: https://www.radcalnet.org/ (accessed on 4 February 2025).
- RadCalNet Data Format Specification:CEOS Reference:QA4EO–WGCV–RadCalNet–R2, 2019.
- Lake Tahoe: Test Sites Catalog. Available online: https://calval.cr.usgs.gov/apps/lake-tahoe (accessed on 4 February 2025).
- McCorkel, J.; Bachmann, C.M.; Coburn, C.; Gerace, A.; Leigh, L.; Czapla–Myers, J.; Helder, D.; Cook, B. Overview of the 2015 Algodones Sand Dunes Field Campaign to Support Sensor Intercalibration. J. Appl. Remote Sens. 2017, 12, 012003. [Google Scholar] [CrossRef]
- Pathiranage, D.S.; Leigh, L.; Pinto, C.T. Evaluation of Low–Cost Radiometer for Surface Reflectance Retrieval and Orbital Sensor’s Validation. Remote Sens. 2023, 15, 2444. [Google Scholar] [CrossRef]
- Libya 4: Test Sites Catalog. Available online: https://calval.cr.usgs.gov/apps/libya-4 (accessed on 4 February 2025).
- Shaw, J.A.; Nugent, P.W. Physics Principles in Radiometric Infrared Imaging of Clouds in the Atmosphere. Eur. J. Phys. 2013, 34, S111. [Google Scholar] [CrossRef]
- Landsat 8–9 Operational Land Imager (OLI)—Thermal Infrared Sensor (TIRS) Collection 2 Level 1 (L1) Data Format Control Book (DFCB). 2020. Available online: https://d9-wret.s3.us-west-2.amazonaws.com/assets/palladium/production/s3fs-public/atoms/files/LSDS-1822_Landsat8-9-OLI-TIRS-C2-L1-DFCB-v6.pdf (accessed on 2 May 2024).
- Thuillier, G.; Hersé, M.; Labs, D.; Foujols, T.; Peetermans, W.; Gillotay, D.; Simon, P.C.; Mandel, H. The Solar Spectral Irradiance from 200 to 2400 nm as Measured by the SOLSPEC Spectrometer from the Atlas and Eureca Missions. Sol. Phys. 2003, 214, 1–22. [Google Scholar]
- Fajardo Rueda, J.; Leigh, L.; Kaewmanee, M.; Byregowda, H.; Teixeira Pinto, C. Derivation of Hyperspectral Profiles for Global Extended Pseudo Invariant Calibration Sites (EPICS) and Their Application in Satellite Sensor Cross–Calibration. Remote Sens. 2025, 17, 216. [Google Scholar] [CrossRef]
- Uncertainty of Measurement–Part 3: Guide to the Expression of Uncertainty in Measurement (GUM:1995) Copyright Protected Document ISO/IEC GUIDE 98–3:2008(E). Available online: https://www.bsigroup.com/contentassets/fb7f1499fa6f43c6b9084be8c2378bc9/iso_iec_guide_98-3_2008_suppl_1_2008e---propagation-of-distributions-using-a-monte-carlo-method.pdf (accessed on 25 January 2024).
- Freund, R.J.; Wilson, W.J. Statistical Methods; Elsevier: Amsterdam, The Netherlands, 2003; ISBN 0080498221. [Google Scholar]
- Mohr, D.L. Statistical Methods; Academic Press: New York, NY, USA, 2010; ISBN 0080961037. [Google Scholar]
- Ott, R.L.; Longnecker, M. An Introduction to Statistical Methods and Data Analysis; Cengaaage Learning: Boston, MA, USA, 2015; ISBN 978-1305269477. [Google Scholar]
- Bruegge, C.J.; Coburn, C.; Elmes, A.; Helmlinger, M.C.; Kataoka, F.; Kuester, M.; Kuze, A.; Ochoa, T.; Schaaf, C.; Shiomi, K.; et al. Bi–Directional Reflectance Factor Determination of the Railroad Valley Playa. Remote Sens. 2019, 11, 2601. [Google Scholar] [CrossRef]
- Lu, Z.; Yuan, K.-H. Welch’s t Test. In Encyclopedia of Research Design; Sage: Thousand Oaks, CA, USA, 2010; pp. 1620–1623. [Google Scholar]

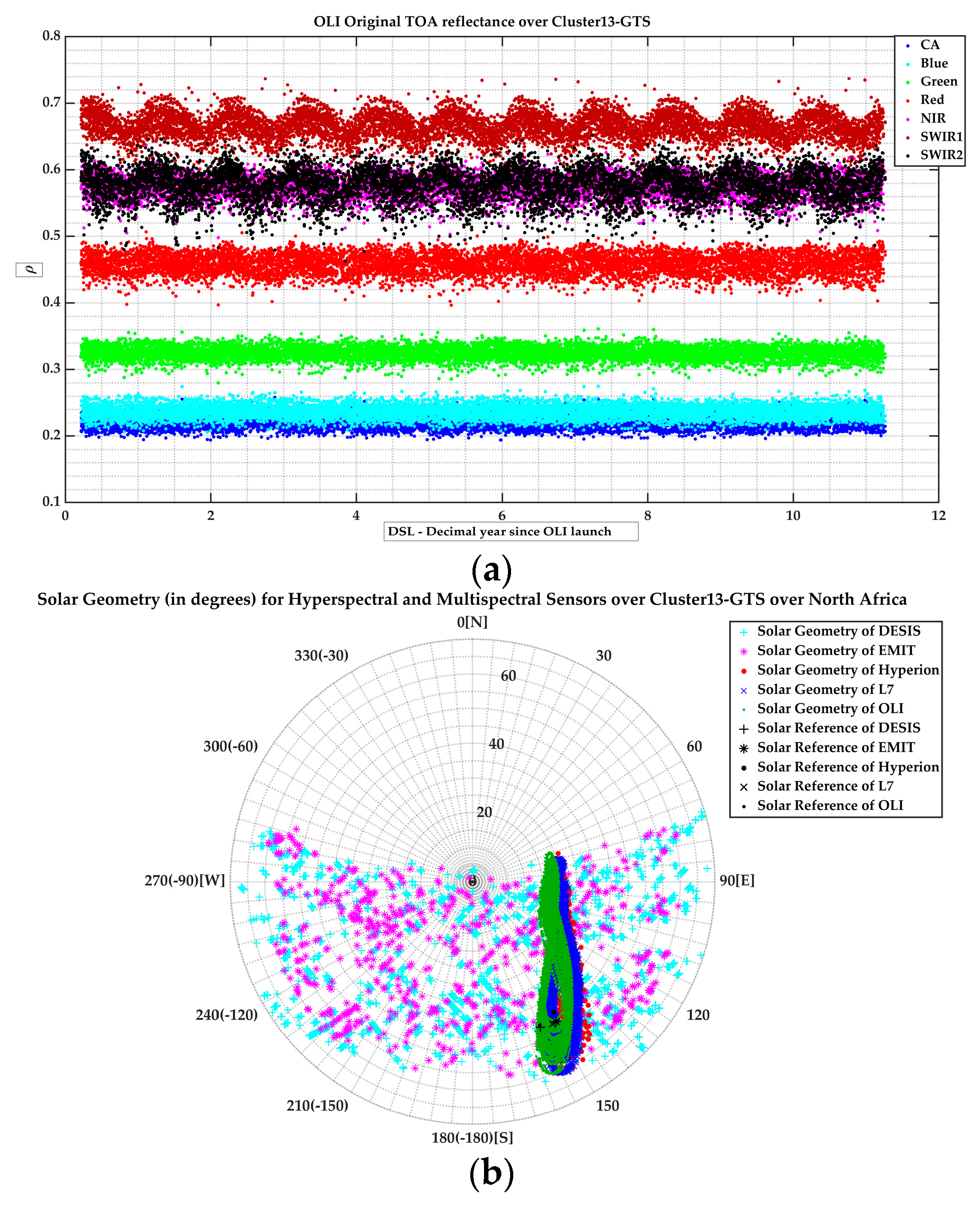
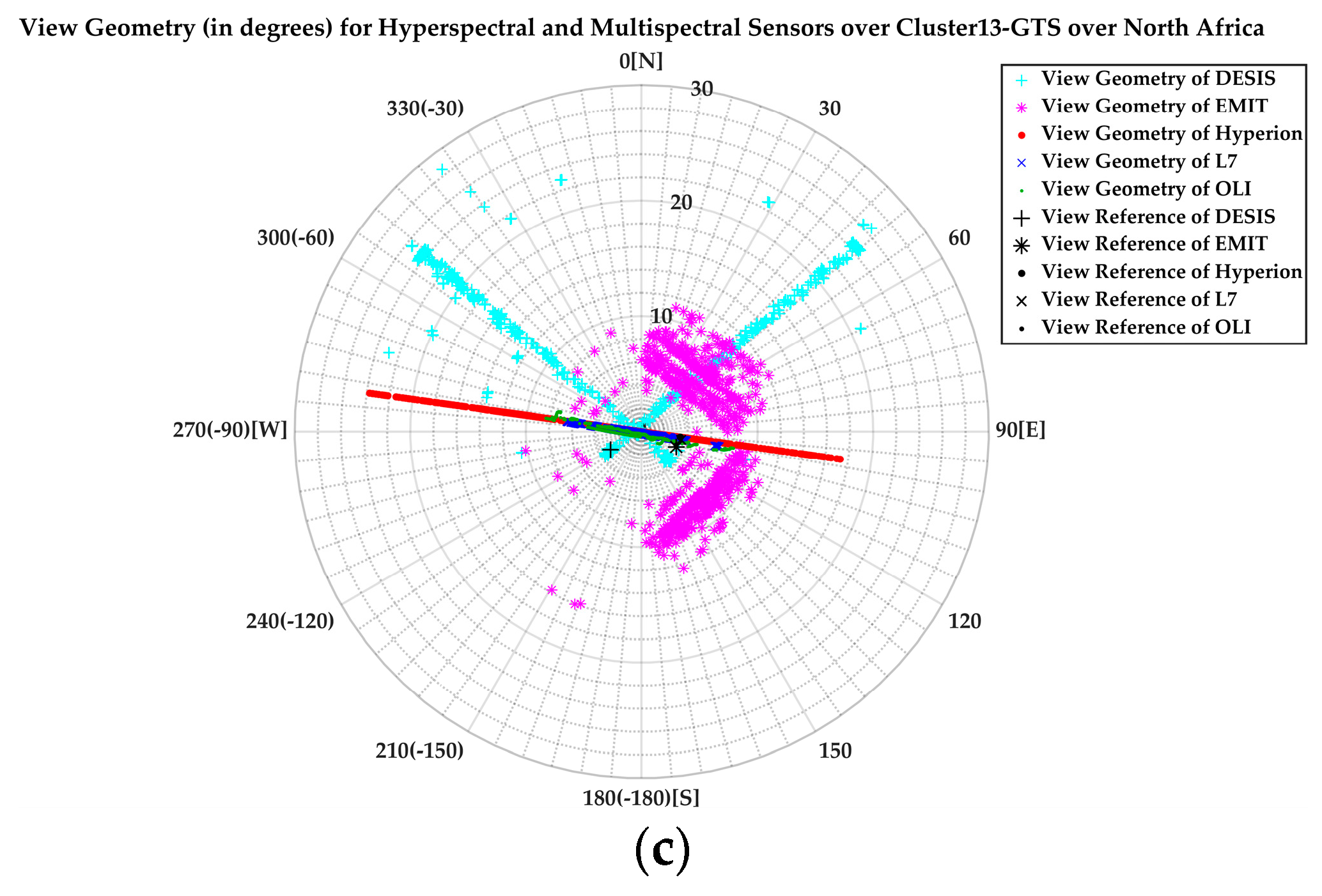









| Sensors/Angles | Solar Azimuth (SAA) | Solar Zenith (SZA) | View Azimuth (VAA) | View Zenith (VZA) |
|---|---|---|---|---|
| DESIS | 154.9° | 46.2° | −120.3° | 3.1° |
| EMIT | 149° | 46.9° | 113.7° | 3.3° |
| Hyperion | 147.9° | 44.3° | 98° | 3.4° |
| ETM+ | 150.6° | 47° | 101.7° | 3.5° |
| OLI | 154.8° | 45.6° | 111.1° | 3.2° |
| Dates/Sites | RVUS | BSCN | GONA | LCFR |
|---|---|---|---|---|
| Coinciding | 13 | 4 | 19 | 6 |
| Near Coinciding | 7 | 1 | 8 | 6 |
| Total | 20 | 5 | 27 | 12 |
| Sites | RVUS | BSCN | LCFR | Lake Tahoe (LT) | Algodones Dunes (AD) | SDSU |
|---|---|---|---|---|---|---|
| Dates | 7 | 1 | 3 | 3 | 1 | 2 |
| Band | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|
| SBAF | 1.0025 | 0.9977 | 0.9915 | 1.0832 | 1.0083 | 1.0657 |
| Scaling Factor | 0.9983 | 0.9830 | 0.9876 | 0.9990 | 1.0097 | 0.9792 |
| Uncertainty Sources (%) | Sensor | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|---|
| Cluster Uncertainty | ETM+ | – | 4.7159 | 2.8821 | 3.7549 | 3.5434 | 3.6418 | 4.8787 |
| OLI | 4.2456 | 4.2348 | 3.1057 | 3.3724 | 2.9888 | 3.2714 | 4.4229 | |
| BRDF | ETM+ | – | 2.6950 | 1.5944 | 1.9861 | 1.7830 | 1.8928 | 2.7666 |
| OLI | 2.2604 | 2.2949 | 1.7633 | 1.8990 | 1.7958 | 1.8948 | 2.7576 | |
| Sensor’s Uncertainty | ETM+ | – | 5 | 5 | 5 | 5 | 5 | 5 |
| OLI | 3 | 3 | 3 | 3 | 3 | 3 | 3 | |
| SBAF | ETM+ | – | 0.4958 | 0.5115 | 0.6782 | 1.0822 | 0.9482 | 0.6462 |
| Total Uncertainty | ETM+ | – | 7.3992 | 6.0092 | 6.5957 | 6.4735 | 6.5379 | 7.5414 |
| OLI | 5.6687 | 5.6745 | 4.6642 | 4.8969 | 4.5997 | 4.8262 | 6.0138 |
| Time Frame (Sensor) | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | |
|---|---|---|---|---|---|---|---|---|
| 1999–2012 (ETM+) | Slope +/− std | – | −9.09 × 10−5 +/− 1.65 × 10−4 | −3.34 × 10−5 +/− 1.93 × 10−4 | 3.30 × 10−4 +/− 2.94 × 10−4 | 4.31 × 10−4 +/− 3.52 × 10−4 | 6.18 × 10−4 +/− 4.06 × 10−4 | 7.29 × 10−4 +/− 4.28 × 10−4 |
| p–value | – | 0.5825 | 0.8629 | 0.2622 | 0.2207 | 0.1276 | 0.0885 | |
| 2013–2024 (OLI) | Slope +/− std | 1.17 × 10−5 +/− 8.46 × 10−5 | −5.74 × 10−6 +/− 8.97 × 10−5 | −1.10 × 10−4 +/− 9.92 × 10−5 | −5.39 × 10−5 +/− 1.48 × 10−4 | −1.12 × 10−4 +/− 1.77 × 10−4 | −2.32 × 10−4 +/− 2.14 × 10−4 | −1.44 × 10−4 +/− 2.28 × 10−4 |
| p–value | 0.8898 | 0.9490 | 0.2680 | 0.7167 | 0.5253 | 0.2803 | 0.5270 |
| Criteria | Models | CA | Blue | Green | Red | NIR |
|---|---|---|---|---|---|---|
| Residual Standard Error | Linear | 0.2967 | 0.3306 | 0.3281 | 0.3485 | 0.3474 |
| Exponential | 1.349 | 1.355 | 0.9443 | 0.7366 | 0.6028 | |
| poly2 | 0.275 | 0.3282 | 0.3282 | 0.3481 | 0.3474 | |
| poly4 | 0.2745 | 0.3282 | 0.3274 | 0.3475 | 0.3452 | |
| F–statistics | Linear | 640.8 | 170.3 | 99.94 | 38.03 | 61.6 |
| Exponential | 629.8 | 171.6 | 98.77 | 35.79 | 58.01 | |
| poly2 | 505.8 | 98.71 | 50.3 | 21.53 | 31.28 | |
| poly4 | 255.8 | 49.81 | 27.6 | 12.54 | 21.52 | |
| p–value for F–statistics | Linear | 2.20 × 10−16 | 2.20 × 10−16 | 2.20 × 10−16 | 8.77 × 10−10 | 7.58 × 10−15 |
| Exponential | 2.20 × 10−16 | 2.20 × 10−16 | 2.20 × 10−16 | 2.70 × 10−9 | 4.42 × 10−14 | |
| poly2 | 2.20 × 10−16 | 2.20 × 10−16 | 2.20 × 10−16 | 5.91 × 10−10 | 4.69 × 10−14 | |
| poly4 | <2.2 × 10−16 | <2.2 × 10−16 | <2.2 × 10−16 | 4.79 × 10−10 | <2.2 × 10−16 | |
| Significance of coefficients | Linear | Constant | Constant | Constant | All | All |
| Exponential | Constant | Constant | All | All | All | |
| poly2 | All | All | Constant, 1st order term | Constant, 2nd order term | Constant term | |
| poly4 | All | All | All | Constant, 1st term | All |
| Criteria | Models | CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 |
|---|---|---|---|---|---|---|---|---|
| Residual Standard Error | Linear | 0.3605 | 0.3847 | 0.387 | 0.42 | 0.4034 | 0.3725 | 0.4169 |
| Exponential | 1.715 | 1.703 | 1.188 | 0.903 | 0.6943 | 0.5811 | 0.7634 | |
| poly2 | 0.3578 | 0.3815 | 0.3883 | 0.4114 | 0.3947 | 0.3672 | 0.394 | |
| Logarithmic | 0.3599 | 0.385 | 0.3892 | 0.4211 | 0.4025 | 0.3712 | 0.4135 | |
| Linear–Log | 0.3572 | 0.3807 | 0.3868 | 0.4142 | 0.3995 | 0.3701 | 0.3945 | |
| poly2–Log | 0.3575 | 0.381 | 0.3866 | 0.4116 | 0.3932 | 0.3664 | 0.3932 | |
| F–statistics | Linear | 0.1996 | 1.003 | 0.1266 | 3.285 | 0.6146 | 5.045 | 0.8116 |
| Exponential | 0.1064 | 1.274 | 0.0581 | 2.998 | 0.7239 | 5.315 | 0.9911 | |
| poly2 | 5.068 | 5.98 | 2.675 | 14.89 | 14.24 | 11.67 | 36.86 | |
| Logarithmic | 2.157 | 0.02011 | 1.665 | 0.2207 | 3.311 | 9.156 | 11 | |
| Linear–Log | 6.22 | 7.314 | 5.16 | 10.63 | 6.742 | 6.844 | 36 | |
| poly2–Log | 4.142 | 4.869 | 3.948 | 10.09 | 11.48 | 9.014 | 25.82 | |
| p–value for F–statistics | Linear | 0.6552 | 0.317 | 0.7221 | 0.07043 | 0.4334 | 0.02505 | 0.368 |
| Exponential | 0.7444 | 0.2594 | 0.8096 | 0.08386 | 0.3952 | 0.02149 | 0.3199 | |
| poly2 | 0.00657 | 0.002681 | 0.06975 | 4.89 × 10−7 | 9.05 × 10−7 | 1.06 × 10−5 | 8.03 × 10−16 | |
| Logarithmic | 0.1425 | 0.8873 | 0.1974 | 0.6387 | 0.0693 | 0.002586 | 0.000964 | |
| Linear–Log | 0.00212 | 0.000727 | 0.006002 | 2.92 × 10−5 | 0.001272 | 0.001151 | 1.73 × 10−15 | |
| poly2–Log | 0.0064 | 0.00236 | 0.008336 | 1.72 × 10−6 | 2.51 × 10−7 | 7.60 × 10−6 | 1.03 × 10−15 | |
| Significance of coefficients | Linear | Constant | Constant | Constant | Constant | Constant | All | Constant |
| Exponential | Constant | Constant | Constant | Constant | Constant | Constant | Constant | |
| poly2 | All | All | All | All | All | All | All | |
| Logarithmic | Constant | Constant | Constant | Constant | Constant | All | All | |
| Linear–Log | All | All | All | All | All | All | All | |
| poly2–Log | Constant | Constant | Constant, Log–term | All except Log–term | All | All except Log–term | Constant, 2nd order term |
| Sensors | p–Value | ||||||
|---|---|---|---|---|---|---|---|
| CA | Blue | Green | Red | NIR | SWIR1 | SWIR2 | |
| OLI vs. DESIS | 0.9944 | 0.9949 | 0.9951 | 0.9962 | 0.9950 | – | – |
| OLI vs. EMIT | 0.9916 | 0.9907 | 0.9920 | 0.9921 | 0.9913 | 0.9907 | 0.9926 |
| OLI vs. Hyperion | 0.9908 | 0.9921 | 0.9918 | 0.9957 | 0.9907 | 0.9905 | 0.9923 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Adrija, H.M.; Leigh, L.; Kaewmanee, M.; Pathiranage, D.S.; Fajardo Rueda, J.; Aaron, D.; Teixeira Pinto, C. Absolute Vicarious Calibration, Extended PICS (EPICS) Based De-Trending and Validation of Hyperspectral Hyperion, DESIS, and EMIT. Remote Sens. 2025, 17, 1301. https://doi.org/10.3390/rs17071301
Adrija HM, Leigh L, Kaewmanee M, Pathiranage DS, Fajardo Rueda J, Aaron D, Teixeira Pinto C. Absolute Vicarious Calibration, Extended PICS (EPICS) Based De-Trending and Validation of Hyperspectral Hyperion, DESIS, and EMIT. Remote Sensing. 2025; 17(7):1301. https://doi.org/10.3390/rs17071301
Chicago/Turabian StyleAdrija, Harshitha Monali, Larry Leigh, Morakot Kaewmanee, Dinithi Siriwardana Pathiranage, Juliana Fajardo Rueda, David Aaron, and Cibele Teixeira Pinto. 2025. "Absolute Vicarious Calibration, Extended PICS (EPICS) Based De-Trending and Validation of Hyperspectral Hyperion, DESIS, and EMIT" Remote Sensing 17, no. 7: 1301. https://doi.org/10.3390/rs17071301
APA StyleAdrija, H. M., Leigh, L., Kaewmanee, M., Pathiranage, D. S., Fajardo Rueda, J., Aaron, D., & Teixeira Pinto, C. (2025). Absolute Vicarious Calibration, Extended PICS (EPICS) Based De-Trending and Validation of Hyperspectral Hyperion, DESIS, and EMIT. Remote Sensing, 17(7), 1301. https://doi.org/10.3390/rs17071301






