Optimization of Multi-Source Remote Sensing Soil Salinity Estimation Based on Different Salinization Degrees
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Materials
2.2.1. Field Sampling and Soil Salinity Measurement
2.2.2. Acquisition of Remote Sensing Data
- (1)
- Satellite imagery
- (2)
- In situ hyperspectral data
2.3. Methods
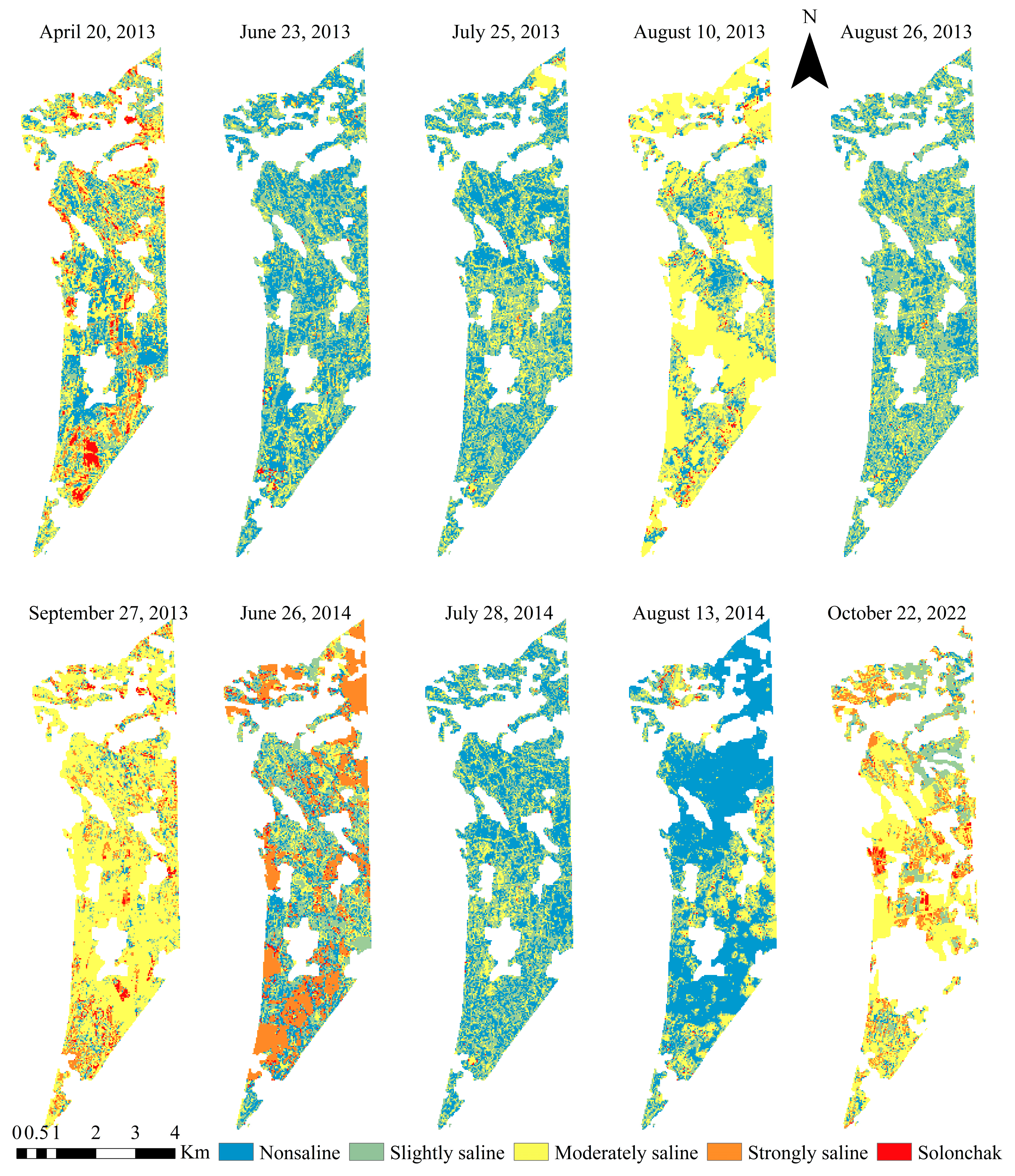
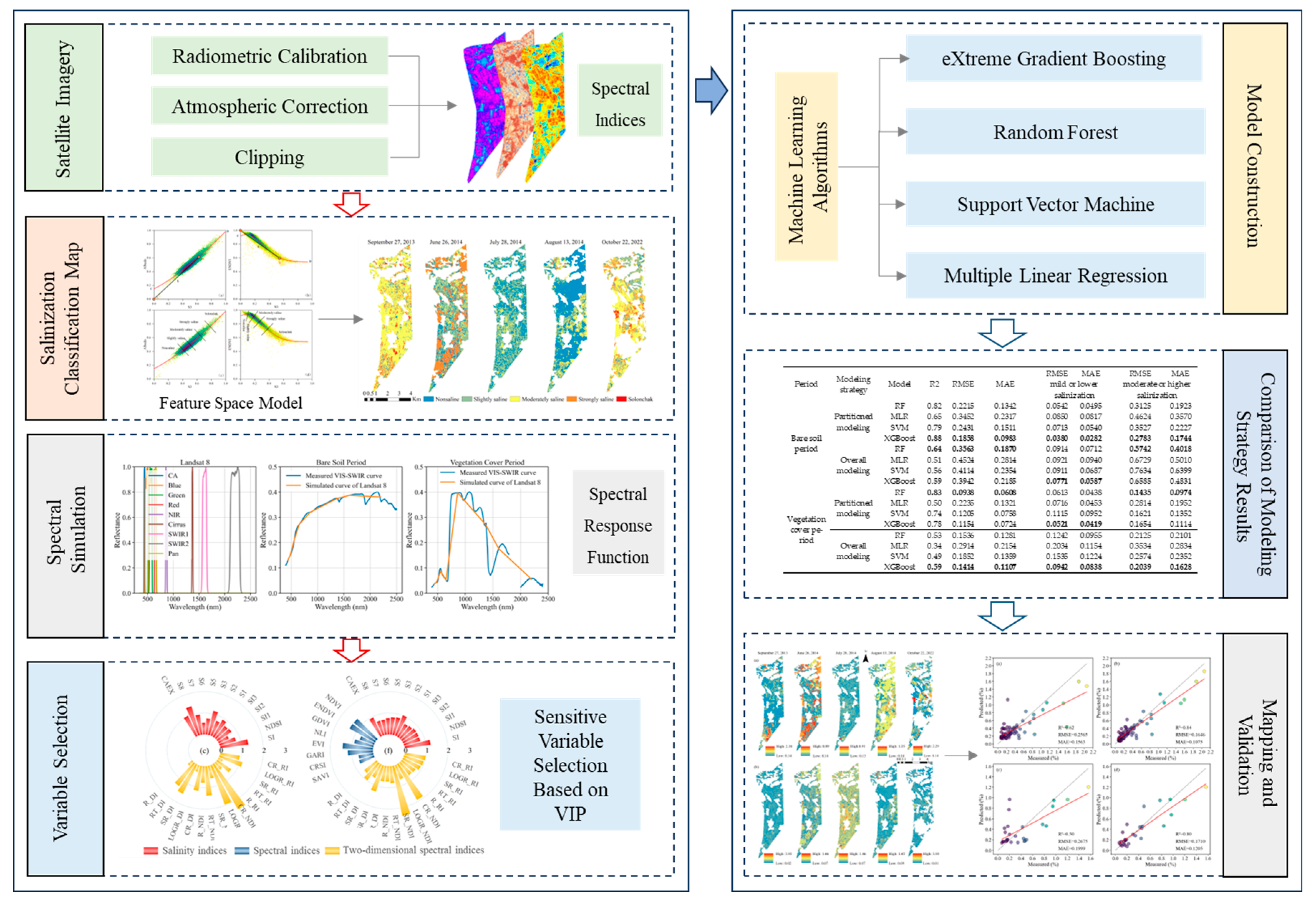
2.3.1. Soil Salinization Classification
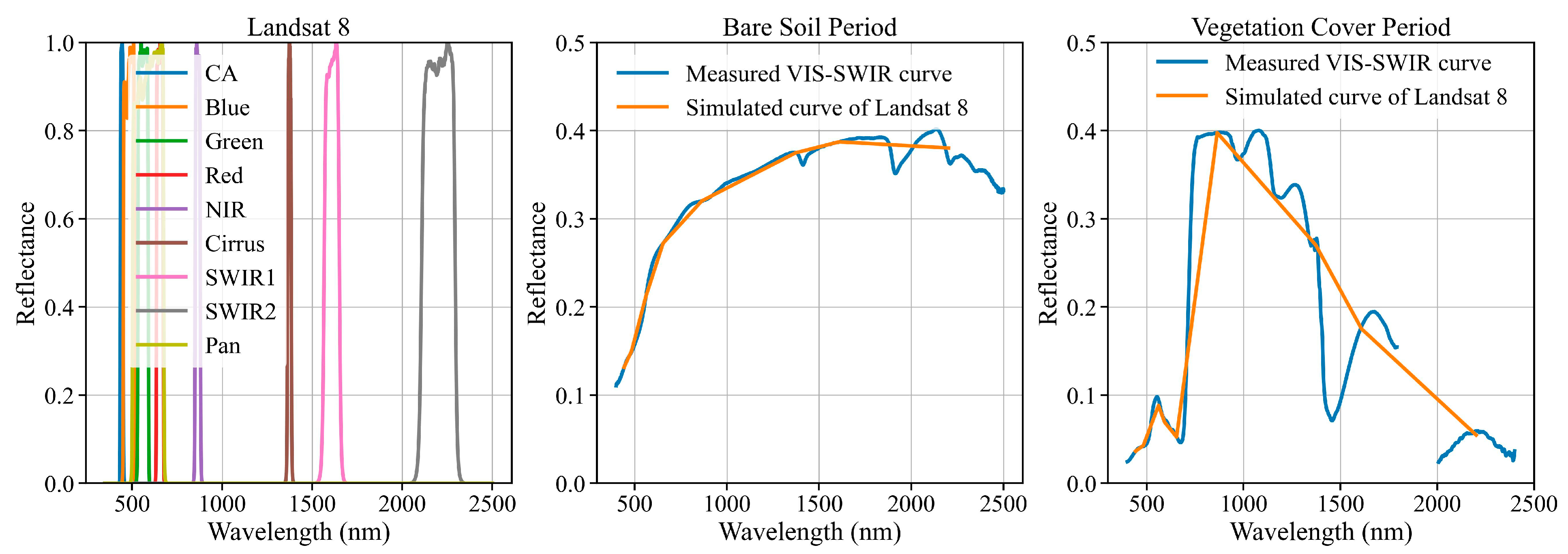
2.3.2. Spectral Simulations
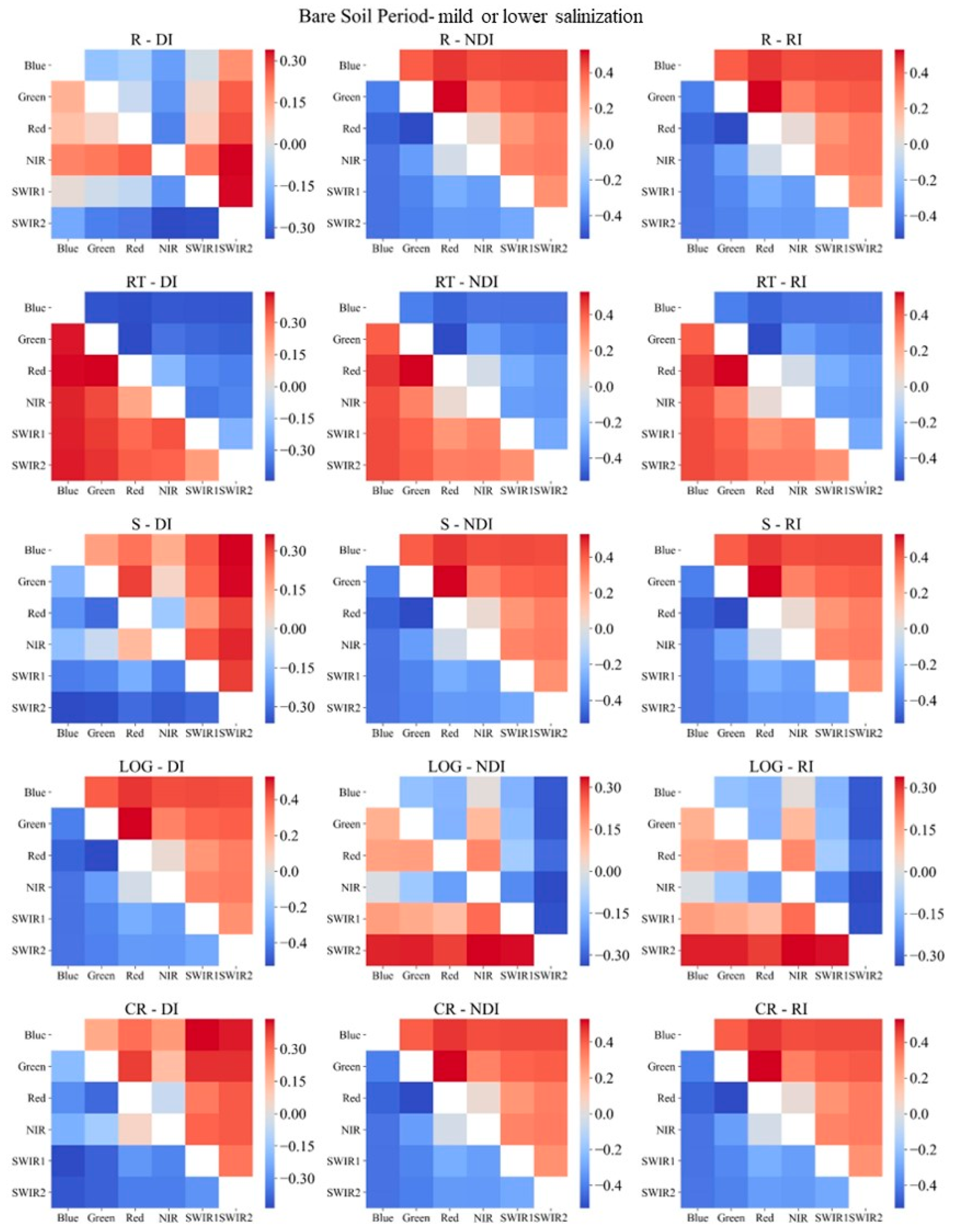
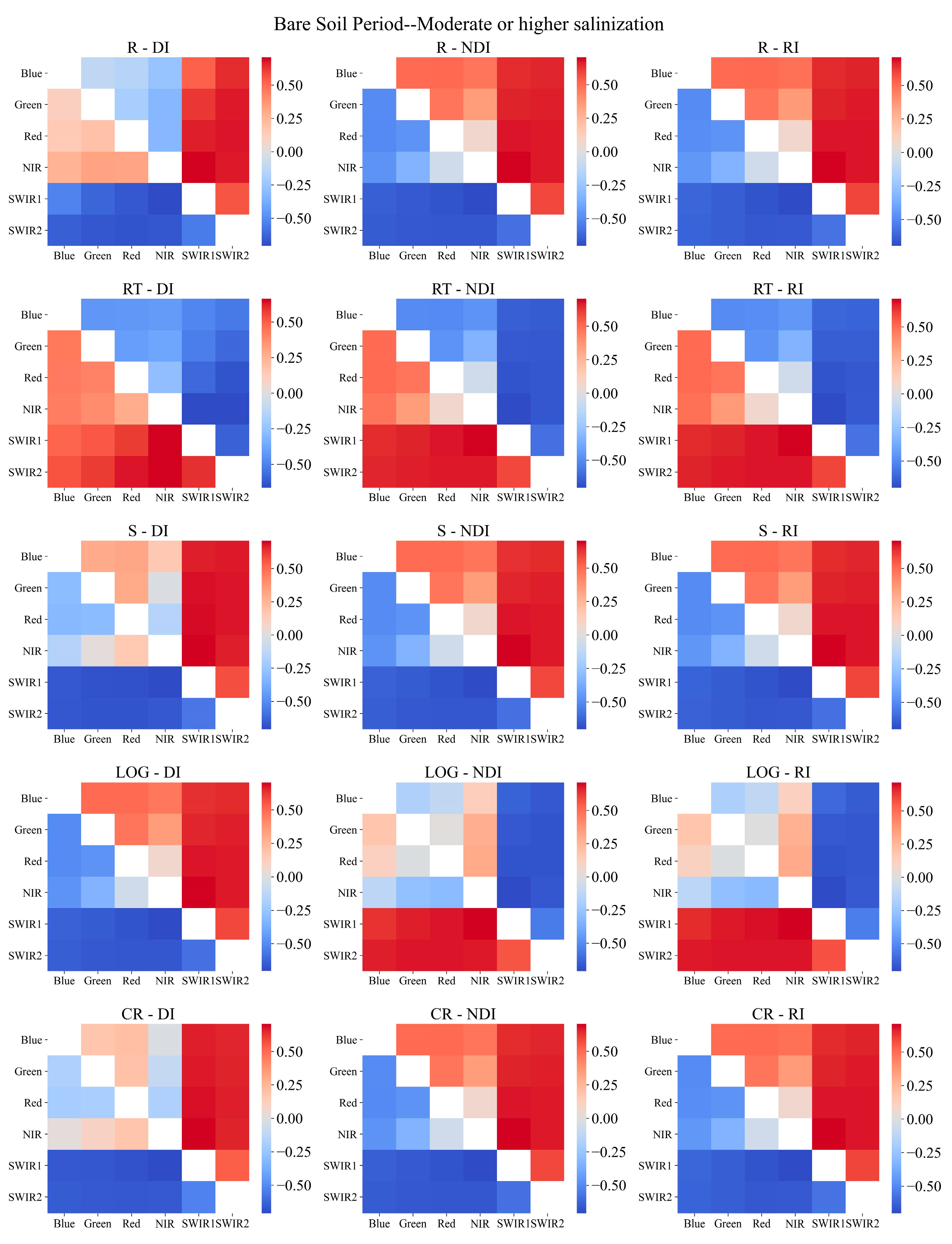
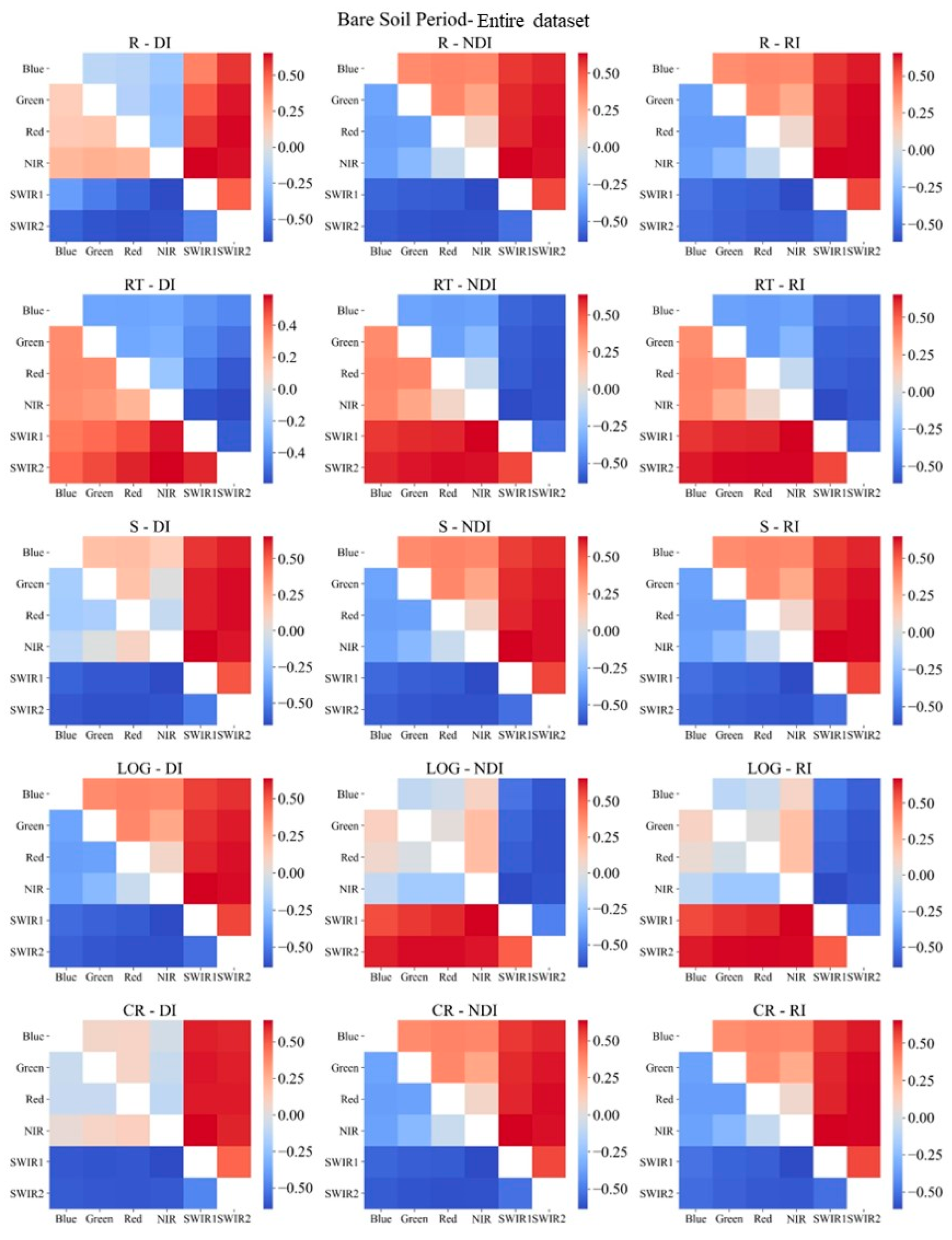
2.3.3. Spectral Index Construction
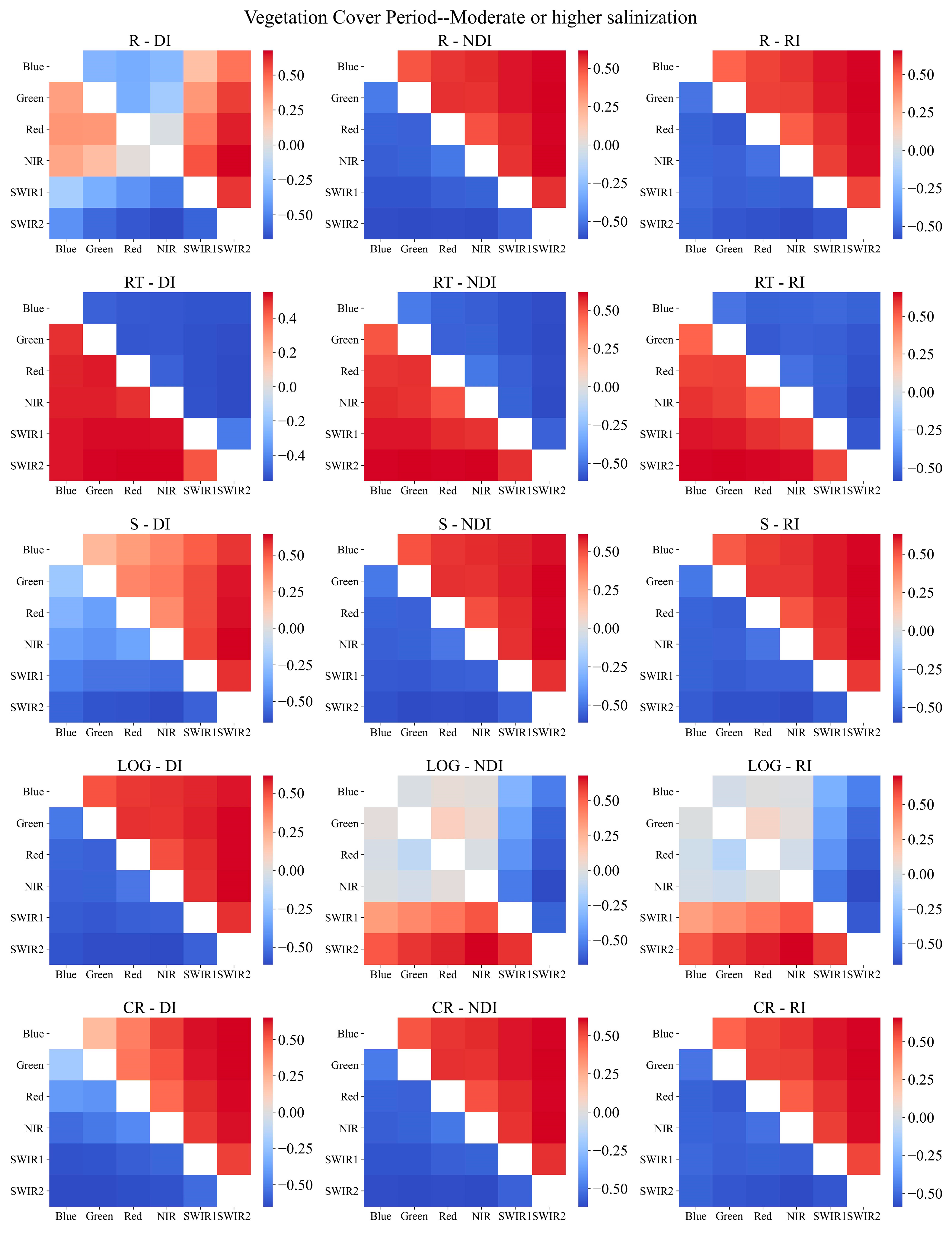
2.3.4. Sensitive Spectral Index Selection Method
2.3.5. Soil Salinity Estimation Model Construction and Model Performance Evaluation
- (1)
- Soil salinity estimation model construction
- (2)
- Model evaluation metrics
3. Results and Analysis
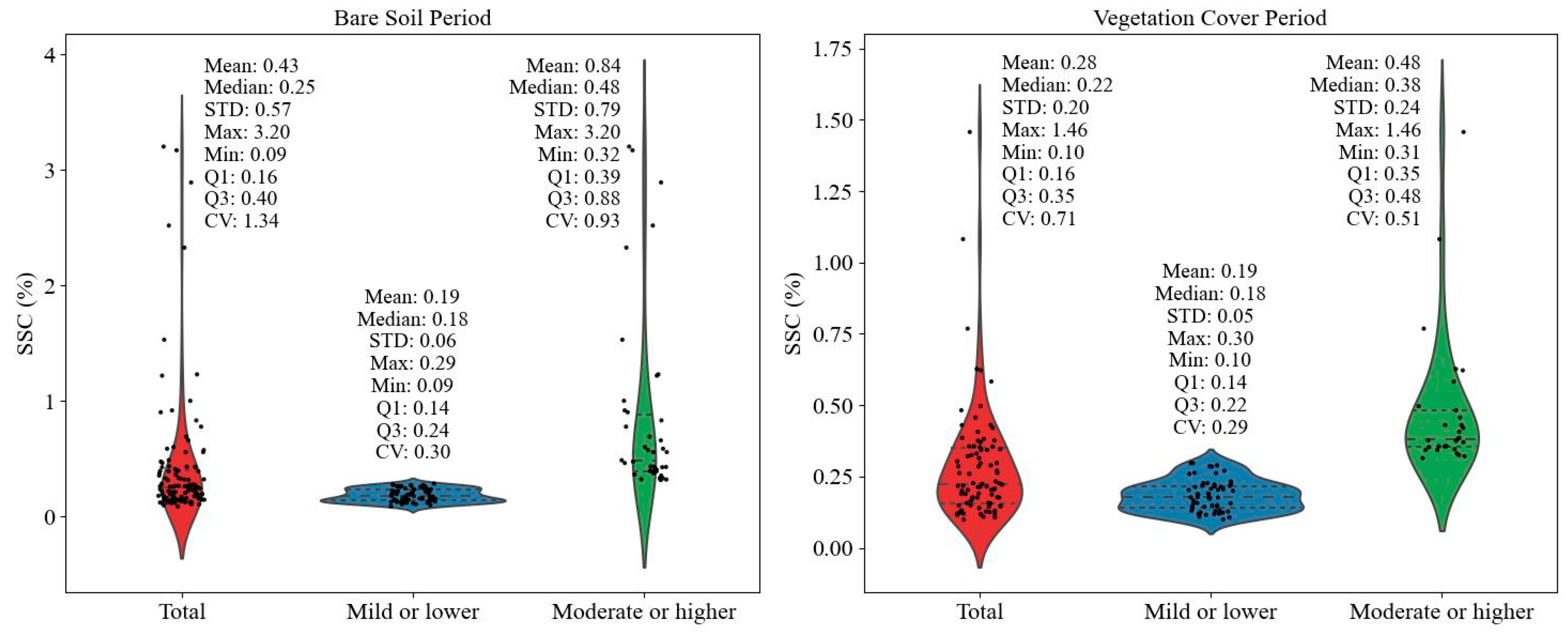
3.1. Statistical Characteristics of the Measured Soil Salinity Data
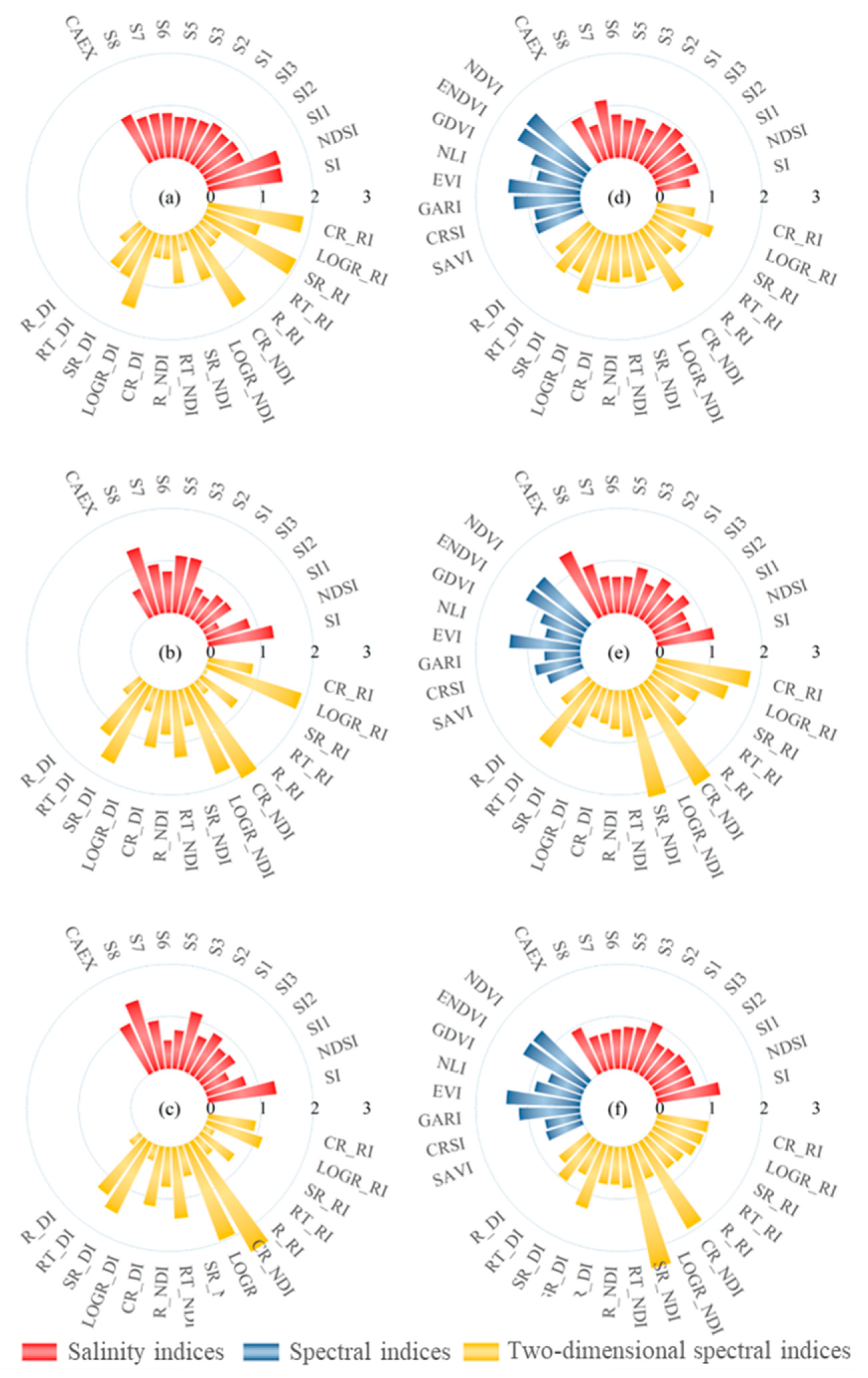
3.2. Sensitive Spectral Index Selection
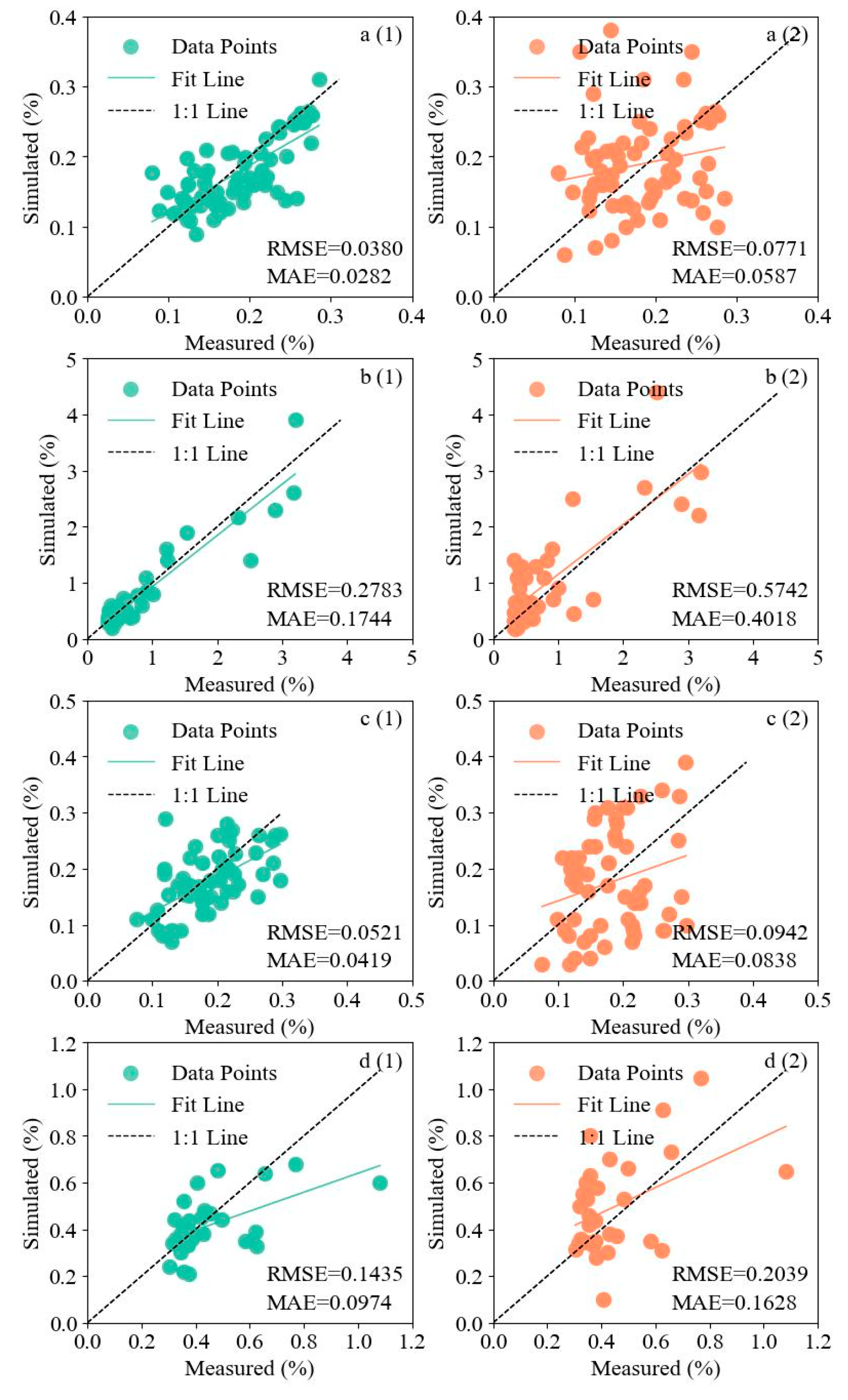
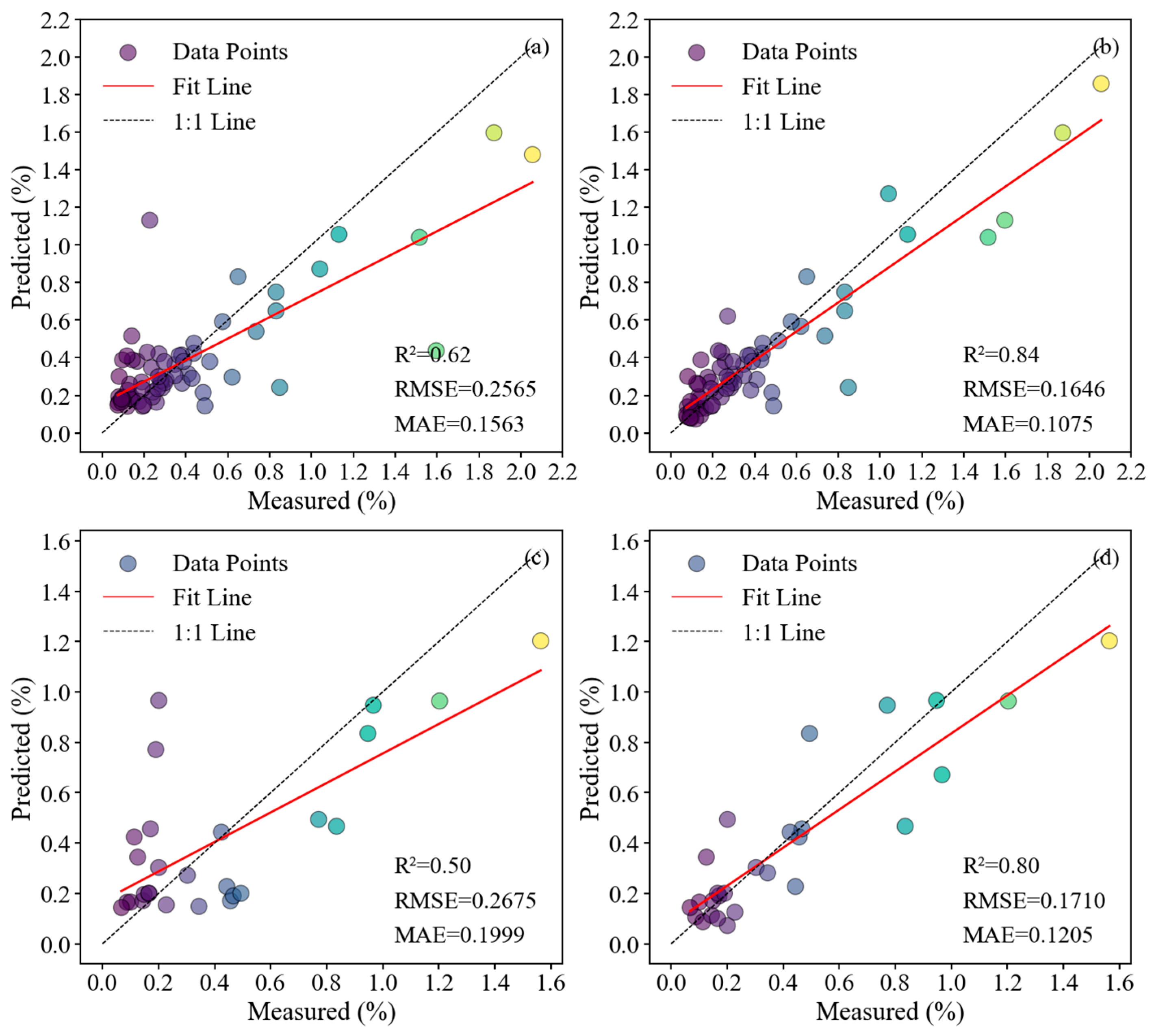
3.3. Evaluation of Soil Salinity Estimation Models with Different Modeling Approaches
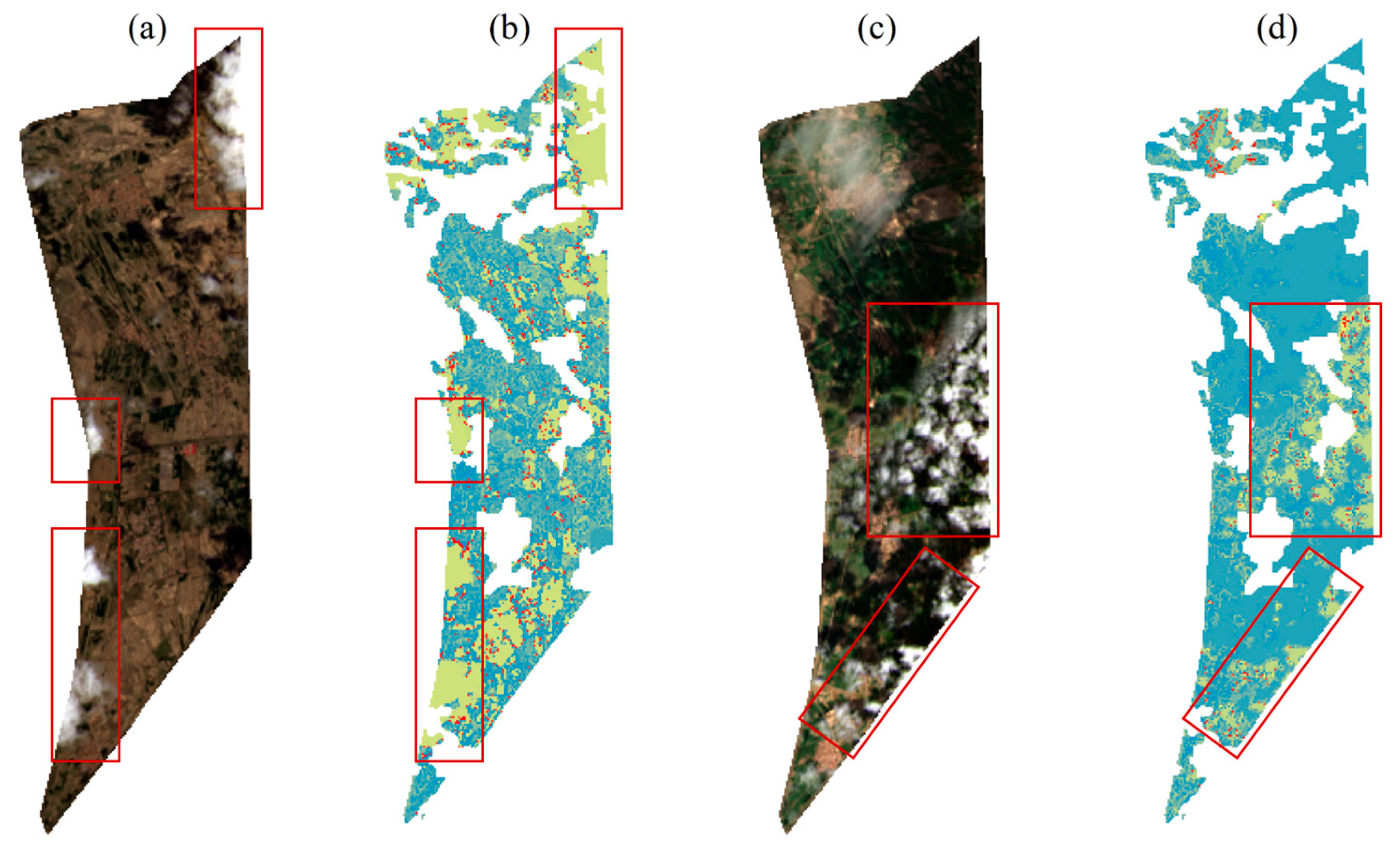
3.4. Application and Validation of Partitioned Model Based on Different Salinization Degrees
4. Discussion
- (1)
- Necessity of soil salinization classification during the bare soil and vegetation cover periods
- (2)
- Potential of multi-source data fusion
- (3)
- Prediction models and digital mapping
- (4)
- Limitations and future perspectives
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

| Period | Soil Salinization Classification | Range |
|---|---|---|
| Bare soil period (SAI model) | Nonsaline | ≤0.598 |
| Slightly saline | 0.598 < SAI ≤ 0.733 | |
| Moderately saline | 0.733 < SAI ≤ 0.902 | |
| Strongly saline | 0.902 < SAI ≤ 1.096 | |
| Solonchak | >1.096 | |
| vegetation cover period (VENS model) | Nonsaline | ≤0.123 |
| Slightly saline | 0.123 < VENS ≤ 0.235 | |
| Moderately saline | 0.235 < VENS ≤ 0.342 | |
| Strongly saline | 0.342 < VENS ≤ 0.461 | |
| Solonchak | >0.461 |
| Model | Salinization Degrees | Predicted | Precision (%) | Recall (%) | F1-Score (%) | Accuracy (%) | Kappa | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonsaline | Slightly Saline | Moderately Saline | Strongly Saline | Solonchak | ||||||||
| SAI | Measured | nonsaline | 59 | 7 | 2 | 0 | 0 | 86.76 | 88.06 | 87.41 | 85.64 | 0.80 |
| slightly saline | 5 | 33 | 2 | 1 | 0 | 80.49 | 78.57 | 79.52 | ||||
| moderately saline | 3 | 2 | 39 | 0 | 0 | 88.64 | 86.67 | 87.64 | ||||
| strongly saline | 0 | 0 | 1 | 11 | 1 | 84.62 | 84.62 | 84.62 | ||||
| solonchak | 0 | 0 | 1 | 1 | 13 | 86.67 | 92.86 | 89.66 | ||||
| VENS | Measured | nonsaline | 37 | 5 | 2 | 1 | 0 | 82.22 | 90.24 | 86.05 | 82.61 | 0.76 |
| slightly saline | 3 | 22 | 2 | 0 | 0 | 81.48 | 75.86 | 78.57 | ||||
| moderately saline | 1 | 2 | 26 | 2 | 1 | 81.25 | 83.87 | 82.54 | ||||
| strongly saline | 0 | 0 | 1 | 6 | 0 | 85.71 | 66.67 | 75.00 | ||||
| solonchak | 0 | 0 | 0 | 0 | 4 | 100.00 | 80.00 | 88.89 | ||||


References
- Metternicht, G.I.; Zinck, J.A. Remote sensing of soil salinity: Potentials and constraints. Remote Sens. Environ. 2003, 85, 1–20. [Google Scholar]
- Xin, P.; Wilson, A.; Shen, C.; Ge, Z.; Moffett, K.B.; Santos, I.R.; Chen, X.; Xu, X.; Yau, Y.Y.Y.; Moore, W.; et al. Surface water and groundwater interactions in salt marshes and their impact on plant ecology and coastal biogeochemistry. Rev. Geophys. 2022, 60, e2021RG000740. [Google Scholar]
- Chen, H.; Wu, J.; Xu, C. Monitoring Soil Salinity Classes through Remote Sensing-Based Ensemble Learning Con-cept: Considering Scale Effects. Remote Sens. 2024, 16, 642. [Google Scholar] [CrossRef]
- Taylor, G.R.; Mah, A.H.; Kruse, F.A.; Kierein-Young, K.S.; Hewson, R.D.; Bennett, B.A. Characterization of saline soils using airborne radar imagery. Remote Sens. Environ. 1996, 57, 127–142. [Google Scholar]
- Abbas, A.; Khan, S.; Hussain, N.; Hanjra, M.; Akbar, S. Characterizing soil salinity in irrigated agriculture using a remote sensing approach. Phys. Chem. Earth A/B/C 2013, 55–57, 43–52. [Google Scholar]
- Scudiero, E.; Skaggs, T.; Corwin, D. Regional-scale soil salinity assessment using Landsat ETM+ canopy reflectance. Remote Sens. Environ. 2015, 169, 335–343. [Google Scholar]
- Abuelgasim, A.; Ammad, R. Mapping soil salinity in arid and semi-arid regions using Landsat 8 OLI satellite data. Remote Sens. Appl. Soc. Environ. 2019, 13, 415–425. [Google Scholar]
- Periasamy, S.; Ravi, K. A novel approach to quantify soil salinity by simulating the dielectric loss of SAR in three-dimensional density space. Remote Sens. Environ. 2020, 251, 112059. [Google Scholar] [CrossRef]
- Zhang, T.; Qi, J.; Gao, Y.; Ouyang, Z.; Zeng, S.; Zhao, B. Detecting soil salinity with MODIS time series VI data. Ecol. Indic. 2015, 52, 480–489. [Google Scholar] [CrossRef]
- Jia, J.; Chen, C.; Liu, Q.; Ding, B.; Ren, Z.; Jia, Y.; Bai, X.; Du, R.; Chen, Q.; Wang, S.; et al. Soil salinity monitoring model based on the synergistic construction of ground-UAV-satellite data. Soil Use Manag. 2024, 40, e12980. [Google Scholar] [CrossRef]
- Fan, X.; Liu, Y.; Tao, J.; Weng, Y. Soil salinity retrieval from advanced multi-spectral sensor with partial least square regression. Remote Sens. 2015, 7, 488–511. [Google Scholar] [CrossRef]
- Wu, S.; Wang, C.; Liu, Y.; Li, Y.; Liu, J.; Xu, A.; Pan, K.; Li, Y.; Pan, X. Mapping the salt content in soil profiles using Vis-NIR hyperspectral imaging. Soil Sci. Soc. Am. J. 2018, 82, 1259–1269. [Google Scholar] [CrossRef]
- Cao, X.; Chen, W.; Ge, X.; Chen, X.; Wang, J.; Ding, J. Multidimensional soil salinity data mining and evaluation from different satellites. Sci. Total Environ. 2022, 846, 157416. [Google Scholar] [CrossRef] [PubMed]
- Allbed, A.; Kumar, L.; Aldakheel, Y. Assessing soil salinity using soil salinity and vegetation indices derived from IKONOS high-spatial resolution imageries: Applications in a date palm dominated region. Geoderma 2014, 230–231, 1–8. [Google Scholar] [CrossRef]
- Ding, J.; Yu, D. Monitoring and evaluating spatial variability of soil salinity in dry and wet seasons in the Werigan-Kuqa Oasis, China, using remote sensing and electromagnetic induction instruments. Geoderma 2014, 235–236, 316–322. [Google Scholar] [CrossRef]
- Rahmati, M.; Hamzehpour, N. Quantitative remote sensing of soil electrical conductivity using ETM+ and ground measured data. Int. J. Remote Sens. 2017, 38, 123–140. [Google Scholar] [CrossRef]
- Tilley, D.R.; Ahmed, M.; Son, J.H.; Badrinarayanan, H. Hyperspectral reflectance response of freshwater macrophytes to salinity in a brackish subtropical marsh. J. Environ. Qual. 2007, 36, 780–789. [Google Scholar] [CrossRef]
- Chi, Y.; Sun, J.; Liu, W.; Wang, J.; Zhao, M. Mapping coastal wetland soil salinity in different seasons using an improved comprehensive land surface factor system. Ecol. Indic. 2019, 107, 105517. [Google Scholar] [CrossRef]
- Peng, J.; Biswas, A.; Jiang, Q.; Zhao, R.; Hu, J.; Hu, B.; Shi, Z. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China. Geoderma 2019, 337, 1309–1319. [Google Scholar] [CrossRef]
- Geng, J.; Lv, J.; Pei, J.; Liao, C.; Tan, Q.; Wang, T.; Fang, H.; Wang, L. Prediction of soil organic carbon in black soil based on a synergistic scheme from hyperspectral data: Combining fractional-order derivatives and three-dimensional spectral indices. Comput. Electron. Agric. 2024, 220, 108905. [Google Scholar] [CrossRef]
- Wu, W.; Zucca, C.; Muhaimeed, A.S.; Al Shafie, W.M.; Fadhil Al Quraishi, A.M.; Nangia, V.; Zhu, M.; Liu, G. Soil salinity prediction and mapping by machine learning regression in Central Mesopotamia, Iraq. Land Degrad. Dev. 2018, 29, 4005–4014. [Google Scholar] [CrossRef]
- Fathizad, H.; Hakimzadeh Ardakani, M.A.; Sodaiezadeh, H.; Kerry, R.; Taghizadeh-Mehrjardi, R. Investigation of the spatial and temporal variation of soil salinity using random forests in the central desert of Iran. Geoderma 2020, 365, 114233. [Google Scholar] [CrossRef]
- Peng, Y.; Liu, Z.; Lin, C.; Hu, Y.; Zhao, L.; Zou, R.; Wen, Y.; Mao, X. A new method for estimating soil fertility using extreme gradient boosting and a backpropagation neural network. Remote Sens. 2022, 14, 3311. [Google Scholar] [CrossRef]
- Farifteh, J.; Van der Meer, F.; Atzberger, C.; Carranza, E.J.M. Quantitative analysis of salt-affected soil reflectance spectra: A comparison of two adaptive methods (PLSR and ANN). Remote Sens. Environ. 2007, 110, 59–78. [Google Scholar] [CrossRef]
- Zhang, H.; Fu, X.; Zhang, Y.; Qi, Z.; Zhang, H.; Xu, Z. Mapping multi-depth soil salinity using remote sensing-enabled machine learning in the Yellow River Delta, China. Remote Sens. 2023, 15, 5640. [Google Scholar] [CrossRef]
- Wang, F.; Yang, S.; Wei, Y.; Shi, Q.; Ding, J. Characterizing soil salinity at multiple depths using electromagnetic induction and remote sensing data with random forests: A case study in Tarim River Basin of southern Xinjiang, China. Sci. Total Environ. 2021, 754, 142030. [Google Scholar] [CrossRef]
- Vermeulen, D.; Van Niekerk, A. Machine learning performance for predicting soil salinity using different combinations of geomorphometric covariates. Geoderma 2017, 299, 1–12. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Jafari, A.; Tajik, S.; Finke, P. Digital mapping of soil properties using multiple machine learning in a semi-arid region, central Iran. Geoderma 2019, 338, 445–452. [Google Scholar] [CrossRef]
- Zeraatpisheh, M.; Ayoubi, S.; Mirbagheri, Z.; Mosaddeghi, M.; Xu, M. Spatial prediction of soil aggregate stability and soil organic carbon in aggregate fractions using machine learning algorithms and environmental variables. Geoderma Reg. 2021, 27, e00440. [Google Scholar]
- Wang, F.; Shi, Z.; Biswas, A.; Yang, S.; Ding, J. Multi-algorithm comparison for predicting soil salinity. Geoderma 2020, 365, 114211. [Google Scholar] [CrossRef]
- Naimi, S.; Ayoubi, S.; Di Raimo, L.A.D.L.; Demattê, J.A.M. Quantification of some intrinsic soil properties using proximal sensing in arid lands: Application of Vis-NIR, MIR, and pXRF spectroscopy. Geoderma Reg. 2022, 28, e00484. [Google Scholar] [CrossRef]
- Xu, C.; Zeng, W.; Huang, J.; Wu, J.; van Leeuwen, W. Prediction of soil moisture content and soil salt concentration from hyperspectral laboratory and field data. Remote Sens. 2016, 8, 42. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Z.; Chen, J.; Chen, H.; Jin, J.; Han, J.; Wang, X.; Song, Z.; Wei, G. Estimating soil salinity with different fractional vegetation cover using remote sensing. Land Degrad. Dev. 2021, 32, 597–612. [Google Scholar] [CrossRef]
- Cui, X.; Han, W.; Zhang, H.; Dong, Y.; Ma, W.; Zhai, X.; Zhang, L.; Li, G. Estimating and mapping the dynamics of soil salinity under different crop types using Sentinel-2 satellite imagery. Geoderma 2023, 440, 116738. [Google Scholar] [CrossRef]
- Domínguez-Beisiegel, M.; Castañeda, C.; Mougenot, B.; Herrero, J. Analysis and map ping of the spectral characteristics of fractional green cover in saline wetlands (NE Spain) using field and remote sensing data. Remote Sens. 2016, 8, 590. [Google Scholar] [CrossRef]
- Wang, L.; Hu, P.; Zheng, H.; Liu, Y.; Cao, X.; Hellwich, O.; Liu, T.; Luo, G.; Bao, A.; Chen, X. Integrative modeling of heterogeneous soil salinity using sparse ground samples and remote sensing images. Geoderma 2023, 430, 116321. [Google Scholar] [CrossRef]
- Bannari, A.; El-Battay, A.; Bannari, R.; Rhinane, H. Sentinel-MSI VNIR and SWIR Bands Sensitivity Analysis for Soil Salinity Discrimination in an Arid Landscape. Remote Sens. 2018, 10, 855. [Google Scholar] [CrossRef]
- Lv, Q.; Jiang, L.; Ma, B.; Zhao, B.; Huo, Z. A study on the effect of the salt content on the solidification of sulfate saline soil solidified with an alkali-activated geopolymer. Constr. Build. Mater. 2018, 176, 68–74. [Google Scholar] [CrossRef]
- Ge, X.; Ding, J.; Teng, D.; Xie, B.; Zhang, X.; Wang, J.; Han, L.; Bao, Q.; Wang, J. Exploring the capability of Gaofen-5 hyperspectral data for assessing soil salinity risks. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102969. [Google Scholar] [CrossRef]
- Lao, C.; Yu, X.; Zhan, L.; Xin, P. Monitoring soil salinity in coastal wetlands with sentinel-2 msi data: Combining fractional-order derivatives and stacked machine learning models. Agric. Water Manag. 2024, 306, 109147. [Google Scholar] [CrossRef]
- Wei, G.; Li, Y.; Zhang, Z.; Chen, Y.; Chen, J.; Yao, Z.; Lao, C.; Chen, H. Estimation of soil salt content by combining UAV-borne multispectral sensor and machine learning algorithms. PeerJ 2020, 8, e9087. [Google Scholar] [CrossRef] [PubMed]
- Xiong, L.; Xu, X.; Engel, B.; Huang, Q.; Huo, Z.; Xiong, Y.; Han, W.; Huang, G. Modeling agro-hydrological processes and analyzing water use in a super-large irrigation district (Hetao) of arid upper Yellow River basin. J. Hydrol. 2021, 603, 127014. [Google Scholar] [CrossRef]
- Du, R.; Xiang, Y.; Chen, J.; Lu, X.; Zhang, F.; Zhang, Z.; Yang, B.; Tang, Z.; Wang, X.; Qian, L. The daily soil water content monitoring of cropland in irrigation area using Sentinel-2/3 spatio-temporal fusion and machine learning. Int. J. Appl. Earth Obs. Geoinf. 2024, 132, 104081. [Google Scholar] [CrossRef]
- Wang, G.; Shi, H.; Li, X.; Guo, J.; Wang, W.; Wu, D. Estimation of salt transport and relationship with groundwater depth in different land types in Hetao irrigation area. Trans. Chin. Soc. Agric. Mach. 2020, 51, 252–261. [Google Scholar]
- Xu, C. Information Retrieval of Four-Dimensional Soil Moisture Content and Salt Concentration in Salted Farmland Based on Remote Sensing Data. Ph.D. Thesis, Wuhan University, Wuhan, China, 2016. [Google Scholar]
- Liu, J.; Zhang, L.; Dong, T.; Wang, J.; Fan, Y.; Wu, H.; Geng, Q.; Yang, Q.; Zhang, Z. The applicability of remote sensing models of soil salinization based on feature space. Sustainability 2021, 13, 13711. [Google Scholar] [CrossRef]
- Rouse, J.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great plains with ERTS. NASA Spec. Publ. 1973, 351, 309. [Google Scholar]
- Abbas, A.; Khan, S. Using remote sensing techniques for appraisal of irrigated soil salinity. In Advances and Applications for Management and Decision Making Land, Water and Environmental Management, Subtitle of host publication, Integrated Systems for Sustainability MODSIM07, Proceedings of the International Congress on Modelling and Simulation (MODSIM), Christchurch, New Zealand, 10–13 December 2007; Modelling and Simulation Society of Australia and New Zealand: Christchurch, New Zealand, 2007. [Google Scholar]
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Trigg, S.; Flasse, S. Characterizing the spectral-temporal response of burned savannah using in situ spectroradiometry and infrared thermometry. Int. J. Remote Sens. 2000, 21, 3161–3168. [Google Scholar] [CrossRef]
- Douaoui, A.; Nicolas, H.; Walter, C. Detecting salinity hazards within a semiarid context by means of combining soil and remote-sensing data. Geoderma 2006, 134, 217–230. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Yu, D.; Ma, X.; Zhang, Z.; Ge, X.; Teng, D.; Li, X.; Liang, J.; Lizaga, I.; et al. Capability of Sentinel-2 MSI data for monitoring and mapping of soil salinity in dry and wet seasons in the Ebinur Lake region, Xinjiang, China. Geoderma 2019, 353, 172–187. [Google Scholar] [CrossRef]
- Khan, N.; Rastoskuev, V.; Sato, Y.; Shiozawa, S. Assessment of hydrosaline land degradation by using a simple approach of remote sensing indicators. Agric. Water Manag. 2005, 77, 96–109. [Google Scholar]
- Bannari, A.; Guedon, A.; El-Harti, A.; Cherkaoui, F.; El-Ghmari, A. Characterization of slightly and moderately saline and sodic soils in irrigated agricultural land using simulated data of advanced land imaging (EO-1) sensor. Commun. Soil Sci. Plant Anal. 2008, 39, 2795–2811. [Google Scholar]
- Wu, W.; Al-Shafie, W.; Mhaimeed, A.; Ziadat, F.; Nangia, V.; Payne, W. Soil salinity mapping by multiscale remote sensing in Mesopotamia, Iraq. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 4442–4452. [Google Scholar]
- Goel, N.; Qin, W. Influences of canopy architecture on relationships between various vegetation indices and LAI and FPAR. Remote Sens. Rev. 1994, 10, 309–347. [Google Scholar]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.; Gao, X.; Ferreira, L. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar]
- Gitelson, A.; Kaufman, Y.; Merzlyak, M. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sens. Environ. 1996, 58, 289–298. [Google Scholar]
- Scudiero, E.; Skaggs, T.; Corwin, D. Regional scale soil salinity evaluation using Landsat 7, western San Joaquin Valley, California, USA. Geoderma Reg. 2014, 2–3, 82–90. [Google Scholar]
- Huete, A. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar]
- Yang, N.; Yang, S.; Cui, W.; Zhang, Z.; Zhang, J.; Chen, J. Effect of spring irrigation on soil salinity monitoring with UAV-borne multispectral sensor. Int. J. Remote Sens. 2021, 42, 8952–8978. [Google Scholar] [CrossRef]
- Chen, Z.; Jin, J.; Zhang, R.; Zhang, T.; Chen, J.; Yang, J.; Ou, C.; Guo, Y. Comparison of different missing-imputation methods for MAIAC (Multiangle Implementation of Atmospheric Correction) AOD in estimating daily PM2.5 levels. Remote Sens. 2020, 12, 3008. [Google Scholar] [CrossRef]
- Gao, H.; Wang, C.; Wang, G.; Fu, H.; Zhu, J. A novel crop classification method based on ppfSVM classifier with time-series alignment kernel from dual-polarization SAR datasets. Remote Sens. Environ. 2021, 264, 112580. [Google Scholar]
- Zhang, Z.; Wei, G.; Miao, H.; Wang, S.; Yang, X.; Han, J. Soil salinity inversion model based on UAV multispectral remote sensing. Trans. Chin. Soc. Agric. Mach. 2019, 50, 101–110. [Google Scholar]
- Sun, Y.; Li, X.; Shi, H.; Ma, H.; Wang, W.; Cui, J.; Chen, C. Optimizing the inversion of soil salt in salinized wasteland using hyperspectral data from remote sensing. Trans. Chin. Soc. Agric. Eng. 2022, 38, 101–111. [Google Scholar]
- Wang, D.; Chen, H.; Wang, Z.; Ma, Y. Inversion of soil salinity according to different salinization grades using multi-source remote sensing. Geocarto Int. 2022, 37, 1274–1293. [Google Scholar]
- Farifteh, J.; Farshad, A.; George, R.J. Assessing salt-affected soils using remote sensing, solute modelling, and geophysics. Geoderma 2006, 130, 191–206. [Google Scholar] [CrossRef]
- Dehaan, R.L.; Taylor, G.R. Field-derived spectra of salinized soils and vegetation as indicators of irrigation-induced soil salinization. Remote Sens. Environ. 2002, 80, 406–417. [Google Scholar]
- Sun, M.; Liu, H.; Li, P.; Gong, P.; Yu, X.; Ye, F.; Guo, Y.; Wu, Z. Effects of salt content and particle size on spectral reflectance and model accuracy: Estimating soil salt content in arid, saline-alkali lands. Microchem. J. 2024, 207, 111666. [Google Scholar] [CrossRef]
- Allbed, A.; Kumar, L.; Sinha, P. Soil salinity and vegetation cover change detection from multi-temporal remotely sensed imagery in Al Hassa Oasis in Saudi Arabia. Geocarto Int. 2018, 33, 830–846. [Google Scholar]
- Guo, Y.; Zhou, Y.; Zhou, L.; Liu, T.; Wang, L.; Cheng, Y.; He, J.; Zheng, G. Using proximal sensor data for soil salinity management and mapping. J. Integr. Agric. 2019, 18, 340–349. [Google Scholar]
- Wang, J.; Ding, J.; Yu, D.; Teng, D.; He, B.; Chen, X.; Ge, X.; Zhang, Z.; Wang, Y.; Yang, X.; et al. Machine learning-based detection of soil salinity in an arid desert region, Northwest China: A comparison between Landsat-8 OLI and Sentinel-2 MSI. Sci. Total Environ. 2020, 707, 136092. [Google Scholar] [CrossRef]
- Ge, J.; Zhao, L.; Yu, Z.; Liu, H.; Zhang, L.; Gong, X.; Sun, H. Prediction of greenhouse tomato crop evapotranspiration using XGBoost machine learning model. Plants 2022, 11, 1923. [Google Scholar] [CrossRef] [PubMed]
- Asselman, A.; Khaldi, M.; Aammou, S. Enhancing the prediction of student performance based on the machine learning XGBoost algorithm. Interact. Learn. Environ. 2023, 31, 3360–3379. [Google Scholar] [CrossRef]
- Jas, K.; Dodagoudar, G. Explainable machine learning model for liquefaction potential assessment of soils using XGBoost-SHAP. Soil Dyn. Earthq. Eng. 2023, 165, 107662. [Google Scholar] [CrossRef]
- Sun, J.; Dang, W.; Wang, F.; Nie, H.; Wei, X.; Zhang, S.; Feng, Y.; Li, P. Prediction of TOC content in organic-rich shale using machine learning algorithms: Comparative study of random forest, support vector machine, and XGBoost. Energies 2023, 16, 4159. [Google Scholar] [CrossRef]
- Song, J.; Wang, Y.; Fang, Z.; Peng, L.; Hong, H. Potential of ensemble learning to improve tree-based classifiers for landslide susceptibility mapping. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4642–4662. [Google Scholar]
- Liang, T.; Liang, S.; Zou, L.; Sun, L.; Li, B.; Lin, H.; He, T.; Tian, F. Estimation of aerosol optical depth at 30 m resolution using Landsat imagery and machine learning. Remote Sens. 2022, 14, 1053. [Google Scholar] [CrossRef]
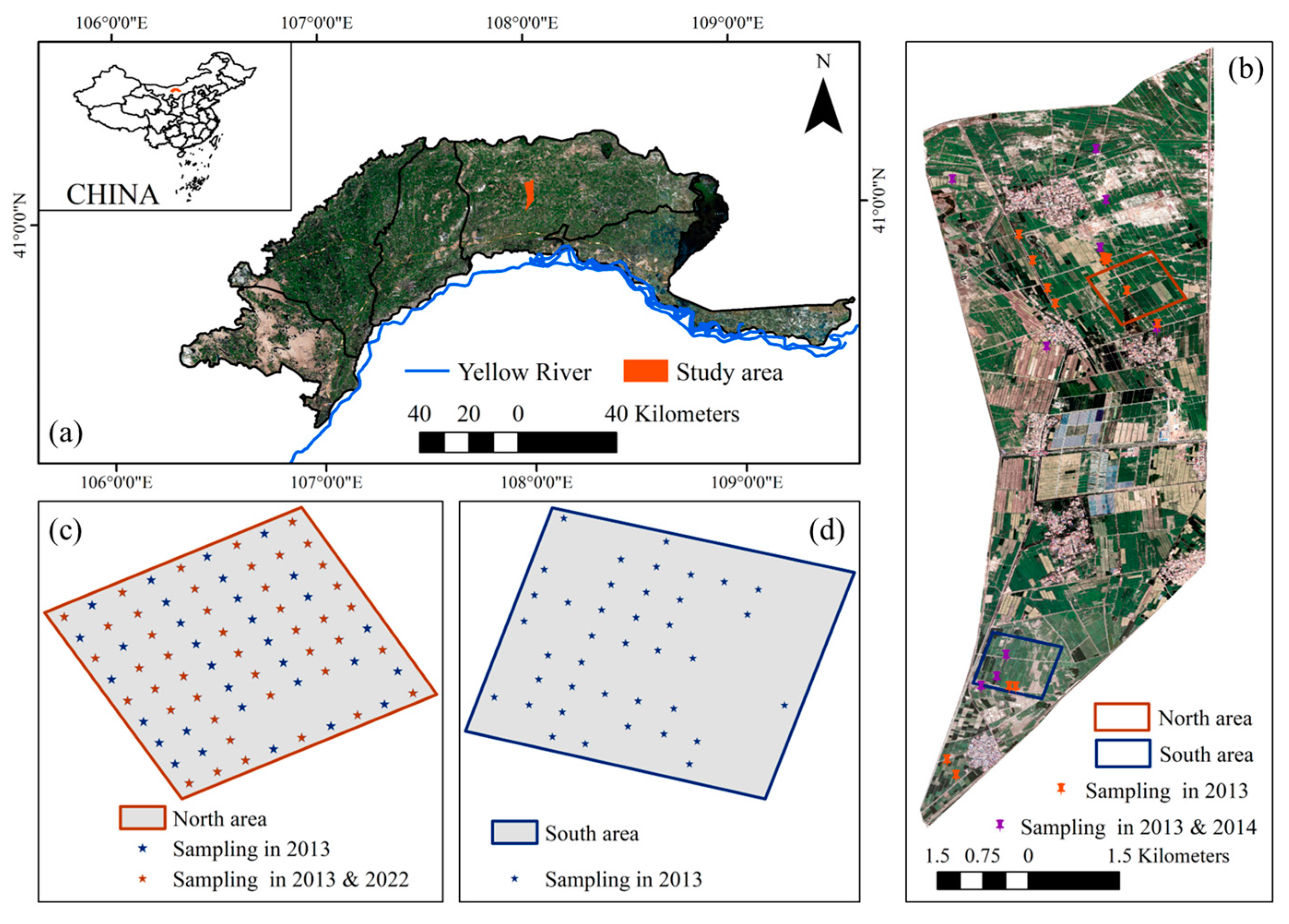
| Period | Sampling Time | Sampling Number | Sampling Area |
|---|---|---|---|
| Bare soil period | 26 April 2013 | 115 | (c,d) |
| 22 September 2013 | 22 | (b) | |
| 26 October 2022 | 44 | (c) | |
| Vegetation cover period | 7 July 2013 | 22 | (b) |
| 28 July 2013 | 22 | (b) | |
| 8 August 2013 | 22 | (b) | |
| 28 August 2013 | 22 | (b) | |
| 30 June 2014 | 9 | (b) | |
| 1 August 2014 | 9 | (b) | |
| 9 August 2014 | 9 | (b) | |
| 16 August 2014 | 9 | (b) |
| Period | Soil Sampling Time | Image Acquisition | Row/Column | Image Source |
|---|---|---|---|---|
| Bare soil period | 26 April 2013 | 20 April 2013 | 129/31 | Landsat 8 |
| 22 September 2013 | 27 September 2013 | 129/31 | ||
| 26 October 2022 | 22 October 2022 | 129/31 | Landsat 9 | |
| Vegetation cover period | 7 July 2013 | 23 July 2013 | 129/31 | Landsat 8 |
| 28 July 2013 | 25 July 2013 | 129/31 | ||
| 8 August 2013 | 10 August 2013 | 129/31 | ||
| 28 August 2013 | 26 August 2013 | 129/31 | ||
| 30 June 2014 | 26 June 2014 | 129/31 | ||
| 1 August 2014 | 28 August 2014 | 129/31 | ||
| 9 August 2014 | 13 August 2014 | 129/31 | ||
| 16 August 2014 | 13 August 2014 | 129/31 |
| Spectral Indices | Formula | Reference | |
|---|---|---|---|
| Salinity indices | SI | (B4 × B2)0.5 | [53] |
| NDSI | (B4 − B5)/(B4 + B5) | ||
| SI1 | (B4 × B3)0.5 | [51] | |
| SI2 | [(B5)2 + (B4)2 + (B3)2]0.5 | ||
| SI3 | [(B4)2 + (B3)2]0.5 | ||
| S1 | B2/B4 | [48] | |
| S2 | (B2 − B4)/(B2 + B4) | ||
| S3 | B3 × B4/B2 | ||
| S5 | B2 × B4/B3 | ||
| S6 | B4 × B5/B3 | ||
| S7 | B6/B7 | [54] | |
| S8 | (B6 − B7)/(B6 + B7) | ||
| CAEX | B4/B3 | ||
| Vegetation indices | NDVI | (B5 − B4)/(B5 + B4) | [47] |
| ENDVI | (B5 − B4 + B7)/(B5 + B4 + B7) | ||
| GDVI | (B52 − B42)/(B52 + B42) | [55] | |
| NLI | (B52 − B4)/(B52 + B4) | [56] | |
| EVI | g × (B5 − B4)/(B5 + C1 × B4 − C2 × B2 + L) | [57] | |
| GARI | {B5 − [B3 + γ × (B2 − B4)]}/{B5 + [B3 + γ × (B2 − B4)]} | [58] | |
| CRSI | {[(B5 × B4) − (B3 × B2)]/[(B5 × B4) + (B3 × B2)]}0.5 | [59] | |
| SAVI | [(B5 − B4) × (1 + L)]/(B5 + B4 + L) | [60] | |
| Period | Modeling Strategy | Model | R2 | RMSE | MAE | RMSE | MAE | RMSE | MAE |
|---|---|---|---|---|---|---|---|---|---|
| Mild or Lower Salinization | Moderate or Higher Salinization | ||||||||
| Bare soil period | Partitioned modeling | RF | 0.82 | 0.2215 | 0.1342 | 0.0542 | 0.0495 | 0.3125 | 0.1923 |
| MLR | 0.65 | 0.3452 | 0.2317 | 0.0850 | 0.0817 | 0.4624 | 0.3570 | ||
| SVM | 0.79 | 0.2431 | 0.1511 | 0.0713 | 0.0540 | 0.3527 | 0.2227 | ||
| XGBoost | 0.88 | 0.1858 | 0.0983 | 0.0380 | 0.0282 | 0.2783 | 0.1744 | ||
| Overall modeling | RF | 0.64 | 0.3563 | 0.1870 | 0.0914 | 0.0712 | 0.5742 | 0.4018 | |
| MLR | 0.51 | 0.4524 | 0.2814 | 0.0921 | 0.0940 | 0.6729 | 0.5010 | ||
| SVM | 0.56 | 0.4114 | 0.2354 | 0.0911 | 0.0687 | 0.7634 | 0.6399 | ||
| XGBoost | 0.59 | 0.3942 | 0.2185 | 0.0771 | 0.0587 | 0.6585 | 0.4831 | ||
| Vegetation cover period | Partitioned modeling | RF | 0.83 | 0.0938 | 0.0608 | 0.0613 | 0.0438 | 0.1435 | 0.0974 |
| MLR | 0.50 | 0.2235 | 0.1321 | 0.0716 | 0.0453 | 0.2814 | 0.1952 | ||
| SVM | 0.74 | 0.1205 | 0.0758 | 0.1115 | 0.0952 | 0.1621 | 0.1352 | ||
| XGBoost | 0.78 | 0.1154 | 0.0724 | 0.0521 | 0.0419 | 0.1654 | 0.1114 | ||
| Overall modeling | RF | 0.53 | 0.1536 | 0.1281 | 0.1242 | 0.0955 | 0.2125 | 0.2101 | |
| MLR | 0.34 | 0.2914 | 0.2154 | 0.2034 | 0.1154 | 0.3534 | 0.2834 | ||
| SVM | 0.49 | 0.1852 | 0.1359 | 0.1535 | 0.1224 | 0.2574 | 0.2352 | ||
| XGBoost | 0.59 | 0.1414 | 0.1107 | 0.0942 | 0.0838 | 0.2039 | 0.1628 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Wu, J.; Xu, C. Optimization of Multi-Source Remote Sensing Soil Salinity Estimation Based on Different Salinization Degrees. Remote Sens. 2025, 17, 1315. https://doi.org/10.3390/rs17071315
Chen H, Wu J, Xu C. Optimization of Multi-Source Remote Sensing Soil Salinity Estimation Based on Different Salinization Degrees. Remote Sensing. 2025; 17(7):1315. https://doi.org/10.3390/rs17071315
Chicago/Turabian StyleChen, Huifang, Jingwei Wu, and Chi Xu. 2025. "Optimization of Multi-Source Remote Sensing Soil Salinity Estimation Based on Different Salinization Degrees" Remote Sensing 17, no. 7: 1315. https://doi.org/10.3390/rs17071315
APA StyleChen, H., Wu, J., & Xu, C. (2025). Optimization of Multi-Source Remote Sensing Soil Salinity Estimation Based on Different Salinization Degrees. Remote Sensing, 17(7), 1315. https://doi.org/10.3390/rs17071315





