Multi-Directional Dual-Window Method Using Fractional Optimal-Order Fourier Transform for Hyperspectral Anomaly Detection
Abstract
:1. Introduction
- (1)
- To more effectively address non-stationary signals in HSI and improve the separation between the background and anomalous pixels, a new criterion is proposed to automatically identify the optimal FrFT order. This criterion integrates entropy, standard deviation, and signal-to-noise ratio (SNR) across all bands, enabling a more global and comprehensive optimization strategy.
- (2)
- To improve AD accuracy, a multi-directional dual-window RAD detector is designed. This detector fully exploits neighborhood and local background information, significantly improving detection performance by providing a more nuanced analysis of spatial relationships.
- (3)
- To effectively integrate the spatial and spectral data of HSI and improve the robustness and precision of detection, a saliency weighting strategy is proposed. This strategy is based on the spatial–spectral union, combining the Euclidean distance, spectral gradient, and Spearman correlation coefficient to achieve more precise anomaly discrimination.
2. Materials and Methods
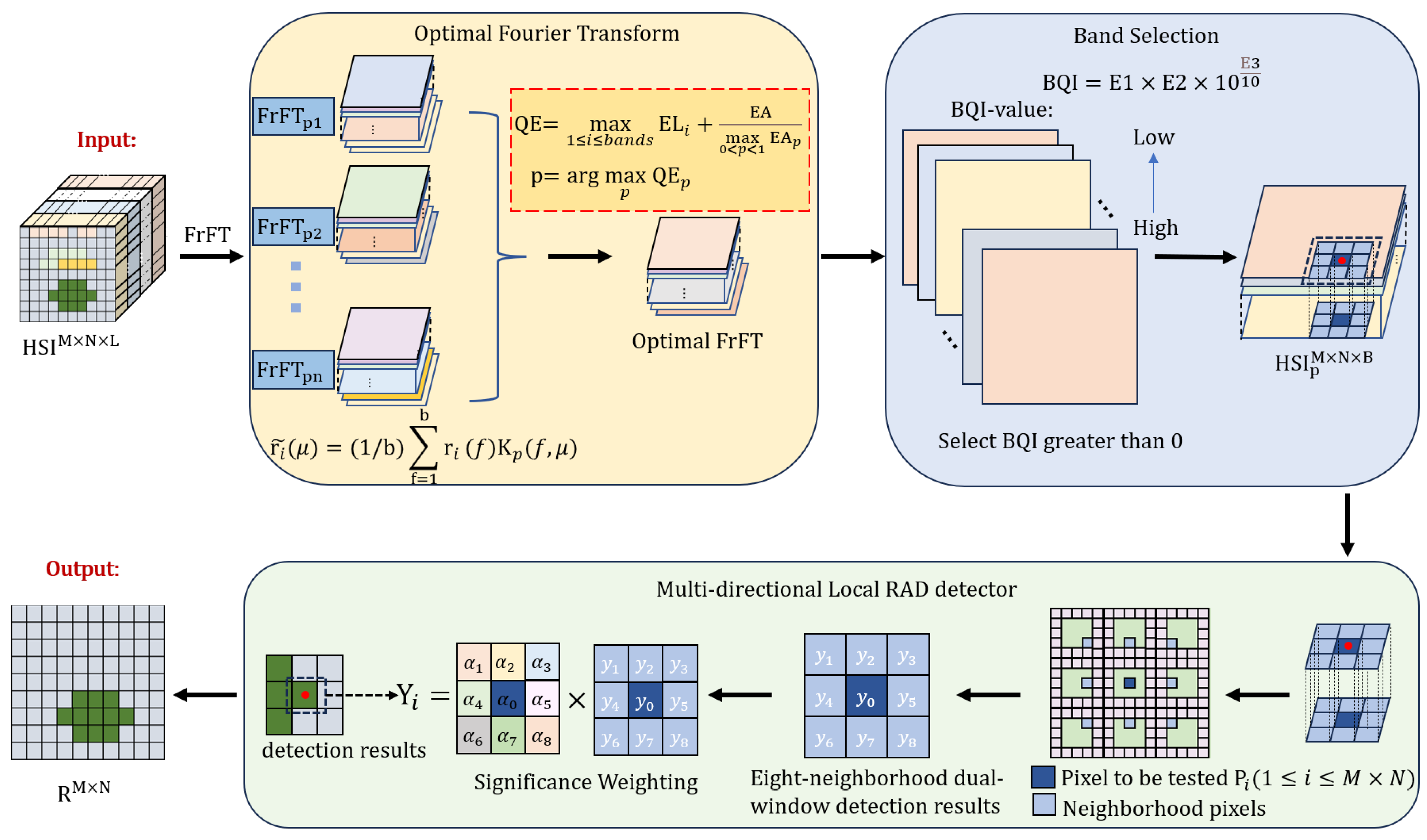
2.1. Overall Framework
2.2. Optimal Fourier Transform
2.3. Entropy-Enhanced Band Selection
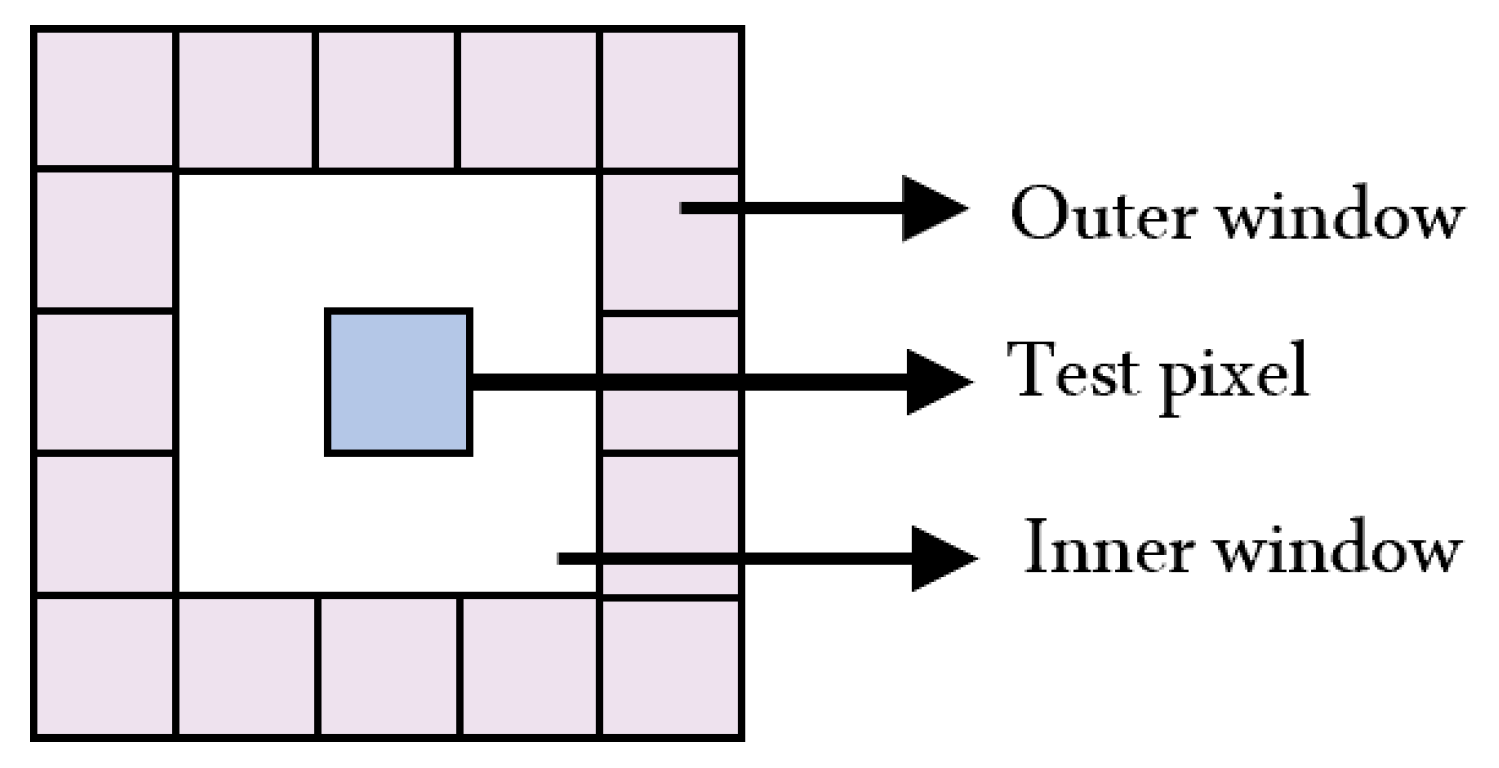
2.4. Multi-Directional Local RAD Detector
3. Experimental Analysis
3.1. Hyperspectral Datasets
3.2. Experimental Design
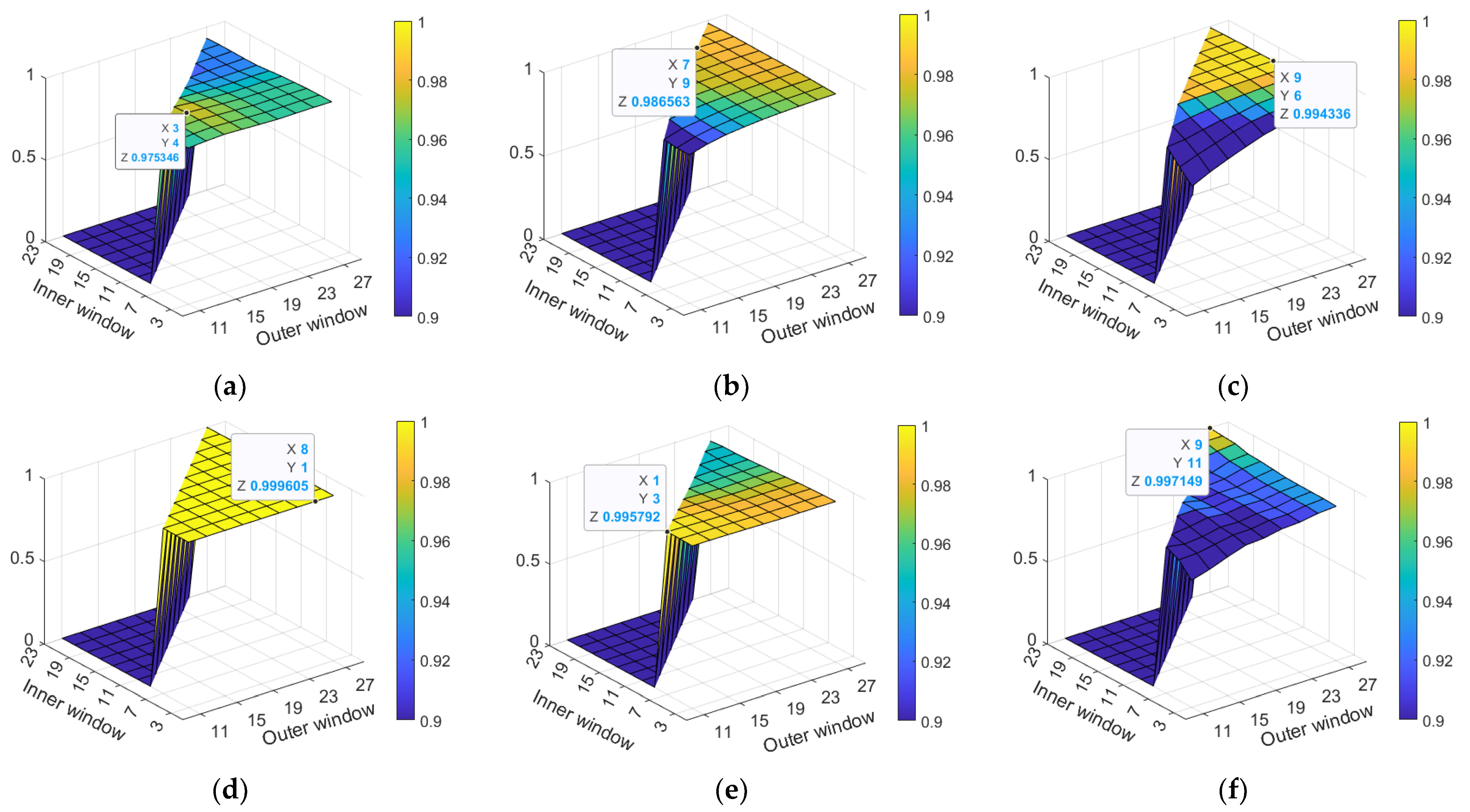
3.3. Parameter Analysis
3.4. Detection Performance
3.5. Ablation Experiment
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Z.; Ma, L.; Du, Q. Class-Wise Distribution Adaptation for Unsupervised Classification of Hyperspectral Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2021, 59, 508–521. [Google Scholar] [CrossRef]
- Li, F.; Song, M. Sequential Band Fusion for Hyperspectral Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5516324. [Google Scholar]
- Wang, Y.; Chen, X.; Zhao, E.; Zhao, C.; Song, M.; Yu, C. An Unsupervised Momentum Contrastive Learning Based Transformer Network for Hyperspectral Target Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 9053–9068. [Google Scholar]
- Khonina, S.N.; Kazanskiy, N.L.; Oseledets, I.V.; Nikonorov, A.V.; Butt, M.A. Synergy between Artificial Intelligence and Hyperspectral Imagining—A Review. Technologies 2024, 12, 163. [Google Scholar] [CrossRef]
- Li, F.; Song, M.; Yu, C.; Wang, Y.; Chang, C.-I. Progressive Band Subset Fusion for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5532724. [Google Scholar]
- Ji, L.; Geng, X. Hyperspectral Target Detection Methods Based on Statistical Information: The Key Problems and the Corresponding Strategies. Remote Sens. 2023, 15, 3835. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar]
- Li, Z.; Zhang, Y.; Zhang, J. Hyperspectral Anomaly Detection via Optimal Kernel and High-Order Moment Correlation Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3925–3937. [Google Scholar]
- Zhao, C.; Li, C.; Feng, S.; Su, N. Spectral-Spatial Stacked Autoencoders Based on the Bilateral Filter for Hyperspectral Anomaly Detection. In Proceedings of the IGARSS 2020—2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, HI, USA, 26 September–2 October 2020; pp. 2209–2212. [Google Scholar]
- Kayabol, K.; Aytekin, E.B.; Arisoy, S.; Kuruoglu, E.E. Skewed t-Distribution for Hyperspectral Anomaly Detection Based on Autoencoder. IEEE Geosci. Remote Sens. Lett. 2022, 19, 5510705. [Google Scholar]
- Zhang, X.; Ma, X.; Huyan, N.; Gu, J.; Tang, X.; Jiao, L. Spectral-Difference Low-Rank Representation Learning for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2021, 59, 10364–10377. [Google Scholar]
- Wu, Z.; Su, H.; Tao, X.; Han, L.; Paoletti, M.E.; Haut, J.M.; Plaza, J.; Plaza, A. Hyperspectral Anomaly Detection with Relaxed Collaborative Representation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5533417. [Google Scholar] [CrossRef]
- Hou, Z.; Li, W.; Tao, R.; Ma, P.; Shi, W. Collaborative representation with background purification and saliency weight for hyperspectral anomaly detection. Sci. China Inf. Sci. 2022, 65, 112305. [Google Scholar] [CrossRef]
- Ren, L.; Wang, M.; Sun, X.; Gao, L.; Huang, M. Hyperspectral Anomaly Detection Via Nonconvex Low-Rank Representation. In Proceedings of the 2023 13th Workshop on Hyperspectral Imaging and Signal Processing: Evolution in Remote Sensing (WHISPERS), Athens, Greece, 31 October–2 November 2023; pp. 1–5. [Google Scholar]
- Qin, H.; Shen, Q.; Zeng, H.; Chen, Y.; Lu, G. Generalized Nonconvex Low-Rank Tensor Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5526612. [Google Scholar] [CrossRef]
- Zhang, X.; Song, M. Go Decomposition-Based Model with Independent Component Analysis for Hyperspectral Anomaly Detection. In Proceedings of the IGARSS 2024—2024 IEEE International Geoscience and Remote Sensing Symposium, Athens, Greece, 7–12 July 2024; pp. 8303–8306. [Google Scholar]
- Cheng, T.; Wang, B. Graph and Total Variation Regularized Low-Rank Representation for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2020, 58, 391–406. [Google Scholar] [CrossRef]
- Wang, Q.; Zeng, J.; Wu, H.; Wang, J.; Sun, K. Self-Adaptive Low-Rank and Sparse Decomposition for Hyperspectral Anomaly Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 3672–3685. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Qu, Y.; Zhao, C.; Tao, R.; Du, Q. Prior-Based Tensor Approximation for Anomaly Detection in Hyperspectral Imagery. IEEE Trans. Neural Netw. Learn. Syst. 2022, 33, 1037–1050. [Google Scholar] [CrossRef]
- Li, W.; Yuan, F.; Zhang, H.; Lv, Z.; Wu, B. Hyperspectral Object Detection Based on Spatial–Spectral Fusion and Visual Mamba. Remote Sens. 2024, 16, 4482. [Google Scholar] [CrossRef]
- Li, Y.; Zhong, J.; Xie, W.; Gamba, P. Representation-Learning-Based Graph and Generative Network for Hyperspectral Small Target Detection. Remote Sens. 2024, 16, 3638. [Google Scholar] [CrossRef]
- Yang, Z.; Zhao, R.; Meng, X.; Yang, G.; Sun, W.; Zhang, S.; Li, J. A Multi-Scale Mask Convolution-Based Blind-Spot Network for Hyperspectral Anomaly Detection. Remote Sens. 2024, 16, 3036. [Google Scholar] [CrossRef]
- Tao, R.; Zhao, X.; Li, W.; Li, H.-C.; Du, Q. Hyperspectral Anomaly Detection by Fractional Fourier Entropy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 4920–4929. [Google Scholar] [CrossRef]
- Li, F.; Song, M.; Xue, B.; Yu, C. Abundance Estimation Based on Band Fusion and Prioritization Mechanism. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5532621. [Google Scholar]
- Song, M.; Li, F.; Yu, C.; Chang, C.-I. Sequential Band Fusion for Hyperspectral Anomaly Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5504916. [Google Scholar] [CrossRef]
- Molero, J.M.; Garzón, E.M.; García, I.; Plaza, A. Analysis and Optimizations of Global and Local Versions of the RX Algorithm for Anomaly Detection in Hyperspectral Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 801–814. [Google Scholar]
- Chen, Z.; Lu, Z.; Gao, H.; Zhang, Y.; Zhao, J.; Hong, D.; Zhang, B. Global to Local: A Hierarchical Detection Algorithm for Hyperspectral Image Target Detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5544915. [Google Scholar]
- Liu, H. Description Methods of Spatial Wind Along Railways. In Wind Forecasting in Railway Engineering; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Lei, W.; Ren, X.; Sun, Y.; Wang, D. Spectral-spatial Joint Method for Hyperspectral Anomaly Detection. Electro-Opt. Technol. Appl. 2016, 31, 36. [Google Scholar]
- Wang, S.; Feng, W.; Quan, Y.; Bao, W.; Dauphin, G.; Gao, L.; Zhong, X.; Xing, M. Subfeature Ensemble-Based Hyperspectral Anomaly Detection Algorithm. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 5943–5952. [Google Scholar] [CrossRef]
- Li, L.; Wu, Z.; Wang, B. Hyperspectral Anomaly Detection via Merging Total Variation into Low-Rank Representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 14894–14907. [Google Scholar] [CrossRef]
- Chang, C.-I.; Chiang, S.-S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar]
- Ma, Y.; Fan, G.; Jin, Q.; Huang, J.; Mei, X.; Ma, J. Hyperspectral Anomaly Detection via Integration of Feature Extraction and Background Purification. IEEE Geosci. Remote Sens. Lett. 2021, 18, 1436–1440. [Google Scholar] [CrossRef]
- Yuan, S.; Shi, L.; Yao, B.; Li, F.; Du, Y. A Hyperspectral Anomaly Detection Algorithm Using Sub-Features Grouping and Binary Accumulation. IEEE Geosci. Remote Sens. Lett. 2022, 19, 6007505. [Google Scholar] [CrossRef]
- Zhao, C.; Li, C.; Feng, S.; Su, N.; Li, W. A Spectral–Spatial Anomaly Target Detection Method Based on Fractional Fourier Transform and Saliency Weighted Collaborative Representation for Hyperspectral Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5982–5997. [Google Scholar] [CrossRef]
- Chang, C.-I. An Effective Evaluation Tool for Hyperspectral Target Detection: 3D Receiver Operating Characteristic Curve Analysis. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5131–5153. [Google Scholar]


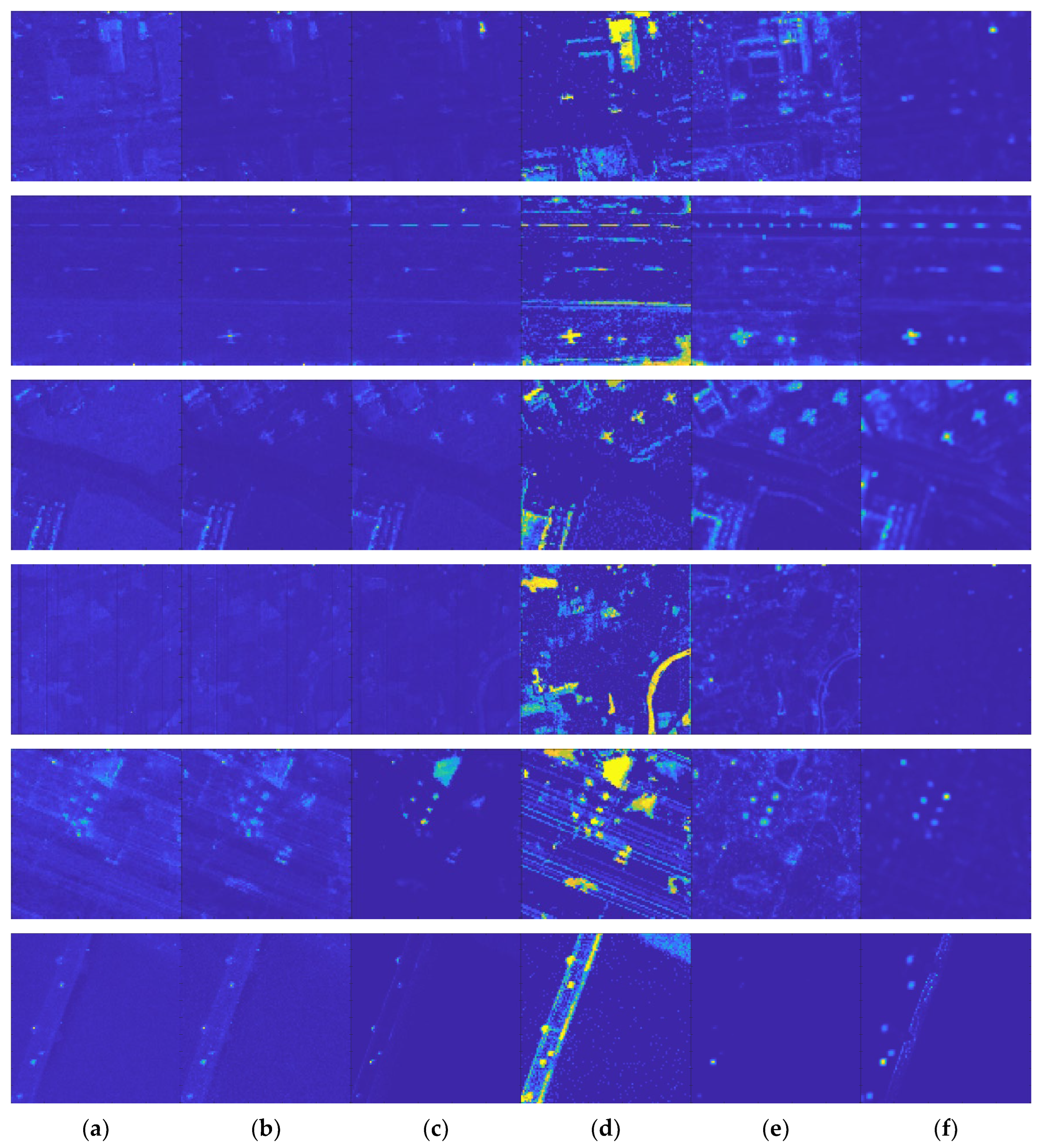


| Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|
| RAD | 0.8180 | 0.0998 | 0.0442 | 0.9178 | 0.7738 | 0.0556 | 1.0556 | 2.2579 |
| FrFE-RX | 0.8836 | 0.0439 | 0.0164 | 0.9275 | 0.8672 | 0.0275 | 1.0275 | 2.6768 |
| FEBPAD | 0.9092 | 0.0181 | 0.0079 | 0.9273 | 0.9013 | 0.0102 | 1.0102 | 2.2911 |
| SFBA-AD | 0.7639 | 0.3002 | 0.0983 | 1.0641 | 0.6656 | 0.2019 | 1.2019 | 3.0539 |
| SSFAD | 0.9518 | 0.2852 | 0.0524 | 1.2370 | 0.8994 | 0.2328 | 1.2328 | 5.4427 |
| proposed | 0.9753 | 0.1299 | 0.0149 | 1.1052 | 0.9604 | 0.1150 | 1.1150 | 8.7181 |
| Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|
| RAD | 0.9519 | 0.0707 | 0.0250 | 1.0226 | 0.9269 | 0.0457 | 1.0457 | 2.8280 |
| FrFE-RX | 0.9790 | 0.1319 | 0.0209 | 1.1109 | 0.9581 | 0.1110 | 1.1110 | 6.3110 |
| FEBPAD | 0.9631 | 0.0953 | 0.0226 | 1.0584 | 0.9405 | 0.0727 | 1.0727 | 4.2168 |
| SFBA-AD | 0.9758 | 0.7917 | 0.1019 | 1.7675 | 0.8739 | 0.6898 | 1.6898 | 7.7694 |
| SSFAD | 0.9781 | 0.4584 | 0.0388 | 1.4365 | 0.9393 | 0.4196 | 1.4196 | 11.8144 |
| proposed | 0.9866 | 0.2927 | 0.0165 | 1.2793 | 0.9701 | 0.2762 | 1.2762 | 17.7394 |
| Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|
| RAD | 0.8632 | 0.0655 | 0.0381 | 0.9287 | 0.8251 | 0.0274 | 1.0274 | 1.7192 |
| FrFE-RX | 0.9660 | 0.0880 | 0.0196 | 1.0540 | 0.9464 | 0.0684 | 1.0684 | 4.4898 |
| FEBPAD | 0.9766 | 0.1327 | 0.0266 | 1.1093 | 0.9500 | 0.1061 | 1.1061 | 4.9887 |
| SFBA-AD | 0.9837 | 0.7506 | 0.0827 | 1.7343 | 0.9010 | 0.6679 | 1.6679 | 9.0762 |
| SSFAD | 0.9829 | 0.3345 | 0.0358 | 1.3174 | 0.9471 | 0.2987 | 1.2987 | 9.3436 |
| proposed | 0.9943 | 0.3737 | 0.0487 | 1.3680 | 0.9456 | 0.3250 | 1.3250 | 7.6735 |
| Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|
| RAD | 0.9969 | 0.2165 | 0.0404 | 1.2134 | 0.9565 | 0.1761 | 1.1761 | 5.3589 |
| FrFE-RX | 0.9953 | 0.2331 | 0.0327 | 1.2284 | 0.9626 | 0.2004 | 1.2004 | 7.1284 |
| FEBPAD | 0.9927 | 0.1624 | 0.0197 | 1.1551 | 0.9730 | 0.1427 | 1.1427 | 8.2437 |
| SFBA-AD | 0.9362 | 0.5882 | 0.1260 | 1.5244 | 0.8102 | 0.4622 | 1.4622 | 4.6683 |
| SSFAD | 0.9790 | 0.2322 | 0.0241 | 1.2112 | 0.9549 | 0.2081 | 1.2081 | 9.6349 |
| proposed | 0.9996 | 0.1896 | 0.0037 | 1.1892 | 0.9959 | 0.1859 | 1.1859 | 51.2432 |
| Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|
| RAD | 0.9904 | 0.3240 | 0.0587 | 1.3144 | 0.9317 | 0.2653 | 1.2653 | 5.5196 |
| FrFE-RX | 0.9891 | 0.3001 | 0.0426 | 1.2892 | 0.9465 | 0.2575 | 1.2575 | 7.0446 |
| FEBPAD | 0.9820 | 0.3356 | 0.0106 | 1.3176 | 0.9714 | 0.3250 | 1.3250 | 31.6604 |
| SFBA-AD | 0.9591 | 0.8547 | 0.1463 | 1.8138 | 0.8128 | 0.7084 | 1.7084 | 5.8421 |
| SSFAD | 0.9951 | 0.4341 | 0.0352 | 1.4292 | 0.9599 | 0.3989 | 1.3989 | 12.3324 |
| proposed | 0.9957 | 0.1972 | 0.0600 | 1.1929 | 0.9357 | 0.1372 | 1.1372 | 3.2867 |
| Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|
| RAD | 0.9934 | 0.1604 | 0.0297 | 1.1538 | 0.9637 | 0.1307 | 1.1307 | 5.4007 |
| FrFE-RX | 0.9868 | 0.1812 | 0.0264 | 1.1680 | 0.9604 | 0.1548 | 1.1548 | 6.8636 |
| FEBPAD | 0.9840 | 0.1090 | 0.0025 | 1.0930 | 0.9815 | 0.1065 | 1.1065 | 43.6000 |
| SFBA-AD | 0.9921 | 0.9211 | 0.0872 | 1.9132 | 0.9049 | 0.8339 | 1.8339 | 10.5631 |
| SSFAD | 0.9960 | 0.1793 | 0.0041 | 1.1753 | 0.9819 | 0.1652 | 1.1652 | 12.7168 |
| proposed | 0.9971 | 0.2395 | 0.0141 | 1.2366 | 0.9930 | 0.2354 | 1.2354 | 58.4146 |
| Dataset | Method | AUC(D,F) | AUC(D,τ) | AUC(F,τ) | AUCTD | AUCBS | AUCTDBS | AUCODP | AUCSNPR |
|---|---|---|---|---|---|---|---|---|---|
| Los Angeles | FrFE-RX | 0.8836 | 0.0439 | 0.0164 | 0.9275 | 0.8672 | 0.0275 | 1.0275 | 2.6768 |
| FrFEBP-RX | 0.8960 | 0.0406 | 0.0130 | 0.9366 | 0.8830 | 0.0276 | 1.0276 | 3.1231 | |
| Gulfport | FrFE-RX | 0.9790 | 0.1319 | 0.0209 | 1.1109 | 0.9581 | 0.1110 | 1.1110 | 6.3110 |
| FrFEBP-RX | 0.9671 | 0.0796 | 0.0185 | 1.0467 | 0.9486 | 0.0611 | 1.0611 | 4.3027 | |
| San Diego | FrFE-RX | 0.9660 | 0.0880 | 0.0196 | 1.0540 | 0.9464 | 0.0684 | 1.0684 | 4.4898 |
| FrFEBP-RX | 0.9678 | 0.0597 | 0.0219 | 1.0275 | 0.9459 | 0.0378 | 1.0378 | 2.7260 | |
| Hyperion | FrFE-RX | 0.9953 | 0.2331 | 0.0327 | 1.2284 | 0.9626 | 0.2004 | 1.2004 | 7.1284 |
| FrFEBP-RX | 0.9976 | 0.2084 | 0.0258 | 1.2060 | 0.9718 | 0.1826 | 1.1826 | 8.0775 | |
| Texas Coast | FrFE-RX | 0.9891 | 0.3001 | 0.0426 | 1.2892 | 0.9465 | 0.2575 | 1.2575 | 7.0446 |
| FrFEBP-RX | 0.9903 | 0.2903 | 0.0442 | 1.2806 | 0.9461 | 0.2461 | 1.2461 | 6.5679 | |
| Pavia | FrFE-RX | 0.9868 | 0.1812 | 0.0264 | 1.1680 | 0.9604 | 0.1548 | 1.1548 | 6.8636 |
| FrFEBP-RX | 0.9893 | 0.2520 | 0.0257 | 1.2413 | 0.9636 | 0.2263 | 1.2263 | 9.8054 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Li, F.; Wang, L.; He, J. Multi-Directional Dual-Window Method Using Fractional Optimal-Order Fourier Transform for Hyperspectral Anomaly Detection. Remote Sens. 2025, 17, 1321. https://doi.org/10.3390/rs17081321
Wang J, Li F, Wang L, He J. Multi-Directional Dual-Window Method Using Fractional Optimal-Order Fourier Transform for Hyperspectral Anomaly Detection. Remote Sensing. 2025; 17(8):1321. https://doi.org/10.3390/rs17081321
Chicago/Turabian StyleWang, Jiahui, Fang Li, Liguo Wang, and Jianjun He. 2025. "Multi-Directional Dual-Window Method Using Fractional Optimal-Order Fourier Transform for Hyperspectral Anomaly Detection" Remote Sensing 17, no. 8: 1321. https://doi.org/10.3390/rs17081321
APA StyleWang, J., Li, F., Wang, L., & He, J. (2025). Multi-Directional Dual-Window Method Using Fractional Optimal-Order Fourier Transform for Hyperspectral Anomaly Detection. Remote Sensing, 17(8), 1321. https://doi.org/10.3390/rs17081321







