Analysis of Grassland Vegetation Coverage Changes and Driving Factors in China–Mongolia–Russia Economic Corridor from 2000 to 2023 Based on RF and BFAST Algorithm
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Research Data
2.2.1. Time-Series Remote Sensing Data Products
2.2.2. Land Cover Data
2.2.3. Topographic Data
2.2.4. Meteorological Data
2.2.5. The Field Measurement Data
2.3. Research Methodology
2.3.1. Machine Learning Regression
2.3.2. Technology Roadmap
2.3.3. BFAST Mutation Detection
2.3.4. Partial Correlation Analysis
2.3.5. Multiple Linear Regression
3. Results
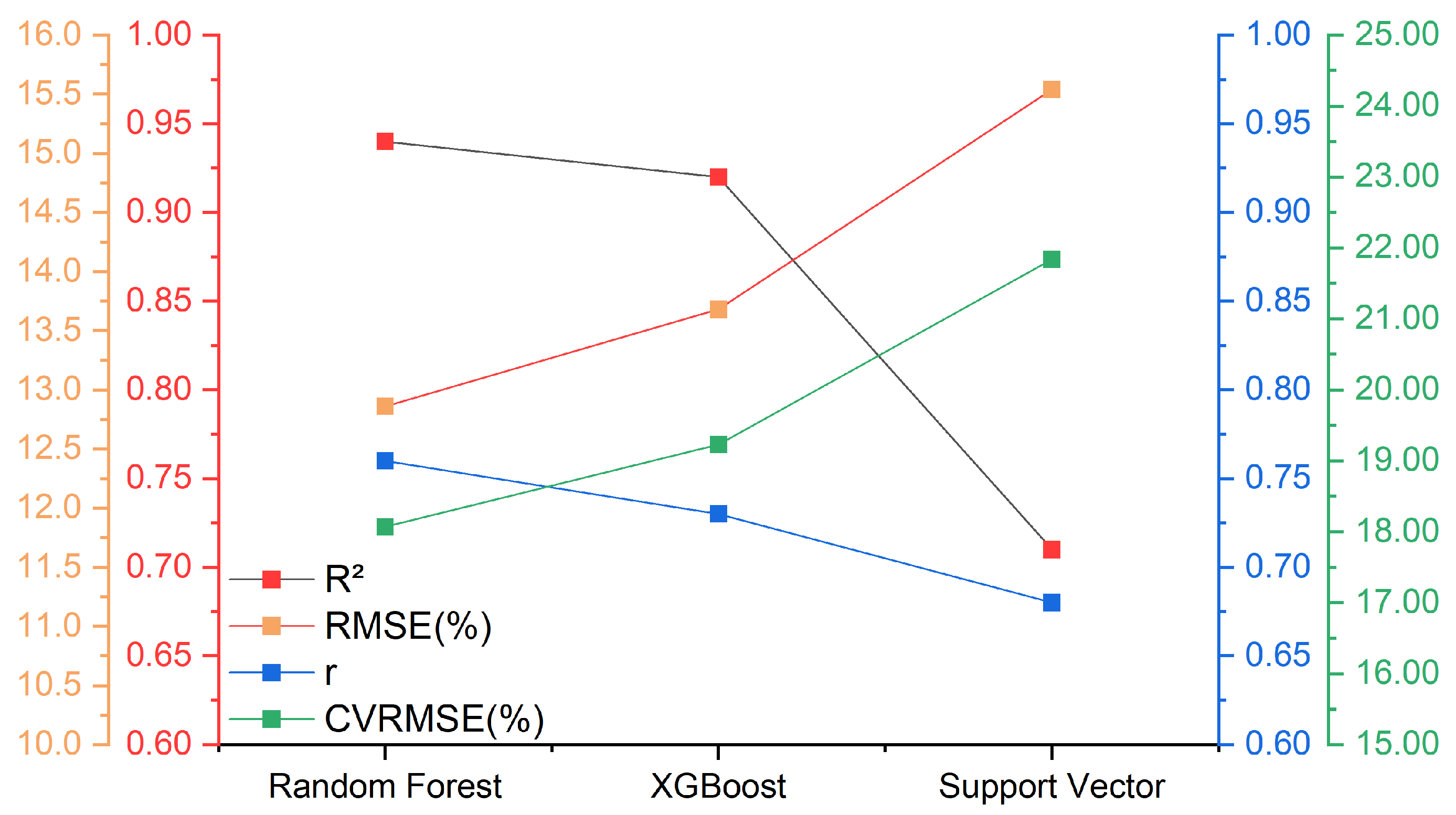
3.1. Evaluation of the Accuracy of the Regression Model
3.2. Spatial Distribution of Grassland Vegetation Cover
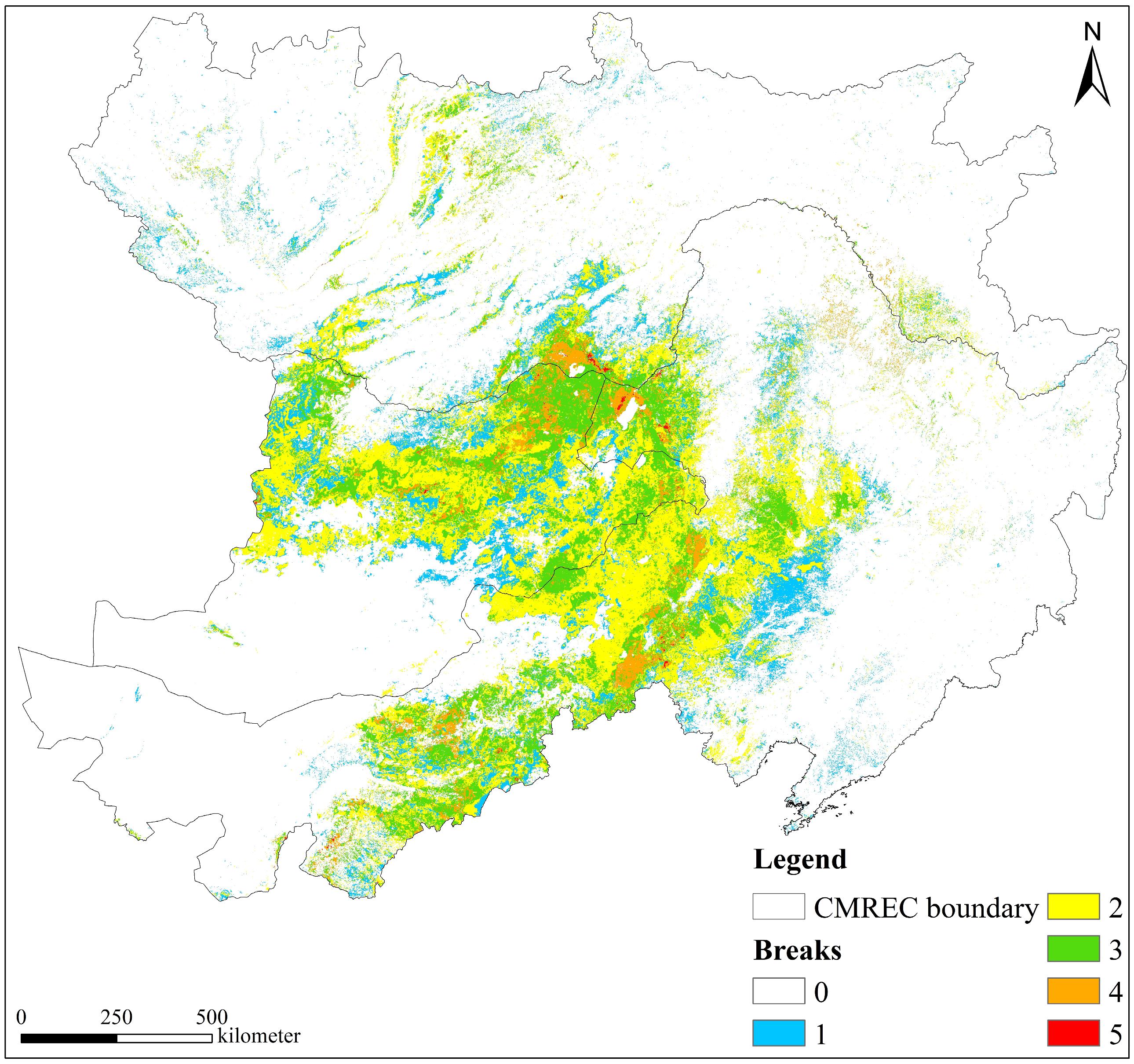
3.3. BFAST Mutation Information Extraction
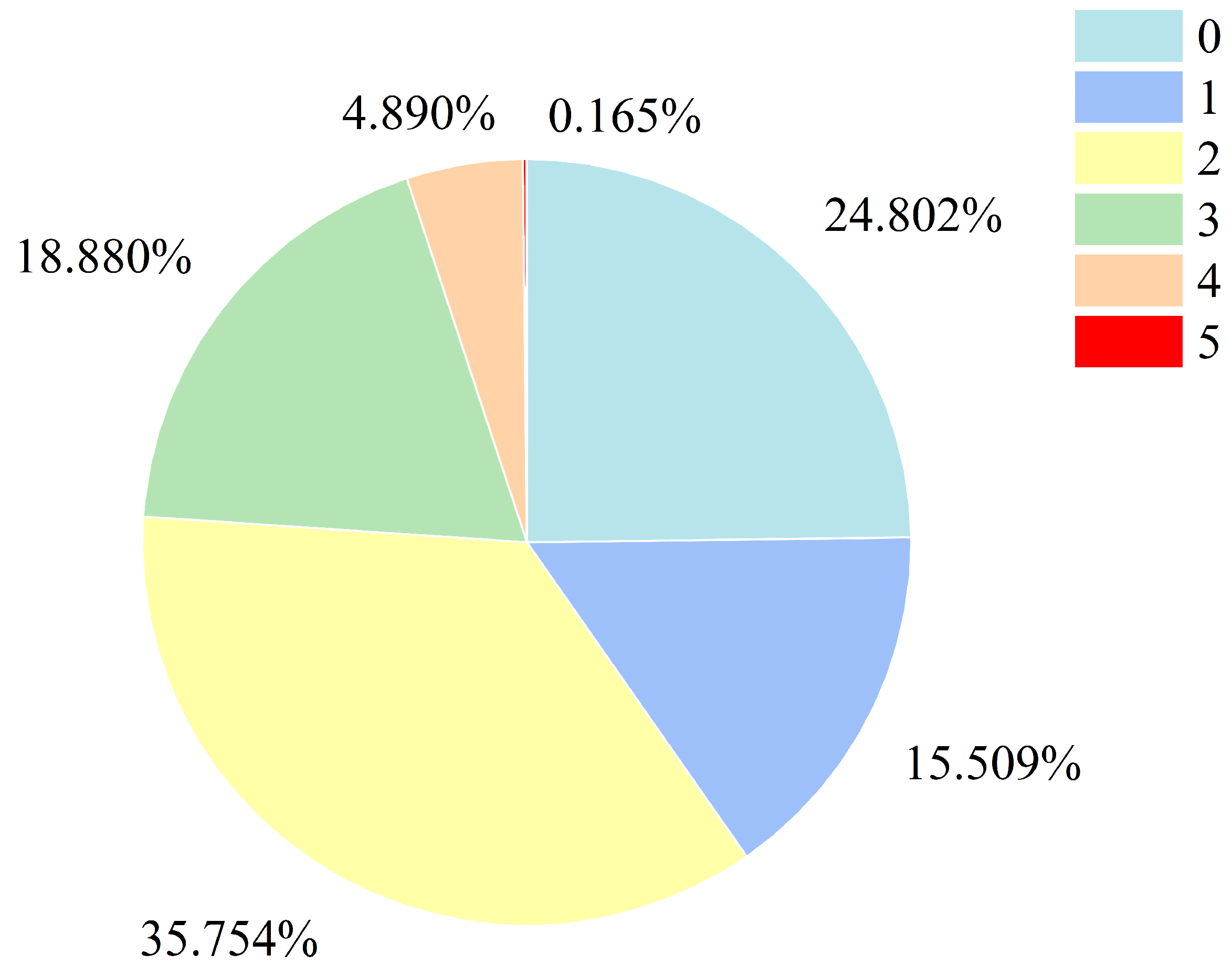
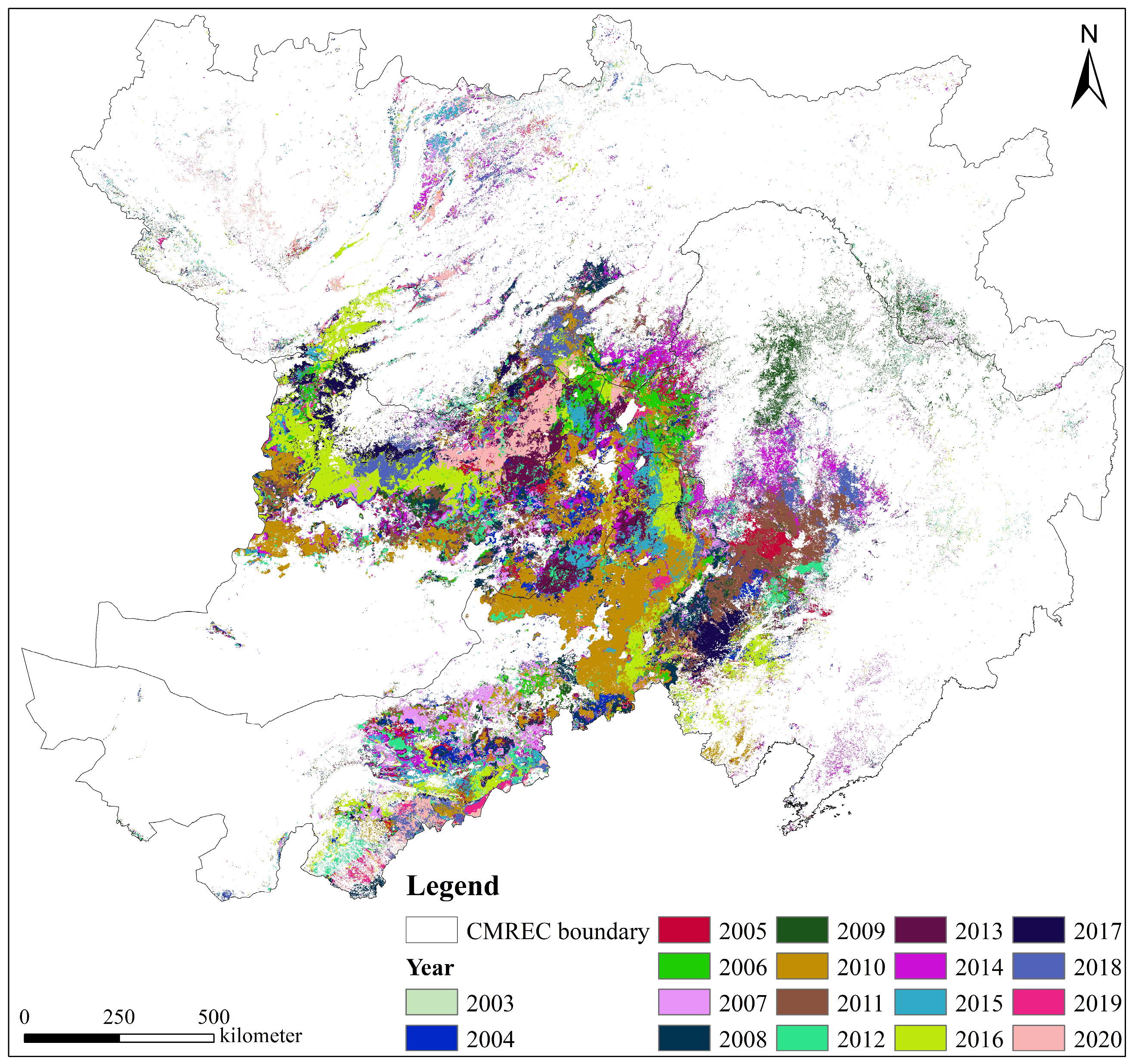
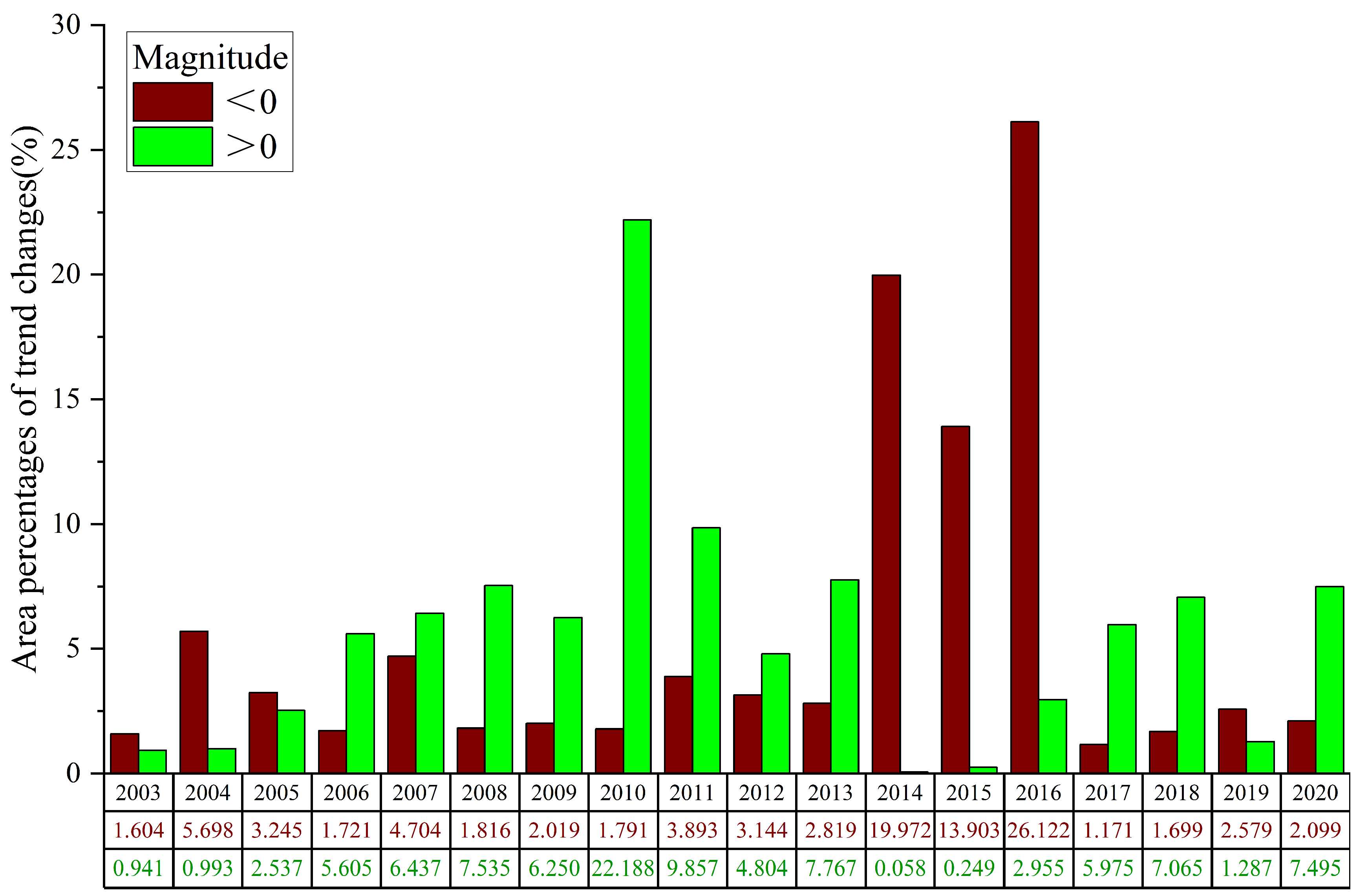
3.3.1. Number of Mutations
3.3.2. Year of Maximum Mutations
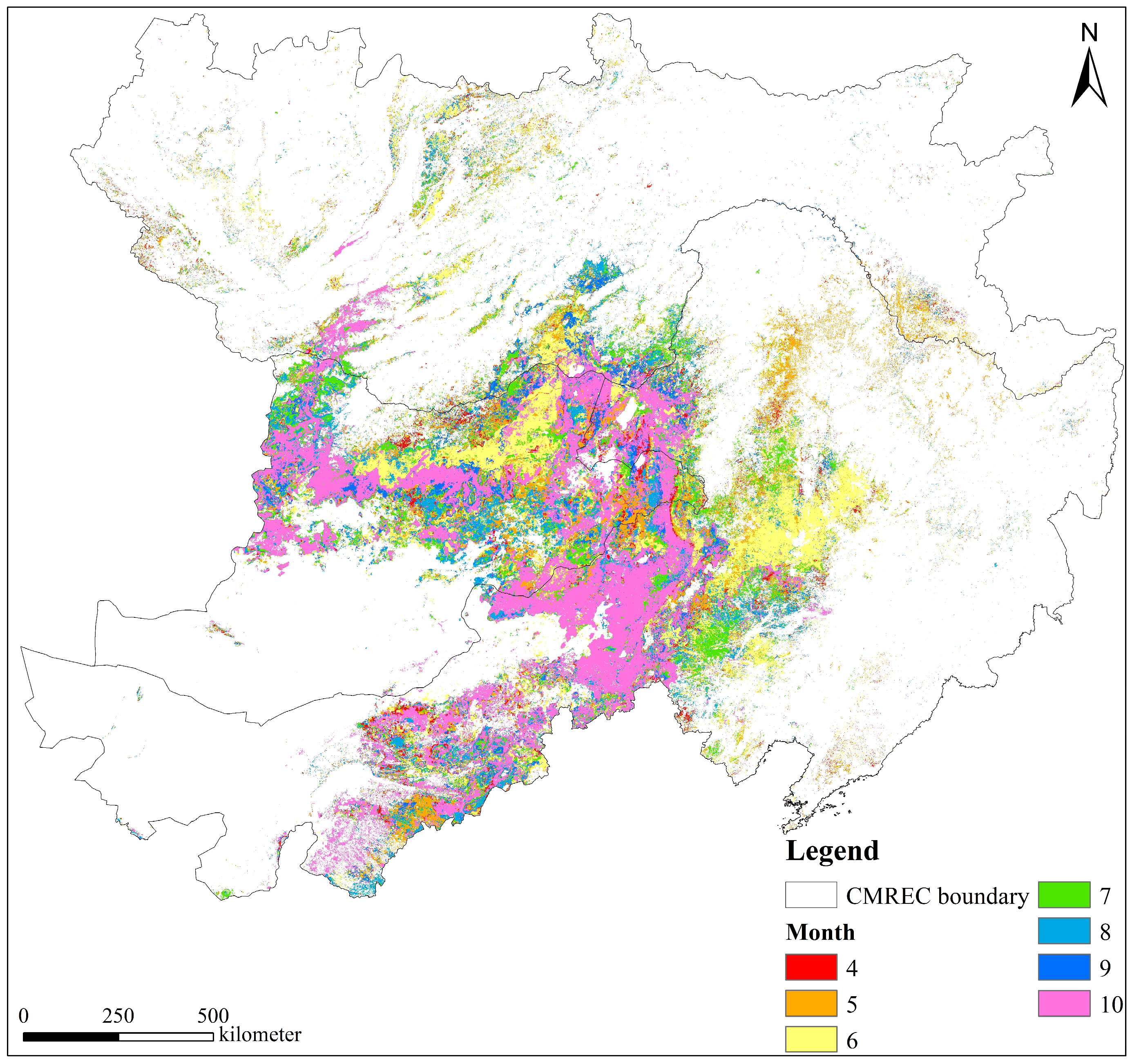
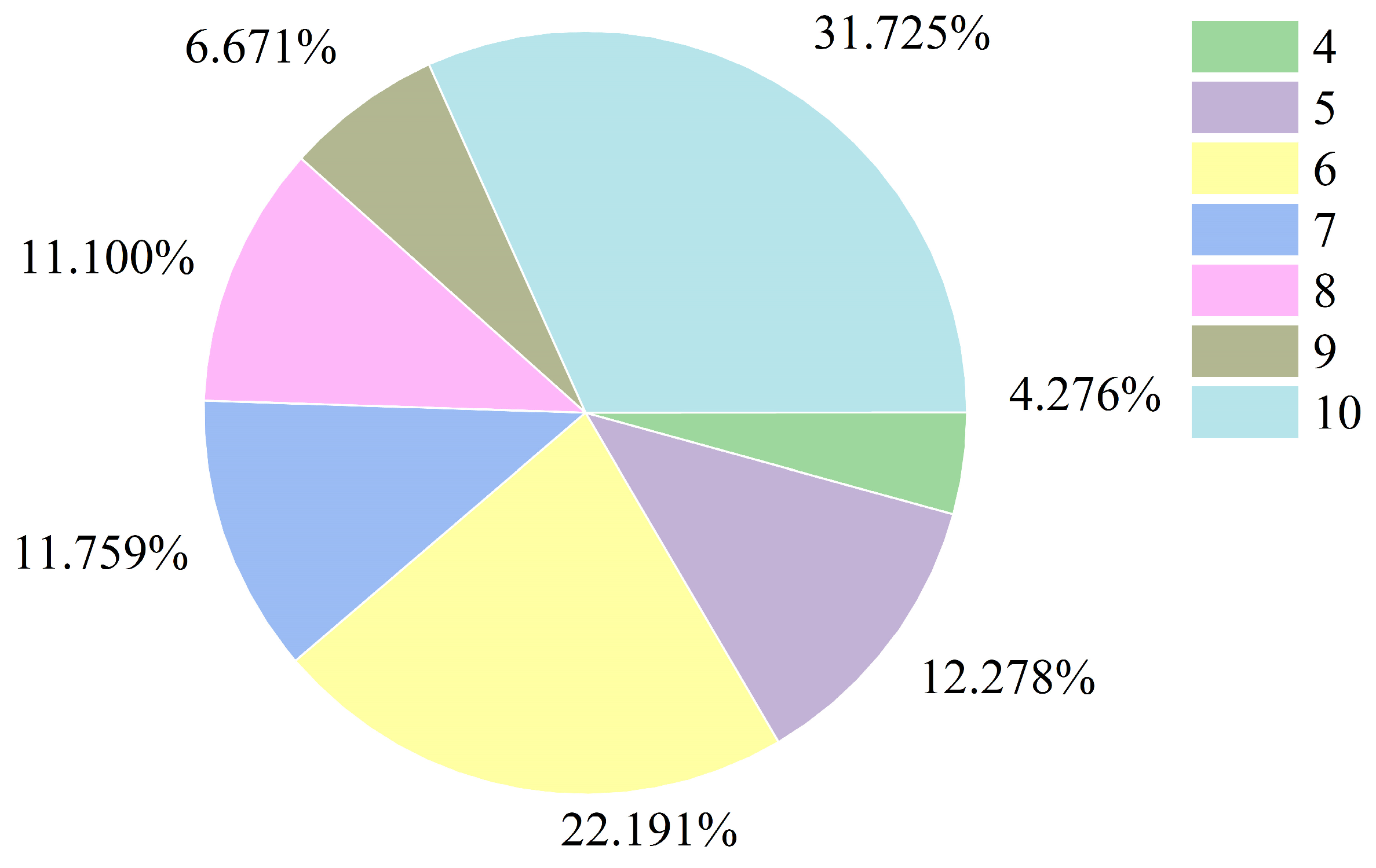
3.3.3. Month of Maximum Mutations
3.3.4. Magnitude of Mutations
3.4. Driving Factor Analysis
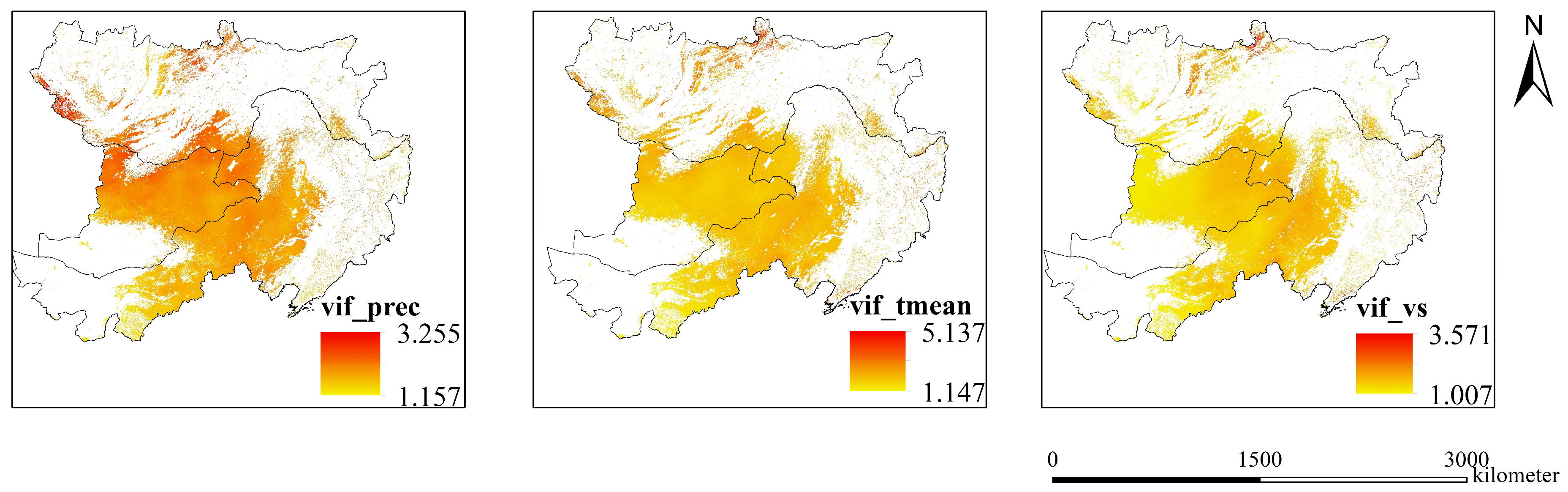
3.4.1. Multicollinearity Test
3.4.2. Partial Correlation Analysis Results Analysis
3.4.3. Multiple Linear Regression Results Analysis
3.4.4. Policy Implications
4. Discussion
5. Conclusions
- (1)
- The RF model is the optimal model for GVC inversion in this region. Compared to other machine learning regression models, such as XGBoost and SVM, the correlation coefficients (r) of the RF model improved by 3.94% and 11.76%, respectively, while the RMSE values decreased by 0.82% and 2.68%, respectively.
- (2)
- There was significant spatial heterogeneity in the distribution of GVC in CMREC. The overall trend of GVC in the study area showed a gradual decrease from northeast to southwest, as indicated by the constructed RF model, with only small differences in coverage between years.
- (3)
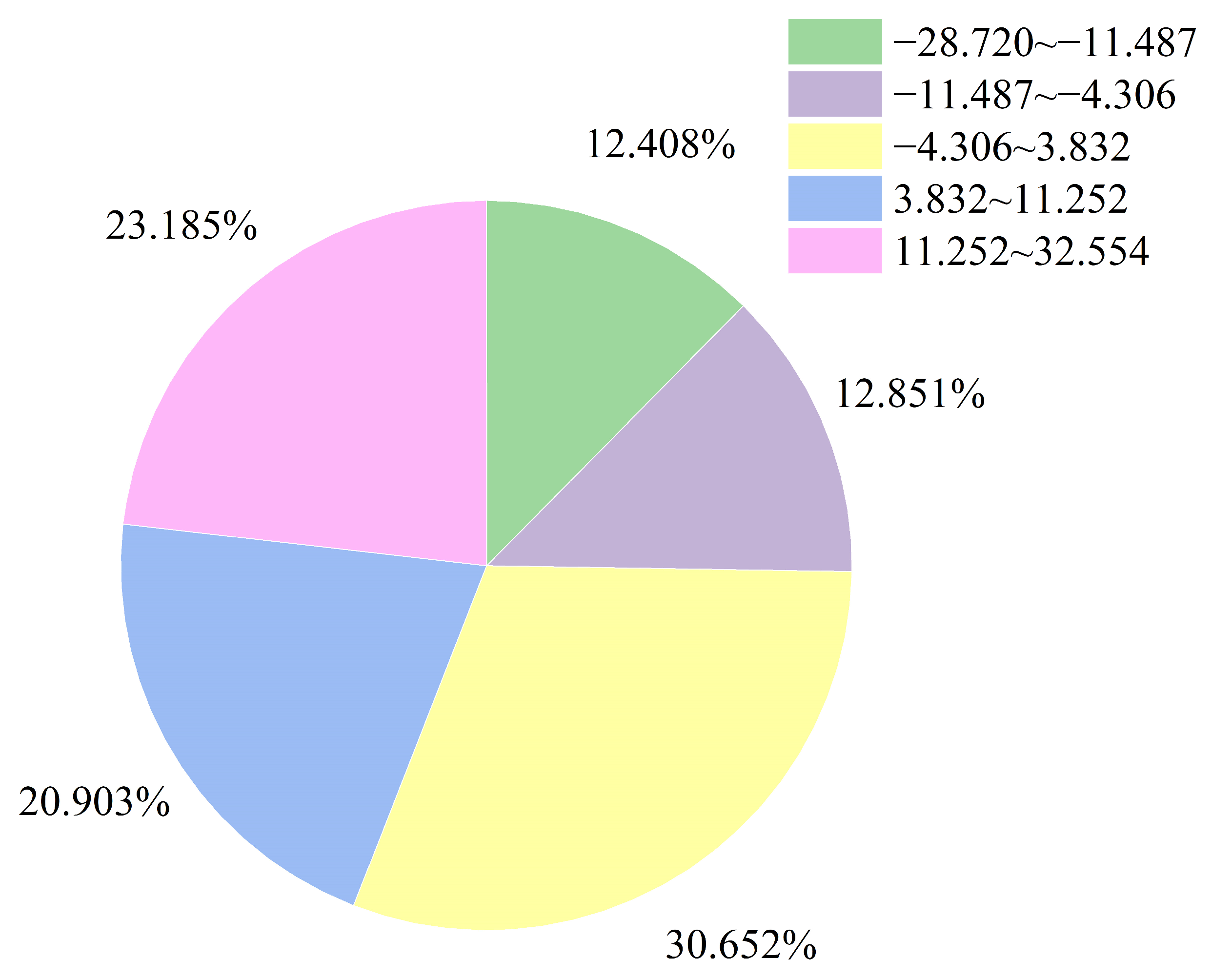
- The mutation information obtained from BFAST was analyzed, revealing that the most mutations occurred in 2010 and 2016, with area percentages of 14.573% and 11.604%, respectively. The majority of mutations occurred in October and June, accounting for 31.725% and 22.191% of all mutations, respectively. Spatially, positive mutations were mostly observed in the central region of Inner Mongolia, China, while negative mutations were primarily found in more desertified areas, particularly in Mongolia and the border region of China, Mongolia, and Russia. As the number of mutations increased, the proportion of intervals with mutations of magnitude 11.252 or more also increased, indicating that the overall GVC in the study area was trending positively.
- (4)
- Partial correlation and multiple linear regression analyses were conducted on precipitation, average temperature, and wind speed before and after the maximum mutations. The results concluded that precipitation is the most important factor influencing GVC mutations in CMREC, with a 43% positive impact enhancement, and it is relatively continuous and stable. Wind speed, on the other hand, had a 45% negative impact, primarily in the Mongolian region and the China–Mongolia–Russia tri-border area, which was unfavorable to grassland growth. Understanding the causes of mutations in GVC will help predict future changes and impacts on vegetation ecosystems, promoting grassland ecological conservation and sustainable development in the CMREC region.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, Y.; Liu, Z.; Wu, J. Grassland ecosystem services: A systematic review of research advances and future directions. Landsc. Ecol. 2020, 35, 793–814. [Google Scholar] [CrossRef]
- Shi, P.; Li, P.; Li, Z.; Sun, J.; Wang, D.; Min, Z. Effects of grass vegetation coverage and position on runoff and sediment yields on the slope of Loess Plateau, China. Agric. Water Manag. 2022, 259, 107231. [Google Scholar] [CrossRef]
- Li, M.; Bai, L.; Yang, L.; Wang, Q.; Zhu, J. Amount, distribution and controls of the soil organic carbon storage loss in the degraded China’s grasslands. Sci. Total Environ. 2024, 944, 173848. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Zhu, W.; He, B. Regional differences in the impact paths of climate on aboveground biomass in alpine grasslands across the Qinghai-Tibet Plateau. Sci. Total Environ. 2024, 947, 174421. [Google Scholar] [CrossRef]
- Fu, L.; Bo, T.; Du, G.; Zheng, X. Modeling the responses of grassland vegetation coverage to grazing disturbance in an alpine meadow. Ecol. Model. 2012, 247, 221–232. [Google Scholar] [CrossRef]
- Fan, Z.; Bai, R.; Yue, T.-X. Scenarios of land cover in Eurasia under climate change. J. Geogr. Sci. 2020, 30, 3–17. [Google Scholar] [CrossRef]
- Fan, Z.; Fan, B.; Yue, T.-X. Terrestrial ecosystem scenarios and their response to climate change in Eurasia. Sci. China Earth Sci. 2019, 62, 1607–1618. [Google Scholar] [CrossRef]
- Sternberg, T.; Rueff, H.; Middleton, N. Contraction of the Gobi Desert, 2000–2012. Remote Sens. 2015, 7, 1346–1358. [Google Scholar] [CrossRef]
- Cleland, E.; Collins, S.; Dickson, T.; Farrer, E.; Gherardi, L.; Hallett, L.; Hobbs, R.; Hsu, J.; Turnbull, L.; Suding, K. Sensitivity of grassland plant community composition to spatial vs. temporal variation in precipitation. Ecology 2013, 94, 1687–1696. [Google Scholar] [CrossRef]
- Gang, C.; Zhaoqi, W.; Yang, Y.; Chen, Y.Z.; Zhang, Y.; Li, J.L.; Cheng, J.M. The NPP spatiotemporal variation of global grassland ecosystems in response to climate change over the past 100 years. Acta Pratacult. Sin. 2016, 25, 1–14. [Google Scholar] [CrossRef]
- Mu, X.; Hu, M.; Song, W.; Ruan, G.; Ge, Y.; Wang, J.; Huang, S.; Yan, G. Evaluation of Sampling Methods for Validation of Remotely Sensed Fractional Vegetation Cover. Remote Sens. 2015, 7, 16164–16182. [Google Scholar] [CrossRef]
- Ding, Y.; Ge, Y.; Hu, M.; Zhang, H. Comparison of different spatial sampling methods for validation of GEOV1 FVC product over heterogeneous and homogeneous surfaces. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology XVIII, Edinburgh, UK, 25 October 2016; pp. 134–143. [Google Scholar]
- Weltz, M.; Ritchie, J.; Fox, H. Comparison of laser and field measurements of vegetation height and canopy cover. Water Resour. Res. 1994, 30, 1311–1320. [Google Scholar] [CrossRef]
- Gao, X.; Dong, S.; Li, S.; Xu, Y.; Liu, S.; Zhao, H.; Yeomans, J.; Li, Y.; Shen, H.; Wu, S.; et al. Using the random forest model and validated MODIS with the field spectrometer measurement promote the accuracy of estimating aboveground biomass and coverage of alpine grasslands on the Qinghai-Tibetan Plateau. Ecol. Indic. 2020, 112, 106114. [Google Scholar] [CrossRef]
- Tang, L.; He, M.; Li, X. Verification of Fractional Vegetation Coverage and NDVI of Desert Vegetation via UAVRS Technology. Remote Sens. 2020, 12, 1742. [Google Scholar] [CrossRef]
- Du, M.; Li, M.; Noguchi, N.; Ji, J.; Ye, M. Retrieval of Fractional Vegetation Cover from Remote Sensing Image of Unmanned Aerial Vehicle Based on Mixed Pixel Decomposition Method. Drones 2023, 7, 43. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, S.; Feng, K.; Kang, W.; Chen, X. Machine Learning-Based Remote Sensing Inversion of Non-Photosynthetic/Photosynthetic Vegetation Coverage in Desertified Areas and Its Response to Drought Analysis. Remote Sens. 2024, 16, 3226. [Google Scholar] [CrossRef]
- Weber, D.; Schwieder, M.; Ritter, L.; Koch, T.; Psomas, A.; Huber, N.; Ginzler, C.; Boch, S. Grassland-use intensity maps for Switzerland based on satellite time series: Challenges and opportunities for ecological applications. Remote Sens. Ecol. Conserv. 2023, 10, 312–327. [Google Scholar] [CrossRef]
- Ge, J.; Meng, B.; Liang, T.; Feng, Q.; Gao, J.; Yang, S.; Huang, X.; Xie, H. Modeling alpine grassland cover based on MODIS data and support vector machine regression in the headwater region of the Huanghe River, China. Remote Sens. Environ. 2018, 218, 162–173. [Google Scholar] [CrossRef]
- Wu, H.; An, S.; Meng, B.; Chen, X.; Li, F.; Ren, S. Retrieval of grassland aboveground biomass across three ecoregions in China during the past two decades using satellite remote sensing technology and machine learning algorithms. Int. J. Appl. Earth Obs. Geoinf. 2024, 130, 103925. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Y.; Qin, X.; Cai, J.; Cai, M.; Hou, X.; Yang, K.; Zhang, H. Assessing the Potential of UAV for Large-Scale Fractional Vegetation Cover Mapping with Satellite Data and Machine Learning. Remote Sens. 2024, 16, 3587. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, T.; Tong, X.; Duan, L.; Jia, T.; Ji, Y. Inversion of vegetation coverage based on multi-source remote sensing data and machine learning method in the Horqin Sandy Land, China. J. Desert Res. 2022, 42, 187. [Google Scholar]
- Yang, D.; Yang, Z.; Wen, Q.; Ma, L.; Guo, J.; Chen, A.; Zhang, M.; Xing, X.; Yuan, Y.; Lan, X.; et al. Dynamic monitoring of aboveground biomass in inner Mongolia grasslands over the past 23 Years using GEE and analysis of its driving forces. J. Environ. Manag. 2024, 354, 120415. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zeng, N.; Ren, X.; He, H.; Zhang, L.; Zhao, D.; Ge, R.; Li, P.; Niu, Z. Estimating grassland aboveground biomass on the Tibetan Plateau using a random forest algorithm. Ecol. Indic. 2019, 102, 479–487. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. Remote Sens. 2019, 154, 189–201. [Google Scholar] [CrossRef]
- Kennedy, R.; Yang, Z.; Cohen, W. Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sens. Environ. 2010, 114, 2897–2910. [Google Scholar] [CrossRef]
- Li, M.; Huang, C.; Zhu, Z.; Shi, H.; Lu, H.; Peng, S. Assessing rates of forest change and fragmentation in Alabama, USA, using the vegetation change tracker model. For. Ecol. Manag. 2009, 257, 1480–1488. [Google Scholar] [CrossRef]
- Jamali, S.; Jönsson, P.; Eklundh, L.; Ardö, J.; Seaquist, J. Detecting changes in vegetation trends using time series segmentation. Remote Sens. Environ. 2015, 156, 182–195. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Zhong, X.; Li, J.; Wang, J.; Zhang, J.; Liu, L.; Ma, J. Linear and Nonlinear Characteristics of Long-Term NDVI Using Trend Analysis: A Case Study of Lancang-Mekong River Basin. Remote Sens. 2022, 14, 6271. [Google Scholar] [CrossRef]
- Luo, S.; Liu, H.; Gong, H. Nonlinear trends and spatial pattern analysis of vegetation cover change in China from 1982 to 2018. Acta Ecol. Sin. 2022, 42, 8331–8342. [Google Scholar] [CrossRef]
- Schultz, M.; Clevers, J.G.P.W.; Carter, S.; Verbesselt, J.; Avitabile, V.; Quang, H.; Herold, M. Performance of vegetation indices from Landsat time series in deforestation monitoring. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 318–327. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Liu, Q.; Ding, M.; Mondal, P. Regional differences in shifts of temperature trends across China between 1980 and 2017. Int. J. Climatol. 2018, 39, 1157–1165. [Google Scholar] [CrossRef]
- Dupas, R.; Minaudo, C.; Gruau, G.; Ruiz, L.; Gascuel-Odoux, C. Multidecadal Trajectory of Riverine Nitrogen and Phosphorus Dynamics in Rural Catchments. Water Resour. Res. 2018, 54, 5327–5340. [Google Scholar] [CrossRef]
- Horion, S.; Ivits, E.; Keersmaecker, W.; Tagesson, T.; Vogt, J.; Fensholt, R. Mapping European ecosystem change types in response to land-use change, extreme climate events and land degradation. Land Degrad. Dev. 2019, 30, 951–963. [Google Scholar] [CrossRef]
- Ersi, C.; Bayaer, T.; Bao, Y.; Bao, Y.; Yong, M.; Zhang, X. Temporal and Spatial Changes in Evapotranspiration and Its Potential Driving Factors in Mongolia over the Past 20 Years. Remote Sens. 2022, 14, 1856. [Google Scholar] [CrossRef]
- Guo, E.; Wang, Y.; Wang, C.; Bao, Y.; Mandula, N.; Jirigala, B.; Bao, Y.; Li, H. NDVI Indicates Long-Term Dynamics of Vegetation and Its Driving Forces from Climatic and Anthropogenic Factors in Mongolian Plateau. Remote Sens. 2021, 13, 688. [Google Scholar] [CrossRef]
- Wu, D.; Zhao, X.; Liang, S.; Zhou, T.; Huang, K.; Tang, B.; Zhao, W. Time-lag Effects of Global Vegetation Responses to Climate Change. Glob. Change Biol. 2015, 21, 3520–3531. [Google Scholar] [CrossRef]
- Yiming, W.; Zhang, Z.; Chen, X. Quantifying Influences of Natural and Anthropogenic Factors on Vegetation Changes Based on Geodetector: A Case Study in the Poyang Lake Basin, China. Remote Sens. 2021, 13, 5081. [Google Scholar] [CrossRef]
- Offiong, R.; Iwara, A. Quantifying the Stock of Soil Organic Carbon using Multiple Regression Model in a Fallow Vegetation, Southern Nigeria. Ethiop. J. Environ. Stud. Manag. 2012, 5, 166–172. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Xu, X. Precipitation and Anthropogenic Activities Jointly Green the China–Mongolia–Russia Economic Corridor. Remote Sens. 2022, 14, 187. [Google Scholar] [CrossRef]
- Shi, H.; Gao, Q.; Qi, Y.; Liu, J.; Hu, Y. Wind erosion hazard assessment of the Mongolian Plateau using FCM and GIS techniques. Environ. Earth Sci. 2009, 61, 689–697. [Google Scholar] [CrossRef]
- Fang, J.; Bai, Y.; Wu, J. Towards a better understanding of landscape patterns and ecosystem processes of the Mongolian Plateau. Landsc. Ecol. 2015, 30, 1573–1578. [Google Scholar] [CrossRef]
- Fan, Z.; Li, S.; Fang, H. Explicitly Identifying the Desertification Change in CMREC Area Based on Multisource Remote Data. Remote Sens. 2020, 12, 3170. [Google Scholar] [CrossRef]
- Meng, B.; Jinlong, G.; Liang, T.; Cui, X.; Ge, J.; Yin, J.; Feng, Q.; Xie, H. Modeling of Alpine Grassland Cover Based on Unmanned Aerial Vehicle Technology and Multi-Factor Methods: A Case Study in the East of Tibetan Plateau, China. Remote Sens. 2018, 10, 320. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, Y.; Chen, C. Analysis of the Spatiotemporal Characteristics and Influencing Factors of the NDVI Based on the GEE Cloud Platform and Landsat Images. Remote Sens. 2023, 15, 4980. [Google Scholar] [CrossRef]
- Fu, B.; Yang, W.; Yao, H.; He, H.; Lan, G.; Gao, E.; Qin, J.; Donglin, F.; Chen, Z. Evaluation of spatio-temporal variations of FVC and its relationship with climate change using GEE and Landsat images in Ganjiang River Basin. Geocarto Int. 2022, 37, 13658–13688. [Google Scholar] [CrossRef]
- Wang, J.; Meng, S.; Zhu, W.; Xu, Z. Phenological Changes and Their Influencing Factors under the Joint Action of Water and Temperature in Northeast Asia. Remote Sens. 2023, 15, 5298. [Google Scholar] [CrossRef]
- De Cáceres, M.; Martin-StPaul, N.; Turco, M.; Cabon, A.; Granda, V. Estimating daily meteorological data and downscaling climate models over landscapes. Environ. Model. Softw. 2018, 108, 186–196. [Google Scholar] [CrossRef]
- Castro, W.; Junior, J.; Polidoro, C.; Osco, L.; Gonçalves, W.; Rodrigues, L.; Santos, M.; Jank, L.; Barrios, S.; Borges do Valle, C.; et al. Deep Learning Applied to Phenotyping of Biomass in Forages with UAV-Based RGB Imagery. Sensors 2020, 20, 4802. [Google Scholar] [CrossRef]
- Karila, K.; Alves de Oliveira, R.; Ek, J.; Kaivosoja, J.; Koivumäki, N.; Korhonen, P.; Niemeläinen, O.; Nyholm, L.; Näsi, R.; Pölönen, I.; et al. Estimating Grass Sward Quality and Quantity Parameters Using Drone Remote Sensing with Deep Neural Networks. Remote Sens. 2022, 14, 2692. [Google Scholar] [CrossRef]
- Yan, Y.; Liu, X.; Wen, Y.; Ou, J. Quantitative analysis of the contributions of climatic and human factors to grassland productivity in northern China. Ecol. Indic. 2019, 103, 542–553. [Google Scholar] [CrossRef]
- Yang, Y.; Zhaoqi, W.; Li, J.; Gang, C.; Zhang, Y.; Zhang, Y.; Odeh, I.; Qi, J. Comparative assessment of grassland degradation dynamics in response to climate variation and human activities in China, Mongolia, Pakistan and Uzbekistan from 2000 to 2013. J. Arid Environ. 2016, 135, 164–172. [Google Scholar] [CrossRef]
- Yan, X.; Li, J.; Shao, Y.; Hu, Z.; Yang, Q.; Shouqiang, Y.; Cui, L. Driving forces of grassland vegetation changes in Chen Barag Banner, Inner Mongolia. GISci. Remote Sens. 2020, 57, 753–769. [Google Scholar] [CrossRef]
- Chen, L.; Li, H.; Zhang, P.; Zhao, X.; Zhou, L.; Liu, T.; Hu, H.; Bai, Y.; Shen, H.; Fang, J. Climate and native grassland vegetation as drivers of the community structures of shrub-encroached grasslands in Inner Mongolia, China. Landsc. Ecol. 2014, 30, 1627–1641. [Google Scholar] [CrossRef]
- Zemmrich, A.; Manthey, M.; Zerbe, S.; Oyunchimeg, D. Driving environmental factors and the role of grazing in grassland communities: A comparative study along an altitudinal gradient in Western Mongolia. J. Arid Environ. 2010, 74, 1271–1280. [Google Scholar] [CrossRef]
- Yang, H.; Auerswald, K.; Gong, X.; Schnyder, H.; Bai, Y. Climate and anthropogenic drivers of changes in abundance of C4 annuals and perennials in grasslands on the Mongolian Plateau. Grassl. Res. 2022, 1, 131–141. [Google Scholar] [CrossRef]
- Pazur, R.; Prishchepov, A.; Mjachina, K.; Verburg, P.; Levykin, S.; Ponkina, E.; Kazachkov, G.; Yakovlev, I.; Akhmetov, R.; Rogova, N.; et al. Restoring steppe landscapes: Patterns, drivers and implications in Russia’s steppes. Landsc. Ecol. 2021, 36, 407–425. [Google Scholar] [CrossRef]
- Matasov, V.; Prishchepov, A.; Jepsen, M.; Müller, D. Spatial determinants and underlying drivers of land-use transitions in European Russia from 1770 to 2010. J. Land Use Sci. 2019, 14, 362–377. [Google Scholar] [CrossRef]
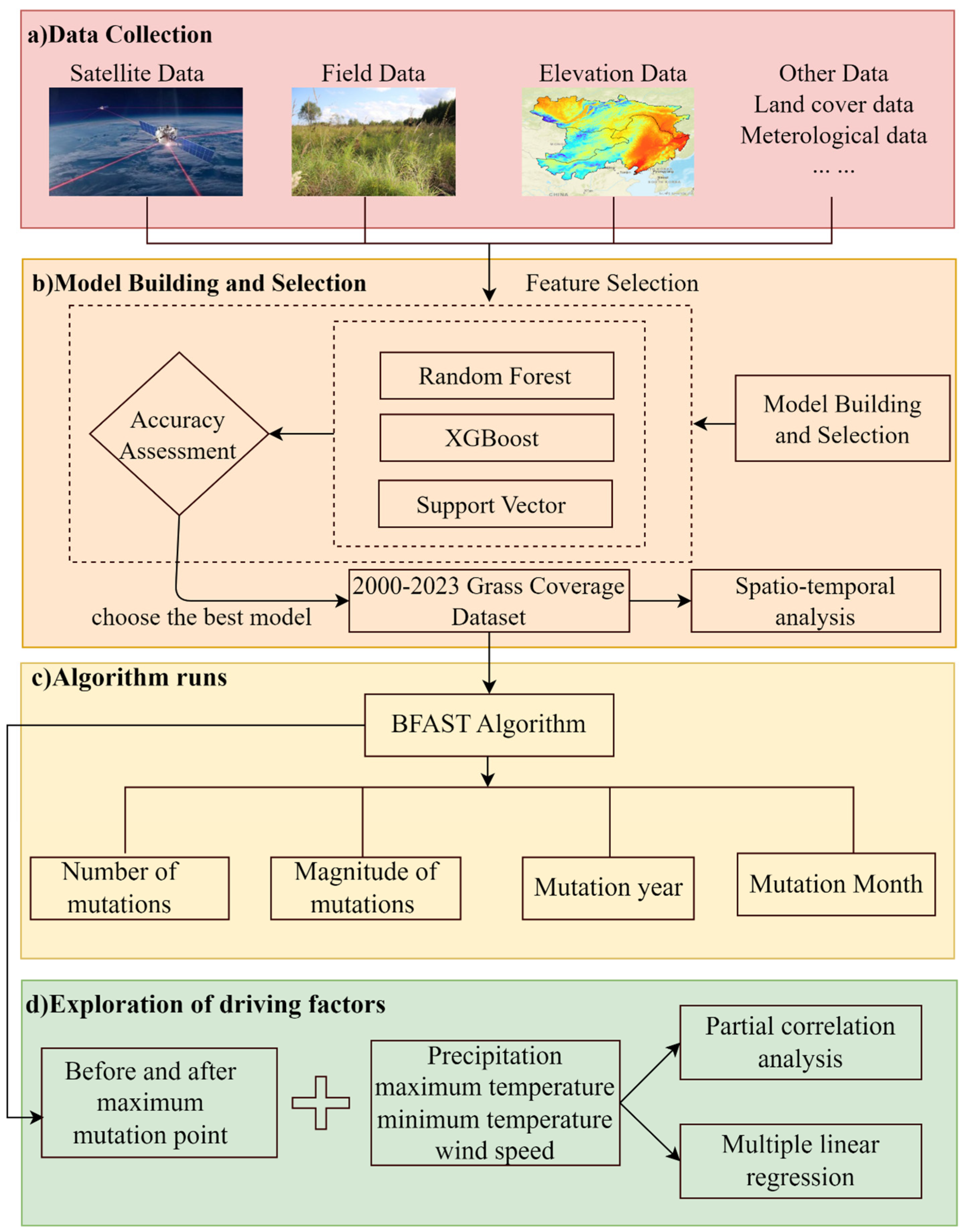




| Type of Data | Secondary Data Type | Spatial Resolution | Years | Data Sources |
|---|---|---|---|---|
| Vegetation Index Data | NDVI | 1 km | 2000–2023 April–October | MOD13A3 |
| EVI | ||||
| SAVI | 500 m → 1 km | MOD09A1 | ||
| Topography Data | DEM | 30 m → 1 km | / | SRTM Version 4 |
| Meteorological Data | Tmmx | 4.6 km → 1 km | 2000–2023 April–October | TerraClimate |
| Tmmn | ||||
| Precipitation | ||||
| Wind speed | ||||
| Soil moisture | ||||
| Air pressure | 11.1 km → 1 km | ERA5Land |
| Breakpoints | −28.720~−11.487 | −11.487~−4.306 | −4.306~3.832 | 3.832~11.252 | 11.252~32.554 |
|---|---|---|---|---|---|
| 1 | 7.108% | 13.151% | 29.279% | 46.051% | 4.411% |
| 2 | 18.524% | 23.165% | 3.093% | 28.200% | 27.018% |
| 3 | 18.763% | 11.940% | 1.036% | 17.427% | 50.834% |
| 4 | 22.383% | 5.531% | 0.158% | 7.712% | 64.215% |
| 5 | 27.765% | 2.866% | 0.029% | 6.630% | 62.710% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiu, C.; Zhang, C.; Ma, J.; Yang, C.; Wang, J.; Mandakh, U.; Ganbat, D.; Myanganbuu, N. Analysis of Grassland Vegetation Coverage Changes and Driving Factors in China–Mongolia–Russia Economic Corridor from 2000 to 2023 Based on RF and BFAST Algorithm. Remote Sens. 2025, 17, 1334. https://doi.org/10.3390/rs17081334
Qiu C, Zhang C, Ma J, Yang C, Wang J, Mandakh U, Ganbat D, Myanganbuu N. Analysis of Grassland Vegetation Coverage Changes and Driving Factors in China–Mongolia–Russia Economic Corridor from 2000 to 2023 Based on RF and BFAST Algorithm. Remote Sensing. 2025; 17(8):1334. https://doi.org/10.3390/rs17081334
Chicago/Turabian StyleQiu, Chi, Chao Zhang, Jiani Ma, Cuicui Yang, Jiayue Wang, Urtnasan Mandakh, Danzanchadav Ganbat, and Nyamkhuu Myanganbuu. 2025. "Analysis of Grassland Vegetation Coverage Changes and Driving Factors in China–Mongolia–Russia Economic Corridor from 2000 to 2023 Based on RF and BFAST Algorithm" Remote Sensing 17, no. 8: 1334. https://doi.org/10.3390/rs17081334
APA StyleQiu, C., Zhang, C., Ma, J., Yang, C., Wang, J., Mandakh, U., Ganbat, D., & Myanganbuu, N. (2025). Analysis of Grassland Vegetation Coverage Changes and Driving Factors in China–Mongolia–Russia Economic Corridor from 2000 to 2023 Based on RF and BFAST Algorithm. Remote Sensing, 17(8), 1334. https://doi.org/10.3390/rs17081334






