Estimating Spatiotemporal Dynamics of Carbon Storage in Roinia pseudoacacia Plantations in the Caijiachuan Watershed Using Sample Plots and Uncrewed Aerial Vehicle-Borne Laser Scanning Data
Abstract
1. Introduction
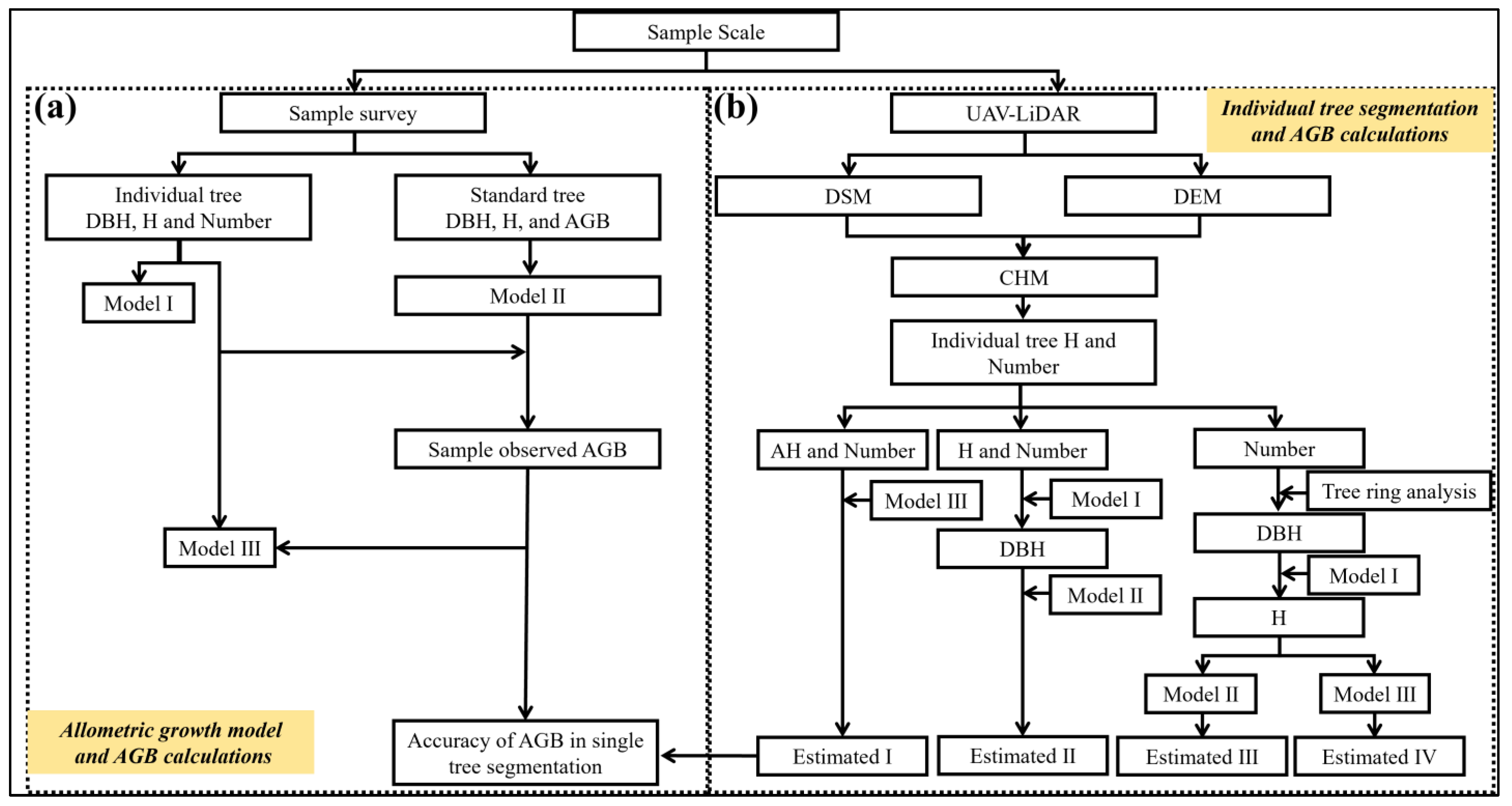
2. Materials and Methods
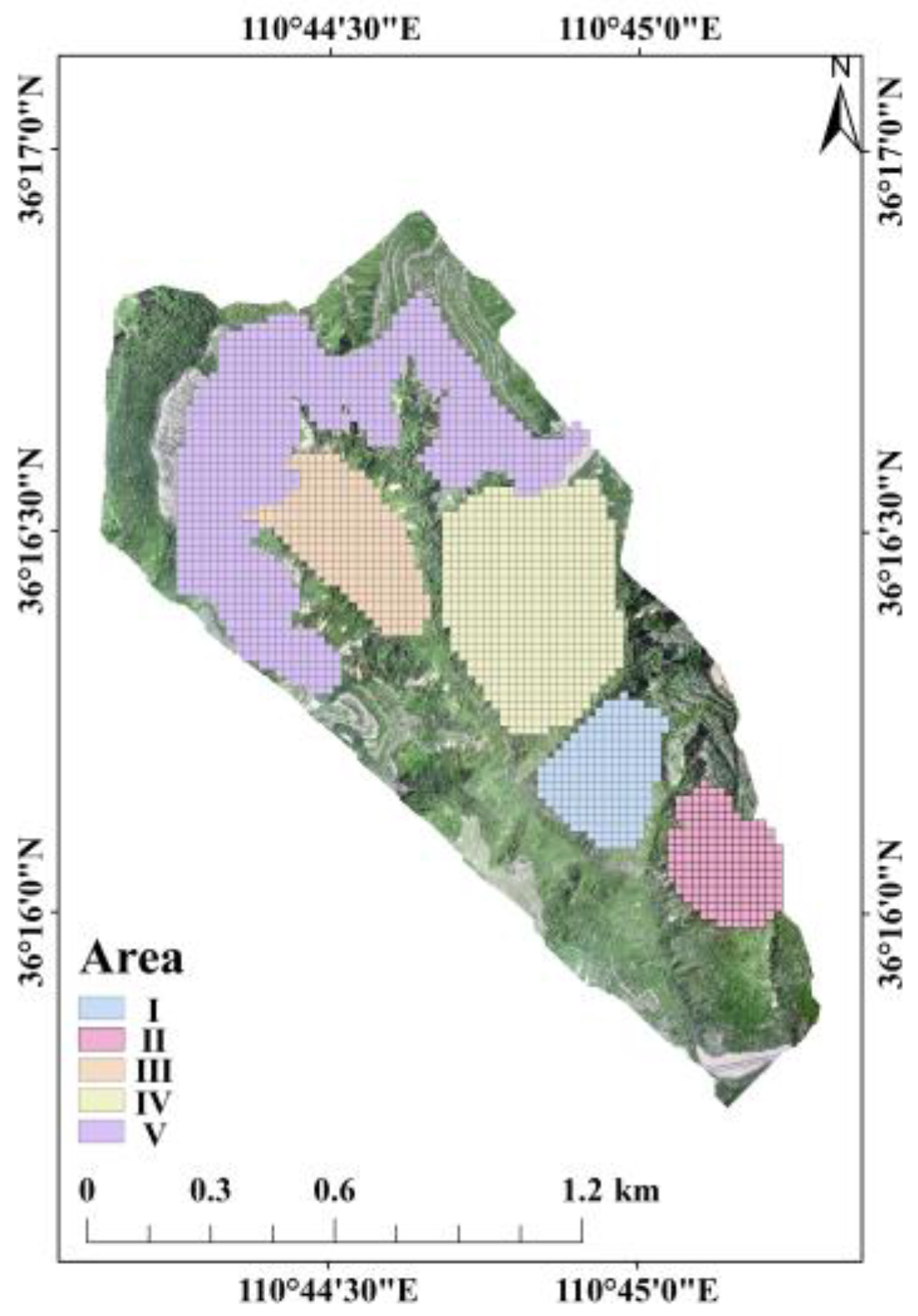
2.1. Study Area
2.2. Field Data Collection
2.3. R. pseudoacacia AGB Survey
2.4. Disk Collection, Processing, and Analysis
2.5. Individual Tree AGB Model and H-DBH Model Construction
2.6. Sample Plot AGB of R. pseudoacacia Model Construction
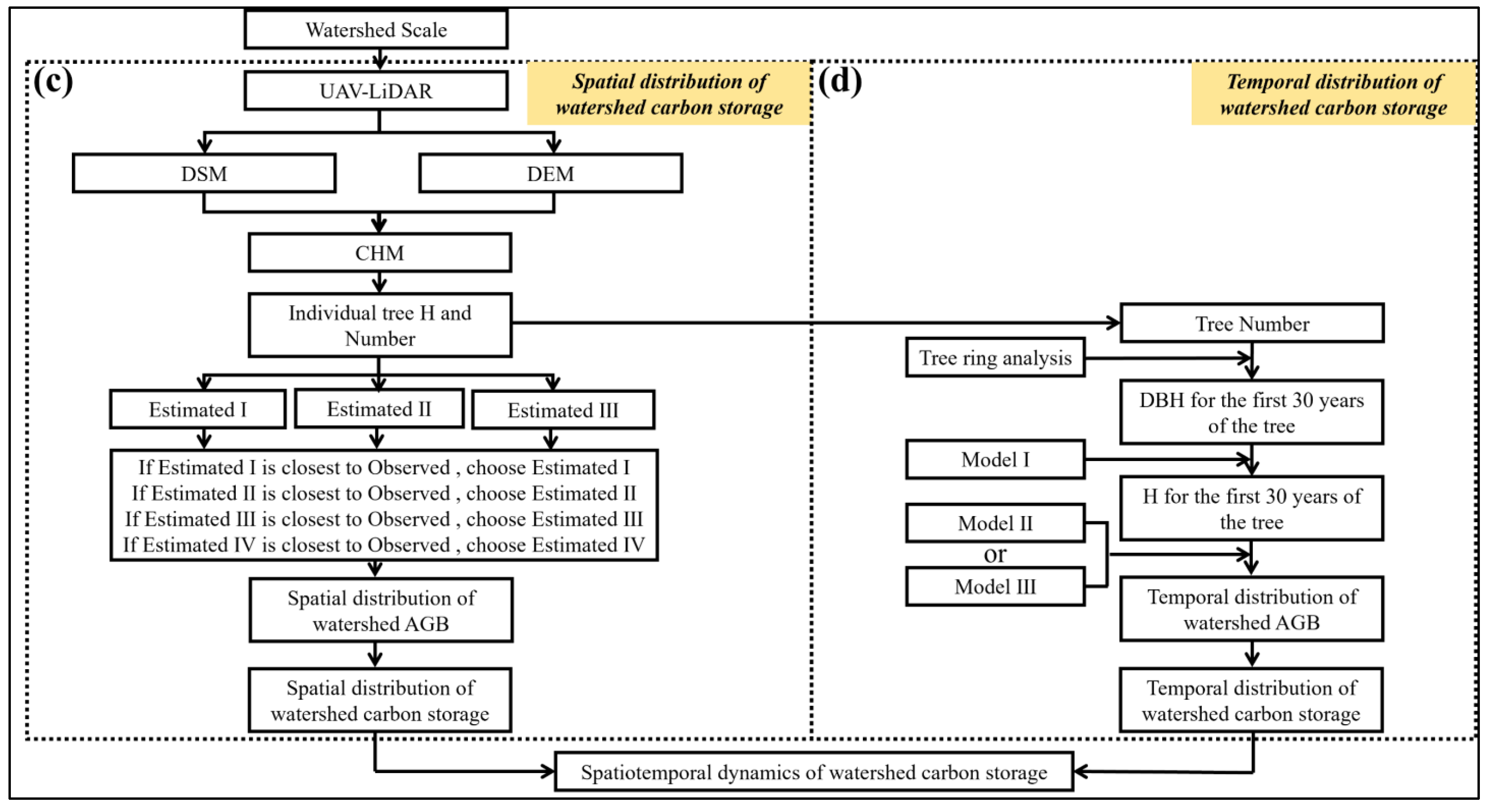
2.7. Carbon Storages Calculation
2.8. Data Acquisition and Preprocessing
2.8.1. Data Acquisition
2.8.2. Data Preprocessing
2.8.3. ITS and Forest Stand Parameter Extraction
2.8.4. Accuracy of ITS
2.8.5. Extraction Error of Forest Stand Parameters
2.8.6. Biomass Estimation Methods
2.9. Mapping the Spatiotemporal Distribution of Carbon Sink Capacity at the Watershed Scale
3. Results
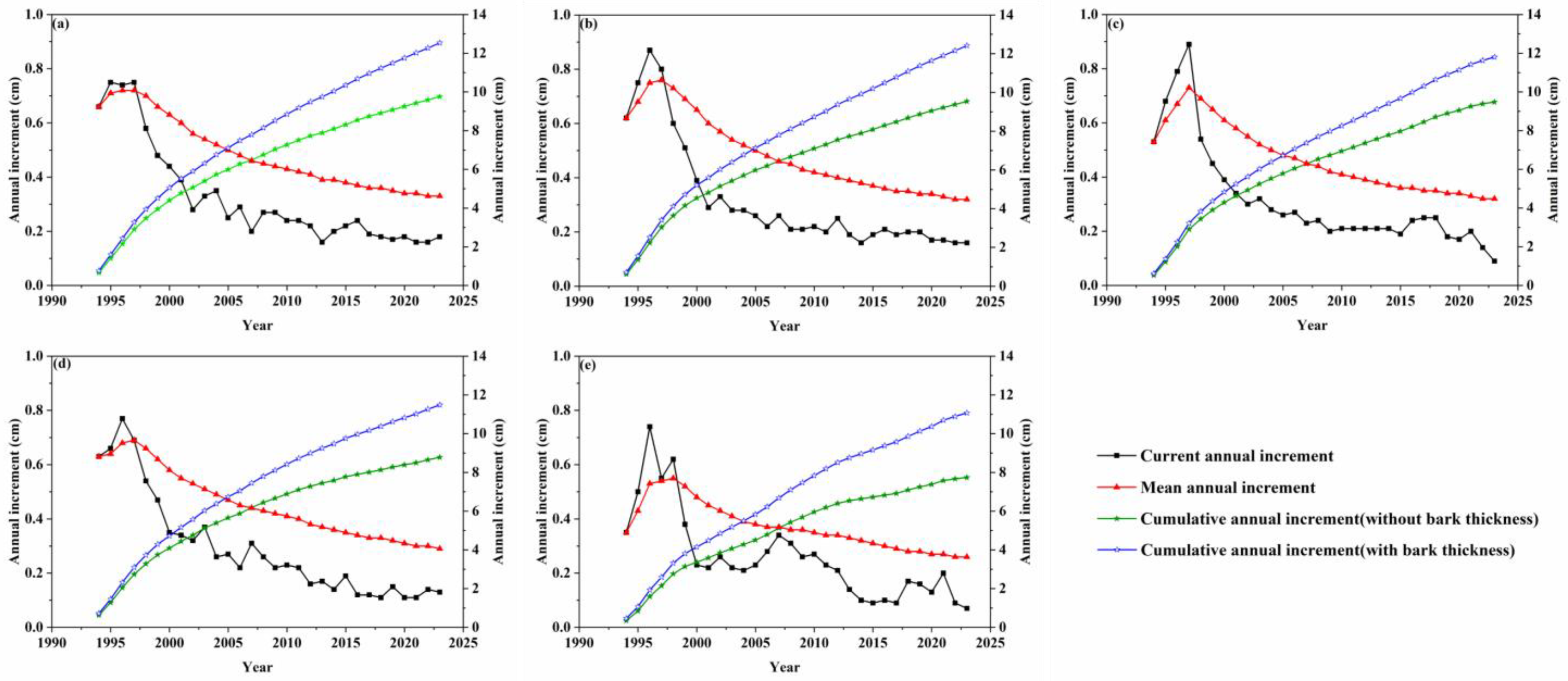
3.1. Growth Process and AGB Estimation of R. pseudoacacia
3.1.1. R. pseudoacacia Growth Curve
3.1.2. H-DBH Model
3.1.3. Individual Tree AGB of R. pseudoacacia Model Construction
3.1.4. Sample Plot Observed AGB of R. pseudoacacia Observed
3.1.5. Sample Plot AGB of R. pseudoacacia Model
3.2. The Effect of Point Cloud Data Segmentation Window Size on ITS
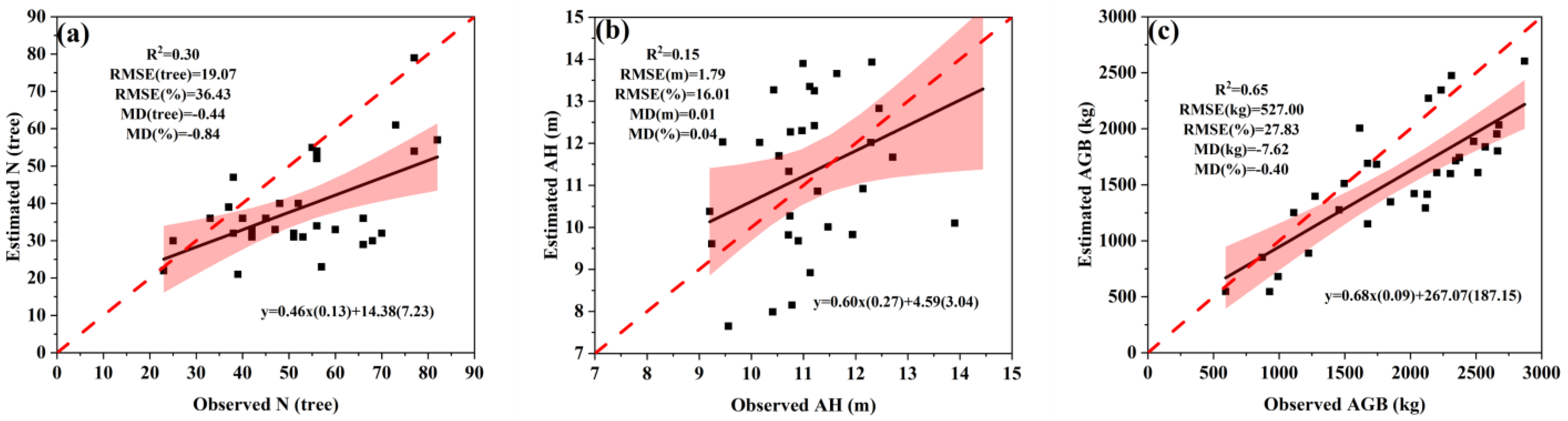
3.2.1. ITS Accuracy
3.2.2. Error of N, AH and AGB
3.3. Spatial Distribution Characteristics of Stand Parameters at the Watershed Scale
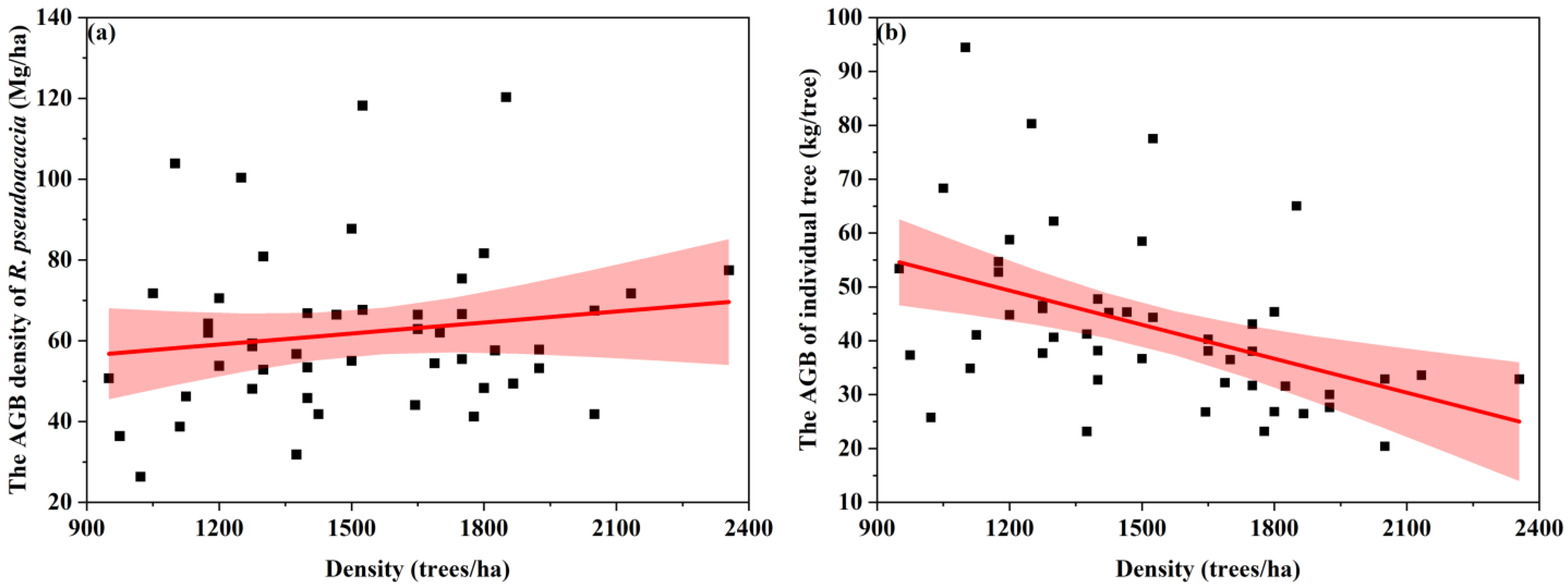
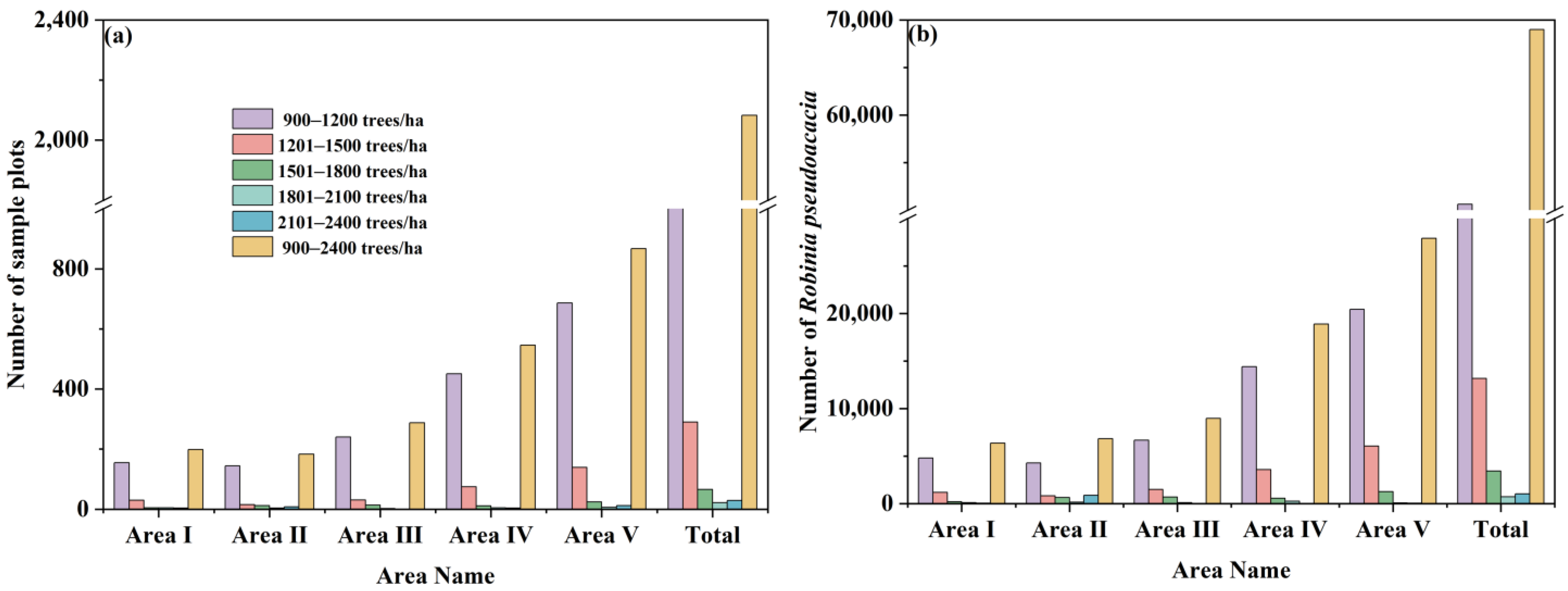
3.3.1. R. pseudoacacia Density at the Watershed Scale
3.3.2. The Average Tree Height at the Watershed
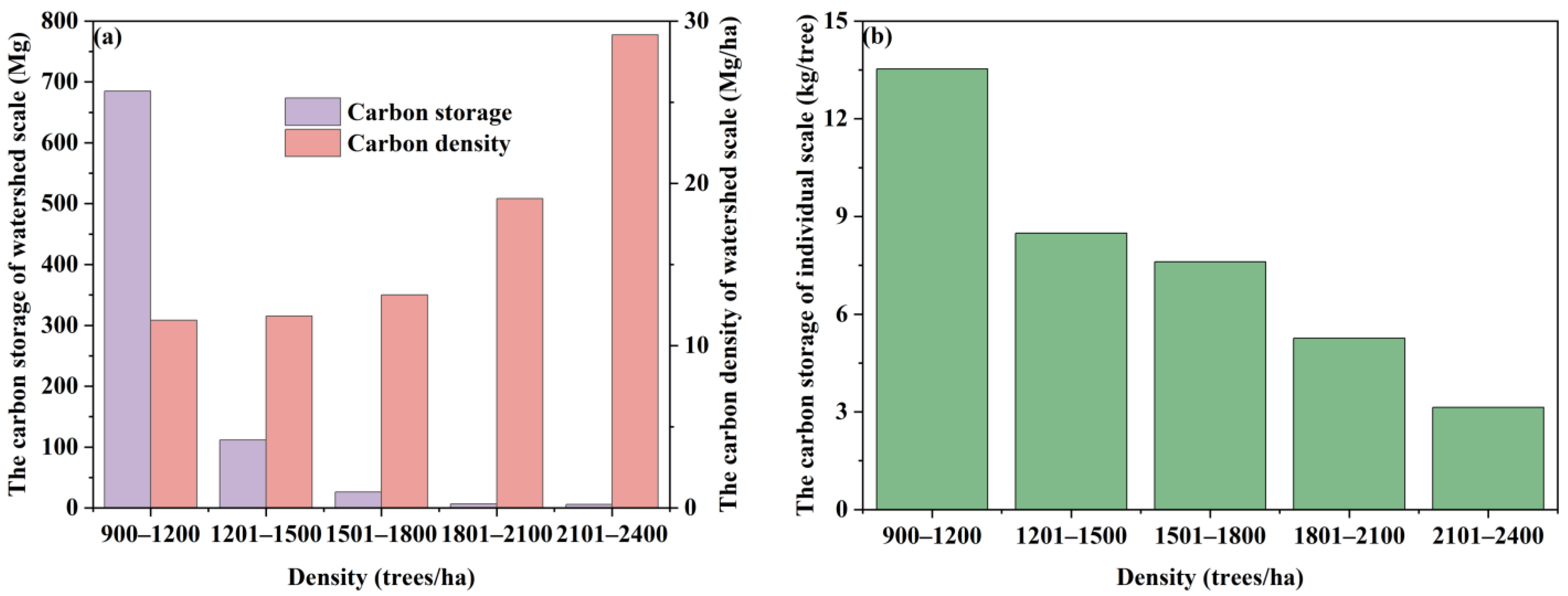
3.3.3. Estimating the Spatial Distribution of Carbon Storage and Carbon Density at the Watershed
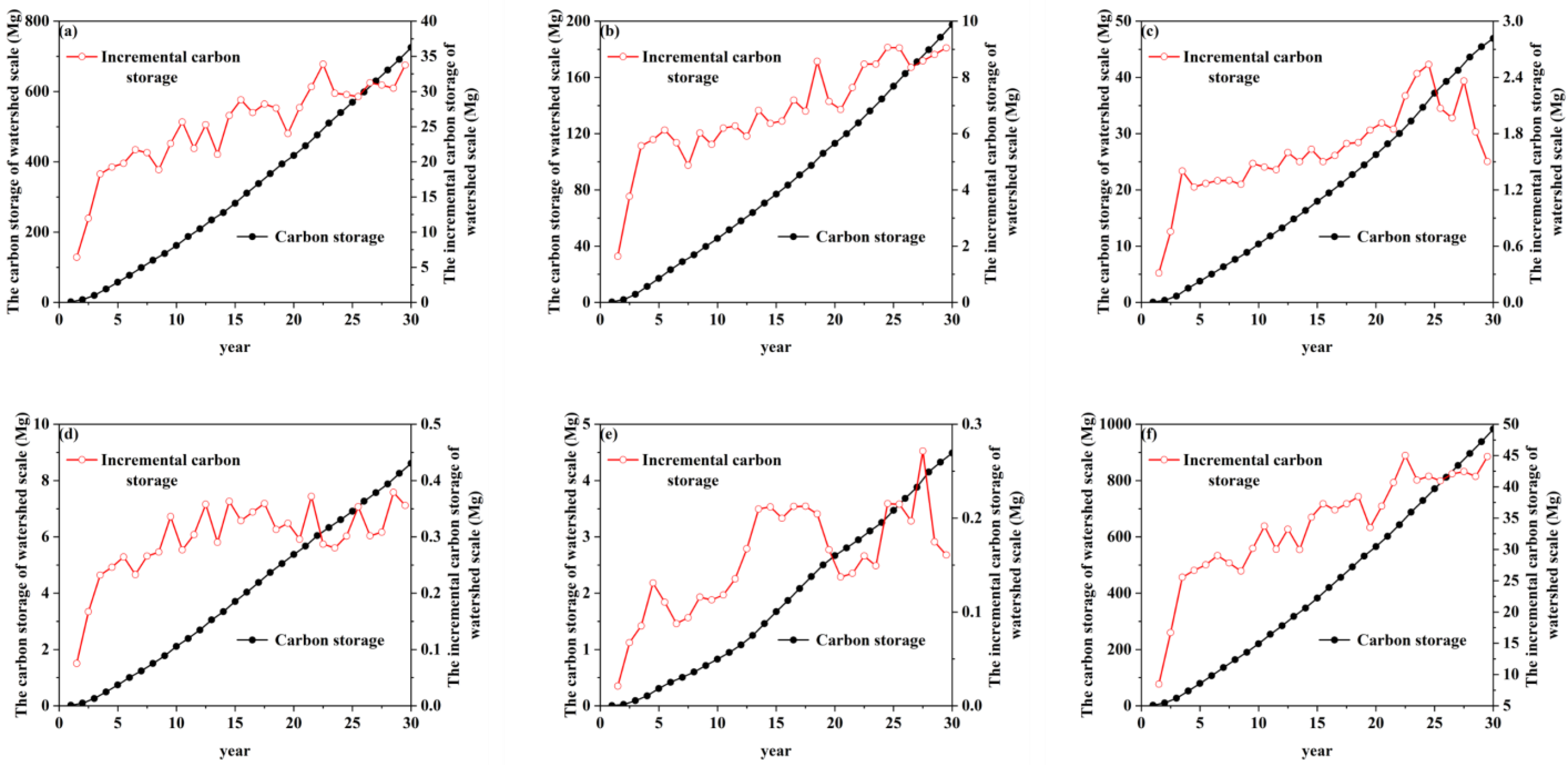
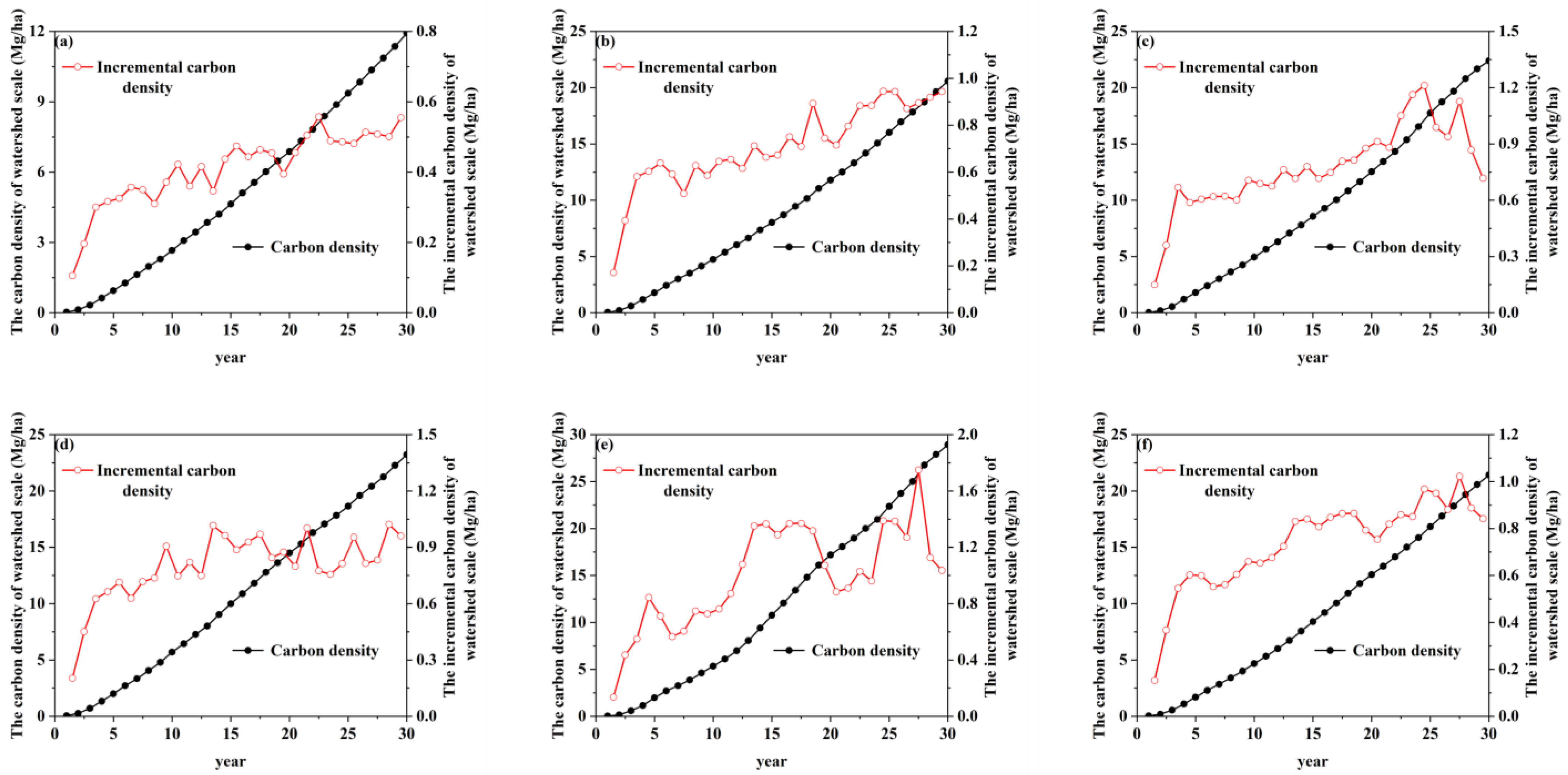
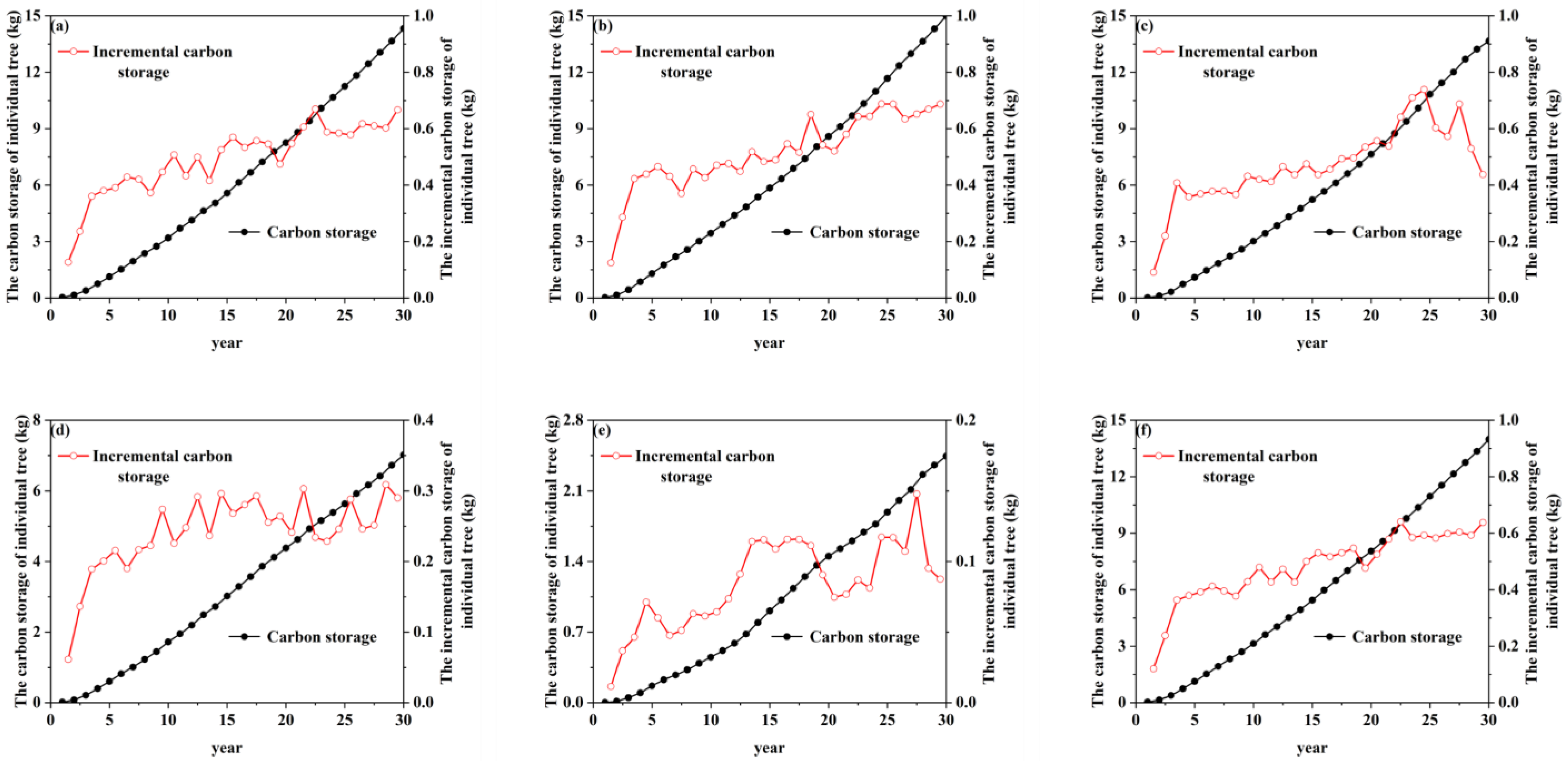
3.4. The Spatiotemporal Distribution of R. pseudoacacia Carbon Storage and Carbon Density at the Watershed Scale
4. Discussion
4.1. The Sample Plot Scale AGB of R. pseudoacacia
4.2. The Watershed Carbon Storage and Carbon Density of R. pseudoacacia
4.3. Overcoming the Challenges of Mapping the Spatiotemporal Changes in Carbon Storage of R. pseudoacacia Plantations Forest at the Watershed Scale
4.4. Future Research Directions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeng, W.; Zou, W.; Chen, X.; Yang, X. A Three-Level Model System of Biomass and Carbon Storage for All Forest Types in China. Forests 2024, 15, 1305. [Google Scholar] [CrossRef]
- Ni-Meister, W.; Rojas, A.; Lee, S. Direct Use of Large-Footprint Lidar Waveforms to Estimate Aboveground Biomass. Remote Sens. Environ. 2022, 280, 113147. [Google Scholar] [CrossRef]
- Zhao, M.; Yang, J.; Zhao, N.; Liu, L.; Du, L.; Xiao, X.; Yue, T.; Wilson, J.P. Spatially Explicit Changes in Forest Biomass Carbon of China over the Past 4 Decades: Coupling Long-Term Inventory and Remote Sensing Data. J. Clean. Prod. 2021, 316, 128274. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, C.; Ji, L.; Zuo, Z.; Beckline, M.; Hu, Y.; Li, X.; Xiao, X. Development of Forest Aboveground Biomass Estimation, Its Problems and Future Solutions: A Review. Ecol. Indic. 2024, 159, 111653. [Google Scholar] [CrossRef]
- Chang, J.; Huang, C. Three Decades of Spatiotemporal Dynamics in Forest Biomass Density in the Qinba Mountains. Ecol. Inform. 2024, 81, 102566. [Google Scholar] [CrossRef]
- Jin, X.-L.; Liu, Y.; Yu, X.-B. UAV-RGB-Image-Based Aboveground Biomass Equation for Planted Forest in Semi-Arid Inner Mongolia, China. Ecol. Inform. 2024, 81, 102574. [Google Scholar] [CrossRef]
- Viana, H.; Aranha, J.; Lopes, D.; Cohen, W.B. Estimation of Crown Biomass of Pinus Pinaster Stands and Shrubland Above-Ground Biomass Using Forest Inventory Data, Remotely Sensed Imagery and Spatial Prediction Models. Ecol. Model. 2012, 226, 22–35. [Google Scholar] [CrossRef]
- Lu, L.; Luo, J.; Xin, Y.; Duan, H.; Sun, Z.; Qiu, Y.; Xiao, Q. How Can UAV Contribute in Satellite-Based Phragmites Australis Aboveground Biomass Estimating? Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103024. [Google Scholar] [CrossRef]
- Wang, D.; Wan, B.; Liu, J.; Su, Y.; Guo, Q.; Qiu, P.; Wu, X. Estimating Aboveground Biomass of the Mangrove Forests on Northeast Hainan Island in China Using an Upscaling Method from Field Plots, UAV-LiDAR Data and Sentinel-2 Imagery. Int. J. Appl. Earth Obs. Geoinf. 2020, 85, 101986. [Google Scholar] [CrossRef]
- Hu, Y.; Sun, Z. Assessing the Capacities of Different Remote Sensors in Estimating Forest Stock Volume Based on High Precision Sample Plot Positioning and Random Forest Method. Nat. Environ. Pollut. Technol. 2022, 21, 1113–1123. [Google Scholar] [CrossRef]
- Ma, T.; Hu, Y.; Wang, J.; Beckline, M.; Pang, D.; Chen, L.; Ni, X.; Li, X. A Novel Vegetation Index Approach Using Sentinel-2 Data and Random Forest Algorithm for Estimating Forest Stock Volume in the Helan Mountains, Ningxia, China. Remote Sens. 2023, 15, 1853. [Google Scholar] [CrossRef]
- Reichstein, M.; Carvalhais, N. Aspects of Forest Biomass in the Earth System: Its Role and Major Unknowns. Surv. Geophys. 2019, 40, 693–707. [Google Scholar] [CrossRef]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and Limitations of Landsat and Land Cover Data for Aboveground Woody Biomass Estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Velasco Pereira, E.A.; Varo Martínez, M.A.; Ruiz Gómez, F.J.; Navarro-Cerrillo, R.M. Temporal Changes in Mediterranean Pine Forest Biomass Using Synergy Models of ALOS PALSAR-Sentinel 1-Landsat 8 Sensors. Remote Sens. 2023, 15, 3430. [Google Scholar] [CrossRef]
- Paris, C.; Valduga, D.; Bruzzone, L. A Hierarchical Approach to Three-Dimensional Segmentation of LiDAR Data at Single-Tree Level in a Multilayered Forest. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4190–4203. [Google Scholar] [CrossRef]
- Meng, Q.; Chen, X.; Zhang, J.; Sun, Y.; Li, J.; Jancsó, T.; Sun, Z. Canopy Structure Attributes Extraction from LiDAR Data Based on Tree Morphology and Crown Height Proportion. J. Indian Soc. Remote Sens. 2018, 46, 1433–1444. [Google Scholar] [CrossRef]
- Salum, R.B.; Souza-Filho, P.W.M.; Simard, M.; Silva, C.A.; Fernandes, M.E.B.; Cougo, M.F.; Do Nascimento, W.; Rogers, K. Improving Mangrove Above-Ground Biomass Estimates Using LiDAR. Estuar. Coast. Shelf Sci. 2020, 236, 106585. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, F.; Sun, Z.; Lister, A.; Gao, X.; Li, W.; Peng, D. The Laser Vegetation Detecting Sensor: A Full Waveform, Large-Footprint, Airborne Laser Altimeter for Monitoring Forest Resources. Sensors 2019, 19, 1699. [Google Scholar] [CrossRef]
- Ren, C.; Jiang, H.; Xi, Y.; Liu, P.; Li, H. Quantifying Temperate Forest Diversity by Integrating GEDI LiDAR and Multi-Temporal Sentinel-2 Imagery. Remote Sens. 2023, 15, 375. [Google Scholar] [CrossRef]
- Huang, H.; Liu, C.; Wang, X.; Zhou, X.; Gong, P. Integration of Multi-Resource Remotely Sensed Data and Allometric Models for Forest Aboveground Biomass Estimation in China. Remote Sens. Environ. 2019, 221, 225–234. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, K.; Zhu, Y.; Wang, X.; Yun, T. Individual Tree Crown Segmentation Directly from UAV-Borne LiDAR Data Using the PointNet of Deep Learning. Forests 2021, 12, 131. [Google Scholar] [CrossRef]
- Liu, J.; Skidmore, A.K.; Jones, S.; Wang, T.; Heurich, M.; Zhu, X.; Shi, Y. Large Off-Nadir Scan Angle of Airborne LiDAR Can Severely Affect the Estimates of Forest Structure Metrics. ISPRS J. Photogramm. Remote Sens. 2018, 136, 13–25. [Google Scholar] [CrossRef]
- Jiang, R.; Lin, J.; Li, T. Refined Aboveground Biomass Estimation of Moso Bamboo Forest Using Culm Lengths Extracted from TLS Point Cloud. Remote Sens. 2022, 14, 5537. [Google Scholar] [CrossRef]
- Beland, M.; Parker, G.; Sparrow, B.; Harding, D.; Chasmer, L.; Phinn, S.; Antonarakis, A.; Strahler, A. On Promoting the Use of Lidar Systems in Forest Ecosystem Research. For. Ecol. Manag. 2019, 450, 117484. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An Integrated UAV-Borne Lidar System for 3D Habitat Mapping in Three Forest Ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Balsi, M.; Esposito, S.; Fallavollita, P.; Nardinocchi, C. Single-Tree Detection in High-Density LiDAR Data from UAV-Based Survey. Eur. J. Remote Sens. 2018, 51, 679–692. [Google Scholar] [CrossRef]
- Hu, T.; Sun, X.; Su, Y.; Guan, H.; Sun, Q.; Kelly, M.; Guo, Q. Development and Performance Evaluation of a Very Low-Cost UAV-Lidar System for Forestry Applications. Remote Sens. 2020, 13, 77. [Google Scholar] [CrossRef]
- Tian, Y.; Huang, H.; Zhou, G.; Zhang, Q.; Tao, J.; Zhang, Y.; Lin, J. Aboveground Mangrove Biomass Estimation in Beibu Gulf Using Machine Learning and UAV Remote Sensing. Sci. Total Environ. 2021, 781, 146816. [Google Scholar] [CrossRef]
- Da Costa, M.B.T.; Silva, C.A.; Broadbent, E.N.; Leite, R.V.; Mohan, M.; Liesenberg, V.; Stoddart, J.; Do Amaral, C.H.; De Almeida, D.R.A.; Da Silva, A.L.; et al. Beyond Trees: Mapping Total Aboveground Biomass Density in the Brazilian Savanna Using High-Density UAV-Lidar Data. For. Ecol. Manag. 2021, 491, 119155. [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Broadbent, E.N.; Zambrano, A.M.A.; Wilkinson, B.E.; Ferreira, M.E.; Chazdon, R.; Meli, P.; Gorgens, E.B.; Silva, C.A.; Stark, S.C.; et al. Monitoring the Structure of Forest Restoration Plantations with a Drone-Lidar System. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 192–198. [Google Scholar] [CrossRef]
- Madsen, B.; Treier, U.A.; Zlinszky, A.; Lucieer, A.; Normand, S. Detecting Shrub Encroachment in Seminatural Grasslands Using UAS LiDAR. Ecol. Evol. 2020, 10, 4876–4902. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Wang, H.; Qin, S.; Cao, L.; Pu, R.; Li, G.; Sun, J. Estimation of Aboveground Biomass of Robinia Pseudoacacia Forest in the Yellow River Delta Based on UAV and Backpack LiDAR Point Clouds. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102014. [Google Scholar] [CrossRef]
- Li, W.; Guo, Q.; Jakubowski, M.K.; Kelly, M. A New Method for Segmenting Individual Trees from the Lidar Point Cloud. Photogramm. Eng. Remote Sens. 2012, 78, 75–84. [Google Scholar] [CrossRef]
- Guerra-Hernández, J.; Cosenza, D.N.; Rodriguez, L.C.E.; Silva, M.; Tomé, M.; Díaz-Varela, R.A.; González-Ferreiro, E. Comparison of ALS- and UAV(SfM)-Derived High-Density Point Clouds for Individual Tree Detection in Eucalyptus Plantations. Int. J. Remote Sens. 2018, 39, 5211–5235. [Google Scholar] [CrossRef]
- Xu, X.; Ma, F.; Lu, K.; Zhu, B.; Li, S.; Liu, K.; Chen, Q.; Li, Q.; Deng, C. Estimation of Biomass Dynamics and Allocation in Chinese Fir Trees Using Tree Ring Analysis in Hunan Province, China. Sustainability 2023, 15, 3306. [Google Scholar] [CrossRef]
- Cao, L.; Coops, N.C.; Innes, J.L.; Sheppard, S.R.J.; Fu, L.; Ruan, H.; She, G. Estimation of Forest Biomass Dynamics in Subtropical Forests Using Multi-Temporal Airborne LiDAR Data. Remote Sens. Environ. 2016, 178, 158–171. [Google Scholar] [CrossRef]
- Bollandsås, O.M.; Gregoire, T.G.; Næsset, E.; Øyen, B.-H. Detection of Biomass Change in a Norwegian Mountain Forest Area Using Small Footprint Airborne Laser Scanner Data. Stat. Methods Appl. 2013, 22, 113–129. [Google Scholar] [CrossRef]
- Økseter, R.; Bollandsås, O.M.; Gobakken, T.; Næsset, E. Modeling and Predicting Aboveground Biomass Change in Young Forest Using Multi-Temporal Airborne Laser Scanner Data. Scand. J. For. Res. 2015, 30, 458–469. [Google Scholar] [CrossRef]
- Hu, Y.; Zhao, J.; Li, Y.; Tang, P.; Yang, Z.; Zhang, J.; Sun, R. Biomass and Carbon Stock Capacity of Robinia Pseudoacacia Plantations at Different Densities on the Loess Plateau. Forests 2024, 15, 1242. [Google Scholar] [CrossRef]
- Cheng, J.; Zhang, X.; Zhang, J.; Zhang, Y.; Hu, Y.; Zhao, J.; Li, Y. Estimating the Aboveground Biomass of Robinia Pseudoacacia Based on UAV LiDAR Data. Forests 2024, 15, 548. [Google Scholar] [CrossRef]
- Zhao, J. Effects of Land Uses and Rainfall Regimes on Surface Runoff and Sediment Yield in a Nested Watershed of the Loess Plateau, China. J. Hydrol. 2022, 44, 101277. [Google Scholar] [CrossRef]
- Li, X.; Ramos Aguila, L.C.; Wu, D.; Lie, Z.; Xu, W.; Tang, X.; Liu, J. Carbon Sequestration and Storage Capacity of Chinese Fir at Different Stand Ages. Sci. Total Environ. 2023, 904, 166962. [Google Scholar] [CrossRef] [PubMed]
- Wang, C. Biomass Allometric Equations for 10 Co-Occurring Tree Species in Chinese Temperate Forests. For. Ecol. Manag. 2006, 222, 9–16. [Google Scholar] [CrossRef]
- Lin, J.; Chen, D.; Wu, W.; Liao, X. Estimating Aboveground Biomass of Urban Forest Trees with Dual-Source UAV Acquired Point Clouds. Urban For. Urban Green. 2022, 69, 127521. [Google Scholar] [CrossRef]
- Pan, H.-L.; Huang, C.-M.; Huang, C. Mapping Aboveground Carbon Density of Subtropical Subalpine Dwarf Bamboo (Yushania niitakayamensis) Vegetation Using UAV-Lidar. Int. J. Appl. Earth Obs. Geoinf. 2023, 123, 103487. [Google Scholar] [CrossRef]
- Liu, K.; Shen, X.; Cao, L.; Wang, G.; Cao, F. Estimating Forest Structural Attributes Using UAV-LiDAR Data in Ginkgo Plantations. ISPRS J. Photogramm. Remote Sens. 2018, 146, 465–482. [Google Scholar] [CrossRef]
- Brede, B.; Lau, A.; Bartholomeus, H.; Kooistra, L. Comparing RIEGL RiCOPTER UAV LiDAR Derived Canopy Height and DBH with Terrestrial LiDAR. Sensors 2017, 17, 2371. [Google Scholar] [CrossRef]
- Brede, B.; Terryn, L.; Barbier, N.; Bartholomeus, H.M.; Bartolo, R.; Calders, K.; Derroire, G.; Krishna Moorthy, S.M.; Lau, A.; Levick, S.R.; et al. Non-Destructive Estimation of Individual Tree Biomass: Allometric Models, Terrestrial and UAV Laser Scanning. Remote Sens. Environ. 2022, 280, 113180. [Google Scholar] [CrossRef]
- Goodbody, T.R.H.; Coops, N.C.; Hermosilla, T.; Tompalski, P.; Crawford, P. Assessing the Status of Forest Regeneration Using Digital Aerial Photogrammetry and Unmanned Aerial Systems. Int. J. Remote Sens. 2018, 39, 5246–5264. [Google Scholar] [CrossRef]
- Chen, Q.; Gao, T.; Zhu, J.; Wu, F.; Li, X.; Lu, D.; Yu, F. Individual Tree Segmentation and Tree Height Estimation Using Leaf-Off and Leaf-On UAV-LiDAR Data in Dense Deciduous Forests. Remote Sens. 2022, 14, 2787. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, X.; Wu, B. Automatic Detection of Individual Oil Palm Trees from UAV Images Using HOG Features and an SVM Classifier. Int. J. Remote Sens. 2019, 40, 7356–7370. [Google Scholar] [CrossRef]
- Lin, Y.-C.; Liu, J.; Fei, S.; Habib, A. Leaf-Off and Leaf-On UAV LiDAR Surveys for Single-Tree Inventory in Forest Plantations. Drones 2021, 5, 115. [Google Scholar] [CrossRef]
- Birdal, A.C.; Avdan, U.; Türk, T. Estimating Tree Heights with Images from an Unmanned Aerial Vehicle. Geomat. Nat. Hazards Risk 2017, 8, 1144–1156. [Google Scholar] [CrossRef]
- Hadush, T.; Girma, A.; Zenebe, A. Tree Height Estimation from Unmanned Aerial Vehicle Imagery and Its Sensitivity on Above Ground Biomass Estimation in Dry Afromontane Forest, Northern Ethiopia. Momona Ethiop. J. Sci. 2022, 13, 256–280. [Google Scholar] [CrossRef]
- Dalla Corte, A.P.; Rex, F.E.; Almeida, D.R.A.D.; Sanquetta, C.R.; Silva, C.A.; Moura, M.M.; Wilkinson, B.; Zambrano, A.M.A.; Cunha Neto, E.M.D.; Veras, H.F.P.; et al. Measuring Individual Tree Diameter and Height Using GatorEye High-Density UAV-Lidar in an Integrated Crop-Livestock-Forest System. Remote Sens. 2020, 12, 863. [Google Scholar] [CrossRef]
- Zhao, M.; Zhou, G.-S. Carbon Storage of Forest Vegetation in China and Its Relationship with Climatic Factors. Clim. Change 2006, 74, 175–189. [Google Scholar] [CrossRef]
- Hou, H.; Zhang, S.; Ding, Z.; Huang, A.; Tian, Y. Spatiotemporal Dynamics of Carbon Storage in Terrestrial Ecosystem Vegetation in the Xuzhou Coal Mining Area, China. Environ. Earth Sci. 2015, 74, 1657–1669. [Google Scholar] [CrossRef]
- Wang, N. Study on Distribution Patterns of Carbon Density and Carbon Stock in the Forest Ecosystem of Shanxi; Beijing Forestry University: Beijing, China, 2014. [Google Scholar]
- Wang, J.J.; Hu, C.X.; Bai, J.; Gong, C.M. Carbon Sequestration of Mature Black Locust Stands on the Loess Plateau, China. Plant Soil Environ. 2015, 61, 116–121. [Google Scholar] [CrossRef]
- Liu, Y.; Fang, Y.; An, S. How C:N:P Stoichiometry in Soils and Plants Responds to Succession in Robinia Pseudoacacia Forests on the Loess Plateau, China. For. Ecol. Manag. 2020, 475, 118394. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, W.; Xu, M.; Deng, J.; Han, X.; Yang, G.; Feng, Y.; Ren, G. Response of Forest Growth to C:N:P Stoichiometry in Plants and Soils during Robinia Pseudoacacia Afforestation on the Loess Plateau, China. Geoderma 2019, 337, 280–289. [Google Scholar] [CrossRef]
- Bai, X.; Wang, B.; An, S.; Zeng, Q.; Zhang, H. Response of Forest Species to C:N:P in the Plant-Litter-Soil System and Stoichiometric Homeostasis of Plant Tissues during Afforestation on the Loess Plateau, China. Catena 2019, 183, 104186. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, P.; Chen, Y. Soil C:N:P Stoichiometry in Plantations of N-Fixing Black Locust and Indigenous Pine, and Secondary Oak Forests in Northwest China. J. Soils Sediments 2018, 18, 1478–1489. [Google Scholar] [CrossRef]
- Liu, Z. Study on Carbon Distribution Patterns of Three Plantation Ecosystems in Western Shanxi; Beijing Forestry University: Beijing, China, 2019. [Google Scholar]
- Wang, Y.; Wang, Q.-X.; Wang, M.-B. Similar Carbon Density of Natural and Planted Forests in the Lüliang Mountains, China. Ann. For. Sci. 2018, 75, 87. [Google Scholar] [CrossRef]
- Lin, J.; Chen, D.; Yang, S.; Liao, X. Precise Aboveground Biomass Estimation of Plantation Forest Trees Using the Novel Allometric Model and UAV-Borne LiDAR. Front. For. Glob. Change 2023, 6, 1166349. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Brienen, R.J.W.; Gloor, E.; Phillips, O.L.; Prior, L.D. Detecting Trends in Tree Growth: Not so Simple. Trends Plant Sci. 2013, 18, 11–17. [Google Scholar] [CrossRef]
- Toro-Herrera, M.A.; Pennacchi, J.P.; Vilas Boas, L.V.; Honda Filho, C.P.; Barbosa, A.C.M.C.; Barbosa, J.P.R.A.D. On the Use of Tree-ring Area as a Predictor of Biomass Accumulation and Its Climatic Determinants of Coffee Tree Growth. Ann. Appl. Biol. 2021, 179, 60–74. [Google Scholar] [CrossRef]
- Anderson, K.J.; Herrmann, V.; Rollinson, C.R.; Gonzalez, B.; Gonzalez, E.B.; Pederson, N.; Alexander, M.R.; Allen, C.D.; Alfaro, R.; Awada, T.; et al. Joint Effects of Climate, Tree Size, and Year on Annual Tree Growth Derived from Tree-ring Records of Ten Globally Distributed Forests. Glob. Change Biol. 2022, 28, 245–266. [Google Scholar] [CrossRef]
- Tang, X.; Lu, Y.; Fehrmann, L.; Forrester, D.I.; Guisasola-Rodríguez, R.; Pérez-Cruzado, C.; Kleinn, C. Estimation of Stand-Level Aboveground Biomass Dynamics Using Tree Ring Analysis in a Chinese Fir Plantation in Shitai County, Anhui Province, China. New For. 2016, 47, 319–332. [Google Scholar] [CrossRef]



| Number | Equation Form | Parameters | Variate |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 |
| Number | Equation Form | Parameters | Variate |
|---|---|---|---|
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 | |||
| 6 | |||
| 7 |
| Density (Trees ha−1) | Model | R2 | n |
|---|---|---|---|
| 900–1200 | H = 2.889D0.5043 | 0.5819 | 402 |
| 1201–1500 | H = 2.741D0.5274 | 0.6306 | 745 |
| 1501–1800 | H = 2.505D0.5501 | 0.6307 | 796 |
| 1801–2100 | H = 2.682D0.4970 | 0.5107 | 502 |
| 2101–2400 | H = 2.462D0.5337 | 0.6310 | 94 |
| Equation Form | Coefficients | R2 | RMSE (kg) | RMSE (%) | MD (kg) | MD (%) | n | ||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | |||||||
| 0.2257 | 2.144 | — | 0.9520 | 13.35 | 23.54 | 0.02 | 0.03 | 63 | |
| 0.0031 | 3.866 | — | 0.8406 | 24.33 | 42.91 | −0.05 | −0.09 | 63 | |
| 0.0693 | 0.8714 | — | 0.9689 | 10.76 | 18.96 | −0.003 | −0.006 | 63 | |
| 0.0477 | 1.608 | 1.154 | 0.9694 | 10.57 | 18.64 | −0.01 | −0.02 | 63 | |
| 11.18 | −80.8 | — | 0.9210 | 17.14 | 30.21 | 0.002 | 0.003 | 63 | |
| 16.18 | −131.9 | — | 0.7155 | 32.51 | 57.33 | 0.001 | 0.002 | 63 | |
| 10.85 | 0.6095 | −83.9 | 0.9199 | 17.11 | 30.17 | 0.001 | 0.001 | 63 | |
| Equation Form | Coefficients | R2 | RMSE (kg) | RMSE (%) | MD (kg) | MD (%) | N | ||
|---|---|---|---|---|---|---|---|---|---|
| a | b | c | |||||||
| 183.9 | 0.6333 | — | 0.1928 | 828.29 | 35.86 | 0.1152 | 0.0050 | 49 | |
| 15.81 | 2.015 | — | 0.5131 | 643.27 | 27.85 | −0.0538 | −0.0023 | 49 | |
| 16.76 | 0.4797 | — | 0.3963 | 757.91 | 32.82 | 5.5429 | 0.2400 | 49 | |
| 0.1067 | 0.988 | 2.437 | 0.9099 | 273.78 | 11.85 | 0.0056 | 0.0002 | 49 | |
| 28.18 | 752.9 | — | 0.1773 | 836.16 | 36.20 | 0.0030 | 0.0001 | 49 | |
| 412.5 | −2538 | — | 0.5090 | 645.96 | 27.97 | −0.0024 | −0.0001 | 49 | |
| 38.41 | 478.4 | −5434 | 0.8616 | 339.33 | 14.69 | 0.0063 | 0.0003 | 49 | |
| Segmentation Windows Size | Number of Trees | Number of Segmented Trees | TP | FN | FP | r /(%) | p /(%) | F /(%) |
|---|---|---|---|---|---|---|---|---|
| 0.035 m × 0.035 m | 1623 | 1895 | 1123 | 500 | 772 | 70.99 | 66.24 | 64.39 |
| 0.040 m × 0.040 m | 1623 | 1392 | 1093 | 530 | 299 | 69.56 | 80.84 | 72.09 |
| 0.045 m × 0.045 m | 1623 | 1246 | 1096 | 527 | 150 | 69.50 | 88.23 | 75.84 |
| 0.050 m × 0.050 m | 1623 | 1199 | 1093 | 530 | 106 | 69.37 | 91.50 | 77.25 |
| 0.055 m × 0.055 m | 1623 | 1166 | 1097 | 526 | 69 | 69.50 | 94.42 | 78.46 |
| 0.060 m × 0.060 m | 1623 | 1151 | 1107 | 516 | 44 | 69.84 | 96.10 | 79.52 |
| 0.065 m × 0.065 m | 1623 | 1120 | 1084 | 539 | 36 | 68.58 | 96.78 | 79.28 |
| 0.070 m × 0.070 m | 1623 | 1108 | 1078 | 545 | 30 | 68.41 | 97.41 | 78.93 |
| 0.075 m × 0.075 m | 1623 | 1098 | 1078 | 545 | 20 | 68.04 | 98.08 | 78.88 |
| 0.080 m × 0.080 m | 1623 | 1092 | 1071 | 552 | 21 | 67.56 | 98.16 | 78.67 |
| Segmentation Windows Size | N/tree | AH/m | N Error/% | AH Error/% |
|---|---|---|---|---|
| 0.035 m × 0.035 m | 1895 | 10.18 | 62.04 | 17.51 |
| 0.040 m × 0.040 m | 1392 | 10.98 | 31.32 | 14.73 |
| 0.045 m × 0.045 m | 1246 | 11.33 | 28.15 | 14.17 |
| 0.050 m × 0.050 m | 1199 | 11.50 | 26.95 | 14.40 |
| 0.055 m × 0.055 m | 1166 | 11.69 | 28.21 | 15.25 |
| 0.060 m × 0.060 m | 1151 | 11.74 | 28.37 | 15.06 |
| 0.065 m × 0.065 m | 1120 | 11.81 | 30.09 | 15.50 |
| 0.070 m × 0.070 m | 1108 | 11.85 | 30.58 | 15.63 |
| 0.075 m × 0.075 m | 1098 | 11.89 | 31.37 | 15.50 |
| 0.080 m × 0.080 m | 1092 | 11.90 | 32.02 | 15.24 |
| Segmentation Windows Size | Observed/kg | Estimated I Error/% | Estimated II Error/% | Estimated III Error/% | Estimated IV Error/% |
|---|---|---|---|---|---|
| 0.035 m × 0.035 m | 1627.23 | 24.55 | 123.33 | 49.72 | 44.31 |
| 0.040 m × 0.040 m | 1543.65 | 22.86 | 98.84 | 30.14 | 36.64 |
| 0.045 m × 0.045 m | 1523.09 | 24.31 | 86.26 | 31.39 | 38.73 |
| 0.050 m × 0.050 m | 1526.14 | 24.22 | 82.80 | 31.93 | 37.72 |
| 0.055 m × 0.055 m | 1544.14 | 24.37 | 84.74 | 31.22 | 38.85 |
| 0.060 m × 0.060 m | 1546.49 | 24.57 | 86.22 | 31.25 | 39.26 |
| 0.065 m × 0.065 m | 1526.70 | 24.54 | 82.88 | 31.16 | 39.53 |
| 0.070 m × 0.070 m | 1525.33 | 24.51 | 83.17 | 30.50 | 40.67 |
| 0.075 m × 0.075 m | 1517.08 | 25.02 | 81.84 | 31.37 | 41.12 |
| 0.080 m × 0.080 m | 1515.46 | 25.18 | 81.77 | 30.49 | 41.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Sun, R.; He, M.; Zhao, J.; Li, Y.; Huang, S.; Zhang, J. Estimating Spatiotemporal Dynamics of Carbon Storage in Roinia pseudoacacia Plantations in the Caijiachuan Watershed Using Sample Plots and Uncrewed Aerial Vehicle-Borne Laser Scanning Data. Remote Sens. 2025, 17, 1365. https://doi.org/10.3390/rs17081365
Hu Y, Sun R, He M, Zhao J, Li Y, Huang S, Zhang J. Estimating Spatiotemporal Dynamics of Carbon Storage in Roinia pseudoacacia Plantations in the Caijiachuan Watershed Using Sample Plots and Uncrewed Aerial Vehicle-Borne Laser Scanning Data. Remote Sensing. 2025; 17(8):1365. https://doi.org/10.3390/rs17081365
Chicago/Turabian StyleHu, Yawei, Ruoxiu Sun, Miaomiao He, Jiongchang Zhao, Yang Li, Shengze Huang, and Jianjun Zhang. 2025. "Estimating Spatiotemporal Dynamics of Carbon Storage in Roinia pseudoacacia Plantations in the Caijiachuan Watershed Using Sample Plots and Uncrewed Aerial Vehicle-Borne Laser Scanning Data" Remote Sensing 17, no. 8: 1365. https://doi.org/10.3390/rs17081365
APA StyleHu, Y., Sun, R., He, M., Zhao, J., Li, Y., Huang, S., & Zhang, J. (2025). Estimating Spatiotemporal Dynamics of Carbon Storage in Roinia pseudoacacia Plantations in the Caijiachuan Watershed Using Sample Plots and Uncrewed Aerial Vehicle-Borne Laser Scanning Data. Remote Sensing, 17(8), 1365. https://doi.org/10.3390/rs17081365






