Next Article in Journal
Comparing Satellite-Derived and Model-Based Surface Soil Moisture for Spring Barley Yield Prediction in Central Europe
Previous Article in Journal
Spatiotemporal Dynamics and Future Projections of Carbon Use Efficiency on the Mongolian Plateau: A Remote Sensing and Machine Learning Approach
Previous Article in Special Issue
SSegRef2Surf—Near Real-Time Photogrammetric Flood Monitoring and Refinement of Classified Water Surfaces
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 17
Issue 8
10.3390/rs17081393
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Study on the Spatial Distribution Patterns and Driving Forces of Rainstorm-Induced Flash Flood in the Yarlung Tsangpo River Basin

by
Fei He
1,2,
Chaolei Zheng
3,
Xingguo Mo
1,2,
Zhonggen Wang
1,4 and
Suxia Liu
1,2,*
1
Key Laboratory of Water Cycle and Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China
2
College of Resources and Environment/Sino-Danish College, University of Chinese Academy of Sciences, Beijing 100190, China
3
Key Laboratory of Remote Sensing and Digital Earth, Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100101, China
4
National Institute of Natural Hazards, Ministry of Emergency Management of the People’s Republic of China, Beijing 100085, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2025, 17(8), 1393; https://doi.org/10.3390/rs17081393
Submission received: 29 January 2025 / Revised: 9 April 2025 / Accepted: 10 April 2025 / Published: 14 April 2025
(This article belongs to the Special Issue Application of Remote Sensing to Flood and Drought Analysis, Monitoring and Risk Management)
Browse Figures
Versions Notes

Abstract

:
Flash floods, typically triggered by natural events such as heavy rainfall, snowmelt, and dam failures, are characterized by abrupt onset, destructive power, unpredictability, and challenges in mitigation. This study investigates the spatial distribution patterns and driving mechanisms of rainstorm-induced flash flood disasters in the Yarlung Tsangpo River Basin (YTRB) by integrating topography, hydrometeorology, human activity data, and historical disaster records. Through a multi-method spatial analysis framework—including kernel density estimation, standard deviation ellipse, spatial autocorrelation (Moran’s I and Getis–Ord Gi*), and the optimal parameter geographic detector (OPGD) model (integrating univariate analysis and interaction detection)—we reveal multiscale disaster dynamics across county, township, and small catchment levels. Key findings indicate that finer spatial resolution (e.g., small catchment scale) enhances precision when identifying high-risk zones. Temporally, the number of rainstorm-induced flash floods increased significantly and disaster-affected areas expanded significantly from the 1980s to the 2010s, with a peak spatial dispersion observed during 2010–2019, reflecting a westward shift in disaster distribution. Spatial aggregation of flash floods persisted throughout the study period, concentrated in the central basin. Village density (TD) was identified as the predominant human activity factor, exhibiting nonlinear amplification through interactions with short-duration heavy rainfall (particularly 3 h [P3] and 6 h [P6] maximum precipitations) and GDP. These precipitation durations demonstrated compounding risk effects, where sustained rainfall intensity progressively heightened disaster potential. Topographic and ecological interactions, particularly between elevation (DEM) and vegetation type (VT), further modulate disaster intensity. These findings provide critical insights for risk zonation and targeted prevention strategies in high-altitude river basins.

1. Introduction

Flash flood disasters manifest as rapid inundation processes within mountain drainage systems, primarily triggered by natural drivers such as extreme precipitation events, snowmelt pulses, or dam failures. These phenomena frequently initiate cascading geomorphic hazards, including fluvial flooding, debris flows, and slope instabilities [1,2], exhibiting distinctive characteristics of abrupt onset, high destructive potential, and significant challenges in predictive modeling [3,4,5,6]. As a critical component of the ecological security barrier on the Tibetan Plateau, the Yarlung Tsangpo River Basin (YTRB) exhibits complex topography, diverse climatic conditions, and highly uneven spatiotemporal distribution of precipitation under the context of global warming [7,8,9]. The frequent occurrence of extreme precipitation events in this region has led to the increased frequency, suddenness, and severity of flash flood disasters, posing severe threats to lives, property, and infrastructure development [10,11]. Notably, rainstorm-induced flash flood disasters represent the predominant form of flood hazards within the study area [12,13]. Therefore, systematic investigation of spatiotemporal distribution patterns and multi-scale influencing factors of such events in the YTRB is of critical importance for enhancing risk assessment accuracy and optimizing disaster prevention/mitigation strategies in this vulnerable region.
Flash floods arise from the combined effects of meteorological, hydrological, geological, geomorphological, and anthropogenic factors [14,15,16] These factors can be broadly categorized into two groups: conditional factors and triggering factors. Conditional factors represent the environmental conditions that predispose an area to flash floods and include elements such as topography, soil, hydrology, and geological features [17,18,19]. In contrast, triggering factors are dynamic forces, such as rainfall, earthquakes, snowmelt, and human activities, that directly induce flash floods by rapidly altering the foundational environment [20,21,22]. Among conditional factors, topographical and geological features are particularly significant. Steep slopes and the conduit effect of narrow valleys enhance runoff velocity, thereby increasing the likelihood of storm-induced flash floods. Among triggering factors, human activities also play a critical role. For instance, irrational land use, such as excessive cultivation or hillside construction, destroys vegetation and reduces water retention capacity, while deforestation exacerbates soil erosion and diminishes river channel flow capacity. Furthermore, in the process of urbanization, inadequate flood prevention infrastructure, such as poorly designed drainage systems, can intensify the severity of disasters [23]. Importantly, rainfall remains the most critical triggering factor and is often identified as the primary cause of flash flood events in small-scale watersheds [24,25]. However, existing studies predominantly incorporate rainstorm-induced flash floods into comprehensive assessment frameworks with heterogeneous disaster types, leading to the ineffective decoupling of driving contributions from extreme precipitation events and human activities at the mechanistic level, thereby resulting in systematic underestimation [26]. Furthermore, conventional geodetector-based analyses of flash flood driving forces exhibit methodological limitations, particularly in handling continuous environmental variables: the criticality of discretization processes is frequently overlooked, with empirical classification schemes predominating and robust quantitative validation remaining insufficient [27,28]. These shortcomings substantially compromise the explanatory power of driving factors regarding disaster probability.
Previous studies on rainstorm-induced flash flood disasters and their association with extreme precipitation in the YTRB have predominantly focused on three aspects: extreme precipitation patterns, small-catchment flood modeling, and flash flood susceptibility assessment. Fan et al. [29], through satellite-derived gridded datasets, observed that both the frequency and intensity of extreme precipitation events in the YTRB have shown increasing trends over the past six decades. Similarly, Liu et al. [30] reported moistening trends in extreme precipitation indices across 15 meteorological stations during 1970–2017, with extreme precipitation demonstrating increasing contribution rates to total rainfall. These findings collectively indicate a growing influence of extreme precipitation on flash flood disasters [11]. Shen et al. [31] pioneered a quantitative risk assessment framework for dam-break floods caused by landslide dams in the main tributaries, systematically evaluating their societal impacts. Regarding rainstorm-induced flash floods, scholars have conducted multi-scale investigations, as follows: He et al. [32] employed the H2O auto-ML interpretable machine learning model to unravel the spatiotemporal evolution patterns of flash flood susceptibility across the entire basin, identifying topographic factors as the dominant drivers. Focusing on the Lhasa River sub-basin, Fu et al. [33] developed an integrated assessment framework combining GIS technology with subjective-objective weighting methods, enabling the multidimensional quantification of flash flood risks. It is noteworthy that current research predominantly concentrates on dam-break floods and paleo-flood events [34,35], while systematic studies on rainfall-triggered flash floods remain insufficient. In particular, there exists a notable research gap in elucidating the interaction mechanisms among driving factors, which warrants further in-depth investigation.
Synthesizing the aforementioned research advancements, three critical limitations persist in flash flood disaster studies within this basin: (1) scarcity of basin-scale investigations, with existing achievements predominantly focused on small-catchment process modeling or localized outburst events, lacking systematic analysis of basin-wide disaster patterns; (2) methodological constraints in driving force analysis, where traditional geographic detectors employ the empirical classification-based discretization of continuous variables, resulting in the biased interpretation of factor influences; and (3) unquantified interactive effects among driving factors, particularly the underexplored interactions among driving factors.
To address these gaps, this study investigates the spatial distribution patterns of rainstorm-induced flash flood disasters using historical event records from 1980 to 2019 in the YTRB. We integrate three driver categories—subsurface characteristics, rainfall parameters, and anthropogenic factors. Through the optimal parameter geographic detector (OPGD) selection, we identify the parameter combination yielding the highest q-statistic to generate optimally discretized factors from continuous rainfall, topographic, and human activity variables. This methodology enables the detection of primary drivers and their spatial heterogeneity, ultimately aiming to enhance flash flood early warning systems and zoning prevention strategies in this climatically sensitive basin.

2. Materials and Methods

2.1. Study Area

The YTRB is located between longitudes 82°00′E and 97°07′E and latitudes 28°00′N and 31°16′N. The main river stretches for 2057 km (Figure 1), ranking as the fifth longest river in China [36]. The basin encompasses an area of approximately 240,480 square kilometers, constituting 20% of Tibet’s total area. As the world’s highest altitude major river, the YTRB has an average elevation exceeding 4000 m and exhibits the steepest gradient within China. The YTRB is characterized by its unique plateau climate, with clearly defined dry and wet seasons [37]. The wet season typically spans from May to September, during which approximately 65% to 80% of the annual precipitation occurs. In contrast, the dry season extends from October to April, during which precipitation is significantly reduced and unevenly distributed throughout the basin [38]. The river’s runoff is predominantly sustained by atmospheric precipitation, while glacial meltwater has become an increasingly significant source due to the ongoing development and melting of glaciers [39]. The total water resources of the Yarlung Tsangpo River are estimated at 165.4 billion cubic meters, accounting for 6.1% of China’s total water resources. The river boasts abundant runoff, with an annual average flow rate of 4425 cubic meters per second and a total annual runoff of 139.54 billion cubic meters, ranking third in the nation [36,40]. Overall, the basin is characterized by a complex terrain and precipitation patterns that exhibit significant temporal and spatial variability, often marked by randomness and instability. The concentrated and intense rainfall during the wet season results in frequent flash floods, which can severely affect local communities. These flash floods cause damage to homes, disrupt transportation infrastructure, and pose serious threats to resident safety, ultimately hindering economic activities and recovery efforts [24,41]. The impact of such disasters underscores the vulnerability of the region during the summer months.

2.2. Datasets

The data utilized in this study comprise the following components: (1) Historical flood event data related to major flash flood disasters from the results of the “Second Comprehensive Scientific Expedition and Research on the Tibetan Plateau”, which includes information on the timing (year and month), location (longitude and latitude), and type of disasters, and which, in this context allows for the exclusion of non-extreme rainfall-induced flood events, such as dam break floods, while retaining only the floods that are associated with heavy rainfall; (2) precipitation data sourced from the China Regional Ground Meteorological Element Driven Dataset (1979–2018); (3) SRTM DEM data of the Tibetan Plateau (2012), used to generate slope data; (4) soil type data obtained from the spatial distribution dataset of Chinese soil types; (5) river network density data derived from the 1 km grid river network density dataset of China (2019); (6) vegetation type data acquired from the spatial distribution dataset of vegetation types at a 1:1,000,000 scale in China; (7) population density data from the kilometer grid dataset of the spatial distribution of the population in China; (8) GDP data sourced from the kilometer grid dataset of China’s GDP spatial distribution; (9) land use data obtained from the Chinese land use dataset (1981–2015); (10) village density data derived from the Chinese village point dataset. Prior to the data analysis, all raster data were resampled to a consistent spatial resolution of 1 km. All operations were conducted using ArcGIS 10.8 software. Detailed information about the datasets can be found in Table 1.

2.3. Methods

2.3.1. Time Series Analysis of Rainstorm-Induced Flash Flood Frequency

Mann–Kendall (M-K) test: The M-K test is a widely used non-parametric method for analyzing time series data, especially in environmental science and hydrology. It detects trends and changes in data sequences without requiring specific distribution assumptions, making it robust against outliers [42]. The test calculates the Z value, where a positive Z indicates an upward trend and a negative Z indicates a downward trend, with significance at the 0.05 level when |Z| > 1.96. For abrupt changes, the statistical sequence (UFK) derived from the time series (X1, X2, …, Xn) is assessed, with |UFK| > 1.96 indicating a significant trend. The inverse series gives the corresponding UBK series (UBK = −UFK), and their intersection at a critical point signifies the onset of a mutation [43].

2.3.2. Analysis of the Spatial Distribution Patterns of Rainstorm-Induced Flash Floods

Kernel density estimation (KDE): The KDE is utilized to estimate the density of point or line features around each output raster cell. Through the use of a two-dimensional grayscale or three-dimensional surface representation of the computed flash flood density, distribution characteristics such as the clustering or dispersion of flash flood point groups can be easily and intuitively identified [41].
f x = 1 n h ∑ i = 1 n K x − X i h
where n represents the number of raster cells within the bandwidth range; K x − X i h is the kernel function; h is the bandwidth; and ( x − X i ) denotes the distance between the estimation point and the sample point X i .
Standard deviation ellipse: In analyzing the spatial distribution of flash floods, the standard deviation ellipse is a useful tool for identifying the spatial distribution characteristics of historical flash flood disaster points. It further illustrates changes in the central location and movement trends [44]. The specific formula is defined as follows:
C = 1 n ∑ i = 1 n x ~ i 2 ∑ i = 1 n   x ~ i y ~ i ∑ i = 1 n   x ~ i y ~ i ∑ i = 1 n   y ~ i 2
x ~ i = x i − x ¯ y ~ i = y i − y ¯
where x i and y i are the coordinates of element i ; ( x ¯ , y ¯ ) represents the mean center of the elements; n denotes the total number of elements; and C is the ellipticity of the standard deviation ellipse.

2.3.3. Study on Spatial Autocorrelation

Local autocorrelation analysis is employed to identify localized spatial clustering characteristics within the study area, facilitating the discovery of regional hotspots and cold spots. Such analysis enables the examination of the spatial autocorrelation of flash flood intensity both across the entire study area and within specific local regions. The Getis–Ord G i * statistic and the local Moran’s I are widely used tools for local autocorrelation analysis. The Getis–Ord G i * is used as the dependent variable Y in the OPGD analysis.
Getis–Ord G i * statistic: This analytical tool is employed to identify areas with high or low value concentrations. A larger G i * value signifies a region of high-value concentration, commonly referred to as a hotspot. The formula is defined as follows:
G i * = ∑ j   w i j x j − X ¯ ∑ j   w i j S ( N ∑ j   w i j 2 − ( ∑ j   w i j ) 2 ) N − 1
The local Moran’s I is utilized to analyze the spatial autocorrelation of individual units. This form of local autocorrelation analysis is capable of uncovering local features that global analyses might overlook. It is particularly significant when the study area exhibits heterogeneity, as it offers insights into localized spatial patterns and variations.
I i = ( x i − x ¯ ) ∑ j   w i j ( x j − x ¯ )
At various spatial scales, the procedure for plotting Moran scatterplots for flash flood intensity involves several steps: Firstly, the average value of flash flood intensity across all analytical units is calculated, along with the spatial lag mean of these values. Based on these two averages, the plane is divided into four quadrants. These quadrants represent different types of local spatial autocorrelation between each analytical unit and its neighboring units, namely high-high correlation, low-high correlation, low-low correlation, and high-low correlation.

2.3.4. Methods for the Causal Mechanisms of Rainstorm-Induced Flash Floods

The OPGD is a model utilized for analyzing spatial heterogeneity and exploring influencing factors and is grounded in the geographical detector method. It enhances the model’s explanatory power through steps such as optimizing discretization strategies, selecting variables, and detecting interactions [45]. The primary objective is to identify the optimal explanatory relationship between the dependent variable (spatial phenomenon) and the independent variables (influencing factors). In this study, the spatial distribution of historical flash flood disasters serves as the analysis phenomenon, while 14 potential factors proposed within the framework are employed as detection variables to investigate the driving forces of flash floods in a specific research area. The detectors chosen here are factor detectors and interaction detectors. The factor detector primarily aims to measure the extent to which a given factor (X) explains the spatial variation of an attribute (Y), using the q value as a metric. The expression is as follows:
    q = 1 − ∑ h = 1 L   N h σ h 2 N σ
S S W = ∑ h = 1 L   N h σ h 2 , S S T = N h σ 2
where h = 1, …, L represents the strata of variable Y or X, which are the classifications or partitions; N h and N denote the number of units in stratum h and the entire region, respectively; and σ h   2 and σ 2 are the variances of the Y values for stratum h and the entire region, respectively.   S S W and S S T represent the sum of squares within the strata (within sum of squares) and the total variance of the entire region (total sum of squares). q indicates the explanatory power (driving force) of a single factor X on the spatial distribution of flash flood intensity Y, with a range of [0, 1]. A larger value suggests a more pronounced spatial differentiation of Y.
Interaction detection can identify the interactions between different influencing factors (Xs), specifically assessing whether the combined effect of factors X1 and X2 increases or diminishes their explanatory power on the dependent variable (Y), or if the impacts of these factors on Y are independent of each other. The evaluation method begins by separately calculating the q values for the two factors, q(X1) and q(X2), in relation to Y. Additionally, the q value when these factors interact (forming a new polygon distribution where the layers of X1 and X2 intersect) is calculated as q(X1 ∩ X2). Finally, a comparison is made among q(X1), q(X2), and q(X1 ∩ X2) [46].
In the application of geographical detectors, the independent variable X must be discrete data. If the independent variable is continuous, it must undergo discretization. This is because the discretization method can significantly affect the size of the q value and the explanatory power of the model. In this study, based on the optimal parameter geographical detector, we calculated the q values for each continuous factor using different classification methods (including equal interval classification, natural interval classification, quantile classification, geometric interval classification, and standard deviation interval classification) and varying numbers of breaks to select the parameter combination with the highest q value, including the classification method and the number of breaks. The analysis here was performed using R programming language (version 4.2.3.), with initial breaks set between 5 and 9 classes. Selecting proper grouping methods and determining the number of groups are crucial for optimizing the geographical detector parameters, as this enhances both the model’s scientific validity and its explanatory power.

3. Results

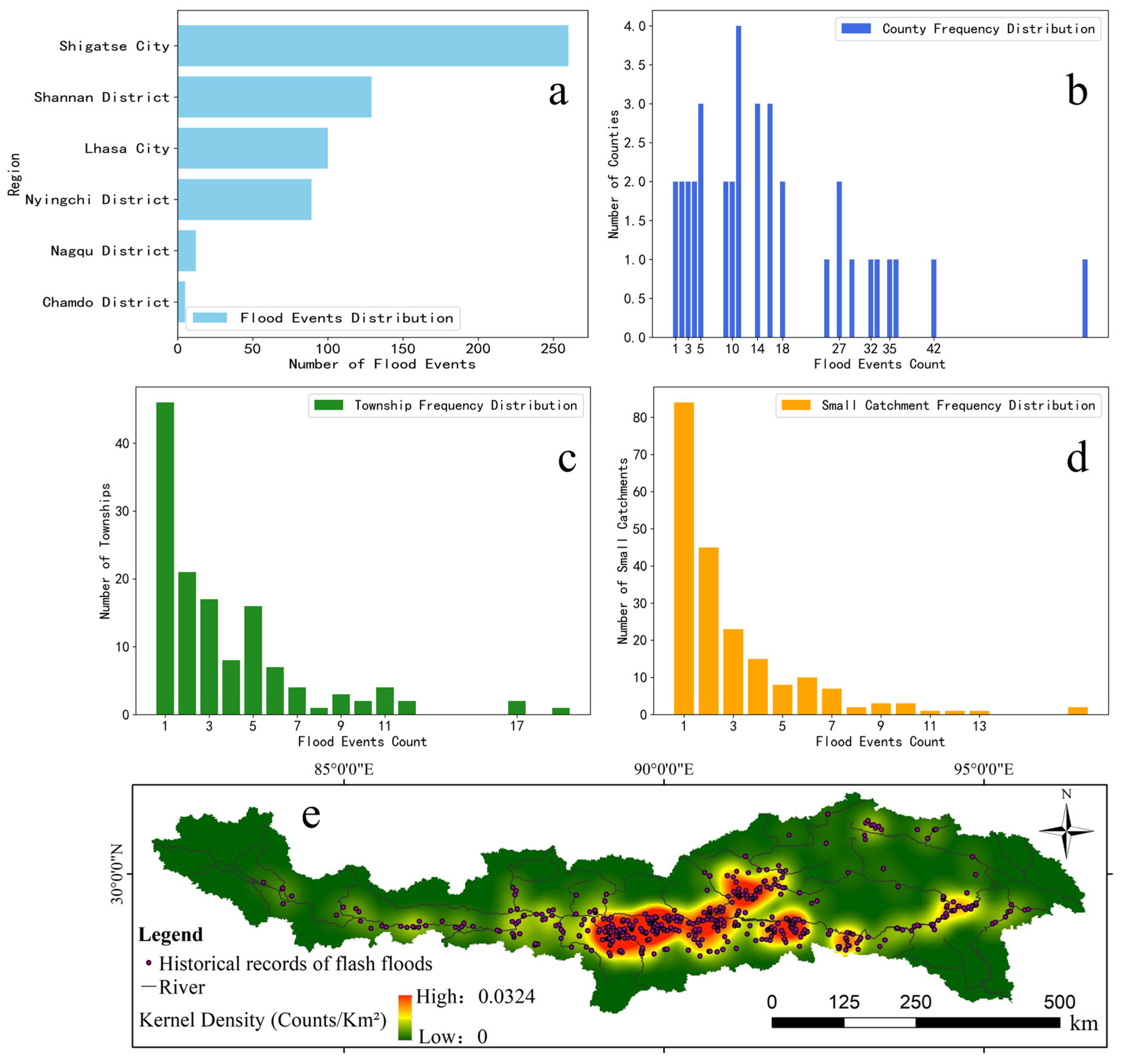
3.1. Spatiotemporal Distribution Patterns of Rainstorm-Induced Flash Floods

3.1.1. Temporal Variation of Rainstorm-Induced Flash Floods

The analysis of the variation in the frequency of rainstorm-induced flash floods from 1980 to 2019 reveals a significant upward trend in such events during this period. As shown in Figure 2a, the annual occurrence of flash floods remained relatively low, ranging between 0 and 5 events per year during the initial period (1980–2000). However, after 2000, the frequency of rainstorm-induced flash floods began to increase significantly, reaching a peak in 2014. The reason for the relatively low number of rainstorm-induced flash flood events after 2015 is largely due to the fact that these data are supplementary and not very comprehensive. Overall, this upward trend suggests a strong association with environmental factors such as climate change and land use changes.
The Mann–Kendall test results (Figure 2b) reveal a statistically significant increasing trend in flash flood frequency. The UFk statistic (red line) follows a stable upward trajectory and exceeds the 95% confidence interval threshold in 1997, indicating a significant trend. The intersection of UFk and UBk (blue line) around 1996 suggests a potential change point in the time series. Following this, UFk continues to rise, while UBk exhibits a declining trend in the early years before stabilizing after 2000. These findings suggest that the observed increase in flash flood frequency is not due to random variability but is likely influenced by environmental and climatic factors.
Through standard deviation ellipse analysis, we have revealed significant changes in the spatial characteristics of flash flood disasters from 1980 to 2019. This analysis focuses on the historical concentration trend, dispersion trend, and directionality of flash flood occurrences. We calculated the standard deviation ellipses for four different time periods: 1980–1989, 1990–1999, 2000–2009, and 2010–2019. As shown in Figure 3 and Table 2, these ellipses illustrate the distribution patterns, central locations, and displacement distances of the disasters. This phenomenon warrants attention, and the possible explanations primarily focus on changes in precipitation. In recent years, the rainfall in the central region has significantly increased, particularly under the influence of an enhanced westerly wind belt, which has led to an increase in moist airflow and accompanying localized heavy rainfall events. This change has resulted in a higher frequency of flash floods in the mountainous areas of the central region, prompting a westward shift in the spatial distribution of the disasters [47]. Additionally, changes in land use, such as urbanization, agricultural expansion, and increased human activities, may have led to greater soil erosion and enhanced surface runoff in the central region [48], further elevating the risk of flash floods. Therefore, the combined effects of changes in precipitation patterns and human activities comprehensively explain the directional shift of flash flood disasters.
The ellipse for 2010–2019 had the largest area, at 68,256.3 square kilometers, indicating the most extensive impact of flash floods during this period, something which is related to the enhanced westerlies that increased precipitation in the western plateau [47], as well as localized heavy rainfall in tributary valleys. Conversely, the smallest ellipse area, 27,931.5 square kilometers, occurred in 1990–1999, possibly due to the weakening of the monsoon from strong El Niño events [8]. The semi-major and semi-minor axes showed variations in the primary and secondary directions of flash flood distribution, with the semi-major axis being the longest in 2010–2019 (358.6 km), indicating a wide distribution along the primary direction (close to north-south, with a rotation angle of 88.25°), while the semi-minor axis was relatively large in 1980–1989 (61.2 km), suggesting more noticeable variations in the secondary direction, which may be linked to orographic lift effects. Differences in the rotation angle reflected the interplay between topography and rainfall patterns, with a smaller R angle in the 1980s (78.07°) showing the east–west orientation of the main river channel constraining disaster spread, and a nearly vertical angle in the 2010s (88.25°) indicating disturbances from enhanced local convective precipitation in north-south tributaries, although the main axis of spread was still dominated by the main river channel topography. These changes show that the spatial distribution of flash flood disasters is influenced by a combination of atmospheric circulation reorganizations, topographical features, and variations in rainfall patterns.

3.1.2. Spatial Distribution Patterns of Rainstorm-Induced Flash Floods

Figure 4 illustrates the spatial distribution of average annual precipitation and elevation at the flash flood disaster points in the YTRB, where the X-axis and Y-axis represent longitude and latitude, respectively, and the Z-axis represents average annual precipitation and elevation. From Figure 4a, it can be observed that the average annual precipitation at the flash flood disaster points shows a decreasing trend from east to west. This indicates that the eastern region experiences higher precipitation, which may be related to the climatic conditions and topographical features of the area, such as being situated on the windward slope of the monsoon, thus receiving more rainfall. However, the area with the highest concentration of flash flood disaster points is located in the central part of the basin, where the average annual precipitation is not the greatest. This suggests that, while precipitation is an important factor influencing flash flood disasters, it is not the sole determinant. Other factors, such as terrain steepness, soil permeability, and vegetation cover, may also play a critical role in the occurrence of flash flood disasters. From Figure 4b, it can be seen that the elevation distribution of flash flood disasters is primarily concentrated above 3500 m, while there are fewer disaster points below 3000 m. This indicates that high-altitude areas, due to their steep terrain and significant slopes, facilitate the rapid convergence of water flow, thereby increasing the risk of flash floods. Combining the precipitation and topographical characteristics of the YTRB, we can further explain the distribution of flash flood disasters. Although the eastern region has higher precipitation, the intricate network of ravines and complex terrain makes it difficult for water to form concentrated flash floods. In contrast, the central region, despite not having the highest precipitation, has complex terrain and numerous river valleys that allow water to converge quickly within a short time, resulting in flash flood disasters. These topographical features make the central region a high-incidence area for flash flood disasters.
Based on this, we analyzed the kernel density of flash flood disasters as shown in Figure 5e. High-density areas are predominantly concentrated in the central part of the basin, where the density of flash flood occurrences can reach up to 0.03 incidents per km2, significantly exceeding those in the upstream and downstream regions. Moreover, the historical distribution of these disasters exhibits a strong correlation with the river systems, being particularly prevalent in valley areas and at river confluences. According to statistics, 76.1% of the storm-induced flash flood disaster points are distributed within a 10 km buffer zone of river systems. This observation suggests that intense short-duration rainfall events, coupled with dramatic topographical variations, are likely the primary factors triggering flash flood disasters.
By analyzing the distribution of flash flood disasters across various spatial scales, high-density and low-density areas can be identified, thereby providing a comprehensive understanding of the overall disaster situation from macro to micro levels. According to statistical data (Figure 5a), the regions with the highest occurrences of rainstorm-induced flash floods are Shigatse City, Shannan Prefecture, Lhasa City, and Nyingchi Prefecture, with 260, 129, 100, and 89 occurrences, respectively. In contrast, Nagqu Prefecture and Chamdo Prefecture have fewer occurrences, with only 12 and 5, respectively. At the district and county level (Figure 5b), flash flood disasters have occurred in 37 districts and counties, accounting for 66.1% of the total. Of these, 2 districts and counties experienced over 40 occurrences, and 8 experienced between 20 and 40 occurrences. At the township level (Figure 5c), 134 townships experienced rainstorm-induced flash flood disasters, representing 34.4% of the total number of townships. Among these townships, 125 experienced 10 or fewer occurrences, while 9 experienced more than 10 occurrences, with the highest being 19. At the small catchment scale (Figure 5d), 205 small catchments experienced rainstorm-induced flash floods, accounting for 15.0% of all small catchments. Among these, 175 small catchments experienced 5 or fewer occurrences, while 30 experienced more than 5 occurrences. This indicates that most small catchments affected by flash floods have a relatively low frequency of occurrence, whereas only a minority have a higher frequency of these disasters.

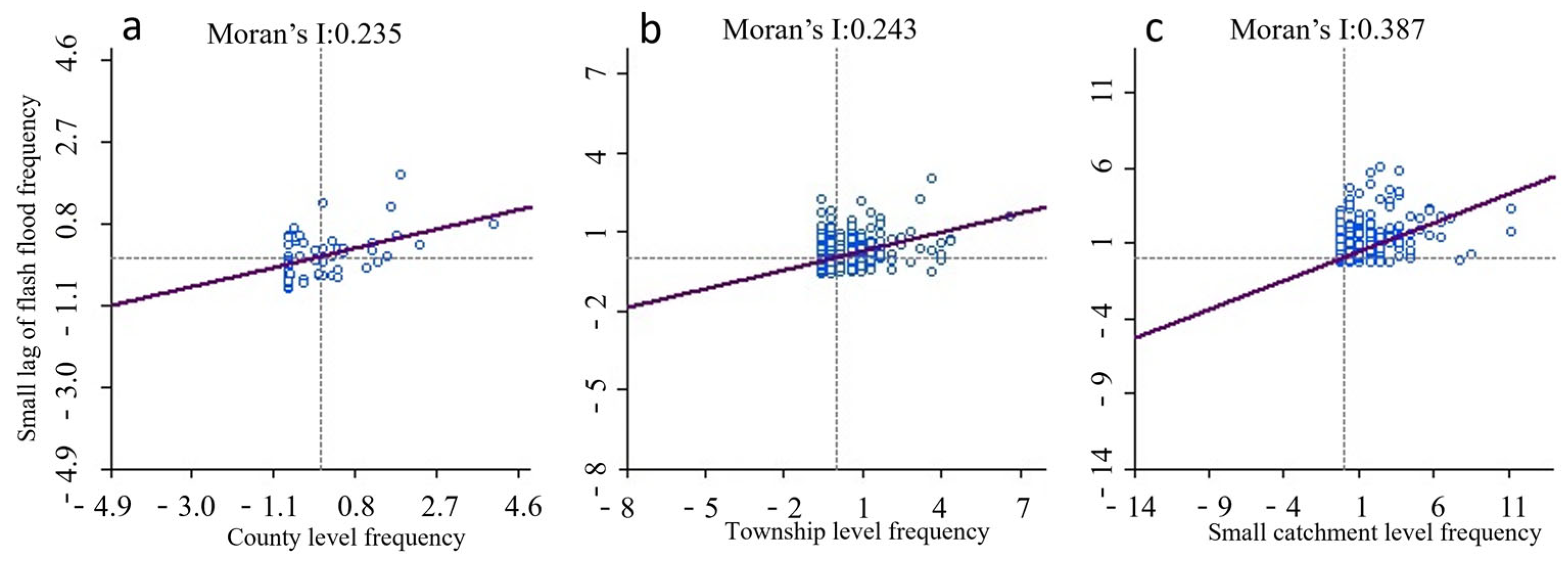
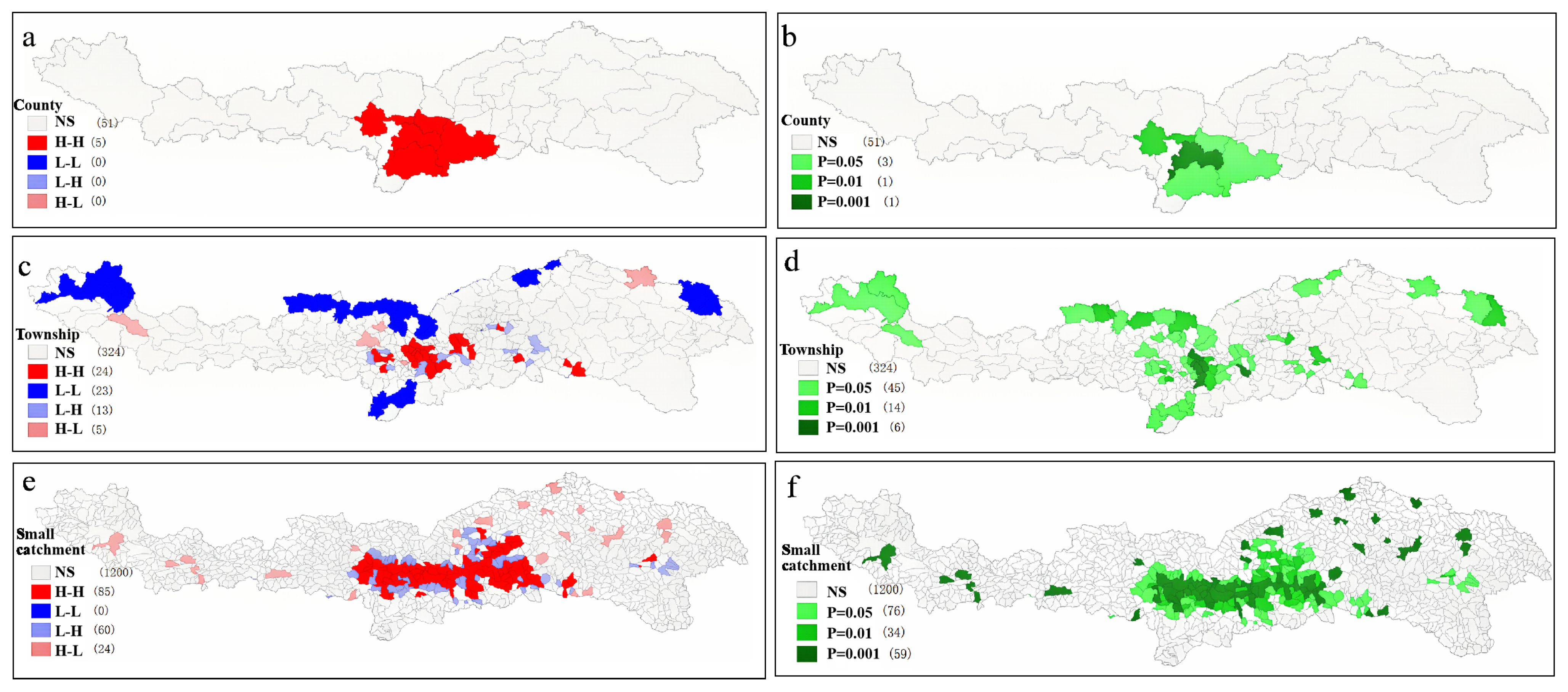
3.2. Spatial Autocorrelation Analysis of Rainstorm-Induced Flash Floods

To explore the spatial dependency of rainstorm-induced flash floods across different spatial scales, this study performed spatial autocorrelation analysis at the district, township, and small catchment levels. The corresponding Moran’s I, Z-scores, and associated probabilities (p-values) were calculated. As presented in Table 3, the Moran’s I reveals an increasing trend of positive spatial autocorrelation across these scales, rising from 0.235 at the district level to 0.243 at the township level, and reaching 0.387 at the small catchment scale. This indicates a tendency for similar levels of flash flood severity to spatially cluster. Moreover, the analysis of Z-scores and associated probabilities (p-values) provides further evidence for the statistical significance of this spatial autocorrelation, confirming the observed pattern of clustering among similar flash flood occurrences.
The local Moran’s I is instrumental in identifying specific clustering areas. Utilizing this metric, a local autocorrelation analysis of rainstorm-induced flash floods was conducted. Figure 6 presents the Moran scatter plots at the district, township, and small catchment scales (Figure 6a–c, respectively). As indicated by the results of the local autocorrelation analysis (Figure 7a,c,e), the patterns of rainstorm-induced flash floods can be categorized into five types across different spatial scales: “High-High (H-H)”, “High-Low (H-L)”, “Low-High (L-H)”, “Low-Low (L-L)”, and “Not Significant (NS)”.
At the county level (Figure 7a), “H-H” clustering is prominently observed in regions such as Samzhubzê District, Gyangzê County, Kangmar County, and Renbu County in Shigatse, as well as Langkazi County in Shannan. This pattern reflects significant spatial autocorrelation, likely due to steep terrain, high-intensity precipitation, and limited vegetation cover. Other clustering categories are not distinctly evident at this scale, possibly due to data resolution limitations. At the township level (Figure 7c), “H-H” clustering is concentrated in specific townships, including Lado Township and Zhongda Town in Nyingchi, Releong Township in Gyangzê County, and several townships in Renbu County and Shannan. “L-L” clustering appears in the basin’s periphery, suggesting low flash flood intensity. “L-H” clusters surround “H-H” areas, possibly due to upstream topography or land use changes. “H-L” clusters are more widespread, indicating diffusion into areas with different land use or human interventions like reservoirs. At the small catchment level (Figure 7e), “H-H” clusters dominate the central basin, covering 85 catchments. This concentration may stem from steep slopes, concentrated rainfall, and land use practices. “L-H” clusters encircle these central areas, reflecting upstream flood propagation or localized land cover changes. “H-L” clusters are dispersed, indicating areas where floods dissipate due to vegetation, wetlands, or efficient drainage. These patterns highlight the complex interplay of natural and anthropogenic factors across scales.

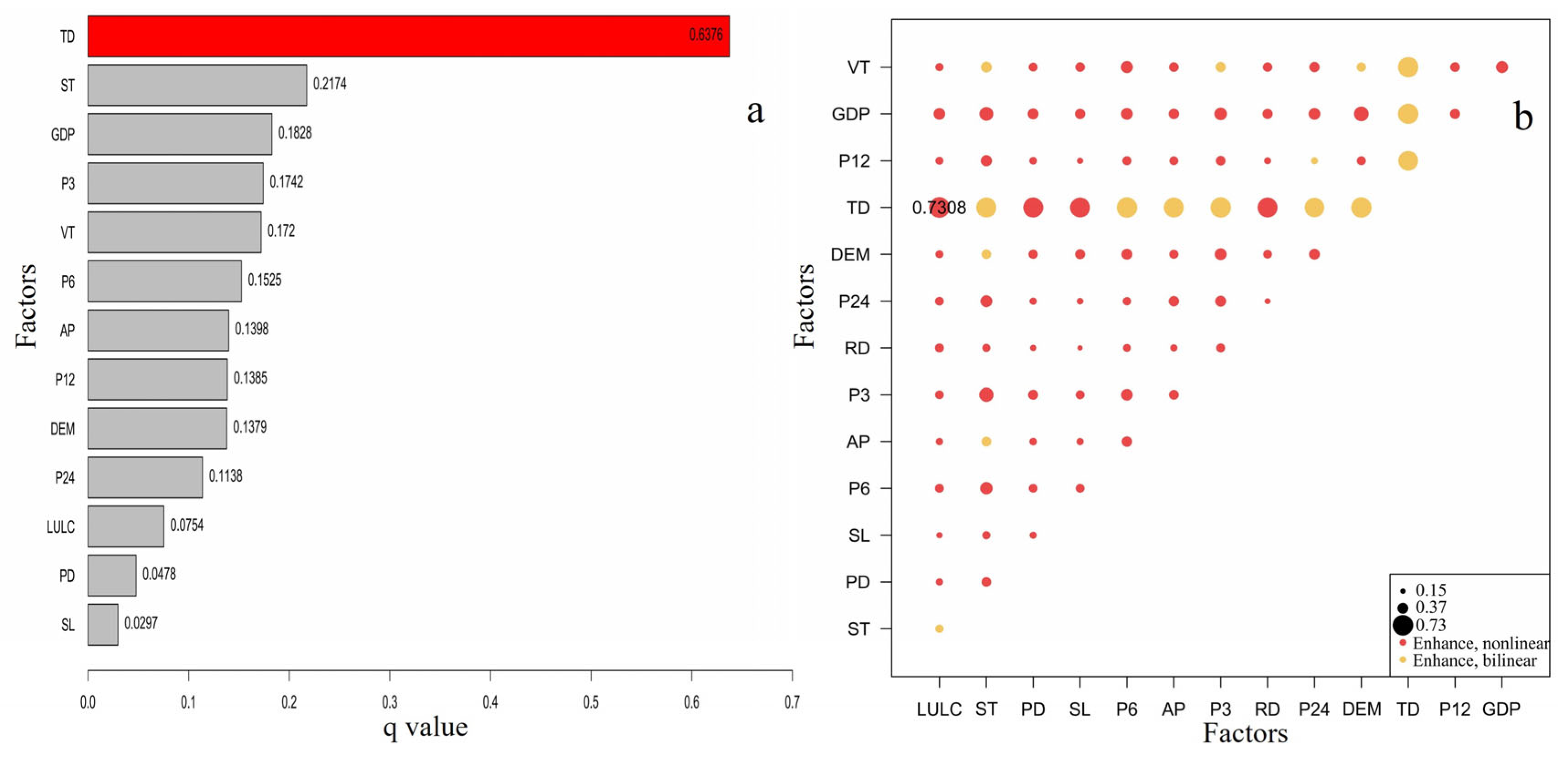
3.3. Analysis of Driving Factors for Rainstorm-Induced Flash Floods

In the OPGD model, the classification methods and the number of categories for each continuous factor have been optimized to enhance the scientific validity and explanatory power of the model (Table 4). Specifically, the continuous factors DEM, SL, RD, P3, P6, PD, and GDP, were classified using quantile classification and divided into 8 or 9 intervals. AP and P12 were classified using standard deviation classification and divided into 9 intervals. P24 was classified using the natural breaks method and divided into 9 intervals. TD was classified using equal interval classification and divided into 9 intervals. For categorical variables such as LULC, ST, and VT, the division was made directly according to categories. The selection of these classification methods and the number of categories aims to optimize the parameters of the geographical detector model, thereby improving the accuracy and reliability of the model. The classification of continuous factors is illustrated in Figure 8.
We evaluated the explanatory power of various influencing factors on the spatial distribution of historical rainstorm-induced flash floods using the q value. The single-factor detection results (Figure 9a) show that TD is the most critical factor influencing the spatial distribution of flash flood disasters, with a q value of 0.6376. This may indicate that multiple influences are at play, as areas with high village density typically indicate a concentration of more population and economic activities within specific geographical spaces, which exacerbates the exposure to flash flood disasters. Furthermore, the hydrological conditions of high village density areas, coupled with changes in impervious surfaces caused by human activities, increase the risk of flash floods. This finding suggests that the prominence of village density as a major factor may be related to human activities, land use intensity, and disaster vulnerability. ST and GDP emerge as second-tier critical factors, with q values of 0.2174 and 0.1828, respectively. This also somewhat supports the discourse on the relevance of village density. ST directly influences surface runoff and infiltration capacity, whereas economic development may indirectly affect disaster risk through infrastructure construction and disaster prevention capabilities. Meteorological factors (P3, P6, AP, P12, P24) significantly impact the spatial distribution of the target variable, particularly P3 and P6, with respective q values of 0.1742 and 0.1525. This underscores short-duration intense rainfall as a critical meteorological trigger for disasters. Among the terrain factors (DEM, SL), DEM exhibits relatively high explanatory power (q = 0.1379), whereas the influence of SL is weaker (q = 0.0297). DEM indirectly influences disaster risks through its impact on precipitation distribution, vegetation types, and soil characteristics, while slope has a limited direct effect on disaster occurrence. VT and LULC also exhibit moderate influence on the spatial distribution of the target variable, with q values of 0.1720 and 0.0754, respectively. VT may impact disaster risk by regulating surface runoff and soil stability, whereas land-use type reflects the extent of human modification of the natural environment. However, RD and PD show relatively weak impacts, with q values of 0.0188 and 0.0478, respectively. River network density may indirectly influence disaster risk by affecting surface runoff and drainage capacity, while the influence of population density is likely related to disaster vulnerability.
Interaction detection results (Figure 9b) indicate that the interaction effects between TD and other key factors significantly impact the target variable. In particular, the nonlinear enhancement effect between VD and short-duration intense precipitation (q = 0.7236), alongside the dual-factor enhancement effect between VD and GDP (q = 0.7219), reveals primary driving mechanisms in high-risk areas. In regions with high VD, the cumulative effect of short-duration intense precipitation is pronounced; in areas with high economic activity, the presence of high VD further amplifies the risk. Furthermore, among precipitation factors, the cumulative effect of P3 and P6 (q = 0.3943) indicates that the combined influence of precipitation intensity and duration is a critical meteorological risk driver. The interaction between topographic and ecological factors, specifically DEM and VT (q = 0.3073), demonstrates that ecological protection is more effective under specific terrain conditions. Conversely, the interaction between SL and RD (q = 0.1500) is not significant, suggesting that their combined effect on the target variable is relatively limited.

4. Discussion

4.1. The Importance of Spatial Scale in Studying Rainstorm-Induced Flash Floods

This study investigates the distribution patterns of rainstorm-induced flash floods across various spatial scales in the YTRB. We found that reducing spatial scale enables more precise identification of high-incidence disaster areas, which is crucial for formulating effective disaster management and mitigation strategies. The research initiated with a macro perspective at the district and county levels, gradually refining to the township and small catchment levels to elucidate details of disaster distribution. Results indicate that, as the spatial scale is reduced, the accuracy of identifying disaster distribution significantly improves [49]. Furthermore, disaster distribution exhibits significant spatial clustering and notable scale differences, providing a strong basis for accurately identifying high-risk areas.
Studies have shown that, at the local scale, the impact of topography on the transformation of rainfall into floods is complex. For instance, steep slopes may accelerate the formation of surface runoff, while complex valley terrain may slow down flood development by dispersing water flow or increasing soil permeability [50]. Local phenomena, such as snowmelt/glacial melt, ice rain, and snow rain, can also lead to runoff, resulting in floods on the Tibetan Plateau [51]. The spatial scale variation of flash flood hydrological processes has a significant impact on the simulation of hydrological processes at different scales within a watershed. This scale dependency reflects the differentiated patterns of energy and material exchange in the hydrological cycle [52]. At the mesoscale, convective systems dominate extreme rainfall events in the eastern Tibetan Plateau. These systems encompass the Tibetan Plateau vortex and tropical cyclones [53]. For example, Kukulies, et al. [54] have demonstrated that extreme summer rainfall events in the eastern Tibetan Plateau are characterized by long durations and extensive coverage, 70% of which are associated with mesoscale convective systems. In summary, the differences in spatial scales significantly influence the distribution patterns of mountain flood disasters. From local to regional scales, the triggering mechanisms transition from being primarily dominated by topography to being controlled by broader climatic systems. Moreover, the impact of human activities becomes more pronounced at the meso-to-small scales, further complicating these interactions. Ultimately, understanding these scale-dependent dynamics is crucial for improving flood risk assessment and management strategies, as it enables more accurate predictions and targeted interventions tailored to specific spatial contexts.

4.2. Discussion on the Trigger Mechanisms and Key Driving Factors

In the investigation of driving forces behind rainstorm-induced flash floods in the YTRB, our findings suggest that village density, short-duration intense precipitation, elevation, and vegetation type are the primary drivers of disaster risk. These findings offer vital references for identifying high-risk areas and developing control measures. Village density, a factor related to human activity, emerges as the most significant driver, exhibiting a notable nonlinear enhancement effect when interacting with short-duration intense precipitation (q = 0.7236) and GDP (q = 0.7219). He, Fang, Wang and Huang [55] underscore the substantial contribution of building density to flash flood intensity, emphasizing that, as per capita housing area increases, so does the intensity of flash floods, corroborating our findings.
Among precipitation factors, the cumulative effect of P3 and P6 highlights their role as critical meteorological risk drivers. Furthermore, the cumulative effect of P3 and P6 precipitation corroborates previous research, suggesting that extreme precipitation remains the predominant influence on flash flood intensity. This includes shifts in precipitation patterns, storm volumes, and storm frequency, collectively contributing 26.6% to the overall impact [56,57]. In terms of the relationship between extreme precipitation changes and flood occurrence trends, analyzing their correlation is challenging due to limitations in specific debris flow disaster data (such as missing dates). In specific flood events in the YTRB, the relationship between extreme precipitation and flood response is quite complex, exhibiting both direct associations and lag effects. Huang et al. [58] analyzed the relationship between extreme precipitation and extreme runoff at the Nuxia hydrological station in the YTRB, finding that 46% to 75% of extreme runoff events occur on the same day as precipitation, indicating a direct connection between the two. However, factors such as soil moisture, vegetation cover, and watershed scale effects can lead to delays in flood response. For example, when the soil is not yet saturated, the flood response may lag by one day. Furthermore, extreme precipitation events with a 1% occurrence probability (precipitation intensity exceeding 18.5 mm/d) can offset the spatial lag effects at the watershed scale and directly trigger rapid runoff, suggesting that precipitation intensity is a critical threshold determining the speed of flood response. This duality of direct response and lag effects reveals the nonlinear characteristics of watershed hydrological processes, providing important scientific evidence for understanding the complex relationship between extreme precipitation and flooding.
Additionally, our results also indicate that interaction between elevation and vegetation type significantly contributes to flash flood disasters among topographic and ecological factors. DEM increases the likelihood of flooding by influencing precipitation distribution, particularly in high-altitude and steep slope areas [59]. VT, on the other hand, plays a crucial role in regulating surface runoff and soil stability through its coverage and root systems, thereby mitigating the risks of flash flood. For instance, forests and grasslands tend to reduce sensitivity to flash floods, while artificial surfaces and cultivated areas increase this sensitivity [60]. The interaction between elevation and vegetation type affects the distribution and intensity of flash flood disasters by influencing precipitation patterns, soil characteristics, terrain slope, and human activities. A deeper understanding of these interactions can provide a solid scientific basis for effective flood prevention and control measures.

4.3. Contributions and Limitations of the Study

This study contributes to the understanding of rainfall-induced flash flood disasters by exploring the spatial distribution at multiple scales, from county to small catchments levels. The identification of high-high (H-H) risk clusters in central regions, along with low-high (L-H) and high-low (H-L) anomalies, offers insights into how disaster risks are spatially differentiated. Additionally, by utilizing the OPGD model, this study reveals the nonlinear relationship between human activities and natural factors from a more effective and reasonable perspective, particularly emphasizing the impact of village density and regional economic level on disaster vulnerability. The results of this study provide the following insights for relevant stakeholders: In terms of planning and land use management, given the significant impact of VD on flood risk (q = 0.6376), it is essential to optimize the layout of villages and cities to avoid the over-concentration of population and economic activities in high-risk areas. Additionally, there should be a strengthening of land use intensity management to reduce the increase of impervious surfaces caused by human activities. Regarding infrastructure construction and optimization, based on the influence of DEM and SL, it is necessary to enhance the construction of water conservancy infrastructure and ecological protection in high-risk areas, such as building flood control levees and drainage systems to improve flood resilience. Furthermore, the layout of transportation and communication infrastructure should be optimized so as to ensure smooth rescue and material transport during flooding events. In terms of disaster monitoring and early warning system construction, by utilizing the triggering effects of short-duration heavy rainfall (P3, P6) and other meteorological factors on floods, more accurate meteorological monitoring and flood warning systems should be established to issue warning information in a timely manner, allowing for the effective evacuation of residents and a rapid emergency response.
However, the study is not without limitations. The reliance on static historical data restricts our ability to fully capture the dynamic nature of disasters under climate change. Inconsistencies in temporal and spatial resolution of the data, along with limited indicator comprehensiveness, may lead to potential biases in the findings. Moreover, the subjective selection of indicators could affect the overall objectivity of the research. Future work could benefit from developing a multi-scale dynamic risk assessment model that integrates real-time meteorological data and land use changes. This approach would enhance the accuracy of rainfall intensity thresholds and permeability assessments, allowing for more tailored prevention and control strategies. While this study has its limitations, it aims to provide a useful foundation for further research and practical applications in disaster risk management.

5. Conclusions

This study conducts an in-depth analysis of the spatial distribution characteristics and driving mechanisms of rainfall-induced flash floods. In terms of spatial distribution, disaster risk exhibits a clear differentiation pattern as the spatial scale is refined from the county level to township and small catchment levels: high-risk areas gradually concentrate from widespread distributions in regions such as Shigatse and Shannan, ultimately manifested at the small catchment level as significant high-high (H-H) clusters in the central region, while low-high (L-H) and high-low (H-L) anomalies are predominantly located at the edges and in the middle to lower reaches of the catchments. In terms of driving mechanisms, the interaction between human activities and natural factors is the dominant factor in the differentiation of the flash flood. The critical human +activity indicator, village density, demonstrates a nonlinear synergistic enhancement effect with short-duration heavy rainfall (P3 and P6, with an interaction coefficient q value reaching 0.7236) and regional economic level (GDP, q = 0.7219), highlighting that areas with tense human–environment relationships are more susceptible to extreme meteorological events. Additionally, the interaction between DEM and VT (q = 0.3073) suggests that, under specific topographic conditions, ecological protection projects may be more effective.
The conclusions of this study emphasize the importance of refined spatial analysis in identifying high-risk areas and reveal the impact of the synergistic effects of human activities and natural factors on disaster risk differentiation, providing scientific support for disaster prevention and control. In practical applications, it is recommended to optimize the layout of villages and cities to avoid excessive concentration in high-risk areas. Additionally, in regions with significant elevation differences, such as Shigatse and Shannan, it is essential to strengthen the construction of water conservancy infrastructure and ecological protection. Prioritizing the establishment of more precise meteorological monitoring and flood warning systems will enable timely issuance of warning information.
This study is limited by the use of static historical data, making it challenging to comprehensively capture the dynamic evolution of disasters under climate change. Moreover, the inconsistency in the temporal and spatial resolution of data, limited availability, and insufficient comprehensiveness in indicator selection may introduce certain errors. Future research should construct a multi-scale dynamic risk assessment model that integrates meteorological forecasting data and land use changes to precisely quantify the physical thresholds of rainfall intensity and underlying surface permeability, thereby achieving accurate zoning of rainfall-induced mountain floods and formulating customized prevention and control strategies.

Author Contributions

Conceptualization, F.H. and S.L.; formal analysis, F.H. and S.L.; funding acquisition, S.L., C.Z., Z.W. and X.M.; methodology, F.H.; software, F.H.; supervision, S.L., C.Z., X.M. and Z.W.; validation, F.H. and S.L.; writing—original draft, F.H.; writing—review and editing, F.H., S.L., C.Z., X.M. and Z.W. All authors have read and agreed to the published version of the manuscript.

Funding

This study was funded by the National Natural Science Foundation of China (Grant No. 42171039), the Second Tibetan Plateau Scientific Expedition and Research (STEP) Program of China (Grant No. 2019QZKK0903), and the National Key Research and Development Program of China (Grant No. 2022YFF0801804).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors would like to thank the reviewers for their constructive comments and suggestions.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kahraman, A.; Kendon, E.J.; Chan, S.C.; Fowler, H.J. Quasi-Stationary Intense Rainstorms Spread Across Europe Under Climate Change. Geophys. Res. Lett. 2021, 48, e2020GL092361. [Google Scholar] [CrossRef]
  2. Westra, S.; Fowler, H.J.; Evans, J.P.; Alexander, L.V.; Berg, P.; Johnson, F.; Kendon, E.J.; Lenderink, G.; Roberts, N.M. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef]
  3. El Gharamti, M.; Rafieeinasab, A.; McCreight, J.L. Leveraging a novel hybrid ensemble and optimal interpolation approach for enhanced streamflow and flood prediction. Hydrol. Earth Syst. Sci. 2024, 28, 3133–3159. [Google Scholar] [CrossRef]
  4. Ngo, P.T.T.; Pham, T.D.; Nhu, V.H.; Le, T.T.; Tran, D.A.; Phan, D.C.; Hoa, P.V.; Amaro-Mellado, J.L.; Bui, D.T. A novel hybrid quantum-PSO and credal decision tree ensemble for tropical cyclone induced flash flood susceptibility mapping with geospatial data. J. Hydrol. 2021, 596, 125682. [Google Scholar] [CrossRef]
  5. Shabou, S.; Ruin, I.; Lutoff, C.; Debionne, S.; Anquetin, S.; Creutin, J.D.; Beaufils, X. MobRISK: A model for assessing the exposure of road users to flash flood events. Nat. Hazards Earth Syst. 2017, 17, 1631–1651. [Google Scholar] [CrossRef]
  6. Yuan, W.L.; Liu, M.Q.; Wan, F. Calculation of Critical Rainfall for Small-Watershed Flash Floods Based on the HEC-HMS Hydrological Model. Water Resour. Manag. 2019, 33, 2555–2575. [Google Scholar] [CrossRef]
  7. Chen, X.; Liu, Y.L.; Zhang, J.Y.; Guan, T.S.; Jin, J.L.; Liu, C.S.; Wang, G.Q.; Bao, Z.X.; Tang, L.S. Changes in soil organic carbon and its response to environmental factors in the Yarlung Tsangpo River basin. Ecol. Indic. 2023, 155, 111039. [Google Scholar] [CrossRef]
  8. Sang, Y.F.; Singh, V.P.; Gong, T.L.; Xu, K.; Sun, F.B.; Liu, C.M.; Liu, W.B.; Chen, R.Z. Precipitation variability and response to changing climatic condition in the Yarlung Tsangpo River basin, China. J. Geophys. Res-Atmos. 2016, 121, 8820–8831. [Google Scholar] [CrossRef]
  9. Zhao, B.; Su, L.J. Complex spatial and size distributions of landslides in the Yarlung Tsangpo River (YTR) basin. J. Rock. Mech. Geotech. 2025, 17, 897–914. [Google Scholar] [CrossRef]
  10. Wang, P.; Wang, H.Y.; Hu, G.; Liu, T.; Qin, J.T.; Wang, Y.Z.; Xu, B.; Zhang, J.Y.; Shi, X.N.; Liu, J.H. Catastrophic outburst floods along the middle Yarlung Tsangpo River: Responses to coupled fault and glacial activity on the Southern Tibetan Plateau. Earth Planet. Sci. Lett. 2024, 646, 119004. [Google Scholar] [CrossRef]
  11. Guo, Y.Q.; Ge, Y.G.; Mao, P.N.; Liu, T. A comprehensive analysis of Holocene extraordinary flood events in the Langxian gorge of the Yarlung Tsangpo River valley. Sci. Total Environ. 2023, 863, 160942. [Google Scholar] [CrossRef] [PubMed]
  12. Yuan, W.L.; Jing, B.H.; Xu, H.S.; Tang, Y.J.; Zhang, S.H. A Dynamic Early Warning Model for Flash Floods Based on Rainfall Pattern Identification. Int. J. Disast Risk Sci. 2024, 15, 769–788. [Google Scholar] [CrossRef]
  13. Yuan, W.L.; Lu, L.; Song, H.Z.; Zhang, X.; Xu, L.J.; Su, C.G.; Liu, M.Q.; Yan, D.H.; Wu, Z.N. Study on the Early Warning for Flash Flood Based on Random Rainfall Pattern. Water Resour. Manag. 2022, 36, 1587–1609. [Google Scholar] [CrossRef]
  14. Wu, Y.Y.; Ouyang, W.; Hao, Z.C.; Lin, C.Y.; Liu, H.B.; Wang, Y.D. Assessment of soil erosion characteristics in response to temperature and precipitation in a freeze-thaw watershed. Geoderma 2018, 328, 56–65. [Google Scholar] [CrossRef]
  15. Delire, C.; Ngomanda, A.; Jolly, D. Possible impacts of 21st century climate on vegetation in Central and West Africa. Glob. Planet Change 2008, 64, 3–15. [Google Scholar] [CrossRef]
  16. Rasouli, K.; Pomeroy, J.W.; Whitfield, P.H. Are the effects of vegetation and soil changes as important as climate change impacts on hydrological processes? Hydrol. Earth Syst. Sci. 2019, 23, 4933–4954. [Google Scholar] [CrossRef]
  17. Gu, X.H.; Zhang, Q.; Li, J.F.; Singh, V.P.; Liu, J.Y.; Sun, P.; Cheng, C.X. Attribution of Global Soil Moisture Drying to Human Activities: A Quantitative Viewpoint. Geophys. Res. Lett. 2019, 46, 2573–2582. [Google Scholar] [CrossRef]
  18. Liu, J.; Wu, Z.; Zhang, H.W. Analysis of Changes in Landslide Susceptibility according to Land Use over 38 Years in Lixian County, China. Sustainability 2021, 13, 10858. [Google Scholar] [CrossRef]
  19. Lu, M.Q.; Lall, U.; Schwartz, A.; Kwon, H. Precipitation predictability associated with tropical moisture exports and circulation patterns for a major flood in France in 1995. Water Resour. Res. 2013, 49, 6381–6392. [Google Scholar] [CrossRef]
  20. Hettiarachchi, S.; Wasko, C.; Sharma, A. Increase in flood risk resulting from climate change in a developed urban watershed—The role of storm temporal patterns. Hydrol. Earth Syst. Sci. 2018, 22, 2041–2056. [Google Scholar] [CrossRef]
  21. Johnson, F.; White, C.J.; van Dijk, A.; Ekstrom, M.; Evans, J.P.; Jakob, D.; Kiem, A.S.; Leonard, M.; Rouillard, A.; Westra, S. Natural hazards in Australia: Floods. Clim. Change 2016, 139, 21–35. [Google Scholar] [CrossRef]
  22. Liu, J.Y.; You, Y.Y.; Li, J.F.; Sitch, S.; Gu, X.H.; Nabel, J.E.M.S.; Lombardozzi, D.; Luo, M.; Feng, X.Y.; Arneth, A.; et al. Response of global land evapotranspiration to climate change, elevated CO2 and land use change. Agric. For. Meteorol. 2021, 311, 108663. [Google Scholar] [CrossRef]
  23. Mallakpour, I.; Villarini, G. The changing nature of flooding across the central United States. Nat. Clim. Change 2015, 5, 250–254. [Google Scholar] [CrossRef]
  24. Asadieh, B.; Krakauer, N.Y. Global trends in extreme precipitation: Climate models versus observations. Hydrol. Earth Syst. Sci. 2015, 19, 877–891. [Google Scholar] [CrossRef]
  25. Yu, X.J.; Gu, X.H.; Kong, D.D.; Zhang, Q.; Cao, Q.; Slater, L.J.; Ren, G.Y.; Luo, M.; Li, J.F.; Liu, J.Y.; et al. Asymmetrical Shift Toward Less Light and More Heavy Precipitation in an Urban Agglomeration of East China: Intensification by Urbanization. Geophys. Res. Lett. 2022, 49, e2021GL097046. [Google Scholar] [CrossRef]
  26. Sikorska, A.E.; Viviroli, D.; Seibert, J. Flood-type classification in mountainous catchments using crisp and fuzzy decision trees. Water Resour. Res. 2015, 51, 7959–7976. [Google Scholar] [CrossRef]
  27. Wang, Y.A.; Nie, J.; Xing, Z.X.; Wang, Z.B.; Xu, C.D.; Li, H. Assessing and mitigating dwelling collapse risk due to extreme precipitation: A comprehensive study using CNN-RF and GeoDetector. Int. J. Disaster Risk Reduct. 2024, 114, 104918. [Google Scholar] [CrossRef]
  28. Wan, W.Y.; Zhou, Y. Spatiotemporal patterns in persistent precipitation extremes of the Chinese mainland (1961–2022) and association with the dynamic factors. Atmos. Res. 2024, 310, 107600. [Google Scholar] [CrossRef]
  29. Fan, J.A.; Sun, W.C.; Zhao, Y.; Xue, B.L.; Zuo, D.P.; Xu, Z.X. Trend Analyses of Extreme Precipitation Events in the Yarlung Zangbo River Basin, China Using a High-Resolution Precipitation Product. Sustainability 2018, 10, 396. [Google Scholar] [CrossRef]
  30. Liu, C.Y.; Li, Y.G.; Ji, X.; Luo, X.; Zhu, M.T. Observed Changes in Temperature and Precipitation Extremes Over the Yarlung Tsangpo River Basin during 1970–2017. Atmosphere 2019, 10, 815. [Google Scholar] [CrossRef]
  31. Shen, D.Y.; Shi, Z.M.; Peng, M.; Zheng, H.C.; Yang, J.T.; Zhang, L.M. Efficient risk assessment of landslide dam breach floods in the Yarlung Tsangpo river basin. Landslides 2024, 21, 2673–2694. [Google Scholar] [CrossRef]
  32. He, F.; Liu, S.X.; Mo, X.G.; Wang, Z.G. Interpretable flash flood susceptibility mapping in Yarlung Tsangpo River Basin using H2O Auto-ML. Sci. Rep. 2025, 15, 1702. [Google Scholar] [CrossRef] [PubMed]
  33. Fu, X.R.; Wang, Z.G.; Sun, H.Q.; Wang, D.; Tian, J.Y.; Sun, P.P.; Su, X.; Liang, L.F. Spatio-Temporal Variation in Pluvial Flash Flood Risk in the Lhasa River Basin, 1991–2020. ISPRS Int. J. Geo-Inf. 2024, 13, 387. [Google Scholar] [CrossRef]
  34. Liu, W.M.; Carling, P.A.; Hu, K.H.; Wang, H.; Zhou, Z.; Zhou, L.Q.; Liu, D.Z.; Lai, Z.P.; Zhang, X.B. Outburst floods in China: A review. Earth-Sci. Rev. 2019, 197, 102895. [Google Scholar] [CrossRef]
  35. Yang, A.N.; Wang, H.; Liu, W.M.; Hu, K.H.; Liu, D.Z.; Wu, C.H.; Hu, X.D. Two megafloods in the middle reach of Yarlung Tsangpo River since Last-glacial period: Evidence from giant bars. Glob. Planet Change 2022, 208, 103726. [Google Scholar] [CrossRef]
  36. Shi, X.N.; Zhang, F.; Lu, X.X.; Wang, Z.Y.; Gong, T.L.; Wang, G.X.; Zhang, H.B. Spatiotemporal variations of suspended sediment transport in the upstream and midstream of the Yarlung Tsangpo River (the upper Brahmaputra), China. Earth Surf. Proc. Land. 2018, 43, 432–443. [Google Scholar] [CrossRef]
  37. Wu, Y.L.; Wang, L.; Yang, J.; Jiang, X.; Niu, Y. Characteristics of hydrochemical and stable isotopes in the Upper and Middle Reaches of the Yarlung Tsangpo River. J. Environ. Chem. Eng. 2023, 11, 110716. [Google Scholar] [CrossRef]
  38. Li, F.P.; Xu, Z.X.; Liu, W.F.; Zhang, Y.Q. The impact of climate change on runoff in the Yarlung Tsangpo River basin in the Tibetan Plateau. Stoch. Environ. Res. Risk A 2014, 28, 517–526. [Google Scholar] [CrossRef]
  39. You, Q.L.; Kang, S.C.; Wu, Y.H.; Yan, Y.P. Climate change over the yarlung zangbo river basin during 1961–2005. J. Geogr. Sci. 2007, 17, 409–420. [Google Scholar] [CrossRef]
  40. Qu, B.; Zhang, X.N.; Pappenberger, F.; Zhang, T.; Fang, Y.H. Multi-Model Grand Ensemble Hydrologic Forecasting in the Fu River Basin Using Bayesian Model Averaging. Water 2017, 9, 74. [Google Scholar] [CrossRef]
  41. Alikadic, A.; Pertot, I.; Eccel, E.; Dolci, C.; Zarbo, C.; Caffarra, A.; De Filippi, R.; Furlanello, C. The impact of climate change on grapevine phenology and the influence of altitude: A regional study. Agric. For. Meteorol. 2019, 271, 73–82. [Google Scholar] [CrossRef]
  42. Mann, H.B. Nonparametric Tests against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
  43. Shi, W.Z.; Huang, S.Z.; Liu, D.F.; Huang, Q.; Han, Z.M.; Leng, G.Y.; Wang, H.; Liang, H.; Li, P.; Wei, X.T. Drought-flood abrupt alternation dynamics and their potential driving forces in a changing environment. J. Hydrol. 2021, 597, 126179. [Google Scholar] [CrossRef]
  44. Li, Y.; Osei, F.B.; Hu, T.A.; Stein, A. Urban flood susceptibility mapping based on social media data in Chengdu city, China. Sustain. Cities Soc. 2023, 88, 104307. [Google Scholar] [CrossRef]
  45. Xiang, S.Y.; Li, Y.Q.; Li, D.A.; Yang, S. An analysis of heavy precipitation caused by a retracing plateau vortex based on TRMM data. Meteorol. Atmos. Phys. 2013, 122, 33–45. [Google Scholar] [CrossRef]
  46. Qiao, P.W.; Yang, S.C.; Lei, M.; Chen, T.B.; Dong, N. Quantitative analysis of the factors influencing spatial distribution of soil heavy metals based on geographical detector. Sci. Total Environ. 2019, 664, 392–413. [Google Scholar] [CrossRef]
  47. Ma, Q.H.; Zhang, C.Y.; Wang, D.H.; Pang, Z.H. Summer Atmospheric Water Cycle under the Transition Influence of the Westerly and Summer Monsoon over the Yarlung Zangbo River Basin in the Southern Tibetan Plateau. Adv. Atmos. Sci. 2024, 41, 830–846. [Google Scholar] [CrossRef]
  48. Wang, L.; Zhang, F.; Fu, S.H.; Shi, X.N.; Chen, Y.; Jagirani, M.D.; Zeng, C. Assessment of soil erosion risk and its response to climate change in the mid-Yarlung Tsangpo River region. Environ. Sci. Pollut. Res. 2020, 27, 607–621. [Google Scholar] [CrossRef]
  49. Huang, F.M.; Xiong, H.W.; Yao, C.; Catani, F.; Zhou, C.B.; Huang, J.S. Uncertainties of landslide susceptibility prediction considering different landslide types. J. Rock. Mech. Geotech. 2023, 15, 2954–2972. [Google Scholar] [CrossRef]
  50. Braud, I.; Ayral, P.A.; Bouvier, C.; Branger, F.; Delrieu, G.; Le Coz, J.; Nord, G.; Vandervaere, J.P.; Anquetin, S.; Adamovic, M.; et al. Multi-scale hydrometeorological observation and modelling for flash flood understanding. Hydrol. Earth Syst. Sci. 2014, 18, 3733–3761. [Google Scholar] [CrossRef]
  51. Yang, L.; Yang, Y.X.; Villarini, G.; Li, X.; Hu, H.C.; Wang, L.C.; Blöschl, G.; Tian, F.Q. Climate More Important for Chinese Flood Changes Than Reservoirs and Land Use. Geophys. Res. Lett. 2021, 48, e2021GL093061. [Google Scholar] [CrossRef]
  52. Yu, Z.B.; Lu, Q.G.; Zhu, J.T.; Yang, C.G.; Ju, Q.; Yang, T.; Chen, X.; Sudicky, E.A. Spatial and Temporal Scale Effect in Simulating Hydrologic Processes in a Watershed. J. Hydrol. Eng. 2014, 19, 99–107. [Google Scholar] [CrossRef]
  53. Chen, A.F.; Ho, C.H.; Chen, D.L.; Azorin-Molina, C. Tropical cyclone rainfall in the Mekong River Basin for 1983–2016. Atmos. Res. 2019, 226, 66–75. [Google Scholar] [CrossRef]
  54. Kukulies, J.; Chen, D.L.; Curio, J. The Role of Mesoscale Convective Systems in Precipitation in the Tibetan Plateau Region. J. Geophys. Res.-Atmos. 2021, 126, e2021JD035279. [Google Scholar] [CrossRef]
  55. He, X.J.; Fang, Y.P.; Wang, B.S.; Huang, X.Y. Towards a verifiable, uncertainty-controlled assessment of the spatiotemporal dynamics of social vulnerability to flash floods. Ecol. Indic. 2024, 166, 112323. [Google Scholar] [CrossRef]
  56. Davenport, F.V.; Burke, M.; Diffenbaugh, N.S. Contribution of historical precipitation change to US flood damages. Proc. Natl. Acad. Sci. USA 2021, 118, e2017524118. [Google Scholar] [CrossRef]
  57. Thomas, V.; Albert, J.R.G.; Hepburn, C. Contributors to the frequency of intense climate disasters in Asia-Pacific countries. Clim. Change 2014, 126, 381–398. [Google Scholar] [CrossRef]
  58. Huang, G.F.; Sun, H.; Yao, T.D. The relationship between extreme precipitation and extreme streamflow at the Nuxia Hydrological Station in the Yarlung Zangbo River basin. J. Glaciol. Geocryol. 2024, 46, 1099–1112. [Google Scholar] [CrossRef]
  59. Chen, C.F.; Hu, B.J.; Li, Y.Y. Easy-to-use spatial random-forest-based downscaling-calibration method for producing precipitation data with high resolution and high accuracy. Hydrol. Earth Syst. Sci. 2021, 25, 5667–5682. [Google Scholar] [CrossRef]
  60. Sun, X.Y.; Zhang, G.T.; Wang, J.; Li, C.Y.; Wu, S.N.; Li, Y. Spatiotemporal variation of flash floods in the Hengduan Mountains region affected by rainfall properties and land use. Nat. Hazards 2022, 111, 465–488. [Google Scholar] [CrossRef]
Remotesensing 17 01393 g001
Figure 1. Location map of the Yarlung Tsangpo River Basin (YTRB).
Figure 1. Location map of the Yarlung Tsangpo River Basin (YTRB).
Remotesensing 17 01393 g001
Remotesensing 17 01393 g002
Figure 2. Temporal variation of rainstorm-induced flash flood events. (a) The number of flash flood occurrences from 1981 to 2015. (b) The results of the Mann–Kendall test analyzing the trend in the frequency of rainstorm-induced flash floods, including the UFk and UBk statistics, indicating a significant upward trend.
Figure 2. Temporal variation of rainstorm-induced flash flood events. (a) The number of flash flood occurrences from 1981 to 2015. (b) The results of the Mann–Kendall test analyzing the trend in the frequency of rainstorm-induced flash floods, including the UFk and UBk statistics, indicating a significant upward trend.
Remotesensing 17 01393 g002
Remotesensing 17 01393 g003
Figure 3. Standard deviational ellipse analysis. The historical rainstorm-induced flash flood points in different colors represent different decades, consistent with the colors of the ellipses.
Figure 3. Standard deviational ellipse analysis. The historical rainstorm-induced flash flood points in different colors represent different decades, consistent with the colors of the ellipses.
Remotesensing 17 01393 g003
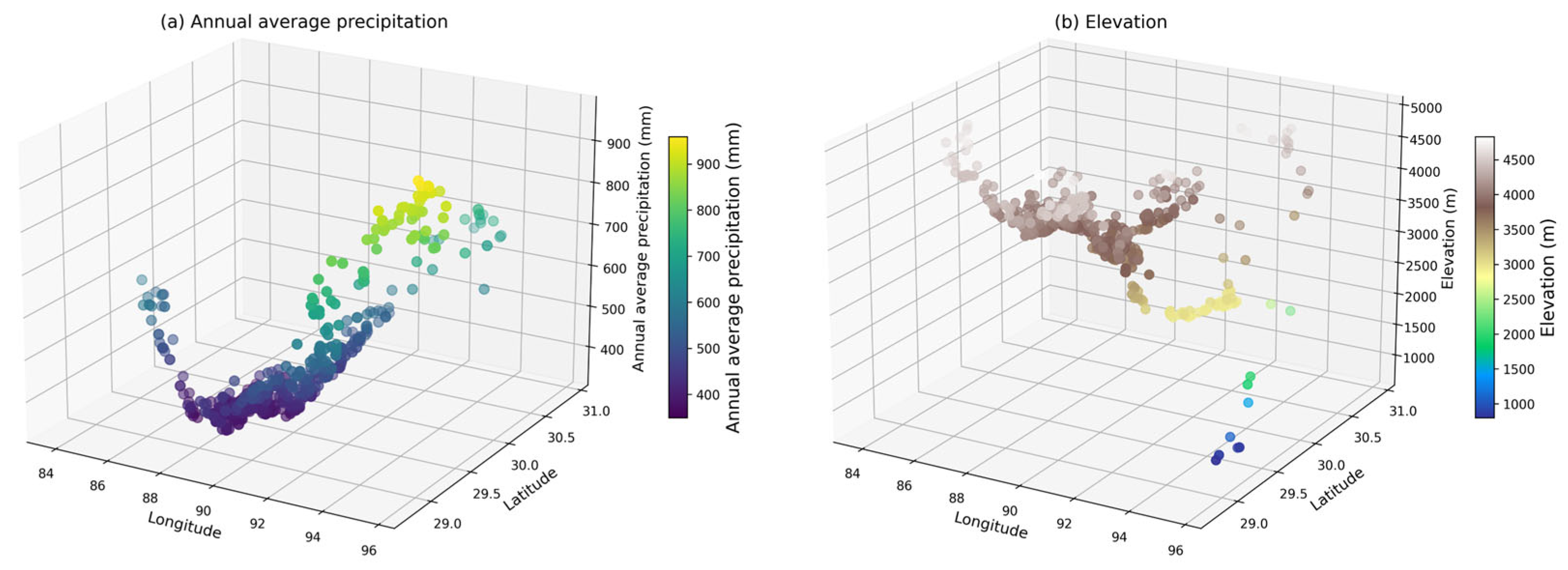
Remotesensing 17 01393 g004
Figure 4. Spatial distribution of annual average precipitation and elevation at rainstorm-induced flash flood points in the YTRB: (a) Annual average precipitation; (b) elevation.
Figure 4. Spatial distribution of annual average precipitation and elevation at rainstorm-induced flash flood points in the YTRB: (a) Annual average precipitation; (b) elevation.
Remotesensing 17 01393 g004
Remotesensing 17 01393 g005
Figure 5. Statistical chart of rainstorm-induced flash flood occurrences across multiple spatial scales. (a) The number of flash flood occurrences in different regions. (b) The number of districts and counties affected by disasters alongside their corresponding occurrence counts. (c) and (d) are the same as (b), but focus on the township and small catchment scale, respectively. (e) The result of kernel density estimation of flash flood disasters.
Figure 5. Statistical chart of rainstorm-induced flash flood occurrences across multiple spatial scales. (a) The number of flash flood occurrences in different regions. (b) The number of districts and counties affected by disasters alongside their corresponding occurrence counts. (c) and (d) are the same as (b), but focus on the township and small catchment scale, respectively. (e) The result of kernel density estimation of flash flood disasters.
Remotesensing 17 01393 g005
Remotesensing 17 01393 g006
Figure 6. Scatter plot of Moran’s I for rainstorm-induced flash floods at multiple spatial scales. (a–c) Moran scatter plots for the county, township, and small catchments, respectively.
Figure 6. Scatter plot of Moran’s I for rainstorm-induced flash floods at multiple spatial scales. (a–c) Moran scatter plots for the county, township, and small catchments, respectively.
Remotesensing 17 01393 g006
Remotesensing 17 01393 g007
Figure 7. The clustering patterns and significance levels of rainstorm-induced flash flood across various spatial scales. (a,c,e) The local autocorrelation patterns of flash flood at these scales. (b,d,f) The significance of local autocorrelation for flash floods at the county, township, and small catchment levels, respectively.
Figure 7. The clustering patterns and significance levels of rainstorm-induced flash flood across various spatial scales. (a,c,e) The local autocorrelation patterns of flash flood at these scales. (b,d,f) The significance of local autocorrelation for flash floods at the county, township, and small catchment levels, respectively.
Remotesensing 17 01393 g007
Remotesensing 17 01393 g008
Figure 8. The parameter discretization process (the red line indicates the interval condition of the factor).
Figure 8. The parameter discretization process (the red line indicates the interval condition of the factor).
Remotesensing 17 01393 g008
Remotesensing 17 01393 g009
Figure 9. The results of single factor exploration and factor interactions exploration. (a) The ranking of explanatory power of individual factors for flash flood disasters. (b) The results of the factor interactions.
Figure 9. The results of single factor exploration and factor interactions exploration. (a) The ranking of explanatory power of individual factors for flash flood disasters. (b) The results of the factor interactions.
Remotesensing 17 01393 g009
Table 1. Introduction and sources of basic data.
Table 1. Introduction and sources of basic data.
CategorysFactorsAbbreviationData Year (s)Spatial ResolutionData TypeData Source
Disaster-inducing environmental factorsElevationDEM201290 mRasterhttps://data.tpdc.ac.cn/ (accessed on 21 November 2024)
slopeSL201290 mRasterhttps://data.tpdc.ac.cn/ (accessed on 21 November 2024)
Soil typeST20141 kmRasterhttps://www.resdc.cn/data.aspx?DATAID=125/ (accessed on 21 November 2024)
River network densityRD20191 kmRasterhttps://www.scidb.cn/en/ (accessed on 21 November 2024)
Vegetation typeVT20101 kmRasterhttps://www.resdc.cn/da-ta.aspx?DATAID=125/ (accessed on 21 November 2024)
Annual average PrecipitationAP1980–20151 kmRasterhttps://www.resdc.cn/data.aspx?DATAID=125/ (accessed on 21 November 2024)
maximum 3 h PrecipitationP32011–20150.1°Rasterhttps://data.tpdc.ac.cn/ (accessed on 21 November 2024)
Rainfall factormaximum 6 h PrecipitationP62011–20150.1°Rasterhttps://data.tpdc.ac.cn/ (accessed on 21 November 2024)
maximum 12 h PrecipitationP122011–20150.1°Rasterhttps://data.tpdc.ac.cn/ (accessed on 21 November 2024)
maximum 24 h orecipitationP242011–20150.1°Rasterhttps://data.tpdc.ac.cn/ (accessed on 21 November 2024)
Population DensityPD20151 kmRasterhttps://www.resdc.cn/data.aspx?DATAID=125/ (accessed on 21 November 2024)
Gross domestic product (GDP)GDP20151 kmRasterhttps://www.resdc.cn/data.aspx?DATAID=125/ (accessed on 21 November 2024)
Human activity factorLand useLULC20151 kmRasterhttps://www.resdc.cn/data.aspx?DATAID=125/ (accessed on 21 November 2024)
Village densityTD20101 kmVector layerhttps://www.resdc.cn/data.aspx?DATAID=125/ (accessed on 21 November)
Flash flood intensityHistorical flood disaster dataFF1980–20181 kmVector layerhttps://data.tpdc.ac.cn/ (accessed on 21 November)
Table 2. Ellipse Parameters.
Table 2. Ellipse Parameters.
PeriodEllipse Area (km2)Ellipse Perimeter (km)Centroid LongitudeCentroid LatitudeSemi-Major Axis (km)Semi-Minor Axis (km)Orientation Angle (°)
2010–201968,256.31012.590.7829.34358.660.688.25
2000–200958,771.1963.890.6229.29331.958.284.96
1990–199927,931.5666.690.4329.25252.535.588.17
1980–198936,043.5838.490.4929.20190.661.278.07
Table 3. Calculation results of the Moran’s I for multi-scale rainstorm-induced flood disasters.
Table 3. Calculation results of the Moran’s I for multi-scale rainstorm-induced flood disasters.
Spatial ScaleMoran’s IZ-ScoreAssociated Probability p
County0.2352.8630.008
Township0.2437.8830.001
Small catchment0.38724.5030.001
Table 4. Factors discretization.
Table 4. Factors discretization.
NameTypeClassification MethodIntervalsDescription of Interval Ranges
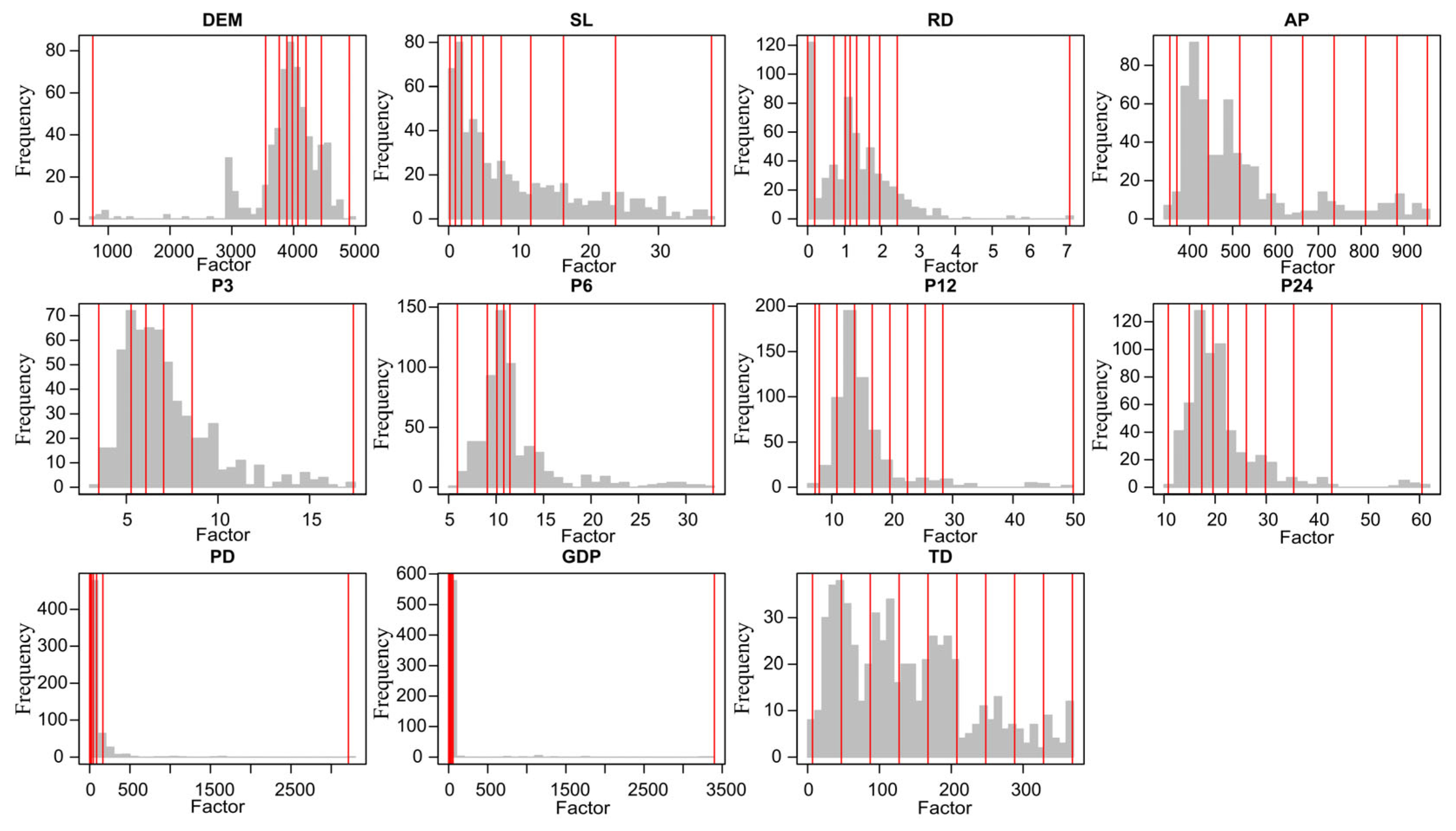
DEMContinuous variableQuantile8[751, 3547.25]–[4449.5, 4902]
SLContinuous variableQuantile9[0.171, 0.962]–[23.9, 37.6]
RDContinuous variableQuantile9[0, 0.19]–[2.43, 7.1]
APContinuous variableStandard deviation9[354, 370]–[884, 954]
P3Continuous variableQuantile5[3.5, 5.26]–[8.59, 17.4]
P6Continuous variableQuantile6[5.92, 9.07]–[14.1, 32.9]
P12Continuous variableStandard deviation9[7.24, 7.92]–[28.4, 50]
P24Continuous variableNatural breaks9[10.8, 14.9]–[42.8, 60.5]
PDContinuous variableQuantile9[0, 2]–[164, 3213]
GDPContinuous variableQuantile9[0, 1]–[56, 3400]
TDContinuous variableEqual9[6.76, 47]–[328, 369]
LULCCategorical variableNoneClassBy Class Number
STCategorical variableNoneClassBy Class Number
VTCategorical variableNoneClassBy Class Number
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

He, F.; Zheng, C.; Mo, X.; Wang, Z.; Liu, S. Study on the Spatial Distribution Patterns and Driving Forces of Rainstorm-Induced Flash Flood in the Yarlung Tsangpo River Basin. Remote Sens. 2025, 17, 1393. https://doi.org/10.3390/rs17081393

AMA Style

He F, Zheng C, Mo X, Wang Z, Liu S. Study on the Spatial Distribution Patterns and Driving Forces of Rainstorm-Induced Flash Flood in the Yarlung Tsangpo River Basin. Remote Sensing. 2025; 17(8):1393. https://doi.org/10.3390/rs17081393

Chicago/Turabian Style

He, Fei, Chaolei Zheng, Xingguo Mo, Zhonggen Wang, and Suxia Liu. 2025. "Study on the Spatial Distribution Patterns and Driving Forces of Rainstorm-Induced Flash Flood in the Yarlung Tsangpo River Basin" Remote Sensing 17, no. 8: 1393. https://doi.org/10.3390/rs17081393

APA Style

He, F., Zheng, C., Mo, X., Wang, Z., & Liu, S. (2025). Study on the Spatial Distribution Patterns and Driving Forces of Rainstorm-Induced Flash Flood in the Yarlung Tsangpo River Basin. Remote Sensing, 17(8), 1393. https://doi.org/10.3390/rs17081393

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop