Comparing Satellite-Derived and Model-Based Surface Soil Moisture for Spring Barley Yield Prediction in Central Europe
Abstract
1. Introduction
1.1. Soil Moisture in the Context of Yield Prediction
1.2. Scope of This Study
2. Materials and Methods
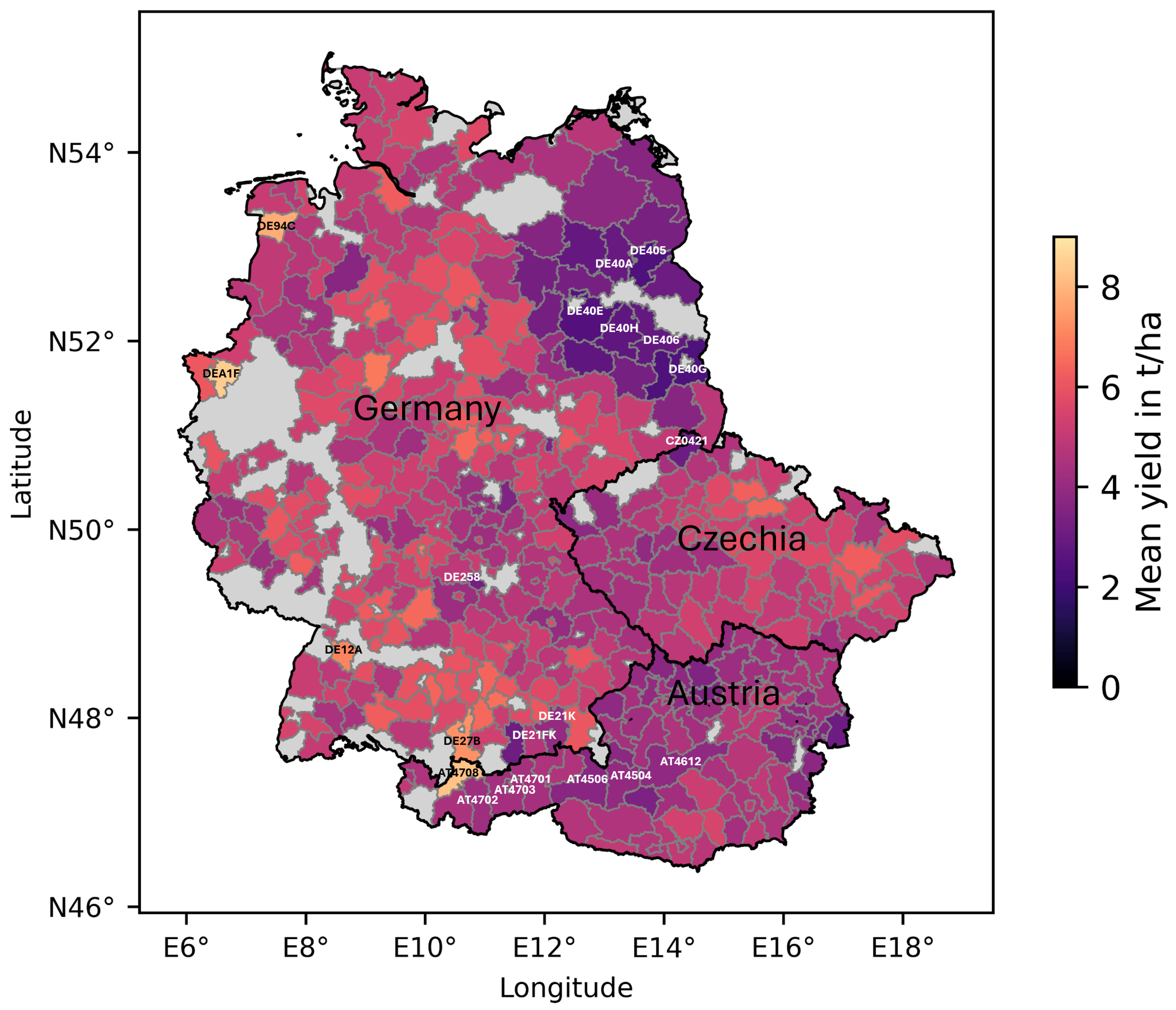
2.1. Study Region
2.2. Cultivation of Spring Barley
2.3. Crop Yield Data
2.4. Surface Soil Moisture Data
2.5. Feed Forward Neural Network
2.6. Model Design and Training
2.7. Accuracy Assessment
- Root Mean Square Error (RMSE): RMSE quantifies the average magnitude of prediction errors by taking the square root of the mean of the squared differences between predicted and actual values. RMSE gives more weight to larger errors, making it particularly useful when large deviations are undesirable or critical in a model’s performance [55].
- Mean Absolute Error ( MAE): MAE measures the average magnitude of prediction errors by calculating the mean of the absolute differences between predicted and actual values. In contrast to RMSE, it treats all errors equally, making it less sensitive to outliers.
- Pearson’s R (correlation coefficient): PearsonR measures the strength and direction of a linear relationship between two continuous variables. It ranges from −1 to +1, where +1 indicates a perfect positive correlation and −1 a perfect negative correlation; 0 suggests no linear correlation. PearsonR is only sensitive to linear relationships, so it does not capture non-linear associations effectively [56].
- R2 (coefficient of determination): R2 measures the proportion of variance in the dependent variable that is explained by the independent variable(s) in a regression model. However, the exact definition and associated calculation of the coefficient of determination varies. In this study, R2 was determined using the Scikit-learn r2_score function, which defines R2 as the ratio of the explained sum of squares to the total sum of squares. An R2 value closer to 1 means that the model explains most of the variability, while values close to 0 or negative indicate a low explained variability [57].
- Unbiased Root Mean Square Error (ubRMSE): ubRMSE provides insight into how well a model captures the dynamics or variability in the data while ignoring any consistent bias. A low ubRMSE indicates that the model predictions closely follow the pattern of the actual data, even if there is a consistent offset. It is defined as the square root of the difference of the squared RMSE and the squared bias. This metric is only used in Section 3.2 and Section 4.2.
- F-statistic: The F-statistic in regression analysis tests whether the model explains a significant proportion of the variance in the dependent variable compared to random chance. It evaluates the null hypothesis that all regression coefficients (except the intercept) are zero, meaning that the predictors have no collective effect. A large F-statistic indicates that the model is statistically significant and at least one predictor contributes meaningfully to explaining the variance [58].
3. Results
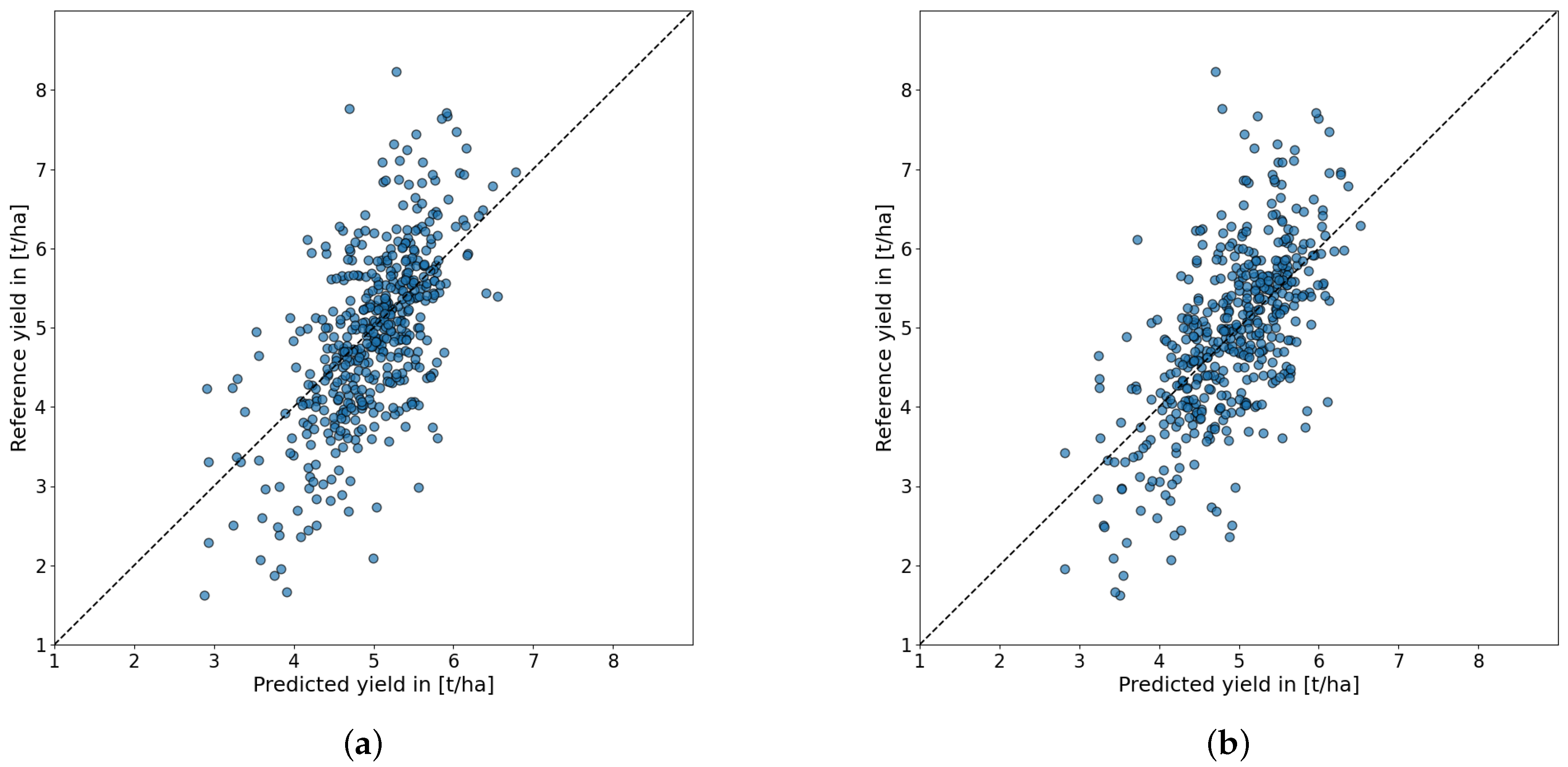
3.1. Explained Variability by Surface Soil Moisture
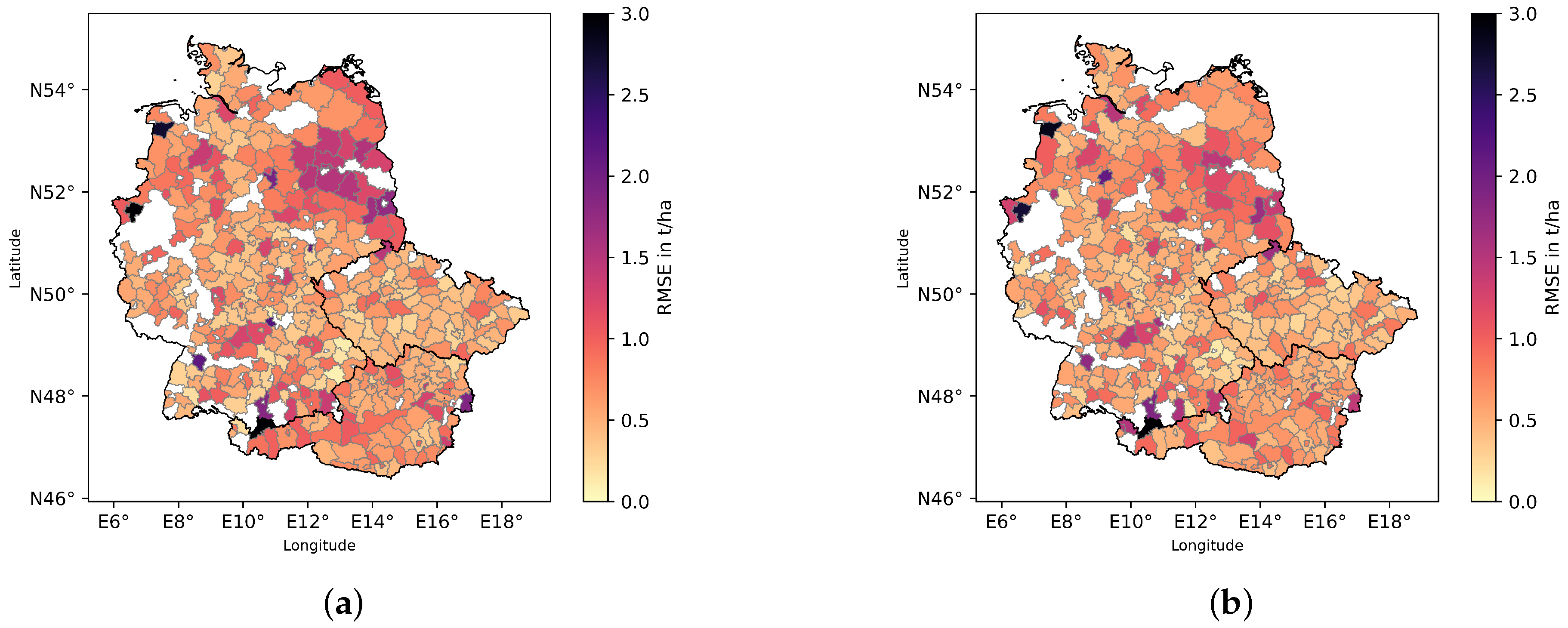
3.2. Spatial Evaluation of the Models
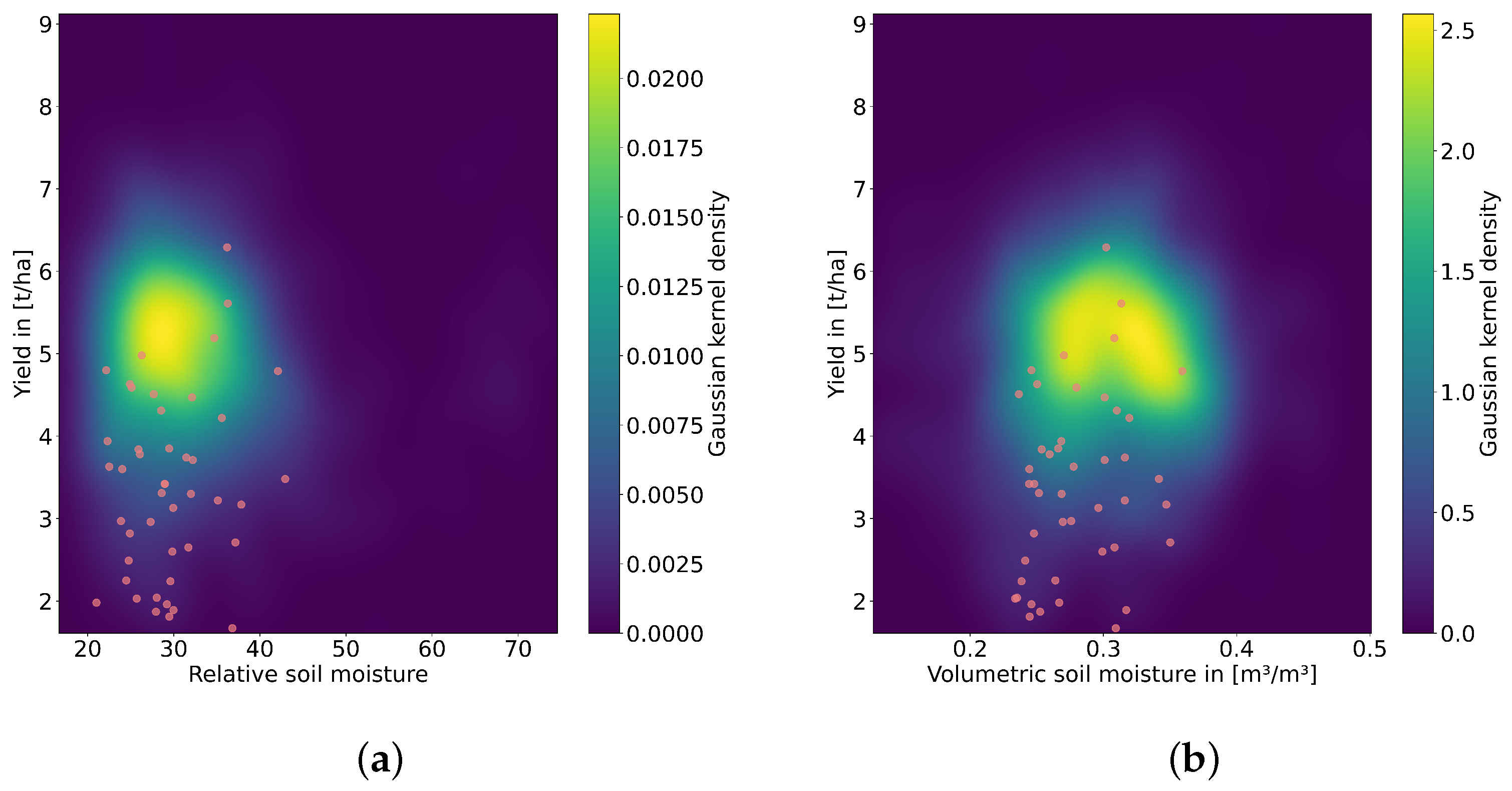
3.3. Comparison of ERA5 SWVL1 and H SAF SSM
4. Discussion
4.1. Value of SSM for Spring Barley Yield Prediction
4.2. Spatial Error Distribution
4.3. Comparison of the Two SSM Products
4.4. Limitations of the Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artifical Neural Network |
| ASCAT | Advanced Scatterometer |
| AT | Austria |
| CZ | Czechia |
| DE | Germany |
| ECMWF | European Centre for Medium-Range Weather Forecasts |
| EUMETSAT | European Organisation for the Exploitation of Meteorological Satellites |
| FFNN | Feed-Forward Neural Network |
| H SAF | EUMETSAT Satellite Application Facility on Support to Operational Hydrology and Water Management |
| MAE | Mean Absolute Error |
| ML | Machine Learning |
| NUTS | Nomenclature Des Unités Territoriales Statistiques |
| RMSE | Root Mean Square Error |
| SM | Soil Moisture |
| SSM | Surface Soil Moisture |
| SWI | Soil Water Index |
| SWVL1 | Volumetric Soil Water Layer 1 |
| ubRMSE | unbiased Root Mean Square Error |
References
- Shah, A.; Dubey, A.; Hemnani, V.; Gala, D.; Kalbande, D.R. Smart Farming System: Crop Yield Prediction Using Regression Techniques. In Proceedings of the International Conference on Wireless Communication, Mumbai, India, 19–20 January 2018; Vasudevan, H., Deshmukh, A.A., Ray, K.P., Eds.; Springer: Singapore, 2018; pp. 49–56. [Google Scholar] [CrossRef]
- Jang, S.J.; Kim, J.S.; Kim, T.W.; Lee, H.J.; Ko, S. A Wafer Map Yield Prediction Based on Machine Learning for Productivity Enhancement. IEEE Trans. Semicond. Manuf. 2019, 32, 400–407. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, M.; Kumar, P.; Singh, J. Crop Selection Method to maximize crop yield rate using machine learning technique. In Proceedings of the 2015 International Conference on Smart Technologies and Management for Computing, Communication, Controls, Energy and Materials (ICSTM), Chennai, India, 6–8 May 2015; pp. 138–145. [Google Scholar] [CrossRef]
- Zaloom, C. How to Read the Future: The Yield Curve, Affect, and Financial Prediction. Public Cult. 2009, 21, 245–268. [Google Scholar] [CrossRef]
- Mahmoodi-Eshkaftaki, M.; Rafiee, M.R. Optimization of irrigation management: A multi-objective approach based on crop yield, growth, evapotranspiration, water use efficiency and soil salinity. J. Clean. Prod. 2020, 252, 119901. [Google Scholar] [CrossRef]
- Lukina, E.V.; Freeman, K.W.; Wynn, K.J.; Thomason, W.E.; Mullen, R.W.; Stone, M.L.; Solie, J.B.; Klatt, A.R.; Johnson, G.V.; Elliott, R.L.; et al. Nitrogen fertilization optimization algorithm based on In-Season estimates of yield and plant nitrogen uptake. J. Plant Nutr. 2001, 24, 885–898. [Google Scholar] [CrossRef]
- Chen, C.; Wang, X.; Chen, H.; Wu, C.; Mafarja, M.; Turabieh, H. Towards Precision Fertilization: Multi-Strategy Grey Wolf Optimizer Based Model Evaluation and Yield Estimation. Electronics 2021, 10, 2183. [Google Scholar] [CrossRef]
- Felix Kogan, W.G.; Yang, W. Drought and food security prediction from NOAA new generation of operational satellites. Geomat. Nat. Hazards Risk 2019, 10, 651–666. [Google Scholar] [CrossRef]
- Kang, Y.; Khan, S.; Ma, X. Climate change impacts on crop yield, crop water productivity and food security—A review. Prog. Nat. Sci. 2009, 19, 1665–1674. [Google Scholar] [CrossRef]
- Kumar, M. Impact of climate change on crop yield and role of model for achieving food security. Environ. Monit. Assess. 2016, 188, 465. [Google Scholar] [CrossRef]
- Eurostat. Agricultural Production—Crops. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Agricultural_production_-_crops#Cereals (accessed on 16 October 2024).
- Verstegen, H.; Köneke, O.; Korzun, V.; von Broock, R. The World Importance of Barley and Challenges to Further Improvements. In Biotechnological Approaches to Barley Improvement; Springer: Berlin/Heidelberg, Germany, 2014; pp. 3–19. [Google Scholar] [CrossRef]
- Day, A.D.; Thompson, R.K. Effects of Soil-Moisture Regimes on the Growth of Barley. Agron. J. 1975, 67, 430–433. [Google Scholar] [CrossRef]
- Streda, T.; Stredova, H.; Kohut, M.; Roznovsky, J.; Bougares, F.; Schwenk, H.; Bengio, Y. Yield of spring barley in dependence of soil moisture balance. In Proceedings of the 61. Tagung der Vereinigung der Pflanzenzüchter und Saatgutkaufleute Österreichs 2010, Raumberg-Gumpenstein, Austria, 23–25 November 2010; Vereinigung der Pfl anzenzüchter und Saatgutkaufleute: Vienna, Austria, 2011; pp. 171–174. [Google Scholar]
- Parkinson, K.J.; Day, W. The Influence of Water Stress on Photosynthesis in a Barley Crop. In Effects of Stress on Photosynthesis: Proceedings of a Conference Held at the ‘Limburgs Universitair Centrum’ Diepenbeek, Belgium, 22–27 August 1982; Marcelle, R., Clijsters, H., van Poucke, M., Eds.; Springer: Dordrecht, The Netherlands, 1983; pp. 65–74. [Google Scholar] [CrossRef]
- Power, J.F.; Grunes, D.L.; Reichman, G.A. The Influence of Phosphorus Fertilization and Moisture on Growth and Nutrient Absorption by Spring Wheat: I. Plant Growth, N Uptake, and Moisture Use. Soil Sci. Soc. Am. J. 1961, 25, 207–210. [Google Scholar] [CrossRef]
- Hargreaves, G.H. Moisture Availability and Crop Production. Trans. ASAE 2013, 18, 980–984. [Google Scholar] [CrossRef]
- Zhao, F.; Wang, G.; Li, S.; Hagan, D.F.T.; Ullah, W. The combined effects of VPD and soil moisture on historical maize yield and prediction in China. Front. Environ. Sci. 2023, 11, 1117184. [Google Scholar] [CrossRef]
- Bushong, J.T.; Mullock, J.L.; Miller, E.C.; Raun, W.R.; Klatt, A.R.; Arnall, D.B. Development of an in-season estimate of yield potential utilizing optical crop sensors and soil moisture data for winter wheat. Precis. Agric. 2016, 17, 451–469. [Google Scholar] [CrossRef]
- White, J.; Berg, A.A.; Champagne, C.; Zhang, Y.; Chipanshi, A.; Daneshfar, B. Improving crop yield forecasts with satellite-based soil moisture estimates: An example for township level canola yield forecasts over the Canadian Prairies. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102092. [Google Scholar] [CrossRef]
- Bueechi, E.; Fischer, M.; Crocetti, L.; Trnka, M.; Grlj, A.; Zappa, L.; Dorigo, W. Crop yield anomaly forecasting in the Pannonian basin using gradient boosting and its performance in years of severe drought. Agric. For. Meteorol. 2023, 340, 109596. [Google Scholar] [CrossRef]
- Boas, T.; Bogena, H.R.; Ryu, D.; Vereecken, H.; Western, A.; Hendricks Franssen, H.J. Seasonal soil moisture and crop yield prediction with fifth-generation seasonal forecasting system (SEAS5) long-range meteorological forecasts in a land surface modelling approach. Hydrol. Earth Syst. Sci. 2023, 27, 3143–3167. [Google Scholar] [CrossRef]
- Bojanowski, J.S.; Sikora, S.; Musiał, J.P.; Woźniak, E.; Dąbrowska-Zielińska, K.; Slesiński, P.; Milewski, T.; Łączyński, A. Integration of Sentinel-3 and MODIS Vegetation Indices with ERA-5 Agro-Meteorological Indicators for Operational Crop Yield Forecasting. Remote Sens. 2022, 14, 1238. [Google Scholar] [CrossRef]
- Ines, A.V.; Das, N.N.; Hansen, J.W.; Njoku, E.G. Assimilation of remotely sensed soil moisture and vegetation with a crop simulation model for maize yield prediction. Remote Sens. Environ. 2013, 138, 149–164. [Google Scholar] [CrossRef]
- Potopová, V.; Trnka, M.; Hamouz, P.; Soukup, J.; Castraveț, T. Statistical modelling of drought-related yield losses using soil moisture-vegetation remote sensing and multiscalar indices in the south-eastern Europe. Agric. Water Manag. 2020, 236, 106168. [Google Scholar] [CrossRef]
- Saf, H. EUMETSAT SAF on Support to Operational Hydrology and Water Management. ASCAT Surface Soil Moisture Climate Data Record v7 12.5 km Sampling—Metop. 2021. Available online: https://user.eumetsat.int/catalogue/EO:EUM:DAT:0656 (accessed on 19 August 2024).
- C3S. ERA5 Hourly Data on Single Levels from 1940 to Present; C3S: Chennai, India, 2015. [Google Scholar] [CrossRef]
- Guitard, A.A. The Influence of Variety, Temperature, and Stage of Growth on the Response of Spring Barley to Photoperiod. Can. J. Plant Sci. 1960, 40, 65–80. [Google Scholar] [CrossRef]
- Svobodová, I.; Misa, P. Effect of drought stress on the formation of yield elements in spring barley and the potential of stress expression reduction by foliar application of fertilizers and growth stimulator. Plant Soil Environ. 2004, 50, 439–446. [Google Scholar] [CrossRef]
- Hlavinka, P.; Trnka, M.; Eitzinger, J.; Smutny, V.; Thaler, S.; Žalud, Z.; Rischbeck, P.; Kren, J. The performance of CERES-Barley and CERES-Wheat under various soil conditions and tillage practices in Central Europe. Die Bodenkult. 2010, 61, 5–17. [Google Scholar]
- Eitzinger, J.; Kubu, G.; Thaler, S. Climate Change Impacts And Adaptation Options for Agriculture in Complex Terrain and Small Scale Agricultural Systems—Results from Case Studies in Austria. In Proceedings of the Extended Abstracts of the International Symosium, University of Natural Resources and Applied Life Sciences (BOKU); Eitzinger, J., Kubu, G., Eds.; University of Natural Resources and Applied Life Sciences (BOKU): Vienna, Austria, 2009; Volume 6, p. 159. [Google Scholar]
- Eitzinger, J.; Daneu, V.; Bodner, G.; Kubu, G.; Loiskandl, W.; Macaigne, P.; Thaler, S.; Schaumberger, A.; Wittmann, C.; Weidle, F.; et al. Drought Monitoring System for Austrian Agriculture—AgroDroughtAustria (Final Scientific Report of Project “AgroDroughtAustria” of the Austrian Climate Change Research Program; Technical Report; University of Natural Resources and Applied Life Sciences (BOKU): Vienna, Austria, 2016. [Google Scholar]
- Grosse, M.; Hierold, W.; Ahlborn, M.C.; Piepho, H.P.; Helming, K. Long-term field experiments in Germany: Classification and spatial representation. Soil 2020, 6, 579–596. [Google Scholar] [CrossRef]
- Váňová, M.; Palík, S.; Hajšlová, J.; Burešová, I. Grain quality and yield of spring barley in field trials under variable growing conditions. Plant Soil Environ. 2006, 52, 211–219. [Google Scholar] [CrossRef]
- Gebeltová, Z. Exploitation of Agricultural Land in the Czech Republic and EU Countries. AGRIS On-Line Pap. Econ. Inform. 2017, 9, 33–44. [Google Scholar] [CrossRef][Green Version]
- Brumer, A.; Wezel, A.; Dauber, J.; Breland, T.A.; Grard, B. Development of agroecology in Austria and Germany. Open Res. Eur. 2023, 3, 25. [Google Scholar] [CrossRef] [PubMed]
- Bundesministerium für Ernährung und Landwirtschaft. Cereal Production and Types of Cereals in Austria. Available online: https://info.bml.gv.at/en/topics/agriculture/agriculture-in-austria/plant-production-in-austria/cereal-production-and-types-of-cereals-in-austria.html (accessed on 22 January 2025).
- Janovska, V.; Simova, P.; Vlasak, J.; Sklenicka, P. Factors affecting farm size on the European level and the national level of the Czech Republic. Agric. Econ. 2017, 63, 1–12. [Google Scholar] [CrossRef]
- Vaishar, A.A.; Šťastná, M.A. Transformation of agriculture in Czechia in the period 1990–2020. Studia Obszarów Wiejskich 2020, 56, 103–118. [Google Scholar] [CrossRef]
- Office, C.S. Harvest Estimates—June 2024. Available online: https://csu.gov.cz/rychle-informace/harvest-estimates-june-2024l (accessed on 16 March 2025).
- Jasib, L.; Donnellan, T.; Lennon, J. The Inequality of Farmland Size in Western Europe. In Proceedings of the Agricultural Economics Society—AES > 90th Annual Conference, Dublin, Ireland, 24–26 April 2017. [Google Scholar] [CrossRef]
- Zakrzewska, A.; Nowak, A. Diversification of Agricultural Output Intensity across the European Union in Light of the Assumptions of Sustainable Development. Agriculture 2022, 12, 1370. [Google Scholar] [CrossRef]
- Wagner, W.; Lemoine, G.; Rott, H. A Method for Estimating Soil Moisture from ERS Scatterometer and Soil Data. Remote Sens. Environ. 1999, 70, 191–207. [Google Scholar] [CrossRef]
- Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An Improved Soil Moisture Retrieval Algorithm for ERS and METOP Scatterometer Observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Fan, Y.; Liu, Y.; Yue, J.; Jin, X.; Chen, R.; Bian, M.; Ma, Y.; Yang, G.; Feng, H. Estimation of potato yield using a semi-mechanistic model developed by proximal remote sensing and environmental variables. Comput. Electron. Agric. 2024, 223, 109117. [Google Scholar] [CrossRef]
- Gómez, D.; Salvador, P.; Sanz, J.; Casanova, J.L. Modelling wheat yield with antecedent information, satellite and climate data using machine learning methods in Mexico. Agric. For. Meteorol. 2021, 300, 108317. [Google Scholar] [CrossRef]
- De Clercq, D.; Mahdi, A. Feasibility of machine learning-based rice yield prediction in India at the district level using climate reanalysis and remote sensing data. Agric. Syst. 2024, 220, 104099. [Google Scholar] [CrossRef]
- Lawrence, J. Introduction to Neural Networks; California Scientific Software: Saratoga, CA, USA, 1993. [Google Scholar]
- Kim, N.; Ha, K.J.; Park, N.W.; Cho, J.; Hong, S.; Lee, Y.W. A Comparison Between Major Artificial Intelligence Models for Crop Yield Prediction: Case Study of the Midwestern United States, 2006–2015. ISPRS Int. J.-Geo-Inf. 2019, 8, 240. [Google Scholar] [CrossRef]
- Kaul, M.; Hill, R.L.; Walthall, C. Artificial neural networks for corn and soybean yield prediction. Agric. Syst. 2005, 85, 1–18. [Google Scholar] [CrossRef]
- Ji, B.; Sun, Y.; Yang, S.; Wan, J. Artificial neural networks for rice yield prediction in mountainous regions. J. Agric. Sci. 2007, 145, 249–261. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Chollet, F. Keras; GitHub: San Francisco, CA, USA, 2015. [Google Scholar]
- Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Zar, J.H. Spearman rank correlation. In Encyclopedia of Biostatistics; Wiley: Hoboken, NJ, USA, 2005; Volume 7. [Google Scholar]
- Wright, S. Correlation and causation. J. Agric. Res. 1921, 20, 557. [Google Scholar]
- Olson, C.L. On choosing a test statistic in multivariate analysis of variance. Psychol. Bull. 1976, 83, 579–586. [Google Scholar] [CrossRef]
- Chmielewski, F.M.; Köhn, W. Impact of weather on yield components of spring cereals over 30 years. Agric. For. Meteorol. 1999, 96, 49–58. [Google Scholar] [CrossRef]
- Yiğit, A.; Chmielewski, F.M. A Deeper Insight into the Yield Formation of Winter and Spring Barley in Relation to Weather and Climate Variability. Agronomy 2024, 14, 1503. [Google Scholar] [CrossRef]
- Trnka, M.; Eitzinger, J.; Kapler, P.; Dubrovský, M.; Semerádová, D.; Žalud, Z.; Formayer, H. Effect of Estimated Daily Global Solar Radiation Data on the Results of Crop Growth Models. Sensors 2007, 7, 2330–2362. [Google Scholar] [CrossRef] [PubMed]
- Savin, R.; Nicolas, M.E. Effects of timing of heat stress and drought on growth and quality of barley grains. Aust. J. Agric. Res. 1999, 50, 357. [Google Scholar] [CrossRef]
- Groß, J.; Gentsch, N.; Boy, J.; Heuermann, D.; Schweneker, D.; Feuerstein, U.; Brunner, J.; Von Wirén, N.; Guggenberger, G.; Bauer, B. Influence of small-scale spatial variability of soil properties on yield formation of winter wheat. Plant Soil 2023, 493, 79–97. [Google Scholar] [CrossRef]
- Thi Huyen, T.; Sonoko, D.; Bellingrath-Kimura, C.H.; Barkusky, D. Effect of long-term fertiliser regimes and weather on spring barley yields in sandy soil in North-East Germany. Arch. Agron. Soil Sci. 2020, 66, 1812–1826. [Google Scholar] [CrossRef]
- Appiah, M.; Bracho-Mujica, G.; Ferreira, N.C.; Schulman, A.H.; Rötter, R.P. Projected impacts of sowing date and cultivar choice on the timing of heat and drought stress in spring barley grown along a European transect. Field Crops Res. 2023, 291, 108768. [Google Scholar] [CrossRef]
- Finke, P.A.; Goense, D. Differences in barley grain yields as a result of soil variability. J. Agric. Sci. 1993, 120, 171–180. [Google Scholar] [CrossRef]
- Bondareva, L.; Danilov, D.; Kartashova, L. Breeding spring barley for ecological plasticity and adaptability in the North-Western Region. BIO Web Conf. 2020, 27, 00067. [Google Scholar] [CrossRef]
- Hlisnikovský, L.; Zemanová, V.; Roman, M.; Menšík, L.; Kunzová, E. Long-Term Study of the Effects of Environment, Variety, and Fertilisation on Yield and Stability of Spring Barley Grain. Plants 2024, 13, 2745. [Google Scholar] [CrossRef] [PubMed]
- NeSmith, D.; Ritchie, J. Maize (Zea mays L.) response to a severe soil water-deficit during grain-filling. Field Crops Res. 1992, 29, 23–35. [Google Scholar] [CrossRef]
- Milics, G.; Kovács, A.J.; Pörneczi, A.; Nyéki, A.; Varga, Z.; Nagy, V.; Lichner, L.; Németh, T.; Baranyai, G.; Neményi, M. Soil moisture distribution mapping in topsoil and its effect on maize yield. Biologia 2017, 72, 847–853. [Google Scholar] [CrossRef]
- Ding, D.; Zhang, M.; Pan, X.; Yang, M.; He, X. Modeling extreme events in time series prediction. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 1114–1122. [Google Scholar]
- Pierdicca, N.; Fascetti, F.; Pulvirenti, L.; Crapolicchio, R.; Muñoz-Sabater, J. Quadruple Collocation Analysis for Soil Moisture Product Assessment. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1595–1599. [Google Scholar] [CrossRef]
- Pierdicca, N.; Fascetti, F.; Pulvirenti, L.; Crapolicchio, R.; Muñoz-Sabater, J. Analysis of ASCAT, SMOS, in-situ and land model soil moisture as a regionalized variable over Europe and North Africa. Remote Sens. Environ. 2015, 170, 280–289. [Google Scholar] [CrossRef]
- Modanesi, S.; Massari, C.; Camici, S.; Brocca, L.; Amarnath, G. Do Satellite Surface Soil Moisture Observations Better Retain Information About Crop-Yield Variability in Drought Conditions? Water Resour. Res. 2020, 56, e2019WR025855. [Google Scholar] [CrossRef]
- Gaona, J.; Bavera, D.; Fioravanti, G.; Hahn, S.; Stradiotti, P.; Filippucci, P.; Camici, S.; Ciabatta, L.; Mossaffa, H.; Puca, S.; et al. Soil moisture products consistency for operational drought monitoring in Europe. Hydrol. Earth Syst. Sci. Discuss. 2024, 1–36. [Google Scholar] [CrossRef]
- Hahn, S.; Melzer, T.; Wagner, W. Error Assessment of the Initial Near Real-Time METOP ASCAT Surface Soil Moisture Product. IEEE Trans. Geosci. Remote Sens. 2012, 50, 2556–2565. [Google Scholar] [CrossRef]
- Paulik, C.; Dorigo, W.; Wagner, W.; Kidd, R. Validation of the ASCAT Soil Water Index using in situ data from the International Soil Moisture Network. Int. J. Appl. Earth Obs. Geoinf. 2014, 30, 1–8. [Google Scholar] [CrossRef]
- Hemm, M.; Hoffmann, A.; Mischke, U.; Nixdorf, B. Natürliche Seen Deutschlands—Aktueller Stand zur Dokumentation, Typisierung und Bewertung anhand des Phytoplanktons; Technical Report; Deutsche Gesellschaft für Limnologie (DGL): Essen, Germany, 2002. [Google Scholar]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Massart, S.; Vreugdenhil, M.; Bauer-Marschallinger, B.; Navacchi, C.; Raml, B.; Wagner, W. Mitigating the impact of dense vegetation on the Sentinel-1 surface soil moisture retrievals over Europe. Eur. J. Remote Sens. 2024, 57, 2300985. [Google Scholar] [CrossRef]
- Kerr, Y.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
- Njoku, E.; Jackson, T.; Lakshmi, V.; Chan, T.; Nghiem, S. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Ray, D.K.; Gerber, J.S.; MacDonald, G.K.; West, P.C. Climate variation explains a third of global crop yield variability. Nat. Commun. 2015, 6, 5989. [Google Scholar] [CrossRef]
- Gibon, F.; Pellarin, T.; Román-Cascón, C.; Alhassane, A.; Traoré, S.; Kerr, Y.; Lo Seen, D.; Baron, C. Millet yield estimates in the Sahel using satellite derived soil moisture time series. Agric. For. Meteorol. 2018, 262, 100–109. [Google Scholar] [CrossRef]


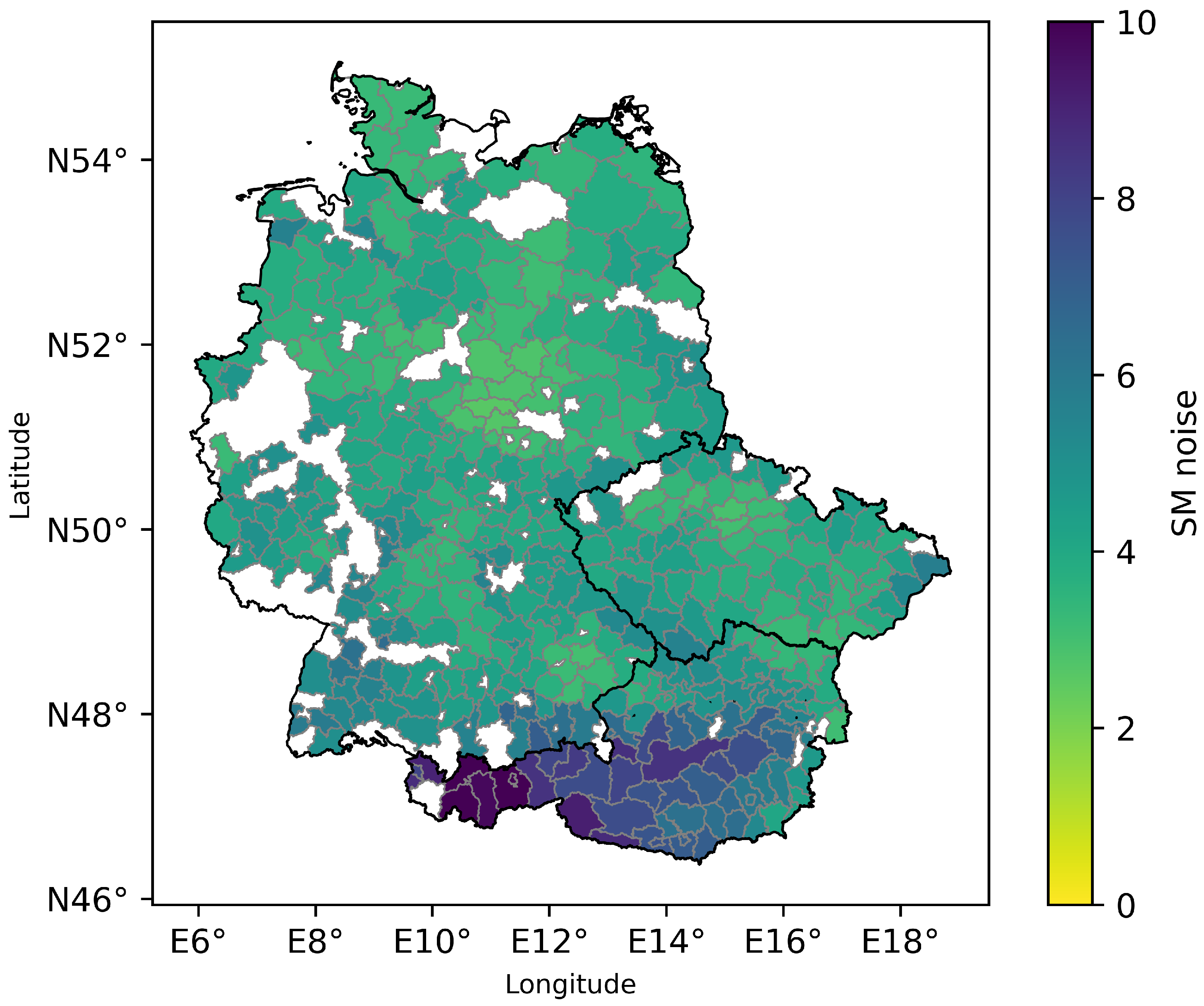
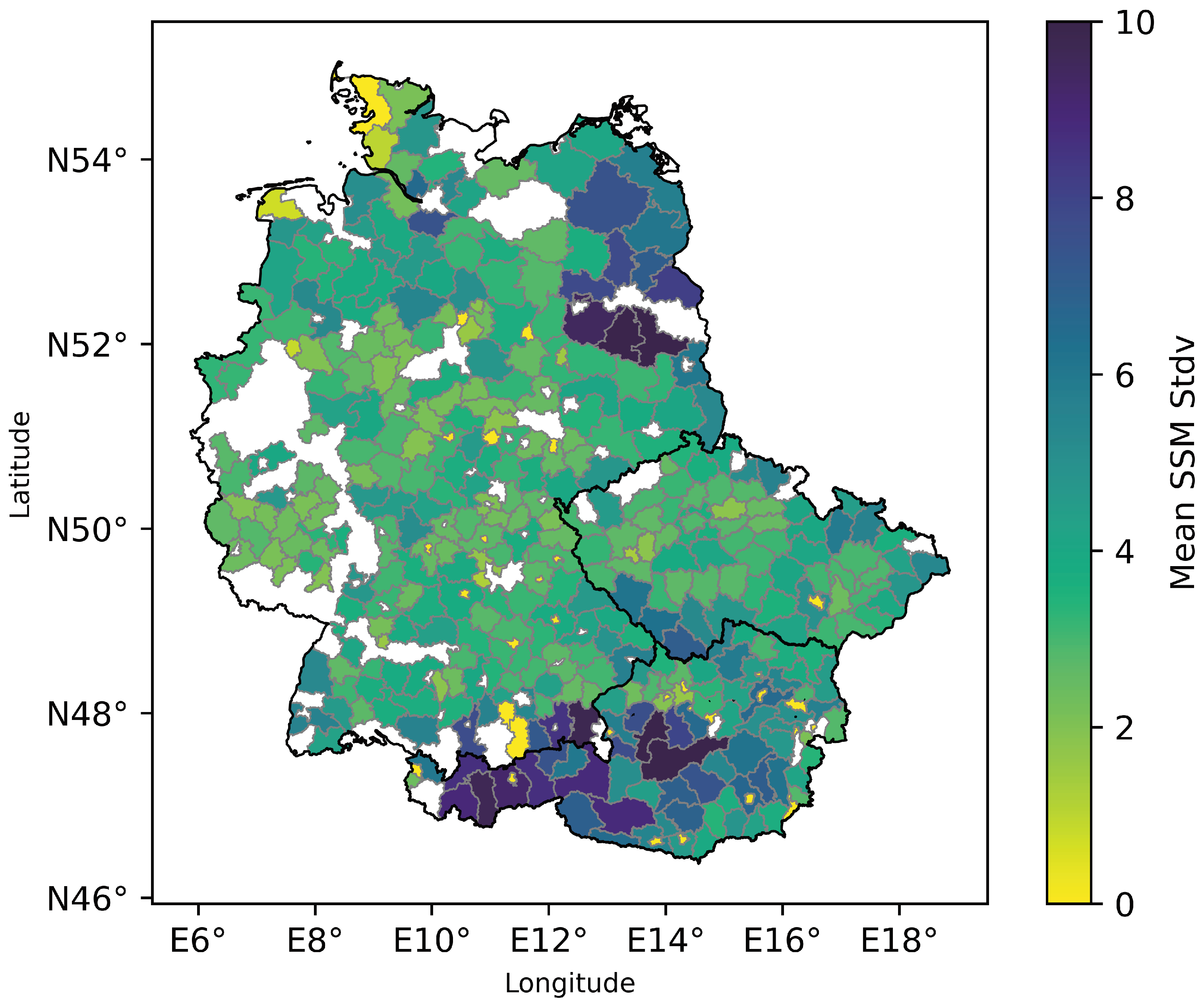
| H SAF SSM | ERA5 SWVL1 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| PearsonR | R2 | RMSE | MAE | F-Statistic | PearsonR | R2 | RMSE | MAE | F-Statistic |
| 0.59 | 0.33 | 0.89 | 0.68 | 9.9 | 0.61 | 0.37 | 0.86 | 0.65 | 8.0 |
| H SAF SSM | ERA5 SWVL1 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PearsonR | R2 | RMSE | ubRMSE | MAE | PearsonR | R2 | RMSE | ubRMSE | MAE | |
| AT | 0.50 | 0.17 | 0.89 | 0.84 | 0.70 | 0.53 | 0.23 | 0.85 | 0.83 | 0.67 |
| CZ | 0.52 | 0.26 | 0.70 | 0.70 | 0.54 | 0.53 | 0.28 | 0.70 | 0.70 | 0.53 |
| DE | 0.53 | 0.28 | 0.94 | 0.94 | 0.72 | 0.58 | 0.34 | 0.89 | 0.89 | 0.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reuß, F.; Vreugdenhil, M.; Bueechi, E.; Wagner, W. Comparing Satellite-Derived and Model-Based Surface Soil Moisture for Spring Barley Yield Prediction in Central Europe. Remote Sens. 2025, 17, 1394. https://doi.org/10.3390/rs17081394
Reuß F, Vreugdenhil M, Bueechi E, Wagner W. Comparing Satellite-Derived and Model-Based Surface Soil Moisture for Spring Barley Yield Prediction in Central Europe. Remote Sensing. 2025; 17(8):1394. https://doi.org/10.3390/rs17081394
Chicago/Turabian StyleReuß, Felix, Mariette Vreugdenhil, Emanuel Bueechi, and Wolfgang Wagner. 2025. "Comparing Satellite-Derived and Model-Based Surface Soil Moisture for Spring Barley Yield Prediction in Central Europe" Remote Sensing 17, no. 8: 1394. https://doi.org/10.3390/rs17081394
APA StyleReuß, F., Vreugdenhil, M., Bueechi, E., & Wagner, W. (2025). Comparing Satellite-Derived and Model-Based Surface Soil Moisture for Spring Barley Yield Prediction in Central Europe. Remote Sensing, 17(8), 1394. https://doi.org/10.3390/rs17081394









