Super-Resolution of Landsat-8 Land Surface Temperature Using Kolmogorov–Arnold Networks with PlanetScope Imagery and UAV Thermal Data
Abstract
:1. Introduction
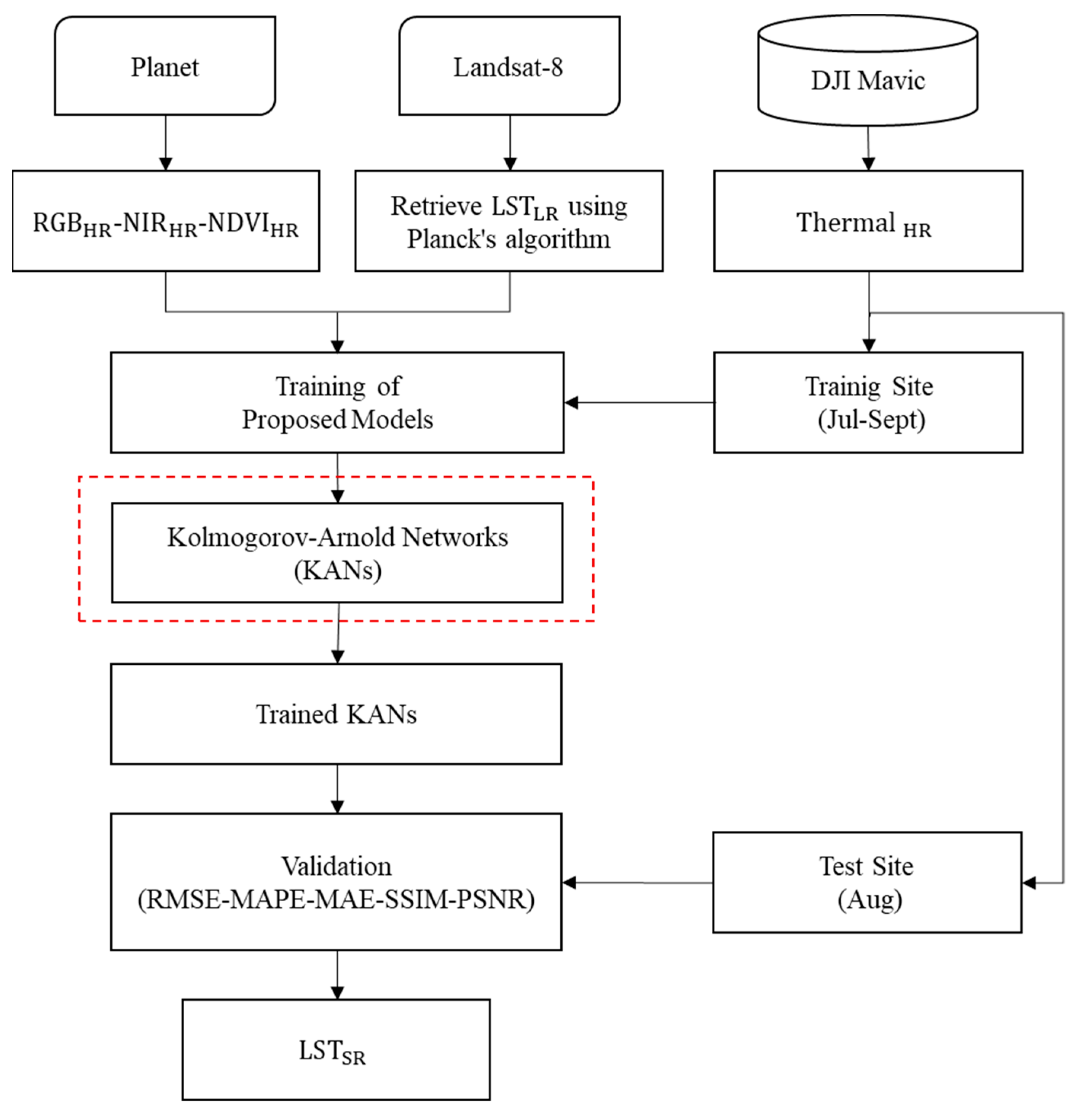
2. Materials and Methods
2.1. Study Area
2.2. Dataset
Processing of Thermal Drone Images for Temperature Retrieval
2.3. Methodology
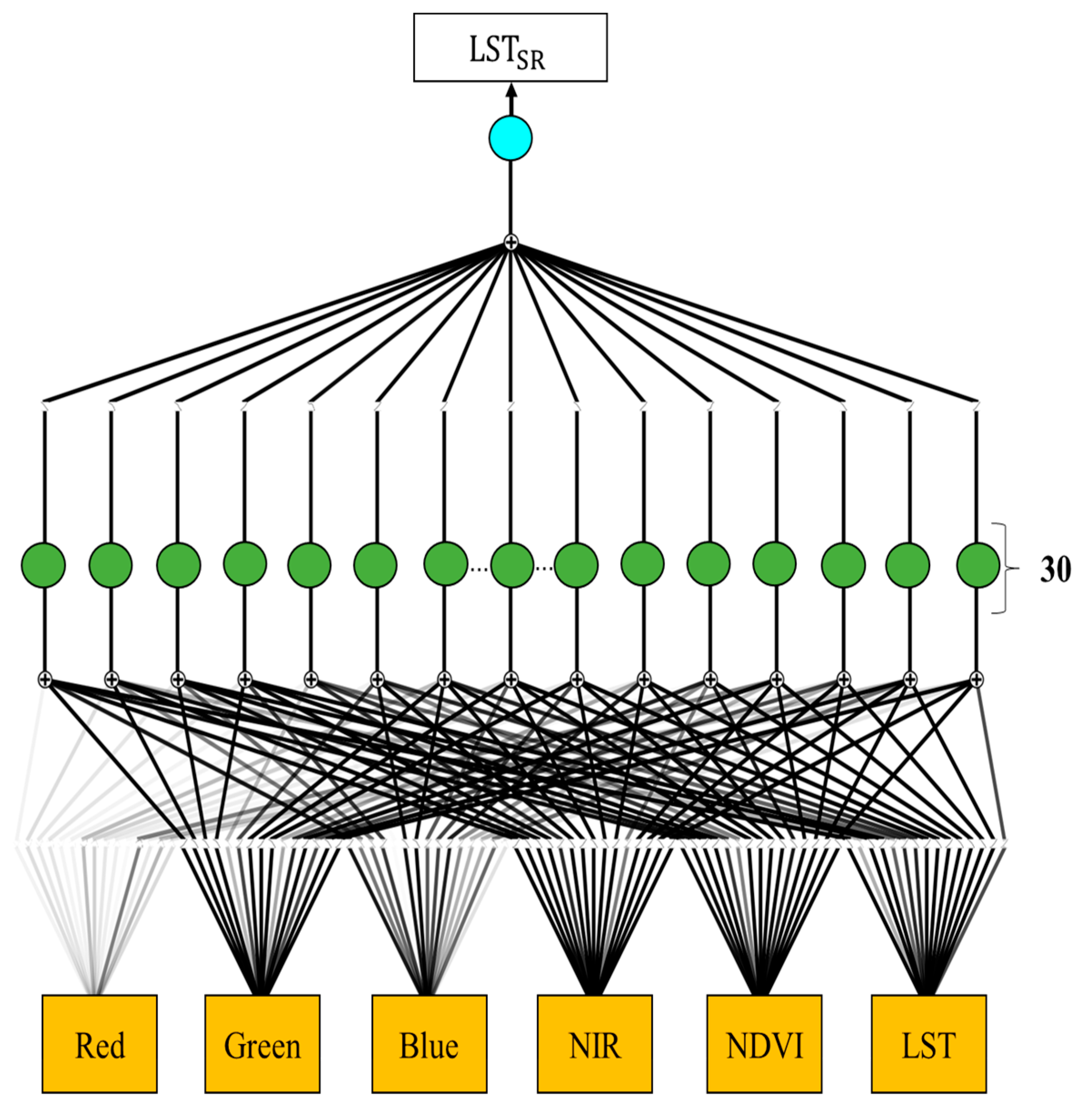
2.3.1. Kolmogorov–Arnold Network Architecture
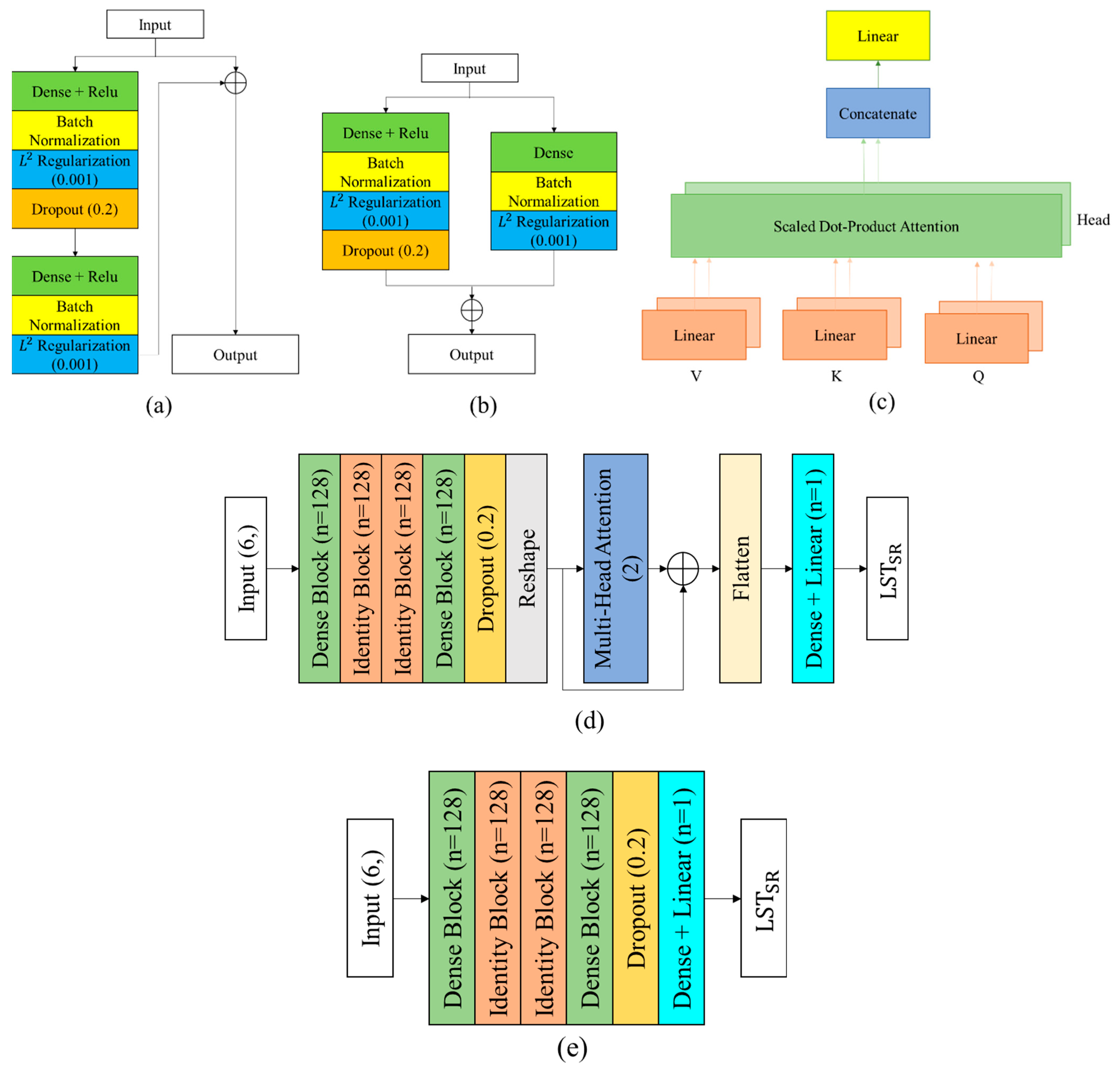
2.3.2. Comparison Models
ResDenseNet Architecture
Multi-Head Residual Attention Block
LightGBM
XGBoost
2.3.3. Model Training and Experimental Setup
2.4. Evaluation Metrics
3. Result
3.1. Evaluation of KAN Model Performance Using PlanetScope and Landsat-8 Imagery Combinations
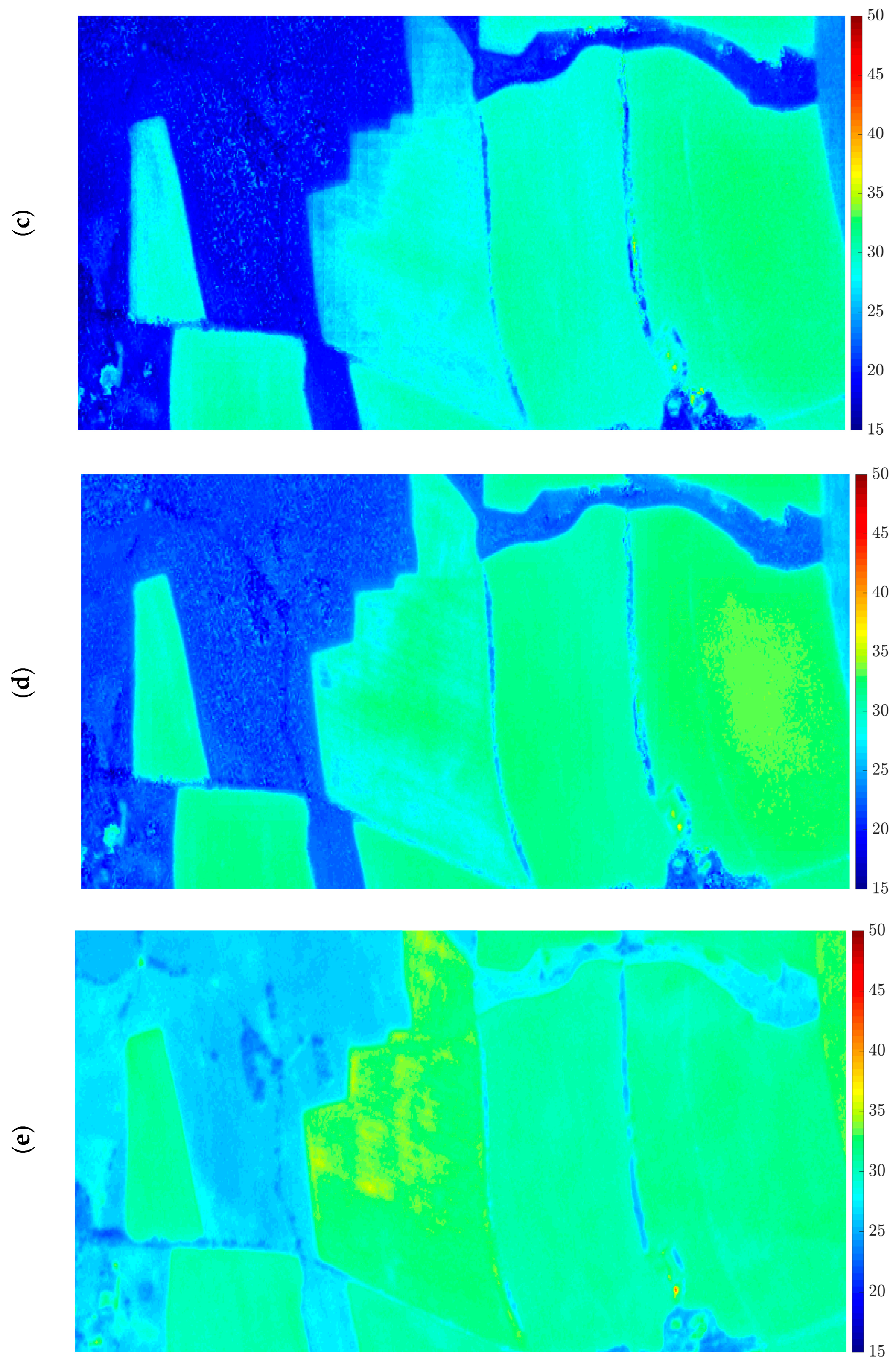
3.2. Visual Comparison
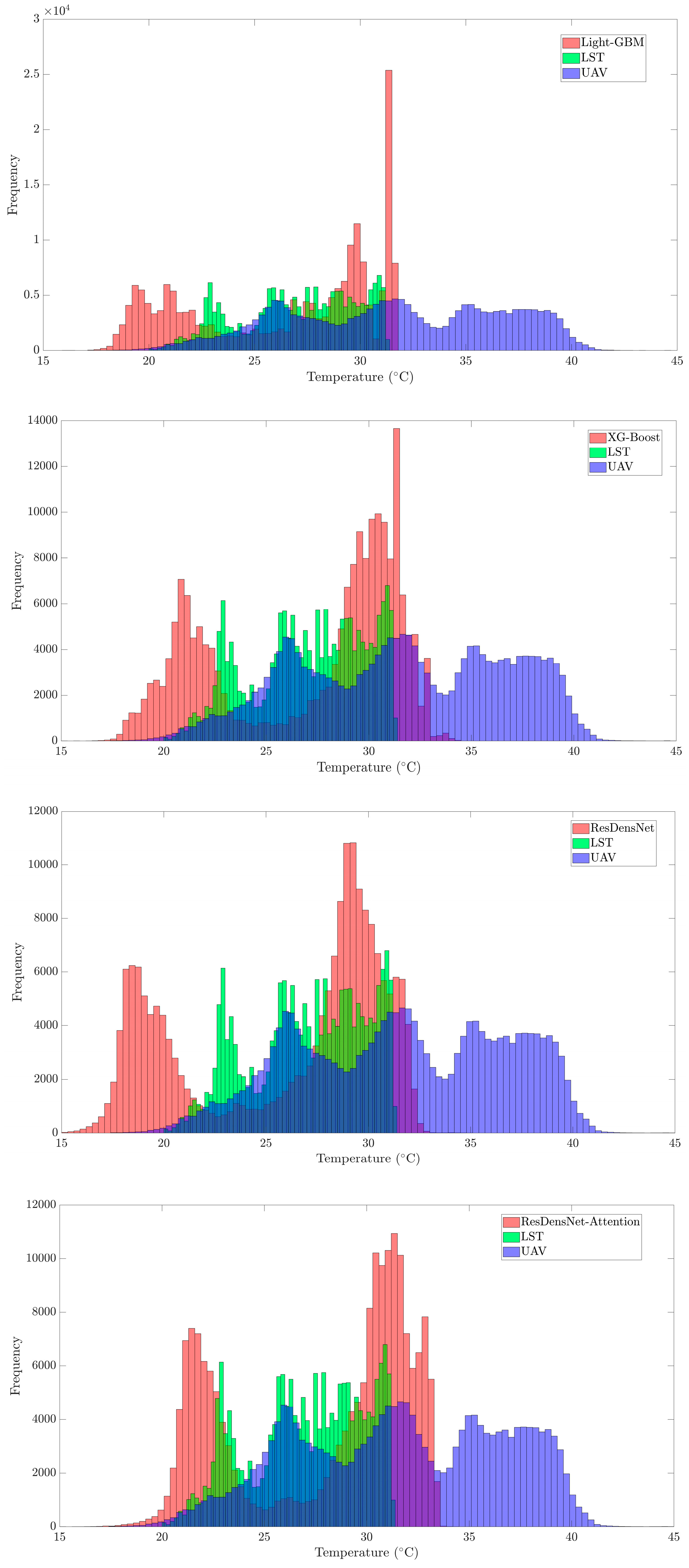
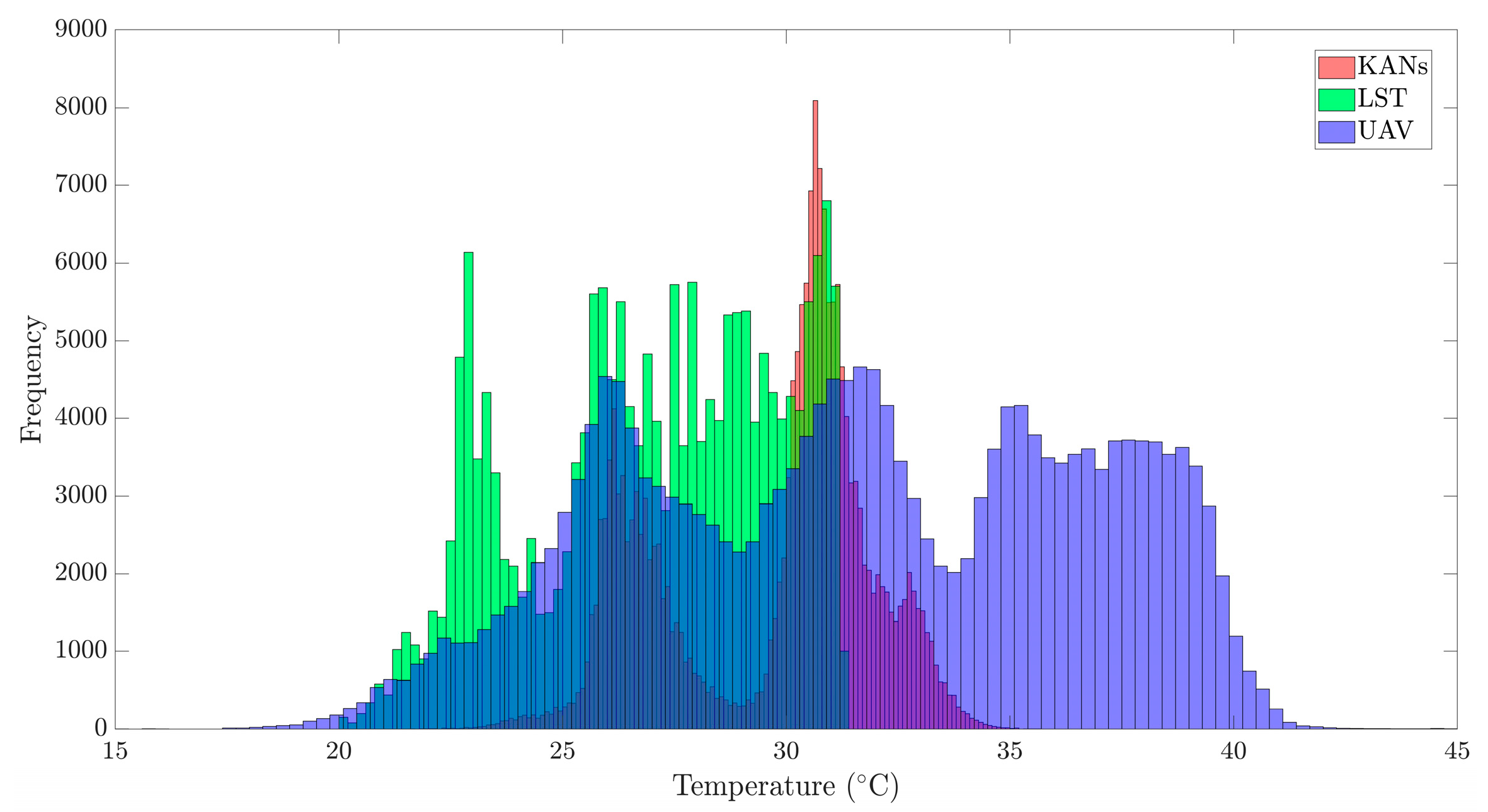
3.3. Histogram and Distribution Analysis
3.4. Error Map Evaluation
3.5. Profile Comparisons
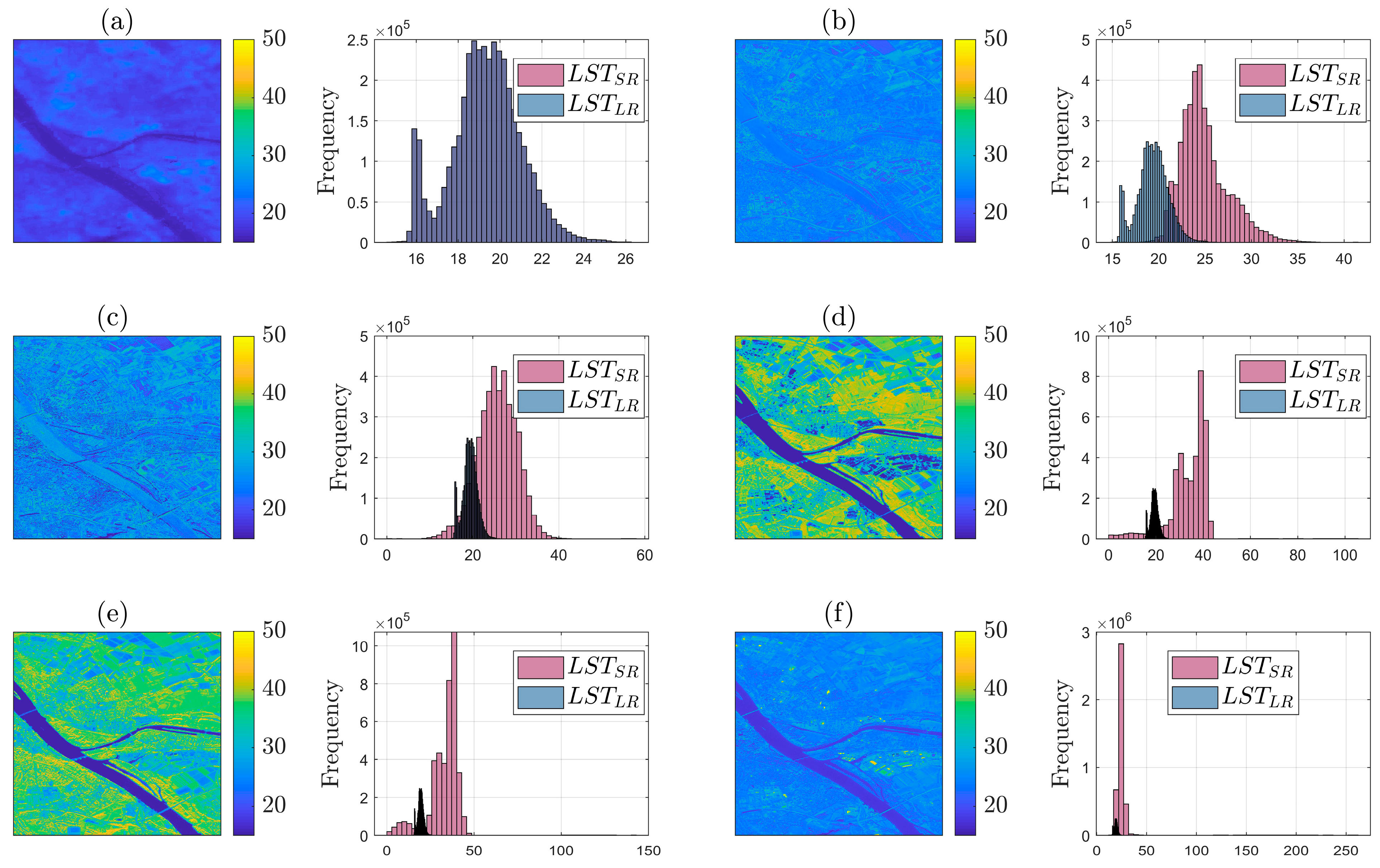
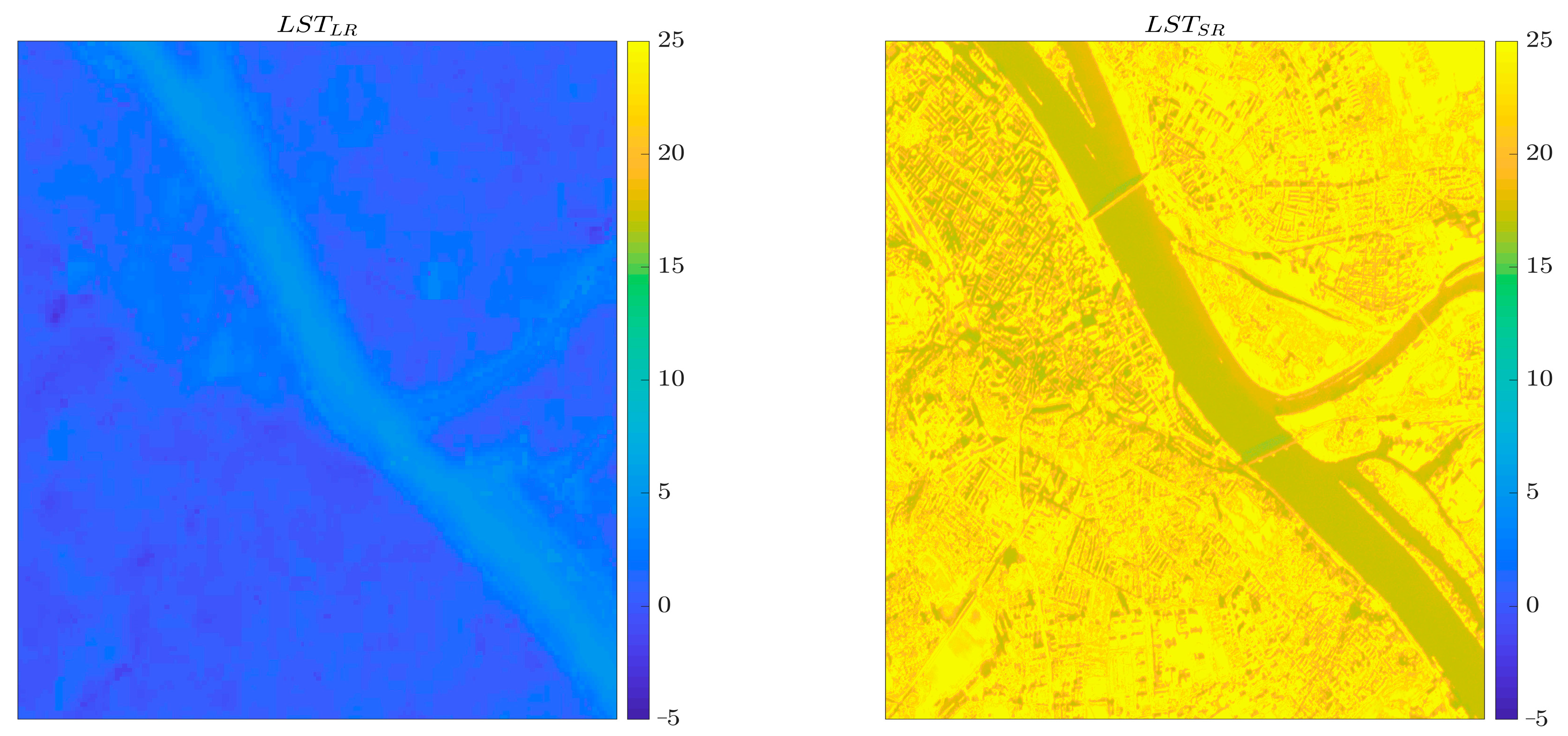
3.6. Generating the LSTSR Using Different Models in Mainz, Germany
Comparing LSTSR Using Different Models to LST Landsat-8
4. Discussion
4.1. LST and Its Importance
4.2. Challenges in LST Data Accuracy
4.3. Technological Impact on LST Accuracy
4.4. Downscaling LST Data
4.5. Limitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Malbéteau, Y.; Parkes, S.; Aragon, B.; Rosas, J.; McCabe, M.F. Capturing the Diurnal Cycle of Land Surface Temperature Using an Unmanned Aerial Vehicle. Remote Sens. 2018, 10, 1407. [Google Scholar] [CrossRef]
- Aboutalebi, M.; Torres-Rua, A.F.; McKee, M.; Kustas, W.P.; Nieto, H.; Alsina, M.M.; White, A.; Prueger, J.H.; McKee, L.; Alfieri, J.; et al. Downscaling UAV Land Surface Temperature Using a Coupled Wavelet-Machine Learning-Optimization Algorithm and Its Impact on Evapotranspiration. Irrig. Sci. 2022, 40, 553–574. [Google Scholar] [CrossRef]
- Heidarimozaffar, R.G.M.; Arefi, A.S.H. Land Surface Temperature Analysis in Densely Populated Zones from the Perspective of Spectral Indices and Urban Morphology. Int. J. Environ. Sci. Technol. 2023, 20, 2883–2902. [Google Scholar] [CrossRef]
- Asadi, A.; Arefi, H.; Fathipoor, H. Simulation of Green Roofs and Their Potential Mitigating Effects on the Urban Heat Island Using an Artificial Neural Network: A Case Study in Austin, Texas. Adv. Space Res. 2020, 66, 1846–1862. [Google Scholar] [CrossRef]
- He, B.J.; Fu, X.; Zhao, Z.; Chen, P.; Sharifi, A.; Li, H. Capability of LCZ Scheme to Differentiate Urban Thermal Environments in Five Megacities of China: Implications for Integrating LCZ System into Heat-Resilient Planning and Design. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2024, 17, 18800–18817. [Google Scholar] [CrossRef]
- Sahoo, S.; Singha, C.; Govind, A.; Moghimi, A. Environmental and Sustainability Indicators Review of Climate-Resilient Agriculture for Ensuring Food Security: Sustainability Opportunities and Challenges of India. Environ. Sustain. Indic. 2025, 25, 100544. [Google Scholar] [CrossRef]
- Elfarkh, J.; Johansen, K.; Angulo, V.; Camargo, O.L.; McCabe, M.F. Quantifying Within-Flight Variation in Land Surface Temperature from a UAV-Based Thermal Infrared Camera. Drones 2023, 7, 617. [Google Scholar] [CrossRef]
- Ferreira, F.L.e.S.; Pereira, E.B.; Gonçalves, A.R.; Costa, R.S.; Bezerra, F.G.S. An Explicitly Spatial Approach to Identify Heat Vulnerable Urban Areas and Landscape Patterns. Urban Clim. 2021, 40, 101021. [Google Scholar] [CrossRef]
- Jiménez-Muñoz, J.C.; Sobrino, J.A. Error Sources on the Land Surface Temperature Retrieved from Thermal Infrared Single Channel Remote Sensing Data. Int. J. Remote Sens. 2006, 27, 999–1014. [Google Scholar] [CrossRef]
- Wang, J.; Ouyang, W. Attenuating the Surface Urban Heat Island within the Local Thermal Zones through Land Surface Modification. J. Environ. Manag. 2017, 187, 239–252. [Google Scholar] [CrossRef]
- Addas, A.; Goldblatt, R.; Rubinyi, S. Utilizing Remotely Sensed Observations to Estimate the Urban Heat Island Effect at a Local Scale: Case Study of a University Campus. Land 2020, 9, 191. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Jiménez-Muñoz, J.C. Land Surface Temperature Retrieval from Thermal Infrared Data: An Assessment in the Context of the Surface Processes and Ecosystem Changes Through Response Analysis (SPECTRA) Mission. J. Geophys. Res. D Atmos. 2005, 110. [Google Scholar] [CrossRef]
- Mathew, K.; Nagarani, C.M.; Kirankumar, A.S. Split-Window and Multi-Angle Methods of Sea Surface Temperature Determination: An Analysis. Int. J. Remote Sens. 2001, 22, 3237–3251. [Google Scholar] [CrossRef]
- Feng, X.; Foody, G.; Aplin, P.; Gosling, S.N. Enhancing the Spatial Resolution of Satellite-Derived Land Surface Temperature Mapping for Urban Areas. Sustain. Cities Soc. 2015, 19, 341–348. [Google Scholar] [CrossRef]
- Jawak, S.D.; Luis, A.J. A Comprehensive Evaluation of PAN-Sharpening Algorithms Coupled with Resampling Methods for Image Synthesis of Very High Resolution Remotely Sensed Satellite Data. Adv. Remote Sens. 2013, 2, 332–344. [Google Scholar] [CrossRef]
- Kumar, D.L.; Rajaan, R.; Choudhary, D.N.; Sharma, D.A. A Comprehensive Review and Comparison of Image Super-Resolution Techniques. Int. J. Adv. Eng. Manag. Sci. 2024, 10, 40–45. [Google Scholar] [CrossRef]
- Sarp, G. Spectral and Spatial Quality Analysis of Pan-Sharpening Algorithms: A Case Study in Istanbul. Eur. J. Remote Sens. 2014, 47, 19–28. [Google Scholar] [CrossRef]
- González-Audícana, M.; Saleta, J.L.; Catalán, R.G.; García, R. Fusion of Multispectral and Panchromatic Images Using Improved IHS and PCA Mergers Based on Wavelet Decomposition. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1291–1299. [Google Scholar] [CrossRef]
- Wady, S.M.A.; Bentoutou, Y.; Bengermikh, A.; Bounoua, A.; Taleb, N. A New IHS and Wavelet Based Pansharpening Algorithm for High Spatial Resolution Satellite Imagery. Adv. Space Res. 2020, 66, 1507–1521. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Ahn, H.; Chung, B.; Yim, C. Super-Resolution Convolutional Neural Networks Using Modified and Bilateral ReLU. In Proceedings of the ICEIC 2019—International Conference on Electronics, Information, and Communication, Auckland, New Zealand, 22–25 January 2019. [Google Scholar]
- Kim, J.; Lee, J.K.; Lee, K.M. Deeply-Recursive Convolutional Network for Image Super-Resolution. In Proceedings of the Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition 2016, Las Vegas, NV, USA, 27–30 June 2016. [Google Scholar]
- Li, C.; Hao, X.; Jing, T. Blind Image Super-Resolution Using Joint Interpolation-Restoration Scheme. In Proceedings of the ISPACS 2010—2010 International Symposium on Intelligent Signal Processing and Communication Systems, Chengdu, China, 6–8 December 2010. [Google Scholar]
- Talab, M.A.; Awang, S.; Najim, S.A.D.M. Super-Low Resolution Face Recognition Using Integrated Efficient Sub-Pixel Convolutional Neural Network (ESPCN) and Convolutional Neural Network (CNN). In Proceedings of the 2019 IEEE International Conference on Automatic Control and Intelligent Systems, Selangor, Malaysia, 29 June 2019. [Google Scholar]
- Cristóbal, G.; Gil, E.; Šroubek, F.; Flusser, J.; Miravet, C.; Rodríguez, F.B. Superresolution Imaging: A Survey of Current Techniques. In Proceedings of the Optical Engineering + Applications, San Diego, CA, USA, 10–14 August 2008. [Google Scholar] [CrossRef]
- Daniels, J.; Bailey, C.P. Reconstruction and Super-Resolution of Land Surface Temperature Using an Attention-Enhanced CNN Architecture. Int. Geosci. Remote Sens. Symp. 2023, 2023, 4863–4866. [Google Scholar] [CrossRef]
- Chen, J.; Jia, L.; Zhang, J.; Feng, Y.; Zhao, X.; Tao, R. Super-Resolution for Land Surface Temperature Retrieval Images via Cross-Scale Diffusion Model Using Reference Images. Remote Sens. 2024, 16, 1356. [Google Scholar] [CrossRef]
- Nguyen, B.M.; Tian, G.; Vo, M.T.; Michel, A.; Corpetti, T.; Granero-Belinchon, C. Convolutional Neural Network Modelling for MODIS Land Surface Temperature Super-Resolution. Eur. Signal Process. Conf. 2022, 2022, 1806–1810. [Google Scholar] [CrossRef]
- Molliere, C.; Gottfriedsen, J.; Langer, M.; Massaro, P.; Soraruf, C.; Schubert, M. Multi-Spectral Super-Resolution of Thermal Infrared Data Products for Urban Heat Applications. Int. Geosci. Remote Sens. Symp. 2023, 2023, 4919–4922. [Google Scholar] [CrossRef]
- Lloyd, D.T.; Abela, A.; Farrugia, R.A.; Galea, A.; Valentino, G. Optically Enhanced Super-Resolution of Sea Surface Temperature Using Deep Learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5000814. [Google Scholar] [CrossRef]
- Yin, Z.; Wu, P.; Foody, G.M.; Wu, Y.; Liu, Z.; Du, Y.; Ling, F. Spatiotemporal Fusion of Land Surface Temperature Based on a Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2021, 59, 1808–1822. [Google Scholar] [CrossRef]
- Zou, R.; Wei, L.; Guan, L. Super Resolution of Satellite-Derived Sea Surface Temperature Using a Transformer-Based Model. Remote Sens. 2023, 15, 5376. [Google Scholar] [CrossRef]
- Passarella, L.S.; Mahajan, S.; Pal, A.; Norman, M.R. Reconstructing High Resolution ESM Data Through a Novel Fast Super Resolution Convolutional Neural Network (FSRCNN). Geophys. Res. Lett. 2022, 49, e2021GL097571. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.; Li, J. Remote Sensing Single-Image Superresolution Based on a Deep Compendium Model. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1432–1436. [Google Scholar] [CrossRef]
- Sattari, F.; Hashim, M. A Breif Review of Land Surface Temperature Retrieval Methods from Thermal Satellite Sensors. Middle-East J. Sci. Res. 2014, 22, 757–768. [Google Scholar]
- Science, E. Correlation Analysis of Land Surface Temperature (LST) Measurement Using DJI Mavic Enterprise Dual Thermal and Landsat 8 Satellite Imagery (Case Study: Surabaya City). In Proceedings of the Geomatics International Conference 2021 (GEOICON 2021), Virtual, 27 July 2021. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Vaidya, S.; Ruehle, F.; Halverson, J.; Soljačić, M.; Hou, T.Y.; Tegmark, M. KAN: Kolmogorov-Arnold Networks. arXiv 2024, arXiv:2404.19756. [Google Scholar]
- Valman, S.J.; Boyd, D.S.; Carbonneau, P.E.; Johnson, M.F.; Dugdale, S.J. An AI Approach to Operationalise Global Daily PlanetScope Satellite Imagery for River Water Masking. Remote Sens. Environ. 2024, 301, 113932. [Google Scholar] [CrossRef]
- Acharya, T.D.; Yang, I.T. Exploring Landsat 8. Int. J. IT Eng. Appl. Sci. Res. 2015, 4, 4–10. [Google Scholar]
- Zahrotunisa, S. Comparison of Split Windows Algorithm and Planck Methods for Surface Temperature Estimation Based on Remote Sensing Data in Semarang. J. Geografi 2022, 14, 11–21. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- Girosi, F.; Poggio, T. Representation Properties of Networks: Kolmogorov’s Theorem Is Irrelevant. Neural Comput. 1989, 1, 465–469. [Google Scholar] [CrossRef]
- Wang, H.; Tu, M. Enhancing Attention Models via Multi-Head Collaboration. In Proceedings of the 2020 International Conference on Asian Language Processing, IALP 2020, Kuala Lumpur, Malaysia, 4–6 December 2020. [Google Scholar]
- Chen, D.; Hu, F.; Nian, G.; Yang, T. Deep Residual Learning for Nonlinear Regression. Entropy 2020, 22, 193. [Google Scholar] [CrossRef]
- Fathi, M.; Shah-Hosseini, R.; Moghimi, A. 3D-ResNet-BiLSTM Model: A Deep Learning Model for County-Level Soybean Yield Prediction with Time-Series Sentinel-1, Sentinel-2 Imagery, and Daymet Data. Remote Sens. 2023, 15, 5551. [Google Scholar] [CrossRef]
- Fathi, M.; Shah-Hosseini, R.; Moghimi, A.; Arefi, H. MHRA-MS-3D-ResNet-BiLSTM: A Multi-Head-Residual Attention-Based Multi-Stream Deep Learning Model for Soybean Yield Prediction in the U.S. Using Multi-Source Remote Sensing Data. Remote Sens. 2025, 17, 107. [Google Scholar] [CrossRef]
- Duta, I.C.; Liu, L.; Zhu, F.; Shao, L. Improved Residual Networks for Image and Video Recognition. In Proceedings of the International Conference on Pattern Recognition, Milan, Italy, 10–15 January 2021. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Ndajah, P.; Kikuchi, H.; Yukawa, M.; Watanabe, H.; Muramatsu, S. An Investigation on the Quality of Denoised Images. Int. J. Circuits Syst. Signal Process. 2011, 5, 423–434. [Google Scholar]
- Kawahara, D.; Ozawa, S.; Saito, A.; Nagata, Y. Image Synthesis of Effective Atomic Number Images Using a Deep Convolutional Neural Network-Based Generative Adversarial Network. Reports Pract. Oncol. Radiother. 2022, 27, 848–855. [Google Scholar] [CrossRef] [PubMed]
- Nandhini, B.; Sruthakeerthi, B. Investigating the Quality Measures of Image Enhancement by Convoluting the Coefficients of Analytic Functions. Eur. Phys. J. Spec. Top. 2024, 123. [Google Scholar] [CrossRef]
- Kim, D.; Yu, J.; Yoon, J.; Jeon, S. Comparison of Accuracy of Surface Temperature Images from Unmanned Aerial Vehicle and Satellite for Precise Thermal Environment Monitoring of Urban Parks Using In Situ Data. Remote Sens. 2021, 13, 1977. [Google Scholar] [CrossRef]
- Somantri, L.; Himayah, S. Urban Heat Island Study Based on Remote Sensing and Geographic Information System: Correlation between Land Cover and Surface Temperature. E3S Web Conf. 2024, 600, 06001. [Google Scholar] [CrossRef]
- Heinemann, S.; Siegmann, B.; Thonfeld, F.; Muro, J.; Jedmowski, C.; Kemna, A.; Kraska, T.; Muller, O.; Schultz, J.; Udelhoven, T.; et al. Land Surface Temperature Retrieval for Agricultural Areas Using a Novel UAV Platform Equipped with a Thermal Infrared and Multispectral Sensor. Remote Sens. 2020, 12, 1075. [Google Scholar] [CrossRef]
- Abu El-Magd, S.A.; Masoud, A.M.; Hassan, H.S.; Nguyen, N.M.; Pham, Q.B.; Haneklaus, N.H.; Hlawitschka, M.W.; Maged, A. Towards Understanding Climate Change: Impact of Land Use Indices and Drainage on Land Surface Temperature for Valley Drainage and Non-Drainage Areas. J. Environ. Manag. 2024, 350, 119636. [Google Scholar] [CrossRef]
- Shafia, A.; Nimish, G.; Bharath, H.A. Dynamics of Land Surface Temperature with Changing Land-Use: Building a Climate ResilientSmart City. In Proceedings of the 2018 3rd International Conference for Convergence in Technology (I2CT), Pune, India, 6–8 April 2018. [Google Scholar]
- Kayet, N.; Pathak, K.; Chakrabarty, A.; Sahoo, S. Spatial Impact of Land Use/Land Cover Change on Surface Temperature Distribution in Saranda Forest, Jharkhand. Model. Earth Syst. Environ. 2016, 2, 127. [Google Scholar] [CrossRef]
- Tan, J.; Yu, D.; Li, Q.; Tan, X.; Zhou, W. Spatial Relationship between Land-Use/Land-Cover Change and Land Surface Temperature in the Dongting Lake Area, China. Sci. Rep. 2020, 10, 9245. [Google Scholar] [CrossRef]
- Mohamed, A.A.; Odindi, J.; Mutanga, O. Land Surface Temperature and Emissivity Estimation for Urban Heat Island Assessment Using Medium- and Low-Resolution Space-Borne Sensors: A Review. Geocarto Int. 2017, 32, 455–470. [Google Scholar] [CrossRef]
- Awais, M.; Li, W.; Hussain, S.; Cheema, M.J.M.; Li, W.; Song, R.; Liu, C. Comparative Evaluation of Land Surface Temperature Images from Unmanned Aerial Vehicle and Satellite Observation for Agricultural Areas Using In Situ Data. Agriculture 2022, 12, 184. [Google Scholar] [CrossRef]





| Data Source | Type | Name | Resolution (m) | Simbol |
|---|---|---|---|---|
| DJI Mavic 3T drone | Thermal (High Resolution) | Temperature | 0.23 | THR |
| Landsat-8 | Thermal (Low Resolution) | LST | 30 | LSTLR |
| PlanetScope | Surface Reflectance | Blue, Green, Red, and NIR | 3 | IHR |
| Spectral Index | NDVI |
| Date (UAV and Landsat-8) | Date (PlanetScope) | Site | Air Temperature (°C) | Humidity (%) | Air Pressure (hPa) |
|---|---|---|---|---|---|
| 2024/07/29 | 2024/07/29 | Oberfischbach | 23 | 59.66 | 977.23 |
| 2024/08/17 | 2024/08/14 | Konigshain | 27 | 66.75 | 979 |
| 2024/09/07 | 2024/09/07 | Oberfischbach | 21.32 | 83 | 966 |
| 2024/09/07 | 2024/09/07 | Mittelfischbach | 22.66 | 75.33 | 967.7 |
| - | 2024/10/23 | Mainz | - | - | - |
| Items | Camera Configuration | Detailed Specifications |
|---|---|---|
 DJI Mavic 3T |  Camera configuration | Weight: 920 g Max. Flight Time: 45 min Max. Speed: 21 m/s Operating Temperature: −10 to 40 °C |
 Sample thermal image |  Thermal camera | Sensor: Uncooled VOx Microbolometer Resolution: 640 × 512 pixels Spectral Range: 8–14 μm Accuracy: ±2 °C Field of View (FOV): 61° Focal Length: 40 mm |
 Sample RGB image |  Telephoto Camera | Sensor: 1/2-inch CMOS Resolution: 4000 × 3000 pixels Field of View (FOV): 15° Focal Length: 162 mm |
 Sample RGB image |  Wide Camera | Sensor: 1/2-inch CMOS Resolution: 8000 × 6000 pixels Field of View (FOV): 84° Focal Length: 24 mm |
| Metric | Formula | Description | Ref |
|---|---|---|---|
| Measures error magnitude, penalizing large errors. | [50] | ||
| Measures the average absolute difference between predicted and actual values, indicating model accuracy. | [51] | ||
| Calculates the relative error as a percentage, allowing easy comparison of models across different data scales. | [51] | ||
| Evaluates image prediction quality, with higher values indicating better quality. | [52] | ||
| Assesses perceived image quality, considering luminance, contrast, and texture. | [50] | ||
| R2 | Measures how well predictions match observations; closer to 1 means better fit. | [46] |
| Model | RMSE (°C) | MAE (°C) | MAPE (%) | PSNR | SSIM | R2 |
|---|---|---|---|---|---|---|
| LightGBM | 6.17 | 5.36 | 16.68 | 18.58 | 0.76 | −0.48 |
| XGBOOST | 5.45 | 4.72 | 14.79 | 19.66 | 0.70 | −0.15 |
| ResDensNet | 6.42 | 5.80 | 18.41 | 18.18 | 0.78 | −0.62 |
| ResDensNet-Attention | 4.74 | 4.08 | 12.72 | 20.87 | 0.81 | 0.12 |
| KAN | 4.06 | 3.09 | 9.32 | 22.22 | 0.83 | 0.35 |
| Planet | Landsat-8 | Evaluation Metrics | ||||||
|---|---|---|---|---|---|---|---|---|
| RGB | NIR | NDVI | LST | RMSE (°C) | MAE (°C) | MAPE (%) | PSNR | SSIM |
| ✓ | 5.93 | 4.86 | 14.27 | 18.92 | 0.82 | |||
| ✓ | ✓ | 4.92 | 3.96 | 12.18 | 20.55 | 0.82 | ||
| ✓ | ✓ | ✓ | 4.56 | 3.67 | 11.58 | 21.21 | 0.82 | |
| ✓ | ✓ | ✓ | ✓ | 4.06 | 3.09 | 9.32 | 22.22 | 0.83 |
| ✓ | ✓ | ✓ | 5.43 | 4.40 | 13.32 | 19.69 | 0.80 | |
| ✓ | ✓ | 4.81 | 3.89 | 11.52 | 20.73 | 0.82 | ||
| Model | RMSE (°C) | MAE (°C) | Correlation |
|---|---|---|---|
| LightGBM | 6.21 | 5.66 | 0.27 |
| XGBoost | 7.87 | 6.79 | 0.08 |
| ResDensNet | 17.46 | 16.10 | 0.25 |
| ResDensNet-Attention | 15.95 | 14.72 | 0.23 |
| KAN | 5.75 | 4.98 | 0.55 |
| Model | Mean (°C) | Median (°C) | Std |
|---|---|---|---|
| Landsat-8 | 19.32 | 19.37 | 1.69 |
| LightGBM | 24.92 | 24.45 | 2.60 |
| XGBoost | 25.63 | 25.75 | 4.54 |
| ResDensNet | 30.72 | 35.20 | 13.57 |
| ResDensNet-Attention | 32.93 | 36.26 | 8.57 |
| KAN | 24.28 | 24.54 | 3.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fathi, M.; Arefi, H.; Shah-Hosseini, R.; Moghimi, A. Super-Resolution of Landsat-8 Land Surface Temperature Using Kolmogorov–Arnold Networks with PlanetScope Imagery and UAV Thermal Data. Remote Sens. 2025, 17, 1410. https://doi.org/10.3390/rs17081410
Fathi M, Arefi H, Shah-Hosseini R, Moghimi A. Super-Resolution of Landsat-8 Land Surface Temperature Using Kolmogorov–Arnold Networks with PlanetScope Imagery and UAV Thermal Data. Remote Sensing. 2025; 17(8):1410. https://doi.org/10.3390/rs17081410
Chicago/Turabian StyleFathi, Mahdiyeh, Hossein Arefi, Reza Shah-Hosseini, and Armin Moghimi. 2025. "Super-Resolution of Landsat-8 Land Surface Temperature Using Kolmogorov–Arnold Networks with PlanetScope Imagery and UAV Thermal Data" Remote Sensing 17, no. 8: 1410. https://doi.org/10.3390/rs17081410
APA StyleFathi, M., Arefi, H., Shah-Hosseini, R., & Moghimi, A. (2025). Super-Resolution of Landsat-8 Land Surface Temperature Using Kolmogorov–Arnold Networks with PlanetScope Imagery and UAV Thermal Data. Remote Sensing, 17(8), 1410. https://doi.org/10.3390/rs17081410







