A Multi-Stage Optimization Approach for Satellite Orbit Pursuit–Evasion Games Based on a Coevolutionary Mechanism
Abstract
:1. Introduction
2. Related Work
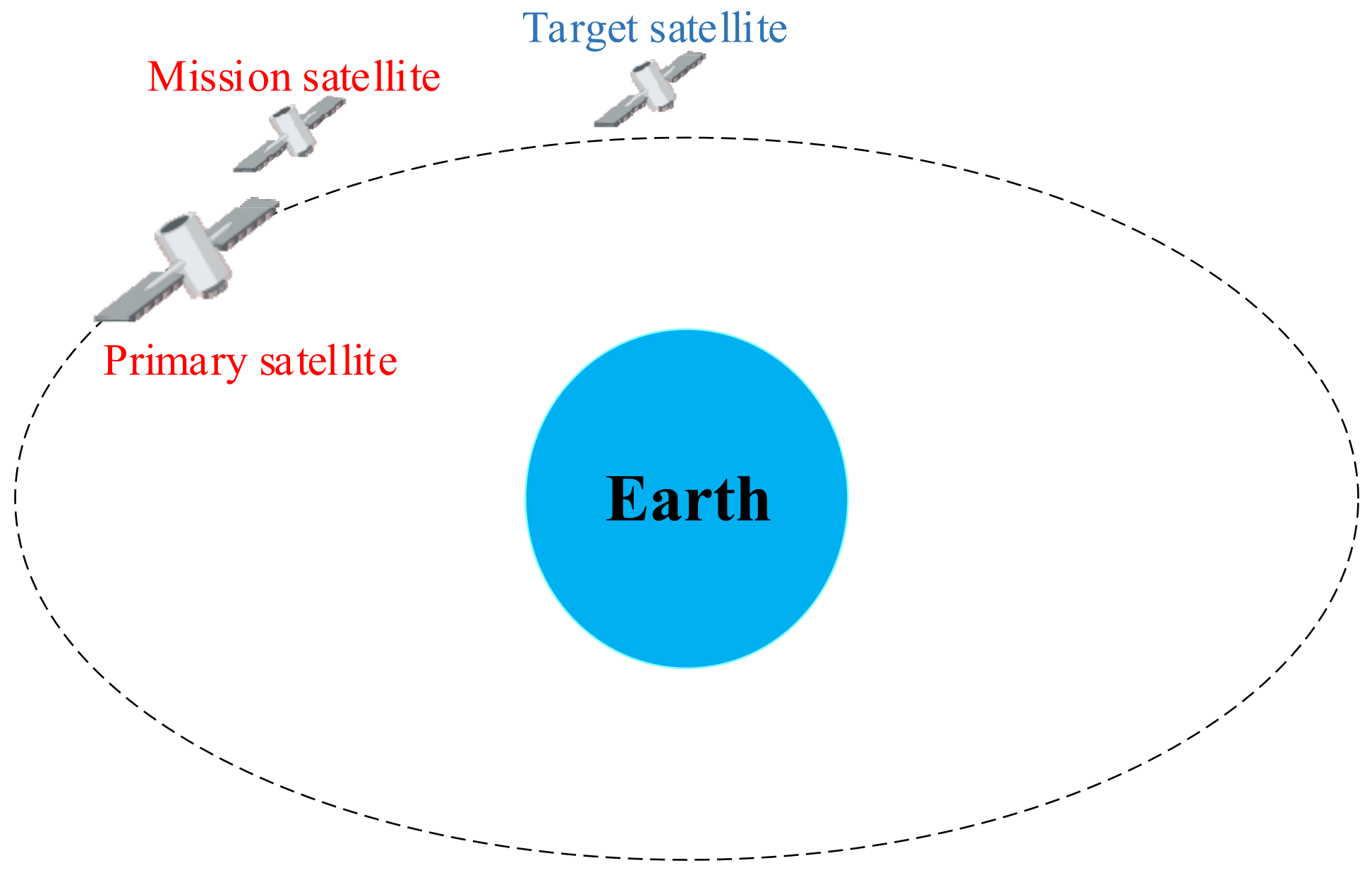
3. Problem Description
4. Constraint Conditions
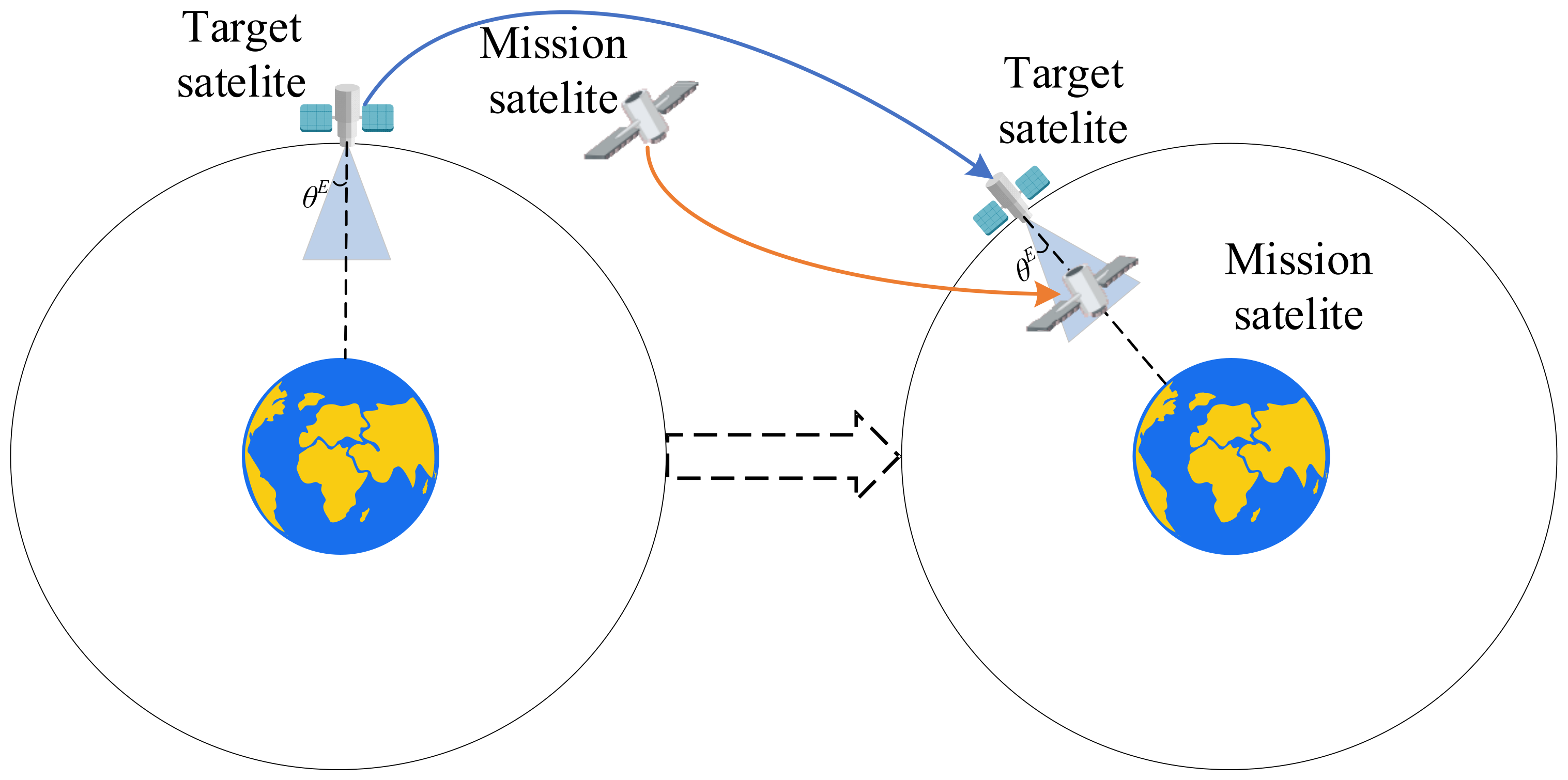
4.1. Mission Condition Constraints
- (1)
- Relative distance constraint
- (2)
- Capture angle constraint
- (3)
- Duration constraint
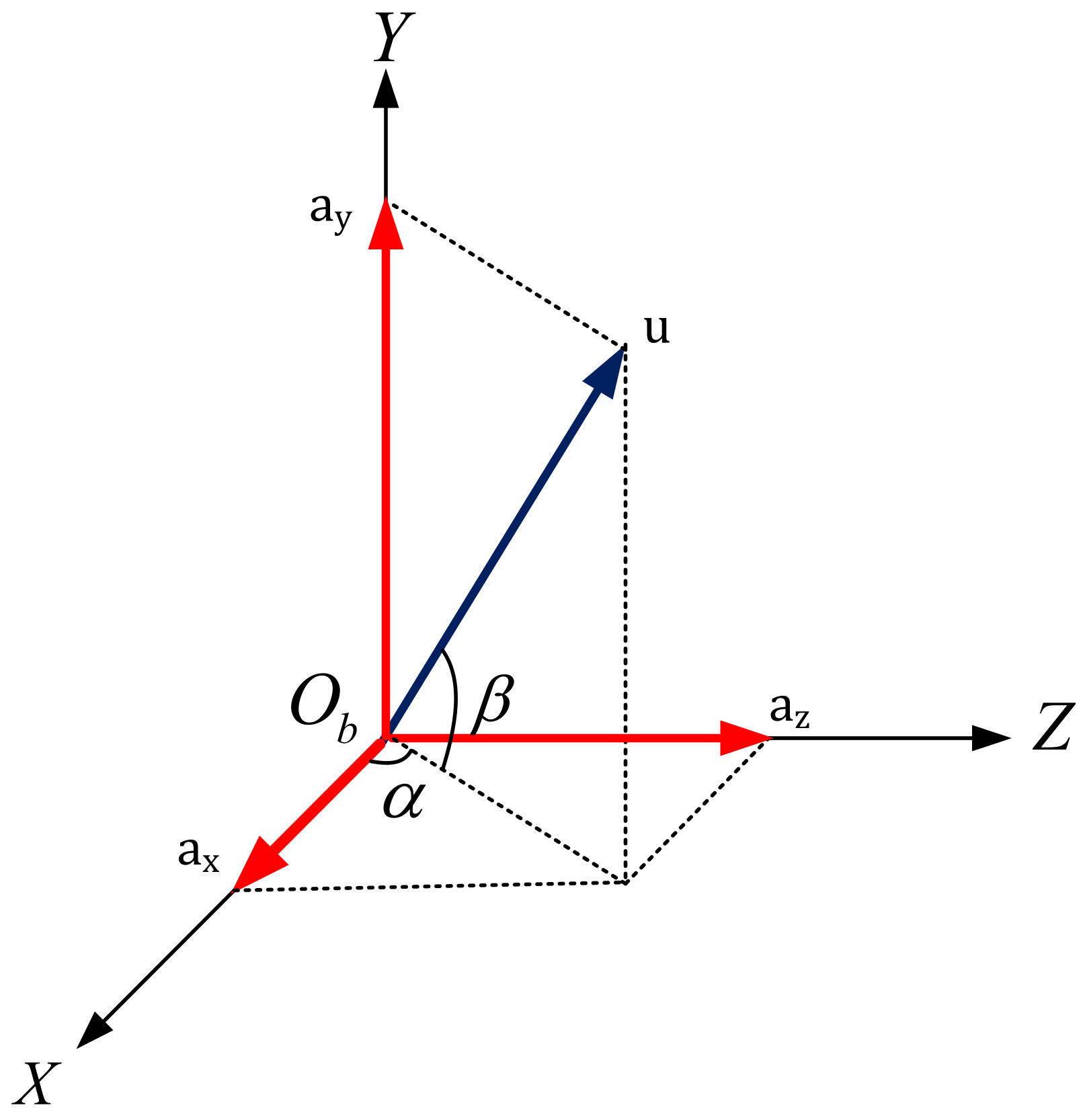
4.2. Velocity Impulse Control Constraint
- (1)
- Impulse magnitude constraint
- (2)
- Pulse interval constraint
- (3)
- Energy consumption constraint
4.3. Time Constraint
5. Design and Implementation of Hybrid Cooperative Evolutionary Algorithm
5.1. Design of Fitness Function
5.2. Differential Game Model
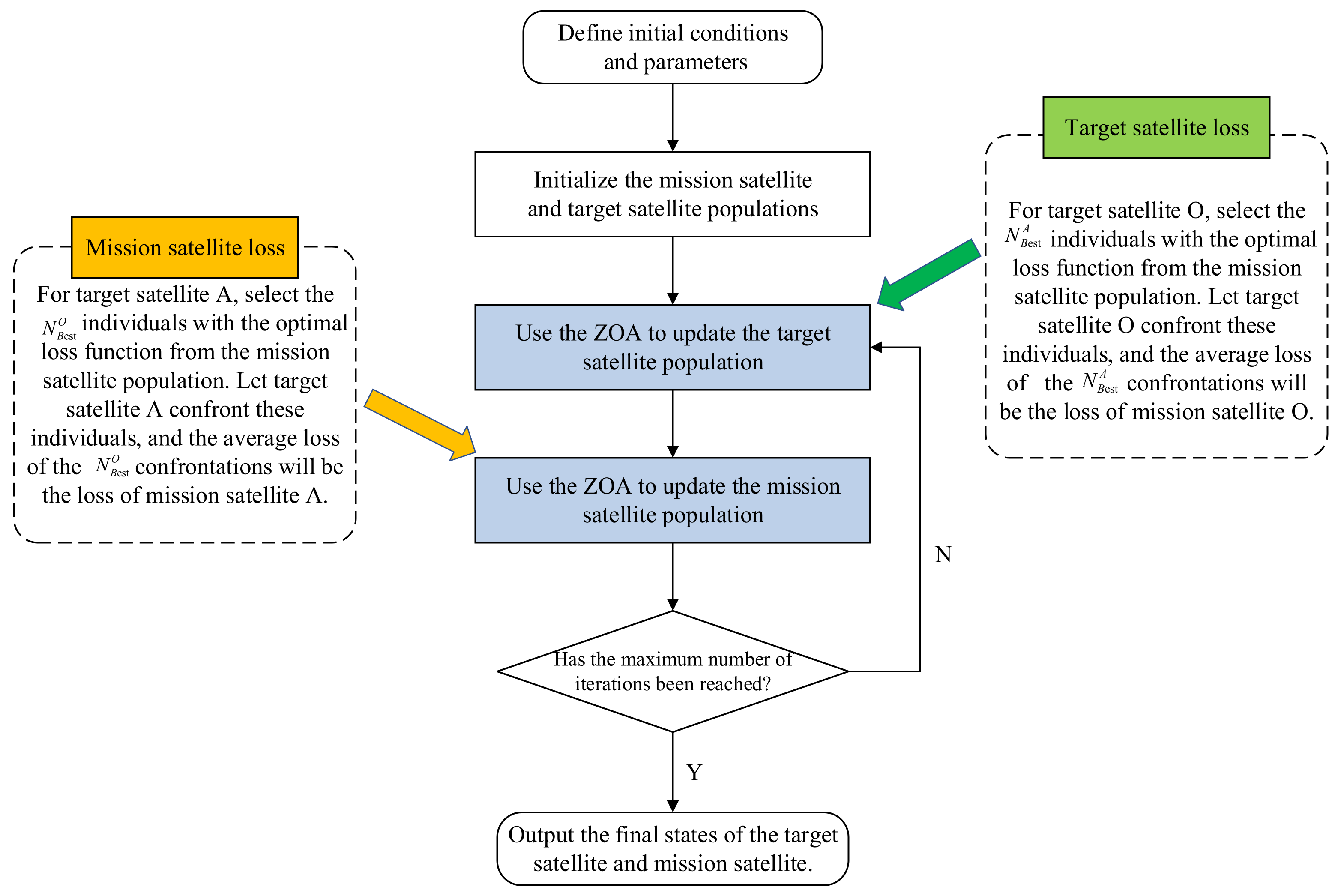
5.3. Design of Strategy Update and Co-Evolution Mechanisms
- (1)
- Population initialization
- (2)
- Fitness evaluation
- (3)
- Zebra behavior simulation
- (4)
- Solution Process
6. Simulation Results and Analysis
6.1. Scenario 1: The Agility of the Mission Satellite Is Twice That of the Target Satellite
6.2. Scenario 2: The Agility of the Mission Satellite Is 1.5 That of the Target Satellite
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liao, T. Research on Pursuit-Evasion Game Control and Solution Methods for Spacecraft. Master’s Thesis, Harbin Institute of Technology, Harbin, China, 2021; pp. 1–2. [Google Scholar]
- Shen, D.; Pham, K.; Blasch, E.; Chen, H.; Chen, G. Pursuit-evasion orbital game for satellite interception and collision avoidance. In Sensors and Systems for Space Applications IV; SPIE: San Francisco, CA, USA, 2011; Volume 8044, pp. 89–97. [Google Scholar]
- Luo, Y.Z.; Li, Z.Y.; Zhu, H. Survey on spacecraft orbital pursuit-evasion differential games. Sci. Sin. Technol. 2020, 50, 1533–1545. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, L.R.; Dang, Z.H.; Zhang, Y.L. Orbital game: Concepts, principles and methods. J. Command Control 2021, 7, 215–224. (In Chinese) [Google Scholar]
- Isaacs, R. Differential Games I: Introduction. 1954. Available online: https://www.rand.org/pubs/research_memoranda/RM1391.html (accessed on 17 March 2025).
- Ho, Y.; Bryson, A.; Baron, S. Differential games and optimal pursuit-evasion strategies. IEEE Trans. Autom. Control 1965, 10, 385–389. [Google Scholar] [CrossRef]
- Pontani, M.; Conway, B.A. Numerical solution of the three-dimensional orbital pursuit-evasion game. J. Guid. Control. Dyn. 2009, 32, 474–487. [Google Scholar] [CrossRef]
- Carr, R.W.; Cobb, R.G.; Pachter, M.; Pierce, S. Solution of a pursuit–evasion game using a near-optimal strategy. J. Guid. Control. Dyn. 2018, 41, 841–850. [Google Scholar] [CrossRef]
- Pang, B.; Wen, C.X.; Han, H.W.; Qiao, D. Solving Pursuit/Evasion Game Along Elliptical Orbit by Providing Precise Gradient. J. Guid. Control. Dyn. 2024, 47, 797–807. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Cheng, Y.; Qiao, D.; Huo, Z.X. An adaptive surrogate model-based fast planning for swarm safe migration along halo orbit. Acta Astronaut. 2022, 194, 309–322. [Google Scholar] [CrossRef]
- Armellin, R. Collision avoidance maneuver optimization with a multiple-impulse convex formulation. Acta Astronaut. 2021, 186, 347–362. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Huang, X.; Li, S.; Yang, B.; Sun, P.; Liu, X.; Liu, X. Spacecraft guidance and control based on artificial intelligence: Review. Acta Aeronaut. Astronaut. Sin. 2021, 42, 106–121. (In Chinese) [Google Scholar]
- Izzo, D.; Martens, M.; Pan, B.F. A survey on artificial intelligence trends in spacecraft guidance dynamics and control. Astrodynamics 2019, 3, 287–299. [Google Scholar] [CrossRef]
- Zhu, Q.; Shao, Z.J. Missile real-time receding horizon pursuit and evasion games guidance based on neural network. Syst. Eng. Elect 2019, 41, 1597–1605. [Google Scholar]
- Yang, B.; Liu, P.; Feng, J.; Li, S. Two-stage pursuit strategy for incomplete-information impulsive space pursuit-evasion mission using reinforcement learning. Aerospace 2021, 8, 299. [Google Scholar] [CrossRef]
- Chu, X.; Alfriend, K.T.; Zhang, J.; Zhang, Y. Q-learning algorithm for path-planning to maneuver through a satellite cluster. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Snowbird, UT, USA, 19–23 August 2018; Univelt Inc.: Escondido, CA, USA, 2018; pp. 2063–2082. [Google Scholar]
- Liu, B.Y.; Ye, X.B.; Gao, Y.; Wang, X.B.; Ni, L. Solution of non-cooperative pursuit-evasion game strategy based on branch deep reinforcement learning. Acta Aeronaut. Astronaut. Sin. 2020, 41, 348–358. (In Chinese) [Google Scholar]
- Xu, X.S.; Dang, C.H.; Song, B.; Yuan, Q.F.; Xiao, Y.Z. Orbital pursuit-evasion game method based on multi-agent reinforcement learning. Aerosp. Shanghai 2022, 39, 24–31. (In Chinese) [Google Scholar]
- Zhao, L.; Zhang, Y.; Dang, Z. PRD-MADDPG: An efficient learning-based algorithm for orbital pursuit-evasion game with impulsive maneuvers. Adv. Space Res. 2023, 72, 211–230. [Google Scholar] [CrossRef]
- Prince, E.R.; Hess, J.A.; Cobb, R.G.; Carr, R.W. Elliptical orbit proximity operations differential games. In Handbook of Scholarly Publications from the Air Force Institute of Technology (AFIT), Volume 1, 2000–2020; CRC Press: Boca Raton, FL, USA, 2022; pp. 243–275. [Google Scholar]
- Yu, D.T. Research on Maneuvering Methods for Spacecraft Safety Protection and Evasion. Master’s Thesis, National University of Defense Technology, Changsha, China, 2017. (In Chinese). [Google Scholar]
- Qi, Y.H. Research on Tracking Interception Guidance for Small Satellites. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2009; pp. 21–25. (In Chinese). [Google Scholar]
- Wu, W.; Chen, J.; Liu, J. A hybrid optimisation method for intercepting satellite trajectory based on differential game. Aeronaut. J. 2023, 127, 900–922. [Google Scholar] [CrossRef]
- Stupik, J.; Pontani, M.; Conway, B. Optimal pursuit/evasion spacecraft trajectories in the hill reference frame. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4882. [Google Scholar]
- Sun, S.; Zhang, Q.; Loxton, R.; Li, B. Numerical solution of a pursuit-evasion differential game involving two spacecraft in low earth orbit. J. Ind. Manag. Optim. (JIMO) 2015, 11, 1127–1147. [Google Scholar] [CrossRef]
- Liu, Y.; She, H.; Meng, B.; Huang, J. A Method of Surrounding Escapable Space Target by Combining Game with Optimization. In Proceedings of the 2023 42nd Chinese Control Conference (CCC), Tianjin, China, 24–26 July 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 8088–8093. [Google Scholar]
- Wu, Q.C.; Zhang, H.B. Spacecraft pursuit-evasion strategy and numerical solution based on survival-type differential game. Control. Inf. Technol. 2019, 4, 39–43. (In Chinese) [Google Scholar]
- Chen, W.; Hu, Y.; Gao, C.; Jing, W. Luring cooperative capture guidance strategy for the pursuit-evasion game under incomplete target information. Astrodynamics 2024, 8, 675–688. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Y. Multi-population improved whale optimization algorithm for high dimensional optimization. Appl. Soft Comput. 2021, 112, 107854. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N. Ensemble of constraint handling techniques. IEEE Trans. Evol. Comput. 2010, 14, 561–579. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xiao, J.; Zhang, X.; Jin, Y. A coevolutionary framework for constrained multiobjective optimization problems. IEEE Trans. Evol. Comput. 2020, 25, 102–116. [Google Scholar] [CrossRef]
- He, C.; Li, M.; Zhang, C.; Chen, H.; Zhong, P.; Li, Z.; Li, J. A self-organizing map approach for constrained multi-objective optimization problems. Complex Intell. Syst. 2022, 8, 5355–5375. [Google Scholar] [CrossRef]
- Trojovská, E.; Dehghani, M.; Trojovský, P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access 2022, 10, 49445–49473. [Google Scholar] [CrossRef]
- Zhu, H. Optimal Control Strategy for Spacecraft Orbital Pursuit-Evasion Based on Differential Game. Master’s Thesis, National University of Defense Technology, Changsha, China, 2017. (In Chinese). [Google Scholar]
- Zhu, H.; Luo, Y.Z.; Li, Z.Y.; Yang, Z. Orbital pursuit-evasion games with incomplete information in the hill reference frame. In Proceedings of the 27th International Symposium on Space Flight Dynamics (ISSFD), Melbourne, Australia, 24–28 February 2019; pp. 1–6. [Google Scholar]
- Wang, Z.K. Research on Dynamics Modeling and Control of Distributed Satellites. Ph.D. Thesis, National University of Defense Technology, Changsha, China, 2006; pp. 18–41. (In Chinese). [Google Scholar]
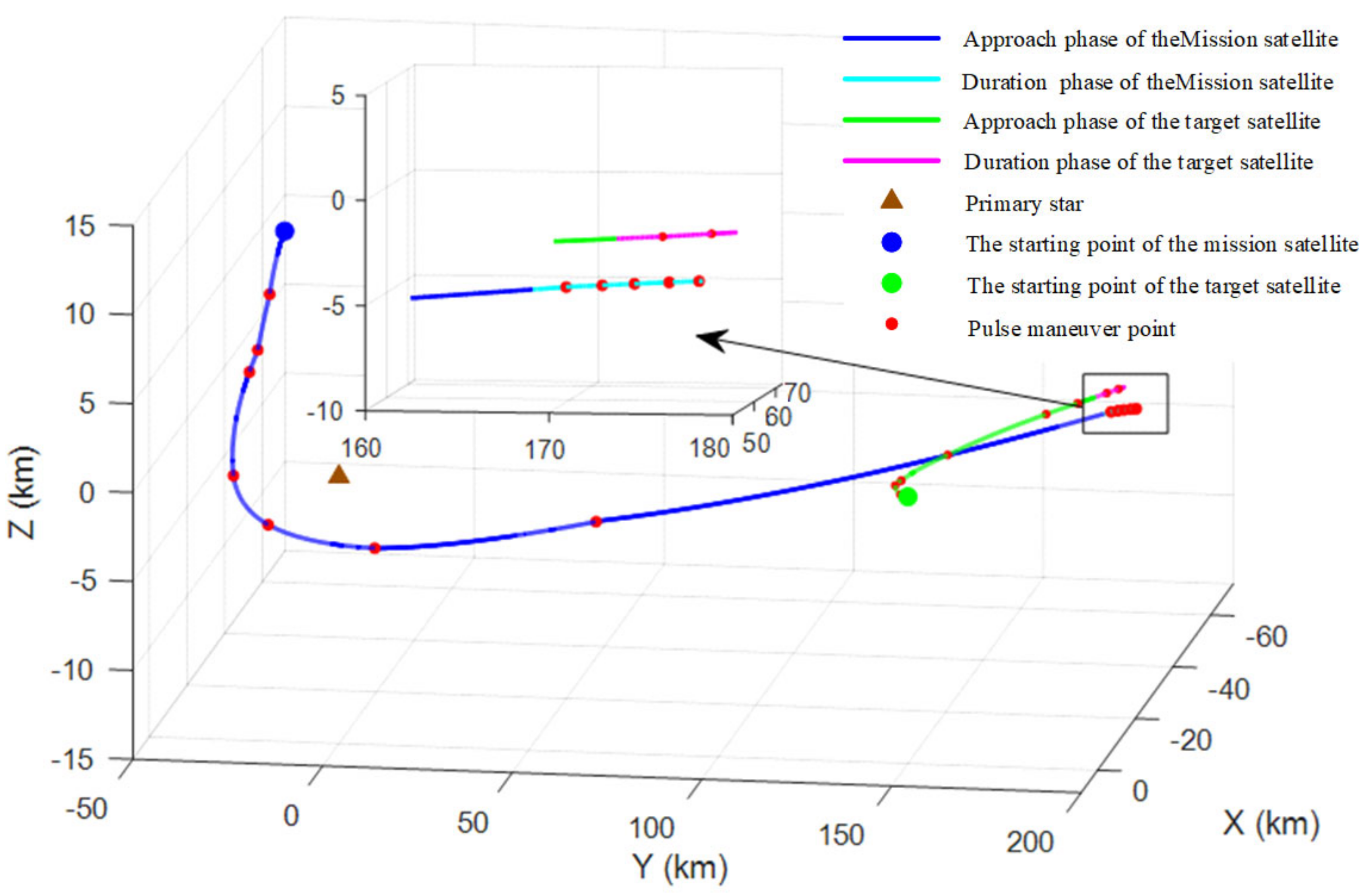
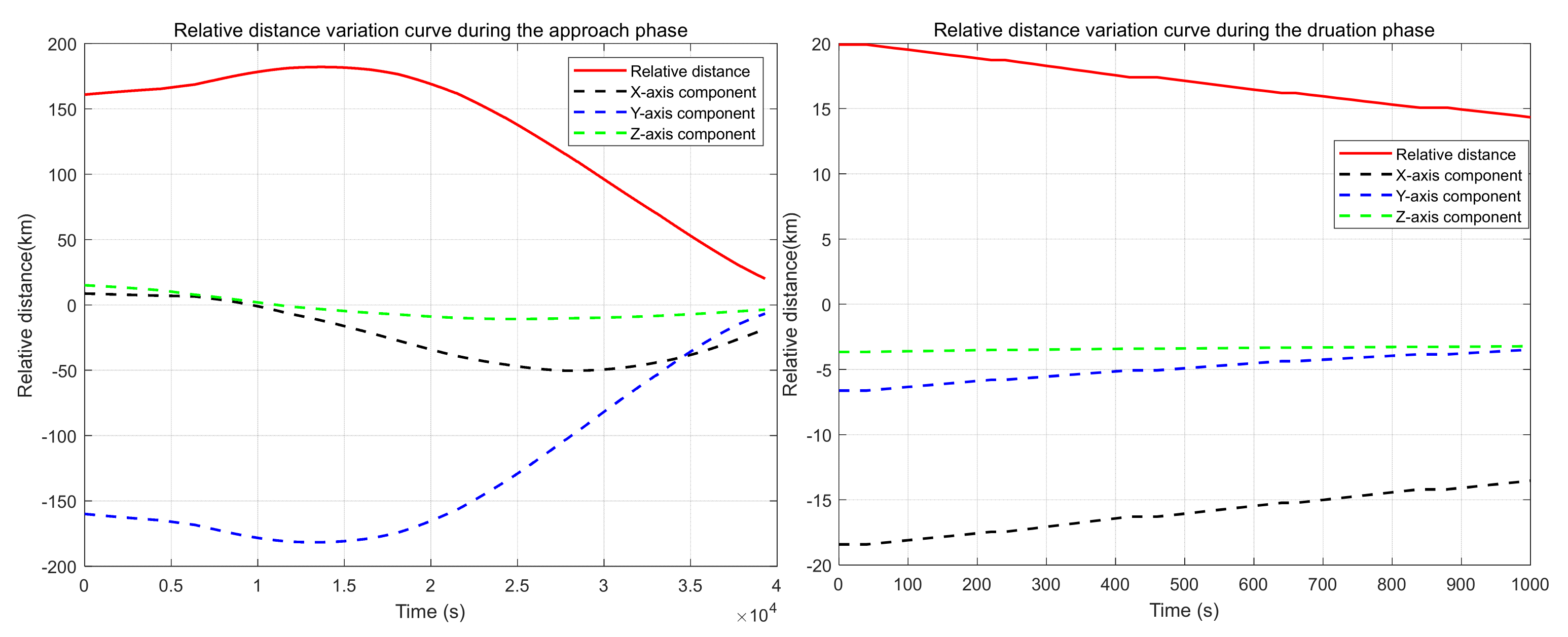
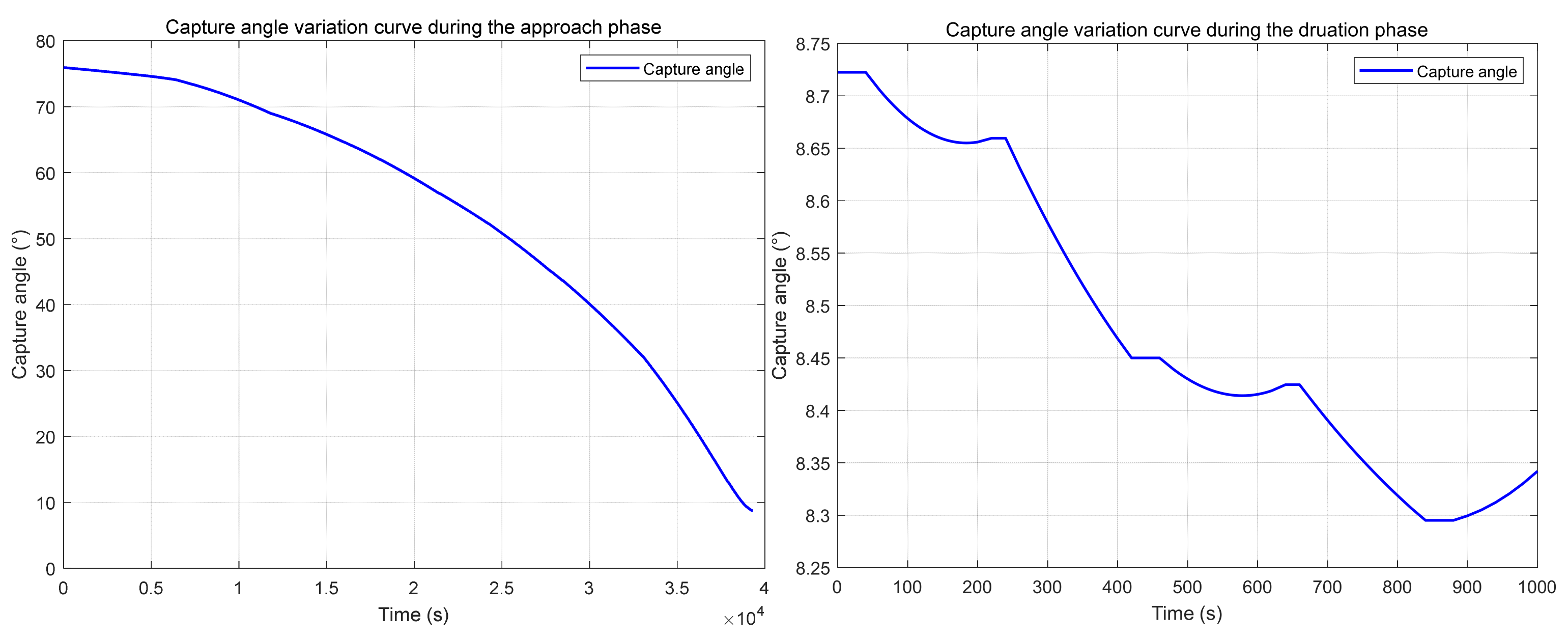


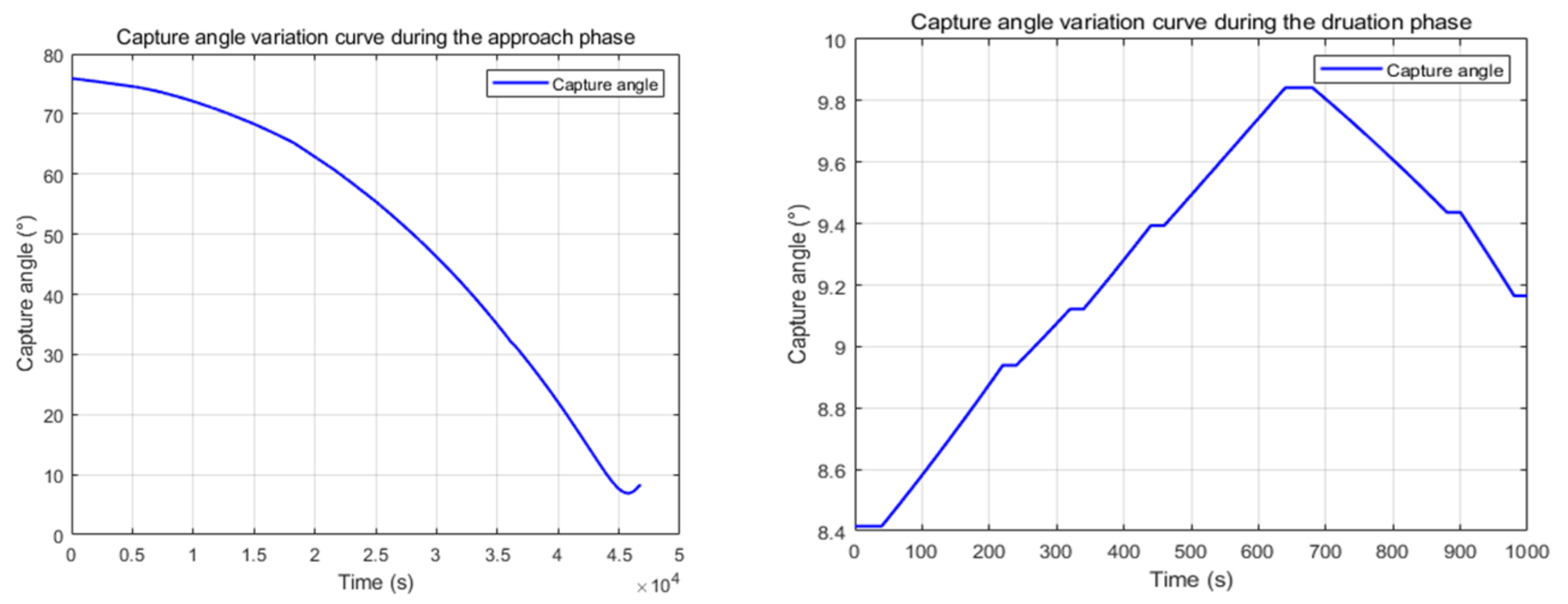
| States | ||||||
|---|---|---|---|---|---|---|
| Mission Satellite | −8.660254 | −10.0 | 15.0 | −0.000361 | −0.001253 | −0.000626 |
| Target Satellite | 0 | 150.0 | 0 | 0 | 0 | 0 |
| Distance (km) | Illumination Angle (°) | Duration (s) | Maximum Mission Time (s) |
|---|---|---|---|
| 1000 | 100,000 |
| Phase | Time (s) | Frequency | |||
|---|---|---|---|---|---|
| Approach Phase | 4368 | 1 | 1.047 | −1.329 | −0.502 |
| 6312 | 2 | 1.803 | −2.163 | 0.188 | |
| 7334 | 3 | 0.361 | −0.822 | −0.384 | |
| 11,775 | 4 | 1.168 | 0.287 | 0.570 | |
| 16334 | 5 | 0.307 | 1.036 | 0.111 | |
| 21,326 | 6 | 0.192 | 0.384 | 0.657 | |
| 27,645 | 7 | 0.456 | 0.128 | −0.257 | |
| End of Approach Phase | 39,320 | ||||
| Sustained Phase | 39,520 | 8 | 1.150 | −0.334 | −0.230 |
| 39,720 | 9 | 0.505 | 0.865 | 0.148 | |
| 39,920 | 10 | 0.781 | −1.839 | −0.171 | |
| 40,120 | 11 | 0.052 | −1.743 | 0.048 | |
| 40,320 | 12 | 0.965 | −0.469 | −0.230 | |
| End of Sustained Phase | 40,320 |
| Phase | Time (s) | Frequency | |||
|---|---|---|---|---|---|
| Approach Phase | 15,908 | 1 | 0.116 | 0.367 | −0.792 |
| 17,943 | 2 | 0.792 | −1.723 | 0.170 | |
| 21,295 | 3 | 0.867 | −2.022 | −0.061 | |
| 24,124 | 4 | 0.571 | −0.940 | −0.405 | |
| 28,311 | 5 | 0.256 | −1.360 | 0.311 | |
| 32,867 | 6 | 0.975 | −1.388 | −0.043 | |
| 37,728 | 7 | 0.506 | 0.485 | 0.126 | |
| 38,782 | 8 | 0.080 | 0.290 | 0.653 | |
| End of Approach Phase | 39,320 | ||||
| Sustained Phase | 39,725 | 9 | 1.000 | 0.340 | 0.172 |
| 40,130 | 10 | 0.336 | −0.781 | −0.062 | |
| End of Sustained Phase | 40,320 |
| Phase | Time (s) | Frequency | |||
|---|---|---|---|---|---|
| Approach Phase | 1618 | 1 | 0.451 | 2.542 | 0.942 |
| 5164 | 2 | 1.598 | −1.670 | 0.096 | |
| 18,037 | 3 | 0.980 | 2.425 | −0.657 | |
| 36,101 | 4 | 0.891 | −1.220 | 0.408 | |
| 46,508 | 5 | 0.345 | 0.067 | 0.636 | |
| End of Approach Phase | 46,780 | ||||
| Sustained Phase | 46,980 | 6 | 0.444 | −0.614 | 0.804 |
| 47,181 | 7 | 0.805 | −0.353 | −0.260 | |
| 47,382 | 8 | 1.509 | −1.183 | 0.239 | |
| 47,583 | 9 | 1.054 | −0.070 | 0.730 | |
| End of Sustained Phase | 47,780 |
| Phase | Time (s) | Frequency | |||
|---|---|---|---|---|---|
| Approach Phase | 6524 | 1 | 0.230 | −1.394 | −0.008 |
| 14,564 | 2 | 0.187 | 0.253 | 1.380 | |
| 21,307 | 3 | 0.337 | −0.751 | −0.141 | |
| 24,709 | 4 | 0.194 | 0.079 | 0.907 | |
| 36,273 | 5 | 0.569 | −0.354 | 0.636 | |
| End of Approach Phase | 46,780 | ||||
| Sustained Phase | 47,080 | 6 | 0.649 | 0.094 | 0.506 |
| 47,381 | 7 | 0.739 | −0.093 | −0.131 | |
| 47,683 | 8 | 0.431 | 1.420 | −0.026 | |
| End of Sustained Phase | 47,780 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Xu, X.; Yuan, Q.; Han, H.; Zhou, D. A Multi-Stage Optimization Approach for Satellite Orbit Pursuit–Evasion Games Based on a Coevolutionary Mechanism. Remote Sens. 2025, 17, 1441. https://doi.org/10.3390/rs17081441
Wu J, Xu X, Yuan Q, Han H, Zhou D. A Multi-Stage Optimization Approach for Satellite Orbit Pursuit–Evasion Games Based on a Coevolutionary Mechanism. Remote Sensing. 2025; 17(8):1441. https://doi.org/10.3390/rs17081441
Chicago/Turabian StyleWu, Jian, Xusheng Xu, Qiufan Yuan, Haodong Han, and Daming Zhou. 2025. "A Multi-Stage Optimization Approach for Satellite Orbit Pursuit–Evasion Games Based on a Coevolutionary Mechanism" Remote Sensing 17, no. 8: 1441. https://doi.org/10.3390/rs17081441
APA StyleWu, J., Xu, X., Yuan, Q., Han, H., & Zhou, D. (2025). A Multi-Stage Optimization Approach for Satellite Orbit Pursuit–Evasion Games Based on a Coevolutionary Mechanism. Remote Sensing, 17(8), 1441. https://doi.org/10.3390/rs17081441





