Undifferenced Ambiguity Resolution for Precise Multi-GNSS Products to Support Global PPP-AR
Abstract
:1. Introduction
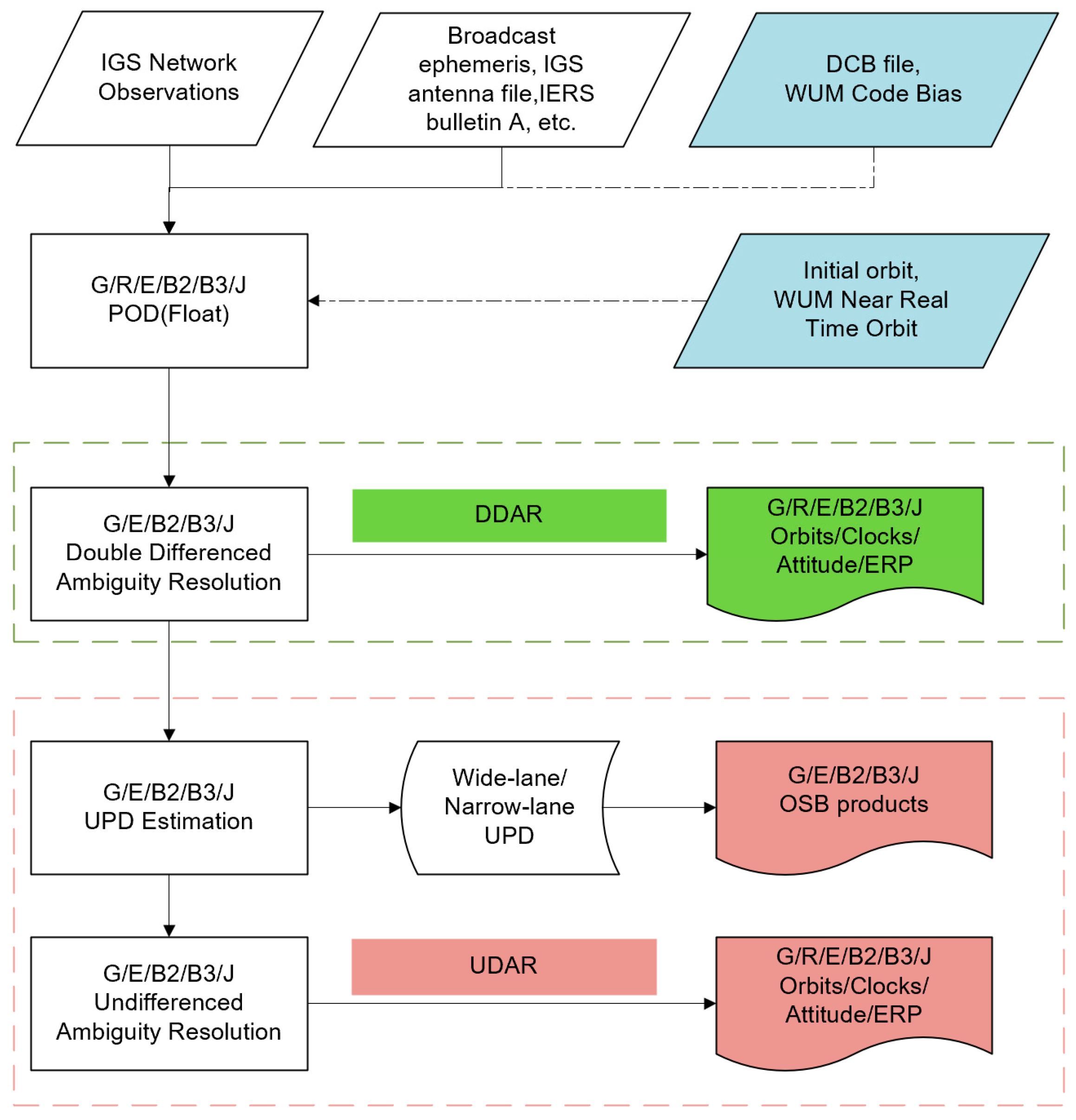
2. Method
2.1. GNSS Observational Model
2.2. Undifferenced Ambiguity Resolution
2.3. Obervable-Specific Bias
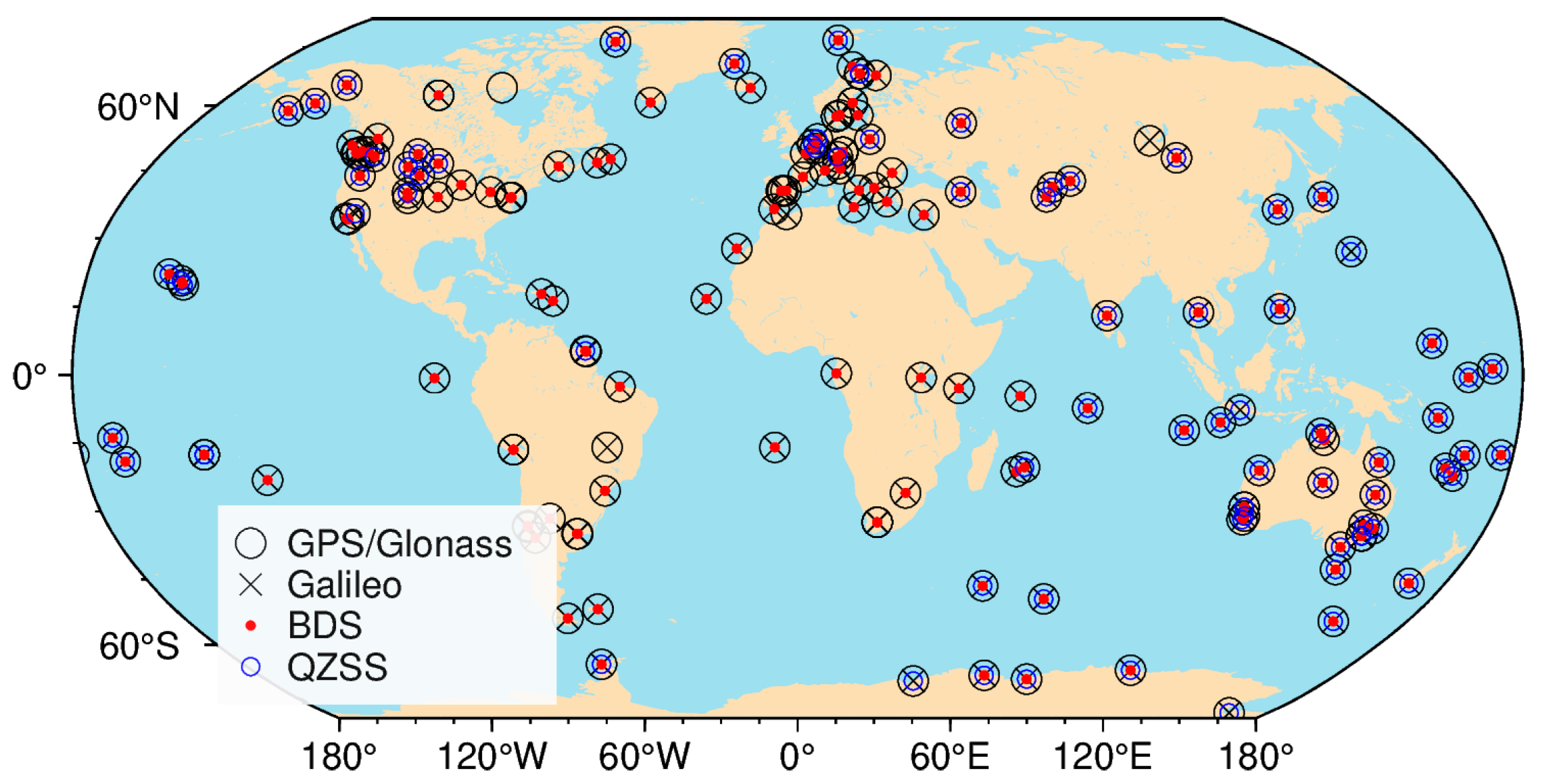
3. Data and Experiments
- Initial estimation: Data from six constellations—GPS, GLONASS, Galileo, BDS-2, BDS-3, and QZSS—are processed simultaneously.
- DDAR solution: Orbits, clocks, Earth rotation parameters, tropospheric delays, coordinates, and receiver clock offsets are estimated based on double-differenced ambiguity resolution. After constraining the double-differenced ambiguities, the parameters for satellites, stations, and other parameters, such as the troposphere and Earth’s rotation parameters, achieve a high level of precision. Products generated at this step are so-called IGS legacy products.
- UDAR solution: Following the DDAR solution, satellite-specific wide-lane and narrow-lane UPDs are derived using between-satellite single-difference ambiguities under a zero-mean condition. With these UPD products, undifferenced ambiguities are fixed and applied as constraints in the normal equations to obtain the final solutions. PPP-AR can be conducted based on products generated at this step.
| Item | Strategy |
|---|---|
| Observable | Undifferenced ionosphere-free dual-frequency code and phase combination GPS C1P/C2P L1P/L2P GLONASS C1P/C2P L1P/L2P Galileo C1X/C5X L1X/L5X, C1C/C5Q, L1C/L5Q BDS-2 C2I/C6I L2I/L6I BDS-3 C2I/C6I L2I/L6I QZSS C1X/C2X L1X/L2X |
| POD arc length | 24 h |
| Sampling rate | 300 s |
| Elevation angle cutoff | 7° |
| Weighting | Code: 0.2 m; phase: 2 mm Elevation-dependent weighting: E > 30°: 1; E ≤ 30°: 1/(2sin(E)) |
| Antenna PCO/PCV | Igs20_wwww.atx for satellites and stations |
| Tidal displacement | Solid Earth tide [40] Ocean tide loading (FES2014b) [41] Solid Earth pole tide (FES2014b) [41] |
| Tropospheric delay | Global Pressure and Temperature (GPT) model with Global Mapping Function (GMF) [42] |
| Earth rotation | IERS Bulletin A Ocean tidal: diurnal/semidiurnal varriations applied UT1 libration applied HF EOP based on Desai model |
| Relativity effect | Applied based on IERS Conventions 2010 |
| Geopotential | Earth Gravitational Model 2008 (EGM08) 12 12 |
| Tidal variations in geopotential | Solid Earth tides Ocean tides Solid Earth pole tide Oceanic pole tide |
| Third body | Sun, Moon, Mercury, Venus, Mars, Jupiter, Saturn, Uranus, Neptune, Pluto with JPL Planetary Ephemeris 405 (DE405) |
| Solar radiation | GPS and GLONASS: Box-wing+ECOM2 (D, Y, B, Bc, Bs, Dc2, Ds2) [33]. Galileo: ECOM1 with a priori SRP model [36] BDS-2 GEO: 5-parameter ECOM1 with a priori SRP model [43] BDS-2 IGSO and MEO: ECOM1 with a constant parameter in the along-track direction [24] BDS-3 MEO: ECOM1 with a priori SRP model [25] |
| Attitude model | GPS [27]; GLONASS [28]; Galileo [29] BDS GEO: orbit nominal mode BDS-2 C07, C08, C09, C10, C12, C13: yaw-steering and orbit normal mode [30] The BDS-2 and BDS-3 MEO/IGSO CAST satellites [31] BDS-3 MEO SECM satellites [32] |
| Earth albedo radiation | Applied based on [39] |
| Satellite antenna thrust | Applied with the satellite transmit power [38] GPS: IIR-A/B 60 W, IIR-M 145 W, IIF 240 W, IIIA 300 W GLONASS: M 20–85 W, K1 105–135 W, M+ 100 W Galileo IOV: 135 W, FOC 260 W BDS-2: IGSO 185 W, MEO 130 W BDS-3: MEO-CAST 310 W, MEO-SECM 280 W QZSS: 2I 550 W, 2G 550 W, 2A 460 W |
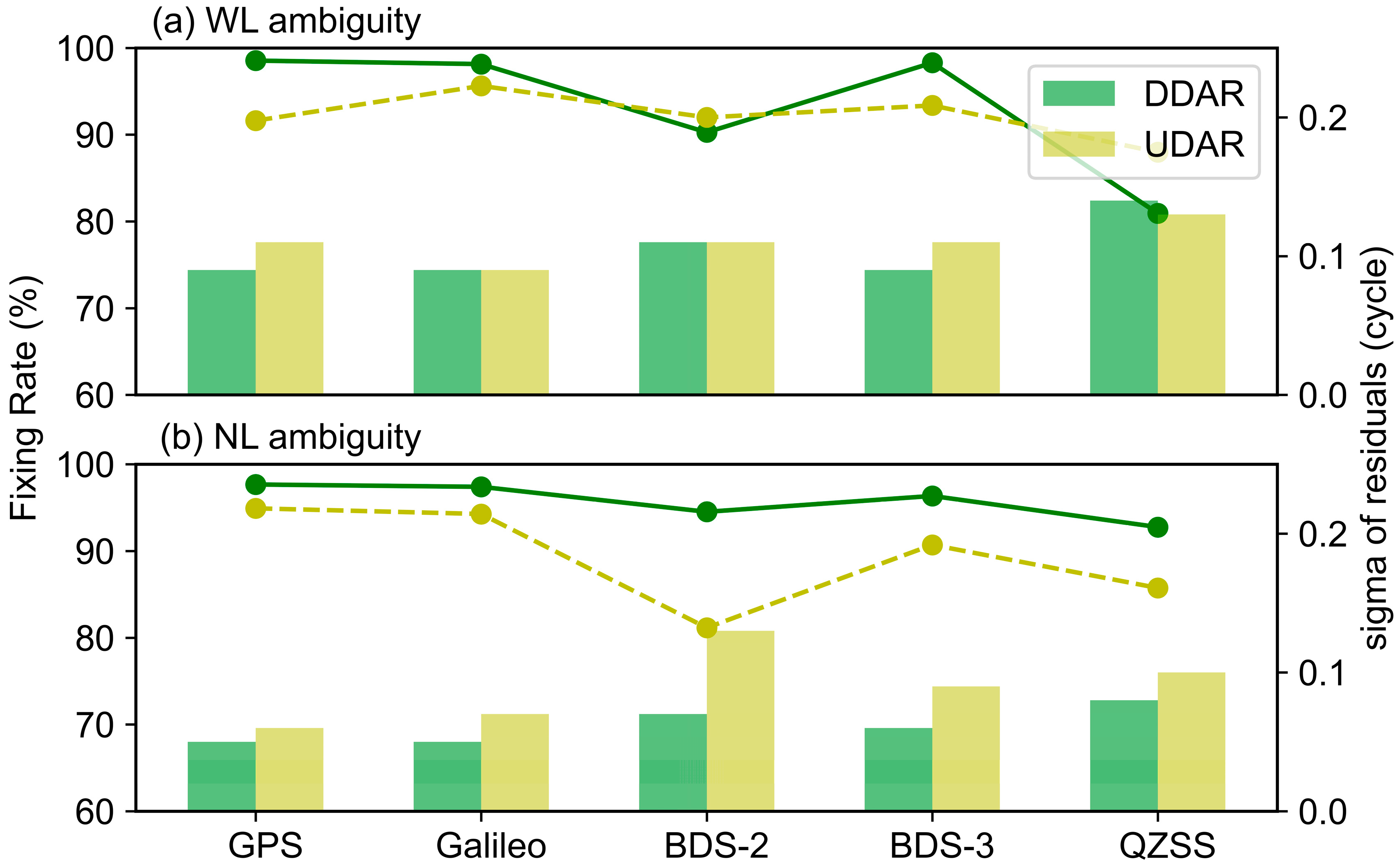
| Ambiguty resolution | DDAR for GPS/Galileo/BDS-2/BDS-3/QZSS, with an additional UDAR step in the UDAR solution The tolerance of WL/NL ambiguity residuals is 0.20/0.12 cycle |
4. Results
4.1. Ambiguity Resolution
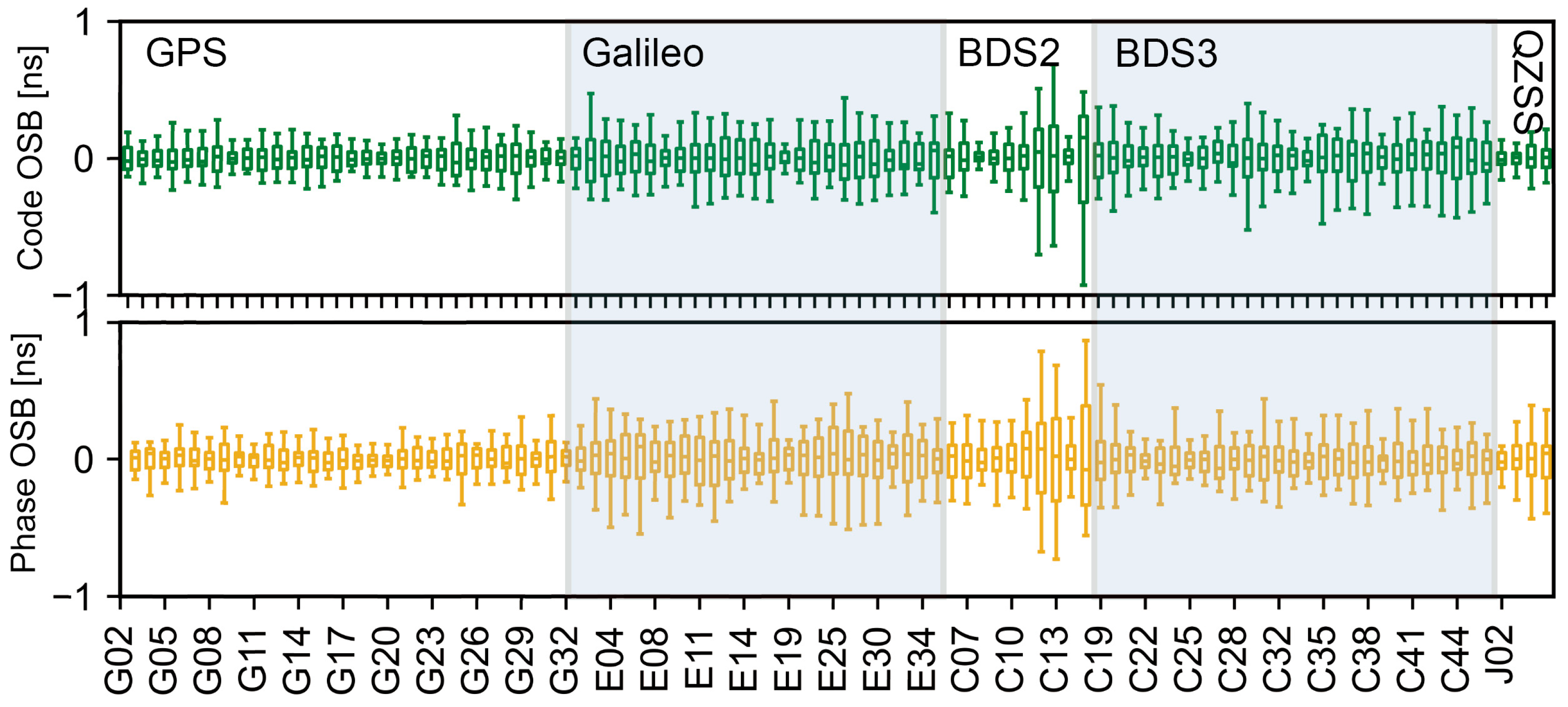
4.2. OSB Products
4.3. Orbit
4.3.1. Orbit Boundary Discontinuity
4.3.2. Comparison with Other Products
4.3.3. Satellite Laser Ranging Validation
4.4. Global Multi-GNSS PPP-AR
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UD | Undifferenced |
| DD | Double-Differenced |
| AR | Ambiguity Resolution |
| PPP | Precise Point Positioning |
| UDAR | Undifferenced Ambiguity Resolution |
| DDAR | Double-Differenced Ambiguity Resolution |
| PPP-AR | Precise Point Positioning Ambiguity Resolution |
| WL | Wide-Lane |
| NL | Narrow-Lane |
| IF | Ionosphere-Free |
| MW | Melbourne–Wübbena |
| AC | Analysis Center |
| MGEX | Multi-GNSS Experiment |
| WUM | Wuhan University |
| IGS | International GNSS Service |
| ESA | European Space Agency |
| DOY | Day of Year |
| OBD | Orbit Boundary Discontinuity |
| SLR | Satellite Laser Ranging |
| POD | Precise Orbit Determination |
| UPD | Uncalibrated Phase Delay |
| OSB | Observable-Specific Bias |
| DCB | Differential Code Bias |
| RMS | Root Mean Square |
| STDev | Standard Derivation |
| MEO | Medium Earth Orbit |
| IGSO | Inclined Geosynchronous Satellite Orbit |
| GEO | Geosynchronous Earth Orbit |
References
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophys. Res. Solid Earth 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Dong, D.-N.; Bock, Y. Global Positioning System Network analysis with phase ambiguity resolution applied to crustal deformation studies in California. J. Geophys. Res. Solid Earth 1989, 94, 3949–3966. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P.; Rothacher, M. A New Data Processing Strategy for Huge GNSS Global Networks. J. Geod. 2006, 80, 199–203. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in Precise Point Positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- Geng, J.; Shi, C.; Ge, M.; Dodson, A.H.; Lou, Y.; Zhao, Q.; Liu, J. Improving the estimation of fractional-cycle biases for ambiguity resolution in precise point positioning. J. Geod. 2012, 86, 579–589. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.-P.; Broca, P.; Cerri, L. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Collins, P.; Bisnath, S.; Lahaye, F.; Héroux, P. Undifferenced GPS Ambiguity Resolution Using the Decoupled Clock Model and Ambiguity Datum Fixing. Navigation 2010, 57, 123–135. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Teferle, F.N. Integer ambiguity resolution in precise point positioning: Method comparison. J. Geod. 2010, 84, 569–581. [Google Scholar] [CrossRef]
- Shi, J.; Gao, Y. A comparison of three PPP integer ambiguity resolution methods. GPS Solut. 2014, 18, 519–528. [Google Scholar] [CrossRef]
- Banville, S.; Geng, J.; Loyer, S.; Schaer, S.; Springer, T.; Strasser, S. On the interoperability of IGS products for precise point positioning with ambiguity resolution. J. Geod. 2020, 94, 10. [Google Scholar] [CrossRef]
- Bertiger, W.; Desai, S.D.; Haines, B.; Harvey, N.; Moore, A.W.; Owen, S.; Weiss, J.P. Single receiver phase ambiguity resolution with GPS data. J. Geod. 2010, 84, 327–337. [Google Scholar] [CrossRef]
- Teunissen, P.J.G.; Khodabandeh, A. Review and principles of PPP-RTK methods. J. Geod. 2015, 89, 217–240. [Google Scholar] [CrossRef]
- Deng, Z.; Wang, J.; Ge, M. The GBM Rapid Product and the Improvement from Undifferenced Ambiguity Resolution. In Proceedings of the EGU General Assembly 2022, Vienna, Austria, 23–27 May 2022. [Google Scholar] [CrossRef]
- Chen, H.; Jiang, W.; Ge, M.; Wickert, J.; Schuh, H. An enhanced strategy for GNSS data processing of massive networks. J. Geod. 2014, 88, 857–867. [Google Scholar] [CrossRef]
- Geng, J.; Mao, S. Massive GNSS Network Analysis Without Baselines: Undifferenced Ambiguity Resolution. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021558. [Google Scholar] [CrossRef]
- Johnston, G.; Riddell, A.; Hausler, G. The International GNSS Service. In Springer Handbook of Global Navigation Satellite Systems; Teunissen, P.J.G., Montenbruck, O., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 967–982. ISBN 978-3-319-42928-1. [Google Scholar]
- Schaer, S.; Villiger, A.; Arnold, D.; Dach, R.; Prange, L.; Jäggi, A. The CODE ambiguity-fixed clock and phase bias analysis products: Generation, properties, and performance. J. Geod. 2021, 95, 81. [Google Scholar] [CrossRef]
- Strasser, S.; Mayer-Gürr, T.; Zehentner, N. Processing of GNSS constellations and ground station networks using the raw observation approach. J. Geod. 2019, 93, 1045–1057. [Google Scholar] [CrossRef]
- Geng, J.; Zhang, Q.; Li, G.; Liu, J.; Liu, D. Observable-specific phase biases of Wuhan multi-GNSS experiment analysis center’s rapid satellite products. Satell. Navig. 2022, 3, 23. [Google Scholar] [CrossRef]
- Geng, J.; Chen, X.; Pan, Y.; Zhao, Q. A modified phase clock/bias model to improve PPP ambiguity resolution at Wuhan University. J. Geod. 2019, 93, 2053–2067. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Dick, G.; Zhang, F.P. Improving carrier-phase ambiguity resolution in global GPS network solutions. J. Geod. 2005, 79, 103–110. [Google Scholar] [CrossRef]
- Wang, N.; Li, Z.; Duan, B.; Hugentobler, U.; Wang, L. GPS and GLONASS observable-specific code bias estimation: Comparison of solutions from the IGS and MGEX networks. J. Geod. 2020, 94, 74. [Google Scholar] [CrossRef]
- Liu, J.; Ge, M. PANDA software and its preliminary result of positioning and orbit determination. Wuhan Univ. J. Nat. Sci. 2003, 8, 603–609. [Google Scholar] [CrossRef]
- Guo, J.; Xu, X.; Zhao, Q.; Liu, J. Precise orbit determination for quad-constellation satellites at Wuhan University: Strategy, result validation, and comparison. J. Geod. 2016, 90, 143–159. [Google Scholar] [CrossRef]
- Guo, J.; Wang, C.; Chen, G.; Xu, X.; Zhao, Q. BDS-3 precise orbit and clock solution at Wuhan University: Status and improvement. J. Geod. 2023, 97, 15. [Google Scholar] [CrossRef]
- Montenbruck, O.; Schmid, R.; Mercier, F.; Steigenberger, P.; Noll, C.; Fatkulin, R.; Kogure, S.; Ganeshan, A.S. GNSS satellite geometry and attitude models. Adv. Space Res. 2015, 56, 1015–1029. [Google Scholar] [CrossRef]
- Kouba, J. A simplified yaw-attitude model for eclipsing GPS satellites. GPS Solut. 2009, 13, 1–12. [Google Scholar] [CrossRef]
- Kouba, J. A Note on the December 2013 Version of the eclips.f Subroutine. Available online: http://acc.igs.org/orbits/eclipsDec2013note.pdf (accessed on 4 February 2024).
- GSA. Galileo Satellite Metadata. 2021. Available online: https://www.gsc-europa.eu/support-to-developers/galileo-satellite-metadata (accessed on 28 November 2021).
- Zhao, Q.; Wang, C.; Guo, J.; Wang, B.; Liu, J. Precise orbit and clock determination for BeiDou-3 experimental satellites with yaw attitude analysis. GPS Solut. 2018, 22, 4. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Yaw attitude modeling for BeiDou I06 and BeiDou-3 satellites. GPS Solut. 2018, 22, 117. [Google Scholar] [CrossRef]
- Yang, C.; Guo, J.; Zhao, Q. Yaw attitudes for BDS-3 IGSO and MEO satellites: Estimation, validation and modeling with intersatellite link observations. J. Geod. 2023, 97, 6. [Google Scholar] [CrossRef]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89, 775–791. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U. Enhanced solar radiation pressure model for GPS satellites considering various physical effects. GPS Solut. 2021, 25, 42. [Google Scholar] [CrossRef]
- Duan, B.; Hugentobler, U.; Hofacker, M.; Selmke, I. Improving solar radiation pressure modeling for GLONASS satellites. J. Geod. 2020, 94, 72. [Google Scholar] [CrossRef]
- Montenbruck, O.; Steigenberger, P.; Hugentobler, U. Enhanced solar radiation pressure modeling for Galileo satellites. J. Geod. 2015, 89, 283–297. [Google Scholar] [CrossRef]
- Zhao, Q.; Chen, G.; Guo, J.; Liu, J.; Liu, X. An a priori solar radiation pressure model for the QZSS Michibiki satellite. J. Geod. 2018, 92, 109–121. [Google Scholar] [CrossRef]
- Steigenberger, P.; Thoelert, S.; Montenbruck, O. GNSS satellite transmit power and its impact on orbit determination. J. Geod. 2018, 92, 609–624. [Google Scholar] [CrossRef]
- Rodriguez-Solano, C.J.; Hugentobler, U.; Steigenberger, P.; Lutz, S. Impact of Earth radiation pressure on GPS position estimates. J. Geod. 2012, 86, 309–317. [Google Scholar] [CrossRef]
- Petit, G.; Luzum, B. The IERS Conventions 2010; No. 36 in IERS Technical Note; Verlag des Bundesamtes für Kartographie und Geodäsie: Frankfurt am Main, Germany, 2010. [Google Scholar]
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 global ocean tides atlas: Design and performances. Ocean Sci. 2020, 17, 615–649. [Google Scholar] [CrossRef]
- Boehm, J.; Heinkelmann, R.; Schuh, H. Short note: A global model of pressure and temperature for geodetic applications. J. Geod. 2007, 81, 679–683. [Google Scholar] [CrossRef]
- Wang, C.; Guo, J.; Zhao, Q.; Liu, J. Empirically derived model of solar radiation pressure for BeiDou GEO satellites. J. Geod. 2019, 93, 791–807. [Google Scholar] [CrossRef]
- Geng, J.; Yang, S.; Guo, J. Assessing IGS GPS/Galileo/BDS-2/BDS-3 phase bias products with PRIDE PPP-AR. Satell. Navig. 2021, 2, 17. [Google Scholar] [CrossRef]
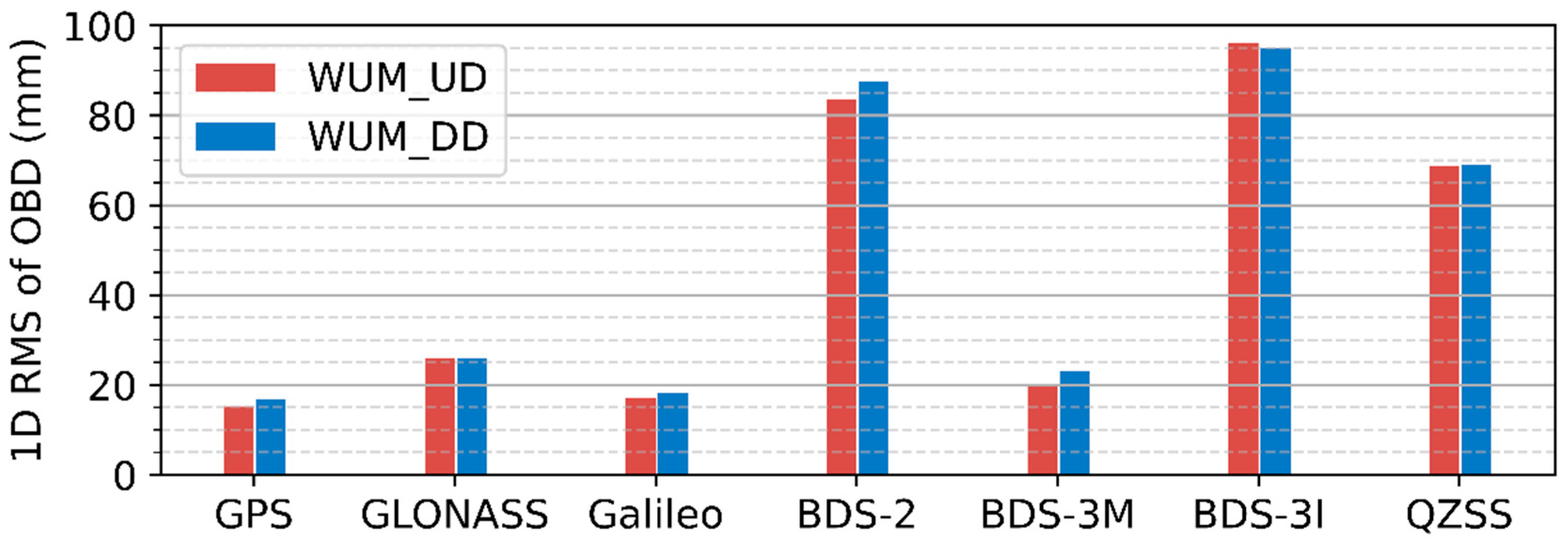

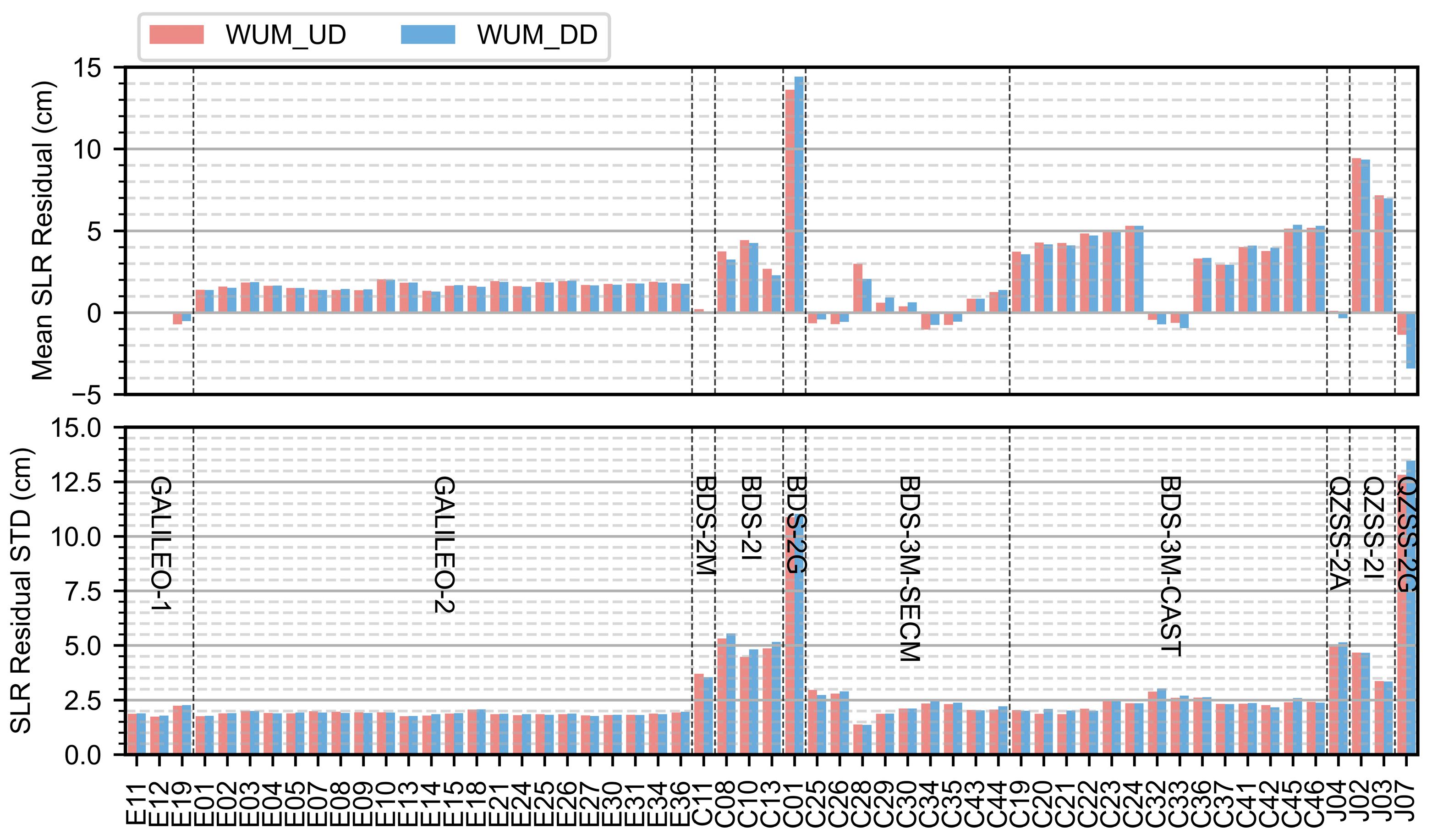
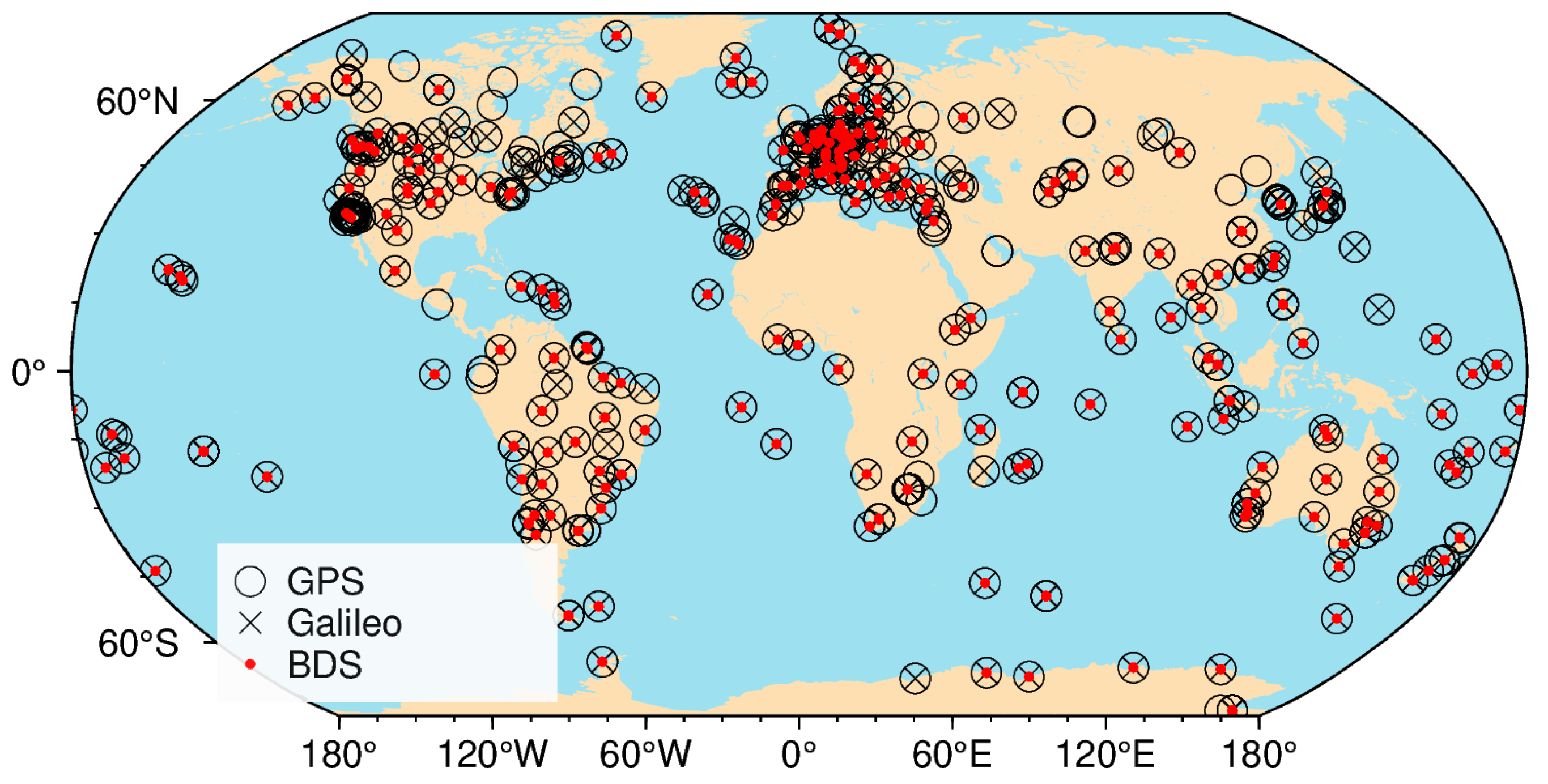
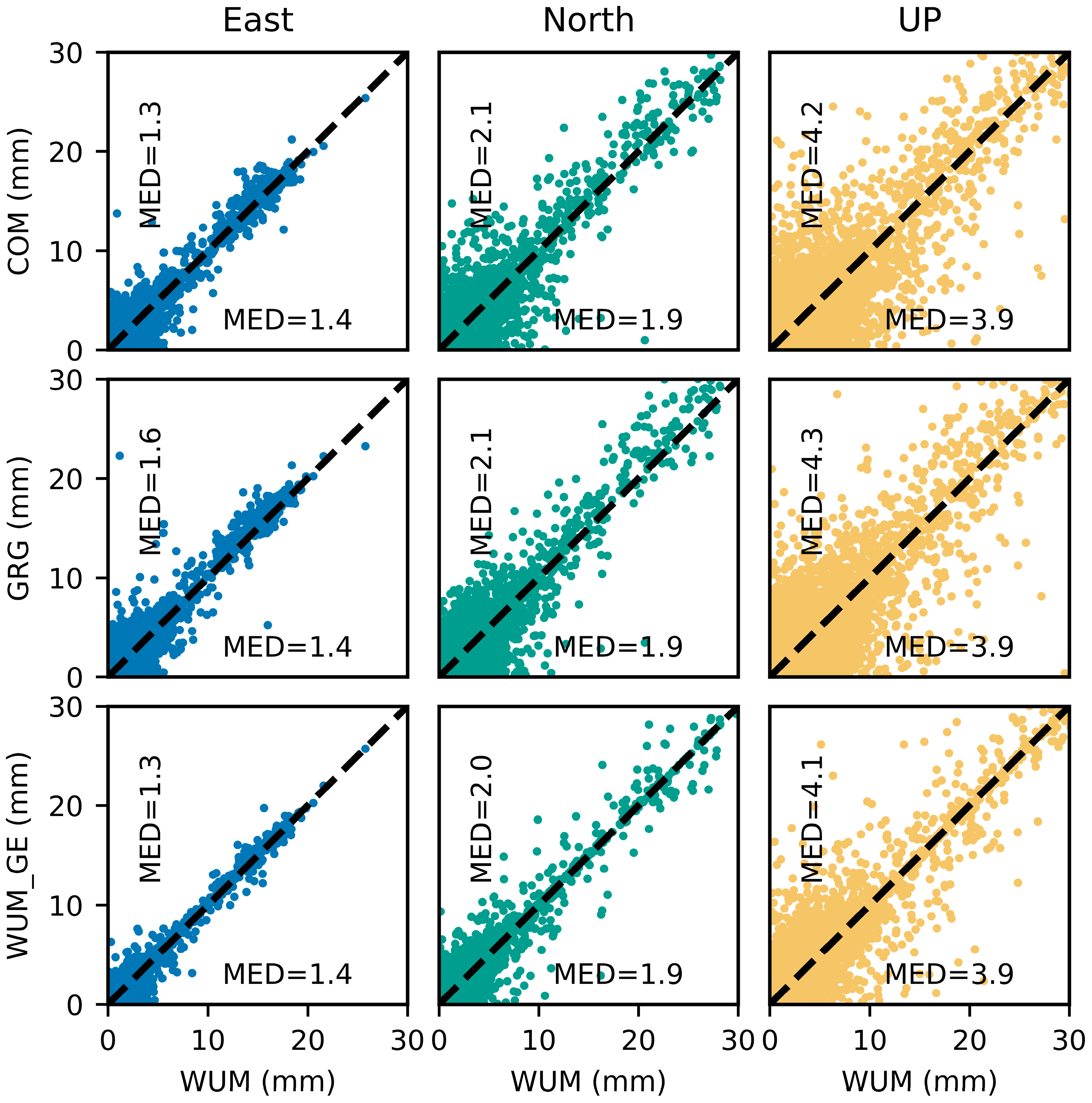
| Type | WUM_UD (mm) | WUM_DD (mm) | Improvement (%) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| A | C | R | A | C | R | A | C | R | |
| GPS | 16.3 | 13.7 | 15.5 | 18.5 | 15.8 | 16.3 | 11.9 | 13.3 | 4.9 |
| GLONASS | 31.8 | 25.8 | 18.3 | 32.1 | 25.8 | 18.4 | 0.9 | 0.0 | 0.5 |
| Galileo | 17.8 | 15.6 | 17.7 | 19.5 | 17.0 | 18.3 | 8.7 | 8.2 | 3.3 |
| BDS-2 | 84.7 | 71.2 | 93.2 | 95.4 | 75.5 | 90.3 | 11.2 | 5.7 | −3.2 |
| BDS-3 MEO | 21.5 | 18.9 | 19.4 | 25.9 | 22.0 | 21.2 | 17.0 | 14.1 | 8.5 |
| BDS-3 IGSO | 69.9 | 103.3 | 110.4 | 59.6 | 103.4 | 113.4 | −17.3 | 0.1 | 2.6 |
| QZSS | 40.7 | 45.8 | 101.9 | 44.2 | 48.0 | 100.2 | 7.9 | 4.6 | −1.7 |
| GPS | Galileo | GLONASS | BDS-2 (MEO) | BDS-2 (IGSO/GEO) | BDS-3 (MEO) | BDS-3 (IGSO) | QZSS | |
|---|---|---|---|---|---|---|---|---|
| WUM_UD | 9.1 | 12.4 | 31.2 | 73.7 | 86.3 | 20.1 | 98.5 | 71.8 |
| WUM_DD | 9.8 | 13.7 | 31.2 | 74.2 | 86.7 | 23.7 | 93.8 | 71.2 |
| COM | 10.1 | 13.1 | 32.8 | 60.0 | 113.4 | 25.8 | 118.5 | 77.5 |
| GBM | 11.4 | 14.5 | 38.8 | 75.8 | 100.4 | 28.1 | 112.2 | 103.7 |
| GRG | 11.2 | 14.4 | 36.9 | / | / | / | / | / |
| JAX | 11.6 | 15.4 | 31.7 | / | / | / | / | 82.5 |
| IAC | 12.7 | 14.9 | 34.4 | 38.6 | 62.9 | 25.6 | 123.3 | 95.7 |
| AC | GPS | Galileo | BDS-2 | BDS-3 |
|---|---|---|---|---|
| WUM | 90.3/99.2 | 97.2/99.2 | 87.4/88.8 | 91.1/98.6 |
| COM | 90.6/99.0 | 97.5/98.7 | ||
| GRG | 90.8/95.2 | 95.5/98.2 | ||
| WUM_GE | 90.3/99.1 | 97.2/99.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Guo, J.; Xu, S.; Zhao, Q. Undifferenced Ambiguity Resolution for Precise Multi-GNSS Products to Support Global PPP-AR. Remote Sens. 2025, 17, 1451. https://doi.org/10.3390/rs17081451
Li J, Guo J, Xu S, Zhao Q. Undifferenced Ambiguity Resolution for Precise Multi-GNSS Products to Support Global PPP-AR. Remote Sensing. 2025; 17(8):1451. https://doi.org/10.3390/rs17081451
Chicago/Turabian StyleLi, Junqiang, Jing Guo, Shengyi Xu, and Qile Zhao. 2025. "Undifferenced Ambiguity Resolution for Precise Multi-GNSS Products to Support Global PPP-AR" Remote Sensing 17, no. 8: 1451. https://doi.org/10.3390/rs17081451
APA StyleLi, J., Guo, J., Xu, S., & Zhao, Q. (2025). Undifferenced Ambiguity Resolution for Precise Multi-GNSS Products to Support Global PPP-AR. Remote Sensing, 17(8), 1451. https://doi.org/10.3390/rs17081451





